Experimental Demonstration of an Efficient Mach–Zehnder Modulator Bias Control for Quantum Key Distribution Systems
Abstract
:1. Introduction
2. Method
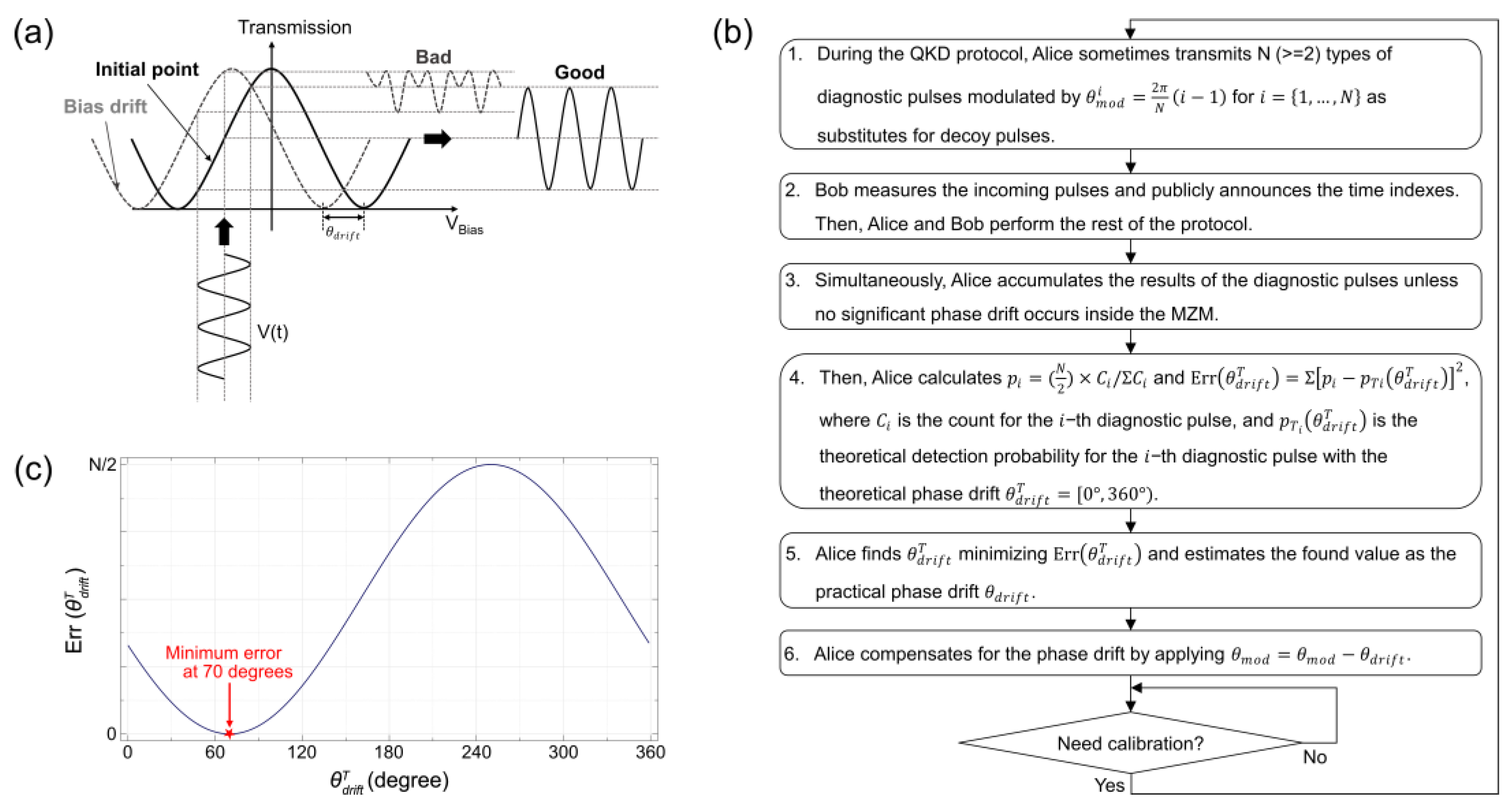
- During the QKD protocol, Alice prepares N (≥2) types of diagnostic pulses whose MZM phases are modulated by with uniformly distributed probabilities for . Thereafter, Alice sometimes transmits them to Bob as substitutes for the decoy pulses. Similar to the signal and decoy pulses, the diagnostic pulses are attenuated to single-photon levels. This method does not weaken the security of the QKD significantly because nobody except Alice can distinguish between the decoy and diagnostic pulses.
- Bob receives and measures the incoming pulses using single-photon detectors (SPDs). After measuring, he publicly announces the time indexes where the signals are detected. Thereafter, Alice and Bob perform the remaining protocols, such as key sifting, error correction and privacy amplification.
- Simultaneously, Alice accumulates the detection results of the diagnostic pulses unless there are no significant phase drifts. The optimal accumulation time strongly depends on the ambient environment, channel loss, detection efficiencies and pulse intensities.
- After accumulation, Alice calculates the normalized detection probabilities as [53,54]where is the count for the i-th diagnostic pulse. can be easily obtained from Bob’s announcement. Subsequently, Alice builds the following error model based on the least-squares method [53,54]:where is the theoretical detection probability for the i-th diagnostic pulse with corresponding phase value and theoretical phase drift . Alice may calculate the theoretical values each time the probability is examined or may use a look-up table that has been created in advance.
- Alice finds minimizing by adjusting from –. Subsequently, the found value is estimated as because the error is minimized when maximally matches the practical value . For example, Alice can assume with the smallest at , as shown in Figure 1c. The estimation accuracy depends on the adjustment interval of . As the interval becomes smaller, the prediction accuracy becomes better. However, more computational power and time are required.
- Finally, Alice compensates for the estimated phase drift by applying ; therefore, the MZM bias point is maintained at the desired point. Accordingly, as the term of the MZM output intensity is erased, Equation (1) becomes
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wright, K.; Beck, K.M.; Debnath, S.; Amini, J.M.; Nam, Y.; Grzesiak, N.; Chen, J.-S.; Pisenti, N.C.; Chmielewski, M.; Collins, C.; et al. Benchmarking an 11-qubit quantum computer. Nat. Commun. 2019, 10, 5464. [Google Scholar] [CrossRef] [PubMed]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef] [Green Version]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kjaergaard, M.; Schwartz, M.E.; Braumüller, J.; Krantz, P.; Wang, J.I.-J.; Gustavsson, S.; Oliver, W.D. Superconducting Qubits: Current State of Play. Annu. Rev. Condens. Matter Phys. 2020, 11, 369–395. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Bao, W.-S.; Cao, S.; Chen, F.; Chen, M.-C.; Chen, X.; Chung, T.-H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Pezzagna, S.; Meijer, J. Quantum computer based on color centers in diamond. Appl. Phys. Rev. 2021, 8, 011308. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Liao, S.-K.; Cai, W.-Q.; Handsteiner, J.; Liu, B.; Yin, J.; Zhang, L.; Rauch, D.; Fink, M.; Ren, J.-G.; Liu, W.-Y.; et al. Satellite-Relayed Intercontinental Quantum Network. Phys. Rev. Lett. 2018, 120, 030501. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Li, Y.-H.; Yang, K.-X.; Jiang, Y.-F.; Li, S.-L.; Hu, X.-L.; Abulizi, M.; Li, C.-L.; Zhang, W.; Sun, Q.-C.; et al. Long-Distance Free-Space Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2020, 125, 260503. [Google Scholar] [CrossRef]
- Wei, K.; Li, W.; Tan, H.; Li, Y.; Min, H.; Zhang, W.-J.; Li, H.; You, L.; Wang, Z.; Jiang, X.; et al. High-Speed Measurement-Device-Independent Quantum Key Distribution with Integrated Silicon Photonics. Phys. Rev. X 2020, 10, 031030. [Google Scholar] [CrossRef]
- Chen, J.-P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.-J.; Han, Z.-Y.; Ma, S.-Z.; Hu, X.-L.; Li, Y.-H.; Liu, H.; et al. Twin-field quantum key distribution over a 511 km optical fibre linking two distant metropolitan areas. Nat. Photonics 2021, 15, 570–575. [Google Scholar] [CrossRef]
- Zhong, X.; Wang, W.; Qian, L.; Lo, H.-K. Proof-of-principle experimental demonstration of twin-field quantum key distribution over optical channels with asymmetric losses. NPJ Quantum Inf. 2021, 7, 8. [Google Scholar] [CrossRef]
- Pittaluga, M.; Minder, M.; Lucamarini, M.; Sanzaro, M.; Woodward, R.I.; Li, M.-J.; Yuan, Z.; Shields, A.J. 600-km repeater-like quantum communications with dual-band stabilization. Nat. Photonics 2021, 15, 530–535. [Google Scholar] [CrossRef]
- Muller, A.; Herzog, T.J.; Huttner, B.; Tittel, W.; Zbinden, H.; Gisin, N. “Plug and play” systems for quantum cryptography. Appl. Phys. Lett. 1997, 70, 793–795. [Google Scholar] [CrossRef]
- Yuan, Z.L.; Fröhlich, B.; Lucamarini, M.; Roberts, G.L.; Dynes, J.F.; Shields, A.J. Directly Phase-Modulated Light Source. Phys. Rev. X 2016, 6, 031044. [Google Scholar] [CrossRef] [Green Version]
- Park, B.K.; Lee, M.S.; Woo, M.K.; Kim, Y.-S.; Han, S.-W.; Moon, S. QKD system with fast active optical path length compensation. Sci. China Ser. G Phys. Mech. Astron. 2017, 60, 060311. [Google Scholar] [CrossRef]
- Wang, C.; Yin, Z.-Q.; Wang, S.; Chen, W.; Guo, G.-C.; Han, Z.-F. Measurement-device-independent quantum key distribution robust against environmental disturbances. Optica 2017, 4, 1016–1023. [Google Scholar] [CrossRef]
- Xie, H.-B.; Li, Y.; Jiang, C.; Cai, W.-Q.; Yin, J.; Ren, J.-G.; Wang, X.-B.; Liao, S.-K.; Peng, C.-Z. Optically injected intensity-stable pulse source for secure quantum key distribution. Opt. Express 2019, 27, 12231–12240. [Google Scholar] [CrossRef]
- Yin, H.-L.; Zhu, W.; Fu, Y. Phase self-aligned continuous-variable measurement-device-independent quantum key distribution. Sci. Rep. 2019, 9, 49. [Google Scholar] [CrossRef] [Green Version]
- Yanikgonul, S.; Guo, R.; Xomalis, A.; Vetlugin, A.N.; Adamo, G.; Soci, C.; Zheludev, N.I. Phase stabilization of a coherent fiber network by single-photon counting. Opt. Lett. 2020, 45, 2740–2743. [Google Scholar] [CrossRef]
- Wang, D.; Song, X.; Zhou, L.; Zhao, Y. Real-Time Phase Tracking Scheme with Mismatched-Basis Data for Phase-Coding Quantum Key Distribution. IEEE Photonics J. 2020, 12, 7600307. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, Y.; Im, D.-G.; Lee, C.-H.; Chae, J.-W.; Scarcelli, G.; Kim, Y.-H. Noise-resistant quantum communications using hyperentanglement. Optica 2021, 8, 1524. [Google Scholar] [CrossRef]
- Trapani, J.; Teklu, B.; Olivares, S.; Paris, M.G.A. Quantum phase communication channels in the presence of static and dynamical phase diffusion. Phys. Rev. A 2015, 92, 012317. [Google Scholar] [CrossRef] [Green Version]
- Rosati, M.; Mari, A.; Giovannetti, V. Coherent-state discrimination via nonheralded probabilistic amplification. Phys. Rev. A 2016, 93, 062315. [Google Scholar] [CrossRef] [Green Version]
- Adnane, H.; Teklu, B.; Paris, M.G.A. Quantum phase communication channels assisted by non-deterministic noiseless amplifiers. J. Opt. Soc. Am. B 2019, 36, 2938. [Google Scholar] [CrossRef]
- Hwang, W.-Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lo, H.-K.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [Green Version]
- Brassard, G.; Lutkenhaus, N.; Mor, T.; Sanders, B. Limitations on Practical Quantum Cryptography. Phys. Rev. Lett. 2000, 85, 1330–1333. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-B. Beating the Photon-Number-Splitting Attack in Practical Quantum Cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef] [Green Version]
- Cho, P.S.; Khurgin, J.B.; Shpantzer, I. Closed-Loop Bias Control of Optical Quadrature Modulator. IEEE Photonics Technol. Lett. 2006, 18, 2209–2211. [Google Scholar] [CrossRef]
- Sekine, K.; Hasegawa, C.; Kikuchi, N.; Sasaki, S. A Novel Bias Control Technique for MZ Modulator with Monitoring Power of Backward Light for Advanced Modulation Formats. In Proceedings of the OFC/NFOEC 2007—2007 Conference on Optical Fiber Communication and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 25–29 March 2007. [Google Scholar] [CrossRef]
- Sotoodeh, M.; Beaulieu, Y.; Harley, J.; McGhan, D.L. Modulator Bias and Optical Power Control of Optical Complex E-Field Modulators. J. Light. Technol. 2011, 29, 2235–2248. [Google Scholar] [CrossRef]
- Kim, M.-H.; Yu, B.-M.; Choi, W.-Y. A Mach-Zehnder Modulator Bias Controller Based on OMA and Average Power Monitoring. IEEE Photonics Technol. Lett. 2017, 29, 2043–2046. [Google Scholar] [CrossRef]
- Hofer, L.R.; Schaeffer, D.; Constantin, C.G.; Niemann, C. Bias Voltage Control in Pulsed Applications for Mach–Zehnder Electrooptic Intensity Modulators. IEEE Trans. Control Syst. Technol. 2017, 25, 1890–1895. [Google Scholar] [CrossRef]
- Wang, L.L.; Kowalcyzk, T. A Versatile Bias Control Technique for Any-Point Locking in Lithium Niobate Mach–Zehnder Modulators. J. Light. Technol. 2010, 28, 1703–1706. [Google Scholar] [CrossRef]
- Yoshida, T.; Sugihara, T.; Uto, K.; Bessho, H.; Sawada, K.; Ishida, K.; Shimizu, K.; Mizuochi, T. A study on automatic bias control for arbitrary optical signal generation by dual-parallel Mach-Zehnder modulator. In Proceedings of the 36th European Conference and Exhibition on Optical Communication, Turin, Italy, 19–23 September 2010. [Google Scholar] [CrossRef]
- Kawakami, H.; Kobayashi, T.; Yoshida, E.; Miyamoto, Y. Auto bias control technique for optical 16-QAM transmitter with asymmetric bias dithering. Opt. Express 2011, 19, B308–B312. [Google Scholar] [CrossRef]
- Kawakami, H.; Yoshida, E.; Miyamoto, Y. Auto Bias Control Technique Based on Asymmetric Bias Dithering for Optical QPSK Modulation. J. Light. Technol. 2012, 30, 962–968. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, Y. Any Bias Point Control Technique for Mach–Zehnder Modulator. IEEE Photonics Technol. Lett. 2013, 25, 2412–2415. [Google Scholar] [CrossRef]
- Gui, T.; Li, C.; Yang, Q.; Xiao, X.; Meng, L.; Li, C.; Yi, X.; Jin, C.; Li, Z. Auto bias control technique for optical OFDM transmitter with bias dithering. Opt. Express 2013, 21, 5833–5841. [Google Scholar] [CrossRef] [Green Version]
- Kawakami, H.; Kobayashi, T.; Yoshida, M.; Kataoka, T.; Miyamoto, Y. Auto bias control and bias hold circuit for IQ-modulator in flexible optical QAM transmitter with Nyquist filtering. Opt. Express 2014, 22, 28163–28168. [Google Scholar] [CrossRef]
- Li, X.; Deng, L.; Chen, X.; Cheng, M.; Fu, S.; Tang, M.; Liu, D. Modulation-format-free and automatic bias control for optical IQ modulators based on dither-correlation detection. Opt. Express 2017, 25, 9333–9345. [Google Scholar] [CrossRef]
- Li, X.; Deng, L.; Chen, X.; Song, H.; Liu, Y.; Cheng, M.; Fu, S.; Tang, M.; Zhang, M.; Liu, D. Arbitrary Bias Point Control Technique for Optical IQ Modulator Based on Dither-Correlation Detection. J. Light. Technol. 2018, 36, 3824–3836. [Google Scholar] [CrossRef]
- Fröhlich, B.; Dynes, J.F.; Lucamarini, M.; Sharpe, A.W.; Yuan, Z.; Shields, A.J. A quantum access network. Nature 2013, 501, 69–72. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Y.-L.; Yin, H.-L.; Zhao, Q.; Liu, H.; Sun, X.-X.; Huang, M.-Q.; Zhang, W.-J.; Chen, S.-J.; Zhang, L.; You, L.-X.; et al. Measurement-Device-Independent Quantum Key Distribution over Untrustful Metropolitan Network. Phys. Rev. X 2016, 6, 011024. [Google Scholar] [CrossRef] [Green Version]
- Dynes, J.F.; Wonfor, A.; Tam, W.W.-S.; Sharpe, A.W.; Takahashi, R.; Lucamarini, M.; Plews, A.; Yuan, Z.L.; Dixon, A.R.; Cho, J.; et al. Cambridge quantum network. NPJ Quantum Inf. 2019, 5, 101. [Google Scholar] [CrossRef] [Green Version]
- Woo, M.K.; Park, B.K.; Kim, Y.-S.; Cho, Y.-W.; Jung, H.; Lim, H.-T.; Kim, S.; Moon, S.; Han, S.-W. One to Many QKD Network System Using Polarization-Wavelength Division Multiplexing. IEEE Access 2020, 8, 194007–194014. [Google Scholar] [CrossRef]
- Park, B.K.; Woo, M.K.; Kim, Y.-S.; Cho, Y.-W.; Moon, S.; Han, S.-W. User-independent optical path length compensation scheme with sub-nanosecond timing resolution for a 1 × N quantum key distribution network system. Photonics Res. 2020, 8, 296–302. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-A.; Zhang, Q.; Chen, T.-Y.; Cai, W.-Q.; Liao, S.-K.; Zhang, J.; Chen, K.; Yin, J.; Ren, J.-G.; Chen, Z.; et al. An integrated space-to-ground quantum communication network over 4,600 kilometres. Nature 2021, 589, 214–219. [Google Scholar] [CrossRef]
- Li, G.; Welstand, R.; Chen, W.; Zhu, J.; Pappert, S.; Sun, C.; Liu, Y.; Yu, P. Novel bias control of electroabsorption waveguide modulator. IEEE Photonics Technol. Lett. 1998, 10, 672–674. [Google Scholar] [CrossRef] [Green Version]
- Sisto, M.; LaRochelle, S.; Rusch, L. Carrier-to-noise ratio optimization by modulator bias control in radio-over-fiber links. IEEE Photonics Technol. Lett. 2006, 18, 1840–1842. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, F.; Sun, B.; Li, C. A Novel Bias Angle Control System for LiNbO3 Photonic Sensor Using Wavelength Tuning. IEEE Photonics Technol. Lett. 2013, 25, 1993–1995. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Z.-W.; Zhang, W.; Guan, J.-Y.; Chen, J.-P.; Zhang, C.; Hu, X.-L.; Li, H.; Jiang, C.; Lin, J.; et al. Experimental Twin-Field Quantum Key Distribution through Sending or Not Sending. Phys. Rev. Lett. 2019, 123, 100505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.-P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.; Hu, X.-L.; Guan, J.-Y.; Yu, Z.-W.; Xu, H.; Lin, J.; et al. Sending-or-Not-Sending with Independent Lasers: Secure Twin-Field Quantum Key Distribution over 509 km. Phys. Rev. Lett. 2020, 124, 070501. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Abbreviation | Description | Symbol | Description |
|---|---|---|---|
| BS | Beam splitter | Practical phase drift | |
| CIR | Circulator | ||
| CW | Continuous-wave | Practical detection probability | |
| DC | Direct-current | Theoretical detection probability | |
| DFB | Distributed feedback | ||
| DL | Delay line | Phase modulation | |
| DWDM | Dense wavelength division multiplexer | Phase modulation of the i-th diagnostic pulse | |
| ER | Extinction ratio | Output intensity | |
| FM | Faraday rotator mirror | Insertion loss | |
| FPGA | Field-programmable gate array | Input intensity | |
| MCU | Microcontroller unit | Count for the i-th diagnostic pulse | |
| MZM | Mach–Zehnder modulator | ||
| PBS | Polarization beam splitter | ||
| PD | Photodiode | ||
| PID | Proportional–integral–derivative | ||
| PINPD | P-i-n photodiode | ||
| PM | Phase modulator | ||
| QBER | Quantum bit error rate | ||
| QKD | Quantum key distribution | ||
| SL | Storage line | ||
| SPD | Single-photon detector | ||
| TLD | Tunable laser driver | ||
| VOA | Variable optical attenuator |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, C.-H.; Woo, M.-K.; Park, B.-K.; Jeon, S.-W.; Jung, H.; Kim, S.; Han, S.-W. Experimental Demonstration of an Efficient Mach–Zehnder Modulator Bias Control for Quantum Key Distribution Systems. Electronics 2022, 11, 2207. https://doi.org/10.3390/electronics11142207
Park C-H, Woo M-K, Park B-K, Jeon S-W, Jung H, Kim S, Han S-W. Experimental Demonstration of an Efficient Mach–Zehnder Modulator Bias Control for Quantum Key Distribution Systems. Electronics. 2022; 11(14):2207. https://doi.org/10.3390/electronics11142207
Chicago/Turabian StylePark, Chang-Hoon, Min-Ki Woo, Byung-Kwon Park, Seung-Woo Jeon, Hojoong Jung, Sangin Kim, and Sang-Wook Han. 2022. "Experimental Demonstration of an Efficient Mach–Zehnder Modulator Bias Control for Quantum Key Distribution Systems" Electronics 11, no. 14: 2207. https://doi.org/10.3390/electronics11142207
APA StylePark, C.-H., Woo, M.-K., Park, B.-K., Jeon, S.-W., Jung, H., Kim, S., & Han, S.-W. (2022). Experimental Demonstration of an Efficient Mach–Zehnder Modulator Bias Control for Quantum Key Distribution Systems. Electronics, 11(14), 2207. https://doi.org/10.3390/electronics11142207







