Fuzzy Luenberger Observer Design for Nonlinear Flexible Joint Robot Manipulator
Abstract
:1. Introduction
2. Related Work
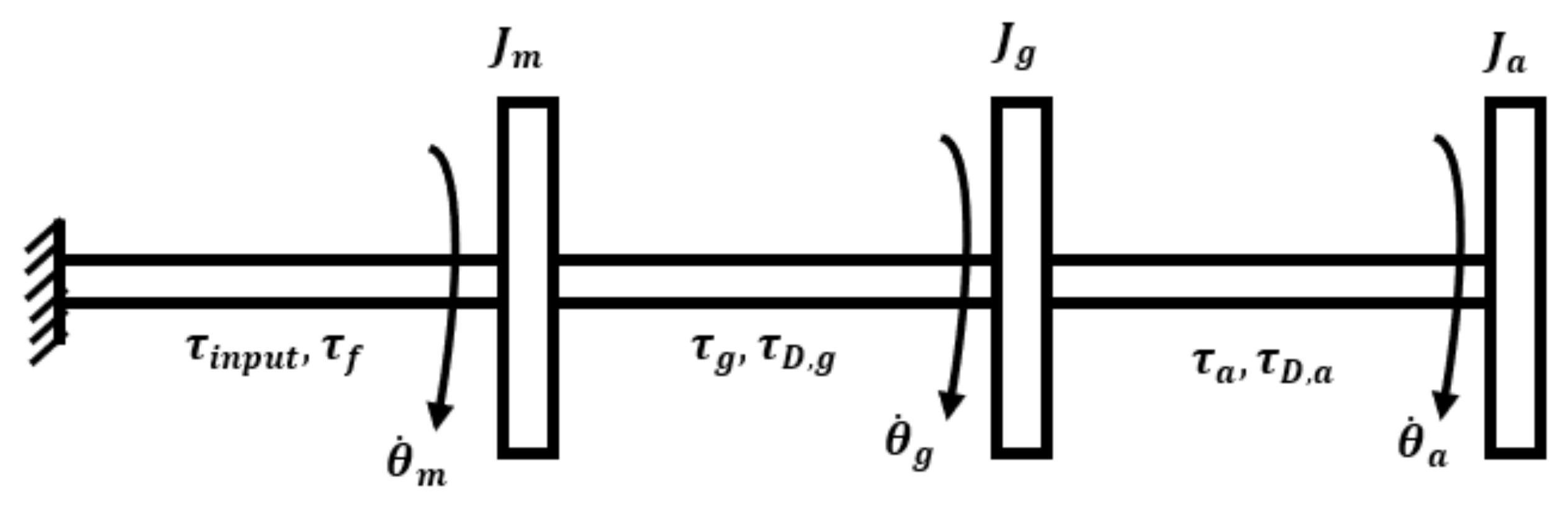
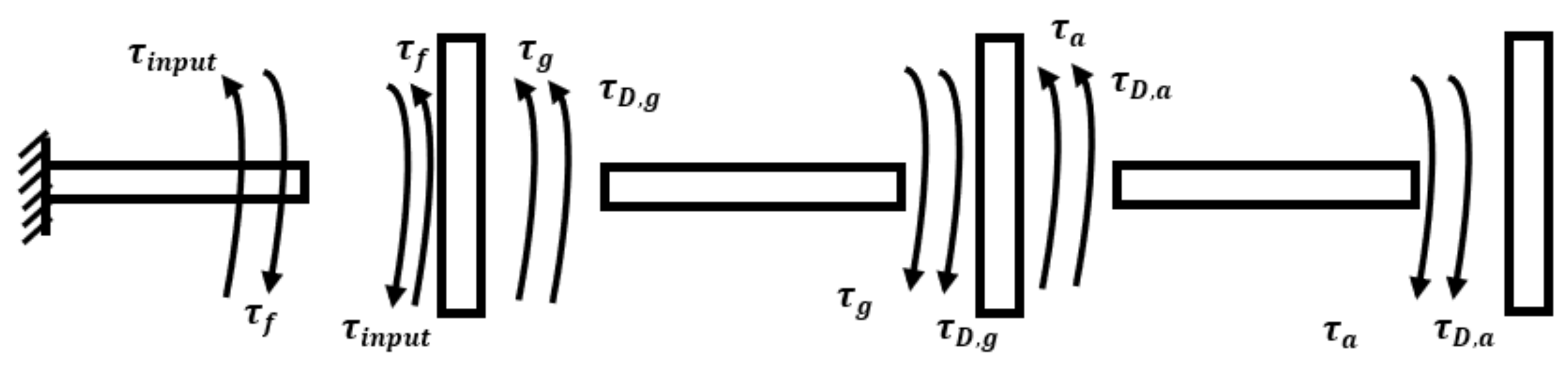
3. Mathematical Models
4. Dynamics Model Linearizing
5. Observer Design
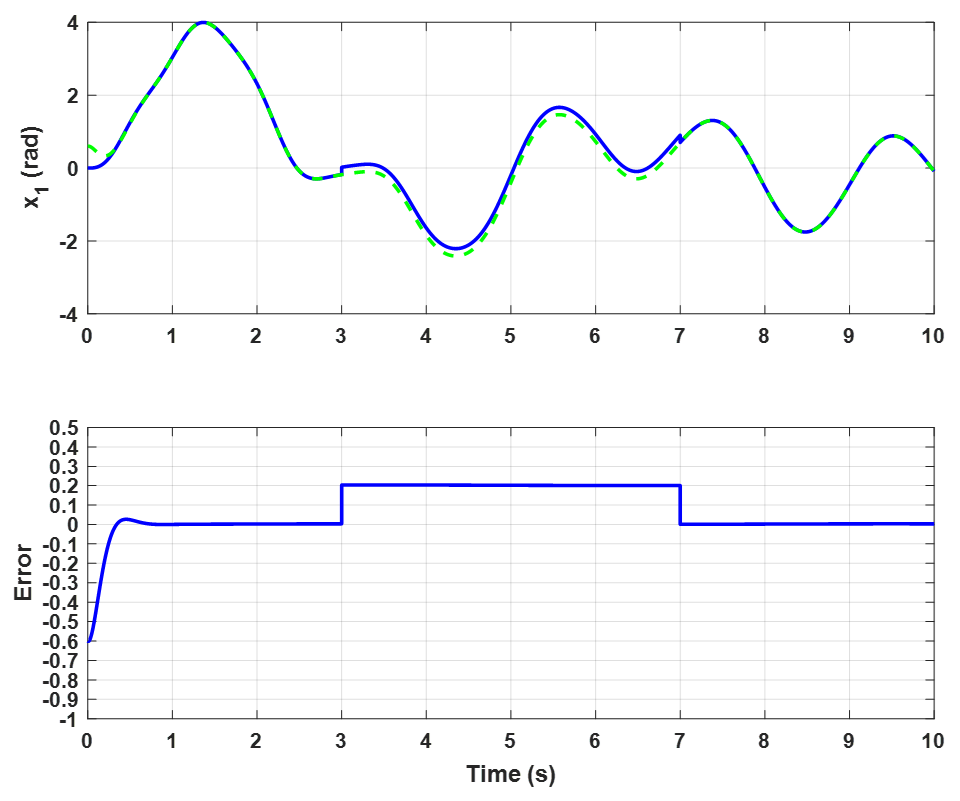
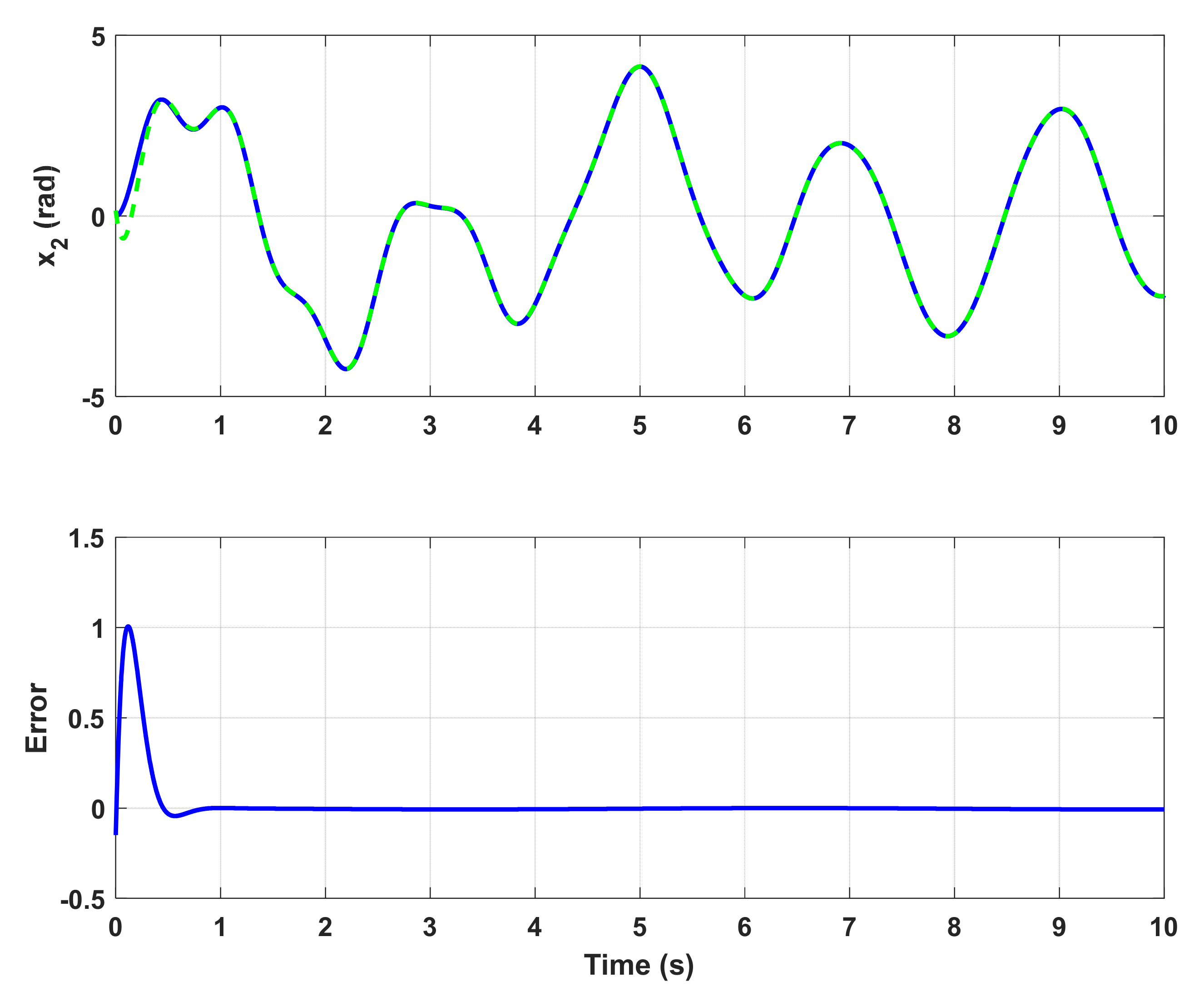
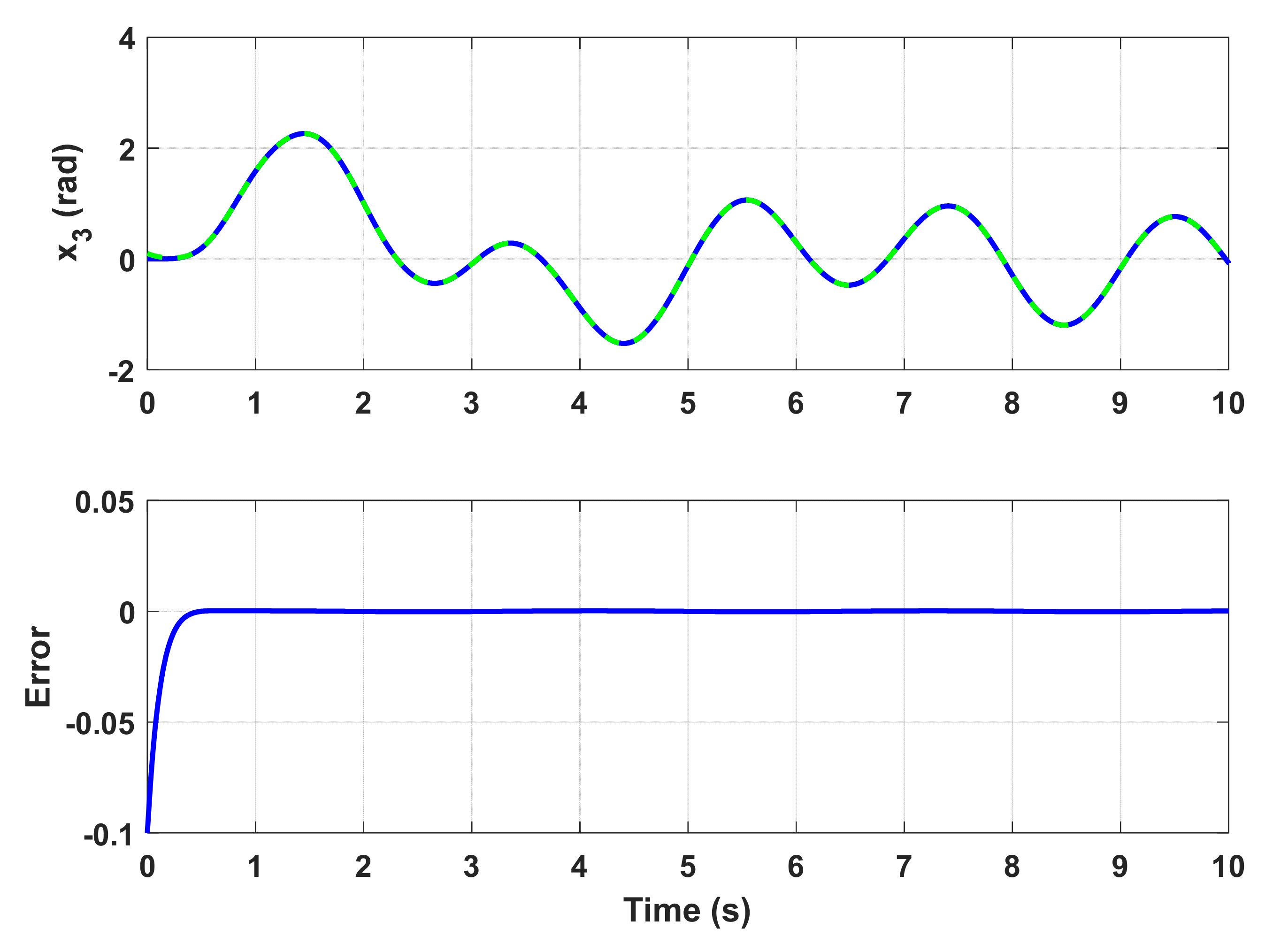
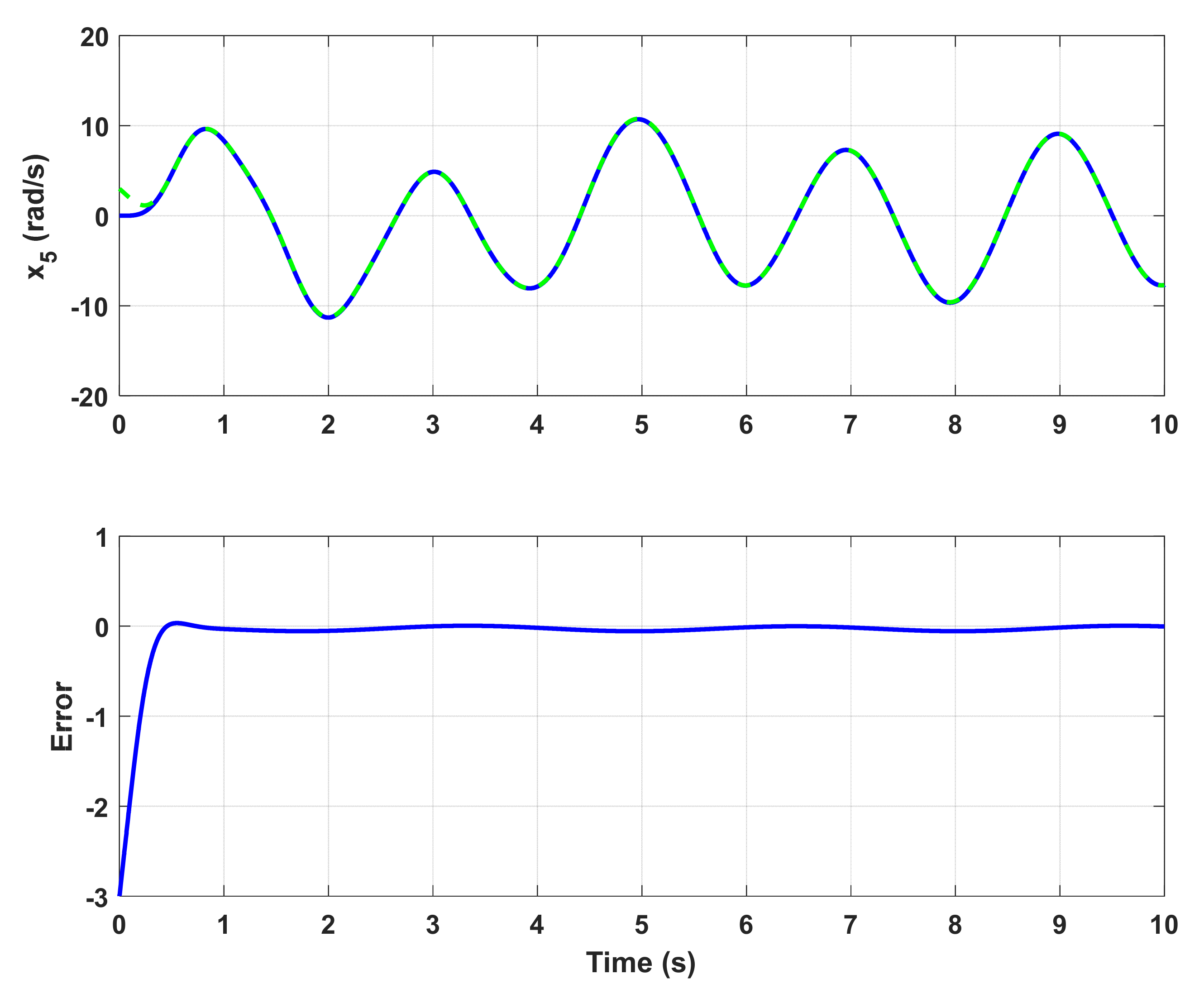
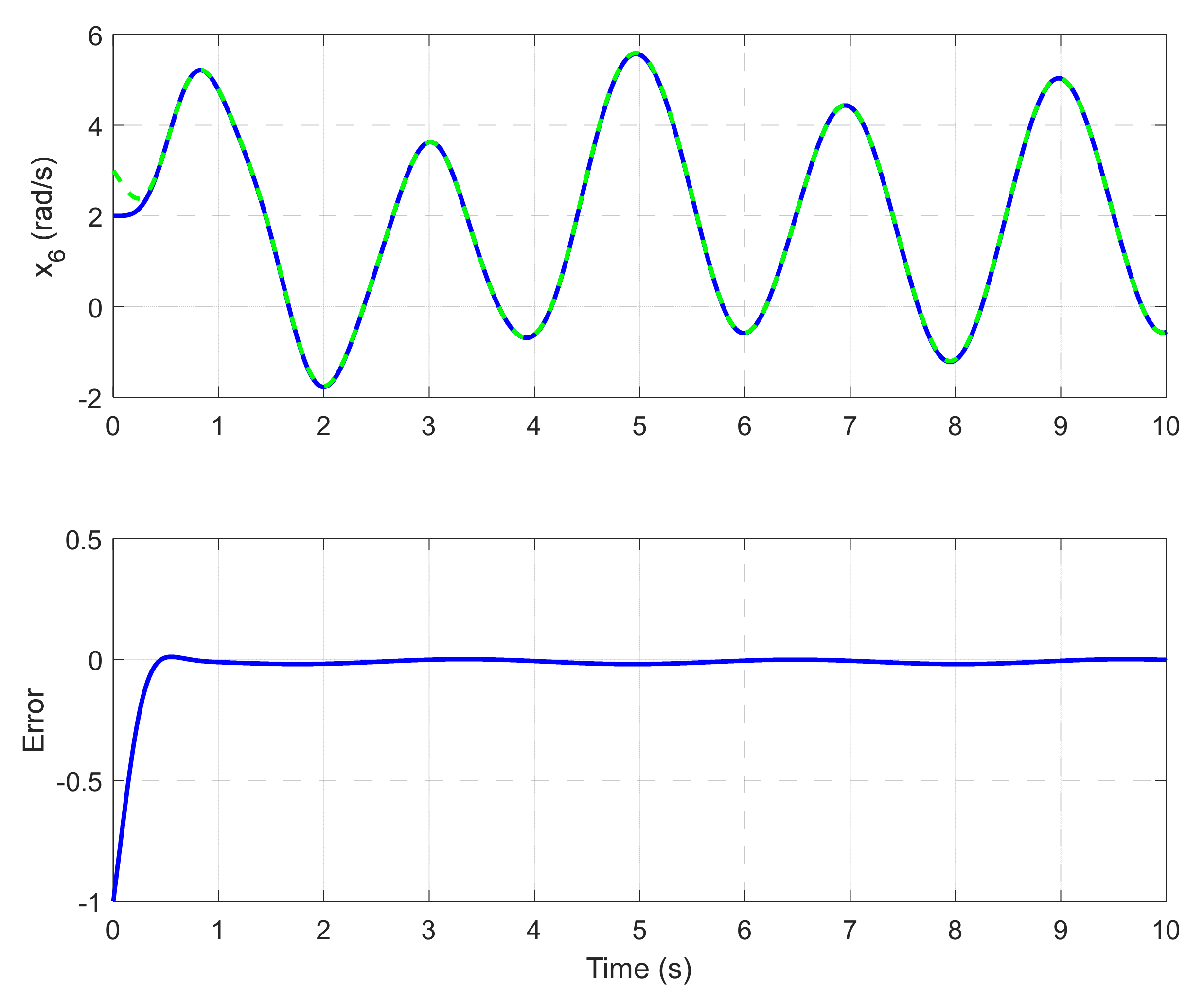
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- García, P.L.; Crispel, S.; Saerens, E.; Verstraten, T.; Lefeber, D. Compact Gearboxes for Modern Robotics: A Review. Front. Robot. AI 2020, 7, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Sinitcyna, Y.V.; Ermolaev, M.M. Influence of Bearing’s Flexibility on the Working of Cycloid Drive. IOP Conf. Ser. Mater. Sci. Eng. 2020, 842, 012021. [Google Scholar] [CrossRef]
- Gaiser, I.; Wiegand, R.; Ivlev, O.; Andres, A.; Breitwieser, H.; Schulz, S.; Bretthauer, G. Compliant Robotics and Automation with Flexible Fluidic Actuators and Inflatable Structures. 2012. Available online: https://www.intechopen.com/chapters/40057 (accessed on 15 March 2022).
- Reutov, A. Modeling of the flexible belt motion on the drive pulley of woodworking equipment. IOP Conf. Ser. Earth Environ. Sci. 2019, 392, 012056. [Google Scholar] [CrossRef]
- Yang, W.; Yuan, H.; Li, H.; Zhang, K. Dynamic Analysis of Flexible Shaft and Elastic Disk Rotor System Based on the Effect of Alford Force. Shock Vib. 2019, 2019, 3545939. [Google Scholar] [CrossRef]
- Al-Darraji, I.; Kılıç, A.; Kapucu, S. Optimal control of compliant planar robot for safe impact using steepest descent technique. In Proceedings of the International Conference on Information and Communication Technology (ICICT ’19), Baghdad, Iraq, 15–16 April 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 233–238. [Google Scholar] [CrossRef]
- Korayem, M.H.; Heidari, H.R. Modeling and testing of moving base manipulators with elastic joints. Latin Am. Appl. Res. 2011, 41, 157–163. [Google Scholar]
- Gao, M.; Wang, Z.; Pang, Z.; Sun, J.; Li, J.; Li, S.; Zhang, H. Electrically Driven Lower Limb Exoskeleton Rehabilitation Robot Based on Anthropomorphic Design. Machines 2022, 10, 266. [Google Scholar] [CrossRef]
- Righettini, P.; Strada, R.; Cortinovis, F. Modal Kinematic Analysis of a Parallel Kinematic Robot with Low-Stiffness Transmissions. Robotics 2021, 10, 132. [Google Scholar] [CrossRef]
- Fu, X.; Ai, H.; Chen, L. Repetitive Learning Sliding Mode Stabilization Control for a Flexible-Base, Flexible-Link and Flexible-Joint Space Robot Capturing a Satellite. Appl. Sci. 2021, 11, 8077. [Google Scholar] [CrossRef]
- Shao, M.; Huang, Y.; Vadim, V. Silberschmidt, Intelligent Manipulator with Flexible Link and Joint: Modeling and Vibration Control. Shock Vib. 2020, 2020, 4671358. [Google Scholar] [CrossRef] [Green Version]
- Ott, C. Modeling of Flexible Joint Robots. In Cartesian Impedance Control of Redundant and Flexible-Joint Robots; Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 49. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, P. Simulation of Manipulator with Flexible Joint. In Applied Mechanics and Materials; Trans Tech Publications, Ltd.: Freinbach, Switzerland, 2013; pp. 999–1003. [Google Scholar]
- Ghorbel, F.; Hung, J.Y.; Spong, M.W. Adaptive control of flexible-joint manipulators. IEEE Control Syst. Mag. 1989, 9, 9–13. [Google Scholar] [CrossRef]
- Aziz, H.; Iqbal, J. Flexible Joint Robotic Manipulator: Modeling and Design of Robust Control Law (Best Paper Award). 2016. Available online: https://ieeexplore.ieee.org/document/7791230 (accessed on 22 December 2016).
- Pavlichenko, D.; Behnke, S. Flexible-Joint Manipulator Trajectory Tracking with Learned Two-Stage Model employing One-Step Future Prediction. In Proceedings of the Fifth IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 15–17 November 2021. [Google Scholar]
- Ahmadi, S.; Fateh, M. Control of flexible joint robot manipulators by compensating flexibility. Iran. J. Fuzzy Syst. 2018, 15, 57–71. [Google Scholar] [CrossRef]
- Zhang, A.; Lin, Z.; Wang, B.; Han, Z. Nonlinear Model Predictive Control of Single-Link Flexible-Joint Robot Using Recurrent Neural Network and Differential Evolution Optimization. Electronics 2021, 10, 2426. [Google Scholar] [CrossRef]
- Abdollahi, F.; Talebi, H.A.; Patel, R.V. A stable neural network-based observer with application to flexible-joint manipulators. IEEE Trans. Neural Netw. 2006, 17, 118–129. [Google Scholar] [CrossRef] [PubMed]
- Nicosia, S.; Tomei, P.; Tornambe, A. A nonlinear observer for elastic robots. IEEE J. Robot. Auto 1988, 4, 45–52. [Google Scholar] [CrossRef]
- De Luca, A.; Schroder, D.; Thummel, M. An Acceleration-based State Observer for Robot Manipulators with Elastic Joints. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 3817–3823. [Google Scholar] [CrossRef]
- Filipescu, A.; Dugard, L.; Dion, J. Flexible Joints Robotic Manipulator Control by Adaptive Gain Smooth Sliding Observer-Controller. Fascicle III, Electrotechnics, Electronics, Automatic Control, Informatics. In The Annals of “Dunarea de Jos” University of Galati; Galati University Press: Galati, Romania, 2003; Volume 26, pp. 5–13. [Google Scholar]
- Bona, B.; Indri, M. Analysis and implementation of observers for robotic manipulators. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20–20 May 1998; Volume 4, pp. 3006–3011. [Google Scholar] [CrossRef]
- Ullah, H.; Malik, F.M.; Raza, A.; Mazhar, N.; Khan, R.; Saeed, A.; Ahmad, I. Robust Output Feedback Control of Single-Link Flexible-Joint Robot Manipulator with Matched Disturbances Using High Gain Observer. Sensors 2021, 21, 3252. [Google Scholar] [CrossRef] [PubMed]
- Seyfferth, W.; Maghzal, A.J.; Angeles, J. Nonlinear modeling and parameter identification of harmonic drive robotic transmissions. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 3, pp. 3027–3032. [Google Scholar] [CrossRef]
- Al-Darraji, I.; Piromalis, D.; Kakei, A.A.; Khan, F.Q.; Stojmenovic, M.; Tsaramirsis, G.; Papageorgas, P.G. Adaptive Robust Controller Design-Based RBF Neural Network for Aerial Robot Arm Model. Electronics 2021, 10, 831. [Google Scholar] [CrossRef]
- Al-Darraji, I.; Derbali, M.; Tsaramirsis, G. Tilting-rotors Quadcopters: A New Dynamics Modelling and Simulation based on the Newton-Euler Method with Lead Compensator Control. In Proceedings of the 2021 8th International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 17–19 March 2021; pp. 363–369. [Google Scholar] [CrossRef]
- Al-Darraji, I.; Kakei, A.A.; Ismaeel, A.G.; Tsaramirsis, G.; Khan, F.Q.; Randhawa, P.; Alrammal, M.; Jan, S. Takagi–sugeno fuzzy modeling and control for effective robotic manipulator motion. Comput. Mater. Contin. 2022, 71, 1011–1024. [Google Scholar]
- Jerbi, H.; Kchaou, M.; Boudjemline, A.; Regaieg, M.A.; Ben Aoun, S.; Kouzou, A.L. H∞ and Passive Fuzzy Control for Non-Linear Descriptor Systems with Time-Varying Delay and Sensor Faults. Mathematics 2021, 9, 2203. [Google Scholar] [CrossRef]
- Kchaou, M.; Jerbi, H.; Ali, N.B.; Alsaif, H. H∞ Reliable Dynamic Output-Feedback Controller Design for Discrete-Time Singular Systems with Sensor Saturation. Actuators 2021, 10, 196. [Google Scholar] [CrossRef]
- Regaieg, M.A.; Kchaou, M.; Jerbi, H.; Boudjemline, A.; Hafaifa, A. Robust Asynchronous H∞ Observer-Based Control Design for Discrete-Time Switched Singular Systems with Time-Varying Delay and Sensor Saturation: An Average Dwell Time Approach. Electronics 2021, 10, 2334. [Google Scholar] [CrossRef]
- Nandam, P.K.; Sen, P.C. A comparative study of a Luenberger observer and adaptive observer-based variable structure speed control system using a self-controlled synchronous motor. IEEE Trans. Indust. Electron. 1990, 37, 127–132. [Google Scholar] [CrossRef]
- Mohan, S.; Liu, J.; Vasudevan, R. Synthesizing the optimal luenberger-type observer for nonlinear systems. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 3658–3663. [Google Scholar] [CrossRef] [Green Version]
- Wernholt, E.; Gunnarsson, S. Nonlinear Identification of a Physically Parameterized Robot Model 1; IFAC Proceedings Volumes; Linköpings Universitet: Linköping, Sweden, 2006; Volume 39, pp. 143–148. ISBN 9783902661029. [Google Scholar]


| Reference Number of Paper | Dynamics Analysis | Nonlinear Order | Accurate Linearization | Number of Reduced Sensors | Stability Analysis | Optimization |
|---|---|---|---|---|---|---|
| [19] | No | 2nd | No | 2 | Yes | No |
| [20] | Yes | 2nd | No | 4 | No | No |
| [21] | Yes | 2nd | No | 4 | No | No |
| [22] | Yes | 2nd | No | 4 | Yes | No |
| [23] | Yes | 1st | No | 4 | No | No |
| [24] | Yes | 2nd | No | 4 | No | No |
| This paper | Yes | 3rd | Yes | 5 | Yes | Yes |
| Module Rule Number | Linguistic Input | Linguistic Output | |||
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 | |||||
| 11 | |||||
| 12 | |||||
| 13 | |||||
| 14 | |||||
| 15 | |||||
| 16 | |||||
| NRA Physical Parameter | Value | Unit |
|---|---|---|
| 0.0059 | ||
| 0.0201 | ||
| 0.00687 | ||
| 0.0206 | ||
| 0.02 | ||
| 0.021 | ||
| 0.0202 | ||
| 0.0624 | ||
| 0.00988 | ||
| 0.000986 | Unitless |
| State Parameter | Description (Unit) | Minimum Range | Maximum Range |
|---|---|---|---|
| Motor angle (rad) | 0 | ||
| Driver gear angle (rad) | 0 | ||
| Arm angle (rad) | 0 | ||
| Motor rate (rad/s) | 0 | 60 | |
| Driver gear rate (rad/s) | 0 | 60 | |
| Arm rate (rad/s) | 0 | 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jerbi, H.; Al-Darraji, I.; Tsaramirsis, G.; Kchaou, M.; Abbassi, R.; AlShammari, O. Fuzzy Luenberger Observer Design for Nonlinear Flexible Joint Robot Manipulator. Electronics 2022, 11, 1569. https://doi.org/10.3390/electronics11101569
Jerbi H, Al-Darraji I, Tsaramirsis G, Kchaou M, Abbassi R, AlShammari O. Fuzzy Luenberger Observer Design for Nonlinear Flexible Joint Robot Manipulator. Electronics. 2022; 11(10):1569. https://doi.org/10.3390/electronics11101569
Chicago/Turabian StyleJerbi, Houssem, Izzat Al-Darraji, Georgios Tsaramirsis, Mourad Kchaou, Rabeh Abbassi, and Obaid AlShammari. 2022. "Fuzzy Luenberger Observer Design for Nonlinear Flexible Joint Robot Manipulator" Electronics 11, no. 10: 1569. https://doi.org/10.3390/electronics11101569
APA StyleJerbi, H., Al-Darraji, I., Tsaramirsis, G., Kchaou, M., Abbassi, R., & AlShammari, O. (2022). Fuzzy Luenberger Observer Design for Nonlinear Flexible Joint Robot Manipulator. Electronics, 11(10), 1569. https://doi.org/10.3390/electronics11101569









