Abstract
Knee injuries are among the most common health problems in the world. They not only affect people who practice sports, but also those who lead a rather sedentary life. Factors such as age, weight, working and leisure activities can affect the health of the knees, causing disorders such as inflammation, edema, deterioration of cartilage and osteoarthritis. Although for the diagnosis and treatment of the various pathologies it is always advisable to contact orthopedists and specialized structures, it would often be useful to monitor the state of health of the knees in order to evaluate the healing (or worsening) process and the effects of sport/motion activities or rehabilitation. In this perspective, a portable knee health monitoring system was developed to be used at home or in gyms and sports environments in general. Besides requiring a simple custom front end, the system relies on a PC audio board capable of a sampling rate of 192 kHz to perform bioimpedance measurements at frequencies in excess of 50 kHz. A simple numerical calibration procedure allows to obtain high accuracy while maintaining low hardware complexity. The software developed for the operation of the system is freely available to any researcher willing to experiment with the bioimpedance measurement approach we propose, ensuring the conditions of portability and low complexity. Primary (intracellular and extracellular resistances and cell membrane capacitance) and secondary (real and imaginary parts of the total impedance) bioimpedance parameters can be obtained and analyzed through direct measurements with reference to an equivalent circuit model. The functionality of the system has been tested on nine subjects with different well-known health conditions, providing encouraging results in terms of the ability to correlate bioimpedance measurements to the health status of the knees. If proper clinical trials were to confirm our preliminary results, a system such as the one we propose could be used for fast and frequent monitoring of knee joints, thus possibly reducing the frequency at which complex and expensive medical exams, sometimes involving long waiting lists, must be performed.
1. Introduction
Knee injuries are certainly the most common cause of problems among individuals who practice sports, at both amateur and professional levels [1,2]. In general, any activity requiring repetitive stresses and high load for the knee joint can lead to knee injury. More sedentary people can be subject to knee injury as well due to the destabilization of the joint as a consequence of atrophied muscles [3]. The diagnosis is generally made by an orthopedic specialist and after the cure (that sometimes may require surgery), the patient can resume his activity or begin a rehabilitation process by undergoing periodic checks consisting in physical examinations [4] or in diagnostic imaging. As far as diagnostic imaging is concerned, depending on the public or private healthcare system organization, long waiting lists may be endured, and in any case, they are time consuming (a magnetic resonance investigation, for example, takes about half an hour plus the time required for the preparation and collection of the medical report, which could take up to a few days) and can be quite expensive [5].
Electrical impedance spectroscopy (EIS) has been widely used in biomedical applications for biological tissues’ characterization [6], for disease identification, such as diabetes [7,8,9], for body composition analysis [10], for cardiac functions monitoring [11,12], for muscles’ condition monitoring during sport activity [13], in dentistry [14] and in many other diagnostic fields.
Innovative methods that can result in simplified procedures for monitoring the health status of the knees would be more than welcome in the scientific and medical community and indeed, a few techniques to pursue this end (such as the analysis of the audio signals of degenerative arthritis [15]) have been proposed.
A few systems based on bioimpedance measurements for determining the progress of osteoarthritis are reported in the scientific literature [16,17]. Acute injury characterized by edema can also be identified [18,19], and a wearable vector electrical bioimpedance system to assess knee joint health has been proposed [20], employing an MP150 data acquisition system for data recording [21].
In consideration of the widespread occurrence of knee injuries, in this paper, we propose a portable system that is easy and safe to use even by individuals who do not have specialized electronic or medical skills. Moreover, the system can be easily reproduced due to its simple structure, its cost effectiveness and the easy availability of all the required components.
To assess the functionality of the new system, it was tested on nine volunteers, with different characteristics of gender, age and activity. Our preliminary results show that a few biological parameters, like the presence of intracellular and extracellular liquids, which are closely related to the state of health of the knee, and the capacitance of the cellular membrane, which is related to the amount of lipids, can be estimated with reference to a simplified model. Different pathologies like osteoarthritis or cartilage damage can be identified as well as the presence of a dominant leg, that is a leg that is subjected to a significantly higher load with respect to the other because of health problems or as a result of asymmetries in posture habits or in sport practices. As part of the study reported in this paper, a new parameter has been investigated as an indicator for comparing the knee conditions between healthy subjects based on the ratio between bioelectrical parameters. Overall, the instrument we propose is suitable to be embedded in a portable system that is a fundamental requirement for many applications.
While we clearly recognize that the limited number of test subjects is insufficient for considering the system and the approach we propose as an established complementary medical device suitable for monitoring the knee health status of any possible individual, we regard our preliminary results as encouraging and worthy of further investigation in the future, including rigorous clinical trials under strict medical supervision.
The hardware and the software components of the system will be discussed in Section 2 and Section 3, respectively. Section 4 will be devoted to a discussion of the methodology adopted for preliminary testing on volunteers, while Section 5 is dedicated to the discussion of the results that have been obtained.
2. Design and Implementation of the Knee Impedance Measurement System
In the design of the knee impedance measurement system, we regarded portability, low hardware complexity and high versatility as the most important goals to be obtained. Portability is required in order to allow testing outside specialized medical facilities, such as sport centers, outdoors training centers or home environment, and low hardware complexity is required to enable other research groups, especially those interested in the medical application of bioimpedance measurements, to easily reproduce the hardware required for performing experimentation with the system. High versatility is required in order to allow for experimenting with different data acquisition and data elaboration approaches. High versatility can be easily obtained whenever Digital Signal Processing (DSP) approaches can be used for signal generation and data elaboration. In recent years, personal computer stereo sound systems capable of sampling frequencies up to 192 kHz and with a resolution of 24 bits for both inputs and outputs have become widespread and are available at quite affordable cost also as standalone USB-based peripherals. With the ability to process signals in a bandwidth extending above 50 kHz (up to about 80 kHz), any such USB audio board, when coupled with the computing power of any mid-range notebook, can represent a rather standard and easily available building block for signal generation, signal acquisition and signal elaboration. Moreover, standard and easily available software libraries can be used for software development that can be made independent of the specific audio board hardware. With these considerations in mind, we developed our system around the USB board Behringer U-PHORIA UMC202HD (192 kHz, 24 bit [22]) and the PortAudio library [23] available in the public domain. Any other audio board with equivalent characteristics can be used. Moreover, if a sound system with the same characteristics is already integrated in the notebook, the external USB audio board is not required. By taking advantage of the audio board and of the computing power of the notebook, the front-end electronics required for the measurement of the bioimpedance can be greatly simplified and can indeed be reduced to the circuit in Figure 1.
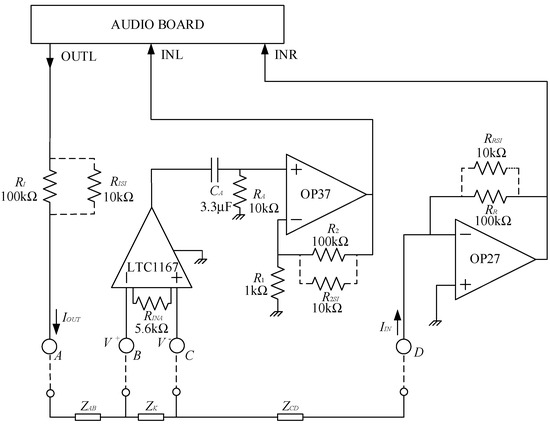
Figure 1.
Circuit schematic of the proposed system. ZK is the impedance of the knee, and ZAB and ZCD are the parasitic impedances between electrodes A and B and C and D, respectively.
The audio board is used for both generating the test signal (OUTL) and measuring the current and the voltage drop across the test region. The circuit is supplied by two 9 V batteries. Using a notebook, besides portability, allows to disconnect the system from the mains during operation (the USB audio board is powered by the notebook, as well), thus ensuring the electrical safety of the test subjects. Moreover, since the maximum DC voltages and currents to which the test subject is exposed are low, insulation and other safeties are not needed for the operation of the prototype according to the standard IEC 60601-1.
With reference to the circuit in Figure 1, ZK is the impedance of the knee, and ZAB and ZCD are the parasitic impedances between electrodes A and B and C and D, respectively. The resistances with the dashed lines (RxSI) can be inserted (snapped in, hence the subscript SI) or removed from the circuit in order to change gains and ranges, as it will be discussed in the following. In the prototype used in this work, these changes must be made manually, and this fact allows to employ an extremely simple electronic board. Manual switches can be used, of course, or programmability can be added if required. It must be noted, however, that changing the resistances in the field is seldom required, since, as it will be discussed in the following, the expected range of possible values for ZK can be easily managed with a fixed setting. Indeed, all testing on actual subjects reported in the following sections have been performed in a fixed configuration with all the RxSI (with RxSI = 10 kΩ) inserted.
The resistance, RI, in Figure 1 is used to limit the maximum current sent toward the patient. When performing bioimpedance measurements, it is preferable to use current signals rather than voltages because the safety of applying electrical signals in vivo is limited by the magnitude of applied current, and therefore a better control is possible. Assuming RISI removed from the circuit, with a maximum value of the voltage at the output OUTL of 1 Vrms, the maximum current toward the patient is limited to 10 μA rms (RI = 100 kΩ). A resistance (RISI) can be snapped in to increase the level of the current. Typically, we employed RISI of 10 kΩ that, in parallel with RI, allows for a maximum current of about 110 μA, that is still well within the safe range for the patient [24]. As we have noted before, the resistance RISI, if present, is installed during initial system configuration and it is never accessible to the operator when performing measurements on a patient. Note that the maximum current can only be obtained if the impedance between nodes A and D (|ZAD| = |ZAB + ZK + ZCD|) is negligible with respect to RI (or to RI in parallel to RISI). This is indeed the case in impedance measurements on a knee, where |ZAD| is typically in the order of 100 Ω or below, as we shall discuss in the following. The current exiting node A reaches node D (virtual ground) at the input of a trans-resistance amplifier (OP 27 and RR or RR//RRSI) with a trans-resistance gain GR = −RR (or GR = −RR//RRSI). The trans-resistance amplifier is used to send a voltage proportional to the actual current through the circuit to the right input INR of the audio board. Clearly, for aligning the output dynamic of the output OUTL with the input dynamic of INR (1 V rms in both cases), we have RI = RR, and, if snap-in resistances are used, they also must match, that is RISI = RRSI. In order to measure the impedance ZK between nodes B and C, the voltage between these nodes must be detected and amplified. The values of |ZK| typically range from few tens of ohms up to about 100 Ω. When working with a maximum current of 10 μA, a gain of about 1000 is required to take advantage of the full dynamic range of the input INL of the audio board (1 V rms), while when operating with RISI = 10 kΩ in place, a gain of 100 is sufficient. To reach a large bandwidth, so that accurate measurements above 50 kHz can be made, we divided the voltage-amplifying chain into two stages. The first stage is a large bandwidth, JFET input instrumentation amplifier LTC1167, that provides for an amplification of 10 of the differential voltage across the impedance ZK with a −3 dB bandwidth of 800 kHz. The second stage is a voltage amplifier based on an OP37 operational amplifier. In its default configuration (R2SI not present), the voltage gain of the second stage is 101 with a −3 dB bandwidth in excess of 600 kHz. When the 10 kΩ snap-in resistance (R2SI) is in place, the gain reduces to 10.1 with a −3 dB bandwidth in excess of 5 MHz. The AC coupling stage RA, CA is used to reject the DC component at the output of the instrumentation amplifier. With RA = 10 kΩ and CA = 3.3 μF, the low corner frequency is about 5 Hz, well below the frequency range in which bioimpedance measurements are usually carried out (above a few kHz [25]).
When performing impedance measurements with the approach outlined in Figure 1, the impedance at any given frequency is obtained by evaluating the ratio between the phasors at the outputs of the trans-resistance and voltage amplifiers in Figure 1 (INL and INR). Because of the division, as long as the left and right acquisition channels of the audio board are well-matched (as it is expected to be the case), the detailed amplitude and phase responses of the audio board channels do not introduce errors in the estimation of the impedance. On the other hand, amplitude and phase deviation from the ideal gain of the voltage and trans-resistance amplification chains in Figure 1 can result in significant errors. As an example, let us assume that we are configuring the circuit with all RXSI removed from the circuit (maximum test current about 10 μA rms). We can resort to SPICE simulation to verify what would be the result of measurements in the particular simple case of ZK = RK = 100 Ω, ZAB = RAB = 10 Ω and ZCD = RCD = 10 Ω. The resulting estimated impedance (ZM) according to such a simulation is reported in Figure 2, where the grey area indicates the frequency region outside the measuring capability of the audio board being used (f > 80 kHz).
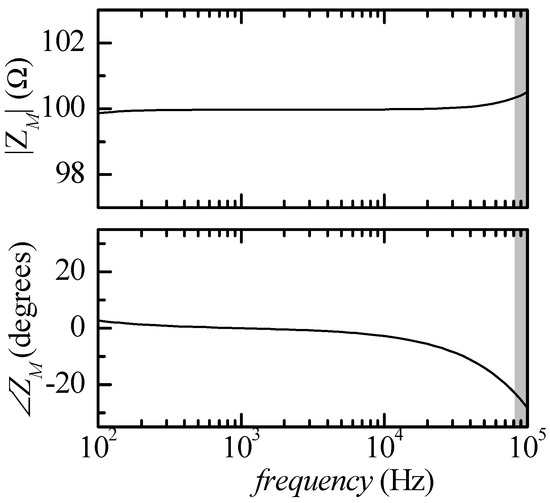
Figure 2.
Simulation of the measurement results with Zk = 100 Ω. The grey area indicates the frequency region outside the measuring capability of the audio board being used.
The deviation with respect to the ideal response |ZM| = 100 Ω and ∠ZM= 0 at low frequencies (f < 500 Hz) is due to the presence of the high pass filter CARA in Figure 1. The effect of the high pass filter could be reduced by decreasing the cut-in frequency (by increasing CA) but, since, as we will discuss presently, we need a calibration procedure for correcting the error at high frequencies, this is not really necessary. Moreover, bioimpedance measurements are rarely performed below a few kHz.
As far as the deviation at higher frequencies is concerned, whereas the error in the modulus of the impedance is small (less than 1%), the error in the phase is much more significant and can be linked to the phase deviation that occurs below the bandwidth limit of the amplifiers in Figure 1. It must be noted that whereas there could be simple ways to extend the bandwidth of the trans-resistance amplifier and of the second-stage voltage amplifier in the circuit in Figure 1, this is not the case as far as the instrumentation amplifier is concerned. As far as we have been able to ascertain, there are not many alternatives to the LT1167 in terms of overall bandwidth and CMMR at the highest frequencies of interest.
Starting from the (simulated) result of the measurement reported in Figure 2, we can however define a complex correction function HC(f), defined as follows:
where ZK is the actual true value of the impedance and ZM is the impedance as obtained from the measurement with the circuit in Figure 1. Suppose now we can ensure that the correction function HC is essentially the same regardless of the actual ZK (in a reasonable and useful range): if this is the case, we can obtain HC(f) from an actual measurement on an actual test impedance (a known calibration impedance ZC) and then obtain the actual value of any impedance by multiplying the measured value ZM at any frequency by HC, as suggested by Equation (1).
In order to verify that this is indeed the case for the specific application we are interested in, we need to mention that the result of bioimpedance measurement on a knee will be interpreted with reference to the equivalent model in Figure 3 [16], where the resistance Rext and Rint, whose physical meaning will be discussed in the following sections, are expected to range between 30 and 100 Ω and the capacitance C in the range between 10 and 15 nF.
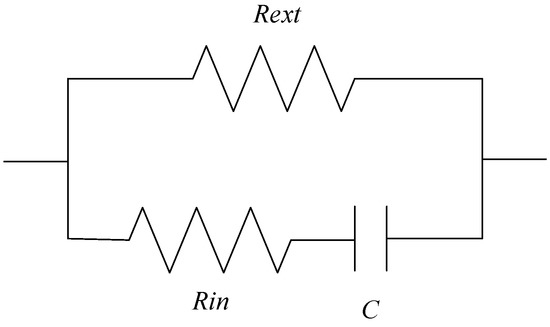
Figure 3.
Equivalent circuit of a knee. Rext models the extracellular liquids, Rin the intracellular liquids and C the capacitance of the cellular membrane.
We therefore performed Monte Carlo SPICE simulations by repeating more than 10,000 spice runs with ZK in the form of Figure 3 with random and uncorrelated values, within the expected ranges, for Rin, Rext and C for each run. The correction function HC was evaluated for each set of values in order to check how much it changed depending on the actual ZK being tested. In a first simulation set-up, we performed the test in the same conditions in which Figure 2 was obtained, that is with all snap-in resistances removed from the circuit. The results are summarized in Figure 4. All curves representing the modulus and the phase of the correction functions lie inside two limiting curves: the deviation is however so small that the limiting curves can be distinguished, with the scale used for the figure, only in the case of the modulus and only for frequencies above about 20 kHz. It can be noticed that in the entire frequency range that can be explored (outside the gray areas), the deviation in the modulus of the correction function is expected to be less than 0.2% and, more importantly, the deviation in the phase is expected to be less than 0.03 degrees. This means that any calibration curve obtained from a calibrated impedance (in the possible range for ZK) can be used to obtain a calibration function HC that can be used for all actual measurements with small errors in the estimation of the modulus (less than 0.2%) and an almost negligible error in the phase.
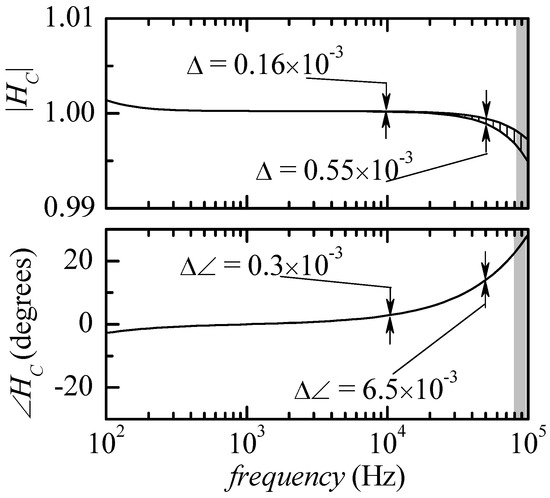
Figure 4.
Modulus and the phase of the correction functions. The deviation is so small that the limiting curves can be distinguished, with the scale used for the figure, only in the case of the modulus and only for frequencies above 20 kHz.
We have investigated in some detail the origin of the spread in the results for HC and the reason why such spread increases for increasing frequency. It is clear that for HC to change as a function of ZK, either the gain of the voltage amplification chain (from VBC to the input INL in Figure 1) or the gain of the current amplification chain (from IIN to the input INR in Figure 1), or both, should depend on the value of ZK. We clearly expect the gain of these two chains to depend on the frequency, but the reason why we observe a dependence, at the same frequency, on the value of ZK and the reason why this change increases with frequency (with ZK changing in the same predefined range) are not obvious. There is certainly no reason, as can also be easily verified through simulation, for the gain of current amplification chain to depend on ZK or in any circuit component to the left of node D in Figure 1. Similarly, if the inverting input of the instrumentation amplifier was actually grounded, there would be no reason for the gain of the voltage amplification chain to depend on ZK. The fact is, however, that the non-inverting input of the instrumentation amplifier is not grounded, and this is indeed the reason why we may obtain a gain that changes with the value of the impedance. In order to understand why, let us assume, for the sake of simplicity, that the impedance ZCD be completely negligible. In this case, we observe that node C is “virtually” grounded through the input of the trans-resistance stage. More in detail, the impedance from node C toward ground (with ZCD = 0) is the input impedance of the trans-resistance stage. Whereas in most applications we may assume this impedance to be negligible, in our particular case in which |ZK| is at most 100 Ω, this is not true in the entire frequency range in which we are interested. In order to estimate such an impedance in our operating conditions, we can safely assume the OP27 to be described by a single pole frequency response with a DC gain AV0 and a pole frequency fop. Since we typically operate at frequencies, f, above 100 Hz (hence f >> fop) and well below the gain bandwidth product of the operational amplifier, we can estimate the modulus of the input impedance ZIT of the transresistance stage to be:
Note that with RR = 100 kΩ and typical values for AV0 and fOP (AV0 × fOP = 8 MHz for the OP27), at the frequency of 10 kHz we have |ZIT|≈125 Ω, that is an input impedance larger than the typical ZK on which we want to perform measurements. The result of this situation is that the common mode voltage at the input of the instrumentation amplifier can be larger than the differential voltage across ZK. More in general, at low frequencies, |ZIT| is small, hence the common mode voltage at the input of the LT1167 is small compared to the differential voltage, and this fact, combined with the high value of the CMRR (105 dB for f < 100 Hz), results in the almost complete rejection of the contribution of the common mode input voltage to the output voltage at node INL in Figure 1. As the frequency increases, however, the common mode input voltage for the same differential voltage across ZK increases because |ZIT| increases (by 20 dB/decade), and, at the same time, the CMRR decreases (−20 dB/decade above 100 Hz). These two effects both cause a larger and larger contribution of the common mode input voltage to the output voltage at INL as the frequency increases. The contribution of the common mode input voltage to the output voltage introduces an error, and we can reasonably expect this error to change as ZK changes and to be larger and larger as the frequency increases. This fact is indeed nicely confirmed by the result of the Monte Carlo simulations reported in Figure 5, where the maximum deviation (∆) in the modulus of the correction function HC is reported vs. frequency in the very same conditions used to obtain Figure 5 (empty squares) and in the case in which 10 kΩ snap-in resistances are inserted in parallel to RI, R2 and RR. We can clearly see that the maximum deviation (∆) increases at a rate of about 40 dB/decade, which can be directly correlated to the increase by 20 dB/decade of the input impedance of the trans-resistance stage and the decrease of the CMRR of the instrumentation amplifier by −20 dB/decade, as discussed above. As a further evidence of the correctness of our interpretation, it can be noticed that when the snap-in resistances are inserted, this causes a reduction by a factor of about 10 in the input impedance of the trans-resistance stage, and this, according to the mechanism discussed above, causes in turn a decrease of the maximum deviation (∆) by the same factor at all frequencies, as can be seen in Figure 5. Since there is not much that can be done about the CMRR of the instrumentation amplifier, it is clear that the only way to further reduce the maximum deviation would be to design a trans-resistance amplifier with a much smaller equivalent input impedance. On the other hand, especially when the snap-in resistances are present, the maximum deviation is sufficiently small and there is no need to increase the complexity of the circuit. With the snap-in resistances in place, the maximum deviation in the modulus of HC at 50 kHz is about 0.05 × 10−3 and, at the same frequency, the maximum deviation in the phase can be estimated to be below 10−3 degrees.
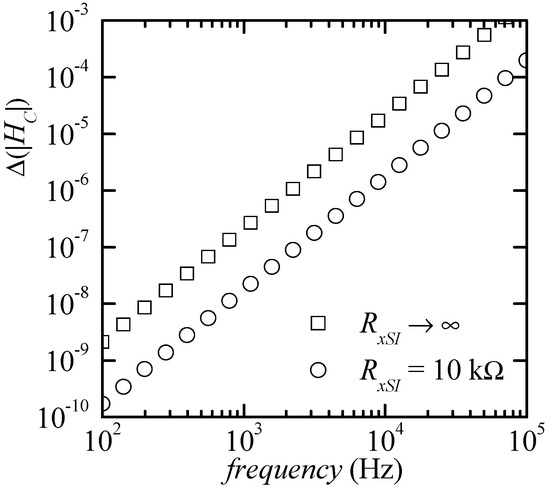
Figure 5.
Maximum deviation of the modulus of the correction function HC vs. frequency. The empty squares refer to the same simulation condition in which Figure 4 has been obtained. In the case of the empty circles, the only change was the presence of 10 kΩ snap-in resistances in parallel to RI, R2 and RR in Figure 1.
With these results and given that whenever possible we will employ the circuit in Figure 1 with all snap-in resistance inserted (larger test current and, hence, larger signal and large signal-to-noise ratio at the input of the audio board), we can conclude that, provided that a calibration measurement is performed on a calibrated impedance, the accuracy that can be obtained with the simple circuit we propose is more than adequate for its application in bioimpedance measurements.
The calibrated impedance does not really need to be in the form of Figure 3, as long as its modulus is within the expected range for the actual measurement. Indeed, we typically employ a single high-accuracy (0.1%) 100 Ω resistor for ZK with ZAB = ZCD = 10 Ω. Using a single resistor greatly simplifies performing the calibration measurement while remaining effective. To demonstrate this fact, we first extracted the calibration function HC from actual measurements on the 100 Ω resistor, and then used HC for correcting the actual measurements on a test impedance in the form of Figure 3, with Rext = 100 Ω, C = 10 nF, Rin = 100 Ω. The results of such procedure are summarized in Figure 6. The measurements obtained without correction (black dots) are shown together with the measurement modified using the correction function HC obtained from a previous measurement on the calibration impedance (empty squares) and with the calculated values for the modulus and the phase of the impedance being tested (continuous black line). As it can be noticed, after correction, the measured values are essentially coincident with the expected ones.
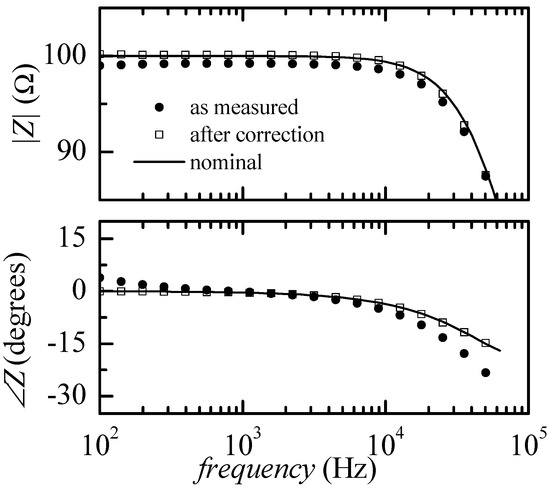
Figure 6.
Measurements on a test impedance as in in Figure 3 with Rext = 100, C = 10 nF and Rin = 100. The black dots are the measurement results when no correction is applied. The empty squares are the measurement results corrected with the calibration function HC obtained from a previous measurement on a single 100 Ω resistor. As it can be noticed, after correction, the measurement essentially coincides with the nominal value of the tested impedance at each frequency (black line).
3. Knee Impedance Measurement System: Software
The software must allow to perform impedance measurements vs. frequency, but, in view of the possibility of expanding the application of the system we propose, should also allow to monitor the fluctuations of the impedance vs. time at fixed frequencies. While this last feature has not been implemented yet, the software architecture was designed to enable this functionality in future work. A schematic diagram of the operation of the Digital Signal Processing (DSP) section of the system software is reported in Figure 7.
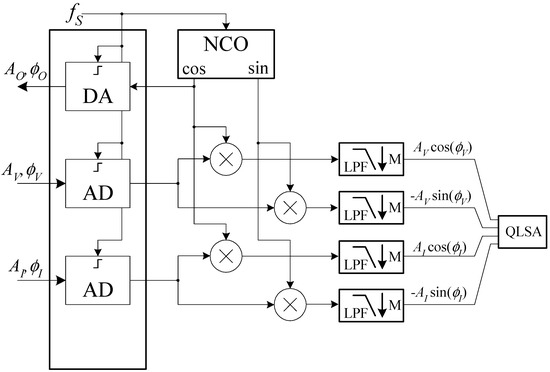
Figure 7.
Schematic diagram of the operation of the Digital Signal Processing (DSP) section of the system software.
The NCO in Figure 7 is a Numerically Controlled Oscillator working at the audio board sampling frequency. The NCO is based on a 30 bits phase accumulator resulting in a frequency resolution ∆f well below 1 mHz (∆f = 179 μHz). The NCO produces two sinusoidal signals that we will assume to be zero-phase cosine and sine functions with an amplitude of 1 V. The cosine signal generated by the NCO is sent to the audio board, resulting in a voltage signal VO(t) given by:
As a result of the stimulus VO, we obtain a sinusoidal current ik (t) through the impedance chain ZAB, ZK and ZCD that, in turn, results in a sinusoidal voltage drop vk(t) across the impedance of interest ZK. The board in Figure 1 amplifies both signals to produce the voltages VV and VI at the left and right input of the audio board:
where we have numerically multiplied GR by −1 so that we obtain the same phase for the voltage and the current in the case of a pure resistance for ZK and we have assumed, for the sake of simplicity, real gains independent of the frequency. We have, however, explicitly noted the fact that both the amplitude and the phase of the signals can depend on the time as a result of physiological causes, such as the cardiac activity. Both amplitude and phase changes are expected to be small and occurring over a time much longer than the signal period. After analog to digital conversion, each of the input signals is sent to a coherent demodulator implemented in software, so that their amplitude and phase can be extracted. The cut-off frequency of the fourth-order IIR low pass filters (LPF in Figure 7) is set in such a way that, besides eliminating the high-frequency components at the output of the multipliers, the numerical signal can be decimated by a factor M = 16, thus reducing the data rate from 192 down to 12 kHz. This sampling frequency is largely sufficient to retain the information due to the possible modulation in the amplitudes and phases of the detected signals. At the outputs of the decimation stages, the in-phase and in-quadrature components can be further low pass filtered in order to reduce noise before the estimation of the impedance. Depending on whether or not we want to retain information on the amplitude and phase fluctuations due to physiological activities, we may have to employ different cut-off frequencies to distinguish phenomena occurring in different frequency bands. In order to simplify such a process and to maintain high flexibility in the data elaboration process, we resorted to the QLSA public domain library [26]. While QLSA is mainly intended for multi-channel spectral analysis, as part of its inner working operation, it performs multi-stage low pass filtering and decimation on the incoming signal stream. More precisely, for each input signal sequence, QLSA is used to perform the filtering operations schematically shown in Figure 8.
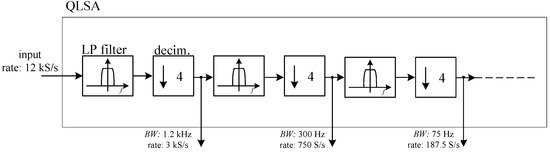
Figure 8.
Filtering and decimation as performed by QLSA (Quasi-Logarithmic Spectrum Analyzer).
The LP filters in Figure 7 are low pass FIR filters with a flat response from 0 to 0.1 times the frequency fR corresponding to the input sampling rate and with an attenuation larger than 70 dB above fR/4 [26]. In this way, we can obtain several low pass filtered outputs with geometrically decreasing bandwidth limits (by a factor of 4 at each step) and correspondingly lower sampling rate, thus lowering the load for analysis algorithms at lower sampling rates.
As it is discussed in Reference [26], adding more filtering and decimation stages after the first two or three has a negligible computational cost, and for this reason, we set the number of stages to 8, although it is rare that one may be interested to the lowest bandwidth obtained in this way (about 70 mHz).
Using any one of the output stages at the output of QLSA, it is trivial to obtain an estimate of the modulus and the impedance of ZK at any given time from the knowledge of the quantities AVcos(ΦV), AVsin(ΦV), AIcos(ΦI), AIsin(ΦI) and from the knowledge of the voltage and trans-resistance gains GV and GR.
In impedance vs. frequency measurements, as used in this work, estimates of the impedance at each frequency are averaged over time in order to reduce the error due to noise (average time is typically one to two seconds).
The software required for the operation of the system is freely available to any researcher willing to experiment with the bioimpedance measurement approach we propose.
4. System Testing
Nine volunteers with different ages (in the range 17–83 years old) and different knee history and conditions participated to the test of the proposed system, after having been thoroughly informed about the measurement procedures and after having signed an informed consent. As we stated in Section 2, the system is used without any connection to the mains, DC voltages and currents are very low and, therefore, insulation and other safeties are not needed for the operation of the prototype, according to the standard IEC 60601-1. Prior to actual measurements, the test impedance used for calibration can be connected to the system in order to check that it is in good working order. Measurements were performed employing standard Ag/AgCl electrodes, disposed to maximize the path of the current within the knee region and to minimize the influence of possible unwanted variables, such as muscle mass, for example. While a few electrode arrangements were tested, the solution employed to obtain the data discussed in this work is the one shown in Figure 9, together with a picture of the measurement system. The upper and lower (on the back) electrodes are dedicated to the injection and detection of the current and correspond to electrodes A and D in Figure 1, whereas the electrodes for measuring the voltage across the region of interest are the ones in the middle (electrodes B and C in Figure 1). This positioning allows to exclude the contribution by the quadriceps and the calf muscles. Moreover, the four-electrodes configuration allows to remove parasitic effects due to cables, electrodes resistances and skin-electrode impedances that could change with skin hydration state and sweat [27]. To ensure consistency among different test sessions for each single individual, the position of the electrodes with respect to the center of the patella, determined with the help of a measuring tape, was recorded. In this way, we were able to perform consistent measurements on both knees of the same patient, even in different trials, in reproducible conditions. High consistency in the positioning of the electrodes from one individual to another is not necessary, since the interpretation of the measurement result does not rely on the comparison of data obtained from different patients.
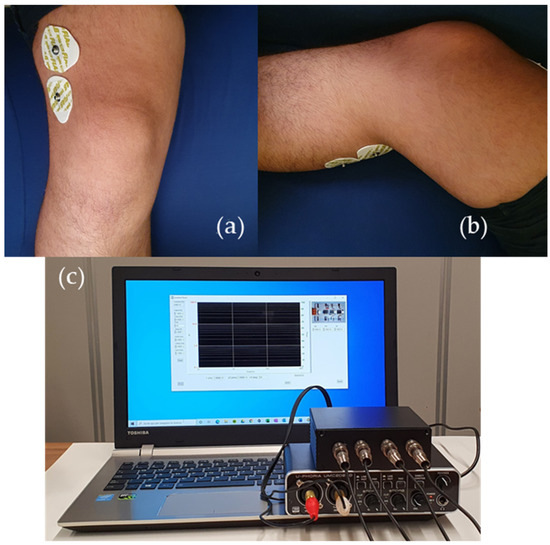
Figure 9.
Electrodes arrangement (a,b) and developed measurement system (c).
No significant differences have been noticed between the execution of the measurements with the subject seated (with the leg extended) or standing. However, since even small involuntary movement can cause fluctuations in the measurements, it was determined to have the patient sitting with the leg extended as this was deemed to be the most stable and most easily reproducible configuration for the leg of the individual during the time required for completing the measurement.
Notice that, on the other hand, significant changes are observed if the leg is bent instead of being extended, possibly because it is difficult to exactly reproduce the same posture in successive trials.
Measurements were performed in the frequency range 10–60 kHz, because this range allows both to reduce losses due to the skin–electrode interface and to employ lower current amplitudes, thus allowing to use the system in better safety conditions [25]. A few bioimpedance parameters were obtained and analyzed through direct measurements and through the study of an equivalent circuit model. In particular, intracellular and extracellular resistances and the real and imaginary parts of the equivalent impedance have been correlated, together with the anamnesis of the volunteers, with the state of health of the knee of each individual.
The results of the measurements are consistent with the knee being modeled as an RC network as in Figure 3, where Rext models the extracellular liquids, Rin the intracellular liquids and C the capacitance of the cellular membrane [16,28]. The ratio Rext/Rin was found to be an important indicator for identifying osteoarthritis or cartilage damage [16,17]. Moreover, the ratio of the intracellular resistances of the two knees allows to identify the dominant leg (if any). In addition to this term, the real part (RE) and the imaginary part (X) of the impedance were also discriminating factors for determining the health status of the knee, and their value at 50 kHz [29] was used. Parameters Rext, Rin and C (not used for the study) where extracted by fitting the experimental data (using OriginPro 8 by OriginLab Corporation) against the real (RE) and imaginary (X) parts of the impedance in Figure 3:
5. Results and Discussion
To verify the effectiveness of the system, nine volunteers with known health conditions were chosen, in order to verify the correlation between the measured parameters and the actual state of the joints, also in accordance with results reported in the literature [16,17,18,19,20]. The subjects can be divided into three groups: (1) two elderly individuals (E1 and E2), (2) five individuals who normally practice some type of sport activities (S1 to S5) and (3) two individuals (NS1 and NS2) who do not exercise with regularity. All the subjects were in good health, for their age range, and did not suffer from any pathology, other than, in the case of some of them (all subjects except S3 and S4), for medical conditions strictly related to their knees. To facilitate the interpretation of the experimental data, Table 1 summarizes the medical diagnosis for each subject and the methodology (or methodologies) employed to reach such diagnosis. Nothing is reported for subjects S3 and S4 since, as it was stated before, these subjects never suffered from knee joint discomfort of any kind. The relevance of each diagnosis in our study will be discussed in a case-by-case basis in the following. The relevant bioimpedance parameters estimated for each subject starting from the measurements performed using the developed instrumentation are reported in Table 2. Parameters RE and X are the real and the imaginary part of the impedance at 50 kHz, ∆R and ∆X are the differences between the real and imaginary parts of the impedance obtained for the right and for the left knee (right minus left), Rext/Rin is the ratio between the extracellular and the intracellular resistances and Rinr/Rinl is the ratio between the intracellular resistances of the right and of the left knee.

Table 1.
Medical diagnosis and related investigation techniques for all the examined subjects. Subjects S3 and S4 do not suffer from any knee-related medical condition.

Table 2.
Bioimpedance parameter values for all the examined subjects.
5.1. Data Discussion: ∆R and ∆X
It has been demonstrated in References [18,20] that a good method to assess knee joint health consists in detecting the differences between the right and left knees resistances and reactances, that result higher in the case of injured subjects. In particular, it has been observed that subjects with an acute inflammatory state have lower resistance and (negative) reactance with respect to healthy subjects. However, this method is only reliable in the case of edema [18,20]. Indeed, edema is more conductive than other biological tissues [30] and its presence lowers the resistance of the knee joint.
The repetition of the measurements on different days and several times a day on the same subject has shown that, in the absence of traumatic events, the spread in the measured values is in the order of 3 Ω. This observation is consistent with what reported in literature [20]. For this reason, it has been assumed that only differences significantly larger than 3 Ω have to be assumed as conclusive indication of some kind of injury as they cannot be justified with random errors due to the measurement procedure and normal day-to-day physiological changes. According to these considerations, measurement results indicated that six of the examined subjects potentially suffered from knee joint problems. According to the data, Subjects S1 and S2 exhibit an inflammatory state accompanied by edema in the left knee (this observation is consistent with the medical history of the individuals) and our results are in agreement with References [18,20]. Subjects of groups 1 and 3 show relevant values of ∆R and ∆X but only one of them (NS1) has a slight edema. The other subjects did not have edema but all reported damage to the cartilage or osteoarthritis. Data suggest, then, that in the case in which there is no significant edema but the knee is still in a state of pain, mainly due to the deterioration of the cartilage, an increase in resistance is observed. At this point, it is important to understand if the difference ∆R is due to a lowering of extracellular resistance due to the presence of edema, or to an increase in extracellular and intracellular resistance due to an osteo-cartilage problem. All the subjects who have documented osteo-cartilaginous problems present, in addition to a relevant ∆R value, also have a relevant ∆X value. On the other hand, subjects who have no particular damage but are in an acute inflammatory state characterized by edema, have a significant ∆R value but a small ∆X.
Based on these observations, it seems useful to cross-reference ∆R data with ∆X data. If there is a high ∆R without large variations of X, we are in the presence of edema, whereas if the high ∆R is accompanied by an appreciable ∆X, the problem is, according to the results acquired so far, osteo-cartilaginous. This result, if confirmed by a future more in-depth experimentation, would be relevant. In fact, at present, studies have been conducted either on knees with only inflammatory states characterized by edema [18,19,20], or on knees with only osteoarthritis diagnosis [16,17], but a method based on bioimpedance measurements that allows to distinguish between the two cases in “blind mode” has not yet been proposed. Measurements performed on subject S3, who can be considered the “reference subject”, having never suffered from trauma and having always practiced symmetrical sports activities such as running and swimming, show that in the absence of injuries, the left and the right knees behave essentially in the same way from the point of view of the measured bioimpedance, as it is shown in Figure 10. The situation of subjects NS1 and NS2 seems to be the same. Nevertheless, these results suggest that the ratio between the bioelectrical parameters would be a better indicator than their difference, used as an indicator in previous works in literature. For example, for NS1 the ratio RE(left)/RE(right) is 1.06, while for NS2 it is 0.85, thus indicating that in the first case, there is a deviation of 6%, while in the second of 15%. The same is true for X: for NS1 the ratio X(left)/X(right) is 1.08, while for NS2 it is 0.79, thus indicating that in the first case, there is a deviation of 8%, while in the second of 21%.
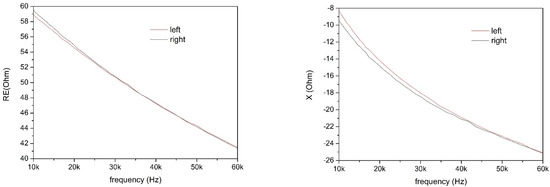
Figure 10.
Resistance and reactance of the bioimpedance of subject S3 vs. frequency.
From the study of the ratio (and not of the differences), therefore, it is evident that the NS1 subject has less of a serious problem than NS2. NS1 is in fact a young overweight woman with a slight inflammation (probably due to her physical condition) characterized by a slight edema at the right knee joint (the one with lower RE and X), while NS2 is an ex-sportsman with third-grade chondropathy in the right knee (which is the knee with the higher values of RE and X). According to this data interpretation, for subjects S1 and S2, it is confirmed that they show an inflammation of the knee joint without serious damage. Indeed, assuming a deviation of at least 10% to be significant, the real part (RE) of the impedance shows a deviation of about 13% between left and right knee for both the subjects, while the variations in reactance are less than 8%.
Subject S5 has a particular situation: the data shown in Table 2 refer to the last measurement performed at the end of a control process that lasted months. The subject (44-year-old woman), in fact, suffered from chondropathy patellae of a maximum grade on the left knee joint and underwent surgery more than twenty years ago. When the knee is subjected to intense sporting activity, the resistance and reactance increase compared to the other knee, probably because of mechanisms similar to the ones that will be described for osteoarthritic knees in the next subsection. After all, according to specialists, those who suffer from chondropathy are destined to have arthritis problems [31], so it is possible, given the time elapsed since the surgery, that the subject is in an initial state of arthritis. In correspondence with these events, the subject feels pain and the classic “crunch” of the knee, even in the absence of evident edema. In Figure 11, the evolution of an acute inflammation is shown. Figure 11a shows the reactance and resistance of the (left) suffering knee and of the (right) healthy knee at the beginning of inflammation (identified by the fact that the subject experiences pain). Figure 11b shows the situation after two weeks of sport activity (running and cardiotonic activity). The situation worsened. Figure 11c shows the situation after another 10 days of training, during which the subject tried to load less on the leg in pain. Figure 11d shows the situation after about 3 months of less stressful activity for the joints (walking and swimming) and ice therapy. As it can be observed, although a difference is still present, it is strongly reduced. The situation shown in Figure 11d coincides with the period in which the subject no longer feels pain. The subject then resumed knee joint-heavy activities and a new increase in RE and X was observed (not reported in the figure).
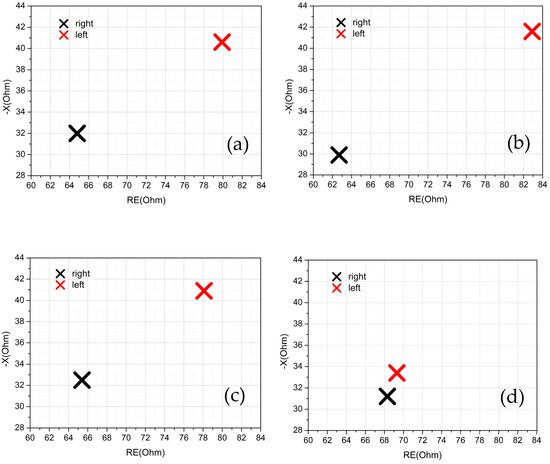
Figure 11.
Reactance vs. resistance for left (injured) knee and right (healthy) knee. (a) Acute phase of injury, (b) situation after two weeks from (a), during which the subject performed heavy sport activity, (c) situation after another 10 days of training, during which the subject tried to load less on the leg in pain, (d) situation after about 3 months of less stressful activity for the joints (walking and swimming) and ice therapy.
Subject E2 is an elderly man (83 years old) with a cartilaginous pain (the “crunch” can be heard) in his left knee (in accordance with the considerations made up to now), while the data of subject E1 will be commented on in the next subsection.
5.2. Data Discussion: Rext/Rin
All the subjects, except one, have a ratio Rext/Rin lower than one. The only subject who has the Rext/Rin > 1 (for both right and left knee) belongs to group 1 (subject E1 in Table 2) and is an elderly subject (woman, 77 years old) who has been diagnosed with advanced osteoarthritis. None of the other subjects had a diagnosis of osteoarthritis. This first observation is in accordance with what is reported in References [16,17]. Indeed, in healthy knees, the resistivity of the extracellular environment is lower than that of the intracellular. Since Rext is associated with the extracellular liquids, its increase in osteoarthritic knees is justified by an increase of apatite crystals and pyrophosphate of calcium (that can be considered as non-conductive particles) in the synovial fluid due to disease [32,33]. Moreover, an increase of the number of leucocytes (size of 10–20 μm) in the synovial liquid of an osteoarthritic knee has been observed [34] and this can contribute to the increase of Rext. Finally, when the knee is in an inflammatory status, cytokines are released into the synovial fluid [35], thus resulting in a further increase of the extracellular resistance. For non-osteoarthritic knees, a mean value of Rext/Rin = 0.63 has been registered, with a minimum value of 0.3 and a maximum of 0.82. The variations of Rext/Rin are due to inflammatory states (different values of Rext) or to different values of Rin. This topic will be discussed in more detail in the next subsection.
5.3. Data Discussion: Rinl/Rinr
The index Rinl/Rinr in Table 2 is the ratio between the intracellular resistance of the right and the left knees.
Although this paper in mainly focused on the instrumentation we have developed, in order to address the topic covered in this subsection, it might be useful to briefly discuss some aspects relative to the physiological parameters associated with the intracellular resistance of the knees. The resistance Rin is mainly associated to the articular cartilage cells’ metabolism [36] (chondrocytes are the only cell type in the cartilage tissue [37]). This metabolism is stimulated by mechanical loading, detected by the mechanoreceptors on the cell surface [38]. In Reference [36], it is explained that through the process of mechanotransduction: mechanical signals modulate the biochemical activity of chondrocytes, regulating metabolic activities by influencing the state of the knee joints. In particular, dynamic compressions during moderate exercise generate mechanical stimuli that can regulate the metabolic balance, thus preventing the progression of cartilage damage [38]. A proper mechanical loading is crucial for the health of knee joints, as it has been demonstrated that insufficient biomechanical stimuli, due, for example, to a forced immobilization, can lead to reduced thickness and softening of the cartilage [39], whereas, conversely, an excessive load can inhibit the articular cartilage regenerative capacity, leading to damage or, in extreme cases, to irreversible destruction [38]. In the case of high load, cytokines are released in the intracellular fluid. Based on these considerations, we have chosen to identify the dominant leg as the one with a higher Rin value, because it seems legitimate to correlate, for the same subject, the higher Rin value with a higher load condition for the relative knee joint.
As a criterion, we have chosen to consider a leg to be dominant if the knee is characterized by a higher value of Rin of at least 10% compared to the other. If this difference is not noticed, it is assumed that there is no dominant leg. The resistance Rin is related to the intracellular fluid and to the metabolic activity of the knee cells, therefore it is reasonable to assume that a higher value of this resistance indicates a greater workload for the knee. Among the examined subjects, four of them show a dominant leg. Among the subjects of group 2 (group of people who regularly practice sport), subjects S1 and S4 show the right leg and the left leg to be dominant, respectively. This result has been verified. In fact, S1 is a (woman, 43 years old) fitness coach with a meniscus problem causing inflammation and edema in the left knee (as also discussed in Section 5.1). Therefore, during workouts, the subject loads on the right knee to avoid making the injured knee problem worse. Subject S4 is a young right-handed basketball player not yet very skilled in the use of his left hand and who consequently mainly jumps on the left leg (think of the lay-up movement in the basketball game).
For both subjects in group 1, it appears that the left leg is dominant, but contrary to the case of the other subjects, we have not been able to find any obvious correlation of these results with their lifestyles. However, since they are affected by cartilage or osteoarthritic suffering, the larger value of Rin of the left knee may not only be due to a greater load but also to a decrease in the pH of the knee. Indeed, a strong negative correlation between the pH variations and the quantity of intracellular liquid has been observed in References [40,41], and in the case of osteoarthritic knees (or with damage to cartilage), the concentration of hyaluronic acid decreases and the pH of the synovial fluid increases, which could be an explanation for a higher intracellular resistance.
6. Conclusions
A bioimpedance measurement system for knee joint health assessment and monitoring has been designed, developed and tested. The system is based on a conventional audio board, it requires minimum additional hardware so that it is quite easy, for anyone interested in its applications, to reproduce it with minimum cost since there is no need for buying complex and/or expensive data acquisition and elaboration systems. A simple calibration procedure has been proposed, that allows to obtain reliable measurement results. The system was tested on nine subjects with known medical history and bioimpedance parameters have been measured and derived that, compared to the results presented in previous works in this field, seem to allow to identify whether the problem of the knee joint is due to an inflammatory state accompanied by edema or whether it is an osteocartilaginous problem; moreover, the results obtained so far suggest that the evaluation of the ratio between right and left resistances and between right and left reactances rather than their difference has proved to be more reliable. The estimation of the intracellular resistance led to the introduction of a new parameter (the ratio between the right and left intracellular resistances), which seems to provide useful information on the load to which the joints are subjected. Although we realize that much more experimentation is required to assess the reliability of the methodology we proposed, the results obtained so far are very encouraging and, in our view, demonstrate the effectiveness of the proposed measurement system and justify further investigation in this field. In fact, we want to point out that the work carried out so far does not intend to emphasize the medical interpretation of the results (although it seems to be reliable), for which a longer and in-depth experimentation is undoubtedly needed under the supervision of experts in the medical field, but on the effectiveness and the simplicity of the proposed instrumentation.
Author Contributions
Conceptualization, G.S.; methodology, G.S. and C.C.; software, C.C.; validation, G.S., C.C. and G.G.; formal analysis, G.S., R.G. and E.A.; investigation, G.S. and C.C.; data curation, E.C.; writing—original draft preparation, G.S. and C.C.; writing—review and editing G.G., E.C. and E.A.; visualization, R.G.; supervision, G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Ethical review and approval were waived for this study, because the proposed system is used without any connection to the mains, the measurements are no invasive, the procedure respects all the safety requirements of the standard IEC 60601-1 and there is no risk for users, whom have been duly informed about the experiment.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
The authors want to thank Silvia Federico and Alessio Solano for their kind availability and the positive discussions on the physiology of the knee.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nicolini, A.P.; de Carvalho, R.T.; Matsuda, M.M.; Sayum, J.F.; Cohen, M. Common injuries in athletes’ knee: Experience of a specialized center. Acta Ortop Bras. 2014, 22, 127–131. [Google Scholar] [CrossRef]
- Resta, P.; Presti, D.L.; Schena, E.; Massaroni, C.; Formica, D.; Kim, T.; Shin, D. A wearable system for knee flexion/extension monitoring: Design and assessment. In Proceedings of the IEEE International Workshop on Metrology for Industry 4.0 & IoT, Roma, Italy, 3–5 June 2020; pp. 273–277. [Google Scholar]
- Hootman, J.M.; Macera, C.A.; Ainsworth, B.E.; Addy, C.L.; Martin, M.; Blair, S.N. Epidemiology of musculoskeletal injuries among sedentary and physically active adults. Med. Sci. Sports Exerc. 2002, 34, 838–844. [Google Scholar] [CrossRef] [PubMed]
- Calmbach, W.L.; Hutchens, M. Evaluation of patients presenting with knee pain: Part I. History physical examination radiographs and laboratory tests. Am. Fam. Physician 2003, 68, 907–912. [Google Scholar] [PubMed]
- Friedman, L.; Finlay, K.; Jurriaans, E. Ultrasound of the knee. Skelet. Radiol. 2001, 30, 361–377. [Google Scholar] [CrossRef]
- Tsai, B.; Xue, H.; Birgersson, E.; Ollmar, S.; Birgersson, U. Dielectrical properties of living epidermis and dermis in the frequency range from 1 khz to 1 mhz. J. Electr. Bioimpedance 2019, 10, 14–23. [Google Scholar] [CrossRef]
- Rodríguez Timaná, L.C.; Castillo García, J.F. Characterization of people with type II diabetes using electrical bioimpedance. In AETA 2019—Recent Advances in Electrical Engineering and Related Sciences: Theory and Application. AETA 2019; Cortes Tobar, D., Hoang Duy, V., Trong Dao, T., Eds.; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2019; Volume 685. [Google Scholar]
- Arpaia, P.; Cesaro, U.; Frosolone, M.; Moccaldi, N.; Taglialatela, M. A micro-bioimpedance meter for monitoring insulin bioavailability in personalized diabetes therapy. Sci. Rep. 2020, 10, 13656. [Google Scholar] [CrossRef] [PubMed]
- Coates, J.; Chipperfield, A.; Clough, G. Wearable Multimodal Skin Sensing for the Diabetic Foot. Electronics 2016, 5, 45. [Google Scholar] [CrossRef]
- Nuñez, C.; Gallagher, D.; Visser, M.; Pi-Sunyer, F.X.; Wang, Z.; Heymsfield, S.B. Bioimpedance analysis: Evaluation of leg-to-leg system based on pressure contact footpad electrodes. Med. Sci. Sports Exerc. 1997, 29, 524–531. [Google Scholar] [PubMed]
- Kubicek, W.G.; Patterson, R.P.; Witsoe, D.A. Impedance cardiography as a noninvasive method of monitoring cardiac function and other parameters of the cardiovascular system. Ann. N. Y. Acad. Sci. 1970, 170, 724–732. [Google Scholar] [CrossRef]
- Zink, M.D.; König, F.; Weyer, S.; Willmes, K.; Leonhardt, S.; Marx, N.; Napp, A. Segmental bioelectrical impedance spectroscopy to monitor fluid status in heart failure. Sci. Rep. 2020, 10, 3577. [Google Scholar] [CrossRef]
- Jotta, B.; Coutinho, A.B.B.; Pino, A.V.; Souza, M.N. Lactate threshold by muscle electrical impedance in professional rowers. Rev. Sci. Instrum. 2017, 88, 045105. [Google Scholar] [CrossRef] [PubMed]
- Morais, A.P.; Pino, A.V.; Souza, M.N. Detection of questionable occlusal carious lesions using an electrical bioimpedance method with fractional electrical model. Rev. Sci. Instrum. 2016, 87, 084305. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.T.; Tai, C.C.; Chou, W.; Tang, S.T.; Lin, J.H. Analyzing the audio signals of degenerative arthritis with an electronic stethoscope. Rev. Sci. Instrum. 2018, 89, 085111. [Google Scholar] [CrossRef]
- Neves, E.B.; Pino, A.V.; Almeida, R.M.V.R.D.; Souza, M.N.D. Knee bioelectric impedance assessment in healthy/with osteoarthritis subjects. Physiol. Meas. 2010, 31, 207–219. [Google Scholar] [CrossRef]
- Alvarenga, R.L.; Souza, M.N. Assessment of knee osteoarthritis by bioelectrical impedance. In Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Cancun, Mexico, 17–21 September 2003; pp. 3118–3121. [Google Scholar]
- Hersek, S.; Töreyin, H.; Inan, O.T. A robust system for longitudinal knee joint edema and blood flow assessment based on vector bioimpedance measurements. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 545–555. [Google Scholar] [CrossRef]
- Shandhi, M.M.H.; Hersek, S.; Inan, O.T. A finite element model of knee electrical bioimpedance for facilitating edema quantification. In Proceedings of the IEEE EMBS International Conference on Biomedical & Health Informatics, Orlando, FL, USA, 16–19 February 2017; pp. 73–76. [Google Scholar]
- Hersek, S.; Toreyin, H.; Teague, C.N.; Millard-Stafford, M.L.; Jeong, H.-K.; Bavare, M.M.; Wolkoff, P.; Sawka, M.N.; Inan, O.T. Wearable vector electrical bioimpedance system to assess knee joint health. IEEE. Trans. Biomed. Eng. 2017, 64, 2353–2360. [Google Scholar] [CrossRef]
- MP150 System, Biopac Systems Inc. Available online: https://www.biopac.com/wp-content/uploads/MP150-Systems.pdf (accessed on 17 November 2020).
- USB Audio Board Behringer U-PHORIA UMC202HD. Available online: https://www.behringer.com/behringer/product?modelCode=P0BJZ (accessed on 17 November 2020).
- PortAudio Libraries. Available online: www.portaudio.com (accessed on 11 January 2021).
- Olson, W.H. Electrical safety. In Medical Instrumentation: Application and Design, 5th ed.; Wiley: New York, NY, USA, 2020; pp. 803–847. [Google Scholar]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gomez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.-C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef]
- Ciofi, C.; Scandurra, G.; Giusi, G. QLSA: A software library for spectral estimation in low-frequency noise measurement applications. Fluct. Noise Lett. 2019, 18, 1940004-1–1940004-12. [Google Scholar] [CrossRef]
- McAdams, E.; Jossinet, J.; Lackermeier, A.; Risacher, F. Factors affecting electrode-gel-skin interface impedance in electrical impedance tomography. Med. Biol. Eng. Comput. 1996, 34, 397–408. [Google Scholar] [CrossRef] [PubMed]
- Cole, K.S. Membranes Ions and Impulses: A Chapter of Classical Biophysics; University of California Press: Berkeley, CA, USA, 1968. [Google Scholar]
- Lukaski, H.; Moore, M. Bioelectrical impedance assessment of wound healing. J. Diabetes Sci. Technol. 2012, 6, 209–212. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef] [PubMed]
- Janssen, G. Die Chondropathia patellae als Prägonarthrose-Zur Atiologie und Therapie anhand von Ergebnissen nach Abrasio patellae [Chondropathy of the patella as pre-arthrosis of the knee. Its causes and treatment, based on results after “abrasio patellae” (author’s transl)]. Z. Orthop. Ihre Grenzgeb. 1974, 112, 1036–1044. [Google Scholar] [PubMed]
- Nero, P.; Nogueira, I.; Vilar, R.; Pimentão, J.B.; Branco, J.C. Identificação de cristais no líquido sinovialpor por microscopia eletrônica. Acta Reum. Port. 2006, 31, 75–81. [Google Scholar]
- Doherty, M.; Belcher, C.; Regan, M.; Jones, A.; Ledingham, J. Association between synovial fluid levels of inorganic pyrophosphate and short term radiographic outcome of knee osteoarthritis. Ann. Rheum. Dis. 1996, 55, 432–436. [Google Scholar] [CrossRef] [PubMed]
- Melo, R.G. O l’ıquido Sinovial. Acta Reum. Port. 2003, 28, 249–266. [Google Scholar]
- Webb, G.R.; Westacott, C.I.; Elson, C. Osteoarthritic synovial fluid and synovium supernatants up-regulate tumor necrosis factor receptors on human articular chondrocytes. Osteoarthr. Cartilage 1998, 6, 167–176. [Google Scholar] [CrossRef][Green Version]
- Primorac, D.; Molnar, V.; Rod, E.; Jeleč, Ž.; Čukelj, F.; Matišić, V.; Vrdoljak, T.; Hudetz, D.; Hajsok, H.; Borić, I. Knee Osteoarthritis: A Review of Pathogenesis and State-Of-The-Art Non-Operative Therapeutic Considerations. Genes 2020, 11, 854. [Google Scholar] [CrossRef]
- Goldring, S.R.; Goldring, M.B. Changes in the osteochondral unit during osteoarthritis: Structure, function and cartilage bone crosstalk. Nat. Rev. Rheumatol. 2016, 12, 632–644. [Google Scholar] [CrossRef] [PubMed]
- Musumeci, G. The Effect of Mechanical Loading on Articular Cartilage. J. Funct. Morphol. Kinesiol. 2016, 1, 154–161. [Google Scholar] [CrossRef]
- Vanwanseele, B.; Eckstein, F.; Knecht, H.; Spaepen, A.; Stüssis, E. Longitudinal Analysis of Cartilage Atrophy in the Knees of Patients with Spinal Cord Injury. Arthritis Rheum. 2003, 48, 3377–3381. [Google Scholar] [CrossRef]
- Mohan, K.R.; Raymer, G.H.; Moran, G.R.; Marsh, G.; Thompson, R.T. Changes in tissue water content measured with multiple-frequency bioimpedance and metabolism measured with 31P-MRS during progressive forearm exercise. J. Appl. Physiol. 2006, 101, 1070–1075. [Google Scholar]
- Damon, B.M.; Gregory, C.D.; Hall, K.L.; Stark, H.J.; Gulani, V.; Dawson, M.J. Intracellular acidification and volume increases explain R(2) decreases in exercising muscle. Magn. Reson. Med. 2002, 47, 14–23. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).