Planning and Research of Distribution Feeder Automation with Decentralized Power Supply

Abstract

The high penetration of distributed generation in distributed energy systems causes the variation of power loss and makes the power grid become more complicated, so this paper takes various types of optimal algorithms into account and simulates the feeder reconfiguration on the IEEE-33 system as well as the Taiwan power system. The simulation verifies linear population size reduction of successful history-based adaptive differential evolution (L-SHADE) and particle swarm optimization (PSO) fitness in different systems and provides the recommended location of distributed energy. The proposed method keeps the voltage bound of 0.95 to 1.03 p.u. of Taiwan regulation. In the IEEE-33 system, we achieved a 52.57% power loss reduction after feeder reconfiguration, and a 70.55% power loss reduction after the distributed generator was implemented and feeder reconfiguration. Under the variation of load demand and power generation of the Taiwan power system, we establish the system models by forecasting one-day load demand. Then, we propose a one-day feeder switch operation strategy by considering the switches’ operation frequency with the reduction of 83.3% manual operation and recommend feeder automation to achieve feeder power loss reduction, voltage profile improvement and get regional power grid resilient configuration.

1. Introduction

The huge and complicated power system will generate fault current when fault occurs, which will have an impact on the stability of power supply. The power system contains distributed power generation, which will cause dual current in different ways on the power system that influences the choice of protective relay. Most state-of-the-art technical skills and power system connection regulations are formulated to maintain the reliability of power transmission and improve the toughness of the power system.

Diversified feeder types were developed [1,2] to facilitate the switching of feeder switches in emergency situations, realize load transfer, stabilize the armature in the transmission and distribution area, enhance the strength of the power grid and improve power quality.

Feeder reconfiguration is one of the effective and common ways to improve power grid-resilient dispatch. In Reference [3], the author presents particle swarm optimization (PSO) for solving feeder reconfiguration of a distributed network with the objective of minimum power loss. Minimum spanning tree (MST) combined with binary particle swarm (BPSO) is presented in References [4,5], and the hybrid PSO with ant colony optimization (ACO) algorithm in Reference [6], to solve the power loss and unstable system voltage.

In recent years, due to the vigorous development of renewable energy, the scale and the number of solar farms have continued to increase. Therefore, the problem of distributed generator (DG) construction is not only to minimize power consumption, but also the need to consider DG grid-connected feeders. In Reference [3], the PSO is used to minimize the power loss of the feeder to select the DG capacity and location method, and Reference [7] used the water cycle algorithm for IEEE 33 bus and IEEE 69 bus to update the algorithm toward the same goal. In Reference [8], the author considers the dynamic distribution of feeders and increasing time dependencies and improving PSO and Grey Wolf Optimizer to complete the optimization calculation of operating costs. To achieve DG establishment optimization, Reference [9] considers the intermittent nature of DG and the energy storage system, then using loss sensitivity factor and multi-objective ant lion optimizer. Among them, it is seldom considered to add renewable energy generation and load-ahead power forecast to do the schedule planning of feeder reorganization. Because of the uncertainty and high proportion of renewable energy, it has a great relationship with the loss of the feeder. It is more significant to do the advance scheduling in practical applications.

This paper proposes size reduction of successful history-based adaptive differential evolution (SHADE) with the linear population size reduction (L-SHADE) algorithm and PSO math models with objectives of minimum power loss in a distributed system which contains distributed generation. By testing on the IEEE 33 standard system and verifying on the Taiwan power system, this paper analyzes the resiliently dispatchable power grid by considering the impact of the distributed generator capacity, establishment location, voltage variation and the load demand effect. According to feeder reorganization, it needs to consider the characteristics of feeder switch reorganization, and combines multiple variables (feeder load, feeder resistance, feeder reactance, etc.) with optimization algorithms. After many iterations, complex high-dimensional problems have been completed according to grid standards. The related and commonly used optimization algorithms [10,11,12,13,14,15,16], including PSO with a rich history of operations [14] and the SHADE with linear population size reduction algorithm improved by differential evolution (DE) [12], were implemented in the feeder reorganize simulation and analysis. Also, L-SHADE has obtained the best configuration of high-output power generation in the discrete optimization problems of the generator configuration of wind power plants [17] and has a significant compensation improvement in optimizing the harmonic parameters of the design circuit [18].

The rest of this paper is organized as follows. In Section 2, reconfiguration problem constraints will be introduced. In Section 3, there are mathematical models of the proposed algorithm L-SHADE and PSO. In Section 4, the optimal algorithms combined with feeder reconfiguration analysis in various scenarios will be compared. Finally, the conclusion in Section 5 will summarize the optimal feeder reconfiguration scheduling.

2. Reconfiguration Problems

2.1. Distributed Generation Characteristics

In the Taiwan power system, there are 17 distributed generators which are all photovoltaic (PV) generation and connected to the distributed network system. The generation characteristics are shown in Table 1.

Table 1. Distributed energy generation characteristics.

Challenge	Statements
Intermittent generation	Time of generation peak is different with peak of load demand so takes the shape of duck curve.
Generation non-smoothing	The severe variation easily makes system voltage and current unstable.
Lack of system inertial	In the severe power accident, generation equipment has no time to respond, and is then disconnected.
Fault current	The fault current comes from the main transformer and distributed generation will cause feeder breaker lack of breaking capacity and increase short current.
Power reverse transmission	Comparing with the single way of electricity transmission before, the multiple transmission ways will easily cause main transformer power reverse transmission.

According to the different irradiance in a day, the generation function per square meter is shown in (1) by Meteorological Information-Based Green Energy Operations Center and power generation records in the Taiwan power company.

$$Pt=SSR\times \eta$$

(1)

where $SSR$ is the amount of irradiance observed by the satellite and $\eta$ is PV panel transformation efficiency.

Considering the PV generation curve and PV panels’ power transformation, this paper simulates the sum of the PV capacity, which is 3057.7 kW, changing in proportion on the day of 20 June 2020.

2.2. Feeder Reconfiguration Constraints

2.2.1. Feeder Current Constraints

In order to keep the power system under normal operation in a distributed network, the various feeder current limits are shown in Table 2.

Table 2. Distributed system feeder current limits.

Type		Wire Diameter	Tolerable Max Current
Underground Cable	Main Feeder	500 MCM	600 A
	Branch	#1 AWG	200 A
Overhead lines	Main Feeder	477 MCM	590 A
	Branch	#2 AWG	165 A

In the simulation, the current of each branch should be less than or equal to the maximum current so that the feeder can tolerate it, as shown in Equation (2). In order to cooperate with the load current on the feeder, which will not exceed the maximum limit when the feeder emergency load transformation occurs, we limit the current variation as in Equation (3).

$$\left|I_{i,i+1}\right|\le \left|I_{i,i+1(max)}\right|$$

(2)

$$△I_{xy}=\frac{V_x-V_y}{R_{loop}+j{X}_{loop}}$$

(3)

Here, $\left|I_{i,i+1(max)}\right|$ is the maximum current between bus $i$ and bus $i+1$, $△I_{xy}$ is the current variation which passes through the feeder, and $V_x$ as well as $V_y$ are voltage at both ends of the feeder. Lastly, $R_{loop}$ and $j{X}_{loop}$ are the impedance of the feeder.

2.2.2. Voltage Variation

During the normal operation, the voltage should maintain the voltage variation in Equation (4), in order to keep the power system in the stable condition:

$$U_{imin} \le U_i\hspace{0.33em}\le \hspace{0.33em}{U}_{imax}$$

(4)

The lowest limit of the feeder voltage variation is $U_{imin}$ (here is 0.95 p.u.), and the highest limit of the feeder voltage variation is $U_{imax}$ (1.03 p.u.), whereas $U_i$ is the voltage difference between the two busses.

2.2.3. Reverse Power Limit

In the IEEE system, this paper assumes the maximum capacity of the distributed generation, which on the feeder is 70% of the load demand, with a view to making sure it is under the reverse current limit. The control limit considers the rated capacity of the main transformer to achieve the balance of supply as well as demand, and meanwhile, keep the system operation stable.

2.2.4. Radial Network

The power system will keep the radial network before and after the feeder reconfiguration to avoid the isolated islands or even the power system shut down. The simulation excludes the feeder switch which could not compose the radial network. By reconfiguring the rest feeder switch iteratively, as shown in (5), we can make sure the system keeps the radial network in the normal operation.

$$g_k \in G_k$$

(5)

In each feeder, $g_k$ is one of the radial feeders after feeder reconfiguration, and $G_k$ is the combination of all types of radial feeder.

3. Optimal Algorithm Math Models

This section describes the math models of L-SHADE and PSO. We first describe L-SHADE, which is modified DE. Contrary to L-SHADE, PSO has rich calculation history which is suitable to solve feeder reconfiguration.

3.1. L-SHADE Optimal Algorithm

L-SHADE is improved by DE, which is called adaptive DE with linear population size reduction [19,20]. In the DE algorithm, the calculation steps are initialization, mutation, reconfiguration (crossover) and selection. According to DE characteristics, it developed the SHADE algorithm and used two corresponding variables, which are the scaling factor (F) and the cross rate (CR), to search in the historic data. Then, SHADE developed into L-SHADE which combined the DE algorithm while linearly reducing the searching population after each iteration to decrease the calculation time.

3.1.1. Initialize Population

In Equation (6), the variable i is selected from 1 to the population size (NP), which is the searching population ($i\in [1, \mathrm{NP}]$), and the variable j is selected from 1 to D, which represents the calculation dimension ($j\in [1, \mathrm{D}]$). We usually set j to the number of the control variables in calculation with the upper limit $x_j^{\max }$ as well as the lower limit $x_j^{\min }$. In order to maintain diversity, $ran{d}_{i,j}[0,1]$ is the variable selected randomly from 0 to 1.

$$x_{i,j}^{(0)}=x_j^{\max }+ran{d}_{i,j}[0,1](x_j^{\max }-x_j^{\min })$$

(6)

3.1.2. Mutation

During the algorithm, each difference will cause the mutation vector in (7) by selecting two unequal vectors and combined with the scaling factor (F) (when a target vector is replaced by a trial vector, the target vector will be added into the archive). However, the calculation should ensure that $x_{R_1^i}^{(G)}$ and $x_{R_2^i}^{(G)}$ are different individuals:

$$V_i^{(G)}=x_i^{(G)}+F_i^{(G)}\cdot (x_{pbest}^{(G)}-x_i^{(G)})+F_i^{(G)}\cdot (x_{R_1^i}^{(G)}-x_{R_2^i}^{(G)})$$

(7)

As shown in (7), $R_i^1$ and $R_i^2$ are two of the variables which are mutually exclusive, selected from the range of [1, NP]. $x_i^{(G)}$ is one of the random individuals, and $x_{pbest}^{(G)}$ is the other individual selected from the contemporary population. While G means the $G$th generation, $F_i^{}$ represents the scaling factor applied on the $i$th individual for scaling at the $G$th.

3.1.3. Parameter Adaption

In each generation, the offspring will vary by the new scaling factor and the cross rate from (8) and (9):

$$F_i^{(t)}=randc(\mu F_r^{(t)}, 0.1)$$

(8)

$$C{R}_i^{(t)}=randn(\mu C{R}_r^{(t)}, 0.1)$$

(9)

The two are randomly selected from the standard distribution and the Cauchy distribution. In each generation, when there is a better generation, the original CR as well as F will be recorded as $S_{CR}$ and $S_F$. After each iteration, $\mu CR$ and $\mu F$ will be renewed, as in (10) and (11):

$$\mu CR=(1-c)\cdot \mu CR+c\cdot mea{n}_A(S_{CR})$$

(10)

$$\mu F=(1-c)\cdot \mu F+c\cdot mea{n}_L(S_F)$$

(11)

$c$ is learning factor which is usually 0.1, $mea{n}_A$ is arithmetic mean and $mea{n}_L$ is known by Lehmer Mean, which is calculated as in Equation (12):

$$mea{n}_L(S_F)=\frac{{\displaystyle \sum _{F\in S_F}^{}{F}^2}}{{\displaystyle \sum _{F\in S_F}^{}{F}^{}}}$$

(12)

3.1.4. Reconfiguration (Crossover)

By means of mutation, the mutation vector $V_i^{(G)}$ will combine with objective vector $x_i^{(G)}$ to take the shape of the next variable vector $u_{i,j}^{(G)}$, shown in (13):

$$u_{i,j}^{(G)}=\left\{{}_{ x_{i,j}^{(0)}, otherwise.}^{v_{i,j}^{(G)}, if j= j_{rand} or ran{d}_{i,j} [1,0) CR{ }_i^{ (G)},}\right.$$

(13)

to generate the new vector and create diversity. In (13), $j_{rand}$ is a random value in 1 to D, where D represents the problem dimension.

3.1.5. Selection

If the performance of the offspring is better than the parent, it will replace into objective vectors in (14):

$$x_{i,j}^{(G+1)}=\left\{{}_{ x_{i,j}^{(G)}, otherwise.}^{u_{i,j}^{(G)}, if f(u_{i,j}^{(G)}) f(x_{i,j}^{(G)}),}\right.$$

(14)

Function F means the function to get the minimum objective. When the new offspring performance is less than or equal to the value of the objective function, it will substitute for the objective vector in the next iteration.

3.1.6. Linear Population Size Reduction Technique

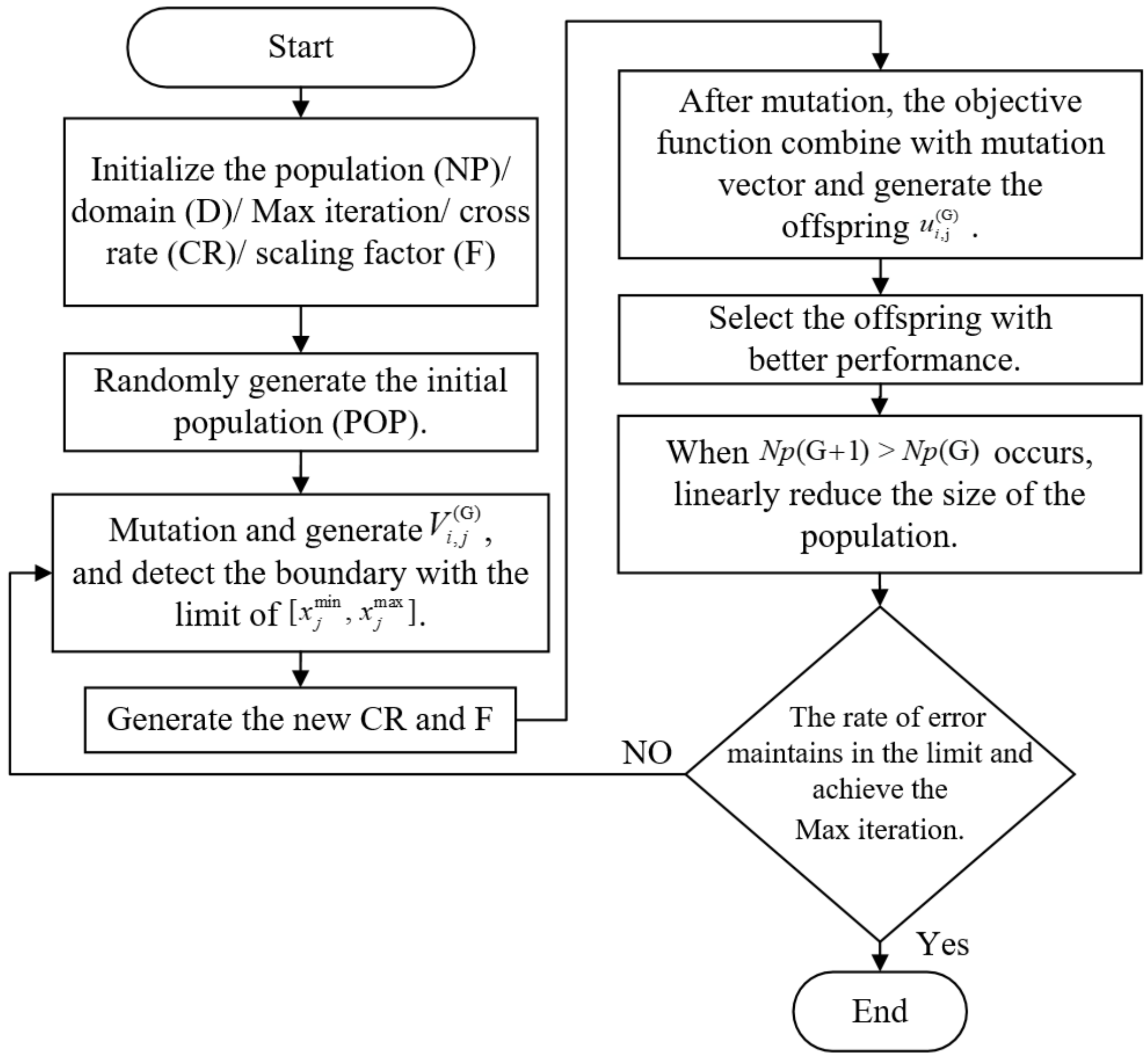
To speed-up the process of the calculation, after every generation iteration, the size of $G+1^{th}$ is NP (G + 1) in (15) for decreasing the range of the searching population. We usually set $N{p}_{\min }$ to 4 because the variables in the mutation process are 4. NFE is the number of fitness evaluations. If $Np (G+1)>Np (G)$, the difference from $(Np (G)-Np (G+1))$ will be deleted. The L-SHADE optimal algorithm simulation procedure is shown in Figure 1.

$$Np(G+1)=round [(\frac{N{p}_{\min }-N{p}_{ini}}{NF{E}_{\max }})\cdot NFE+N{p}_{ini}]$$

(15)

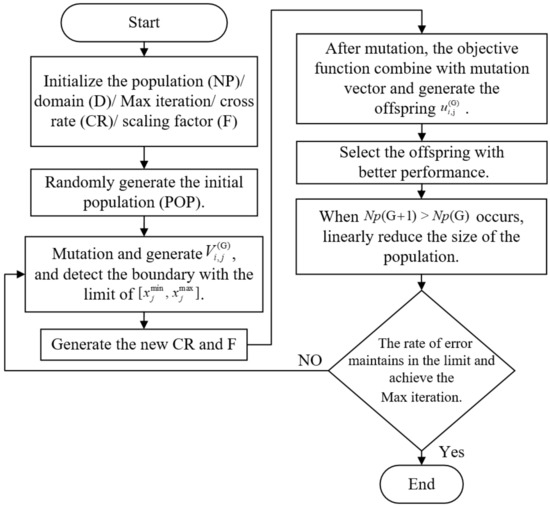
Figure 1. L-SHADE optimal algorithm simulation procedure.

Function F means the function to get the minimum objective. When the new offspring performance is less than or equal to the value of the objective function, it will substitute for the objective vector in the next iteration.

3.2. PSO Optimal Algorithm

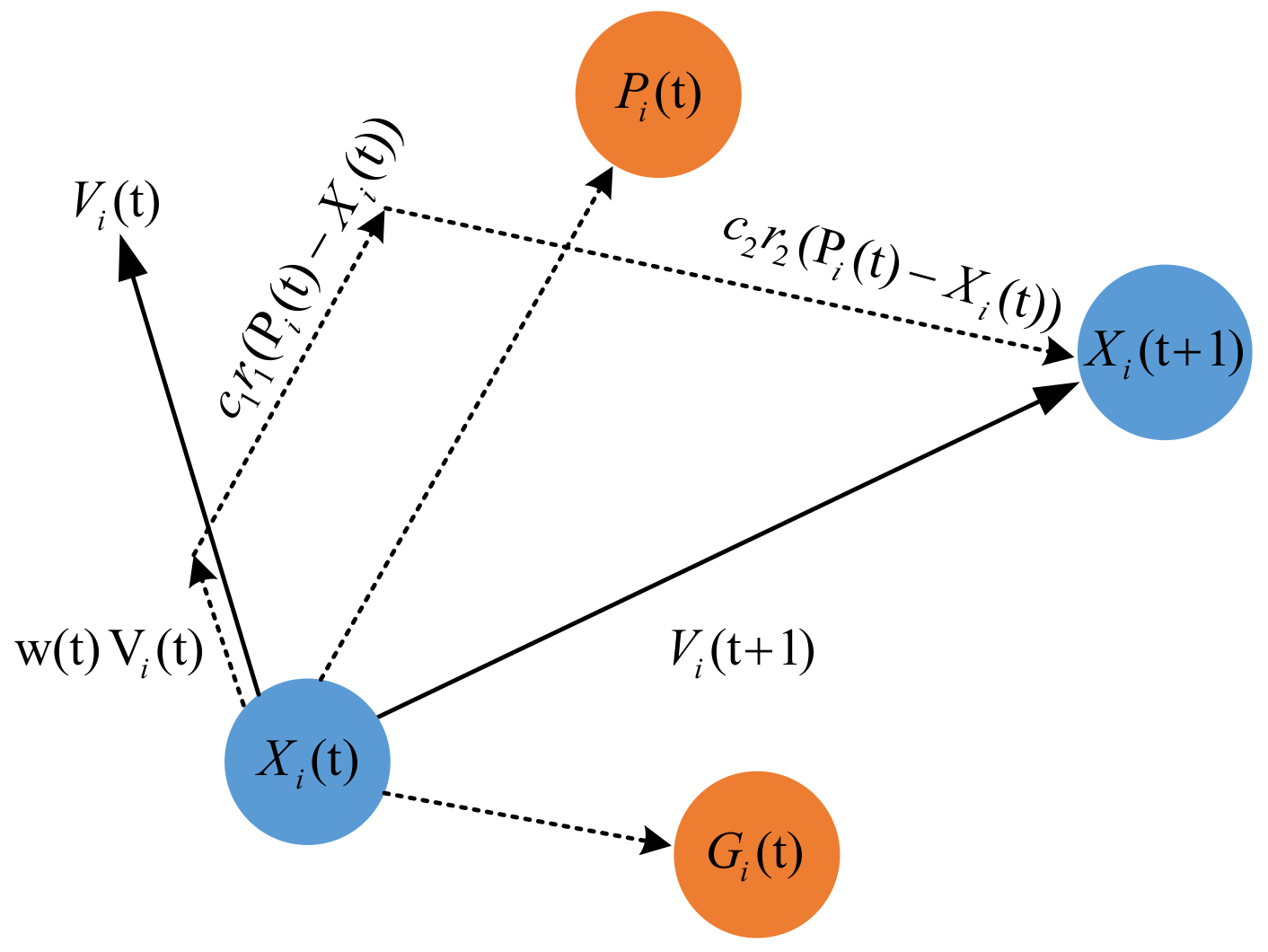
The PSO optimal algorithm iteration math model is as shown in Figure 2. The initial variables contain searching domain (D), the best position of individual particle ($pbest$), the best position of current swarm particles ($gbest$) and maximum iteration times ($ite{r}_{\max }$). The $i^{th}$ particle and velocity are given by (16) and (17).

$$x_i=(x_{i1}, x_{i2}, x_{i3},\dots ,x_{iD})$$

(16)

$$v_i=(v_{i1}, v_{i2}, v_{i3},\dots ,v_{iD})$$

(17)

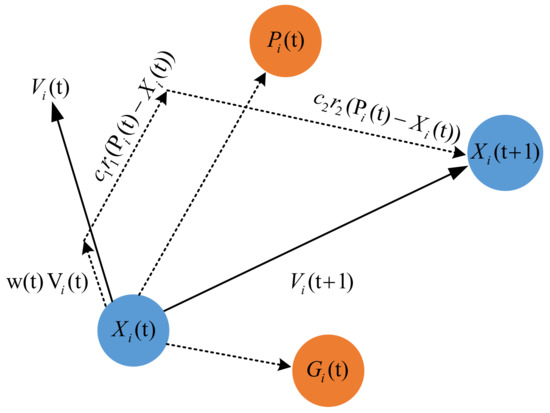
Figure 2. PSO algorithm math models.

The iteration velocity of every step of the particle evolution is defined as in (18), and the new position after iteration is defined as in Equation (19):

$$v_{ij}^{(i+1)}=w\cdot v_{ij}^{(t)}+c_1\cdot r\cdot (pbest-x_{ij}^{(t)})+c_2\cdot r\cdot (gbest-x_{ij}^{(t)})$$

(18)

$$x_{ij}^{(t+1)}=x_{ij}^{(t)}+v_{ij}^{(t+1)}$$

(19)

where $v_{ij}^{(t)}$ is the velocity of the $i^{th}$ particle in the $t^{th}$ iteration, $x_{ij}^{(t)}$ is the position of the $i^{th}$ particle in the $t^{th}$ iteration, $c_1$ and $c_2$ are the learning factors and w is the weight, with the calculation as shown in Equation (20):

$$w=w_{\max }-iter\cdot \frac{w_{\max }-w_{\min }}{ite{r}_{\max }}$$

(20)

The time of the iteration is $iter$, and $w_{\max }$ as well as $w_{\min }$ are the upper and lower limits of the weight. The learning factor $c_1$ will impact the learning efficiency of the particle, and $c_2$ will impact the learning efficiency of the population. The bigger the $w$, the wider range the particle will search to get the global optimal point. On the contrary, the smaller the $w$, the result will get closer to the local optimal point.

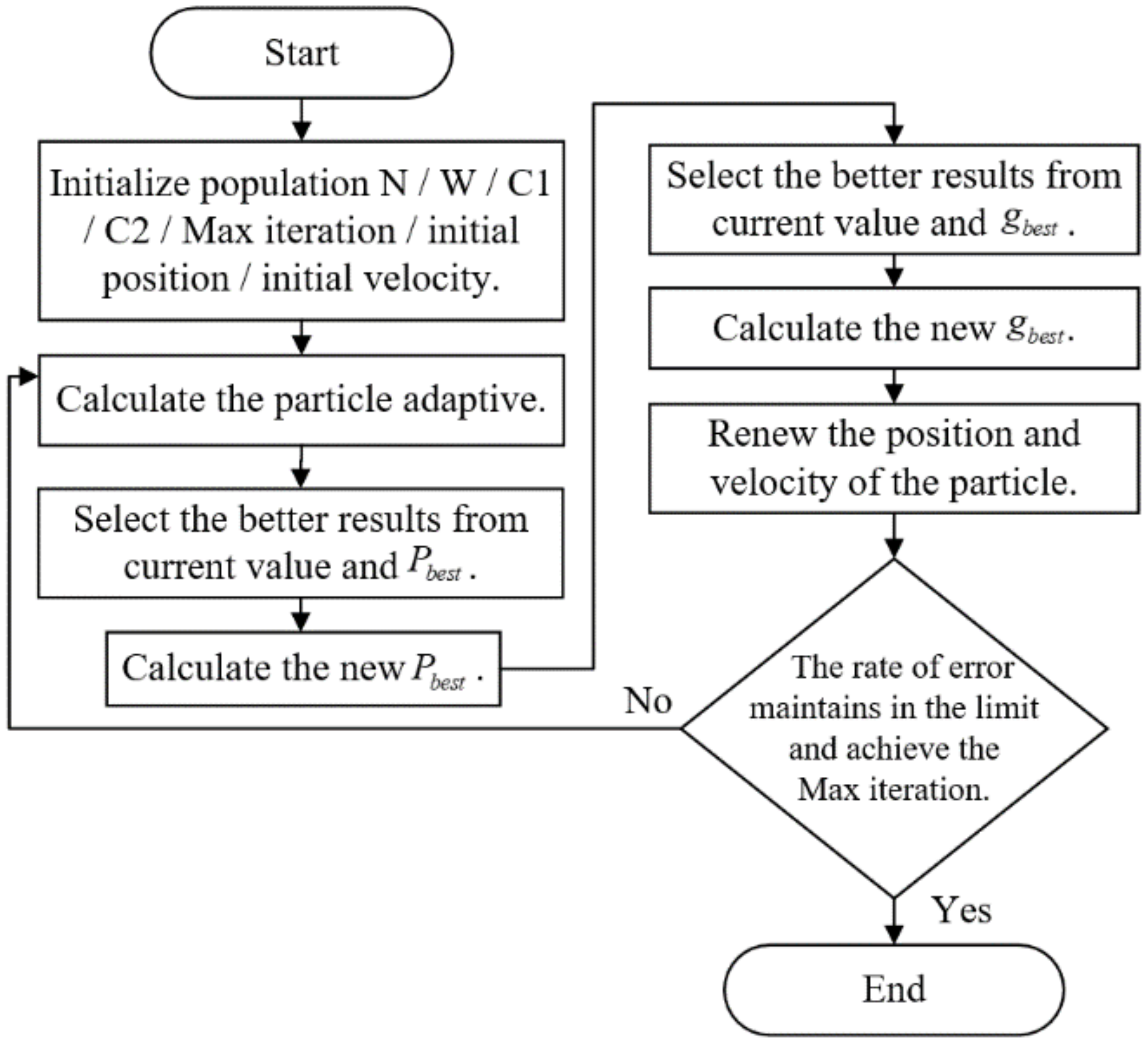
$G_i(t)$ is the best position of the group after training, and $P_i(t)$ is the best position of the individual after training. Before training, $X_i(t)$ is the initial position of the individual particle, $X_i(t+1)$ is the next position after training, $V_i(t)$ is the initial velocity of particle movement and $V_i(t+1)$ is the velocity of particle movement after iteration. The simulation procedure of the PSO optimal algorithm is shown in Figure 3.

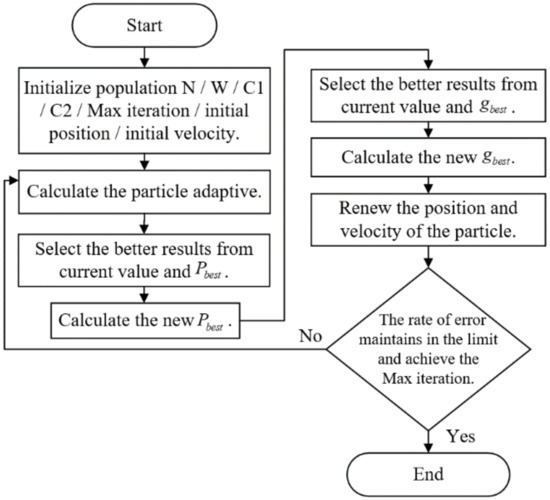
Figure 3. PSO optimal algorithm simulation procedure.

3.3. Objective Function

After the iteration, the objective function of the feeder reconfiguration is to get the feeder configuration with the minimum power loss, as presented in (21):

$$\min P_{loss}={\displaystyle \sum _{i=0}^n\frac{P_i{}^2+Q_i{}^2}{U_i{}^2}{k}_i{r}_i}$$

(21)

Here, $i$ indicates the number of branches in the system feeder, $n$ is the summation of the branch number and $k_i$ presents the switch condition of the branch $i$, in which zero means the switch turns off. By calculating the feeder branch resistance $i$, active power $P_i$, reactive power $Q_i$ and the voltage $U_i$ on the feeder, we can obtain the power loss of the system feeder.

4. Case Study

4.1. System Parameter Definition

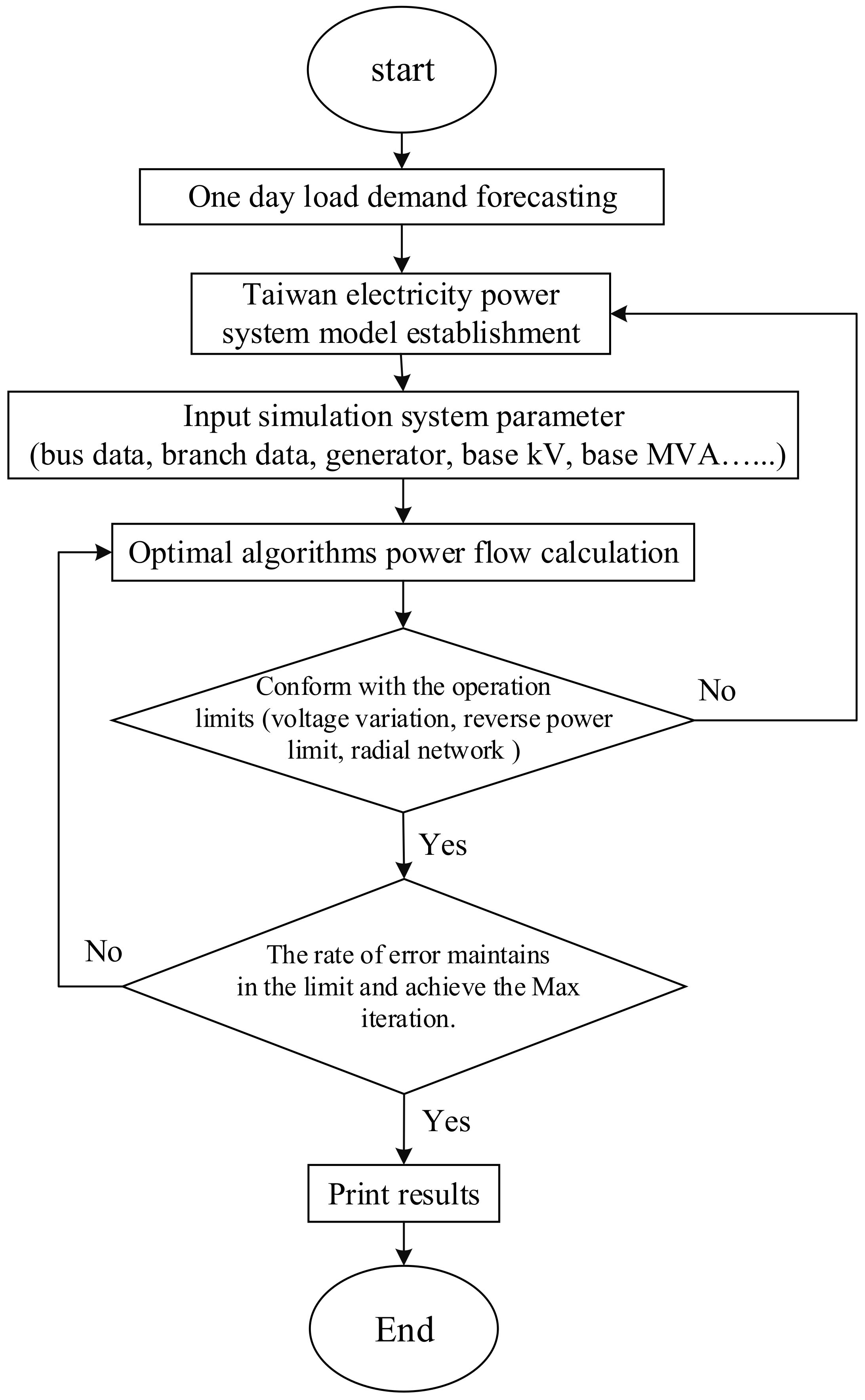
There are three systems in this paper, as shown in Table 3. This paper compared L-SHADE and PSO in three different systems with MATLAB using MATPOWER to calculate the power flow integrated with an optimal algorithm. The flow chart is shown in Figure 4.

Table 3. Scale of the three systems.

System	IEEE 33 [21]	Taiwan Case 1 System	Taiwan Case 2 System
Apparent power (MVA)	100	25	25
System voltage (kV)	12.66	11.4	11.4
Total of system load demand	3715 kW + 2300 kvar	1471.6 kW + 483.7 kvar (one-day average)	2745.6 kW + 902.4 kvar (one-day average)
Branch number	37	78	134
Node number	32	73	126
Tie switch number	5	5	8

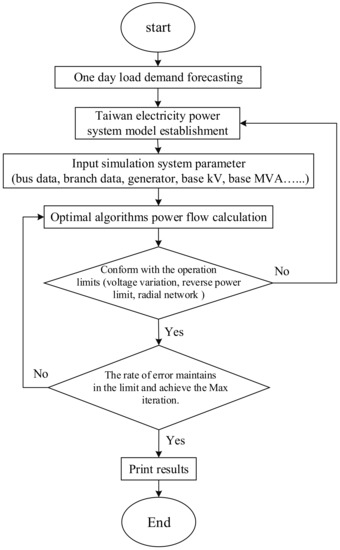
Figure 4. Flow chart.

4.2. Optimal Reconfiguration Analysis

4.2.1. IEEE 33 System Background

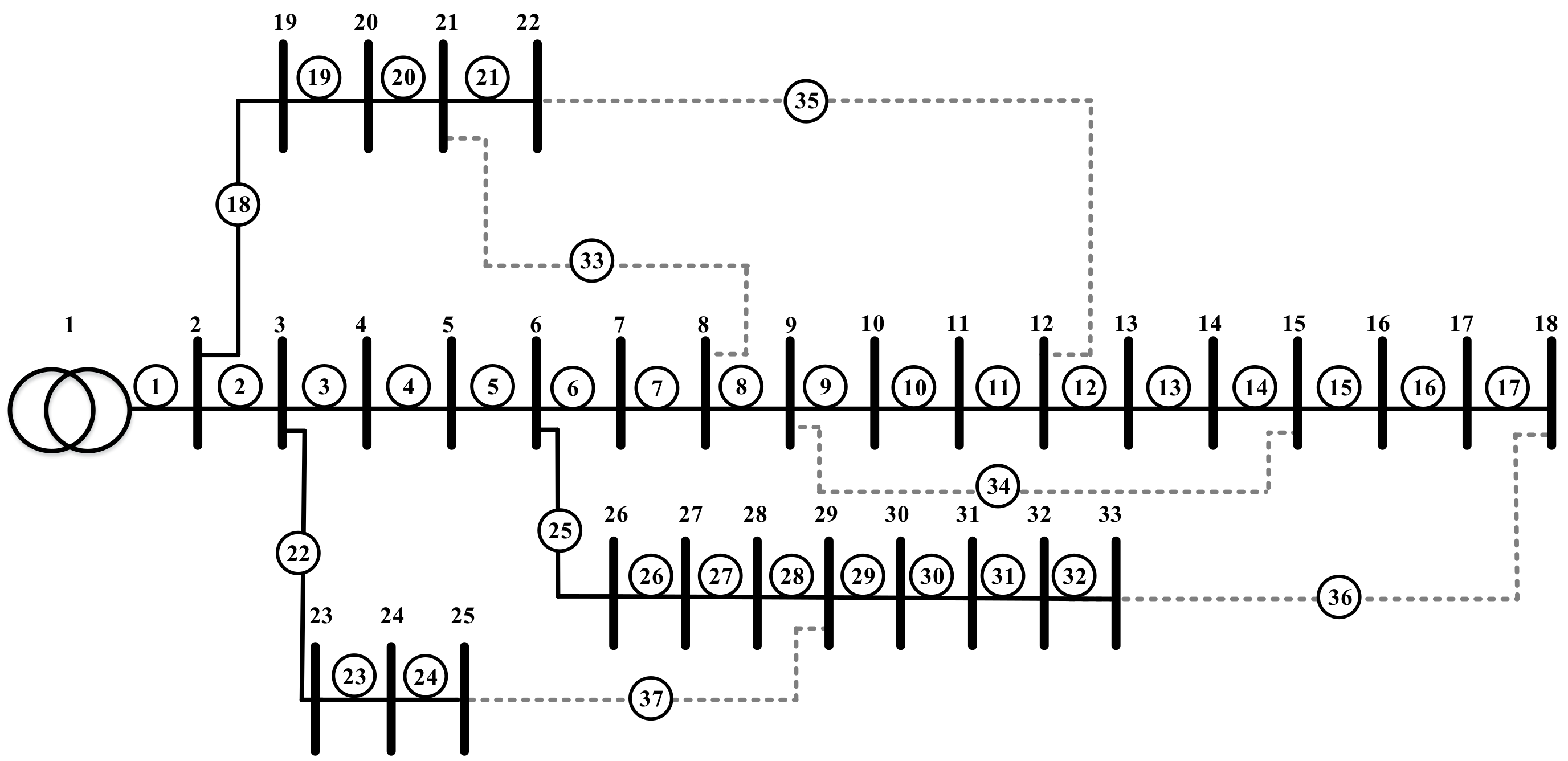
The standard IEEE 33 system is shown in Figure 5. To correspond to the radial network, there are five tie switches, which are often open in the IEEE 33 system.

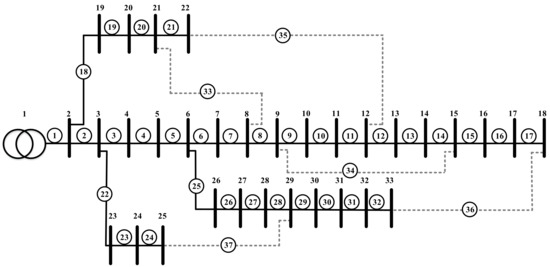
Figure 5. IEEE 33 system feeder.

4.2.2. IEEE 33 Feeder Reconfiguration

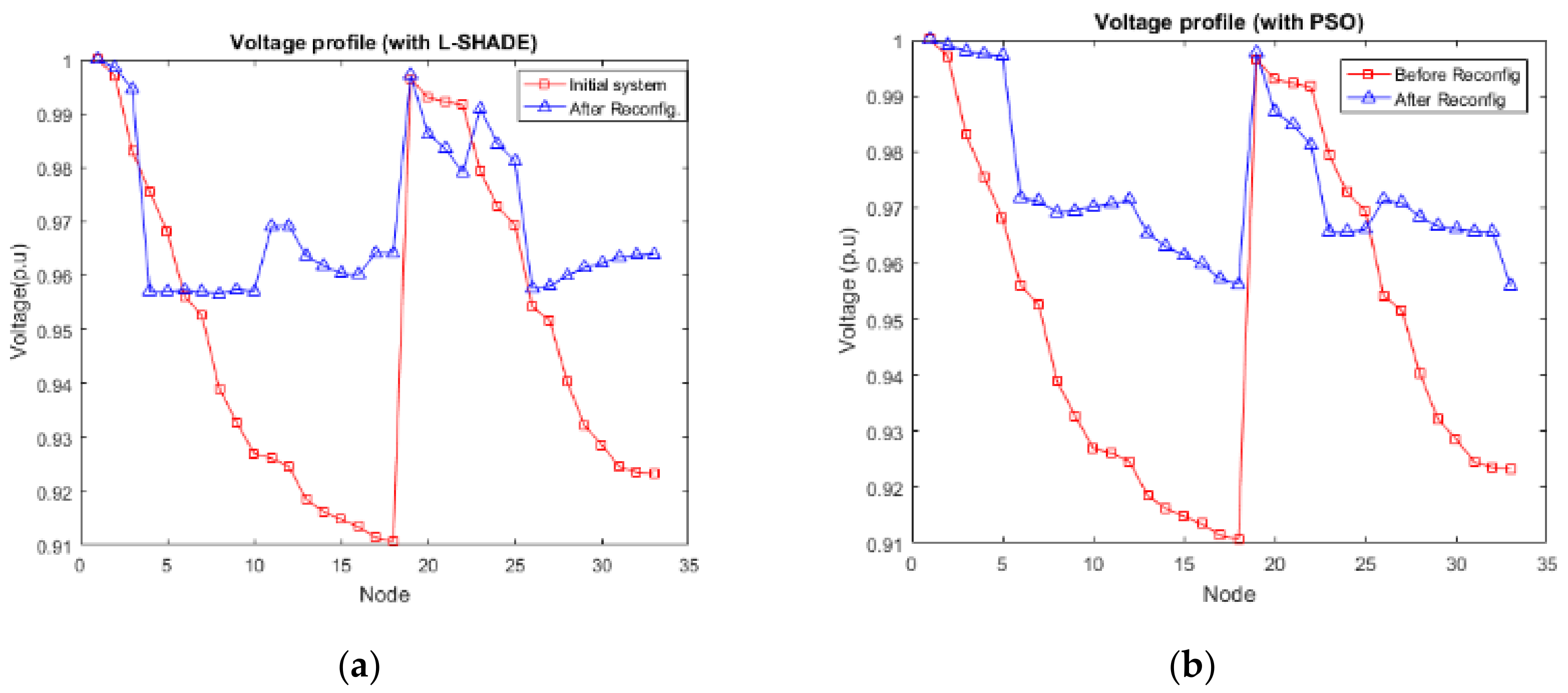
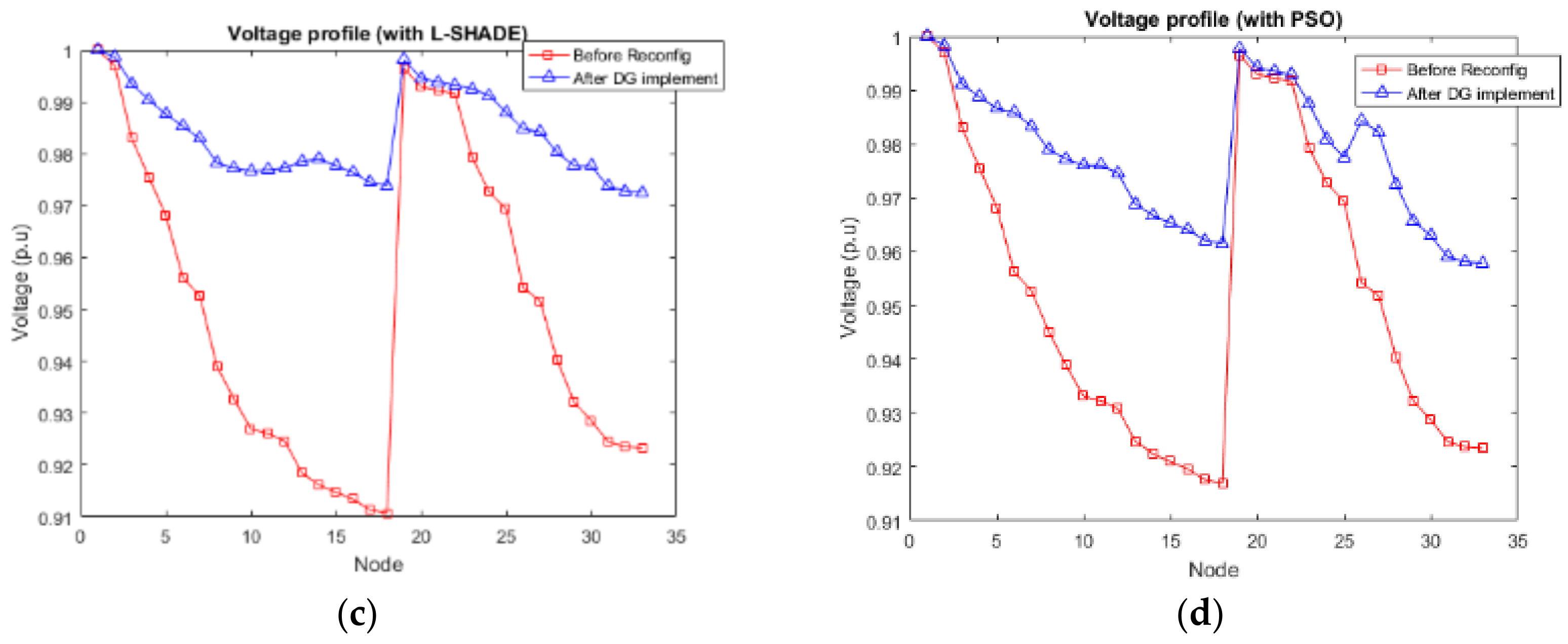
Table 4 summarizes the results obtained with L-SHADE and PSO algorithms in the IEEE 33 node test feeder. By confirming the voltage distribution, it is significant to the stability of the system, as shown in Figure 6 and Figure 7 in different scenarios.

Table 4. Results obtained after execution of the L-SHADE and PSO algorithms in the IEEE 33 node test feeder.

Scenario	Statement	L-SHADE	PSO
Before feeder reconfiguration (Initial System)	Tie switches	33, 34, 35, 36, 37	33, 34, 35, 36, 37
	Power loss (kW)	202.68	202.68
	Power loss reduction percentage (%)	–	–
	Min voltage (bus number)	0.91075 p.u. (18)	0.91075 p.u. (18)
After feeder reconfiguration	Tie switches	3, 10, 16, 33, 37	5, 22, 32, 33, 34
	Power loss (kW)	96.1344	150.6883
	Power loss reduction percentage (%)	52.57	25.65
	Min voltage (bus number)	0.95657 p.u. (8)	0.95603 p.u. (33)
After DG*3 implementation (keep initial system)	Tie switches	33, 34, 35, 36, 37	33, 34, 35, 36, 37
	Power loss (kW)	72.5447	90.7069
	DG capacity (kW) (bus number)	751 (14) 926 (24) 1021 (30)	1220 (6) 650 (11) 200 (30)
	Power loss reduction percentage (%)	64.21	55.25
	Min voltage (bus number)	0.9726 p.u. (33)	0.9578 p.u. (33)

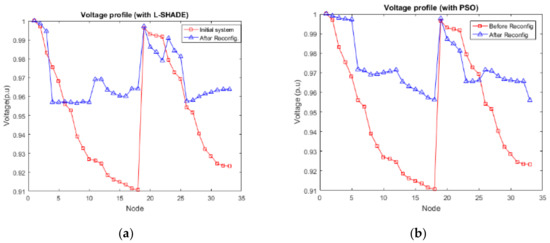
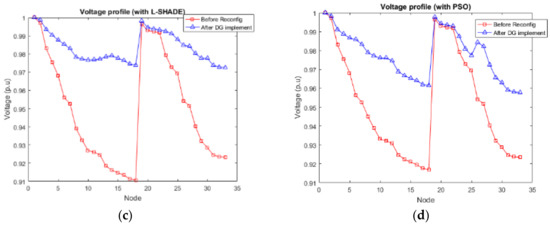
Figure 6. (a) Voltage profile before and after reconfiguration. (b) Voltage profile before and after reconfiguration. (c) Voltage profile after DG implementation. (d)Voltage profile after DG implementation.

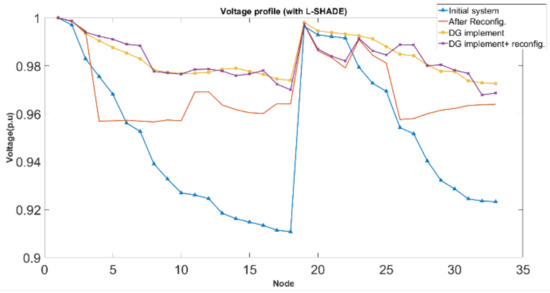
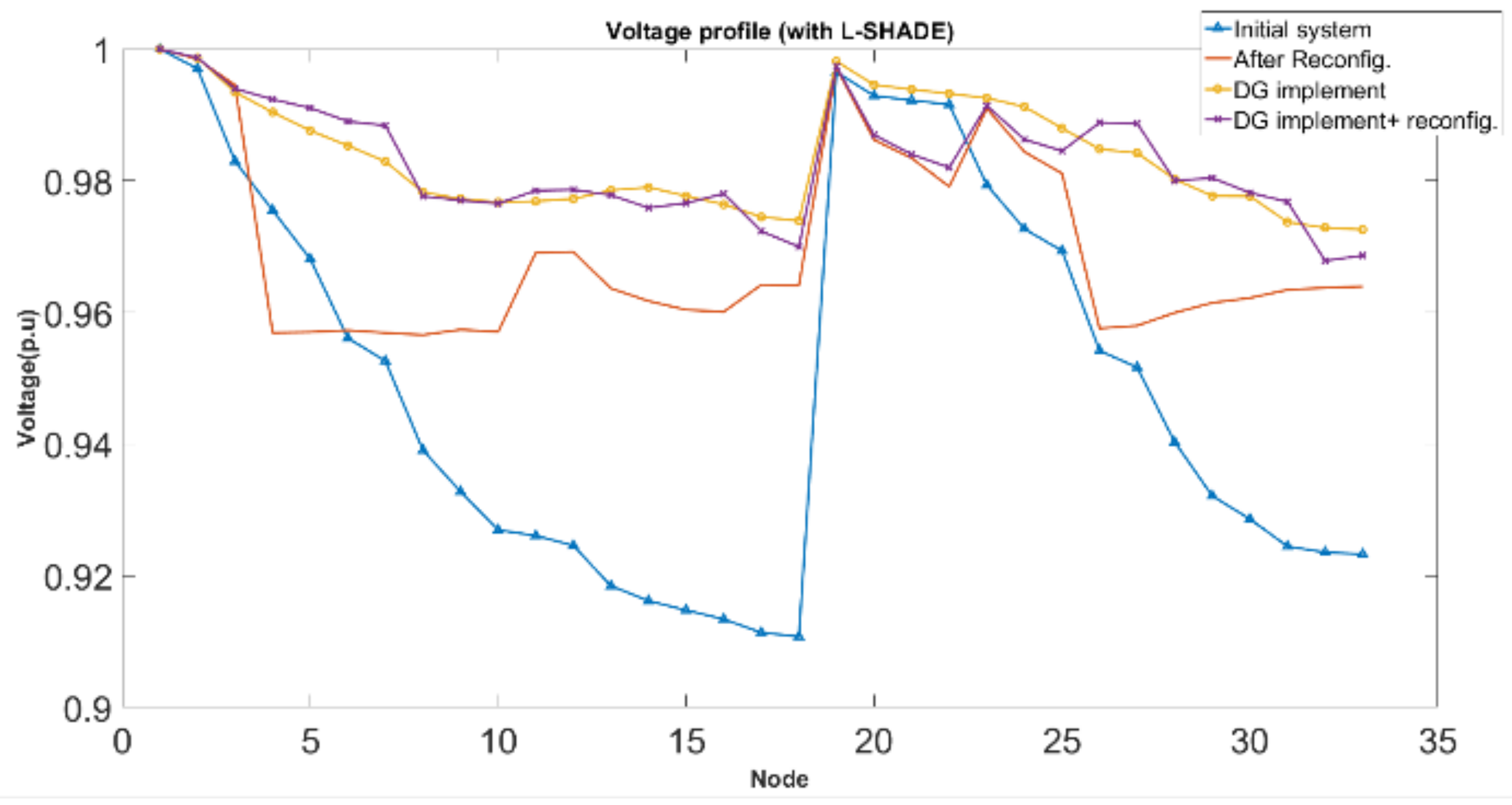
Figure 7. Various feeder bus voltage profile patterns.

In the four different scenario simulations in Figure 7, the power loss reduction percentage could reach up to 70.55% of the IEEE 33 system after DG implementation and feeder reconfiguration, with the tie switches as 6, 10, 12, 27 and 30 and the minimum voltage pf 0.967842 p.u. at bus number 32.

4.3. Impact by Load Variation to the Feeder Switch

4.3.1. Taiwan Case 1 System Background

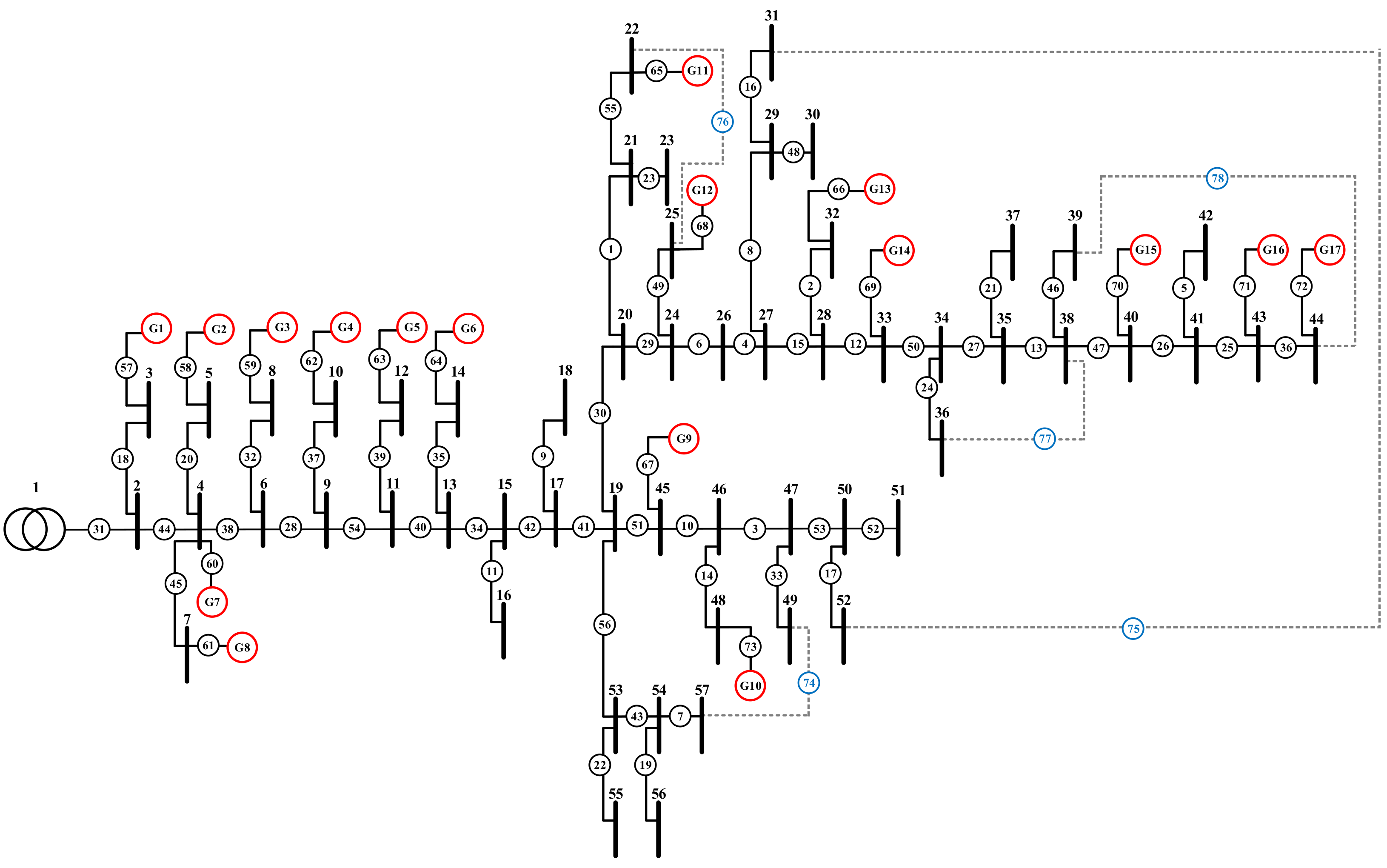
As above, in the IEEE 33 standard test system, we tested the reliability of L-SHADE and PSO optimal algorithms in feeder reconfiguration. Then, we verified two of the algorithms in the Taiwan case 1 system, as shown in Figure 8, and analyzed the impact of the load variation to the feeder switch from light-load to overload.

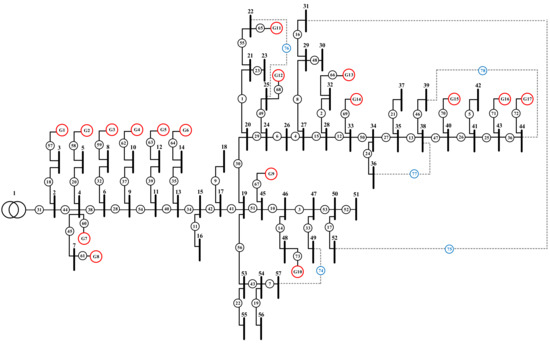
Figure 8. Taiwan case 1 system network with renewable energy sources present.

4.3.2. Taiwan Case 1 Feeder Reconfiguration

In this area, there are numerous households, but no large-scale load demands of the factory. By considering the rapid change at 4:00, 12:00 and 20:00 o’clock respectively, the control variables are the active power as well as reactive power (load demand) in each hour, the condition of the feeder switch and the domain of the calculation is set to eight. The results in Table 5 show the minimum voltage profile and the power loss after simulation with L-SHADE and PSO algorithms.

Table 5. Results obtained after execution of the L-SHADE and PSO algorithms in the Taiwan case 1 system.

Scenario	Statement	Initial system	L-SHADE	PSO
After reconfiguration at 4:00	Tie switches	74, 75, 76, 77, 78	12, 17, 26, 30, 33	6, 10, 24, 30, 47
	Power loss (kW)	13.4505	3.7289	12.3869
	Power loss reduction percentage (%)	–	72.2769%	7.9075%
	Min voltage (bus number)	0.9989 p.u. (18)	0.9991 p.u. (49)	0.9990 p.u. (18)
After reconfiguration at 12:00	Tie switches	74, 75, 76, 77, 78	17, 33, 50, 76, 78	4, 24, 30, 33, 47
	Power loss (kW)	9.9062	9.1997	9.8512
	Power loss reduction percentage (%)	–	7.1319%	0.5552%
	Min voltage (bus number)	0.9992 p.u. (18)	0.9990 p.u. (49)	0.9991 p.u. (18)
After reconfiguration at 20:00	Tie switches	74, 75, 76, 77, 78	17, 24, 30, 33, 78	3, 6, 24, 26, 30
	Power loss (kW)	31.5766	9.3244	31.9362
	Power loss reduction percentage (%)	–	70.4705%	−1.1388%
	Min voltage (bus number)	0.9982 p.u. (18)	0.9987 p.u. (49)	0.9981 p.u. (18)

The Taiwan case 1 system simulation showed two results: in the voltage profile, both L-SHADE and PSO could maintain the minimum voltage in the constraints, while L-SHADE could keep voltage distribution more stable than PSO. In the power loss, L-SHADE efficiently lowered the power loss compared to the initial system and the simulation of PSO from light-load to overload. As a result of the above-mentioned results, the next simulation will mainly use L-SHADE to raise the efficiency of the power grid transmission.

4.3.3. Taiwan Case 2 System Background

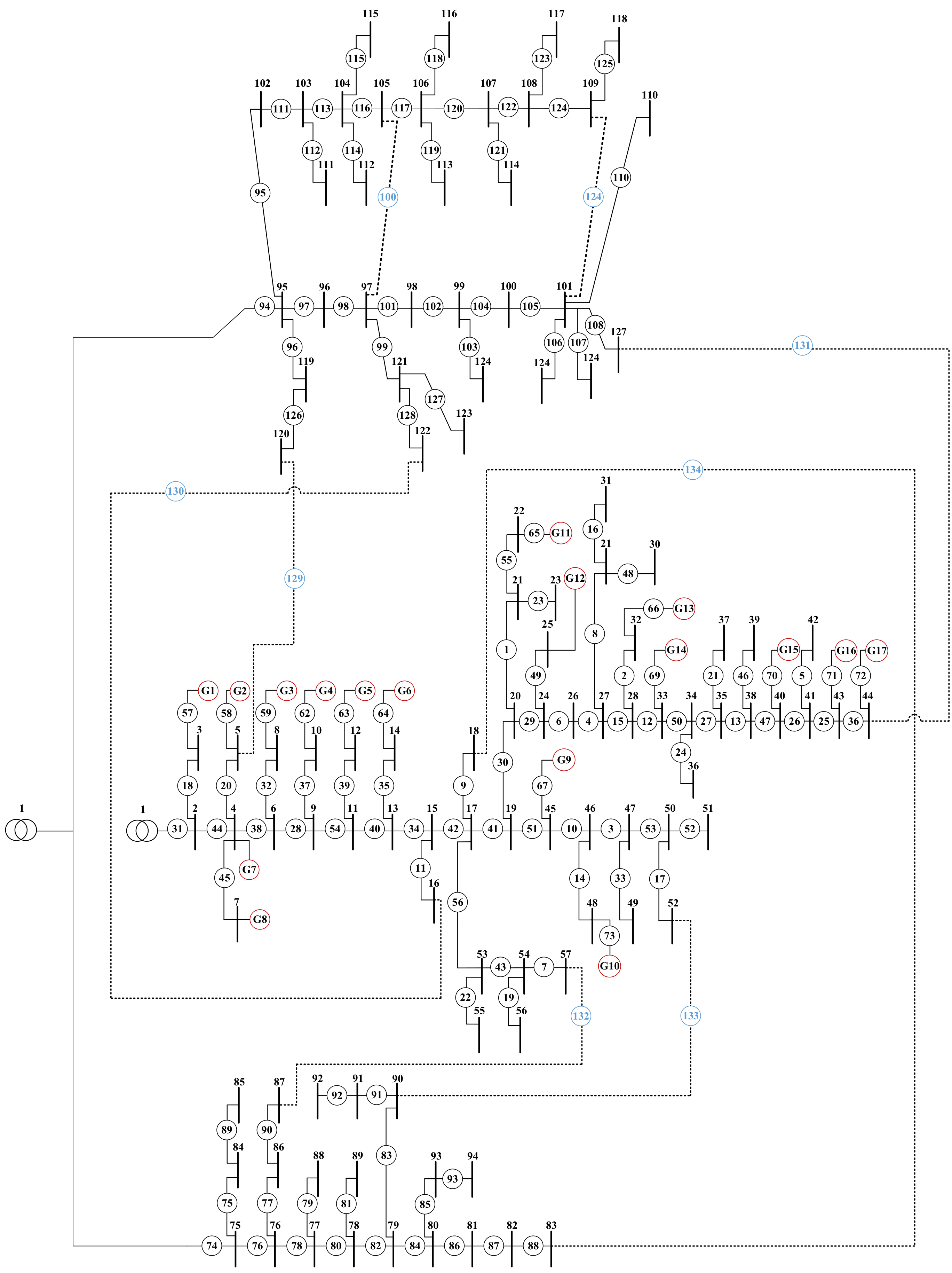
Combined with feeders in neighboring areas, L-SHADE is applied to the Taiwan case 2 system in Figure 9. Considering the changes in load and DG generation in one day, we analyzed the impacts to the feeder switches schedule and proposed the one-day feeder switch configuration and recommendations.

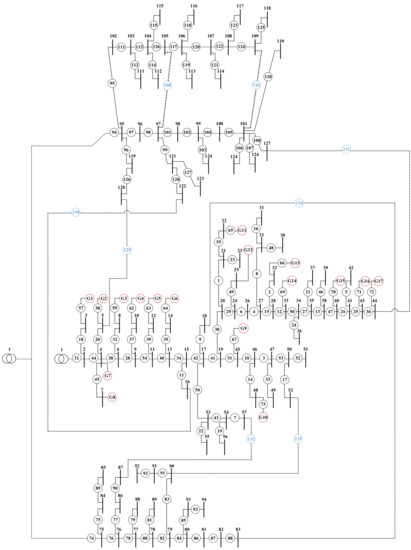
Figure 9. Taiwan case 2 system network with renewable energy sources present.

In Figure 9, the red circles mean the distributed generator connected to the system, which is all PV generators, the blue circles mean the tie-switches, which are often turned on in the system with the dotted line. The whole system is combined with three regions, as shown in Table 6. Only area A contains decentralized renewable energy (here, all are PV), and the load users are mainly agricultural and households, but no large-scale load demand users, such as factories.

Table 6. Taiwan case 2 system feeder data.

System	Area A	Area B	Area C	Area A + B + C
Apparent power (MVA)	25
System voltage (kV)	11.4
Total of system load demand (one-day average)	1471.6 kW + 483.7 kvar	756.7 kW + 248.7 kvar	517.3 kW + 170 kvar	2745.6 kW + 902.4 kvar
Branch number	73	35	20	134
node number	73	33	20	126
DG number	17	0	0	17
Total DG capacity (kW)	3057.7	–	–	3057.7
Tie switch number	–	2	–	8

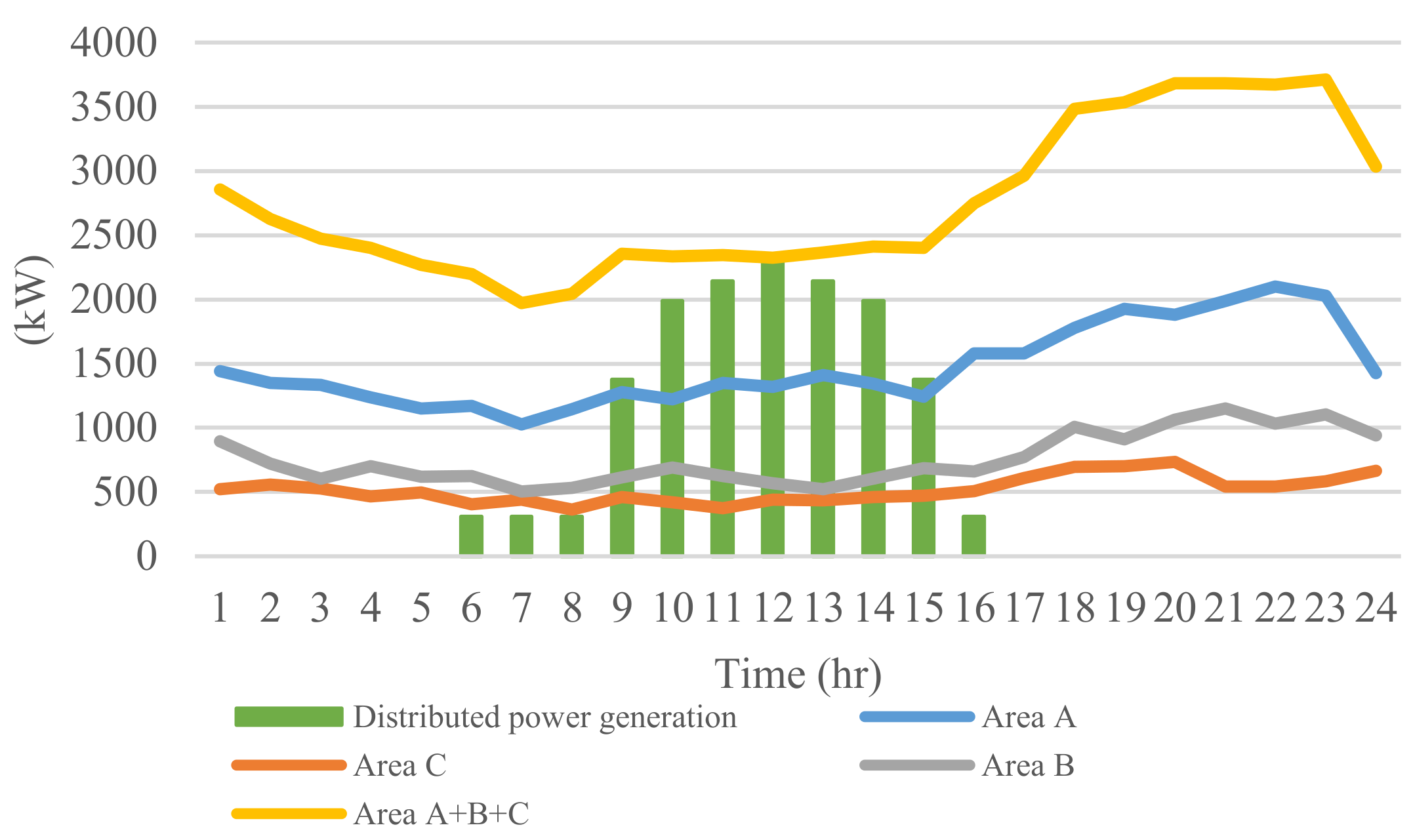
According to the change in the daily load demand of each system, as shown in Figure 10, it can be obviously seen that the peak power consumption time is about 20:00 to 23:00 o’clock, while the light load consumption time focuses on 6:00 to 8:00 o’clock. After 16:00 o’clock, the load demand gradually increases, however, after 23:00 o’clock, the load demand gradually decreases. The light-load in the system is about 0.53 times that of the peak load consumption.

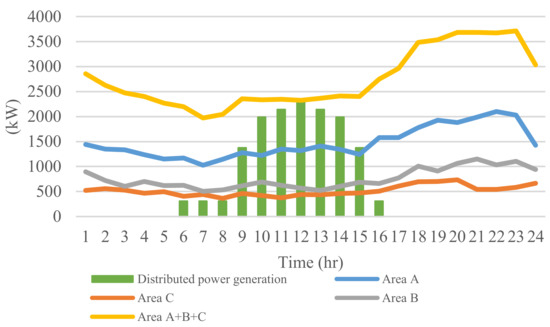
Figure 10. Taiwan case 2 one-day load demand and power generation variation.

4.3.4. Taiwan Case 2 Feeder Reconfiguration

There are 68 feeder switches that can be operated in the system, and the daily switches schedule is summarized in Table 7. The total number of switching operations is 209. According to Table 8, the total number of frequently changed switches under daily load is 85. If we set the eight frequently operated switches in Table 8 into automatic, the number of manually operated switches was reduced to 124 and the number of manual operational times reduced by 40.7%.

Table 7. Feeder switches schedule in daily load demand variation.

Time	Tie Switches Variation
Original system	100	109	129	130	131	132	133	134
00:00	6	53	54	84	99	111	117	132
01:00	3	28	29	84	99	111	124	132
02:00	3	4	28	84	99	113	124	132
03:00	3	7	12	40	84	99	102	116
04:00	3	7	40	50	84	99	116	117
05:00	28	50	51	84	99	104	116	132
06:00	15	34	53	84	99	116	120	132
07:00	3	29	40	84	99	111	124	132
08:00	3	28	50	77	84	99	111	117
09:00	10	12	58	82	84	99	116	124
10:00	12	51	54	77	84	99	101	111
11:00	3	29	54	84	99	113	120	132
12:00	10	30	58	82	84	99	111	120
13:00	15	51	58	84	90	99	113	124
14:00	3	50	54	84	99	111	117	132
15:00	10	50	54	80	84	99	113	117
16:00	41	51	78	84	99	113	117	129
17:00	15	20	51	80	84	99	113	124
18:00	34	50	53	84	90	99	113	124
19:00	6	20	51	82	84	99	116	120
20:00	4	28	53	84	99	113	117	132
21:00	3	15	34	77	84	99	116	120
22:00	41	51	54	78	84	99	116	124
23:00	12	38	51	84	99	105	113	132

Table 8. One-day frequently changed switches.

Switch number	3	51	54	111	113	117	124	132
Operation frequency	10	12	8	10	12	10	12	11

4.3.5. Reconfiguration Considering the Operation Frequency

The excessively frequent switching operations will consume labor costs and time in actual power company operation, so this paper takes the switching operation frequency into account.

Retaining the switches with high operational frequency while limiting the non-action switches or low relational switches can reduce the complexity of the actual feeder. We limit the operable switches from 68 to 28 by setting the switches that are far away from the main transformer and those with fewer occurrences as inoperable. The feeder switches schedule in daily load demand variation by considering the operation frequency is shown in Table 9.

Table 9. Feeder switches schedule in daily load demand variation by considering the operation frequency.

Time	Tie Switches Variation
Original system	100	109	129	130	131	132	133	134
00:00	3	13	34	84	99	113	122	132
01:00	7	13	34	53	84	99	113	122
02:00	3	13	34	84	99	111	124	132
03:00	3	7	13	34	84	99	111	124
04:00	13	34	83	84	99	113	124	132
05:00	34	50	53	84	99	113	122	132
06:00	3	7	13	34	84	99	113	122
07:00	7	13	34	53	84	99	113	124
08:00	7	13	34	53	84	95	99	124
09:00	3	7	34	50	84	95	99	124
10:00	13	34	83	84	95	99	122	132
11:00	3	7	13	34	84	99	111	124
12:00	13	34	53	84	95	99	122	132
13:00	7	34	50	53	84	99	113	124
14:00	3	7	13	34	84	99	113	122
15:00	7	34	50	83	84	99	113	124
16:00	13	34	53	84	99	111	122	132
17:00	10	34	50	84	99	113	122	132
18:00	3	13	34	84	99	113	124	132
19:00	13	34	53	84	99	113	124	132
20:00	13	34	53	84	95	99	124	132
21:00	7	34	50	53	84	99	113	124
22:00	3	7	13	34	84	95	99	124
23:00	34	50	83	84	95	99	122	132

Under the consideration of DG generation and load variation, we proposed the switches operation schedule of every hour. It can be found from Table 9 that the frequently acting switches are numbered 3, 7, 13, 50, 53, 122, 124 and 132. The switch numbers 34, 84 and 99 are almost in the state of normally open switches, so the total switching operation number is 141. Considering the total number of frequently changed switches, as shown in Table 10, there are 106 in total. Setting the eight switches into automatic can effectively reduce the operation number to 35 and significantly reduce labor costs and reduce the number of manual operational times by 83.3%.

Table 10. One-day frequently changed switches by considering the operation frequency.

Switch number	3	7	13	50	53	122	124	132
Operation frequency	14	12	14	14	12	13	12	13

5. Conclusions

This paper compared L-SHADE with PSO in feeder reconfiguration analysis considering distributed generation connection and load variation to achieve the goal of reducing the power loss. We tested the two algorithms in the IEEE 33 standard system under the constraints including voltage, current and DG capacity to improve the power system condition.

Also, we verified L-SHADE and PSO in the Taiwan system. By taking into account the one-day load fluctuation and PV generation, L-SHADE effectively reduces the power loss and keeps the voltage variation and current changes within the limit. In order to save the labor costs and raise system-resilient scheduling, we reduced the feeder switches operation number to 35 by setting the feeder switches with frequent actions to automation.

The contributions of this paper are as follows: (1) We analyzed the PSO and L-SHADE in the feeder reconfiguration by applying them to the IEEE 33 standard system as well as the Taiwan power system. (2) After verifying in the Taiwan system, the algorithm we proposed, L-SHADE, spends less time than PSO in calculating the optimal solution for convergence. Also, L-SHADE effectively reduces the power loss with the limit constraints. (3) The system uses real feeder parameters and a high percentage of solar power plants. The proposed scheduling showed reliability and effectiveness. Also, we achieved the goal of power loss reduction as well as feeder automation planning, with an 83.3% reduction of the manual operation times.