Robust and Fast Converging Cross-Layer Failure Correction in Segment-Routed Networks

Abstract

Due to overlay technologies, service providers have a logical view of the underlay network and can optimize the experience quality without modifying the physical network. However, the cross-layer interaction inevitably causes network fluctuation due to their inconsistent optimization objectives. Aside from that, network failures that occur in both layers not only cause network performance degradation but also significantly increase the frequency of cross-layer interaction. These problems make the network fluctuate for a long time, reduce the network performance, and influence the user experience, especially for time-sensitive applications. In this paper, we design a cross-layer architecture in which the logical layer can satisfy the service function chain demands and maximize the user experience and physical layer so it can optimize the overall network performance. Our cross-layer architecture can make proactive corrections in both layers. Furthermore, we investigate the cross-layer interaction and design two strategies to eliminate fluctuations and make the network converge quickly.

1. Introduction

Over the past few years, a wide variety of overlay networks have been deployed upon the Internet to provide different kinds of service, such as peer-to-peer (P2P) networks, resilient overlay networks (RONs) [1], and content delivery networks (CDNs) [2]. Although the advantages of the overlay network can be used to build many applications that improve the quality of the user experience, in real applications, network failures and cross-layer interactions can still reduce the user experience of the overlay application, especially for time-sensitive applications.

Network function virtualization (NFV) technology has been extensively studied and practiced over the years, in which the network functions are implemented in software running on a common hard device. In NFV, the virtual network functions (VNFs), such as the firewall, load balancer, and deep packet inspection, are chained together in an ordered way for providing services based on different application scenarios, forming a service function chain (SFC). From the perspective of service providers, such services are usually implemented by VNF instances in a cloudlet network composed of a set of data centers and switches. This paper considers VNF instances that provide network services in a cloud network to implement a service chain. The VNF instances in each data center are divided into multiple types, and each type carries a service chain. Overlay networks designed for time-sensitive applications aim to minimize the latency of all applications passing through specific SFC.

However, network failures at both layers can cause network congestion, route reconfiguration, and frequent interaction between the overlay and underlay networks, which will increase the delay of time-sensitive applications. In order to provide better services for time-sensitive applications, we provide three mechanisms in the cross-layer architecture. First, add a failure correction mechanism to the physical layer so that the physical network can satisfy the demands of the logical layer uninterrupted. Second, for invisible SFC failures, add a failure correction mechanism to the logic layer to reduce the impact of SFC failures on the delay performance, and finally, add two fast convergence strategies so that the network can reduce fluctuations and quickly converge.

Segment routing (SR) is a relatively novel source routing approach that is easy to deploy on a large-scale network due to its low overhead, good performance, and compatibility with the current network infrastructure [3]. SR uses a path consisting of the shortest path segment to transmit a packet and encodes the path to the packet’s header. Although SR’s flow control is more flexible and scalable, SR still needs to perform traffic engineering (TE) to optimize resource utilization and network performance [4]. SR can leverage existing IGPs and take advantage of many good features. One of these features is the automatic rerouting of traffic after a failure. Upon a failure, the IGP recomputes all the shortest paths, and the node segments are automatically repaired without any additional intervention. In this paper, we consider using a more robust traffic-allocating algorithm based on segment routing (SR) in the underlay network.

With a robust underlay, the overlay can provide services with less volatility and stable performance for time-sensitive applications. However, there are SFC failures at the logical layer which cannot be observed at the physical layer and can only be resolved at the logical layer. The forward correction method is also applied to the logic layer to correct SFC failures. When we allocate SFC resources, we take into account possible SFC failures and reserve resources in advance so that when failures occur, the network can automatically correct them. In this way, we can largely guarantee the uninterrupted and non-blocking operation of the network [5].

Aside from the failures that may occur in the cross-layer architecture, long-term cross-layer interaction is also one of the key problems affecting the quality of service in the overlay network. Overlay routing and underlay routing have different viewpoints of the network [6]. Underlay TE has a physical view of the network, whereas the overlay has a logical view of the network. The traffic demand of underlay TE is the sum of the overlay demand and background demand. The interaction of two layers is a sequential process, and the two layers take turns to optimize their routes. In the process of interaction, the operation of the overlay changes the traffic pattern of underlay TE, and underlay TE changes the delays of the overlay links [7]. The routing decision of one layer will impact the decision of the other layer. If there is no change between the last two rounds, the network state will be stable.

In this paper, we propose a cross-layer model between low-latency service (LLS) and segment routing with correction (SRC). The model is illustrated by Figure 1. In SRC, we use SR for its easy deployment, near-optimal performance, and built-in rerouting mechanism (IGP-based reroute) to propose an algorithm that automatically corrects control and data plane failures without congestion. In LLS, we care about its latency performance and also use SR to minimize the delay of the overlay. The robustness of each layer of the network has greatly enhanced the stability of the entire system, and the number of network interactions has been reduced, which is very important for time-sensitive applications. Our other focus is on the interaction between SRC and LLS. Obviously, there are two conflicting objectives in the two layers: SRC minimizes the maximum link utilization (MLU) after failure correction, and LLS minimizes the total delay of the overlay. The inconsistency of targets and non-sharing of cross-layer information will lead to network fluctuations. Long-term fluctuations seriously reduce the performance of our LLS and SRC. To achieve better network performance, we provide two strategies to accelerate convergence. Our main contributions are summarized as follows:

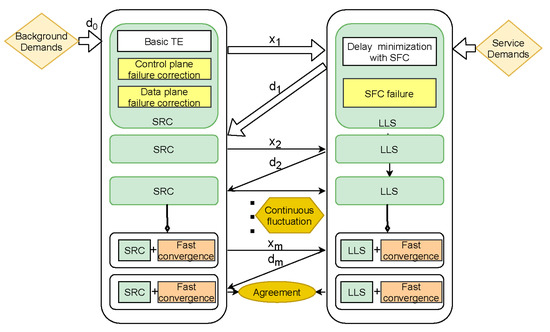
Figure 1. Multilayer architecture with LLS and SRC under failure scenarios.

• In order to achieve better performance for time-sensitive applications, we combine NFV and cross-layer network models and propose SRC and LLS methods as the basic framework of this paper.
• To deal with the network failures in the underlay, we propose a failure correction mechanism for SRC. Our method can handle both data plane failures and control plane failures.
• In order to handle the unique failure types of the logic layer, we add an SFC failure handling mechanism to the LLS to ensure uninterrupted network transmission and ensure the performance of time-sensitive applications.
• We build a cross-layer interaction model regarding LLS and SRC. We treat the interaction as a repeated game [8]. SRC and LLS alternately and selfishly propose conditions until they reach a consensus. We design two strategies in our cross-layer model to accelerate network convergence to reduce the performance degradation caused by fluctuations in networks where errors may occur.
• In the course of our comparative experiment, we gradually add the mechanisms we introduced to the basic version of the framework, observing the impact of different mechanisms on the cross-layer interaction process, proving the effectiveness of our strategy, and the entire framework can guarantee the performance of time-sensitive applications.

Different network error recovery mechanisms have different effects on the quality of service of the cross-layer network. Network failure recovery mechanisms can be divided into two types: proactive and reactive. Because the reactive fault recovery mechanism has the problem of a slow recovery speed and may cause the cross-layer network to enter a fluctuating state, in our paper, a proactive failure recovery mechanism is used. We minimize the MLU in the network after failure recovery to avoid link congestion caused by failure recovery. The congestion of the physical link will lead to a sharp increase in the delay of the logical link, which will cause the network to enter the interactive process and network fluctuations. Compared with the reactive failure recovery mechanism, the proactive failure recovery mechanism can make the network recover from failures faster and reduce the frequency of the network entering a fluctuating state.

The rest of the paper is organized as follows. Section 2 presents the related work. Section 3 introduces the system model and the design objectives of SRC and LLS. In Section 4, we introduce the failure correction mechanism in a cross-layer architecture. In Section 5, we design two strategies to accelerate network convergence. Section 6 presents the experiment results. Section 7 summarizes the paper.

2. Related Work

2.1. SFC

The NFV framework has attracted a lot of attention, especially in the areas of VNF deployment and service chain resiliency. The issues of efficient resource management of NFV, including VNF placement, resource allocation, and flow routing, have been extensively studied in the literature [9]. Sang et al. [10] considered the placement of a minimum number of VNF instances to cover all of the flows in the case of a single type of network function, and Sallam et al. [11] addressed this problem in the case of multiple types of network functions. Cziva et al. [12] formulated the Edge VNF placement problem to allocate VNFs to a distributed edge infrastructure, minimizing end-to-end latency from all users to their associated VNFs. The dynamic placement scheduler minimizes VNF migrations compared with other schedulers and offers quality of service guarantees by not exceeding a maximum number of latency violations that can be tolerated by certain applications. The proactive provisioning for NFV has also attracted growing attention. Fan et al. [13] defined an optimal availability-aware SFC mapping problem and presented a novel online algorithm that can minimize physical resource consumption while guaranteeing the required high availability within a polynomial time. In another work, Fei et al. [14] formulated the VNF provisioning problem so that the cost incurred by inaccurate prediction and VNF deployment would be minimized. In the proposed online algorithm, we first employ an efficient online learning method which aims at minimizing the error in predicting the service chain demands. In this paper, we combine SFC with a cross-layer model. At the logical layer, users using our architecture pay attention to how to meet their needs for the SFC and minimize the delay in their use of services. The tasks generated by the logical layer will have the physical layer to complete the transmission, regardless of the SFC requirements and delays.

2.2. Network Failure Correction

In this paper, we use algorithms based on segment routing (SR) to implement network failure correction. SR is based on the existing IGP protocol, and both can use the fast reroute mechanism. When there is a link or node failure, IGP recomputes all the shortest paths, and the SR is automatically repaired without interruption. There is a lot of research on network correction in segment routing and other traffic engineering methods. In [15], Hao et al. proposed a method to optimize the centralized determination of connections’ primary paths to enable the best sharing of restoration bandwidth over non-simultaneous failures. Pereira et al. [16] proposed a robust semi-oblivious method to meet the flow demands and ensure good network performance after link failures. In [17], the authors proposed an SR method to construct a pairs path to remain disjointed even after an input set of failures to be used for restoration. In [18], the authors initiated a systematic study of such local fast failover mechanisms, which not only provided connectivity guarantees even under multiple link failures but also accounted for the quality of the resulting failover routes for locality and congestion, and they proposed a method called CASA, which provides a high degree of robustness as well as a provable quality of fast rerouting. In [19], Bogle et al. advocated for a novel approach to leverage empirical data to generate a probabilistic model of network failures and maximize bandwidth allocation to network users, subject to an operator-specified availability target. This approach enables network operators to strike the utilization-availability balance that best suits their goals and operational reality, because in a cross-layer architecture, different layers have different perceptions of network failures. In this paper, we enumerate the various types of network errors in the cross-layer system, solve the SFC failures at the logical layer, and solve the control plane and data plane failures at the physical layer.

2.3. Cross-Layer Model

A lot of previous work proved that for users, network-level routing configuration cannot meet everyone’s requirements for network performance [20], but when all users selfishly choose routing paths based on their own needs, the network will suffer serious performance degradation. In order to better meet the needs of users and ensure the overall performance of the network, there has been a lot of work on cross-layer optimization in recent years [7]. Xiao et al. [21] analyzed the interaction of overlays and underlays as a two-stage congestion game and recommended simple operational guidelines to ensure global stability. The paper further explored the use of the Shapley value as an enabler of mutual cooperation in an otherwise competitive environment. In [22], Guck et al. developed a novel function split framework for achieving hard real-time QoS based on SDN. The function split framework can be implemented with any SDN controller that has a global view of the network and can set the queue level flow rules. Wang et al. [23] presented a game theoretic study of the selfish strategic collaboration of multiple overlays when they are allowed to use multipath transfer, which is referred to as the multipath selection game. This research showed analytically the existence and uniqueness of Nash equilibria in these games. Furthermore, the authors found that the loss of efficiency of Nash equilibria can be arbitrarily large if the overlays do not have resource limitations. When there are multiple overlays participating in resource competition, the issue of fairness inevitably becomes the first consideration. Xu et al. [24] proposed a novel cross-layer, fairness-driven, SCTP-based concurrent multipath transfer solution to improve video delivery performance while remaining fair to the competing transmission control protocol (TCP) flows. Wang et al. [6] proposed methods to eliminate the oscillations generated by the interaction between service routing and TE so that the network converges quickly. In [25], Chen et al. proposed a cross-layer resource optimization model and solution to wireless-enabled SFC networks to minimize end-to-end downlink latency, including both wireless and wired delay, by optimizing the VNF placement, routing path, and wireless resources in terms of the resource block for each SFC. In this paper, we consider the influence of various kinds of network failures on the interaction process. Network failures will lead to instability of the cross-layer interaction. We observe the influence of various failures on the cross-layer interaction process through experiments and propose strategies to accelerate convergence.

3. System Model

In this section, we formally define the multilayer SRC architecture with LLS. In order to explain our complex cross-layer model clearly, we introduce the SRC model, the LLS model, and the cross-layer bargaining model.

3.1. SRC Model

First, we introduce SRC as our underlay network to provide physical links for demands from the overlay and background users. We can get an overall overview of our SRC model from Figure 2. In SRC, we studied the MLU minimization problem in a cloud network consisting of multiple data centers to provide different types of service chains. Each router in the SRC may lead to a data center that provides various service chains or may be connected to a group of user nodes. It is worth noting that although SRC, as the actual implementer of overlay requirements, does not pay attention to whether each router is connected to a data center or a user node, SRC focuses on the correct transmission of overlay traffic requirements, minimization of MLU, and various kinds of data and control plane failure correcting.

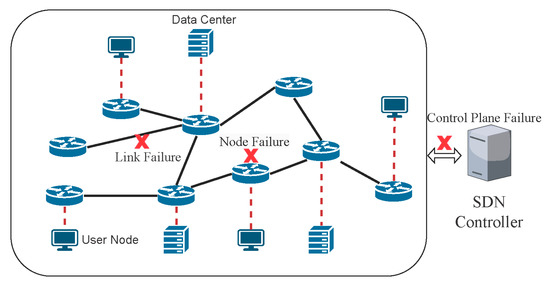
Figure 2. SRC model.

As is shown in Table 1, we used $G\left(V,E\right)$ to denote an underlay network, where $V$ is a set of physical nodes and $E$ is a set of physical links. Then, we defined $C_e$ as the link bandwidth capacity of $e$ and $r\in R$ as a possible flow of the underlay. The demand size of $r$ was denoted by $d_r$.

Table 1. Table of symbols.

Symbols	Description
Symbols in SRC
$G\left(V,E\right)$	Underlay network graph with nodes $V$ and links $E$.
$C_e$	The bandwidth capacity of link e.
$\theta$	The maximum link utilization.
$k\in V$	An intermediate node for segment routing.
$r\in R$	Flows aggregated by ingress and egress switches.
$r_s$	The source switch of flow $r$.
$r_t$	The end switch of flow $r$.
$t_r^k$	A tunnel consisting of two shortest segments.
$d_r^{overlay}$	Underlay demand on flow $r$ arising from the logical link $\left(r_{s^{\prime }}^{\prime },r_{t^{\prime }}^{\prime }\right)$.
$d_r^{underlay}$	Underlay demand on flow $r$ arising from background traffic applications.
$d_r$	The sum of $d_r^{overlay}$ and $d_r^{underlay}$.
$g_r^k\left(e\right)$	The number of times the tunnel $t_r^k$ passes through physical link $e$.
$ne$	Maximum number of link errors that occur simultaneously.
$nv$	Maximum number of switch errors that occur simultaneously.
$nc$	Maximum number of control plane errors that occur simultaneously.
$\left(\mathbf{\beta },\mathbf{\gamma }\right)\in U_{ne,nv}$	A scenario expressing $nv$ node failures and $ne$ link failures at the same time.
$\mathbf{\alpha }\in B_{nc}$	A vector expressing $nc$ control failures at the same time.
${\Phi }_{v,e}$	The total traffic aggregating at link $e$ from flows starting at $v$ if no configuration failure happens.
${\Psi }_{v,e}$	The total traffic aggregating at link $e$ from flows starting at $v$ if there exist configuration failures.
$z_r^k$	The traffic volume on tunnel $t_r^k$.
$g_r^k\left(e,\mathbf{\beta },\mathbf{\gamma }\right)$	The $g_r^k\left(e\right)$ in the failure case $\left(\mathbf{\beta },\mathbf{\gamma }\right)$.
$y_r^k$	The splitting weight of the current period.
$\widehat{y_r^k}$	The splitting weight of the last period.
$hop{\left(r\right)}_{last}$	The total hop count of each flow $r$ after the operation of SRC in the last round.
Symbols in LLS
$G^{\prime }\left(V^{\prime }\cup D{C}^{\prime },E^{\prime }\right)$	Overlay network graph with nodes $V^{\prime }$, data center $D{C}^{\prime }$, and links $E^{\prime }$.
$k^{\prime }\in D{C}^{\prime }$	A data center in $D{C}^{\prime }$.
$r^{\prime }\in R^{\prime }$	Flows aggregated by ingress and egress switches.
$r_{m^{\prime }}^{\prime }\in R_{m^{\prime }}^{\prime }$	Flows that require a type-$m^{\prime }$ service chain aggregated by ingress and egress switches.
$r_s^{\prime }$	The source switch of flow $r^{\prime }$.
$r_t^{\prime }$	The end switch of flow $r^{\prime }$.
$delay\left(r^{\prime }\right)$	The delay of flow $r^{\prime }$.
$link\_delay\left(e^{\prime }\right)$	The link delay of overlay link $e^{\prime }$.
$d_{r^{\prime }}\in D^{\prime }$	The bandwidth demand of flow $r^{\prime }$.
$d_{r^{\prime },m^{\prime }}\in D_{m^{\prime }}$	The bandwidth demand of flow $r^{\prime }$ that requires instances of type-$m^{\prime }$ service chains.
$f_{r^{\prime }}^{e^{\prime }}$	The decision variable to represent the fraction of $d_{r^{\prime }}$ on link $e^{\prime }$.
$m^{\prime }\in M^{\prime }$	A type of service chain.
$S{C}_{m^{\prime }}$	Type-$m^{\prime }$ service chains.
$S{C}_{m^{\prime }}^{k^{\prime }}$	The set of instances of type-$m^{\prime }$ service chains at data center $k^{\prime }$.
$\left|S{C}_{m^{\prime }}^{k^{\prime }}\right|$	The computing resource capacity of $S{C}_{m^{\prime }}^{k^{\prime }}$.
$x_{r^{\prime },m^{\prime }}^{k^{\prime }}$	The bandwidth splitting weight of flow $r_{m^{\prime }}^{\prime }$ on $e^{\prime }$.
$g_{r^{\prime }}^{k^{\prime }}\left(e^{\prime }\right)$	The number of times the tunnel $t_{r^{\prime }}^{k^{\prime }}$ passes through local link $e^{\prime }$.
$ns$	Maximum number of SFC failures that occur simultaneously.
${\mathbf{\lambda }}^{\prime }\in S_{ns}$	A vector expressing ns SFC failures at the same time.
$load{\left(e^{\prime }\right)}_{last}$	The amount of overlay traffic on each link after the operation of overlay routing in the last round.

An important task for SRC is to balance the load and avoid link congestion even when there exist node failures, link failures, and control plane failures. Link congestion causes a performance degradation in SRC, which is intolerable for time-sensitive applications. In order to accomplish our goal, we used segment routing [26] to design our algorithm. Segment routing is a new type of source-routing paradigm. It splits a path into multiple shortest paths and uses the header of the transport protocol to save the shortest path segments that have passed. We used segmented routing for two main reasons. The first was because it could make full use of the existing network facilities based on the shortest path and also give full play to the advantages of the SDN environment. It has the characteristics of easy deployment and strong scalability. The second was that the rerouting mechanism we adopted was also designed according to the shortest path algorithm. In this paper, we use two-segment routing, which is enough to explain our problem, and more segments can be expanded simply by increasing the number of calculations.

Considering that there are many elements involved in our paper, in order to highlight the key points, we used a relatively simplified SFC deployment and two-segment routing. In the actual environment, a data center can directly provide multiple composite services (each composite service represents a complete SFC), such as in the literature [27]. If a packet needs a certain service, it only needs to pass through the data in the chain that provides this service. In the data center, the network flow will pass through a service function chain composed of multiple sub-services (such as firewalls, DPI, and NAT) to meet the demands of users for the specified service. Therefore, the use of two segments can also complete all types of user demands. More segmented segment routing was needed to rewrite our mathematical formulas, such as changing $z_r^k$ to $z_r^{kl}$ and $g_r^k\left(e\right)$ to $g_r^{kl}\left(e\right)$. When the number of segments is small, the expansion of the number of segments will not be difficult. When the number of segments becomes very large, the problem of solving segment routing will become very complicated, which is not the focus of this paper. The authors of [28] proposed CG4SR to provide a fast calculation method for multi-segment routing. Fortunately, according to the conclusion of [26], two segments could be very efficient for us to use, and using too many segments was not necessary.

In this section, we first give the basic formula of segment routing traffic engineering. Then, in the next section, we will introduce a forward correction mechanism that can avoid congestion even if errors occur. We used $\theta$ to represent the MLU as the objective function of our SRC. It is worth noting that our objective function of SRC will change slightly after the error correction mechanism is introduced in the next section. In the next section, our objective function will be to minimize the MLU in the failure correction scenarios. Each SRC demand can be transmitted by a group of tunnels $t_r^k,\forall k\in V$. Here, $t_r^k$ denotes a path consisting of the two shortest segments: one from $r_s$ to $k$ and the other from $k$ to $r_t$. Let $z_r^k$ denote the traffic volume for tunnel $t_r^k$, and we have $\sum _k{z}_r^k=d_r$. Let $y_r^k$ denote the allocation ratio of tunnel $t_r^k$, and we have $\sum _k{y}_r^k=1$. Notice that SRC does not differentiate the overlay demands and background demands. When receiving demands from the LLS and underlay users, SRC performs the operation formulated as

$$minimize \theta$$

(1)

$$\sum _r\sum _k{z}_r^k{g}_r^k\left(e\right)\le C_e\theta ,\forall e\in E$$

(2)

$$\sum _k{z}_r^k\ge d_r,\forall r\in R$$

(3)

$$0\le z_r^k,0\le \theta ,\forall r\in R,k\in V$$

(4)

We used Equation (1) to calculate the MLU. Equation (2) could ensure that all links did not exceed the link bandwidth capacity limit, and Equation (3) could ensure all demands could be satisfied. We used $g_r^k\left(e\right)$ to represent the amount of traffic imposed on edge $e$ when a unit of traffic passed through tunnel $t_r^k$. We used the Equal Cost Multi-path (ECMP) [29] strategy in the traffic transmission of each segment. When there were multiple paths between the two endpoints of the segment, we divided our traffic equally and transmitted it on different paths:

$$g_r^k\left(e\right)=\frac{t_{r_s}^k\left(e\right)n_k^{r_t}+t_k^{r_t}\left(e\right)n_{r_s}^k}{n_k^{r_t}{n}_{r_s}^k}$$

(5)

We used Equation (5) to calculate $g_r^k\left(e\right)$, where $t_a^b\left(e\right)$ represents the number of times that all shortest paths between $a$ and $b$ pass through $e$ and $n_a^b$ represents the number of shortest paths between $a$ and $b$. In the case of one segment, we calculated the number of shortest paths between $r_s$ and $r_t$. The traffic of this segment was divided equally to each path. Let us take the situation in Figure 3 as an example. Assuming that there is a unit of traffic that needs to be transmitted between A and G, there are three shortest paths between A and G, so each path is divided into one third of the unit of traffic. Because the link <A, B> exists on the two shortest paths, there is two-thirds of the unit of traffic on <A, B>. In the case of two segments, the number of paths for $r_s$ and $r_t$ is the number of shortest paths in the first segment multiplied by the number of shortest paths in the second segment. We divided the traffic into equal parts on all paths and used Equation (5) to calculate the value of $g_r^k\left(e\right)$.

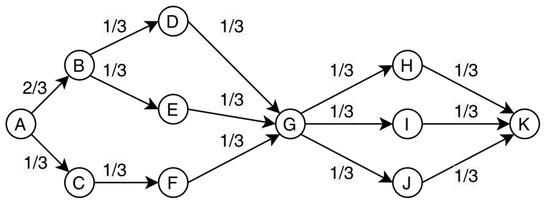
Figure 3. An example of calculating the value of $g_r^k\left(e\right)$.

SRC splits each flow onto multiple paths without considering packet reordering. Mainly for the following considerations, packet reordering is a general problem involved in multipath routing, which is far from limited to this paper. There are more mature solutions to this problem, such as MBD/ADBR [30], TS-EDPF [31], and THR [32]. In addition, this paper focuses on models and analysis, focusing on the convergence framework based on game theory, performance-bound and multipath-routing computing (rather than how to schedule packets after calculating the multipath routing), and other issues. We use the flow-level model for modeling, and our problem is not suitable for the packet-level model. Similar research can be seen in a large number of cross-layer references [6,33,34]. Finally, in practical applications, the packet rearrangement problem can be solved by per-flow traffic splitting methods such as DHTC [35] or a flow cache [36]. Aside from that, we can also use the techniques in THR [32] and FLARE [37] to mitigate packet reordering.

SRC uses a snapshot of the traffic demand matrix to calculate the SR tunnel allocation scheme. The frequency of recalculation depends on the amplitude of change in the traffic matrix or the desired periodicity. Note that networks using only the above descriptions cannot handle network errors, which can result in serious degradation of the load balancing performance when errors occur. LLS’s performance cannot be guaranteed. In the next section, we introduce some methods to improve the robustness of SRC.

3.2. LLS Model

In this subsection, we introduce LLS as our overlay network to provide low-latency service for overlay users.

We can get an overall overview of our LLS model from Figure 4. In LLS, we studied the latency minimization problem to meet the low latency needs of users. Users’ data packets in LLS not only require point-to-point traffic transmission, but they also need to go through a set of specific service function chains to perform specific operations on the packets. A number of instances of service chains have been instantiated in each service chain node corresponding to the data center in SRC.

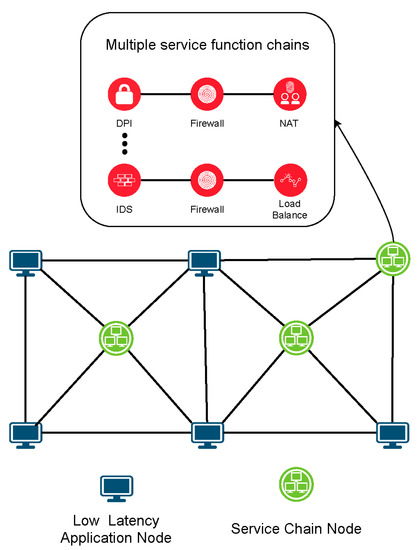
Figure 4. LLS model.

The symbols in LLS are listed in Table 1. An LLS network in an overlay is represented by the graph $G^{\prime }\left(V^{\prime }\cup D{C}^{\prime },E^{\prime }\right)$, where $V^{\prime }$ is a set of logical nodes, $D{C}^{\prime }$ is a set of data centers, and $E^{\prime }$ is a set of logical links. Each overlay node maps onto a physical node, and each overlay link maps onto a group of physical paths. A logical flow $r^{\prime }\in R^{\prime }$ denotes a possible flow of an overlay which contains a set of logical links, and the demand on it is $d_{r^{\prime }}^{\prime }$. Each service chain node $k^{\prime }\in D{C}^{\prime }$ has a computing resource capacity (CPU, RAM, etc.) to implement VNFs. We used $\left|S{C}_{m^{\prime }}^{k^{\prime }}\right|$ to denote the computing resource capacity of type-$m^{\prime }$ service chains in service chain node $k^{\prime }$. We categorized the demand matrix according to the type of service chain required, and $d_{r^{\prime },m}$ denotes the bandwidth demand of flow $r^{\prime }$ that requires instances of type-$m^{\prime }$ service chains. In order to maintain consistency before and after in LLS, we still used segmented routing to design our method, because it can easily transmit user packets through the service function chains to the end nodes.

The goal of LLS is to provide users with the most reliable and lowest-latency services. We set the minimization of the total delay as our objective function. Let $x_{r^{\prime },m^{\prime }}^{k^{\prime }}$ denote the bandwidth splitting weight of flow $r_{m^{\prime }}^{\prime }$ on $k^{\prime }$. Given the topology information of LLS and the demands of the users, the optimal operation of LLS can be formulated as

$$minimize \sum _{r^{\prime }}delay\left(r^{\prime }\right)$$

(6)

$$delay\left(r^{\prime }\right)=\sum _{e^{\prime }\in E^{\prime }}link\_delay\left(e^{\prime }\right)\times f_{r^{\prime }}^{e^{\prime }}$$

(7)

$$link\_delay\left(e^{\prime }\right)=\sum _{e\in E}\frac{f_r^e\times d_r^{overlay}}{C_e-{\sum }_r{f}_r^e\times \left(d_r^{overlay}+d_r^{underlay}\right)}$$

(8)

$$\sum _{k^{\prime }\in D{C}^{\prime }}{x}_{r^{\prime },m^{\prime }}^{k^{\prime }}\ge 1,\forall r^{\prime }\in R^{\prime },m^{\prime }\in M^{\prime }$$

(9)

$$\sum _{r^{\prime }\in R^{\prime }}{x}_{r^{\prime },m^{\prime }}^{k^{\prime }}{d}_{r^{\prime },m^{\prime }}\le \left|S{C}_{m^{\prime }}^{k^{\prime }}\right|,\forall k^{\prime }\in D{C}^{\prime },m^{\prime }\in M^{\prime }$$

(10)

$$f_{r^{\prime }}^{e^{\prime }}{d}_{r^{\prime }}=\sum _{k\in D{C}^{\prime }}\sum _{m^{\prime }\in M^{\prime }}{x}_{r^{\prime },m^{\prime }}^{k^{\prime }}{g}_{r^{\prime }}^{k^{\prime }}\left(e\right)d_{r^{\prime },m^{\prime }},\forall r^{\prime }\in R^{\prime },e^{\prime }\in E^{\prime }$$

(11)

$$d_r^{\prime }=\sum _{m^{\prime }\in M^{\prime }}{d}_{r^{\prime },m^{\prime }},\forall r^{\prime }\in R^{\prime }$$

(12)

$$x_{r^{\prime },m^{\prime }}^{k^{\prime }}\ge 0,\forall r^{\prime }\in R^{\prime },m^{\prime }\in M^{\prime },k^{\prime }\in D{C}^{\prime }$$

(13)

Equation (9) is the demand constraint, and Equation (10) is the computing resource constraint, while $f_{r^{\prime }}^{e^{\prime }}$ represents the fraction of $d_{r^{\prime }}$ on link $e^{\prime }$ and is an intermediate variable for calculating the link delay. Let $link\_delay\left(e^{\prime }\right)$ represent the delay overlay LLS link $e^{\prime }$. Note that we adopted the M/M/1 formula in [38] to calculate the link delay, which is a nonlinear function. We adopted the approach used in [38] to transform the nonlinear programming function into a piece-wise linear increasing and convex function, which can be solved in polynomial time. LLS’s link delay is related to the delay of the SRC links, through which the LLS demands on this LLS link are transmitted. As mentioned above, an overlay link flow is treated as a demand by the underlay. Thus, we denoted $d_r^{overlay}$ as a physical demand from $r_s$ to $r_t$, and the size of $d_r^{overlay}$ is equal to the amount of traffic transmitted by the corresponding link in the overlay. There were also some background traffic demands, defined as $d_r^{underlay}$ in the physical network. The total demands of the physical layer are the sum of the two kinds of demands. Equation (8) calculates the link delay of each logical link.

In our architecture, LLS determines the routing policies for all demands in its logical network. A source node may divide its demand and transmit traffic by different paths. For each flow $r_{m^{\prime }}^{\prime }$, LLS needs to determine how to allocate $d_{r^{\prime },m^{\prime }}$ to different paths. LLS translates the flow scheme into the demands of SRC, and SRC receives the demands of LLS and the underlay users and decides how to allocate the traffic on physical links.

3.3. Cross-Layer Model

SRC and LLS have different perspectives on the same network. As shown in Figure 5, LLS regards the network as a logical network of a set of user application nodes and nodes that provide services, and SRC is the physical network that carries these applications and services. A physical network can carry many logical networks. For the overlay, not all underlay nodes are visible. For the link, a link in the overlay corresponds to a set of paths determined by the underlay controller in the underlay. The service function chain node of the overlay corresponds to a node of the underlay connected to a data center that provides the service function chains. In the cross-layer structure, the main task of LLS is to collect the link usage status in SRC and to deal with the demands of users and allocate them on different service function chain nodes and different logical paths. The main task of SRC is to convert the transmission scheme of LLS to the $d_r^{overlay}$ of the physical layer and then proceed to traffic engineering.

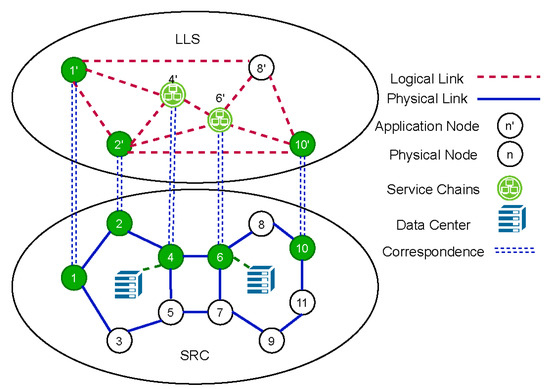
Figure 5. Cross-layer model.

SRC and LLS have different objectives in the multilayer network architecture. The objective of SRC is to balance the load even when there are failures in the underlay network, so SRC tends to allocate traffic to the links that are underutilized and not easily congested by a failure scenario. However, SRC inevitably causes the latency of LLS to become large. In the same way, in order to achieve a smaller delay, LLS tends to configure paths with shorter latency for each demand. In general, a path with a shorter latency may have fewer hops. However, the selfish operation may lead the corresponding SRC link to have a high link load or SRC to become congested due to failures. The objective inconsistency between SRC and LLS makes both layers constantly change their routing configuration, causes network fluctuation, and greatly harms the time-sensitive performance of LLS. It is worth noting that the objective functions of SRC and LLS are indeed not completely opposite. It is not that the increase of the MLU of the SRC will make the delay of the LLS decrease, or vice versa. In [38], Fortz and Thorup used the method of minimizing the M/M/1 queue delay to avoid congestion. To some extent, the increase of the MLU of SRC will also cause the delay of LLS to increase. A more accurate description of the reasons for the fluctuations should be the misalignment between the objectives of SRC and LLS. We understand that the conflict of this relationship is that when one layer reaches the optimum, the other layer is often unable to reach the optimum. The word “conflict” is used in many papers [6,33,34] on cross-layer networks, so we also used the same word to facilitate understanding.

The interaction process can be revealed in Algorithm 1. SRC and LLS take turns to calculate their optimal schemes with inconsistent objectives. In the interaction process, the result of SRC will change the allocation ratio of the tunnels between the demand pairs, which leads to new link latency in LLS. The optimal operation of LLS will change the routes in LLS according to the logical link delay, which is determined by the corresponding physical path and the demand pattern, which will change the allocated scheme of SRC in the next round. We made SRC perform its optimal operation at odd rounds and LLS perform its optimal operation at even rounds. The core calculation of the algorithm is the following two formulas:

$$\left[d_r^{overlay}, dela{y}^{LLS}, ML{U}^{LLS}\right]=LLS\left(y_r^k\right)$$

(14)

$$\left[y_r^k, dela{y}^{SRC}, ML{U}^{SRC}\right]=SRC\left(d_r^{overlay}\right)$$

(15)

At the odd rounds, we used Equation (15) to compute the tunnel splitting weights $y_r^k$, $dela{y}^{LLS}$ with updated $y_r^k$, and $MLU$. Note that SRC is calculated in the underlay, which will change the allocation scheme of the underlay tunnels. At this time, LLS has not calculated the new demand pattern, so the $dela{y}^{LLS}$ can be calculated by using the updated $y_r^k$ and the non-updated $d_r^{overlay}$. SRC’s selfishness leads to a high value for $dela{y}^{LLS}$, so LLS will perform Equation (14) to lower the latency. The input of LLS from SRC is $y_k^r$, and the output of LLS is a new demand matrix $d_r^{overlay}$. At the same time, we can get the $dela{y}^{LLS}$ and $ML{U}^{LLS}$, which can be obtained by allocating the updated $d_r$ with the non-updated $y_r^k$. SRC and LLS take turns to compute the optimal operation for themselves until they reach an agreement, which is the so-called Nash equilibrium [6]. In the Nash equilibrium state, both schemes can produce the same MLU and delays, and the network also enters a stable state without frequently updating the routing configuration.

Algorithm 1 Cross-Layer Model Iterative Algorithm

Input: $G\left(V,E\right)$, $G\left(V^{\prime }\cup D{C}^{\prime },E^{\prime }\right)$, $D^{underlay}$, $\left\{D_{m^{\prime }}^{\prime }\right\}$, ${ϵ}_{mlu}$, ${ϵ}_{delay}$

Output: $\left\{x_{r^{\prime },m^{\prime }}^{k^{\prime }}\right\},\left\{z_r^k\right\}$

1: ${\Delta }_{mlu}=\infty$

2: ${\Delta }_{latency}=\infty$

3: $d_r^{overlay}=0,\forall r$

4: while (${\Delta }_{mlu}\ge {ϵ}_{mlu} \left|\right|{\Delta }_{delay}\ge {ϵ}_{delay}$) do

5:        $\left[y_r^k,dela{y}^{SRC},ML{U}^{SRC}\right]=SRC\left(d_r^{overlay}\right)$

6:        $\left[d_r^{overlay},dela{y}^{LLS},ML{U}^{LLS}\right]=LLS\left(y_r^k\right)$

7:        ${\Delta }_{mlu}=\left|ML{U}^{LLS}-ML{U}^{SRC}\right|$

8:        ${\Delta }_{latency}=\left|dela{y}^{LLS}-dela{y}^{SRC}\right|$

9: end

10: return $\left\{x_{r^{\prime },m^{\prime }}^{k^{\prime }}\right\},\left\{z_r^k\right\}$

SRC and LLS have different objectives in the multilayer network architecture. The objective of SRC is to balance the load even when there are failures in the underlay network, so SRC tends to allocate traffic to the links that are underutilized and not easily congested by a failure scenario. However, SRC inevitably causes the latency of LLS to become large. In the same way, in order to achieve a smaller delay, LLS tends to configure paths with shorter latency for each demand. In general, a path with a shorter latency may have fewer hops. However, selfish operation may lead to the corresponding SRC link to have a high link load or SRC to become congested due to failures. The objective inconsistency between SRC and LLS makes both layers constantly change their routing configuration, causes network fluctuation, and greatly harms the time-sensitive performance of LLS. Inspired by [6,8], we propose two strategies for SRC and LLS to accelerate the convergence of network states in Section 5.

4. Failure Correction in a Cross-Layer Architecture

In a cross-layer network architecture, what affects the performance of time-sensitive applications most are endless interaction and network failures [39]. Network errors may cause the cross-layer network to frequently enter the interactive process. The overlay network uses user demands and the delay of each logical link as input to calculate the traffic distribution on each logical link. The traffic on each logical link will be transformed into a demand pair and a user demand matrix formed by all demand pairs. The underlay processes the user demand matrix and the background demand matrix together to generate a new routing configuration. Therefore, when the demand matrix is input into our cross-layer framework, the calculation results of the overlay will change the input of the underlay, leading to reconfiguration of the underlay which, in turn, affects the input of the overlay and so on, causing continuous fluctuations in the cross-layer network [6]. In the stable state of the cross-layer network, when the user demand matrix or the logical link delay changes beyond the preset range, the overlay will be reconfigured, which will also cause the underlay to enter reconfiguration, which will cause fluctuations in the cross-layer network. The same is true when the input of the underlay (background flow matrix and overlay demand matrix) changes more than the preset amplitude.

Network failure recovery mechanisms can be divided into two types: proactive and reactive [40]. We will first introduce the reactive failure recovery mechanism. When an error occurs in the network, the network detects the failure through some detection mechanisms and repairs it by reconfiguring the route. The reactive failure recovery mechanism has two problems: one is the slow recovery speed, and the other is that it will frequently cause the cross-layer network to enter a fluctuating state. In our paper, a proactive failure recovery mechanism is used. We minimize the MLU in the network after failure recovery to avoid link congestion caused by failure recovery. The congestion of the physical link will lead to a sharp increase in the delay of the logical link, which will cause the network to enter the interactive process, which will cause network fluctuations. Compared with the reactive error recovery mechanism, the proactive failure recovery mechanism can make the network recover from failures faster and reduce the frequency of the network entering a fluctuating state, but the proactive failure mechanism needs to reserve more resources in exchange for availability.

First of all, we try to solve the data plane errors and control plane errors that may occur in the network in SRC. For LLS unique service function chain errors, we solve them at the LLS layer. We use proactive error correction methods to reserve bandwidth in advance for the occurrence of errors and automatically repair them when errors occur instead of recalculating the entire network traffic, which is not only slow but also introduces fluctuations in the process of interaction.

4.1. Failure Correction in SRC

The base version of SRC is slow to respond to congestion caused by control plane and data plane failures. In the base version of SRC, when a failure happens, the network operator detects the failure, recalculates the traffic allocation scheme, and configures it on data plane. LLS is sensitive to congestion, packet drops, or long queuing delays of the underlay, and the bad performance of the underlay may cause an increase in the delay of LLS or a recalculation of the LLS routing scheme, which will reduce the performance of time-sensitive applications. In this subsection, we are inspired by the FFC method [40] to introduce a forward correction mechanism for our SRC method.

4.1.1. Correction of Data Plane Failures

In order to support the better working of LLS, we introduce the IGP-based rerouting mechanism [15] to SRC to correct the node and link failures in the network. In an IGP-based network, when a failure occurs, the switch will update the topology data and recompute the shortest path for every node pair. In SR, because an SR tunnel contains several shortest path segments, the IGP-based rerouting mechanism can be used by our SRC. In Figure 6, we show the paths of tunnel $t_r^k$. When there is no failure in the network, the tunnel $t_r^k$ uses the path $r_s\to k\to r_t$ to transmit the traffic, and when there is a failure in the link of the path, a new shortest path for the node pair $\left(r_s,k\right)$ will be configured in all switches. When a node failure occurs, the network will adopt a similar method.

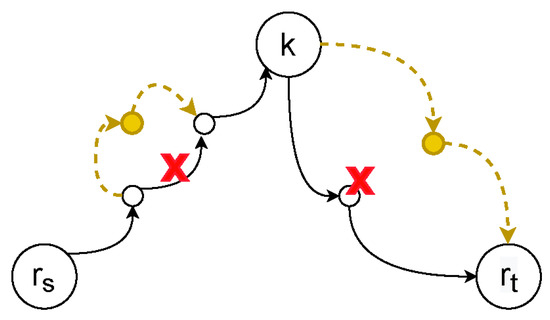
Figure 6. IGP-based rerouting mechanism in SRC.

When a node or link fails, it impacts all tunnels passing through it. When the switches detect the fault, they reconfigure their routing table. The paths of the impacted tunnels also change, which may lead to network congestion. To solve this problem, SRC takes into account the impact of failures when designing the traffic allocation plan. For data plane faults (including node and link failures), we set two parameters, $nv$ and $ne$, to represent the maximum node and link failures that SRC can tolerate; that is to say, if there are $ne$ link failures and $nv$ node failures in the network, congestion will not occur. We introduced the following formulas to handle data plane failures:

$$\sum _r\sum _k{z}_r^k{g}_r^k\left(e,\mathbf{\beta },\mathbf{\gamma }\right)\le C_e\theta ,\forall r\in R,k\in V$$

(16)

$$\sum _k{z}_r^k\ge d_r,\forall r\in R,\left(\mathbf{\beta },\mathbf{\gamma }\right)\in U_{ne,nv}$$

(17)

Let ${\beta }_e=1$ denote that link $e$ has failed and ${\gamma }_v=1$ represent that switch $v$ has failed. On the contrary, if the value is 0, no failure happens on the link or node. A case of a data plane fault can be represented by $\left(\mathbf{\beta },\mathbf{\gamma }\right)$, where vector $\mathbf{\beta }=\left\{{\beta }_e\right|e\in E\}$, and vector $\mathbf{\gamma }=\left\{{\gamma }_v\right|v\in V\}.$ SRC can achieve robustness to $ne$ link failures and $nv$ node failures and require that there is no overloaded link under the set of $U_{ne,nv}=\left\{\left(\mathbf{\beta },\mathbf{\gamma }\right)\right|\sum _e{\beta }_e\le ne,\sum _v{\gamma }_v\le nv\}$. Given a failure case $\left(\mathbf{\beta },\mathbf{\gamma }\right)$, we can easily get the value of $g_r^k\left(e,\mathbf{\beta },\mathbf{\gamma }\right)$, which denotes the $g_r^k\left(e\right)$ in the failure case $\left(\mathbf{\beta },\mathbf{\gamma }\right)$ with an IGP-based rerouting mechanism. Equation (16) calculates the MLU for all given failure cases, and Equation (17) meets all demands for all given failure cases. Note that now the $\theta$ is the maximum link utilization after the reroute of data plane failures. Only the allocation scheme with $\theta$ less than one is the balanced load scheme that can correct the failures accurately.

4.1.2. Correction of Control Plane Failures

Control plane failures are unique to centralized traffic engineering (TE) and may happen when a centralized controller calculates a new traffic allocation scheme and configures each switch. The switch where the control plane error occurs does not update the routing table of the SR tunnels and still uses the routing table of the previous period, which is likely to cause excessive network latency or congestion.

For control plane faults, the goal of SRC is to calculate a new configuration $\{z_r^k,y_r^k\}$ such that no congestion will occur as long as $nc$ or fewer switches fail to update their old configuration $\{\widehat{z_r^k},\widehat{y_r^k\}}$. Let ${\alpha }_v=1$ denote that there exists 1 flow configuration failure at least in the switch $v$. Because SR is a kind of source-routing technology, the control plane failure impacts the flow with $v$ as the source node. If ${\alpha }_v=0$, there is no control plane failure in the switch $v$. Therefore, a case of control plane failures in the network can be represented as a vector $\mathbf{\alpha }=\left\{{\alpha }_v\right|v\in V\}$. We set a parameter $nc$ to denote the protection capability of SRC. SRC can work without congestion under the set of cases $B_{nc}=\left\{\mathbf{\alpha }\right|\sum _{v\in V}{\alpha }_v\le nc$}. To enable the protection, we added the following formula:

$$\sum _{v\in V}\left(1-{\alpha }_v\right){\Phi }_{v,e}+{\alpha }_v{\Psi }_{v,e}\le C_e\theta ,\forall e\in E,\mathbf{\alpha }\in B_{nc}$$

(18)

$${\Phi }_{v,e}=\sum _{\left\{r\right|r_s=v\}}\sum _k{z}_r^k{g}_r^k\left(e\right),\forall e\in E,v\in V$$

(19)

$${\Psi }_{v,e}=\sum _{\left\{r\right|r_s=v\}}\sum _k{b}_r^k{g}_r^k\left(e\right),\forall e\in E,v\in V$$

(20)

$$b_r^k=max\left\{\widehat{y_r^k}{d}_r,z_r^k\right\},\forall r\in R,k\in V$$

(21)

where ${\Phi }_{v,e}$ denotes the total traffic aggregating at link $e$ from flows starting at $v$ if no configuration failure happens. We could get this from Equation (19). ${\Psi }_{v,e}$ denotes the total traffic aggregating at link $e$ from flows starting at $v$ if there exists a configuration failure. When a control plane error occurs in node $v$, its forwarding table cannot be updated correctly. Therefore, all flows starting at node $v$ will be forwarded according to the unupdated forwarding table. $\widehat{y_r^k}$ is the splitting weight of last period. We could get ${\Psi }_{v,e}$ from Equations (20) and (21).

SRC can protect the network from congestion even when network failures are encountered. Therefore, SRC can not only guarantee the low latency performance of LLS but also reduce the number of interactions between LLS and SRC by reducing the number of recalculations of routes in SRC.

4.2. Failure Correction in LLS

We have introduced failure recovery mechanisms for SRC, but in our cross-layer architecture, SRC failure correction cannot solve all failures that may appear in the architecture, such as SFC failures. Because there is no concept of SFC in SRC, LLS passes the calculated routing requirement matrix to SRC for traffic routing configuration. In order to ensure the robustness of our cross-layer network architecture, minimize the number of cross-layer interactions, and ensure the performance of time-sensitive applications, we also introduced an SFC failure correction mechanism in LLS to ensure that when failures occur in certain SFCs, the network can automatically recover and operate normally.

First, we introduced an SFC failure recovery mechanism for the LLS. When a certain SFC node fails, all traffic demands using this type of SFC on this node will be affected. When an SFC failure is detected, the source node of the affected traffic will redistribute the traffic on the currently used tunnel. As is shown in Figure 7, suppose a flow that needs a type-2 service function chain is distributed to three tunnels in the proportion of $\left(0.3,0.3,0.4\right)$. When a failure occurs in the type-2 SFC at the third tunnel, the source node will redistribute the proportional coefficient to $\left(0.5,0.5,0\right)$. This reactive error correction mechanism can ensure that the network recovers from errors quickly and reduces the impact on time-sensitive applications. However, the number of requests that each SFC node can handle is limited. When a failure occurs, the additional allocation request may cause congestion of the service function chain nodes. In order to solve this problem, LLS considers the possibility of error correction of the SFC when calculating the routing plan. We set the parameter $ns$ as the maximum SFC failures that LLS can tolerate. When there are $ns$ SFC failures, the LLS can work well without congestion. For achieving this target, we added following formula to our LLS:

$$\sum _{k^{\prime }\in D{C}^{\lambda }}{x}_{r^{\prime },m^{\prime }}^{k^{\prime }}\ge 1,\forall r^{\prime }\in R^{\prime },m^{\prime }\in M^{\prime },{\mathbf{\lambda }}^{\prime }\in S_{ns}$$

(22)

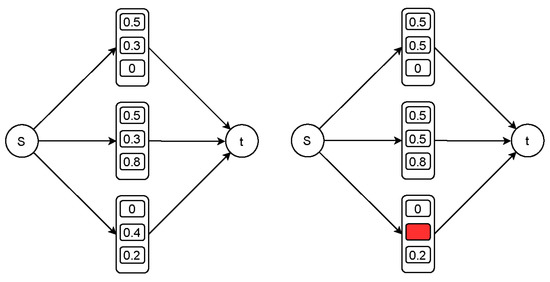
Figure 7. SFC failure correction.

Let ${\lambda }_s^{\prime }=1$ denote that SFC $s$ has failed. If ${\lambda }_s^{\prime }=0$, the service chain $s$ works well. A case of service chiain failure can be represented by ${\mathbf{\lambda }}^{\prime }$, in which vector ${\mathbf{\lambda }}^{\prime }=\left\{{\lambda }_s^{\prime }\right|s\in SC\}$. We used Equation (22) to meet all service chain demands in any scenario where $ns$ failures may occur.

5. Fast Convergence in the Interaction

In the previous part of the article, we completed the construction of the cross-layer architecture and considered the problem of network error correction that affects the cross-layer network. Although we minimized the frequency of network interactions, the difficulty of convergence for each interaction is still a problem that our architecture needs to solve. SRC and LLS serve different objects, so they have different objectives in the multilayer network architecture.

A selfish operation may lead the corresponding SRC link to have a high link load or SRC to become congested due to failures. The objective inconsistency between SRC and LLS makes both layers constantly change their routing configurations, causes network fluctuation, and greatly harms the time-sensitive performance of LLS. In this section, we provide two strategies to eliminate network fluctuation and realize fast convergence.

5.1. SRC Strategy for Fast Convergence

In this subsection, we propose a strategy for SRC to achieve fast convergence in the process of interaction and support time-sensitive applications to perform better in LLS. In SRC, we use a method to make the routing computed achieve less delay for every demand pair at the last round. Then, the links in LLS will not change largely, and the routing of LLS will not change drastically. This strategy makes the latency of LLS a stable value, reduces the fluctuation of LLS, and makes the interaction achieve an agreement fast. In order to adopt our strategy to our architecture, we added Equation (23) to SRC:

$$\sum _{k\in V}\sum _{e\in E}{y}_r^k{g}_r^k\left(e\right)\le hop{\left(r\right)}_{last},\forall r\in R$$

(23)

In Equation (23), we adopted the hop count to approximate the delay of an SRC path. $hop{\left(r\right)}_{last}$ denotes the total hop count of each flow $r$ after the operation of SRC in the last round and can be obtained by ${\displaystyle \sum _{k\in V}}{\displaystyle \sum _{e\in E}}{y}_r^k{g}_r^k\left(e\right)$ in the last round. Notice that in the first round, we did not add the strategy to SRC.

5.2. LLS Strategy for Fast Convergence

In this subsection, we propose a strategy for LLS to achieve fast convergence in the process of interaction and reduce the link load in SRC. In LLS, we adopted an idea that in the current round, the routing operation of LLS ensures the amount of overlay traffic in each overlay link is less than the amount in the last round. Then, the SRC will not notice the change in the value of MLU and will not change the overlay drastically. In this way, our architecture can obtain fast convergence in the process of interaction. To apply our strategy to our architecture, we added Equation (24) to our SRC:

$$\sum _{r^{\prime }\in R^{\prime }}{f}_{r^{\prime }}^{e^{\prime }}{d}_{r^{\prime }}\le load{\left(e^{\prime }\right)}_{last},\forall e^{\prime }\in E^{\prime }$$

(24)

In Equation (24), $load{\left(e^{\prime }\right)}_{last}$ denotes the amount of overlay traffic on each link after the operation of overlay routing in the last round and can be calculated as ${\displaystyle \sum _{r^{\prime }\in R^{\prime }}}{f}_{r^{\prime }}^{e^{\prime }}{d}_{r^{\prime }}$. In the first round, we did not add the strategy to LLS.

6. Performance Evaluation

In this section, we show the interaction process of SRC and LLS and verify that our strategies can help the network converge quickly. We first verified that there were fluctuations in the interaction between the basic LLS and SRC, verified the effectiveness of our strategies in the basic framework, and continued to add components, observe the impact of different components on the interaction experiment, and verify the effectiveness of our strategies in a more complex framework. We conducted experiments on available real-world topology of Ans in repetita [41]. Ans topology has 18 nodes and 50 edges. We set the link bandwidth capacity to a random value between 300 Mbps and 500 Mbps. Before conducting the experiment, we conducted a systematic investigation on the related work of the cross-layer network. The most commonly used link bandwidth capacity in the experiment was simply set to 10–20 Mbps [6]. The link bandwidth range was large, and there is no detailed description of how to select the bandwidth value for each link. This was mainly because different bandwidth settings had almost no effect on the convergence and the speed of convergence in the cross-layer experiment. Because we proposed a novel system model, we redesigned the cross-layer network experiment. We used the real topology from [5] and a set of random numbers between 300 and 500 Mbps as the bandwidth capacity of the links and then adjusted the SFC computing resource capacity according to the link bandwidth capacity. In the actual network, various resources are also flexibly configured according to demand to prevent a certain resource from becoming a bottleneck in the network system. On this basis, we randomly selected the demand matrix that the system could accommodate so that MLU could range from 30% to 100% and adjusted the ratio of user demand to background demand for multiple experiments. The overlay topology was composed of 7 nodes and 28 edges. There were 4 DC nodes in the overlay. Each of these DC nodes contained type-3 complete SFC [27], and the computing resource capacity of the SFC in each node was random from 0 to 100. In the underlay network, there are widespread background traffic demands. The value of the background traffic was set between 1 and 10 randomly. The demand matrix of the overlay follows the uniform distribution of [0, 50]. We mainly observed the process of cross-layer interaction under four failure types: SFC failures ($ns$), link failures ($ne$), node failures ($nv$), and control plane failures ($nc$). We ran these experiments in 100 steps and examined the MLU and latency. Note that we conducted experiments on multiple topologies in repetita, demand sizes, and link capacities, and the results were similar. Thus, we present the results on the Ans topology here to avoid repetition. In the experiment, we did not pursue to set each parameter to a large value, because the occurrence of multiple errors in the network was an event with a small probability [19]. Overprotection would lead to a sharp decline in network performance. Our experimental results prove the effectiveness of our method.

6.1. Interaction between Basic SRC and LLS

In Figure 8, we set $ns=0, ne=0, nv=0, nc=0$ in order to observe the interaction process between basic SRC and LLS. We present the results of the default interaction and new interaction using our strategies between basic SRC and LLS. During the default interaction process, the operations of SRC caused an increase in the total latency of LLS, and the operations of LLS minimized the total delay. The operations of LLS caused an increase in the MLU, and SRC minimized the MLU. Figure 8 clearly shows the existence of conflict between SRC and LLS. We found that the default interaction process did not reach a stable state even after 100 rounds. When applying our strategies, the new interaction converged within six rounds. In the balanced state, we could achieve a latency below the average and reach load balancing. This experiment verifies that the inconsistency of optimization goals between cross-layer networks will indeed cause continuous network oscillations and difficulty in convergence. Our strategies can significantly speed up convergence without affecting performance.

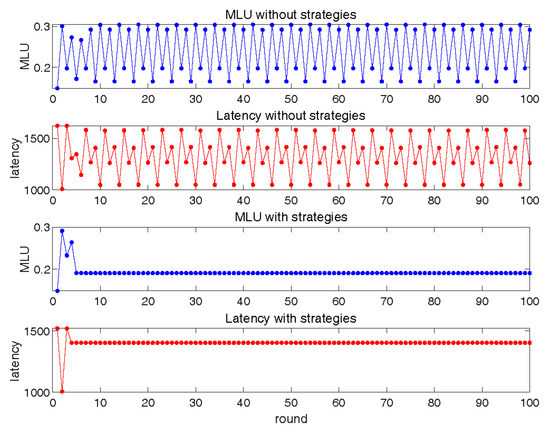
Figure 8. Interaction between basic SRC and LLS.

6.2. Interaction between SRC with Restoration and Basic LLS

In Figure 9, we set $ns=0, ne=1, nv=0, nc=0$ in order to observe the interaction process between basic LLS and SRC with single link failure restoration. In general, after the data plane error recovery function was added, the experiment still obtained similar results to the interaction of the basic version, but we can see that in order to reserve bandwidth for the error recovery function, both the MLU and latency would be slightly larger. The main reason for the increase in MLU is that the MLU of the basic version of SRC and the MLU of the error-corrected version of SRC have different meanings. As mentioned above, the MLU of the error-corrected version is the worst-case MLU after a network error occurs. Obviously, it is bigger than when there is no error (the basic version of SRC). In this experiment, we can still verify that our strategies can effectively accelerate convergence.

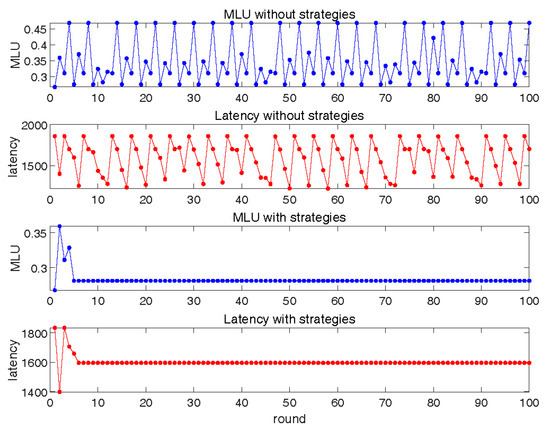
Figure 9. Interaction between SRC with data plane fault correction and LLS.

In Figure 10, we set $ns=0, ne=1, nv=0, nc=1$ to observe the interaction process between basic LLS and SRC with control plane failure correction. In this experiment, SRC may have suffered from a control plane failure and may not have been able to update the routing table configuration at each node, so the routing allocation scheme for the previous two rounds had to be considered in the MLU calculation. We can see that the oscillation amplitude of MLU in control plane failure scenarios was smaller than the oscillation amplitude of MLU in the data plane failure scenarios. This was because in the control plane failure scenario, we required that when a control plane error occurred, the network would not be congested, so the previous round of distribution plan was considered when calculating the traffic distribution scheme. When the SRC calculation was not only considering its own objective function but also considering the previous round of calculation results, it would accelerate the convergence speed of the cross-layer interaction. As shown in Figure 10, even if the accelerated convergence strategy was not used, the MLU and latency also converged within a limited round in this experiment. However, our strategies can still effectively accelerate convergence without a loss of performance.

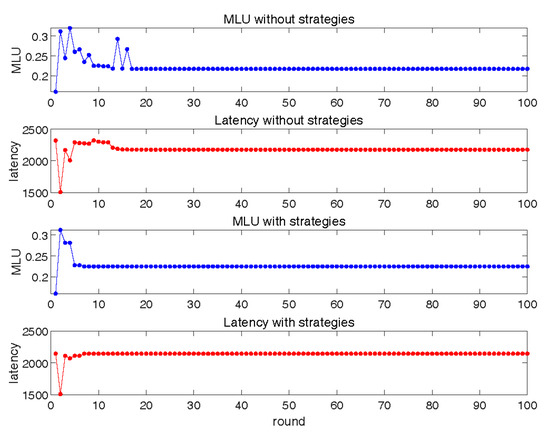
Figure 10. Interaction between SRC with control plane fault correction and LLS.

6.3. Interaction between Basic SRC and LLS with Service Correction

In Figure 11, we set $ns=1, ne=0, nv=0, nc=0$ in order to observe the interaction process between basic SRC and LLS with SFC failure correction. Because the situation of a service error is more complicated than the situation of a network error in SRC, and the network scale of LLS is smaller than that of SRC, LLS has a smaller solution space, and we can see that the amplitude was smaller in this experiment. However, it is worth noting that without the help of fast convergence strategies, convergence is still difficult to achieve. The curve of the latency without any strategies still oscillated with a small amplitude. Our fast convergence strategy in this experiment is still effective.

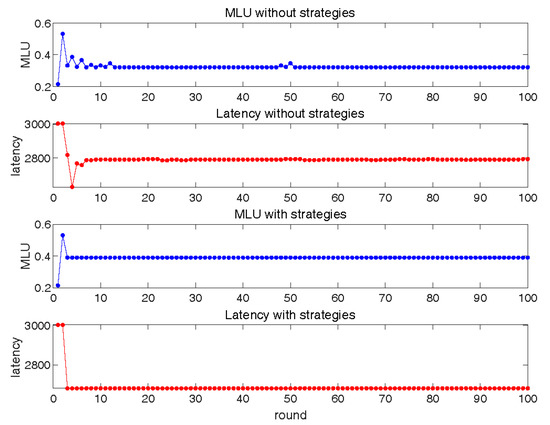
Figure 11. Interaction between SRC and LLS with service fault correction.

6.4. Interaction between SRC and LLS

In Figure 12, we set $ns=1, ne=0, nv=0, nc=1$ in order to observe the interaction process between fully functional SRC and LLS. We can see that after adding all the modules we proposed to the network, the fluctuation of the network presented a disorderly state. The reason for this is that each type of module had a different function, and it has been verified in previous experiments that they have different effects on network fluctuations. Network fluctuations showing this complexity can also be expected. In our complex architecture, the strategies of accelerating convergence can still achieve rapid convergence under the premise of guaranteed performance. Therefore, our cross-layer architecture can calculate and converge quickly when the demand arrives, avoid entering the interactive state, and conduct reactive error correction when errors occur, all of which can effectively guarantee the performance of upper-layer time-sensitive applications.

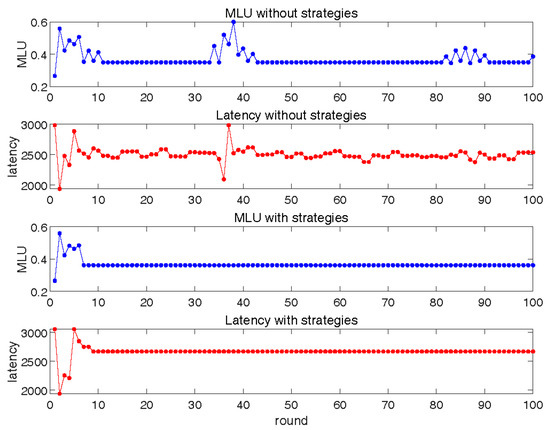
Figure 12. Interaction between fully functional SRC and LLS.

6.5. Convergence Time Varies with Network Size

In the above experiments, we used the fixed topology Ans to conduct all experiments. In this subsection, we explore whether our accelerated convergence strategy will change with the change of the network scale. We choose seven topologies with different numbers of nodes and links in repetita. The specific information of each topology can be obtained from Table 2. According to the above experiment, we knew that different components in our paper had an impact on convergence. In order to investigate the relationship between the convergence time and network size under our accelerated convergence strategy, we set $ns=0, ne=0, nv=0, nc=0$. We used different topologies to replace the models in the underlay, and the number of nodes in these topologies increased by three each time. We decomposed the convergence time into the time to solve the SRC, the time to solve the LLS, and the number of interactive rounds required for convergence, because in different hardware environments, the absolute running time does not have much meaning.

Table 2. Convergence time varies with network size.

Topology	Nodes	Links	SRC	LLS	Convergence
Eunetworks	14	42	0.2633 s	1.0651 s	5 rounds
Agis	17	44	0.6656 s	2.4879 s	5 rounds
EliBackone	20	60	1.8755 s	5.1245 s	5 rounds
Integra	23	64	3.6163 s	9.3239 s	5 rounds
Darkstrand	26	56	5.7526 s	17.1196 s	4 rounds
Cesnet	29	66	10.8048 s	28.2829 s	4 rounds
Canerie	32	82	19.1414 s	126.8002 s	5 rounds

The results of the experiment are shown in Table 2. In the SRC model, as the number of nodes increased, the time to solve the linear programming model was doubled, mainly because the number of variables of the basic SRC model was $O({\left|V\right|}^3)$, and the number of constraints was $O({\left|v\right|}^2+\left|E\right|)$. Therefore, the number of links in the topology had a small effect on the calculation time of the model. For example, although the number of links in Darkstrand was smaller than that of Integra, the calculation time of SRC was doubled. The number of variables and the number of constraints of the LLS model were $O({\left|V\right|}^3)$ and $O({\left|V\right|}^2\left|E\right|)$, respectively, so the calculation time of LLS was more sensitive to the number of links. For the convergence time, we can see that the number of convergence rounds would not become larger as the network topology and calculation time became larger, which also shows the efficiency of our convergence strategy. However, as the network became larger, because the calculation time became longer and longer, the total time for the network to enter convergence would become longer and longer, and a strategy to accelerate convergence was necessary.

According to our observations in the experiment, when no acceleration convergence strategy was used, there would be two situations: one was to reach a consensus after a period of interaction, and the other was to be in an interactive state and fluctuate consistently. Whether the network will continue to fluctuate depends on, among other factors, the topology and the input demands. When using our strategy to accelerate convergence, the network can quickly reach a consensus. In [42,43], the authors explained the reasons for the fluctuations and the process of convergence through theoretical derivation, simple examples, and experimental proofs.

7. Conclusions

In this paper, a cross-layer network architecture based on an overlay that meets user’s SFC requirements and time performance requirements and an underlay that optimizes the performance of a physical network was proposed. We proposed an SR-based method SRC to correct the network failures in the underlay. At the same time, we solved the SFC failures in the overlay through a proactive algorithm. We modeled the interaction of SRC and LLS as a repeated game and designed novel strategies to eliminate the fluctuations of interaction. The experiment results demonstrate the effectiveness of our methods under different failure scenarios and definitely show that our strategies are equally effective in multiple combinations of failure scenarios. Our method can not only reduce congestion caused by network failures but also speed up the convergence of cross-layer interactions due to route reconfiguration. Thus, our approach can greatly improve the performance of applications in the overlay.