Abstract
Deep learning has achieved outstanding results in various tasks in machine learning under the background of rapid increase in equipment’s computing capacity. However, while achieving higher performance and effects, model size is larger, training and inference time longer, the memory and storage occupancy increasing, the computing efficiency shrinking, and the energy consumption augmenting. Consequently, it’s difficult to let these models run on edge devices such as micro and mobile devices. Model compression technology is gradually emerging and researched, for instance, model quantization. Quantization aware training can take more accuracy loss resulting from data mapping in model training into account, which clamps and approximates the data when updating parameters, and introduces quantization errors into the model loss function. In quantization, we found that some stages of the two super-resolution model networks, SRGAN and ESRGAN, showed sensitivity to quantization, which greatly reduced the performance. Therefore, we use higher-bits integer quantization for the sensitive stage, and train the model together in quantization aware training. Although model size was sacrificed a little, the accuracy approaching the original model was achieved. The ESRGAN model was still reduced by nearly 67.14% and SRGAN model was reduced by nearly 68.48%, and the inference time was reduced by nearly 30.48% and 39.85% respectively. What’s more, the PI values of SRGAN and ESRGAN are 2.1049 and 2.2075 respectively.
1. Introduction
Deep learning has been proven to be powerfull on tasks including image classification, objection detection, natural language processing and so on. Super-resolution [1,2,3,4,5,6,7] is one of the important applications of deep learning in computer vision. Its main function is to improve the clarity of enlarged images and reduce the degradation of image quality caused by image enlargement. From simple mathematical methods to methods based on deep learning, such as SRCNN proposed by Dong et al. [2], SRGAN proposed by Ledig et al. [1] and ESRGAN proposed by Wang et al. [3], the performance of super-resolution reconstruction is constantly improving.
With the fast development of neural network research and application, people want more and more accurate predication, and networks grows deeper and deeper. The memory size of network becomes a problem. The model size is not only a memory usage problem, it’s also a memory bandwidth problem. Therefore, the size of the network model becomes one of the main concerns of researchers, especially on especially in an environment with limited resource or power consumption.
Model quantization [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], as a means of compressing model, can be applied to model deployment, so that both the model size and the inference delay can be reduced. At present, the sizes of SR models become larger and larger. For instance, a common SRGAN model is about 16 MB in size and has 259G MACs (Multiply–Accumulate Operations), while a common ESRGAN model is about 32 MB in size and 1804G MACs. Figure 1 lists some models and their model size and MACs. Therefore, many researches focus on the methods to reduce model sizes. Quantization is one of the most effective approaches at present, so it has attracted extensive attentions of researchers. Its main idea is to map a data type with a wider representation range and a larger storage space to another data type with a more narrow representation range and a smaller storage space, and therefore reduce the model size and the time overheads. For example, a mapping from high-precision floating point data type to a low-precision one, or from floating point to integer, etc. When a model is quantized, the mapping process inevitably introduces some information loss, and the accuracy of the result model will be reduced accordingly. Therefore, quantization technology will generally be used with other methods together to ensure that the loss of accuracy is as small as possible while effectively reducing the size of model and MACs.
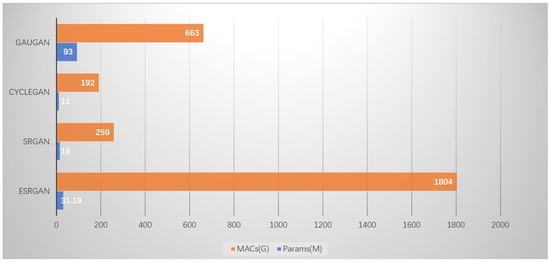
Figure 1.
The model size and calculation amount of super-resolution using deep learning.
However, current model quantization approaches usually have an important drawback, which limits its effectiveness greatly. Existing quantization methods mainly focus on the reduction of model size while ignoring its impact on the model performance (i.e., accuracy). At many cases, quantization effectively compresses the model and shrinks the inference time, but the accucracy of the result also decreased a lot. For example, if simply employing 8-bit integer to replace single-precision floating-point weights, EDSR [6] model will save 73 percent capacity and get a 43 percent performance acceleration, but the accuracy will be decreased by 53 percent. There are some reasons for so much accuracy loss, such as too much information are lost during quantizing. However, for most cases, this is caused because an existing method usually uses a unique quantization strategy to process all stages in the network, ignoring the sensitivity of different stages to data types and results accuracy. For example, for SRGAN and ESRGAN model’s basic blocks and upsampling stage, quantization can reduce the size of the model with little effect on accuracy. However, for other stages, the accuracy will decreases rapidly as the size of the model decreases. The detailed statistical results are shown in Figure 7.
Aiming at the above problems, this paper takes SR model as an example to evaluate the sensitivity of SRGAN and ESRGAN models with quantization aware training at each stage, and identifies the stage with the highest sensitivity. In addition, a mixed quantization method is proposed to obtain a comprehensive quantization results with small model size, short test time and almost unchanged accuracy. In this paper, quantization aware training is selected as the baseline approach when quantizing SR models. The two quantization methods, static post-training quantization and quantization aware training, are used to test the generator part of the SRGAN and ESRGAN models, which ensures the quantization method from the PI value. It is found that the effect of post-training static quantization is far inferior to quantization aware training. Among them, the PI values of SRGAN are 4.6278 and 2.4731 respectively, and ESRGAN is 4.562 and 2.688. In the meanwhile the model size is reduced by nearly 75%.
This paper has two contributions:
- (1)
- The concept of “quantization sensitivity” is proposed, which describes the sensitivity of quantization results of all stages to a quantization approach, from three aspects: model size, test time and result accuracy.
- (2)
- For different stages of the same network with different quantization sensitivities, a hybrid quantization method is proposed to obtain a good quantization results in model size, testing time and accuracy.
Taking two popular SR models (SRGAN and ESRGAN) as the input of quantization and the quantization aware training as the baseline method, we evaluate the performance of our hybrid quantization approach. With our apprach, the ESRGAN model was still reduced by nearly 67.14% and SRGAN model was reduced by nearly 68.48%, and the inference time was reduced by nearly 30.48% and 39.85% respectively. What’s more, the PI values of SRGAN and ESRGAN are 2.1049 and 2.2075 respectively.
The rest of this article is organized as follows. The Section 2 introduces model quantization and super-resolution in brief, and lists some related works. The Section 3 introduces our hybrid quantization method in detail, and discusses how to quantize the training model. The Section 4 lists the experimental environment and eavluates the performance our approach. Finally, the Section 5 gives some conclusions.
2. Background and Related Works
2.1. Super-Resolution
Super-resolution [1,2,3,4,5,6,7] is one of the hottest research areas of low-level image problems in computer vision. Super-resolution technology is mainly to reconstruct images and videos with low-resolution into high-resolution images and videos. This article only studies the problem of image super-resolution. The problem of image super-resolution can be divided into multi-image-based super-resolution reconstruction and single-image-based super-resolution reconstruction. Among them, multi-image-based super-resolution reconstruction refers to a method of obtaining multiple low-resolution images that reflect different positions or pixel shifts that need to be obtained in the same scene, and use multiple low-resolution images to obtain high-resolution images. Such as the continuous motion of the object to capture images, etc. And single-image-based super-resolution reconstruction refers to the method of obtaining high-resolution images from a single low-resolution image. This method only uses the information of a low-resolution image to obtain high-resolution images. In many practical applications, due to hardware devices with limited storage capacity, time-sensitive shooting information and other factors, users often cannot obtain multiple low-resolution images reflecting different angles, such as cameras. Time sequence information of captured objects, satellite imaging images, etc. So the super-resolution technology based on single image has a wide range of applications. This article mainly studies the super-resolution technology based on single image. In real life, due to hardware constraints or data transmission bottlenecks, the directly obtained images are often small in size and difficult to meet users’ needs. Therefore, the size of the image needs to be enlarged to meet the users’ processing requirements. In the process of image enlargement, users hope to reduce the quality loss of the image as much as possible, and the goal of super-resolution technology is just to reduce the quality loss during the image enlargement process. Therefore, super-resolution has a wide range of application scenarios and is of great significance to medical imaging, traffic management and other fields.
The core idea of super-resolution reconstruction based on single images is to predict the enlarged images’ information based on the information of the low-resolution image and improve the resolution of the enlarged image. Before the emergence of deep learning methods, super-resolution reconstruction based on single images mainly relied on traditional mathematical methods, such as coding methods using sparse dictionaries, interpolation methods such as bilinear interpolation. However, these simple super-resolution reconstruction images obtained by using traditional mathematical methods are still unsatisfactory, because these methods mainly rely on simple mathematical calculations to predict the high-resolution images’ RGB pixel values from low-resolution, and the reconstructed images obtained are often blurry, besides, the sensory effect in human eyes is poor, too.
SRCNN [2] applies the model structure of deep learning to the field of super-resolution, and has achieved good results. After SRCNN, the super-resolution reconstruction technology mainly relies on deep learning methods. SRCNN began to use an end-to-end mapping method to directly map low-resolution images to high-resolution images after bicubic interpolation. It fits the nonlinear mapping through a three-layer convolutional network, and finally outputs a high-resolution image result. The structure of the three-layer convolution is explained into three steps: image block extraction and feature representation, feature nonlinear mapping and final reconstruction. Then, in order to solve the problem that the bicubic interpolation destroys the rich image information in the low-resolution image, the model cannot be directly used. Figure 2 is the process of solving super-resolution with the deep learning method.
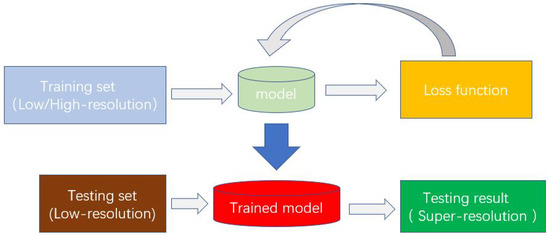
Figure 2.
The process of super-resolution using deep learning.
VDSR [5] takes the low-resolution image in target size obtained by interpolation as the input of the network, and then adds this image and the residual error learned by the network to obtain the final output of the network. Making full use of the idea of residual network, the input low-resolution image and the output high-resolution image are similar to a large extent, that is, the low-frequency information carried by the low-resolution image and the low-frequency information of the high-resolution image Similar, it will take a lot of time to bring this part during training. In fact, we only need to learn the high-frequency part residuals between the high-resolution image and the low-resolution image.
The generative adversarial network [27] is used to solve the super-resolution problem. In addition to the traditional method of using the mean square error as the loss function to obtain a high peak signal-to-noise ratio (PSNR) when training the network, it also uses perceptual loss and adversarial loss to improve the recovery effect of the picture, such as reality, more texture details. Perceptual loss uses the features extracted by the network to compare the differences between the features of the generated image and the target image after passing through the convolutional neural network, so that the generated image and the target image are more similar in semantics and style.
2.2. Model Quantization
Quantization [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], as the name implies, is to let the weight and activation of the forward propagation calculation in the neural network and the 32-bit or 64-bit floating point number of the gradient value of the back propagation calculation are represented by low-bit floating point or fixed-point number, and can even be directly calculated. Figure 3 shows the basic idea of converting floating-point numbers into signed 8-bit fixed-point numbers.
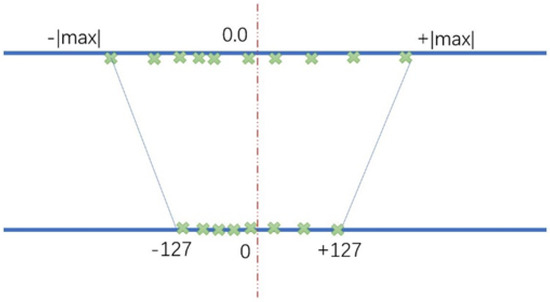
Figure 3.
The process of quantization.
Quantization itself can be divided into linear quantization and non-linear quantization. The steps of non-linear quantization are not fixed, and the method is not fixed, too. Basically, it only reduces the storage size of the model. There is no acceleration and even time complexity in model inference and data processing. So the main discussion is linear quantization. The basic principle of linear quantization is relatively clear. Take the 32-bit floating point to 8-bit integer as an example. Establish the data mapping relationship between the two, from the original data accuracy value to the corresponding quantized value. Its general form can be expressed as:
Among them, x and q are the numbers before and after quantization, s is called the scaling factor, and z is called the zero point. The zero point is the quantized value of “0” in the original value range. There will be a lot of 0 in the weight or activation (such as zero padding, or through the ReLU function), so we need to make “0” accurately represented after quantization when we quantize. In order to quantize in the range of n-bit integers, then:
Among them, the denominators are the lower (min in above equation or in Figure 3) and upper bounds of the value range of the mapping value (such as weight or activation) respectively.
Quantization Method
According to the number of quantization bits, it can be divided into floating-point quantization and fixed-point quantization. Floating-point quantization is to quantize the original high-precision number with 16-bit floating-point or 8-bit floating-point number or even lower-precision floating-point number. Fixed-point quantization means high-precision quantization into 16-bit fixed-point or 8-bit fixed-point quantization or even lower-precision quantization. The quantized data is inferenced or trained in the neural network, and the intermediate data can be calculated and stored with low precision. Generally speaking, this quantization method mainly considers the choice of the number of data mapping bits and the method, and the principle is the same as mentioned above. At present, 8-bit integer quantization has the most stable effect in a variety of tasks, so this article mainly studies 8-bit integer quantization.
On the basis of whether quantization is needed in the quantization process, it is divided into post-training quantization and quantization aware training. Post-training quantization is the quantization operation after the floating-point model training converges, and whether it is necessary to “feed” the data to the model for calibration, it is divided into static quantization and dynamic quantization. The calibration in static quantization is to “feed” data to the model in advance (usually about a few hundred data), and determine the zero point and the scaling factor. For the determination of quantization parameters, sometimes the training environment and training data cannot be obtained, so calibration cannot be used. In dynamic quantization, the weight is quantized in advance, and the activation is dynamically quantized in the forward inference process, that is, the scale value and zero point are calculated once for each layer of the actual floating-point data range, and then quantized. Therefore, calibration is not used, but the maximum and minimum values are determined directly and dynamically based on the input tensor value, and then other parameters are determined. Static quantization is shown in Figure 4.
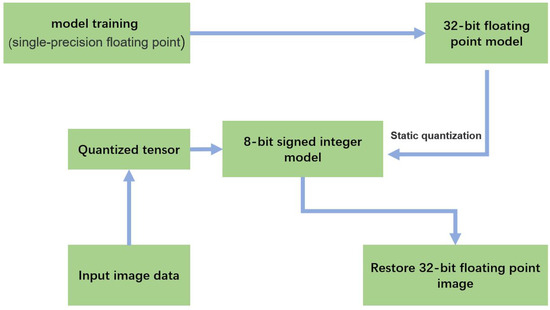
Figure 4.
The static quantization process of the model.
Quantization aware training is model quantization in the process of network training. By using fake quantization in training to simulate the process of training 8-bit integers which use clamping and approximating, so that the weights are able to simulate 8-bit integers to inference and train, but the entire model training is still carried out under the original precision. Quantization aware training is shown in Figure 5.

Figure 5.
Quantization aware training process.
2.3. Super-Resolution Model in Quantization
Super-resolution quantization technology [8,28,29,30,31,32] has recently started to do a lot of work. At the beginning, super-resolution reconstruction focused on the results obtained with the accuracy of each pixel. Comparing with the low-precision model which is compressed and quantized such as classification tasks and semantic text work, many people think that super-resolution model quantization may make the image not clear and true enough, resulting in a substantial decrease in model performance. Therefore, there is not much quantization work on super-resolution. However, the overall framework of the super-resolution model is mainly composed of deep convolutional neural networks. Deep neural networks have a lot of compression and quantization model work in the training and inference stages, including methods of compressing convolutional neural networks. In existing methods, researchers and experts have paid great attention to attempts to limit the weights of convolutional neural networks to low-precision values (such as binary values or bit-quantized values). First, Expected Back Propagation (EBP) [33] is proposed to estimate the posterior distribution of network weights. During the probabilistic feedforward inference, the weights are constrained to be +1 and −1. BinaryConnect [9] extends the former idea. First, it proposes to directly binarize the network weights in the training phase, and update the weights which consist of original values according to the gradient of the binarized weights in backfoward propagation process. The state-of-the-art classification performance is achieved on a small data set, indicating that binary CNNs may have performance very close to the true value network. Based on BinaryConnect, the binary network binarizes the weight and activation. XNOR-net [12] further expands beyond binary networks and binary connections by combining binary convolution operations and binary inputs in the forward inference process. Although accuracy is sacrificed to some extent, it reduces memory usage and greatly increases computing speed. Later, in addition to the above work, there is much other work to train convolutional neural networks with low-precision weights, low-precision activations and even low-precision gradients, such as three-valued weight network [18] (TWN), DoReFa-Net, quantized neural network [11] (QNN) and Incremental Network Quantization [19] (INQ).
From past experience, simply binarizing the entire super-resolution network does not produce satisfying results. Therefore, Yinglan Ma [29] explored the image super-resolution task of neural network binarization, and proposed a binarization strategy, which binarizes the convolution filter by only binarizing the residual block and learnable weights. Without losing too much accuracy, it reaches 80% size of the original model and increases the inference speed by 5 times. However, this work only studies binary weights and full-precision activation models, and convolution calculations are not bit operations, so the inference speed of the model is not simplified enough. On the basis of predecessors, Jingwei Xin [30] once again used binary weights and even intermediate activations in order to find the best approximation of convolution using bit operations and perform image super-resolution tasks on devices with limited computing resources. Among them, the convolution can be estimated through the bit operation, and the speed is about 58 times faster than the equivalent network of single-precision weights (the model size is also about 32 times compressed). The inference can be done efficiently on the CPU. At the same time, a bit accumulation mechanism is proposed, which approximates the full-precision convolution through an iterative scheme of cascading binary weighting and activation. And it only relies on the existing basic model, without introducing any other additional inference modules, to achieve high-precision one-bit estimation of weights and activation values. Experiment results show that this method can achieve better super-resolution performance with a lighter network structure and fewer operations.
3. Quantizton Method Selection of Typical SR Model
SRGAN [1] and ESRGAN [3] are classical super-resolution models in deep learning methods. SRGAN’s job is to fool the discriminator network to determine whether the image obtained was generated by the generator network or the original image in the database so as to let the generator network generate high-resolution images from low-resolution images.
ESRGAN [3] is an improved version of SRGAN. First of all, like EDSR [6], the BN layer is removed to reduce artifacts, which can reduce the amount of calculation and generate richer texture details. Secondly, the GAN loss function is upgraded to RaGAN [7], allowing the relative discriminator to predict the authenticity of the image rather than whether the image is “fake image”, and network interpolation is also added to generate a richer detailed image than the image interpolation. At the same time, the perceptual loss is performed before the activation function, and the structure of the dense network and the residual network is also added. The combination of residual network and dense connection is called RRDB block.
To get higher quality super-resolution images with less cost, and less training and inference time, Ninghui Yuan [34,35,36] proposed a multi-model super-resolution framework (MMSR). In the framework, all input images are classified by an approach called TVAT (Total Variance above the Threshold). And the framework prunes the training set according to the complexity of the images in the training set, which significantly reduces the size of the training set. At the same time, the framework can select the specific depth according to the image features of the images to recover the images, which helps to improve the SR-reconstruction effect.
As mentioned in Section 2, to use quantization in the prosess of training and testing, static quantization and quantization aware training are selected, for select the better quantization method.
At present, pytorch [37] supports eight-bit integer quantization, and supports many model quantization methods. The article uses the pytorch’s method to experiment. The evaluation index uses the PI value, which is the perception index, as the criterion. The PI value and the direct perception of human vision are more matched than traditional evaluation indexes such as PSNR (peak signal to noise ratio). The more natural and clear images human eyes observe, the lower the PI value is, which means the higher the image quality.
All the experiment involved in this article is done on the “CPU+GPU” computing node. The system configuration of the computing node is shown in Table 1:

Table 1.
System parameters of computing nodes.
We test two methods to quantize the SRGAN and ESRGAN models. Using DIV_2K set to train and PRIM dataset to test, which contains 800 and 100 pictures respectively, we measured the model size, reference time and model reconstruction effect (PI value, perception index [4]) and got the results, as shown in Table 2:

Table 2.
Quantized results of ESRGAN and SRGAN models.
Above Table 2, -B represents before quantization, -A represents after quantization. -O represents original model, -S represents post-training static quantization, -Q represents quantization aware training. Inf time represents model’s inferncing time.
Among them, we found that the model size has been reduced by four times, but the inference result is quite different. This is not difficult to understand. Static quantization directly converts the trained model with the original precision into 8-bit integer. The quantization error is directly reflected in the result, and there is no way to solve it. This does not seem to be a problem. Quantization is a numerical mapping of floating-point numbers to integer numbers. The data representation range of its own will be reduced. Errors are certain, but quantization aware training can reduce more errors. Quantization aware training is a quantization method that can achieve high accuracy. When using quantization aware training, all weights and activation are “fake-quantized” during the forward and backward propagation in training, that is, floating-point values will approximate 8-bit integer values, but all calculations will still use floating-point numbers get on. Therefore, all weight adjustments during the training process are performed after “perceiving” the fact that the model will eventually be quantized. Therefore, after quantization, the quantization error will also be invisibly added to the loss function of the original model. Therefore, it usually produces higher accuracy than dynamic quantization or static quantization after training. In conclusion, based on the experiment results, we choose quantization aware training as the quantization method for subsequent experiment and work.
4. Mixed Quantization Method
4.1. The Basic Concept of Sensitivity
The concept quantization sensitivity shows a phenomenon, that is, when we quantize a model or network, different stages of model or network quantized will get a result of huge difference. The reason why quantization sensitivity hapens is that every stage in the model or network has its weight, and some stages don’t influence others althogh get quantized if these stages aren’t sensitive to the quantization and vice versa.
4.2. Mixed Quantization
The main idea of mixed quantization is to select different mapping to combine them to get model or network higher accuracy. We all know that the two super-resolution models of SRGAN and ESRGAN are divided into several stages: feature extraction block, residual and dense blocks (basic blocks), up-sampling block and high-resolution reconstruction block. As shown in Figure 6:
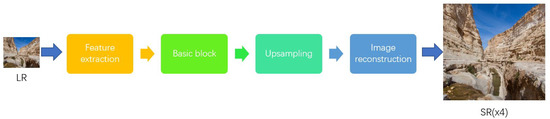
Figure 6.
Super-resolution network framework (generator of GAN network).
Although quantization has many advantages in model size reduction and model inference. But if the entire model is directly quantized, some parts of the model may be sensitive and will not be discovered. Therefore, the four parts of these two models will be individually and partially quantized to see what effect the partial quantization has on the performance of the entire model. The most commonly used testing image sets in super-resolution are Set7 and Set14, which contain 7 and 14 images respectively. However, in order to expand the number of images displayed and the calculated PI value to be more general, we use the PRIM test set. This test set is also a commonly used test set for super-resolution, and there are 100 images in total, which contain richer image content. Therefore, we use PRIM as the test set for experiment, and the image enlarge scale is 4 times.
We use quantization aware training to quantize different parts of SRGAN and ESRGAN during the training, and measure the PI values respectively to study the sensitivity of part quantization to the super-resolution model. The results are shown in Figure 7 below:
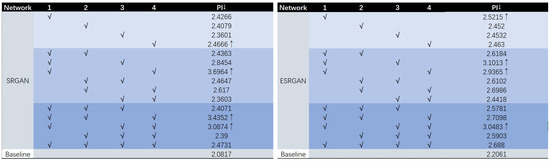
Figure 7.
The results of quantization sensitivity test.
From the above results, it can be seen that when we concern about only one part quantization, the image reconstruction part has the highest sensitivity, followed by the feature extraction part, then the upsampling part, and finally the residual basic block part. The image reconstruction stage is to directly convert the features obtained through a series of convolution and residual connections into RGB three-channel images through convolution operations. The experiment results show that the feature maps obtained by this part of the stage are more sensitively quantized, which has a greater impact on model performance.
From the result of quantizing only one part of the ESRGAN model, the feature extraction part is higher than the remaining three parts. The second higher is the reconstruction part. The results of the quantization of the two parts, the quantization of the feature extraction and reconstruction part, have higher PI. The PI value of the quantized three parts including the two, which is the combination of these parts, is 3.0483, which have the highest PI value.
5. Experiment and Discussion
5.1. Experiment
According to the mixed quantization and the concept quantization sensitivity, we select the two highest stages to quantize in a higher-bit. When the quantization bits of the feature extraction stage and the image reconstruction stage in two model frameworks are respectively increased, the 8-bit integer quantization is changed to 16-bit integer, the PI value is reduced from 2.4266 to 2.1298 in SRGAN, which greatly reduces the overall sensitivity of the model. In this way, when we quantize, we can set different quantization bits for each part according to the sensitivity of each part of the model to quantization, which can ensure that the final accuracy error of the model is minimized, and at the same time it is accelerated. We use 16-bit integer quantization for the feature extraction part and image reconstruction part of SRGAN and ESRGAN, and 8-bit integer quantization for the rest. The results are as follows in Table 3 (-M refers to the model modified (optimized)):

Table 3.
Multi-precision quantized results of ESRGAN and SRGAN models.
It can be seen that after quantizing sensitive part with higher bits, combining the rest parts in quantization aware training, the accuracy of the model is better than that of directly using quantization aware training to entire model. Although some model size is sacrificed under the premise of compressing it, it is still optimized by nearly 67.15% and 68.48%, and the inference time is reduced from 82 s and 138 s to 57 s and 83 s. Although model size is compressed worse than straight quantizing all model to some extent, it gets better super-resolution images comparing with the original from PI value. We select two images in the data set as an example. As is shown in Figure 8. From the figure, we can see that the images quantized in mixed precision have the approximate perfomance compared to the images without mixed quantization.

Figure 8.
Two comparison of our method and the original one.
5.2. Discussion
The operations of feature extraction and image reconstruction are opposite operations. One is to convert the low-resolution image pixel features of the RGB channel into a 64-channel feature map, and the other is to convert the 64-channel feature map back to a super-resolution image of the RGB channel. From the experiment results, quantizing the two parts will get relatively high PI value, and it will be more sensitive if the two parts quantized simultaneously, which will severely affect the effect of the generated image. The detailed operation of the two part is showed in Figure 9:
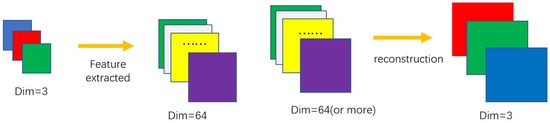
Figure 9.
Two parts’ operations in detail.
We found that the two parts with greater quantization sensitivity are the feature extraction part and the image reconstruction part. The stages in the two parts are mainly convolution kernels. The middle two parts of SRGAN and ESRGAN are mainly residual blocks or dense blocks containing convolution. Basically, the channel dimensions have not changed much, and 64 channels are the main ones (although there is channel concatenating, the data shows that quantization is not particularly sensitive to it).
6. Conclusions
This paper proposes a new concept (i.e., quantization sensitivity) to describe the degree to which a certain stage of a network model is affected by a specific quantization method. Then, based on the experimental results that that the quantization sensitivities usually change in different stages, this paper proposes a hybrid quantization method to obtain a better comprehensive results, which is evaluated from three aspects: model size, test time, and accuracy. Evaluation results indicate that with our hybrid quantization stratagy, the accuracies of two typical SR models are kept almost unchanged while the model size decrease greatly. This combination of multiple quantization mehtods makes the performance of the model be greatly improved, i.e., the PI value of the image getting inferenced is reduced from 2.4731 to 2.1049 when using SRGAN model, and from 2.688 to 2.2075 when using ESRGAN model. Next, we plan to implement an automatic sensitivity evaluation and hybrid quantization method selection framework, and evaluate its performance with more neural network models.
Author Contributions
Conceptualization, J.L., Q.W. and L.S.; methodology, J.L., Q.W., D.Z. and L.S.; validation, J.L. and D.Z.; writing—original draft preparation, J.L.; writing—review and editing, Q.W., D.Z. and L.S.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science Fundation of China grant number 62032001 and 61972407.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CUDA | Compute Unified Device Architecture |
| SR | Super-Resolution |
| GPU | Graphics Processing Unit |
| SRCNN | Image super-resolution using deep convolutional networks |
| SRGAN | Super-resolution using a generative adversarial network |
| ESRGAN | Enhanced SRGAN |
| EDSR | Enhanced Deep Residual Networks for Single Image Super-Resolution |
| OS | Operation System |
| CPU | Central Processing Unit |
| PI | Perceptual Index |
| TWN | Ternary Weight Networks |
| INQ | Incremental Network Quantization |
| QNN | Quantized Neural Network |
| CNN | Convolutional Neural Network |
| DNN | Deep Neural Network |
References
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Loy, C.C.; Qiao, Y.; Tang, X. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Ying, T.; Jian, Y.; Liu, X. Image Super-Resolution via Deep Recursive Residual Network. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Jolicoeur-Martineau, A. The relativistic discriminator: A key element missing from standard GAN. arXiv 2018, arXiv:1807.00734. [Google Scholar]
- Choi, J.; Zhuo, W.; Venkataramani, S.; Chuang, I.J.; Gopalakrishnan, K. PACT: Parameterized Clipping Activation for Quantized Neural Networks. arXiv 2018, arXiv:1805.06085. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J.P. BinaryConnect: Training Deep Neural Networks with Binary Weights during Propagations; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1. arXiv 2016, arXiv:1602.02830. [Google Scholar]
- Wu, J.; Cong, L.; Wang, Y.; Hu, Q.; Jian, C. Quantized Convolutional Neural Networks for Mobile Devices. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Sa, C.D.; Leszczynski, M.; Jian, Z.; Marzoev, A.; Ré, C. High-Accuracy Low-Precision Training. arXiv 2018, arXiv:1803.03383. [Google Scholar]
- Chu, T.; Luo, Q.; Yang, J.; Huang, X. Mixed-precision quantized neural networks with progressively decreasing bitwidth. Pattern Recognit. 2021, 111, 107647. [Google Scholar] [CrossRef]
- Mishra, A.; Nurvita DHi, E.; Cook, J.J.; Marr, D. WRPN: Wide Reduced-Precision Networks. arXiv 2017, arXiv:1709.01134. [Google Scholar]
- Zhuang, B.; Liu, L.; Tan, M.; Shen, C.; Reid, I. Training Quantized Neural Networks with a Full-precision Auxiliary Module. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Li, F.; Liu, B. Ternary Weight Networks. arXiv 2016, arXiv:1605.04711. [Google Scholar]
- Zhou, A.; Yao, A.; Guo, Y.; Xu, L.; Chen, Y. Incremental Network Quantization: Towards Lossless CNNs with Low-Precision Weights. arXiv 2017, arXiv:1702.03044. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations. J. Mach. Learn. Res. 2016, 18, 6869–6898. [Google Scholar]
- Kim, N.; Shin, D.; Choi, W.; Kim, G.; Park, J. Exploiting Retraining-Based Mixed-Precision Quantization for Low-Cost DNN Accelerator Design. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2925–2938. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Lin, J.; Ding, Y.; Liu, Z.; Zhu, J.Y.; Han, S. GAN Compression: Efficient Architectures for Interactive Conditional GANs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Zhuang, B.; Tan, M.; Liu, J.; Liu, L.; Shen, C. Effective Training of Convolutional Neural Networks with Low-bitwidth Weights and Activations. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Cai, H.; Gan, C.; Wang, T.; Zhang, Z.; Han, S. Once-for-All: Train One Network and Specialize it for Efficient Deployment. arXiv 2019, arXiv:1908.09791. [Google Scholar]
- Chang, S.E.; Li, Y.; Sun, M.; Jiang, W.; Shi, R.; Lin, X.; Wang, Y. MSP: An FPGA-Specific Mixed-Scheme, Multi-Precision Deep Neural Network Quantization Framework. arXiv 2020, arXiv:2009.07460. [Google Scholar]
- Vasquez, K.; Venkatesha, Y.; Bhattacharjee, A.; Moitra, A.; Panda, P. Activation Density based Mixed-Precision Quantization for Energy Efficient Neural Networks. arXiv 2021, arXiv:2101.04354. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Bing, X.; Bengio, Y. Generative Adversarial Nets; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Lee, R.; Dudziak, U.; Abdelfattah, M.; Venieris, S.I.; Lane, N.D. Journey Towards Tiny Perceptual Super-Resolution. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Ma, Y.; Xiong, H.; Hu, Z.; Ma, L. Efficient Super Resolution Using Binarized Neural Network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Xin, J.; Wang, N.; Jiang, X.; Li, J.; Huang, H.; Gao, X. Binarized neural network for single image super resolution. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 91–107. [Google Scholar]
- Li, H.; Yan, C.; Lin, S.; Zheng, X.; Zhang, B.; Yang, F.; Ji, R. PAMS: Quantized Super-Resolution via Parameterized Max Scale; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Soudry, D.; Hubara, I.; Meir, R. Expectation Backpropagation: Parameter-Free Training of Multilayer Neural Networks with Continuous or Discrete Weights. In Proceedings of the Neural Information Processing Systems (NIPS), Montreal, QC, USA, 8–13 December 2014. [Google Scholar]
- Yuan, N.; Zhu, Z.; Wu, X.; Shen, L. MMSR: A Multi-model Super Resolution Framework. In Network and Parallel Computing; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Yuan, N.; Liu, J.; Wang, Q.; Shen, L. Customizing Super-Resolution Framework According to Image Features. In Proceedings of the 2020 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), Exeter, UK, 17–19 December 2020. [Google Scholar]
- Yuan, N.; Zhang, D.; Wang, Q.; Shen, L. A Multi-Model Super-Resolution Training and Reconstruction Framework; Network and Parallel Computing; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Imambi, S.; Prakash, K.B.; Kanagachidambaresan, G.R. PyTorch; Programming with TensorFlow; EAI/Springer Innovations in Communication and Computing; Springer: Cham, Switzerland, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).