Abstract
This paper studies the design scalability of a -shaped piezoelectric energy harvester (EH) using the generalized classical Ritz method (GCRM) and differential evolution algorithm. The generalized classical Ritz method (GCRM) is the advanced version of the classical Ritz method (CRM) that can handle a multibody system by assembling its equations of motion interconnected by the constraint equations. In this study, the GCRM is extended for analysis of the piezoelectric energy harvesters with material and/or orientation discontinuity between members. The electromechanical equations of motion are derived for the PE harvester using GCRM, and the accuracy of the numerical simulation is experimentally validated by comparing frequency response functions for voltage and power output. Then the GCRM is used in the power maximization design study that considers four different total masses—15 g, 30 g, 45 g, 60 g—to understand design scalability. The optimized EH has the maximum normalized power density of 23.1 × 103 kg·s·m−3 which is the highest among the reviewed PE harvesters. We discuss how the design parameters need to be determined at different harvester scales.
1. Introduction
The high demand for self-powered electronic devices, such as sensors and small electronics, has increased and energy harvesting is expected to gain more attraction. Piezoelectricity is one of the energy conversion principles used in energy harvesting systems, and it has shown advantages such as a high voltage output and ease of fabrication both in macro- and microscales [1,2,3]. These advantages have led to the use of piezoelectricity in various energy harvesting applications, and their design studies—structural modifications and electric circuit designs—have been actively conducted during the last two decades [4,5]. Previous piezoelectric energy (PE) harvesting studies considered various dynamic energy sources, such as HVAC (heating, ventilation, and air conditioning) systems (outdoor condensing unit, duct, compressor, pipe, fan belt cage) [6,7,8], human motions (vibration [9,10] and shoe compression [11,12,13]), pavements (or tiles) [14,15,16,17], vibrating bridges [18], wind-induced motions [19,20,21], raindrops [22,23], tires [24], and even inside human bodies [25,26,27,28]. The aforementioned works developed numerical models for PE harvesters and performed design studies to reduce the development cost while satisfying the power requirement.
There are three typical methods to develop numerical models for PE harvesters: the finite element method (FEM) [29,30], analytical methods [1,31,32,33], and the classical Ritz method (CRM) [1,34,35,36,37,38,39]. Each method has its advantages and disadvantages. The FEM is advantageous in modeling complicated features such as multiple materials, complex geometric profiles, and various boundary conditions. However, the FEM inherently needs a large number of degrees of freedom (DOFs) and is computationally inefficient [39,40,41,42]. The analytical method shows high computational efficiency, but it is limited to a system having simple structural configurations and a limited number of boundary conditions. The CRM is a preferred method for a model with a moderate geometry complexity and multimaterial configuration, e.g., a two-segment self-charging piezoelectric cantilever [34]. Besides, the CRM does not need many DOFs and has excellent computational efficiency compared to the FEM. Meirovitch and Kwak [39] showed that the convergence speed of the CRM is faster than that of the FEM in the modal analysis for a nonuniform rod in axial vibration. Morales [38] demonstrated how the CRM can be used for N-story framed structures and showed a faster convergence speed of the CRM than FEM. However, there are two disadvantages of the CRM: (1) admissible trial functions satisfying all the geometric boundary conditions of the system must be used to approximate the deformation field, and (2) for systems consisting of multiple bodies as in [38], the so-called kinematical procedure, which represents kinematical quantities (i.e., displacement, velocity, and acceleration) of a certain body based on the adjoining body, has to be included in a derivation process of equations of motion to satisfy the compatibility condition. Given that the aforementioned disadvantages prevent the CRM being used to model general systems having multiple structures and many PE harvesters that consist of multiple structures (e.g., L-shape [32,33], M-shape [43,44], zigzag [45,46,47], E-shape [48], multiple cantilevers [49], and -shape in this study) have better performance than a cantilever PE harvester in terms of power output or broadband characteristic, the CRM needs to be upgraded.
Jeong and Yoo [41,42] developed a modified version of the CRM, so-called generalized CRM (GCRM), that always uses the same set of trial functions regardless of the system. Their studies focused on modeling and analyzing structures with geometrical nonlinearity. This study extends the use of GCRM for electromechanical linear PE harvesters with general geometry, by including the piezoelectric constitutive relations. For simplicity, the proposed modified GCRM for PE harvesters is referred to as GCRM-P hereafter. The efficiency of the proposed GCRM-P method enables its smooth adaptation to a shape optimization process for PE harvesters to enhance design compactness and durability while meeting power requirements. This paper performs a design optimization study for a specific harvester configuration named -shaped PE harvester (EH) that assembles two uniform beams at a right angle (90°) (Figure 1a). This configuration has uniform strain distribution along its vertical structure, whereas a cantilevered PE harvester (CEH) (Figure 1b) has nonuniform strain distribution. The EH is analyzed using the GCRM-P model and experimentally validated by comparing the voltage frequency response. In the design optimization study, four different mass constraints (15 g, 30 g, 45 g, 60 g) are considered, to understand design scalability. Furthermore, the energy harvesting performance of its optimal design is evaluated based on the normalized power density (NPD) [4,50].
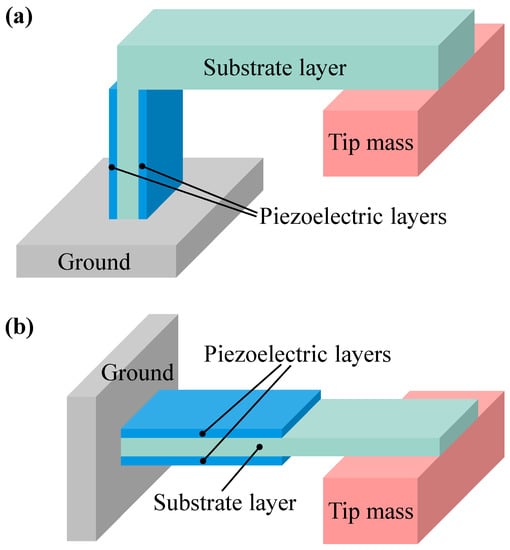
Figure 1.
Configurations for (a) proposed -shaped piezoelectric energy harvester (EH) and (b) cantilever-shaped piezoelectric energy harvester (CEH). Both systems consist of piezoelectric layers, substrate layer, and tip mass. The CEH consists of a single beam whereas the EH consists of two beams which are perpendicular to each other.
The goals of this study are summarized as follows:
- Development of a GCRM-P model to predict linear electromechanical behaviors of PE harvesters having multiple structural members,
- Experimental validation for the GCRM-P model in terms of energy harvesting performance,
- Study of design scalability—design optimization of EH under different mass scales, and comparison of the power output performance with the other recent PE harvester studies.
2. Generalized CRM for Piezoelectric Harvester (GCRM-P)
This section derives electromechanical equations of motion for a piezoelectric harvester system using GCRM-P. The system is assumed to exhibit 2D linear stress−strain behavior and the material properties are assumed to be constant. We also assume that the beam is so slender that the rotary inertia effect of the cross-section is negligible. In the piezoelectric beam, the perfect bonding condition is assumed between the piezoelectric and substrate layers.
2.1. Description for a Unit Element
Figure 2 shows the configuration of a unit piezoelectric beam element (before and after deformation) as well as its electrical connection to a load resistor. The beam element is a composite having both piezoelectric layers (top and bottom layers) and substrate layer (middle layer). In Figure 2a, the coordinate system () is fixed to the Newtonian reference frame (N) with the origin point of , one local coordinate system () is fixed to the ground (G) with the origin point of . and describe the velocity components of the ground along and , respectively. The other local coordinate system () is fixed to the kth beam element (E(k)) with the origin point of . A generic point between two nodal points and lies on the neutral axis of the beam, and is distanced from by along . The displacement vectors of , , and are given as , , and . The initial angle between and is denoted as , and the rotations at , , and are given as , , and . The nodal masses at and are denoted as , and their moments of inertia along (=) is given as , , respectively. The load resistance in Figure 2b can be connected in either serial or parallel depending on the choice of the poling direction of the piezoelectric material and the wiring between the layers.
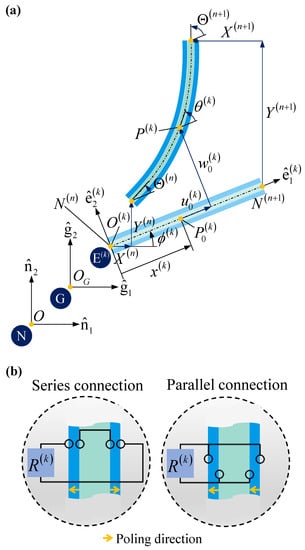
Figure 2.
(a) Configuration of the unit piezoelectric beam element before and after deformation. (b) Two possible choices of electrical connection: series and parallel connections of the piezoelectric layers. The arrows show the poling directions of the piezoelectric layers.
2.2. Electromechanical Energy Formulations
According to [1], the potential energy term where the piezoelectric constitutive relation is
where is the length of the beam and is the voltage across the load resistance. The superscripts and denote that the variable is differentiated with respect to the spatial variable once and twice, respectively. and are the elastic moduli of the substrate and piezoelectric layers. The superscript E in denotes that the constant is evaluated at the constant electric field. and are the areas of the cross-sections of the substrate and piezoelectric layers, given as
where is the width of the beam, and and are the thicknesses of the substrate and piezoelectric layers. and are the second moments of area for the substrate and piezoelectric cross-sections as
where is the location of the generic point along . is the equivalent coupling term for the voltage and the bending deformation, selected as:
where
The kinetic energy term for the element is
and the kinetic energy terms and for the nodes are
where denotes time differentiation and is the mass per unit length given as
The internal electrical energy in the piezoelectric layers is given as
is the equivalent internal capacitance of the piezoelectric layer given as
where
and is the permittivity of the piezoelectric material at constant strain.
2.3. Constraint Equations
The GCRM uses constraint equations and the Lagrange multiplier method to meet compatibility and boundary conditions. The constraint equations for the unit element in Figure 1a are given as
The constraint equations impose the continuity of DOFs across the neighboring elements. The boundary conditions can be applied by assigning corresponding values to Equations (15)–(20). For example, a fixed-free boundary condition can be implemented by setting = = = 0 in Equations (15), (17) and (19).
2.4. Spatial Discretization and Electromechanical Equations of Motion
The deformation variables and are approximated as follows:
where and are the coordinates for the deformation variables and are trial functions. The choice of the trial function affects the rate of convergence, computational time, and numerical stability [51]. Different from the CRM, the GCRM can use nonadmissible trial functions. Among others, this study selects the Legendre polynomials (Figure 3) that were successfully used for both GCRM-based static [41] and dynamic [42] analyses. A mathematical expression for the Legendre polynomials is given as follows:
where is the binomial coefficient, or where ! denotes the factorial of the given integer.
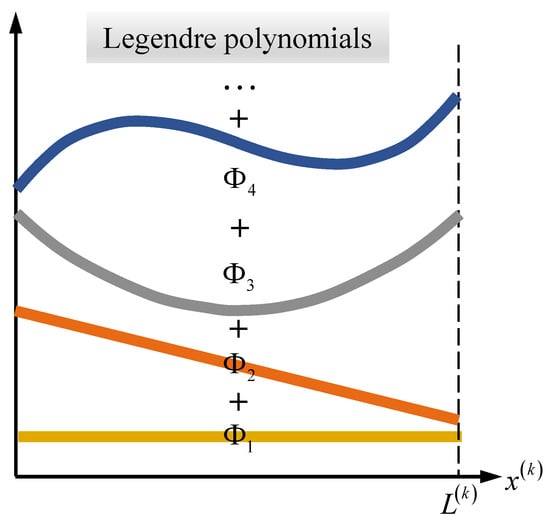
Figure 3.
Graphical representation for the first four Legendre polynomials used to approximate the deformation variables of the beam element.
According to the electromechanical Lagrange equations of motion with Lagrange multipliers, we have
where and are the total numbers of elements and nodes. In Equation (24), represents a coordinate in the system, i.e., , , , and . represents either a mechanical forcing function (when is a coordinate for displacement) or an electrical charge output () of the piezoelectric layers (when = ). It is noted that the mechanical forcing effect by ground movement is already included in the kinetic energy formulations.
Between the two types of usual damping mechanisms—viscous air damping and strain-rate damping—only the latter one is considered because the system is assumed not to be operated in viscous fluids or microscale devices. The strain-rate damping effect is modeled by adding the modal damping matrix to the derived equations of motion [1,52]. Following previous studies [31,36,53], the modal damping ratio of 0.025 is employed for the first mode response.
3. System Descriptions for the EH
3.1. Uniform Strain Distribution in -Shaped Structure
The CEH and EH consist of piezoelectric and substrate layers and tip mass. In this section, however, the simplified structures without the piezoelectric layers and tip mass are analyzed for the simplicity of the analysis (detailed analysis and design are conducted in Section 4). Figure 4a shows the simplified CEH whose length, Young’s modulus, and the second moment of the cross-section area are , , and . is the coordinate of the arbitrary point from the origin point along axis. Similarly, Figure 4b shows the simplified EH whose vertical length, horizontal length, Young’s modulus, and the second moments of the vertical and horizontal beams’ cross-section areas are , , , , and . is the coordinate of the arbitrary point on the vertical beam from the origin point along axis. The vertical beam is to be implemented as a piezoelectric sandwiched beam (Section 4).
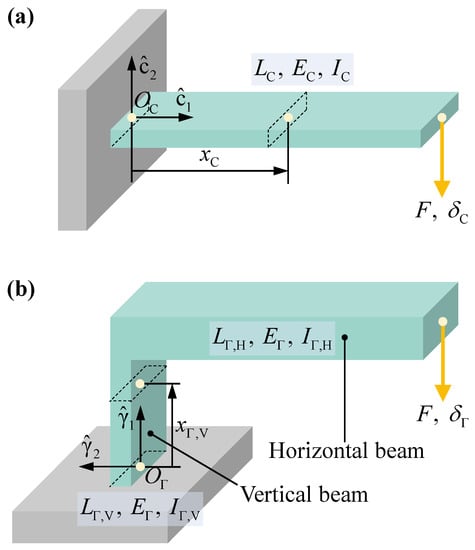
Figure 4.
Simplified structures for (a) CEH and (b) EH. L, E, I, F, , and O are the length, Young’s modulus, second moment of the cross-section area, applied load, tip displacement, and origin point. The subscripts C, , , and denote cantilever, -shaped structure, vertical beam of the -shaped structure, and horizontal beam of the -shaped structure.
This section performs a simply static analysis to explain how a uniform strain is generated in EH. In both structures in Figure 4, the tip load F is applied so that it causes the tip displacements, and , respectively. The internal moments from each structure are given as
Based on the Euler−Bernoulli beam theory, the curvatures are represented as
where w is the transverse displacement and the superscript means that the variable is differentiated with respect to the spatial variable ( or ) twice. Substituting Equations (25) and (26) into Equations (27) and (28) gives
To conclude, the bending curvature of the cantilever () linearly decreases, whereas that of the vertical beam in -shaped structure () is constant and uniform. The uniform curvature results in a uniform strain distribution and higher power generation. It is noted that one previous study—the L-shaped PE harvesters [32,33]—had a similar angled geometry, but had a different contribution to increase the bandwidth.
It is necessary to validate the uniform strain distribution of the -shaped structure by finite element analysis (FEA). For the FEA analysis, a commercial software ANSYS v19.2 (Ansys, Inc., Canonsburg, PA, USA) was employed to conduct a static analysis. In the FEA model, 1500 and 3764 quadratic hexahedron solid elements were used for the simplified CEH and EH, respectively. The specifications in terms of geometry and material are not given here because the point of this FEA is to show the uniform strain distribution of the proposed structure rather than values. Figure 5 shows the strain distributions, boundary conditions, and loading conditions of the FEA models. The color in Figure 5 shows the magnitude of the von Mises strain induced by the applied static load (the red and blue colors mean high and low strains). It is noted that the simplified CEH had the nonuniform strain distribution in its longitudinal direction as predicted in the analytical solution (Equation (29)), i.e., its strain varied from high (red) to low (blue) along the longitudinal direction (Figure 5a), whereas the simplified EH had the uniform strain distribution (Figure 5b) in its vertical beam.
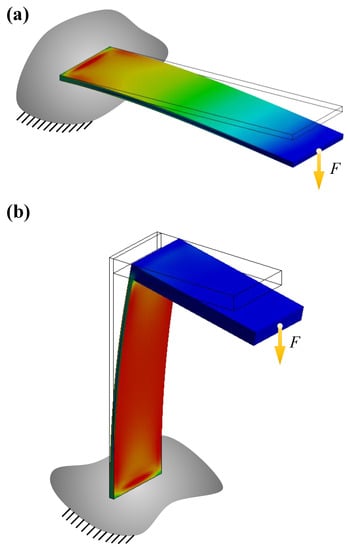
Figure 5.
Finite element analysis results for the simplified (a) CEH and (b) ΓEH. All structures are under the same transverse load acting downward and each root of the structure is assumed to be rigidly fixed to the ground. The color shows the von Mises strain level (high and low strain levels are colored by red and blue, respectively).
3.2. Configuration of -Shaped Harvester
The configuration of the EH is given in Figure 6. The PIC151 ceramic (PI-Ceramic GmbH, Lederhose, Germany), polylactic acid (PLA), and lead were used for the piezoelectric layers, substrate layers, and tip mass, and their material properties (Table 1) were assigned to the numerical model. The piezoelectric layers were placed only in the vertical part where a uniform strain distribution was observed.
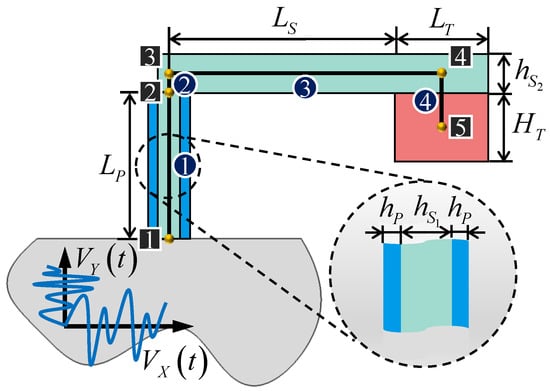
Figure 6.
Side view of the EH. The nodes, elements, and design variables are given in the figure. The width of the beam (b), the width of the tip mass (bT), and the load resistance (R) connected to the energy harvester, which are not shown in the figure, are remaining design variables to be determined in the design problem.

Table 1.
Material properties for the energy harvester.
The GCRM-P model does not need the serious mesh generation as required in an FEM model, but only a few nodes where there is a change in material property, cross-sectional property, or orientation of a structural member. Considering that the vertical beam is not fully covered by piezoelectric material, there needs to be a dummy element (which is rigid and massless) to place a gap between vertical and horizontal beams. The tip mass is modeled as a point mass at the center of the tip mass. Therefore, a node has to be defined there and is connected to the tip of the horizontal beam with a dummy element. Accordingly, five nodes (boxed numbers) and four elements (circled numbers) ware assigned as shown in Figure 6. In the design problem of this study, there are nine (, and R for the CEH) design variables as explained in Table 2 and Figure 6. The piezoelectric layer thickness () is fixed to 0.21 mm which is the manufacturer’s specification, i.e., PIC 151. The ground velocity term is defined based on the measurement signal from an outdoor condensing unit as shown in Figure 7. A wireless accelerometer, Slam Stick X (Mide Technology Corporation, Woburn, MA, USA), was used to acquire the time-domain data and was transformed into the frequency domain by the fast Fourier transform (FFT). The Y directional acceleration component was found to have 40 Hz frequency with the amplitude of 0.16 g (g denotes the gravitational acceleration, i.e., 9.81 m/s2), or
where A and f are 0.16 g and 40 Hz, respectively, and is assumed to be zero.

Table 2.
Geometrical specifications of the EH used for the experimental validation.
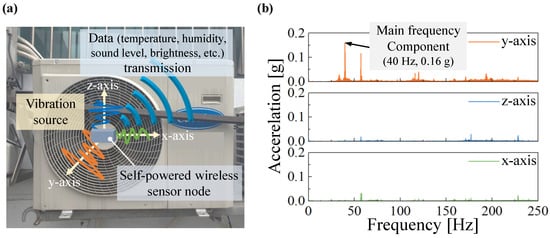
Figure 7.
(a) Demonstration of the typical self-powered wireless sensor node and the outdoor condensing unit from which the electricity is generated by the energy harvester attached to the vibrating surface. (b) FFT results for the acceleration data in three axes. The acceleration in the y-axis is the most dominant and the main frequency component has 40 Hz and 0.16 g.
4. Shape Optimization
This section introduces the experimental validation of the GCRM-P model developed in Section 2 and the design formulation for the ΓEH. In the experimental validation, the accuracy of the GCRM-P model was verified by comparing the voltage output FRFs from the experiment and simulation. With the experimentally validated model, the shape optimization was performed and the design change trend was discussed when the total mass of the harvester changed.
4.1. Experimental Validation of the GCRM-P Model for EH
In this section, the simulation analysis result is validated experimentally, using the EH prototype as specified in Table 2. For prototyping, the substrates of the EH were fabricated part by part using a 3D printer (Prusa I3 MK3, Prusa Research, Prague, Czech Republic), with a 100% infill density, and assembled afterward. Then, the piezoelectric layers with the electrode and tip mass made of the lead were glued on the substrate using the cyanoacrylate adhesive.
The experimental setup in Figure 8 was prepared to measure the frequency response function (FRF) for the voltage and power output of the fabricated prototype. An electromagnetic shaker (Type 4809, Brüel & Kjær, Nærum, Denmark), a function generator (33250A, Agilent, Santa Clara CA, USA), and a power amplifier (Type 2718, Brüel & Kjær, Nærum, Denmark) were used to excite the energy harvesting beam, and the accelerometer in Section 4 was used to measure the acceleration of the base. The energy harvester was connected to a variable load resistance from which the voltage output was obtained using an oscilloscope (Tektronix DPO4054B, Tektronix, Beaverton, OR, USA). Then, the power output could be calculated by applying Ohm’s law.

Figure 8.
Experimental setup used for measuring the electromechanical frequency response functions (FRFs).
The experimental and numerical FRFs for the voltage and power outputs are shown in Figure 9. The symbols and lines denote the experimental and numerical results, respectively. It is noted that the results are normalized by gravitational acceleration (g). The voltage outputs were measured at two load resistance conditions: one was the open-circuit condition () and the other was the optimized load resistance condition ( 1/(ω)) given in Table 2, and the power output was measured only at the optimized load resistance condition. In both voltage and power results, the experimental FRFs were slightly shifted to the right-hand side. This stiffening effect could result from the thickness of electrodes in between the layers, unevenly distributed adhesive, substrates more thickly printed than intended, or a combined effect of some of the aforementioned possible causes. Nonetheless, we conclude that both results showed a reasonable agreement—the errors on the maximum open-circuit voltage output, voltage output at the optimized load resistance, and power output were about 11.4%, 2.6%, and 5.5%, respectively.
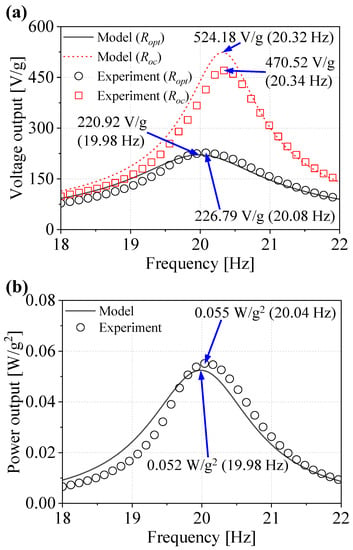
Figure 9.
Measured (symbol) and predicted (line) voltage and power output FRFs of the EH. Both quantities are normalized by gravitational acceleration (g). (a) voltage output; (b) power output.
4.2. Design Formulation
The energy harvester design problem is formulated to maximize the peak value of power output. The design constraints consider cost-effectiveness and compactness as well as durability, and are formulated to limit: total mass (), horizontal length (), vertical length (), closest vertical distance between the bottom surface of the tip mass and the ground (), piezoelectric material volume (), and the maximum stress at piezoelectric material () as follows:
Maximize power at the load resistance subject to
where , , and are density values of the materials given in Table 1. in Equation (38) is the amplitude of the downward nodal displacement at node 5. The subscript “” indicates that the value is evaluated considering static (gravity effect) and dynamic (base excitation) loads. It is noted that the gravity effect can be removed or changed based on the installation orientation of the harvester. The value of 30 MPa in Equation (40) is decided by applying a safety factor of 1.5 to the tensile strength of the PIC 151, i.e., 45 MPa [54]. The lower/upper bounds in this design problem are
We select to use the differential evolution (DE) algorithm for design optimization [55,56], which evolves a pool of design candidate populations generation to generation. Let’s suppose at Gth generation we have NP populations of D-dimensional vectors, i.e., . The initial populations are generated by sampling random real numbers within lower and upper bounds and . In the mutation operation, the DE employs mutation strategies to produce a mutant vector . After the mutation operation, a crossover operation is employed to each pair of the target and mutant vectors and to generate a trial vector . The binomial crossover is the most commonly used crossover operation given as
where CR is a user-defined crossover rate (0 < CR < 1) that controls the fraction of vector components copied from the mutant vector, rand j (0, 1) is jth random real number in the range of [0, 1], and is a randomly selected integer within the range [1, D].
After the trial vectors have been generated, the selection operation determines the survivors for the next (G + 1)th generation. The operator compares each pair of the target and trial vectors and , keeping the vector having a better fitness value in the population as follows:
where the function is a fitness function to be maximized. These three operations—mutation, crossover, and selection—are repeated until the termination criterion is met in terms of the number of maximum function evaluations.
In this study, we chose one of the DE variants, L-SHADE-EIG [57,58], combined with the oracle penalty method [59] to handle a constrained problem. This DE variant gained great attention as it won the first prize in a real-parameter single objective optimization competition at 2015 IEEE congress on evolutionary computation. In the algorithm implementation, the numbers of initial populations and the maximum function evaluation for the algorithm termination are set depending on the number of design variables (D = 9) to be and (or 90 and 9000) respectively, and other settings are adopted from the original L-SHADE-EIG algorithm. The fitness function is chosen as the peak value of power output obtained with the given input acceleration conditions.
4.3. Shape Optimization Results and Discussions
In this section, four different system mass values are attempted ( = 15 g, 30 g, 45 g, and 60 g) for the optimization and the corresponding design change trend is studied. The optimal design parameters at different values are found as shown in Table 3, Figure 10 (in the normalized scale), as well as Figure 11. The normalized values in Figure 10 were calculated by the following formulation.

Table 3.
Optimized design variables depending on the allowed total mass (15 g, 30 g, 45 g and 60 g).
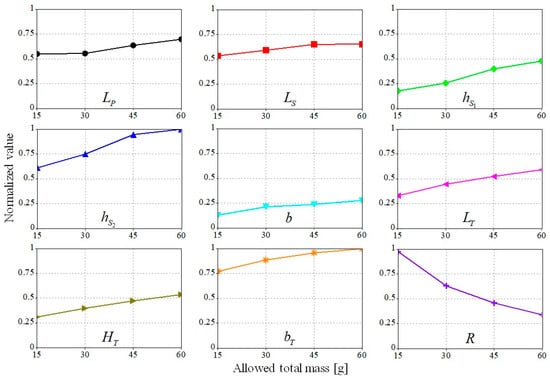
Figure 10.
Changes of the normalized design variables depending on the allowed total mass.
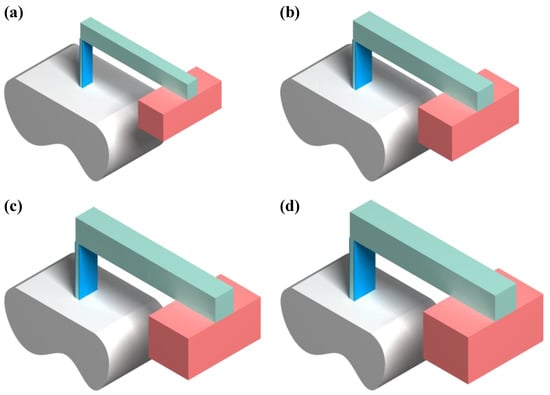
Figure 11.
Graphical demonstrations of the four optimized EHs having different allowed total mass: (a) 15 g, (b) 30 g, (c) 45 g, and (d) 60 g.
In all four cases, the mass constraint (Equation (32)) is found active, obviously indicating that a larger power is generated from a heavier harvester. More interesting observations include: (1) the tip mass dimension parameters (, , and ) are dominant factors to increase the total mass and base excitation forcing effect, (2) the external resistor (R) is the only decreasing parameter due to the impedance matching issue—the increased piezoelectric internal capacitance by and b [60], and (3) and also increase so that the beam stiffness is increased and the natural frequency of the system stays close to the excitation frequency (40 Hz).
It is noted from the optimization results (Figure 10) that both the length and the width of vertical piezoelectric beam ( and b) increase but their increasing trends are different. Basically, (flexibility) and b (stiffness) increase at the same time to maintain the beam’s natural frequency. When is changed from 15 g to 30 g, the stress condition is satisfactory ( < 30 MPa) and there is a substantial increase of b (61.19%) rather than increase (1.01%). On the other hand, when the design scale becomes larger and the stress constraint becomes more active ( ≈ 30 MPa when is changed from 30 g to 45 g), more increase of is preferred rather than increasing b (the slope of between 30 g and 45 g is 2.05 times stiffer than that of b) to maintain the stress within the bound while keeping the similar natural frequency by increased and . This observation indicates there exists a preferable way to increase the stiffness depending on the stress condition. The increase of piezo-substrate width (b) is preferred when there is no stress violation issue because it can increase the power using more piezoelectric material. On the other hand, the increase of substrate thicknesses ( and ) is preferred as the stress violation is concerned—the bending moment of inertia is a cubic function of the thickness, which is more effective to decrease stress than the width (linear function). The tip mass parameters are increased correspondingly to maintain the harvester’s resonant frequency.
Several performance measures are compared from four different designs as shown in Figure 12. The stress values increase as a larger mass is allowed as shown in Figure 12a. In this figure, and are the maximum stresses of the piezoelectric material induced by the static and dynamic loads, respectively. This result confirms the gravity-induced initial stress must be considered given that the proportion of is almost 40% of . Especially, no consideration of in the last two cases ( = 45 g and 60 g) will violate the maximum stress constraint (Equation (37)) and deteriorate the durability of the energy harvester.
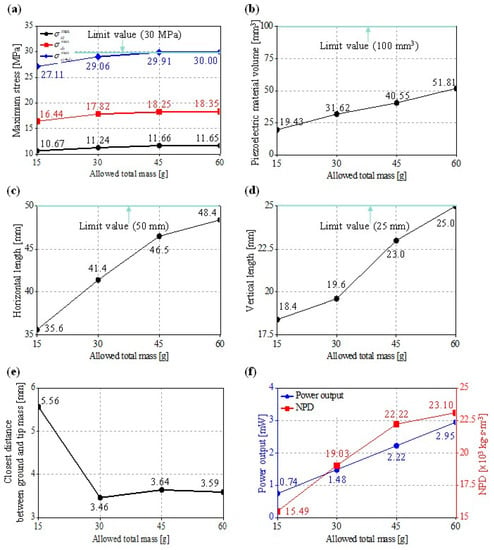
Figure 12.
Results for the four optimized EHs: (a) maximum stress induced by static, dynamic, and combined loadings, (b) piezoelectric material volume, (c) horizontal length, (d) vertical length, (e) closest distance between ground and tip mass, (f) power output and NPD.
Figure 12b shows the change of the piezoelectric material volume that increases gradually. However, the piezoelectric material volumes are found not active (100 mm3) in all of the cases. This implies that using the maximum allowable piezoelectric material does not necessarily guarantee the higher power output, because of increased stiffness and decreased strain generation in the piezoelectric material. The harvester clearance from the ground (, Figure 12e) is found positive from all of the cases by satisfying Equation (35).
The power output and the normalized power density (NPD) is compared in Figure 12f. The NPD is defined as
The power output (in mW) shows almost linear behavior with respect to (in g), and it can be approximated by linear regression formula as
with the R2 (coefficient of determination) of 0.999. Based on this formula, energy harvester designers can approximately estimate a total mass that will be needed to meet the power requirement. An additional optimization study at = 37.5 g found the power output 1.857 mW (the optimized design variables can be found in Table 4) and confirms this linear relation—only 0.6% different from a predicted value (1.845 mW).

Table 4.
Optimized design variables where the allowed total mass is 37.5 g.
Table 5 [61,62,63,64,65,66,67] shows the NPDs and modified NPDs of various PE harvesters and their specification in terms of piezoelectric material, excitation amplitude, piezoelectric material volume, system volume, power output, and total mass. The modified NPD is a new index defined similarly as the NPD. However, the power output is divided by the volume of the system rather than that of the piezoelectric material. Therefore, the modified NPD can be referred to when the compactness is more important than the cost. All four optimized EHs in this study show higher NPDs (15.49 × 103~23.10 × 103 kg·s·m−3) than those of any other PE harvesters reviewed in this table (0.016 × 103~11.55 × 103 kg·s·m−3). It is noted that the highest NPD among the referenced works, i.e., 11.55 × 103 kg·s·m−3 by Yang et al. [63], was enabled by its large mass (100 g) and the high piezoelectric coupling constant of 275 pC/N. However, more than doubled NPD can be obtained from our design using a smaller mass ( = 60 g) and a smaller piezoelectric coupling constant (210 pC/N). In terms of the modified NPD, the proposed designs with = 45 g and 60 g have higher values than the design in [63]. This shows the effectiveness of the optimized EH. By the way, the NPD increases as the mass becomes larger, but shows a saturated trend (around 24 × 103 kg·s·m−3), because the constraints of vertical dimension and stress (Equations (34) and (36)) become active.

Table 5.
NPD and other information on various mesoscale PE harvesters.
5. Conclusions
This paper performed design optimization of a new EH using the GCRM-P and DE algorithm. Some conclusive remarks are as follows:
- (1)
- The accuracy of the proposed GCRM-P model used for the frequency response analysis of the EH was experimentally validated with the error 5.5% for the peak power frequency.
- (2)
- The proposed DE-based approach successfully provided the optimized solutions with the high NPDs, while satisfying the six design constraints. Specifically, we could obtain higher harvester NPDs than the multiple mesoscale PE harvesters from recent studies.
- (3)
- The linear relation between the harvester mass (Mallowed) and power performance does not necessarily mean that all the design variables are linearly scaled—they need to be carefully chosen to maximize the power output while satisfying all of the constraints, especially the stress and the natural frequency measures.
This study focused on the power and NPD at a fixed frequency as a performance index. A more practical design study considering broadband characteristics, durability, manufacturing cost, and compactness of the EH remains as future work.
Author Contributions
Conceptualization, S.J. and S.L.; methodology, S.J.; software, S.J.; validation, S.J.; formal analysis, S.J.; investigation, S.J.; resources, S.J.; data curation, S.J.; writing—original draft preparation, S.J.; writing—review and editing, S.J., S.L. and H.Y.; visualization, S.J.; supervision, S.L. and H.Y.; project administration, S.L. and H.Y.; funding acquisition, S.L. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request due to privacy.
Acknowledgments
This research was supported by the MOTIE (Ministry of Trade, Industry, and Energy) in Korea, under the Fostering Global Talents for Innovative Growth Program (P0008748, Global Human Resource Development for Innovative Design in Robot and Engineering) supervised by the Korea Institute for Advancement of Technology (KIAT).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons Ltd: Hoboken, NJ, USA, 2011. [Google Scholar]
- Cook-Chennault, K.A.; Thambi, N.; Sastry, A.M. Powering MEMS portable devices—a review of non-regenerative and re-generative power supply systems with special emphasis on piezoelectric energy harvesting systems. Smart Mater. Struct. 2008, 17, 043001. [Google Scholar] [CrossRef] [Green Version]
- Jeon, Y.; Sood, R.; Jeong, J.-H.; Kim, S.-G. MEMS power generator with transverse mode thin film PZT. Sens. Actuators A Phys. 2005, 122, 16–22. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef] [Green Version]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Lee, S.; Youn, B.D.; Jung, B.C. Robust segment-type energy harvester and its application to a wireless sensor. Smart Mater. Struct. 2009, 18, 095021. [Google Scholar] [CrossRef]
- Lee, S.; Youn, B.D. A design and experimental verification methodology for an energy harvester skin structure. Smart Mater. Struct. 2011, 20, 057001. [Google Scholar] [CrossRef]
- Miller, L.M.; Halvorsen, E.; Dong, T.; Wright, P.K. Modeling and experimental verification of low-frequency MEMS energy harvesting from ambient vibrations. J. Micromech. Microeng. 2011, 21, 045029. [Google Scholar] [CrossRef]
- Izadgoshasb, I.; Lim, Y.Y.; Lake, N.; Tang, L.; Padilla, R.V.; Kashiwao, T. Optimizing orientation of piezoelectric cantilever beam for harvesting energy from human walking. Energy Convers. Manag. 2018, 161, 66–73. [Google Scholar] [CrossRef]
- Izadgoshasb, I.; Lim, Y.Y.; Tang, L.; Padilla, R.V.; Tang, Z.S.; Sedighi, M. Improving efficiency of piezoelectric based energy harvesting from human motions using double pendulum system. Energy Convers. Manag. 2019, 184, 559–570. [Google Scholar] [CrossRef]
- Turkmen, A.C.; Celik, C. Energy harvesting with the piezoelectric material integrated shoe. Energy 2018, 150, 556–564. [Google Scholar] [CrossRef]
- Qian, F.; Xu, T.-B.; Zuo, L. Piezoelectric energy harvesting from human walking using a two-stage amplification mechanism. Energy 2019, 189, 116140. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Hwang, W.S.; Cho, J.Y.; Jeong, J.C.; Ahn, J.H.; Kim, K.B.; Hong, S.D.; Song, G.J.; Jeon, D.H.; Sung, T.H. Piezoelectric device operating as sensor and harvester to drive switching circuit in LED shoes. Energy 2019, 177, 87–93. [Google Scholar] [CrossRef]
- Song, G.J.; Cho, J.Y.; Kim, K.-B.; Ahn, J.H.; Song, Y.; Hwang, W.; Hong, S.D.; Sung, T.H. Development of a pavement block piezoelectric energy harvester for self-powered walkway applications. Appl. Energy 2019, 256, 113916. [Google Scholar] [CrossRef]
- Cho, J.Y.; Kim, K.-B.; Hwang, W.S.; Yang, C.H.; Ahn, J.H.; Hong, S.D.; Jeon, D.H.; Song, G.J.; Ryu, C.H.; Woo, S.B.; et al. A multifunctional road-compatible piezoelectric energy harvester for autonomous driver-assist LED indicators with a self-monitoring system. Appl. Energy 2019, 242, 294–301. [Google Scholar] [CrossRef]
- Hwang, W.; Kim, K.B.; Cho, J.Y.; Yang, C.H.; Kim, J.H.; Song, G.J.; Kim, J. Watts-level road-compatible piezo-electric energy harvester for a self-powered temperature monitoring system on an actual roadway. Appl. Energy 2019, 243, 313–320. [Google Scholar] [CrossRef]
- Wang, S.; Wang, C.; Yu, G.; Gao, Z. Development and performance of a piezoelectric energy conversion structure applied in pavement. Energy Convers. Manag. 2020, 207, 112571. [Google Scholar] [CrossRef]
- Peigney, M.; Siegert, D. Piezoelectric energy harvesting from traffic-induced bridge vibrations. Smart Mater. Struct. 2013, 22, 095019. [Google Scholar] [CrossRef] [Green Version]
- Usman, M.; Hanif, A.; Kim, I.-H.; Jung, H.-J. Experimental validation of a novel piezoelectric energy harvesting system employing wake galloping phenomenon for a broad wind spectrum. Energy 2018, 153, 882–889. [Google Scholar] [CrossRef]
- Bolat, F.C.; Basaran, S.; Sivrioglu, S. Piezoelectric and electromagnetic hybrid energy harvesting with low-frequency vibrations of an aerodynamic profile under the air effect. Mech. Syst. Signal Process. 2019, 133, 106246. [Google Scholar] [CrossRef]
- Jia, J.; Shan, X.; Upadrashta, D.; Xie, T.; Yang, Y.; Song, R. An asymmetric bending-torsional piezoelectric energy harvester at low wind speed. Energy 2020, 198, 117287. [Google Scholar] [CrossRef]
- Bao, B.; Chen, W.; Wang, Q. A piezoelectric hydro-energy harvester featuring a special container structure. Energy 2019, 189, 116261. [Google Scholar] [CrossRef]
- Wong, V.-K.; Ho, J.-H.; Chai, A.-B. Performance of a piezoelectric energy harvester in actual rain. Energy 2017, 124, 364–371. [Google Scholar] [CrossRef]
- Lee, J.; Choi, B. Development of a piezoelectric energy harvesting system for implementing wireless sensors on the tires. Energy Convers. Manag. 2014, 78, 32–38. [Google Scholar] [CrossRef]
- Eshghi, A.T.; Lee, S.; Sadoughi, M.K.; Hu, C.; Kim, Y.-C.; Seo, J.-H. Design optimization under uncertainty and speed variability for a piezoelectric energy harvester powering a tire pressure monitoring sensor. Smart Mater. Struct. 2017, 26, 105037. [Google Scholar] [CrossRef]
- Dagdeviren, C.; Yang, B.D.; Su, Y.; Tran, P.L.; Joe, P.; Anderson, E.; Xia, J.; Doraiswamy, V.; Dehdashti, B.; Feng, X.; et al. Conformal piezoelectric energy harvesting and storage from motions of the heart, lung, and diaphragm. Proc. Natl. Acad. Sci. USA 2014, 111, 1927–1932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, H.; Zhang, X.-S.; Cheng, X.; Liu, Y.; Han, M.; Xue, X.; Wang, S.; Yang, F.; Smitha, A.S.; Zhang, H.; et al. A flexible and implantable piezoelectric generator harvesting energy from the pulsation of ascending aorta: In vitro and in vivo studies. Nano Energy 2015, 12, 296–304. [Google Scholar] [CrossRef]
- Lü, C.; Zhang, Y.; Zhang, H.; Zhang, Z.; Shen, M.; Chen, Y. Generalized optimization method for energy conversion and storage efficiency of nanoscale flexible piezoelectric energy harvesters. Energy Convers. Manag. 2019, 182, 34–40. [Google Scholar] [CrossRef]
- Khazaee, M.; Rosendahl, L.; Rezania, A. A comprehensive electromechanically coupled model for non-uniform piezoelectric energy harvesting composite laminates. Mech. Syst. Signal Process. 2020, 145, 106927. [Google Scholar] [CrossRef]
- Hwang, W.-S.; Park, H.C. Finite element modeling of piezoelectric sensors and actuators. AIAA J. 1993, 31, 930–937. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Erturk, A.; Renno, J.; Inman, D.J. Modeling of Piezoelectric Energy Harvesting from an L-shaped Beam-mass Structure with an Application to UAVs. J. Intell. Mater. Syst. Struct. 2008, 20, 529–544. [Google Scholar] [CrossRef]
- Li, H.; Liu, D.; Wang, J.; Shang, X.; Hajj, M.R. Broadband bimorph piezoelectric energy harvesting by exploiting bending-torsion of L-shaped structure. Energy Convers. Manag. 2020, 206, 112503. [Google Scholar] [CrossRef]
- Anton, S.R.; Erturk, A.; Inman, D.J. Multifunctional self-charging structures using piezoceramics and thin-film batteries. Smart Mater. Struct. 2010, 19, 115021. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Assumed-modes formulation of piezoelectric energy harvesters: Euler-bernoulli, rayleigh and timoshenko models with axial deformations. In Proceedings of the ASME 2010 10th Biennial Conference on Engineering Systems Design and Analysis, Istanbul, Turkey, 12–14 July 2010; Volume 3, pp. 405–414. [Google Scholar] [CrossRef]
- Jeong, S.-W.; Cho, J.Y.; Sung, T.H.; Yoo, H.H. Electromechanical modeling and power performance analysis of a piezoelectric energy harvester having an attached mass and a segmented piezoelectric layer. Smart Mater. Struct. 2016, 26, 035035. [Google Scholar] [CrossRef]
- Jung, H.J.; Lee, S.; Jeong, S.-W.; Yoo, H.H. Segmented impact-type piezoelectric energy harvester for self-start impedance matching circuit. Smart Mater. Struct. 2018, 27, 114006. [Google Scholar] [CrossRef]
- Morales, C. Dynamic analysis of frames by a Rayleigh–Ritz based substructure synthesis method. Eng. Struct. 2000, 22, 1632–1640. [Google Scholar] [CrossRef]
- Meirovitch, L.; Kwak, M.K. Convergence of the classical Rayleigh-Ritz method and the finite element method. AIAA J. 1990, 28, 1509–1516. [Google Scholar] [CrossRef]
- Jeong, S.; Yoo, H.H. Flexibility modeling of a beam undergoing large deflection using the assumed mode meth-od. Int. J. Mech. Sci. 2017, 133, 611–618. [Google Scholar] [CrossRef]
- Jeong, S.; Yoo, H.H. Nonlinear structural analysis of a flexible multibody system using the classical Rayleigh–Ritz method. Int. J. Non-Linear Mech. 2019, 110, 69–80. [Google Scholar] [CrossRef]
- Jeong, S.; Yoo, H.H. Generalized classical Ritz method for modeling geometrically nonlinear flexible multibody systems having a general topology. Int. J. Mech. Sci. 2020, 181, 105687. [Google Scholar] [CrossRef]
- Leadenham, S.; Erturk, A. M-shaped asymmetric nonlinear oscillator for broadband vibration energy harvesting: Harmonic balance analysis and experimental validation. J. Sound Vib. 2014, 333, 6209–6223. [Google Scholar] [CrossRef]
- Leadenham, S.; Erturk, A. Nonlinear M-shaped broadband piezoelectric energy harvester for very low base accel-erations: Primary and secondary resonances. Smart Mater. Struct. 2015, 24, 055021. [Google Scholar] [CrossRef] [Green Version]
- Essink, B.C.; Hobeck, J.D.; Owen, R.B.; Inman, D.J. Magnetoelastic energy harvester for structural health monitoring applications. In Active and Passive Smart Structures and Integrated Systems; SPIE: Bellingham, WA, USA, 2015; Volume 9431, p. 943123. [Google Scholar]
- Hobeck, J.D.; Inman, D.J., Sr. Simultaneous passive broadband vibration suppression and energy harvesting with multifunctional metastructures. In A Tribute Conference Honoring Daniel Inman; SPIE: Bellington, WA, USA, 2017; Volume 10172, p. 101720K. [Google Scholar]
- Zhou, S.; Chen, W.; Malakooti, M.H.; Cao, J.; Inman, D.J. Design and modeling of a flexible longitudinal zigzag structure for enhanced vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2016, 28, 367–380. [Google Scholar] [CrossRef]
- Ramírez, J.; Gatti, C.; Machado, S.; Febbo, M. Energy harvesting for autonomous thermal sensing using a linked E-shape multi-beam piezoelectric device in a low frequency rotational motion. Mech. Syst. Signal Process. 2019, 133, 106267. [Google Scholar] [CrossRef]
- Li, X.; Upadrashta, D.; Yu, K.; Yang, Y. Analytical modeling and validation of multi-mode piezoelectric energy harvester. Mech. Syst. Signal Process. 2019, 124, 613–631. [Google Scholar] [CrossRef]
- Beeby, S.; Torah, R.; Tudor, M.J.; Glynne-Jones, P.; O’Donnell, T.; Saha, C.; Roy, S. A micro electromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 2007, 17, 1257–1265. [Google Scholar] [CrossRef]
- Moreno-García, P.; Dos Santos, J.V.A.; Lopes, H. A Review and Study on Ritz Method Admissible Functions with Emphasis on Buckling and Free Vibration of Isotropic and Anisotropic Beams and Plates. Arch. Comput. Methods Eng. 2017, 25, 785–815. [Google Scholar] [CrossRef]
- Inman, D.J.; Singh, R.C. Engineering Vibration; Prentice Hall: Englewood Cliffs, NJ, USA, 1994; Volume 3. [Google Scholar]
- Dutoit, N.E.; Wardle, B.L. Experimental Verification of Models for Microfabricated Piezoelectric Vibration Energy Harvesters. AIAA J. 2007, 45, 1126–1137. [Google Scholar] [CrossRef]
- Fett, T.; Munz, D.; Thun, G. Tensile and bending strength of piezoelectric ceramics. J. Mater. Sci. Lett. 1999, 18, 1899–1902. [Google Scholar] [CrossRef]
- Storn, R.; Price, K.V. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Guo, S.-M.; Yang, C.-C. Enhancing Differential Evolution Utilizing Eigenvector-Based Crossover Operator. IEEE Trans. Evol. Comput. 2015, 19, 31–49. [Google Scholar] [CrossRef]
- Guo, S.-M.; Tsai, J.S.-H.; Yang, C.-C.; Hsu, P.-H. A self-optimization approach for L-SHADE incorporated with eigenvector-based crossover and successful-parent-selecting framework on CEC 2015 benchmark set. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 24–28 May 2015; pp. 1003–1010. [Google Scholar]
- Schlüter, M.; Gerdts, M. The oracle penalty method. J. Glob. Optim. 2009, 47, 293–325. [Google Scholar] [CrossRef]
- Paquin, S.; St-Amant, Y. Improving the performance of a piezoelectric energy harvester using a variable thickness beam. Smart Mater. Struct. 2010, 19, 105020. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y. A nonlinear piezoelectric energy harvester with magnetic oscillator. Appl. Phys. Lett. 2012, 101, 094102. [Google Scholar] [CrossRef]
- Yang, Z.; Zu, J. Comparison of PZN-PT, PMN-PT single crystals and PZT ceramic for vibration energy harvesting. Energy Convers. Manag. 2016, 122, 321–329. [Google Scholar] [CrossRef]
- Yang, Z.; Zu, J.; Luo, J.; Peng, Y. Modeling and parametric study of a force-amplified compressive-mode piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2017, 28, 357–366. [Google Scholar] [CrossRef]
- Pan, D.; Dai, F. Design and analysis of a broadband vibratory energy harvester using bi-stable piezoelectric com-posite laminate. Energy Convers. Manag. 2018, 169, 149–160. [Google Scholar] [CrossRef]
- Li, X.; Upadrashta, D.; Yu, K.; Yang, Y. Sandwich piezoelectric energy harvester: Analytical modeling and experi-mental validation. Energy Convers. Manag. 2018, 176, 69–85. [Google Scholar] [CrossRef]
- Gao, X.; Qiu, C.; Li, G.; Ma, M.; Yang, S.; Xu, Z.; Li, F. High output power density of a shear-mode piezoelectric energy harvester based on Pb (In1/2Nb1/2) O3-Pb (Mg1/3Nb2/3) O3-PbTiO3 single crystals. Appl. Energy 2020, 271, 115193. [Google Scholar] [CrossRef]
- Lee, H.; Sharpes, N.; Abdelmoula, H.; Abdelkefi, A.; Priya, S. Higher power generation from torsion-dominant mode in a zigzag shaped two-dimensional energy harvester. Appl. Energy 2018, 216, 494–503. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).