Efficient Chaos-Based Substitution-Box and Its Application to Image Encryption

Abstract

Chaotic systems are vital in designing contemporary cryptographic systems. This study proposes an innovative method for constructing an effective substitution box using a 3-dimensional chaotic map. Moreover, bouyed by the efficiency of the proposed chaos-based substitution boxes’ effectiveness, we introduce a new chaos-based image cryptosystem that combines the adeptness of Gray codes, a non-linear and sensitive hyper-chaotic system, and the proposed S-box. The generated secret key emanating from the cryptosystem is correlated to the input image to produce a unique key for each image. Extensive experimental outcomes demonstrate the utility, effectiveness, and high performance of the resulting cryptosystem.

1. Introduction

In various graphics applications such as military, medicine, homeland security, etc., advanced image encryption techniques are increasingly needed for the safe transfer, storage, and recuperation of digital images. A well-designed image cryptosystem should meet the two principles: diffusion and confusion [1]. Confusion indicates that all possible traces or information related to the plaintext or key are deleted from the ciphertext. Diffusion indicates that any tiny modification in either the plaintext or the key leads to a huge modification in the ciphertext. The substitution-box (S-box) is a nonlinear unit used in many cryptographic applications to guarantee the confusion characteristic [2]. The diffusion feature can be checked with chaotic dynamical maps. In actuality, chaotic maps have numerous ultimate features, such as ergodicity, sensitivity to primary conditions. They show a random behavior that can cause confusion and diffusion in the plaintext to get secure ciphertext [3].

Recently, various researchers have used chaotic maps in constructing S-boxes and designing image encryption mechanisms [4,5,6,7,8,9,10,11,12,13]. Chaotic systems play an important role in designing S-boxes. For example, Tang et al. [14] presented a different scheme for constructing S-box using a 2D discretized chaotic system, and in [7], a four-step strategy to construct S-boxes using a chaotic system is proposed. In [15], Chen et al. developed the scheme presented in [14] by utilizing 3D Backer system. In [16], Fatih et al. introduced a new method for S-box constructions using chaotic Lorenz map. Furthermore, Khan et al. [17] presented a new S-box construction scheme for block cipher using multi-chaotic maps. A popular characteristic of the above approaches is that they construct S-boxes using only the randomness properties of chaotic systems. This is why we need a new chaotic map with good randomness properties to build strong S-boxes. In [18], Tlelo-Cuautle et al. presented a new 3D chaotic map with infinite numbers of equilibrium points and good effective performance. Based on the advantages of the presented map in [18], we design a new chaos-based S-box that utilizes the randomness property of the chaotic map.

Data security performs a vital task in our daily life, in which chaotic systems are popularly utilized in the development of modern encryption mechanisms [19,20,21]. Based on chaos, several image cryptosystems have been introduced. Most of them are dependent on a one-dimensional or multi-dimensional chaotic system to generate pseudorandom numbers for constructing the cipher image. For example, in [22], a skew tent map is employed to design an image encryption approach, and in [8], a 1D chaotic map is obtained through coupling sine and tent maps, which is then adjusted to encrypt the plain image. Hua et al. in [23] employ a 2D Sine Logistic modulation system to produce an image cryptosystem, and Liu et al. [24] suggest a color image cryptosystem by utilizing a hyper-chaotic map and Choquet fuzzy integral. In [9], a chaos-based image block encryption approach is presented using S-box, and Wang et al. [24] suggested an image cryptosystem in the form of block cipher using a chaotic map and dynamic random growth mechanism. In [25], an image cryptosystem based on a 3D cat map is proposed. Although the previous schemes have some good results, they are not enough to raise the effectiveness of potential applications for the image encryption field. Most of them present vulnerabilities [26,27,28].

Based on the presented chaos-based substitution box efficiency, we present a new chaos-based image cryptosystem using Gray code, 3D chaotic map [18], and the proposed substitution box strategy. The provided image cryptosystem can be implemented on both grey-scale and colored images. Experimental outcomes demonstrate that the presented approach posses high performance and security.

To clarify, the main contributions of our study are twofold, as follows:

• Designing a new chaos-based S-box and validating its randomness property as required in efficient chaotic maps [18].
• Utilising the designed S-box as the fulcrum of a new image cryptosystem that also integrates the Gray code and the chaotic mapping [18] to generate unique encryption signatures with high sensitivity for each image.

This work’s organization is as follows: Section 2 gives the preliminary work for the suggested schemes. In Section 3, the new approach of designing the S-box is illustrated, and the criteria for assessing the S-box and the performance evaluation of the suggested S-box are presented and compared with other chaos-based S-boxes. In Section 4, a new chaos-based image cryptosystem is presented, while its performance evaluations are provided in Section 5. Finally, a conclusion is given in Section 6.

2. Preliminary Knowledge

This section presents the preliminary knowledge needed for constructing the S-box and designing the image encryption mechanism. In what follows, we provide the preliminary knowledge regarding the chaotic system [18] and Gray code.

2.1. 3D Chaotic Map

Tlelo-Cuautle et al. [18] introduced a new 3D chaotic map with infinite numbers of equilibrium points and good effective performance, which the following equation can express:

$$\left\{\begin{array}{c}\dot{x}=-z\hfill \\ \dot{y}=x{z}^2\hfill \\ \dot{z}=x-a{e}^y+z\left(y^2-z^2\right)\hfill \end{array}\right.$$

(1)

where a is the system parameter, and $x,y,z$ are state variables. For more information about the chaotic map, refer to Reference [18]. To present the cryptographic applications of the chaotic system provided in Equation (1), we adjust the system as given in Equation (2).

$$\left\{\begin{array}{c}{x}_{i+1}=\left(-z_i\right)mod1\hfill \\ y_{i+1}=\left(x_i{z}_i^2\right)mod1\hfill \\ z_{i+1}=\left(x_i-a{e}^{y_i}+z_i\left(y_i^2-z_i^2\right)\right)mod1\hfill \end{array}\right.$$

(2)

2.2. Gray Code

Gray code is a representation of two consecutive values that should differ in only one bit. This feature has proven useful in many applications. The representation of Gray code can be defined as given in Equation (3).

$$G\left(b\right)=b\oplus (b\gg 1),$$

(3)

where ≫ denotes the binary right shift, and ⊕ is the binary XOR operation. Table 1 provides an illustrated example of Gray code operation.

Table 1. Illustrative example of 3-bit Gray code equivalence.

Binary Format	Gray Code
000	000
001	001
010	011
011	010
100	110
101	111
110	101
111	100

3. Proposed S-box Approach

In this part, we present the new approach of designing the S-box, its performance evaluation, and compared it with other chaos-based S-boxes.

3.1. S-box Construction

Chaotic systems perform a vital task in constructing S-boxes. Utilizing the powers of the presented chaotic map in [18], we proposed a new chaos-based S-box that utilizes the randomness property of the chaotic map. The proposed algorithm for producing a new $8\times 8$ S-box is described in Algorithm 1.

Algorithm 1: S-box construction

Parameters: Primary conditions and control parameters for acting the 3D chaotic map ($x_0,y_0,z_0,a$)    Output: An $8\times 8$ S-box (SBox) 1 $[X,Y,Z]\leftarrow chaoticSystem(x_0,y_0,z_0,a,256)$ // Operate the chaotic map using primary requirements 256 times 2 $V\leftarrow order\left(X\right)$ // Order the elements in ascending structure 3 $SB\leftarrow index\left(VinX\right)$ // Get the index of every element of the sequence V in the sequence X 4 $SBox\leftarrow reshape(SB,P,Q,R)$ // Remodeling $SB$ sequence into $16\times 16$ structure to generate the S-box

In this paper, the primary key parameters for acting the chaotic system (2) to generate the stated S-box are given as ($x_0=0.7486$, $y_0=0.5935$, $z_0=0.6535$, and $a=0.6582$). The generated S-box by the presented method is shown in Table 2.

Table 2. S-box by the proposed scheme.

130	181	146	11	143	99	155	89	201	87	27	158	202	16	153	157
165	206	248	178	10	44	237	7	5	247	119	208	73	40	31	232
184	29	90	207	82	57	145	141	219	170	32	144	148	172	15	140
97	188	42	41	118	107	228	253	111	204	62	17	242	189	183	231
154	46	126	180	200	229	167	92	56	109	129	96	100	70	195	169
198	187	245	18	149	142	222	30	71	84	210	80	35	177	19	213
103	234	134	246	36	239	128	139	74	9	135	226	131	218	216	116
104	255	243	25	51	168	34	233	28	161	33	179	251	48	61	65
236	196	182	175	138	209	101	102	132	230	85	215	123	164	150	55
162	192	199	93	203	124	45	37	244	75	79	83	249	24	13	94
220	8	64	174	117	53	38	122	121	95	240	112	193	22	63	254
136	238	171	190	78	60	137	1	2	52	176	14	194	185	147	156
20	86	235	76	12	98	217	127	163	39	205	115	23	191	197	211
110	69	66	173	160	241	108	47	250	133	91	43	212	21	106	151
54	88	114	214	227	152	67	0	72	225	105	26	50	221	113	3
4	6	59	68	77	223	58	186	81	125	252	166	159	49	224	120

3.2. Performance Analysis

In [29,30,31], the most important criteria for a strong S-box are presented. These criteria include bijectivety, strict avalanche criterion (SAC), differential and linear approximation probability, and the bit independence criterion (BIC).

3.2.1. Bijective Property

An $n\times n$ S-box is bijective when it has all distinct outcome integers in the period $[0,2^n-1]$. From Table 2, our produced S-box has distinct outcome integers in the period $[0,255]$. Consequently, the produced S-box fulfills the bijective characteristic.

3.2.2. Nonlinearity Criterion

The non-linearities of the produced S-box and S-boxes displayed in [7,14,15,16,32] are shown in Table 3. We notice that the average non-linearity given by the suggested approach is superior to that of the S-boxes in References [7,14,15,16] and lower than Wang’s S-box [32].

Table 3. Comparison of the non-linearities.

S-box	Non-Linearity
	Minimum	Maximum	Average
Proposed scheme	104	110	106
[14]	99	106	103.3
[7]	98	108	103.2
[15]	100	106	103
[16]	100	106	103.2
[32]	108	108	108

3.2.3. Strict Avalanche Criterion

The dependence matrix of the created S-box is provided in Table 4. The average value of the proposed S-box’s dependence matrix is 0.4993, which is very near to the optimal value of 0.5. The maximum, minimum, and average values of our S-box and other S-boxes’ dependence matrix are provided in Table 5. The outcomes demonstrate that the generated S-box using our strategy has good SAC features.

Table 4. Dependence matrix of the proposed S-box.

0.5156	0.4531	0.5000	0.4531	0.5781	0.5938	0.5000	0.4688
0.5156	0.5000	0.4688	0.5000	0.5000	0.4844	0.4688	0.5156
0.4531	0.5469	0.5156	0.5469	0.4531	0.5469	0.5156	0.5781
0.5000	0.5000	0.4688	0.4844	0.5000	0.5625	0.5313	0.4219
0.4688	0.5313	0.4844	0.4219	0.5156	0.4688	0.4844	0.5156
0.4844	0.4844	0.4844	0.4844	0.4844	0.3750	0.5313	0.4844
0.5313	0.5156	0.5000	0.5000	0.5313	0.5000	0.5313	0.5156
0.5156	0.5938	0.4375	0.4844	0.4531	0.5000	0.5000	0.5000

Table 5. Comparison of strict avalanche criterion.

S-box	Strict Avalanche Criterion
	Minimum	Maximum	Average
Proposed scheme	0.3750	0.5938	0.4993
[14]	0.4140	0.6015	0.4987
[7]	0.3671	0.5975	0.5058
[15]	0.4218	0.6093	0.5000
[16]	0.4218	0.5937	0.5048
[32]	0.4062	0.5781	0.5068

3.2.4. Output Bits Independence Criterion (BIC)

The outcomes of BIC for our S-box are provided in Table 6 and Table 7. Table 6 displays the BIC non-linearity, in which the minimum BIC non-linearity is 100, and the average value exceeds 104.2143. Table 7 shows the BIC-SAC, in which the average BIC-SAC is 0.5030, which is very near to the optimal value of 0.5. Consequently, the presented S-box fulfills the BIC criterion. Additionally, the comparison of the nonlinearities BIC and BIC-SAC are given in Table 8. Table 8 proves that the outcomes obtained from our S-box realize a practically acceptable range.

Table 6. Bits Independence Criterion (BIC) nonlinearity of the proposed S-box.

-	104	106	102	102	108	106	100
104	-	106	104	104	102	102	108
106	106	-	106	106	100	106	102
102	104	106	-	104	102	102	104
102	104	106	104	-	104	106	110
108	102	100	102	104	-	100	104
106	102	106	102	106	100	-	108
100	108	102	104	110	104	108	-

Table 7. BIC-SAC criterion of the proposed S-box.

-	0.5244	0.5132	0.4818	0.5154	0.5176	0.5064	0.5132
0.4952	-	0.4952	0.5154	0.5154	0.4885	0.5087	0.5042
0.4997	0.5132	-	0.4975	0.4997	0.5042	0.4952	0.5289
0.5154	0.4818	0.5064	-	0.4952	0.5020	0.5333	0.4908
0.4930	0.4751	0.4751	0.4840	-	0.4930	0.5356	0.4930
0.4930	0.5176	0.5132	0.5109	0.5445	-	0.4952	0.5087
0.4908	0.5221	0.4796	0.5266	0.4952	0.5154	-	0.4975
0.4706	0.4796	0.4908	0.4908	0.5020	0.5064	0.5087	-

Table 8. Comparison of BIC.

S-box	Average BIC-Non Linearity	Average BIC-SAC
Proposed scheme	104.2143	0.5030
[14]	103.3	0.4995
[7]	104.2	0.5031
[15]	103.1	0.5024
[16]	103.7	0.5009
[32]	103.36	0.5017

3.2.5. The Equiprobable Input/Output XOR Distribution

The differential approximation tables for our S-box are listed in Table 9. The differential approximate probability (DP) of the presented S-box is 0.039062, demonstrating that the presented method is secure against differential attacks. The PDs of other S-boxes are provided in Table 10, in which our S-box has an acceptable DP value compared to other S-boxes.

Table 9. Differential approximate probability (DP) for the proposed S-box.

6	8	6	8	8	8	6	8	8	6	8	6	8	8	6	8
8	8	6	6	4	8	8	6	6	8	6	6	6	8	8	8
6	8	6	6	6	6	6	6	6	8	8	6	6	6	6	8
6	6	6	10	6	8	6	6	8	6	6	10	8	6	10	8
8	6	6	8	6	6	10	6	6	6	6	8	6	8	8	8
8	8	6	6	6	8	6	6	6	6	6	6	8	8	10	8
6	6	8	6	8	8	10	6	8	6	6	6	6	8	6	6
8	8	4	6	6	6	8	8	6	6	8	6	6	6	6	8
6	6	6	6	10	6	6	6	6	8	6	8	6	8	6	8
6	6	6	6	6	6	8	8	8	6	4	6	10	6	6	8
8	6	8	8	6	6	6	6	6	6	8	6	8	6	8	8
8	6	8	6	6	6	6	8	8	6	6	6	8	10	8	6
6	8	10	6	6	8	6	8	6	4	6	6	4	6	6	8
8	6	8	8	6	6	6	6	8	6	6	8	8	6	6	6
6	8	6	8	6	6	10	8	8	8	6	6	6	8	6	8
6	10	6	8	6	6	8	8	10	8	8	10	6	10	6	-

Table 10. Differential approximate probability (DP) comparison.

S-box	Max DP
Proposed scheme	0.039062
[14]	0.039062
[7]	0.046875
[15]	0.054687
[16]	0.039062
[32]	0.039062

3.2.6. Linear Approximation Probability (LP)

The probability of linear approximation for the compared S-boxes is given in Table 11. Obviously, our S-box has an LP value of 0.1250 and is comparable with the value of other S-boxes. Consequently, the proposed S-box has acceptable LP characteristics.

Table 11. A comparison of Linear approximation probability (LP).

S-box	LP
Proposed scheme	0.125000
[14]	0.132813
[7]	0.128906
[15]	0.128906
[16]	0.128906
[32]	0.140625

3.3. Discussion

From the above performance evaluations of our S-box compared with prior S-boxes, we can conclude that:

• Table 2 demonstrates the bijective feature of our proposed S-box.
• From Table 3, we can notice that our S-box have good performance compared to prior S-boxes in References [7,14,15,16].
• The average value of BIC-SAC for the proposed S-box is 0.5030, which is very near the optimal value.
• The maximum DP value, Table 10, is acceptable.
• The LP value of our S-box, Table 11, is acceptable.

4. Proposed Encryption Approach

In this part, we present a new image cryptosystem based on S-box, 3D chaotic system (2), and Gray code. In the substitution phase, the presented S-box in Section 3 is utilized to demonstrate its fitness for various cryptographic applications.

4.1. Encryption Process

The detailed steps of the encryption process for the presented cryptosystem are outlined in Figure 1 and defined in Algorithm 2.

Algorithm 2: Encryption procedure

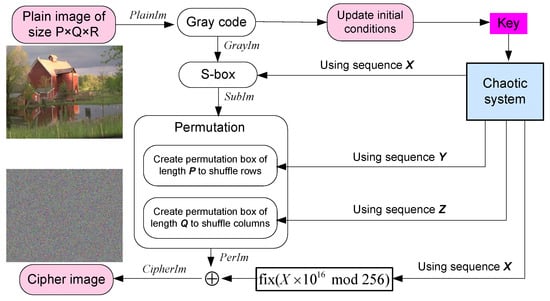
Figure 1. Block diagram of the proposed encryption algorithm.

4.2. Decryption Process

The decryption process consists of applying the encryption steps in reverse order. The proposed algorithm is symmetric; i.e., the same secret key is used at the reception to decipher the encrypted images correctly. Thus, the secret key of (2) and the parameter $\delta$ must be transferred to the receiver using a secure exchange like the Diffie-Hellman key exchange. The steps of the decryption process are illustrated in Figure 2 and detailed in Algorithm 3.

Algorithm 3: Decryption procedure

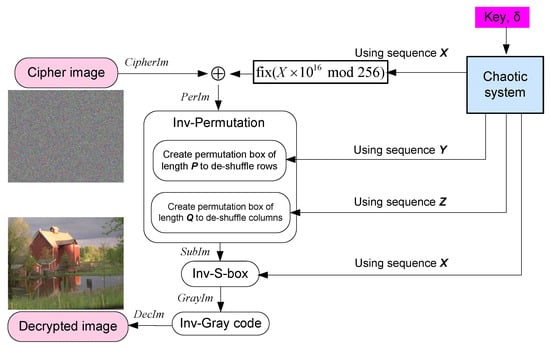
Figure 2. Block diagram of the proposed decryption algorithm.

5. Performance and Security Analyses

In this part, various analyses are employed to evaluate the security and performance of the suggested encryption scheme. A dataset of images taken from Kodak [33] of dimension $512\times 768$ were employed to evaluate the proposed cryptosystem (see Figure 3). The primary values and control parameter for acting the 3D chaotic map (2) are given as ($x_0=0.7486$, $y_0=0.5935$, $z_0=0.6535$, and $a=0.6582$). These simulation results were obtained using Matlab software, which was performed on an Intel Core i5-2450M 2.5 CPU with 6 GB RAM.

Figure 3. Image dataset utilized for evaluating the proposed cryptosystem (a–d) and its corresponding ciphered ones (e–h).

5.1. Key Space Analysis

The key space is defined as the whole set of keys employed throughout the encryption process. It must be amply large to make brute-force attacks ineffective. The key space of the proposed cryptosystem consists of the initial conditions $(x_0,y_0,z_0,a)$ of (2). The computational precision of digital computers is assumed to be ${10}^{-16}$. The possible values of $x_0$ are ${10}^{16}$, as are the values of $y_0$, $z_0$, and a. Therefore, the proposed scheme holds a ${10}^{64}\approx 2^{213}$ key space, which is enough to defend against potential brute-force-based attacks.

5.2. Statistical Analysis

In this part, various statistical analyses are utilized to evaluate the performance of the suggested cryptosystem, including correlation analysis, histogram analysis, global entropy, and local entropy.

5.2.1. Correlation Analysis

The correlation of neighboring pixels in the original images and their ciphered ones are displayed in this subsection. It is understood that the values of correlation for original images are very near to 1, whilst encrypted images with a good encryption mechanism are very near to 0. The correlations among each pair of two neighboring pixels can be measured as follows:

$$C_{xy}=\frac{{\sum }_{i=1}^N\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{\sum }_{i=1}^N{\left(x_i-\overline{x}\right)}^2{\sum }_{i=1}^N{\left(y_i-\overline{y}\right)}^2}},$$

(4)

where $x_i$ and $y_i$ are gray-scale values of two selected adjacent pixels, and N is the complete number of pairs $(x_i,y_i)$ collected from the image. The correlation coefficients of 10,000 randomly selected pairs of neighboring pixels in the original image and its encrypted ones are provided in Table 12. The correlation coefficients of original images are close to 1, whilst those of ciphered images are approximately equal to 0. Then, the adjacent pixels in the encrypted image are de-correlated in each direction. This feature is displayed graphically in Figure 4, Figure 5 and Figure 6, which contains plots of the correlation distributions in each direction of the original Houses image and the Cipher-Houses image for each color component. Consequently, the presented encryption scheme fulfills zero correlation, and it has a high privilege towards statistical attacks.

Table 12. Correlation values for combinations of images in the dataset in Figure 3.

Image	Direction
	Hor.			Ver.			Diag.
	R	G	B	R	G	B	R	G	B
Houses	0.9211	0.9227	0.9106	0.8906	0.8938	0.8646	0.8216	0.8247	0.7889
Cipher-Houses	0.0006	0.0014	0.0009	−0.0015	0.0009	0.0004	−0.0006	0.0008	−0.0002
Flowers	0.9556	0.9442	0.9519	0.9660	0.9590	0.9665	0.9339	0.9151	0.9285
Cipher-Flowers	−0.0011	−0.0005	0.0004	0.0006	−0.0004	0.0008	−0.0002	−0.0013	0.0010
Rustic	0.9595	0.9529	0.9629	0.9561	0.9482	0.9569	0.9322	0.9207	0.9343
Cipher-Rustic	0.0006	−0.0013	−0.0008	0.0012	−0.0004	0.0006	0.0014	−0.0001	0.0002
Lighthouse	0.8965	0.9067	0.9212	0.9491	0.9537	0.9588	0.8648	0.8821	0.9016
Cipher-Lighthouse	0.0013	−0.0003	−0.0005	−0.0011	−0.0007	0.0004	−0.0013	−0.0005	−0.0010

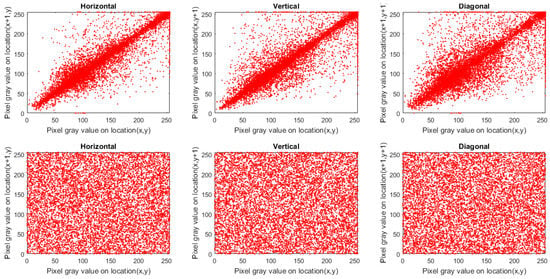
Figure 4. Correlation distribution of plain and ciphered Houses images for the red channel.

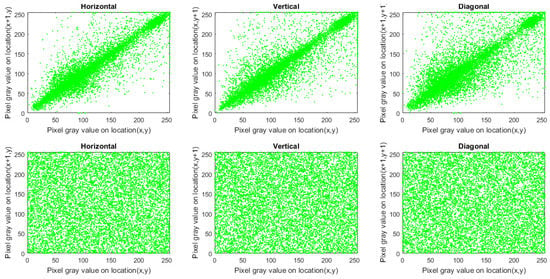
Figure 5. Correlation distribution of plain and ciphered Houses image for the green channel.

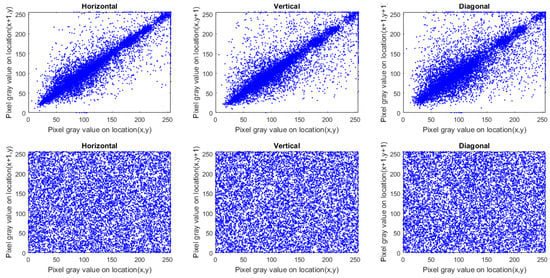
Figure 6. Correlation distribution of plain and ciphered Houses image for the blue channel.

5.2.2. Histogram Analysis

The histogram exposes the intensity of the grey level of an image. This information can be beneficial in the event of a histogram attack with an uneven distribution. Images created using a well-designed image cryptosystem should have identical histograms to increase resistance to statistical analysis. Histograms of plain images and their ciphered ones are shown in Figure 7. Obviously, the histograms of the ciphered images are somewhat identical and differ significantly from the corresponding plain images. Therefore, we can deduce that the suggested encryption mechanism can withstand histogram attacks.

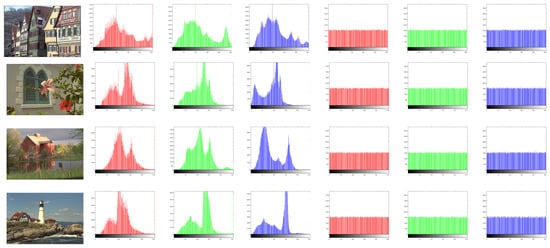
Figure 7. Histograms of the studied images, which the encrypted images (displayed in the last three columns) have a completely identical distribution.

5.2.3. Global Entropy

Information entropy is a statistical examination of randomness. The entropy value can be measured as given in (5).

$$H\left(X\right)=\sum _{k}p\left(x_k\right)lo{g}_2\left(\frac{1}{p\left(x_k\right)}\right)bits,$$

(5)

where $p\left(x_k\right)$ denotes the appearance probability of each symbol $x_k$. The optimal entropy value (i.e., $lo{g}_2\left(2^8\right)=8$ bits) is achieved if all the pixels appeared with equal probability, which implies that the pixel distribution is identical. The entropy values of experimented images are given in Table 13, in which the entropy values for the presented cryptosystem are approximately equal to 8. Thus, the presented image cryptosystem has the ability to withstand entropy attacks.

Table 13. Global information entropy for the examined dataset.

Image	Original	Encrypted
Houses	7.67379	7.99986
Flowers	7.30985	7.99985
Rustic	7.38525	7.99982
Lighthouse	7.25947	7.99983

5.2.4. Local Entropy

The global entropy is the average amount of information, so it does not reflect the randomness within each region of the image; i.e., the insufficiency of randomness inside some local regions of the image may be hidden. Therefore, it is recommended to apply another entropy analysis that works at the block level, namely, the local entropy [34]. The local entropy computation is conducted following the steps reported in [34]. The local entropy outcomes are listed in Table 14, where the entropies are very close to the optimal empiric value $7.9024693$ [34].

Table 14. Local information entropy for the examined dataset.

Image	Original	Encrypted
Houses	6.55206	7.90218
Flowers	5.44114	7.90284
Rustic	5.59077	7.90293
Lighthouse	5.39785	7.90178

5.3. Sensitivity Analysis

A well-designed cryptosystem must present a very high sensitivity of the ciphered image to slight modifications in either the key or the plain image. In this part, we present the suggested cryptosystem sensitivity analyses, including key sensitivity and plaintext sensitivity.

5.3.1. Key Sensitivity

A robust encryption scheme always warrants a high sensitivity to the secret key. That is, any slight change in such a key would provide a diametrically different encrypted image. Figure 8 shows the outcomes of key sensitivity for the proposed image cryptosystem, in which it demonstrates a high sensitivity to the secret key. Consequently, the proposed cryptosystem is extremely sensitive to tiny changes in the secret key.

Figure 8. Outcomes of key sensitivity for the proposed image cryptosystem.

5.3.2. Plaintext Sensitivity

Like the key sensitivity, the plaintext sensitivity measures the rate of changes in the ciphertext when inducing a slight alteration to the plaintext. In this regard, two well-known quantitative tools were used: unified average changing intensity (UACI) and the number of pixel change rate (NPCR). We performed NPCR to calculate the number of different pixels between two ciphered images encrypted with one key and differing only in one bit of the plain image. Whereas the UACI criteria provide the average intensity variation. The NPCR and UACI are represented in (6) and (7), respectively.

$$NPCR=\frac{{\sum }_{i,j}\varphi (i,j)}{W}\times 100\%,$$

(6)

where W is the complete number of pixels in the image and $\varphi (i,j)$ is obtained as:

$$\varphi (i,j)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{F}_1(i,j)=F_2(i,j)\hfill \\ 1,\hfill & \mathrm{if}{F}_1(i,j)\ne F_2(i,j)\hfill \end{array}\right..$$

$$UACI=\frac{1}{W}\frac{{\sum }_{i,j}|F_1(i,j)-F_2(i,j)|}{2^n-1}\times 100\%,$$

(7)

where, $F_1$ and $F_2$ are two ciphered images; the $(i,j)th$ pixel of $F_1$ and $F_2$ are indicated as $F_1(i,j)$ and $F_2(i,j)$, respectively; and n is the number of bits utilized to form a greyscale pixel value. The results of NPCR and UACI values are provided in Table 15. It can be observed from Table 15 that all of the NPCR values are over than $99.6\%$, which confirms the high sensitivity of the encryption method, and UACI values for all experimented dataset are very near to $33\%$, which verifies that the degree of influence is very high. Accordingly, the proposed cryptosystem is immensely sensitive to minor changes in the original image, and no valuable information can be deduced from the algorithm.

Table 15. NPCR and UACI values for the investigated dataset by changing one bit in the plain image.

Image	NPCR (%)	UACI (%)
Houses	99.61107	33.44665
Flowers	99.61277	33.48629
Rustic	99.60047	33.46803
Lighthouse	99.60895	33.48006

5.4. Robustness Analysis

When transmitted over a communication channel, the encrypted images are susceptible to data losses, which causes degradations in the quality of the decrypted images. Furthermore, the transmission channels are noisy, and the encrypted images are susceptible to noise-based attacks. In this part, we present the robustness analyses of the suggested cryptosystem, including occlusion attack and noise attack.

5.4.1. Occlusion Attack

An occlusion attack generally tests an encryption scheme’s ability to retain the original image’s features when the corresponding encrypted image is subjected to a loss of information. Figure 9a–d depict the encrypted images of Lighthouse under data losses of (a) $6.25\%$, (b) $12.5\%$, (c) $25\%$, and (d) $50\%$, respectively. Their decrypted images are displayed in Figure 9e–h, respectively. Although half of the encrypted image information is lost, the corresponding decrypted image reserves enough visual information of the original image. As a result, the proposed cryptosystem can resist occlusion-based attacks.

Figure 9. Occlusion attacks: encrypted images with (a) $6.25\%$, (b) $12.5\%$, (c) $25\%$, and (d) $50\%$ data loss; their corresponding decrypted images (e–h).

5.4.2. Noise Attack

A strong encryption scheme should not be concerned with such noises. To check the robustness of the proposed cryptosystem to noise-based attacks, the encrypted image of the Lighthouse is tainted by the salt and pepper noise with several densities. The corresponding decrypted images are displayed in Figure 10. It is shown that the image maintains the original image’s features, although the noise density is set to 0.3. Therefore, the proposed cryptosystem exhibits strong immunity against noise-based attacks.

Figure 10. Decrypted images undergo the salt and pepper noise with a density of: (a) 0.005, (b) 0.05, (c) 0.100, and (d) 0.300.

5.5. Known-Plaintext and Chosen-Plaintext Attacks

The main task of cryptanalysis is to recover the entire secret key or some parts of it to completely or partially decipher the ciphertexts produced by a given encryption scheme. Moreover, in some attack scenarios, the attacker can retrieve the correct plaintext from a given ciphertext without needing the secret key. Indeed, he/she tries to find any similarities between plaintexts and ciphertexts. According to how the cryptanalyst performed such a search, four different attacks are presented and listed here from the hardest to the easiest attacks: the ciphertext-only attack, the known-plaintext attack, the chosen-plaintext attack, and the chosen-ciphertext attack. Among these attacks, the known-plaintext and chosen-plaintext attacks are considered the powerful ones, and if an encryption scheme can withstand them, it can resist the other attacks as well. In the proposed cryptosystem, the secret key is fully correlated to the input image, which leads to a unique key for each different image. Accordingly, the cryptanalyst cannot establish any link between plaintext/ciphertext pairs. The proposed cryptosystem has the power to hold facing known-plaintext and chosen-plaintext attacks.

5.6. Comparative and Speed Analysis

To appraise our image cryptosystem’s performance, its experimental outcomes are compared to other related encryption schemes. Table 16 provides a comparison analysis, proving our encryption mechanism’s high performance. Apart from performance and security evaluations of the presented approach, a speed performance is also needed. Table 17 provides the speed performance of our cryptosystem and the competitive image cryptosystem for various sizes of grey-scale of images as reported in [35]. Table 16 and Table 17 confirm the supremacy of our cryptosystem alongside those related image cryptosystems.

Table 16. Comparative study of the average values of information entropy, correlation coefficients, UACI, and NPCR of the suggested cryptosystem image with respect of other similar cryptosystems.

Cryptosystem	Correlation			NPCR (%)	UACI (%)	Entropy
	Hor.	Ver.	Diag.
Proposed scheme	0.00007	0.00007	−0.00014	99.60832	33.47026	7.99984
[10]	−0.0042	−0.0049	−0.0045	99.6101	33.5252	7.99954
[36]	−0.0033	−0.0008	−0.0002	99.6061	33.4548	-
[24]	−0.00165	−0.0336	0.0279	99.7044	33.47125	7.98759
[37]	0.001906	0.003817	−0.001948	99.58648	33.2533	7.99698

Table 17. Comparative analysis of encryption speed (ms) for the suggested cryptosystem and other cryptosystems.

Cryptosystem	Image Dimensional
	$\mathbf{128}\times \mathbf{128}$	$\mathbf{256}\times \mathbf{256}$	$\mathbf{512}\times \mathbf{512}$	$\mathbf{1024}\times \mathbf{1024}$
Proposed scheme	67.487	298.131	1304.873	5270.002
[35]	153.1	634.7	2491.3	9918.5

6. Conclusions

A new approach to building a strong S-box using a 3D chaotic map was presented in this paper. The performance results show that the presented S-box has better cryptographic features than prior S-box approaches. Furthermore, a new chaotic-based image cryptosystem using the proposed S-Box and Gray code was introduced. It employs a key generation process that relies on the input image and acts as its signature to make high key sensibility. Various numerical and simulation methods were used to analyze the performance of the proposed image encryption approach. We will focus on designing a new video encryption scheme using the presented S-Box, chaotic maps, and Gray code in the near future.