Closed-Form Expressions for Numerical Evaluation of Self-Impedance Terms Involved on Wire Antenna Analysis by the Method of Moments

Abstract

This paper proposes new closed expressions of self-impedance using the Method of Moments with the Point Matching Procedure and piecewise constant and linear basis functions in different configurations, which allow saving computing time for the solution of wire antennas with complex geometries. The new expressions have complexity $O\left(1\right)$ with well-defined theoretical bound errors. They were compared with an adaptive numerical integration. We obtain an accuracy between 7 and 16 digits depending on the chosen basis function and segmentation used. Besides, the computing time involved in the calculation of the self-impedance terms was evaluated and compared with the time required by the adaptative quadrature integration solution of the same problem. Expressions have a run-time bounded between 50 and 200 times faster than an adaptive numerical integration assuming full computation of all constant of the expressions.

1. Introduction

The radiation and scattering produced by antennas is the foundation of modern wireless communications. In particular, wire antennas have been widely studied due to their ease of manufacture and multifaceted functional capabilities in a wide range of HF/VHF/UHF applications [1,2,3,4,5,6,7]. They have been used since the beginning of amateur radio, television, and AM/FM radio for transmitters and receivers [8]. Due to their adaptability to many problems, wire antennas have been extensively tested with experiments [9] and they have been designed using several numerical approaches [10,11,12,13] employing arbitrary geometries [14], parasitic elements [15], arrays [16], and single probes [17,18,19,20].

The geometry and variables used to define wire antennas with an arbitrary form and constant radius $\left(a\right)$ are shown in Figure 1. The unknown current $I\left(s^{\prime }\right)$ is found through the solution of the Electric Field Integral Equation (EFIE) [21,22,23], which is expressed by

$$E_s^i\left(s\right)=i\frac{\eta }{4\pi k}\underset{C}{\int }\{k^2\hat{\mathbf{s}}·{\hat{\mathbf{s}}}^{\prime }I\left(s^{\prime }\right)+\frac{d}{d{s}^{\prime }}I\left(s^{\prime }\right)\frac{\partial }{\partial s}\}G(r,r^{\prime })d{s}^{\prime }$$

(1)

where $G(r,r^{\prime })$ is the free-space Green’s function, given by

$$G(r,r^{\prime })=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}\frac{e^{-ik·R}}{R}d{\varphi }^{\prime }$$

(2)

and $R=\parallel \overrightarrow{R}\parallel =\parallel \overrightarrow{r}-{\overrightarrow{r}}^{\prime }\parallel$ is the scalar distance between the current source on the wire and the observation point (OP), $k=2\pi /\lambda$ is the angular wavenumber, $\lambda$ is the wavelength $\left[\mathrm{m}\right]$ of the electromagnetic wave, $\eta \simeq 120\pi \left[\mathsf{\Omega }\right]$ is the wave impedance for free space, ${\overrightarrow{s}}^{\prime }$ and $\overrightarrow{s}$ are unit direction vectors (i.e., $\parallel \overrightarrow{s}\parallel =\parallel {\overrightarrow{s}}^{\prime }\parallel =1$), and $E_s^i\left(s\right)$ is the printed source in the wire.

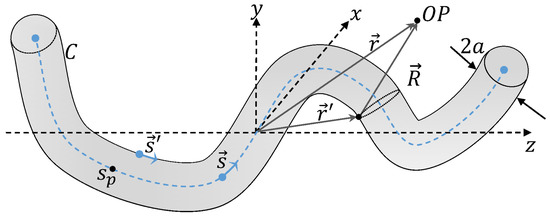
Figure 1. Wire antenna geometry, where a is the radius, and C is the Arc length.

The EFIE’s solution can be approached by the Method of Moments [24]. In that methodology, we divided the domain of the wire into convenient domains, denoted by $C_q$. The unknown current is approximated by the linear combination of basis functions $f_q\left(s^{\prime }\right)$ with support $C_q$ (i.e., $\mathrm{supp}\left\{f_q\right\}=C_q$), by means of

$$I^M\left(s^{\prime }\right)=\sum _{q=1}^M{I}_q{f}_q\left(s^{\prime }\right).$$

(3)

In particular, the Point Matching Procedure (PM-P) allows us to find the unknown constants $I_q$ with a low computational cost. Those unknown constants are found through the solution of the linear equation system

$$\left[\begin{array}{ccc}{Z}_{11}& \cdots & Z_{1M}\\ ⋮& \ddots & ⋮\\ Z_{M1}& \cdots & Z_{MM}\end{array}\right]\left[\begin{array}{c}{I}_1\\ ⋮\\ I_M\end{array}\right]=\left[\begin{array}{c}{E}_s^i\left(s_1\right)\\ ⋮\\ E_s^i\left(s_M\right)\end{array}\right],$$

(4)

where the matrix entries are given by

$$Z_{pq}={\left.i\frac{\eta }{4\pi k}\underset{C_q}{\int }\{k^2\hat{\mathbf{s}}·{\hat{\mathbf{s}}}^{\prime }{f}_q\left(s^{\prime }\right)+\frac{d}{d{s}^{\prime }}{f}_q\left(s^{\prime }\right)\frac{\partial }{\partial s}\}G(r,r^{\prime })d{s}^{\prime }\right|}_{s=s_p}.$$

(5)

In that approach, the diagonal terms (i.e., $Z_{pp}$ ) of the involved matrices are commonly known as self-impedances. Unfortunately, the numerical evaluation of the self-impedance is computationally expensive because the Green’s function (2) has a quasi-singularity for $R\le 0.1\lambda$. Although modern computers can deal with this situation using adaptive numerical integration, the time consumed is relevant for several applications. For instance, when the designer is searching the wire geometry for some particular application [14,25,26], such as maximum power transfer or maximum (or minimum) radiation toward some spatial region, the iterations of optimization algorithms might require many evaluations of $Z_{pp}$.

On the other hand, the straight wire, shown in Figure 2, has been extensively studied in the literature. Assuming the hypotheses of zero azimuthal variations of the density current and zero current density at boundaries $(\pm L/2)$[27,28,29], it is possible to simplify (5) because $\hat{\mathbf{s}}·{\hat{\mathbf{s}}}^{\prime }=1$ and $G(r,r^{\prime })\cong \frac{e^{-ik·R}}{R}$. As a result, it is found that

$$Z_{pq}=i\frac{\eta }{4\pi k}\underset{z^{\prime }=-L/2}{\overset{z^{\prime }=+L/2}{\int }}{f}_q\left(z^{\prime }\right)K_{ap}(z_p,z^{\prime })d{z}^{\prime }$$

(6)

where

$$K_{ap}(z,z^{\prime })=\frac{e^{-i·kR}}{R^5}\left(k^2{a}^2{R}^2+\left(1+ikR\right)(2R^2-3a^2)\right).$$

(7)

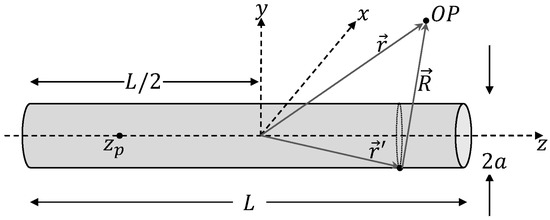
Figure 2. Straight wire antenna geometry, where a is the radius, and L is the length.

Although the application of (6)–(7) is limited for $0<a\le {10}^{-2}\lambda$ and $a\ll L$, it has been used in many commercial software such as NEC-2, NEC-4, MININEC and EZ-NEC.

Several techniques have been proposed to reduce the computational cost of calculating the matrix coefficients for straight wires, such as series with special functions [30,31] (e.g., Hankel or Bessel functions) or custom-made series [32,33,34,35,36,37,38]. Nowadays, the most frequently used approaches are applying the transformation of variables in the integral [39,40,41,42], and to make a convenient additive separation of the integrand [43,44,45,46,47,48].

Although it is highly desirable to have an analytical closed expression for $Z_{pp}$, the complexity of the expressions does not allow a deduction of it for arbitrary geometries. The closed expressions allow saving computing time for the solution of complex problems, particularly in the design of arbitrary wire geometries. Additionally, closed expressions for self-impedances allow reducing the numerical error of the solution of (5) because ${\left[Z_{pq}\right]}_{M\times M}$ is a nearly-diagonal dominant matrix. Therefore, errors ${ϵ}_Z$ in $Z_{pp}+{ϵ}_Z$ could be reflected in large errors in the estimation of $I\left(s^{\prime }\right)$. This situation is particularly relevant when the matrix begins to be ill-conditioned [49], which frequently arises in the solution of MoM.

To the best knowledge of the authors, despite the necessity of the aforementioned closed expressions, only a few are reported and evaluated in the literature. Particularly, the authors of [43] use the additive separation technique to find a closed self-impedance using the Maclaurin series approximation of $R^{-5}{e}^{-jkR}$ and the piecewise constant basis function with an observation point $z_p$ located at the middle of the segment $\mathsf{\Delta }$. A closed self-impedance using [43] can be extended to an arbitrary source, with the following result

$$\begin{array}{cc}\hfill {\tilde{Z}}_{pp}^{0)}& =\mathsf{\Delta }\frac{1}{36}\frac{\eta }{\lambda }\left\{12k-k^3\left(h^2+3a^2\right)\right\}+i\mathsf{\Delta }\frac{1}{4}\frac{\eta }{\lambda }\left\{\begin{array}{c}{h}^{-1}\left(2-\frac{1}{2}{k}^2{a}^2\right)ln\left(\frac{h+r}{a}\right)-r^{-1}{P}_0\end{array}\right\},\hfill \end{array}$$

(8)

where $P_0=1+\frac{1}{2}{k}^2{r}^2+2k^{-2}{r}^{-2}$, $r^2=h^2+a^2$ and $h=\mathsf{\Delta }/2$.

In [48], the authors use the Euler indentity $e^{-jkR}=cos\left(kR\right)-j·sin\left(kR\right)$ and the Maclaurin series of $cos(·)$ and $sin(·)$ treated independently to have fast convergence with low truncation of the summations for modeling small wire antennas. Using that methodology, it is possible to find closed expressions for the self-impedance using piecewise constant and linear basis functions in useful configurations applied for straight wire antennas with size $8a\le L\le 0.1\lambda$.

The motivation of this paper is to improve the evaluation (in time and accuracy) of $Z_{pp}$ in (5) for arbitrary geometries. Our future application will be the design of electric probes using wire antennas for EMC applications [50]. Our approach is to divide the $C_q$ domain into a nearly straight part and a curved part, as shown the Figure 3.

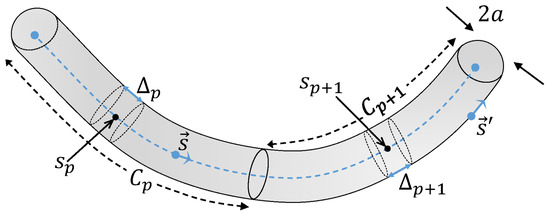
Figure 3. Simplification for the evaluation of $Z_{pp}$ in curved wire antennas.

In the straight part ($\left|s-s_p\right|<\frac{1}{2}{\mathsf{\Delta }}_p$), we evaluate the basis functions as a local combination of piecewise constant and linear basis functions, shown in Figure 4. For the curved part, we will evaluate $Z_{pp}$ by means of adaptive numerical methods using any convenient $f_p\left(s\right)$ function. For our approach to be effective, we will assume that $8a\le {\mathsf{\Delta }}_p\le 0.1\lambda$ is large enough to contain the quasi-singularity, and small enough for $\hat{\mathbf{s}}·{\hat{\mathbf{s}}}^{\prime }\cong 1$ to hold. Therefore, the solution and simplification from (7) would be valid.

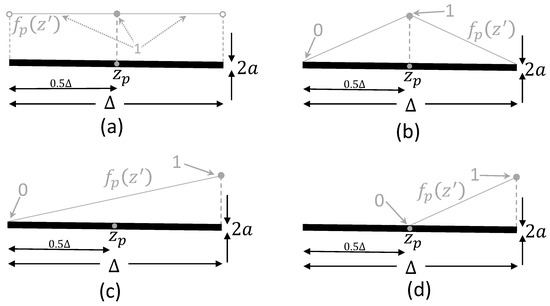
Figure 4. Piecewise basis functions analyzed in this paper. (a) Piecewise standard constant basis function. (b) Piecewise standard linear basis function. (c) Piecewise full linear basis function. (d) Piecewise truncated linear basis function.

In this article, we detail the first part of our strategy, where we find the expressions of the self-impedance for $\left|s-s_p\right|<\frac{1}{2}{\mathsf{\Delta }}_p$ and $8a\le {\mathsf{\Delta }}_p\le 0.1\lambda$, and we evaluate it in detail. The rest of the article is divided as follows. Section 3 presents the methodology of [48] and its main results. Section 4 presents the new closed expressions for the four cases show in Figure 4. Section 5 evaluates the new expressions by comparison with an adaptive numerical integration. The performance measures were the enhancements in accuracy and computational time. Finally, the last sections present the conclusions, future work and appendices.

2. Methodology

We define the variable $\xi =\left(z-z^{\prime }\right)a^{-1}=\left(n-n^{\prime }\right)a_N^{-1}$, where $z=\lambda n$, $z^{\prime }=\lambda n^{\prime }$, $a=\lambda a_N$, $\mathsf{\Delta }={\mathsf{\Delta }}_N\lambda$ and $L=L_N\lambda$. If $\mathsf{\Delta }\le 0.1\lambda$ and $0<a\le {10}^{-2}\lambda$, then it is possible to simplify (6) using Euler’s formula $e^{-i·kR}=cos\left(kR\right)-i·sin\left(kR\right)$ and the Maclaurin series of $cos(·)$ and $sin(·)$. As a result of that procedure, we can transform (6)–(7) in

$$-2\pi i{\eta }^{-1}{a}_N^2{E}_n^i(n_p,a_N)=\underset{\left(n_p-L_N/2\right)a_N^{-1}}{\overset{\left(n_p+L_N/2\right)a_N^{-1}}{\int }}\hat{I}(n_p-a_N\xi ){\hat{K}}_{ap}(\xi ,a_N)d\xi ,$$

(9)

where $z_p=\lambda n_p$, ${\hat{K}}_{ap}(\xi ,a_N)=P\left(\xi ,a_N\right)+i·Q\left(\xi ,a_N\right)$, and

$$\begin{array}{c}P\left(\xi ,a_N\right)={\pi }^3{a}_N^3{\displaystyle \sum _{k=0}^2}\frac{C_k}{{\left({\pi }^2{a}_N^2{\xi }^2+{\pi }^2{a}_N^2\right)}^{\frac{5}{2}-k}}\\ +{\pi }^3{a}_N^3{\displaystyle \sum _{k=0}^{M_r}}{A}_k{\left({\pi }^2{a}_N^2{\xi }^2+{\pi }^2{a}_N^2\right)}^{(2k+1)/2}+{ϵ}_P\left(\xi ,a_N\right)\end{array}$$

(10)

$$\begin{array}{ccc}Q\left(\xi ,a_N\right)& =& {\pi }^3{a}_N^3{\displaystyle \sum _{k=0}^{M_i}}{E}_k{\left(\pi a_N\xi \right)}^{2k}+{ϵ}_Q\left(\xi ,a_N\right)\hfill \end{array},$$

(11)

where $M_r,M_i\in \{0,1,2,...\}$, and $A_k,C_k$ and $E_k$ constants can be found in Appendix A. After simplification of (7), it is found that the error functions ${ϵ}_P\left(\xi ,a_N\right)$ and ${ϵ}_Q\left(\xi ,a_N\right)$ are limited by

$$\left|{ϵ}_P\left(\xi ,a_N\right)\right|\le a_N^3{C}_P\frac{{\left(2\pi \right)}^{2M_r+6}}{(2M_r+8)!}{\left(a_N^2{\xi }^2+a_N^2\right)}^{M_r+3/2}$$

(12)

$$\left|{ϵ}_Q\left(\xi ,a_N\right)\right|\le a_N^3{C}_Q\frac{{\left(2\pi \right)}^{2M_i+4}}{(2M_i+7)!}{(a_N^2{\xi }^2+a_N^2)}^{M_i+1},$$

(13)

where $C_P=\pi a_N^2·\left(4M_r^2+36M_r+83\right)+{\pi }^{-1}{\left(2M_r+7\right)}^2\left(M_r+4\right)$ and $C_Q=8M_i^3+252+$ $8{\pi }^2{a}_N^2{M}_i^2+76M_i^2+64{\pi }^2{a}_N^2{M}_i+240M_i+132{\pi }^2{a}_N^2$.

Using this approach in (6), the self-impedance is

$$\begin{array}{cc}\hfill Z_{pp}& ={\tilde{Z}}_{pp}+{ϵ}_Z=\eta i\frac{a_N^{-2}}{2\pi }\underset{\left(n_p-L_N/2\right)a_N^{-1}}{\overset{\left(n_p+L_N/2\right)a_N^{-1}}{\int }}{\hat{f}}_p(n_p-a_N\xi ){\hat{K}}_{ap}(\xi ,a_N)d\xi ,\hfill \end{array}$$

(14)

where ${\tilde{Z}}_{pp}$ is the closed self-impedance approximation and ${ϵ}_Z$ is its error. In particular, using $M_i=3$ and $M_r=1$, it is possible to obtain several closed expressions for the self-impedance with high accuracy and well-defined bounded errors for piecewise constant and linear basis functions because

$$\left|{ϵ}_Z\right|\le 4{\pi }^2\eta {\int }_{\left|u\right|<{10}^{-1}}\left|{\hat{f}}_p(n_p-u)\right|{(u^2+a_N^2)}^{2}du.$$

(15)

3. Proposed Self-Impedance Expressions

The results (10)–(11), and (15) are applicable in two ways, with basis functions using arbitrary wire antennas that include a straight segment. The first is shown in Figure 4a,b, where the basis functions are defined on the segment in the conventional way. The second is shown in Figure 4c,d, where only a special linear basis function is defined on the segment. With these four basis functions, we can locally describe sophisticated basis functions $f_q\left(s^{\prime }\right)$ with the first two nonzero Taylor coefficients (i.e., $c_0+c_1(s^{\prime }-s_q)$) in $\left|s^{\prime }-s_q\right|<\frac{1}{2}{\mathsf{\Delta }}_q$.

In all of the cases, we assumed a middle observation point $\left(z_p\right)$ in the segment with normalized size ${\mathsf{\Delta }}_N\le 0.1$ and normalized radius $0<a_N\le {10}^{-2}$. Although the expressions and constants depend on $a_N$ and ${\mathsf{\Delta }}_N$, we simplify the notation by $Z_{pp}^{k)}={\tilde{Z}}_{pp}^{k)}+{ϵ}_{Z^{k)}}$, where the super index notation $k)$ is used to distinguish the self-impedance cases in Figure 4.

3.1. Case 1

The self-impedance could be calculated from (14) using (10)–(11) and the piecewise constant basis function illustrated in Figure 4a. The resulting expression is

$$\begin{array}{cc}\hfill {\tilde{Z}}_{pp}^{1)}=& \eta ·{\mathsf{\Delta }}_N·R_1\left({\mathsf{\Delta }}_N\right)+\eta ·i·X_1({\mathsf{\Delta }}_N)·h({\mathsf{\Delta }}_N,\frac{1}{2})+\eta ·i·X_L·L({\mathsf{\Delta }}_N,\frac{1}{2})\hfill \end{array}$$

(16)

where $R_1(·),$$X_1(·)$ and $X_L$ are defined in Appendix B. The functions $h(v,w)$ and $L(v,w)$ are

$$h(v,w)=v^{-2}{\left(a_N^2{v}^{-2}+w^2\right)}^{-\frac{3}{2}}$$

(17)

$$L(v,w)=ln\left(\frac{\sqrt{a_N^2{v}^{-2}+w^2}+w}{\sqrt{a_N^2{v}^{-2}+w^2}-w}\right).$$

(18)

The bounded error is

$$\left|{ϵ}_{Z^{1)}}\right|\le {\pi }^2\eta {\mathsf{\Delta }}_N\left(\frac{1}{20}{\mathsf{\Delta }}_N^4+\frac{2}{3}{\mathsf{\Delta }}_N^2{a}_N^2+4a_N^4\right)$$

(19)

3.2. Case 2

The self-impedance could be calculated from (14) using (10)–(11) and the piecewise linear basis function illustrated in Figure 4b. The resulting expression is

$$\begin{array}{cc}\hfill {\tilde{Z}}_{pp}^{2)}=& \frac{\eta }{2}·{\mathsf{\Delta }}_N·R_2(\frac{1}{2}{\mathsf{\Delta }}_N)+\eta ·i·X_2(\frac{1}{2}{\mathsf{\Delta }}_N)·h(\frac{1}{2}{\mathsf{\Delta }}_N,1)\hfill \\ \hfill +& \eta ·i·X_L·L(\frac{1}{2}{\mathsf{\Delta }}_N,1)+\eta ·i·X_3·g(\frac{1}{2}{\mathsf{\Delta }}_N,1)\hfill \end{array}$$

(20)

where $R_2(·),$$X_2(·)$ and $X_3$ are defined in Appendix C. The function $g(v,w)$ is

$$g(v,w)=v^{-1}\left\{a_N^{-3}-v^{-1}·h(v,w)\right\}.$$

(21)

The bounded error is

$$\left|{ϵ}_{Z^{2)}}\right|\le {\pi }^2\eta {\mathsf{\Delta }}_N\left(\frac{4}{15}{\mathsf{\Delta }}_N^4+\frac{4}{3}{\mathsf{\Delta }}_N^2{a}_N^2+4a_N^4\right).$$

(22)

3.3. Case 3

The self-impedance could be calculated from (14) using (10)–(11) and the piecewise linear basis function illustrated in Figure 4c. The resulting expression is

$${\tilde{Z}}_{pp}^{3)}=\frac{1}{2}{\tilde{Z}}_{pp}^{1)}$$

(23)

where the bounded error is

$$\left|{ϵ}_{Z^{3)}}\right|\le \frac{1}{2}\left|{ϵ}_{Z^{1)}}\right|.$$

(24)

3.4. Case 4

The self-impedance could be calculated from (14) using (10)–(11) and the piecewise linear basis function illustrated in Figure 4d. The resulting expression is

$${\tilde{Z}}_{pp}^{4)}=\frac{1}{2}{\tilde{Z}}_{pp}^{1)}-\frac{1}{2}{\tilde{Z}}_{pp}^{2)}$$

(25)

where the bounded error is

$$\left|{ϵ}_{Z^{4)}}\right|\le \frac{1}{2}\left|{ϵ}_{Z^{1)}}\right|+\frac{1}{2}\left|{ϵ}_{Z^{2)}}\right|.$$

(26)

4. Evaluation of the Proposed Expressions

The closed expressions were compared with an adaptive numerical integration using MATLAB^® in a computer Intel(R) Core(TM) i7-8850H CPU @2.6 GHz with 64 bits and 32 GB in RAM. We used the function $integral(·)$ with an absolute and relative error tolerance of ${10}^{-10}$. That function uses a global adaptive quadrature [51] to obtain $Z_{pp}^{k)}$. In order to compare both approaches, we evaluate the absolute relative error, defined by $e_r^{k)}=\left|1-{\tilde{Z}}_{pp}^{k)}/Z_{pp}^{k)}\right|$, in Figure 5 for a typical example of $a_N={10}^{-4}$.

Figure 5. Absolute relative error for different ${\mathsf{\Delta }}_N$ using $a_N={10}^{-4}$. The absolute relative error $e_r^{0)}$ has been found using (8). The absolute relative errors $e_r^{1)},...,e_r^{4)}$ have been found using (16), (20), (23) and (25), respectively.

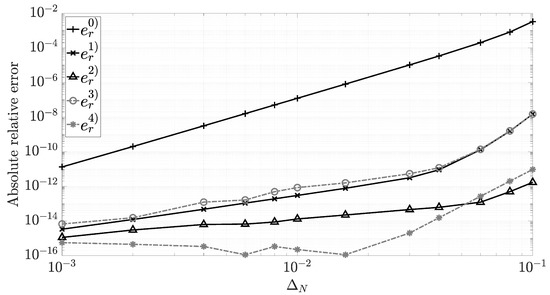
As we show, the absolute relative error of $e_r^{1)}$ reduces $e_r^{0)}$ in several decades. Therefore, it follows that ${\tilde{Z}}_{pp}^{1)}$ has much better accuracy than ${\tilde{Z}}_{pp}^{0)}$. Additionally, the absolute relative errors $e_r^{1)},\dots ,e_r^{4)}$ are less than ${10}^{-7}$. For smaller segmentation, for example $\mathsf{\Delta }={10}^{-2}$, we obtain an accuracy better than ${10}^{-12}$. In the limits of ${\mathsf{\Delta }}_N=10a_N={10}^{-3}$, we obtain an accuracy better than ${10}^{-14}$. Consequently, it is inferred that ${\tilde{Z}}_{pp}^{k)}$ with $k=1,2,3,4$ allows a very good approximation of the theoretical integrals.

Besides, the time involved in the calculation of the self-impedance terms was evaluated using the figure of merit defined as $S^{k)}=\mathrm{time}(Z_{pp}^{k)})/\mathrm{time}({\tilde{Z}}_{pp}^{k)})$, where $\mathrm{time}(Z_{pp}^{k)})$ is the average of the computing time obtained with the adaptive quadrature integration and $\mathrm{time}({\tilde{Z}}_{pp}^{k)})$ is the average of the time consuming obtained by the closed expression. The variable $S^{k)}$ measures the run-time in terms of how faster the proposed expressions are compared to an adaptive numerical integration, for a particular segmentation. For instance, Figure 6 shows the evaluation of $S^{k)}$ for the case $a_N={10}^{-4}$. Conclusively, the closed expressions are at least (on average) 50 times faster than the adaptive quadrature integration. In particular, the case $k=0$ is around 3000 times faster. However, its accuracy is bounded by ${10}^{-2}$. The cases $k=1$ and $k=3$ are around 200 times faster with an accuracy bounded by ${10}^{-7}$. The case $k=2$ is around 150 times faster with an accuracy bounded by ${10}^{-11}$. Finally, case $k=4$ is around 50 times faster with an accuracy bounded by ${10}^{-11}$. If it is assumed that the radius of the wire is constant throughout the antenna, then $S^{k)}$ increases considerably because the constants $A_k,C_k,E_k,F_k,G_k,H_k,X_L$ are evaluated only once for an arbitrary $M\times M$ matrix.

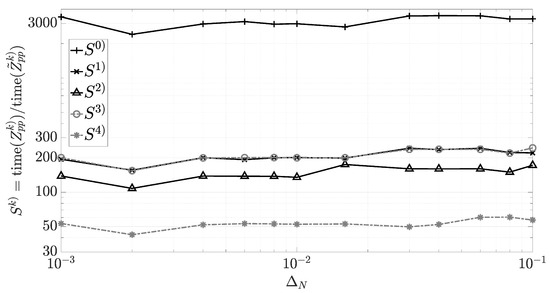
Figure 6. Normalized time consumed for different ${\mathsf{\Delta }}_N$ for $a_N={10}^{-4}$ using the same computer; Intel(R) Core(TM) i7-8850H CPU @2.6 GHz with 64 bits and 32 GB in RAM.

On the other hand, we found that $\mathrm{Im}\{{\tilde{Z}}_{pp}^{1)}\}\ge 0$ for a normalized radius $a_N\le 2.3\times {10}^{-6}$ and normalized segmentation $0.05<{\mathsf{\Delta }}_N<0.1$, which is not related to the error of the approximation. Therefore, the use of the piecewise constant basis function has the disadvantage of requiring smaller segmentation (with respect to the wavelength) for the smallest radius in order to capture the well-known physical capacitive behavior of the self-impedance in wire antennas. Although we find a similar issue with the self-impedance using the basis functions of Figure 4c,d, the capacitive behavior depends on adjunct-impedances $\left(Z_{p,p\pm 1}\right)$ in both cases.

We find that the real part of the closed self-impedance has a better approximation because that component does not have a quasi-singularity. For instance, the worst case, $a_N=0.01$ and ${\mathsf{\Delta }}_N=0.1$, obtains $\mathrm{Re}\{{\tilde{Z}}_{pp}^{2)}\}=39.38244194237$ using (20), and $\mathrm{Re}\{Z_{pp}^{2)}\}\approx 39.38244194243$ using the numerical adaptive integration. Conclusively, the closed bound errors are more related with the error of the imaginary part. However, by the methodology used, the closed bound error is strictly related to the magnitude of the self-impedance.

Finally, there is a loss of the logarithm behavior of the self-impedance using $K_{ap}(z,z^{\prime })$ at $▵<8a$ caused by ${lim}_{▵\to 0^{+}}\mathrm{Im}\left\{Z_{pp}\right\}\to 0^{-}$. As a consequence, the solution cannot be used in smallest segmentation because the approximated kernel (7) is nonphysical and the matrix’s solution will be very ill-conditioned.

5. Conclusions

This paper presents several closed expressions for the self-impedance of wire antennas modeled by the Method of Moments using the Point Matching Procedure. The new expressions can be used with piecewise linear and constant basis functions in configurations useful for integration into models of curved wire antennas. Additionally, the expressions have closed bound errors, which allow us to study the errors related to the methodology of the solution of the linear equation system.

In summary, the closed expressions are at least (on average) 50 times faster than an adaptive quadrature integration with an accuracy better than ${10}^{-7}$. In particular, the case $k=0$ is around 3000 times faster. However, its accuracy is bounded by ${10}^{-2}$. The cases $k=1$ and $k=3$ are around 200 times faster with an accuracy bounded by ${10}^{-7}$. The case $k=2$ is around 150 times faster with an accuracy bounded by ${10}^{-11}$. Finally, case $k=4$ is around 50 times faster with an accuracy bounded by ${10}^{-11}$. At the lower limit of the segmentation ($\mathsf{\Delta }=8a$), we find that the accuracy for $k=0,1,\dots ,4$ is bounded by ${10}^{-11}$, ${10}^{-14}$, ${10}^{-15}$, ${10}^{-14}$, and ${10}^{-15}$, respectively.

From a numerical point of view, the new expressions are simple formulas to implement in numerical code, which use basis functions with the first two nonzero Taylor’s coefficients around the sampling point in the wire.

6. Future Work

We wrote this paper because we need very fast computational code to design wideband electromagnetic probes for EMC applications using curved wire antennas. This work will continue with the second phase of our research, which is to develop a complete in-house MoM solution to design these probes for the research project “Radiation exposure dosimetry of electromagnetic fields emitted by 3G and 4G cellular base station antennas” funded by the Pontificia Universidad Javeriana.