Abstract
This paper proposes a Field-Programmable Gate Array (FPGA)-based hardware accelerator for assisting the embedded MicroBlaze soft-core processor in calculating population count. The population count is frequently required to be executed in cyber-physical systems and can be applied to large data sets, such as in the case of molecular similarity search in cheminformatics, or assisting with computations performed by binarized neural networks. The MicroBlaze instruction set architecture (ISA) does not support this operation natively, so the count has to be realized as either a sequence of native instructions (in software) or in parallel in a dedicated hardware accelerator. Different hardware accelerator architectures are analyzed and compared to one another and to implementing the population count operation in MicroBlaze. The achieved experimental results with large vector lengths (up to 217) demonstrate that the best hardware accelerator with DMA (Direct Memory Access) is ~31 times faster than the best software version running on MicroBlaze. The proposed architectures are scalable and can easily be adjusted to both smaller and bigger input vector lengths. The entire system was implemented and tested on a Nexys-4 prototyping board containing a low-cost/low-power Artix-7 FPGA.
1. Introduction
Cyber-physical systems (CPS) are a ground for the Internet of Things, smart cities, smart grid, and, actually, smart “anything” (cars, domestic appliances, hospitals). CPS tightly integrates computing, communication, and control technologies to achieve safety, stability, performance, reliability, adaptability, robustness, and efficiency [1,2]. Frequently, CPSs are built on reconfigurable hardware devices such as Field-Programmable Gate Arrays (FPGA) and Programmable Systems-on-Chip (PSoC). This is a logical choice since modern reconfigurable platforms combine on a single chip high-capacity programmable logic and state-of-the art general-purpose and graphic processors, achieving a tight integration of computational and physical elements. Moreover, inherent FPGA reconfigurability provides direct support for run-time system adaptation, one of the requirements of CPS paradigm [2]. FPGA are also able to provide high energy efficiency by exploiting low-level fine-grained parallelism through customizing data paths to the requirements of a specific algorithm/application [3,4,5,6,7].
In this paper, I study one of the operations that is frequently executed by CPSs but is not directly supported by MicroBlaze, which is a population count. Population count, also called Hamming weight, is the number of nonzero elements in a (binary) vector. Albeit the operation itself seems very simple, it is used in several disciplines including information theory, coding theory, cheminformatics, and cryptography. Modern hard-core processors provide direct support for population count by including such instructions as popcnt in Intel Core [8] and vcnt in ARM [9].
The main contributions of this study are the following:
- Analysis and relative comparison of population count computations in software running on MicroBlaze processor;
- Analysis and relative comparison of parallel dedicated accelerators for population count computation in hardware;
- A hardware/software co-design technique implemented and tested in a low-cost FPGA of Artix-7 from Xilinx;
- The result of experiments and comparisons demonstrating increase of throughput of hardware-accelerated computations comparing to the best software alternative.
The remainder of this paper is organized as follows. The background is presented in Section 2. Overview of the related work in software/hardware support for population count is reported in Section 3. The detailed description of explored hardware accelerator architectures is done in Section 4. The results are presented and discussed in Section 5. The conclusion is given in Section 6.
2. Background
2.1. FPGA and MicroBlaze
FPGAs can be configured to implement an instruction-set architecture and other microcontroller components augmented, if required, with new peripherals and functionality. A microprocessor implemented in an FPGA at the cost of reconfigurable logic resources is known as a soft-core processor. Soft-core processors are slower than custom silicon processors (hard-core processors) with equivalent functionality, but they are nonetheless attractive because they are highly customizable. Besides, multiple soft-core processors may be instantiated in an FPGA to create a multicore processor.
One of the most popular soft-core processors is Xilinx’s MicroBlaze [10]. MicroBlaze is a 32/64-bit configurable RISC processor with three preset configurations: (1) suitable for running baremetal code; (2) providing deterministic real-time processing on a real-time operating system; and (3) supporting embedded Linux. MicroBlaze features a three/five/eight-stage pipeline (depending on the desired optimization) and represents a Harvard architecture with instruction and data accesses done in separate address spaces. MicroBlaze ISA (Instruction Set Architecture) supports two instruction formats (register-register and register-immediate) and includes traditional RISC arithmetic, logical, branch, and load/store instructions augmented with special instructions [10].
2.2. Population Count
Population count operation calculates the number of bits set to 1 in a binary vector. It can also be defined for any vector (not obligatory binary) as the number of the vector’s nonzero elements. If the source vector has N bits, the result is (-bit long. This operation has many practical applications; some examples are given below.
- Binarized Neural Networks (BNN) are reduced precision neural networks, having weights and activations restricted to single-bit values [11,12,13]. One of the computations executed in BNNc is to multiply a binarized vector of input neurons against a binarized weight matrix. Such operation can be done using variant of a population count [11]. The parameter N tends to be large (64–1200) as it equals the number of input neurons for a fully connected layer and to the product of the size of the convolution filter in one dimension and the number of input channels for a convolution layer [12]. An example of using BNNs in a robot design for agricultural cyber-physical systems is reported in [14].
- Cryptographic applications—in [15] the population count operation is used to identify pairs of vectors that are likely to lie at a small angle to each other. In [16] Hamming weight is computed to describe an attack that recovers the private key from the public key for a public-key encryption scheme based on Mersenne numbers. Hamming distance (which is the population count of the number of mismatches between a pair of vectors) needs to be determined to prevent intrusion and detect anomalies in CPSs reviewed in [17].
- Telecommunications—error detection/correction in a communication channel recurring to Hamming weight calculus is reported in [18].
- Cheminformatics—a high-performance molecular similarity search system is described in [19] executing similarity search of bitstring fingerprints and combining fast population count evaluation and pruning algorithms. A fingerprint for chemical similarity is a description of a molecule such that the similarity between two descriptions gives some idea of the similarity between two molecules [19]. The most widely used fingerprints have a length ranging from 166 to 2048 bits. The most popular way to compare two fingerprints is to calculate their Tanimoto similarity, which can be reduced to one population count evaluation per comparison [19]. Millions of fingerprints have to be processed for most corporate compound collections.
- Bioinformatics—in [20], a tool is proposed to remove duplicated and near-duplicated reads from next generation sequencing datasets.
Population count is also used in computer chess to evaluate the mobility of pieces from their attack sets and quickly match blocks of text in the implementation of hash arrays and hash trees. Execution time for population count computations over vectors has an impact on overall performance of systems that use the results of such computations [11,12,13,14,15,16,17,18,19,20]. Therefore, several research efforts have been directed to efficiently implement this operation in both software and hardware.
3. Related Work
Most efficient population count implementation would be by a native dedicated instruction but since MicroBlaze ISA does not include one, I will limit my review to listing known software and hardware realizations.
3.1. Software Implementations of Population Count
Let us consider 32-bit long vectors (N = 32). The simplest way is to compute the population count by checking and accumulating the value of each of the 32 bits individually (until no more bits are set), like in the following C code snippet:

This approach is slow and highly inefficient since it requires multiple operations for each bit in the vector. Brian Kernighan’s algorithm reduces the number of cycle iterations to the actual population count value. This is achieved by iteratively subtracting one from the given vector, which flips all the bits to the right of the rightmost set bit, including the rightmost set bit, and calculating bitwise AND with the previous vector’s value:

One of the possibilities reported in [21] is to count the set bits in parallel. In this code, the given vector is divided into smaller chunks, for which the population counts are computed and then added:

The fastest counting method would be to use a lookup table (LUT). This approach is not practical for big values of N, but it is feasible to have a relatively small LUT; for instance, LUT 8:4 (storing population counts for all 8-bit vectors), and then to calculate the result by summing N/8 intermediate results. An example for N = 32 is given below:

3.2. Hardware Implementations of Population Count
State-of-the-art hardware implementations of population count computations have been exhaustively analyzed in [22,23,24,25,26,27,28,29]. The basic ideas of these methods are summarized below [22]:
- Parallel counters from [24] are tree-based circuits that are built from full-adders.
- The designs from [25] are based on sorting networks, which have known limitations; in particular, when the number of source data items grows, the occupied resources are increased considerably.
- Counting networks [26] eliminate propagation delays in carry chains that appear in [24] and give very good results especially for pipelined implementations. However, they occupy many general-purpose logical slices.
- The designs [28] are based on embedded to FPGA digital signal processing (DSP) slices, organized as a tree of DSP adders.
- LUT-based circuits [29] are very competitive but they are hardly scalable and resource consuming for big values of N.
- A combination of counting networks, LUT- and DSP- based circuits is proposed in [22]. It is noticed that LUT-based circuits and counting networks are the fastest solutions for small length sub-vectors (up to 128 bits). The result is produced as a combinational sum of the accumulated population counts of the sub-vectors that can be either done in DSP slices or in a circuit built from logical slices.
Architectures that are more recent are reported in [30,31,32,33]. In [30] a generic system architecture is proposed for binary string comparisons that is based on a Virtex UltraScale+ FPGA. The system is adaptable to different bit widths and the number of parallel processing elements and exhibits high throughput for streaming data. The adopted approach is definitely interesting for high-end applications as it requires PCIe-based connection to a host CPU but is not suitable for a low-cost CPS.
A LUT-efficient compressor architecture for performing population count operation is described in [31] to be used in matrix multiplications of variable precision. The authors started with a population count unit built as a tree of 6:3 LUTs and adders requiring a large number of LUTs and many stages to pipeline the adder tree. Therefore, a carry-free bit heap compression was applied, which executes a carry-save addition using regular full adders operating in parallel (except for the last addition, which requires carry propagation). This work resembles parallel counters from [24,33].
The paper [32] states that modern FPGA LUT-based architectures are not particularly efficient for implementation of compressor trees (which can be considered parallel counters with explicit carry-in and carry-out signals to be connected to adjacent compressors in the same stage) and suggests to augment existing commercial FPGA logic elements with a 6-input XOR gate. The authors demonstrate that the proposed modifications improve compressor tree synthesis using generalized parallel counters.
It is clear that none of the analyzed related work targets specifically CPSs incorporating the MicroBlaze processor, which can be essential for cost-sensitive applications.
4. Proposed Hardware Accelerators for Population Count
4.1. Hardware Population Count Accelerators Architectures
Six different architectures have been analyzed for the hardware accelerator module, specified in VHDL. In all the cases, 32-bit sub-vectors arriving from DMA (Direct Memory Access) are processed in parallel and the intermediate results are summed up at the speed of AXI (Advanced eXtensible Interface) DMA transfers. The analyzed architectures are the following:
- A1—trivial counting the set bits;
- A2—using tables 8:4 and adders;
- A3—using double layer of tables 8:4;
- A4—counting the set bits in parallel with 16- and 32-bit chunks processed through multiplication;
- A5—counting bits set in parallel without multiplication, like in Section 3.1;
- A6—dedicated LUT-based circuit from [29].
The first architecture (A1) is implemented as for loop VHDL construction and results in a long sequence of 31 adders that does not seem particularly interesting except for the sake of comparison:

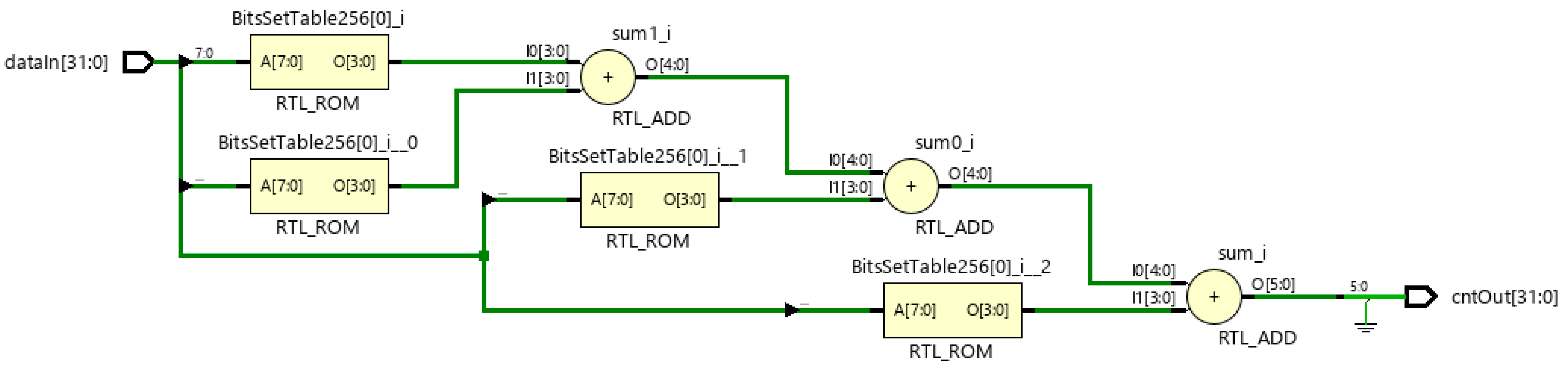
The second architecture A2 uses four tables 8:4 to quickly process 8-bit chunks and three adders to sum up the previous results. The elaborated design is presented in Figure 1 (albeit 6 bits are sufficient to keep the result, 32-bit output is used with the most significant bits set to 0).
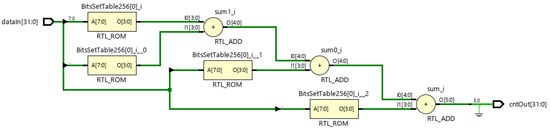
Figure 1.
Schematic of A2 architecture: tables 8:4 and adders.
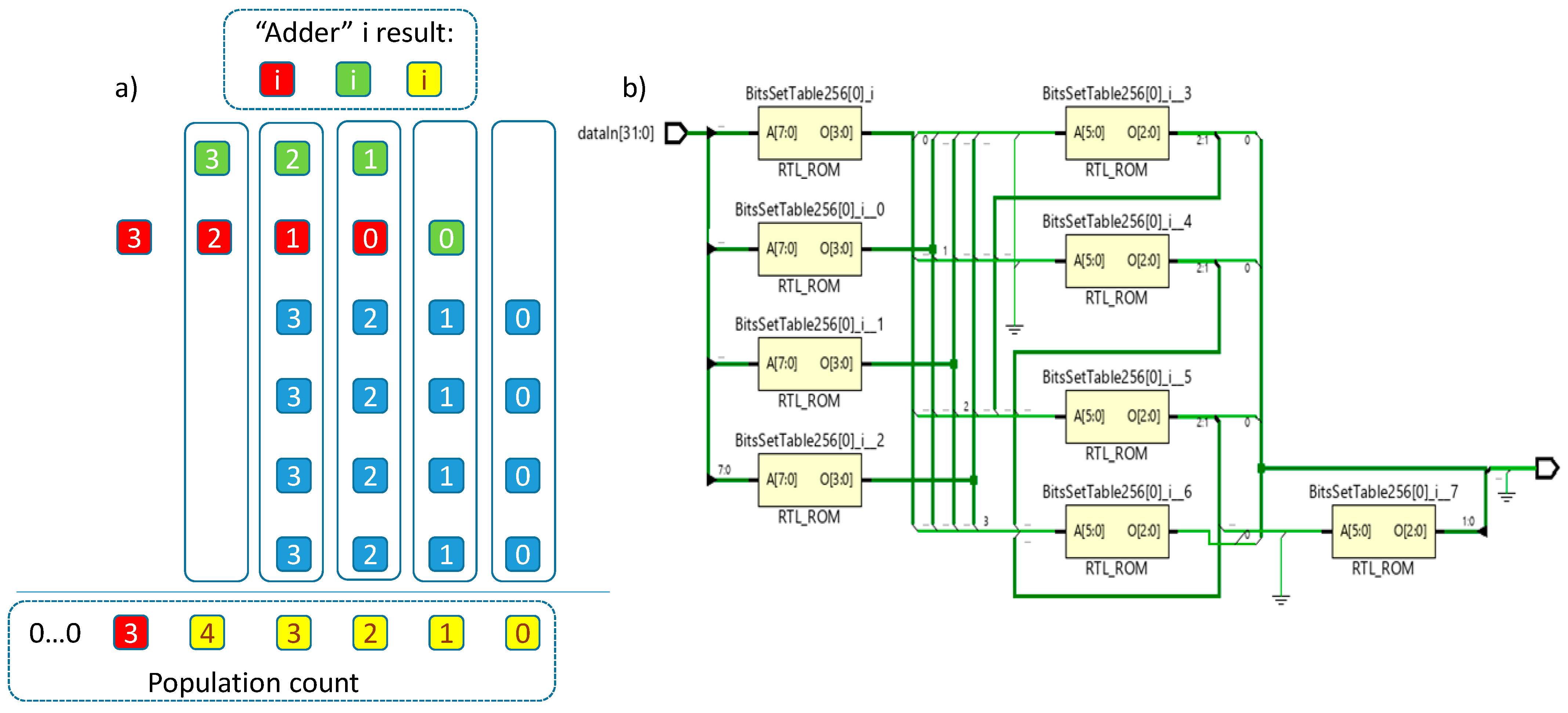
The third architecture A3 is similar to A2, but instead of adders, reutilizes the 8:4 table as illustrated in Figure 2. The first layer of four tables 8:4 calculates the population counts for 8-bit chunks. The second layer executes table-based “addition” operation over the same-order bits and the correct carries from the previous lowest order results as illustrated in Figure 2a). Blue squares are individual bits of the four 4-bit values that have to be summed up. The possible result in every column never exceeds 3 bits: red square is the most significant bit, green square is the middle bit, and yellow square is the least significant bit. Note that at position 4 the result can only be either 1 or 0, with carry always equal to 0. This is because after processing the 8-bit chinks the maximum number of set bits that each of these may have is equal to 8. Solid rectangles represent five instances of the 8:4 table to be used at the second layer (see Figure 2b). The architecture resembles a compressor tree executing a single 4-input addition operation.
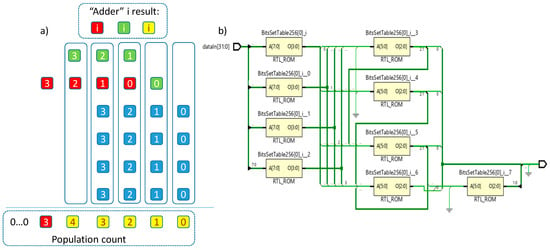
Figure 2.
Executing the addition with 8:4 tables (a); schematic of A3 architecture (b).
The fourth architecture A4 executes counting the set bits in parallel with 16- and 32-bit chunks processed through multiplication. The following VHDL code fragment illustrates the idea:

The architecture A5 is very similar to the previous one, with the only difference being the multiplication operation substituted by the following combination of ANDs and shifts (as this might have influence on the critical path):

Finally, the last architecture is taken straight from Figure 3.32 in [29] which constructs a 32-bit Hamming weight counter/comparator by directly instantiating and configuring Artix-7′s LUTs. This approach is definitely the most difficult to implement and less portable, as the respective VHDL code uses Xilinx-specific LUT components (declared in UNISIM library) and all the LUTs in the layers have to be configured with proper constants; this operation is obviously error-prone.
4.2. System Architecture
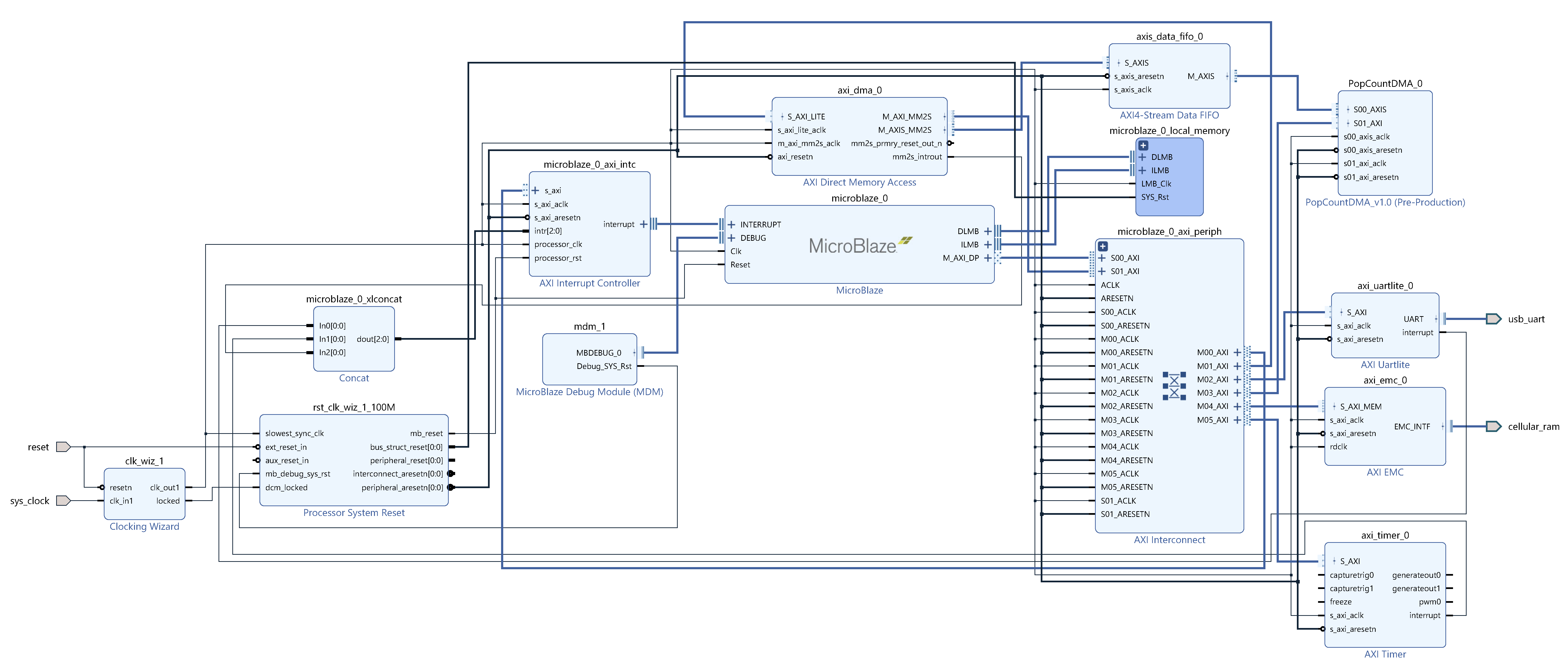
Different hardware accelerators for MicroBlaze for population count computation have been designed and implemented in Xilinx Vivado 2020.2 design suite and Vitis 2020.2 core development kit. All the designs have been tested on a low-cost and low-power xc7a100tcsg324-1 FPGA [34] from Artix-7 family available on Nexys-4 prototyping board [35]. The system architecture was described using the Vivado IP integrator, with various population count accelerators specified in VHDL. The software was written in C language and built using Vitis. The system consists of the following blocks:
- A 32-bit MicroBlaze processor optimized for performance with instruction and data caches disabled, the debug module enabled, and the peripheral AXI data interface enabled. The processor has two interfaces for memory accesses: local memory bus and AXI4 for peripheral access.
- A mixed-mode clock manager (MMCM)—to generate the 100 MHz clock for the design from signal arriving from the crystal clock oscillator available on Nexys-4.
- MicroBlaze local memory configured to 128 KB and connected to the MicroBlaze instance through the local memory bus core providing fast connection to on-chip block RAM storing instruction and data.
- MicroBlaze debug module interfacing with the JTAG port of the FPGA to provide support for software debugging tools.
- MicroBlaze concat for concatenating bus signals to be used in the interrupt controller.
- AXI interrupt controller supporting interrupts from the AXI timer, the UARTLite module and DMA. It concentrates three interrupt inputs from these devices to a single interrupt output to the MicroBlaze.
- AXI timer—hardware timer for measuring execution times. The timer counter is configured to 32 bits.
- Reset module that provides customized resets for the entire system, including the processor, the interconnect, the DMA, and peripherals.
- AXI interconnect with two slave and six master interfaces. The interconnect core connects AXI memory-mapped master devices to one or more memory-mapped slave devices. The two slave ports of the interconnect are connected to the MicroBlaze and the DMA controller. The six master ports are linked with the interrupt controller, DMA controller, UARTLite module, population count accelerator, external memory controller, and timer.
- UARTLite module implementing AXI4-Lite slave interface for interacting with the FPGA through UART from the host PC. A serial port terminal is used to get and print the results.
- AXI External Memory Controller (EMC)—controller for the onboard external cellular 16 MB RAM which is used to store source data for processing.
- AXI DMA controller configured to 32 bits data width with the buffer length register width of 24 bits (allowing transfers up to 224-1 bytes) and providing high-bandwidth direct memory access between the cellular 16MB memory (memory controller) and the population count accelerator module.
- AXI4-Stream data FIFO with 4096 depth for buffering AXI4-Stream data.
- The population count accelerator receiving stream data for processing through DMA from the cellular 16 MB RAM and providing memory-mapped interface to the MicroBlaze for reading the result (sum of the population counts of x 32-bit binary vectors, which is equivalent to processing bits).
The final block diagram is illustrated in Figure 3. The block automation and connection automation features have been used to put together the basic microprocessor system, the accelerator, the DMA/EMC controllers, and connecting ports to external I/O ports.
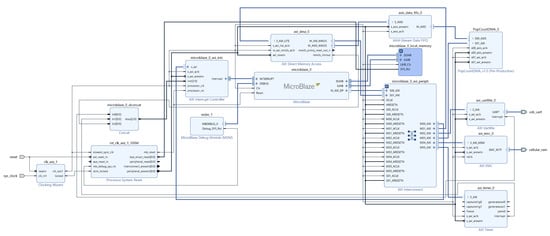
Figure 3.
Block diagram of the microprocessor system equipped with the population count accelerator.
4.3. Experimental Setup
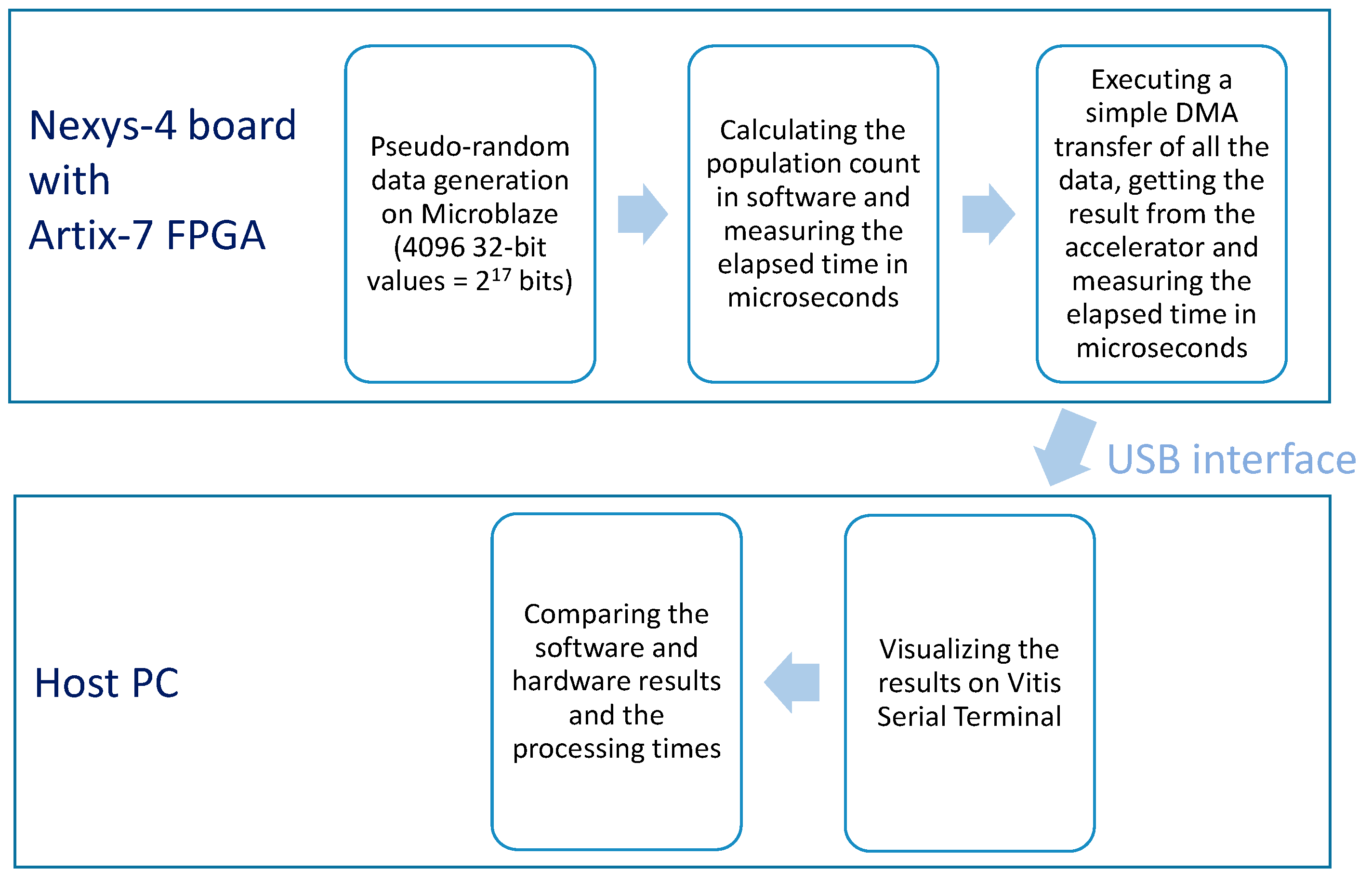
Figure 4 illustrates the overall experimental setup.
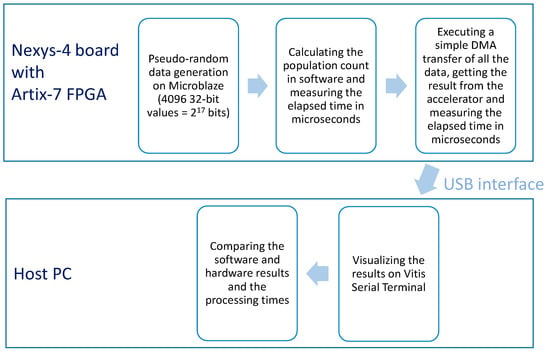
Figure 4.
The experimental setup.
The MicroBlaze is executed in standalone mode. BSS (Block Starting Symbol segment keeping uninitialized data), heap and stack memory areas are mapped to external cellular RAM. Memory is initialized with N = 4096 (configurable value) 32-bit pseudo-randomly generated values, stored in the stack area. Then a C software routine is started to calculate the total population count of all these values and the required execution time is measured with the aid of the hardware timer:

In the PopulationCountSw function, five different methods described in Section 3.1 have been tested; namely:
- trivial accumulation of the values of each of the 217 bits in a loop;
- B. Kernighan’s method;
- counting the set bits in parallel as illustrated in Section 3.1;
- counting the set bits in parallel with 16- and 32-bit chunks processed through multiplication:
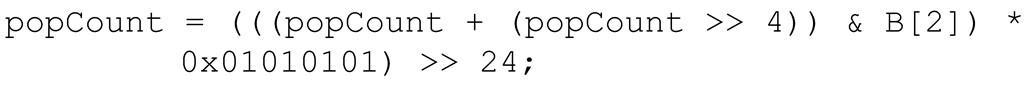
- using LUTs 8:4 and adding up the intermediate results.
I found that the best results are achieved with the LUT-based method similar to that reported at the end of Section 3.1:

After running the software routine to calculate the population count, the hardware timer is reset, a simple DMA transfer of the same source data to the hardware accelerator is executed and, once the transfer is complete, the result is read from the memory-mapped accelerator’s register. Finally, the timer is stopped and the timer’s counter register value is used to measure the elapsed time in microseconds. The following C code illustrates the procedure:
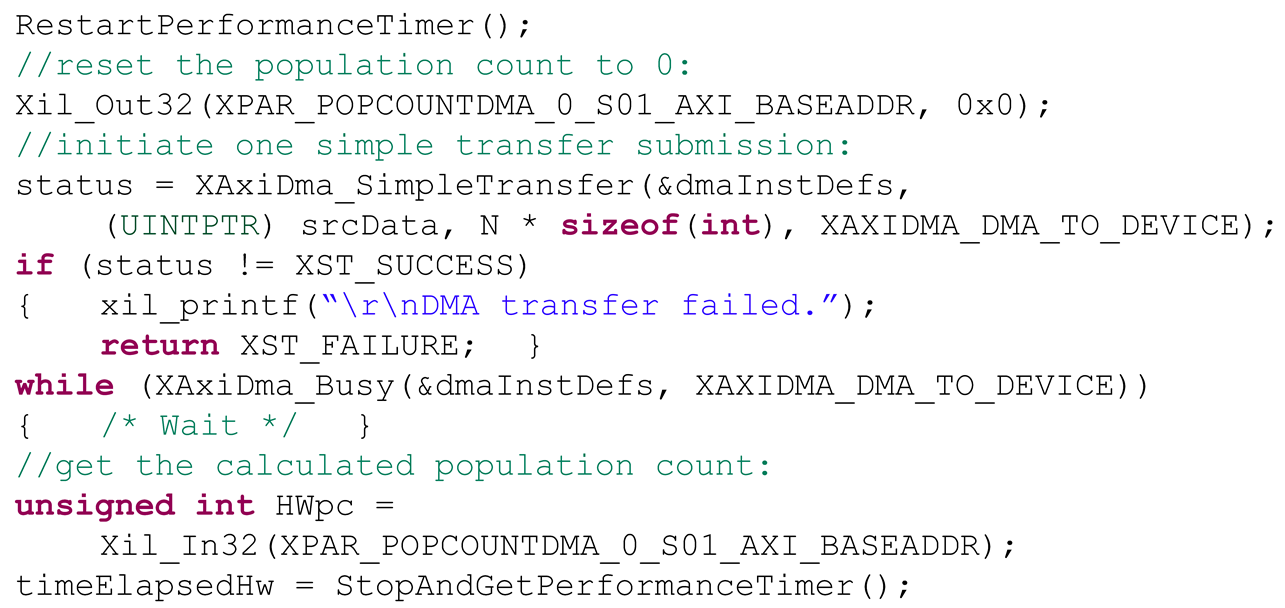
All the results and eventual error messages are visualized on Vitis Serial Terminal communicating with the MicroBlaze through the UARTLite module.
5. Discussion of the Results
The software execution time was measured for all the considered in Section 4.3 software implementations as the calculated timer counter register value multiplied by the known clock period of 10 ns. I found that the best results are achieved with the LUT-based method, followed by a 4-input adder. The selected embedded software module takes 23,786 µs to execute and is 19 times faster than the trivial bit count, 7 times faster than the B. Kernighan’s method and 1.2–1.6 times faster compared to counting the set bits in parallel (depending on how to process 16- and 32-bit chunks). Therefore, the fastest C code listed in Section 4.3 for calculating the population count in software was chosen for further comparison with hardware accelerators.
All the hardware architectures A1–A6 take exactly the same number of clock cycles to execute (77,042 cycles), as this is bounded by AXI DMA transactions, and, assuming 100 MHz clock frequency, this amounts to 770 µs for processing the same 217 bits of randomly-generated data, which is 30.8 times faster than calculating the population count in software running on MicroBlaze. This is, however, a theoretical speed-up as not all the architectures are capable of executing at 100MHz. In particular, I found that A4 and A5 exhibit negative values of worst slack, and the greatest positive slack is demonstrated by A1 architecture. Table 1 summarizes the timing performance of A1–A6 for the considered implementations and the required for the complete system resources (including all the modules listed in Section 4.2). In terms of the occupied resources, all the architectures exhibit comparable results with negligible differences, with the most resource-angry approaches being A4 and A5. It is a big surprise, however, that the architecture A1 (a long sequence of 31 adders) demonstrates the best maximum operating frequency and comparable to counterparts resources. I believe that this is due to the very efficient carry chain optimization realized by the Vivado synthesis tool. Compressor trees employed in A3 are slower and grant a negligible resource gain.

Table 1.
Timing performance of A1–A6 accelerator architectures for the considered implementations, the resources occupied by the complete system and the total on-chip power.
The total on-chip power calculated by Vivado power analysis tool from the implemented netlist for the whole system with A1–A6 accelerators is also reported in Table 1. The power losses are scaled to one clock frequency (100 MHz) and the results indicate that the variation in power losses among the architectures A1–A6 is negligible.
All the designs reported in this paper have been fully implemented and tested on the Nexys-4 board connected to the host PC through a USB cable. The designs are however self-contained and do not require a host PC to operate. The computer was only used to facilitate experiments and the results analysis.
6. Conclusions
I found that a low-cost, low-power Artix-7 FPGA in which the soft-core processor offloads the computation of the population count to a hardware accelerator implemented in FPGA logic resources can perform the calculation at a speed 31× greater than what the processor achieves without hardware acceleration. The experiments have been carried out with 217-bit randomly generated vectors stored in external cellular memory. The system architecture is scalable to support smaller (no changes are required) or longer bit vectors (it might be necessary to adjust the buffer length register width of the DMA controller which is currently configured to support 224-1 bit transactions). As the analyzed accelerators occupy negligible FPGA resources, several accelerator instances could be instantiated and run in parallel; however, as reported in [22], I believe that the bottleneck would be in communication links and protocols.
Funding
This work was supported by National Funds through the FCT—Foundation for Science and Technology, in the context of the project UIDB/00127/2020.
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Kim, K.D.; Kumar, P.R. An overview and some challenges in cyber-physical systems. J. Indian Inst. Sci. 2013, 93, 341–352. [Google Scholar]
- Mosterman, P.J.; Zander, J. Cyber-physical systems challenges: A needs analysis for collaborating embedded software systems. Softw. Syst. Model 2016, 15, 5–16. [Google Scholar] [CrossRef]
- Rodríguez, A.; Valverde, J.; Portilla, J.; Otero, A.; Riesgo, T.; de la Torre, E. FPGA-Based High-Performance Embedded Systems for Adaptive Edge Computing in Cyber-Physical Systems: The ARTICo3 Framework. Sensors 2018, 18, 1877. [Google Scholar] [CrossRef]
- Qasaimeh, M.; Denolf, K.; Vissers, J.L.K.; Zambreno, J.; Jones, P.H. Comparing Energy Efficiency of CPU, GPU and FPGA Implementations for Vision Kernels. In Proceedings of the 2019 IEEE International Conference on Embedded Software and Systems (ICESS), Las Vegas, NV, USA, 2–3 June 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Hong, T.; Kang, Y.; Chung, J. InSight: An FPGA-Based Neuromorphic Computing System for Deep Neural Networks. J. Low Power Electron. Appl. 2020, 10, 36. [Google Scholar] [CrossRef]
- Spagnolo, F.; Perri, S.; Frustaci, F.; Corsonello, P. Energy-Efficient Architecture for CNNs Inference on Heterogeneous FPGA. J. Low Power Electron. Appl. 2020, 10, 1. [Google Scholar] [CrossRef]
- Sarwar, I.; Turvani, G.; Casu, M.R.; Tobon, J.A.; Vipiana, F.; Scapaticci, R.; Crocco, L. Low-Cost Low-Power Acceleration of a Microwave Imaging Algorithm for Brain Stroke Monitoring. J. Low Power Electron. Appl. 2018, 8, 43. [Google Scholar] [CrossRef]
- Intel Corp. Intel® 64 and IA-32 Architectures Software Developer’s Manual, Volume 2 (2A, 2B, 2C & 2D): Instruction Set Reference, A–Z. 2016. Available online: https://www.intel.com/content/dam/www/public/us/en/documents/manuals/64-ia-32-architectures-software-developer-instruction-set-reference-manual-325383.pdf (accessed on 14 March 2021).
- Arm, Lda., Arm Armv8-A A32/T32 Instruction Set Architecture. Available online: https://developer.arm.com/documentation/ddi0597/2020-12/SIMD-FP-Instructions/VCNT—Vector-Count-Set-Bits-?lang=en (accessed on 14 March 2021).
- Xilinx, Inc. MicroBlaze Processor Reference Guide. UG081 (v9.0). 2008. Available online: https://www.xilinx.com/support/documentation/sw_manuals/mb_ref_guide.pdf (accessed on 14 March 2021).
- Nurvitadhi, E.; Sheffield, D.; Sim, J.; Mishra, A.; Venkatesh, G.; Marr, D. Accelerating Binarized Neural Networks: Comparison of FPGA, CPU, GPU, and ASIC. In Proceedings of the 2016 International Conference on Field-Programmable Technology (FPT), Xi’an, China, 7–9 December 2016; pp. 77–84. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, J.; Anderson, J.H. FPGA Architecture Enhancements for Efficient BNN Implementation. In Proceedings of the 2018 International Conference on Field-Programmable Technology (FPT), Naha, Japan, 10–14 December 2018; pp. 214–221. [Google Scholar] [CrossRef]
- Agrawal, A.; Jaiswal, A.; Roy, D.; Han, B.; Srinivasan, G.; Ankit, A.; Roy, K. Xcel-RAM: Accelerating Binary Neural Networks in High-Throughput SRAM Compute Arrays. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3064–3076. [Google Scholar] [CrossRef]
- Huang, C.H.; Chen, P.J.; Lin, Y.J.; Chen, B.W.; Zheng, J.X. A robot-based intelligent management design for agricultural cyber-physical systems. Comput. Electron. Agric. 2021, 181. [Google Scholar] [CrossRef]
- Schanck, J. Improving Post-Quantum Cryptography through Cryptanalysis. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2020. Available online: https://uwspace.uwaterloo.ca/bitstream/handle/10012/16060/Schanck_John.pdf?sequence=3&isAllowed=y (accessed on 14 March 2021).
- Coron, J.S.; Gini, A. Improved cryptanalysis of the AJPS Mersenne based cryptosystem. J. Math. Cryptol. 2020, 14, 218–223. [Google Scholar] [CrossRef]
- Mitchell, R.; Chen, I.R. A Survey of Intrusion Detection Techniques for Cyber-Physical Systems. ACM Comput. Surv. 2014, 55. [Google Scholar] [CrossRef]
- John, I.N.; Kamaku, P.W.; Macharia, D.K.; Mutua, N.M. Error Detection and Correction Using Hamming and Cyclic Codes in a Communication Channel. Pure Appl. Math. J. 2016, 5, 220–231. [Google Scholar] [CrossRef]
- Dalke, A. The chemfp project. J. Cheminform. 2019, 11, 76. [Google Scholar] [CrossRef]
- Gonzalez-Domínguez, J.; Schmidt, B. ParDRe: Faster parallel duplicated reads removal tool for sequencing studies. Bioinformatics 2016, 32, 1562–1564. [Google Scholar] [CrossRef]
- Anderson, S.E. Bit Twiddling Hacks. Available online: http://graphics.stanford.edu/~seander/bithacks.html#CountBitsSetTable (accessed on 14 March 2021).
- Sklyarov, V.; Skliarova, I.; Silva, J. On-chip reconfigurable hardware accelerators for popcount computations. Int. J. Re Config. Comput. 2016, 2016, 8972065. [Google Scholar] [CrossRef]
- Sklyarov, V.; Skliarova, I. Hamming Weight Counters and Comparators based on Embedded DSP Blocks for Implementation in FPGA. Adv. Electr. Comput. Eng. 2014, 14, 63–68. [Google Scholar] [CrossRef]
- Parhami, B. Efficient Hamming weight comparators for binary vectors based on accumulative and up/down parallel counters. IEEE Trans. Circuits Syst. Ii Express Briefs 2009, 56, 167–171. [Google Scholar] [CrossRef]
- Piestrak, S.J. Efficient Hamming weight comparators of binary vectors. Electron. Lett. 2007, 43, 611–612. [Google Scholar] [CrossRef]
- Sklyarov, V.; Skliarova, I. Design and implementation of counting networks. Computing 2015, 97, 557–577. [Google Scholar] [CrossRef]
- El-Qawasmeh, E. Beating the Popcount. Int. J. Inf. Technol. 2003, 9, 1–18. Available online: http://intjit.org/cms/journal/volume/9/1/91_1.pdf (accessed on 14 March 2021).
- Sklyarov, V.; Skliarova, I. Multi-core DSP-based vector set bits counters/comparators. J. Signal. Process. Syst. 2015, 80, 309–322. [Google Scholar] [CrossRef]
- Sklyarov, V.; Skliarova, I.; Barkalov, A.; Titarenko, L. Synthesis and Optimization of FPGA-Based Systems; Springer: Berlin, Germany, 2014. [Google Scholar]
- Pilz, S.; Porrmann, F.; Kaiser, M.; Hagemeyer, J.; Hogan, J.M.; Rückert, U. Accelerating Binary String Comparisons with a Scalable, Streaming-Based System Architecture Based on FPGAs. Algorithms 2020, 13, 47. [Google Scholar] [CrossRef]
- Umuroglu, Y.; Conficconi, D.; Rasnayake, L.K.; Preußer, T.B.; Själander, M. Optimizing Bit-Serial Matrix Multiplication for Reconfigurable Computing. ACM Trans. Reconfig. Technol. Syst. 2019, 12, 1–24. [Google Scholar] [CrossRef]
- Rasoulinezhad, S.; Siddhartha; Zhou, H.; Wang, L.; Boland, D.; Leong, P.H.W. LUXOR: An FPGA Logic Cell Architecture for Efficient Compressor Tree Implementations. In Proceedings of the 2020 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 26–28 February 2020; pp. 161–171. [Google Scholar] [CrossRef]
- Preußer, T.B. Generic and Universal Parallel Matrix Summation with a Flexible Compression Goal for Xilinx FPGAs. In Proceedings of the 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Xilinx, Inc. 7 Series FPGAs Data Sheet: Overview. 2020. Available online: https://www.xilinx.com/support/documentation/data_sheets/ds180_7Series_Overview.pdf (accessed on 21 March 2021).
- Digilent, Nexys 4 Reference Manual. Available online: https://reference.digilentinc.com/reference/programmable-logic/nexys-4/reference-manual (accessed on 21 March 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).