Abstract
This paper contains the description of a successful system dynamics (SD) modeling approach used for almost a quarter-century in secondary schools, both in algebra classes and in a year-long SD modeling course. Secondary school students have demonstrated an ability to build original models from the news, write technical papers explaining their models, and present a newfound understanding of dynamic feedback behavior to an audience. The educational learning theory and instructional methods used for both the algebra and modeling courses are detailed, with examples. Successful student SD modeling experiences suggest the SD approach can expand the sophistication of topics that secondary school students can understand.
1. Introduction
Jay Forrester, the father of system dynamics (SD), developed the system dynamics analytical approach at Massachusetts Institute of Technology in the mid 1950s. He described system dynamics as “a method for analyzing complex systems that uses computer simulation models to reveal how known structures and policies often produce unexpected and troublesome behavior” [1]. Professor Forrester lamented the lack of understanding of dynamic systemic behavior by decision makers who are tasked with designing policies that try to modify/mitigate the undesirable side effects of troublesome systems, which are often caused by previous short-sighted policies [2]. Forrester’s recommendation for increasing the design of successful policies that address systemic problems was to have system dynamics infused into pre-college education [2]. Thus, all educated people would have a foundational understanding of the dynamics inherent in systems.
It would seem that such a recommendation would be welcome in the pre-college educational community. Teaching secondary school students to build mathematical models has been a goal in the United States for decades [3,4]. Some mathematics educators consider merely translating a story problem from the mathematics textbook into an equation as modeling, which, in the literal sense, it is. This translation process from story problem description to symbolic (equation) representation has proven difficult for a significant number of students [5,6]. SD presents a new mathematical representation that has potential for addressing the translation issue from description to symbolic representation. However, the equation representation holds a sacred place in the teaching of mathematics. Science educators, on the other hand, seem to be heading in the direction of Forrester’s vision, with stronger educational cross-cutting concept statements supporting systems and systems modeling, cause and effect, structure and function, and stability and change [7], which are all foundational concepts in SD.
An additional issue for pre-college infusion of SD is that SD is inherently cross-discipline, and U.S. secondary schools are not structured in this way. Moreover, teacher training is siloed. Consequently, when educators start teaching, they are not prepared for the broader background needed to facilitate the discussions that support systems modeling [8]. An interesting historical note is that one of Forrester’s major contributions to science and society was applying SD (based on the science of control theory) in the social sciences. This is a powerful message to mathematics and science educators that collaboration with social science teachers in SD modeling lessons is not only possible, but important. Yet another issue that teachers mention when asked about teaching modeling using technology, is a fear of losing (discipline) control of their class [9]. Siloed instructions and the changing dynamics in classroom management are not trivial concerns and create barriers for SD infusion in secondary school mathematics (and some science) classrooms.
Nevertheless, the current movement toward instruction that is focused on “student learning” rather than on “teacher teaching” is making headway. Flipped classrooms, student-centered activities, and inquiry approaches in mathematics and science place more emphasis on students accepting responsibility for their own learning, rather than being receptacles for information. There is more technology in classrooms and students are becoming ever more facile using multiple technology tools [10]. Teachers have often used student assistants to help with technology applications in the classroom. Using student assistants has worked well for this author when infusing SD into secondary school mathematics and science classes.
A final question might arise as you read this introduction. Can pre-college students actually understand dynamic system behavior? Can secondary school students learn to build SD models to explain the dynamics of complex systems. The answer is an unequivocal yes! In selected elementary and secondary schools, children from pre-school (age 4) to the end of secondary school (age 18) have demonstrated the ability to analyze dynamic behavior using behavior over time graphs, causal-loop diagrams, and SD modeling [10]. Secondary school students have been able to demonstrate an understanding of feedback control, non-linear dynamics, and delays by designing and building SD models [10,11,12]. All of this work has been going on in select pre-college schools for over a quarter-century.
Within this paper a description will be presented about how one might go about teaching students at the middle and secondary school level (ages 14 to 18) to create models of dynamic feedback systems using the SD modeling method. Before proceeding to that discussion, however, it is useful to review some important insights that we gain from learning theory.
2. Learning Theory
One of the overarching goals that society is called upon to provide for our children is to have them learn with understanding. As educators, we strive to have students internalize concepts and make them their own so that the concepts become tools for further learning, a foundation upon which intellectual growth can take place [13,14].
Deep understanding implies that the information is well-represented and well-connected. The greater the number and strength of the connections, the deeper the understanding. New information can be well-connected to existing knowledge and/or the pieces of the new information can be well-connected from within.([15], p. 3)
Although good teaching within individual content areas attempts to connect discipline-specific concepts, it is not often the case that those connections are extended across disciplines. Complex problems require multi-disciplinary approaches to develop a deep understanding of the concepts relevant to the dynamics of the problem. Learning theorists provide insights into this process.
Lev Vygotsky suggested that learning should be a socially active endeavor, where students are expressing their thinking and the teacher is facilitating the process. Learning should support student interaction and collaboration (i.e., the teacher uses demonstrations and leading questions) in order to be effective. Teachers do not transmit concepts.
If concept development is to be effective in the formation of scientific concepts [those new ideas learned in school] instruction must be designed to foster conscious awareness of concept form and structure and thereby allow for individual access and control over acquired scientific concepts.([16], p. 312)
Vygotsky is best known for “Zone of Proximal Development” (ZPD), representing a gap between what the student could learn by him/herself and what he/she could learn with the help of more knowledgeable peers and/or the teacher. Vygotsky indicated that the trajectories for individual student learning in this zone are quite open and follow dynamic and divergent paths. The objective of the “instruction”, however, is to help the student eventually internalize the new knowledge. Vygotsky [17] indicated that essential (good) learning should create a ZPD (“awaken a variety of internal developmental processes in the child that are activated by working cooperatively with peers and other people in his/her environment”, p. 90) that is forward-looking, developmentally, rather than testing, which is backward (ineffective) looking. Once the processes become internalized, they lead to independent developmental achievement ([18], italix added).
Jerome Bruner [19] suggested that there were three modes of acquiring new ideas. He referred to these as his three modes of representation: enactive, iconic, and symbolic. The first mode, enactive, involves students working with concrete objects. Students manipulate objects or act out a part in a story. The effective use of physical play-acting or manipulating devices when teaching students to create SD models is evidenced in the most popular books/lessons developed by pre-college teachers who have used SD modeling in their instruction for many years. Popsicle sticks in a jar represent trees being planted or cut in a forest. Students stand in a circle and move vertically up or down to represent the two types of feedback (positive/reinforcing or negative/balancing). Students walk in front of a motion detector to replicate linear behavior patterns. These experiences are often used as precursors to modeling activities [20,21,22].
Bruner’s second mode of representation is iconic. In the iconic mode, students use images, pictures, diagrams, or graphs to represent concrete ideas or situations that they experienced in the first mode. The iconic representation is still rather concrete as the representation is directly connected to the physical activity (from the enactive mode). For SD learning, this would be the use of graphs to represent change over time, perhaps representing the level of curiosity of a character from a story that was read, or the graph of motion displayed by a computer projector on the overhead screen in a classroom as a student walks in front of a motion detector. In both the enacting and iconic representations, students are developing mental models of how their activity represents some concept that the teacher is trying to convey.
The third mode of representation that Bruner proposes is symbolic. Here, the abstract concepts of numbers and words, or other symbols, are used to allow a student to organize his/her thinking. The intention is that the abstraction does not require a direct connection to the concrete activity from which it arose. In this stage, SD reaches its most powerful application. The symbols are the stocks, flows, converters, and connectors that students use to represent the elements they experienced in the enacting representation. They connect the elements, define the components, and finally, execute the symbolic model to produce a graph that should display the same type of behavior that was evidenced in the iconic mode. Ideally, these simple models may be applied to scenarios that the student did not experience in the enacting mode.
From this research, we conclude that modeling exercises include students working together on experiential activities to better understand the problem, and where a lesson evolves from concrete to a more abstract analysis. This strategy provides a fertile environment for assimilating new ideas about dynamic behavior.
Let us turn, for a moment, to the issue of choice of representation for constructing models. Kaput and Roschelle [23] make an interesting historical point regarding the traditional equation symbolic representation used in mathematics. This representation was designed for an intellectual elite group of mathematicians and scientists in the 17th and 18th centuries so they could communicate with each other regarding their work “largely without regard to learnability outside the community of intellectual elite involved” (p. 4). Kaput et al. mention how communication using writing or using pictures, or methods of transportation have improved when brought to scale for general public consumption. No such enhancement has been made with regard to the use of the abstract symbolism used in mathematics classes that all students are expected to master. This suggests that perhaps it might be time to transition to representations that are more user-friendly, at least as an option/alternative for quantitative analysis for some of our general student population.
Additional research points to the power of providing multiple representations for modeling using technology. De Jong, Ainsworth, Dobson, van der Hulst, Levonen, et al. [24] suggest that multiple representations can add value to a learning situation because each representation can bring different information to the learner, providing a more complete picture of the situation. It is important to note that each additional representation should bring some level of value with respect to the efficient representation of information. They also suggest that experts in a given domain are able to integrate different representations, thus multiple representation integration is a valuable learning experience for students. In a later article, van der Meij and de Jong (2006) [25] suggest that using technology to dynamically link representations can improve retention of domain knowledge and the ability of students to translate between representations.
SD modeling integrates a visual, schematic representation of the core system elements and interconnections with a graphical display of the systemic behavior under study. It shows element dependencies and makes feedback relationships visible. When executing the model, each component has its value displayed within its icon, graphically, over time. Moreover, a graph and/or table can display values for elements that are related (on the same grid or table) over time and the simulation time can be scrubbed back and forth to display, erase, and redisplay multiple model component values, allowing for comparison of dynamics between components (i.e., comparing the graphs of births and deaths over time with the population dynamics).
Forrester [2] explains that most decisions that people make are based upon their mental models, which are formed from their observations and experiences. He cautions, however, that although mental models contain significant information that allows us to function well in many situations, when it comes to complex decisions, it can have serious shortcomings. Seel [26] cites research on the importance of “making thinking visible” to advance learning. He states that encouraging students to create their own visual representations can advance learning, and mentions research involving students who created dynamic visualizations of their mental models relating to a science concept outperforming students who created static visualizations. Forrester would go further, stressing the need to test whether one’s mental model is valid by creating a dynamic model to test the structure and behavior of the mental model [2]. Forrester admits that a computer model cannot actually capture the true behavior of a mental model because all models are simplifications of the real world. However, he states that creating computer models helps to refine one’s mental model, which can then be used to refine the computer model, and thus they work in a synergetic fashion to lead to more accurate and useful understanding of the problem under study.
Green [27] has written a book that highlights some of the characteristics of quality teaching. It is no surprise that effective student learning is heavily influenced by having effective classroom teachers. Part of learning theory must focus on those qualities that help teachers become more effective in their classrooms. Research supports the move from teacher on the stage to guide on the side. Effective teachers design a positive learning environment using many subtle management strategies. One of the highly effective teacher/researcher educators, Deborah Loewenberg Ball, identified five high-leverage practices of effective teachers. The top five practices include the following: (1) making content explicit through explanation, modeling, representations, and examples; (2) leading a whole class discussion; (3) eliciting and interpreting individual students’ thinking; (4) recognizing particular common patterns of student thinking in a subject-matter domain; and (5) identifying and implementing an instructional response to common patterns of student thinking. It is evident from Green’s book that teachers who can stimulate learning must themselves continue to be students of their craft.
Let us turn now to a discussion about how SD captures the structure of a systemic problem, how SD has been used to enhance the learning of functions in algebra, and how SD has been used to enable students to design original SD models in an SD modeling course.
3. Introduction to the System Dynamics Modeling Icons
There are four basic modeling icons that are used when building beginning and intermediate level SD models with students. These icons are displayed in Figure 1.
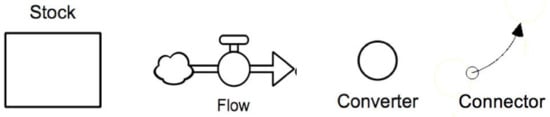
Figure 1.
The four main icons used when creating system dynamics (SD) models.
The stock icon is used to represent the variable(s) whose value we want to track in the model. It is an accumulator, increasing or decreasing in quantity during the simulation. Some simple examples of variables that might be designated as stocks could include money in a bank account, population in a city, pollution in a river, or more abstract variables such as concern for safety in a community or job satisfaction.
The flow, if it contains only one arrowhead, will be drawn with the arrow pointing toward the stock or away from the stock. Pointing toward the stock, the flow value will increase the stock value and represents the rate of increase of the stock. Pointing away from the stock, the flow value will decrease the stock value and represents the rate of decrease of the stock. For the first two stock examples listed in the previous paragraph, an inflow for money in the bank could be interest added to the account (or deposits added to the account) and an outflow could be monthly expenditures. For population in a city, an inflow could be births and/or immigration and outflows could be deaths and/or emigration.
The converter (auxiliary) is used to hold additional values or formulas needed for calculating the flow values. If the reader examines Figure 2 below, which contains a simple population model, it becomes apparent that a modeler might want to display an icon that holds the constant value “percent of births per year” or “percent of deaths per year” in order to bring attention to the importance of these parameters. Converters allow the modeler to make these components visible in the model.
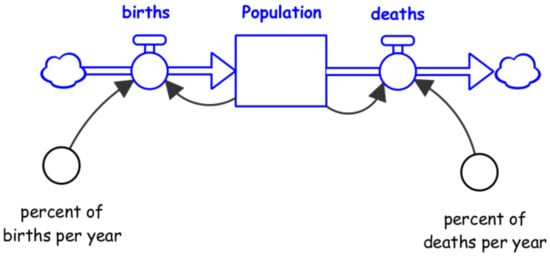
Figure 2.
Simple Population SD model.
The connector is used to connect stocks to flows, stocks to converters, converters to flows, flows to other flows, or converters to other converters. It sends numeric information from one icon to another, allowing for values to be updated as simulations are executed recursively in small, discrete time steps. Again, looking at Figure 2, the connectors allow the modeler and the client to see dependencies of one component upon another explicitly. They are also extremely valuable in helping one identify feedback in the model.
A simple population SD model diagram is presented in Figure 2. The population stock value increases via births (flow) and decreases via deaths (flow). Births are calculated as the product of the current population value and the (constant) percent of births per year value. Deaths are calculated similarly, using the population stock value and the (constant) percent of deaths per year value.
4. Teaching System Dynamics Modeling
What follows is an approach to teaching SD modeling that has been used successfully with secondary school students for over 20 years. At secondary school level, the activity of building SD models has been implemented in two ways. One use of SD modeling was to reinforce student understanding of the typical behavior of generic functions studied in algebra. That is, which stock/flow structures produce behavior that is linear, parabolic, exponential, goal-seeking (convergent), logistic, or sinusoidal? Following these basic lessons, students then combined these function structures to build models to study more sophisticated dynamics. Some example models that students built include drug pharmacokinetics, population with resource depletion, and predator/prey populations.
The other use of SD modeling was in the design of a year-long (nine-month) SD modeling course for students aged 15 to 18, which culminated in students designing an original model (model topic of their choice), writing a technical paper explaining how their model worked, and finally, giving a presentation about their model to the class. This application of SD modeling is explained in Section 4.2.2. An example of a student’s original model is displayed and explained in Figure 6.
4.1. Model-Building in Algebra Classes
For the past few decades, U.S. mathematics education standards have recommended that algebra be taught using multiple representations when studying generic functions [3,4]. These representations included the typical equation for the function, the graphical output for the function, identifying functions from numerical (tabular) data, and identifying functions from reading a story problem. The stock/flow SD representation was added to this set of function representations by this author. Moreover, a “verbal” differentiation of the behavior of the functions was implemented by focusing on the function’s rate of change. That is, the functions were introduced using a conceptual calculus approach. Examples of this conceptual calculus approach include a focus on the fact that linear stock behavior is produced by constant inflow and/or outflow values, that exponential stock behavior is produced when inflow and/or outflow values are defined to be proportional to the stock value, and that when a bi-directional flow1 value changes sign, the stock behavior changes direction (thus producing a local maximum or local minimum, etc.), to name a few. This entire description is done without the overhead of describing derivatives and integrals via the equations associated with traditional calculus.
Pre-Lessons
In teaching the use of stock/flow SD modeling in algebra, an initial lesson started with some motion detector activities. For these activities, a motion probe2, connected to a computer that displayed a graph of the position (distance from the probe) of the person moving in front of the probe, was used. A student was asked to move in front of the detector to create different linear motion graphs (see Figure 3). When introducing quadratic functions, a ball was tossed above the motion probe (which was placed on the floor with the sensor pointing upward) to produce parabolic motion graphs. When introducing sine and cosine functions, the probe (with the sensor pointing toward the floor) was rotated using a circular motion to produce sinusoidal graphs. The instructional emphasis was to focus on the pattern of the velocity of the movement and use it to explain why this pattern of velocity produced the shape of the position over time graph that was displayed by the motion sensor (i.e., the point was to understand how the flow behavior could be used to predict the stock behavior) [21].
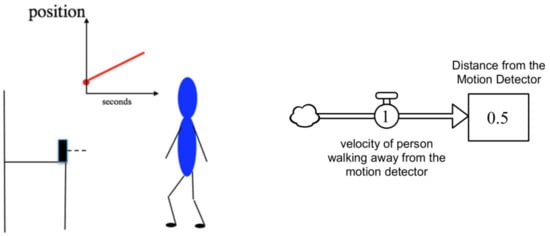
Figure 3.
Student walking in front of a motion detector, and the SD model used to capture the idea of distance changing (linearly) over time. Assume the student initially stands 0.5 m away from the detector and then moves away from the detector at a velocity of 1 m per second for 4 s.
These kinesthetic lessons were instrumental in helping students understand why the stock/flow model for each function had the designated structure. This activity applies all three of Bruner’s learning modes.
The stock/flow structure was regularly compared to the traditional generic function graph, numeric data, and equation for each function type (see Figure 4). Once students understood the basic stock/flow structure for each generic function, they were ready to start combining these generic structures to study problems that contained more complexity.
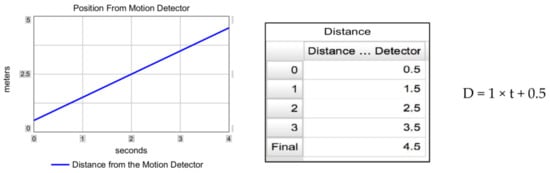
Figure 4.
The graph and table produced by the SD software, and the equation for the situation described in Figure 3. In the equation, D represents the student’s current distance from the motion detector and t represents the time lapsed (in seconds) since the simulation commenced.
Using guided story scenarios, students built models to analyze drug pharmacokinetics (combining linear and exponential function structures), population and resource consumption (introducing non-linear modeling components and analyzing the transfer of loop dominance), and oscillations (two stock models containing a balancing feedback loop that connects them). An example of an oscillating predator/prey model that was used in an algebra class is displayed below (see Figure 5).
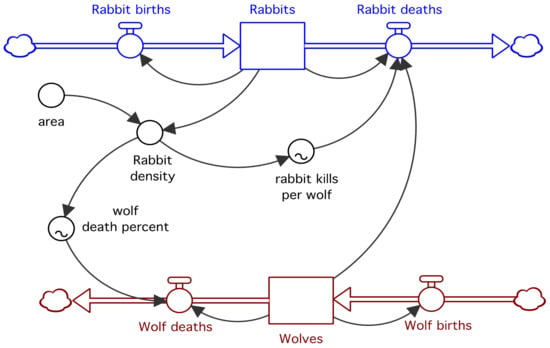
Figure 5.
The stock/flow diagram that secondary school algebra students built and analyzed in a 45 min class period in the second half of the academic year.
These lessons were all short and directed toward very specific reinforcement of individual and combined generic function behavior. The emphasis in the lessons was for students to use the stock/flow model structure and the feedback within the structure to explain the behavior of the model, which was displayed graphically. The SD core principle applied here is “structure (of the model) determines the behavior (of the model)” and supports the important core SD principle that system behavior is generated endogenously [28].
Some action research experiments were conducted in the algebra classes over the years. In this research, it was found that students felt more comfortable using SD modeling software to build multi-function models, rather than setting up piece-wise defined functions [29]; were able to predict (more than 60% of the time) whether the value of the stock in a one-stock SD model would increase or decrease over time [30]; and felt that they learned important information (94% in class 1, 73% in class 2) building the pharmacokinetic models [31]. Moreover, Dr. Edward Gallaher, a research pharmacologist who uses SD modeling in his drug research, was invited—several years in succession—to participate in the final stages of the SD drug model sequence of lessons with my algebra students. Dr. Gallaher also taught pharmacokinetics to second-year medical students at Oregon Health and Sciences University. He observed, “I came to the realization that these [SD] modeling exercises enabled high school students to meet or exceed our expectations for the medical students!”
The previous section described how some teachers have used SD modeling to reinforce mathematics concepts (especially functions) in a traditional algebra classroom. In such an environment, there are constraints on the time that can be allotted to modeling due to the large number of topics that are required to be included in most mathematics classes. The next section describes the structure of a year-long SD modeling course for secondary school students. In this course, the focus was on enhancing students’ SD modeling skills so that they could build original models and explain complex dynamic systems in more detail.
4.2. The Nine-Month System Dynamics Modeling Course
Students (aged 15 to 18) who decided to take this elective SD modeling course tended to be self-motivated and willing to take risks. These characteristics were necessary for student success in the course because there were no lectures, no tests, and no homework. All of the instruction was done, with one exception, within the printed lesson scenarios that were given to the students. All of the students had previously taken an introductory algebra course and had, at minimum, an average ability in algebra. Many students had no previous experience in building SD models. Students progressed through the lessons at their own pace (with a minimum pace specified by the teacher). Additional extra credit assignments and other challenges were provided for students who progressed at a very quick pace. The class met four times per week. Three of the sessions were 48 min and one session was 80 min. The class was held in a computer lab in which each student had his/her individual computer to work on each class session. Each modeling lesson required students to read a story, start to build an SD model (incrementally), anticipate model behavior, capture graphical output from the models they built, and explain any discrepancy between anticipated model behavior and the output produced by simulating the model on the computer. Students were also asked to look for other applications of the models they built. These lessons were graded.
The overarching goals of the SD modeling class were the following:
- To prepare students to identify and analyze problems in the world from which they could gain understanding by building and analyzing SD models.
- To develop the student’s skill in model building, analyzing model design, identifying and explaining feedback control and how it is evidenced in model output, and explaining clearly what they have learned in the modeling process.
The SD modeling method provided the foundation for the majority of the structure for the lessons. The specific SD modeling method is spelled out in detail in Sterman’s [32] book:
- Problem Articulation: Selecting an appropriate problem, determining the necessary time boundary for the problem that captures the problematic behavior, determining the key variables, and sketching appropriate reference graphs (behavior over time graphs of key variables).
- Formulating a Dynamic Hypothesis: Identifying key feedback loops that can produce the problematic system behavior identified in problem articulation.
- Formulating a Simulation Model: Creating the stock/flow model that can produce the problematic behavior identified in problem articulation.
- Testing the Model: Testing occurs throughout model development, as model development is an iterative process. Tests include sensitivity analysis on parameters and reasonable model behavior recovery from introducing extreme values in certain model components.
- Policy Design and Evaluation: Identifying practical policies that can be implemented within the system that could mitigate the undesirable behavior of the system. Model structure may need to be altered to make the new policy work.
Different lessons in the course focused on having students develop skill with one or more concepts from the SD modeling method.
Before describing the sequence of modeling topics, it is important to remember the purpose of SD modeling. An SD model is built to help the modeler (and client) better understand the underlying structure and causal nature within the system that produces its troublesome behavior.
Forecasting of future conditions is not a measure of model suitability because forecasting is nearly impossible, and the goal is to understand how changes in policies affect behavior.([33], p.23)
Some specific details about the organization of the SD modeling course will now be presented.
4.2.1. The First Modeling Lesson
Before students are ready to build models, they need to learn to navigate the modeling software. To that end, a lesson was given to students requiring them to design a model from an explanation that is very directive in its instruction. In this activity, students learned to place, name, and define modeling icons; create and read numerical data from graphs; refine precision for variables; and revise model settings. The first lesson also set the expectation for quality when students responded to questions. Student responses were often too short and poorly organized in this first lesson. Significant teacher feedback was provided to help students learn how to improve their responses to questions.
4.2.2. The Sequence of System Dynamics Modeling Lessons
The two expectations that were announced to students at the beginning of their SD modeling efforts were that (1) units for every model diagram element must be identified and all units in the model must be consistent, and (again) (2) explanations required in the lessons must be thoughtful, clear, and in complete sentences. Significant weight for the grade was based on following both of these rules. Students were encouraged to talk and work together on modeling assignments, but each explanation had to be his/her own.
The entire modeling course was based on the philosophy that students learn how to understand the dynamics of a particular situation by building models to capture the dynamics present in that scenario. Students not only practiced translating the story description into stock/flow model diagrams, but were expected to use the feedback present in the model to describe the model behavior. Students were introduced to special constructs, like designing multipliers, in context. The sequence of learning activities is presented below:
- Build small generic structures: There are a few generic modeling structures that capture important dynamics that are often parts of larger models. Having students develop some skill building and analyzing these small models and applying them to multiple scenarios was a useful early modeling experience. Some typical behaviors that were captured by generic structures included the following: exponential growth, exponential decay, convergent (goal-seeking) behavior, logistic (or more generally s-shaped) behavior, and overshoot and collapse behavior. Note: oscillating behavior was treated separately, later in the course.
- Combine generic structures: A logical next step was to create stories in which the dynamic behavior is produced by a combination of the generic structures already studied. As an example, a pharmacokinetic model would involve a patient connected to an intravenous drip. The inflow was constant, but the outflow (metabolizing the drug) was exponential. Many scenarios contained basic population structures (i.e., births/deaths, immigration/emigration, aging chains) and fitted within this category.
At this stage a core SD principle is reinforced: feedback loops are responsible for the dynamics that we see in SD models because they control the changes that we experience in systems over time [34]. Moreover, these feedback loops are a consequence of the endogenous viewpoint that is fundamental to SD analysis [35].
- Learn to build a dimensionless multiplier (DM): Most SD components are defined using either constant values or simple mathematical formulas. However, SD modeling also allows components to be defined graphically. Best practice usually requires the graphical definition to follow a prescribed design that produces a component known as a dimension multiplier. Learning to implement dimensionless multipliers in an SD model moves the modeler to a higher level of expertise. It is essential that the students understand why one would want to use, where to apply in a model, how to design, and how to implement a dimensionless multiplier in an SD model. Dimensionless multipliers are used to implement the non-linear behavior of the system within an SD model. They are essential to producing transfer of loop dominance. In early lessons, students built scripted models that incorporated dimensionless multipliers. Students were asked to explain how the dimensionless multiplier affected the behavior of the model (by interpreting the purpose of the (DM) graphical shape, the reason for the (1,1) stability point, and the choice of scale boundaries). Thus, students were gaining experience in the use of a DM before actually implementing one independently.
- Learn why systems oscillate: Oscillations can be produced wherever an SD model contains two stocks that are connected within a balancing feedback loop. One of the virtues of SD modeling is that students come to understand the structures that produce oscillations in a system, rather than just using trigonometric functions within a model to produce this behavior.
- Capture delays: Another extremely valuable feature of SD modeling is the ability to capture material delays (i.e., the time it takes for a letter to travel from sender to recipient) and information delays (i.e., the average time it takes for a person to change his/her mind about an issue) in SD models. These delays were incorporated in earlier lessons, without explicitly identifying them as delays. When delays were formally introduced, students were expected to reflect on the earlier models and identify the delays that were included in those models. Students were then to implement delay structures and explain the correct delay concepts when delays appeared in future story scenarios.
- Practice creating a stock/flow diagram from a news article: This is the one lesson in which direct instruction was used. Students were asked to read a news article. Then, as a class, students decided which variables might be important in the article. They identified which of those variables might be stocks. For the stocks, a reference behavior graph was developed, the time horizon was chosen, and the time units were chosen for the model. A stock/flow diagram was then developed, progressing until the first major feedback (containing more than three components) was closed. Finally, the feedback loop was identified and its polarity was determined. Students were then told to repeat the process on an article from the news that was of interest to them. Students have mentioned that this lesson was one of the most important lessons in preparing them to start to build their own (original) model for their project. Note: In this lesson, students did not simulate these models on the computer. The models were simply stock/flow maps without equations.
- Build and test an original system dynamics model from scratch: Building an original model from scratch was done in teams of two students. Students spent approximately two weeks selecting and researching two system problem ideas. Two topics were researched because students sometimes found one topic too difficult for them to understand or found they could not locate sufficient data for one of the topics. Students were also required to find an expert on their topic who would agree to talk to them periodically throughout their model-building phase, because it would become clear to them that they could not model a topic they did not understand well. (It was a pleasant surprise to find that an overwhelming number of adults who were solicited by the student modelers were quite willing to help them understand their project topic by answering student questions.3) By the end of the two weeks, students had to settle on one topic. The model was built and tested in stages, following the strong recommendation from SD modelers, “always have a working model.” This process took about four weeks. Students were given extra credit if they could get their model to start in equilibrium. Thus, the time frame for this part of the project included two weeks for initial research, two weeks to develop a draft model that simulates,4 and one to two weeks to polish the model. Forrester states that the process of building models is more important than the models arising from it [36].
- Write a technical paper explaining model behavior, model testing process, and a policy recommendation: Students wrote a technical paper explaining the model and the testing protocol that was followed to “validate” the model. Sterman [32] claims that it is not possible to actually validate or verify a model, since all models are wrong. However, there are procedures that should be followed to give the modeler (and the client) some confidence that the model may provide useful information about the problem being analyzed. Firstly, units had to be consistent. Secondly, sensitivity analysis had to be used to determine which parameters were most sensitive. Thirdly, students needed to conduct extreme value tests. In the final stage of this project a reasonable, realistic policy had to be designed, tested, and explained in an attempt to help mitigate the undesirable behavior produced by the system (which was captured by the model). A paper outline format was provided as no student had ever written a technical paper before (at secondary school level). The paper took between 1.5 and two weeks to produce, with a draft paper submitted after one week and feedback on the draft provided by the teacher so students could polish their final paper and resubmit. Paper drafts were not started until students had received feedback on their model drafts from the teacher.
You may notice the sequence of steps used to move the student from reading about a systemic problem to building and analyzing the model that is described in this bullet to be slightly different from the sequence listed by John Sterman (Section 4.2). The difference concerns when to create a dynamic hypothesis. Forrester [37] created the model before developing the dynamic hypothesis. Forrester’s sequence has been very effective with pre-college students. The students do not create a detailed dynamic hypothesis loop diagram. The students create an aggregate dynamic hypothesis diagram, which they present in their technical papers, as recommended by Khalid Saeed [33]. Aggregate dynamic hypothesis diagrams show the high-level module segments of the model and the simple feedback connecting these modules.
- Present modeling insights to an audience: Students were given the option of doing a videotaped presentation of their model to the class or producing a poster to explain their model to an audience. Guidelines for the video presentation and the poster presentation were given to the students.
An example of one of the original models created by an 18-year-old student in this course is presented in Figure 6. The output of the model is displayed in Figure 7.
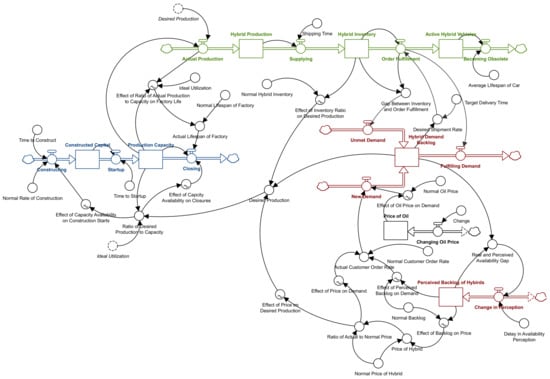
Figure 6.
Model of hybrid car production and sale created by an 18-year-old student. The model includes segments representing hybrid car factory capacity (blue), car inventory (green), and delay and perceived delay (brown) in ability to purchase a hybrid car [11].
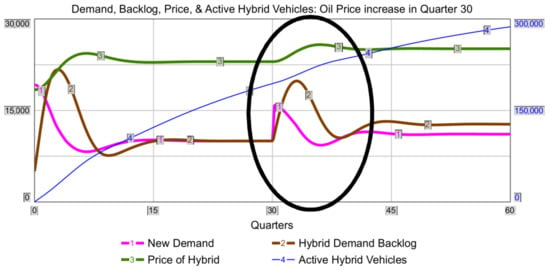
Figure 7.
The output of the model displayed in Figure 6. Adopted from [11].
In 2007, there was a global oil crisis and oil prices soared. In the United States, this prompted an increase in the demand for more fuel-efficient hybrid gasoline–electric cars. However, factories could not produce enough cars to meet the demand. This caused a significant backlog in the demand for hybrid cars. Some potential buyers became frustrated at the length of time they had to wait for a hybrid car and so changed their minds about buying this type of car. All of these concepts are captured in this student’s model. You will notice, in the lower left of the model displayed in Figure 6, that the model segment includes factory production of hybrid cars. In the top of the model, you will find a third-order material delay representing the supply chain for hybrid cars from production to final sale. The lower right portion of the model, the largest segment, captures the effect of the demand backlog and the perceived backlog, which led some customers to decide to change their minds about purchasing a hybrid car.
The output of this model can be seen in Figure 7 below. The important behavior of the model is shown in quarter 30, when an artificial spike in oil price is activated.5
In the graph, you can see the result of activating an artificial increase in oil prices in quarter 30. Hybrid car demand increases in this quarter, then demand backlog increases, which increases the price of hybrid cars. Eventually, the demand is being met by the production and sale of hybrid cars and by people taking themselves out of the queue of customers for purchase of a hybrid car.
More student model diagrams, student technical papers, and some student videos explaining their models can be found at ccmodelingsystems.com.
5. Assessments
How can one assess the discipline-specific learning that is occurring from the SD model-building activities used in, say, an algebra class? Instructors who use SD modeling at the pre-college level believe that SD modeling is more effective than other activities in helping their students learn concepts more deeply [10]. While these teachers used some combination of tests, oral presentation, student models, written narrative, and/or teacher observation to make their judgment, they did not conduct formal scientific research. Interested educational researchers are needed to partner with these teachers in order to conduct the research. SD modeling brings to the algebra classroom a representation that allows students to build models that help them analyze the dynamics created by combinations of the functions they typically study in a traditional algebra classroom. Examples of the multiple function scenarios mentioned earlier in this paper include the pharmacokinetic models, resource-depletion models, and the predator/prey model (Figure 5). Some of these models contain feedback and non-linear components that students are expected to (and do) explain. The multi-function analysis used with SD model-building activities is certainly not part of the traditional approach to teaching algebra, thus standard assessments (state and national exams) would not access this “multi-function” learning.
Stanford Research Institute (SRI) has published research that focused on assessing reasoning that occurs when students build models. One document describes an assessment strategy called the Principled Assessment Design for Inquiry (PADI) [38]. PADI breaks the modeling process into seven stages. Each stage can have assessment tasks developed to try to capture the specific stage of model-building identified. The seven stages are as follows: model formulation (translating a real-world situation to some mathematical representation), model use (explaining the model representation structure), model elaboration (adding detail to an existing model), model articulation (explaining the system, connecting the real world and its representation), model evaluation (testing the model against the real-world system behavior), model revision (modifying the model to make it align more reasonably with real-world behavior), and model-based inquiry (applying metacognitive strategies for model design). Mislevy, Riconscente, and Rutstein [38] provide examples, layered evidence-based designs for assessments, and sample rubrics for PADI. These stages can be used to compare the traditional mathematical equation representation and the SD modeling representation for those story problem scenarios that involve dynamic behavior.
Another important characteristic of SD modeling is the claim that its visual, schematic representation provides the ability to transfer structure to other applications with similar behavior. The hope is that ease in transferring structure supports the transfer of understanding associated with how the model functions in the new application. Goldstone and Wilensky [39] describe the ability to transfer understanding from the original model-building activity to other similarly structured scenarios as an important student assessment criterion for learning.
Within the year-long modeling course, a student’s original modeling project, involving the construction of original SD simulation models, technical papers, and a video presentation explaining his/her model, provide ample evidence of learning. Rubrics are used to assess both the models and the papers. Another possible validation of the value of the learning process for students comes from university professors who have read some of the technical papers that secondary school students have produced, explaining their original models, or from professors who have observed SD-trained student problem-solving processes as they tackle a new systems problem. This is exactly what was accomplished during the Sym*Bowl Competition held in Portland, Oregon, in the years 1994–2000. There were three to five secondary schools that sent SD modeling students to complete in the Sym*Bowl each year. Dr. Wayne Wakeland, chair of the System Science Doctoral Program at Portland State University, was in charge of the judges and judging process for the Sym*Bowl events.
During one of the Sym*Bowl events, we included a “Hotshots Challenge” problem that gave a non-trivial modeling challenge to the HS [high school] students to be solved within one hour. The problem we chose was highly relevant to HS students, and involved a person who goes to a party, and begins consuming alcohol at a relatively modest rate. The challenge is to predict when they will start feeling “under the influence” and, responsibly, stop drinking. The problem goes on to ask if, at the end of the party, fours hours after it began, was the person’s blood alcohol low enough for them to be safe to drive. Several of the HS students correctly solved the problem. I was very impressed. Since then I have given this problem to PhD students on their comprehensive exams, and not all of them solve the problem as well as the HS students.(Dr. Wayne Wakeland)
Dr. Edward Gallaher—mentioned earlier in this paper—who also participated as a judge for the quality of SD secondary school student models and papers, had this observation:
The breadth, and depth of these inquiries were impressive! In particular, the SD modeling and simulation fostered led students to ask perceptive, in-depth, and insightful questions far beyond their years. One project still stands out. Two girls with an interest in forensics developed a simple model of exponential heat loss [of a dead body]. They then conducted systematic experiments to monitor temperature loss from one-gallon milk bottles exposed to various ambient temperatures and various levels of wet and dry ‘clothing’. This information allowed them to extrapolate back in time to determine a ’time of death’ under various environmental conditions. Innovative and experiential learning at its best!
The students of modeling teacher, Tim Joy, took their modeling efforts one step further and presented to three members of the Portland, Oregon Metro Urban Planning Board. Here, we see the real value of a systems education. Two of the members of the Metro board were systems analysts. Before the meeting, Mr. Joy’s students had built, tested, and experimented with a simplified version of Jay Forrester’s Urban Dynamics model. The students gave a 30 min presentation to the Metro Board. One of the planners asked about household size, one of the variables in the model, indicating that Portland had a smaller household size than was used in the model. Mr. Joy suggested that the students predict what they thought should happen differently in the model behavior. The students looked at the model diagram, and some of the earlier model runs they had executed back at school, and described what they thought would happen. They ran the model and were correct. Then, one of the senior Metro planners looked around the table of his peers and said, “Guess I’m out of a job”.
In this story, we see the ultimate validation of modeling, empowering students to improve problems in their communities. That is, in the words of the late system dynamicist, Barry Richmond, creating better systems citizens is the goal of an SD-infused education.
6. Conclusions
Within this paper, an argument has been made for the importance of infusing the study of the dynamic behavior of complex systems for secondary school students. Learning theory and research evidence have been presented that indicate the characteristics of a learning environment that have been shown to provide fertile ground for enhancing understanding and retention of ideas presented in the classroom. Typical icons used to create SD models were introduced, as well as example SD model-building scenarios that are included in some secondary school algebra classes. The purpose of the SD models in algebra is to reinforce the characteristics of the structure of typical algebraic functions and how these structures produce their attendant behavior. The use of SD modeling to extend the story problem scenarios to those including multiple function structures, feedback, and non-linear dynamics was discussed. The design and implementation of a nine-month SD modeling course was described in some detail, culminating with the display of one example of an original student model and the behavior of that model. Finally, the issue of assessment was presented. SD modeling brings a new view—the characteristic behavior of dynamic systems—to the algebra classroom and to the secondary school learning environment. Secondary school students have shown they are quite competent to handle a dynamic view of the world.
It is interesting to reflect on the characteristics that make learning interesting. Some personal observations about teaching SD to secondary school students come to mind. Firstly, the active model-building process was an essential part of this learning process. Forrester stresses the importance of testing one’s perception of how a systemic problem is structured and behaves [2]. He indicates that one cannot rely on systems thinking to analyze systemic problems without validating one’s mental model. To Forrester, validation means building computer models and observing whether the computer simulation matches one’s mental model. Secondly, students liked building models of problems that were based on topics they learned in other classes and that were appropriate for their age group. Thirdly, they enjoyed creating original models. This final point should be underscored. SD provided students with a representation that is relatively easy to use for building models. One need only look at the problems that students can study using closed-form equations and those problems that students can study (and explain) using SD. Building original models was very empowering for students, but it was uncomfortable (initially) for teachers. Teachers mentioned concerns about losing control of their class [9] and were concerned about not knowing the content that was required for building any model that a student might decide to build [8]. There is no solution to the dilemma made by this third point. A teacher must take a chance. This author started by telling students that she had a new idea she wanted to try with them, and that the idea was new to her, and asked if they were willing to be part of the experiment. The students were willing. She indicated that if they chose model topics about which she did not have knowledge, they (the teacher and students) would have to work together to determine how to proceed with the model design. Students were still willing. Model size was restricted during the early years of SD model experimentation. Intermediate size models had to be built and tested in stages. The assessment evolved, becoming more precise, as both the teacher and students became more proficient. The teacher had to become a student again, and the students were very receptive, enjoying the times they could teach her some special modeling technique. This model-building instructional approach was transformative for the teacher (the author of this paper).
Conflicts of Interest
The author declares no conflict of interest.
References
- Forrester, J.W. System Dynamics and K-12 Teachers. Lecture at the University of Virginia School of Education. 1996. Available online: http://ocw.alfaisal.edu/NR/rdonlyres/Sloan-School-of-Management/15-988Fall-1998-Spring-1999/D2310653-E3BA-4924-BE64-96C719E4B692/0/teachers.pdf (accessed on 10 April 2018).
- Forrester, J.W. Learning through System Dynamics as Preparation for the 21st century. Presented at the K-12 Systems Thinking and Dynamic Modeling Conference, Concord Academy, Concord, MA, USA, 27–29 July 2009; Available online: http://static.clexchange.org/ftp/documents/whyk12sd/Y_2009-02Learning ThroughSD.pdf (accessed on 24 March 2018).
- National Council of Teachers of Mathematics (NCTM). Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000; ISBN 978-0873534840. [Google Scholar]
- National Governors Association Center for Best Practices, Council of Chief State School Officers. Common Core State Standards—Mathematics; National Governors Association Center for Best Practices, Council of Chief State School Officers: Washington DC, USA, 2000; Available online: http://www.corestandards.org/Math/Practice/ (accessed on 24 March 2018).
- Clement, J.; Lochhead, J.; Monk, G.S. Translation difficulties in learning mathematics. Am. Math. Mon. 1981, 88, 286–290. [Google Scholar] [CrossRef]
- Pawley, D.; Ayres, P.; Cooper, M.; Sweller, J. Translating words into equations: A cognitive load theory approach. Educ. Psychol. 2005, 25, 75–97. [Google Scholar] [CrossRef]
- NGSS Lead States. Next Generation Science Standards: For States, by States (Cross-Cutting Goals); The National Academies Press: Washington, DC, USA, 2013; Available online: https://www.nextgenscience.org/sites/default/files/Appendix%20G%20%20Crosscutting%20Concepts%20FINAL%20edited%204.10.13.pdf (accessed on 24 March 2018).
- Hmelo-Silver, C.E.; Azevedo, R. Understanding complex systems: Some core challenges. J. Learn. Sci. 2006, 15, 53–61. [Google Scholar] [CrossRef]
- Skaza, H.; Crippen, K.J.; Carroll, K.R. Teachers’ barriers to introducing system dynamics in K-12 STEM curriculum. Syst. Dyn. Rev. 2013, 29, 157–169. [Google Scholar] [CrossRef]
- Fisher, D.M. The next 25 years in pre-college education: A move toward global understanding of complex systems. In Proceedings of the International System Dynamics Conference, Cambridge, MA, USA, 16–20 July 2017. [Google Scholar]
- Fisher, D.M. “Everybody thinking differently”: K–12 is a leverage point. Syst. Dyn. Rev. 2011, 27, 394–411. [Google Scholar] [CrossRef]
- Fisher, D.M. Modeling Dynamic Systems: Lessons for a First Course: Teacher’s Guide; Isee Systems, Inc.: Lebanon, NH, USA, 2011; ISBN 978-0-9704921-6-6. [Google Scholar]
- Mansilla, V.B.; Jackson, A. Educating for Global Competence: Preparing Our Youth to Engage the World; Asia Society: New York, NY, USA, 2011; pp. 15–108. Available online: http://www.pz.harvard.edu/sites/default/files/book-globalcompetence.pdf (accessed on 19 February 2018).
- Organization for Economic Cooperation and Development. 21st Century Learning: Research, Innovation and Policy. In Proceedings of the Organization for Economic Cooperation and Development/Centre for Educational Research and Innovation International Conference, Paris, France, 15–16 May 2008; Available online: http://www.oecd.org/site/educeri21st/40554299.pdf (accessed on 19 February 2018).
- Grotzer, T. Booklet 1: Cognitive Issues that Affect Math and Science. In Math/Science Matters: Resource Booklets on Research in Math and Science Learning; Project Zero; Harvard Graduate School of Education: Cambridge, MA, USA, 1996; pp. 1–12. [Google Scholar]
- Daniels, H.; Cole, M.; Wertsch, J.V. The Cambridge Companion to Vygotsky; Cambridge University Press: New York, NY, USA, 2007; ISBN 978-0521537872. [Google Scholar]
- Vygotsky, L. Interaction between learning and development. In L.S. Vygotsky Mind in Society: The Development of Higher Psychological Processes; Cole, M., John-Steiner, V., Scribner, S., Souberman, E., Eds.; Harvard University Press: Cambridge, MA, USA, 1978; pp. 79–91. ISBN 9780674576292. [Google Scholar]
- Vygotsky, L.S. The history of the development of higher mental functions. In The Collected Works of L. S. Vygotsky. Volume 4; Rieber, R.W., Ed.; Plenum Press: New York, NY, USA, 1997; pp. 1–26. ISBN 9780306456091. [Google Scholar]
- Bruner, J.S. Toward a Theory of Instruction; Harvard University Press: Cambridge, MA, USA, 1966; pp. 1–21. ISBN 978-0-674-89701-3. [Google Scholar]
- Booth-Sweeney, L.; Meadows, D. The Systems Thinking Playbook; Chelsea Green Publishing, Inc.: White River Junction, VT, USA, 2010; ISBN 978-1-60358-258-2. [Google Scholar]
- Fisher, D.M. Lessons in Mathematics: A Dynamic Approach with Applications across the Sciences: Teacher’s Guide; Isee Systems, Inc.: Lebanon, NH, USA, 2005; ISBN 978-0-9753169-1-5. [Google Scholar]
- Quaden, R.; Ticotsky, A.; Lyneis, D. The Shape of Change and the Shape of Change: Stocks and Flows; The Creative Learning Exchange: Acton, MA, USA, 2008; ISBN 978-0-9753169-4-8. [Google Scholar]
- Kaput, J.; Roschelle, J. Shifting representational infrastructures and reconstituting content to democratize access to the math of change and variation: Impacts on cognition, curriculum, learning and teaching. Available online: https://pdfs.semanticscholar.org/87bf/eba674d274267a3c6b916f6b839491dd0e6e.pdf (accessed on 24 March 2018).
- De Jong, T.; Ainsworth, S.; Dobson, M.; van der Hulst, A.; Levonen, J.; Reimann, P.; Sime, J.-A.; Van Someren, M.; Spada, H.; Swaak, J. Acquiring knowledge in science and mathematics: The use of multiple representations in technology based learning environments. In Learning with Multiple Representations; van Someren, M., Reimann, P., Boshuizen, H., de Jong, T., Eds.; Elsevier Science: Oxford, UK, 1998; pp. 9–41. ISBN 9780080433431. [Google Scholar]
- Van der Meij, J.; de Jong, T. Supporting students’ learning with multiple representations in a dynamic simulation-based learning environment. Learn. Instr. 2006, 16, 199–212. [Google Scholar] [CrossRef]
- Seel, N.M. Model-based learning: A synthesis of theory and research. Educ. Technol. Res. Dev. 2017, 65, 931–966. [Google Scholar] [CrossRef]
- Green, E. Building a Better Teacher: How Teaching Works (and How to Teach It to Everyone); WW Norton & Company: New York, NY, USA, 2014; ISBN 978-0-393-08159-6. [Google Scholar]
- Forrester, J.W. Principles of Systems; Productivity Press: Cambridge, MA, USA, 1968; ISBN 978-0-915299-87-9. [Google Scholar]
- Fisher, D.M. Building slightly more complex models: Calculators vs. STELLA. In Proceedings of the International System Dynamics Conference, Athens, Greece, 20–24 July 2008. [Google Scholar]
- Fisher, D.M. How well can students determine simple growth and decay patterns from a diagram. In Proceedings of the International System Dynamics Conference, Albuquerque, NM, USA, 26–30 July 2009. [Google Scholar]
- Fisher, D.M. How drugs work in the human body: Analysis of a modeling unit used in a second year algebra class. In Proceedings of the International System Dynamics Conference, New York, NY, USA, 20–24 July 2003. [Google Scholar]
- Sterman, J.D. Business Dynamics: Systems Thinking and Modeling for a Complex World; McGraw-Hill: Boston, MA, USA, 2000; ISBN 978-0-07-231135-5. [Google Scholar]
- Saeed, K. Circumscribing System Dynamics Modeling and Building Confidence in Models a Personal Perspective. 2017. Available online: https://ssrn.com/abstract=3093080 (accessed on 19 February 2018).
- Richardson, G.; Pugh, A., III. Introduction to System Dynamics Modeling with Dynamo; Productivity Press: Portland, OR, USA, 1981; ISBN 978-0-915299-24-0. [Google Scholar]
- Richardson, G. Reflections on the foundations of system dynamics. Syst. Dyn. Rev. 2011, 27, 219–243. [Google Scholar] [CrossRef]
- Forrester, J.W. “The” model versus a modelling “process”. Syst. Dyn. Rev. 1985, 1, 133–134. [Google Scholar] [CrossRef]
- Saeed, K. System Dynamics: A Disruptive Science? Transcript of a Fireside Chat with Jay Forrester. 2013. Available online: https://www.researchgate.net/publication/304460184_System_Dynamics_A_Disruptive_Science_Transcript_of_a_fireside_chat_with_Jay_Forrester_July_2013 (accessed on 19 February 2018).
- Mislevy, R.J.; Riconscente, M.M.; Rutstein, D.W. Design Patterns for Assessing Model-Based Reasoning (Large-Scale Assessment Technical Report 6); SRI International: Menlo Park, CA, USA, 2009. [Google Scholar]
- Goldstone, R.L.; Wilensky, U. Promoting transfer by grounding complex systems principles. J. Learn. Sci. 2008, 17, 465–516. [Google Scholar] [CrossRef]
| 1 | Bi-directional flows (bi-flows) are not displayed in Figure 1. Bi-flows have an arrowhead at each end of the flow pipe (one is a dotted arrowhead in order to differentiate the arrowheads). Positive flow values flow numeric information toward one arrowhead (perhaps filling the stock) whereas negative flow values flow numeric information toward the other arrowhead (perhaps emptying the stock). |
| 2 | Vernier Software & Technology, (Go!Motion), vernier.com. |
| 3 | Students were cautioned that they should not contact their expert frequently, that they should have their questions written out in advance, that they should use professional etiquette in email correspondence or phone conversations, and that they had to respect the time constraints on their expert with regard to responding to their questions. |
| 4 | The draft model was submitted to the teacher who gave students recommendations for improvements. |
| 5 | This student was unable to get his model to start in dynamic equilibrium. This is a flaw in the model definition, but not a fatal one. It is still possible to see that a rise in oil prices in quarter 30 produces reasonable model behavior. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).