Exploring Metacognitive Experiences by Simulating Internal Decisions of Information Access

Abstract

Research claims that metacognitive experiences can be classified as types of metacognitive regulation. Formulated in terms of the theory of Attention as Internal Action, this view raises questions about the timing of metacognitive experiences that occur in response to internal experiences. To investigate these questions, this work presents a method for cognitive computation that simulates consecutive internal decisions occurring during the process of taking a digital exam. A new version of the General Internal Model of Attention is proposed and supported by research. It is applied as cognitive architecture in a simulation system to reproduce cognitive phenomena such as the cognitive cycle, internal decision-making, imagery, body actions, learning, and metacognition. Two corresponding groups of Markov Decision Processes were designed as information stores for goal influence and learning, and a Hebbian machine learning algorithm was applied as an operator on the learning models. The timing and consecutiveness of metacognitive experiences were analyzed based on the cognitive cycle results, and several hypotheses were derived. One of them suggests that the first engagement in a metacognitive experience for each question in the exam is delayed over the course of the exam-taking process.

1. Introduction

A model of metacognition claims that there are three types of metacognitive regulation: planning, monitoring, and evaluation [1]. A systematic analysis shows that the model is well accepted across different scientific fields, as the analysis shows a growth in the number of publications that refer to it [2]. Furthermore, the systematic review shows an interrelation between the model and other concepts from cognitive science. Viewed in a dichotomic relation between metacognitive knowledge [3], a metacognitive experience is shown to correspond to metacognitive regulation. What is more, the significant amount of research showing interrelation between the concepts of metacognitive experience and the model of metacognition suggests that types of metacognitive experiences should be studied as a form of self-regulation [2]. If a system of rules is formulated to define the relations between memory and conscious processes, it becomes possible to simulate mental processes that include metacognitive experiences.

In order to investigate the timing of cognitive phenomena, a view is required that explains human cognition in terms of iterations. An explanation exists regarding the cognitive cycle as being equivalent to the gamma activity coherence of the brain [4]. Supported by neuroscientific and experimental psychology studies, the authors conduct a simulation of the cognitive cycle via a simple reaction time task. Another study involving human participants uses a continuous reaction time task to measure the cognitive cycle [5]. Showing persistent results of the cognitive cycle duration, the theory in the experimental research was decided to be used to reproduce other cognitive phenomena based on the presented formulations. That is why the theory of Attention as Internal Action was targeted as a foundation for developing the digital information system, which is going to simulate MEs.

A sustainable general classification of types of cognitive experiences is hard to formulate. Cognitive architectures aim at achieving this, but their representations are often directed entirely at memory processes and rarely define internal imagery experiences. David Marks and his General Theory of Behavior have brought the Action Cycle Theory [6]. It comes with a system of six modules that are based on his investigations into imagery experiences. Focusing on human consciousness, the Action Cycle Theory is shown to have relations with the theory behind the LIDA cognitive architecture [7], which was formulated in terms of the theoretical approach of Attention as Action [8]. Following the strive to generalize imagery experiences as events of internal attention, the first step towards a General Internal Model of Attention (GIMA) was performed [2]. A decision was made to use the knowledge of this first attempt and to implement the knowledge of GIMA into a digital information system for the simulation of a simple task. The follow-up work of this decision is the main topic of this article.

The first section of this paper has two parts, which consecutively present the following content: Firstly, we present the theory of Attention as Internal Action, together with the knowledge representation framework. Secondly, the designed GIMA cognitive architecture and its components are intended to be simulated. In the Methods Section, the system design, the simulation technique, the task, and the experimental setup are described. The Results Section reports important observations derived from the conducted simulation. Lastly, a discussion is presented that analyzes the observations and provides directions for reproducing the simulated task in a real experimental environment with humans.

2. Theoretical Views

The emerging theoretical approach of Attention as Action shows applicability in explaining cognitive experiences that arise immediately after the occurrence of a Sensory Event [9]. The approach is dedicated to elucidating conscious cognitive processes as brief experiences of learning, imagery, perception, and metacognition occurring in the cognitive cycle. The foundational idea of the approach suggests that decision-making should be investigated as a brief internal experience involving the observation of various available information resources and selection among them. Thus, the concepts of internal action (IA), internal decision-making, and internal agent emerged as foundational concepts for explaining cognitive phenomena in a consecutive (cyclic) manner [2,8,9]. However, the framework of the theoretical approach does not provide a specific formulation of how body (external) actions are executed in terms of the ongoing flow of cognitive experiences. Also, in the context of the theoretical approach, the IA concept is defined as an execution that produces a conscious attentional experience as a result of accessing information generated by a memory process [2], but there is a lack of clarity on how the information is retrieved in the cognitive cycle by the memory process in the first place. The answers to these questions require a systematized formulation in order to make it possible to design a digital information system that recreates such cognitive experiences.

2.1. Glossary

The context of each theoretical approach is important for the researcher, which is why providing clarity on the terms is essential. For this purpose, the glossary below presents the main theoretical concepts:

• Attention as Internal Action (AIA): The understanding that a conscious experience is a volitional act of accessing information that has been previously generated automatically and unconsciously.
• Automatic Unconscious Process (AUP): A habitual cognitive process that gathers, transforms, and provides information without the awareness of the personality.
• Internal Action (IA): An act of volitional access to information that leads to a conscious experience of perceptual or mental imagery.
• Internal Agent: An actor that decides which information to access and generates an internal action.
• Two-Cause Internal Conjunction (TIC): A conscious experience that is due to the simultaneously occurring phenomena of an internal action and information provisioning by an Automatic Unconscious Process.
• General Internal Model of Attention (GIMA): A cognitive model whose purpose is to generally identify types of Two-Cause Internal Conjunction Phenomena and to represent relational knowledge between them.
• Stream of Incoming Sensory Information (SISI): The process of continuous and consecutive input of unprocessed sensory information.
• Sensory Event (SE): An occurrence in which information from the stream of incoming sensory information is packaged and ready for access by other processes.

These concepts and their interrelations are explained in the following subsections. Their purpose is to serve as a tool for researchers to integrate subjective experiences into a cognitive system that provides classificatory and relational knowledge.

2.2. Attention as Internal Action

It was considered that the theoretical approach can serve as a good foundation for a theory that explains interconnected automatic processes that are run by the cognitive system in the absence of awareness of the simulated subject. Such an organization of memory processes works in unison to “ignite” a single conscious experience in terms of a single iteration of the cognitive cycle. Franklin and Baar’s explanation of attention, which is implemented in the LIDA cognitive architecture, states that attention is the act of “bringing contents to consciousness” [10] (p. 5). Following this direction, it can be claimed that during a conscious experience, an automatic unconscious (memory) process provides information to the internal agent at a certain stage, leading to the generation of an imagery experience. This process is known as the occurrence of an “internal attentional experience” [2] (p. 7). If this phenomenon is more specifically formulated and classified, fields of research could be established for linking memory process types to imagery experiences and eventually integrating them into a general, comprehensive cognitive architecture (the GIMA model).

2.2.1. Two-Cause Internal Conjunction

In resemblance to the Computational Theory of Mind, the theory of Attention as Internal Action (AIA) views the human brain as a complex computational system. However, AIA holds that there is a second cause of a conscious experience, and that cause is the internal agent that goes through internal decision-making and performs an IA as a result. Based on this understanding, the theory of AIA defines the Two-Cause Internal Conjunction (TIC) phenomenon as a discrete conscious perceptual or mental imagery experience. During a TIC, the internal agent is performing an act of observation—IA—of the information provided by a selected automatic unconscious (memory) process (AUP), as shown in Figure 1. Therefore, AIA strictly holds to the claims that:

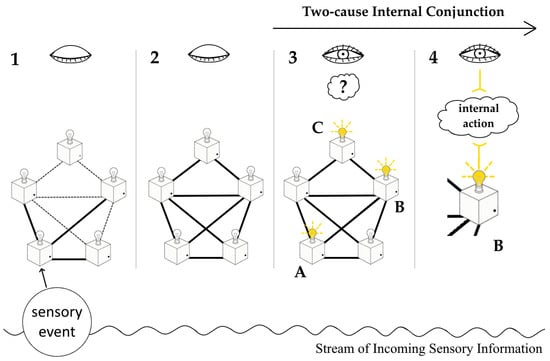
Figure 1. The four phases of the cognitive cycle, as defined in the theory of Attention as Internal Action. The first two phases involve Automatic Unconscious Processing of sensory and memory information, respectively. The third phase begins when an Automatic Unconscious Process emits an event A (a bulb lights up), prompting the internal agent C (the eye) to enter a conscious state and make an internal decision. In the fourth phase, the agent performs an internal action B based on this decision, during which a conscious imagery experience arises from the provided information. The final two phases constitute the Two-Cause Internal Conjunction (TIC), a phenomenon lasting about 100 ms.

• A TIC phenomenon includes an imagery experience;
• An IA type is a brief conscious learning type;
• An AUP is a memory process that unconsciously retrieves, organizes, and/or generates information.

Of importance is the understanding of the stream of incoming sensory information (SISI) as it links to the established co-existence of the concepts of continuous input of sensory information and metacognition [11]. Sensory information is constantly being provided by the senses, but the human brain cannot process all of it with attention. That is why the mechanism of SISI explains the formation of a so-called Sensory Event [2] as an occurrence of a noticeable change in the external environment. However, it is required of AIA to strictly explain how a Sensory Event is formed by SISI and how this event is later processed in terms of several consecutive cognitive cycle iterations. To achieve this, a formulation of a knowledge representation framework would be fruitful, as it can systematically represent several consecutive iterations in which AUPs form information transitions.

2.2.2. Knowledge Representation Framework

Based on the semiotic knowledge representation techniques from Attention as Action research [2,8,9], the theory of AIA formulates a system of visual semiotics that allows representing a variety of cognitive phenomena. Specific rules are formulated for the signs to allow the expression of cognitive events that occur simultaneously within a single iteration of a cognitive cycle or across a series of such iterations. The following concept types are formulated in the framework and can be used for representing a scenario of cognitive events (Figure 2):

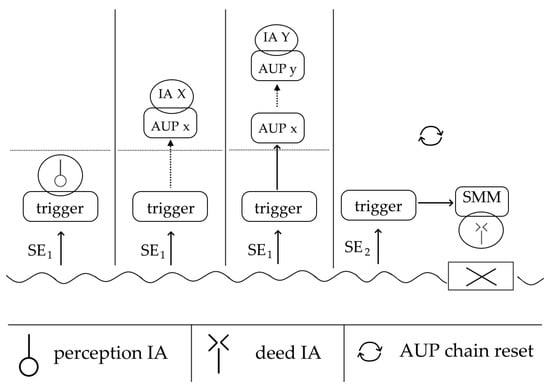
Figure 2. Example application of the knowledge representation framework. Sensory Events (SE) are packaged from the stream for each cognitive cycle iteration. If sensory information does not significantly differ, an SE remains approximately the same, so it is denoted with the same index. The trigger processes an SE, sending it to a perceptual internal action (IA) or another Automatic Unconscious Process (AUP). Eventually, the personality may decide to access sensorimotor memory (SMM) and perform a body action.

• The SISI: Denoted by a wavy line usually placed at the bottom of the representation.
• A Sensory Event (SE): Denoted with an acronym and a sequential number.
• An AUP type: An acronym or a name surrounded by a rectangle.
• An IA type: A semiotic symbol or an acronym surrounded by an ellipse.
• A motor plan execution: A rectangle with a cross in it.
• An unconscious information transition: An arrow.
• The link between two consecutively chosen AUPs: A dashed arrow.
• Reset of an AUP chain: Circular arrows representing a refresh.

The theory of AIA strictly follows the module relations described by Norman and Shallice in their Supervisory Attentional System model [12]. When a Sensory Event (SE) is formed, it always initially reaches the trigger AUP (Figure 2). The latter corresponds to the trigger database, while the SISI explains the sensory input and the sensory-perceptual module.

The theory of AIA includes the Discrete Motor Execution Hypothesis, which explains how a short and conscious motor plan is executed [5]. Being a conscious act of sensory motor learning, the performance of the deed IA is in parallel to the motor plan execution (Figure 2). The latter is also known as body action signaling [2], as it represents a single or several signals from the motor cortex that reach the body muscles and make them contract. Each signal corresponds to a muscle evoked potential, which is known to be around 20 ms [13]. As shown in Figure 2, the execution of the deed IA corresponds to the sensory motor memory (SMM) AUP. It is inspired by a module of the same name in LIDA, which holds motor plan templates that are loaded in a reactive fashion as a response to sensory content [14].

A crucial idea of the knowledge representation framework is the AUP chaining and resetting (Figure 2). The latter is also known as the phenomenon of a cognitive cycle reset and has been explained in terms of the performance of a continuous reaction time task [5]. A Sensory Event (SE) is formed by the SISI on each cognitive cycle iteration, but the information difference between two consecutive SEs might be exceedingly small. That is why the framework allows representing several consecutive SEs with the same designator. In Figure 2, three consecutive cognitive cycles process SE₁, but when SE₂—significantly varying from SE₁—occurs, a reset of the AUP chaining takes place. This technique can be used to provide new explanations of how attention shifting occurs and how it affects working memory [15].

An important note is that the duration of an iteration of the cognitive cycle is hypothesized to be between 260 and 390 ms [4]. This means that the cognitive phenomena represented in Figure 2 occur within the span of a second. However, the way in which the duration of a cognitive cycle iteration is computed when it is based on the Discrete Motor Execution Hypothesis [5] is slightly different from the one used in the simulation with the LIDA model [4]. This is because of the understanding of the motor plan execution, which formulates that a volitional motor response is included in the iteration of the cognitive cycle.

2.2.3. Defining Data, Information, and Knowledge

One of the main goals of the applied theory is to create a general comprehension of how data, information, and knowledge are processed by a cognitive system. A useful source for achieving this goal was considered to be the emerging field of infodynamics [16]. The first lines of the content in the referenced review describe information as an abstract concept with divergent meanings. In terms of infodynamics, it can be stated that information is the foundation that entangles other concepts like knowledge, memory, and consciousness [16]. The theory of AIA accepts the definition of terms presented in Jaffe’s article and additionally formulates data as content that a system needs to process in order to transform into information. In the context of cognitive systems, data is provided by body receptors and can be referred to as sensory input [6,7,17]. In the framework of AIA, data is thought to be continuously provided by the receptors and processed by the SISI module, which in turn produces a Sensory Event per a cognitive cycle iteration. The Sensory Event can correspond to a digital stimulus as produced by a digital information system [2] or it can be referred to as an internal or external sensory stimulus [7,18]. In order to store perceptual information in memory, the cognitive system—via the SISI module—has to initially transform the sensory input data into a Sensory Event. The Supervisory Attentional System (SAS) model and its neuroscientific support [17,19] have been used as underpinnings for defining the trigger AUP [5]. At this initial point, perceptual information is available to an AUP and can be further processed and provided to the internal agent for conscious access.

In infodynamics, knowledge is defined as “information that allows an agent to predict behaviors or features of a system even if it has access to only partial information of the system” [16] (p. 2). In the context of the theory of AIA, “system” is a cognitive system of interconnected AUPs that compete for consciousness (Phase 3, Figure 1), and “agent” is the internal agent that predicts behaviors or features of the cognitive system. Knowledge is present when the information is accessed by the internal agent from the AUP (Phase 4, Figure 1). It is the conscious availability that the internal agent uses to navigate through the cognitive system. By following these understandings, the concept of memory [16] (p. 3) begs to be explained in terms of the theory of AIA.

The theory of AIA envisions a memory process in the form of an AUP. In order to provide an explanation that aligns with cognitive science, AIA relies on the established Atkinson–Shiffrin model, which by itself is a “general framework” [20] for formulating models. An AUP is viewed as a process that unconsciously (with a lack of awareness of the internal agent) retrieves information from a memory store and organizes it for eventual access. It is unclear whether a new generation of information is being processed by the AUP, but it certainly processes information from a memory store in its own manner, which is why it is claimed that it organizes it. When the information is accessed by the internal agent in the form of an internal act of observation (IA), it turns into knowledge that is stowed in the short-term store (Figure 3). An IA is a cognitive process of learning [8] that produces a learning experience, which is viewed as an internal attentional experience [2] and as a TIC in terms of AIA (Figure 1). What is more, a TIC is recognized as a discrete event of consciousness [4,5] that interacts with working memory [21]. This resonates with the previously stated claim that IA stores knowledge in the short-term store.

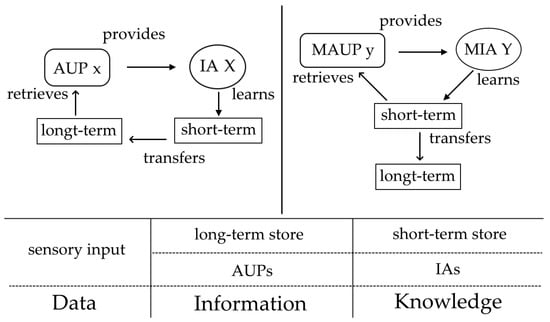
Figure 3. Conceptual explanation of how memory stores cooperate with learning processes in the context of Attention as Internal Action theory. The arrows represent the flow of information. An Automatic Unconscious Process (AUP) provides information necessary for executing an internal action (IA). A classical AUP gathers information from long-term memory, whereas a metacognitive AUP (MAUP) collects information from short-term memory to support the execution of a metacognitive internal action (MIA).

An important observation to be made is that an IA always stores (learns) knowledge in the short-term store, whereas an AUP may retrieve information from either the long-term or the short-term stores (Figure 3). This classifies two general types of AUPs based on which memory store they retrieve information from. They are conceptually depicted in Figure 3 and are termed as classical and metacognitive. The timing of both classical and metacognitive modes of information provisioning (from an AUP or an MAUP) aligns with the fourth phase of the cognitive cycle iteration (Section 2.2.1, Figure 1).

2.2.4. Entitative and Linkative Knowledge Types

It was shown in the previous subsection how memory stores interact with the cognitive processes defined in the theoretical framework of AIA. It is now necessary that a more precise understanding be formulated about what general types of knowledge are generated during a single TIC experience. If a supported scientific approach is provided that defines general modes of IAs, then TIC types are also going to be formulated as a conjunction between an AUP and its corresponding IA. An established dichotomous view in cognitive science generally defines cognitive processes as either explicit or implicit. It finds application in the CLARION cognitive architecture [22]. It directs researchers toward explaining representations of implicit and explicit knowledge that are either action-centered or non-action-centered. This approach could be applied to define IA modes, but implicit learning is rather viewed as an unconscious process. Given that an IA is a conscious process, the theory of AIA follows the established understanding of learning provided by the theory that backs up the LIDA cognitive architecture. The Global Workspace Theory states that most of the learning occurs consciously [23]. Furthermore, it is claimed that conscious events are guidance “even for implicit learning” [24], as implicit learning requires “conscious attention to the stimuli” [25].

In terms of AIA, the second stage in a TIC experience (Phase 4, Figure 1) and its corresponding cognitive process of learning—IA—are formulated to be conscious. An IA is performed as a result of an internal demand for knowledge, like the aim to recall an experienced event, to compare a current event to a past event, or to execute a motor plan, like shooting a basketball. The extraction of specific information provided by a targeted AUP may be experienced by the internal agent in different ways. For example, the internal demand might be to recall what objects are contained in a bag. If the personality has recently arranged the bag, then the images of a bottle, a pen, and a notebook might appear one after another in the mind. In contrast, if the personality often uses the bag and its arrangement remains the same, the image of the bag itself can appear in the mind, bearing the inferred knowledge that there is a bottle, a pen, and a notebook in it. The internal agent might consciously aim to apply a large quantity of knowledge without explicating it. In the article by Sun, Slusarz, and Terry, it is discussed that knowledge generated from implicit learning “is always richer”, and that it is hard to explicate [22].

Setting aside the claims for a moment, the question is asked: if implicit learning is perceived as a “process by which information is learned outside of conscious awareness” [26], then how can it be explained as a conscious act of learning in a dichotomic relation to explicit learning? Baars and Gage provide an answer to this question by stating that implicit learning is misleadingly associated with unconscious learning, but it occurs during conscious input, which by itself leads to implicit “inferences” [24]. Additionally, it can be stated that knowledge content is inside conscious awareness when the internal agent is aware of its possession in the short-term store. The fact that the knowledge cannot be explicated does not mean that the internal agent is not aware of its current possession. Therefore, in terms of the theoretical framework, it can be said that implicit knowledge can be loaded in the short-term store. Atkinson and Shiffrin also used the term “working memory” [20] before Baddeley and Hitch’s model, which strongly suggests that the short-term store holds conscious content that undergoes attentional control. Based on all of the evidence in this paragraph, it can be stated that this content can be viewed as either a standalone explicit entity or as one that is used for the creation of “binding representations” [27].

By accepting AIA’s claims discussed thus far in this section, a TIC experience, as one that corresponds to a perceptual or mental imagery experience [6] (more in Section 2.2), is an event of knowledge generation. With the demand to formulate general types of knowledge produced during a single TIC, the concepts of explicit and implicit learning can be used to define two brief conscious learning processes, each generating content that can be:

• Entitative type: The content is generated by an explicit IA and is represented by a knowledge entity.
• Linkative type: The content is generated by an implicit IA and is represented by one or several knowledge entities, linked to each other.

An important reminder is that the generated TIC content corresponds to a single conscious experience occurring in a cognitive cycle iteration (Section 2.2.1). Both the entitative and linkative knowledge types correspond to the occurrence of a perceptual or mental imagery experience [6]. As produced by IAs, the knowledge entities and the implicit links between them are stowed in the short-term store (Section 2.2.3). This formulation resonates with the explanation of conscious implicit learning provided by Baars and Gage. The link between two or more knowledge entities corresponds to the implicit inferences “that are learned, along with the conscious aspects of the task” [24]. The theory of AIA does not limit itself to explaining implicit learning only as gaining knowledge about how to procedurally conduct a task, but allows theorization of any kind of links between explicit knowledge entities. This is because the theory views learning simply as storing knowledge in the short-term store. Information that is retrieved and organized in different ways: perceptual, sensorimotor, procedural, episodic [14] or other types, corresponding to each of the defined AUPs in the cognitive architecture, can be the cause of learning.

The GIMA cognitive architecture can now be extended by defining two modes of short conscious learning processes. Thus, a rule can be formulated: each IA presented so far in GIMA [2,5] has one mode that observes information entitatively and produces explicit knowledge, and another mode that accesses the same organized information but produces implicit links between entities in the short-term store.

2.3. General Internal Model of Attention

The striving towards forming a general mental model [28], based on the theory of AIA, which comprehensively explains types of short cognitive phenomena, has been demanded by research related to metacognition [2]. More specifically, metacognitive regulation has been viewed as a metacognitive experience that is classified into three types: planning, monitoring, and evaluation [2]. The knowledge representation framework (Section 2.2.2) is usually used to depict scenarios of internal decision-making [8,9] but it can also be used for designing cognitive architecture models. The GIMA model can now be extended by acquiring knowledge from the CLARION architecture to explain metacognition as a short act of learning. The view of metacognitive regulation as an active and consequent process [29] links to the established understanding of the cognitive cycle, which involves discrete conscious experiences [4]. The latter are now viewed as TICs in terms of the theory of AIA and can be defined as corresponding to perceptual or mental imagery experience [6]. The CLARION architecture emphasizes self-monitoring and regulation of cognitive processes [29], which leads to the following question. Are self-planning, self-monitoring, and self-evaluation types of metacognitive regulation (1), or can the three concepts be defined alongside regulation (2)? By taking path (2), the “alternative model” of metacognitive regulation appears as a scientific support [2] and leads to the classification of four types of metacognitive experiences.

2.3.1. Extending the Cognitive Architecture

It has been decided that the alternative model of metacognitive regulation is going to serve to clarify GIMA’s layer 3 [2]. However, a solid establishment is required to explain the processes defined in layer 2 of cognitive architecture. Such a solid foundation built upon neuroscientific evidence can be found in the Common Model of Cognition [30]. What is more, a newer study on anticipatory thinking depicts declarative long-term memory based on its established classification, representing it through semantic and episodic memory modules [31]. Jones and Laird accentuate the general aspects of cognition and unambiguously point out that semantic memory stores general concepts and facts such as “the meanings of words” [31]. The episodic nature of long-term memory is oriented towards providing information on specific events, which the agent has experienced, while the semantic memory delivers general concepts that can be linked to objects or actions, contained in the knowledge of the experienced events.

The theoretical approach of Attention as Action has been shown to explain relations between imagery experiences of objects, affect, schemata, and goals [8] based on knowledge derived from the Action Cycle Theory model [6]. However, clarity is lacking on how words and concepts are internally experienced. In order to formulate an understanding of the theoretical context of AIA, this work focuses on developing a new IA that targets the information provided by the semantic memory. By following the formulation in Section 2.2.4 principle of the general knowledge types, it is stated that a semantic AUP exists that provides information, which can be internally observed in an entitative or linkative mode. This act of internal observation was decided to be referred to as the conceptual IA (Figure 4).

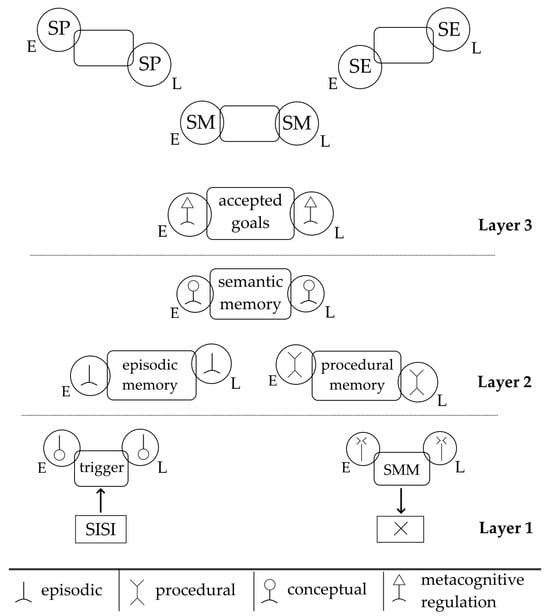
Figure 4. The formulated General Internal Model of Attention (GIMA). Each type of internal action (IA) is represented by two symbols, each signifying an entitative and a linkative mode, denoted by the letters E and L, respectively. Layer 1, which links cognitive architecture with the external world, includes the stream of incoming sensory information (SISI) and the sensory motor memory (SMM). The metacognitive layer (Layer 3) includes the internal actions of self-planning (SP), self-monitoring (SM), and self-evaluation (SE). Their corresponding Automatic Unconscious Processes are yet to be investigated. Layer 2 plays the linking role between the metacognitive layer and the externally connected layer.

The extended version of GIMA, presented in Figure 4, introduces the Common Model of Cognition [30,31], representing it via the episodic, procedural, and semantic memory AUPs. The other two components—the SMM and the trigger AUPs—correspond to the perception IA and the deed IA [2,5,8], which are described in Section 2.2.2. The dotted lines separate the three layers and represent the formulated rules in the cognitive architecture. They dictate which IA can be performed as a follow-up internal decision to a previous one. Also, the rules provide knowledge about how IAs are related to the receipt of a Sensory Event, as based on the knowledge representation framework of AIA (Section 2.2.2). To simplify and systematically formulate the switching rules, it is proposed that the performance of one of the defined IAs is viewed as a brief system state. Depending on the process layer index (i), a switch from an initial state (X) to a decided state (Y) is possible if:

• X is in layer (i) and Y is in layer (i);
• X is in layer (i) and Y is in layer (i + 1);
• X is in layer (i) and Y is in layer (i − 1);
• X is in any layer, Y is in layer (1), and a new significantly varying SE has occurred.

By following these simple rules, the conceptual model of the cognitive architecture may avoid representing possible state switches with many arrows and thus depict the IAs in a clearer way. To explain the represented knowledge in different words, in the internal decision-making phase (Phase 3, Figure 1), only AUPs that are adjacent to the current layer (i) may emit an internal event. However, if there is a new SE that has significantly varying sensory information compared to the last one (more in Section 2.2.2), the perception IA or the deed IA can be performed no matter of the previous IA. Currently, it is accepted that X cannot be equal to Y—two cognitive cycle iterations cannot involve the performance of the same IA.

This extended version of GIMA focuses on linking semantic memory [31] to metacognitive control and regulation, as inspired by CLARION [29]. The latter is a hybrid cognitive architecture as it combines the connectionist as well as the symbolic approaches [32]. Implementing the GIMA model in a digital information system may allow integrating neural network models that serve the function of the defined AUPs. In this way, an AUP can be seen as a computational process that produces information with specific purposes. The software implementation presented in this article does not focus on the connectionist path but explains the interconnections between the IAs defined in the extended GIMA. It is important to note that this paper explains TIC experiences based on Marks’ well-defined concepts of visual perceptual imagery and visual mental imagery [6]. Additionally, it leaves the door open for hypotheses on imagery experiences occurring “in other sensory modalities” [33]. In the following paragraphs, the IA types and their corresponding AUP are explained and scientifically supported with established understandings of imagery and memory types.

2.3.2. Model Components

The perception IA produces a perceptual imagery experience that corresponds to the Object type in the Action Cycle Theory (ACT) model [6]. In ACT, the Object imagery type is associated with the occipital cortex and is claimed to be related both to perceptual and mental imagery. In the theory of AIA, the perception IA is limited only to the generation of a perceptual imagery experience. This tallies with the claims of the SAS model, that the trigger database, represented by the trigger AUP (Figure 4), is fed with sensory information [17]. The trigger AUP produces a perceptual information entity, which is delivered to all of the adjacent AUPs (in layers 2 and 1). After that, the adjacent AUPs, including the trigger AUP, begin to retrieve relevant information and, when finished, emit an internal event, which makes them targetable by the internal agent for the production of an imagery. This corresponds to the unconscious phase of understanding in the cognitive cycle and to the “competition between different ‘actors’” [34], in which the ‘actors’ can be metaphorically addressed to the AUPs that gather relevant information.

The procedural IA generates a mental imagery experience of an activity procedure. It is represented by the access to relevant information provided by the procedural AUP. The knowledge generated during this experience is supported by the understanding of procedural learning as defined in LIDA [14]. Schemes that are “relevant and reliable” [14] for loading behavioral knowledge in the short-term memory resembles the understanding of the Schemata in the ACT model. However, Marks defines three types of schemata processes, which operate in unconscious and rapid ways [6]. This, however, does not mean that the content—the stowed in short-term memory knowledge (from Section 2.2.3)—of the schemata is unconscious. This is supported by the fact that schemata are explained as mental models and as being related to the cerebellum, the output of which can be perceived as images and a “felt sense of doing” [6,35].

The deed IA targets the sensory motor memory process, which—inspired by LIDA—is viewed as an AUP that loads relevant templates of motor plans that are further provided for execution [14]. The execution of the deed IA is simultaneous with a volitional execution of a body motor plan (the Discrete Motor Execution Hypothesis [5]). Motor imagery modalities have been researched as “imagining performing movements” [36], which corresponds to the understanding of the imagery type occurring during the execution of the deed IA. In research related to LIDA, it is explained that the executed action, based on the selected motor plan, may change the “environment, or an internal representation, or both” [7]. This solidifies the understanding of the nature of the deed IA as one that generates an imagery (TIC) experience.

The episodic IA targets the AUP that gathers and organizes information from the episodic long-term memory. The knowledge that is born in an episodic TIC experience is simply an imagery of an experienced event. The episodic IA corresponds to the episodic learning in LIDA [14]. It is also recognized as an IA of feeling [8] that produces an imagery of affect [6]. The episodic IA is viewed as a process of bringing emotional unconscious content to consciousness, turning it into a feeling, which links to Damasio’s theory [37] and the definition of Voluntary and Automatic Attention in the Global Workspace Theory [10].

The conceptual IA generates a priori knowledge of a concept based on information provided by the semantic AUP (Figure 4). The imagery produced by this IA is a mental imagery experience involving one or more objects, occurring “in the absence” [6,38] of relevant sensory input for those objects. This work focuses on exploring the interaction between the conceptual IA and the metacognitive IAs, as semantic memory has been shown to support creating working-memory bindings [27]. The aim is to provide a new explanation of how an aggregation of “meanings of words” [31] is first loaded by a conceptual IA and then processed by a metacognitive AUP and provided to a metacognitive IA for regulation or control. This can be achieved by adhering to AIA’s view on how a metacognitive AUP retrieves information from the short-term memory (Figure 3).

The metacognitive regulation IA (or just regulation IA) has the aim to reorganize and control knowledge that is being stowed in the short-term memory. In research related to the CLARION cognitive architecture, regulation and control are closely related [29]. This led to the conclusion that one of the two corresponds to one of the knowledge generation modes (Section 2.2.4) of the regulation IA. Sun, Zhang, and Mathews refer to Flavell’s famous model of metacognition by pointing out that regulation and control are “in the service of some goal” [29]. That is why the idea was adopted that the AUP, which serves the regulation entitative and linkative IAs, processes information related to previously accepted goals (Figure 4). Being viewed as an ME type [2], an occurrence of metacognitive regulation is explained as a brief learning phenomenon that is a TIC experience produced by the execution of the regulation IA. As such, a single TIC is claimed to correspond to one of the two modes of knowledge generation (based on Section 2.2.4):

• Regulation entitative IA: The process of approving or rejecting the veracity of a knowledge entity based on its relevance to an accepted goal. It is related to the control aspect of regulation.
• Regulation linkative IA: The process of generating a relevant but opposing knowledge entity in contrast to another, with the purpose of attaining an accepted goal.

Formulated in this manner, these two processes serve to: organize the actual order of experienced episodes (episodic knowledge), ensure the accuracy of schemata (procedural knowledge), and confirm the proper meanings of words or statements (semantic knowledge), all for the purpose of an accepted demand for knowledge.

3. Methods

Grounded in the formulated theory, this section presents the implemented system design and explains the reasons behind the different techniques used in the computations underlying the simulation. The projected task for the simulation was envisioned to be used in a real environment, which, when investigated with a real-world experiment, would provide results for comparison with the data simulated in this work. This section consecutively introduces the simulation system, the simulated task, and the system parameters. At the end of this section, the experimental setup is explained.

3.1. Simulation System

The main requirement of the information system is to simulate consecutive discrete conscious experiences [4,5] viewed as TIC phenomena (Section 2.2.1) produced by the defined in the GIMA cognitive architecture IAs and their corresponding AUPs (Figure 4). Satisfying this requirement demands representing an IA as a possible brief system state, which led to the application of Markov Decision Process (MDP) models. Specific internal demand for knowledge leads to defining a value set of probabilities. With every decision on performing an IA by the internal agent, a change in a set of probabilities occurs. Inspired by Hebbian theory, a learning algorithm was designed that dictates these changes. A task was projected, which allowed addressing internal experiences related to word meaning, evaluation of sentences, simple motor activities, and knowledge regulations for achieving a goal.

3.1.1. Simulating Internal Decisions

An internal decision in terms of the theory of AIA is the outcome of the process of deciding which AUP information to access and which IA mode to use for the observation of it (Phase 3, Figure 1). This means that the performance of an IA can be viewed as the outcome of the internal decision-making phase. Based on the rules defined for GIMA (Section 2.3.1), different IA state switches can occur as a result of an input IA state. That is why it was decided that an MDP model should be used for retaining data on probabilities of states and state switching. An MDP model in the context of this work is defined as a data structure specified by M:

$$\mathrm{M} = (\mathrm{S}, \mathrm{A}, \mathrm{P}\mathrm{)},$$

(1)

where S is a finite set of possible states corresponding to one of the IA types defined in GIMA; A is a finite set of internal decisions (state switches) that are possible in a given IA state; and P is a finite set of probabilities of state switches. Each of the probability values is in the range p = [0, 1] and corresponds to a single state switch—an arrow in Figure 5.

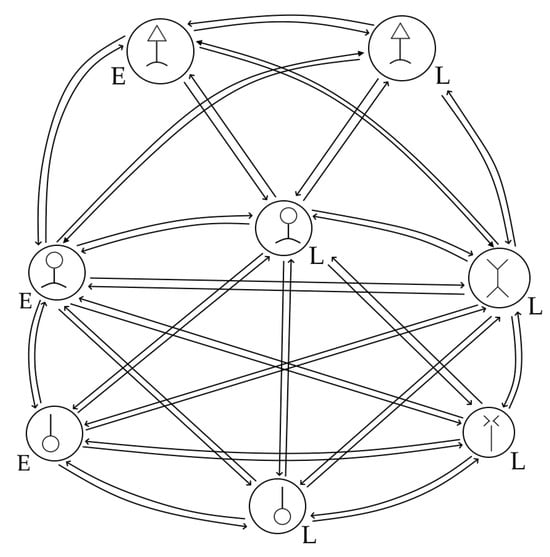
Figure 5. A Markov Decision Process (MDP) model representing simulated internal actions (IAs) from the GIMA cognitive architecture. An IA is viewed as a state, and each arrow represents the possibility of a state switch. Each arrow also represents the probability of switching from one IA to another. The two defined types of knowledge generation (entitative and linkative) are denoted with the letters E and L. The symbols represent the IAs defined in terms of the GIMA model.

By following the understanding that an internal decision is made due to a demand for knowledge (from Section 2.2.4), a single MDP model shall exist corresponding to a goal that the simulated subject has to achieve in the external environment. This means that for every goal, an internal demand for knowledge can be defined. Also, the demand changes over time as new knowledge is accumulated. To simulate this, it was decided that different MDP models can be defined for different goals that have to be achieved in the process of the task. Figure 5 presents an MDP model that is used in the simulation of the projected task. In this work, it was decided that only eight of the eighteen IAs in GIMA are going to be simulated.

A learning method had to be designed that simulates knowledge gaining and long-term learning. A key question arises: if an internal decision is made, what effect does it have on the probability values? To answer this question, reinforcement learning must first be discussed in terms of GIMA. It is shown that reinforcement learning is commonly applied within MDP frameworks [39]. Moreover, there is a clear effort to formulate a general framework for applying reinforcement learning in cognitive architectures [40]. These approaches view the agent as a cognitive architecture that operates with the external environment [40]. However, the theoretical framework of AIA formulates the agent as operating inside the cognitive architecture. Therefore, the latter is the environment itself, and the internal events emitted by the AUPs are the environmental events. That is why, in terms of AIA, the agent is referred to as an ‘internal agent’, and its attention is considered internal as well (Figure 6). Such design approach can be seen in a study on intrinsic motivation [41].

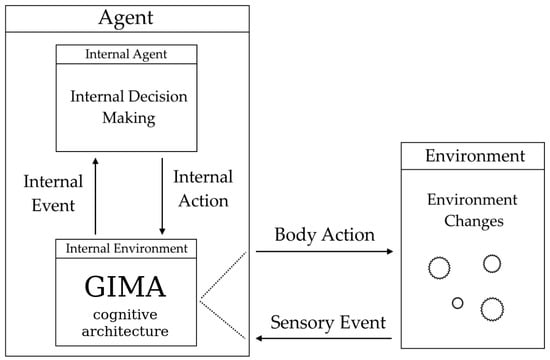
Figure 6. This conceptual model represents a cognitive architecture, in this case GIMA, as an internal environment in which the internal agent operates by making internal decisions based on internal events produced by Automatic Unconscious Processes (AUPs). The internal environment is represented by interconnected states of internal actions (IAs)—the outcomes of internal decision-making. The external environment is represented by environment changes, some of which are perceived as sensory events by the agent. Based on the current internal action, the internal agent produces a body action that is reflected in the environment as a change.

To comply with this design approach, it was decided that inspiration shall be gained from Hebbian theory, which explains how learning occurs on a neuroscientific level. It is shown in a recent article that Hebbian learning is useful in providing solutions for prediction tasks [42]. In the referenced work, Graph Neural Networks are used, which are relatable to the MDP model as defined in this section. To simulate the cognitive phenomena specified in this work, the internal demand for knowledge and the long-term learning effect have to be addressed in MDP models. That is why, in the context of the simulation system, two types of MDP models were declared:

• Learning MDP model (MDP-L): One for each goal that must be achieved in the external environment.
• Influencing MDP model (MDP-I): One for each L, with the purpose of simulating an internal demand for knowledge.

For each defined goal, the MDP-I model influences the probabilities within the dynamic MDP-L model. On the other hand, with every internal decision, the MDP-L probability values are updated towards strengthening the connection of the made decision. This means that for every cognitive cycle iteration, a new Hebbian update is made. The methodology can be more evidently understood if the MDP models are represented by matrices (Figure 7).

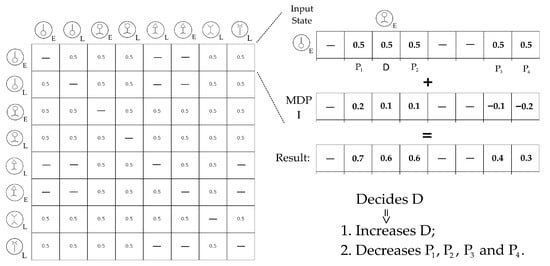
Figure 7. An example of an MDP-L model (for learning) influenced by an MDP-I model. Each row represents an internal action (IA) serving as the source state. The values in each row represent the probabilities of transitioning from the IA of the row to another IA—the output state. Dashes indicate transitions that are not possible according to the rules defined in the GIMA cognitive architecture. When a decision is about to be made based on a source state, the corresponding rows from the two matrices—one from MDP-L and one from MDP-I—are summed. The result is used as input to the stochastic selection algorithm, which outputs an index. Based on this index, the Hebbian learning algorithm is applied to the corresponding row in the MDP-L matrix. The probability of the selected IA is increased, while the probabilities of the non-selected IAs are decreased.

For every internal decision, the computational system increases the probability value of the decided state switch and decreases the other possible state switch probabilities. The following equation is used to calculate the new probability for each undecided IA state switch for every simulated cognitive cycle iteration:

$${P’}_i=P_i-{\displaystyle \frac{a}{n-1}},$$

(2)

where a is the value that is added to the probability of the decided state, n is the number of possible state switches from the source state, P is the initial probability value, and P′ is the new probability stored in the corresponding state switch value of the MDP-L matrix. With each iteration of the cognitive cycle, the likelihood of selecting the decided IA based on the source state increases, but only if the same goal (internal demand for knowledge) is present.

On every cognitive cycle iteration, a stochastic selection algorithm is used to randomly pick the next possible IA state based on the probabilities corresponding to the source state. For example, if the source state is the perception entitative IA (the first line in Figure 7), the algorithm may select the conceptual entitative IA (third from left to right in Figure 7). The higher the probability value, the greater the chance that the cognitive cycle iteration will be simulated using the corresponding IA state. An important note is that in Figure 7, the values in the MDP-L model (on the left) are all 0.5, as it was decided that at the beginning of the simulation, all learning models have an initial probability value (0.5). In this way, several simulation sessions can be conducted, starting from the same probability values, and their evolution will be analyzed.

3.1.2. Simulated Task

If the task were to be performed by actual subjects, it could be described to them as a simple exam that involves confirming the veracity of a statement. In this study, a single veracity confirmation will be referred to as a ‘trial’, which involves several short mental activities. The task is envisioned as a tool that can be applied in digital education environments to conduct online exams over the internet. A single execution of the digital task is projected to have a specified number of statements, each of which has to be marked by the subject as being either true or false. The count of the statements corresponds to the trials count in terms of a single task execution. The projected task begins with the appearance of the first statement, and below it are two buttons: True and False. Immediately after clicking on one of the buttons, the next statement is loaded. Even though this task has a simple design, simulating the internal experiences of the subject is still a challenge, as there are many possibilities due to the short time of the iteration of the cognitive cycle.

In order to simulate internal demands for knowledge based on goals (Section 3.1.1), it is important to define specific short objectives that are pursued during the simulated task. The defined IA and AUP types in GIMA (Figure 4) can be addressed to different short-term internal experience—TICs (from Section 2.2.1)—that occur in the process of performing the projected task. The direction for defining them is the internal demand for knowledge engendered by the current goal of the subject. For a given statement that has to be verified by the subject in the task (conducting a single trial), three consecutive goals were defined:

• Reading the statement;
• Resolve (mentally) whether the statement is true or false (veracity-resolving);
• Execute a motor operation to click one of the buttons, depending on the decision.

It is possible that any of the IAs used in the experiment (Figure 5 and Figure 7) may be executed in the process of pursuing any of these three goals. However, an MDP-L model stores the state switch probabilities for each goal, and a static (its probabilities do not change) MDP-I model influences the internal decisions. Due to the influence on the latter, the MDP-I model also affects the long-term internal learning information stored in the MDP-L model. To simulate the task realistically, the three influencing (MDP-I) models have to learn the stochastic selection algorithm for picking specific IAs for every goal. Corresponding to the three goals defined above, the following actions have to be of preference for the selection algorithm:

• Reading: Perception entitative IA, perception linkative IA, conceptual entitative IA, and conceptual linkative IA.
• Veracity-resolving: Regulation entitative IA and regulation linkative IA.
• Button clicking: Procedural IA and deed IA.

These are general directions for IAs that should be a predominant decision in the three goals (internal demands for knowledge). However, the leaning towards specific IAs is precisely specified by the probability values of the MDP-I models. The values of the MDP-I models used in the experiment are presented further below, where the system parameters are described.

In order for a goal to be attained, specific conditions must be met based on the IAs executed during one of the three trial stages (reading, veracity-resolving, and button clicking). The conditions were hypothetically defined according to the understanding of the nature of the different IA types. For the reading goal to be attained, the sum of execution counts of the perception entitative IA and perception linkative IA in the first stage has to be equal to the word count of the trial sentence. The goal is fulfilled at the point when the subject executes the perception IA (linkative or entitative) with a sequence number after the start equal to the word count. For the veracity-resolving goal, it is considered that a single execution of the regulation entitative IA by the subject marks the internal achievement of the goal. It is theorized that during the performance of this IA, the subject visualizes, to some degree of vividness [6,43,44], an imagery representing the decision on the veracity of the statement in the task trial. For achieving the button clicking goal, it was accepted that two executions of the deed IA have to be made during the third trial stage. They are based on the Discrete Motor Execution Hypothesis [5] of the underpinning theory of AIA. The consecutive executions of the deed IA represent the eventual pointing of the mouse and the click on the button corresponding to the decision on the veracity.

3.1.3. Software Implementation

The digital simulation system was developed using the Python 3.10 language and the Django 5.2 programming framework. The IAs were represented by a PostgreSQL table via Django model classes. The MDP model representations were also developed via model classes and, during computations, were used as matrices of probability values, each falling in the range: [0.1, 1.0]. A Django command, which is simply an executable Python script, was developed as a tool that runs a single simulation session. The command allows the researcher to simulate several executions of the task with the same input of statements and parameters. The values of the MDP-L models are stored in the database and can be reset only at the beginning of the command execution. They are never reset between task executions. The statements input was designed to be a list of strings, each of which is a sentence corresponding to a single statement. The stochastic selection algorithm was implemented using Python’s built-in random module. It takes a list of probabilities, which is the sum of the MDP-L and the MDP-I matrices. The function responsible for the next state selection was programmed to ensure that probability values do not fall below 0.1 or exceed 1.0. In this way, it is always, even though slightly, possible that an unexpected IA is selected by the algorithm. A single simulated execution of the task was based on a for loop that iterates over the list of statements. For every iteration of the for loop (for every task trial), the code consecutively calls three functions that correspond to the three defined goals—internal demands for knowledge (from Section 3.1.2). Each of the functions is responsible for consecutively storing a data structure that represents a single cognitive cycle iteration with its simulated internal decision—the selected IA. All of the functions use the lastly stored data structure to receive the IA from it and apply it as a source state for the stochastic selection. The three functions, presented in the next three paragraphs, are consecutively called to simulate a single task trial.

The first function simulates the reading of the statement. It processes a loop that iterates over the words of the current sentence. It was accepted that a perceptual imagery experience occurring in a single cognitive cycle iteration can correspond to a single word. In the loop, the selected internal decision determines whether the next word should be processed. Going to the next word of the sentence happens only if the selected IA is defined as one that generates perceptual imagery. This corresponds to the claim that the simulated subjects cannot mentally process a word without first perceiving it with either a perception entitative IA or perception linkative IA. After processing all the words, the function exits.

The second function reproduces how the simulated subject resolves the statement’s veracity. Again, a loop is used to reproduce cognitive cycle iterations until the stochastic algorithm selects a regulation entitative IA for the first time. This IA corresponds to the resolution of the veracity decided by the simulated subject. After a selection of this IA occurs, it is considered that the veracity-resolving goal is fulfilled, and the function exits its code processing.

The third function reproduces the simulated subject’s persuasion of the goal to click on one of the buttons. Whether the veracity of the statement was resolved to be true or false is not of importance. It is significant to set the probability values of the influencing MDP model to highly lean towards picking the deed IA. The simulation of the latter was programmed according to AIA’s Discrete Motor Execution Hypothesis [5]. As corresponding to a single motor plan, the execution of the deed IA was required to occur twice in order to confirm that the third goal (clicking a button) is fulfilled. It is envisioned that the subject has to: (1) move the mouse to the “True” or “False” button and (2) click the targeted button. That is why the function was programmed to count occurrences of the deed IA, and a rule was implemented that breaks the loop and exits the function on the second occurrence of the deed IA. Keep in mind that even with the high leaning towards the deed IA, the stochastic algorithm may still select a different IA.

3.1.4. Simulation Parameters

Several parameters were designed for the software command, with some designated for configuring the simulation process and others for the cognitive cycle reproduction:

• Count of simulated task executions (rounds): A single execution of the command can simulate several executions of the task.
• Statements for a task execution: A list of strings, each of which corresponds to a trial statement that is going to be processed in the loop of a single execution of the task.
• Reset MDP-L values: If set to true, all of the probability values of the three MDP-L models will be set to 0.5.
• Three MDP-I matrices: Corresponding to the three defined goals.
• Duration of a single cognitive cycle iteration: A single value, considered as average, was used for all the iterations. This value is used to measure the durations of the different simulated processes.
• IA for veracity-resolving: The IA, which, when selected during the veracity-resolving fulfillment, leads to exiting the function that reproduces this goal.
• Count of deed IA occurrences for the fulfillment of the clicking goal: When as many deed IAs are selected as specified by this parameter, the function responsible for reproducing the button-click goal fulfillment exits its code processing.
• Probability addition: Corresponds to the variable a from Equation (2).

A technique for representing the probability values of the MDP-I models was designed to more easily depict the influence on the IA state desired by the researcher. In Figure 8, the IA state switches, which are demanded for the specified goal, are represented with a capital “P” (for positive), indicating that the MDP-I model influences the algorithm to select the corresponding IA. On the other hand, the state switches, which are not fulfilling the goal, are set to “N” (for negative). Additionally, “p” and “n” were defined as values indicating an intermediate degree of wanted or avoided state switch influence.

Figure 8. The matrices corresponding to the three Markov Decision Process (MDP) models that influence the selection of an internal action (IA). These are referred to as MDP-I and are summed with the corresponding MDP-L matrix to form probability rows, which are then passed to a stochastic selection function simulating state switches between IAs. For example, reading a newly displayed sentence is simulated using the first matrix. If the source state is the perception entitative IA (first row), the stochastic selection algorithm is likely to select a perception linkative IA (second column), as the state-switch probability is increased by 0.2 in the MDP-I matrix.

3.2. Experimental Setup

Several simulations (command executions) can be conducted to investigate the possible outcomes of the MDP-L models by setting the reset parameter to true (Parameter 3, Section 3.1.4). In this experiment, three different probability evolutions of the MDP-L matrices were analyzed with the same simulation parameters (Section 3.1.4):

• Parameter 1: Ten rounds per simulation.
• Parameter 2: A list of 10 strings representing the statements, which means that a single simulation involves the reproduction of 100 trials. The statement list contained one string with 20 words, one with 18, two with 17, and six with 19 words.
• Parameter 3: At the start of each of the three simulations, the MDP-L model values are reset to 0.5.
• Parameter 4: The MDP-I matrices are represented in Figure 8.
• Parameter 5: Average duration of a single cognitive cycle iteration was set to 327.87 (reasons below).
• Parameter 6: The IA that leads to completing a single veracity-resolving goal was set to be the regulation entitative IA for all simulations.
• Parameter 7: Two-deed IA executions were set to complete the button-clicking goal in all simulations.
• Parameter 8: This parameter was set to 0.02 for all simulations—on every simulated internal decision, the probability value corresponding to the state switch is increased by 0.02.

The value of Parameter 5 needs consideration, as the timing of the cognitive cycle duration may vary for different subjects. The hypothesized timing of 260–390 ms [4] was investigated with a small experiment with real subjects [5]. The latter suggested that “the currently accepted” [5] hypothesized time range may have to be expanded. However, it was decided that the Parameter 5 value shall not be less than the lower limit of the hypothesized timing. Inspiration was sought in research on words reading times [45]. The actual execution of the task would involve subjects reading the statements silently; however, it was accepted that, as an online exam, the subjects would read the sentences with higher attention. That is why the speed of reading aloud—183 words per minute [45]—was selected for calculating the duration of an average cognitive cycle iteration. Based on this value, the average duration of a single cognitive iteration is calculated to be 327.87.

Two-deed IA executions were set on Parameter 7, as the simulated task is simple enough for the subject to only move the mouse and click one of two buttons. These two actions constitute the two-deed IA executions. The selected values for the other parameters were chosen because several simulations with the software produced results that did not heuristically match real-world examples. A stopwatch was used to record the time each selected statement was read and processed by a research team member. These times were then used to adjust Parameter 8.

3.2.1. Software Code and Data Structures

In summary, the software implementation represents a command that uses and manipulates the learning models (MDP-L) by applying the constant influencing models (MDP-I). For the reproduction of every cognitive cycle iteration, an internal decision is selected using a simple stochastic selection algorithm developed with Python’s random module, as shown in Figure 9. At each decision, representing a state switch from one IA to another, the corresponding probability value in the MDP-L matrix is increased by 0.02. When the three goals (reading, resolving, and button-clicking) are fulfilled for a conscious process, the latter is added to the result list. Once all statements are processed—that is, after a single round is simulated—the state of the MDP-L models and information on the shortest and longest processes are stored in a file.

Figure 9. Pseudocode presenting the Django command that performs a single cognitive simulation. Before a simulation, the data structures storing the probability values of the MDP models are reset. A simulated cognitive process corresponds to one complete resolution of a statement (reading, resolving, and button-clicking). The three methods, which correspond to the three stages of statement resolution, append cognitive cycle iterations to the ‘process’ variable. After all statements are processed, the information is stored in a file representing the current state of the MDP models and the longest and shortest cognitive processes.

The software generates a results file at the end of each execution that describes the probability values of the MDP-L models and other cognitive processes data generated in the round. This way, it can be analyzed how the MDP-L models evolve throughout the consecutive executions (rounds) of the whole simulation. Of interest is how fast the simulated subject conducts a single trial of the task—reads the statement, resolves its veracity, and clicks the corresponding button. Also, it is of interest to investigate which IAs are picked, and at what point in time since the beginning of the trial. That is why, except for the MDP-L probability values, each results file also stores the following data for a single execution:

• The average count of cognitive cycle iterations per trial;
• Data for the shortest trial;
• Data for the longest trial.

Trial data in the file includes the following variables:

• Duration of the trial (in milliseconds);
• Count of cognitive cycle iterations in the trial;
• Count of words in the statement;
• Order of the IAs that were selected in the trial.

These values are going to be analyzed in order to investigate the different ways in which the MDP-L models transform and how their values impact the timing of the metacognitive experiences and the duration of the trials. Also, the Hebbian machine learning algorithm will be analyzed by observing the evolution of the average trial duration throughout the ten simulated task executions.

3.2.2. Used Software Tools

Except for the Python programming language and the Django development framework, other software tools were used for presenting the data. For charts generation, the Canva website was used: https://www.canva.com/graphs/ (accessed on 28 October 2025) for the average durations chart and the Chart.js framework: https://www.chartjs.org/ (accessed on 28 October 2025) for everything else. Also, Microsoft’s Paint.NET application was used to make the conceptual models and figures in this work.

4. Results

The results from the generated files were organized in a spreadsheet, which is publicly available—check the Data Availability Statement at the bottom of the article. The simulations were performed on a computer with an AMD Ryzen 5 3600 6-Core processor with six cores and 3593 megahertz. The durations of the three analyzed simulations (formatted as min:s) were 2:35, 2:28, and 2:25. The system generated files for each of the 10 executions of the three simulations. The file’s data was analyzed to investigate the average durations of the simulated task trials, the dynamics of MDP-L probability values, and the timing of the metacognitive experience.

4.1. Durations of Statement Verification Trials

Based on the data acquired from the files, the durations of the simulated trials can be analyzed based on the count of the cognitive cycle iterations stored in the files generated by the system. The time results are computed based on the Parameter 5 value (Section 3.1.4), which is applied as an average cognitive cycle iteration duration for the calculations of the time length of a trial. The result files also provided data on the cognitive cycle iterations count, which can be used to analyze the duration of a trial process in a general way. In Figure 10, a table is presented that depicts the line graphs corresponding to the three evolutions of the average cognitive cycle iterations count for each simulated execution of the task.

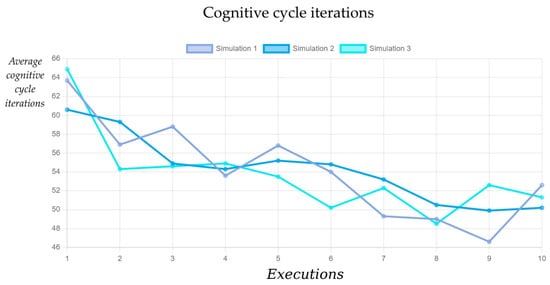
Figure 10. Line graphs depicting the average number of cognitive cycle iterations per trial of an execution. Each of the three simulations was performed with the same input parameters. The variety of data in the different simulations depended on the stochastic selection algorithm.

It can be observed in Figure 10 that the Hebbian learning algorithm decreases the average cognitive cycle iterations throughout the executions. However, the simulations follow different trajectories on the graph. For example, the Simulation 3 line fluctuates sharply during the first executions (1–5), while Simulation 2 shows a comparatively steady decrease in the average iterations count. An important note is that for each execution, 10 trials are reproduced, and the three MDP-L models are updated via the Hebbian learning algorithm on each decision made. This makes a total of 10 × the average iterations count per execution.

To observe how the longest and shortest trials of the executions evolve throughout the simulations, a stacked bar chart was created (Figure 11). It can be noticed how the minimum and maximum durations decrease with each consecutive execution.

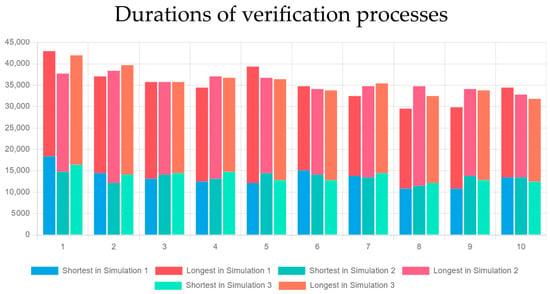
Figure 11. Stacked bar chart of shortest and longest trial durations in milliseconds for every execution in the three simulations. Each of the three simulations has the duration of its longest and shortest process presented for each execution (1–10).

4.2. Evolution of Probability Values

With the possibility to extract the probability values of the different IA state transitions throughout the simulation process, the metacognitive experience IAs could be analyzed. Of interest are the matrix values corresponding to the four state transitions between the conceptual IAs and the regulation IAs:

• Conceptual entitative—regulation linkative;
• Conceptual entitative—regulation entitative;
• Conceptual linkative—regulation linkative;
• Conceptual linkative—regulation entitative.

These four transitions represent the internal act of deciding to engage in a metacognitive experience (metacognitive regulation), which is why they are of interest for the study. To analyze these values, it was decided to investigate the values from the MDP-L model, corresponding to the veracity-resolving goal—the second consecutive goal in a trial. That is why each of the three simulations (Figure 12, Figure 13 and Figure 14) was investigated by analyzing the targeted probability values in line charts, where the x-axis shows the first, fifth, and tenth execution and the y-axis—the probability values.

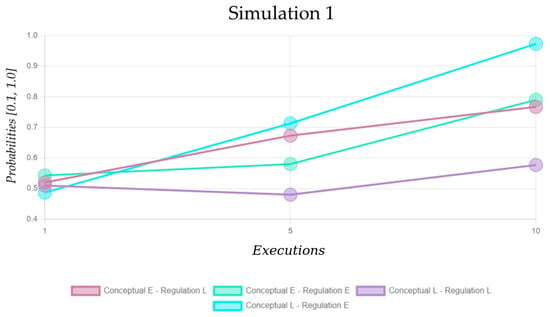
Figure 12. The probability values of the learning Markov Decision Process (MDP-L) model responsible for veracity-resolving in Simulation 1. The entitative and linkative modes of the internal actions (Conceptual and Regulation) are, respectively, represented by E and L.

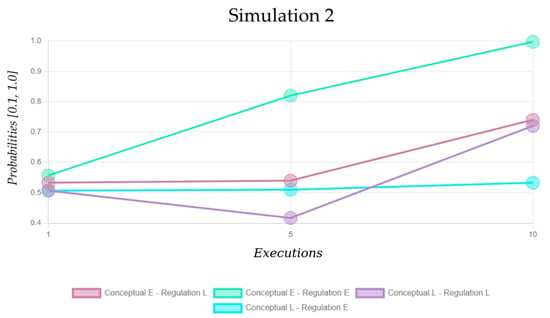
Figure 13. The probability values of the learning Markov Decision Process (MDP-L) model responsible for veracity-resolving in Simulation 2. The entitative and linkative modes of the internal actions (Conceptual and Regulation) are, respectively, represented by E and L.

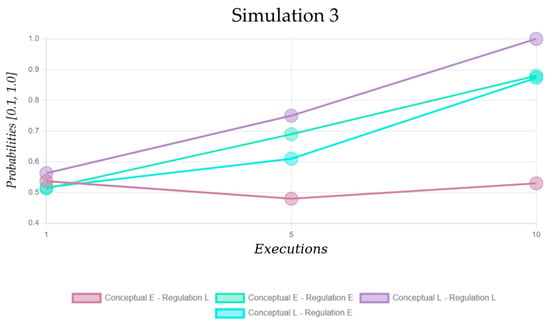
Figure 14. The probability values of the learning Markov Decision Process (MDP-L) model responsible for veracity-resolving in Simulation 3. The entitative and linkative modes of the internal actions (Conceptual and Regulation) are, respectively, represented by E and L.

It appears that there are different ways for the evolution of the MDP-L model responsible for the goal of resolving the statement’s veracity. It is important to note that the regulation entitative IA marks the fulfillment of the veracity-resolving goal. Therefore, it is expected that the higher the probability values of the transitions marked in green and blue (Figure 12, Figure 13 and Figure 14), the lower the trial durations are going to be. However, the duration of a single statement verification process in the task is also dictated by the other two goals—reading the sentence and clicking the button corresponding to the veracity that was mentally resolved.

4.3. The Timing of Metacognitive Experiences

The data from the files generated by the system regarding the order of IA decisions was analyzed by an additional Python script, which provides information on timing and occurrence counts. As mentioned earlier in Section 3.2, it is of interest for this research to investigate the time point at which the first metacognitive experience is engaged. The time points of the first occurrence of the two IAs—regulation entitative (Reg. E.) and regulation linkative (Reg. L.)—were extracted. Each of the files generated by the system provided two strings describing the IAs and the order in which they were selected. Each of the two strings corresponds to the longest and the shortest trial in the execution. The strings were analyzed by the additional Python script to produce the data presented in the six tables (Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6).

Table 1. The longest trials for each execution in Simulation 1.

Execution	Words	CCIs	Reg. E. Count	Reg. L. Count	First Reg. E. Occurrence Time	First Reg. L. Occurrence Time	Reading Time	First Reg. E. Time After Reading
1	20	75	2	5	0.656	4.918	19.344	19.672
2	20	69	2	5	15.41	5.902	14.426	21.639
3	20	69	3	2	6.557	3.934	17.049	19.344
4	20	67	2	4	17.377	15.082	13.443	18.689
5	19	83	4	2	6.23	1.639	18.689	25.574
6	18	60	1	3	16.393	6.23	14.426	16.393
7	18	57	2	3	15.41	9.836	13.443	17.377
8	19	57	4	1	7.541	16.066	14.754	16.393
9	20	58	1	2	16.066	5.902	14.098	16.066
10	17	64	2	1	5.574	15.41	13.771	17.705

Table 2. The shortest trials for each execution in Simulation 1.

Execution	Words	CCIs	Reg. E. Count	Reg. L. Count	First Reg. E. Occurrence Time	First Reg. L. Occurrence Time	Reading Time	First Reg. E. Time After Reading
1	19	56	1	1	16.393	14.426	15.738	16.393
2	17	44	1	0	11.475	—	10.492	11.475
3	17	40	1	2	11.148	2.295	9.508	11.148
4	18	38	1	1	10.82	10.492	8.852	10.82
5	17	37	1	1	9.18	8.852	8.197	9.18
6	17	46	1	0	13.115	—	12.131	13.115
7	17	42	2	1	9.18	11.148	10.492	11.475
8	17	33	1	0	8.852	—	8.525	8.852
9	17	33	1	0	8.852	—	8.525	8.852
10	19	41	2	0	0.656	—	11.148	11.803

Table 3. The longest trials for each execution in Simulation 2.

Execution	Words	CCIs	Reg. E. Count	Reg. L. Count	First Reg. E. Occurrence Time	First Reg. L. Occurrence Time	Reading Time	First Reg. E. Time After Reading
1	19	70	5	4	3.934	3.607	18.033	19.672
2	19	80	4	1	1.311	6.23	15.082	22.623
3	20	66	3	2	4.918	11.475	14.754	19.672
4	19	73	4	2	3.279	2.951	13.771	22.951
5	20	68	4	3	10.82	2.951	15.738	19.672
6	18	61	2	3	3.279	2.951	14.426	17.377
7	19	65	2	2	4.918	14.426	13.771	18.361
8	19	71	4	5	3.279	12.459	12.131	20.984
9	19	62	1	2	18.689	4.918	15.738	18.689
10	20	59	1	4	17.377	0.656	16.066	17.377

Table 4. The shortest trials for each execution in Simulation 2.

Execution	Words	CCIs	Reg. E. Count	Reg. L. Count	First Reg. E. Occurrence Time	First Reg. L. Occurrence Time	Reading Time	First Reg. E. Time After Reading
1	18	45	1	1	10.492	11.148	10.164	10.492
2	17	37	1	1	10.492	8.197	10.164	10.492
3	20	43	1	0	12.459	—	12.131	12.459
4	17	40	2	0	3.934	—	10.82	11.475
5	19	44	2	1	11.803	11.475	10.82	13.443
6	17	43	3	2	6.557	5.902	11.803	12.459
7	17	41	1	2	11.475	10.492	9.836	11.475
8	17	35	1	0	9.508	—	8.197	9.508
9	17	42	1	0	11.803	—	11.148	11.803
10	19	41	2	1	1.311	12.459	10.82	11.148

Table 5. The longest trials for each execution in Simulation 3.

Execution	Words	CCIs	Reg. E. Count	Reg. L. Count	First Reg. E. Occurrence Time	First Reg. L. Occurrence Time	Reading Time	First Reg. E. Time After Reading
1	17	78	4	5	0.328	0.656	17.049	22.295
2	20	78	4	3	9.508	17.705	14.098	23.279
3	20	65	1	2	18.689	14.098	11.475	18.689
4	19	67	2	3	10.492	2.295	19.016	19.672
5	19	72	2	6	6.23	13.443	12.459	19.672
6	19	64	4	5	4.262	3.934	17.705	18.689
7	17	64	5	3	6.885	2.623	16.066	17.377
8	19	62	3	3	2.623	2.295	14.426	19.016
9	19	64	3	3	9.18	14.754	13.115	18.033
10	20	59	2	5	13.443	12.131	11.803	16.393

Table 6. The shortest trials for each execution in Simulation 3.

Execution	Words	CCIs	Reg. E. Count	Reg. L. Count	First Reg. E. Occurrence Time	First Reg. L. Occurrence Time	Reading Time	First Reg. E. Time After Reading
1	17	50	1	4	13.115	4.918	11.803	13.115
2	18	43	2	0	1.639	—	10.164	10.82
3	17	44	2	1	5.246	5.574	10.82	11.148
4	20	45	1	1	12.459	4.262	12.131	12.459
5	17	39	2	1	3.279	11.148	9.836	10.82
6	20	39	1	0	11.148	—	10.492	11.148
7	18	44	2	1	10.492	9.18	10.164	11.148
8	19	37	2	0	9.836	—	9.508	10.492
9	17	39	1	1	10.82	11.148	10.492	10.82
10	19	38	2	1	9.508	9.18	8.525	11.475

Each of the six tables presents the same variables, which the longest (Table 1, Table 3 and Table 5) and the shortest (Table 2, Table 4 and Table 6) trials showed. The times of the first occurrences of the Reg. E. IA and the Reg. L. IA in the trials are presented, along with the occurrence counts per trial. The tables also present the time point when the reading goal is fulfilled and the veracity-resolving is started (column is denoted with “Reading time”). Also shown is the time at which the goal-fulfilling Reg. E. IA is selected during the veracity-resolving goal (“First Reg. E. time after reading”).

5. Discussion

By observing the results from a general perspective, it can be stated that the Hebian learning method successfully simulated an improvement in the (long-term learning) effect on task performance. The presented machine learning method appears applicable to human-centered models designed to replicate actual subjects and cognitive events, which was the aim of this study. For simulating a faster improving effect, the designed system allows increasing the probability addition parameter (Parameter 8, Section 3.1.4). No research has been performed yet to investigate if the chosen probability addition value (0.02) corresponds to task learning effects in actual subjects.

The analysis of the probability values of the state switches leading to metacognitive regulation experiences (Section 4.2) showed that the different simulations produced different evolutions of the probability values in the MDP-L models. Based on the line graphs, it can be stated that at least one state switch probability value of the ones investigated will reach or will be close to the maximum at the tenth execution. Of course, the conditions required for achieving this circumstance are the specified system parameter values (Section 3.1.4).

With its main focus on the timing of the metacognitive experiences, the analysis required an additional Python script to investigate the evolution of several variables across the ten executions. It was demanded that the time elapsed until the occurrence of the first metacognitive experience in each trial be investigated. This means that the selection time point corresponding to one of the two metacognitive regulation IAs must be extracted for every trial. This will allow analysis of the elapsed time values, each representing the occurrence of either a regulation entitative (Reg. E.) or a regulation linkative (Reg. L.) IA, using a scatter plot in which the x-axis represents the execution number.

5.1. Analyzing the Occurrences of Metacognitive Experiences

In the tables in Section 4.3, it is observable that longer trial durations are associated with higher occurrence counts of metacognitive experiences (Reg. E. and Reg. L.). This seems natural simply because longer trials provide more time, which increases the likelihood of the algorithm selecting the regulation IAs. However, the linear regression of the elapsed time until the first metacognitive experience in each trial showed results deserving attention. The linear regression graph in Figure 15 reveals that the time values increase slightly as the x-axis executions progress.

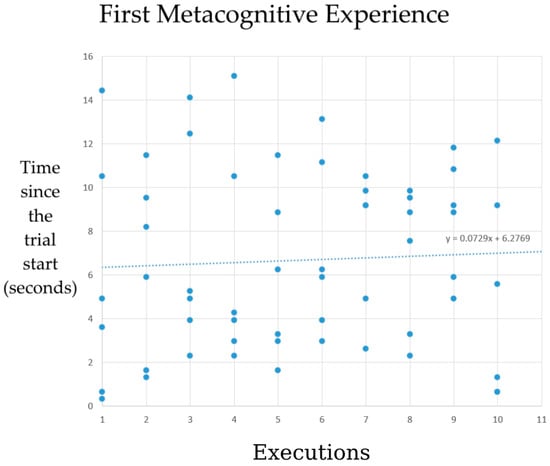
Figure 15. Linear regression analysis of the time points of the first occurrence of a metacognitive experience in the simulated task trials in the ten executions. Each y-value is the elapsed time from the beginning of the trial until the first recorded occurrence of a metacognitive experience.

The results in Figure 15 were unexpected, as the decrease in the average trial duration suggested that the first metacognitive experience would occur earlier in the trial process. This finding suggests that, based on the theory of AIA and the simulation system, subjects tend to engage in metacognitive experiences later as the exam task progresses. The graph in Figure 15 analyzes the first metacognitive experience, whether it is of a Reg. E. or a Reg. L. IA. This leads to the question: Is the IA that attains the veracity-resolving goal—the Reg E. IA—occurring earlier over the simulation course? To answer this question, further linear regression analyses were performed (Figure 16 and Figure 17).

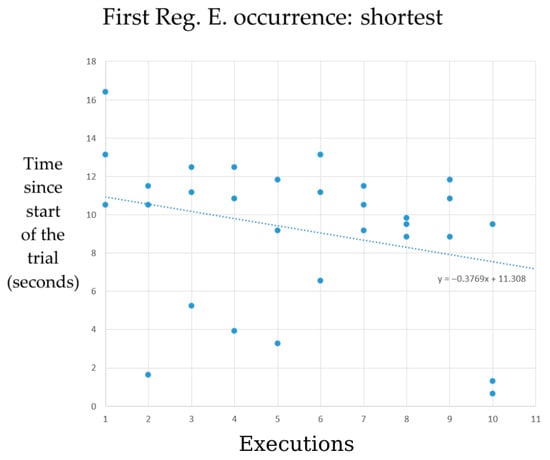
Figure 16. Linear regression analysis of the elapsed time points from the trial onset until the first occurrence of the regulation entitative (Reg. E.) internal action. The data pertains to the shortest task trials from each of the 10 consecutive task executions, reproduced in three simulation sessions.

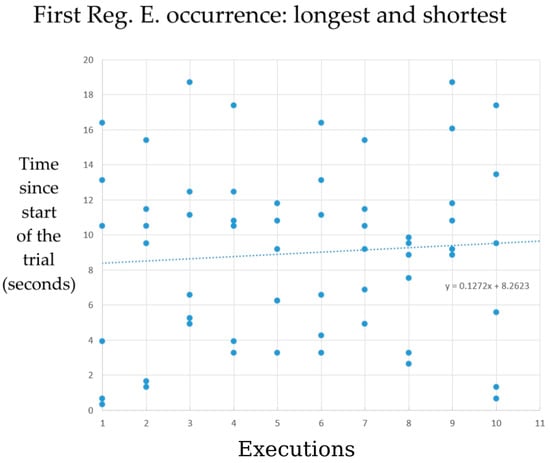
Figure 17. Linear regression analysis of the elapsed time points from the trial onset until the first occurrence of the regulation entitative (Reg. E.) internal action. The data pertains to the shortest and longest trials from each of the 10 consecutive task executions, reproduced in three simulation sessions. In general, the duration of statement resolution increases over time.

These results were surprising due to the reasoning that the trial duration is expected to shorten if an earlier selection of a goal-filling IA is made (the Reg. E. IA for the veracity-resolving stage). Also, the selection of the goal-filling IA leads to Hebbian update of the corresponding state switch probability, which was expected to additionally increase the chance of an earlier Reg. E. IA selection. Figure 16 confirms this expectation, showing how the time of the first occurrence of the Reg. E. IA naturally decreases over the course of the executions. However, the graph in Figure 16 analyzes only the shortest trials recorded in the executions. When observing the whole picture by including the longest trials as well, a delay is once again evident (Figure 17). The elapsed time from the trial onset until the first Reg. E. occurrence increases by 127.2 ms for each execution. This additionally supports the earlier suggested hypothesis claiming that the subjects tend to engage in a metacognitive experience later over the course of the exam task.

5.2. Comparison with Real Cognitive Effects

Knowledge can be extracted from the data generated in the three simulations. What is certain is that the duration of the shortest statement resolutions decreases, while that of the longest resolutions increases. This divergence in performance dynamics can be related to real-life situations, where individuals are well-prepared for certain topics in an exam but less prepared for others. Therefore, over the course of the exam, questions related to familiar topics are answered more quickly due to performance improvement effects, while those concerning unfamiliar topics become increasingly difficult for the subjects to answer. The effect of vigilance decrement [46] is related to the decrease in answering speed for the exam statements. On the other hand, the increased speed in resolving statements in known topics can be attributed to effects like the impact of familiarity with the exam [47] and practice due to serial assessment [48].

5.3. Limitations

This approach for simulating internal experiences allows researchers to address rapid events. However, a key problem remains: the duration of a cognitive cycle iteration cannot be directly determined for a given subject [5]. The average duration used in this experiment remained constant across the three simulations, which certainly makes them less realistic. Another limitation is that some components of the GIMA cognitive architecture, such as the AUPs corresponding to metacognitive IAs, lack empirical support. The GIMA model certainly requires further research to substantiate its explanations for short-term and long-term memory access (Figure 3). A step toward this challenge is conducting real-life experiments based on the presented simulated task design. Data from human subjects could be used to adjust the simulation parameters to match real-world results, thereby confirming or refuting the findings presented in Section 5.2.

5.4. System Applications

Based on the conducted experiment, it was shown that the simulation system can provide an understanding of how fast different subjects can complete a simple exam. The latter is represented by statements that participants must confirm or reject by clicking on one of two buttons. Such rather simple exams can be used for the quick knowledge evaluation of students, job applicants, driver candidates, and specialist trainees. The time results that the system generates are expected to correspond to participants who are prepared for the exam. Yet, the varying value states of the MDP-L models produced throughout the simulation process can represent to participants with different levels of preparation. It can be argued that Parameter 5’s input value of 327.87 (Section 3.1.4) might be inconsistent with reality, as this is the time for which a word is read out loud, while during an exam, the subjects can read a lot faster, especially if they have studied the content. However, the average duration of a trial in the task can be calculated with different average duration values, as data on the counts of the cognitive cycle iterations was extracted in the files for each task execution.

An idea planned for future research in our laboratory involves conducting a psychological experiment to investigate whether the simulated time results align with the ones produced by actual subjects. Such an experiment would produce time results by itself, which, if they do not align, would allow adapting the simulation system parameters towards reproducing them. Achieving time results alignment would mean that the adapted system parameter can be used for measuring the execution time based on different exam content—statements, which the subjects have to verify as true or false. A future challenge is to extend the functionalities of the system to allow reproducing exams with answers other than true or false. This would require designing the reproduction of an additional internal demand for reading the provided answers.

Another application of this system is the possibility to simulate different internal demands for knowledge based on the theory of AIA and the new version of the GIMA cognitive architecture. The MDP-I models allow the researcher to precisely define the way in which the internal demand leads to the selection of specific IAs and thus to represent particular cognitive experiences. However, a challenge, which demands heuristic decisions, is to specify the influence values of the MDP-I matrices to achieve realistic simulated internal behavior. The MDP-I values have to be in harmony with the probability addition parameter (Parameter 8, Section 3.1.4). This is because if higher influence values are used, the likelihood of selecting the same IA increases due to the updates of the Hebbian learning algorithm.

6. Conclusions

This work presented the theory of Attention as Internal Action and its application in designing cognitive architectures for conscious imagery experiences. The new version of the General Internal Model of Attention (GIMA) was utilized to design a simulation system that reproduces internal decisions of information access occurring during the process of taking an exam. Based on the conducted experiment, this study presents a new hypothesis on the timing of metacognitive experiences during exam-taking. The results suggest that metacognitive experiences are delayed at the beginning of each new question as the exam progresses. Real-world cognitive effects, such as vigilance decrement and serial practice impact, were considered in relation to the findings. The developed simulation system can also have applications beyond scientific experiments. Supplied with exam statements, it can be used to generate results on the duration of a digital exam as performed by participants with different levels of preparation.