Abstract
Multimodal sentiment analysis is an actively growing field of research, where tensor-based techniques have demonstrated great expressive efficiency in previous research. However, existing sequential sentiment analysis methods only focus on a single fixed-order representation space with a specific order, which results in the local optimal performance of the sentiment analysis model. Furthermore, existing methods could only employ a single sentiment analysis strategy at each layer, which indeed limits the capability of exploring comprehensive sentiment properties. In this work, the mixed-order polynomial tensor pooling (MOPTP) block is first proposed to adaptively activate the much more discriminative sentiment properties among mixed-order representation subspaces with varying orders, leading to relatively global optimal performance. Using MOPTP as a basic component, we further establish a tree-based mixed-order polynomial fusion network (TMOPFN) to explore multi-level sentiment properties via the parallel procedure. Indeed, TMOPFN allows using multiple sentiment analysis strategies at the same network layer simultaneously, resulting in the improvement of expressive power and the great flexibility of the model. We verified TMOPFN on three multimodal datasets with various experiments, and find it can obtain state-of-the-art or competitive performance.
1. Introduction
Multimodal sentiment analysis is an important research topic in the field of affective computing, which observes the fusion of multiple sentimental modalities [1,2,3,4,5,6,7]. Compared to multimodal sentiment analysis, unimodality-based sentiment analysis may result in the ambiguous sentiment. For instance, the text message “This movie is sick” can be either positive or negative. However, if the speaker is also smiling at the same time, then the above text is related to the positive. In contrast, if the speaker is frowning at the same time, then the above text will be perceived as negative. Indeed, multiple sentiment modalities (spoken language, visual and acoustic signals) [8,9,10,11,12] consist of consistency and complementarity. Therefore, the joint multimodal sentiment representation can effectively reason about more accurate sentiment properties, allowing us to further boost the task performance of a sentiment analysis model. Currently, extensive fusion research aims at capturing the potential correlation among multiple sentimental modalities [8,13,14,15].
The multimodal fusion techniques attempt to incorporate the message collected from various modalities into a precise outcome. Reasonable integration of multimodal information can give full play to the role of each modality. Traditional multimodal fusion can be divided into early fusion, late fusion, and hybrid fusion [16,17]. Early fusion treats the concatenation of the unimodal presentation as the input of the model [18,19]. In contrast, late fusion performs the fusion process at the decision level by voting on or averaging the results [20,21]. As to hybrid fusion, the output depends on the combination of unimodal prediction and early fusion [4,22]. Although traditional fusion techniques are effective for some simple tasks, the expressive capability of the model is limited to the oversimplified linear combination of multiple modalities, i.e., the linear combination-based fusion models could only capture linear cross-modal interactions, which may fail to highlight sophisticated multimodal intercorrelations.
The recent bilinear or trilinear multimodal fusion models aim to exploit nonlinear and high-order cross-modal interactions using tensor product representations [23,24,25,26]. Additionally, Liu et al. [27,28] employed the low-rank tensor to model trilinear multimodal fusion, which significantly reduces the parameters of the fusion framework. Please note that the above models are not applicable to consider much more sophisticated intercorrelations as the fusion tensor is restricted to the order. For instance, the order of fusion tensor is only up to three, contributing to the trilinear interaction. To overcome this issue, [29] proposed the sequential hierarchical architecture HPFN to measure the multilinear multimodal intercorrelations. However, existing sentiment analysis techniques only address the fixed-order representation space with a specific order. The fixed-order representation space refers to a specific N-order space, where N denotes the order of the corresponding space. Please note that the relative low-order representation subspace consists of coarse-grained sentiment characteristics. The relative high-order sentiment subspace includes fine-grained properties. If we only focus on the analysis of a single fixed-order representation space, this may result in the local optimal performance of the sentiment analysis model, i.e., the fixed-order analysis fails to effectively obtain the potential and comprehensive sentiment properties among representation subspaces with varying orders (Figure 1). More importantly, existing sequential learning architecture could only use a single fusion strategy at each network layer. This indeed limits the complete expressive power of the multimodal sentiment analysis model and results in the significant deterioration of task prediction.
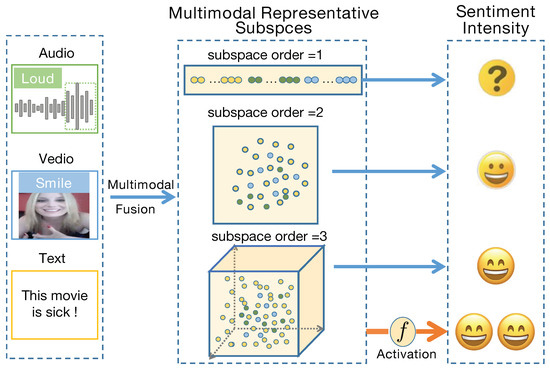
Figure 1.
The relative low-order representation subspace consists of coarse-grained sentiment characteristics. The relative high-order subspace includes fine-grained properties. If we only focus on the analysis of a single fixed-order representation space (1-order, 2-order, or 3-order subspace), which may result in the local optimal performance of the sentiment analysis model.
In this work, the mixed-order polynomial tensor pooling (MOPTP) block is proposed to adaptively activate the much more discriminative sentiment properties among representation subspaces with varying orders. Please note that this does indeed allow for much more capability to obtain global optimal performance among multiple representation subspaces, leading to more discriminative and comprehensive sentiment characteristics. Taking MOPTP as a basis, we further establish a tree-based mixed-order polynomial fusion network (TMOPFN), which could be broadened and deepened concurrently, i.e., the network could be broadened by using multiple sentiment analysis strategies at the same network layer simultaneously, which allows for exploring multi-level sentiment properties with the multi-spect view. Moreover, low-level sentiment information can be transmitted to the high-level one via the deepen procedure (i.e., in a recursive manner). Actually, incorporating a ‘tree-based structure’ with ‘MOPTP’ further boosts the flexibility and expressive capability of the multimodal sentiment analysis model.
The main contribution of our paper are summarized as follows:
- •
- We propose the mixed-order polynomial tensor pooling (MOPTP) block to adaptively activate the much more discriminative sentiment properties among representation subspaces with varying orders. Compared to the existing fixed-order methods, the proposed mixed-order model can effectively integrate multiple local sentiment properties into the more discriminative one, leading to the relatively global optimal performance.
- •
- We propose a novel tree-based multimodal sentiment learning architecture (TMOPFN) that allows for using multiple sentiment analysis strategies on the same network layer simultaneously. Compared to the existing sequential sentiment analysis model, our parallel framework naturally provides us the great benefit of capturing multi-level sentiment properties via the parallel procedure.
- •
- We conduct various experiments on three public multimodal sentiment benchmarks to evaluate our proposed model. Empirical performance demonstrated the effectiveness of the mixed-order-based techniques and tree-based learning architecture. Please note that sentiment is part of emotion, i.e., the emotion recognition also covers sentiment analysis. Thus, we evaluated our model on two sentiment analysis benchmarks and one emotion recognition benchmark.
2. Related Work
The existing study of multimodal sentiment analysis includes two major groups: Non-temporal models average the features along the temporal dimension. These models demonstrated the effectiveness in the early work of multimodal emotion analysis [30]. Recently, tensor fusion network (TFN) [24] employs tensor product to explore non-temporal bimodal and trimodal sentiment interactions. Moreover, Low-rank multimodal fusion network (LMF) [27] is proposed to further enhance the compressibility of non-temporal fusion with modality-specific low-rank factors. The above manners attempt to capture all multimodal correlations at once, without using temporal message. Therefore, they are not able to explore the intra-modal and inter-modal sentiment dependency along the temporal domain, leading to the deterioration of sentiment analysis performance.
Multimodal temporal models attempt to process multimodal sentiment interactions along the temporal dimension. The long-short term memory (LSTM) [31] facilitated various applications in sequential multimodal sentiment learning. Among them, in order to capture both view-specific and cross-view sentiment properties, multi-view LSTM (MV-LSTM) [32] partitions the memory cell corresponding to specific modality. The bidirectional contextual LSTM (BC-LSTM) [33] focuses on the context-dependent sentiment analysis and emotion recognition tasks. The memory fusion network (MFN) [8] employs multi-view gated memory to store cross-modal and intra-modal interactions. The multi-attention recurrent network (MARN) [34] uses a multi-attention component to highlight cross-modal sentiment interaction via the attention mechanism. The recurrent multistage fusion network (RMFN) [13] decomposes the sentiment analysis into several stages, and focuses on only a subset of the signal in each stage. The multimodal factorization model (MFM) [35] factorizes multimodal sentiment representations into two sets of independent factors, including multimodal discriminative and modality-specific generative factors. The multimodal baseline model (MMB) [15] proposes two simple but strong multimodal learning baselines. The first baseline factorizes the utterance into unimodal factors conditioned on the joint embeddings. The second baseline factorizes the utterance into unimodal, bimodal, and trimodal factors. The deep multimodal multilinear fusion with high-order polynomial pooling (HPFN) proposed sequential fusion architecture to model multilinear multimodal sentiment interactions within the fixed-order representation space. More recently, transformer-based models have exhibited great predictive performance with the help of the self-attention mechanism. For instance, the Conversational Transformer Network (CTNet) [35] employs the transformer to model inter-modality and intra-modality sentiment interactions via transformer pairs. The Low Rank Fusion based Transformers (LMF-MulT) [36] combine the low-rank tensor framework with a cross-modality attention block to exploit the low-rank cross-modality sentiment information via a single transformer. The attention-based modality-gated networks (AMGN) [37] propose an attention-based method to learn the discriminative features and the close correlation between visual and text modality. Additionally, graph-based models have been largely applied to multimodal sentiment learning tasks. For example, the Multimodal Graph [38] uses a graph convolutional and pooling network to explore intra-modal and inter-model sentiment dynamics. The Multimodal Temporal Graph Attention Networks (MTGAT) [39] propose a novel graph operation called multimodal temporal graph attention to focus on both multimodal sentiment fusion and alignment. The Heterogeneous Graph-based Fusion (HGMF) [40] constructs a transductive learning-based heterogeneous hyper-node graph to leverage the inter-modality sentiment information among multiple modality patterns.
However, the aforementioned sentiment analysis manners only focus on the fixed-order representation space with a specific order, leading to the local optimal sentiment analysis performance, i.e., exiting methods fail to effectively highlight the more discriminative sentiment properties among representation subspaces with varying orders. More essentially, existing sequential architecture could only use a single fusion strategy at each network layer, with the restricted sequence of sentiment analysis strategy. This indeed limits the complete expressive capability of capturing the comprehensive and multi-level sentiment properties.
3. Preliminaries
Tensors are the multi-dimensional generalization of matrixes [41]. We denote a P-order tensor with P modes. The is the -th entry of tensor with for all . Given two tensors and , the corresponding tensor product is performed as
where . Actually, the tensor could be performed on vector inputs. For instance, the CP decomposition [42] of can be denoted as a sum of rank-1 tensors as , where R is defined as tensor rank. Tensor networks (TNs) [43,44,45] are the extension of original decomposition (CP, Tucker [46]) and consist of a set of interconnected low-order tensors, which greatly reduces the effect of high tensor order.
4. Methodology
In this section, we first introduce the mixed-order polynomial tensor pooling (MOPTP), which is the core operation of our tree-based mixed-order polynomial fusion network (TMOPFN). The MOPTP block is proposed to adaptively activate the discriminative sentiment properties among representation subspaces with varying orders. Treating MOPTP as a basis, TMOPFN is further established to exploit multi-level sentiment properties via the parallel procedure.
4.1. Mix-Order Polynomial Tensor Pooling (MOPTP)
Compared to our previous work, ‘PTP’ (high-order polynomial tensor pooling), MOPTP can adaptively activate the more discriminative sentiment properties among multiple representation subspaces, which contributes to global optimal performance. The MOPTP block is formulated in Algorithm 1.
| Algorithm 1 Mix-order Polynomial Tensor Pooling (MOPTP) |
| Input: text , video , audio , the number of subspaces ‘N’, tensor rank ‘R’. Output: The multimodal fusion representation ‘’. 1: ← concat (, , ) 2: for to N do 3: for to n do 4: for to R do 5: ← 6: end for 7: ← ( + ⋯ + ) 8: ←· 9: end for 10: ← 11: end for 12: ← ( + ⋯ + ) 13: return x |
The MOPTP block attempts to merge the sentiment features into the joint message by adaptively activating the discriminative sentiment information among multiple representation subspaces with varying orders. Figure 2 demonstrates the detailed operation of MOPTP. The ‘M’ refers to the number of modalities. For instance, if the dataset consists of audio, text, and video modality, then ‘M’ equals to 3. Initially, a set of M modality representation vectors are concatenated together into a long representation vector :
Then, the fixed P-order representation tensor is formulated as
where are a series of tensor product operators. The pooling weight tensor is introduced to analyze the high-order multimodal sentiment properties within a P-order representation subspace:
where , corresponds to the h-th element of the H-dimension x. The high-order term in the n-th mode is indicated by .
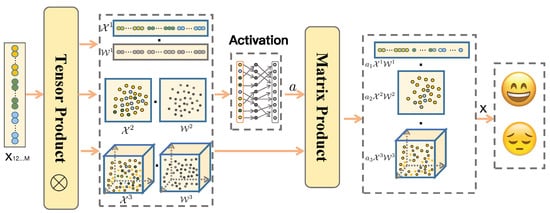
Figure 2.
The scheme of 3-order polynomial tensor pooling (MOPTP) block for fusing , , and modalities. First, is used to construct the N-order multimodal representation subspace via tensor product, e.g., , and indicates the N-order weight tensor. Furthermore, MOPTP attempts to employ a pooling function to adaptively activate the more discriminative sentiment properties among representation subspaces with varying orders (, , and ).
It is important to note that each fixed-order representation subspace is comprised of corresponding sentiment granularity. The relative low-order representation subspace (such as 1-order subspace) consists of coarse-grained sentiment characteristics, where the elements of the low-order subspace indicate explicit and general sentiment characteristics. The relative high-order representation subspace (such as N-order subspace) is comprised of fine-grained sentiment properties, where the elements of the high-order subspace refer to implicit and specific sentiment properties. Please note that PTP only considers the sentiment properties within a single representation subspace with a fixed order, leading to the local optimal performance of the sentiment analysis model. To overcome the above issue, we extend the ‘PTP’ to ‘MOPTP’ for adaptively activating local sentiment properties among multiple subspaces with varying orders, then (4) is rewritten as
where N indicates the number of fixed-order (P-order) representation subspaces. Each element of can fully absorbs the contribution from mixed-order representation subspaces {1-order subspace, ⋯, N-order subspace}, leading to more discriminative and comprehensive sentiment properties.
Specifically, the sentiment activation coefficient is employed to adaptively activate the sentiment-related elements of all the representation subspaces, i.e., the above activation procedure provides us with the great benefit of adaptively modifying each element of representation with the help of all the representation subspaces, leading to more discriminative sentiment properties. This indeed bears the potential to reduce the redundancy information to some extent. Moreover, the above operation can integrate the local sentiment properties into the global one, leading to more discriminative and comprehensive representations. Please note that the sentiment activation coefficient is received based on specific linear function. In this paper, we use the identity function to activate all representation subspaces, which supports the investigation of both coarse-grained and fine-grained sentiment properties. Additionally, the piecewise function is leveraged to activate one of the multimodal representation subspaces, contributing to the relatively sparse sentiment representation.
Please note that the dimension of in (5) increases exponentially with the number of interaction order P. Therefore, we employ the low-rank tensor network to approximate the , then (5) is rewritten as the following vector-based form:
If admits a TR format, then the following formula can be derived from (5) as
where the block vectors are the parameters of our proposed multimodal sentiment analysis model. are defined as ranks of a tensor ring network, where . With the help of low-rank tensor formulation, the sentiment analysis model can effectively employ the parallel decomposition of both representation tensor and weight tensor . Therefore, we can capture the corresponding representation without actually creating and storing the original large tensor, and avoid the curse of dimensionality on representation tensor and weight tensor.
4.2. Tree-Based Mix-Order Polynomial Fusion Network (TMOPFN)
Based on the proposed MOPTP block, a tree-based mixed-order polynomial fusion network (TMOPFN) is further established to analyze the multilevel sentiment properties in a recursive fashion. Please note that the proposed tree-based network refers to a hierarchical tree structure with a set of connected nodes, where each node refers to the hidden layer or output layer. In general, the multimodal sentiment series is rearranged into a ‘2D map’, and the ‘window’ is used to cover local representation across temporal and modality dimensions. Then, the MOPTP block is used to capture the potential sentiment properties within the ‘window’. Moreover, the local integration is transmitted to the global one, recursively.
A simple instance of three-layer-based sentiment analysis network is shown in Figure 3. At the first hidden layer, a MOPTP block is used to analyze the receptive ‘window’ that covers sentiment features across all 4 time steps and 3 modalities. Each MOPTP is comprised of multiple representation subspaces, where each subspace refers to a distinct N-order space. Please note that each fixed-order representation subspace is composed of corresponding sentiment granularity. Then, we can effectively capture the multimodal interactions within the ‘window’ that includes total 12 features (i.e., 4 time-steps × 3 modalities), leading to new modality representation H1-1. At the second hidden layer, MOPTP is used to model local sentiment properties in a ‘window’ that includes 2 time steps and 2 modalities. For example, the MOPTP is applied to merge the text and video representation spanning time T3 and T4, resulting in the third hidden node of new modality H2-1. Similarly, the first hidden node of H2-2 is retrieved by fusing the video and audio features of T1 and T2. Please note that the first hidden layer focuses on the general sentiment properties among three modalities, while the second hidden layer attempts to highlight the local sentiment properties of each modality pair. At the output layer, the MOPTP is used to integrate the message of the first and second hidden layers into the final global sentiment properties.
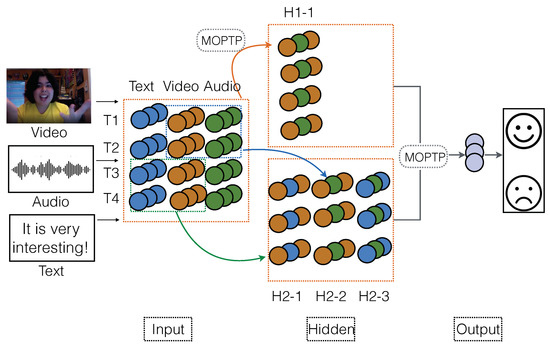
Figure 3.
TMOPFN-L3-S1. At the first hidden layer H1, a MOPTP block is used to analyze the receptive “window” that covers features across all four time steps and time modalities, leading to the new modality representation ‘H1-1’. At the second hidden layer H2, the MOPTP is used to model local interactions in the “window” that consider two time steps and two modalities, allowing for new modality representation ‘H2-1’, ‘H2-2’, and ‘H2-3’. The tree-based structure naturally allows for using multiple sentiment analysis strategies on the same network layer simultaneously, resulting in the significant improvement of expressive power.
As shown in Figure 3 and Figure 4, and attempt to further integrate the local sentiment properties into the much more comprehensive one within the same ‘2D map’. Compared to the , employs the skip operation to the multimodal sentiment analysis network, allowing for the additional sentiment information captured from the preceding layer. Initially, modality is transmitted to the first hidden layer . Then, MOPTP is used to search for the latent inter-correlation between modality and the coarse-grained sentiment message of the preceding layer. Note that is the essential modality that consists of abundant sentiment knowledge, and the coarse-grained sentiment message is comprised of the global sentiment properties. Therefore, aims at further exploiting subtle sentiment dependency between and , where is the strong backbone and is employed to guide the sentiment analysis process.
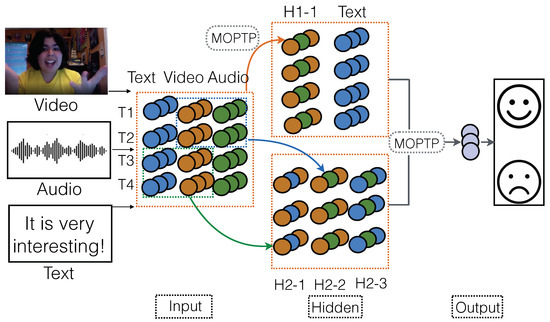
Figure 4.
TMOPFN-L3-S2. Compared to TMOPFN-L3-S1, TMOPFN-L3-S2 introduces the skip operation to the fusion framework, allowing for the additional information captured from the preceding layer.
Additionally, Figure 5 demonstrates a tree-based structure that is associated with segmentation sentiment analysis strategy and skip sentiment analysis strategy. Initially, the local sentiment message of the modality pair is transmitted to the next hidden layer. For instance, the first hidden node of H1-1 is captured by integrating text and video representation of T3 and T4. Then, the audio representation of the input layer is directly delivered to the same hidden layer . Furthermore, we can capture the inter-correlations between audio and H1-1. This strategy allows our model to highlight the fine-grained and multi-stage sentiment inter-correlations among multiple modalities. Note that each modality serves as the backbone and guide the multimodal sentiment analysis process in diverse fashions, leading to comprehensive sentiment properties. Taking advantage of the tree-based structure, the original sentiment analysis framework could be extended to diverse variants that enjoy a significant improvement of expressive power.

Figure 5.
TMOPFN-L3-S3. Taking the advantage of segmentation fusion strategy and skip operation, each modality can serve as the backbone and guide the multimodal fusion process in diverse fashion. This indeed contributes to more fine-grained and explicit correlations among multiple modalities.
5. Experiments
5.1. Experiment Setups
Datasets. IEMOCAP dataset [2] is comprised of 302 videos of recorded dyadic dialogues. The segments of videos are annotated with basic emotions (neutral, fearful, happy, angry, disappointed, sad, frustrated, excited, surprised), as well as the dimension-based labels (dominance, valance, and arousal). There are 6373 segments in the training set, 1775 segments in the validation set and 1807 segments in the test set. CMU-MOSI dataset [47] collects the movie reviews from YouTube, and contains 2199 opinion video clips. Each clip is associated with a sentiment label in the range from high negative to high positive. The division of the train, validation, and test sets is 1284, 229, and 686, respectively. CMU-MOSEI dataset [48] is a generation of CMU-MOSI, which consists of 23,453 annotated video segments from 1000 distinct speakers and 250 topics. Each sentence is annotated for a sentiment on the Likert scale. It can be ensured that the specified speaker can only belong to one of the three sets, which means the splits of three datasets are speaker-independent.
Features and alignment. In this part, we attempt to provide more details about feature extraction and alignment of the text, visual and audio modalities. Please note that words and audio are aligned at the phoneme level, with the help of the P2FA forced alignment model [49]. Since words are considered as the basic units of text modality, we use the interval duration of each word utterance as a time step. Then, the visual and audio modalities are aligned by calculating the average value over the utterance interval of each word [8,35].
(1) Text: Glove word embeddings [50] are used to capture the word vectors from the video segment transcripts, and the obtained vectors are used to represent the text modality feature. Additionally, the 300-dimension Glove word embeddings are trained on 840 billion tokens from the crawl dataset.
(2) Visual: The Emotient FACET [48] is leveraged to extract a set of six basic emotions from the static faces. MultiComp OpenFace [51] is used to capture 68 facial landmarks, 20 facial shape parameters, facial HOG features, head pose, gaze tracking and facial landmarks.
(3) Audio: The software COVAREP [1] is used to explore the 12 Mel-frequency cepstral coefficients, pitch tracking, voiced/unvoiced segmenting features, glottal source parameters, peak slope parameters, and maxima dispersion quotients. The above audio features are related to sentiment status and tone of speech.
Training details of baselines. We compare the performance of TMOPFN with the following state-of-the-art tensor and non-tensor-based frameworks: tensor fusion network (TFN) [24], low-rank multimodal fusion network (LMF) [27], multimodal factorization model (MFM) [35], memory fusion network (MFN) [8], multi-attention recurrent network (MARN) [34], and hierarchical polynomial fusion network (HPFN) [29], as well as transformer-based and graph-based models.
For all baselines and our proposed TMOPFN, the grid-search is performed over the hyper-parameters to select the model with the best validation classification or regression loss, and the models are then tested on the testing trials. The models are trained using the Adam optimizer [52], and the training duration of the models is governed by an early stopping strategy with patience of 6 to 20 epochs. The splits of the training, validation, and testing trials (sets) are exactly the same for all models. Furthermore, all the baselines include the same number of trails. Additionally, all of the experiments are performed independent of the speaker, where no speaker is shared between training, validation, and testing trails. For all models, the trials splits of three benchmarks ([training trails, validation trails, testing trails]) are summarized as follows: IEMOCAP [6373, 1775, 1807], CMU-MOSI [1284, 229, 686], CMU-MOSEI [15, 290, 2291, 4832]. Moreover, we also used five-fold cross-validation in our work.
Implementation details of TMOPFN. Based on LMF [27], we use a low-rank CP network to compress the weight tensor of MOPTP. The candidate CP ranks are . Due to the property of element-wise multiplication, the value of output presentation may be too small, raising a question on effectively performing classification tasks. In order to make the model numerically more stable, we could adopt power normalization (element-wise signed squared root) or normalization, which is similar to [53]. In this paper, the computing resources we leveraged to conduct corresponding experiments are several CPUs and GPUs. In detail, the CPUs are Intel(R) Core(TM) i9-10900X CPU @ 3.70 GHz, and the GPUs are GeForce RTX 3080. Additionally, we use PyTorch and python to implement all our experiments.
Model architectures and evaluation metrics. The proposed models are described in Table 1, including the new TMOPFN TMOPFN-L3-S1, TMOPFN-L3-S2, and TMOPFN-L3-S3. Furthermore, the corresponding model complexity analysis is demonstrated in Table 2. As to the input of models, only tensor-based models attempt to perform the multimodal fusion on the tensor input, while the non-tensor-based models take the vector as input. Additionally, we report the model results with the following measure metrics: MAE = mean absolute error, Corr = Pearson correlation, Acc-2 = accuracy across two classes, Acc-7 = accuracy across seven classes, and F1 = F1 score. For a fair comparison, we follow ([24,27]) to report the above evaluation metrics. Specifically, the binary acc/F1 is calculated based on positive/negative sentiments. When the value of the label is larger than 0, the corresponding data are annotated with ‘positive sentiment’.

Table 1.
Specifications of network architecture of TMOPFN and MOPFN. MOPFN indicates that we replace the ’PTP’ with ’MOPTP’ in the original HPFN. [-] indicates the configuration of a specific layer. denotes the ‘m’th fused feature node in the layer ‘k’.

Table 2.
Comparison of model complexity for TFN, LMF and our TMOPFN. Specifically, is the length of output feature, M is the number of modalities, R is the tensor rank, [T, S] is the local ’window’ size with , and indicates the dimension of message from modality m at time t. The amount of parameters of the L-layer TMOPFN is linearly related to the total number of MOPTP ’windows’ , where is the number of ‘windows’ at layer . Actually, is small and decreasing along layers, e.g., . Generally, the parameter of TMOPFN is larger than or comparable to LMF, but significantly less than that of TFN.
Performance comparison with state-of-the-art models. First, we analyze the baselines that focus on sentiment analysis and emotion recognition tasks. The bottom rows in Table 3 show the best performance of our model. It is obvious that our model surpasses the existing models in most of the metrics. Please note that the proposed TMOPFN outperforms the previous HPFN, which demonstrates the effectiveness of the operation MOPTP and the tree-based structure. Particularly, on the sentiment task, our ’TMOPFN-L3-S2, 2 subspaces’ exceeds the previous best MFM on the metric ‘Acc-7’ with an improvement of . The overall best performance is received by ’TMOPFN-L3-S1, 2 subspaces’ on the metric ‘MAE’. This implies that the tree-based structure is able to highlight the multi-level sentiment properties via the parallel procedure. It is important to note that, our ’TMOPFN-L1, 2 subspaces’ achieves the best performance on ‘Corr’, ‘Acc-2’ and ‘F1’. This implies the superior expressive capability of MOPTP that attempts to further capture the more discriminative sentiment properties among multiple representation subspaces. The results of the number of modalities are demonstrated in (Table 4). Furthermore, we further investigate the performance of transformer-based and graph-based models which recently have exhibited great expressive power in multimodal learning. As shown in Table 5 and Table 6, we observe that our model can still obtain state-of-the-art or competitive performance, implying the superiority of our work. In particular, TMOPFN exceeds the other models by a significant margin of 5.4 on ‘Acc-7’. This demonstrates that TMOPFN is capable of effectively investigating the discriminative sentiment properties with the help of ‘MOPTP’ and tree-based framework. Additionally, we also report the UA+WA (Table 7) and the variance and standard deviation of TMOPFN (Table 8). The results demonstrate the robustness of the proposed model.

Table 3.
Results for sentiment analysis on CMU-MOSI & CMU-MOSEI and emotion recognition on IEMOCAP.

Table 4.
Results for number of modalities on CMU-MOSI & CMU-MOSEI and emotion recognition on IEMOCAP.

Table 5.
Performance of Transformer-based model, Graph-based model and TMOPFN on CMU-MOSI.

Table 6.
Performance of Transformer-based model, Graph-based model and TMOPFN on IEMOCAP.

Table 7.
The UA (unweighted accuracy) and WA (weighted accuracy) of TMOPFN on CMU-MOSI, CMU-MOSEI and IEMOCAP.

Table 8.
The mean, variance and standard deviation of TMOPFN on CMU-MOSI, CMU-MOSEI and IEMOCAP. Please note that each performance metric is executed for 5 times (5-fold cross validation).
5.2. Experimental Results
Effect of the order of multimodal sentiment subspace. In our work, our MOPTP is proposed to capture sentiment properties among multiple representation subspaces with varying orders. Hence, in this part, we attempt to analyze the correlation between order and emotion. For simplicity, the test setting is ’TMOPFN-L1, 1 subspace’, where the multimodal representation is non-temporal that is obtained by averaging along the temporal domain. The ‘1 subspace’ indicates that ‘TMOPFN’ is only associated with a single fix-order representation subspace. The order of the corresponding subspace is denoted by which ranges from 1 to 9. As shown in Figure 6, ’TMOPFN-L1, 1 subspace’ can obtain competitive performance with respect to the specified orders. We can observe that ’TMOPFN-L1, 1 subspace’ reaches the peak value at order 4 on the CMU-MOSI dataset. As to the IEMOCAP dataset, it is important to note that the best performance is received at the order of 3 in the ‘neutral’ emotion, while the other emotions reach the highest point at the order that varies from 6 to 8. Indeed, ‘neutral’ is a kind of straightforward emotion, and may only need to search for the relatively simple or general properties among multiple modalities from the low-order feature space, i.e., the low-order multimodal fusion space is comprised of low-level interactions that refer to the general properties of ‘Neutral’, leading to the good performance of the recognition task. This is quite analogous to the process of the shallow network. In contrast, ‘Angry’, ‘Happy’, and ‘Sad’ are relative strong emotions, and those emotions may attempt to exploit the sophisticated properties from high-order space. In other words, the high-order polynomial space consists of much more polynomial terms, and each term corresponds to a local intercorrelation among multiple modalities. Then, employing the operation block associated with a high-order representation space to recognize the strong emotion. This allows us to effectively integrate comprehensive local interactions into the sophisticated global one.
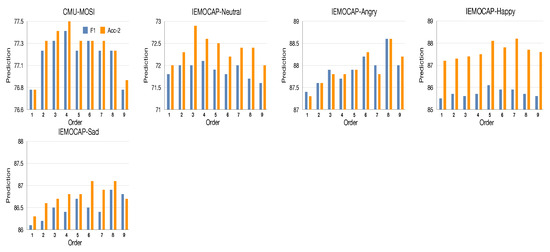
Figure 6.
Results of the effect of orders of multimodal sentiment subspace on IEMOCAP and CMU-MOSI. The fusion operation is associated with single fix-order sentiment subspace.
Effect of the subspace number of mixed-order polynomial fusion (MOPTP). Based on the high-order block, we extend the original operation (PTP) to the mixed-order case (MOPTP), which allows us to adaptively activate the discriminative sentiment properties among representation subspaces with varying orders. Hence, we are interested in examining how various subspaces associated with distinct orders influence the predictive results. For simplicity, the testing architecture is TMOPFN-L1, where the non-temporal multimodal presentation is retrieved by averaging along the temporal domain. The number of subspaces ranges from 1 to 9, where the setting means that corresponding MOPTP includes 1-order and 2-order representation subspaces.
In Figure 7, TMOPFN-L1, is able to achieve fairly good performance with respect to the representation subspaces. Compared to the performance demonstrated in Figure 6, MOPTP outperforms the fixed-order manner, which indicates the necessity and effectiveness of activating the discriminative sentiment properties among representation subspaces with varying orders. In particular, our model reaches the peak value at the subspace of 3 and 2 in the ‘neutral’ and ‘happy’ emotions, while the other emotions maximize the performance at the subspace of 7 and 8 on IEMOCAP. Actually, ‘angry’ and ‘sad’ are relative negative emotion that is comprised of more complex sentiment properties. Therefore, we need to exploit the sophisticated sentiment message that includes the comprehensive sentiment granularity within the receptive ‘window’. Actually, the relative low-order sentiment subspace consists of the coarse-grained sentiment characteristics, and the high-order sentiment subspace is comprised of the fine-grained sentiment properties. Essentially, in the ‘happy’ emotion, the setting (Figure 7) exceeds the 1-order and 2-order based settings (Figure 6). Moreover, the fixed-order manner reaches the highest point at order 5, while ‘MOPTP’ maximizes the performance only at subspace 2. Since ‘happy’ is a kind of positive emotion, which may only require explicit or general sentiment properties highlighted from the ‘window’. Compared to the fixed-order manner, ‘MOPTP’ focuses on highlighting the more discriminative sentiment properties between ‘1-order subspace’ and ‘2-order subspace’. Note that the above two low-order subspaces include distinct general sentiment properties. This may contribute to a more comprehensive general message, and bring forth the improvement of expressive power. Hence, ‘MOPTP’ is able to exceed fixed-order manner only with the integration of low-order representation subspaces.
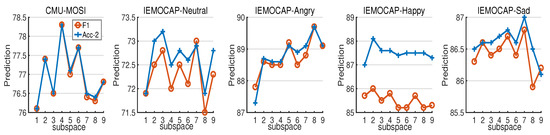
Figure 7.
Results of the effect of mixed-order sentiment subspaces on IEMOCAP and CMU-MOSI. The fusion operation is associated with multiple mixed-order sentiment subspaces (MOPTP).
Effect of the depth and tree-based structure. Due to the flexibility of our proposed model, we attempt to compare our new proposed TMOPFN with a series of HPFN variants. For simplicity, the test is performed on the non-temporal multimodal representation. Considering the impact of depth, the validation models are: HPFN-L1, HPFN-L2, HPFN-L3 and HPFN-L4. Furthermore, our TMOPFN also serve as the testing case: TMOPFN-L3-S1, TMOPFN-L3-S2, TMOPFN-L3-S3. In Table 9, we observe that two-layer- and three-layer-based frameworks achieve better overall performance than both one-layer and four-layer case. Thanks to the hierarchical architecture and recursive learning strategy, the local intercorrelations of the previous layer can be easily transmitted to the next layer. Therefore, the relative deeper model consists of comprehensive sentiment properties, which naturally outperform the shallow one (i.e., one-layer case). However, the four-layer-based network contains too much redundancy that may overlook the presence of the core message. In particular, TMOPFN-L3-S3 reaches the best precision on almost all metrics. Compared to the sequential hierarchical architecture of HPFN, TMOPFN could leverage multiple fusion strategies at the same network layer simultaneously, leading to multi-level sentiment properties. Compared to the rest of tree-based networks, TMOPFN-L3-S3 employs the segmentation fusion strategy to analyze the data. Consequently, each modality could serve as the backbone and guide the fusion procedure in turn, contributing to the exhaustive multimodal fusion representation.

Table 9.
Results of TMOPFN and HPFN on non-temporal multimodal features regarding the depth and dense connectivity.
Effect of skip operation. In this test, we attempt to assess how skip operation affects the architecture performance. For simplicity, we validate only on the following cases: HPFN-L2-based and TMOPFN-L3-based. In Table 9, we find that TMOPFN-L3-S3 achieves the best performance on almost all metrics. Compared to TMOPFN-L3-S3, HPFN-L2-S1 and HPFN-L2-S2 only directly absorb the original modality from the preceding layer, where unimodality does not serve as the backbone and guide the multimodal fusion process. Additionally, TMOPFN-L3-S1 only pays close attention to the text modality and overlooks the importance of audio and video modality. Actually, employing audio or video modality to guide the fusion procedure allows for much more complementarity and consistency among multiple modalities. Essentially, TMOPFN-L3-S3 involves much more ‘window’, and each ‘window’ focuses on exploiting the corresponding sentiment properties from the same preceding ‘2D map’, leading to multi-level multimodal properties. In conclusion, adopting skip operation would help to incorporate additional knowledge captured from the preceding layer, allowing for superior expressive power.
Effect of the temporal domain. The aforementioned experiments are performed on the non-temporal multimodal presentation, lacking the analysis of the temporal domain. In this part, we are interested to investigate how the temporal domain affects the model performance. The temporal TMOPFN-L2 is applied with a scanning ‘window’ at the input layer, where the size is and the stride step is set as 2 along the temporal domain. Initially, we employ the ‘MOPTP’ to cope with the modality representation within the scanning ‘window’ along the temporal dimension. As shown in Figure 8, compared to the weight-shared cases, the non-weight-shared model seems to receive comparable or relative higher performance. Actually, the share strategy may peel off the dynamic dependency of multimodal interactions along the temporal domain. Hence, sharing the same ‘MOPTP’ to various small ‘windows’ may do not bring forth additional improvement of task performance. As to the non-weight-shared models, it is interesting to find that there is a general upward trend in the size of ‘window’. This may imply that a large ‘window’ is comprised of much more common pattern among multiple modalities, as well as the intra-modal and inter-modal temporal consistency. Therefore, employing the non-share strategy may further exploit the latent temporal consistency and common associations among multiple modalities, and boost the task performance.
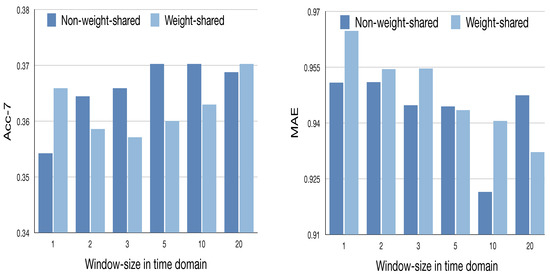
Figure 8.
Results of the effect of window-size in temporal domain on CMU-MOSI. The validation framework is TMOPFN-L2.
Effect of the ‘PTP’ and ‘MOPTP’ on various TMOPFN and MOPFN architecture. Based on different design strategies, the original one-layer MOPFN architecture is extended to distinct variants.
Meanwhile, as ‘MOPTP’ plays a key role in our work, we are interested to investigate the specific impact of ‘MOPTP’ on various TMOPFN and MOPFN architectures (as shown in Figure 9 and Figure 10). Specifically, the number of fix-order subspaces ranges from 2 to 5. For simplicity, we only demonstrate the TMOPFN and MOPFN cases that exhibit the best performance. Moreover, we also compared the new fusion operation ‘MOPTP’ with the original ‘PTP’ on the same TMOPFN and MOPFN frameworks. To focus on the effect of ‘MOPTP’ on the depth, we only validate the proposed architectures on the non-temporal multimodal data. The validation models are MOPFN-L1, MOPFN-L2, MOPFN-L2-S1, MOPFN-L2-S2, MOPFN-L3 and MOPFN-L4. We also validate the ‘MOPTP’ on the new proposed tree-based multimodal fusion frameworks: TMOPFN-L3-S1, TMOPFN-L3-S2, TMOPFN-L3-S3.
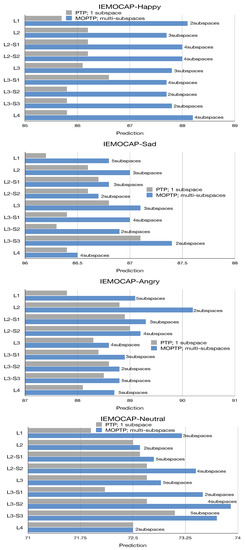
Figure 9.
Results on predictions of ‘PTP’ and ‘MOPTP’ on IEMOCAP. Specifically, the ‘n subspaces’ attached to the blue bar indicates a MOPTP with n high-order subspaces.
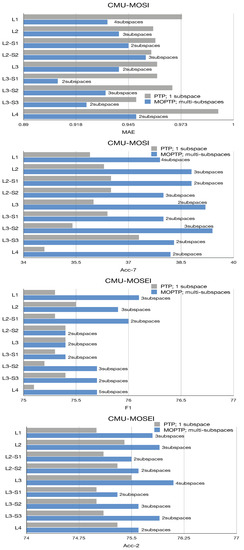
Figure 10.
Results on predictions of ‘PTP’ and ‘MOPTP’ on MOSI and MOSEI.
Generally, ‘MOPTP’ outperforms ‘PTP’ on all TMOPFN and MOPFN architectures, which demonstrates the superiority of ‘MOPTP’ in processing multiple modalities. In other words, the result indicates the necessity of further activating the discriminative sentiment properties among representation subspaces with varying orders. In particular, we observe that ‘MOPTP’ exceeds ‘PTP’ by a significant margin on ‘Happy’ and ‘Neutral’ emotions on TMOPFN architecture (TMOPFN-L3-S1, TMOPFN-L3-S2, TMOPFN-L3-S3). Indeed, ‘Happy’ and ‘Neutral’ are relatively positive emotions and may require the comprehensive explicit properties highlighted by the multimodal information. Note that tree-based architecture allows us to capture multi-level sentiment properties from the same ‘2D feature map’ simultaneously. Therefore, associating ‘MOPTP’ with the ‘TMOPFN’ can further boost the expressive capability of ‘MOPTP’, leading to the good performance of the positive emotion analysis tasks.
It is important to find that the TMOPFN and MOPFN variants associated with the skip operation receive good performance in ‘happy’ and ‘neutral’, when the number of fix-order sentiment subspaces is relatively large. Actually, the skip operation allows for original or additional information captured from the preceding layer. Therefore, applying ‘MOPTP’ that consists of much more representation subspaces to the next process layer allows us to make full use of the additional information of the preceding layer. Then, the message of the preceding and next layer could be fused efficiently by exploiting more discriminative sentiment properties among representation subspaces.
On the CMU-MOSI dataset, it is important to find that ‘MOPTP’ outperforms ‘PTP’ by a large margin on all the TMOPFN and MOPFN frameworks. This may demonstrate the superiority and effectiveness of ‘MOPTP’ in the emotion recognition tasks. Compared to ‘PTP’ which only considers a single representation subspace with a specific order, ‘MOPTP’ consists of multiple representation subspaces with varying orders. As mentioned before, each fixed-order representation subspace includes corresponding sentiment properties. For instance, the relative low-order subspace includes coarse-grained sentiment properties that correspond to explicit interaction among multiple modalities. The high-order subspace consists of fine-grained sentiment properties that correspond to implicit interaction. Therefore, ‘PTP’ only can obtain the local optimal sentiment properties from the single representation subspace. In contrast, ‘MOPTP’ attempts to adaptively activate more discriminative sentiment properties among representation subspaces with varying orders, resulting in the significant improvement of expressive capability.
Effect of the adaptive activation function. In this part, we are interested to investigate how distinct activation function influence the performance of ‘MOPTP’. Specifically, we designed two effective activation functions which include identity function and the piecewise functions. As shown in Figure 11, we observe that the ‘identity function’ outperforms the ‘piecewise function’ by a large margin in ‘happy’ emotion. Indeed, ‘happy’ is a kind of relative positive emotion that consists of explicit sentiment properties. Thus, we need to capture the comprehensive explicit knowledge for the ‘happy’ analysis task. In addition, the ‘identity function’ attempts to temperately integrate the information from distinct representation subspaces without destroying the consistency of each subspace, i.e., ‘identity function’ allows us to capture coarse-grained sentiment characteristics and fine-grained sentiment properties simultaneously, leading to a much more expressive representation. In contrast, the ‘piecewise function’ focuses on the most essential context of each representation subspace, which may damage the consistency within the same representation subspace. Therefore, when employing a ‘piecewise function’ to analyze ‘happy’ emotion, the final representation may only include the fine-grained sentiment properties. Furthermore, the corresponding coarse-grained sentiment properties is missed. In particular, we can find that the ‘piecewise function’ exceeds the ‘identity function’ on ‘angry’. Actually, ‘angry’ is a strong negative emotion that is comprised of much more complex sentiment properties. Please note that the ‘piecewise function’ can integrate all the essential sentiment properties into the more sophisticated representation, leading to good performance in the ‘angry’ classification task. In Figure 12, we also find that ‘identity function’ outperforms ‘piecewise function’ on CMU-MOSI dataset. In conclusion, various activation function helps us to activate the potential sentiment properties among multiple modalities, which can further boost the performance of multimodal sentiment analysis task.
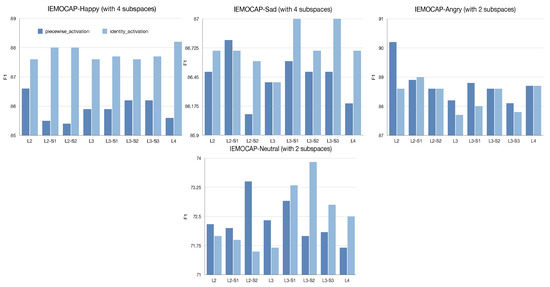
Figure 11.
Results on predictions w.r.t activation method on IEMOCAP.
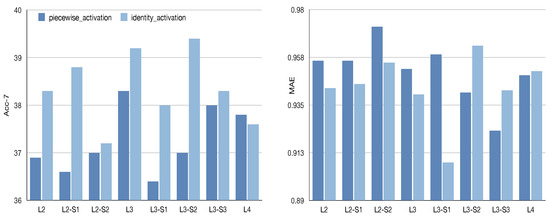
Figure 12.
Results on predictions w.r.t activation method on CMU-MOSI. The MOPTP is associated with two high-order subspaces.
Comparison of 2D/3D DenseNet and TMOPFN. Since the TMOPFN is proposed based on ConvAC, and given the stark similarity between ConvAC and CNN, we employ the 2D and 3D DenseNet to analyze multiple modalities based on the same input of Equation (3). The detailed performance is demonstrated in Table 10. As shown in Table 10, we observe that our proposed model outperforms 2D/3D DenseNet by a large margin, which demonstrates the superiority and effectiveness of MOPTP and tree-based structure. Particularly, on the sentiment task, our TMOPFN exceeds 3D-DenseNet on the metric ‘Acc-7’ with an improvement of 10.4%. Essentially, compared to our TMOPFN, 2D/3D DenseNet is comprised of a large number of model parameters. Compared to 2D/3D DenseNet which only considers a single low-order representation subspace, ‘MOPTP’ consists of multiple representation subspaces with varying orders. The relative low-order representation subspace is comprised of coarse-grained sentiment characteristics, allowing for general and low-level sentiment knowledge. Therefore, 2D/3D DenseNet may is not applicable to effectively exploit comprehensive sentiment characteristics within the feature map. In contrast, ‘MOPTP’ focuses on underlining the more discriminative sentiment properties among multiple representation subspaces. This indeed contributes to the more comprehensive and discriminative sentiment message and brings forth the significant improvement of expressive capability.

Table 10.
Comparison of 2D/3D DenseNet and TMOPFN on CMU-MOSI and IEMOCAP.
6. Conclusions
In this paper, we proposed a mixed-order polynomial tensor pooling block (MOPTP) for adaptively activating the more discriminative sentiment properties among representation subspaces with varying orders. This indeed provides much more capability to effectively obtain global optimal performance in the multimodal sentiment analysis task. Treating MOPTP as the basic component, we further established a tree-based mixed-order polynomial fusion network (TMOPFN), which allows for using multiple sentiment analysis strategies at the same network layer simultaneously. Indeed, this naturally provides us with the great benefit of exploiting multi-level and sophisticated sentiment properties via the parallel procedure.
An earlier version of this paper was presented at the Thirty-third Conference on Neural Information Processing Systems, Vancouver CANADA, 2019.
(1) In this version, we propose a new mixed-order polynomial tensor pooling manner (MOPTP) as the building block of our framework. The original operation ‘PTP’ only focuses on the analysis of a specific N-order representation space with a fixed order. This may result in the local optimal performance of the multimodal sentiment analysis model. In contrast, ‘MOPTP’ is capable of adaptively activating the much more discriminative sentiment properties among representation subspaces with varying orders. This can effectively integrate multiple local sentiment properties into the more discriminative one, leading to the relatively global optimal performance.
(2) Furthermore, we propose a new framework ‘TMOPFN’: , and . Compared to the original sequential framework, ‘HPFN’, ‘TMOPFN’ allows for using multiple sentiment analysis strategies on the same network layer simultaneously. Indeed, this naturally provides us the great benefit of capturing multi-level sentiment properties via the parallel procedure.
(3) Additionally, a new multimodal dataset (MOSEI dataset) is introduced in this work, and we verified the new manner (MOPTP) on three multimodal datasets. Various experiments demonstrate that our new proposed model can exceed the best performance of the original version. Furthermore, our new model can achieve state-of-the-art or competitive results compared to the baselines, which indicates the superiority and effectiveness of MOPTP and TMOPFN. The code will be posted on Github later.
Author Contributions
Conceptualization, J.T.; methodology, J.T. and M.H.; software, J.T.; formal analysis, J.T., M.H., X.J., J.Z. and Q.Z.; writing—original draft preparation, J.T.; writing—review and editing, J.T., M.H., X.J., J.Z. and Q.Z.; visualization, J.T. and X.J.; supervision, W.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key R&D Program of China for Intergovernmental International Science and Technology Innovation Cooperation Project (No. 2017YFE0116800), Key Research and Development Project of Zhejiang Province (No. 2023C03026, No. 2021C03001, No. 2021C03003), JSPS KAKENHI (No. 20H04249, No. 20H04208), National Natural Science Foundation of China (No. U20B2074, No. U1909202, No. 62071132), and supported by Key Laboratory of Brain Machine Collaborative Intelligence of Zhejiang Province (No. 2020E10010).
Data Availability Statement
The data presented in the study are available on request from the first author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shoumy, N.J.; Ang, L.M.; Seng, K.P.; Rahaman, D.M.; Zia, T. Multimodal big data affective analytics: A comprehensive survey using text, audio, visual and physiological signals. J. Netw. Comput. Appl. 2020, 149, 102447. [Google Scholar] [CrossRef]
- Yu, Y.; Kim, Y.J. Attention-LSTM-attention model for speech emotion recognition and analysis of IEMOCAP database. Electronics 2020, 9, 713. [Google Scholar] [CrossRef]
- Rahman, W.; Hasan, M.K.; Lee, S.; Zadeh, A.; Mao, C.; Morency, L.P.; Hoque, E. Integrating multimodal information in large pretrained transformers. In Proceedings of the Conference Association for Computational Linguistics, Online, 6–8 July 2020; Volume 2020, p. 2359. Available online: https://aclanthology.org/2020.acl-main.214/ (accessed on 20 December 2022).
- Yadav, A.; Vishwakarma, D.K. Sentiment analysis using deep learning architectures: A review. Artif. Intell. Rev. 2020, 53, 4335–4385. [Google Scholar] [CrossRef]
- Peng, Y.; Qin, F.; Kong, W.; Ge, Y.; Nie, F.; Cichocki, A. GFIL: A unified framework for the importance analysis of features, frequency bands and channels in EEG-based emotion recognition. IEEE Trans. Cogn. Dev. Syst. 2021, 14, 935–947. [Google Scholar] [CrossRef]
- Lai, Z.; Wang, Y.; Feng, R.; Hu, X.; Xu, H. Multi-Feature Fusion Based Deepfake Face Forgery Video Detection. Systems 2022, 10, 31. [Google Scholar] [CrossRef]
- Shen, F.; Peng, Y.; Dai, G.; Lu, B.; Kong, W. Coupled Projection Transfer Metric Learning for Cross-Session Emotion Recognition from EEG. Systems 2022, 10, 47. [Google Scholar] [CrossRef]
- Zadeh, A.; Liang, P.P.; Mazumder, N.; Poria, S.; Cambria, E.; Morency, L.P. Memory fusion network for multi-view sequential learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 2–3 February 2018. [Google Scholar]
- Chandrasekaran, G.; Antoanela, N.; Andrei, G.; Monica, C.; Hemanth, J. Visual Sentiment Analysis Using Deep Learning Models with Social Media Data. Appl. Sci. 2022, 12, 1030. [Google Scholar] [CrossRef]
- Atmaja, B.T.; Sasou, A. Sentiment Analysis and Emotion Recognition from Speech Using Universal Speech Representations. Sensors 2022, 22, 6369. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, W.; Li, Y.; Huang, S.L.; Zhang, L. Learning better representations for audio-visual emotion recognition with common information. Appl. Sci. 2020, 10, 7239. [Google Scholar] [CrossRef]
- Atmaja, B.T.; Sasou, A.; Akagi, M. Survey on bimodal speech emotion recognition from acoustic and linguistic information fusion. Speech Commun. 2022, 140, 11–28. [Google Scholar] [CrossRef]
- Liang, P.P.; Liu, Z.; Zadeh, A.B.; Morency, L.P. Multimodal language Analysis with recurrent multistage fusion. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 150–161. [Google Scholar]
- Boehm, K.M.; Khosravi, P.; Vanguri, R.; Gao, J.; Shah, S.P. Harnessing multimodal data integration to advance precision oncology. Nat. Rev. Cancer 2022, 22, 114–126. [Google Scholar] [CrossRef]
- Liang, P.P.; Lim, Y.C.; Tsai, Y.H.H.; Salakhutdinov, R.; Morency, L.P. Strong and simple baselines for multimodal utterance embeddings. arXiv 2019, arXiv:1906.02125. [Google Scholar]
- Bayoudh, K.; Knani, R.; Hamdaoui, F.; Mtibaa, A. A survey on deep multimodal learning for computer vision: Advances, trends, applications, and datasets. Vis. Comput. 2022, 38, 2939–2970. [Google Scholar] [CrossRef]
- Poria, S.; Cambria, E.; Bajpai, R.; Hussain, A. A review of affective computing: From unimodal analysis to multimodal fusion. Inf. Fusion 2017, 37, 98–125. [Google Scholar] [CrossRef]
- Sharma, K.; Giannakos, M. Multimodal data capabilities for learning: What can multimodal data tell us about learning? Br. J. Educ. Technol. 2020, 51, 1450–1484. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, Z.; Chen, P.; Nichele, S. Emotion recognition using multi-modal data and machine learning techniques: A tutorial and review. Inf. Fusion 2020, 59, 103–126. [Google Scholar] [CrossRef]
- Mai, S.; Hu, H.; Xu, J.; Xing, S. Multi-fusion residual memory network for multimodal human sentiment comprehension. IEEE Trans. Affect. Comput. 2020, 13, 320–334. [Google Scholar] [CrossRef]
- Li, Q.; Gkoumas, D.; Lioma, C.; Melucci, M. Quantum-inspired multimodal fusion for video sentiment analysis. Inf. Fusion 2021, 65, 58–71. [Google Scholar] [CrossRef]
- Li, W.; Zhu, L.; Shi, Y.; Guo, K.; Cambria, E. User reviews: Sentiment analysis using lexicon integrated two-channel CNN–LSTM family models. Appl. Soft Comput. 2020, 94, 106435. [Google Scholar] [CrossRef]
- Chen, L.; Li, S.; Bai, Q.; Yang, J.; Jiang, S.; Miao, Y. Review of image classification algorithms based on convolutional neural networks. Remote Sens. 2021, 13, 4712. [Google Scholar] [CrossRef]
- Zadeh, A.; Chen, M.; Poria, S.; Cambria, E.; Morency, L.P. Tensor fusion network for multimodal sentiment analysis. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 9–11 September 2017; pp. 1103–1114. [Google Scholar]
- Zhang, Y.; Cheng, C.; Wang, S.; Xia, T. Emotion recognition using heterogeneous convolutional neural networks combined with multimodal factorized bilinear pooling. Biomed. Signal Process. Control 2022, 77, 103877. [Google Scholar] [CrossRef]
- Wang, J.; Ji, Y.; Sun, J.; Yang, Y.; Sakai, T. MIRTT: Learning Multimodal Interaction Representations from Trilinear Transformers for Visual Question Answering. In Proceedings of the Findings of the Association for Computational Linguistics: EMNLP 2021, Punta Cana, Dominican Republic, 16–20 November 2021; pp. 2280–2292. [Google Scholar]
- Liu, Z.; Shen, Y.; Lakshminarasimhan, V.B.; Liang, P.P.; Zadeh, A.B.; Morency, L.P. Efficient low-rank multimodal fusion with modality-specific factors. In Proceedings of the Annual Meeting of the Association for Computational Linguistics, Melbourne, Australia, 15–20 July 2018; pp. 2247–2256. [Google Scholar]
- Choi, D.Y.; Kim, D.H.; Song, B.C. Multimodal attention network for continuous-time emotion recognition using video and EEG signals. IEEE Access 2020, 8, 203814–203826. [Google Scholar] [CrossRef]
- Hou, M.; Tang, J.; Zhang, J.; Kong, W.; Zhao, Q. Deep multimodal multilinear fusion with high-order polynomial pooling. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 12136–12145. [Google Scholar]
- Huan, R.H.; Shu, J.; Bao, S.L.; Liang, R.H.; Chen, P.; Chi, K.K. Video multimodal emotion recognition based on Bi-GRU and attention fusion. Multimed. Tools Appl. 2021, 80, 8213–8240. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Khalid, H.; Gorji, A.; Bourdoux, A.; Pollin, S.; Sahli, H. Multi-view CNN-LSTM architecture for radar-based human activity recognition. IEEE Access 2022, 10, 24509–24519. [Google Scholar] [CrossRef]
- Poria, S.; Cambria, E.; Hazarika, D.; Majumder, N.; Zadeh, A.; Morency, L.P. Context-dependent sentiment analysis in user-generated videos. In Proceedings of the Annual Meeting of the Association for Computational Linguistics, Vancouver, BC, Canada, 30 July–4 August 2017; pp. 873–883. [Google Scholar]
- Zadeh, A.; Liang, P.P.; Poria, S.; Vij, P.; Cambria, E.; Morency, L.P. Multi-attention recurrent network for human communication comprehension. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 2–3 February 2018. [Google Scholar]
- Tsai, Y.H.; Liang, P.P.; Zadeh, A.; Morency, L.; Salakhutdinov, R. Learning Factorized Multimodal Representations. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Sahay, S.; Okur, E.; Kumar, S.H.; Nachman, L. Low Rank Fusion based Transformers for Multimodal Sequences. arXiv 2020, arXiv:2007.02038. [Google Scholar]
- Huang, F.; Wei, K.; Weng, J.; Li, Z. Attention-based modality-gated networks for image-text sentiment analysis. ACM Trans. Multimed. Comput. Commun. Appl. (TOMM) 2020, 16, 1–19. [Google Scholar] [CrossRef]
- Mai, S.; Xing, S.; He, J.; Zeng, Y.; Hu, H. Analyzing Unaligned Multimodal Sequence via Graph Convolution and Graph Pooling Fusion. arXiv 2020, arXiv:2011.13572. [Google Scholar]
- Yang, J.; Wang, Y.; Yi, R.; Zhu, Y.; Rehman, A.; Zadeh, A.; Poria, S.; Morency, L.P. MTGAT: Multimodal Temporal Graph Attention Networks for Unaligned Human Multimodal Language Sequences. arXiv 2020, arXiv:2010.11985. [Google Scholar]
- Chen, J.; Zhang, A. HGMF: Heterogeneous Graph-based Fusion for Multimodal Data with Incompleteness. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 1295–1305. [Google Scholar]
- Hong, D.; Kolda, T.G.; Duersch, J.A. Generalized canonical polyadic tensor decomposition. SIAM Rev. 2020, 62, 133–163. [Google Scholar] [CrossRef]
- Little, A.; Xie, Y.; Sun, Q. An analysis of classical multidimensional scaling with applications to clustering. Inf. Inference J. IMA 2022. [Google Scholar] [CrossRef]
- Reyes, J.A.; Stoudenmire, E.M. Multi-scale tensor network architecture for machine learning. Mach. Learn. Sci. Technol. 2021, 2, 035036. [Google Scholar] [CrossRef]
- Phan, A.H.; Cichocki, A.; Uschmajew, A.; Tichavskỳ, P.; Luta, G.; Mandic, D.P. Tensor networks for latent variable analysis: Novel algorithms for tensor train approximation. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4622–4636. [Google Scholar] [CrossRef] [PubMed]
- Asante-Mensah, M.G.; Ahmadi-Asl, S.; Cichocki, A. Matrix and tensor completion using tensor ring decomposition with sparse representation. Mach. Learn. Sci. Technol. 2021, 2, 035008. [Google Scholar] [CrossRef]
- Zhao, M.; Li, W.; Li, L.; Ma, P.; Cai, Z.; Tao, R. Three-order tensor creation and tucker decomposition for infrared small-target detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Zadeh, A.; Zellers, R.; Pincus, E.; Morency, L.P. MOSI: Multimodal corpus of sentiment intensity and subjectivity analysis in online opinion videos. arXiv 2016, arXiv:1606.06259. [Google Scholar]
- Zadeh, A.B.; Liang, P.P.; Poria, S.; Cambria, E.; Morency, L.P. Multimodal language analysis in the wild: Cmu-mosei dataset and interpretable dynamic fusion graph. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, Melbourne, Australia, 15–20 July 2018; Volume 1, Long Papers. pp. 2236–2246. [Google Scholar]
- Zhang, H. The Prosody of Fluent Repetitions in Spontaneous Speech. In Proceedings of the 10th International Conference on Speech Prosody 2020, Hong Kong, China, 25–28 May 2020; pp. 759–763. [Google Scholar]
- Kamyab, M.; Liu, G.; Adjeisah, M. Attention-based CNN and Bi-LSTM model based on TF-IDF and glove word embedding for sentiment analysis. Appl. Sci. 2021, 11, 11255. [Google Scholar] [CrossRef]
- Khalane, A.; Shaikh, T. Context-Aware Multimodal Emotion Recognition. In Proceedings of the International Conference on Information Technology and Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 51–61. [Google Scholar]
- Melinte, D.O.; Vladareanu, L. Facial expressions recognition for human–robot interaction using deep convolutional neural networks with rectified adam optimizer. Sensors 2020, 20, 2393. [Google Scholar] [CrossRef]
- Hashemi, A.; Dowlatshahi, M.B. MLCR: A fast multi-label feature selection method based on K-means and L2-norm. In Proceedings of the 2020 25th International Computer Conference, Computer Society of Iran (CSICC), Tehran, Iran, 1–2 January 2020; pp. 1–7. [Google Scholar]
- Xia, H.; Yang, Y.; Pan, X.; Zhang, Z.; An, W. Sentiment analysis for online reviews using conditional random fields and support vector machines. Electron. Commer. Res. 2020, 20, 343–360. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, Z.; He, X.; Deng, L. Multimodal intelligence: Representation learning, information fusion, and applications. IEEE J. Sel. Top. Signal Process. 2020, 14, 478–493. [Google Scholar] [CrossRef]
- Lian, Z.; Liu, B.; Tao, J. CTNet: Conversational Transformer Network for Emotion Recognition. IEEE/ACM Trans. Audio, Speech, Lang. Process. 2021, 29, 985–1000. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).