Abstract
To study the effect of the local corrosion of prestressed steel strands on the shear failure mode and shear bearing capacity of concrete beams, unilateral steel strands in four post-tensioning prestressed concrete (PC) beams are corroded, and the shear test of four PC beams are performed. Moreover, a simplified calculation method for the shear bearing capacity of concrete beams with diagonal steel bars is proposed considering the effect of cross-sectional reduction of steel bars, the degradation of mechanical properties, and the cross-sectional damage of concrete. Results shows that the crack propagation mode and failure mode are unrelated to the corrosion of prestressed steel bars when the shear span ratio of beam is the same. The shear capacity of the beam decreases with the increase of corrosion rate, but the decreasing rate is lower than the increasing rate of the corrosion rate. The growth rate of stirrup stress is much greater than that of load after concrete tension and compression loss cracking, and the yield of stirrup can be used as a sign of the ultimate bearing capacity of the beam. In addition, by comparing the experimental and numerical simulation results, the proposed simplified calculation method for the shear bearing capacity of concrete beams is of high accuracy.
1. Introduction
Post-tensioning and pre-tensioning are the two most commonly used technologies for tensioning prestressed steel tendons in concrete structures [1]. Compared with pre-tensioning PC structures, post-tensioning PC structures have better structural performance and are more suitable for the curved arrangement of steel tendons in long-span structures [2]. As a result, post-tensioning PC structures has become the most widely used structural form in long-span bridge construction. However, with the increase of service time, various diseases such as corrosion of steel tendons, reduction of the effective area of steel tendons, and shedding of protective layers gradually appear [3,4,5]. This will not only lead to the degradation of structural safety performance but also reduce the normal service performance of the bridge [6,7]. Compared with bending failure, the shear failure of structure is mostly brittle, and there are almost no predictable symptoms. This means that the damage caused by the shear failure of corroded PC components is more serious [8,9]. Therefore, it is very important to study the degradation mechanism of shear mechanical properties of corroded PC structure and reasonably evaluate the residual shear capacity.
At present, some scholars have carried out research on the shear performance of corroded concrete structures, but they mainly focus on ordinary reinforced concrete (RC) specimens. For example, based on the bearing capacity test results of corroded reinforced concrete specimens, Ye [10] found that the structural shear strength decreased gradually with the increase of the corrosion degree of stirrups. Zhang [11] studied the corrosion-induced spalling of cover concrete and its effects on shear behavior of RC beams, and the results showed that both the concrete damage and bond degradation do not significantly affect the shear resistance of reinforced concrete beams at a small degree of corrosion. Based on the experimental and numerical analysis results, Huang [12] believed that the shear resistance of corroded RC beams in terms of initial stiffness, cracking load, ultimate bearing capacity, post-peak behavior and energy dissipation capacity is significantly degraded, and this degradation becomes more obvious with the increase of corrosion degree. Lu [13] studied the influence of different concrete strength grades and stirrup arrangement on the shear strength of RC structure, and found that the shear strength of structures is more sensitive to the change of stirrup yield strength. Compared with the RC structure, the stress characteristics of the PC structure and the elements that provide shear resistance inside the structure are significantly different, which leads to a more complex variation law of the shear resistance of the PC structure. Therefore, it is necessary to study the shear resistance of corroded PC structures.
To reasonably evaluate the shear performance of concrete structures, some scholars have proposed a calculation model of the shear capacity of corroded concrete members based on the experimental and theoretical analysis results. By refining the shear design model provided by American Concrete Institute (ACI), Soltani [14] proposed a model to estimate the reduced shear capacity for RC beams. Based on the modified compression field theory, Spinella [15] proposed a calculation model of the ultimate shear force of reinforced concrete beams with corroded stirrups. El-Sayed [16] presented a proposed design procedure for quantifying the residual shear strength of RC beams with corrosion-damaged stirrups. Da [17] developed a calculation model for the ultimate shear capacity of reinforced coral aggregate concrete beam by considering the influence of high-strength coral aggregate concrete and stirrup corrosion. Although the above models provide meaningful references for reasonably evaluating the degradation of shear capacity of corroded concrete structures, most of these models are proposed based on the assumption of uniform corrosion. In service concrete structures, the spatial variability of material properties, structural dimensions, and environmental parameters as well as grouting defects lead to uneven corrosion of steel strands, which makes the existing shear capacity calculation model no longer applicable. Therefore, it is necessary to further propose a shear capacity model that considers the effect of local corrosion of steel strands.
The main purpose of this paper is to study the change law of the shear capacity of PC structure considering the effect of local corrosion and to propose the corresponding theoretical calculation model. First, the crack development, failure mode, deflection change and ultimate bearing capacity development law are analyzed based on local corrosion test of PC member bearing capacity. Second, a simplified calculation model of shear capacity is proposed considering the effect of local corrosion of steel strands. Finally, the shear resistance of locally corroded PC structures is studied based on numerical simulations. Among them, studying the effect of local corrosion on the shear capacity of PC structures and proposing a calculation method of shear performance of PC structures considering the effect of local corrosion are the novelties of this paper.
2. Test Profile
A total of four post-tensioning PC beams, numbered as B1, B2, B3, and B4, are designed in this experiment. The test beams are 3000 mm in length and 160 mm × 450 mm in cross-sectional dimensions. The thickness of concrete cover is 30 mm. Prestressed tendons are made of seven wire twisted steel strands with a nominal diameter of 15.2 mm, and the controlled tensile stress is 1395 MPa. In addition, the 2Φ25 HRB400 reinforcing steel bars is used as ordinary tensile bars, 2Φ10 HRB400 steel bars are used as erection bars, and Φ6 HRB400 steel bars are selected as stirrups. The average measured cubic compressive strength of concrete is 42.2 MPa. The cross-sectional dimensions of test beams and the concrete layout of steel bars are shown in Figure 1, and the mechanical property parameters of ordinary and prestressed steel bars are presented in Table 1.
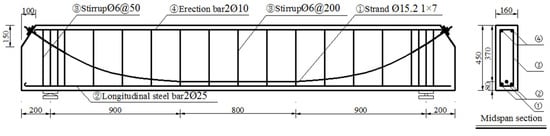
Figure 1.
Dimensions and reinforcement of test beams (unit: mm).

Table 1.
Mechanical parameters of steel strands and ordinary steel bars.
Among these test beams, the B1 beam is not corroded, while the bending-shear segment at the side of B2 to B4 beams are corroded by electrochemical rapid corrosion method. In this experiment, the 5% NaCl solution is adopted. After completing the rapid corrosion, the static load tests of all beams are carried out, as shown in Figure 2. As a result, the spacing between center lines of supports for simply supported beams is 2.6 m, the pure bending segment is 1.0 m, and the shear span ratio is 2.1. Here, the multi-stage loading method is implemented through a jack. The loading level of the test beam before cracking is 5 kN, and the loading level after cracking is adjusted to 10 kN. The loading rate above two processes are 5 kN/min. When the actual loading value is close to the ultimate load, the loading level is adjusted to 5 kN, and the loading rate at this time is set to 2 kN/min. Here, the loading is stopped when the concrete is crushed or unstable deformation occurs, and then the structure is considered to be damaged at this time. Finally, after the static load test, the corroded steel bars inside the structure were taken out, and the corrosion rate of steel strands is determined by using the relatively accurate sectional profile method [18]. The corrosion time and corrosion rate of steel strands in different beams are presented in Table 2.
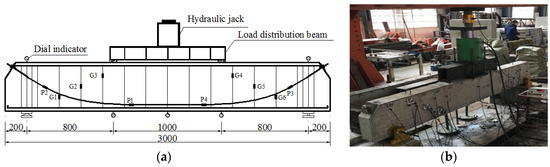
Figure 2.
Loading diagram and measuring point layout. (a) Loading and measuring point layout (unit: mm), (b) Loading photo.

Table 2.
Corrosion time and corrosion rate η.
3. Shear Performance Analysis
3.1. Crack Propagation
Although steel strands varied in corrosion rate, the crack propagation modes of test beams are basically consistent. Under the loading action, a vertical bending crack firstly appears in the pure bending segment between loading points. As the load continues to grow, multiple diagonal cracks pointing to loading points successively appear in the bending-shear segment at the corrosion treatment side, while diagonal cracks appear later at the side without corrosion treatment. Due to the difference between steel strands in corrosion rate, the cracking load of test beams is varied. The load value upon the appearance of the first bending crack and that upon the appearance of the first diagonal crack in B1–B4 are listed in Table 3. It could be seen that with the increase of corrosion rate, both the load upon the appearance of the first bending crack and that upon the appearance of the first diagonal crack in B1–B4 are gradually reduced, and both bending load and diagonal cracking load are inversely proportional to the change in corrosion rate. The more seriously the prestressed steel bars are corroded, the greater their effective cross-sectional area loss. The more serious the concrete bonding degradation, the greater the loss of the effective prestress, and the earlier the test beam cracked under the loading action. At the corrosion rate of 7.9%, 19.4%, and 31.7%, the loads leading to the initiation of bending crack and diagonal crack in test beams declines by 11.3%, 23.9%, and 40.8%, and 10%, 19% and 37.8%, respectively, in comparison with the uncorroded beam. This means that the bending crack is more sensitive to corrosion rate.

Table 3.
Main test results.
The crack distribution in B1–B4 under the ultimate load is given in Figure 3. For all test beams, the principal diagonal crack leading to the failure is a bending-shear crack, accompanied by avulsion phenomenon of longitudinal steel bars close to the beam bottom. The number of cracks in all test beams is within 11 to 12, the beam spacing is basically identical, the height distribution of each crack shows no obvious changes relative to the comparison beam (basically equivalent), and the crack distribution in the concrete beams is not evidently influenced by the corrosion of the prestressed steel bars.
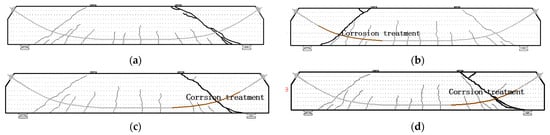
Figure 3.
Crack distribution under the ultimate loading state. (a) B1 beam; (b) B2 beam; (c) B3 beam; (d) B4 beam.
3.2. Failure Mode
Despite different corrosion rates of steel strands, the failure modes of test beams are basically identical. In the initial loading stage, the pure bending segment is the first to start cracking (vertical bending tensile crack). With the increase in the load, the bending-shear segments at both sides are subjected to 3–5 diagonal cracks. As the load continued to increase, a web-shear diagonal crack pointing to the loading point firstly appears nearby the support of the bending-shear segment at the corrosion side, while the diagonal crack appears at the uncorroded side slightly later. Subsequently, the load is further increased, the vertical crack in the pure bending zone no longer developes towards the beam top, but the web-shear diagonal crack nearby the support at the corroded side developes simultaneously towards two directions and extended beneath the beam-top loading point, becoming a critical diagonal crack. The width of the principal diagonal crack increases with the load. When the ultimate load is reached and cannot be further increased, the test beam made a cracking sound and a transverse crack appears in the concrete nearby the lower part of load board at the top of the diagonal crack. As a result, the concrete is crushed and peels off. Moreover, the crack width in the zone between erection bars and steel strands at the lower end of the crack continued to grow, a horizontal avulsed crack appears on the upper surface of erection steel bars, and test beams are subjected to failures. The failure modes as shown in Figure 4. The failure modes of test beams do not go through any obvious change due to the corrosion of the steel strands, all of which experienced typical shear-compression failures.

Figure 4.
Failure sections of B1–B4. (a) B1 beam; (b) B2 beam; (c) B3 beam; (d) B4 beam.
3.3. Deflection Analysis
Deflection is the main index reflecting the overall stiffness of a structure. In this study, the deflections at midspan under the action of each stage of load are selected to appear in Figure 5. It appears that the curves presented indicate three-stage characteristics:
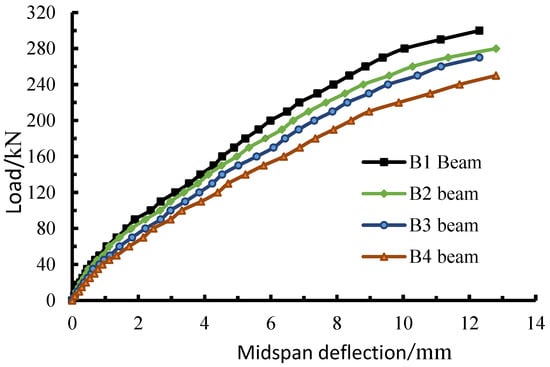
Figure 5.
Load–midspan deflection curves.
In the initial loading stage, the midspan deflection of each test beam is basically linearly correlated with the load and showed elastic structural characteristics, and the deflection difference is very minor. This is because each test beam is in an elastic deformation stage, and the structural stiffness is mainly controlled by concrete. At this time, the structure is not crack yet, and the overall stiffness difference is not large. After the load reaches the cracking load, the slope of the load-deflection curve of each test beam declines. The growth rate of deflection is higher than that of the load, and the structure is inelastic, indicating that the structural stiffness declines due to cracking. However, the stiffness decrements of different test beams are inconsistent. The load–deflection curves of B1 and B2 are basically overlapped in this stage, but the slope of the load–deflection curves of B3 and B3 is apparently smaller than that of B1. This indicates that the decline degree of structural stiffness is associated with the corrosion rate of steel strands. The reason is that due to the corrosion of steel strands, the structure cracked in advance in comparison with B1. In this case, the concrete with a cracking cross section exit from the work, and thus the concrete stress is redistributed. With the appearance of cracks, the bonding performance between steel strands and concrete is damaged, between which slipping occurs with the degradation of the overall stiffness.
When the load approaches the ultimate load, the structure is evidently plastic; namely, the load growth is small but the structural deflection increases rapidly. Compared with the B1 test beam, the ultimate midspan deflections of the B2–B4 beams increases by 2.7%, 8.0%, and 11.6%, respectively.
3.4. Ultimate Load
The ultimate loads of the test beams (Table 4) are significantly influenced by the corrosion of steel strands, which could result in the degradation of structural shear bearing capacity. With the increase in the corrosion rate, moreover, the structural shear bearing capacity is degraded more significantly. In this test, the shear bearing capacity of the test beams decreases by 5.8%, 9.1%, and 15.5%, respectively, at the steel strands’ area corrosion rate of 7.9%, 19.4%, and 31.7%. All test beams experienced a brittle shear failure. The relative ultimate shear strength ω is defined as the ratio of the ultimate load of corroded beam to that of uncorroded beam. The area corrosion rate η and relative ultimate shear strength ω of test beams are listed in Table 4.

Table 4.
Corrosion rate η and relative shear strength ω of test beams.
The data in Table 4 are linearly fitted to obtain η-ω relations, as shown in Figure 6. Due to the corrosion of the prestressed steel bars, the shear bearing capacity of component declines, and the area corrosion rate η shows a good linear relation with the relative ultimate shear strength ω.
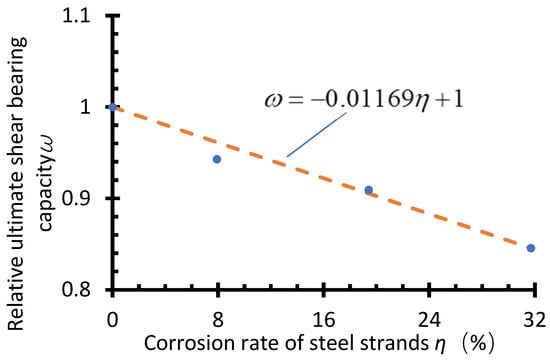
Figure 6.
ω-η curves.
4. Calculation of Ultimate Shear Bearing Capacity
4.1. Simplified Computational Analysis of Shear Bearing Capacity
In accordance with Code for Design of Concrete Structures (GB 50010-2020) [19], the oblique cross-sectional shear bearing capacity of PC flexural members configured with stirrups and bent-up bars can be calculated through the following equations:
where Vu is the shear bearing capacity of component and Vcs represents the shear bearing capacity provided by stirrups and concrete. Vp denotes the shear bearing capacity provided by the prestress, which is 0, since the structure will reach the ultimate bearing capacity when cracking, and it is stipulated in the code that the contribution made by the prestress component to shear resistance should not be considered. Asb and Apb represent the cross-sectional areas of bent-up bars and prestressed steel bars, respectively. αs and αp are the included angle of the longitudinal axis of the component with bent-up bars and bent-up prestressed steel bars on the oblique section, respectively. λ is the shear span ratio of each test beam; ft stands for the design axial tensile strength of concrete, which can be calculated as per ft = 0.26 fcu2/3. fcu is the cubic compressive strength of concrete, fyv is the design tensile strength of stirrups, Asv is the cross-sectional area of stirrups, s represents the spacing of stirrups, b and h0 denote the rectangular cross-sectional with and without effective height, respectively.
According to the test beam design and the existing literature [20], the shear bearing capacity of test beams is expressed as
where , and represent the shear bearing capacity of concrete, stirrups and diagonal steel strands, respectively. denotes the longitudinal reinforcement ratio, and is the compressive strength of concrete, taken as . is the arm of force, taken as 0.875 h0, stands for the included angle between principal diagonal crack and beam axis, is the included angle between stirrups and beam axis, represents the included angle between steel strands on the principal diagonal rupture plane and beam axis. It could be seen from the test results that stirrups already yielded upon a failure, so the actual yield value is taken during the stirrup calculation, and the standard value (1860 MPa) is selected for steel strands.
In Equations (3) and (4), the corrosion of steel strands is not yet considered. The design parameters of B1 are substituted into such equations to calculate the shear bearing capacity as 293.8 kN, whose error relative to the test value is −1.4%, indicating a high accuracy.
The corrosion of steel strands influences the structural shear bearing capacity mainly in two ways: On the one hand, the corrosion causes the cross-sectional damage of steel strands and reduces the strength of the steel strand. On the other hand, the corrosion led to the bonding degradation and uncoordinated strain between steel strands and concrete and stress hysteresis of prestressed steel bars. Consequently, steel strands fail to give full play to their strength, and they may not reach the standard strength upon the structural shear-compression failure. Hence, the effect of corrosion should be considered in order to correctly evaluate the shear bearing capacity of components with corroded steel strands. Given this, the concept of strength utilization rate [21] of the corroded prestressed steel bars for the PC beams is introduced to calculate the shear bearing capacity of the test beams with corroded steel strands. Through the strength utilization rate , the actual effective prestress of corroded steel strands under the ultimate load can be solved as:
where is the actual prestress of corroded prestressed steel bars, is the standard strength of uncorroded prestressed steel bars, is the strength utilization rate; η is the area corrosion rate, is the actual effective area of prestressed steel bars, is the cross-sectional area of uncorroded prestressed steel bars, k is the corrosion influencing factor, and is the distance from the gravity center of prestressed steel bars to the concrete top.
Then, Equation (1) is corrected according to Equations (7)–(10), thereby acquiring the ultimate shear bearing capacity of test beams as follows
The calculation results for the ultimate bearing capacity of the test beams according to Equation (12) are presented in Table 5.

Table 5.
Comparison between test results and theoretical calculation results of B1–B4.
As seen in Table 5, the average error between test value and theoretical value of shear bearing capacity is 2.2%. The value obtained through simplified calculation as per the code coincides with the test value very well, thus verifying the reasonability of the simplified calculations.
4.2. Numerical Simulation Analysis of Shear Performance
A finite element calculation model of each damaged concrete beam is established via ABAQUS. The structure is constructed with a separated-type model. Therein, concrete is simulated using reduced integral hexahedral elements (C3D8R) and expressed by a constitutive concrete damage plasticity model. Load boards and supports are simulated using rigid elements (R3D4) to avoid stress concentration, and boundary conditions are set and loading is performed through the rigid body reference point (RP). Ordinary steel bars and prestressed steel bars are both simulated using truss elements (T3D2), and strong hardening constitutive relation models [22,23] such as double broken lines are chosen.
The bond-slip between steel strands and concrete is simulated using nonlinear spring elements (SPRING2), specifically by setting elements parallel and perpendicular to the steel bars at the co-node between concrete and steel strands. To simulate the rupture of steel strands, the elements are inactivated and activated by using the model change in the interaction module. In Stage 1, all structural elements are inactivated, and the elements in the corresponding stage are activated according to experimental steps, thus completing the simulation of the whole test process.
The calculated value and measured value of ultimate bending load of each test beam are listed in Table 5. It could be seen that the relative error between test value and the value obtained through numerical analysis and calculation was small, with the maximum error of only 3.9%, and all calculated values relatively agree with the test values.
The test value and the calculated value of midspan deformation of each beam under different load conditions are displayed in Figure 7. It could be observed from Figure 7 that the test value is relatively consistent with the calculated value, which further verifies the effectiveness of the calculation model.
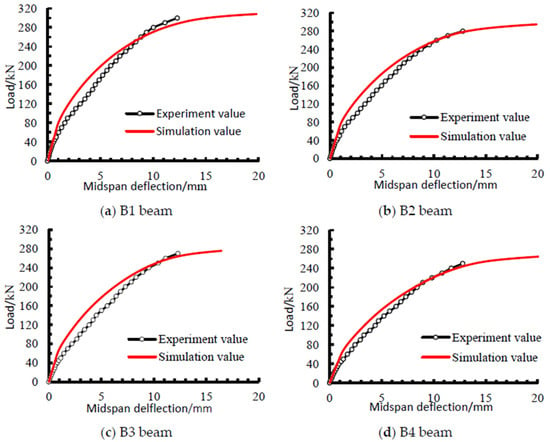
Figure 7.
Comparison of midspan load–deflection curves between test results and calculation results.
To compare the concrete damage status and the stress state of stirrups under the same stage of loading action and theoretically analyze the influence of the corrosion of steel strands on structural shear bearing capacity, the load is taken as 252 kN by reference to the ultimate bearing capacity of each beam. The concrete damage and cracking conditions of beams under a tensile-compressive state as well as the stress state of stirrups are exhibited in Figure 8, Figure 9 and Figure 10. It can be observed that in each test beam, tensile cracks are firstly generated at the bottom of the midspan pure bending segment. As the load continued to grow, and bending-shear diagonal cracks are formed in the bending-shear segment and pointed to the support along the loading point. It can be judged that the failure mode of the beam is not changed due to the increase in the corrosion rate of steel strands. That is, the shear-compression failure is a dominated factor. Relative to the comparison beam B1, the increasing corrosion rate of steel strands exerts a minor influence on the tensile damage and cracking of concrete in the pure bending segment but generates a great impact on the tensile-compression damage and cracking of concrete in the bending-shear segment. Meanwhile, as the load increases, the stress of stirrups develops at a high speed after the tensile-compressive damage and cracking of concrete. Under the action of 252 kN, the maximum stress of comparison beam B1, B2, B3, and B4 are 197 MPa, 200 MPa, 342 MPa, and 476 MPa, respectively. The greater the corrosion rate of steel strands, the earlier the stirrups would enter a yield state. The stress growth rate of stirrups is much greater than the load increasing rate, and meanwhile, the diagonal crack induced by the tensile-compressive damage of concrete already run through the whole beam body. By comparing the finite element simulation results (Figure 8 and Figure 9) with the experimental results (Figure 3), we can find that the crack development laws of the two cases are consistent. This further proves the effectiveness of the calculation model proposed in this paper. Therefore, the yield of stirrups can serve as a sign for beams to reach their ultimate bearing capacity in practical applications.
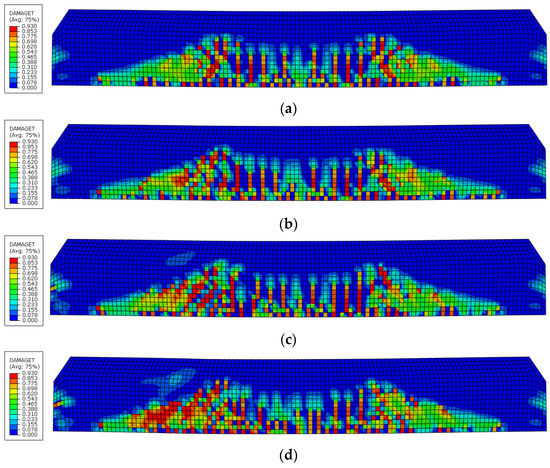
Figure 8.
Tensile damage and cracking of concrete in test beams. (a) B1 beam; (b) B2 beam; (c) B3 beam; (d) B4 beam.
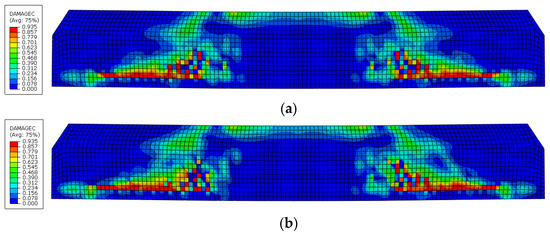

Figure 9.
Compressive damage and cracking of concrete in test beams. (a) B1 beam; (b) B2 beam; (c) B3 beam; (d) B4 beam.
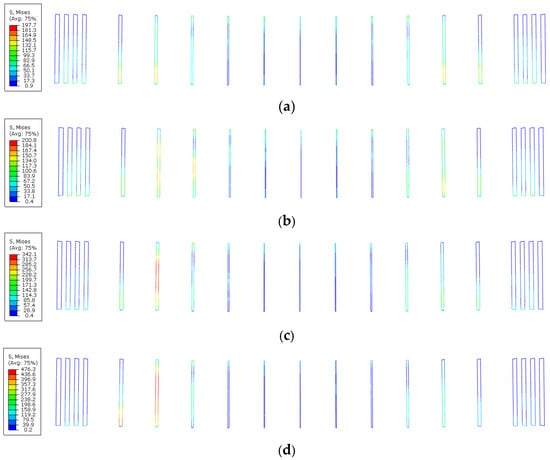
Figure 10.
Stress diagram of stirrups. (a) B1 beam; (b) B2 beam; (c) B3 beam; (d) B4 beam.
5. Conclusions
In this paper, the crack development, failure mode, deflection change, and ultimate shear bearing capacity development law of the PC structure with locally corroded steel strands were analyzed, and the calculation model of ultimate shear bearing capacity considering the effect of local corrosion was also proposed. The conclusions are summarized as follows:
(1) The crack development mode and failure mode of PC structure are not affected by the corrosion of prestressed steel strands, but its shear bearing capacity gradually decreases with the increase of the corrosion rate of the steel strand section, and the corrosion rate of prestressed steel strand has a linear relationship with the degradation of the relative ultimate shear strength.
(2) The calculation method of shear capacity of PC structure considering the effect of local corrosion proposed in this paper has high prediction accuracy, and the average error of all prediction results in this experiment is only 2.6%.
(3) The larger the cross-section corrosion rate of the steel strand, the earlier the stirrup enters the yield state. In the service state evaluation of the corroded PC structure, the yield of stirrups can be used as a sign of the ultimate shear bearing capacity of the structure.
Author Contributions
Conceptualization, R.Y.; methodology, R.Y., X.W. and P.L.; software, R.Y.; validation, R.Y. and Y.Y.; writing—original draft preparation, R.Y. and Y.Y.; writing—review and editing, R.Y., Y.Y., X.W. and P.L.; supervision, X.W. and P.L.; funding acquisition, R.Y., Y.Y., P.L. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. 52208166), the Hunan Provincial Natural Science Foundation of China (grants no. 2021JJ50156, 2022JJ40024, and 2021JJ50153), the National Science Foundation for Distinguished Young Scholars of Hunan Province (grant no. 2022JJ10075), and the Research Foundation of Education Bureau of Hunan Province (grants no. 18A401, 21B0723, and 19C0343).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank the anonymous reviewers and the editor for their valuable comments and remarks that helped us to improve the original manuscript.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Yang, Y.M.; Peng, J.X.; Liu, X.H.; Cai, C.S.; Zhang, J.R. Probability analysis of web cracking of corroded prestressed concrete box-girder bridges considering aleatory and epistemic uncertainties. Eng. Struct. 2020, 228, 111486. [Google Scholar] [CrossRef]
- Shen, X.W.; Wang, R.H. Mechanics Effect Analysis of Pre-tensioned and Post-tensioned Pre-stressed Concrete Simply-supported Box Beams on High-speed Railway. China Railw. Sci. 2004, 25, 100–104. [Google Scholar]
- Yang, Y.M.; Tang, H.; Wang, X.Z. Failure probability analysis of corroded RC structures considering the effect of spatial variability. Mag. Concrete Res. 2022. ahead of print. [Google Scholar] [CrossRef]
- Yang, Y.M.; Peng, J.X.; Cai, C.S.; Zhang, J.R. Improved interval evidence theory–based fuzzy AHP approach for comprehensive condition assessment of long-span PSC continuous box-girder bridges. J. Bridge Eng. 2019, 24, 04019113. [Google Scholar] [CrossRef]
- Peng, J.X.; Yang, Y.M.; Bian, H.B.; Zhang, J.R.; Wang, L. Optimisation of maintenance strategy of deteriorating bridges considering sustainability criteria. Struct. Infrastruct. Eng. 2022, 18, 395–411. [Google Scholar] [CrossRef]
- Ma, Y.F.; Xu, F.Y.; Wang, L.; Zhang, J.R.; Zhang, X.H. Influence of corrosion-induced cracking on structural behavior of reinforced concrete arch ribs. Eng. Struct. 2016, 117, 184–194. [Google Scholar] [CrossRef]
- Yang, Y.M.; Peng, J.X.; Cai, C.S.; Zhou, Y.D.; Wang, L.; Zhang, J.R. Time-dependent reliability assessment of aging structures considering stochastic resistance degradation process. Reliab. Eng. Syst. Safe 2022, 217, 108105. [Google Scholar] [CrossRef]
- Juarez, C.A.; Guevara, B.; Fajardo, G.; Castro-Borges, P. Ultimate and nominal shear strength in reinforced concrete beams deteriorated by corrosion. Eng. Struct. 2011, 33, 3189–3196. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wang, L.; Zhang, J.R. Experimental RC beams research of shear performance of corroded arranged with diagonal reinforcement. Bridge Constr. 2017, 47, 77–82. [Google Scholar]
- Ye, Z.; Zhang, W.P.; Gu, X.L. Modeling of Shear Behavior of Reinforced Concrete Beams with Corroded Stirrups Strengthened with FRP Sheets. J. Compos. Constr. 2018, 22, 04018035. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhang, Y.; Liu, B.; Liu, B.W.; Wu, W.P.; Yang, C.Q. Corrosion-induced spalling of concrete cover and its effects on shear strength of RC beams. Eng. Fail. Anal. 2021, 127, 105538. [Google Scholar] [CrossRef]
- Huang, L.; Ye, H.L.; Jin, X.Y.; Jin, N.G.; Xu, Z.N. Corrosion-induced shear performance degradation of reinforced concrete beams. Constr. Build. Mater. 2020, 248, 118668. [Google Scholar] [CrossRef]
- Lu, Z.H.; Li, H.; Li, W.; Zhao, Y.G.; Tang, Z.; Sun, Z. Shear behavior degradation and failure pattern of reinforced concrete beam with chloride-induced stirrup corrosion. Adv. Struct. Eng. 2019, 22, 2998–3010. [Google Scholar] [CrossRef]
- Soltani, M.; Abu-Abaileh, A.; Scott-Rowe, B. Statistical Approach to Modeling Reduced Shear Capacity of Corrosion-Damaged Reinforced Concrete Beams. Pract. Period. Struct. Des. Constr. 2021, 26, 04020073. [Google Scholar] [CrossRef]
- Spinella, N.; Colajanni, P.; Recupero, A.; Tondolo, F. Ultimate Shear of RC Beams with Corroded Stirrups and Strengthened with FRP. Buildings 2019, 9, 34. [Google Scholar] [CrossRef]
- El-Sayed, A.K. Shear capacity assessment of reinforced concrete beams with corroded stirrups. Constr. Build. Mater. 2017, 134, 176–184. [Google Scholar] [CrossRef]
- Da, B.; Yu, H.F.; Ma, H.Y.; Yu, B.; Wu, Z.Y.; Guo, J.B. Study on shear behavior of reinforced coral aggregate concrete beam. Adv. Struct. Eng. 2020, 23, 2388–2398. [Google Scholar] [CrossRef]
- Zhang, X.H. Strain Compatibility between Corroded Prestressing Strand and Concrete & Calculation Theory of Beam Capacity; Changsha University of Science & Technology: Changsha, China, 2016; pp. 22–23. [Google Scholar]
- GB 50010-2020; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2019.
- Guo, Z.H. Reinforced Concrete Theory, 3rd ed.; Tsinghua University Press: Beijing, China, 2012; pp. 246–259. [Google Scholar]
- Yang, R.H.; Dai, L.Z.; Wang, L.; Zhang, J.R. Calculation of flexural capacity of PC beams considering strength utilization of corroded prestressing tendon. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 2593–2602. [Google Scholar]
- Fang, Z.H.; Zhou, H.J.; Lai, S.Y. Choose of ABAQUS concrete stress-strain curve. Build. Struct. 2013, 43, 559–561. [Google Scholar]
- Alfarah, B.; López-Almansa, F.; Oller, S. New methodology for calculating damage variables evolution in plastic damage model for RC structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).