Study of 3-D Prandtl Nanofluid Flow over a Convectively Heated Sheet: A Stochastic Intelligent Technique

Abstract

In this article, we examine the three-dimensional Prandtl nanofluid flow model (TD-PNFM) by utilizing the technique of Levenberg Marquardt with backpropagated artificial neural network (TLM-BANN). The flow is generated by stretched sheet. The electro conductive Prandtl nanofluid is taken through magnetic field. The PDEs representing the TD-PNFM are converted to system of ordinary differential equations, then the obtained ODEs are solved through Adam numerical solver to compute the reference dataset with the variations of Prandtl fluid number, flexible number, ratio parameter, Prandtl number, Biot number and thermophoresis number. The correctness and the validation of the proposed TD-PNFM are examined by training, testing and validation process of TLM-BANN. Regression analysis, error histogram and results of mean square error (MSE), validates the performance analysis of designed TLM-BANN. The performance is ranges 10⁻¹⁰, 10⁻¹⁰, 10⁻¹⁰, 10⁻¹¹, 10⁻¹⁰ and 10⁻¹⁰ with epochs 204, 192, 143, 20, 183 and 176, as depicted through mean square error. Temperature profile decreases whenever there is an increase in Prandtl fluid number, flexible number, ratio parameter and Prandtl number, but temperature profile shows an increasing behavior with the increase in Biot number and thermophoresis number. The absolute error values by varying the parameters for temperature profile are 10⁻⁸ to 10⁻³, 10⁻⁸ to 10⁻³, 10⁻⁷ to 10⁻³, 10⁻⁷ to 10⁻³, 10⁻⁷ to 10⁻⁴ and 10⁻⁸ to 10⁻³. Similarly, the increase in Prandtl fluid number, flexible number and ratio parameter leads to a decrease in the concentration profile, whereas the increase in thermophoresis parameter increases the concentration distribution. The absolute error values by varying the parameters for concentration profile are 10⁻⁸ to 10⁻³, 10⁻⁷ to 10⁻³, 10⁻⁷ to 10⁻³ and 10⁻⁸ to 10⁻³. Velocity distribution shows an increasing trend for the upsurge in the values of Prandtl fluid parameter and flexible parameter. Skin friction coefficient declines for the increase in Hartmann number and ratio parameter Nusselt number falls for the rising values of thermophoresis parameter against N_b.

1. Introduction

Nanofluid is a mixture of base liquid and nanosize particles, and the size of these nanoparticles is between 1 to 100 nanometer. There are two types of fluids; first one is Newtonian fluid and the second is non-Newtonian fluid. Nanofluids consist of rods, fibers and nanometer sized particles suspended in base fluids [1]. The base fluid is usually water, ethylene glycol or oil. There are some articles published, that investigate the progress of nanofluids [2,3,4]. Some researchers study the applications of nanofluids in heat exchange [5], car radiators [6], medical appliances [7] and solar collectors [8].

Heat generation is a phenomenon of generation, conversion, use and exchange of thermal energy between the two objects. Conduction, convection and Radiation are the different modes of heat transfer. Heat transfer of nanofluids is also examined by research workers [9,10,11]. Three-dimensional flows mean that the flow is describing in three space coordinates. Any physical flow is three dimensional. Three-dimensional flow over a stretched sheet was studied by Wang [12], Ariel [13], Xu et al. [14] and Liu et al. [15].

The main purpose of this article is to study the three-dimensional flow of Prandtl nanofluid containing nanoparticles. Hayat [16,17] examined the peristaltic flow of Prandtl nanoliquid and Kumar [18] examined the impact of mass transfer in Prandtl liquid flow. Hayat [19] also analyzed the Prandtl liquid flow with Cattaneo-Christov double diffusion. Nadeem et al. [20] studied the Prandtl liquid model in an endoscope. Some researchers have carried out tremendous work using the Prandtl nanofluid model, i.e., Akbar [21,22], Sooppy Nisar [23] and Hamid [24], examined the flow of Prandtl fluid flow in their research models. Over a deformable surface, Soomro et al. [25] examined the passive control of nanoparticles in Prandtl nanofluid flow. Nilankush [26,27] examined the Spectral quasi linearization simulation of radiative nanofluidic transport over a permeable inclined disk and a bended surface in his two research articles. Sabu [28] explored the role of nanoparticle form and thermo-hydrodynamic slip limitations in Magnetohydrodynamic alumina-water nanofluid flows across a rotating hot surface. Virmani [29] reviewed the nanostructured materials for exterior panel elements in automotive.

There are many models examined by the scientist over a convectively heated surface. Uddin [30] examined the mixed convective Prandtl-Eyring flow over a surface. Zaka Ullah [31] and Patil [32] demonstrated the flow of Prandtl fluid over a convectively heated surface. Over a convectively heated sheet, Hosseinzadeh [33] analyzed the flow of Maxwell liquid. Ahmed [34] explore the chemically reacting fluid flow through a convectively heated sheet. Alamri et al. [35] investigated the novel viewpoint of Cattaneo-Christove heat flux model. Yausif et al. [36] implemented the numerical technique for heat transfer analysis subjected to fluid flow system under the impacts of thermal radiation and internal heat source/sink. Ellahi et al. [37,38] analyzed the heat transfer impacts on bi-phase flow coatings. The authors also studied the entropy optimized fluid flow system under the influence of heat transfer and magneto hydrodynamics. Moreover, heat transfer generation, heat transfer consumption and thermal radiation for non-Newtonian fluid flow are studies by Saeed et al. [39].

The three-dimensional flow of Prandtl nanofluid is examined by using different numerical and analytical method, but stochastic numerical methods are well known due to their effectiveness, robustness and worth. Research workers already applied stochastic numerical technique on their research problems [40,41,42,43,44]. Some research models examined by implementing the artificial intelligence techniques are Ree-Eyring fluid model [45], third-grade fluid model [46], MHD boundary layer flow model [47] and Maxwell nanofluid model [48].

To analyze the Prandtl fluid models based on differential equations, many scholars employed various numerical simulations. However, no one has applied the solution method which is based on the Levenberg-Marquardt approach in artificial neural networks to improve the solver technique’s computing power and precision level. Due to their usefulness, efficiency, and reliability, stochastic numerical approaches are effective and reliable to investigate the Prandtl fluid flow related problems. All of these motivating factors encourage authors to use a precise and consistent AI algorithm-based mathematical simulation framework for mathematical solution of Prandtl fluid flow over a convectively heated surface by performing numerical and graphical research to analyze the influence of all variations on velocity, concentration, and temperature distributions, which is the novelty of this study.

In this article, Mathematica (version 12) and MATLAB (version R2019b) software are used for numerical treatment.

The innovative contributions of computing procedure are as follows:

• The numerical computation has been designed through the technique of Levenberg Marquardt with backpropagated artificial neural network (TLM-BANN) for the comparative study of three dimensional Prandtl nanofluid flow model (TD-PNFM) with convectively heated surface.
• The TLM-BANN coupled PDEs representing TD-PNFM are transformed into system of ODEs by utilizing suitable transformation.
• The Mathematica software command ‘NDSolve’ is used to compute the dataset for designed TLM-BANN for the variation of Prandtl fluid number, flexible number, ratio parameter, Prandtl number, Biot number and thermophoresis number.
• The MATLAB software is used to interpret the solution and the AE analysis plots of TD-PNFM.
• The correctness and the validation of the proposed TD-PNFM is examined by training, testing and validation process of TLM-BANN.
• Regression analysis, error histogram and results of mean square error (MSE), validates the performance analysis of designed TLM-BANN.

2. Mathematical Modeling

We examine the 3D flow of Prandtl nanofluid with a convectively heated surface. Thermal convection and zero nanoparticles mass flux are the two boundary conditions discussed in this model. Thermophoretic and Brownian motion impacts are also examined. The fluid is electro conductive with the magnetic field applied in the direction of z-axis, shown by the geometrical interpretation represented through Figure 1. The figure shows that the sheet is extended in x and y- direction, and the fluid is moving at that extended sheet. The model is discussed in Cartesian coordinates system. The velocity U_w is along the x-axis and the velocity V_w is along the y-axis at z = 0. Along z-axis, magnetic field B₀ is applied. The current hall and magnetic field impacts are ignored for a small value of Reynold number. Then the resulting ODEs along with the boundary conditions after solving the system of PDEs [49] are:

$${\beta }_1{f}^{‴}+\left(f+g\right)f^{″}-{f^{\prime }}^2+{\beta }_2{f^{″}}^2{f}^{‴}-{\left(Ha\right)}^2{f}^{\prime }=0,$$

(1)

$${\beta }_1{g}^{‴}+\left(f+g\right)g^{″}-{g^{\prime }}^2+{\beta }_2{g^{″}}^2{g}^{‴}-{\left(Ha\right)}^2{g}^{\prime }=0,$$

(2)

$${\theta }^{″}+\mathrm{Pr}\left(\left(f+g\right){\theta }^{\prime }+N_b{\theta }^{\prime }{\varphi }^{\prime }+N_t{{\theta }^{\prime }}^2\right)=0,$$

(3)

$${\varphi }^{″}+Sc(f+g){\varphi }^{\prime }+\frac{N_t}{N_b}{\theta }^{″}=0,$$

(4)

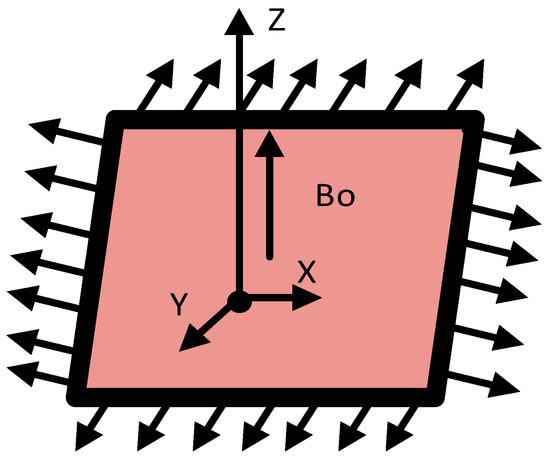
Figure 1. Flow Diagram.

And the BCs are;

$$\begin{array}{l}f(0)=g(0)=0,f^{\prime }(0)=1,g^{\prime }(0)=\alpha ,\\ {\theta }^{\prime }(0)=-\gamma (1-\theta (0)),N_b{\varphi }^{\prime }(0)+N_t{\theta }^{\prime }(0)=0,\end{array}$$

(5)

$$f^{\prime }(\infty )\to 0,g^{\prime }(\infty )\to 0,\theta (\infty )\to 0,\varphi (\infty )\to 0,$$

(6)

3. Solution Methodology

The TLM-BANN coupled with PDEs representing TD-PNFM are converted into system of ODEs by applying suitable transformation. Adam numerical method is used to compute the reference dataset for all the six scenarios of TD-PNFM. The MATLAB command ‘nftool’ is used to execute the technique of Levenberg Marquardt with backpropagated artificial neural network (TLM-BANN) for the study of TD-PNFM.

The neural network figure for LMT-BANN is given below as Figure 2 and the flow chart is shown in Figure 3.

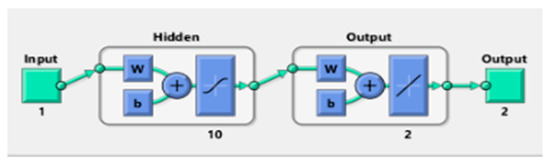
Figure 2. Neural Network diagram for TD-PNFM.

Figure 3. Flow chart for TD-PNFM.

The current model is discussed for six scenarios and the scenarios consist of the variations of Prandtl fluid number, flexible number, ratio parameter, Prandtl number, Biot number and thermophoresis parameter. Each scenario has further four cases and the values for all the cases are written below in Table 1. With Ha= 0.4, N_b= 0.9 and Sc = 1.0. We can easily see the impact of variations of physical parameters on temperature profile and concentration profile. There are 10 hidden neurons with the input lies between 0 and 8 and the step size is 0.08. The dataset is computed for 101 points in which 81 points are for training, 10 points for testing and 10 points for validation.

Table 1. Variation of parameters of TD-PNFM.

Scenarios	Cases	Physical Quantities
		β1	β2	α	γ	Pr	Nt
01	1	0.2	0.6	0.2	0.8	1.1	0.8
	2	0.4	0.6	0.2	0.8	1.1	0.8
	3	0.6	0.6	0.2	0.8	1.1	0.8
	4	0.8	0.6	0.2	0.8	1.1	0.8
02	1	0.2	0.0	0.2	0.8	1.1	0.8
	2	0.2	0.4	0.2	0.8	1.1	0.8
	3	0.2	0.8	0.2	0.8	1.1	0.8
	4	0.2	1.2	0.2	0.8	1.1	0.8
03	1	0.2	0.6	0.0	0.8	1.1	0.8
	2	0.2	0.6	0.15	0.8	1.1	0.8
	3	0.2	0.6	0.30	0.8	1.1	0.8
	4	0.2	0.6	0.45	0.8	1.1	0.8
04	1	0.2	0.6	0.2	0.1	1.1	0.8
	2	0.2	0.6	0.2	0.5	1.1	0.8
	3	0.2	0.6	0.2	1.0	1.1	0.8
	4	0.2	0.6	0.2	1.5	1.1	0.8
05	1	0.2	0.6	0.2	0.8	0.75	0.8
	2	0.2	0.6	0.2	0.8	1.0	0.8
	3	0.2	0.6	0.2	0.8	1.25	0.8
	4	0.2	0.6	0.2	0.8	1.50	0.8
06	1	0.2	0.6	0.2	0.8	1.1	0.1
	2	0.2	0.6	0.2	0.8	1.1	0.7
	3	0.2	0.6	0.2	0.8	1.1	1.2
	4	0.2	0.6	0.2	0.8	1.1	1.9

4. Discussion of Results

The six scenarios of TD-PNFM by the variation of Prandtl fluid number, flexible number, ratio parameter, Prandtl number, Biot number and thermophoresis parameter are formulated for four different cases for both, temperature and concentration profile of three-dimensional Prandtl nanofluid flow model as elaborated in Table 1.

The Prandtl number described as the ratio of momentum to thermal diffusivity. As the Prandtl number increases, the temperature decreases. As Pr increases, thermal diffusivity reduces, resulting in a drop in temperature. The Biot number represents the ratio of inner to outside thermal resistance for a solid item that transfers heat to a liquid flow. This ratio indicates if the inside temperature of a body fluctuate considerably in space when it heated or cools over time due to a thermal gradient given to its sheet. A rise in the Biot number induces intense convection, resulting in an increase in thermal profile. Thermophoresis is a force caused by the difference of temperature among the cold wall and hot gas that causes particulate particles to migrate more toward the cold wall. This variable is caused by nanoparticles. Nanoparticles increased the nanoliquids thermal conductivity. The thermal conductivity of nanoliquids enhances with temperature. As a result, an increase in temperature is noticed for a better estimation of N_t.

The dataset for the designed TLM-BANN is computed with the help of Adam numerical method, for which, the input lies between 0 and 8 with 0.08 step size for all the four cases of six different scenarios of TLM-BANN of TD-PNFM. The solution for three-dimensional Prandtl nanofluid flow is determined by using the command ‘nftool’ in MATLAB. The dataset is generated for 101 points in which 81 points are for training, 10 points for testing and 10 points for validation of designed TLM-BANN.

The performance, state transition, fitness, error histogram and regression for the case I of the scenarios I, II, III, IV, V and VI are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, respectively. The MSE based performance reflects the difference between observation and simulation; the lower the MSE value, the higher the performance. The performance is 10⁻¹⁰, 10⁻¹⁰, 10⁻¹⁰, 10⁻¹¹, 10⁻¹⁰ and 10⁻¹⁰ with epochs 204, 192, 143, 20, 183 and 176, as depicted in the performance graphs. The histogram displays the technique’s dependability by displaying the difference between the anticipated and targeted results after neural network training. A histogram plot has twenty vertical bars, which are referred to as bins. The data is distributed evenly between positive and negative components is shown by the zero line, which is the red vertical line in the histogram plot. The regression plots demonstrate the output and the target relationship. Regression R measures that how accurately measured values fit a straight line or curve, and the straight line reflecting the perfect fit. If R = 1, the outputs and the targets relation is accurate. The fitness graph depicts the relation of training, testing, and validation of output and training, where overlap of all three indicating that algorithm is properly trained and provides an accurate answer. Inside the training state, there is a portion of error plot that represents the error related to output. Moreover, the data for MSE, performance, epochs, Mu and time taken is given in Table 2. The Mu and gradient values corresponding to epoch reflect whether the convergence is gradual or rapid; as the epoch advances, the values of gradient and Mu fall, indicating the convergence is quick using the Levenberg-Marquardt solver.

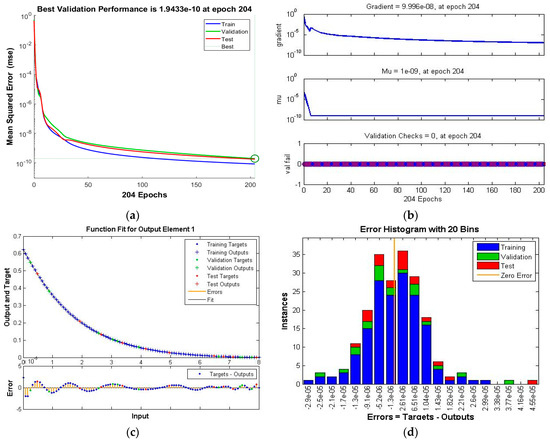
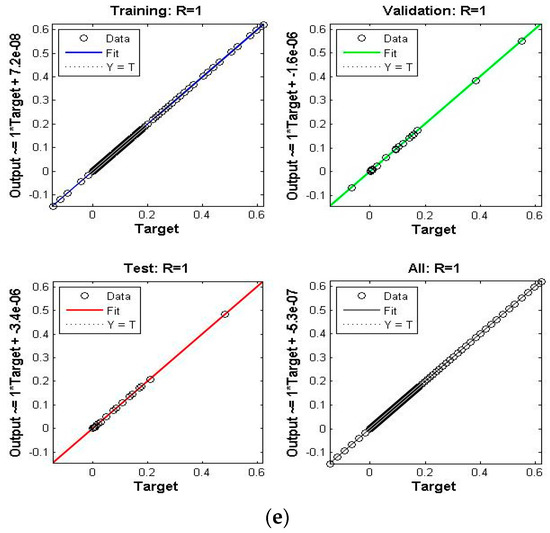
Figure 4. Scenario I Case I of TD-PNFM. (a) MSE Results: Scenario I Case I; (b) Transition state: Scenario I Case I; (c) Fitness: Scenario I Case I; (d) Error Histogram: Scenario I Case I; (e)regression: Scenario I Case I.

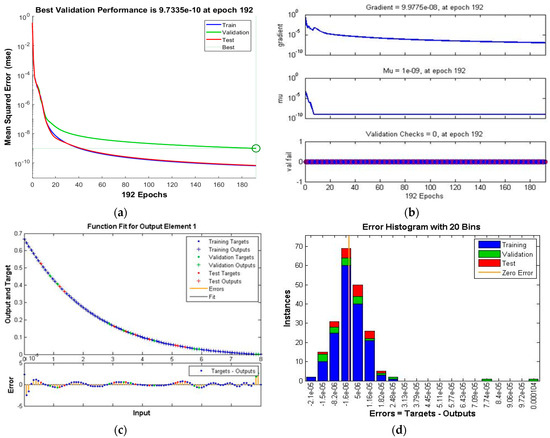
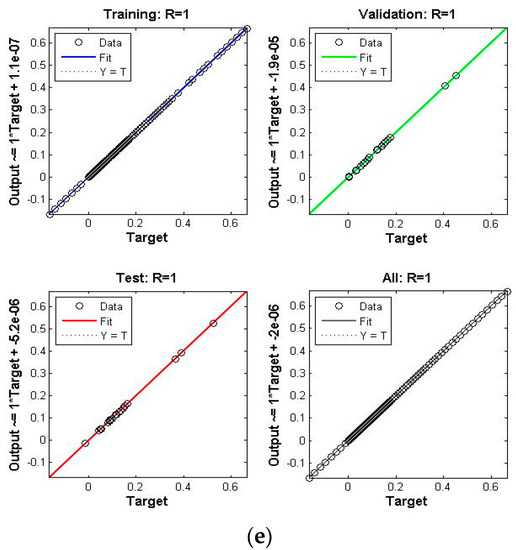
Figure 5. Scenario II Case I of TD-PNFM. (a) MSE Results: Scenario II Case I; (b) Transition state: Scenario II Case I; (c) Fitness: Scenario II Case I; (d) Error Histogram: Scenario II Case I; (e)regression: Scenario II Case I.

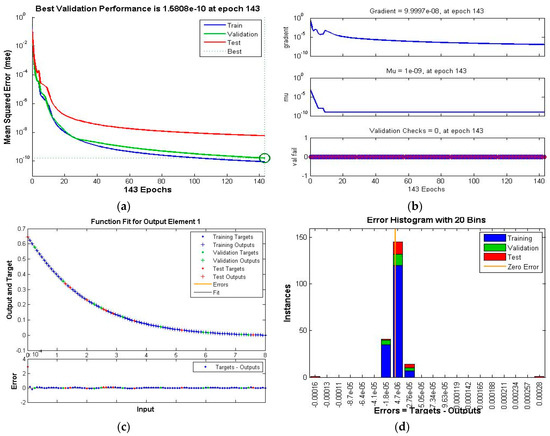
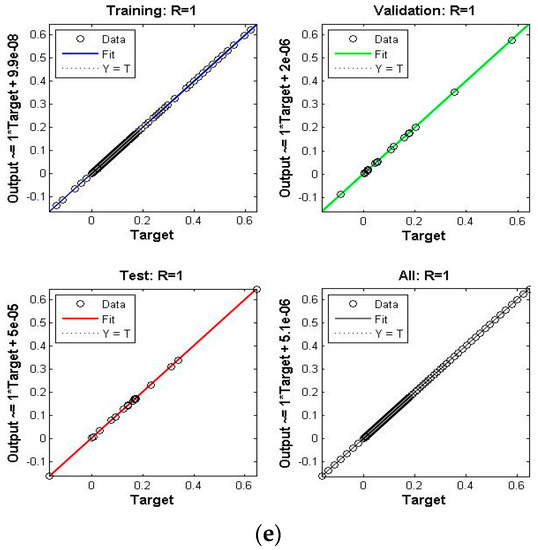
Figure 6. Scenario III Case I of TD-PNFM. (a) MSE Results: Scenario III Case I; (b) Transition state: Scenario III Case I; (c) Fitness: Scenario III Case I; (d) Error Histogram: Scenario III Case I; (e)regression: Scenario III Case I.

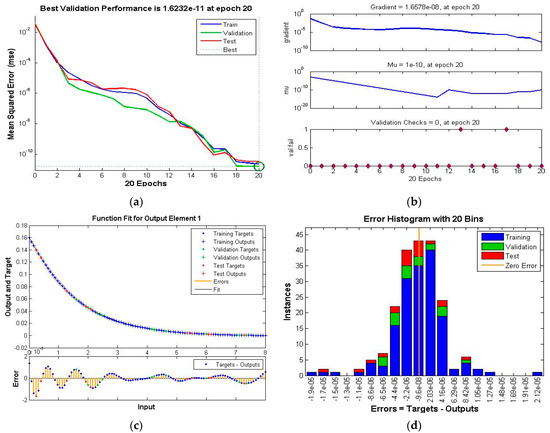
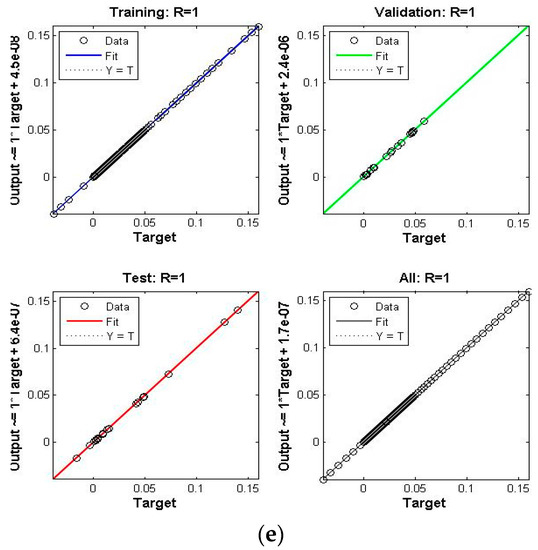
Figure 7. Scenario IV Case I of TD-PNFM. (a) MSE Results: Scenario IV Case I; (b) Transition state: Scenario IV Case I; (c) Fitness: Scenario IV Case I; (d) Error Histogram: Scenario IV Case I; (e)regression: Scenario IV Case I.

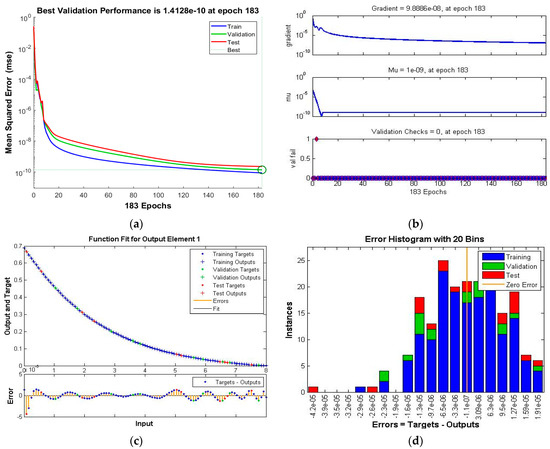
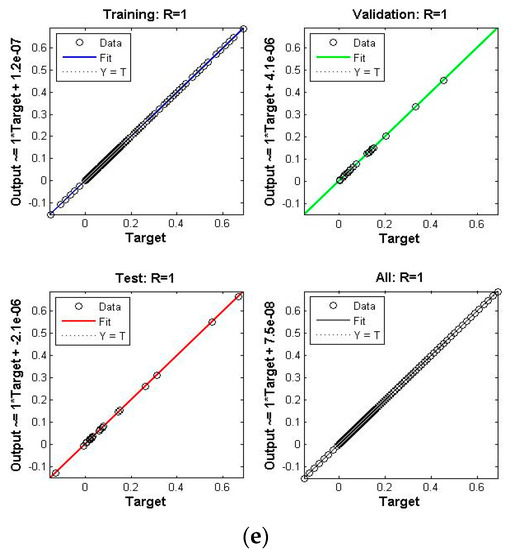
Figure 8. Scenario V Case I of TD-PNFM. (a) MSE Results: Scenario V Case I; (b) Transition state: Scenario V Case I; (c) Fitness: Scenario V Case I; (d) Error Histogram: Scenario V Case I; (e)regression: Scenario V Case I.

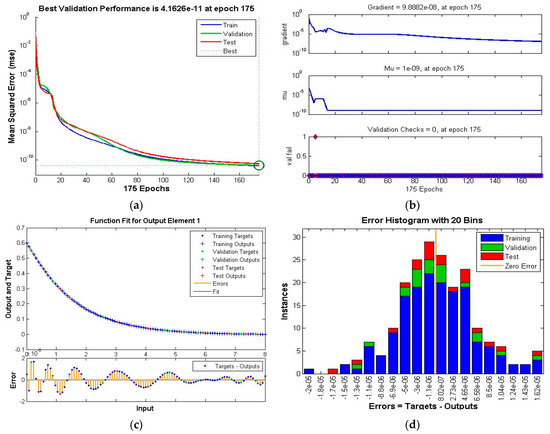
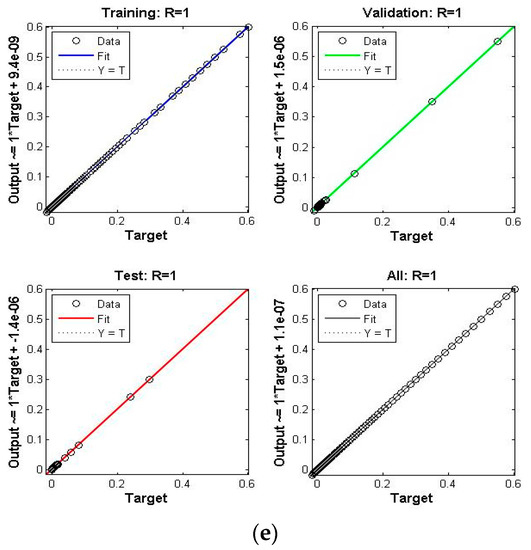
Figure 9. Scenario VI Case I of TD-PNFM. (a) MSE Results: Scenario VI Case I; (b) Transition state: Scenario VI Case I; (c) Fitness: Scenario VI Case I; (d) Error Histogram: Scenario VI Case I; (e) regression: Scenario VI Case I.

Table 2. Outcomes of TLM-BANN of TD-PNFM.

Scenario	Case	MSE Data			Performance	Gradient	Mu	Final Epoch	Time
		Training	Validation	Testing
1	1	8.42 × 10−11	1.94 × 10−10	1.78 × 10−10	8.42 × 10−11	1.00 × 10−07	1.00 × 10−09	204	5 s
	2	3.02 × 10−11	1.01 × 10−10	5.59 × 10−10	3.02 × 10−11	9.85 × 10−08	1.00 × 10−09	188	2 s
	3	2.82 × 10−09	3.07 × 10−09	4.17 × 10−09	1.75 × 10−09	6.68 × 10−06	1.00 × 10−09	43	<1 s
	4	2.26 × 10−11	2.17 × 10−11	6.99 × 10−09	2.26 × 10−11	9.79 × 10−08	1.00 × 10−09	134	1 s
2	1	6.30 × 10−11	9.73 × 10−10	6.64 × 10−11	6.30 × 10−11	9.98 × 10−08	1.00 × 10−09	192	2 s
	2	4.98 × 10−11	1.16 × 10−10	5.26 × 10−11	4.98 × 10−11	9.88 × 10−08	1.00 × 10−09	27	2 s
	3	7.24 × 10−12	1.40 × 10−11	1.06 × 10−11	7.24 × 10−12	9.90 × 10−08	1.00 × 10−10	164	2 s
	4	1.19 × 10−08	7.42 × 10−09	1.46 × 10−08	5.11 × 10−09	1.45 × 10−05	1.00 × 10−09	25	<1 s
3	1	8.81 × 10−11	1.58 × 10−10	5.75 × 10−09	8.81 × 10−11	1.00 × 10−07	1.00 × 10−09	143	1 s
	2	8.70 × 10−10	3.56 × 10−09	1.67 × 10−09	8.71 × 10−10	1.00 × 10−07	1.00 × 10−08	278	3 s
	3	4.60 × 10−11	6.79 × 10−11	1.05 × 10−09	4.60 × 10−11	9.96 × 10−08	1.00 × 10−09	204	2 s
	4	4.58 × 10−11	1.91 × 10−10	2.47 × 10−10	4.58 × 10−11	9.89 × 10−08	1.00 × 10−09	139	1 s
4	1	2.25 × 10−11	1.62 × 10−11	3.48 × 10−11	2.25 × 10−11	1.66 × 10−08	1.00 × 10−10	20	<1 s
	2	4.71 × 10−11	2.35 × 10−11	9.08 × 10−12	4.71 × 10−11	9.92 × 10−08	1.00 × 10−11	106	1 s
	3	5.50 × 10−11	4.25 × 10−11	5.92 × 10−11	5.50 × 10−11	9.93 × 10−08	1.00 × 10−09	212	2 s
	4	1.50 × 10−08	2.71 × 10−08	1.58 × 10−08	1.12 × 10−08	2.11 × 10−08	1.00 × 10−08	68	<1 s
5	1	8.90 × 10−11	1.41 × 10−10	2.30 × 10−10	8.91 × 10−11	9.89 × 10−08	1.00 × 10−09	183	2 s
	2	7.41 × 10−11	8.25 × 10−11	1.50 × 10−10	7.41 × 10−11	9.99 × 10−08	1.00 × 10−09	191	2 s
	3	4.80 × 10−11	7.13 × 10−11	3.81 × 10−10	4.81 × 10−11	9.91 × 10−08	1.00 × 10−09	165	2 s
	4	5.51 × 10−11	5.72 × 10−11	1.69 × 10−10	5.52 × 10−11	9.90 × 10−08	1.00 × 10−09	142	1 s
6	1	3.87 × 10−11	4.16 × 10−11	5.47 × 10−11	3.88 × 10−11	9.89 × 10−08	1.00 × 10−09	175	2 s
	2	2.27 × 10−08	9.76 × 10−09	2.75 × 10−08	7.32 × 10−09	9.00 × 10−06	1.00 × 10−09	26	<1 s
	3	4.07 × 10−11	7.95 × 10−10	7.77 × 10−11	4.07 × 10−11	9.84 × 10−08	1.00 × 10−09	169	2 s
	4	2.30 × 10−10	3.84 × 10−09	2.97 × 10−10	2.30 × 10−10	9.92 × 10−08	1.00 × 10−08	308	4 s

The solution for three-dimension Prandtl nanofluid model for the temperature profile is depicted in Figure 10a,c,e,g,i,k, whereas the AE analysis plots for the temperature profile is given in Figure 10b,d,f,h,j,l. Similarly the solution plots for the concentration profile is shown in Figure 11a,c,e,g. The AE analysis plots are given in Figure 11b,d,f,h. The solution plots for the velocity distribution are shown in Figure 12a,b. The outcomes for the skin friction and Nusselt number are depicted in Figure 13a–c and Figure 14a, respectively.

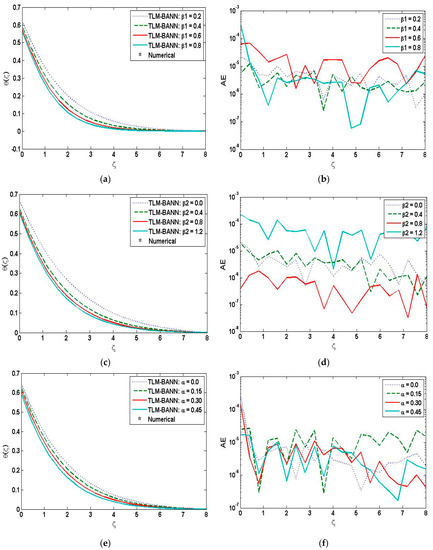
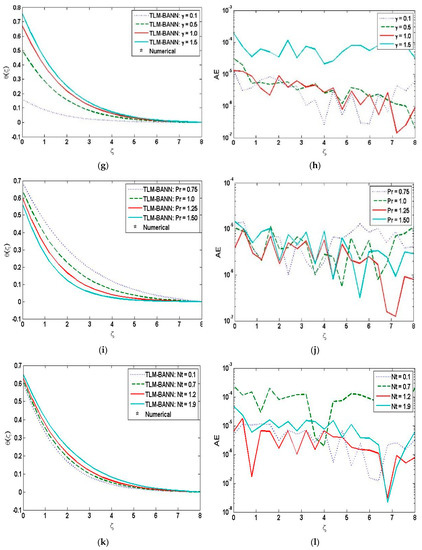
Figure 10. Assessment of TLM-BANN for θ with reference dataset of TD-PNFM (a) Variation of β₁ for θ; (b) AE analysis in variation of β₁ for θ; (c) Variation of β₂ for θ; (d) AE analysis in variation of β₂ for θ; (e) Variation of α for θ; (f) AE analysis in variation of α for θ; (g) Variation of γ for θ; (h) AE analysis in variation of γ for θ; (i) Variation of Pr for θ; (j) AE analysis in variation of Pr for θ; (k) Variation of N_t for θ (l) AE analysis in variation of N_t for θ.

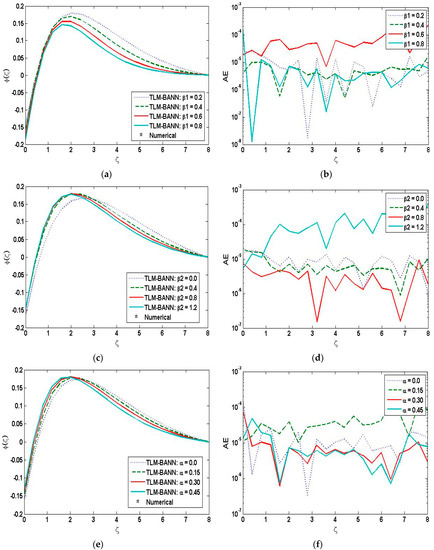
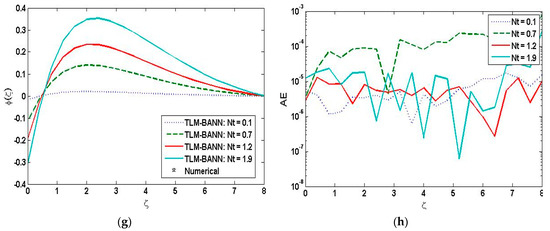
Figure 11. Assessment of TLM-BANN for φ with reference dataset of TD-PNFM. (a) Variation of β₁ for φ; (b) AE analysis in variation of β₁ for φ; (c) Variation of β₂ for φ; (d) AE analysis in variation of β₂ for φ; (e) Variation of α for φ; (f) AE analysis in variation of α for φ; (g) Variation of N_t for φ; (h) AE analysis in variation of N_t for φ.

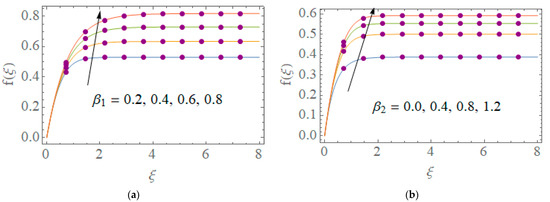
Figure 12. Assessment of TLM-BANN for f with reference dataset of TD-PNFM. (a) Variation of β₁ for f; (b) Variation of β₂ for f.

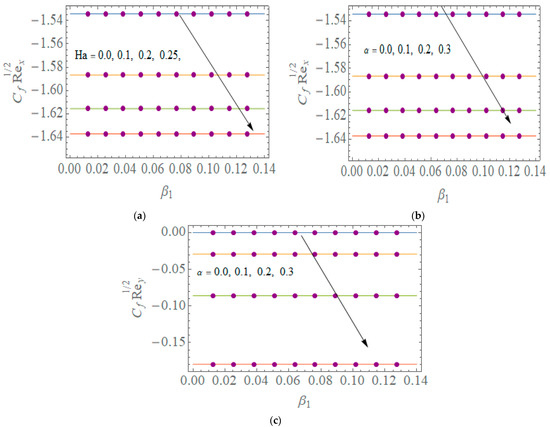
Figure 13. Assessment of TLM-BANN for f with reference dataset of TD-PNFM. (a) Variation of Ha for $C_f{\mathrm{Re}}_x^{1/2}$; (b) Variation of α for $C_f{\mathrm{Re}}_x^{1/2}$; (c) Variation of α for $C_f{\mathrm{Re}}_y^{1/2}$.

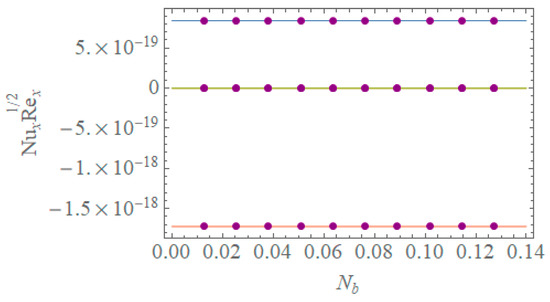
Figure 14. Assessment of TLM-BANN for f with reference dataset of TD-PNFM. Variation of N_t for $N{u}_x{\mathrm{Re}}_x^{-1/2}$.

4.1. Impact of Variation on θ(ζ)

The MATLAB software is utilize to interpret the effects of variation β₁, β₂, α, Pr, γ and N_t on temperature profile. Figure 10 shows the solution plots and AE analysis plots for the temperature profile by varying of Prandtl fluid number, flexible number, ratio parameter, Prandtl number, Biot number and thermophoresis number. The absolute error values for the following variations are 10⁻⁸ to 10⁻³, 10⁻⁸ to 10⁻³, 10⁻⁷ to 10⁻³, 10⁻⁷ to 10⁻³, 10⁻⁷ to 10⁻⁴ and 10⁻⁸ to 10⁻³, respectively.

One may witness that:

• The temperature profile increases with the increase in Biot number.
• Temperature distribution shows decreasing behavior with the increase in Prandtl fluid number and flexible number.
• Increase in thermophoresis number leads to an increase in temperature profile.
• Temperature profile decreases with the increase in the values of Prandtl number and ratio parameter.

4.2. Impact of Variation on

Software MATLAB is used to interpret the AE analysis plots and the solution plots to examine the variation of β₁, β₂, α and N_t on the concentration profile. Figure 11 depicts the solution and AE analysis plots for the concentration profile by the variation of Prandtl fluid number, flexible number, ratio parameter and thermophoresis number. It can be easily seen that Prandtl fluid number, flexible number and ratio parameter have the same impact on the concentration profile, but thermophoresis number has the opposite effect, which is an upsurge in the trend of concentration distribution. The absolute error values for the following variations are 10⁻⁸ to 10⁻³, 10⁻⁷ to 10⁻³, 10⁻⁷ to 10⁻³ and 10⁻⁸ to 10⁻³, respectively.

One may witness that:

• The concentration profile shows decreasing behavior when the value of Prandtl fluid parameter increases.
• Increase in flexible number causes a decrease in concentration profile.
• Increasing values of ratio parameter leads to a decrease in the behavior of concentration profile.
• The concentration profile increases with the increase in thermophoresis parameter. The reason is, raising thermophoresis parameter induces a rise in the system’s thermal conductivity, which adds to an increase in concentration.

4.3. Impact of Variation on f(ζ)

The effects of variation β₁ and β₂ on velocity distribution is shown in Figure 12. Figure 12 shows the solution plots for the velocity profile by varying of Prandtl fluid number and flexible number.

One may witness that:

• Velocity distribution shows an increasing trend with the increase in Prandtl fluid number.
• Increase in flexible number leads to an increase in velocity profile.

4.4. Skin Friction Coefficient

The effects of variation of Ha and α on skin friction ($C_f{\mathrm{Re}}_x^{1/2}$ and $C_f{\mathrm{Re}}_y^{1/2}$) is shown in Figure 13. Figure 13 shows the plots for the skin friction by varying of Hartmann number and ratio parameter.

One may witness that:

• $C_f{\mathrm{Re}}_x^{1/2}$ shows a declining trend with the increase in Hartmann number and ratio parameter against Prandtl fluid parameter.

• Rise in ratio parameter leads to a decrease in $C_f{\mathrm{Re}}_y^{1/2}$ against Prandtl fluid parameetr.

4.5. Nusselt Number

The effects of variation of thermophoresis parameter on Nusselt number ($N{u}_x{\mathrm{Re}}_x^{-1/2}$) is shown in Figure 14. Figure 14 shows the plots for the Nusselt number by varying of thermophoresis parameter against Brownian motion parameter.

One may witness that:

• $N{u}_x{\mathrm{Re}}_x^{-1/2}$ shows a falling pattern with the increase in thermophoresis parameter against Brownian motion parameter.

5. Conclusions

The technique of Levenberg-Marquardt with backpropagated neural network is used to study the three-dimensional Prandtl nanofluid flow model with a convectively heated surface by the variations of Prandtl fluid number, flexible number, ratio parameter, Prandtl number, Biot number and thermophoresis number. The governing PDEs are transformed to system of ordinary differential equations by applying suitable transformation. The Mathematica command ‘ND Solve’ is utilized to compute the reference dataset for 101 points, in which there are 81 points for training, 10 point for testing and 10 points for validation. The regression analysis, error histogram and MSE data validates the performance of TLM-BANN.

There are few points drawn from the results are written below:

• The temperature profile shows increasing behavior with the increase in Biot number.
• Temperature distribution is decreasing with the increase in Prandtl fluid number and flexible number.
• Increase in thermophoresis number leads to an increase in temperature profile.
• Temperature profile decreases when the values of Prandtl number and ratio parameter increase.
• The concentration profile decreasing when the value of Prandtl fluid parameter increases.
• Increase in flexible number causes a decrease in concentration profile.
• Increasing values of ratio parameter causes a decrease in concentration profile.
• The concentration profile increases with the increasing values of thermophoresis parameter.
• Velocity distribution shows an increasing trend for the upsurge in the values of Prandtl fluid parameter and flexible parameter.
• Skin friction coefficient declines for the increase in Hartmann number and ratio parameter
• Nusselt number falls for the rising values of thermophoresis parameter against Nb.

6. Future Work

In future, some new soft computing architectures may be implemented for different fluidic models provided in [50,51,52] successfully.