Optical Nonreciprocity Based on the Four-Wave Mixing Effect in Semiconductor Quantum Dots
Abstract
1. Introduction
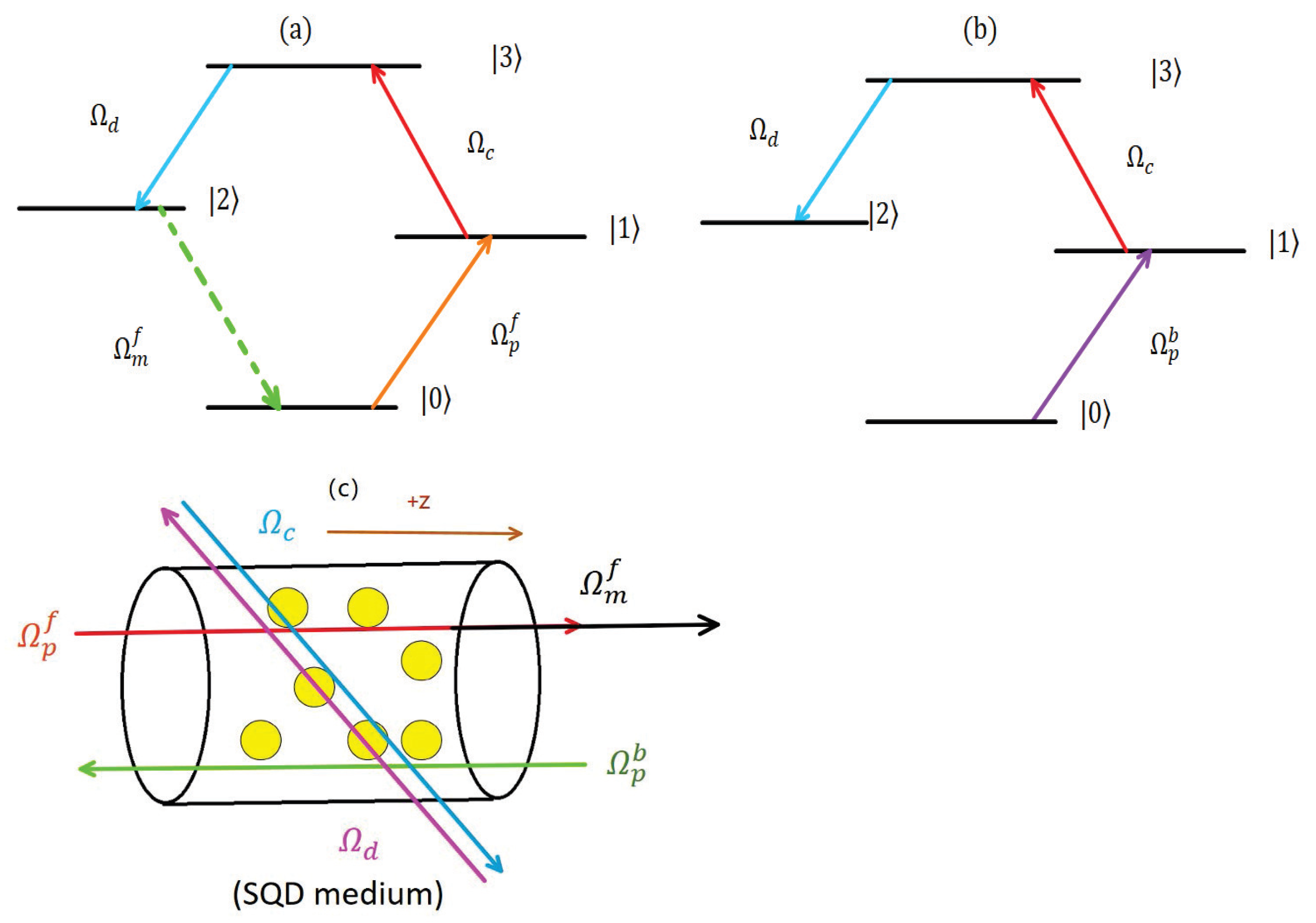
2. Theoretical Model and Equations
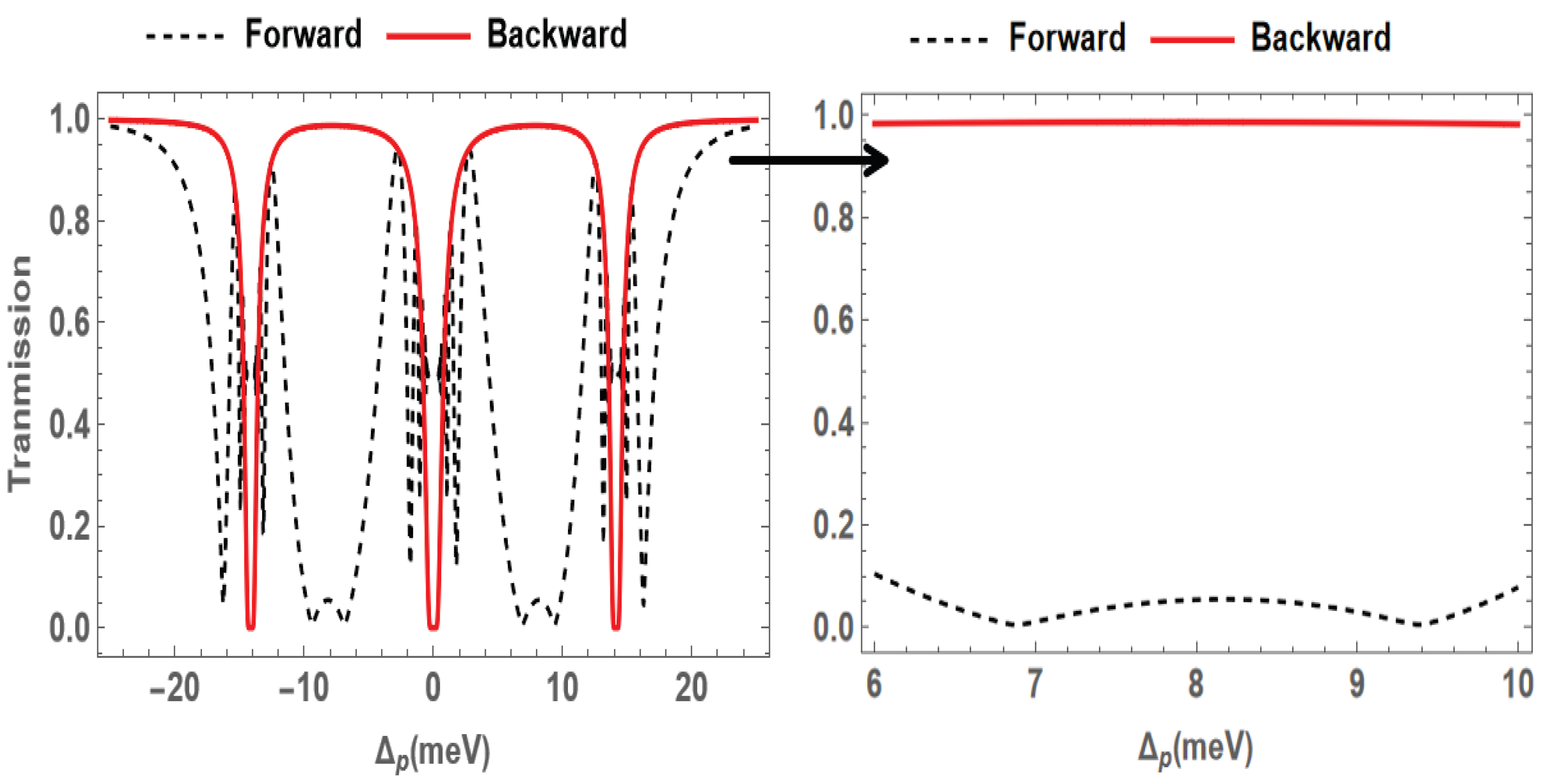
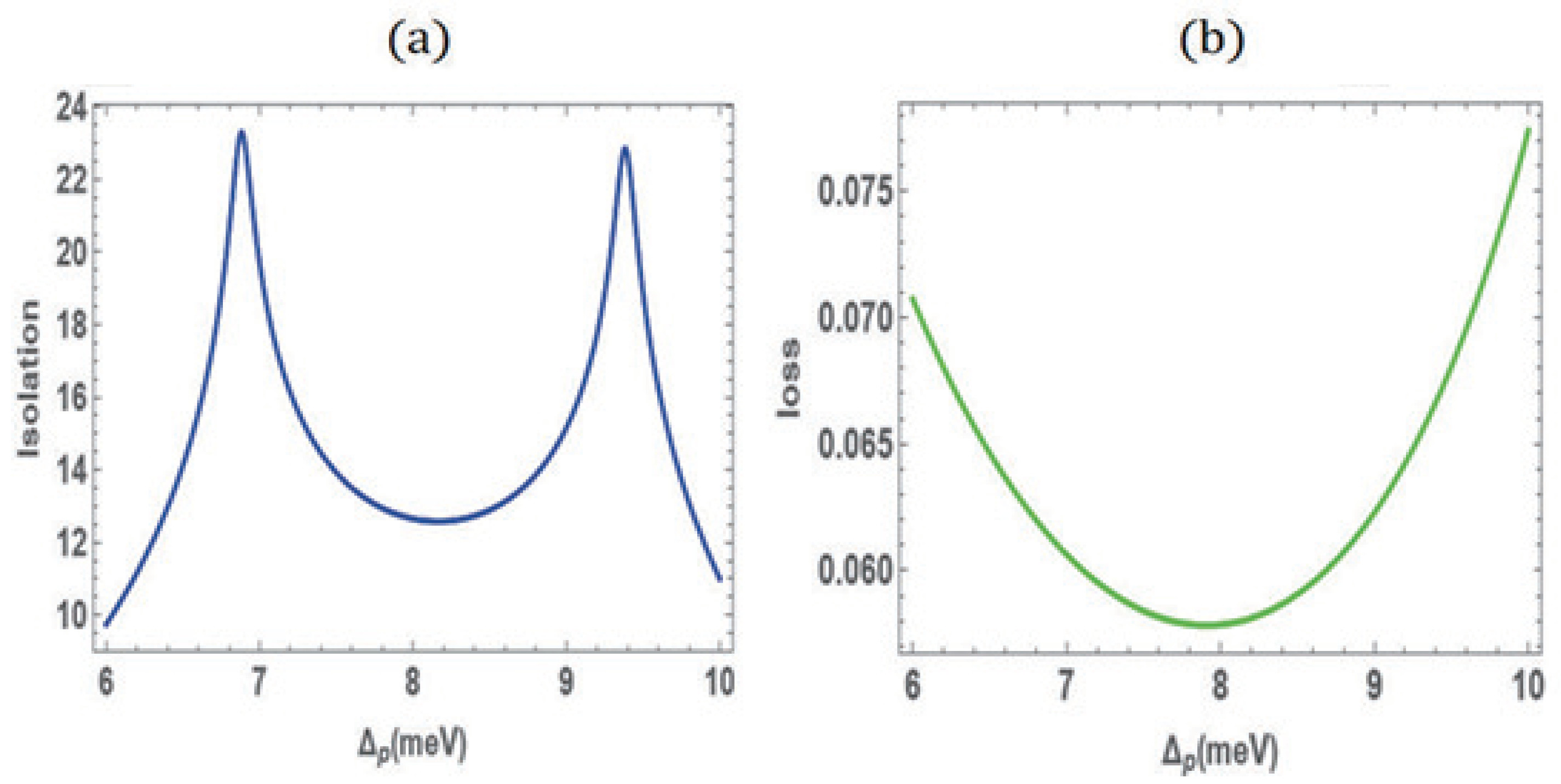
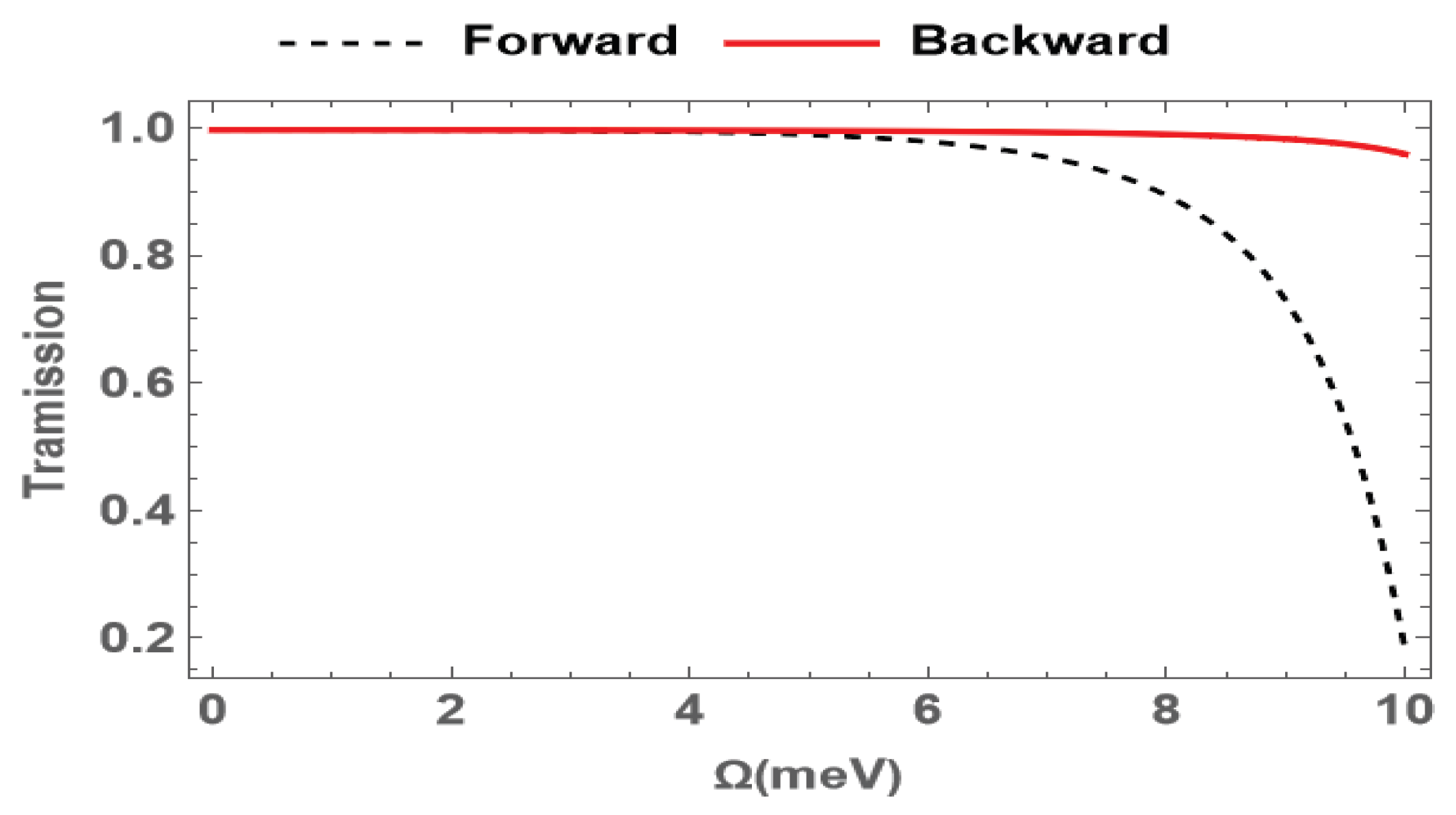
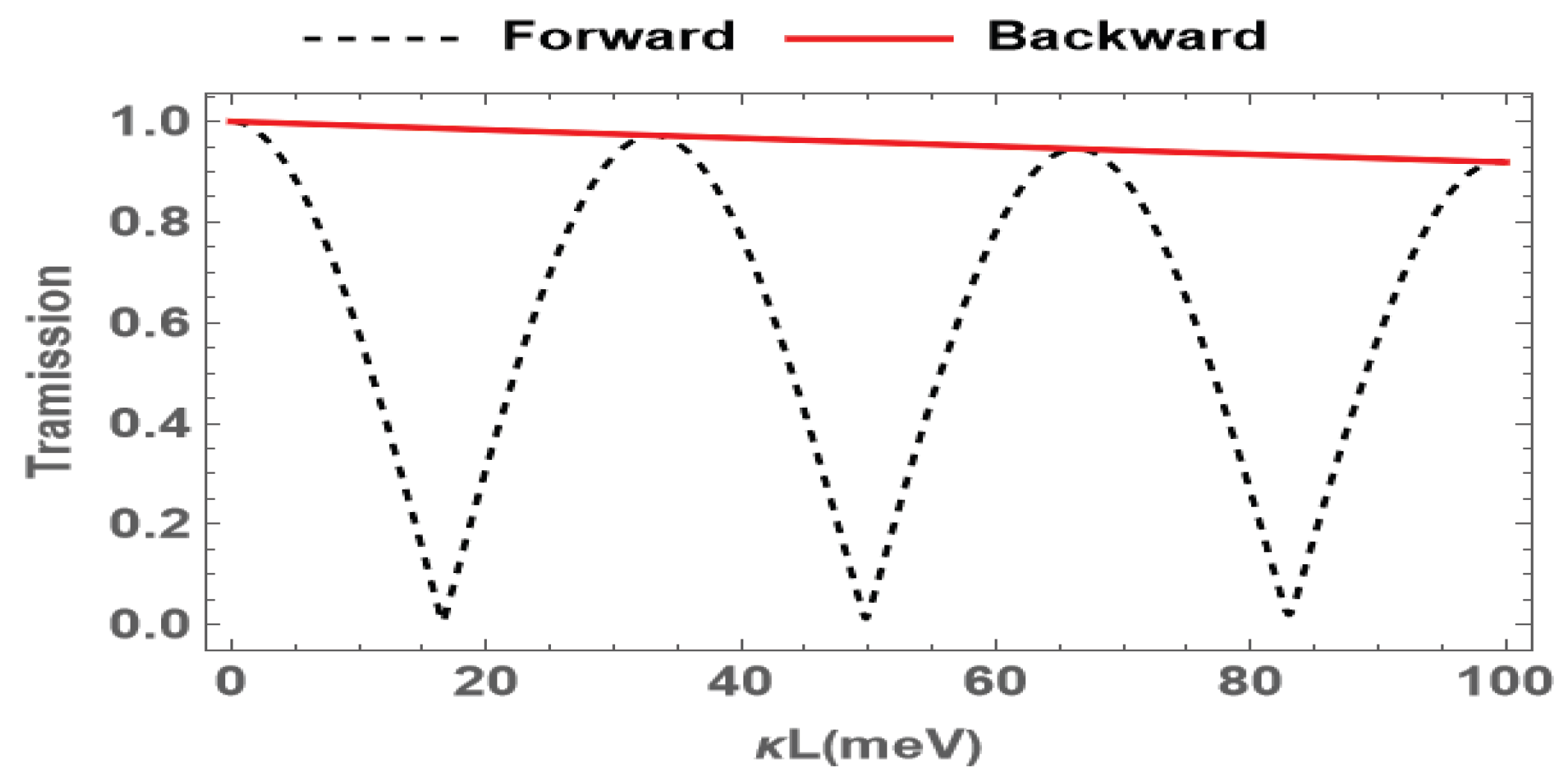
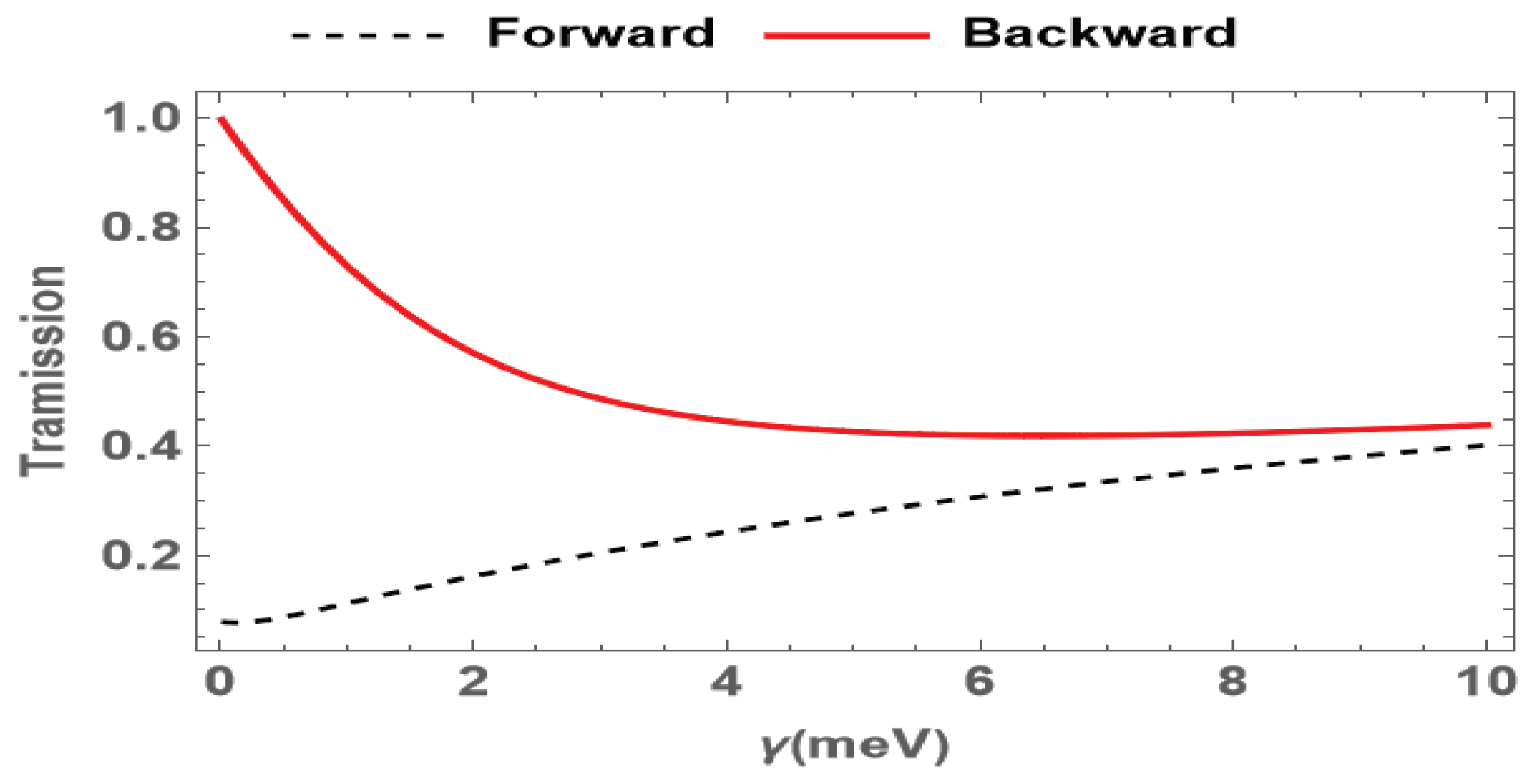
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khanikaev, A.B.; Alù, A. Nonlinear dynamic reciprocity. Nat. Photon. 2015, 9, 359–361. [Google Scholar] [CrossRef]
- Yu, Z.; Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photon. 2009, 3, 91–94. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S.; Rauschenbeutel, A.; Schneeweiss, P.; Volz, J.; Pichler, H.; Zoller, P. Chiral quantum optics. Nature 2017, 541, 473–480. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Mousavi, S.H.; Shvets, G.; Kivshar, Y.S. One-way extraordinary optical transmission and nonreciprocal spoof plasmons. Phys. Rev. Lett. 2010, 105, 126804. [Google Scholar] [CrossRef] [PubMed]
- Bi, L.; Hu, J.; Jiang, P.; Kim, D.H.; Dionne, G.F.; Kimerling, L.C.; Ross, C.A. On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nat. Photon. 2011, 5, 758–762. [Google Scholar] [CrossRef]
- Fan, L.; Wang, J.; Varghese, L.T.; Shen, H.; Niu, B.; Xuan, Y.; Weiner, A.M.; Qi, M. An all-silicon passive optical diode. Science 2012, 335, 447–450. [Google Scholar] [CrossRef]
- Fan, L.; Varghese, L.T.; Wang, J.; Xuan, Y.; Weiner, A.M.; Qi, M. Silicon optical diode with 40 db nonreciprocal transmission. Opt. Lett. 2013, 38, 1259–1261. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, X.; Hua, S.; Yang, C.; Wen, J.; Jiang, L.; Li, G.; Wang, G.; Xiao, M. Parity–time symmetry and variable optical isolation in active–passive-coupled microresonators. Nat. Photon. 2014, 8, 524–529. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, J.; Shen, Z.; Cao, J.; Chen, X.; Liang, X.; Wan, W. Optically induced transparency in a micro-cavity. Light. Sci. Appl. 2016, 5, e16072. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Li, X.; Zhou, H.-T.; Xue, J.-J.; Li, R.-N.; Wang, D.; Yang, B.-D.; Zhang, J.-X. Optical reciprocity-nonreciprocity-amplification conversion based on degenerate four-wave mixing. J. Opt. Soc. Am. B 2024, 41, 984–991. [Google Scholar] [CrossRef]
- Xia, K.; Lu, G.; Lin, G.; Cheng, Y.; Niu, Y.; Gong, S.; Twamley, J. Reversible nonmagnetic single-photon isolation using unbalanced quantum coupling. Phys. Rev. A 2014, 90, 043802. [Google Scholar] [CrossRef]
- Scheucher, M.; Hilico, A.; Will, E.; Volz, J.; Rauschenbeutel, A. Quantum optical circulator controlled by a single chirally coupled atom. Science 2016, 354, 1577–1580. [Google Scholar] [CrossRef]
- Hafezi, M.; Rabl, P. Optomechanically induced non-reciprocity in microring resonators. Opt. Express 2012, 20, 7672–7684. [Google Scholar] [CrossRef] [PubMed]
- Ruesink, F.; Miri, M.-A.; Alù, A.; Verhagen, E. Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat. Commun. 2016, 7, 13662. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, Y.-L.; Chen, Y.; Zou, C.-L.; Xiao, Y.-F.; Zou, X.-B.; Sun, F.-W.; Guo, G.-C.; Dong, C.-H. Experimental realization of optomechanically induced non-reciprocity. Nat. Photon. 2016, 10, 657–661. [Google Scholar] [CrossRef]
- Chen, L.-T.; Qin, L.-G.; Tian, L.-J.; Huang, J.-H.; Zhou, N.-R.; Gong, S.-Q. Effects of cross-Kerr coupling on transmission spectrum of double-cavity optomechanical system. Chin. Phys. B 2024, 33, 064204. [Google Scholar] [CrossRef]
- Wang, D.-W.; Zhou, H.-T.; Guo, M.-J.; Zhang, J.-X.; Evers, J.; Zhu, S.-Y. Optical diode made from a moving photonic crystal. Phys. Rev. Lett. 2013, 110, 093901. [Google Scholar] [CrossRef]
- Ramezani, H.; Jha, P.K.; Wang, Y.; Zhang, X. Nonreciprocal localization of photons. Phys. Rev. Lett. 2018, 120, 043901. [Google Scholar] [CrossRef]
- Horsley, S.; Wu, J.-H.; Artoni, M.; Rocca, G.L. Optical nonreciprocity of cold atom bragg mirrors in motion. Phys. Rev. Lett. 2013, 110, 223602. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Hu, Y.; Lin, G.; Niu, Y.; Xia, K.; Gong, J.; Gong, S. Thermal-motion-induced non-reciprocal quantum optical system. Nat. Photon. 2018, 12, 744–748. [Google Scholar] [CrossRef]
- Xia, K.; Nori, F.; Xiao, M. Cavity-free optical isolators and circulators using a chiral cross-Kerr nonlinearity. Phys. Rev. Lett. 2018, 121, 203602. [Google Scholar] [CrossRef]
- Fan, S.; Qi, Y.; Lin, G.; Niu, Y.; Gong, S. Broadband optical nonreciprocity in an n-type thermal atomic system. Opt. Commun. 2020, 462, 125343. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, L.; Zhang, S.; Li, X.; Qian, J.; Lin, G.; Niu, Y.; Gong, S. Low insertion loss optical isolator with widely tunable frequency. Opt. Commun. 2021, 489, 126861. [Google Scholar] [CrossRef]
- Liang, C.; Liu, B.; Xu, A.N.; Wen, X.; Lu, C.; Xia, K.; Tey, M.K.; Liu, Y.C.; You, L. Collision-induced broadband optical nonreciprocity. Phys. Rev. Lett. 2020, 125, 123901. [Google Scholar] [CrossRef]
- Song, F.; Wang, Z.; Li, E.; Huang, Z.; Yu, B.; Shi, B. Optical nonreciprocity using four-wave mixing in hot atoms. Appl. Phys. Lett. 2021, 119, 024101. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, S.; Niu, Y.; Gong, S. Ultra-strong nonreciprocal amplification with hot atoms. Opt. Commun. 2022, 515, 128195. [Google Scholar] [CrossRef]
- Ge, Y.-R.; Kang, Z.; Ding, C.-L.; Hao, X.-Y.; Jin, R.-B. Efficient optical nonreciprocity based on four-wave mixing effect in semiconductor quantum well. Acta Phys. Sin. 2024, 73, 014201. [Google Scholar] [CrossRef]
- Veisi, M.; Kazemi, S.H.; Mahmoudi, M. Tunneling-induced optical limiting in quantum dot molecules. Sci. Rep. 2020, 10, 16304. [Google Scholar] [CrossRef]
- Hao, X.; Wu, J.; Wang, Y. Steady-state absorption–dispersion properties and four-wave mixing process in a quantum dot nanostructure. J. Opt. Soc. Am. B 2012, 29, 420–428. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubariry, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Singh, M.R.; Meng, Q.; Jiang, X. A Study of Degenerate Four-Wave Mixing and Phase Conjugation in Metallic Nanohybrids. Adv. Opt. Mater. 2024, 12, 2401741. [Google Scholar] [CrossRef]
- Yu, C.; Sun, L.; Zhang, H.; Chen, F. High efficiency four-wave mixing in double asymmetry quantum dots. Optik 2019, 180, 295–301. [Google Scholar] [CrossRef]
- Ramirez, H.Y.; Lin, C.H.; Chao, C.C.; Hsu, Y.; You, W.T.; Huang, S.Y.; Chen, Y.T.; Tseng, H.C.; Chang, W.H.; Lin, S.D.; et al. Optical fine structures of highly quantized InGaAs/GaAs self-assembled quantum dots. Phys. Rev. B 2010, 81, 245324. [Google Scholar] [CrossRef]
- Bayer, M.; Forchel, A. Temperature dependence of the exciton homogeneous linewidth in in 0.60 ga 0.40 as/gaas self-assembled quantum dots. Phys. Rev. B 2002, 65, 041308. [Google Scholar] [CrossRef]
- Yu, C.; Sun, L.; Zhang, H.; Chen, F. Controllable optical bistability in double quantum dot molecule. IET Optoelectron. 2018, 12, 215–219. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Yang, H.; Xu, F.; Qi, Y.; Niu, Y.; Gong, S. Optical Nonreciprocity Based on the Four-Wave Mixing Effect in Semiconductor Quantum Dots. Nanomaterials 2025, 15, 380. https://doi.org/10.3390/nano15050380
Lin Z, Yang H, Xu F, Qi Y, Niu Y, Gong S. Optical Nonreciprocity Based on the Four-Wave Mixing Effect in Semiconductor Quantum Dots. Nanomaterials. 2025; 15(5):380. https://doi.org/10.3390/nano15050380
Chicago/Turabian StyleLin, Zelin, Han Yang, Fei Xu, Yihong Qi, Yueping Niu, and Shangqing Gong. 2025. "Optical Nonreciprocity Based on the Four-Wave Mixing Effect in Semiconductor Quantum Dots" Nanomaterials 15, no. 5: 380. https://doi.org/10.3390/nano15050380
APA StyleLin, Z., Yang, H., Xu, F., Qi, Y., Niu, Y., & Gong, S. (2025). Optical Nonreciprocity Based on the Four-Wave Mixing Effect in Semiconductor Quantum Dots. Nanomaterials, 15(5), 380. https://doi.org/10.3390/nano15050380





