Abstract
Cognitive modeling of response time distributions has seen a huge rise in popularity in individual differences research. In particular, several studies have shown that individual differences in the drift rate parameter of the diffusion model, which reflects the speed of information uptake, are substantially related to individual differences in intelligence. However, if diffusion model parameters are to reflect trait-like properties of cognitive processes, they have to qualify as trait-like variables themselves, i.e., they have to be stable across time and consistent over different situations. To assess their trait characteristics, we conducted a latent state-trait analysis of diffusion model parameters estimated from three response time tasks that 114 participants completed at two laboratory sessions eight months apart. Drift rate, boundary separation, and non-decision time parameters showed a great temporal stability over a period of eight months. However, the coefficients of consistency and reliability were only low to moderate and highest for drift rate parameters. These results show that the consistent variance of diffusion model parameters across tasks can be regarded as temporally stable ability parameters. Moreover, they illustrate the need for using broader batteries of response time tasks in future studies on the relationship between diffusion model parameters and intelligence.
1. Introduction
Being quick on the uptake or being quick-witted are popular idioms when describing smart individuals. Decades of research on the relationship between general intelligence and behavioral response times established the close link between mental abilities and the speed of information processing. A recent review of 172 studies reported an average correlation of r = −.24 between mental abilities and different measures of information processing speed [1]. More specifically, the correlations between mean response times in elementary cognitive tasks and general intelligence ranged from r = −.25 to r = −.40. In general, composite measures of response times tend to show higher correlation with general intelligence than single response time measures. For example, canonical correlations between test batteries of response time tasks and general intelligence ranged from C = .55 to C = .72 [2,3,4]. This suggests that it is the variance shared by different response time tasks—general mental speed—that is closely related to general intelligence.
Typically, mental speed is assessed by calculating the mean or median of each participant’s intra-individual response time distribution in an experimental task. Because mean response times should exhibit ideal psychometric properties under assumptions of classical test theory, they are usually preferred over other parameters describing an individual’s response time distribution such as the standard deviation, skewness, or kurtosis. However, there are a couple of findings suggesting that inter-individual differences in various parameters of intra-individual response time distributions may be of particular interest for explaining individual differences in mental abilities. First, previous research has indicated that the intra-individual standard deviation of response times is sometimes more strongly related to general intelligence than mean or median response times [5,6]. However, a recent meta-analysis of 24 studies found no consistent difference in the size of correlations between these measures [7]. Second, the worst performance rule [8] describes the phenomenon that when individual response times are ranked from fastest to slowest, the slowest response times are more predictive of general intelligence than the mean or best response times [9,10]. Third, using means as a measure of central tendency to summarize the information contained in individual response time distributions may not be the ideal choice, as response time distributions are strongly positively skewed, which contradicts the assumption of a Gaussian distribution.
Moreover, when only mean response times are used as measures of mental speed, information contained in the shape of response time distributions is inevitably lost. Response time distributions can be described as combined Gaussian and exponential distributions. Shifts in both of these elements of response time distributions can lead to a similar increase in mean response times, just like a shift in the response time distribution or an increase in skewness can result in higher mean response times [11,12]. Taken together, these phenomena suggest that it may be worthwhile to consider the complete distribution of response times when analyzing the relationship between mental speed and mental abilities.
Beyond that, the distinction between decision times and movement times has proven to be another critical issue for the study of individual differences in mental chronometry. Some experimental setups require participants to rest their finger(s) on a home button that they are instructed to release as soon as the stimulus is presented and their decision is made. Subsequently, they have to press one of several response keys. Home-button setups are supposed to allow dissociating between the time required for the stimulus to be perceived, encoded, and processed (decision time, DT), and the time required for response execution (motor time, MT). Although DT and MT tend to load on two orthogonal factors [13], moderate correlations between DT and MT are reported in many studies [6]. The view that some degree of process contamination exists in both of these measures is supported by two experiments showing that participants release the home key immediately after detecting the stimulus, but before finalizing their decision, in anticipation of their response [14]. These results suggest that a clear-cut distinction between decision times and movement times cannot be easily achieved by a home-button setup and that other methods have to be employed to obtain a process-pure measurement of the speed of information processing.
1.1. The Diffusion Model: A Process Model of Speeded Binary Decision Making
Mathematical models of response times can overcome the aforementioned problems (i.e., providing adequate parameters for the description of a response time distribution, analyzing the complete distribution, allowing a more valid distinction between the time required for decision processes and for non-decision processes such as movement times), because they provide a process-based account of decision making that uses a participant’s whole response time distribution to estimate parameters reflecting various elements of the decision process. The most prominent mathematical model of binary response time tasks is the diffusion model, which is a random-walk model that assumes a continuous information accumulation during a binary decision until one of two decision thresholds is reached [15]. This information accumulation process can be described by a Wiener diffusion process consisting of a constant systematic component, the drift, and normally distributed random noise.
The basic diffusion model contains four parameters (see Figure 1): The drift rate (v) reflects the strength and direction of the systematic influence on the diffusion process and is a direct performance measure for the speed of information uptake. Boundary separation (a) reflects the amount of information considered for a decision, which is for example influenced by a participant’s cautiousness or by instructions stressing speed over accuracy and vice versa, e.g., [16,17]. The starting point (z) reflects a priori biases in decision making that can be influenced by asymmetric pay-off matrices [16]. Finally, the non-decision time () reflects the time required for all sorts of decision-unrelated processes such as encoding or motor programming and execution.
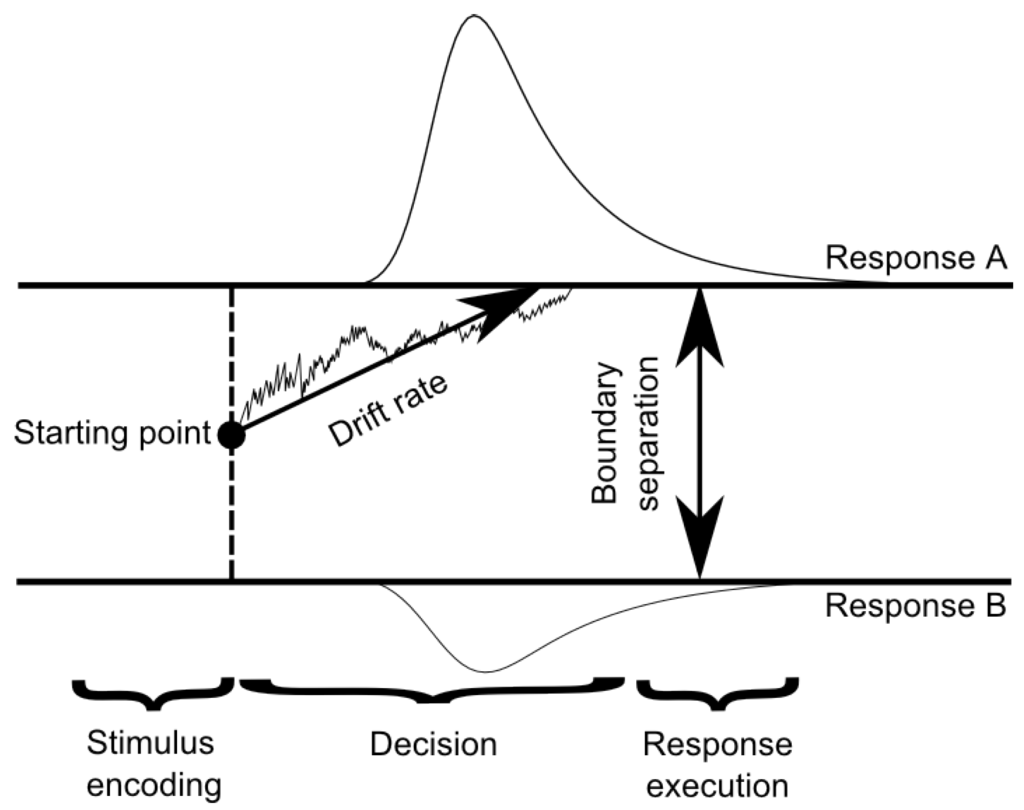
Figure 1.
A simplified illustration of the basic diffusion model. Information accumulation begins at the starting point z and continues with a mean drift rate v (affected by random noise) until one of two thresholds is hit. Boundary separation a represents the amount of information that has to be accumulated before a decision is made. Outside of the information accumulation process, non-decision time (not shown here) quantifies the time of non-decision processes such as stimulus encoding and response execution. This figure was inspired by the illustration of the diffusion model in Voss et al. [18].
For each participant, a set of parameters is estimated by permuting parameter values until the predicted response time distribution closely resembles the empirical response time distributions. One advantage of the diffusion model is that it maps different cognitive processes to different model parameters and provides process-pure measures of these parameters that have been empirically validated [16]. Hence, the diffusion model takes into account the whole distribution of response times and allows separating the speed of information uptake—reflected in the drift rate parameter—from the speed of the motor response—reflected in the non-decision time parameter.
The diffusion model has seen a recent rise in popularity thanks to the publication of software solutions that allow fitting the model without extensive programming knowledge [19,20,21,22]. Applications in individual differences research include studies on individual differences in attention [23], in impulsivity, e.g., [24], in mental abilities, e.g., [25,26,27,28], in numeracy [29], and in word recognition [30].
1.2. Correlations between Diffusion Model Parameters and Mental Abilities
First studies on the relationship between diffusion model parameters and mental abilities have supported the notion that the diffusion model may help to identify the speed of specific cognitive processes and their specific associations with intelligence. This research is based on the assumption that individual differences in these model parameters reflect trait-like properties of cognitive processes. Four studies analyzing the relation between diffusion model parameters and mental abilities reported substantial correlations between drift rate and mental abilities ranging from r = .18 to .90 [25,26,27,28]. Ratcliff et al. [25] asked participants in three age groups (college age, 60–74 years old, 75–90 years old) to complete the vocabulary and matrix reasoning subtests of the Wechsler intelligence test and analyzed correlations with a latent drift rate factor from a numerosity discrimination, recognition memory, and lexical decision response time task. Correlations ranged from r = .60 to .90 for the vocabulary subtest, and from r = .36 to .85 for the matrix reasoning subtest. Moreover, the same participants also completed an item and associative recognition task. Manifest correlations between drift rate parameters estimated from response time distributions of these tasks ranged from r = .18 to .67 with the matrix reasoning subtest, and from r = .28 to .68 with the verbal subtest [26]. Schmiedek et al. [27] reported a latent correlation of r = .79 between reasoning ability and drift rates in eight response time tasks (including verbal, numerical, and spatial tasks) in a student sample, and Schubert et al. [28] reported a correlation of r = .50 between general intelligence and a drift rate factor derived from three response time tasks (choice response task, recognition task, semantic discrimination task). Taken together, these results indicate that smarter individuals have a greater speed of information uptake as reflected in the drift rate parameter.
Previous studies have reported less consistent associations between non-decision time and mental abilities. Ratcliff et al. [25] found latent correlations ranging from r = −.14 to .40 for the vocabulary subtest, and from r = −.04 to −.50 for the matrix reasoning subtest, and Ratcliff et al. [26] reported manifest correlations ranging from r = −.29 to .37 between non-decision times in item recognition tasks and associative recognition tasks and intelligence, leading them to conclude that non-decision times were not reliably associated with intelligence. Schmiedek et al. [27], however, reported a small but significant positive correlation between a latent non-decision time factor and reasoning ability, r = .25. Schubert et al. [28] also found evidence for an association between the non-decision time parameter and general intelligence, but in the direction that more intelligent individuals had shorter non-decision times, r = −.42. More research is needed to conclude whether intelligence is consistently associated with the non-decision time parameter. Because the non-decision time parameter captures to some degree movement times, it would be consistent with previous research if it was not related to intelligence. However, the non-decision time parameter does not only reflect motor speed, but also the time required for encoding and for memory-related processes [31] and may thus be related to general intelligence.
Finally, some studies have found associations between boundary separation and mental abilities. Ratcliff et al. [25] found latent correlations ranging from r = −.02 to .52 for the vocabulary subtest, and from r = .15 to .37 for the matrix reasoning subtest, and Ratcliff et al. [26] reported manifest correlations ranging from r = −.32 to .14 between boundary separation parameters in item and associative recognition tasks and intelligence. Schmiedek et al. [27] reported a negative latent correlation between a boundary separation factor and reasoning ability, r = −.48. Again, the results seem largely inconsistent, because greater intelligence has been found to be associated both with a smaller and a larger boundary separation, i.e., with less and more decision cautiousness.
Taken together, these first studies strongly support the view that more intelligent individuals have a higher drift rate across a broad variety of response time tasks and participant samples. In comparison, associations between intelligence and non-decision time/boundary separation parameters were smaller and largely inconsistent within and across studies. The number of studies relating diffusion model parameters to mental abilities is still too small to allow identifying variables moderating the size and direction of these associations such as sample characteristics or task difficulties.
1.3. Diffusion Model Parameters as Personality Traits
Before a claim can be made that diffusion model parameters reflect trait-like properties of cognitive processes, it has to be shown that they qualify as trait-like variables themselves. Several authors have previously suggested an integration of item response theory (IRT) and the diffusion model into a latent variable model, which takes into account that the mean drift rate consists of a person part and an item part [32,33,34]. It has been shown that diffusion IRT models can account for psychometric responses on tests of bipolar traits [33] as well as for ability tests under the assumption that abilities have a natural zero point [34]. Moreover, Vandekerckhove [35] has suggested a cognitive latent variable model based on Bayesian hierarchical modeling for the simultaneous analysis of response time data and personality or ability test data. This framework allows estimating latent task abilities, which are reflected in diffusion model parameters across different tasks and which can be related to external covariates. However, none of these approaches explicitly takes into consideration the core assumption of many personality theories, which consists of the temporal stability and trans-situational consistency of personality traits [36,37,38]. Showing that diffusion model parameters can be accounted for with a latent variable model is a necessary, but not a sufficient condition to conclude that they can be treated as trait-like variables, as state variables can also be modeled as latent variables [38]. Hence, diffusion model parameters only qualify as trait-like variables if it can be shown that they are stable across time and consistent over different tasks/situations.
Moreover, because diffusion model parameters can be affected by task properties [16], it is important to identify to what extent specific parameter values reflect person properties common to different tasks and to what extent they reflect specific person-task interactions. This knowledge would facilitate the planning of future studies on the relationship between mental speed and intelligence by helping to determine how many response time tasks are needed for a reliable assessment of common model parameters. Moreover, estimates of the consistency of task-specific model parameters would allow evaluating the associations between these model parameters and intelligence. From the viewpoint of classical test theory (CTT), the effects of the situation and the effects of the person–situation interaction act as nuisance variables when estimating the diffusion model parameters, i.e., these effects add to the error variance. In turn, the variance portions that are not due to individual differences in a latent trait attenuate the correlations between diffusion model parameters and intelligence. Thus, the estimates of consistency inform us about the maximum correlation that may be expected in empirical investigations of the relationship between diffusion model parameters and intelligence (the coefficient of consistency indicates an upper bound of the correlation between the diffusion model parameters and intelligence). Therefore, knowing the consistencies helps to interpret the empirical correlations that have been reported in previous research and that may be reported in future research.
Previous research has suggested that response times may be experimentally influenced by fatigue and performance-dependent rewards [39,40]. However, it is as of yet unclear whether such situational factors affect the relative performance in response time tasks when not experimentally induced and how this might be reflected in diffusion model parameters. Previous research on the temporal stability of diffusion model parameters is scarce, but first studies suggest a moderate temporal stability over a period of one week. One week test-retest correlations of drift rate, threshold separation, and non-decision time parameters ranged from r = .48 to .86 (mean r = .66) in lexical decisions tasks [30,41], from r = .35 to .77 (mean r = .56) in a recognition memory task [41], and from r = .30 to .79 (mean r = .67) in an associative priming task [41].
However, a period of one week may be suited to estimate the reliability with test-retest correlations, but it does not convey much information about the temporal stability and trans-situational consistency of model parameters in a broader sense. Because intelligence is known to show a great temporal stability over longer periods of time, e.g., [13,42], diffusion model parameters should show a similar temporal stability if considered to reflect processes giving rise to individual differences in general intelligence. Moreover, if diffusion model parameters are to be considered as trait-like properties of cognitive processes, not only the temporal stability of parameters in specific tasks, but the temporal stability of model parameters across tasks—i.e., of hierarchical or latent model parameters—is of particular interest for individual differences research.
To evaluate whether diffusion model parameters (namely: drift rate, boundary separation, and non-decision time) qualify as trait-like variables, we asked participants to complete three response time tasks at two laboratory sessions approximately eight months apart. The tasks were so-called elementary cognitive tasks (ECTs) that are the most widely used tasks in individual differences research on the relationship between mental speed and mental abilities [1]. ECTs are tasks with minimal cognitive demands that minimize unwanted sources of variance such as strategy use and learning effects. The first task we used was a visual choice response time task in which participants had to decide in which of four squares a cross appeared. Previous research has shown that an increase of stimulus alternatives leads to a linear increase in response times [43]. This linear increase indicates that evidence is accumulated continuously until a decision point is reached and that this process takes longer the more stimulus alternatives are presented, either because more evidence has to be considered or because the process gets noisier. We know that other cognitive models such as the linear ballistic accumulator (LBA [44]) or the leaky competing accumulator (LCA [45]) model may be better suited to model response times in this task, but we are aware of at least one study that previously used the diffusion model to model behavioral data of this task and came to similar results as a study that used the LCA model [28,46]. The second task we used was the Sternberg memory scanning task [47], in which participants have to decide whether a probe item was part of a previously presented memory set. As Ratcliff [15] has shown, performance in this task can be adequately described by the diffusion model under the assumption of parallel diffusion processes for each memory set item. The third task we used was the Posner letter matching task [48], in which participants have to decide whether two letters have (a) the same physical and (b) the same name identity. While participants decide whether the letters are identical, they may either accumulate information simultaneously from both letters regarding their similarity until reaching a threshold, or they may first encode one of the letters and then apply a decision process to the second one. In the first case, one common diffusion process or two parallel ones might be occurring, whereas in the latter case only a single diffusion process should occur reflecting the comparison process to the previously encoded stimulus. Moreover, evaluating the name identity of letters may require additional processing demands due to the access of long-term memory, which should be reflected in the non-decision time [31].
We used latent state-trait (LST) models to quantify the amount of variance in model parameters that can be attributed to a common trait, to situational influences, to specific experimental tasks, and to measurement error [49,50]. If diffusion model parameters qualify as trait-like properties of cognitive processes affecting response times in a variety of tasks , they should show at least moderate consistencies and low occasion-specificities.
2. Experimental Section
2.1. Participants
We recruited N = 134 participants (81 females, 53 males, = 37.1, = 13.8) from different educational and occupational backgrounds. Of these, N = 114 (66 females, 48 males, = 36.9, = 13.5) attended both the first and the second experimental session that were approximately eight months apart. Participants who did not attend the second laboratory session tended to have smaller drift rates, average d = −0.46, greater boundary separation parameters, average d = 0.44, and negligible differences in non-decision time parameters, average d = −0.06. We only included participants who attended both experimental sessions in our analyses. All participants had normal or corrected to normal vision. As a reward for their participation, they received 100€ and feedback about their personal results.
2.2. Measures
Response Time Tasks
Visual choice response time task. We used a choice response time (CRT) task with either two (CR2) or four (CR4) response alternatives. Four white squares were presented in a row on a black screen. Participants’ middle and index fingers rested on four keys directly underneath the squares. After a delay of 1000–1500 ms, a cross appeared in one of the four squares and participants had to press the corresponding key as fast as possible. In the two-choice response time condition, the choice space was reduced to two squares in which the cross could appear for 50 subsequent trials. After completing a block of 50 trials, participants were informed that the cross could now only appear in a different combination of squares (outer left and left squares, outer right and right squares, inner squares, outer squares). In the four-choice response time condition, the cross could appear in any of the four squares. Both conditions began with ten practice trials with immediate feedback followed by 200 test trials without feedback. The order of conditions was counterbalanced across participants.
Sternberg memory scanning task. Participants were shown a memory set consisting of one (set size one, S1), three (set size three, S3), or five (set size five, S5) digits from 0 to 9 on a black computer screen. Subsequently, participants were shown a probe digit and had to decide whether the probe was contained in the previously presented memory set by pressing one of two keys. This was the case in 50% of the trials. The position of keys indicating whether the probe item was part of the memory set was counterbalanced across participants. Each of the three conditions began with ten practice trials with immediate feedback followed by 100 test trials without feedback. The order of conditions was counterbalanced across participants.
Posner letter matching task. Participants were shown two letters and had to decide whether they were identical. In the physical identity (PI) condition, participants had to decide whether they were physically identical, and in the the name identity (NI) condition, they had to decide whether the two presented letters had the same name. The position of keys indicating whether the letters were identical was counterbalanced across participants. Both conditions began with ten practice trials with immediate feedback followed by 300 test trials without feedback. All participants started with the PI condition at the first laboratory session, whereas all participants started with the NI condition at the second laboratory session.
2.3. Procedure
The two experimental sessions were approximately eight months apart. We administered the CRT task first, followed by the Sternberg memory scanning task and the Posner letter matching task. The order of tasks was the same for all participants at both experimental sessions. An EEG was recorded while participants completed the tasks (data are not reported here). Each session took approximately three hours.
2.4. Data Analysis
2.4.1. Response Time Data
We discarded any RTs faster than 100 ms or slower than 3000 ms. In a second step, we discarded any trials with logarithmized RTs exceeding ± 3 SDs of the mean of each condition on an intra-individual level. Diffusion model parameters were estimated with fast-dm-30 [19] for each participant, each condition, and each experimental session separately. We analyzed the data in such a way that responses to the upper threshold reflected correct decisions and that responses to the lower threshold reflected incorrect decisions. For the CR4 task, this implied that responses to any of the three incorrect locations were aggregated into one RT distribution of incorrect trials. The starting point z was fixed to a/2, and the difference in speed of response execution d and the trial-to-trial variability parameters of the drift and the starting point were fixed to 0. Thus, four parameters were estimated for each participant, each condition, and each experimental session: The drift rate v, the boundary separation a, the non-decision time , and the variability of the non-decision time . Model parameters were estimated with the Kolmogorov-Smirnov statistic. Model fit was evaluated graphically by plotting predicted values against empirical values for the 25, 50, and 75 quantiles of the RT distribution separately for each task and each laboratory session (see Figure A1, Appendix A).
2.4.2. Statistical Analysis
We used latent state-trait models to assess the relationship between diffusion model parameters estimated for the three response time tasks across the two experimental sessions. We specified a structural equation model with a common trait T, a state residual for each of the two measurement occasions i, and a method factor for each of the three experimental tasks j. The path coefficients of the common trait T as well as the path coefficients of the state residuals on the latent states were fixed to 1. Moreover, the path coefficients of the method factors were also fixed to 1. Finally, the path coefficients of the latent states were estimated with the exception of the path coefficient loading on the CR2 task, which was fixed to 1. The variances of error residuals were set equal across measurement occasions. In addition, we also specified LST models separately for diffusion model parameter and each experimental task. These structural equation models were specified as above with the exceptions that method factors reflected experimental conditions within the task and that all paths were fixed to 1. We did not analyze the mean structure in any of the models and fixed the intercepts to 0, because the diffusion model parameters were z-standardized prior to being entered into structural equation models. Note that the assumption of measurement invariance is not necessary to explore the relative temporal stability of latent model parameter states [38]. All in all, we calculated four LST models for each diffusion model parameter (v, a, ): One model across all experimental tasks and three separate models for each of the experimental tasks (CRT task, Sternberg memory scanning task, Posner letter matching task).
Moreover, we calculated several LST parameters to assess the reliability, consistency, occasion-specificity, and method-specificity of the model parameters [38]. The coefficient of consistency is computed as / and reflects the proportion of variance of the manifest variable that can be accounted for by individual differences in the latent trait T. The coefficient of occasion-specificity is computed as / and reflects the proportion of variance that is due to situational effects . Similarly, the coefficient of method-specificity is computed as / and reflects the proportion of variance that can be accounted for by a specific method . Taken together, these different sources of systematic variation contribute to the reliability of a manifest variable , which can thus be computed as /. For the purposes of our analyses, we defined LST parameters ≤.30 as small, between .30 and .60 as moderate, and ≥.60 as great, as consistencies of well-known intelligence and personality tests all exceeded this threshold value [51,52]. Note that these cut-offs should only be treated as heuristics. For the evaluation of LST parameters, we sighted the literature carefully for previous evaluations of these parameters. In their formulation of LST theory, Steyer et al. [49] did not offer any guidelines for the interpretation of LST parameters. Hence, we used previous applications of LST theory in individual differences research on mental abilities and personality traits as benchmarks. Danner et al. [51] calculated the LST parameters of intelligence tests and reported consistencies ranging from .67 to .72 and reliabilities ranging from .86 to .83, which they evaluated as “great”. In comparison, method-specificities of intelligence tests ranged from .13 to .24 and were evaluated as “small”. Deinzer et al. [52] evaluated the trait characteristics of different personality questionnaires (Freiburg Personality Inventory (FPI), NEO Five-Factor Inventory (NEO-FFI), Eysenck Personality Questionnaire (EPI)) and reported consistencies ranging from .73 to .94 for the FPI, from .62 to .92 for the NEO-FFI, and from .72 to .83 for the E and N scales of the EPI. In comparison, occasion-specificities ranged from .00 to .17 for the FPI, from .00 to .22 for the NEO-FFI, and from 0 to .16 for the E and N scales of the EPI. These results led the authors to conclude that situational and/or interactional influences explained a significant proportion of variance of these personality questionnaires and that test scores depended both on latent traits and (albeit to a lesser degree) on situational and/or interactional influences.
Structural equation models were estimated with MPlus 7 [53] (the data and analysis files for all structural equation models are provided in the supplementary materials online). Model fit was evaluated with the chi-square test, the comparative fit index (CFI) and root-mean-square error of approximation (RMSEA). According to Browne and Cudeck [54] and Hu and Bentler [55], we considered CFI values > .90 and RMSEA values < .08 to indicate acceptable model fit, and CFI values > .95 and RMSEA values < .06 to indicate good model fit. Missing values were accounted for using the ML algorithm implemented in MPlus.
3. Results and Discussion
3.1. Descriptive Data
Table 1 shows the mean RTs and accuracies for each condition of the three response time tasks at both experimental sessions. All in all, accuracies were relatively high due to the low complexity of the response time tasks. Moreover, RTs tended to increase with increasing information-processing demands within each task.

Table 1.
Mean accuracies (ACC), mean RTs (RT), and mean diffusion model parameters (v, a, , and ) across conditions in the three response time tasks at both measurement occasions (SDs in parantheses).
3.2. Diffusion Model Analysis
Results from one participant in the set size one condition of the Sternberg memory scanning task and results from one participant in the name identity condition of the Posner letter matching task had to be discarded, because the predicted RTs deviated strongly from the empirical RTs across all four quantiles (Figure A1 in Appendix A displays the relation of empiric vs. predicted response times for the remaining data).
Drift rates tended to decrease and boundary separation and non-decision parameters tended to increase with increasing information-processing demands within each task. Drift rates of experimental tasks were comparable across experimental sessions, all 0.13, except for the name identity condition of the Posner letter matching task. Here, drift rates were slightly greater at the second than at the first laboratory session, d = 0.24. Boundary separation parameters were also comparable across sessions, all 0.19, except for the Sternberg memory scanning task. Here, boundary separation parameters decreased from the first to the second session, all 0.27. Finally, non-decision time parameters were also comparable across sessions, all 0.16, except for the set size one condition of the Sternberg memory scanning task, in which non-decision time parameters increased across sessions, d = 0.21, and the physical identity condition of the Posner letter matching task, in which non-decision time parameters decreased across sessions, d = 0.48.
3.2.1. Drift Rate
Manifest correlations of drift rate parameters are shown in Table A1 in Appendix B. The LST model for drift rate across experimental tasks provided a good fit for the data, (94) = 136.44, p = .003, CFI = .95, RMSEA = .06 [.04; .09]. However, the variances of the latent state residuals and of the method factor for the Posner letter matching task were non-significant (VAR() = 0.03, p = .660; VAR() = 0.03, p = .643; VAR() = 0.00, p = .992). Hence, these variances were fixed to zero. These modifications did not impair model fit, (97) = 143.94, p = .001, CFI = .94, RMSEA = .07 [.04; .09]. Although the test indicated significant differences between the implied and empirical covariance structure, the goodness-of-fit indices CFI and RMSEA indicated acceptable model fit [54,55]. See Figure 2 for the modified model.
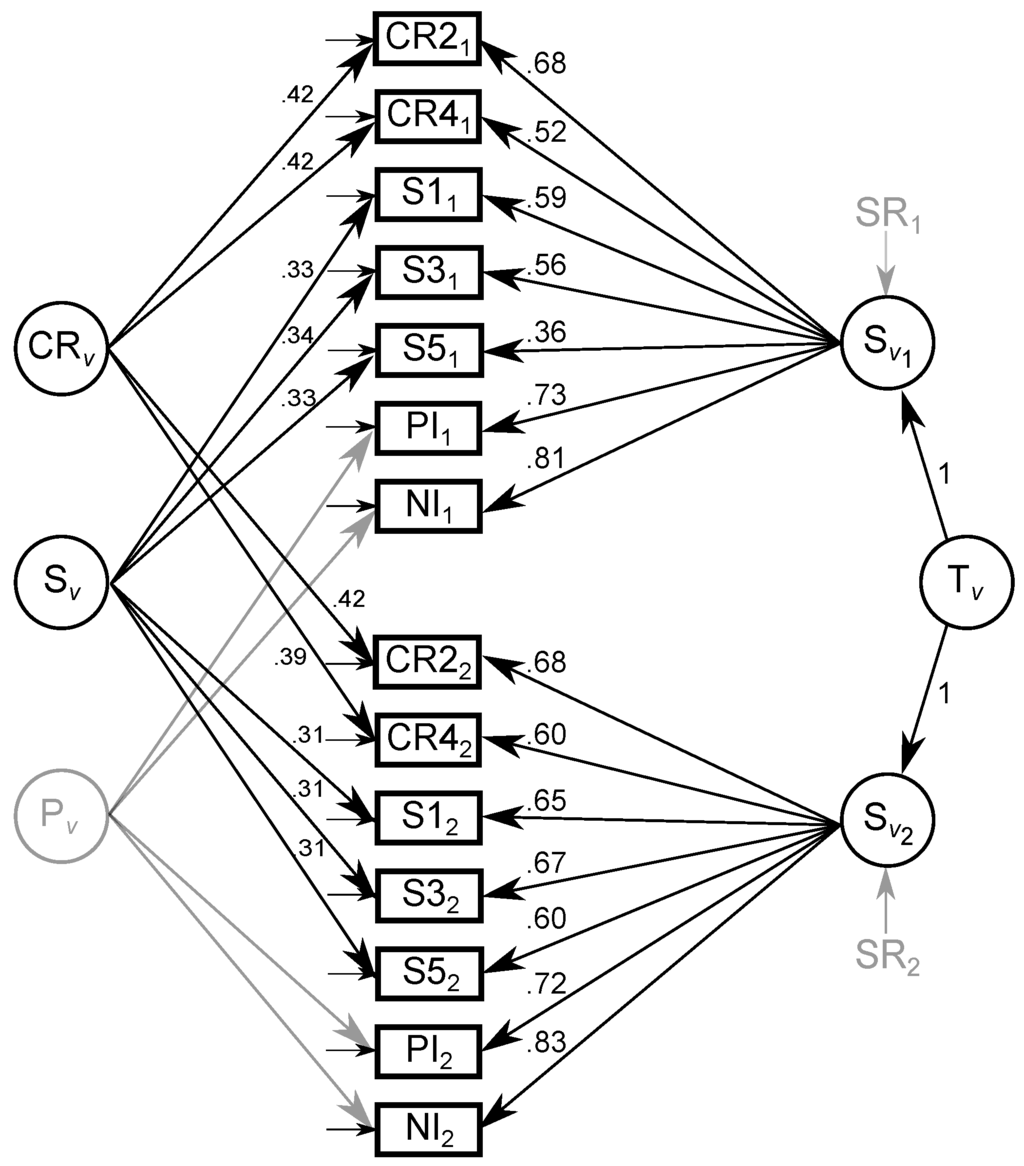
Figure 2.
The latent state-trait model of drift rate parameters consists of a common trait T, a state residual for each of the two measurement occasions i, and a method factor for each of the three experimental tasks. CR2/4 = choice response time task with two/four alternatives; S1 = set size one; S3 = set size three; S5 = set size five; PI = physical identity; NI = name identity. Latent variables displayed in gray were non-significant.
Subsequently, we calculated the coefficients of reliability, consistency, occasion-specificity, and method-specificity based on LST theory (see Table 2). Drift rate parameters estimated in the CRT and Sternberg memory scanning task showed moderate consistencies and low method-specificities. Drift rate parameters estimated in the Posner letter matching task showed the highest consistencies and no method-specificities. Overall, the temporal stabilities of the latent drift rate states were great as state residuals were not significant and occasion-specificities were therefore zero, but the reliabilities of the manifest drift rate parameters were only moderate, with coefficients of reliability ranging from .38 to .69.

Table 2.
Latent state-trait theory parameters of diffusion model parameters. Occ. Spec. = Occasion-specificity; Meth. Spec. = Method-specificity.
CRT task. The LST model provided a good fit for the data, (7) = 6.90, p = .440, CFI = 1, RMSEA = .00 [.00; .11]. However, the variances of the latent state residuals and of the method factor for the four choice condition were negative and/or non-significant (VAR() = −0.03, p = .659; VAR() = 0.05, p = .413; VAR() = 0.01, p = .948). Hence, these variances were fixed to zero. These modifications did not impair model fit, (10) = 7.67, p = .661, CFI = 1, RMSEA = .01 [.00; .08]. See the upper part of Figure 3A (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
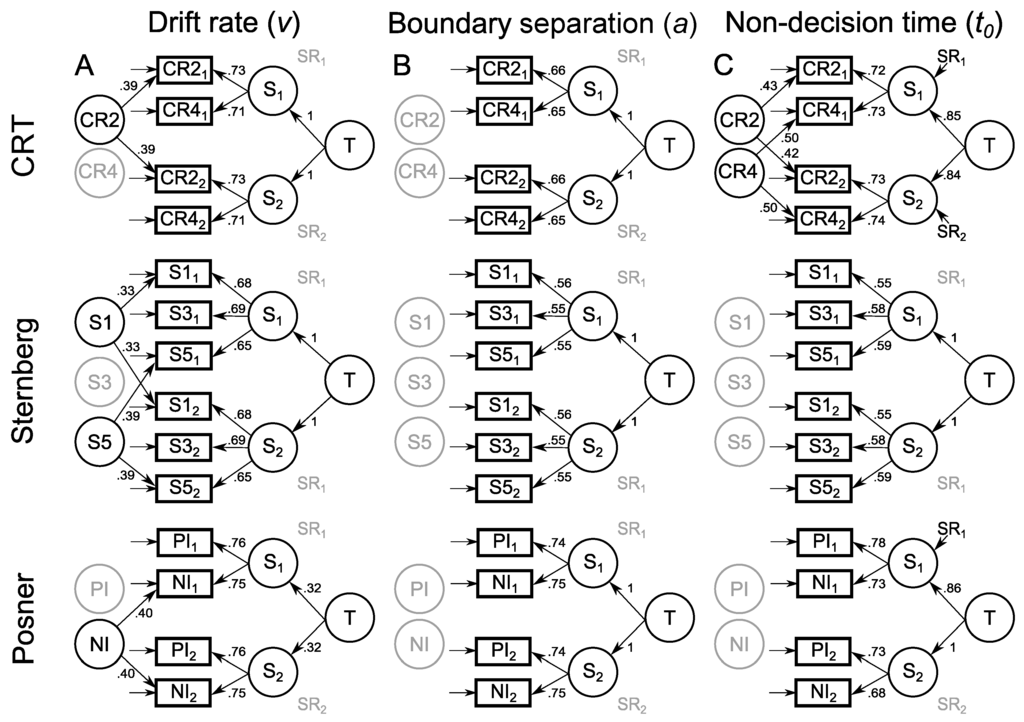
Figure 3.
Seperate LST models for the three parameters of the diffusion model: drift rate v, boundary separation a, and non-decision time —estimated for each of the three tasks.

Table 3.
LST parameters for the LST models by task (see Figure 3). Cond. = Condition; Occ. Spec. = Occasion-specificity; Meth. Spec. = Method-specificity; Rel. = Reliability; Boundary sep. = Boundary separation; Non-dec. time = Non-decision time.
Sternberg memory scanning task. The LST model provided an acceptable fit for the data, (18) = 26.53, p = .088, CFI = .96, RMSEA = .06 [.00; .11]. However, the variances of the latent state residuals and of the method factor for the set size 3 condition were non-significant (VAR() = 0.02, p = .748; VAR() = 0.90, p = .099; VAR() = 0.01, p = .851). Hence, these variances were fixed to zero. These modifications did not impair model fit, (21) = 31.38, p = .068, CFI = .96, RMSEA = .07 [.00; .11]. See the middle part of Figure 3A (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
Posner letter matching task. The LST model provided a good fit for the data, (7) = 7.44, p = .385, CFI = 1, RMSEA = .02 [.00; .12]. However, the variances of the latent state residuals and of the method factor for the physical identity condition were non-significant (VAR() = 0.06, p = .301; VAR() = 0.12, p = .063; VAR() = 0.07, p = .322). Hence, these variances were fixed to zero. Afterwards, model fit was still acceptable, (10) = 16.08, p = .097, CFI = .97, RMSEA = .07 [.00; .14]. See the lower part of Figure 3A (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
3.2.2. Boundary Separation
Manifest correlations between boundary-separation parameters across tasks and measurements are shown in Table A2 in Appendix B. The LST model for boundary separation across the three experimental tasks provided a good fit for the data, (94) = 124.78, p = .019, CFI = .94, RMSEA = .05 [.02; .08]. Because the variances of the latent state residuals and of the method factor for the Posner letter matching task were negative and/or non-significant again (VAR() = −0.04, p = .181; VAR() = 0.10, p = .156; VAR() = 0.08, p = .227), we also fixed these variances to zero. These modifications did not impair model fit, (97) = 134.26, p = .007, CFI = .93, RMSEA = .06 [.03; .08]. Again, the test indicated significant differences between the implied and empirical covariance structure, but the CFI and the RMSEA indicated an acceptable model fit [54,55]. See Figure 4 for the modified model.
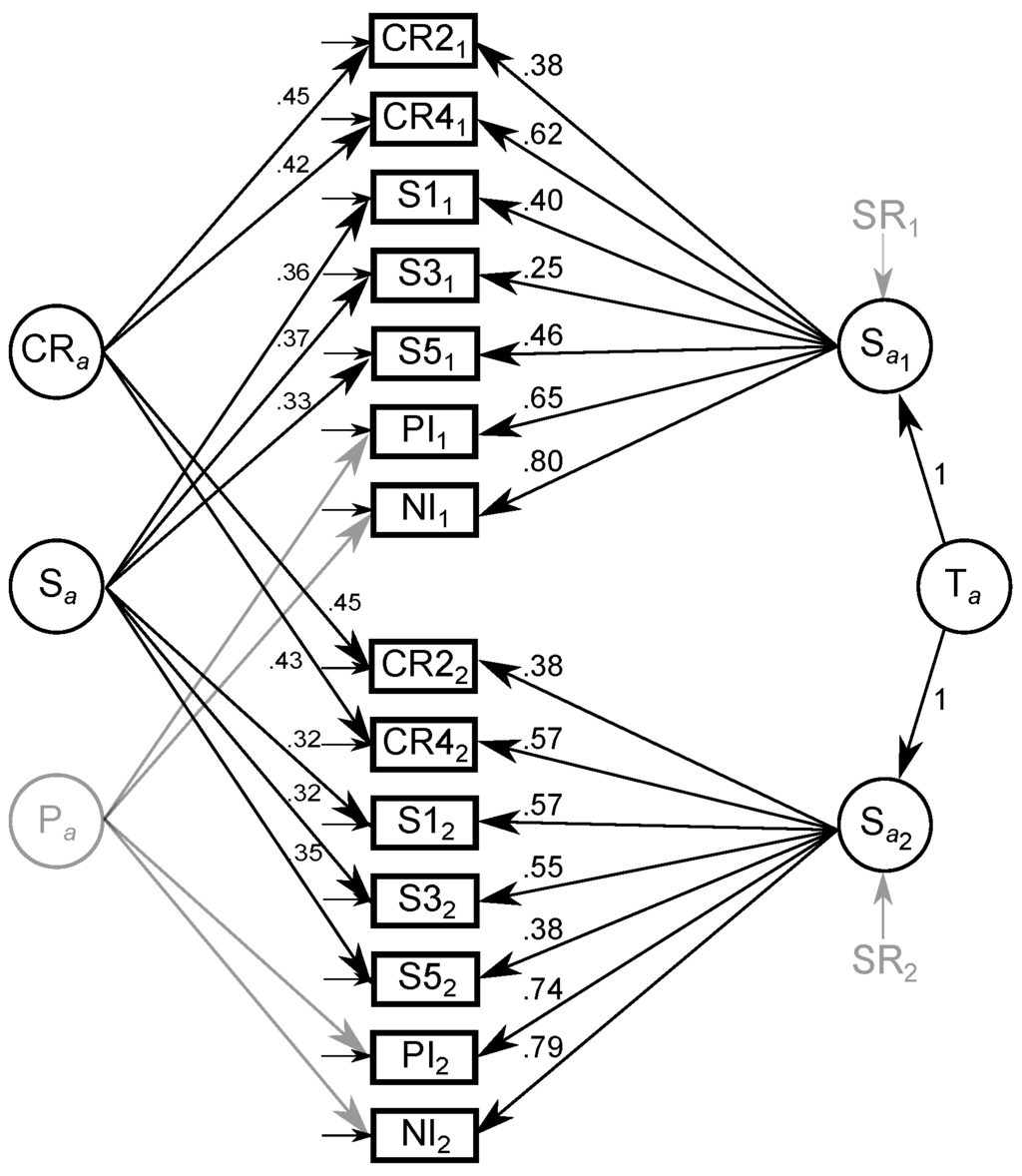
Figure 4.
The latent state-trait model of boundary separation parameters consists of a common trait T, a state residual for each of the two measurement occasions i, and a method factor for each of the three experimental tasks. CR2/4 = choice response time task with two/four alternatives; S1 = set size one; S3 = set size three; S5 = set size five; PI = physical identity; NI = name identity. Latent variables displayed in gray were non-significant.
Coefficients of reliability, consistency, occasion-specificity, and method-specificity are shown in the middle part of Table 2. Consistencies of boundary separation parameters were low to moderate and highest in the Posner letter matching task. Methods-specificities were low in the SRT, CRT, and Sternberg memory scanning task, whereas method factors explained no variance in boundary separation parameters in the Posner letter matching task. While the temporal stabilities were as great for the latent boundary separation states as for the latent drift rate states, the reliabilities of manifest boundary separation parameters were notably lower ranging from .27 to .64.
CRT task. The LST model provided a good fit for the data, (7) = 2.43, p = .933, CFI = 1, RMSEA = .00 [.00; .03]. However, the variances of the latent state residuals and of the method factors were non-significant (VAR() = 0.04, p = .536; VAR() = 0.11, p = .134; VAR() = 0.08, p = .303; VAR() = 0.15, p = .079). Hence, these variances were fixed to zero. These modifications did not impair model fit, (11) = 8.38, p = .679, CFI = 1, RMSEA = .00 [.00; .08]. See the upper part of Figure 3B (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
Sternberg memory scanning task. The LST model provided an acceptable fit for the data, (18) = 24.78, p = .131, CFI = .94, RMSEA = .06 [.00; .11]. However, the variances of the latent state residuals and of the method factors were non-significant and/or negative (VAR() = −0.04, p = .465; VAR() = 0.11, p = .100; VAR() = 0.08, p = .330; VAR() = −0.09, p = .247; VAR() = 0.05, p = .529). Hence, these variances were fixed to zero. These modifications did not impair model fit, (23) = 31.51, p = .111, CFI = .93, RMSEA = .06 [.00; .10]. See the middle part of Figure 3B (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
Posner letter matching task. The LST model provided a good fit for the data, (7) = 5.52, p = .597, CFI = 1, RMSEA = .00 [.00; .10]. However, the variances of the latent state residuals and of the method factors were negative and/or non-significant (VAR() = −0.03, p = .652; VAR() = 0.05, p = .429; VAR() = −0.11, p = .071, VAR() = 0.13, p = .079). Hence, these variances were fixed to zero. These modifications did not impair model fit, (11) = 11.55, p = .398, CFI = 1, RMSEA = .02 [.00; .10]. See the lower part of Figure 3B (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
3.2.3. Non-Decision Time
Manifest correlations for non-decision time parameters across tasks and measurements are shown in Table A3 in Appendix B. The LST model for non-decision time provided a mediocre fit for the data, (94) = 274.01, p < .001, CFI = .76, RMSEA = .13 [.11; .15]. Because the variances of the latent state residuals and of the method factor for the Sternberg and the Posner letter matching task were non-significant or negative (VAR() = 0.02, p = .667; VAR() = −0.02, p = .718; VAR() = −0.06, p = .053; VAR() = 0.03, p = .542), we also fixed these variances to zero. These modifications did not impair model fit, (98) = 292.27, p < .001, CFI = .76, RMSEA = .13 [.11; .15]. This time, both the test and the CFI and RMSEA indicated significant differences between the implied and empirical covariance structure [54,55]. See Figure 5 for the modified model.
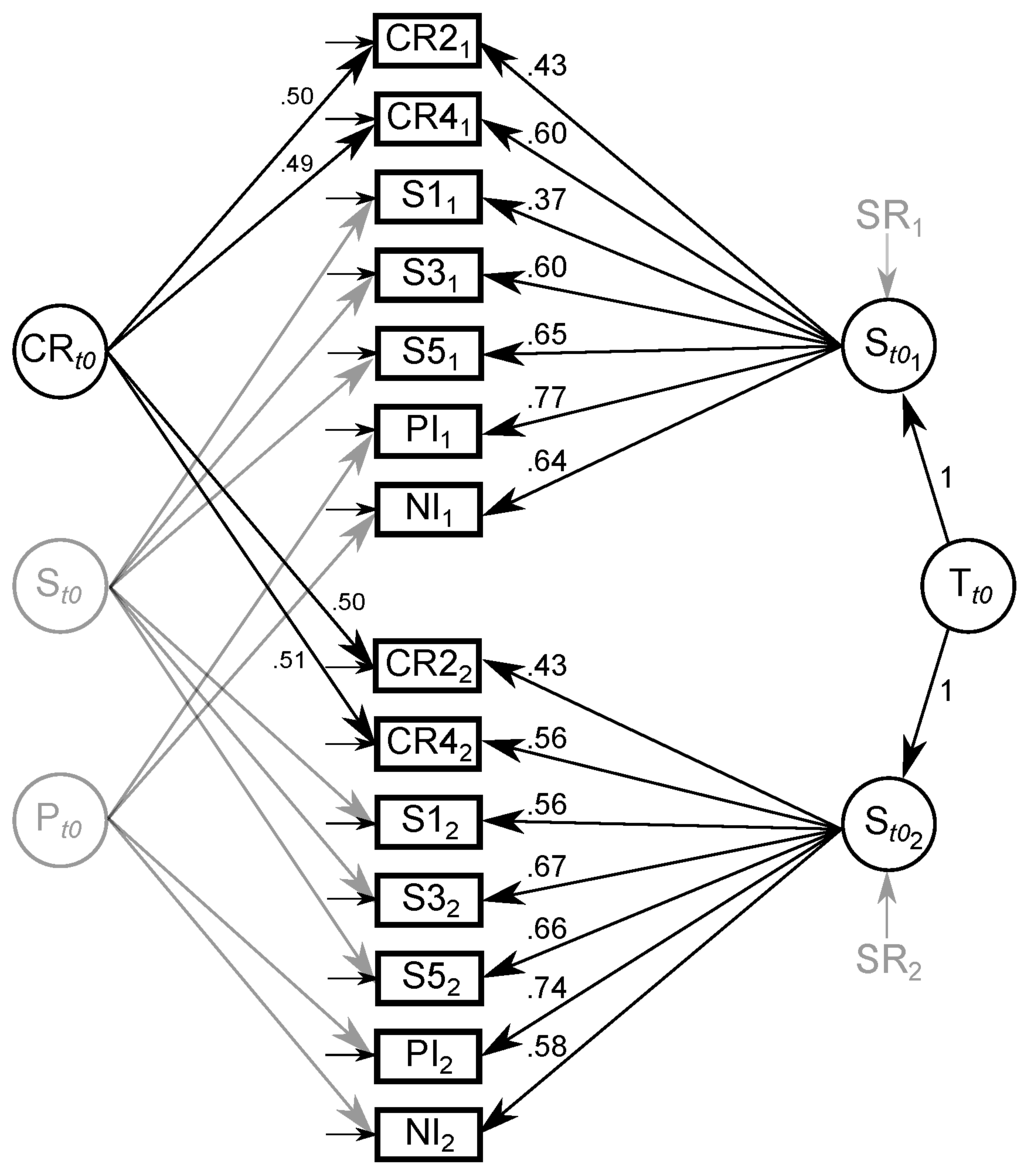
Figure 5.
The latent state-trait model of non-decision time parameters consists of a common trait T, a state residual for each of the two measurement occasions i, and a method factor for each of the three experimental tasks. CR2/4 = choice response time task with two/four alternatives; S1 = set size one; S3 = set size three; S5 = set size five; PI = physical identity; NI = name identity. Latent variables displayed in gray were non-significant.
Coefficients of reliability, consistency, occasion-specificity, and method-specificity are shown in the lower part of Table 2. Consistencies of non-decision time parameters were overall low to moderate and highest in the Posner letter matching task. We observed low method-specificities only in the SRT/CRT task; for the other two tasks, we found no effect of task-specific characteristics. Again, the temporal stabilities of the latent states were great, but reliabilities of the manifest non-decision time parameters were low to moderate, ranging from .14 to .60.
CRT task. The LST model provided a good fit for the data, (7) = 2.21, p = .947, CFI = 1, RMSEA = .00 [.00; .01]. See the upper part of Figure 3C (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
Sternberg memory scanning task. The LST model did not provide an acceptable fit for the data, (18) = 62.32, p < .001, CFI = .78, RMSEA = .15 [.11; .19]. The variances of the latent state residuals and of the method factors were non-significant and/or negative (VAR() = −0.06, p = .316; VAR() = 0.05, p = .473; VAR() = −0.07, p = .377; VAR() = −0.24, p = .002; VAR() = −0.17, p = .016). Hence, these variances were fixed to zero. These modifications did not change model fit to a great degree, (23) = 83.49, p < .001, CFI = .67, RMSEA = .15 [.12; .19]. See the middle part of Figure 3C (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
Posner letter matching task. The LST model provided a good fit for the data, (7) = 1.77, p = .971, CFI = 1, RMSEA = .00 [.00; .10]. However, the variances of the latent state residual reflecting the second measurement occasion and of the method factor for the name identity condition were negative and/or non-significant (VAR() = 0.13, p = .086; VAR() = −0.10, p = .145. Hence, these variances were fixed to zero. These modifications did not impair model fit, (9) = 8.13, p = .521, CFI = 1, RMSEA = .00 [.00; .10]. Now, however, the method factor for the physical identity condition was non-significant, VAR() = 0.11, p = .110, and was subsequently fixed to zero. The final model still provided a good fit for the data, (10) = 10.99, p = .359, CFI = .99, RMSEA = .03 [.00; .11]. See the lower part of Figure 3C (p. 12) for the final model and Table 3 (p. 13) for the associated LST parameters.
3.3. Discussion
The present study evaluated whether diffusion model parameters (drift rate, boundary separation, non-decision time) qualify as trait-like variables that may be considered temporally stable person properties of cognitive processes. For this purpose, we used LST models to assess the amount of variance in model parameters that can be attributed to a common trait. If diffusion model parameters from elementary cognitive tasks are to be treated as trait-like variables in individual differences research, they have to be stable across time and consistent over situations [38].
First, we evaluated the temporal stability of the latent drift rate, boundary separation, and non-decision time states across a time period of eight months in three tasks. The variance of model parameters consistent across tasks was not affected by situational influences or influences of person-situation interactions such as fatigue, motivation, or familiarization with the testing environment, as reflected in the result that the state residuals in all LST models could be fixed to zero without impairing model fit. These results are consistent with previous research on the reliability of diffusion model parameters reporting moderate to good test-retest correlations over a period of one week [30,41]. They support the notion that the variances of diffusion model parameters that are consistent across tasks can be considered trait-like properties of cognitive processes. Moreover, because their temporal stability is comparable to the temporal stability of intelligence tests [13,42,51], these results are consistent with the view that individual differences in diffusion model parameters reflect elementary person properties that may give rise to general intelligence.
Second, we evaluated the consistency of diffusion model parameters across three elementary cognitive tasks, which showed a great variability. Only manifest (note that in this context “manifest” refers to the estimates of the latent diffusion model parameters that were entered into structural equation models as manifest variables) drift rate variables showed a moderate consistency, whereas the coefficients of consistency of boundary separation and non-decision time parameters were rather low. On average, 44 percent of the variance of each manifest drift rate parameter was accounted for by the common trait. Based on these results, individual differences in drift rate can be considered as a temporally stable and trans-situationally consistent trait across different tasks, as they are likely to reflect an ability of a person. Nevertheless, the consistencies of drift rate parameters were still lower than the consistencies typically observed in intelligence tests [51], which is why we suggest administering more than one response time task in future studies on individual differences in drift rates to reliably capture the common variance across tasks.
In comparison, on average only 32 to 36 percent of the variance of each manifest boundary separation and non-decision time parameter was accounted for by the common trait across the three tasks. Moreover, the LST model of non-decision times did not even provide a good account for the data due to the complex factorial structure with several low covariances between manifest parameters. These results suggest that while latent variables of boundary separation and non-decision times showed a great temporal stability, the manifest parameters are likely to reflect mostly narrower and more task-specific skills as well as measurement error. Hence, an individual does not have one boundary separation or one non-decision time. Instead, an individual has task-specific boundary separation and non-decision time parameters that are only weakly correlated across tasks. This result is most intuitive for the non-decision time parameter, which reflects the speed of different non-decisional processes such as encoding, memory retrieval, or response execution [31]. As such, it is not a process-pure parameter. Individual differences in non-decision time may thus reflect mostly individual differences in encoding speed in one kind of task, and individual differences in response execution in another kind of task.
Third, we repeated these analyses separately for each task and each model parameter. While the results of these task-specific analyses were largely consistent with the results of the LST models across tasks, we observed that consistencies for all model parameters tended to increase when evaluated at a task-specific level. This finding supports the notion that model parameters consist to a considerable degree of task-specific variance. Interestingly, we found that even at a task-specific level a common trait model was not suited to describe the non-decision times in the Sternberg memory scanning task as reflected in the bad model fits. Correlations between non-decision times in the set size three and five conditions were substantially greater than correlations between non-decision times in the set size one condition and any of the other conditions, as can be seen in Table A3 in Appendix B. We believe that the additional short-term memory access demands of any set size larger than one are reflected in the non-decision time parameter [28,31], which explains why non-decision time parameters from these conditions are less strongly related to a non-decision time parameter from a condition without short-term memory access. Again, this result suggests that non-decision time parameters should not be treated as trait-like variables, as they contain different sources of variation. On a side note, we would like to point out that the model specifications of the task-specific analyses allow a weak test of relative measurement invariance, as all paths were fixed to one and error variances for each condition were constrained to be equal across sessions. This weak test of measurement invariance suggests that at least the assumption of relative measurement invariance holds for the majority of diffusion model parameters, as indicated by the acceptable model fits under these model specifications except for the LST model of non-decision times in the Sternberg memory scanning task.
4. Conclusions
All in all, our analysis of the psychometric properties of diffusion model parameters may help understanding why only drift rate parameters have been consistently positively associated with mental abilities, whereas the associations between boundary separation and non-decision time parameters have been inconsistent and sometimes even in opposite directions [25,26,27,28]. First, drift rate parameters showed overall slightly higher consistencies than boundary separation and non-decision time parameters. Second and more importantly, drift rate parameters had fewer extremely small consistencies than boundary separation and non-decision time parameters (smallest consistencies: .26 (drift rate), .09 (boundary separation), .18 (non-decision time)). Future studies should thus consider using broader batteries of response time tasks to capture the small amount of temporally stable common variance in boundary separation and non-decision time parameters across different tasks and to minimize the effect of tasks with extremely low consistencies, or focus on studying task-specific associations with mental abilities. However, when analyzing only the association between drift rates and mental abilities, a small test battery consisting of only a few response time tasks will be sufficient to reliably estimate the common drift rate trait. Moreover, we caution against treating the non-decision time parameter as a trait-like variable, as it is not a process-pure parameter and contains substantial task-specific sources of variation.
There are several limitations to the present study. First, we only used elementary cognitive tasks, which are relatively simple response time tasks with low error rates. Whether cognitively more demanding tasks such as recognition memory or lexical decision tasks yield comparable results is an open question. Second, we applied the diffusion model to the CRT task, although it is not clear whether the decision process in this task reflects a diffusion process or whether it requires only a spatial identification of the stimulus position. There is some evidence that the decision process reflects at least an evidence accumulation process, as Leite and Ratcliff [46] successfully fitted sequential sampling models to data from a similar task. Moreover, factor loadings of the structural equation models and the resulting consistencies in Figure 2, Figure 3, Figure 4 and Figure 5 and Table 2 do not suggest that the CRT task stands out from the rest of the tasks. Nevertheless, we do not presume that the diffusion model captures the true diffusion process, but rather that it provides a simplifying description related to the true process. As such, it describes the data in terms of parameters that are likely related to a substantial (but unknown) degree to the true parameters characterizing evidence accumulation, boundary separation, and non-decision time. This important distinction between the true process and its description in terms of model parameters has important implications for the interpretation of the resulting parameters estimates. In particular, other process models may be better suited to describe the cognitive processes involved in the CRT task than the diffusion model. It would be interesting to explore the convergent validity of diffusion model parameters with conceptually related parameters from sequential sampling models in the CRT task in future studies. Third, we only used the Kolmogorov-Smirnov statistic to estimate diffusion model parameters and previous research has suggested that other estimation algorithms such as the statistic and the maximum likelihood estimation may yield different test-retest correlations [41]. Fourth, we did not evaluate the temporal stability of manifest variables on a latent level, because an odd-even split of trials within each condition was not feasible without affecting the stability of parameter estimates due to relatively low trial numbers. Hence, we do not know to what degree manifest variables reflect task-specific skills and to what extent they reflect measurement error.
Taken together, our results show that the consistent variance of diffusion model parameters across tasks can be regarded as temporally stable ability parameters. We have shown that only the drift rate parameter can be regarded as a trait-like variable that is stable across time and consistent over different tasks [38]. Because the diffusion model allows an elegant, process-pure measurement of the speed of information uptake with trait-like characteristics, we believe that the mathematical modeling of response times provides a promising avenue for identifying the cognitive processes giving rise to individual differences in general intelligence.
Author Contributions
Dirk Hagemann, Anna-Lena Schubert, and Andreas Voss designed the experiment; Anna-Lena Schubert performed the experiment; Anna-Lena Schubert and Gidon T. Frischkorn analyzed the data; Anna-Lena Schubert wrote the paper; Gidon T. Frischkorn, Dirk Hagemann, and Andreas Voss gave conceptual and technical advice. All authors discussed the results and commented on the paper.
Conflicts of Interest
All authors declare no conflict of interest.
Appendix A. QQ-Plot Evaluating the Fit of Diffusion Model Parameters
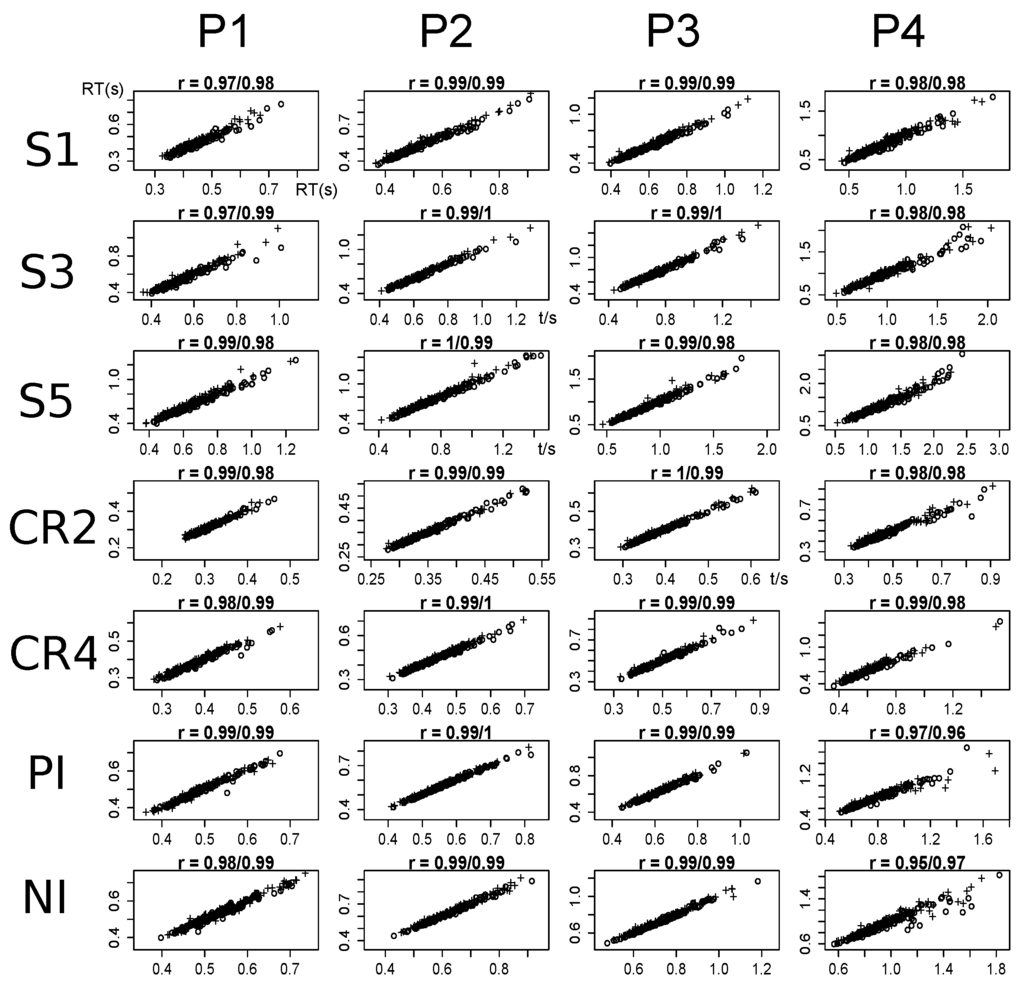
Figure A1.
Correlations between empirical and predicted mean response times in seconds across four percentiles (P1 to P4) after the removal of outliers in all tasks. Dots represent mean response times at the first laboratory session and crosses represent mean response times at the second laboratory session.
Appendix B. Correlation Tables for Diffusion Model Parameters Across Measurement Points

Table A1.
Product–moment correlations between drift rate parameters at the first and second laboratory session.
| Session 1 | Session 2 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CR2 | CR4 | S1 | S3 | S5 | PI | NI | CR2 | CR4 | S1 | S3 | S5 | PI | NI | ||
| Ses. 1 | CR2 | 1 | 0.43 | 0.28 | 0.35 | 0.25 | 0.51 | 0.55 | 0.60 | 0.47 | 0.51 | 0.45 | 0.47 | 0.48 | 0.56 |
| CR4 | 1 | 0.26 | 0.37 | 0.21 | 0.31 | 0.45 | 0.39 | 0.44 | 0.42 | 0.43 | 0.33 | 0.35 | 0.41 | ||
| S1 | 1 | 0.41 | 0.30 | 0.37 | 0.37 | 0.37 | 0.22 | 0.53 | 0.42 | 0.32 | 0.23 | 0.23 | |||
| S3 | 1 | 0.31 | 0.44 | 0.40 | 0.30 | 0.15 | 0.43 | 0.52 | 0.35 | 0.39 | 0.40 | ||||
| S5 | 1 | 0.38 | 0.45 | 0.25 | 0.26 | 0.30 | 0.53 | 0.53 | 0.32 | 0.44 | |||||
| PI | 1 | 0.56 | 0.35 | 0.36 | 0.56 | 0.53 | 0.42 | 0.60 | 0.57 | ||||||
| NI | 1 | 0.39 | 0.37 | 0.46 | 0.56 | 0.53 | 0.49 | 0.71 | |||||||
| Ses. 2 | CR2 | 1 | 0.64 | 0.52 | 0.43 | 0.38 | 0.37 | 0.30 | |||||||
| CR4 | 1 | 0.36 | 0.30 | 0.32 | 0.35 | 0.31 | |||||||||
| S1 | 1 | 0.60 | 0.50 | 0.49 | 0.51 | ||||||||||
| S3 | 1 | 0.59 | 0.59 | 0.66 | |||||||||||
| S5 | 1 | 0.47 | 0.60 | ||||||||||||
| PI | 1 | 0.70 | |||||||||||||
| NI | 1 | ||||||||||||||
Note: Ses.1/2 = measures at measurement point one or two; CR2/4 = choice response time task with two/four alternatives; S1 = set size one; S3 = set size three; S5 = set size five; PI = physical identity; NI = name identity.

Table A2.
Product–moment correlations between boundary separation parameters at the first and second laboratory session.
| Session 1 | Session 2 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CR2 | CR4 | S1 | S3 | S5 | PI | NI | CR2 | CR4 | S1 | S3 | S5 | PI | NI | ||
| Ses. 1 | CR2 | 1 | 0.39 | 0.06 | 0.15 | 0.26 | 0.22 | 0.17 | 0.46 | 0.33 | 0.40 | 0.26 | 0.15 | 0.18 | 0.13 |
| CR4 | 1 | 0.02 | 0.12 | 0.24 | 0.42 | 0.54 | 0.41 | 0.51 | 0.46 | 0.30 | 0.22 | 0.48 | 0.49 | ||
| S1 | 1 | 0.09 | 0.11 | 0.07 | 0.23 | 0.18 | 0.19 | 0.20 | 0.14 | 0.05 | 0.16 | 0.07 | |||
| S3 | 1 | 0.15 | 0.09 | 0.20 | 0.24 | 0.07 | 0.23 | 0.22 | 0.22 | 0.23 | 0.15 | ||||
| S5 | 1 | 0.29 | 0.45 | 0.25 | 0.35 | 0.32 | 0.47 | 0.34 | 0.24 | 0.36 | |||||
| PI | 1 | 0.56 | 0.27 | 0.33 | 0.43 | 0.36 | 0.22 | 0.47 | 0.53 | ||||||
| NI | 1 | 0.32 | 0.33 | 0.39 | 0.55 | 0.24 | 0.57 | 0.60 | |||||||
| Ses. 2 | CR2 | 1 | 0.50 | 0.48 | 0.28 | 0.20 | 0.29 | 0.35 | |||||||
| CR4 | 1 | 0.52 | 0.33 | 0.26 | 0.49 | 0.48 | |||||||||
| S1 | 1 | 0.55 | 0.33 | 0.45 | 0.44 | ||||||||||
| S3 | 1 | 0.45 | 0.38 | 0.47 | |||||||||||
| S5 | 1 | 0.22 | 0.39 | ||||||||||||
| PI | 1 | 0.57 | |||||||||||||
| NI | 1 | ||||||||||||||
Note: Ses.1/2 = measures at measurement point one or two; CR2/4 = choice response time task with two/four alternatives; S1 = set size one; S3 = set size three; S5 = set size five; PI = physical identity; NI = name identity.

Table A3.
Product–moment correlations between non-decision time parameters at the first and second laboratory session.
| Session 1 | Session 2 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CR2 | CR4 | S1 | S3 | S5 | PI | NI | CR2 | CR4 | S1 | S3 | S5 | PI | NI | ||
| Ses. 1 | CR2 | 1 | 0.48 | 0.25 | 0.31 | 0.28 | 0.39 | 0.41 | 0.26 | 0.28 | 0.22 | 0.21 | 0.24 | 0.33 | 0.27 |
| CR4 | 1 | 0.17 | 0.33 | 0.37 | 0.48 | 0.44 | 0.17 | 0.26 | 0.33 | 0.43 | 0.28 | 0.34 | 0.40 | ||
| S1 | 1 | 0.16 | 0.11 | 0.28 | 0.21 | 0.32 | 0.27 | 0.44 | 0.22 | 0.13 | 0.31 | 0.22 | |||
| S3 | 1 | 0.61 | 0.42 | 0.29 | 0.30 | 0.18 | 0.33 | 0.55 | 0.53 | 0.23 | 0.20 | ||||
| S5 | 1 | 0.54 | 0.34 | −0.01 | 0.03 | 0.23 | 0.61 | 0.54 | 0.29 | 0.34 | |||||
| PI | 1 | 0.59 | 0.21 | 0.38 | 0.40 | 0.56 | 0.45 | 0.63 | 0.63 | ||||||
| NI | 1 | 0.33 | 0.36 | 0.31 | 0.35 | 0.20 | 0.55 | 0.56 | |||||||
| Ses. 2 | CR2 | 1 | 0.99 | 0.12 | −0.03 | −0.06 | −0.09 | −0.22 | |||||||
| CR4 | 1 | 0.15 | 0 .01 | −0.02 | −0.04 | −0.14 | |||||||||
| S1 | 1 | 0.49 | 0.35 | 0.28 | 0.37 | ||||||||||
| S3 | 1 | 0.53 | 0.29 | 0.34 | |||||||||||
| S5 | 1 | 0.27 | .30 | ||||||||||||
| PI | 1 | 0.66 | |||||||||||||
| NI | 1 | ||||||||||||||
Note.: Ses.1/2 = measures at measurement point one or two; CR2/4 = choice response time task with two/four alternatives; S1 = set size one; S3 = set size three; S5 = set size five; PI = physical identity; NI = name identity.
References
- Sheppard, L.D.; Vernon, P.A. Intelligence and speed of information-processing: A review of 50 years of research. Personal. Individ. Differ. 2008, 44, 535–551. [Google Scholar] [CrossRef]
- Kranzler, J.H.; Jensen, A.R. The nature of psychometric g: Unitary process or a number of independent processes? Intelligence 1991, 15, 397–422. [Google Scholar] [CrossRef]
- Miller, L.T.; Vernon, P.A. Intelligence, reaction time, and working memory in 4- to 6-year-old children. Intelligence 1996, 22, 155–190. [Google Scholar] [CrossRef]
- Saccuzzo, D.P.; Larson, G.E.; Rimland, B. Speed of Information Processing and Individual Differences In Intelligence; Research Report NPRDC TR 86-23; Navy Personnel Research and Development Center: San Diego, CA, USA, 1986. [Google Scholar]
- Jensen, A.R. The importance of intraindividual variation in reaction time. Personal. Individ. Differ. 1992, 13, 869–881. [Google Scholar] [CrossRef]
- Jensen, A.R. Clocking the Mind: Mental Chronometry and Individual Differences; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Doebler, P.; Scheffler, B. The relationship of choice reaction time variability and intelligence: A meta-analysis. Learn. Individ. Differ. 2015. [Google Scholar] [CrossRef]
- Larson, G.E.; Alderton, D.L. Reaction time variability and intelligence: A “worst performance” analysis of individual differences. Intelligence 1990, 14, 309–325. [Google Scholar] [CrossRef]
- Coyle, T.R. A review of the worst performance rule: Evidence, theory, and alternative hypotheses. Intelligence 2003, 31, 567–587. [Google Scholar] [CrossRef]
- Fernandez, S.; Fagot, D.; Dirk, J.; de Ribaupierre, A. Generalization of the worst performance rule across the lifespan. Intelligence 2014, 42, 31–43. [Google Scholar] [CrossRef]
- Heathcote, A.; Popiel, S.J.; Mewhort, D.J. Analysis of response time distributions: An example using the Stroop task. Psychol. Bull. 1991, 109, 340–347. [Google Scholar] [CrossRef]
- Spieler, D.H.; Balota, D.A.; Faust, M.E. Levels of selective attention revealed through analyses of response time distributions. J. Exp. Psychol. Hum. Percept. Perform. 2000, 26, 506–526. [Google Scholar] [CrossRef] [PubMed]
- Carroll, J.B. Human Cognitive Abilities: A Survey of Factor-Analytic Studies; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1993. [Google Scholar]
- Smith, G.A.; Carew, M. Decision time unmasked: Individuals adopt different strategies. Aust. J. Psychol. 1987, 39, 339–351. [Google Scholar] [CrossRef]
- Ratcliff, R. A theory of memory retrieval. Psychol. Rev. 1978, 85, 59–108. [Google Scholar] [CrossRef]
- Voss, A.; Rothermund, K.; Voss, J. Interpreting the parameters of the diffusion model: An empirical validation. Memory Cogn. 2004, 32, 1206–1220. [Google Scholar] [CrossRef]
- Ratcliff, R.; Spieler, D.; McKoon, G. Explicitly modeling the effects of aging on response time. Psychon. Bull. Rev. 2000, 7, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Nagler, M.; Lerche, V. Diffusion models in experimental psychology: A practical introduction. Exp. Psychol. 2013, 60, 385–402. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Voss, J. Fast-dm: A free program for efficient diffusion model analysis. Behav. Res. Methods 2007, 39, 767–775. [Google Scholar] [CrossRef] [PubMed]
- Vandekerckhove, J.; Tuerlinckx, F. Fitting the Ratcliff diffusion model to experimental data. Psychon. Bull. Rev. 2007, 14, 1011–1026. [Google Scholar] [CrossRef] [PubMed]
- Vandekerckhove, J.; Tuerlinckx, F. Diffusion model analysis with MATLAB: A DMAT primer. Behav. Res. Methods 2008, 40, 61–72. [Google Scholar] [CrossRef] [PubMed]
- Wagenmakers, E.J.; van der Maas, H.L.J.; Grasman, R.P.P.P. An EZ-diffusion model for response time and accuracy. Psychon. Bull. Rev. 2007, 14, 3–22. [Google Scholar] [CrossRef] [PubMed]
- Nunez, M.D.; Srinivasan, R.; Vandekerckhove, J. Individual differences in attention influence perceptual decision making. Front. Psychol. 2015, 8, 18. [Google Scholar] [CrossRef] [PubMed]
- Stahl, C.; Voss, A.; Schmitz, F.; Nuszbaum, M.; Tuscher, O.; Lieb, K.; Klauer, K.C. Behavioral components of impulsivity. J. Exp. Psychol. Gen. 2014, 143, 850–886. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R.; Thapar, A.; Mckoon, G. Individual differences, aging, and IQ in two-choice tasks. Cogn. Psychol. 2010, 60, 127–157. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R.; Thapar, A.; Mckoon, G. Effects of aging and IQ on item and associative memory. J. Exp. Psychol. Gen. 2011, 140, 464–487. [Google Scholar] [CrossRef] [PubMed]
- Schmiedek, F.; Oberauer, K.; Wilhelm, O.; Suss, H.M.; Wittmann, W.W. Individual differences in components of reaction time distributions and their relations to working memory and intelligence. J. Exp. Psychol. Gen. 2007, 136, 414–429. [Google Scholar] [CrossRef] [PubMed]
- Schubert, A.L.; Hagemann, D.; Voss, A.; Schankin, A.; Bergmann, K. Decomposing the relationship between mental speed and mental abilities. Intelligence 2015, 51, 28–46. [Google Scholar] [CrossRef]
- Ratcliff, R.; Thompson, C.A.; Mckoon, G. Modeling individual differences in response time and accuracy in numeracy. Cognition 2015, 137, 115–136. [Google Scholar] [CrossRef] [PubMed]
- Yap, M.J.; Balota, D.A.; Sibley, D.E.; Ratcliff, R. Individual differences in visual word recognition: Insights from the English Lexicon Project. J. Exp. Psychol. Hum. Percept. Perform. 2012, 38, 53–79. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R.; Mckoon, G. The diffusion decision model: Theory and data for two-choice decision tasks. Neural Comput. 2008, 20, 873–922. [Google Scholar] [CrossRef] [PubMed]
- Molenaar, D.; Tuerlinckx, F.; van der Maas, H.L.J. Fitting Diffusion Item Response Theory Models for Responses and Response Times Using the R Package diffIRT. J. Stat. Softw. 2015, 66. [Google Scholar] [CrossRef]
- Tuerlinckx, F.; Boeck, P.D. Two interpretations of the discrimination parameter. Psychometrika 2005, 70, 629–650. [Google Scholar] [CrossRef]
- Van der Maas, H.L.J.; Molenaar, D.; Maris, G.; Kievit, R.A.; Borsboom, D. Cognitive psychology meets psychometric theory: On the relation between process models for decision making and latent variable models for individual differences. Psychol. Rev. 2011, 118, 339–356. [Google Scholar] [CrossRef] [PubMed]
- Vandekerckhove, J. A cognitive latent variable model for the simultaneous analysis of behavioral and personality data. J. Math. Psychol. 2014, 60, 58–71. [Google Scholar] [CrossRef]
- Allport, G.W. Personality, a Psychological Interpretation; Holt: New York, NY, USA, 1937. [Google Scholar]
- Cattell, R. Personality: A Systematic Theoretical and Factual Study; McGraw-Hill: New York, NY, USA, 1950. [Google Scholar]
- Steyer, R.; Schmitt, M.; Eid, M. Latent state–trait theory and research in personality and individual differences. Eur. J. Personal. 1999, 13, 389–408. [Google Scholar] [CrossRef]
- Langner, R.; Steinborn, M.B.; Chatterjee, A.; Sturm, W.; Willmes, K. Mental fatigue and temporal preparation in simple reaction-time performance. Acta Psychol. 2010, 133, 64–72. [Google Scholar] [CrossRef] [PubMed]
- Doll, T.J. Motivation, reaction time, and the contents of active verbal memory. J. Exp. Psychol. 1971, 87, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Lerche, V.; Voss, A. Retest reliability of the parameters of the ratcliff diffusion model. Psychol. Res. 2016, 2016, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Larsen, L.; Hartmann, P.; Nyborg, H. The stability of general intelligence from early adulthood to middle-age. Intelligence 2008, 36, 29–34. [Google Scholar] [CrossRef]
- Hick, W.E. On the rate of gain of information. Q. J. Exp. Psychol. 1952, 4, 11–26. [Google Scholar] [CrossRef]
- Brown, S.D.; Heathcote, A. The simplest complete model of choice response time: Linear ballistic accumulation. Cogn. Psychol. 2008, 57, 153–178. [Google Scholar] [CrossRef] [PubMed]
- Usher, M.; McClelland, J.L. The time course of perceptual choice: The leaky, competing accumulator model. Psychol. Rev. 2001, 108, 550–592. [Google Scholar] [CrossRef] [PubMed]
- Leite, F.P.; Ratcliff, R. Modeling reaction time and accuracy of multiple-alternative decisions. Atten. Percept. Psychophys. 2010, 72, 246–273. [Google Scholar] [CrossRef] [PubMed]
- Sternberg, S. Memory-scanning: Mental processes revealed by reaction-time experiments. Am. Sci. 1969, 57, 421–457. [Google Scholar] [PubMed]
- Posner, M.I.; Mitchell, R.F. Chronometric analysis of classification. Psychol. Rev. 1967, 74, 392–409. [Google Scholar] [CrossRef] [PubMed]
- Steyer, R.; Ferring, D.; Schmitt, M.J. States and traits in psychological assessment. Eur. J. Psychol. Assess. 1992, 8, 79–98. [Google Scholar]
- Steyer, R.; Mayer, A.; Geiser, C.; Cole, D.A. A theory of states and traits–revised. Annu. Rev. Clin. Psychol. 2015, 11, 71–98. [Google Scholar] [CrossRef] [PubMed]
- Danner, D.; Hagemann, D.; Schankin, A.; Hager, M.; Funke, J. Beyond IQ: A latent state-trait analysis of general intelligence, dynamic decision making, and implicit learning. Intelligence 2011, 39, 323–334. [Google Scholar] [CrossRef]
- Deinzer, R.; Steyer, R.; Eid, M.; Notz, P.; Schwenkmezger, P.; Ostendorf, F.; Neubauer, A. Situational effects in trait assessment: The FPI, NEOFFI, and EPI questionnaires. Eur. J. Personal. 1995, 9, 1–23. [Google Scholar] [CrossRef]
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 7th ed.; Muthén & Muthén: Los Angeles, CA, USA, 1998–2012. [Google Scholar]
- Browne, M.W.; Cudeck, R. Alternative Ways of Assessing Model Fit. Sociol. Methods Res. 1992, 21, 230–258. [Google Scholar] [CrossRef]
- Hu, L.T.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. 1999, 6, 1–55. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).