Abstract
Aiming at the characteristics of limited actuation capability of the semi-active control system and strong nonlinearity of the hydro-pneumatic suspension, a constrained nonlinear control strategy of a semi-active hydro-pneumatic suspension system is proposed. According to the mathematical model of nonlinear hydro-pneumatic suspension, the static stiffness and linear damping coefficient based on the equivalent energy are calculated, and then the control-oriented dynamic equation whose expression minimizes the nonlinear term is constructed. Combined with actuation capacity constraints, an optimization model with constraints is established to minimize the deviation between the actual overall control force and the expected optimal control force, and the optimal approximation from nonlinear control to linear quadratic optimal control is realized. The control simulation results of various methods show that the nonlinear control with constraints of the semi-active hydro-pneumatic suspension system, which effectively combines the actuation capacity constraints and nonlinear characteristics of the system, achieves a good comprehensive control effect for the nonlinear suspension control with constraints.
1. Introduction
With the development of modern vehicle electronic control technology, controllable suspension systems can adapt to different road surfaces and vehicle conditions, breaking the inherent limitations of traditional suspension systems and showing broad application prospects. In various driving conditions such as steering, acceleration, and braking, an active suspension system can not only improve ride comfort but also limit the roll and pitch movements of the vehicle body in both transient and steady states. However, active suspension systems have shortcomings such as high cost and large energy consumption, which restrict their application in commercial vehicles. Compared with active suspension, semi-active suspension has great potential in improving ride comfort and maneuverability, and balances cost and performance well. At the same time, semi-active suspension also has a certain fault-tolerant capability. Once the control system fails, it can still work like passive suspension [1,2].
Semi-active control suspensions mostly adopt continuously adjustable damping devices. The principle of such suspensions is mainly realized by variable orifices or intelligent materials, whose viscosity changes with control current (electrorheological damping or magnetorheological damping) [3,4,5]. In terms of cost, variable orifice shock absorbers are more valuable for market application than magnetorheological and electrorheological shock absorbers, with broad application prospects and mature commercial products available. Continuously adjusting damping by changing the opening of flow orifices remains the main implementation method in current commercial vehicle semi-active suspension systems. Hydro-pneumatic suspension, developed by Citroen in the 1950s, features compact structure and strong controllability. Its variable-volume nitrogen accumulator can provide good nonlinear elastic characteristics, and it is widely used in heavy vehicles such as engineering vehicles and military vehicles. Compared with other suspension systems, this suspension itself contains an actuating cylinder, making it easy to realize active and semi-active control [6].
The design of active and semi-active suspension controllers is basically the same. The main difference is that the control output force of semi-active suspension is limited by the current state (such as the relative velocity or relative displacement of the suspension) [7,8], and suboptimal control results are often obtained through the shear force method in many cases, while active suspension generally only limits the power of the actuation force output, which has stronger control capability. At present, most linear control strategies are adopted for active or semi-active hydro-pneumatic suspensions, such as PID control, linear quadratic Gaussian (LQG) control, and linear model predictive control [9,10,11,12,13]. For systems with high nonlinearity like hydro-pneumatic suspensions, it is difficult to achieve ideal control performance with linear control methods. In recent years, many researchers have proposed nonlinear control methods for controllable hydro-pneumatic suspension systems. Wang et al. derived approximate solutions based on data-driven reinforcement learning algorithms to achieve constrained H∞ optimal control for nonlinear active suspensions [14]. However, data-driven control is a black-box control model, and for boundary ranges or control sequences that are not trained, it can lead to significant degradation in control performance or instability issues. Jibril et al. proposed a fuzzy model predictive control method for active suspension systems to stabilize the displacement of active suspensions under different road profiles [15]. In fact, the model predictive control method is suitable for linear or weakly nonlinear systems; otherwise, the linear model cannot accurately describe their behavior, resulting in degraded control performance or even instability. Saglam adopted a control method based on state-dependent Riccati equations to design a self-adjusting suboptimal nonlinear controller for active hydro-pneumatic suspension systems [6]. To obtain the Riccati equation form represented by state variables, a polynomial expression was used to fit the elastic force. Shi et al. established a nonlinear dynamic model for vehicle active hydro-pneumatic suspensions, transformed the nonlinear system into a linear system through feedback linearization, and achieved nonlinear control of the active hydro-pneumatic suspension system using sliding mode control [16]. Feedback linearization control generally requires relatively accurate control equations. However, in this study, the elastic force of the hydro-pneumatic suspension was approximated by a first-order Taylor expansion, and the influence of the active system flow rate on the damping force was ignored, making it difficult to ensure the reliability of the actual control system. Hao et al. proposed a new multi-objective command filter adaptive control strategy for active suspension systems with nonlinear hydraulic actuators [17]. Hu et al. combined the actuation force output model with the suspension system to establish a nonlinear dynamic model of the electromagnetic active suspension and designed a multi-objective particle swarm robust hybrid controller based on adaptive filter compensation using the filtered recursive least square method [18]. Pan et al. focused on communication optimization and state constraints and proposed an adaptive event-triggered control method for nonlinear vehicle active suspension systems [19]. Yan et al. focused on the multi-actuator fault problem of the full-vehicle active suspension system and put forward a joint fault-tolerant control and fault diagnosis strategy [20]. Feng et al. aimed at the time-varying motion constraint problem of active suspension systems and proposed a neural adaptive control method based on nonlinear state-dependent functions (NSDF) [21]. However, they only considered the nonlinearity of the actuator without considering the nonlinearity of the suspension system itself. In summary, these nonlinear control methods rarely involve control under actuation capability constraints, and a generalized nonlinear control method for constrained controllable suspension systems has not yet been formed.
In recent years, the development of bionics has brought new ideas and methods for the nonlinear control of suspension systems. Yan et al. proposed a new bionic vibration isolation structure inspired by the leg structure of kangaroos and verified its excellent performance in low-frequency vibration isolation through theoretical modeling and experimental validation [22]. Cao et al. constructed a bionic limb-like quasi-zero stiffness vibration isolation system and conducted a comparative analysis of its vibration isolation characteristics with those of linear and traditional quasi-zero stiffness vibration isolation systems [23]. Pan et al., based on the phenomenon of Grus japonensis landing safely from high places, designed a bionic polygonal skeleton structure and carried out a systematic study on its nonlinear characteristics and vibration isolation performance [24]. These bionic vibration isolators, relying on their unique structural configurations and nonlinear mechanical properties, have shown significant advantages in low-frequency vibration isolation, load-bearing capacity, and stability, injecting new vitality into the development of vibration isolation technology. However, the current research on bionic vibration isolators is still in the exploratory stage, and there is a great deal of work to be done in depth in terms of structural optimization, performance improvement, and expansion of practical engineering applications.
In response to this, based on the establishment of the mathematical model of the nonlinear hydro-pneumatic suspension, this paper constructs a nonlinear dynamic equation with minimized nonlinear terms according to the linear damping coefficient and static stiffness obtained by energy equivalence. Furthermore, an optimization model with actuation capability constraints is established to minimize the difference between the actual overall control force term and the linear quadratic optimal control force term, forming a generalized nonlinear control method for constrained controllable suspension systems.
The rest of this paper is structured as follows: Section 2 establishes a mathematical model of vehicle dynamics with semi-active hydro-pneumatic suspension; Section 3 introduces the constrained nonlinear control method for the semi-active hydro-pneumatic suspension system; Section 4 conducts simulations of the hydro-pneumatic suspension system using four control methods; Section 5 analyzes the simulation results of the hydro-pneumatic suspension control system and compares the performance of different control methods; Section 6 summarizes the research conclusions of this paper.
2. Vehicle Dynamics Modeling with Semi-Active Hydro-Pneumatic Suspension
2.1. Quarter Vehicle Dynamic Equations
Figure 1 shows a quarter-vehicle model with a semi-active hydro-pneumatic suspension: mw and mb represent the unsprung mass and sprung mass, respectively; xg, xw and xb denote the random displacement of the road surface, the displacement of the unsprung mass, and the displacement of the sprung mass, respectively; kt and ct are the stiffness and damping of the tire. Based on the traditional passive hydro-pneumatic suspension, this model adds an adjustable damping valve, which can adjust the damping force of the suspension system according to the actual road conditions. The controllable hydro-pneumatic suspension system generally adopts a hydro-pneumatic separated structure, that is, the accumulator is connected to the hydro-pneumatic suspension cylinder through an external pipeline, as specifically referred to in Reference [25].
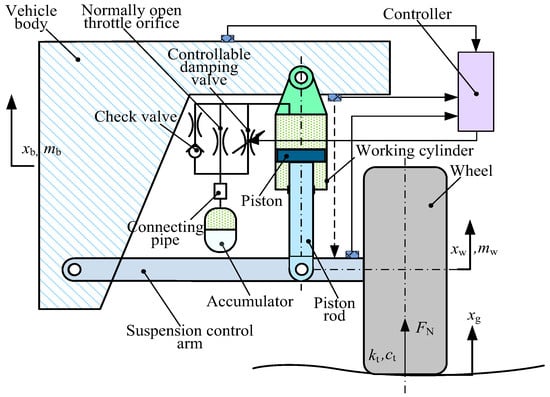
Figure 1.
A quarter-vehicle model of the semi-active oil-gas suspension.
Considering that the semi-active hydro-pneumatic suspension adopts the form of an external accumulator, the mathematical model of the suspension force needs to take into account the effects of the adjustable damping orifice, the along way pressure loss of the pipeline, and the local pressure loss at the outlet of the accumulator [16]. Therefore, the mathematical model of the suspension force is as follows:
where is the damping force generated by the pressure loss of the thin-walled orifice, ; is the damping force generated by the pressure loss in the pipeline, ;; Sc is the effective cross-sectional area of the piston rod; P1 and V1 are the accumulator pressure and volume under static balance, respectively; A01 is the equivalent area of the damping orifice, A02 is the equivalent area of the one-way damping orifice, and A03 is the equivalent area of the variable damping orifice; Cd1, Cd2, and Cd3 are the flow coefficients of the normally open damping orifice, one-way damping orifice, and variable damping orifice, respectively; lp, Dp, and Sp are the pipeline length, diameter, and cross-sectional area, respectively; ξ is the local pressure loss coefficient; Sa is the cross-sectional area of the accumulator outlet; Ff is the sealing friction force [26].
2.2. Dynamic Equations Relative to Static Equilibrium Position
Figure 2 is a schematic diagram of the quarter-vehicle model with a semi-active hydro-pneumatic suspension.
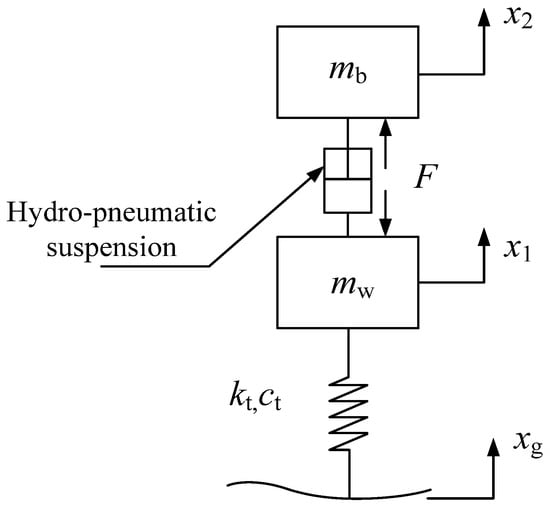
Figure 2.
Schematic diagram of the quarter-vehicle model.
According to the schematic diagram of the quarter-vehicle model shown in Figure 2, its dynamic equation relative to the static equilibrium position is as follows:
where F is the suspension force and x1 and x2 are the displacements of the unsprung mass and sprung mass relative to their static equilibrium positions, respectively. Other variables have been defined in Section 2.1.
2.3. Static Stiffness and Equivalent Damping Coefficient
According to Taylor’s expansion, we obtain the following:
where is the static stiffness of the gas spring.
In engineering practice, most of the damping existing in vibration systems is non-viscous damping, and the mathematical description of non-viscous damping is relatively complex. For the convenience of vibration analysis, energy methods are usually used to simplify non-viscous damping into equivalent viscous damping. The equivalent principle is that the energy consumed by viscous damping in one cycle is equal to the energy consumed by non-viscous damping in one cycle.
Considering that one of the damping valves is controllable and the effective area varies in the range of 0~, combining the opening and closing conditions of the unidirectional damping valve during extension and compression, let:
where and are the coefficients preceding in the calculation formula of damping force generated by the pressure loss of the thin-walled orifice. Since the suspension has different damping in the stretching and compressing strokes, these preceding coefficients are different. Specifically, is the coefficient for the stretching stroke, and is the coefficient for the compressing stroke.
Set , , , the equivalent viscous damping coefficient of the oil-gas suspension is , according to the calculation formula of damping force work, we have the following:
Substitute the above equation into the expressions for z, and dz, and simplify to obtain the following:
And because of , it follows that:
In the above equation, Bω represents the amplitude of the relative velocity of the oil-gas suspension. For a vehicle suspension system with random road input, the root mean square (RMS) value of the relative velocity of the passive suspension is generally used to approximately calculate the equivalent damping coefficient. To minimize the influence of nonlinear factors and enable the nonlinear control system to approach the linear optimal control system as much as possible, the next section constructs a vehicle dynamic equation containing static stiffness and equivalent damping coefficient and uses a constrained optimization method to seek the optimal control force at each moment.
3. Nonlinear Control of Semi-Active Hydro-Pneumatic Suspension System
3.1. Dynamic Equation for Nonlinear Term Minimization
According to the static stiffness and equivalent damping coefficient, let and . Adding and subtracting the same terms on the right sides of Equations (2) and (3), the equations still hold, that is:
Let:
where ; , u can be regarded as an overall control input force, which is a nonlinear function of , and . Further, Equations (10) and (11) can be rearranged as follows:
In a controlled suspension vehicle, real-time values of and can be easily obtained through the measurement results of the suspension displacement sensor. Therefore, when the cross-sectional area of the controllable damping orifice is given, the actual overall control force u can be determined.
It can be seen from Equations (13) and (14) that the linear suspension force obtained by using the static stiffness and equivalent damping coefficient, namely , can largely reflect the inherent characteristics of the system, and the influence of the remaining nonlinear terms is already small at this time. Therefore, by using the form of the traditional state-space equation and constructing a quadratic performance function based on the ride comfort performance indicators, the desired linear optimal overall control force is obtained. However, the controllable capability of the semi-active suspension system is limited, and it may not be able to achieve the desired optimal control force. Therefore, Section 3.4 will realize the optimal approximation between the actual overall control force and the desired overall control force by constructing a constrained optimization model.
3.2. State Space Equations of the System with Road Random Inputs
Filtered white noise can directly express the road roughness displacement in the form of a differential, which facilitates its extension into Equations (13) and (14). In this regard, the random road displacement xg is written in the form of filtered white noise [27]:
where is the vertical velocity of the random road surface, f0 is the lower cutoff frequency, generally taken as 0.0628 Hz; w(t) is a Gaussian white noise with a power spectral density amplitude of 1, n0 is the frequency index, and n0 = 0.1 m−1.
According to the actual sensor configuration, the outputs of the sensors are the suspension displacement x2(t) − x1(t), the suspension velocity 2(t) − 1(t), the acceleration of the unsprung mass, and the acceleration of the sprung mass. Combining with Equation (15), Equations (13) and (14) are extended to obtain the state space equations of the system with road random inputs:
where:
3.3. Linear Quadratic Optimal Control Under Ride Comfort Indexes
Three performance indicators of ride comfort: tire dynamic deflection x1(t) − xg(t), suspension dynamic travel x2(t) − x1(t), and acceleration of sprung mass 2. Expressed in matrix form with state xa(t) and overall control force u(t), we have the following:
where:
Note: For the sake of convenience, one of the performance indicators of ride comfort is defined here as the dynamic deflection of the tire, which is slightly different from the common indicator of tire dynamic load, i.e., there is a difference of a tire stiffness coefficient.
Treat u(t) as the overall control input of the system, and construct a quadratic performance function based on the ride comfort indexes and the input quantity u(t).
After further sorting out, we have the following:
In the above formula, q1, q2, q3, and q4 are the weight coefficients of tire dynamic deflection, suspension dynamic travel, sprung mass acceleration, and the overall control force u, respectively.
According to the Riccati algebraic equation, the optimal control gain is obtained:
where P is the solution to the following Riccati algebraic equation.
Therefore, the optimal control is as follows:
3.4. Constrained Optimization Model for Optimal Control
The optimal control force uopt = −Kx(t), while the actual overall control force u can be obtained according to Equation (12). Considering that the adjustment of the controllable damping valve is limited (i.e., the effective flow area can only vary within a limited range), to obtain the optimal control A03(t) under this condition, a constrained optimization model is established to minimize |uopt − u|. For this purpose, the optimization model is established as follows:
- (1)
- Design variable: A03, which represents the effective acting area of the controllable damping valve at each moment.
- (2)
- Objective function:
- (3)
- Constraint condition: .
When the relative velocity of the suspension is large, the controllability is strong, and the desired overall vehicle control force can usually be achieved; when the relative velocity of the suspension is small, the controllability is weak, and the optimization model can ensure that the desired and ideal overall control forces are closest. Therefore, it can realize the approximation of nonlinear control to linear quadratic optimal control.
Based on the actual sensor data, z and ż at each moment are obtained. Then, an appropriate state estimator (such as the Unscented Kalman Filter [28]) is used to estimate the system state so that an optimization model only related to the design variable A03 can be obtained. After that, an optimization algorithm is called for solution, and the optimal effective acting area of the controllable damping valve in the nonlinear control system at each moment is obtained.
4. Simulation of Hydro-Pneumatic Suspension Control System
Assuming that all system states are observable, simulations of the hydro-pneumatic suspension system using various control methods and comparative studies thereof are carried out based on the nonlinear control method proposed in the previous section. It should be emphasized that for the closed-loop system constructed in the control simulation of the constrained semi-active hydro-pneumatic suspension, regardless of the opening area of the actuating damping valve, the closed-loop system can always be linearized into a state-space equation under each state. Moreover, the system matrix of this state equation is negative definite, indicating that the closed-loop system is stable, which can be known from Lyapunov’s first approximation theory [29].
4.1. Dynamic Simulation Parameters of the Suspension System
Table 1 shows the dynamic simulation parameters of a certain mining dump truck. In addition, based on the results of dynamic responses, considering the three ride comfort index quantities (yr1, yr2, yr3) and the overall control force u, we first analyze the order of magnitude of these performance index quantities and then make appropriate fine-tuning in combination with the response results to determine their weight coefficients.

Table 1.
Dynamic simulation parameters of semi-active hydro-pneumatic suspension system.
4.2. Simulation Settings and Results of Four Control Systems
- (1)
- Passive control. It refers to the situation when the controllable damping valve is closed, i.e., A03 is constantly equal to 0.
- (2)
- Unconstrained control. The difference between it and the constrained semi-active hydro-pneumatic suspension is that its actuation capability is not constrained (or its actuation capability is relatively large), which means that the system can provide an actuation force of any magnitude at each moment and can achieve the desired overall control force (i.e., u = uopt). In this case, such a controller degenerates into a linear quadratic optimal control. For the convenience of comparison, this paper presents the simulation results of the unconstrained semi-active hydro-pneumatic suspension nonlinear control.
- (3)
- Skyhook control. Skyhook damping control mainly realizes an “on-off” switch control mode through a two-state damping, and the control algorithm can be referred to in reference [30]. It has the advantages of simple control law and good effect, and is one of the most commonly used suspension control strategies in commercial vehicles at present.
- (4)
- Constrained control. The “constrained control” mentioned in this section is the abbreviation of the nonlinear control method proposed in this paper for the semi-active suspension system.
Figure 3, Figure 4, Figure 5 and Figure 6 show the simulation results of the four control methods when the vehicle is traveling on a Class D road at 20 km/h. In Figure 3 and Figure 4, (a) represents the simulation results from 0 to 60 s; (b) represents the simulation results from 20 to 21 s. In Figure 5 and Figure 6, (a) represents the simulation results within the range of 0 to 35 Hz; (b) represents the simulation results within the range of 0 to 6 Hz. Subgraph (b) clearly shows the differences between the four control results. ·
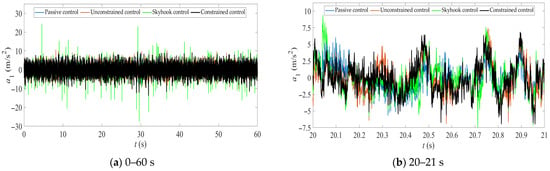
Figure 3.
Time-domain response of unsprung mass acceleration under four control methods. (a) Simulation Results from 0 to 60 s, (b) Simulation results from 20 to 21 s.
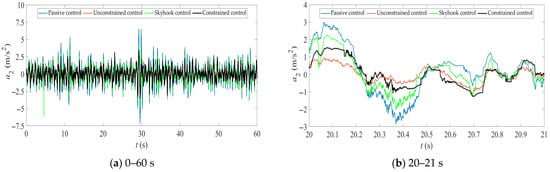
Figure 4.
Time-domain response of sprung mass acceleration under four control methods. (a) simulation results from 0 to 60 s, (b) simulation results from 20 to 21 s.
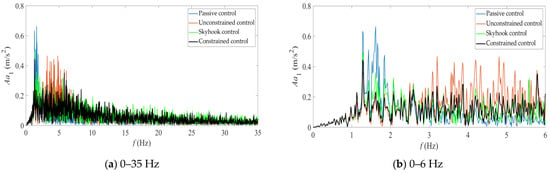
Figure 5.
Amplitude spectra of unsprung mass acceleration under four types of control. (a) simulation results from 0 to 35 Hz, (b) simulation results from 0 to 6 Hz.
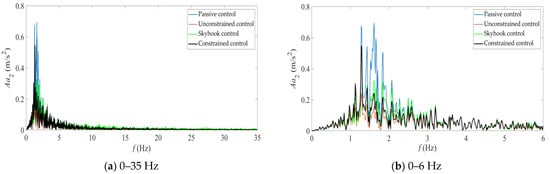
Figure 6.
Amplitude spectra of sprung mass acceleration under four types of control. (a) simulation results from 0 to 35 Hz, (b) simulation results from 0 to 6 Hz.
5. Analysis of Simulation Results for Hydro-Pneumatic Suspension Control
Based on the control simulation results, the concerned indicators are statistically summarized, as shown in Table 2.

Table 2.
Statistical results of simulations for four control methods.
Taking the passive control results as the benchmark, the improvement degrees of three ride comfort indicators (i.e., the root mean square values of sprung mass acceleration, suspension dynamic travel, and tire dynamic load) under unconstrained control, skyhook control, and constrained control are obtained. The improvement degrees of sprung mass acceleration are 56.764%, 28.661%, and 36.541%; the improvement degrees of suspension dynamic travel are −38.191%, −4.356%, and −27.292%; the improvement degrees of tire dynamic load are 47.362%, 26.794%, and 35.645%. It can be seen that the suspension dynamic travel of the controllable suspension system deteriorates to a certain extent, but both the sprung mass acceleration and tire dynamic load are significantly improved. Considering the structural design and installation stroke of the hydro-pneumatic suspension, the suspension dynamic travel (maximum and minimum suspension displacement) does not reach the limit position, and there is a certain redundancy. This indicates that the unconstrained control has the best effect, followed by the constrained control, and the skyhook control has the worst effect. It can be seen from Figure 3 and Table 2 that skyhook control significantly deteriorates the vibration of the unsprung mass, especially increasing its maximum and minimum values, and is accompanied by large impacts (see the response results around 29.6 s in Figure 3a). It can be seen from Figure 5 and Figure 6 that unconstrained control significantly improves the amplitude of sprung acceleration response in each frequency band of the hydro-pneumatic suspension system but at the same time increases the amplitude of unsprung mass acceleration, especially in the 3–6 Hz frequency band.
To sum up, unconstrained control can better suppress the vibration of the sprung mass, but it does not take into account the constraints on the actuation capability of the actual suspension system, thus failing to ensure the actual control effect. The constrained nonlinear control for the semi-active hydro-pneumatic suspension system balances the constraint issues well in the actual semi-active suspension control. When the system has strong damping force adjustment capability, it will approach the results of linear quadratic optimal control.
6. Conclusions
On the basis of establishing a vehicle dynamics model containing a semi-active hydro-pneumatic suspension, a nonlinear dynamic equation with minimized nonlinear terms was constructed according to the linear damping coefficient and static stiffness obtained from energy equivalence. To take into account the actuation capability constraints of the semi-active suspension system, a constrained optimization model for optimal control was established, thus forming a nonlinear control method for the suspension system with constraints.
Simulation results from multiple methods indicate that the nonlinear control method for semi-active hydro-pneumatic suspensions with constraints effectively combines unconstrained control and actuation capability constraints, achieving a control effect with excellent comprehensive performance. The control-oriented dynamic equation takes into account the nonlinearity of the hydro-pneumatic suspension (such as stiffness, damping, and seal friction) and actuation capability constraints, which not only improves the control accuracy but also better conforms to the actual working conditions of the vehicle.
In this study, by constructing a control-oriented nonlinear dynamic equation with minimized nonlinear terms and establishing an optimization model that minimizes the difference between the actual overall control force term and the expected control force, the optimal approximation effect of nonlinear control to linear quadratic optimal control is achieved. This provides an effective design method for the nonlinear control of suspension systems.
Author Contributions
Conceptualization, B.Q. and C.J.; methodology, B.Q. and C.J.; software, B.Q.; validation, B.Q. and C.J.; investigation, B.Q.; resources, B.Q. and C.J.; data curation, B.Q.; writing—original draft preparation, B.Q.; writing—review and editing, B.Q. and C.J.; formal analysis, B.Q.; supervision, C.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wagh, R.R. A Review on Controlling Methods for Semi-Active Suspension Systems. Int. J. Res. Appl. Sci. Eng. 2024, 12, 3188–3193. [Google Scholar] [CrossRef]
- Ni, F.; Luo, Y.; Xu, J.; Liu, D.; Sun, Y.; Ji, W. Review of Fault-Tolerant Control Methods for Suspension Systems: From Road Vehicles to Maglev Trains. Mathematics 2024, 12, 2576. [Google Scholar] [CrossRef]
- Wang, X.; Huang, D.; Qin, N.; Chen, C.; Zhang, K. Modeling and Second-Order Sliding Mode Control for Lateral Vibration of High-Speed Train With MR Dampers. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10299–10308. [Google Scholar] [CrossRef]
- Ab Talib, M.H.; Muhammad Afandi, M.A.D.; Mat Darus, I.Z.; Mohd Yatim, H.; Asus, Z.; Mohd Yamin, A.H.; Hadi, M.S. Magnetorheological Damper Control for Semi-Active Suspension System Using Skyhook-Differential Evolution. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2021; pp. 161–171. [Google Scholar] [CrossRef]
- Kumar, S.; Chandramohan, S.; Sujatha, S. Geometric Optimization of Magnetorheological Damper for Prosthetic Ankles Using Artificial Neural Networks. Mechatronics 2024, 98, 103108. [Google Scholar] [CrossRef]
- Saglam, F.; Unlusoy, Y.S. Adaptive ride comfort and attitude control of vehicles equipped with active hydro-pneumatic suspension. Int. J. Veh. Des. 2016, 71, 31–51. [Google Scholar] [CrossRef]
- Soh, M.; Jang, H.; Park, J.; Sohn, Y.; Park, K. Development of Preview Active Suspension Control System and Performance Limit Analysis by Trajectory Optimization. Int. J. Automot. Technol. 2018, 19, 1001–1012. [Google Scholar] [CrossRef]
- Brezas, P.; Smith, M.C.; Hoult, W. A Clipped-Optimal Control Algorithm for Semi-Active Vehicle Suspensions: Theory and Experimental Evaluation. Automatica 2015, 53, 188–194. [Google Scholar] [CrossRef]
- Sun, Q.; Yin, C.; Wang, B. Experimental Validation of Truck Cab Suspension Model and Ride Comfort Improvement under Various Semi-Active Control Strategies. Processes 2024, 12, 1880. [Google Scholar] [CrossRef]
- Likaj, R.; Shala, A. Optimisation and Control of Vehicle Suspension Using Linear Quadratic Gaussian Control. Stroj. časopis-J. Mech. Eng. 2018, 68, 61–68. [Google Scholar] [CrossRef]
- Shehata Gad, A. Preview Model Predictive Control Controller for Magnetorheological Damper of Semi-Active Suspension to Improve Both Ride and Handling. SAE Int. J. Veh. Dyn. Stab. NVH 2020, 4, 305–326. [Google Scholar] [CrossRef]
- Yang, L.; Wang, R.; Ding, R.; Liu, W.; Zhu, Z. Investigation on the Dynamic Performance of a New Semi-Active Hydro-Pneumatic Inerter-Based Suspension System with MPC Control Strategy. Mech. Syst. Signal Process. 2021, 154, 107569. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, R.; Yang, L.; Sun, Z.; Meng, X. Modelling and Control of a Semi-Active Dual-Chamber Hydro-Pneumatic Inerter-Based Suspension System. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2355–2370. [Google Scholar] [CrossRef]
- Wang, G.; Deng, J.; Duan, D.; Zhou, T.; Liu, S. Constrained H∞ Optimal Control for Nonlinear Active Suspensions Via Data-Driven Reinforcement Learning Algorithm. J. Comput. Nonlinear Dyn. 2025, 20, 071007. [Google Scholar] [CrossRef]
- Jibril, M.; Tadese, M.; Hassen, N. Nonlinear Active Suspension System Based on Fuzzy Model Predictive Controller. J. Eng. Appl. Sci. 2021, 16, 289–295. [Google Scholar] [CrossRef]
- Shi, J.-W.; Li, X.-W.; Zhang, J.-W. Feedback Linearization and Sliding Mode Control for Active Hydropneumatic Suspension of a Special-Purpose Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2009, 224, 41–53. [Google Scholar] [CrossRef]
- Hao, R.; Wang, H.; Liu, S.; Yang, M.; Tian, Z. Multi-Objective Command Filtered Adaptive Control for Nonlinear Hydraulic Active Suspension Systems. Nonlinear Dyn. 2021, 105, 1559–1579. [Google Scholar] [CrossRef]
- Hu, Y.M.; Li, Y.N.; Zheng, L. Hybrid control of electromagnetic active suspension based on nonlinear actuators. China Mech. Eng. 2022, 33, 134–142. [Google Scholar]
- Pan, H.; Sun, W.; Zhang, J.; Yan, S.; Lin, W. Adaptive Event-Triggered Control for Vehicle Active Suspension Systems With State Constraints. IFAC-Pap. 2018, 51, 955–960. [Google Scholar] [CrossRef]
- Yan, S.; Sun, W.; Xia, Y. A Joint Fault-Tolerant and Fault Diagnosis Strategy for Multiple Actuator Faults of Full-Vehicle Active Suspension Systems. IEEE Trans. Automat. Sci. Eng. 2025, 22, 1928–1940. [Google Scholar] [CrossRef]
- Feng, Z.; Li, R.-B.; Jing, X. Neuroadaptive Control for Active Suspension Systems With Time-Varying Motion Constraints: A Feasibility-Condition-Free Method. IEEE Trans. Cybern. 2024, 54, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Yan, G.; Zou, H.-X.; Wang, S.; Zhao, L.-C.; Wu, Z.-Y.; Zhang, W.-M. Bio-Inspired Vibration Isolation: Methodology and Design. Appl. Mech. Rev. 2021, 73, 020801. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, M.; Huang, J.; Mohammed, S. Load-Transfer Suspended Backpack With Bioinspired Vibration Isolation for Shoulder Pressure Reduction Across Diverse Terrains. IEEE Trans. Robot. 2025, 41, 3059–3077. [Google Scholar] [CrossRef]
- Pan, H.; Jing, X.; Sun, W.; Gao, H. A Bioinspired Dynamics-Based Adaptive Tracking Control for Nonlinear Suspension Systems. IEEE Trans. Contr. Syst. Technol. 2018, 26, 903–914. [Google Scholar] [CrossRef]
- Bosso, N.; Zampieri, N.; Somà, A.; Mocera, F.; Conte, E. Simulation of a Hydropneumatic Suspension for Agricultural Working Vehicles. In Advances in Mechatronics and Mechanical Engineering; IGI Global: Hershey, PA, USA, 2021; pp. 268–287. [Google Scholar] [CrossRef]
- Yin, Y.; Rakheja, S.; Yang, J.; Boileau, P.-E. Characterization of a Hydro-Pneumatic Suspension Strut with Gas-Oil Emulsion. Mech. Syst. Signal Process. 2018, 106, 319–333. [Google Scholar] [CrossRef]
- Dong, M.M.; Bian, N. Military Vehicle Suspension Design; Beijing Institute of Technology Press: Beijing, China, 2016; pp. 76–99. [Google Scholar]
- Zhang, Y.; Li, M.; Zhang, Y.; Hu, Z.; Sun, Q.; Lu, B. An Enhanced Adaptive Unscented Kalman Filter for Vehicle State Estimation. IEEE Trans. Instrum. Meas. 2022, 71, 6502412. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Lyapunov Exponent Sign Reversal: Stability and Instability by the First Approximation. In Nonlinear Systems and Complexity; Springer International Publishing: Cham, Switzerland, 2013; pp. 41–77. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Fayaz, M.; Qureshi, M.S.; Boujoudar, Y. Hybrid Sliding Mode Control of Full-Car Semi-Active Suspension Systems. Symmetry 2021, 13, 2442. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).