Abstract
In injured arteries, platelets adhere to the subendothelium and initiate the coagulation process. They recruit other platelets and form a plug that stops blood leakage. The formation of the platelet plug depends on platelet activation, a process that is regulated by intracellular calcium signaling. Using an improved version of a previous multiscale model, we study the effects of changes in calcium signaling on thrombus growth. This model utilizes the immersed boundary method to capture the interplay between platelets and the flow. Each platelet can attach to other platelets, become activated, express proteins on its surface, detach, and/or become non-adhesive. Platelet activation is captured through a specific calcium signaling model that is solved at the intracellular level, which considers calcium activation by agonists and contacts. Simulations reveal a contact-dependent activation threshold necessary for the formation of the thrombus core. Next, we evaluate the effect of knocking out the P2Y and PAR receptor families. Further, we show that blocking P2Y receptors reduces platelet numbers in the shell while slightly increasing the core size. An analysis of the contribution of P2Y and PAR activation to intraplatelet calcium signaling reveals that each of the ADP and thrombin agonists promotes the activation of platelets in different regions of the thrombus. Finally, the model predicts that the heterogeneity in platelet size reduces the overall number of platelets recruited by the thrombus. The presented framework can be readily used to study the effect of antiplatelet therapy under different physiological and pathological blood flow, platelet count, and activation conditions.
1. Introduction
Platelets play vital roles in arterial thrombosis. They aggregate and form blood plugs to prevent blood loss. Calcium signaling triggers platelet activation when stimulated by contact with other platelets, von Willebrand factor (vWF), collagen, thrombin, or Adenine nucleotide translocator (ADP). Activated platelets become more adhesive, producing agonists that recruit more platelets. Platelet adhesion and activation are crucial initial steps in arterial and microvascular hemostasis, particularly under conditions of high shear stress. This process can be triggered by the binding of platelets to collagen, by damaged or inflamed endothelial cells, or through the action of soluble biochemical agonists [1,2,3]. The roles of red blood cells (RBCs) in thrombosis and hemostasis are becoming increasingly established. Recent studies highlight their contribution not only through mechanical and rheological effects but also via biochemical responses, aggregation, and participation in cellular signaling [4,5,6]. Excessive activation may cause the formation of larger clots that obstruct blood flow, while reduced activation results in unstable clots that do not stop bleeding.
At the intracellular level of platelets, calcium (Ca2+) is activated through various signaling pathways when agonists bind to their receptors in a dose-dependent manner [7]. Elevated Ca2+ concentrations trigger shape changes, degranulation, and IIb3 integrin activation [8,9], the expression of which increases the adhesiveness of platelets and promotes their aggregation. One of the key mechanisms that contribute to the first steps of platelet recruitment and activation is the GPIb receptors. Upon initial contact, the mechanical stimulation of GPIb receptors in the presence of vWF can lead to the intermediate activation of GPIIb/IIIa integrin receptors [10]. This allows platelets to form weak adhesive bonds, which initiates the aggregation process. If platelets remain in contact for a longer period of time, they become activated and form stronger bonds as they express IIb3 integrins upon activation. As a result, they constitute a stronger aggregate that resists removal by blood flow and stops blood leakage. ADP and thrombin are key agonists that play significant roles in platelet activation by inducing intracellular calcium (Ca2+) mobilization and the subsequent activation of platelets. ADP works through G protein-coupled receptors, P2Y1 and P2Y12, on platelets to trigger intracellular calcium [11], while thrombin activates platelets via protease-activated receptors (PARs) [12]. The combined effects of ADP and thrombin are complex, even though both proteins are expressed by activated platelets. Indeed, ADP has a much larger diffusion rate than thrombin [13], while thrombin generation is amplified within the clot due to the biochemical reactions of the coagulation cascade [14].
The process of platelet aggregation is reinforced by the production of agonists, such as ADP, by activated platelets. Active platelets express negatively charged phospholipids (PSs), thrombin, and other procoagulant factors on their surface, which contribute to the generation of the fibrin polymer. The production of the fibrin mesh is critical for the stabilization of the thrombus as it traps platelets and holds them tightly together. In the later stages of this process, parts of the aggregate are detached from the clot as they get pulled out by blood flow. The fibrin mesh forms a cap that covers platelets and prevents them from making new connections [15]. It also solidifies interplatelet connections, which makes the clot more resistant. Ultimately, the process of platelet aggregation stops when all platelets forming the clot become non-adhesive and no longer secrete agonists.
Various modeling techniques describe blood coagulation in flow, and they fall into three categories: continuous, discrete, and hybrid multiscale models [16,17]. Continuous models use partial differential equations (PDEs) for blood factor concentrations and simulate blood flow with Navier–Stokes equations [18,19,20]. An important technical challenge encountered in this approach is addressing the interaction between the flow and the clot. This can be achieved by considering blood as a viscoelastic non-Newtonian fluid [21], whose viscosity depends on the concentration of fibrin. Another technique entails considering the thrombus as a porous medium whose hydraulic resistance is given according to the concentration of fibrin polymer [22]. This method can also be used for the simulation of arterial thrombus formation by using PDEs to describe the concentration of platelet subtypes and assuming that the clot resistance depends on the concentration of aggregated platelets [13,23,24]. Another class of continuous models uses mixture theory to capture the interactions between platelets, plasma, red blood cells (RBCs), and the clot [25,26,27]. Discrete models track individual cell actions using methods like dissipative particle dynamics (DPD) or Smoothed-Particle Hydrodynamics (SPH) [28,29], while multiscale modeling combines continuous and discrete descriptions of the underlying mechanisms [30,31,32,33,34,35]. The DPD method was particularly successful in capturing platelet adhesion dynamics [36] and the interplay between red blood cells and macrophages during sickle cell disease [37]. In multiscale models, blood flow can be introduced using DPD or Navier–Stokes equations, while platelets can be represented as discrete objects. The kinetics of the coagulation cascade are usually captured using PDEs. This approach enables the integration of various clot growth mechanisms at both the cellular and plasma scales. The immersed boundary method has also been used to describe platelet aggregation under flow [38,39]. Initially, this method was developed to describe the interaction between blood flow and heart valves [40]. Recently, it was successfully applied to study sub-clinical leaflet thrombosis [24]. The advantage of this method is that it can describe the interplay between moving boundaries (shells or solids) and the flow without having to recompute the domain mesh after each step. Alternatively, dynamic adaptive mesh can be used to introduce the effects of wall deformations due to flow pulsations [41]. Overall, there is a lack of multiscale models that integrate calcium signaling dynamics at the platelet level while capturing other effects contributing to thrombus growth, such as hemodynamics and their interplay with the platelet aggregate and the thrombus, as well as thrombin generation and fibrin polymerization. Our previously developed model integrates all of these features into a single framework [39], which makes it suitable for the investigation of the effect of both intraplatelet and extraplatelet mechanisms contributing to thrombus formation. In this work, we improve this framework by validating the intraplatelet dynamics and applying them to study the effects of perturbations in the calcium signaling pathway on the development of the thrombus.
Mathematical modeling was also applied to gain insights into the kinetics of calcium signaling in platelets under various stimulation conditions. Ordinary differential equation (ODE) systems were used to reproduce experiments for Ca2+ activation following the stimulation of the PAR receptors [42]. Another ODE-based model studied the interaction between the different pathways leading to Ca2+ activation, including the nitric oxide (NO)/cGMP/cAMP cascade [43], while a recent work used neural networks trained using experimental data to predict the activation of platelets in response to combinatorial agonists [44,45]. These trained neural networks were subsequently introduced in a multiscale model of platelet aggregation under flow in 3D to describe the response of platelets to various agonist stimuli [46].
In this paper, we will use an improved version of a previously developed multiscale model of platelet–fibrin thrombus growth to study the effects of alterations in intracellular calcium signaling on the dynamics of platelet aggregation and thrombus formation [39]. The model uses the immersed boundary method to capture the interplay between blood flow and platelets, described as elastic spheres. It describes the regulatory dynamics of the coagulation cascade and thrombin generation similarly to our previous studies on venous clot formation [18,47]. The kinetics of platelet aggregation were taken from previous works by Tosenberger et al. [33]. The framework also considers the intracellular kinetics of calcium signaling through a specific model that describes Ca2+ activation due to contacts with other platelets, as well as through the stimulation of the PAR and P2Y receptors. The model successfully reproduces the kinetics of thrombus formation reported in in vivo experiments of platelet aggregation under flow [48]. Using computer simulations, we elucidate the roles of contact stimulation, ADP, and thrombin on the formation of the platelet plug and investigate the effect of platelet size heterogeneity. The computational framework presented in this paper can be readily used to improve our understanding of antiplatelet action and gain insights into the mechanisms regulating thrombus growth at both the intraplatelet and plasma scales.
2. Multiscale Modeling of Platelet–Fibrin Thrombus Formation
We improve our previously developed platelet–fibrin model to explore the effects of intraplatelet calcium signaling on thrombus formation [39]. This model utilizes Navier–Stokes equations to represent blood flow and includes partial differential equations to describe coagulation cascade kinetics, encompassing the main biochemical processes leading to thrombin generation and fibrin mesh formation [18,47]. Platelets are treated as discrete spheres, exhibiting mobility, aggregation, activation, and agonist secretion. Interactions between platelets and blood flow are captured through the immersed boundary method, while platelet aggregation kinetics are taken from a previously developed model [33]. Platelet activation is governed by intracellular calcium (Ca2+) phosphorylation, triggered by interactions with other platelets as well as exposure to agonists such as ADP or thrombin. We fine-tune rate constants for these pathways to approximate experimentally observed kinetics. Figure 1A provides a schematic of the captured mechanisms, while Figure 1B presents a snapshot of a typical numerical simulation conducted using the model.
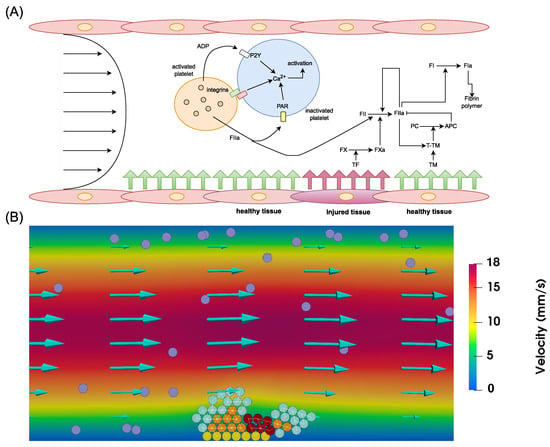
Figure 1.
(A) Schematic representation of the mechanisms regulating thrombus formation captured by the model. The model describes the interactions between platelets in the flow through integrins and their receptors, as well as exposure to ADP and thrombin. The biochemical reactions of the coagulation cascade in the flow are initiated through exposure to injured tissues. They culminate in the generation of thrombin, which forms the fibrin mesh that traps a part of the clot. Thrombin self-amplification is arrested by activated protein C, blood flow, and antithrombin. (B) A snapshot of a numerical simulation showing the formation of a platelet plug under flow. Yellow spheres depict platelets attached to the subendothelium, purple ones correspond to mobile platelets in the flow, cyan spheres represent platelets connected by weak bonds, orange spheres illustrate active platelets, and dark-red spheres indicate platelets covered by fibrin. Interplatelet bonds are represented by white lines.
2.1. The Coagulation Cascade
We use a previously developed model to describe the kinetics of thrombin generation [47]. The advantage of this model is that its parameters can be fitted to reproduce any patient-specific thrombin generation curve. It consists of three equations for the concentrations of prothrombin, thrombin, and factor Xa, obtained by using quasi-stationary approximations of a more complete model [49]. After incorporating the effects of diffusion and advection by the flow, we describe the spatial distributions of factor Xa (U), thrombin (T), and prothrombin (P) as follows:
Here, the second terms on the left-hand side of the three equations describe the diffusion of these three proteins and their transport by blood plasma, and represents the activation of prothrombin by activated platelets as they express negatively charged phospholipids on their surfaces. It takes a constant value on the computational mesh points occupied by activated platelets and is zero elsewhere. The values of the parameters , as well as the initial concentrations of prothrombin () and factor X (), are taken from previous studies [47]. C represents the concentration of activated protein C, which stops the lateral expansion of thrombin self-amplification. We prescribe a zero-flux condition at all boundaries for the three chemical species except for prothrombin, which is subject to the boundary condition at the inlet. We consider zero-flux boundary conditions for thrombin and factor Xa everywhere except for the injury site, where we consider the following condition describing the activation of factor X by the complex TF-FVIIa during the initiation stage [19]:
Here, represents the concentration of factor X in the bloodstream, taken from a previous study [47], and is a positive constant equal to 100 nM−1. Next, we add the equations for fibrin production:
where, and F describe the concentrations of fibrinogen and fibrin, respectively. We prescribe the inlet and initial condition of for fibrinogen. The zero-flux condition is prescribed at the rest of the boundaries. The same condition is applied everywhere for fibrin. We also simulate the concentration of ADP in the flow. ADP is produced by activated platelets and has the ability to activate other platelets through the activation of the P2Y receptors. We describe its concentration as follows:
where is the rate of ADP production by activated platelets. It takes a constant value in nodes occupied by activated platelets and zero elsewhere. To these equations, we added one equation for activated protein C (APC). It is one of the mechanisms that stop the lateral expansion of the thrombin self-amplifying generation loop:
Note that APC is activated by the thrombin–thrombomodulin complex. It results from the interaction of thrombin with thrombomodulin, which is expressed in healthy tissues. We describe the production of this component on intact tissues using the following boundary condition:
Then, we prescribe the following boundary condition for APC in healthy tissues:
The inlet and initial concentrations of the zymogens prothrombin and fibrinogen are set to their physiological values, and the zero-flux boundary condition is used at the remaining boundaries. As for the other coagulation factors, we apply the zero-flux boundary condition at all boundaries.
2.2. Blood Flow and Clot Permeability
Since the study is restricted to high-shear hemodynamics, we describe blood flow as an incompressible Newtonian fluid as follows:
where is the flow velocity, p is the pressure, is the density of the blood, is the dynamic viscosity, considered to be a constant since we are dealing with a Newtonian fluid, and f is obtained from the elastic interplatelet connections described in the next section. The influence of the clot is captured through the third term on the right-hand side of the equation, where is the hydraulic permeability of the clot [50]:
Here, is the normalized concentration of fibrin in the clot, considered to be bounded by a value corresponding to the normal permeability of the clot, and is the radius of the fibers.
The term describes the impermeability of platelets within the clot to flow. Here, assumes a suitably large value to impede flow through platelets residing in the clot. Meanwhile, the function takes the value 1 in nodes hosting attached platelets and 0 elsewhere, with the exception of weakly connected platelets, where is assigned a value of 0 because these platelets are not sufficiently attached to resist removal by the flow.
We use the immersed boundary method to introduce the effects of platelet movement on local hemodynamics [40]. In this method, the forces exerted on the flow, considered in Equation (10), are computed by spreading the forces exerted on all platelets to the computational mesh:
where and are the sum of aggregation and repulsive forces applied on the n-th platelet, and is a radial-basis function [39].
We assume that blood plasma is driven by the pressure difference, and we prescribe the pressure at the inlet and the pressure at the outlet . We consider no-slip boundary conditions at the other boundaries . To set the inlet pressure dependent on shear rate , we use the formula , where L is the length of the vessel, and D is the diameter of the vessel. The outflow pressure is set to zero .
2.3. Platelet Transport and Aggregation
We describe each platelet as a soft sphere characterized by its center and radius. We track its motion by applying Newton’s second law of dynamics to their centers. We consider that each platelet can be subject to three types of forces: drag force by the flow, repulsive forces due to contact with other platelets, and aggregation forces due to the integrins expressed by other platelets [39]:
Here, m is the platelet mass, assumed to be the same for all platelets, and represents its acceleration, while , , and denote the drag, repulsive, and aggregation forces exerted on the platelet. The drag force is exerted by the flow and causes the transport of the platelet. It is given by
where is the drag coefficient, taken to be equal to 0.5 for a sphere, is the surface area exposed to the flow, and is the relative velocity of the particle to the fluid. Next, we introduce the repulsive force between platelets. It prevents the aggregated platelets from overlapping. It is given as the sum of repulsive forces exerted by neighboring platelets:
where
Here, K is a positive constant, is the interplatelet distance, is the radius of the th platelet, and is the normalized vector . Finally, we describe the aggregation force using Hooke’s law. The aggregation force applied on platelets is given as follows:
where
Here, represents the force strength coefficient, which depends on the strength of the connection between the two platelets, and is the distance of force relaxation, calculated as 1.2 times the sum of two platelet radii. When the distance between two platelet centers falls below (connection criterion), they connect and remain so until the distance exceeds (disconnection criterion), set as 1.3 times the sum of the radii of the two platelets. The strength of the existing connection between two platelets () becomes stronger if one of them becomes activated or if both get covered by fibrin:
Here, , , and denote the three strength coefficients for interplatelet connections, chosen such that . These represent the magnitudes of weak bonds due to GP1b receptors, medium bonds due to platelet activation, and strong bonds reinforced by fibrin. represents the fibrin concentration value at coordinates , and represents the threshold value of fibrin concentration that covers the clot. New aggregation forces are only applied on platelets that are not covered by fibrin. Fibrin-covered platelets remain subject to the previously applied aggregation force, in addition to repulsive and drag forces. For a platelet to become trapped by the fibrin mesh, the concentration of fibrin at its center has to exceed a certain threshold ().
2.4. Intraplatelet Calcium Signaling
We describe the activation of platelets through calcium signaling due to stimulation by contact with other platelets as well as the activation of the P2Y and PAR receptors. The concentration of calcium inside of each inactivated platelet is captured as follows:
where represents a time-dependent function, which takes the value of the number of connections with the neighboring platelets, and and describe the concentrations of ADP and thrombin at the center of the i-th platelet, respectively. Platelets become active when the intracellular concentration reaches a certain threshold ([Ca2+] ≥ [Ca2+]*). The baseline values of the parameters were derived from experimental studies, as indicated in Table 1.

Table 1.
The baseline values of the parameters of the calcium signaling model used in the simulations.
2.5. Numerical Implementation
The finite difference method was used to implement the continuous part of the model. The computational domain was discretized into a grid with points. A mesh consistency analysis is provided in Appendix A. We opted for a rather coarse mesh, given the computationally expensive nature of the model. The projection method was used to implement the Navier–Stokes equations [54], while the successive over-relaxation (SOR) method was used for pressure correction. To overcome the convection-dominated nature of the simulation of advection–diffusion–reaction equations, upwinding schemes were adopted for the convection terms. The code was written in an object-oriented structure using the C++ programming language. The Brinkman term was treated implicitly. Further details of the implementation of the model, as well as the values of the parameters describing platelet aggregation and blood flow, were provided in our previous study [39]. Note that the current model was implemented solely in 2D, given its high computational cost. Its extension to 3D requires more validation and code parallelization. The code is available upon request to the corresponding author.
3. Results
3.1. Simulation of Thrombus Growth under Normal Physiological Conditions
We begin by studying the dynamics of thrombus formation in a 2D rectangular domain corresponding to an arteriole of 200 m length and 50 m diameter. In all the considered simulations, the steady-state number of platelets in the domain was set to 98, which corresponds approximately to the physiological platelet count of 250 × 109 L−1. The enforced pressure difference was adjusted to obtain an arterial wall shear rate value of 1440 s−1, and the length of the injured vessel area was set to 10 m in all simulations. Initially, we supposed that six collagen-bound platelets initiate the formation of the plug. We conducted simulations for 60 s of physical time. To eliminate the stochasticity resulting from the random distribution of platelets at the beginning, we considered the results of 15 simulations and calculated the median and confidence intervals. We calibrated the interplatelet adhesive force parameters to reproduce the dynamics of in vitro thrombus growth observed in experimental studies [48], as shown in Appendix B.
The process of thrombus formation begins with platelets getting recruited and forming weak bonds with their collagen-bound counterparts. Due to the relatively low velocity of blood flow in the vicinity of the vessel wall, some platelets remain connected for a long time until they get activated. These active platelets contribute to the generation of thrombin by two means. First, they express procoagulant factors on their surfaces, increasing the conversion of prothrombin into thrombin. Second, they form a permeable medium that allows for the biochemical reactions of the coagulation cascade to take place. The production of fibrin leads to the development of the thrombus core, which consists of strongly connected platelets. A screenshot of a numerical simulation showing the core–shell structure of the thrombus is shown in Figure 2A. In our simulations, it took approximately five seconds of physical time to observe the appearance of the first platelets covered by fibrin and belonging to the thrombus core.
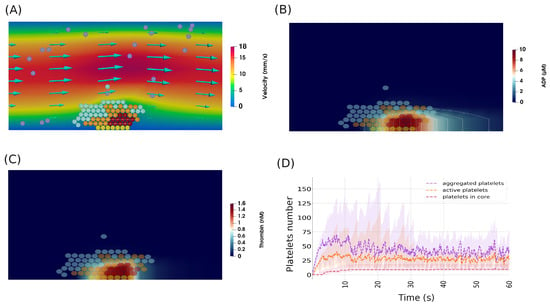
Figure 2.
(A) Numerical simulations showing the formation of a platelet plug in the normal physiological scenario, showing the typical structure of a thrombus, which consists of a shell and a core. Yellow spheres represent platelets attached to the subendothelium, purple ones correspond to mobile platelets in the flow, cyan spheres describe platelets connected by weak bonds, orange spheres represent active platelets, and dark-red spheres indicate platelets covered by fibrin. (B) The concentration of ADP during the same period of thrombus growth. (C) The concentration of thrombin inside the clot. (D) The evolution of the number of aggregated, activated, and fibrin-covered platelets during the simulations. Ribbons indicate 95% confidence intervals.
The recruitment of platelets does not stop after the emergence of the core. Indeed, activated platelets continue to recruit other platelets to the aggregate by producing agonists such as ADP and thrombin. Due to its higher diffusion coefficient, ADP can reach the platelets in the vicinity of the thrombus, which increases their activation and recruitment (Figure 2B). The generation of the fibrin polymer is concentrated at the center of the clot due to the high concentration of thrombin in this area (Figure 2C). The expansion of the thrombus leads to the detachment of parts of the platelet plug due to the drag force exerted by the flow. The aggregation of platelets is attenuated following the exposure of the platelet core to the flow. That is because of the non-adhesive nature of the fibrin-covered platelets. The activation of platelets continues in some simulations, but the size of the clot remains stable, as these platelets do not attach to the clot (Figure 2D).
3.2. Threshold Response of Platelet Core Formation to the Interplatelet Contact-Dependent Activation Rate
We study the effect of the calcium activation rate during contact with other platelets () on the dynamics of platelet recruitment and thrombus formation. We consider three values of the rate of calcium activation, corresponding to faster activation ( = 5 nM·s−1), slower activation ( = 1 nM·s−1), and very reduced activation ( = 0.5 nM·s−1). Figure 3 shows snapshots of numerical simulations as well as the changes in the populations of platelet subtypes over time. In the case of faster contact-dependent activation, the formation of the platelet plug takes place quickly and reaches its maximum extent within the first five seconds of the simulations. At this moment, the first platelets covered by the fibrin polymer are observed. The process of thrombus growth continues with the expansion of the platelet core for approximately ten seconds. After this phase, the platelet plug stops expanding, and the shell of the clot is detached, which leads to the arrest of thrombus formation.
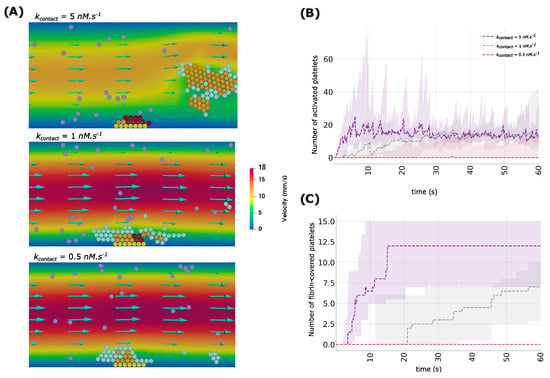
Figure 3.
(A) Snapshots of numerical simulations showing the formation of a platelet plug for three values of the rate of calcium activation by interplatelet contact (). Yellow spheres illustrate platelets attached to the subendothelium, purple ones represent mobile platelets in the flow, cyan spheres describe platelets connected by weak bonds, orange spheres correspond to active platelets, and dark-red spheres indicate platelets covered by fibrin. (B) The evolution of the population of active platelets over time for three values of the contact-dependent calcium activation rate. (C) The number of fibrin-covered platelets over time for three values of the rate of calcium activation through contacts. Ribbons correspond to 95% confidence intervals.
In the case of slower contact-dependent activation ( = 1 nM·s−1), the development of the thrombus follows the same mechanism as the one observed for faster activation. However, the growth rate is significantly reduced. In this case, the process of platelet aggregation does not reach its maximum extent until twenty seconds. The core of the thrombus appears at this moment and starts expanding at a slower rate. It does not reach its maximum extent by the end of the simulation. When considering much slower contact-dependent activation ( = 0.5 nM·s−1), the thrombus core does not emerge at all. In this case, the thrombus remains unstable, as most platelets aggregate and get removed by the flow before they get activated and form stronger bonds.
3.3. P2Y Blockade Reduces Platelet Recruitment in the Thrombus Shell but Does Not Decrease the Number of Cells in the Thrombus Core
We continue our investigation by looking at the effect of blocking the P2Y and PAR receptors, which are responsible for calcium activation by ADP and thrombin, respectively. We studied these questions by running simulations where we set = 0 nM·s−1 or = 0 s−1 and compared the results to the baseline. In the case where P2Y receptors are blocked, the recruitment of platelets at the shell of the clot is reduced because, in this case, all platelets are desensitized to ADP, which is the only agonist that reaches them due to its higher diffusion coefficient. As a result, the clot size is significantly reduced.
By the end of the simulation, the number of active platelets in the clot decreases by 34.61% when the P2Y receptors are knocked out. Interestingly, the number of fibrin-covered platelets slightly increases, possibly due to the stochastic nature of simulations. This suggests that ADP does not restrict the formation of the thrombus core. Indeed, the concentration of other agonists, such as thrombin, tends to be higher in the core region, which makes the role of ADP in this region marginal. Knocking out the PAR receptors in addition to the P2Y ones reduces the number of active platelets by 29.41% while decreasing the number in the core by 50%. Figure 4A shows a snapshot of a numerical simulation in the case where P2Y or/and PAR receptors are blocked, while Figure 4B shows the number of platelets by the end of the simulation under the considered scenarios.
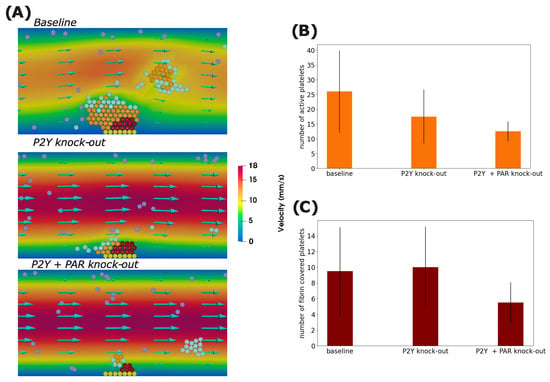
Figure 4.
(A) Screenshots of numerical simulations showing the formation of a platelet plug for three situations where P2Y receptors, PAR receptors, or both are blocked. Yellow spheres represent platelets attached to the subendothelium, purple ones correspond to mobile platelets in the flow, cyan spheres describe platelets connected by weak bonds, orange spheres represent active platelets, and dark-red spheres indicate platelets covered by fibrin. The number of activated platelets (B) and fibrin-covered platelets (C) by the end of the simulation time in each scenario. Error bars correspond to 95% confidence intervals.
To gain further insights into these results, we estimated the contributions of both ADP and thrombin to calcium signaling in each platelet. To achieve this, we calculated the activation of calcium Ca2+ by ADP and thrombin independently as follows:
Figure 5 illustrates the contributions of both thrombin and ADP to calcium signaling during a numerical simulation. Figure 5A shows that thrombin increases the signaling of calcium in platelets in the core region, while Figure 5 suggests that ADP stimulates calcium signaling in cells in the vicinity of the thrombus. The platelets that face the inflow are activated by neither thrombin nor ADP due to the convection of these two molecular species by the flow. Hence, they are activated by mechanical contact. Indeed, in this region, these platelets enjoy higher stability and remain connected for a longer duration because they are trapped between the thrombus and the flow.
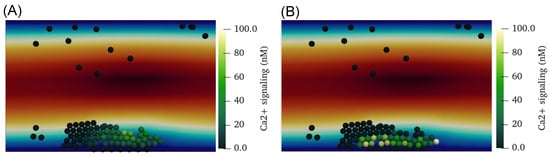
Figure 5.
(A) The concentration of calcium activated through the P2Y receptor () due to ADP stimulation in each platelet. (B) The concentration of calcium activated through the thrombin PAR receptor () in each platelet.
3.4. Platelet Size Heterogeneity Reduces the Size of the Clot
The effect of platelet heterogeneity is another question that we have studied with our framework. Changes in the size of platelets are observed in several conditions, including thrombocytopenia [55] and SARS-CoV-2 infection [56]. Considering that the size of platelets can be variable depending on health conditions [57], it is not clear what effect this would have on the dynamics of thrombus growth. To address this question, we ran four sets of simulations, where the following scenarios were considered: homogeneous platelets with a normal radius of 1 m or an increased radius of 1.5 m, and heterogeneous platelets with a radius sampled from a normal distribution with a mean equal to 1 m and a standard deviation of 0.1 m, or with larger radii sampled from a normal distribution with a 1.5 m mean and a 0.15 m standard deviation. Note that in all the considered simulations, we considered platelets to have the same mass and express the same number of receptors on their surfaces.
In the case where the size of platelets is homogeneous, platelet centers form hexagonal structures similar to a beehive. This enables the formation of strong platelet plugs due to the high number of connections between platelets. Indeed, each platelet inside the plug can have up to six connections with other platelets. Further, the high number of connections accelerates platelet activation. When we consider platelets with a randomly sampled size, the irregularities in platelet size prevent the formation of the beehive structure. As a result, there are fewer bonds between platelets at the center of the plug. As a result, the formed plug is less solid and more easily detached by the flow (Figure 6A). The same observation is also made when considering larger platelets. However, in this case, the formed thrombi consist of fewer platelets because a reduced number of platelets are required to form plugs that get detached. Overall, considering the irregularities in platelet size decreased the number of active platelets in the clot by roughly 12.5% and 16.6% when the considered platelet radius was r = 1 m and r = 1.5 m, respectively (Figure 6B).
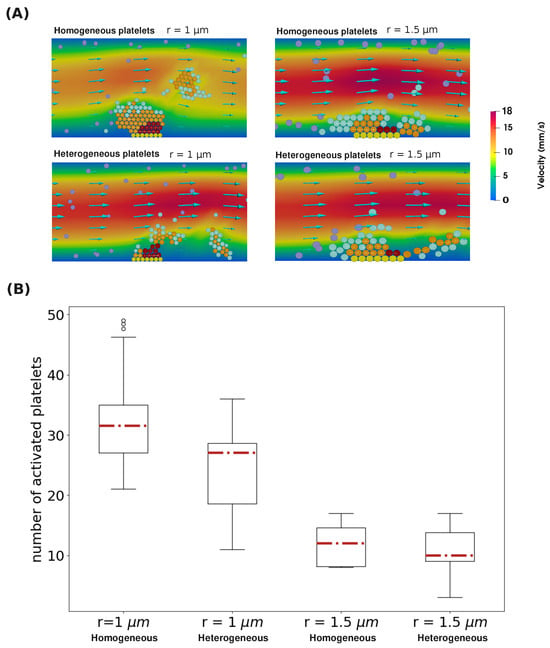
Figure 6.
(A) The structure of the platelet plug when different platelet sizes and distributions of platelet radii are considered. Yellow spheres depict platelets attached to the subendothelium, purple ones correspond to mobile platelets in the flow, cyan spheres represent platelets connected by weak bonds, orange spheres illustrate active platelets, and dark-red spheres indicate platelets covered by fibrin. (B) The distribution of the number of active platelets in the clot by the end of 15 simulations under four different scenarios of platelet size distribution.
4. Discussion
This paper studies the effects of intraplatelet calcium signaling on the dynamics of thrombus formation under flow. To make our previously developed model of platelet–fibrin clot formation more suitable for this study [39], we calibrated the submodel of intracellular calcium signaling using available estimates for the kinetic constants. We also enhanced the thrombin generation part of our model by considering more recently developed models that are validated against thrombin generation assays [47]. Our multiscale framework encompasses the main mechanisms contributing to platelet aggregation and thrombus formation, such as the coagulation cascade, blood flow and clot mechanobiology, thrombin aggregation and activation, and intraplatelet calcium signaling. It qualitatively reproduces the in vivo dynamics of thrombus formation in arteries [48]. Further, the submodels constituting the framework were validated against other experiments for thrombin generation [47], venous thrombosis [18,58], and calcium signaling [51,52,53]. Given the stochastic sources in the model related to the random initial position of platelets in the computational domain, we conducted 15 simulations for each studied scenario and considered the average values of these simulations. We took advantage of the multiscale architecture of the model to investigate the impact of intraplatelet calcium signaling on the dynamics and outcome of thrombus formation under flow.
We started our study by investigating the effects of contact-dependent activation on the initiation and progression of platelet–fibrin thrombus formation. We considered different values for the rate of contact-dependent activation following stimulation by other platelets. The considered values correspond to cases of excessive and restricted activation. Our results have shown that the formation of the platelet core requires a certain threshold for the rate of calcium activation by contact with other platelets. In this context, it was shown that the thrombus core acts as a selective molecular prison that retains soluble procoagulant agonists and increases their effective concentration [59]. Thus, the initial formation of the platelet aggregate provides an appropriate environment that enables the generation of fibrin, which holds the platelet plug together and stabilizes the thrombus, allowing further recruitment of platelets. It was experimentally demonstrated that the formation of the thrombus core depends on thrombin generation. Indeed, the absence of a platelet core was obtained experimentally when the anticoagulant hirudin was administered [60].
Next, we studied the role of ADP and thrombin on platelet recruitment and aggregation by conducting simulations where we knocked out their respective receptor families, P2Y and PAR. In the case where the P2Y receptors were knocked out, we observed a significant reduction in the number of platelets in the thrombus shell, but the number of platelets in the core remained approximately the same. In this case, the thrombus consisted mainly of platelets adhering to the thrombus core. The same result was observed in in vivo experiments when the P2Y antagonist cangrelor was administered to the bloodstream [61]. This confirms the consistency of the model with experimental findings. Indeed, in the experiments by Stalker et al., the administration of P2Y antagonists significantly reduced the area occupied by the shell and slightly increased the core area, which agrees with the results obtained by our model. Other experiments also indicated that blocking contact-dependent signaling and thrombin reduced the size of the core and made the thrombus less stable, which also agrees with our model’s predictions [62,63].
The differences between the roles of thrombin and ADP in the recruitment of platelets can be analyzed by studying their respective spatial distributions within the thrombus. First, ADP diffuses more broadly than thrombin, which allows it to reach platelets in the shell. Second, the amplification of thrombin generation requires a threshold concentration that can only be reached near the injured wall. This is because of (i) the expression of tissue factor in the injured area, (ii) the higher density of active platelets, which increases thrombin production and reduces flow velocity, and (iii) the lower flow velocity in the vicinity of the artery. Hence, the higher thrombin concentration generated due to the triggering of the amplification phase can only be reached near the wall area, which explains the production of fibrin polymer exclusively in the core.
Another key question that we have studied with our model is the effects of irregularities in platelet size on the formation of the thrombus. To elucidate these effects, we ran simulations where the platelet size was either homogeneous or sampled from a random distribution. It is important to note that, in these simulations, we only changed the radius of platelets and did not consider changes in ligand expression, agonist secretion, or platelet mass, which can correlate with the platelet size. Experimentally, studies have shown that larger platelets tend to be more adhesive and procoagulant [64]. In the absence of this effect, our simulations suggest that homogeneous platelets tend to build more compact and dense thrombi than heterogeneous platelets. This is because homogeneous platelets can form beehive structures, which maximizes the number of connections that each platelet can make. This results in a faster activation of platelets and a more resistant thrombus. The simulation results suggest that the effect of platelet size heterogeneity on thrombus compactness is an important question that needs to be further investigated. The effect of the compactness of the platelet plug was investigated experimentally and was shown to play an important role in intra-thrombus transport [65].
This study has a few limitations that need to be discussed. First, the obtained results were from simulations conducted under specific conditions in terms of shear rate and platelet count. To generalize these findings, it is important to test whether they hold under a wide range of physiological conditions. This requires running several simulations, which would demand access to high-performance computing. Second, although the model includes the main components contributing to platelet aggregation and thrombus formation, it does not incorporate the effect of some components, such as thromboxane A2 (TxA2), which is another agonist secreted by platelets, and von Willebrand (vWF) factor. The effect of TxA2 was shown to be similar to that of ADP, as it enhances the recruitment of platelets to the shell due to its higher diffusion [61], while vWF allows the recruitment of platelets under high-shear flow conditions [34], a question that is not studied in the present work. Third, we considered that platelets keep secreting agonists until the end of the simulation, which results in the activation of a few platelets that come close to the thrombus, while experimental studies have shown that activated platelets have a limited number of agonists [66]. The effect of agonist depletion and clot growth arrest was not studied because our simulations were limited to 60 s. Fourth, the effect of changes in the shape of the platelet, as well as their interplay with the fibrin polymer, was not incorporated. This assumption was made to reduce the computational cost, as our main focus is the effect of perturbations in the calcium signaling pathway on the thrombus formation process. Fine-grained models were developed to investigate the role of platelet shape in the coagulation process [67,68,69]. However, these models are computationally expensive, which limits their applicability for quantitative investigations of thrombus growth.
5. Conclusions
Overall, our framework provides a computational platform that can be further improved and used to study the effect of antiplatelet and anticoagulant therapy under a wide range of physiological and pathological conditions. One advantage of the model is that it incorporates the main therapeutic targets for several antiplatelet and anticoagulant treatments. It also links the mechanisms regulating platelet activation at the intracellular level to their function and interactions with their microenvironment. The consistency of the model with experimental observations makes it suitable for systems biology studies that investigate the mechanisms regulating arterial thrombosis at the intracellular and bloodstream scales. After further validation, our framework can be deployed as a decision-making tool using techniques such as machine learning [70,71].
Author Contributions
Conceptualization, A.B. and V.V.; methodology, A.B. and V.V.; software, A.B.; validation, A.B. and V.V.; formal analysis, A.B. and V.V.; investigation, A.B. and V.V.; resources, A.B. and V.V.; data curation, A.B. and V.V.; writing—original draft preparation, A.B.; writing—review and editing, V.V.; visualization, A.B.; supervision, V.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Ministry of Science and Higher Education of the Russian Federation (megagrant agreement No. 075-15-2022-1115).
Data Availability Statement
The simulation code is available upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. The Consistency of the Numerical Mesh
To evaluate the consistency of the considered mesh, we compared the results of simulations to the case where a finer mesh of grid points was used. Enhancing the resolution of the mesh requires reducing the time step to ensure the stability of the numerical scheme. As a result, the simulations become computationally expensive and require tens of hours to complete, depending on the number of platelets recruited by the clot. For this reason, we compared only the changes in the number of platelets during the first 12 s. Figure A1 indicates that the two dynamics of platelet adhesion are pretty close in the two cases.
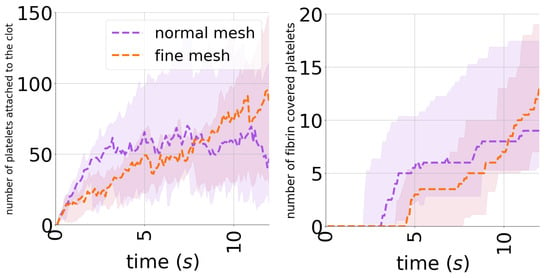
Figure A1.
Mesh consistency analysis showing the number of platelets over time when two meshes are considered: normal and fine meshes with and grid points, respectively.
Appendix B. Model Validation
The model was validated using experimental data from in vitro experiments [48]. These experiments describe the growth of the thrombus in flow conditions that mimic arterial flow. To validate our model, we adjusted the shear rate to the specific value of 1500 s−1. Then, we fine-tuned several model parameters to replicate the clot growth behavior observed in the experiments. Specifically, we modified the interplatelet strength coefficients to achieve the desired outcomes. The model still reproduces the experimental dynamics despite the calibration of intracellular Ca+2 regulation in the model. Figure A2 provides a comparison between the model results and the experimental data.
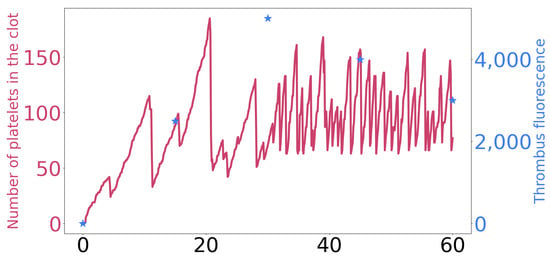
Figure A2.
A comparison between the number of platelets over time in a numerical simulation (represented as a dark pink line) and changes in thrombus fluorescence in in vitro experiments [48], shown in blue stars.
References
- Jackson, S.P.; Nesbitt, W.S.; Westein, E. Dynamics of platelet thrombus formation. J. Thromb. Haemost. 2009, 7, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Brass, L.F.; Diamond, S.L. Transport physics and biorheology in the setting of hemostasis and thrombosis. J. Thromb. Haemost. 2016, 14, 906–917. [Google Scholar] [CrossRef] [PubMed]
- Furie, B.; Furie, B.C. Thrombus formation in vivo. J. Clin. Investig. 2005, 115, 3355–3362. [Google Scholar] [CrossRef] [PubMed]
- Zilberman-Rudenko, J.; Sylman, J.L.; Lakshmanan, H.H.S.; McCarty, O.J.T.; Maddala, J. Dynamics of Blood Flow and Thrombus Formation in a Multi-Bypass Microfluidic Ladder Network. Cell. Mol. Bioeng. 2017, 10, 16–29. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.T.; Aubry, N.; Antaki, J.F.; Massoudi, M. Simulation of blood flow in a sudden expansion channel and a coronary artery. J. Comput. Appl. Math. 2020, 376, 112856. [Google Scholar] [CrossRef] [PubMed]
- Mountrakis, L.; Lorenz, E.; Malaspinas, O.; Alowayyed, S.; Chopard, B.; Hoekstra, A.G. Parallel performance of an IB-LBM suspension simulation framework. J. Comput. Sci. 2015, 9, 45–50. [Google Scholar] [CrossRef]
- Rink, T.; Sage, S. Calcium signaling in human platelets. Annu. Rev. Physiol. 1990, 52, 431–449. [Google Scholar] [CrossRef]
- Shattil, S.; Brass, L. Induction of the fibrinogen receptor on human platelets by intracellular mediators. J. Biol. Chem. 1987, 262, 992–1000. [Google Scholar] [CrossRef]
- Hathaway, D.R.; Adelstein, R.S. Human platelet myosin light chain kinase requires the calcium-binding protein calmodulin for activity. Proc. Natl. Acad. Sci. USA 1979, 76, 1653–1657. [Google Scholar] [CrossRef]
- Chen, Y.; Ju, L.A.; Zhou, F.; Liao, J.; Xue, L.; Su, Q.P.; Jin, D.; Yuan, Y.; Lu, H.; Jackson, S.P.; et al. An integrin αIIbβ3 intermediate affinity state mediates biomechanical platelet aggregation. Nat. Mater. 2019, 18, 760–769. [Google Scholar] [CrossRef]
- Mills, D.C. ADP receptors on platelets. Thromb. Haemost. 1996, 76, 0835–0856. [Google Scholar] [CrossRef]
- Brass, L.F. Thrombin and platelet activation. Chest 2003, 124, 18S–25S. [Google Scholar] [CrossRef] [PubMed]
- Leiderman, K.; Fogelson, A.L. Grow with the flow: A spatial–temporal model of platelet deposition and blood coagulation under flow. Math. Med. Biol. J. IMA 2011, 28, 47–84. [Google Scholar] [CrossRef] [PubMed]
- Davie, E.W.; Fujikawa, K.; Kisiel, W. The coagulation cascade: Initiation, maintenance, and regulation. Biochemistry 1991, 30, 10363–10370. [Google Scholar] [CrossRef] [PubMed]
- Kim, O.V.; Xu, Z.; Rosen, E.D.; Alber, M.S. Fibrin networks regulate protein transport during thrombus development. PLoS Comput. Biol. 2013, 9, e1003095. [Google Scholar] [CrossRef] [PubMed]
- Belyaev, A.; Dunster, J.L.; Gibbins, J.M.; Panteleev, M.A.; Volpert, V. Modeling thrombosis in silico: Frontiers, challenges, unresolved problems and milestones. Phys. Life Rev. 2018, 26, 57–95. [Google Scholar] [CrossRef]
- Leiderman, K.; Fogelson, A. An overview of mathematical modeling of thrombus formation under flow. Thromb. Res. 2014, 133, S12–S14. [Google Scholar] [CrossRef]
- Bouchnita, A.; Terekhov, K.; Nony, P.; Vassilevski, Y.; Volpert, V. A mathematical model to quantify the effects of platelet count, shear rate, and injury size on the initiation of blood coagulation under venous flow conditions. PLoS ONE 2020, 15, e0235392. [Google Scholar] [CrossRef]
- Bouchnita, A.; Galochkina, T.; Kurbatova, P.; Nony, P.; Volpert, V. Conditions of microvessel occlusion for blood coagulation in flow. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2850. [Google Scholar] [CrossRef]
- Zheng, X.; Yazdani, A.; Li, H.; Humphrey, J.D.; Karniadakis, G.E. A three-dimensional phase-field model for multiscale modeling of thrombus biomechanics in blood vessels. PLoS Comput. Biol. 2020, 16, e1007709. [Google Scholar] [CrossRef]
- Bodnár, T.; Sequeira, A. Numerical simulation of the coagulation dynamics of blood. Comput. Math. Methods Med. 2008, 9, 83–104. [Google Scholar] [CrossRef]
- Govindarajan, V.; Rakesh, V.; Reifman, J.; Mitrophanov, A.Y. Computational study of thrombus formation and clotting factor effects under venous flow conditions. Biophys. J. 2016, 110, 1869–1885. [Google Scholar] [CrossRef] [PubMed]
- Leiderman, K.; Fogelson, A.L. The influence of hindered transport on the development of platelet thrombi under flow. Bull. Math. Biol. 2013, 75, 1255–1283. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A.; Brown, J.A.; Smith, M.A.; Woodward, A.; Vavalle, J.P.; Kheradvar, A.; Griffith, B.E.; Fogelson, A.L. A model of fluid–structure and biochemical interactions for applications to subclinical leaflet thrombosis. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3700. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.T.; Jamiolkowski, M.A.; Wagner, W.R.; Aubry, N.; Massoudi, M.; Antaki, J.F. Multi-constituent simulation of thrombus deposition. Sci. Rep. 2017, 7, 42720. [Google Scholar] [CrossRef] [PubMed]
- Bouchnita, A.; Belyaev, A.V.; Volpert, V. Multiphase continuum modeling of thrombosis in aneurysms and recirculation zones. Phys. Fluids 2021, 33, 093314. [Google Scholar] [CrossRef]
- Xu, S.; Xu, Z.; Kim, O.V.; Litvinov, R.I.; Weisel, J.W.; Alber, M. Model predictions of deformation, embolization and permeability of partially obstructive blood clots under variable shear flow. J. R. Soc. Interface 2017, 14, 20170441. [Google Scholar] [CrossRef] [PubMed]
- Filipovic, N.; Kojic, M.; Tsuda, A. Modelling thrombosis using dissipative particle dynamics method. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 3265–3279. [Google Scholar] [CrossRef]
- Al-Saad, M.; Suarez, C.; Obeidat, A.; Bordas, S.; Kulasegaram, S. Application of smooth particle hydrodynamics method for modelling blood flow with thrombus formation. Comput. Model. Eng. Sci. 2020, 122, 831–862. [Google Scholar] [CrossRef]
- Yazdani, A.; Deng, Y.; Li, H.; Javadi, E.; Li, Z.; Jamali, S.; Lin, C.; Humphrey, J.D.; Mantzoros, C.S.; Em Karniadakis, G. Integrating blood cell mechanics, platelet adhesive dynamics and coagulation cascade for modelling thrombus formation in normal and diabetic blood. J. R. Soc. Interface 2021, 18, 20200834. [Google Scholar] [CrossRef]
- Yazdani, A.; Li, H.; Humphrey, J.D.; Karniadakis, G.E. A general shear-dependent model for thrombus formation. PLoS Comput. Biol. 2017, 13, e1005291. [Google Scholar] [CrossRef] [PubMed]
- Kaneva, V.N.; Dunster, J.L.; Volpert, V.; Ataullahanov, F.; Panteleev, M.A.; Nechipurenko, D.Y. Modeling thrombus shell: Linking adhesion receptor properties and macroscopic dynamics. Biophys. J. 2021, 120, 334–351. [Google Scholar] [CrossRef] [PubMed]
- Tosenberger, A.; Ataullakhanov, F.; Bessonov, N.; Panteleev, M.; Tokarev, A.; Volpert, V. Modelling of thrombus growth in flow with a DPD-PDE method. J. Theor. Biol. 2013, 337, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Tsyu, N.G.; Belyaev, A.V. Coarse-grained simulations of von Willebrand factor adsorption to collagen with consequent platelet recruitment. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3747. [Google Scholar] [CrossRef] [PubMed]
- Shankar, K.N.; Zhang, Y.; Sinno, T.; Diamond, S.L. A three-dimensional multiscale model for the prediction of thrombus growth under flow with single-platelet resolution. PLoS Comput. Biol. 2022, 18, e1009850. [Google Scholar] [CrossRef] [PubMed]
- Pivkin, I.V.; Richardson, P.D.; Karniadakis, G. Blood flow velocity effects and role of activation delay time on growth and form of platelet thrombi. Proc. Natl. Acad. Sci. USA 2006, 103, 17164–17169. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Qiang, Y.; Li, H.; Li, X.; Dao, M.; Karniadakis, G.E. In silico and in vitro study of the adhesion dynamics of erythrophagocytosis in sickle cell disease. Biophys. J. 2023, 122, 2590–2604. [Google Scholar] [CrossRef]
- Fogelson, A.L.; Guy, R.D. Immersed-boundary-type models of intravascular platelet aggregation. Comput. Methods Appl. Mech. Eng. 2008, 197, 2087–2104. [Google Scholar] [CrossRef]
- Bouchnita, A.; Volpert, V. A multiscale model of platelet-fibrin thrombus growth in the flow. Comput. Fluids 2019, 184, 10–20. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves. In Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics: Vol. II Problems of Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 214–221. [Google Scholar]
- Terekhov, K.M.; Butakov, I.D.; Danilov, A.A.; Vassilevski, Y.V. Dynamic adaptive moving mesh finite-volume method for the blood flow and coagulation modeling. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3731. [Google Scholar] [CrossRef]
- Lenoci, L.; Duvernay, M.; Satchell, S.; DiBenedetto, E.; Hamm, H.E. Mathematical model of PAR1-mediated activation of human platelets. Mol. BioSyst. 2011, 7, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
- Kleppe, R.; Jonassen, I.; Døskeland, S.O.; Selheim, F. Mathematical modelling of nitric oxide/cyclic GMP/cyclic AMP signalling in platelets. Int. J. Mol. Sci. 2018, 19, 612. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.Y.; Diamond, S.L. A human platelet calcium calculator trained by pairwise agonist scanning. PLoS Comput. Biol. 2015, 11, e1004118. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, M.S.; Purvis, J.E.; Brass, L.F.; Diamond, S.L. Pairwise agonist scanning predicts cellular signaling responses to combinatorial stimuli. Nat. Biotechnol. 2010, 28, 727–732. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Lee, M.Y.; Zhu, S.; Sinno, T.; Diamond, S.L. Multiscale simulation of thrombus growth and vessel occlusion triggered by collagen/tissue factor using a data-driven model of combinatorial platelet signalling. Math. Med. Biol. J. 2017, 34, 523–546. [Google Scholar] [CrossRef] [PubMed]
- Ratto, N.; Bouchnita, A.; Chelle, P.; Marion, M.; Panteleev, M.; Nechipurenko, D.; Tardy-Poncet, B.; Volpert, V. Patient-specific modelling of blood coagulation. Bull. Math. Biol. 2021, 83, 50. [Google Scholar] [CrossRef] [PubMed]
- Falati, S.; Gross, P.; Merrill-Skoloff, G.; Croce, K.; Furie, B.; Furie, B. In vivo real time imaging of arterial thrombus formation reveals P-selectin-and PSGL-1-mediated tissue factor accumulation as a mechanism for fibrin clot generation. In Blood; American Society of Hematology: Washington, DC, USA, 2001; Volume 98, p. 823A. [Google Scholar]
- Krasotkina, Y.V.; Sinauridze, E.I.; Ataullakhanov, F.I. Spatiotemporal dynamics of fibrin formation and spreading of active thrombin entering non-recalcified plasma by diffusion. Biochim. Biophys. Acta (BBA)-Gen. Subj. 2000, 1474, 337–345. [Google Scholar] [CrossRef]
- Wufsus, A.R.; Macera, N.; Neeves, K. The hydraulic permeability of blood clots as a function of fibrin and platelet density. Biophys. J. 2013, 104, 1812–1823. [Google Scholar] [CrossRef] [PubMed]
- Nesbitt, W.S.; Giuliano, S.; Kulkarni, S.; Dopheide, S.M.; Harper, I.S.; Jackson, S.P. Intercellular calcium communication regulates platelet aggregation and thrombus growth. J. Cell Biol. 2003, 160, 1151–1161. [Google Scholar] [CrossRef]
- Covic, L.; Gresser, A.L.; Kuliopulos, A. Biphasic kinetics of activation and signaling for PAR1 and PAR4 thrombin receptors in platelets. Biochemistry 2000, 39, 5458–5467. [Google Scholar] [CrossRef]
- Dolan, A.T.; Diamond, S.L. Systems modeling of Ca2+ homeostasis and mobilization in platelets mediated by IP3 and store-operated Ca2+ entry. Biophys. J. 2014, 106, 2049–2060. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Noris, P.; Biino, G.; Pecci, A.; Civaschi, E.; Savoia, A.; Seri, M.; Melazzini, F.; Loffredo, G.; Russo, G.; Bozzi, V.; et al. Platelet diameters in inherited thrombocytopenias: Analysis of 376 patients with all known disorders. Blood J. Am. Soc. Hematol. 2014, 124, e4–e10. [Google Scholar] [CrossRef]
- Brambilla, M.; Canzano, P.; Becchetti, A.; Tremoli, E.; Camera, M. Alterations in platelets during SARS-CoV-2 infection. Platelets 2022, 33, 192–199. [Google Scholar] [CrossRef]
- Frojmovic, M.M.; Milton, J.G. Human platelet size, shape, and related functions in health and disease. Physiol. Rev. 1982, 62, 185–261. [Google Scholar] [CrossRef] [PubMed]
- Shen, F.; Kastrup, C.J.; Liu, Y.; Ismagilov, R.F. Threshold response of initiation of blood coagulation by tissue factor in patterned microfluidic capillaries is controlled by shear rate. Arterioscler. Thromb. Vasc. Biol. 2008, 28, 2035–2041. [Google Scholar] [CrossRef]
- Tomaiuolo, M.; Stalker, T.J.; Welsh, J.D.; Diamond, S.L.; Sinno, T.; Brass, L.F. A systems approach to hemostasis: 2. Computational analysis of molecular transport in the thrombus microenvironment. Blood J. Am. Soc. Hematol. 2014, 124, 1816–1823. [Google Scholar] [CrossRef]
- Tomaiuolo, M.; Brass, L.F.; Stalker, T.J. Regulation of platelet activation and coagulation and its role in vascular injury and arterial thrombosis. Interv. Cardiol. Clin. 2017, 6, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Stalker, T.J.; Traxler, E.A.; Wu, J.; Wannemacher, K.M.; Cermignano, S.L.; Voronov, R.; Diamond, S.L.; Brass, L.F. Hierarchical organization in the hemostatic response and its relationship to the platelet-signaling network. Blood J. Am. Soc. Hematol. 2013, 121, 1875–1885. [Google Scholar] [CrossRef]
- Welsh, J.D.; Muthard, R.W.; Stalker, T.J.; Taliaferro, J.P.; Diamond, S.L.; Brass, L.F. A systems approach to hemostasis: 4. How hemostatic thrombi limit the loss of plasma-borne molecules from the microvasculature. Blood J. Am. Soc. Hematol. 2016, 127, 1598–1605. [Google Scholar] [CrossRef]
- Neeves, K.; Maloney, S.; Fong, K.; Schmaier, A.; Kahn, M.; Brass, L.; Diamond, S.L. Microfluidic focal thrombosis model for measuring murine platelet deposition and stability: PAR4 signaling enhances shear-resistance of platelet aggregates. J. Thromb. Haemost. 2008, 6, 2193–2201. [Google Scholar] [CrossRef] [PubMed]
- Handtke, S.; Thiele, T. Large and small platelets—(When) do they differ? J. Thromb. Haemost. 2020, 18, 1256–1267. [Google Scholar] [CrossRef] [PubMed]
- Stalker, T.J.; Welsh, J.D.; Tomaiuolo, M.; Wu, J.; Colace, T.V.; Diamond, S.L.; Brass, L.F. A systems approach to hemostasis: 3. Thrombus consolidation regulates intrathrombus solute transport and local thrombin activity. Blood J. Am. Soc. Hematol. 2014, 124, 1824–1831. [Google Scholar] [CrossRef] [PubMed]
- Masalceva, A.A.; Kaneva, V.N.; Panteleev, M.A.; Ataullakhanov, F.; Volpert, V.; Afanasyev, I.; Nechipurenko, D.Y. Analysis of microvascular thrombus mechanobiology with a novel particle-based model. J. Biomech. 2022, 130, 110801. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Z.; Kim, O.; Alber, M. Three-dimensional multi-scale model of deformable platelets adhesion to vessel wall in blood flow. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130380. [Google Scholar] [CrossRef] [PubMed]
- Kim, O.V.; Litvinov, R.I.; Alber, M.S.; Weisel, J.W. Quantitative structural mechanobiology of platelet-driven blood clot contraction. Nat. Commun. 2017, 8, 1274. [Google Scholar] [CrossRef] [PubMed]
- Michael, C.; Pancaldi, F.; Britton, S.; Kim, O.V.; Peshkova, A.D.; Vo, K.; Xu, Z.; Litvinov, R.I.; Weisel, J.W.; Alber, M. Combined computational modeling and experimental study of the biomechanical mechanisms of platelet-driven contraction of fibrin clots. Commun. Biol. 2023, 6, 869. [Google Scholar] [CrossRef] [PubMed]
- Bouchnita, A.; Nony, P.; Llored, J.P.; Volpert, V. Combining mathematical modeling and deep learning to make rapid and explainable predictions of the patient-specific response to anticoagulant therapy under venous flow. Math. Biosci. 2022, 349, 108830. [Google Scholar] [CrossRef] [PubMed]
- Bouchnita, A.; Yadav, K.; Llored, J.P.; Gurovich, A.; Volpert, V. Thrombin Generation Thresholds for Coagulation Initiation under Flow. Axioms 2023, 12, 873. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).