Apple Image Recognition Multi-Objective Method Based on the Adaptive Harmony Search Algorithm with Simulation and Creation

Abstract

Aiming at the low recognition effect of apple images captured in a natural scene, and the problem that the OTSU algorithm has a single threshold, lack of adaptability, easily caused noise interference, and over-segmentation, an apple image recognition multi-objective method based on the adaptive harmony search algorithm with simulation and creation is proposed in this paper. The new adaptive harmony search algorithm with simulation and creation expands the search space to maintain the diversity of the solution and accelerates the convergence of the algorithm. In the search process, the harmony tone simulation operator is used to make each harmony tone evolve towards the optimal harmony individual direction to ensure the global search ability of the algorithm. Despite no improvement in the evolution, the harmony tone creation operator is used to make each harmony tone to stay away from the current optimal harmony individual for extending the search space to maintain the diversity of solutions. The adaptive factor of the harmony tone was used to restrain random searching of the two operators to accelerate the convergence ability of the algorithm. The multi-objective optimization recognition method transforms the apple image recognition problem collected in the natural scene into a multi-objective optimization problem, and uses the new adaptive harmony search algorithm with simulation and creation as the image threshold search strategy. The maximum class variance and maximum entropy are chosen as the objective functions of the multi-objective optimization problem. Compared with HS, HIS, GHS, and SGHS algorithms, the experimental results showed that the improved algorithm has higher a convergence speed and accuracy, and maintains optimal performance in high-dimensional, large-scale harmony memory. The proposed multi-objective optimization recognition method obtains a set of non-dominated threshold solution sets, which is more flexible than the OTSU algorithm in the opportunity of threshold selection. The selected threshold has better adaptive characteristics and has good image segmentation results.

1. Introduction

The harmony search (HS) algorithm [1] is a swarm intelligence algorithm that simulates the process of music players’ repeated tuning of the pitch of each musical instrument through memory to achieve a wonderful harmony process. It has been successfully applied to many engineering problems. Like other swarm intelligence algorithms, the HS algorithm also has problems with premature convergence and stagnant convergence [2,3]. In recent years, scholars have made many improvements to the optimization performance of the HS algorithm, such as the probabilistic idea of applying the distributed estimation algorithm in the [2] to design an adaptive adjustment strategy and improve the search ability of the algorithm. In [3], the HS algorithm and the genetic algorithm (GA) are combined to obtain a better initial solution based on multiple iterations of the genetic algorithm, and then the harmony search algorithm is used to further search for possible solutions in the adjacent region. Zhu et al. linearly combines the optimal harmony vector with the two harmony vectors randomly selected in the population to generate a new harmony and expand the local search area [4]. Wu et al. uses the competitive elimination mechanism to update the harmony memory library to accelerate the process of survival of the fittest. Some studies have designed two key parameters of the HS algorithm to overcome the shortcomings of fixed parameters [5]. These two parameters also have improved from different perspectives and proposed different improved harmony search algorithms in [6,7,8]. The studies in [9,10] apply the improved HS algorithm to multi-objective optimization problems.

Relevant scholars have conducted a large number of basic studies on the HS algorithm, and proposed improvements, achieving good results in application. Simulated annealing and a genetic algorithm are used to optimally adjust the weights for the aggregation mechanism [11]. An innovative tuning approach for fuzzy control systems (CSs) with a reduced parametric sensitivity using the grey wolf optimizer (GWO) algorithm was proposed in [12]. The GWO algorithm is used in solving the optimization problems, where the objective functions include the output sensitivity functions [12]. Echo state networks (ESN) are a special form of recurrent neural networks (RNNs), which allow for the black box modeling of nonlinear dynamical systems. The harmony search (HS) algorithm shows good performance, proposed for training the echo state network in an online manner [13]. The design of the Takagi–Sugeno fuzzy controllers in state feedback formed using swarm intelligence optimization algorithms was proposed in [14], and the particle swarm optimization, simulated annealing and gravitational search algorithms are adopted. In terms of image applications of HS, the following studies have been conducted. A novel approach to visual tracking called the harmony filter is presented. The harmony filter models the target as a color histogram and searches for the best estimated target location using the Bhattacharyya coefficient as a fitness metric [15]. In [16], a new dynamic clustering algorithm based on the hybridization of harmony search (HS) and fuzzy c-means to automatically segment MRI brain images in an intelligent manner was presented. Improvements to Harmony Search (HS) in circle detection was proposed that enables the algorithm to robustly find multiple circles in larger data sets and still work on realistic images that are heavily corrupted by noisy edges [17]. A new approach to estimate the vanishing point using a harmony search (HS) algorithm was proposed in [18]. In the theoretical background of HS, the following studies have been conducted. In order to consider the realistic design situations, a novel derivative for discrete design variables based on a harmony search algorithm was proposed in [19]. In [20], it presents a simple mathematical analysis of the explorative search behavior of harmony search (HS) algorithm. The comparison of the final designs of conventional methods and metaheuristic based structural optimization methods was discussed in [21]. In the improvement of adaptive methods of HS, the following studies have been conducted. An adaptive harmony search algorithm was proposed for solving structural optimization problems to incorporate a new approach for adjusting these parameters automatically during the search for the most efficient optimization process [22]. A novel technique to eliminate tedious and experience-requiring parameter assigning efforts was proposed for the harmony search algorithm in [23]. Pan et al. presents a self-adaptive global best harmony search (SGHS) algorithm for solving continuous optimization problems [24].

Recognition of apple images is one of the most basic aspects of computer processing apple grading [25]. Apple image recognition refers to the separation of apple fruit from branches, leaves, soil, and sky, i.e., image segmentation techniques [26]. The threshold segmentation method is an extremely important and widely used image segmentation method [27]. Among them, the maximum class variance (OTSU) [28] and maximum entropy method [29] are the two most commonly used threshold segmentation methods. Both types of segmentation methods have different degrees of defects [30]. The classical OTSU algorithm has the problem that the ideal segmentation effect cannot be obtained for complex images of natural scenes [30]. Although the OTSU algorithm solves the problem of threshold selection, it has the problems of lacking adaptability, easily causes noise interference and over-segmentation, and requires a great deal of time for computing, and so on. Therefore, the classical OTSU algorithm still needs further improvement. In order to comprehensively utilize the advantages of the two segmentation methods, a multi-objective optimization problem is introduced. In recent years, the HS algorithm has made some progress in solving multi-objective optimization problems, such as the stand-alone scheduling problem [10], the wireless sensor network routing problem [31], the urban one-way traffic organization optimization problem [32], and the distribution network model problem [33]. In [34], the study employed a phenomenon-mimicking algorithm and harmony search to perform the bi-objective trade-off. The harmony search algorithm explored only a small amount of total solution space in order to solve this combinatorial optimization problem. A multi-objective optimization model based on the harmony search algorithm (HS) was presented to minimize the life cycle cost (LCC) and carbon dioxide equivalent (CO₂-eq) emissions of the buildings [35]. A novel fuzzy-based velocity reliability index using fuzzy theory and harmony search was proposed, which is to be maximized while the design cost is simultaneously minimized [36]. These studies are closely integrated with specific application issues and cannot be easily extended to other application areas.

This paper proposes an apple image recognition multi-objective method based on the adaptive harmony search algorithm with simulation and creation (ARMM-AHS). This method transforms the image segmentation problem of natural scenes into a multi-objective optimization problem. It takes the maximum class variance and maximum entropy as the two objective functions of the optimization problem. A new adaptive harmony search algorithm with simulation and creation (SC-AHS) is proposed as a strategy for the image threshold search to achieve natural scene apple image segmentation. The results showed that the SC-AHS algorithm improves the global search ability and the diversity of the solution of the HS algorithm, and has obvious performance advantages of fast convergence. The ARMM-AHS method can effectively segment the apple image.

2. Theory Basis

2.1. Threshold Segmentation Principle of the OTSU Algorithm

The OTSU algorithm is a global threshold selection method. The basic idea is to use the grayscale histogram of the image to dynamically determine the segmentation threshold of the image with the maximum variance of the target and the background.

Suppose that the gray level of an apple image is $L$ the gray value of each pixel is $0,1,\cdots ,L-1$, the number of pixels with gray value $\mathrm{i}$ is $W_i$, the total number of pixels in the image is $\mathrm{W}={\sum }_{i=0}^{L-1}{W}_i$, and the probability of gray value $\mathrm{i}$ is set to $p_i=\raisebox{1ex}{$W_i$}\!\left/ \!\raisebox{-1ex}{$W$}\right.$.

Let the threshold $\mathrm{t}$ divide the image into two classes $C_0$ and $C_1$ (target and background), that is, $C_0$ and $C_1$ respectively correspond to pixels with gray levels $\left\{0,1,\cdots ,\mathrm{t}\right\}$ and $\left\{\mathrm{t}+1,\mathrm{t}+2,\cdots ,\mathrm{L}-1\right\}$, then the variance between the two classes is as shown in Equation (1):

$${\sigma }_B^2={\omega }_0{\left({\mu }_0-{\mu }_T\right)}^2+{\omega }_1{\left({\mu }_1-{\mu }_T\right)}^2$$

(1)

The optimal threshold $t^{*}$ should maximize the variance between classes, which is an optimization problem, as shown in Equation (2):

$$t^{*}=\begin{array}{cc}arg& \underset{0\le t\le L-1}{\max }\left\{{\sigma }_B^2\left(t\right)\right\}\end{array}$$

(2)

Among them, ${\omega }_0$ and ${\omega }_1$ respectively represent the probability of the occurrence of class $C_0$ and class $C_1$. ${\mu }_0$ and ${\mu }_1$ represent the average gray value of the class $C_0$ and class $C_1$, respectively. ${\mu }_T$ represents the average gray level of the entire image. Therefore, the larger the value of ${\sigma }_B^2$, the better the threshold that is selected.

2.2. Maximum Entropy Segmentation Principle

For the same image, let us assume that the threshold t divides the image into two classes $C_0$ and $C_1$. The probability distribution of the class $C_0$ is $\left\{\frac{p_0}{P_t},\frac{p_1}{P_t},\cdots ,\frac{p_t}{P_t}\right\}$, and the probability distribution of the class $C_1$ is $\left\{\frac{p_{t+1}}{1-P_t},\frac{p_{t+2}}{1-P_t},\cdots ,\frac{p_{L-1}}{1-P_t}\right\}$, where $P_t={\sum }_{i=0}^t{p}_i,0\le t\le L-1$.

The entropy formula is as shown in Equation (3):

$$H\left(t\right)=-{\displaystyle \sum _{i=0}^t}\frac{p_i}{P_t}\ln \frac{p_i}{P_t}-{\displaystyle \sum _{i=t+1}^{L-1}}\frac{p_i}{1-P_t}\ln \frac{p_i}{1-P_t}$$

(3)

The optimal threshold should maximize the entropy, which is also an optimization problem, as shown in Equation (4).

$$t^{*}=\begin{array}{cc}arg& \underset{0\le t\le L-1}{\max }\left\{H\left(t\right)\right\}\end{array}$$

(4)

3. Adaptive Harmony Search Algorithm with Simulation and Creation

The inertial particle and fuzzy reasoning were introduced into the bird swarm optimization algorithm (BSA) in [37] to make those birds that are foraging jump out of the local optimal solution to enhance the ability of global optimization. The fast shuffled frog leaping algorithm (FSFLA) proposed in [38] makes each frog individual evolve toward the best individual, which accelerates the individual evolutionary speed and improves the search speed of the algorithm. According to the no-free lunch theorem [39], this paper fuses the ideas of the above two different types of optimization algorithms’ mechanisms and proposes an adaptive harmony search algorithm with simulation and creation (SC-AHS) to improve the HS algorithm optimization performance.

3.1. Theory Basis

3.1.1. Adaptive Factor of Harmony Tone

Definition 1 (Adaptive factor of harmony tone).

Randomly generate Harmony Memory whose Size is HMS to find out the global optimal harmony$x_i^g=\left(x_1^g,x_2^g,\cdots ,x_N^g\right)$, current optimal harmony$x_i^{now}=\left(x_1^{now},x_2^{now},\cdots ,x_N^{now}\right)$, and global worst harmony$x_i^w=\left(x_1^w,x_2^w,\cdots ,x_N^w\right)$in each creation of the harmony memory. The adaptive factor of the harmony tone${\xi }_i$is defined as follows, and it is used to suppress randomness during simulation and creation of harmony tone:

$$\begin{gathered} {\xi }_i=\frac{{\sum }_{i=1}^N{r}_i{x}_i^{now}}{{\sum }_{i=1}^N{r}_i},i=1,2,\cdots ,N \\ {r}_i=\frac{f\left(x_i^g\right)-f\left(x_i^w\right)}{f\left(x_i^{now}\right)} \end{gathered}$$

(5)

3.1.2. Harmony Tone Simulation Operator

Definition 2 (Harmony tone simulation operator).

In one harmony evolution, each tone component$x_i^j,i=1,2,\cdots ,N$of each harmony$x^j,j=1,2,\cdots ,HMS$in the harmony memory adaptively evolves through the harmony tone simulation operator, as follows, to adjust the harmony individuals to evolve to optimal harmony individuals:

$$x_i^{j,new}=x_i^{j,old}+{\xi }_i\left(x_i^g-x_i^{j,old}\right)$$

(6)

3.1.3. Harmony Tone Creation Operator

Definition 3 (Harmony tone creation operator).

In one harmony evolution, each tone component$x_i^j,i=1,2,\cdots ,N$of each harmony$x^j,j=1,2,\cdots ,HMS$in the harmony memory adaptively evolves through the harmony tone creation operator, as follows, to adjust harmony individuals away from the current optimal harmony individual evolution:

$$x_i^{j,new}=x_i^{j,old}-{\xi }_i\left(x_i^{now}-x_i^{j,old}\right)$$

(7)

3.2. Adaptive Evolution Theorem with Simulation and Creation

Theorem 1 (Adaptive evolution theorem with simulation and creation).

In one harmony evolution, each tone component$x^j,j=1,2,\cdots ,HMS$in each harmony$x_i^j,i=1,2,\cdots ,N$in the harmony memory adaptively evolves through the harmony tone simulation operator according to the Equation (6). If$f\left(x^{j,new}\right)<f\left(x^{j,old}\right)$, replace$x_i^{j,old}$with$x_i^{j,new}$, respectively. Otherwise, it evolves through the harmony tone creation operator according to the Equation (7). If$f\left(x^{j,new}\right)\ge f\left(x^{j,old}\right)$still exists, use Equation (8) to randomly generate the harmony tone:

$$x_i^{j,new}=L{B}_i+r\left(U{B}_i-L{B}_i\right)$$

(8)

3.3. SC-AHS Algorithm Process

Algorithm 1. SC-AHS

Input: the maximum number of evolutions $T_{max}$, the size of the harmony memory HMS, the number of tone component N.

Output: global optimal harmony $x^g$.

Step1: Randomly generate initial harmony individuals which number is HMS, marked as $X_{HMS}=\left\{x^j|x^j=\left(x_1^j,x_2^j,\cdots ,x_N^j\right),j=1,2,\cdots ,HMS\right\}$. The harmony memory is initialized according to Equation (1). The fitness of $x^j$ is $f\left(x^j\right)$.

Step2: Each tone component $x_i^j,i=1,2,\cdots ,N$ of each harmony $x^j,j=1,2,\cdots ,HMS$ is updated.

Begin

Sort each harmony by fitness $f\left(x^j\right)$ in descending order to determine $x_i^g$, $x_i^{now}$ and $x_i^w$.

For ($x^j,j=1,2,\cdots ,HMS$)

Begin

Calculated ${\xi }_i$ according to Equation (5)

For ($x_i^j,i=1,2,\cdots ,N$)

Update $x_i^{j,old}$ according to Equation (6) to perform harmony tone simulation

End

if ($f\left(x^{j,new}\right)<f\left(x^{j,old}\right)$)

For ($x_i^j,i=1,2,\cdots ,N$) $$x_i^{j,old}=x_i^{j,new}$$

End

else

For ($x_i^j,i=1,2,\cdots ,N$)

Update $x_i^{j,old}$ according to Equation (7) to perform harmony tone creation

End

If ($f\left(x^{j,new}\right)<f\left(x^{j,old}\right)$)

For ($x_i^j,i=1,2,\cdots ,N$) $$x_i^{j,old}=x_i^{j,new}$$

End

else

For ($x_i^j,i=1,2,\cdots ,N$)

Randomly generate harmony tone $x_i^{j,new}$ according to Equation (8).

End

End

End

Step3: Determine if the number of evolutions has been reached $T_{max}$. If not, go to Step 2. Otherwise, the algorithm stops and outputs $x^g$.

3.4. Efficiency Analysis of SC-AHS

The efficiency analysis of the algorithm shows that the time complexity of the HS algorithm is $O\left(T_{max}\times N\right)$, and the space complexity is $O\left(HMS\times N\right)$, while the time complexity of the SC-AHS algorithm is $O\left(T_{max}\times N\times HMS\right)$, and the space complexity is $O\left(HMS\times N\right)$. Since $T_{max}\gg HMS$, the execution time and storage space of the SC-AHS algorithm and the HS algorithm are of the same order of magnitude. This shows that the SC-AHS algorithm does not increase the computational overhead and space.

4. Apple Image Recognition Multi-Objective Method Based on an Adaptive Harmony Search Algorithm with Simulation and Creation

4.1. Mathematical Problem Description of the Multi-Objective Optimization Recognition Method

Suppose that the gray level of an apple image is $L$, the gray value of each pixel is $0,1,\cdots ,\mathrm{L}-1$. There are two classes to be distinguished in the apple image, and the corresponding harmonic threshold in each class is written as $x^j,j=1,2,\cdots ,HMS,0\le x^j\le L-1$. The optimization process of seeking thresholds for segmentation of apple images can be regarded as a multi-objective optimization problem, in which the maximum class variance and maximum entropy are taken as two objective functions of the multi-objective optimization problem. The proposed SC-AHS algorithm is used as an image threshold search strategy. If we take the calculation of the minimization function as an example, the multi-objective optimization problem can be defined as follows:

$$\{\begin{array}{c}\min f\left(x\right)=\left[f_1\left(x\right),f_2\left(x\right)\right]\\ s.t.x^j=\left(x_1^j,x_2^j,\cdots ,x_N^j\right)\in X\subseteq R^N,N=8\\ \begin{array}{c}X=\left\{x^j,j=1,2,\cdots ,HMS|0\le x^j\le L-1\right\}\\ f_1\left(x^{*}\right)=-\underset{0\le x^j\le L-1}{\min }\left\{{\sigma }_B^2\left(x^j\right)\right\}\\ f_2\left(x^{*}\right)=-\underset{0\le x^j\le L-1}{\min }\left\{H\left(x^j\right)\right\}\end{array}\end{array}$$

(9)

4.2. Process of the Apple Image Recognition Multi-Objective Method Based on an Adaptive Harmony Search Algorithm with Simulation and Creation

Step 1: Read and preprocess the apple image. Count the gray level $L$ of the image and the number of corresponding pixels $W_i$ to calculate the probability $p_i$ of the occurrence of grayscale.

Step 2: Enter the maximum number of evolutions $T_{max}$, the size of the harmony memory bank HMS, and the number of tone components N.

Step 2.1: HMS initial harmony thresholds are generated randomly, which is denoted as $X=\left\{x^j|x^j=\left(x_1^j,x_2^j,\cdots ,x_N^j\right),j=1,2,\cdots ,HMS\right\}$. Each harmonic threshold is binary coded and calculated $f_1\left(X\right)$ and $f_2\left(X\right)$ according to Equation (9) to initialize the harmony memory. The fitness of the harmonic threshold $x^j$ is $f_1\left(x^j\right)$ and $f_2\left(x^j\right)$.

Step 2.2: Construct a Pareto optimal solution set, and note the harmonic threshold deleted from the optimal solution set as $x^{w,old}$.

Step 2.3: Each tone component $x_i^{w,old},i=1,2,\cdots ,N$ of the harmony threshold $x^{w,old}$ is updated according to the SC-AHS algorithm step.

Step 2.4: Determine whether the number of evolutions has been reached $T_{max}$. If not, go to Step 2.2. Otherwise, the algorithm stops and the optimal harmonic threshold solution set is output and noted as $x^{*}$.

Step 3: Use the optimal harmony threshold solution set $x^{*}$ to divide the apple image and output the segmented image.

The apple image recognition multi-objective method based on an adaptive harmony search algorithm with simulation and creation process is shown in Figure 1.

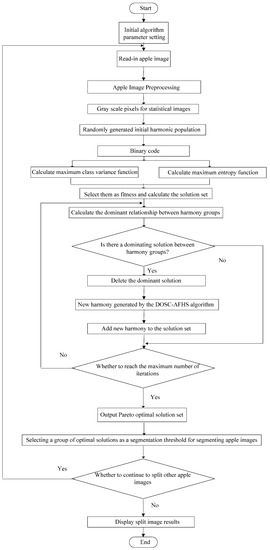
Figure 1. Flowchart of the apple image recognition multi-objective method based on an adaptive harmony search algorithm with simulation and creation.

5. Experiment Design and Results Analysis

5.1. Experiment Design

The experimental samples were chosen from the mature HuaNiu apples. A series of mature HuaNiu apple image segmentation experiments are conducted under six conditions of direct sunlight with strong, medium, and weak illumination, and backlighting with strong, medium, and weak illumination in a natural scene. The experiment contains two parts. Firstly, the benchmark functions are used to test the optimization performance of the SC-AHS algorithm. Secondly, the ARMM-AHS method is used to segment and identify the apple image. The experiment used a Lenovon (Beijing, China) Notebook computer with an Intel Core i5 CPU 2.6 GHz and 4.0 GB of memory. The test platform was Microsoft Visual C++ 6.0 and Matlab 2012.

5.2. Benchmark Function Comparison Experiment and Result Analysis

Five benchmark functions, including Sphere, Rastrigrin, Griewank, Ackley, and Rosenbrock, were used to simulate the individual fitness of harmony. The parameters of each function are shown in Table 1 [40].

$$f_1\left(x\right)={\sum }_{i=1}^N{x}_i^2$$

(10)

$$f_2\left(x\right)={\sum }_{i=1}^N\left[x_i^2-10\cos \left(2\pi x_i\right)+10\right]$$

(11)

$$f_3\left(x\right)=\frac{1}{4000}{\sum }_{i=1}^N{x}_i^2-{\prod }_{i=1}^N\cos \left(\frac{x_i}{\sqrt{i}}\right)+1$$

(12)

$$f_4\left(x\right)=-20\exp \left[-0.2\sqrt{\frac{1}{N}{\sum }_{i=1}^N{x}_i^2}\right]-\exp \left[\frac{1}{N}{\sum }_{i=1}^N\cos \left(2\pi x_i\right)\right]+20+e$$

(13)

$$f_5\left(x\right)={\sum }_{i=1}^N[100{(x_{i+1}-x_i^2)}^2+{(1-x_i)}^2]$$

(14)

Table 1. Parameters of five benchmark functions.

Function	Name	Peak Value	Dimension	Search Cope	Theoretical Optimal Value	Target Accuracy
f1	Sphere	unimodal	30	[−100,100]	0	10−15
f2	Rastrigrin	multimodal	30	[−5.12,5.12]	0	10−2
f3	Griewank	multimodal	30	[−600,600]	0	10−2
f4	Ackley	multimodal	30	[−32,32]	0	10−6
f5	Rosenbrock	unimodal	30	[−30,30]	0	10−15

5.2.1. Fixed Parameters Experiment

The fixed parameters experiment uses a minimum value optimization simulation to compare and test the optimization performance of the HS, Improved Harmony Search (IHS) [7], Global-best Harmony Search (GHS) [41], Self-adaptive Global best Harmony Search (SGHS) [24], and SC-AHS algorithms.

In the fixed parameter experiment, the experimental parameters were set as follows. HMS = 200, HMCR = 0.9, PAR = 0.3, BW = 0.01, $T_{max}$ = 20,000, N = 30. The HCMR is the Harmony memory library probability, the PAR is the tone fine-tuning probability, the BW is the tone fine-tuning bandwidth, and $T_{max}$ is the number of evolutions. In the IHS algorithm, the pitch tune probability minimum value PAR_min = 0.01, the pitch tuning probability maximum value PAR_max = 0.99, the pitch tune bandwidth minimum value BW_min = 0.0001, and the pitch tune bandwidth maximum value ${\mathrm{BW}}_{\max }=1/\left(20\times \left(UB-LB\right)\right)$ [7]. In the GHS algorithm, PAR_min = 0.01, PAR_max = 0.99 [41]. In the SGHS algorithm, the initial probability value of the harmony memory is HMCR_m = 0.98, the standard deviation of the value of the harmony memory is HMCR_s = 0.01, and the probability of the harmony memory is normally distributed within [0.9, 1.0], the average initial value of the bandwidth is PAR_m = 0.9, the standard deviation of the pitch tune bandwidth PAR_s = 0.05, the pitch tune bandwidth is normally distributed within [0.0, 1.0], the specific evolution numbers LP = 100 [24], the pitch tune bandwidth minimum BW_min = 0.0001, and the pitch tune bandwidth maximum ${\mathrm{BW}}_{\max }=1/\left(20\times \left(UB-LB\right)\right)$ [7]. Upper Bound (UB) is the maximum value of the search range of the algorithm, and Lower Bound (LB) is the minimum value of the search range of the algorithm. In the SC-AHS algorithm, ${\alpha }_{init}=0.1$, ${\alpha }_{final}=1.2$. The final test results were averaged after 30 independent runs. The performance evaluation of the algorithm uses the following methods: (1) the method of convergence accuracy and speed of the analysis algorithm under a fixed evolutionary frequency; and (2) the method of comparing the evolution curve of the average optimal value of each function.

The convergence accuracy of each algorithm is shown in Table 2. For both the unimodal Sphere (f1) and Rosenbrock (f5) functions, the data in Table 2 shows that the algorithm has reached the theoretical minimum of 0 for both functions. It shows that the convergence accuracy of this algorithm is very high, and the convergence speed and accuracy of other functions are slightly smaller than the SC-AHS algorithm. For the multimodal Rastrigrin (f2) function, Table 2 shows that the SC-AHS algorithm has reached the theoretical minimum of 0. It indicates that the algorithm has high convergence accuracy, and the convergence accuracy of other functions does not reach the theoretical minimum. For multimodal Griewank (f3) and Ackley (f4) functions, the data in Table 2 shows that the GHS algorithm reached the theoretical minimum value of 0 as it reaches the 5000 iterations in the Griewank (f3) function optimization. At the same time, the convergence accuracy of the GHS algorithm in the Ackley (f4) function optimization is also better than other algorithms, indicating that for these two functions, the SC-AHS algorithm converges faster, and the convergence accuracy is better than the other algorithms, except the GHS algorithm.

Table 2. Comparison of the results of fixed global evolution times.

Algorithm	Optimization Performance	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_5$
HS	Optimum	5.07 × 102	1.76 × 101	4.47 × 100	5.18 × 100	1.13 × 104
	Standard deviation	1.36 × 100	9.17 × 10−2	4.89 × 10−3	1.88 × 10−2	3.06 × 102
IHS	Optimum	3.80 × 102	2.83 × 101	7.62 × 100	6.10 × 100	4.49 × 104
	Standard deviation	6.12 × 10−3	6.81 × 10−1	8.60 × 10−6	1.76 × 10−3	2.26 × 101
GHS	Optimum	1.20 × 102	3.62 × 10−4	0.00 × 100	5.89 × 10−16	3.00 × 101
	Standard deviation	9.19 × 10−2	4.70 × 10−2	6.11 × 10−4	4.90 × 10−29	3.33 × 100
SGHS	Optimum	2.47 × 102	2.98 × 101	5.92 × 100	5.62 × 100	1.89 × 104
	Standard deviation	8.50 × 10−12	1.97 × 10−1	2.67 × 10−5	6.89 × 10−4	1.27 × 101
DOSC-AFHS	Optimum	0.00 × 100	0.00 × 100	1.97 × 10−2	3.27 × 10−6	0.00 × 100
	Standard deviation	0.00 × 100	4.27 × 10−1	1.02 × 10−15	2.72 × 10−5	0.00 × 100

By comparing the minimum values of the HS, HIS [7], GHS [41], and SGHS [24] algorithms, and the SC-AHS algorithm with fixed parameters, the results show that for unimodal Sphere (f1) and Rosenbrock (f5) functions and multimodal Rastrigrin (f2) function, the SC-AHS algorithm has better performance than the other algorithms. For the multimodal Grievenk (f3) and Ackley (f4) functions, the SC-AHS algorithm converges faster than other algorithms. In addition to the GHS algorithm, the SC-AHS algorithm has better convergence accuracy than other algorithms. For each function, compared with the HS algorithm, the convergence accuracy and speed of the SC-AHS algorithm are significantly improved. Compared with other algorithms, the SC-AHS algorithm has the advantage of fast convergence.

5.2.2. Dynamic Parameters Experiment

The dynamic parameters experiment uses two test methods, including varying the number of harmony tone components and varying the harmony memory size, HMS. Under the condition of dynamic parameters, the optimization performance effect of the above algorithms, like HS, HIS [7], GHS [41], SGHS [24], and the SC-AHS is compared. The average value of each function, the relative change rate [42], and the average change value were used as measures of the performance of the algorithm.

Test of Average Optimum with Different Harmony Tone Components of Five Functions

The number of harmony tone components corresponds to the dimension of the function. High-dimensional, multimodal, complex optimization problems can easily cause a local optimum and premature convergence. For this reason, it is extremely necessary to adjust the dimension of the benchmark function (i.e., the number of tone components) and test the optimization performance of each algorithm in high dimensions. The tone components are in the range of 50 to 100, and the other parameters are unchanged. The comparison of the changes in the number of tone components for the optimization performance of each algorithm is shown in Table 3. The average optimal value of each function varied with the number of tone components is shown in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. In Table 3, there is:

$$\begin{array}{l}Relativerateofchange\\ =\frac{\left|averageoptimalvalueofthe50tonecomponents-averageoptimalvalueofthe100tonecomponents\right|}{averageoptimalvalueofthe50tonecomponents}\\ \times 100\%\end{array}$$

(15)

$$Averagechange=\frac{{\sum }_{i=1}^{6}averageoptimalvalueofdifferentnumbersoftonecomponents}{6}\times 100\%$$

(16)

Table 3. Comparison of the optimal performance with different harmony tone components of five functions.

Functions	N	Average Optimal Value of HS	Average Optimal Value of IHS	Average Optimal Value of GHS	Average Optimal Value of SGHS	Average Optimal Value of SC-AHS
$f_1$	50	1.29 × 103	9.48 × 102	2.00 × 102	1.17 × 103	9.62 × 10−19
	60	1.35 × 103	1.96 × 103	2.40 × 102	1.09 × 103	2.49 × 10−21
	70	1.63 × 103	1.92 × 103	1.12 × 103	3.59 × 103	3.34 × 10−17
	80	2.67 × 103	2.82 × 103	3.20 × 102	1.82 × 104	1.00 × 10−18
	90	4.04 × 103	4.49 × 103	3.20 × 101	2.33 × 104	5.78 × 10−17
	100	5.83 × 103	6.08 × 103	3.60 × 103	3.59 × 104	2.57 × 10−25
	Relative rate of change/%	3.52 × 102	5.42 × 102	1.70 × 103	2.97 × 103	1.00 × 102
	Average change	2.80 × 103	3.04 × 103	9.19 × 102	1.39 × 104	1.55 × 10−17
$f_2$	50	3.50 × 101	5.73 × 101	5.81 × 101	7.38 × 102	1.29 × 101
	60	4.76 × 101	7.81 × 101	4.36 × 100	7.09 × 102	1.69 × 101
	70	6.69 × 101	1.18 × 102	7.24 × 100	9.06 × 102	2.29 × 101
	80	6.75 × 101	1.13 × 102	9.30 × 101	1.05 × 102	3.78 × 101
	90	1.09 × 102	1.47 × 102	2.01 × 100	1.19 × 103	4.38 × 101
	100	1.13 × 102	1.75 × 102	2.01 × 100	1.62 × 102	6.07 × 101
	Relative rate of change/%	2.22 × 102	2.06 × 102	9.65 × 101	7.80 × 101	3.69 × 102
	Average change	7.31 × 101	1.15 × 102	2.78 × 101	6.35 × 102	3.25 × 101
$f_3$	50	1.03 × 101	8.13 × 100	2.80 × 100	1.03 × 103	4.93 × 10−3
	60	1.59 × 101	1.66 × 101	1.92 × 10−1	2.00 × 102	9.86 × 10−3
	70	1.77 × 101	1.99 × 101	3.52 × 100	1.66 × 102	1.11 × 10−16
	80	2.94 × 101	3.22 × 101	3.88 × 100	1.52 × 101	1.23 × 10−2
	90	4.81 × 101	3.76 × 101	1.40 × 101	2.78 × 102	4.93 × 10−3
	100	4.67 × 101	4.96 × 101	3.34 × 101	3.52 × 101	1.72 × 10−2
	Relative rate of change/%	3.56 × 102	5.10 × 102	1.09 × 103	9.66 × 101	2.49 × 102
	Average change	2.80 × 101	2.73 × 101	9.63 × 100	2.88 × 102	8.21 × 10−3
$f_4$	50	1.26 × 101	1.22 × 101	1.12 × 101	8.42 × 100	7.10 × 10−5
	60	1.31 × 101	1.25 × 101	1.44 × 100	1.07 × 101	7.73 × 10−6
	70	1.11 × 101	1.25 × 101	3.87 × 100	1.61 × 101	8.51 × 100
	80	8.45 × 100	8.93 × 100	2.11 × 100	2.00 × 101	1.88 × 101
	90	2.79 × 100	3.42 × 100	7.55 × 10−1	2.03 × 101	1.56 × 101
	100	6.41 × 10−1	1.96 × 10−1	4.75 × 10−2	2.05 × 101	2.08 × 101
	Relative rate of change/%	9.49 × 101	9.84 × 101	9.96 × 101	1.43 × 102	2.93 × 107
	Average change	8.11 × 100	8.30 × 100	3.24 × 100	1.60 × 101	1.06 × 101
$f_5$	50	2.62 × 105	1.53 × 105	3.03 × 102	4.33 × 108	1.00 × 10−20
	60	5.24 × 105	7.42 × 105	5.50 × 102	1.16 × 107	1.00 × 10−20
	70	4.95 × 105	9.88 × 105	1.09 × 103	1.08 × 107	1.00 × 10−20
	80	1.26 × 106	1.14 × 106	8.46 × 104	2.29 × 105	1.00 × 10−20
	90	2.04 × 106	1.15 × 106	7.97 × 105	3.56 × 107	1.00 × 10−20
	100	3.37 × 106	1.46 × 106	1.00 × 102	2.30 × 105	1.00 × 10−20
	Relative rate of change/%	1.19 × 103	8.55 × 102	6.70 × 101	9.99 × 101	0.00 × 100
	Average change	1.32 × 106	9.39 × 105	1.47 × 105	8.18 × 107	1.00 × 10−20

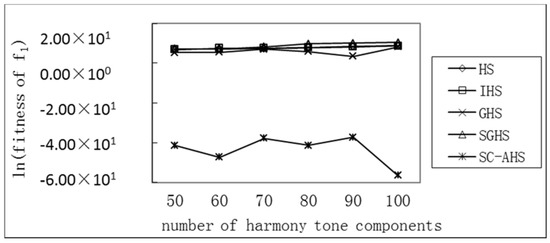
Figure 2. Comparison of the average optimum with different harmony tone components of the Sphere function.

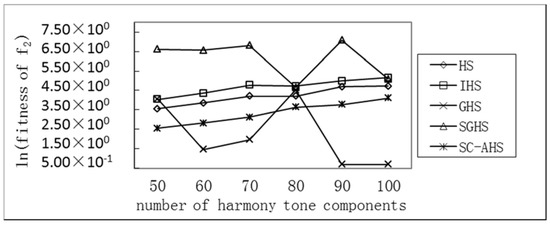
Figure 3. Comparison of the average optimum with different harmony tone components of the Rastrigrin function.

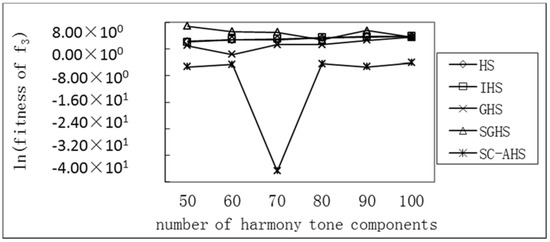
Figure 4. Comparison of the average optimum with different harmony tone components of the Griewank function.

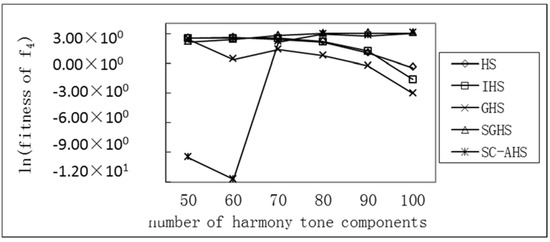
Figure 5. Comparison of the average optimum with different harmony tone components of the Ackley function.

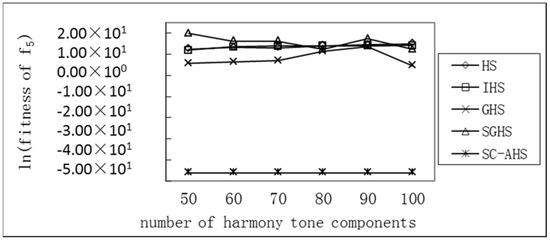
Figure 6. Comparison of the average optimum with different harmony tone components of the Rosenbrock function.

It can be seen from the above that for the uni-peak Sphere (f1) and Rosenbrock (f5) functions, the average optimal value of each algorithm has an increasing trend with the increase of the number of harmonic components, but the SC-AHS algorithm shows a decline. In the trend, the relative change rate of the SC-AHS algorithm in Table 3 is also the lowest. For the multi-peak Rastrigrin (f2), Griewank (f3), and Ackley (f4) functions, the average optimal value of the SC-AHS algorithm varies unstably. The average change value of the SC-AHS algorithm in Table 3 is the lowest among the algorithms. Therefore, the SC-AHS algorithm does not show a significant decrease in convergence accuracy with the increase in the number of tone components. That is, the algorithm still has good convergence performance in high-dimensional cases.

Test of the Average Optimum with Different Harmony Memory Sizes of Five Functions

The population diversity can be affected with the changes of the size of the harmony memory HMS. The range of parameters HMS is 20, 50, 100, 150, and 200. Other parameters are unchanged. The effect of the change in the size of the harmony memory on the optimization performance of each algorithm is shown in Table 4. The comparison of the average optimum value of each function changed with the size of the harmony memory as showed in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.

Table 4. Comparison of the optimal performance with different harmony memory sizes of five functions.

Functions	HMS	Average Optimal Value of HS	Average Optimal Value of IHS	Average Optimal Value of GHS	Average Optimal Value of SGHS	Average Optimal Value of SC-AHS
$f_1$	20	2.09 × 104	1.38 × 104	1.60 × 101	4.65 × 103	8.23 × 10−20
	50	2.59 × 103	5.33 × 103	4.00 × 100	3.07 × 103	2.14 × 10−27
	100	1.02 × 103	2.33 × 103	1.20 × 102	1.68 × 103	7.58 × 10−17
	150	8.41 × 102	1.04 × 103	4.80 × 102	6.58 × 102	4.29 × 10−25
	200	5.05 × 102	6.20 × 102	1.20 × 102	4.31 × 102	1.00 × 10−30
	Relative rate of change/%	9.76 × 101	9.55 × 101	6.50 × 102	9.07 × 101	1.00 × 102
	Average change	5.16 × 103	4.63 × 103	1.48 × 102	2.10 × 103	1.52 × 10−17
$f_2$	20	1.60 × 102	1.82 × 102	3.49 × 101	1.22 × 102	1.59 × 101
	50	7.11 × 101	9.51 × 101	1.16 × 100	1.72 × 102	7.96 × 100
	100	3.23 × 101	5.28 × 101	1.16 × 100	5.40 × 101	1.99 × 100
	150	2.70 × 101	2.87 × 101	2.04 × 100	2.73 × 102	9.95 × 10−1
	200	1.76 × 101	2.68 × 101	4.02 × 100	2.25 × 101	1.78 × 10−15
	Relative rate of change/%	8.91 × 101	8.53 × 101	8.85 × 101	8.15 × 101	1.00 × 102
	Average change	6.17 × 101	7.71 × 101	8.65 × 100	1.29 × 102	5.37 × 100
$f_3$	20	1.77 × 102	1.25 × 102	1.12 × 100	7.10 × 101	6.14 × 10−1
	50	4.32 × 101	5.19 × 101	1.60 × 100	3.30 × 101	2.46 × 10−2
	100	1.70 × 101	1.29 × 101	7.20 × 10−1	6.35 × 100	1.11 × 10−16
	150	6.50 × 100	1.01 × 101	1.92 × 10−1	5.19 × 101	2.22 × 10−2
	200	4.46 × 100	5.21 × 100	2.08 × 100	6.63 × 100	1.97 × 10−2
	Relative rate of change/%	9.75 × 101	9.58 × 101	8.57 × 101	9.07 × 101	9.68 × 101
	Average change	4.97 × 101	4.11 × 101	1.14 × 100	3.38 × 101	1.36 × 10−1
$f_4$	20	1.54 × 101	1.48 × 101	5.89 × 10−16	1.43 × 101	8.97 × 10−1
	50	1.30 × 101	1.24 × 101	5.89 × 10−16	9.69 × 100	8.96 × 10−1
	100	9.06 × 100	9.64 × 100	5.89 × 10−16	5.89 × 100	8.96 × 10−1
	150	6.05 × 100	6.22 × 100	5.89 × 10−16	5.89 × 100	4.16 × 10−5
	200	5.15 × 100	6.81 × 100	4.59 × 100	5.54 × 100	8.48 × 10−7
	Relative rate of change/%	6.66 × 101	5.41 × 101	7.80 × 1017	6.13 × 101	1.00 × 102
	Average change	9.73 × 100	9.98 × 100	9.19 × 10−1	8.27 × 100	5.38 × 10−1
$f_5$	20	1.57 × 107	4.96 × 107	3.00 × 101	1.09 × 106	4.36 × 10−2
	50	4.17 × 106	3.71 × 106	4.66 × 102	9.13 × 104	7.72 × 10−16
	100	2.14 × 105	5.21 × 105	3.76 × 102	7.31 × 104	1.00 × 10−20
	150	1.85 × 104	5.58 × 105	3.00 × 101	1.47 × 106	1.00 × 10−20
	200	1.08 × 104	1.05 × 105	4.66 × 102	1.67 × 104	1.00 × 10−20
	Relative rate of change/%	9.99 × 101	9.98 × 101	1.45 × 103	9.85 × 101	1.00 × 102
	Average change	4.01 × 106	1.09 × 107	2.73 × 102	5.49 × 105	8.72 × 10−3

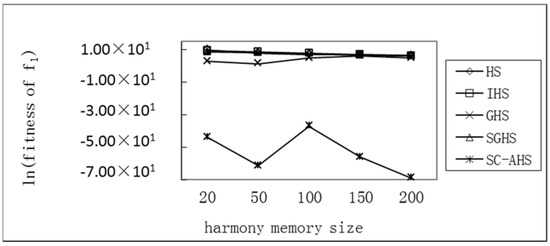
Figure 7. Comparison of the average optimum with different harmony memory sizes of the Sphere function.

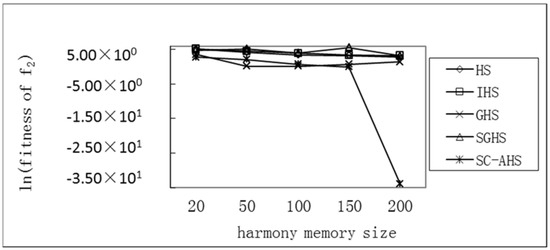
Figure 8. Comparison of the average optimum with different harmony memory sizes of the Rastrigrin function.

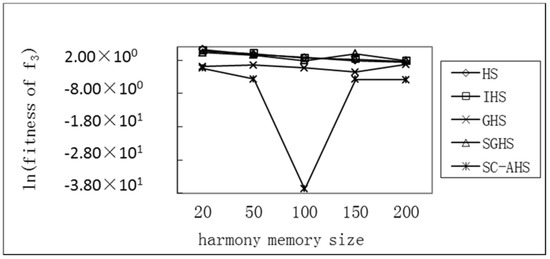
Figure 9. Comparison of the average optimum with different harmony memory sizes of the Griewank function.

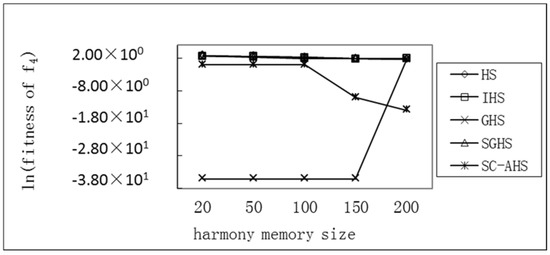
Figure 10. Comparison of the average optimum with different harmony memory sizes of the Ackley function.

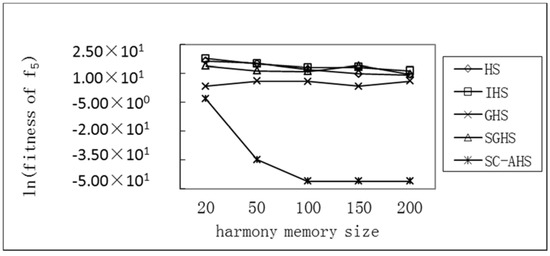
Figure 11. Comparison of the average optimum with different harmony memory sizes of the Rosenbrock function.

In Table 4, there is:

$$\begin{array}{l}Relativerateofchange\\ =\frac{\left|averageoptimalvalueof20fortheharmonymemory-averageoptimalvalueof200fortheharmonymemory\right|}{averageoptimalvalueof20fortheharmonymemory}\times 100\%\end{array}$$

(17)

$$Averagechange=\frac{{\sum }_{i=1}^{5}averageoptimalvalueofdifferentsizesofharmonymemories}{5}\times 100\%$$

(18)

It can be seen that for the single-peak Sphere (f1) and Rosenbrock (f5) functions and the multi-peak Rastrigrin (f2) function, the average value of each algorithm has an increasing trend with the increase of the size of the harmony memory, but the SC-AHS algorithm shows a significant downward trend. The relative change rate of the SC-AHS algorithm in Table 4 is higher than other algorithms, indicating that with the increase of the size of the harmony memory, the diversity of the population is maintained and the convergence accuracy is improved. For the multi-peak Grievenk (f3) and Ackley (f4) functions, the average optimal value of the SC-AHS algorithm is not stable. The average change value of the SC-AHS algorithm in Table 4 is the lowest among the algorithms, and the relative change rate of the algorithm is higher than other algorithms. Therefore, the SC-AHS algorithm increases the convergence accuracy of the algorithm with the increase of the size of the harmonic memory, and it has better convergence than other algorithms.

5.2.3. Test of SC-AHS Algorithm with Dynamic Parameters Experiment

The experiment is mainly to verify that the SC-AHS algorithm has fast convergence performance. The experiment still adopts the conditions of changing parameters, and still adopts two test methods, including varying the number of harmonic components and varying the harmonic memory size, HMS. The effect of changing the parameters under test on the convergence speed of the SC-AHS algorithm is studied. The average optimal value of each function and the number of evolutions are used as a measure of the performance of the SC-AHS algorithm.

Test of Average Optimum with Different Harmony Tone Components of the SC-AHS Algorithm

The range of the number of harmonic components, N, is from 50 to 100. The other parameters are unchanged. The effect of the change in the number of harmonic components on the convergence rate of the SC-AHS algorithm is shown in Table 5. The comparison of the change of the average optimum value and the sum of the tone components of each function is shown in Figure 12. It can be seen that with the increase in the number of tone components, there is no apparent upward trend in the average optimal value of the functions. Table 5 shows that the number of evolutions of the SC-AHS algorithm is less than 20,000 for single-peak Sphere (f1) and Rosenbrock (f5) functions, as well as multi-peak Grievenk function (f3), and the number of tone components is different, indicating that the SC-AHS algorithm still has a high convergence speed in the high-dimensional case.

Table 5. Influences of convergence performance with different harmony tone components of the SC-AHS algorithm.

Function	Optimize Performance	N = 50	N = 60	N = 70	N = 80	N = 90	N = 100
$f_1$	Average optimal value	9.62 × 10−19	2.49 × 10−21	3.34 × 10−17	1.00 × 10−18	5.78 × 10−17	2.57 × 10−25
	Evolution times/times	309	414	480	548	620	765
$f_2$	Average optimal value	1.29 × 101	1.69 × 101	2.29 × 101	3.78 × 101	4.38 × 101	6.07 × 101
	Evolution times/times	20,000	20,000	20,000	20,000	20,000	20,000
$f_3$	Average optimal value	4.93 × 10−3	9.86 × 10−3	1.11 × 10−16	1.23 × 10−2	4.93 × 10−3	1.72 × 10−2
	Evolution times/times	20,000	20,000	19,763	20,000	20,000	20,000
$f_4$	Average optimal value	7.10 × 10−5	7.73 × 10−6	8.51 × 100	1.88 × 101	1.56 × 101	2.08 × 101
	Evolution times/times	20,000	20,000	20,000	20,000	20,000	20,000
$f_5$	Average optimal value	1.00 × 10−20	1.00 × 10−20	1.00 × 10−20	1.00 × 10−20	1.00 × 10−20	1.00 × 10−20
	Evolution times/times	5292	6771	7802	9855	10,441	10,890

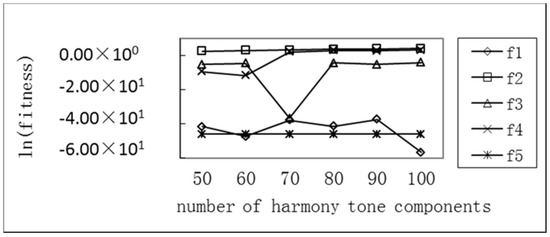
Figure 12. Comparison of the average optimum with different harmony tone components of five functions.

Test of Average Optimum with Different Harmony Memory Sizes of the SC-AHS Algorithm

The value range of the HMS memory size is also 20, 50, 100, 150, and 200, respectively, and the other parameter settings are unchanged. The effect of the change in the size of the harmony memory on the convergence rate of the SC-AHS algorithm is shown in Table 6. The comparison of the average optimum value of each function with the change of the size of the harmony memory is shown in Figure 13. It can be seen that, as the size of the harmonic memory increases, the average optimal value of each function has a more obvious downward trend. This is because the size of the harmonic memory increases, which increases the diversity of the population and the search performance of the algorithm. Table 6 shows that the number of SC-AHS evolutions is lower than 20,000 for single-peak Sphere (f1), Rosenbrock (f5), multi-peak Rastrigrin (f2), and Griewank (f3) functions. It shows that the SC-AHS algorithm has increased the convergence speed when the harmony memory is large.

Table 6. Comparisons of the convergence performance with different harmony memory sizes of the SC-AHS algorithm.

Function	Optimize Performance	HMS = 20	HMS = 50	HMS = 100	HMS = 150	HMS = 200
$f_1$	Average optimal value	8.23 × 10−20	2.14 × 10−27	7.58 × 10−17	4.29 × 10−25	1.00 × 10−30
	Evolution times/times	1606	280	203	219	209
$f_2$	Average optimal value	1.59 × 101	7.96 × 100	1.99 × 100	9.95 × 10−1	1.78 × 10−15
	Evolution times/times	20,000	20,000	20,000	20,000	18,361
$f_3$	Average optimal value	3.06 × 10−2	2.46 × 10−2	1.11 × 10−16	2.22 × 10−2	1.97 × 10−2
	Evolution times/times	20,000	20,000	11,936	20,000	20,000
$f_4$	Average optimal value	2.27 × 10−5	1.60 × 10−8	3.93 × 10−9	2.87 × 10−10	1.31 × 10−11
	Evolution times/times	20,000	20,000	20,000	20,000	20,000
$f_5$	Average optimal value	2.43 × 10−3	4.33 × 10−17	1.00 × 10−20	1.00 × 10−20	1.00 × 10−20
	Evolution times/times	20,000	20,000	4296	3932	3346

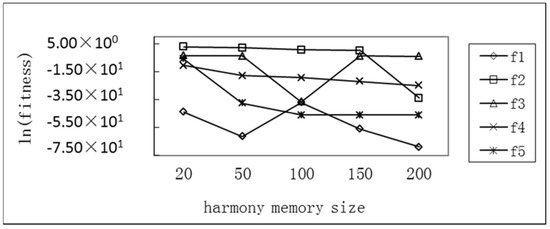
Figure 13. Comparison of the average optimum with different harmony memory sizes of five functions.

5.3. Apple Image Segmentation Experiment

The experiment uses a single apple image as input, and takes the ARMM-AHS method proposed in this paper as the threshold search strategy of images to perform apple image segmentation experiments. The maximum class variance function and the maximum entropy function are used as the two objective fitness functions of the multi-objective optimization method. The main interface of the apple image segmentation program developed with Matlab2012 GUI is shown in Figure 14.

Figure 14. Main interface of the apple image segmentation program.

Five segmentation indicators based on the image recognition rate, such as the segmentation rate (R_Seg), fruit segmentation rate (R_App), branch segmentation rate (R_Bra), segmentation success rate (R_Suc), and missing rate (R_Mis), are respectively defined in this paper. The equations of the five indicators are defined in Equations (19)–(23). Among them, $N_{to}$ is the total number of segmentation targets (including the number of fruits and the number of branches), $N_{po}$ is the total number of targets obtained by manual visualization (including the number of fruits and the number of branches), $N_a$ is the total number of segmentation fruits, $N_{pa}$ is the total number of fruits obtained by manual visualization, and $N_l$ is the total number of segmentation branches. Due to the effects of the illumination condition and interference factors, the experiment sets the fruit size that is greater than 1/4 that of complete fruit as a fruit statistics value, and sets the branch length that is greater than 1/4 that of a complete branch as a branch of the statistics value, and fruits that are too small in the perspective of the image are not counted in the statistics values.

$$R_{Seg}=\frac{N_{to}}{N_{po}}\times 100\%$$

(19)

$$R_{App}=\frac{N_a}{N_{to}}\times 100\%$$

(20)

$$R_{Bra}=\frac{N_l}{N_{to}}\times 100\%=R_{App}=\frac{N_{to}-N_a}{N_{to}}\times 100\%$$

(21)

$$R_{Suc}=\frac{N_a}{N_{pa}}\times 100\%$$

(22)

$$R_{Mis}=\frac{N_{pa}-N_a}{N_{pa}}\times 100\%$$

(23)

Figure 15, Figure 16 and Figure 17 show the comparison of the results of image segmentation under three illumination conditions, including direct sunlight with strong illumination, backlighting with strong illumination, and backlighting with medium illumination. The figures show the original image, the preprocessed image, the Pareto optimal frontier fitness curve using the SC-AHS optimization algorithm, the ARMM-AHS method segmentation result, and the OTSU algorithm segmentation result. Figure 15, Figure 16 and Figure 17 show that the multi-objective optimization method can be used to obtain a set of non-dominated threshold solutions, which can provide more opportunities to select thresholds. The thresholds of the non-dominated solution set under six illumination conditions using the ARMM-AHS method is shown in Table 7. The number of non-dominated solutions under six illumination conditions are different.

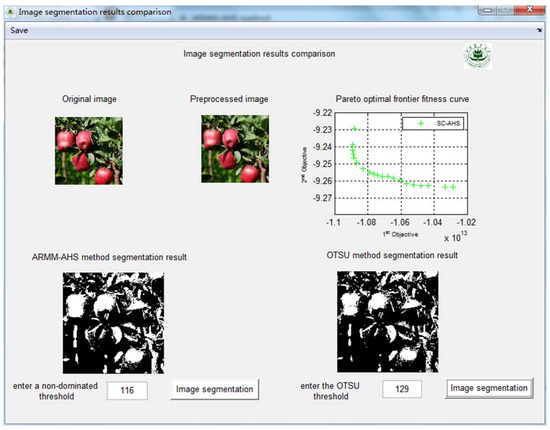
Figure 15. Comparison of the results of image segmentation under direct sunlight under the strong illumination condition.

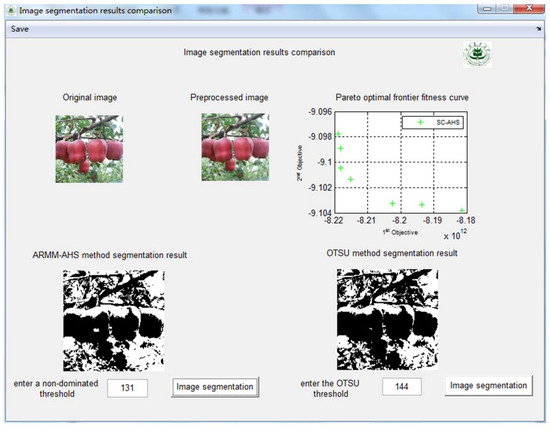
Figure 16. Comparison of the results of image segmentation under backlighting under the strong illumination condition.

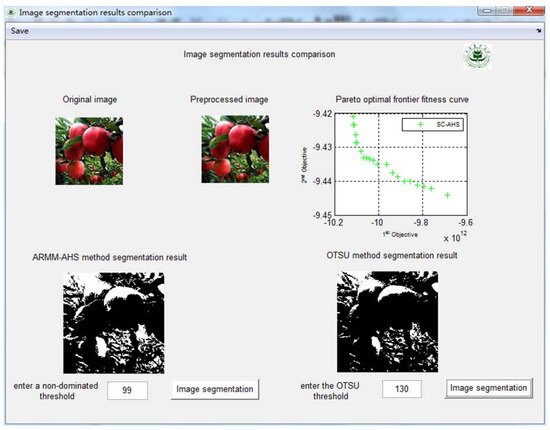
Figure 17. Comparison of the results of image segmentation under backlighting under the medium illumination condition.

Table 7. Thresholds of the non-dominated solution set under six illumination conditions using the ARMM-AHS method.

Direct Sunlight with Strong	Direct Sunlight with Medium	Direct Sunlight with Weak	Backlighting with Strong	Backlighting with Medium	Backlighting with Weak
Non-Dominated Solution Number: 54	Non-Dominated Solution Number: 36	Non-Dominated Solution Number: 28	Non-Dominated Solution Number: 18	Non-Dominated Solution Number: 54	Non-Dominated Solution Number: 62
77	121	130	131	107	146
116	121	130	131	99	152
77	114	130	131	107	129
77	121	130	131	126	113
77	121	130	131	107	152
116	121	130	131	126	152
116	131	130	131	126	152
77	121	130	131	126	115
116	121	130	131	107	115
116	121	130	131	107	115
116	121	130	131	106	113
77	121	130	131	99	113
77	121	130	172	99	113
77	131	130	228	107	122
116	114	130	66	99	152
77	121	130	221	126	113
116	131	130	206	99	113
77	121	130	15	106	113
116	114	130		107	120
77	121	130		106	129
116	121	130		106	120
77	121	46		99	129
77	114	133		106	146
77	121	85		106	129
77	121	72		126	120
77	121	146		107	120
77	114	55		126	152
77	149	45		107	113
77	114			99	152
116	178			126	129
116	243			99	146
116	39			99	115
116	198			126	122
116	66			126	120
77	166			126	146
116	97			126	122
77				107	122
77				126	120
77				107	152
77				106	122
77				106	120
116				126	122
116				106	146
153				168	120
69				70	146
231				230	120
205				98	146
146				106	122
36				159	113
33				163	122
221				70	202
21				10	58
163				208	47
203				91	122
					214
					28
					129
					209
					181
					204
					248
					172

The comparison of the thresholds selected from the non-dominated solution set under six illumination conditions with OTSU thresholds is shown in Table 8. The effect of apple image segmentation under six lighting conditions is shown in Table 9. The data in Table 9 shows that the segmentation rate and segmentation success rate of the direct sunlight with strong illumination and backlighting with strong illumination all reach 100%. When the segmentation result includes branches, the branch segmentation rate and the missing rate are equivalent. This shows that the branches are well segmented and achieve the desired segmentation effect.

Table 8. Comparison of thresholds selected from the non-dominated solution set under six illumination conditions with OTSU thresholds.

Illumination Condition	Select Threshold by SC-AHS	OTSU Threshold
Direct sunlight with strong	116	129
Direct sunlight with medium	121	129
Direct sunlight with weak	130	133
Backlighting with strong	131	144
Backlighting with medium	99	130
Backlighting with weak	113	130

Table 9. Apple image segmentation effect comparison under six illumination conditions.

Illumination Condition	RSeg	RApp	RBra	RSuc	RMis (%)
Direct sunlight with strong	100.0	85.7	14.3	100.0	0.0
Direct sunlight with medium	80.0	75.0	25.0	75.0	25.0
Direct sunlight with weak	80.0	100.0	0.0	80.0	20.0
Backlighting with strong	100.0	83.3	16.7	100.0	0.0
Backlighting with medium	85.7	83.3	16.7	83.3	16.7
Backlighting with weak	66.7	100.0	0.0	66.7	33.3

6. Conclusions

This paper proposes a new adaptive harmony search algorithm with simulation and creation, which expands the search space to maintain the diversity of the solution and accelerates the convergence of the algorithm compared with HS, HIS, GHS, and SGHS algorithms. An apple image recognition multi-objective method based on the adaptive harmony search algorithm with simulation and creation is proposed. The multi-objective optimization recognition method transforms the apple image recognition problem collected in the natural scene into a multi-objective optimization problem, and uses the new adaptive harmony search algorithm with simulation and creation as the image threshold search strategy. The proposed multi-objective optimization recognition method obtains a set of non-dominated threshold solution sets, which is more flexible than the OTSU algorithm in the opportunity of threshold selection. The selected threshold has better adaptive characteristics and has good image segmentation results.