Apple Image Recognition Multi-Objective Method Based on the Adaptive Harmony Search Algorithm with Simulation and Creation
Abstract
1. Introduction
2. Theory Basis
2.1. Threshold Segmentation Principle of the OTSU Algorithm
2.2. Maximum Entropy Segmentation Principle
3. Adaptive Harmony Search Algorithm with Simulation and Creation
3.1. Theory Basis
3.1.1. Adaptive Factor of Harmony Tone
3.1.2. Harmony Tone Simulation Operator
3.1.3. Harmony Tone Creation Operator
3.2. Adaptive Evolution Theorem with Simulation and Creation
3.3. SC-AHS Algorithm Process
| Algorithm 1. SC-AHS |
| Input: the maximum number of evolutions , the size of the harmony memory HMS, the number of tone component N. |
| Output: global optimal harmony . |
| Step1: Randomly generate initial harmony individuals which number is HMS, marked as . The harmony memory is initialized according to Equation (1). The fitness of is . |
| Step2: Each tone component of each harmony is updated. |
| Begin |
| Sort each harmony by fitness in descending order to determine , and . |
| For () |
| Begin |
| Calculated according to Equation (5) |
| For () |
| Update according to Equation (6) to perform harmony tone simulation |
| End |
| if () |
| For ()
|
| End |
| else |
| For () |
| Update according to Equation (7) to perform harmony tone creation |
| End |
| If () |
| For ()
|
| End |
| else |
| For () |
| Randomly generate harmony tone according to Equation (8). |
| End |
| End |
| End |
| Step3: Determine if the number of evolutions has been reached . If not, go to Step 2. Otherwise, the algorithm stops and outputs . |
3.4. Efficiency Analysis of SC-AHS
4. Apple Image Recognition Multi-Objective Method Based on an Adaptive Harmony Search Algorithm with Simulation and Creation
4.1. Mathematical Problem Description of the Multi-Objective Optimization Recognition Method
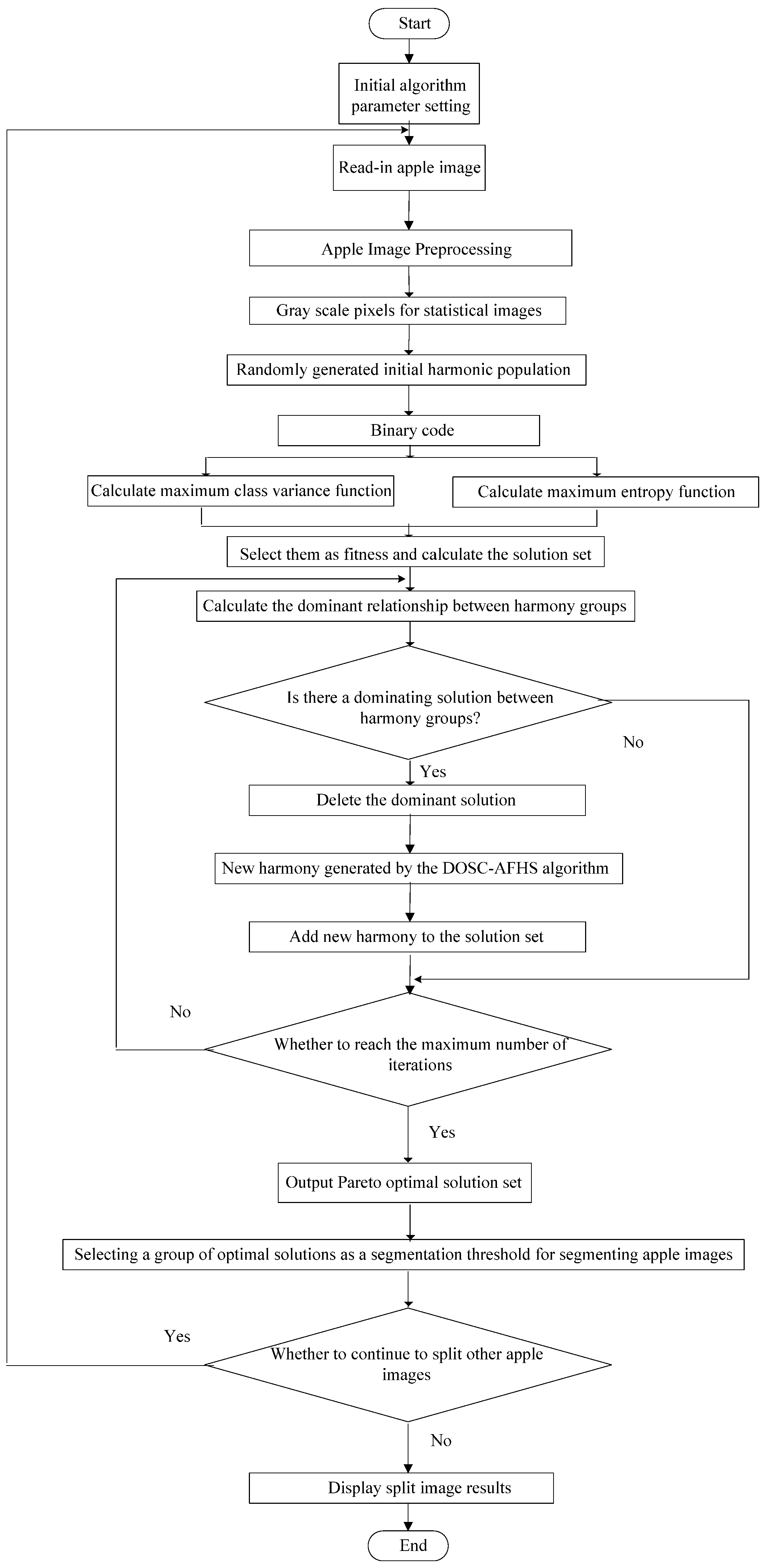
4.2. Process of the Apple Image Recognition Multi-Objective Method Based on an Adaptive Harmony Search Algorithm with Simulation and Creation
5. Experiment Design and Results Analysis
5.1. Experiment Design
5.2. Benchmark Function Comparison Experiment and Result Analysis
5.2.1. Fixed Parameters Experiment
5.2.2. Dynamic Parameters Experiment
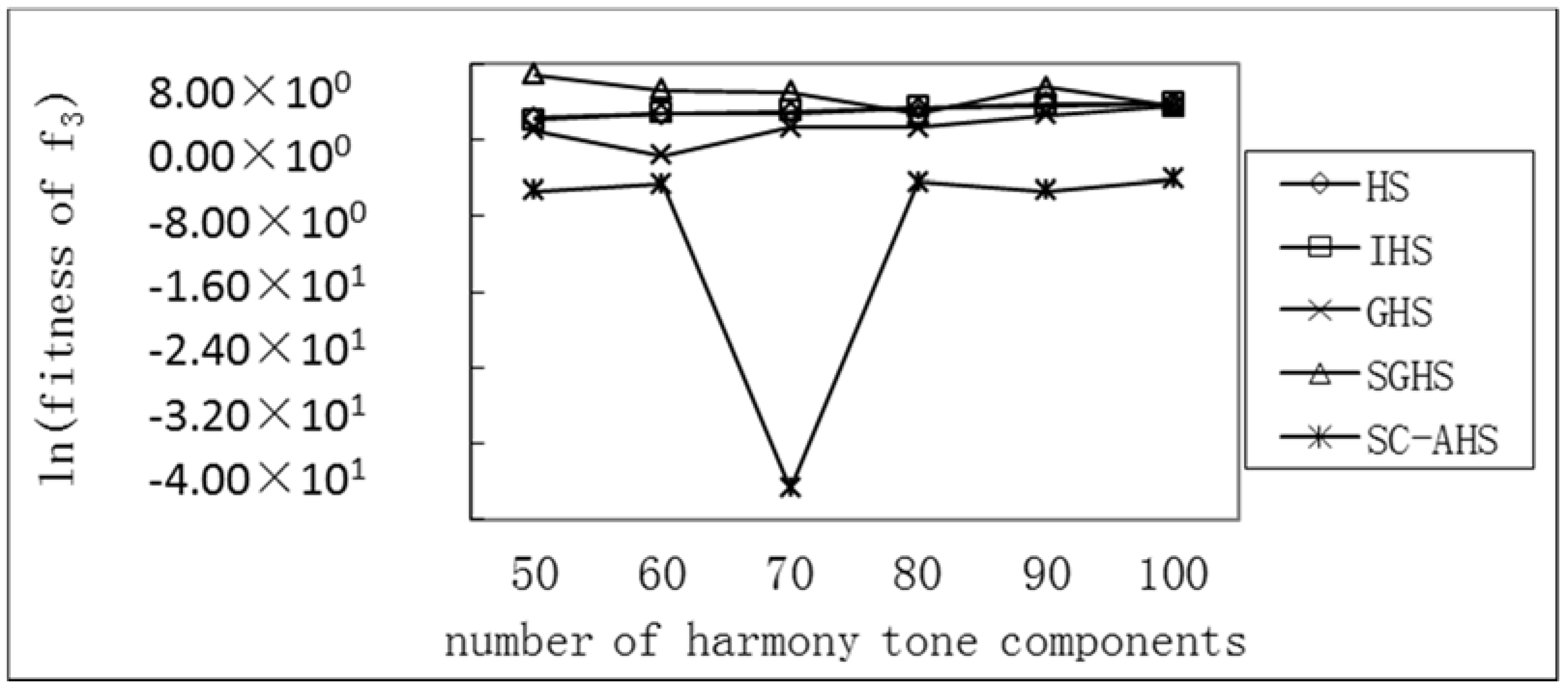
Test of Average Optimum with Different Harmony Tone Components of Five Functions
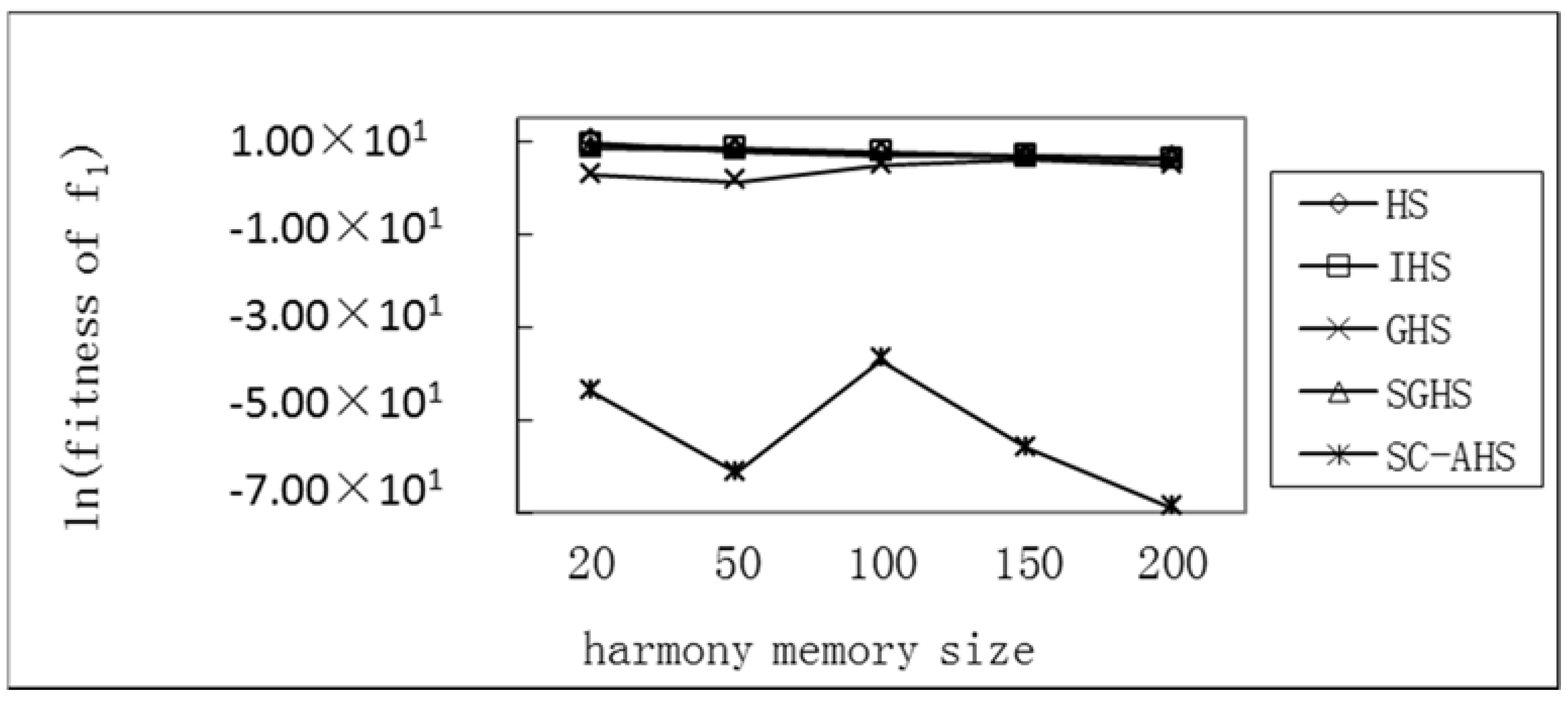
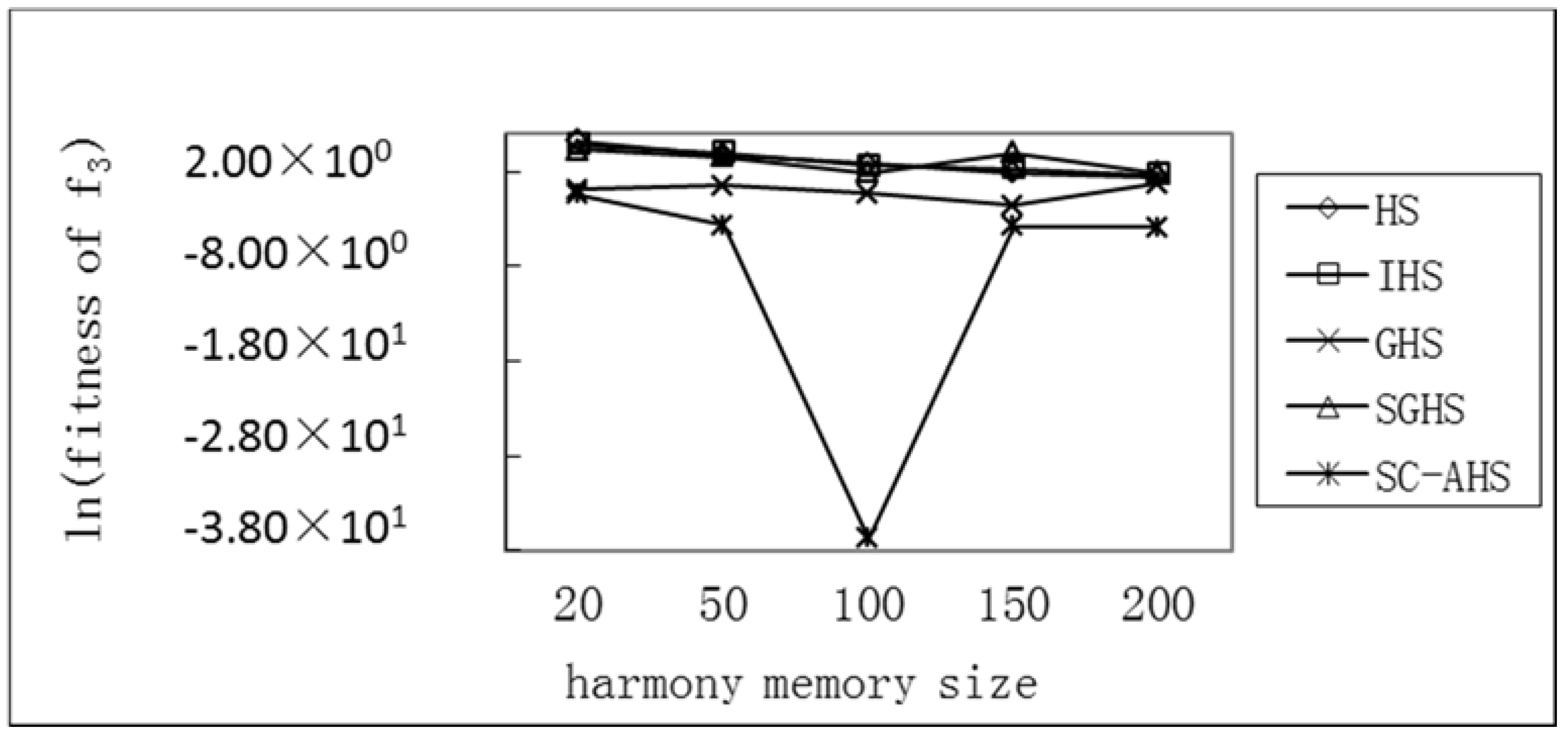
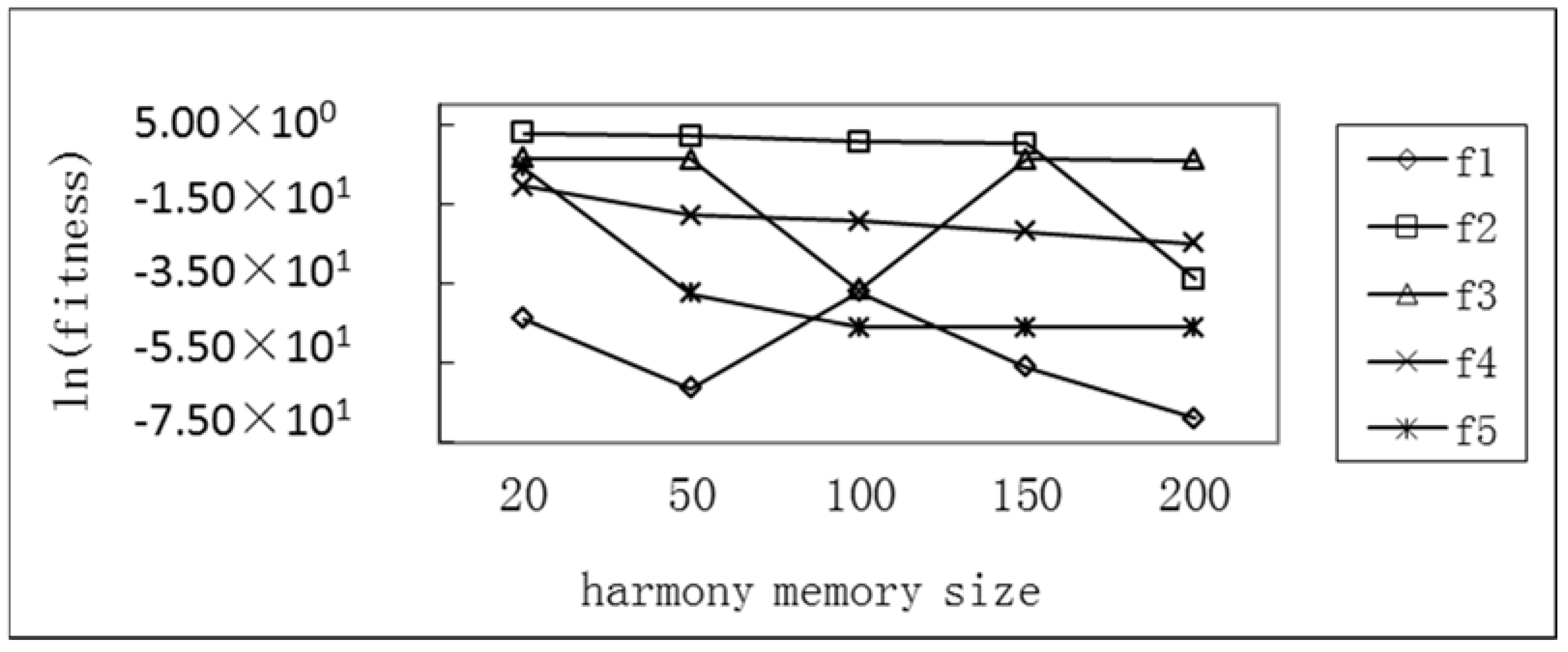
Test of the Average Optimum with Different Harmony Memory Sizes of Five Functions
5.2.3. Test of SC-AHS Algorithm with Dynamic Parameters Experiment
Test of Average Optimum with Different Harmony Tone Components of the SC-AHS Algorithm
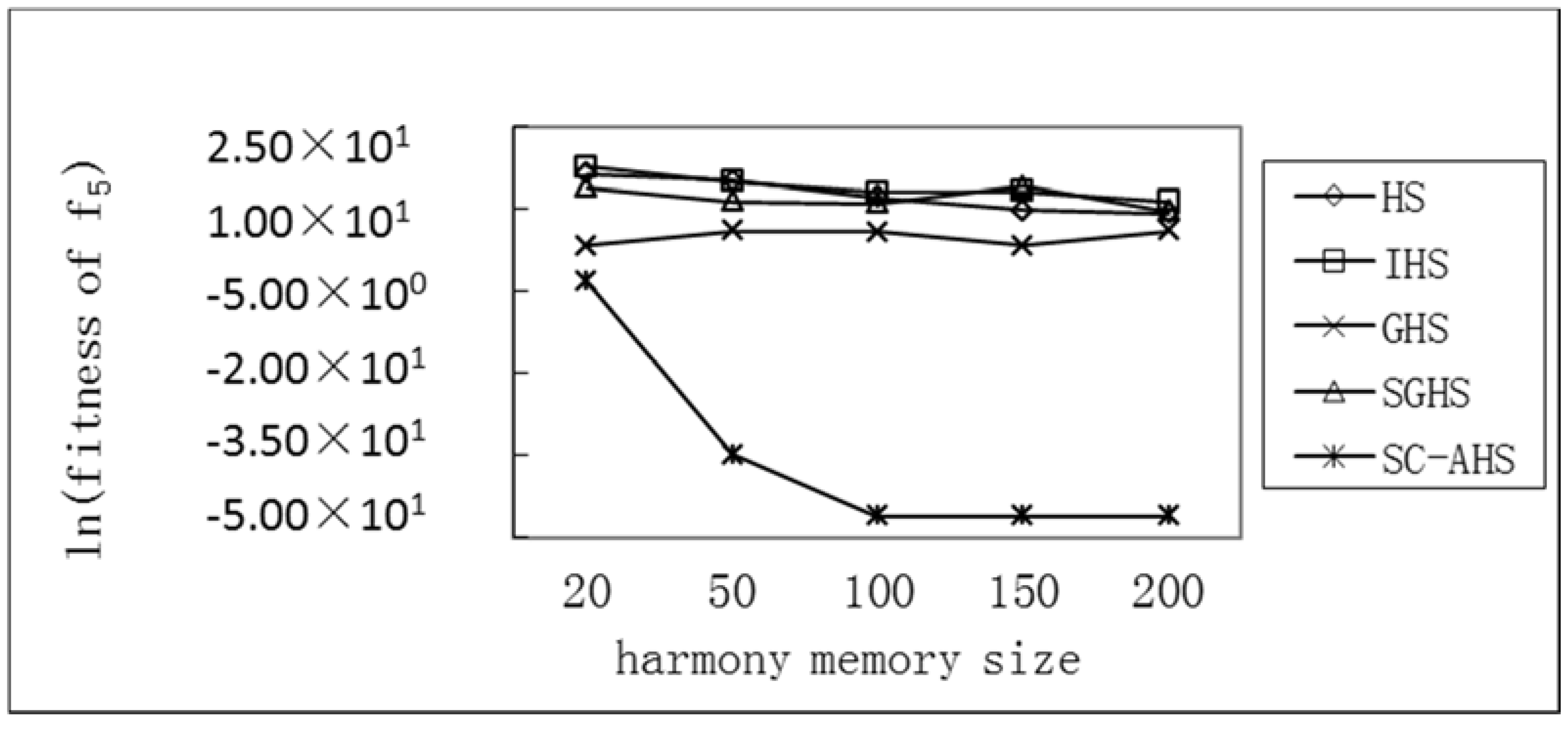
Test of Average Optimum with Different Harmony Memory Sizes of the SC-AHS Algorithm
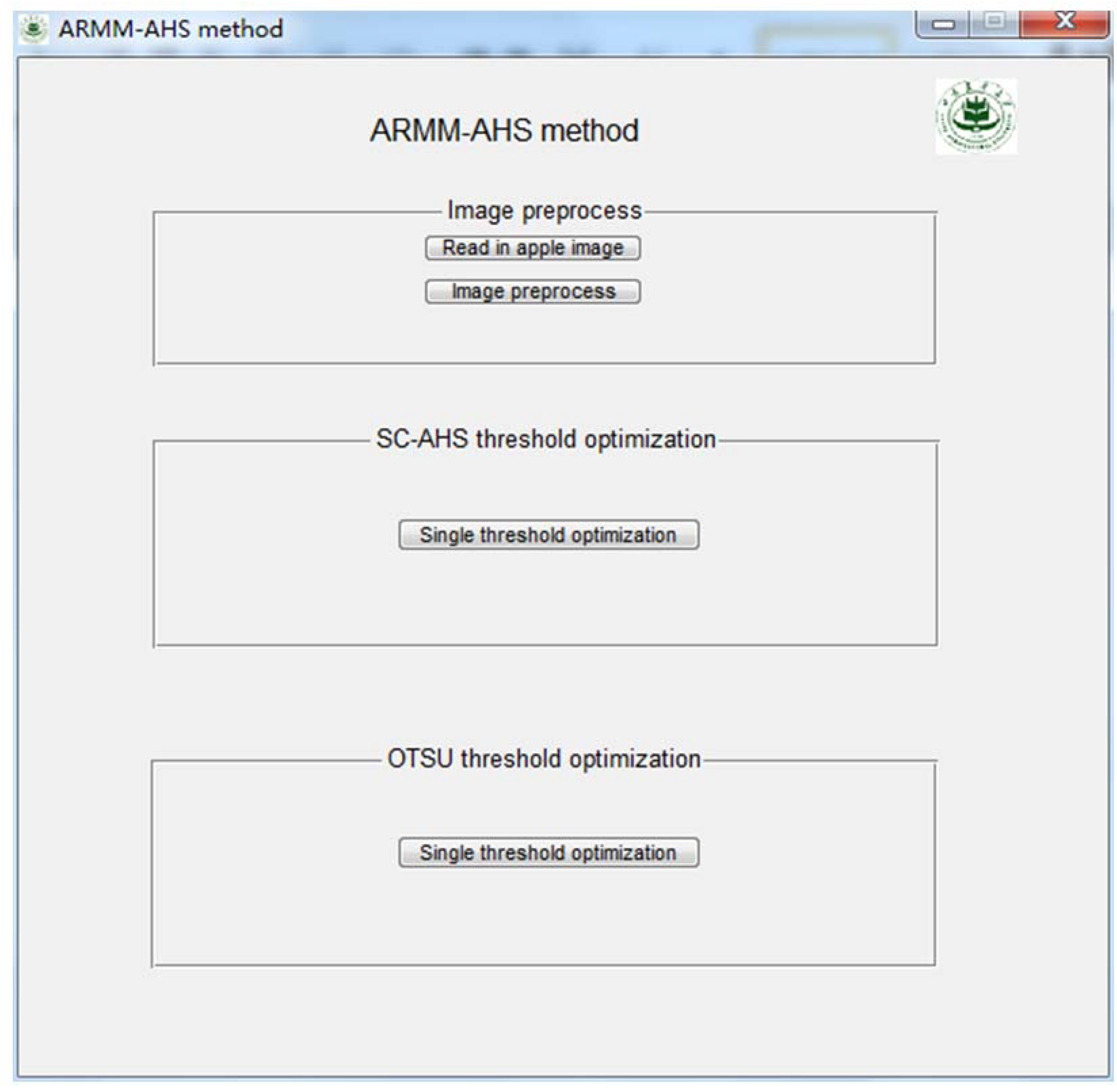
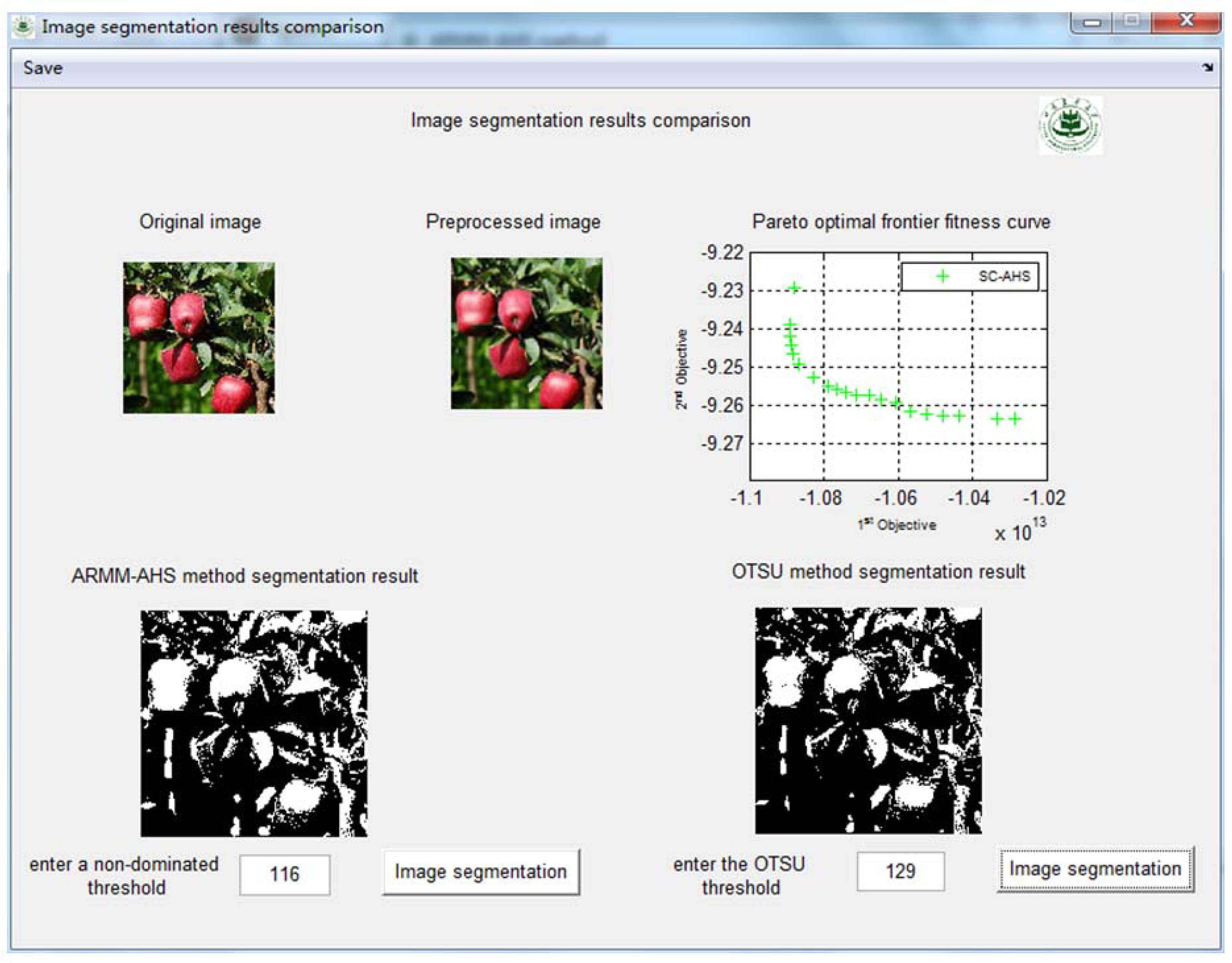
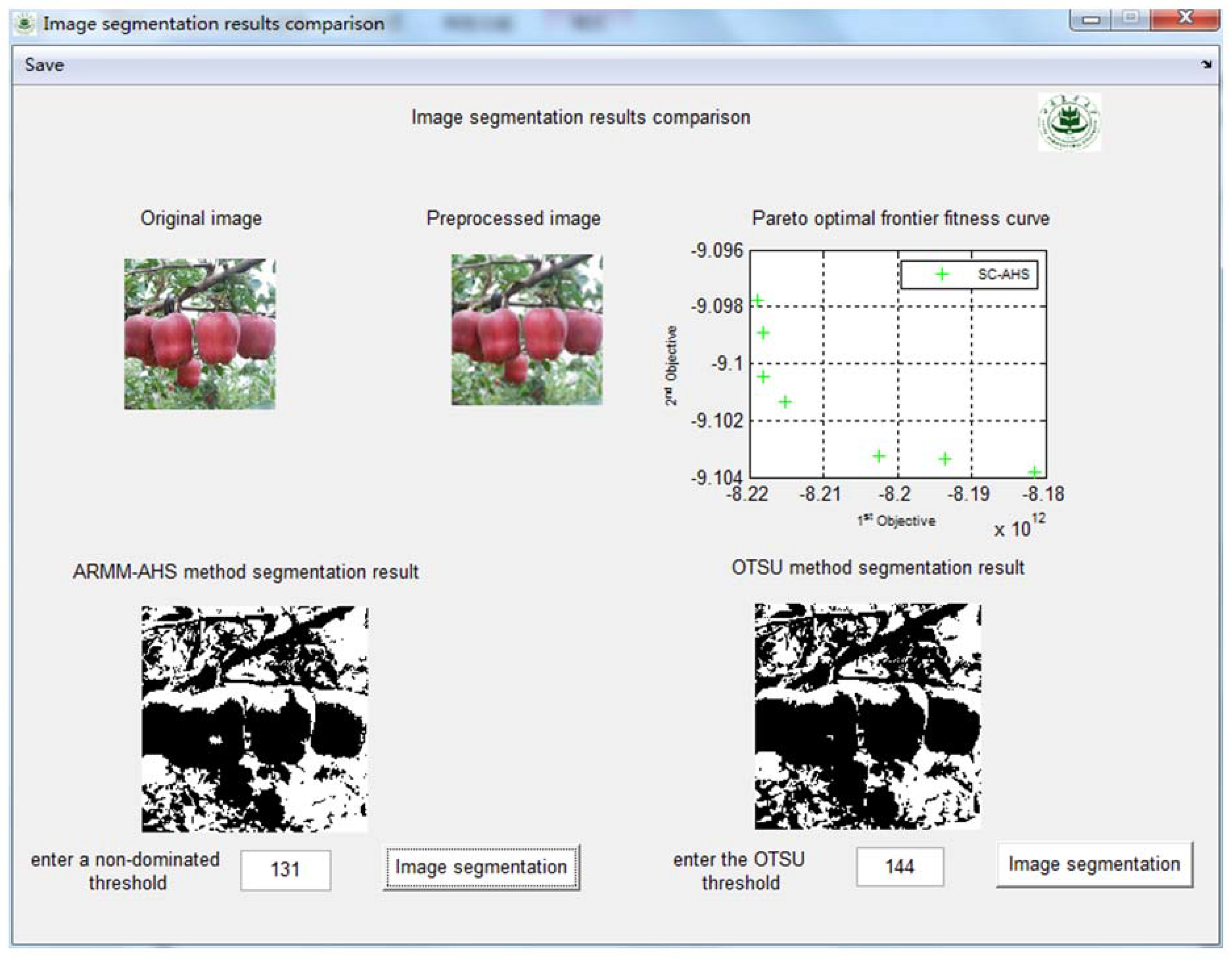
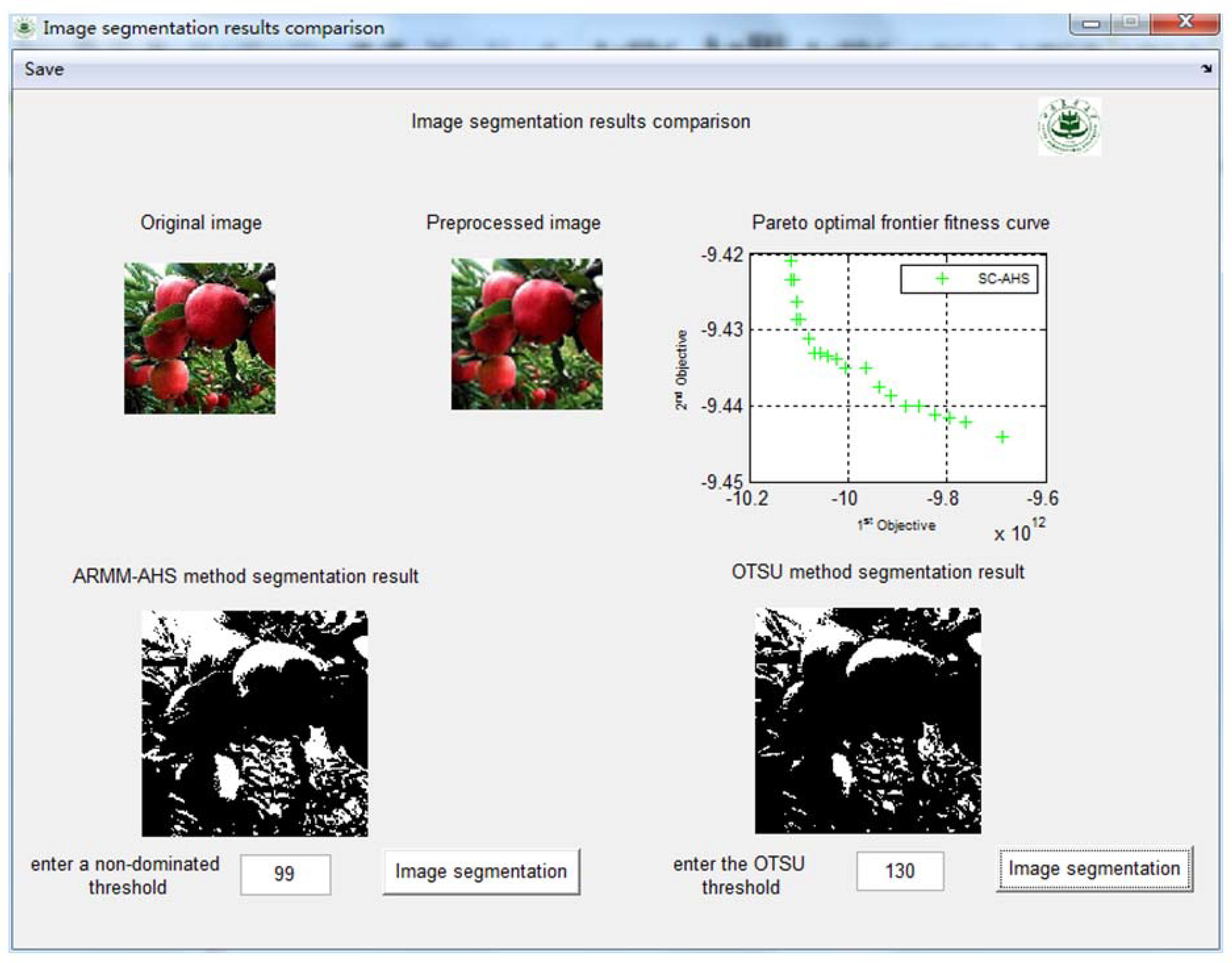
5.3. Apple Image Segmentation Experiment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zong, W.G.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Ouyang, H.B.; Xia, H.G.; Wang, Q.; Ma, G. Discrete global harmony search algorithm for 0–1 knapsack problems. J. Guangzhou Univ. (Nat. Sci. Ed.) 2018, 17, 64–70. [Google Scholar]
- Xie, L.Z.; Chen, Y.J.; Kang, L.; Zhang, Q.; Liang, X.J. Design of MIMO radar orthogonal polyphone code based on genetic harmony algorithm. Electron. Opt. Control. 2018, 1, 1–7. [Google Scholar]
- Zhu, F.; Liu, J.S.; Xie, L.L. Local Search Technique Fusion of Harmony Search Algorithm. Comput. Eng. Des. 2017, 38, 1541–1546. [Google Scholar]
- Wu, C.L.; Huang, S.; Wang, Y.; Ji, Z.C. Improved Harmony Search Algorithm in Application of Vulcanization Workshop Scheduling. J. Syst. Simul. 2017, 29, 630–638. [Google Scholar]
- Peng, H.; Wang, Z.X. An Improved Adaptive Parameters Harmony Search Algorithm. Microelectron. Comput. 2016, 33, 38–41. [Google Scholar]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Han, H.Y.; Pan, Q.K.; Liang, J. Application of improved harmony search algorithm in function optimization. Comput. Eng. 2010, 36, 245–247. [Google Scholar]
- Zhang, T.; Xu, X.Q.; Ran, H.J. Multi-objective Optimal Allocation of FACTS Devices Based on Improved Differential Evolution Harmony Search Algorithm. Proc. CSEE 2018, 38, 727–734. [Google Scholar]
- LIU, L.; LIU, X.B. Improved Multi-objective Harmony Search Algorithm for Single Machine Scheduling in Sequence Dependent Setup Environment. Comput. Eng. Appl. 2013, 49, 25–29. [Google Scholar]
- Hosen, M.A.; Khosravi, A.; Nahavandi, S.; Creighton, D. Improving the quality of prediction intervals through optimal aggregation. IEEE Trans. Ind. Electron. 2015, 62, 4420–4429. [Google Scholar] [CrossRef]
- Precup, R.E.; David, R.C.; Petriu, E.M. Grey wolf optimizer algorithm-based tuning of fuzzy control systems with reduced parametric sensitivity. IEEE Trans. Ind. Electron. 2017, 64, 527–534. [Google Scholar] [CrossRef]
- Saadat, J.; Moallem, P.; Koofigar, H. Training echo state neural network using harmony search algorithm. Int. J. Artif. Intell. 2017, 15, 163–179. [Google Scholar]
- Vrkalovic, S.; Teban, T.A.; Borlea, L.D. Stable Takagi-Sugeno fuzzy control designed by optimization. Int. J. Artif. Intell. 2017, 15, 17–29. [Google Scholar]
- Fourie, J.; Mills, S.; Green, R. Harmony filter: A robust visual tracking system using the improved harmony search algorithm. Image Vis. Comput. 2010, 28, 1702–1716. [Google Scholar] [CrossRef]
- Alia, O.M.; Mandava, R.; Aziz, M.E. A hybrid harmony search algorithm for MRI brain segmentation. Evol. Intell. 2011, 4, 31–49. [Google Scholar] [CrossRef]
- Fourie, J. Robust circle detection using Harmony Search. J. Optim. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Moon, Y.Y.; Zong, W.G.; Han, G.T. Vanishing point detection for self-driving car using harmony search algorithm. Swarm Evol. Comput. 2018, 41, 111–119. [Google Scholar] [CrossRef]
- Zong, W.G. Novel Derivative of Harmony Search Algorithm for Discrete Design Variables. Appl. Math. Comput. 2008, 199, 223–230. [Google Scholar]
- Das, S.; Mukhopadhyay, A.; Roy, A.; Abraham, A.; Panigrahi, B.K. Exploratory Power of the Harmony Search Algorithm: Analysis and Improvements for Global Numerical Optimization. IEEE Trans. Syst. Man Cybern. 2011, 41, 89–106. [Google Scholar] [CrossRef] [PubMed]
- Saka, M.P.; Hasançebi, O.; Zong, W.G. Metaheuristics in Structural Optimization and Discussions on Harmony Search Algorithm. Swarm Evol. Comput. 2016, 28, 88–97. [Google Scholar] [CrossRef]
- Hasançebi, O.; Erdal, F.; Saka, M.P. Adaptive Harmony Search Method for Structural Optimization. J. Struct. Eng. 2010, 136, 419–431. [Google Scholar] [CrossRef]
- Zong, W.G.; Sim, K.B. Parameter-Setting-Free Harmony Search Algorithm. Appl. Math. Comput. 2010, 217, 3881–3889. [Google Scholar]
- Pan, Q.K.; Suganthan, P.N.; Tasgetiren, M.F.; Liang, J.J. A self-adaptive global best harmony search algorithm for continuous optimization problems. Appl. Math. Comput. 2010, 216, 830–848. [Google Scholar] [CrossRef]
- Bao, X.M.; Wang, Y.M. Apple image segmentation based on the minimum error Bayes decision. Trans. Chin. Soc. Agric. Eng. 2006, 22, 122–124. [Google Scholar]
- Qian, J.P.; Yang, X.T.; Wu, X.M.; Chen, M.X.; Wu, B.G. Mature apple recognition based on hybrid color space in natural scene. Trans. Chin. Soc. Agric. Eng. 2012, 28, 137–142. [Google Scholar]
- Lu, B.B.; Jia, Z.H.; He, D. Remote-Sensing Image Segmentation Method based on Improved OTSU and Shuffled Frog-Leaping Algorithm. Comput. Appl. Softw. 2011, 28, 77–79. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Zhao, F.; Zheng, Y.; Liu, H.Q.; Wang, J. Multi-population cooperation-based multi-objective evolutionary algorithm for adaptive thresholding image segmentation. Appl. Res. Comput. 2018, 35, 1858–1862. [Google Scholar]
- Li, M.; Cao, X.L.; Hu, W.J. Optimal multi-objective clustering routing protocol based on harmony search algorithm for wireless sensor networks. Chin. J. Sci. Instrum. 2014, 35, 162–168. [Google Scholar]
- Dong, J.S.; Wang, W.Z.; Liu, W.W. Urban One-way traffic optimization based on multi-objective harmony search approach. J. Univ. Shanghai Sci. Technol. 2014, 36, 141–146. [Google Scholar]
- Li, Z.; Zhang, Y.; Bao, Y.K.; Guo, C.X.; Wang, W.; Xie, Y.Z. Multi-objective distribution network reconfiguration based on system homogeneity. Power Syst. Prot. Control. 2016, 44, 69–75. [Google Scholar]
- Zong, W.G. Multiobjective Optimization of Time-Cost Trade-Off Using Harmony Search. J. Constr. Eng. Manag. 2010, 136, 711–716. [Google Scholar]
- Fesanghary, M.; Asadi, S.; Zong, W.G. Design of low-emission and energy-efficient residential buildings using a multi-objective optimization algorithm. Build. Environ. 2012, 49, 245–250. [Google Scholar] [CrossRef]
- Zong, W.G. Multiobjective optimization of water distribution networks using fuzzy theory and harmony search. Water 2015, 7, 3613–3625. [Google Scholar]
- Shi, X.D.; Gao, Y.L. Improved Bird Swarm Optimization Algorithm. J. Chongqing Univ. Technol. (Nat. Sci.) 2018, 4, 177–185. [Google Scholar]
- Wang, L.G.; Gong, Y.X. A Fast Shuffled Frog Leaping Algorithm. In Proceedings of the 9th International Conference on Natural Computation (ICNC 2013), Shenyang, China, 23–25 July 2013; pp. 369–373. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Wang, L. Intelligent Optimization Algorithms and Applications; Tsinghua University Press: Beijing, China, 2004; pp. 2–6. ISBN 9787302044994. [Google Scholar]
- Omran, M.G.H.; Mahdavi, M. Global-best harmony search. Appl. Math. Comput. 2008, 198, 634–656. [Google Scholar] [CrossRef]
- Han, J.Y.; Liu, C.Z.; Wang, L.G. Dynamic Double Subgroups Cooperative Fruit Fly Optimization Algorithm. Parttern Recognit. Artif. Intell. 2013, 26, 1057–1067. [Google Scholar]







| Function | Name | Peak Value | Dimension | Search Cope | Theoretical Optimal Value | Target Accuracy |
|---|---|---|---|---|---|---|
| f1 | Sphere | unimodal | 30 | [−100,100] | 0 | 10−15 |
| f2 | Rastrigrin | multimodal | 30 | [−5.12,5.12] | 0 | 10−2 |
| f3 | Griewank | multimodal | 30 | [−600,600] | 0 | 10−2 |
| f4 | Ackley | multimodal | 30 | [−32,32] | 0 | 10−6 |
| f5 | Rosenbrock | unimodal | 30 | [−30,30] | 0 | 10−15 |
| Algorithm | Optimization Performance | |||||
|---|---|---|---|---|---|---|
| HS | Optimum | 5.07 × 102 | 1.76 × 101 | 4.47 × 100 | 5.18 × 100 | 1.13 × 104 |
| Standard deviation | 1.36 × 100 | 9.17 × 10−2 | 4.89 × 10−3 | 1.88 × 10−2 | 3.06 × 102 | |
| IHS | Optimum | 3.80 × 102 | 2.83 × 101 | 7.62 × 100 | 6.10 × 100 | 4.49 × 104 |
| Standard deviation | 6.12 × 10−3 | 6.81 × 10−1 | 8.60 × 10−6 | 1.76 × 10−3 | 2.26 × 101 | |
| GHS | Optimum | 1.20 × 102 | 3.62 × 10−4 | 0.00 × 100 | 5.89 × 10−16 | 3.00 × 101 |
| Standard deviation | 9.19 × 10−2 | 4.70 × 10−2 | 6.11 × 10−4 | 4.90 × 10−29 | 3.33 × 100 | |
| SGHS | Optimum | 2.47 × 102 | 2.98 × 101 | 5.92 × 100 | 5.62 × 100 | 1.89 × 104 |
| Standard deviation | 8.50 × 10−12 | 1.97 × 10−1 | 2.67 × 10−5 | 6.89 × 10−4 | 1.27 × 101 | |
| DOSC-AFHS | Optimum | 0.00 × 100 | 0.00 × 100 | 1.97 × 10−2 | 3.27 × 10−6 | 0.00 × 100 |
| Standard deviation | 0.00 × 100 | 4.27 × 10−1 | 1.02 × 10−15 | 2.72 × 10−5 | 0.00 × 100 |
| Functions | N | Average Optimal Value of HS | Average Optimal Value of IHS | Average Optimal Value of GHS | Average Optimal Value of SGHS | Average Optimal Value of SC-AHS |
|---|---|---|---|---|---|---|
| 50 | 1.29 × 103 | 9.48 × 102 | 2.00 × 102 | 1.17 × 103 | 9.62 × 10−19 | |
| 60 | 1.35 × 103 | 1.96 × 103 | 2.40 × 102 | 1.09 × 103 | 2.49 × 10−21 | |
| 70 | 1.63 × 103 | 1.92 × 103 | 1.12 × 103 | 3.59 × 103 | 3.34 × 10−17 | |
| 80 | 2.67 × 103 | 2.82 × 103 | 3.20 × 102 | 1.82 × 104 | 1.00 × 10−18 | |
| 90 | 4.04 × 103 | 4.49 × 103 | 3.20 × 101 | 2.33 × 104 | 5.78 × 10−17 | |
| 100 | 5.83 × 103 | 6.08 × 103 | 3.60 × 103 | 3.59 × 104 | 2.57 × 10−25 | |
| Relative rate of change/% | 3.52 × 102 | 5.42 × 102 | 1.70 × 103 | 2.97 × 103 | 1.00 × 102 | |
| Average change | 2.80 × 103 | 3.04 × 103 | 9.19 × 102 | 1.39 × 104 | 1.55 × 10−17 | |
| 50 | 3.50 × 101 | 5.73 × 101 | 5.81 × 101 | 7.38 × 102 | 1.29 × 101 | |
| 60 | 4.76 × 101 | 7.81 × 101 | 4.36 × 100 | 7.09 × 102 | 1.69 × 101 | |
| 70 | 6.69 × 101 | 1.18 × 102 | 7.24 × 100 | 9.06 × 102 | 2.29 × 101 | |
| 80 | 6.75 × 101 | 1.13 × 102 | 9.30 × 101 | 1.05 × 102 | 3.78 × 101 | |
| 90 | 1.09 × 102 | 1.47 × 102 | 2.01 × 100 | 1.19 × 103 | 4.38 × 101 | |
| 100 | 1.13 × 102 | 1.75 × 102 | 2.01 × 100 | 1.62 × 102 | 6.07 × 101 | |
| Relative rate of change/% | 2.22 × 102 | 2.06 × 102 | 9.65 × 101 | 7.80 × 101 | 3.69 × 102 | |
| Average change | 7.31 × 101 | 1.15 × 102 | 2.78 × 101 | 6.35 × 102 | 3.25 × 101 | |
| 50 | 1.03 × 101 | 8.13 × 100 | 2.80 × 100 | 1.03 × 103 | 4.93 × 10−3 | |
| 60 | 1.59 × 101 | 1.66 × 101 | 1.92 × 10−1 | 2.00 × 102 | 9.86 × 10−3 | |
| 70 | 1.77 × 101 | 1.99 × 101 | 3.52 × 100 | 1.66 × 102 | 1.11 × 10−16 | |
| 80 | 2.94 × 101 | 3.22 × 101 | 3.88 × 100 | 1.52 × 101 | 1.23 × 10−2 | |
| 90 | 4.81 × 101 | 3.76 × 101 | 1.40 × 101 | 2.78 × 102 | 4.93 × 10−3 | |
| 100 | 4.67 × 101 | 4.96 × 101 | 3.34 × 101 | 3.52 × 101 | 1.72 × 10−2 | |
| Relative rate of change/% | 3.56 × 102 | 5.10 × 102 | 1.09 × 103 | 9.66 × 101 | 2.49 × 102 | |
| Average change | 2.80 × 101 | 2.73 × 101 | 9.63 × 100 | 2.88 × 102 | 8.21 × 10−3 | |
| 50 | 1.26 × 101 | 1.22 × 101 | 1.12 × 101 | 8.42 × 100 | 7.10 × 10−5 | |
| 60 | 1.31 × 101 | 1.25 × 101 | 1.44 × 100 | 1.07 × 101 | 7.73 × 10−6 | |
| 70 | 1.11 × 101 | 1.25 × 101 | 3.87 × 100 | 1.61 × 101 | 8.51 × 100 | |
| 80 | 8.45 × 100 | 8.93 × 100 | 2.11 × 100 | 2.00 × 101 | 1.88 × 101 | |
| 90 | 2.79 × 100 | 3.42 × 100 | 7.55 × 10−1 | 2.03 × 101 | 1.56 × 101 | |
| 100 | 6.41 × 10−1 | 1.96 × 10−1 | 4.75 × 10−2 | 2.05 × 101 | 2.08 × 101 | |
| Relative rate of change/% | 9.49 × 101 | 9.84 × 101 | 9.96 × 101 | 1.43 × 102 | 2.93 × 107 | |
| Average change | 8.11 × 100 | 8.30 × 100 | 3.24 × 100 | 1.60 × 101 | 1.06 × 101 | |
| 50 | 2.62 × 105 | 1.53 × 105 | 3.03 × 102 | 4.33 × 108 | 1.00 × 10−20 | |
| 60 | 5.24 × 105 | 7.42 × 105 | 5.50 × 102 | 1.16 × 107 | 1.00 × 10−20 | |
| 70 | 4.95 × 105 | 9.88 × 105 | 1.09 × 103 | 1.08 × 107 | 1.00 × 10−20 | |
| 80 | 1.26 × 106 | 1.14 × 106 | 8.46 × 104 | 2.29 × 105 | 1.00 × 10−20 | |
| 90 | 2.04 × 106 | 1.15 × 106 | 7.97 × 105 | 3.56 × 107 | 1.00 × 10−20 | |
| 100 | 3.37 × 106 | 1.46 × 106 | 1.00 × 102 | 2.30 × 105 | 1.00 × 10−20 | |
| Relative rate of change/% | 1.19 × 103 | 8.55 × 102 | 6.70 × 101 | 9.99 × 101 | 0.00 × 100 | |
| Average change | 1.32 × 106 | 9.39 × 105 | 1.47 × 105 | 8.18 × 107 | 1.00 × 10−20 |
| Functions | HMS | Average Optimal Value of HS | Average Optimal Value of IHS | Average Optimal Value of GHS | Average Optimal Value of SGHS | Average Optimal Value of SC-AHS |
|---|---|---|---|---|---|---|
| 20 | 2.09 × 104 | 1.38 × 104 | 1.60 × 101 | 4.65 × 103 | 8.23 × 10−20 | |
| 50 | 2.59 × 103 | 5.33 × 103 | 4.00 × 100 | 3.07 × 103 | 2.14 × 10−27 | |
| 100 | 1.02 × 103 | 2.33 × 103 | 1.20 × 102 | 1.68 × 103 | 7.58 × 10−17 | |
| 150 | 8.41 × 102 | 1.04 × 103 | 4.80 × 102 | 6.58 × 102 | 4.29 × 10−25 | |
| 200 | 5.05 × 102 | 6.20 × 102 | 1.20 × 102 | 4.31 × 102 | 1.00 × 10−30 | |
| Relative rate of change/% | 9.76 × 101 | 9.55 × 101 | 6.50 × 102 | 9.07 × 101 | 1.00 × 102 | |
| Average change | 5.16 × 103 | 4.63 × 103 | 1.48 × 102 | 2.10 × 103 | 1.52 × 10−17 | |
| 20 | 1.60 × 102 | 1.82 × 102 | 3.49 × 101 | 1.22 × 102 | 1.59 × 101 | |
| 50 | 7.11 × 101 | 9.51 × 101 | 1.16 × 100 | 1.72 × 102 | 7.96 × 100 | |
| 100 | 3.23 × 101 | 5.28 × 101 | 1.16 × 100 | 5.40 × 101 | 1.99 × 100 | |
| 150 | 2.70 × 101 | 2.87 × 101 | 2.04 × 100 | 2.73 × 102 | 9.95 × 10−1 | |
| 200 | 1.76 × 101 | 2.68 × 101 | 4.02 × 100 | 2.25 × 101 | 1.78 × 10−15 | |
| Relative rate of change/% | 8.91 × 101 | 8.53 × 101 | 8.85 × 101 | 8.15 × 101 | 1.00 × 102 | |
| Average change | 6.17 × 101 | 7.71 × 101 | 8.65 × 100 | 1.29 × 102 | 5.37 × 100 | |
| 20 | 1.77 × 102 | 1.25 × 102 | 1.12 × 100 | 7.10 × 101 | 6.14 × 10−1 | |
| 50 | 4.32 × 101 | 5.19 × 101 | 1.60 × 100 | 3.30 × 101 | 2.46 × 10−2 | |
| 100 | 1.70 × 101 | 1.29 × 101 | 7.20 × 10−1 | 6.35 × 100 | 1.11 × 10−16 | |
| 150 | 6.50 × 100 | 1.01 × 101 | 1.92 × 10−1 | 5.19 × 101 | 2.22 × 10−2 | |
| 200 | 4.46 × 100 | 5.21 × 100 | 2.08 × 100 | 6.63 × 100 | 1.97 × 10−2 | |
| Relative rate of change/% | 9.75 × 101 | 9.58 × 101 | 8.57 × 101 | 9.07 × 101 | 9.68 × 101 | |
| Average change | 4.97 × 101 | 4.11 × 101 | 1.14 × 100 | 3.38 × 101 | 1.36 × 10−1 | |
| 20 | 1.54 × 101 | 1.48 × 101 | 5.89 × 10−16 | 1.43 × 101 | 8.97 × 10−1 | |
| 50 | 1.30 × 101 | 1.24 × 101 | 5.89 × 10−16 | 9.69 × 100 | 8.96 × 10−1 | |
| 100 | 9.06 × 100 | 9.64 × 100 | 5.89 × 10−16 | 5.89 × 100 | 8.96 × 10−1 | |
| 150 | 6.05 × 100 | 6.22 × 100 | 5.89 × 10−16 | 5.89 × 100 | 4.16 × 10−5 | |
| 200 | 5.15 × 100 | 6.81 × 100 | 4.59 × 100 | 5.54 × 100 | 8.48 × 10−7 | |
| Relative rate of change/% | 6.66 × 101 | 5.41 × 101 | 7.80 × 1017 | 6.13 × 101 | 1.00 × 102 | |
| Average change | 9.73 × 100 | 9.98 × 100 | 9.19 × 10−1 | 8.27 × 100 | 5.38 × 10−1 | |
| 20 | 1.57 × 107 | 4.96 × 107 | 3.00 × 101 | 1.09 × 106 | 4.36 × 10−2 | |
| 50 | 4.17 × 106 | 3.71 × 106 | 4.66 × 102 | 9.13 × 104 | 7.72 × 10−16 | |
| 100 | 2.14 × 105 | 5.21 × 105 | 3.76 × 102 | 7.31 × 104 | 1.00 × 10−20 | |
| 150 | 1.85 × 104 | 5.58 × 105 | 3.00 × 101 | 1.47 × 106 | 1.00 × 10−20 | |
| 200 | 1.08 × 104 | 1.05 × 105 | 4.66 × 102 | 1.67 × 104 | 1.00 × 10−20 | |
| Relative rate of change/% | 9.99 × 101 | 9.98 × 101 | 1.45 × 103 | 9.85 × 101 | 1.00 × 102 | |
| Average change | 4.01 × 106 | 1.09 × 107 | 2.73 × 102 | 5.49 × 105 | 8.72 × 10−3 |
| Function | Optimize Performance | N = 50 | N = 60 | N = 70 | N = 80 | N = 90 | N = 100 |
|---|---|---|---|---|---|---|---|
| Average optimal value | 9.62 × 10−19 | 2.49 × 10−21 | 3.34 × 10−17 | 1.00 × 10−18 | 5.78 × 10−17 | 2.57 × 10−25 | |
| Evolution times/times | 309 | 414 | 480 | 548 | 620 | 765 | |
| Average optimal value | 1.29 × 101 | 1.69 × 101 | 2.29 × 101 | 3.78 × 101 | 4.38 × 101 | 6.07 × 101 | |
| Evolution times/times | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | |
| Average optimal value | 4.93 × 10−3 | 9.86 × 10−3 | 1.11 × 10−16 | 1.23 × 10−2 | 4.93 × 10−3 | 1.72 × 10−2 | |
| Evolution times/times | 20,000 | 20,000 | 19,763 | 20,000 | 20,000 | 20,000 | |
| Average optimal value | 7.10 × 10−5 | 7.73 × 10−6 | 8.51 × 100 | 1.88 × 101 | 1.56 × 101 | 2.08 × 101 | |
| Evolution times/times | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | |
| Average optimal value | 1.00 × 10−20 | 1.00 × 10−20 | 1.00 × 10−20 | 1.00 × 10−20 | 1.00 × 10−20 | 1.00 × 10−20 | |
| Evolution times/times | 5292 | 6771 | 7802 | 9855 | 10,441 | 10,890 |
| Function | Optimize Performance | HMS = 20 | HMS = 50 | HMS = 100 | HMS = 150 | HMS = 200 |
|---|---|---|---|---|---|---|
| Average optimal value | 8.23 × 10−20 | 2.14 × 10−27 | 7.58 × 10−17 | 4.29 × 10−25 | 1.00 × 10−30 | |
| Evolution times/times | 1606 | 280 | 203 | 219 | 209 | |
| Average optimal value | 1.59 × 101 | 7.96 × 100 | 1.99 × 100 | 9.95 × 10−1 | 1.78 × 10−15 | |
| Evolution times/times | 20,000 | 20,000 | 20,000 | 20,000 | 18,361 | |
| Average optimal value | 3.06 × 10−2 | 2.46 × 10−2 | 1.11 × 10−16 | 2.22 × 10−2 | 1.97 × 10−2 | |
| Evolution times/times | 20,000 | 20,000 | 11,936 | 20,000 | 20,000 | |
| Average optimal value | 2.27 × 10−5 | 1.60 × 10−8 | 3.93 × 10−9 | 2.87 × 10−10 | 1.31 × 10−11 | |
| Evolution times/times | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | |
| Average optimal value | 2.43 × 10−3 | 4.33 × 10−17 | 1.00 × 10−20 | 1.00 × 10−20 | 1.00 × 10−20 | |
| Evolution times/times | 20,000 | 20,000 | 4296 | 3932 | 3346 |
| Direct Sunlight with Strong | Direct Sunlight with Medium | Direct Sunlight with Weak | Backlighting with Strong | Backlighting with Medium | Backlighting with Weak |
|---|---|---|---|---|---|
| Non-Dominated Solution Number: 54 | Non-Dominated Solution Number: 36 | Non-Dominated Solution Number: 28 | Non-Dominated Solution Number: 18 | Non-Dominated Solution Number: 54 | Non-Dominated Solution Number: 62 |
| 77 | 121 | 130 | 131 | 107 | 146 |
| 116 | 121 | 130 | 131 | 99 | 152 |
| 77 | 114 | 130 | 131 | 107 | 129 |
| 77 | 121 | 130 | 131 | 126 | 113 |
| 77 | 121 | 130 | 131 | 107 | 152 |
| 116 | 121 | 130 | 131 | 126 | 152 |
| 116 | 131 | 130 | 131 | 126 | 152 |
| 77 | 121 | 130 | 131 | 126 | 115 |
| 116 | 121 | 130 | 131 | 107 | 115 |
| 116 | 121 | 130 | 131 | 107 | 115 |
| 116 | 121 | 130 | 131 | 106 | 113 |
| 77 | 121 | 130 | 131 | 99 | 113 |
| 77 | 121 | 130 | 172 | 99 | 113 |
| 77 | 131 | 130 | 228 | 107 | 122 |
| 116 | 114 | 130 | 66 | 99 | 152 |
| 77 | 121 | 130 | 221 | 126 | 113 |
| 116 | 131 | 130 | 206 | 99 | 113 |
| 77 | 121 | 130 | 15 | 106 | 113 |
| 116 | 114 | 130 | 107 | 120 | |
| 77 | 121 | 130 | 106 | 129 | |
| 116 | 121 | 130 | 106 | 120 | |
| 77 | 121 | 46 | 99 | 129 | |
| 77 | 114 | 133 | 106 | 146 | |
| 77 | 121 | 85 | 106 | 129 | |
| 77 | 121 | 72 | 126 | 120 | |
| 77 | 121 | 146 | 107 | 120 | |
| 77 | 114 | 55 | 126 | 152 | |
| 77 | 149 | 45 | 107 | 113 | |
| 77 | 114 | 99 | 152 | ||
| 116 | 178 | 126 | 129 | ||
| 116 | 243 | 99 | 146 | ||
| 116 | 39 | 99 | 115 | ||
| 116 | 198 | 126 | 122 | ||
| 116 | 66 | 126 | 120 | ||
| 77 | 166 | 126 | 146 | ||
| 116 | 97 | 126 | 122 | ||
| 77 | 107 | 122 | |||
| 77 | 126 | 120 | |||
| 77 | 107 | 152 | |||
| 77 | 106 | 122 | |||
| 77 | 106 | 120 | |||
| 116 | 126 | 122 | |||
| 116 | 106 | 146 | |||
| 153 | 168 | 120 | |||
| 69 | 70 | 146 | |||
| 231 | 230 | 120 | |||
| 205 | 98 | 146 | |||
| 146 | 106 | 122 | |||
| 36 | 159 | 113 | |||
| 33 | 163 | 122 | |||
| 221 | 70 | 202 | |||
| 21 | 10 | 58 | |||
| 163 | 208 | 47 | |||
| 203 | 91 | 122 | |||
| 214 | |||||
| 28 | |||||
| 129 | |||||
| 209 | |||||
| 181 | |||||
| 204 | |||||
| 248 | |||||
| 172 |
| Illumination Condition | Select Threshold by SC-AHS | OTSU Threshold |
|---|---|---|
| Direct sunlight with strong | 116 | 129 |
| Direct sunlight with medium | 121 | 129 |
| Direct sunlight with weak | 130 | 133 |
| Backlighting with strong | 131 | 144 |
| Backlighting with medium | 99 | 130 |
| Backlighting with weak | 113 | 130 |
| Illumination Condition | RSeg | RApp | RBra | RSuc | RMis (%) |
|---|---|---|---|---|---|
| Direct sunlight with strong | 100.0 | 85.7 | 14.3 | 100.0 | 0.0 |
| Direct sunlight with medium | 80.0 | 75.0 | 25.0 | 75.0 | 25.0 |
| Direct sunlight with weak | 80.0 | 100.0 | 0.0 | 80.0 | 20.0 |
| Backlighting with strong | 100.0 | 83.3 | 16.7 | 100.0 | 0.0 |
| Backlighting with medium | 85.7 | 83.3 | 16.7 | 83.3 | 16.7 |
| Backlighting with weak | 66.7 | 100.0 | 0.0 | 66.7 | 33.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Huo, J. Apple Image Recognition Multi-Objective Method Based on the Adaptive Harmony Search Algorithm with Simulation and Creation. Information 2018, 9, 180. https://doi.org/10.3390/info9070180
Liu L, Huo J. Apple Image Recognition Multi-Objective Method Based on the Adaptive Harmony Search Algorithm with Simulation and Creation. Information. 2018; 9(7):180. https://doi.org/10.3390/info9070180
Chicago/Turabian StyleLiu, Liqun, and Jiuyuan Huo. 2018. "Apple Image Recognition Multi-Objective Method Based on the Adaptive Harmony Search Algorithm with Simulation and Creation" Information 9, no. 7: 180. https://doi.org/10.3390/info9070180
APA StyleLiu, L., & Huo, J. (2018). Apple Image Recognition Multi-Objective Method Based on the Adaptive Harmony Search Algorithm with Simulation and Creation. Information, 9(7), 180. https://doi.org/10.3390/info9070180





