Abstract
A neutrosophic cubic set is the hybridization of the concept of a neutrosophic set and an interval neutrosophic set. A neutrosophic cubic set has the capacity to express the hybrid information of both the interval neutrosophic set and the single valued neutrosophic set simultaneously. As newly defined, little research on the operations and applications of neutrosophic cubic sets has been reported in the current literature. In the present paper, we propose the score and accuracy functions for neutrosophic cubic sets and prove their basic properties. We also develop a strategy for ranking of neutrosophic cubic numbers based on the score and accuracy functions. We firstly develop a TODIM (Tomada de decisao interativa e multicritévio) in the neutrosophic cubic set (NC) environment, which we call the NC-TODIM. We establish a new NC-TODIM strategy for solving multi attribute group decision making (MAGDM) in neutrosophic cubic set environment. We illustrate the proposed NC-TODIM strategy for solving a multi attribute group decision making problem to show the applicability and effectiveness of the developed strategy. We also conduct sensitivity analysis to show the impact of ranking order of the alternatives for different values of the attenuation factor of losses for multi-attribute group decision making strategies.
1. Introduction
While modelling multi attribute decision making (MADM) and multi attribute group decision making (MAGDM), it is often observed that the parameters of the problem are not precisely known. The parameters often involve uncertainty. To deal with uncertainty, Zadeh [1] left an important mark to represent and compute with imperfect information by introducing the fuzzy set. The fuzzy set fostered a broad research community, and its impact has also been clearly felt at the application level in MADM [2,3,4] and MAGDM [5,6,7,8,9].
Atanassov [10] incorporated the non-membership function as an independent component and defined the intuitionistic fuzzy set (IFS) at first to express uncertainty in a more meaningful way. IFSs have been applied in many MADM problems [11,12,13]. Smarandache [14] proposed the notion of the neutrosophic set (NS) by introducing indeterminacy as an independent component. Wang et al. [15] grounded the concept of the single valued neutrosophic set (SVNS), an instance of the neutrosophic set, to deal with incomplete, inconsistent, and indeterminate information in a realistic way. Wang et al. [16] proposed the interval neutrosophic set (INS) as a subclass of neutrosophic sets in which the values of truth, indeterminacy, and falsity membership degrees are interval numbers. Theoretical development and applications of SVNSs and INSs are found in [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] for MADM or MAGDM. Some studies on MADM in single valued neutrosophic hesitant fuzzy set environments are found in [38,39,40,41].
NS and INS are both capable of handling uncertainty and incomplete information. By fusing NS and INS, Ali et al. [42] proposed the neutrosophic cubic set (NCS) and defined external and internal neutrosophic cubic sets, and established some of their properties. In the same study, Ali et al. [42] proposed an adjustable strategy to NCS-based decision making. Jun et al. [43] also defined NCS by combining NS and INS. In decision making process, the advantage of NCSs is that the decision makers can employ the hybrid information comprising of INSs and SVNSs for evaluating and rating of the alternatives with respect to their predefined attributes. However, there are only a few studies in the literature to deal with MADM and MAGDM in the NCS environment. Banerjee et al. [44] established grey relational analysis (GRA) [45,46,47] based on the new MADM strategy in the NCS environment. In the same study, Banerjee et al. [44] proposed the Hamming distances for weighted grey relational coefficients and ideal grey relational coefficients, and offered the concept of relative closeness coefficients for presenting the ranking order of the alternatives based on the descending order of their relative closeness coefficients.
Similarity measure is an important mathematical tool in decision-making problems. Pramanik et al. [48] at first defined similarity measure for NCSs and proved its basic properties. In the same study, Pramanik et al. [48] developed a new MAGDM strategy in the NCS environment. Lu and Ye [49] proposed cosine measures between NCSs and established their basic properties. In the same study, Lu and Ye [49] proposed three new cosine measures-based MADM strategies under a NCS environment.
Due to little research on the operations and application of NCSs, Pramanik et al. [50] proposed several operational rules on NCSs, and defined Euclidean distances and arithmetic average operators of NCSs. In the same study, Pramanik et al. [50] also employed the information entropy scheme to calculate the unknown weights of the attributes, and developed a new extended TOPSIS strategy for MADM under the NCS environment. Zhan et al. [51] proposed a new algorithm for multi-criteria decision making (MCDM) in an NCS environment based on a weighted average operator and a weighted geometric operator. Ye [52] established the concept of a linguistic neutrosophic cubic number (LNCN). In the same study, Ye [52] developed a new MADM strategy based on a LNCN weighted arithmetic averaging (LNCNWAA) operator and a LNCN weighted geometric averaging (LNCNWGA) operator under a linguistic NCS environment.
In the literature, there are only six strategies [44,48,49,50,51,52] for MADM and MAGDM in NCS environment. However, we say that none of them is generally superior to all others. So, new strategies for MADM and MAGDM should be explored under the NCS environment for the development of neutrosophic studies.
TODIM (an acronym in Portuguese for interactive multi-criteria decision making strategy named Tomada de decisao interativa e multicritévio) is an important MADM strategy, since it considers the decision makers’ bounded rationality. Firstly, Gomes and Lima [53] introduced the TODIM strategy based on prospect theory [54]. Krohling and Souza [55] defined the fuzzy TODIM strategy to solve MCDM problems. Several researchers applied the TODIM strategy in various fuzzy MADM or MAGDM problems [56,57,58]. Fan et al. [59] introduced the extended TODIM strategy to deal with the hybrid MADM problems. Krohling et al. [60] extended the TODIM strategy from fuzzy environment to intuitionistic fuzzy environment to process the intuitionistic fuzzy information. Wang [61] introduced TODIM strategy into multi-valued neutrosophic set environment. Zhang et al. [62] proposed the TODIM strategy for MAGDM problems under a neutrosophic number environment. Ji et al. [63] proposed the TODIM strategy under a multi-valued neutrosophic environment and employed it to solve personal selection problems. In 2017, Xu et al. [64] developed the TODIM strategy in a single valued neutrosophic setting and extended it into interval neutrosophic setting. Neutrosophic TODIM [64] is capable of dealing with only single-valued neutrosophic information or interval neutrosophic information.
NCS can be used to express the interval neutrosophic information and neutrosophic information in the process of MADGM. It seems that TODIM in NCSs has an enormous chance of success to deal with group decision making problems. In the NCS environment, the TODIM strategy is yet to appear. Motivated by these, we initiated the study of TODIM in the NCS environment, which we call NC-TODIM.
However, NCSs comprise of hybrid information of INSs and SVNSs simultaneously, which are more flexible and elegant for expressing neutrosophic cubic information. To apply NCSs to MADGM problems, we introduce some basic operations of neutrosophic cubic (NC) numbers and the score, and accuracy functions of NC numbers, and the ranking strategy of NC numbers.
In this paper we develop a TODIM strategy (for short, NC-TODIM strategy) for MAGDM in the NCS environment. The proposed NC-TODIM strategy was proven to be capable of successfully dealing with MAGDM problems by solving an illustrative example. What is more, a comparative analysis ensured the feasibility of the proposed NC-TODIM strategy.
The remainder of the paper is divided into seven sections that are organized as follows: Section 2 presents some basic definitions of NS, SVNS, INS, and NCS. Section 3 presents comparison strategy of two NC-numbers. Section 4 is devoted to present the proposed NC-TODIM strategy. Section 5 presents an illustrative numerical example of MAGDM in the NCS environment. Section 6 is devoted to analyzing the ranking order with different values of attenuation factors of losses. Section 7 presents a comparative analysis between the developed strategy and other existing strategies in the NCS environment. Section 8 presents the conclusion and the future scope of research.
2. Preliminaries
In this section, we review some basic definitions which are important to develop the paper.
Definition 1.
[14] NS. Let U be a space of points (objects) with a generic element in U denoted by u, i.e., u U. A neutrosophic set R in U is characterized by truth-membership function , indeterminacy-membership function , and falsity-membership function , where , , are the functions from U to ]0, 1[ i.e., , , : U]0, 1[ that means (u), (u), (u) are the real standard or non-standard subset of ]0, 1[. The neutrosophic set can be expressed as R = {<u; ((u), (u), (u))>: uU}. Since (u), (u), (u) are the subset of ]0, 1[, there the sum ((u) + (u) + (u)) lies between 0 and 3, where 0 = 0 − and 3 = 3 + , > 0.
Definition 2.
[15] SVNS. Let U be a space of points (objects) with a generic element in U denoted by u. A single valued neutrosophic set H in U is expressed by H = {<u, ((u), (u), (u))>; uU}, where (u), (u), (u)[0, 1]. Therefore for each uU, (u), (u), (u)[0, 1] and 0 ≤ (u) + (u) + (u) ≤ 3.
Definition 3.
[16] INS. Let G be a non-empty set. An interval neutrosophic set in G is characterized by truth-membership function the indeterminacy membership function and falsity membership function . For each gG, (g), (g), (g) [0, 1] and defined as
Here,
and
In real problems it is difficult to express the truth-memberships function, indeterminacy-membership function and falsity-membership function in the form of
Here,
Example 2.
Suppose that G = {, gn} is a non-empty set. Let be an INS. Then is expressed as
Definition 4.
[42,43] NCS. A NCS in a non-empty set G is defined as © = {<g; (g), R(g)>: gG}, where and R are the INS and NS in G respectively. NCS can be presented as an order pair © = <, R>, then we call it as a neutrosophic cubic (NC) number.
Example 3.
Suppose that G = {, gn} is a non-empty set. Let be any NC-number. Then can be expressed as = {<; [0.39, 0.47], [0.17, 0.43], [0.18, 0.36], (0.6, 0.3, 0.4)>: G}.
Some operations of NC-numbers:
i. Union of any two NC-numbers
Let and be any two NC-numbers in a non-empty set G. Then the union of and denoted by and defined as
where = {<g, [max {(g), (g)},max {(g), (g)}], [max {(g), (g)}, max {(g), (g)}], [min {(g), (g)}, min {(g), (g)}]>: gG} and = {<g, max {(g), (g)}, max {(g), (g)}, min {(g), (g)}>:gU}.
Example 4.
Let and be two NC-numbers in G presented as follows:
and
Then
ii. Intersection of any two NC-numbers
Intersection of two NC-numbers denoted and defined as follows:
where = {<g, [min {(g), (g)},min {(g), (g)}], [min {(g), (g)}, min {(g), (g)}], [max {(g), (g)}, max {(g), (g)}]>: gG} and = {<g, min {(g), (g)}, min {(g),(g)}, max {(g), (g)}>:gU}.
Example 5.
Let and be any two NC-numbers in G presented as follows:
and
Then
iii. Compliment of a NC-number
Let be a NCS in G. Then, the compliment of denoted by = {<g, (g), (g)>: gG}.
Here, = {<g, [(g), (g)], [(g), (g)], [(g), (g)]>: gG}, where, (g) = (g), (g) = (g), (g) = {1} − (g), (g) = {1} − (g), (g) = (g), (g) = (g) and (g) = (g) ,(g) = {1} − (g), (g) = (g).
Example 6.
Assume that be any NC-number in G in the form:
Then compliment of is obtained as
Definition 5.
Score function. Let ©1 be a NC-number in a non-empty set G. Then, a score function of ©1, denoted by is defined as:
where, ©1 = <[a1, a2], [b1, b2], [c1, c2], (a, b, c) > and [–1, 1].
Proposition 1.
Score function of two NC-numbers lies between −1 to 1.
Proof.
Using the definition of INS and NS, we have all a1, a2, b1, b2, c1, c2, a, b, and c .
Since,
Adding Equations (2)–(4), we obtain
Again,
Adding (6) and (7), we obtain
Adding (5) and (8) and dividing by 2, we obtain
Hence the proof is complete. ☐
Example 7.
Let and be two NC-numbers in G, presented as follows:
and
Then, by applying Definition 5, we obtain = −0.01 and = 0.07, In this case, we can say that .
Definition 6.
Accuracy function. Let ©1 be a NC-number in a non-empty set G, an accuracy function of ©1 is defined as:
Ac(©1) = ½[½(a1 + a2 − b2(1 − a2) − b1(1 − a1) − c2(1 − b1) − c1(1 − b2) + a − b(1 − a) − c(1 − b)]
Here, [–1, 1].
When the value of increases, we say that the degree of accuracy of the NC-number ©1 increases.
Proposition 2.
Accuracy function of two NC-numbers lies between −1 to 1.
Proof.
The values of accuracy function depend upon
The values of
and
lie between −1 to 1 from [37].
Thus, .
Hence the proof is completed. ☐
Example 8.
Let and be two NC-numbers in G presented as follows:
and
Then, by applying Definition 6, we obtain = 0.14 and = 0.30. In this case, we can say that alternative is better than .
With respect to the score function and the accuracy function , a strategy for comparing NC-numbers can be defined as follows:
3. Comparison Strategy of Two NC-Numbers
Let ©1 and ©2 be any two NC-numbers. Then we define comparison strategy as follows:
- IfSc(©1) > Sc(©2), then ©1 > ©2.
- IfSc(©1) = Sc(©2) and Ac(©1) > Ac(©2), then ©1 > ©2.
- IfSc(©1) = Sc(©2) and Ac(©1) = Ac(©2), then ©1 = ©2.
Example 9.
Let ©1 and ©2 be two NC-numbers in G, presented as follows:
and
Then, applying Definition 5, we obtain = 0.13 and = 0.13. Applying Definition 6, we obtain = −0.20 and = −0.18. In this case, we say that alternative > . (Score values and Accuracy values taking correct up to two decimal places).
Definition 7.
Let ©1 and ©2 be any two NC-numbers, then the distance between them is defined by
where, ©1 = <[a1, a2], [b1, b2], [c1, c2], (a, b, c)> and ©2 = <[d1, d2], [e1, e2], [f1, f2], (d, e, f)>.
Example 10.
Let ©1 and ©2 be two NC-numbers in G presented as follows:
and
Then, applying Definition 7, we obtain ∂ (©1, ©2) = 0.12.
Definition 8.
Let = be any neutrosophic cubic value. used to evaluate i-th alternative with respect to j-th criterion. The normalized form of ©ij is defined as follows:
A conceptual model of the evolution of the neutrosophic cubic set is shown in Figure 1.
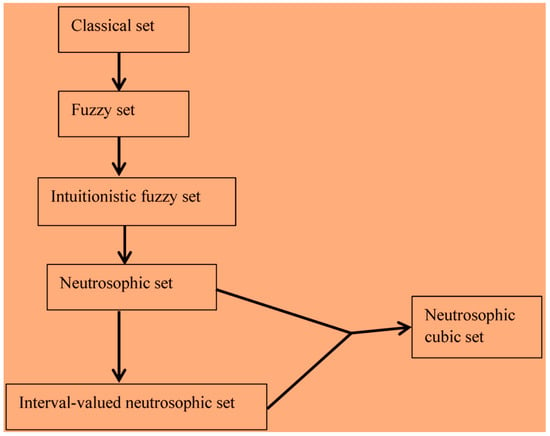
Figure 1.
Evolution of the neutrosophic cubic set.
4. NC-TODIM Based MAGDM under a NCS Environment
Assume that A = {A1, A2, …, Am} (m ≥ 2) and C = {C1, C2, …, Cn} (n ≥ 2) are the discrete set of alternatives and attributes respectively. W = {W1, W2, …, Wn} is the weight vector of attributes Cj (j = 1, 2, …, n), where Wj > 0 and . Let E = {E1, E2, …, Er} be the set of decision makers and be the weight vector of decision makers, where > 0 and .
NC-TODIM Strategy
Now, we describe the NC-TODIM strategy to solve the MAGDM problems with NC-numbers. The NC-TODIM strategy consists of the following steps:
Step 1. Formulate the decision matrix
Assume that = be the decision matrix, where = <> is the rating value provided by the k-th (Ek) decision maker for alternative Ai, with respect to attribute Cj. The matrix form of is presented as:
Step 2. Normalize the decision matrix
The MAGDM problem generally consists of cost criteria and benefit criteria. So, the decision matrix needs to be normalized. For cost criterion Cj, we use the Definition 8 to normalize the decision matrix (Equation (15)) provided by the decision makers. For benefit criterion Cj we don’t need to normalize the decision matrix. When Cj is a cost criterion, the normalized form of decision matrix (see Equation (15)) is presented below.
Here is the normalized form of the NC-number.
Step 3. Determine the relative weight of each criterion
The relative weight of each criterion is obtained by the following equation.
where, = max {W1, W2, …, Wn}.
Step 4. Calculate score values
Using Equation (1), calculate the score value (i = 1, 2, …, m; j = 1, 2, …, n) of if Cj is a cost criterion. Using Equation (1), calculate the score value (i = 1, 2, …, m; j = 1, 2, …, n) of if Cj is a benefit criterion.
Step 5. Calculate accuracy values
Using Equation (9), calculate the accuracy value (I = 1, 2, …, m; j= 1, 2, …, n) of if Cj is a cost criterion. Using Equation (9), calculate the accuracy value (I = 1, 2, …, m; j = 1, 2, …, n) of if Cj is a benefit criterion.
Step 6. Formulate the dominance matrix
Calculate the dominance of each alternative Ai over each alternative Aj with respect to the criteria C (C1, C2, …, Cn), of the k-th decision maker Ek by the following Equations (18) and (19).
(For cost criteria)
(For benefit criteria)
where, parameter represents the attenuation factor of losses and must be positive.
Step 7. Formulate the individual overall dominance matrix
Using Equation (20), calculate the individual total dominance matrix of each alternative Ai over each alternative Aj under the criterion Cj.
Step 8. Aggregate the dominance matrix
Using Equation (21), calculate the collective overall dominance of alternative Ai over each alternative Aj.
Step 9. Calculate global values
We present the global value of each alternative as follows:
Step 10. Rank the priority
Sorting the values of provides the rank of each alternative. A set of alternatives can be preference-ranked according to the descending order of . The highest global value corresponds to the best alternative.
A conceptual model of the NC-TODIM strategy is shown in Figure 2.
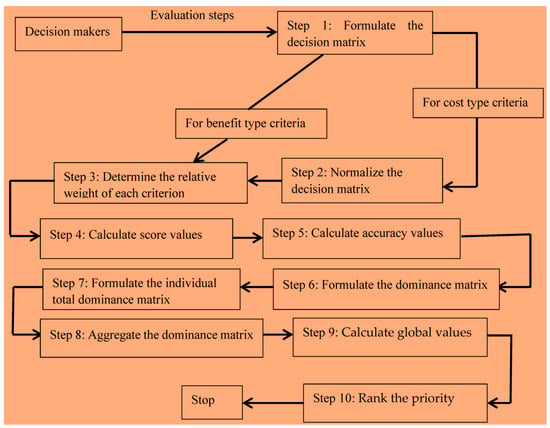
Figure 2.
A flow chart of the proposed neutrosophic cubic set (NC)-TODIM strategy.
5. Illustrative Example
In this section, a MAGDM problem is adapted from the study [18] under the NCS environment. An investment company wants to select the best alternative among the set of feasible alternatives. The feasible alternatives are
- Car company (A1)
- Food company (A2)
- Computer company (A3)
- Arms company (A4).
The best alternative is selected based on the following criteria:
- Risk analysis (C1)
- Growth analysis (C2)
- Environmental impact analysis (C3).
An investment company forms a panel of three decision makers {E1, E2, E3} who evaluate four alternatives in decision making process. The weight vector of attributes and decision makers are considered as W = (0.4, 0.35, 0.25)T = (0.32, 0.33, 0.35)T respectively.
The proposed strategy is presented using the following steps:
Step 1. Formulate the decision matrix
Formulate the decision matrices using the rating values of alternatives with respect to three criteria provided by the three decision makers in terms of NC-numbers. Assume that the NC-numbers = <> present the rating value provided by the decision maker Ek for alternative Ai with respect to attribute Cj. Using these rating values (k = 1, 2, 3; i = 1, 2, 3, 4; j = 1, 2, 3), three decision matrices = (k = 1, 2, 3) are constructed (see Equations (23)–(25)).
Decision matrix for E1
Decision matrix for E2


Decision matrix for E3


Step 2. Normalize the decision matrix
Since all the criteria are benefit type, we do not need to normalize the decision matrix.
Step 3. Determine the relative weight of each criterion
Using Equation (17), we obtain the relative weight vector of criteria as follows:
Wch = (1, 0.875, 0.625)T.
Step 4. Calculate score values
The score values of each alternative relative to each criterion obtained by Equation (1) are presented in the Table 1, Table 2 and Table 3.

Table 1.
Score values for M1.

Table 2.
Score values for M2.

Table 3.
Score values for M3.
Step 5. Calculate accuracy values
The accuracy values of each alternative relative to each criterion obtained by Equation (9) are presented in Table 4, Table 5 and Table 6.

Table 4.
Accuracy values for M1.

Table 5.
Accuracy values for M2.

Table 6.
Accuracy values for M3.
Step 6. Formulate the dominance matrix
Using Equation (19), we construct dominance matrix for = 1. The dominance matrices are represented in matrix form (See Equations (26)–(34)).
The dominance matrix , the dominance matrix
The dominance matrix , the dominance matrix
The dominance matrix , the dominance matrix
The dominance matrix , the dominance matrix
The dominance matrix
Step 7. Formulate the individual overall dominance matrix
The individual overall dominance matrix is calculated by the Equation (20) and the dominance matrices are represented in matrix form (see Equations (35)–(37)).
First decision maker’s overall dominance matrix
Second decision maker’s overall dominance matrix
Third decision maker’s overall dominance matrix
Step 8. Aggregate the dominance matrix
Using Equation (21), the aggregate dominance matrix is constructed (see Equation (38)) as follows:
Step 9. Calculate global values
Using Equation (22), we calculate the values of (i = 1, 2, 3, 4) and represented in Table 7.

Table 7.
Global values of alternatives.
Step 10. Rank the priority
Since > > > , alternatives are then preference ranked as follows: A3 > A2 > A1 > A4.
Hence A3 is the best alternative.
From the illustrative example, we see that the proposed NC-TODIM strategy is more suitable for real scientific and engineering applications because it can handle hybrid information consisting of INS and SVNS information simultaneously to cope with indeterminate and inconsistent information. Thus, NC-TODIM extends the existing decision-making strategies and provides a sophisticated mathematical tool for decision makers.
6. Rank of Alternatives with Different Values of
Table 8 shows that the ranking order of alternatives depends on the values of the attenuation factor, which reflects the importance of the attenuation factor in the NC-TODIM strategy.

Table 8.
Global values and ranking of alternatives for different values of .
Analysis on Influence of the Parameter to Ranking Order
The impact of parameter on ranking order is examined by comparing the ranking orders taken with varying the different values of . When = 0.5, 1, 1.5, 2, 3, ranking order are presented in Table 8. We draw Figure 3 and Figure 4 to compare the ranking order for different values of . When = 0.5, = 1.5 and = 3, the ranking order is unchanged and A3 is the best alternative, while A1 is the worst alternative. When = 1, the ranking order is changed and A3 is the best alternative and A4 is the worst alternative. For = 2, the ranking order is changed and A2 is the best alternative and A1 is the worst alternative. From Table 8, we see that A3 is the best alternative in four cases and A1 is the worst for four cases. We can say that ranking order depends on parameter .
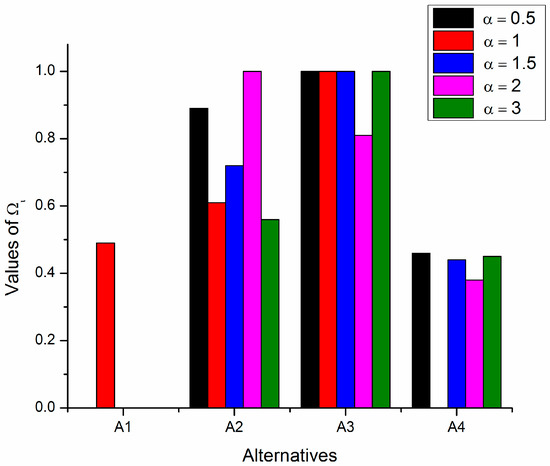
Figure 3.
Global values of the alternatives for different values of attenuation factor = 0.5, 1, 1.5, 2, 3.
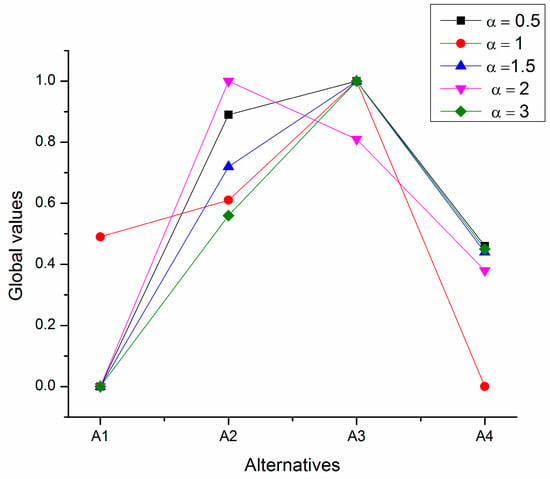
Figure 4.
Ranking of the alternatives for = 0.5, 1, 1.5, 2, 3.
7. Comparative Analysis and Discussion
On comparing with the existing neutrosophic decision making strategies [26,27,28,29,33,34,35,64,65,66,67,68,69], we see that the decision information used in the proposed NC-TODIM strategy is NC numbers, which comprises of interval neutrosophic information and single-valued neutrosophic information simultaneously; whereas the decision information in the existing literature is either SVNSs or INSs. Since NC numbers comprises of much more information, the NC numbers based on the TODIM strategy proposed in this paper is more elegant, typical and more general in applications, while the existing neutrosophic decision-making strategies cannot deal with the NC number decision-making problem developed in this paper.
The first decision making paper in NCS environment was studied by Banerjee et al. [44]. On comparison with existing GRA-based NCS decision making strategies [44], we observe that the proposed NC-TODIM strategy uses the score, and accuracy functions, while the decision making-strategy in [44] uses Hamming distances for weighted grey relational coefficients and standard (ideal) grey relational coefficients, and ranks the alternatives based on the relative closeness coefficients. Hence, the proposed NC-TODIM strategy is relatively simple in the decision making process.
On comparing with cosine measures of NCSs [49], we observe that the proposed NC-TODIM involves multiple decision makers, while in [49] only a single decision maker is involved. This shows that [49] cannot deal with group decision making, while the proposed NC-TODIM strategy is more sophisticated as it can deal with single as well as group decision making in the NCS environment.
On comparison with extended TOPSIS [50] with neutrosophic cubic information, we observe that nine components are present in NCSs. Therefore, by calculation of a weighted decision matrix, a neutrosophic cubic positive ideal solution (NCPIS), and a neutrosophic cubic negative ideal solution, the distance measures of alternatives from NCPIS and NCNIS (NCNIS,) and entropy weight, and use of an aggregation operator are lengthy, time consuming, and hence expensive. The proposed NC-TODIM strategy is free from different kinds of typical aggregation operators. The calculations required for the proposed strategy are relatively straightforward and time-saving. Therefore, the final ranking obtained by the proposed strategy is more conclusive than those produced by the other strategies, and it is evident that the proposed strategy is accurate and reliable.
On comparison with the strategy proposed by Zhan et al. [51], we see that they employ score, accuracy, and certainty functions, and a weighted average operator and weighted geometric operator of NCSs for decision making problem involving only a single decision maker. This reflects that the strategy introduced by Zhan et al. [51] is only applicable for decision making problems involving single decision maker. However, our proposed NC-TODIM strategy is more general as it is capable of dealing with group decision-making problems.
A comparative study is conducted with the existing strategy [48] for group decision making under a NCS environment (See Table 9). Since the philosophy of two strategies are different, the obtained results (ranking order) are different. At a glance, it cannot be said which strategy is superior to the other. However, on comparison with similarity measure-based strategies studied in [48], we observed that ideal solutions are needed for ranking of alternatives but in a real world ideal solution, this is an imaginary case, which means that an indeterminacy arises automatically, whereas in our proposed NC-TODIM strategy we can calculate the rank of the alternatives based on global values of alternatives. So, the proposed NC-TODIM strategy is relatively easy to implement and apply for solving MAGDM problems.

Table 9.
Ranking order of alternatives using three different decision making strategies in the neutrosophic cubic set (NCS) environment.
8. Conclusions
NCSs can better describe hybrid information comprising of INSs and NSs. In this study, we proposed a score function and an accuracy function, and established their properties. We developed a NC-TODIM strategy, which is capable for tackling MAGDM problems affected by uncertainty and indeterminacy represented by NC numbers. The standard TODIM, in its original formulation, is only applicable to a crisp environment. Existing neutrosophic TODIM strategies deal with single valued neutrosophic information or interval neutrosophic information. Therefore, proposed NC-TODIM strategy demonstrates the advantages of presenting and manipulating MAGDM problems with NCSs comprising of the hybrid information of INSs and NSs. Furthermore, NC-TODIM strategy that considers the risk preferences of decision makers, is significant to solve MAGDM problems. The proposed NC-TODIM strategy was verified to be applicable, feasible, and effective by solving an illustrative example regarding the selection problem of investment alternatives. In addition, we investigated the influence of attenuation factor of losses on ranking the order of alternatives.
The contribution of this study can be concluded as follows. First, this study utilized NCSs to present the interval neutrosophic information and neutrosophic information in the MAGDM process. Second, the NC-TODIM strategy established in this paper is simpler and easier than the existing strategy proposed by Pramanik et al. [48] for group decision making with neutrosophic cubic information based on similarity measure and demonstrates the main advantage of its simple and easy group decision making process. Third, TODIM strategy was extended to the NCS environment. Fourth, we defined the NC number. Fifth, we defined the score and accuracy functions and proved their basic properties. Sixth, we developed the ranking of NC numbers using score and accuracy functions. Therefore, two functions namely, score function, accuracy function, and proofs of their basic properties, ranking of NC numbers, and NC-TODIM strategy for MAGDM are the main contributions of the paper.
Several directions for future research are generated from this study. First, this study employs the NC-TODIM strategy to deal with MAGDM. In addition to MAGDM, MAGDM problems in a variety of other fields can be solved using the NC-TODIM strategy, including logistics center selection, personnel selection, teacher selection, renewable energy selection, medical diagnosis, image processing, fault diagnosis, etc. Second, this study considers the risk preferences of decision makers i.e., the essence of TODIM, while the interrelationship between criteria are ignored. In future research, the NC-TODIM strategy will be improved to address this deficiency. Third, the proposed strategy can only deal with crisp weights of attributes and decision makers, rather than NCS, which reflects its main limitation. This limitation will be effectively addressed in our future research. Fourth, in our illustrative example, three criteria are considered as an example. However, in real world group decision making problems, many other criteria should be included. A comprehensive framework for MAGDM problem comprising of all relevant criteria should be designed based on prior studies and the proposed NC-TODIM strategy in future research. Finally, we conclude that the developed NC-TODIM strategy offers a novel and effective strategy for decision makers under the NCS environment, and will open up a new avenue of research into the neutrosophic hybrid environment.
Acknowledgments
The authors would like to acknowledge the constructive comments and suggestions of the anonymous referees.
Author Contributions
Surapati Pramanik conceived and designed the problem; Shyamal Dalapati solved the problem; Surapati Pramanik, Shariful Alam and Tapan Kumar Roy analyzed the results; Surapati Pramanik and Shyamal Dalapati wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Chen, S.J.; Hwang, C.L. Fuzzy Multiple Attribute Decision-Making, Methods and Applications; Lecture Notes in Economics and Mathematical Systems; Springer-Verlag: Berlin/Heidelberg, Germany, 1992; Volume 375. [Google Scholar]
- Chang, T.H.; Wang, T.C. Using the fuzzy multi-criteria decision making approach for measuring the possibility of successful knowledge management. Inf. Sci. 2009, 179, 355–370. [Google Scholar] [CrossRef]
- Pramanik, S.; Mondal, K. Weighted fuzzy similarity measure based on tangent function and its application to medical diagnosis. Int. J. Innovat. Res. Sci. Engg. Tech. 2015, 4, 158–164. [Google Scholar] [CrossRef]
- Chen, C.T. Extension of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, J. An integrated group decision-making method dealing with fuzzy preferences for alternatives and individual judgments for selection criteria. Group Decis. Negot. 2003, 12, 501–515. [Google Scholar] [CrossRef]
- Krohling, R.A.; Campanharo, V.C. Fuzzy TOPSIS for group decision making: A case study for accidents with oil spill in the sea. Expert Syst. Appl. 2011, 38, 4190–4197. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z. A novel method for fuzzy multi-criteria decision making. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 497–519. [Google Scholar] [CrossRef]
- Mehlawat, M.K.; Guptal, P. A new fuzzy group multi-criteria decision making method with an application to the critical path selection. Int. J. Adv. Manuf. Technol. 2016, 83, 1281–1296. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Xu, Z. Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making. Fuzzy Optim. Decis. Mak. 2007, 6, 109–121. [Google Scholar] [CrossRef]
- Mondal, K.; Pramanik, S. Intuitionistic fuzzy multi criteria group decision making approach to quality-brick selection problem. J. Appl. Quant. Methods 2014, 9, 35–50. [Google Scholar]
- Dey, P.P.; Pramanik, S.; Giri, B.C. Multi-criteria group decision making in intuitionistic fuzzy environment based on grey relational analysis for weaver selection in Khadi institution. J. Appl. Quant. Methods 2015, 10, 1–14. [Google Scholar]
- Smarandache, F. A unifying field in logics. In Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, DE, USA, 1999. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistruct. 2010, 4, 410–413. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing; Hexis: Phoenix, AZ, USA, 2005. [Google Scholar]
- Kharal, A. A neutrosophic multi-criteria decision making method. New Math. Nat. Comput. 2014, 10, 143–162. [Google Scholar] [CrossRef]
- Ye, J. Similarity measures between interval neutrosophic sets and their multi criteria decision-making method. J. Intell. Fuzzy Syst. 2014, 26, 165–172. [Google Scholar]
- Ye, J. Multiple attribute group decision-making method with completely unknown weights based on similarity measures under single valued neutrosophic environment. J. Intell. Fuzzy Syst. 2014, 27, 2927–2935. [Google Scholar]
- Mondal, K.; Pramanik, S. Multi-criteria group decision making approach for teacher recruitment in higher education under simplified neutrosophic environment. Neutrosophic Sets Syst. 2014, 6, 28–34. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Entropy based grey relational analysis method for multi-attribute decision making under single valued neutrosophic assessments. Neutrosophic Sets Syst. 2014, 2, 102–110. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. A new methodology for neutrosophic multi-attribute decision-making with unknown weight information. Neutrosophic Sets Syst. 2014, 3, 44–54. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Cosine similarity measure based multi-attribute decision-making with trapezoidal fuzzy neutrosophic numbers. Neutrosophic Sets Syst. 2014, 8, 46–56. [Google Scholar]
- Mondal, K.; Pramanik, S. Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis. Neutrosophic Sets Syst. 2015, 9, 64–71. [Google Scholar]
- Mondal, K.; Pramanik, S. Neutrosophic tangent similarity measure and its application to multiple attribute decision making. Neutrosophic Sets Syst. 2015, 9, 85–92. [Google Scholar]
- Pramanik, S.; Biswas, P.; Giri, B.C. Hybrid vector similarity measures and their applications to multi-attribute decision making under neutrosophic environment. Neural Comput. Appl. 2017, 28, 1163–1176. [Google Scholar] [CrossRef]
- Sahin, R.; Küçük, A. Subsethood measure for single valued neutrosophic sets. J. Intell. Fuzzy Syst. 2015, 29, 525–530. [Google Scholar] [CrossRef]
- Ye, J. An extended TOPSIS method for multiple attribute group decision making based on single valued neutrosophic linguistic numbers. J. Intell. Fuzzy Syst. 2015, 28, 247–255. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. TOPSIS method for multi-attribute group decision-making under single-valued neutrosophic environment. Neural Comput. Appl. 2016, 27, 727–737. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Value and ambiguity index based ranking method of single-valued trapezoidal neutrosophic numbers and its application to multi-attribute decision making. Neutrosophic Sets Syst. 2016, 12, 127–138. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Aggregation of triangular fuzzy neutrosophic set information and its application to multi-attribute decision making. Neutrosophic Sets Syst. 2016, 12, 20–40. [Google Scholar]
- Smarandache, F.; Pramanik, S. (Eds.) New Trends in Neutrosophic Theory and Applications; Pons Editions: Brussels, Belgium, 2016; pp. 15–161. ISBN 978-1-59973-498-9. [Google Scholar]
- Sahin, R.; Liu, P. Maximizing deviation method for neutrosophic multiple attribute decision making with incomplete weight information. Neural Comput. Appl. 2016, 27, 2017–2029. [Google Scholar] [CrossRef]
- Sahin, R. Cross-entropy measure on interval neutrosophic sets and its applications in multi criteria decision making. Neural Comput. Appl. 2017, 28, 1177–1187. [Google Scholar] [CrossRef]
- Sahin, R.; Liu, P. Possibility-induced simplified neutrosophic aggregation operators and their application to multi-criteria group decision-making. J. Exp. Theor. Artif. Intell. 2017, 29, 769–785. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Multi-attribute group decision making based on expected value of neutrosophic trapezoidal numbers. New Math. Natural Comput. 2015. [Google Scholar] [CrossRef]
- Şahin, R. Multi-Criteria Neutrosophic Decision Making Method Based on Score and Accuracy Functions under Neutrosophic Environment. arXiv, 2014; arXiv:1412.5202. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. GRA method of multiple attribute decision making with single valued neutrosophic hesitant fuzzy set information. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; Volume 1, pp. 55–63. ISBN 978-1-59973-498-9. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Some distance measures of single valued neutrosophic hesitant fuzzy sets and their applications to multiple attribute decision making. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; Volume 1, pp. 27–34. ISBN 978-1-59973-498-9. [Google Scholar]
- Sahin, R.; Liu, P. Distance and similarity measure for multiple attribute with single–valued neutrosophic hesitant fuzzy information. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; Volume 1, pp. 35–54. ISBN 978-1-59973-498-9. [Google Scholar]
- Sahin, R.; Liu, P. Correlation coefficient of single-valued neutrosophic hesitant fuzzy sets and its applications in decision making. Neural Comput. Appl. 2017, 28, 1387–1395. [Google Scholar] [CrossRef]
- Ali, M.; Deli, I.; Smarandache, F. The theory of neutrosophic cubic sets and their applications in pattern recognition. J. Intell. Fuzzy Syst. 2016, 30, 1957–1963. [Google Scholar] [CrossRef]
- Jun, Y.B.; Smarandache, F.; Kim, C.S. Neutrosophic Cubic sets. New Math. Natural Comput. 2017, 13, 41–54. [Google Scholar] [CrossRef]
- Banerjee, D.; Giri, B.C.; Pramanik, S.; Smarandache, F. GRA for multi attribute decision making in neutrosophic cubic set environment. Neutrosophic Sets Syst. 2017, 15, 60–69. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Pramanik, S.; Mukhopadhyaya, D. Grey relational analysis based intuitionistic fuzzy multi criteria group decision-making approach for teacher selection in higher education. Int. J. Comput. Appl. 2011, 34, 21–29. [Google Scholar]
- Chang, K.H.; Chang, Y.C.; Tasi, I.T. Enhancing FMEA assessment by integrating grey relational analysis and the decision making trial and evaluation laboratory approach. Eng. Fail. Anal. 2013, 31, 211–224. [Google Scholar] [CrossRef]
- Pramanik, S.; Dalapati, S.; Alam, S.; Roy, T.K.; Smarandache, F. neutrosophic cubic MCGDM method based on similarity measure. Neutrosophic Sets Syst. 2017, 16, 44–56. [Google Scholar] [CrossRef]
- Lu, Z.; Ye, J. Cosine measures of neutrosophic cubic sets for multiple attribute decision-making. Symmetry 2017, 9, 121. [Google Scholar] [CrossRef]
- Pramanik, S.; Dey, P.P.; Giri, B.C.; Smarandache, F. An extended TOPSIS for multi-attribute decision making problems with neutrosophic cubic information. Neutrosophic Sets Syst. 2017, 17, 20–28. [Google Scholar]
- Zhan, J.; Khan, M.; Gulistan, M. Applications of neutrosophic cubic sets in multi-criteria decision-making. Int. J. Uncertain. Quantif. 2017, 7, 377–394. [Google Scholar] [CrossRef]
- Ye, J. Linguistic neutrosophic cubic numbers and their multiple attribute decision-making method. Information 2017, 8, 110. [Google Scholar] [CrossRef]
- Gomes, L.; Lima, M. TODIM: Basics and application to multicriteria ranking of projects with environmental impacts. Found. Comput. Decis. Sci. 1991, 16, 113–127. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econ. J. Econ. Soc. 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Krohling, R.A.; De Souza, T.T.M. Combining prospect theory and fuzzy numbers to multi-criteria decision making. Expert Syst. Appl. 2012, 39, 11487–11493. [Google Scholar] [CrossRef]
- Liu, P.; Teng, F. An extended TODIM method for multiple attribute group decision-making based on 2-dimension uncertain linguistic Variable. Complexity 2014, 21, 20–30. [Google Scholar] [CrossRef]
- Tosun, O.; Akyu, G. A fuzzy TODIM approach for the supplier selection problem. Int. J. Comput. Intell. Syst. 2015, 8, 317–329. [Google Scholar] [CrossRef]
- Gomes, L.F.A.M.; Machado, M.A.S.; Da Costa, F.F.; Rangel, L.A.D. Criteria interactions in multiple criteria decision aiding: A Choquet formulation for the TODIM method. Procedia Comput. Sci. 2013, 17, 324–331. [Google Scholar] [CrossRef]
- Fan, Z.P.; Zhang, X.; Chen, F.D.; Liu, Y. Extended TODIM method for hybrid multiple attribute decision making problems. Knowl. Based Syst. 2013, 42, 40–48. [Google Scholar] [CrossRef]
- Krohling, R.A.; Pacheco, A.G.C.; Siviero, A.L.T. IF-TODIM: An intuitionistic fuzzy TODIM to multi-criteria decision making. Knowl. Based Syst. 2013, 53, 142–146. [Google Scholar] [CrossRef]
- Wang, J.Q. TODIM method with multi-valued neutrosophic set. Control Decis. 2015, 30, 1139–1142. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, P.; Shi, L. An extended multiple attribute group decision-making TODIM method based on the neutrosophic numbers. J. Intell. Fuzzy Syst. 2016, 30, 1773–1781. [Google Scholar] [CrossRef]
- Ji, P.; Zhang, H.; Wang, J. A projection-based TODIM method under multi-valued neutrosophic environments and its application in personnel selection. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Xu, D.S.; Wei, C.; Wei, G.W. TODIM method for single-valued neutrosophic multiple attribute decision making. Information 2017, 8, 125. [Google Scholar] [CrossRef]
- Liu, P.D.; Wang, Y.M. Multiple attribute decision-making method based on single valued neutrosophic normalized weighted Bonferroni mean. Neural Comput. Appl. 2014, 25, 2001–2010. [Google Scholar] [CrossRef]
- Liu, P.D.; Tang, G.L. Some power generalized aggregation operators based on the interval neutrosophic numbers and their application to decision making. J. Intell. Fuzzy Syst. 2016, 30, 2517–2528. [Google Scholar] [CrossRef]
- Liu, P.D.; Wang, Y.M. Interval neutrosophic prioritized OWA operator and its application to multiple attribute decision making. J. Syst. Sci. Complex. 2016, 29, 681–697. [Google Scholar] [CrossRef]
- Liu, P.D. The aggregation operators based on Archimedean t-conorm and t-norm for the single valued neutrosophic numbers and their application to decision making. Int. J. Fuzzy Syst. 2016, 18, 849–863. [Google Scholar] [CrossRef]
- Liu, P.D.; Chu, Y.C.; Li, Y.W.; Chen, Y.B. Some generalized neutrosophic number Hamacher aggregation operators and their application to group decision making. Int. J. Fuzzy Syst. 2014, 16, 242–255. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).