Certain Competition Graphs Based on Intuitionistic Neutrosophic Environment

Abstract

The concept of intuitionistic neutrosophic sets provides an additional possibility to represent imprecise, uncertain, inconsistent and incomplete information, which exists in real situations. This research article first presents the notion of intuitionistic neutrosophic competition graphs. Then, p-competition intuitionistic neutrosophic graphs and m-step intuitionistic neutrosophic competition graphs are discussed. Further, applications of intuitionistic neutrosophic competition graphs in ecosystem and career competition are described.

1. Introduction

Euler [1] introduced the concept of graph theory in 1736, which has applications in various fields, including image capturing, data mining, clustering and computer science [2,3,4,5]. A graph is also used to develop an interconnection between objects in a known set of objects. Every object can be illustrated by a vertex, and interconnection between them can be illustrated by an edge. The notion of competition graphs was developed by Cohen [6] in 1968, depending on a problem in ecology. The competition graphs have many utilizations in solving daily life problems, including channel assignment, modeling of complex economic, phytogenetic tree reconstruction, coding and energy systems.

Fuzzy set theory and intuitionistic fuzzy sets theory are useful models for dealing with uncertainty and incomplete information. However, they may not be sufficient in modeling of indeterminate and inconsistent information encountered in the real world. In order to cope with this issue, neutrosophic set theory was proposed by Smarandache [7] as a generalization of fuzzy sets and intuitionistic fuzzy sets. However, since neutrosophic sets are identified by three functions called truth-membership $(t)$, indeterminacy-membership $(i)$ and falsity-membership $(f)$, whose values are the real standard or non-standard subset of unit interval $]0^{-},1^{+}[$. There are some difficulties in modeling of some problems in engineering and sciences. To overcome these difficulties, Smarandache in 1998 [8] and Wang et al. [9] in 2010 defined the concept of single-valued neutrosophic sets and their operations as a generalization of intuitionistic fuzzy sets. Yang et al. [10] introduced the concept of the single-valued neutrosophic relation based on the single-valued neutrosophic set. They also developed kernels and closures of a single-valued neutrosophic set. The concept of the single-valued intuitionistic neutrosophic set was proposed by Bhowmik and Pal [11,12].

The valuable contribution of fuzzy graph and generalized structures has been studied by several researchers [13,14,15,16,17,18,19,20,21,22]. Smarandache [23] proposed the notion of the neutrosophic graph and separated them into four main categories. Wu [24] discussed fuzzy digraphs. Fuzzy m-competition and p-competition graphs were introduced by Samanta and Pal [25]. Samanta et al. [26] introduced m-step fuzzy competition graphs. Dhavaseelan et al. [27] defined strong neutrosophic graphs. Akram and Shahzadi [28] introduced the notion of a single-valued neutrosophic graph and studied some of its operations. They also discussed the properties of single-valued neutrosophic graphs by level graphs. Akram and Shahzadi [29] introduced the concept of neutrosophic soft graphs with applications. Broumi et al. [30] proposed single-valued neutrosophic graphs and discussed some properties. Ye [31,32,33] has presented several novel concepts of neutrosophic sets with applications. In this paper, we first introduce the concept of intuitionistic neutrosophic competition graphs. We then discuss m-step intuitionistic neutrosophic competition graphs. Further, we describe applications of intuitionistic neutrosophic competition graphs in ecosystem and career competition. Finally, we present our developed methods by algorithms.

Our paper is divided into the following sections: In Section 2, we introduce certain competition graphs using the intuitionistic neutrosophic environment. In Section 3, we present applications of intuitionistic neutrosophic competition graphs in ecosystem and career competition. Finally, Section 4 provides conclusions and future research directions.

2. Intuitionistic Neutrosophic Competition Graphs

We have used standard definitions and terminologies in this paper. For other notations, terminologies and applications not mentioned in the paper, the readers are referred to [34,35,36,37,38,39,40,41,42,43,44].

Definition 1.

[38] Let X be a fixed set. A generalized intuitionistic fuzzy set I of X is an object having the form I=$\{(u,{\mu }_I(u),{\nu }_I(u))|u\in U\}$, where the functions ${\mu }_I(u):\to [0,1]$ and ${\nu }_I(u):\to [0,1]$ define the degree of membership and degree of non-membership of an element $u\in X$, respectively, such that:

$$\min \{{\mu }_I(u),{\nu }_I(u)\}\le 0.5,forallu\in X.$$

This condition is called the generalized intuitionistic condition.

Definition 2.

[11] An intuitionistic neutrosophic set (IN-set) is defined as $\breve{A}=(w$, $t_{\breve{A}}(w)$, $i_{\breve{A}}(w)$, $f_{\breve{A}}(w))$, where:

$$\begin{array}{cc}\hfill t_{\breve{A}}(w)\wedge f_{\breve{A}}(w)& \le 0.5,\hfill \\ \hfill t_{\breve{A}}(w)\wedge i_{\breve{A}}(w)& \le 0.5,\hfill \\ \hfill i_{\breve{A}}(w)\wedge f_{\breve{A}}(w)& \le 0.5,\hfill \end{array}$$

for all, $w\in X$, such that:

$$\begin{array}{cc}\hfill 0& \le t_{\breve{A}}(w)+i_{\breve{A}}(w)+f_{\breve{A}}(w)\le 2.\hfill \end{array}$$

Definition 3.

[12] An intuitionistic neutrosophic relation (IN-relation) is defined as an intuitionistic neutrosophic subset of $X\times Y$, which has of the form:

$$R=\{((w,z),t_R(w,z),i_R(w,z),f_R(w,z)):w\in X,z\in Y\},$$

where $t_R$, $i_R$ and $f_R$ are intuitionistic neutrosophic subsets of $X\times Y$ satisfying the conditions:

1.

one of these $t_R(w$, $z)$, $i_R(w$, $z)$ and $f_R(w$, $z)$ is greater than or equal to $0.5$,

2.

$0\le t_R(w,z)+i_R(w,z)+f_R(w,z)\le 2$.

Definition 4.

An intuitionistic neutrosophic graph (IN-graph) $\mathfrak{G}=(X$, h, $k)$ (in short $\mathfrak{G}$) on X (vertex set) is a triplet such that:

1.

$t_k(w,z)\le t_h(w)\wedge t_h(z)$, $i_k(w,z)\le i_h(w)\wedge i_h(z)$, $f_k(w,z)\le f_h(w)\vee f_h(z)$,

2.

$t_k(w,z)\wedge i_k(w,z)\le 0.5$, $t_k(w,z)\wedge f_k(w,z)\le 0.5$, $i_k(w,z)\wedge f_k(w,z)\le 0.5$,

3.

$0\le t_k(w,z)+i_k(w,z)+f_k(w,z)\le 2$, for all $w,z\in X$,

where,

$$t_h,i_{h}and{f}_h\to [0,1]$$

denote the truth-membership, indeterminacy-membership and falsity-membership of an element $w\in X$ and:

$$t_k,i_{k}and{f}_k\to [0,1]$$

denote the truth-membership, indeterminacy-membership and falsity-membership of an element $(w$, $z)\in E$ (edge set).

We now illustrate this with an example.

Example 1.

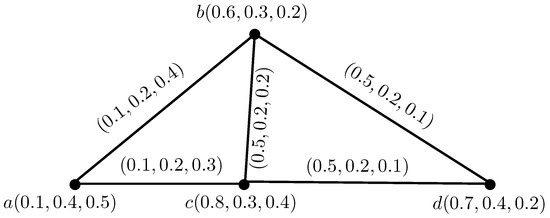
Consider IN-graph $\mathfrak{G}$ on non-empty set X, as shown in Figure 1.

Figure 1. Intuitionistic neutrosophic graph (IN-graph).

Definition 5.

Let $\overrightarrow{\mathfrak{G}}$ be an intuitionistic neutrosophic digraph (IN-digraph), then intuitionistic neutrosophic out-neighborhoods (IN-out-neighborhoods) of a vertex w are an IN-set:

$${\mathbb{N}}^{+}(w)=(X_w^{+},t_w^{+},i_w^{+},f_w^{+}),$$

where,

$$X_w^{+}=\{z|k_1\overrightarrow{(w,z)}>0,k_2\overrightarrow{(w,z)}>0,k_3\overrightarrow{(w,z)}>0\},$$

such that $t_w^{+}:X_w^{+}\to [0,1]$ defined by $t_w^{+}(z)=k_1\overrightarrow{(w,z)}$, $i_w^{+}:X_w^{+}\to [0,1]$ defined by $i_w^{+}(z)=k_2\overrightarrow{(w,z)}$ and $f_z^{+}:X_z^{+}\to [0,1]$ defined by $f_w^{+}(z)=k_3\overrightarrow{(w,z)}$.

Definition 6.

Let $\overrightarrow{\mathfrak{G}}$ be an IN-digraph, then the intuitionistic neutrosophic in-neighborhoods (IN-in-neighborhoods) of a vertex w are an IN-set:

$${\mathbb{N}}^{-}(w)=(X_w^{-},t_w^{-},i_w^{-},f_w^{-}),$$

where,

$$X_w^{-}=\{z|k_1\overrightarrow{(z,w)}>0,k_2\overrightarrow{(z,w)}>0,k_3\overrightarrow{(z,w)}>0\},$$

such that $t_w^{-}:X_w^{-}\to [0,1]$ defined by $t_w^{-}(z)=k_1\overrightarrow{(z,w)}$, $i_w^{-}:X_w^{-}\to [0,1]$ defined by $i_w^{-}(z)=k_2\overrightarrow{(z,w)}$ and $f_w^{-}:X_w^{-}\to [0,1]$ defined by $f_w^{-}(z)=k_3\overrightarrow{(z,w)}$.

Example 2.

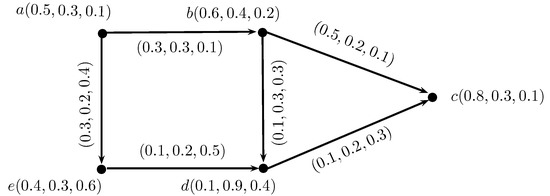
Consider $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ to be an IN-digraph, such that, $X=\{a$, b, c, d, $e\}$, $h=\{($a, $0.5$, $0.3$, $0.1)$, (b, $0.6$, $0.4$, $0.2)$, (c, $0.8$, $0.3$, $0.1)$, (d, $0.1$, $0.9$, $0.4)$, (e, $0.4$, $0.3$, $0.6)\}$ and $k=\{(\overrightarrow{ab}$, $0.3$, $0.3$, $0.1)$, $(\overrightarrow{ae}$, $0.3$, $0.2$, $0.4)$, $(\overrightarrow{bc}$, $0.5$, $0.2$, $0.1)$, $(\overrightarrow{ed}$, $0.1$, $0.2$, $0.5)$, $(\overrightarrow{dc}$, $0.1$, $0.2$, $0.3)$, $(\overrightarrow{bd}$, $0.1$, $0.3$, $0.3)\}$, as shown in Figure 2.

Figure 2. IN-digraph.

Then, ${\mathbb{N}}^{+}(a)=\{(b$, $0.3$, $0.3$, $0.1)$, $(e$, $0.3$, $0.2$, $0.4)\}$, ${\mathbb{N}}^{+}(c)=\varnothing$, ${\mathbb{N}}^{+}(d)=\{(c$, $0.1$, $0.2$, $0.3)\}$, and ${\mathbb{N}}^{-}(b)=\{($a, $0.3$, $0.3$, $0.1)\}$, ${\mathbb{N}}^{-}(c)=\{($b, $0.5$, $0.2$, $0.1)$, (d, $0.1$, $0.2$, $0.3)\}$. Similarly, we can calculate IN-out and in-neighborhoods of the remaining vertices.

Definition 7.

The height of an IN-set $\breve{A}=(w$, $t_{\breve{A}}$, $i_{\breve{A}}$, $f_{\breve{A}})$ is defined as:

$$H(\breve{A})=(\underset{w\in X}{\sup }{t}_{\breve{A}}(w),\underset{w\in X}{\sup }{i}_{\breve{A}}(w),\underset{w\in X}{\inf }{f}_{\breve{A}}(w))=(H_1(\breve{A}),H_2(\breve{A}),H_3(\breve{A})).$$

For example, the height of an IN-set $\breve{A}=\{(a$, $0.5$, $0.7$, $0.2)$, $(b$, $0.1$, $0.2$, $1)$, $(c$, $0.3$, $0.5$, $0.3)\}$ in $X=\{a$, b, $c\}$ is $H(\breve{A})=(0.5$, $0.7$, $0.2)$.

Definition 8.

An intuitionistic neutrosophic competition graph (INC-graph) $\mathbb{C}(\overrightarrow{\mathfrak{G}})$ of an IN-digraph $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is an undirected IN-graph $\mathfrak{G}=($X, h, $k)$, which has the same intuitionistic neutrosophic set of vertices as in $\overrightarrow{\mathfrak{G}}$ and has an intuitionistic neutrosophic edge between two vertices w, $z\in X$ in $\mathbb{C}(\overrightarrow{\mathfrak{G}})$ if and only if ${\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)$ is a non-empty IN-set in $\overrightarrow{\mathfrak{G}}$. The truth-membership, indeterminacy-membership and falsity-membership values of edge $(w$, $z)$ in $\mathbb{C}(\overrightarrow{\mathfrak{G}})$ are:

$$\begin{array}{cc}\hfill t_k(w,z)& =(t_h(w)\wedge t_h(z))H({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)),\hfill \\ \hfill i_k(w,z)& =(i_h(w)\wedge i_h(z))H({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)),\hfill \\ \hfill f_k(w,z)& =(f_h(w)\vee f_h(z))H({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)),respectively.\hfill \end{array}$$

Example 3.

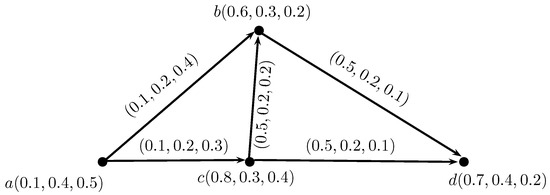
Consider $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ to be an IN-digraph, such that, $X=\{a$, b, c, $d\}$, $h=\{(a$, $0.1$, $0.4$, $0.5)$, $(b$, $0.6$, $0.3$, $0.2)$, $(c$, $0.8$, $0.3$, $0.4)$, $(d$, $0.7$, $0.4$, $0.2)\}$ and $k=\{(\overrightarrow{ab}$, $0.1$, $0.2$, $0.4)$, $(\overrightarrow{ac}$, $0.1$, $0.2$, $0.3)$, $(\overrightarrow{bc}$, $0.5$, $0.2$, $0.2)$, $(\overrightarrow{bd}$, $0.5$, $0.2$, $0.1)$, $(\overrightarrow{cd}$, $0.5$, $0.2$, $0.1)\}$, as shown in Figure 3.

Figure 3. IN-digraph.

By direct calculations, we have Table 1 and Table 2 representing IN-out and in-neighborhoods, respectively.

Table 1. IN-out-neighborhoods.

w	${\mathbb{N}}^{+}(\mathit{w})$
a	{(b, 0.1, 0.2, 0.4), (c, 0.1, 0.2, 0.3)}
b	{(d, 0.5, 0.2, 0.1)}
c	{(b, 0.5, 0.2, 0.2), (d, 0.5, 0.2, 0.1)}
d	∅

Table 2. IN-in-neighborhoods.

w	${\mathbb{N}}^{-}(\mathit{w})$
a	∅
b	{(a, 0.1, 0.2, 0.4), (c, 0.1, 0.2, 0.3)}
c	{(a, 0.1, 0.2, 0.3)}
d	{(b, 0.5, 0.2, 0.1), (c, 0.5, 0.2, 0.1)}

The INC-graph of Figure 3 is shown in Figure 4.

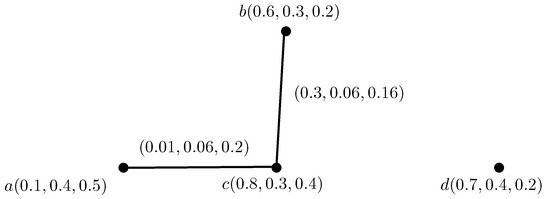
Figure 4. Intuitionistic neutrosophic competition graph (INC-graph).

Therefore, there is an edge between two vertices in INC-graph $\mathbb{C}(\overrightarrow{\mathfrak{G}})$, whose truth-membership, indeterminacy-membership and falsity-membership values are given by the above formula.

Definition 9.

For an IN-graph $\mathfrak{G}=(X$, h, $k)$, where $h=(h_1$, $h_2$, $h_3)$ and $k=(k_1$, $k_2$, $k_3)$, then an edge $(w$, $z)$, w, z $\in X$ is called independent strong if:

$$\begin{array}{cc}\hfill \frac{1}{2}[h_1(w)\wedge h_1(z)]& <k_1(w,z),\hfill \\ \hfill \frac{1}{2}[h_2(w)\wedge h_2(z)]& >k_2(w,z),\hfill \\ \hfill \frac{1}{2}[h_3(w)\vee h_3(z)]& >k_3(w,z).\hfill \end{array}$$

Otherwise, it is called weak.

Theorem 1.

Suppose $\overrightarrow{\mathfrak{G}}$ is an IN-digraph. If ${\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)$ contains only one element of $\overrightarrow{\mathfrak{G}}$, then the edge $(w$, $z)$ of $\mathbb{C}(\overrightarrow{\mathfrak{G}})$ is independent strong if and only if:

$$\begin{array}{cc}\hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_t& >0.5,\hfill \\ \hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_i& <0.5,\hfill \\ \hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_f& <0.5.\hfill \end{array}$$

Proof. 

Suppose, $\overrightarrow{\mathfrak{G}}$ is an IN-digraph. Suppose ${\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)=(a$, $\breve{p}$, q, $r)$, where $\breve{p}$, q and r are the truth-membership, indeterminacy-membership and falsity-membership values of either the edge $(w$, $a)$ or the edge $(z$, $a)$, respectively. Here,

$$\begin{array}{cc}\hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_t& =\breve{p}=H_1({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)),\hfill \\ \hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_i& =q=H_2({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)),\hfill \\ \hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_f& =r=H_3({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)).\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill k_1(w,z)& =\breve{p}\times [h_1(w)\wedge h_1(z)],\hfill \\ \hfill k_2(w,z)& =q\times [h_2(w)\wedge h_2(z)],\hfill \\ \hfill k_3(w,z)& =r\times [h_3(w)\vee h_3(z)].\hfill \end{array}$$

Therefore, the edge $(w$, $z)$ in $\mathbb{C}(\overrightarrow{\mathfrak{G}})$ is independent strong if and only if $\breve{p}>0.5$, $q<0.5$ and $r<0.5$. Hence, the edge $(w$, $z)$ of $\mathbb{C}(\overrightarrow{\mathfrak{G}})$ is independent strong if and only if:

$$\begin{array}{cc}\hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_t& >0.5,\hfill \\ \hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_i& <0.5,\hfill \\ \hfill |[{\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)]{|}_f& <0.5.\hfill \end{array}$$

☐

We illustrate the theorem with an example as shown in Figure 5.

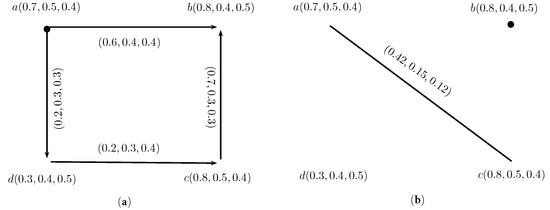
Figure 5. INC-graph. (a) IN-digraph; (b) corresponding INC-graph.

Theorem 2.

If all the edges of an IN-digraph $\overrightarrow{\mathfrak{G}}$ are independent strong, then:

$$\begin{array}{cc}\hfill \frac{k_1(w,z)}{{(h_1(w)\wedge h_1(z))}^2}& >0.5,\hfill \\ \hfill \frac{k_2(w,z)}{{(h_2(w)\wedge h_2(z))}^2}& <0.5,\hfill \\ \hfill \frac{k_3(w,z)}{{(h_3(w)\vee f_3(z))}^2}& <0.5\hfill \end{array}$$

for all edges $(w$, $z)$ in $\mathbb{C}(\overrightarrow{\mathfrak{G}})$.

Proof. 

Suppose all the edges of IN-digraph $\overrightarrow{\mathfrak{G}}$ are independent strong. Then:

$$\begin{array}{cc}\hfill \frac{1}{2}[h_1(w)\wedge h_1(z)]& <k_1\overrightarrow{(w,z)},\hfill \\ \hfill \frac{1}{2}[h_2(w)\wedge h_2(z)]& >k_2\overrightarrow{(w,z)},\hfill \\ \hfill \frac{1}{2}[h_3(w)\vee h_3(z)]& >k_3\overrightarrow{(w,z)},\hfill \end{array}$$

for all the edges $(w$, $z)$ in $\overrightarrow{\mathfrak{G}}$. Let the corresponding INC-graph be $\mathbb{C}(\overrightarrow{\mathfrak{G}})$.

Case (1): When ${\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)=\varnothing$ for all w, $z\in X$, then there does not exist any edge in $\mathbb{C}(\overrightarrow{\mathfrak{G}})$ between w and z. Thus, we have nothing to prove in this case.

Case (2): When ${\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)\ne \varnothing$, let ${\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)=\{(a_1$, $m_1$, $n_1$, ${\breve{p}}_1)$, $(a_2$, $m_2$, $n_2$, ${\breve{p}}_2)$, …, $(a_l$, $m_l$, $n_l$, ${\breve{p}}_l)\}$, where $m_i$, $n_i$ and ${\breve{p}}_i$ are the truth-membership, indeterminacy-membership and falsity-membership values of either $\overrightarrow{(w,a_i)}$ or $\overrightarrow{(z,a_i)}$ for $i=1$, 2, …, l, respectively. Therefore,

$$\begin{array}{cc}\hfill m_i& =[k_1\overrightarrow{(w,a_i)}\wedge k_1\overrightarrow{(z,a_i)}],\hfill \\ \hfill n_i& =[k_2\overrightarrow{(w,a_i)}\wedge k_2\overrightarrow{(z,a_i)}],\hfill \\ \hfill {\breve{p}}_i& =[k_3\overrightarrow{(w,a_i)}\vee k_3\overrightarrow{(z,a_i)}],fori=1,2,\dots ,l.\hfill \end{array}$$

Suppose,

$$\begin{array}{cc}\hfill H_1({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z))& =\max \{m_i,i=1,2,\dots ,l\}=m_{\max },\hfill \\ \hfill H_2({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z))& =\max \{n_i,i=1,2,\dots ,l\}=n_{\max },\hfill \\ \hfill H_3({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z))& =\min \{{\breve{p}}_i,i=1,2,\dots ,l\}={\breve{p}}_{\min }.\hfill \end{array}$$

Obviously, $m_{\max }>k_1\overrightarrow{(w,z)}$ and $n_{\max }<k_2\overrightarrow{(w,z)}$ and ${\breve{p}}_{\min }<k_3\overrightarrow{(w,z)}$ for all edges $\overrightarrow{(w,z)}$ show that:

$$\begin{array}{cc}\hfill \frac{m_{\max }}{h_1(w)\wedge h_1(z)}& >\frac{k_1\overrightarrow{(w,z)}}{h_1(w)\wedge h_1(z)}>0.5,\hfill \\ \hfill \frac{n_{\max }}{h_2(w)\wedge h_2(z)}& <\frac{k_2\overrightarrow{(w,z)}}{h_2(w)\wedge h_2(z)}<0.5,\hfill \\ \hfill \frac{{\breve{p}}_{\min }}{h_3(w)\vee h_3(z)}& <\frac{k_3\overrightarrow{(w,z)}}{h_3(w)\wedge h_3(z)}<0.5,\hfill \end{array}$$

therefore,

$$\begin{array}{cc}\hfill k_1(w,z)& =(h_1(w)\wedge h_1(z))H_1({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)),\hfill \\ \hfill k_1(w,z)& =[h_1(w)\wedge h_1(z)]\times m_{\max },\hfill \\ \hfill \frac{k_1(w,z)}{(h_1(w)\wedge h_1(z))}& =m_{\max },\hfill \\ \hfill \frac{k_1(w,z)}{{(h_1(w)\wedge h_1(z))}^2}& =\frac{m_{\max }}{(h_1(w)\wedge h_1(z))}>0.5,\hfill \end{array}$$

$$\begin{array}{cc}\hfill k_2(w,z)& =(h_2(w)\wedge h_2(z))H_2({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)),\hfill \\ \hfill k_2(w,z)& =[h_2(w)\wedge h_2(z)]\times n_{\max },\hfill \\ \hfill \frac{k_2(w,z)}{(h_2(w)\wedge h_2(z))}& =n_{\max },\hfill \\ \hfill \frac{k_2(w,z)}{{(h_2(w)\wedge h_2(z))}^2}& =\frac{n_{\max }}{(h_2(w)\wedge h_2(z))}<0.5,\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill k_3(w,z)& =(h_3(w)\vee h_3(z))H_3({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z)),\hfill \\ \hfill k_3(w,z)& =[h_3(w)\vee h_3(z)]\times {\breve{p}}_{\min },\hfill \\ \hfill \frac{k_3(w,z)}{(h_3(w)\vee h_3(z))}& ={\breve{p}}_{\min },\hfill \\ \hfill \frac{k_3(w,z)}{{(h_3(w)\vee h_3(z))}^2}& =\frac{{\breve{p}}_{\min }}{(h_3(w)\vee h_3(z))}<0.5.\hfill \end{array}$$

Hence, $\frac{k_1(w,z)}{{(h_1(w)\wedge h_1(z))}^2}>0.5$, $\frac{k_2(w,z)}{{(h_2(w)\wedge h_2(z))}^2}<0.5$, and $\frac{k_3(w,z)}{{(h_3(w)\vee h_3(z))}^2}<0.5$ for all edges $(w$, $z)$ in $\mathbb{C}(\overrightarrow{\mathfrak{G}})$. ☐

Theorem 3.

Let $\mathbb{C}(\overrightarrow{{\mathfrak{G}}_1})=(h_1$, $k_1)$ and $\mathbb{C}(\overrightarrow{{\mathfrak{G}}_2})=(h_2$, $k_2)$ be two INC-graph of IN-digraphs $\overrightarrow{{\mathfrak{G}}_1}=(h_1$, $\overrightarrow{l_1})$ and $\overrightarrow{{\mathfrak{G}}_2}=(h_2$, $\overrightarrow{l_2})$, respectively. Then, $\mathbb{C}(\overrightarrow{{\mathfrak{G}}_1}\square \overrightarrow{{\mathfrak{G}}_2})={\mathfrak{G}}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square \mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}\cup {\mathfrak{G}}^{\square }$ where, ${\mathfrak{G}}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square \mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}$ is an IN-graph on the crisp graph $(X_1\times X_2,E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\square E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }})$, $\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }$ and $\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }$ are the crisp competition graphs of $\overrightarrow{{\mathfrak{G}}_1}$ and $\overrightarrow{{\mathfrak{G}}_2}$, respectively. ${\mathfrak{D}}^{\square }$ is an IN-graph on $(X_1\times X_2,E^{\square })$ such that:

1.

$E^{\square }=\{(w_1,w_2)(z_1,z_2):z_1\in {\mathbb{N}}^{-}{(w_1)}^{\ast },z_2\in {\mathbb{N}}^{+}{(w_2)}^{\ast }\}$

$E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square }{E}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}=\{(w_1,w_2)(w_1,z_2):w_1\in X_1,w_2{z}_2\in E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}\}\cup \{(w_1,w_2)(z_1,w_2):w_2\in X_2,w_1{z}_1\in E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\}.$

2.

$t_{h_1\square h_2}=t_{h_1}(w_1)\wedge t_{h_2}(w_2)$, $i_{h_1\square h_2}=i_{h_1}(w_1)\wedge i_{h_2}(w_2)$, $f_{h_1\square h_2}=f_{h_1}(w_1)\vee f_{h_2}(w_2).$

3.

$t_k((w_1,w_2)(w_1,z_2))=[t_{h_1}(w_1)\wedge t_{h_2}(w_2)\wedge t_{h_2}(z_2)]\times {\vee }_{x_2}\{t_{h_1}(w_1)\wedge t_{\overrightarrow{l_2}}(w_2{x}_2)\wedge t_{\overrightarrow{l_2}}(z_2{x}_2)\},(w_1,w_2)(w_1,z_2)\in E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\square E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }},x_2\in {({\mathbb{N}}^{+}(w_2)\cap {\mathbb{N}}^{+}(z_2))}^{\ast }.$

4.

$i_k((w_1,w_2)(w_1,z_2))=[i_{h_1}(w_1)\wedge i_{h_2}(w_2)\wedge i_{h_2}(z_2)]\times {\vee }_{x_2}\{i_{h_1}(w_1)\wedge i_{\overrightarrow{l_2}}(w_2{x}_2)\wedge i_{\overrightarrow{l_2}}(z_2{x}_2)\},(w_1,w_2)(w_1,z_2)\in E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\square E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }},x_2\in {({\mathbb{N}}^{+}(w_2)\cap {\mathbb{N}}^{+}(z_2))}^{\ast }.$

5.

$f_k((w_1,w_2)(w_1,z_2))=[f_{h_1}(w_1)\vee f_{h_2}(w_2)\vee f_{h_2}(z_2)]\times {\vee }_{x_2}\{f_{h_1}(w_1)\vee f_{\overrightarrow{l_2}}(w_2{x}_2)\vee f_{\overrightarrow{l_2}}(z_2{x}_2)\},(w_1,w_2)(w_1,z_2)\in E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\square E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }},x_2\in {({\mathbb{N}}^{+}(w_2)\cap {\mathbb{N}}^{+}(z_2))}^{\ast }.$

6.

$t_k((w_1,w_2)(z_1,w_2))=[t_{h_1}(w_1)\wedge t_{h_1}(z_1)\wedge t_{h_2}(w_2)]\times {\vee }_{x_1}\{t_{h_2}(w_2)\wedge t_{\overrightarrow{l_1}}(w_1{x}_1)\wedge t_{\overrightarrow{l_1}}(z_1{x}_1)\},(w_1,w_2)(z_1,w_2)\in E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\square E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }},x_1\in {({\mathbb{N}}^{+}(w_1)\cap {\mathbb{N}}^{+}(z_1))}^{\ast }.$

7.

$i_k((w_1,w_2)(z_1,w_2))=[i_{h_1}(w_1)\wedge i_{h_1}(z_1)\wedge i_{h_2}(w_2)]\times {\vee }_{x_1}\{i_{h_2}(w_2)\wedge i_{\overrightarrow{l_1}}(w_1{x}_1)\wedge i_{\overrightarrow{l_1}}(z_1{x}_1)\},(w_1,w_2)(z_1,w_2)\in E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\square E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }},x_1\in {({\mathbb{N}}^{+}(w_1)\cap {\mathbb{N}}^{+}(z_1))}^{\ast }.$

8.

$f_k((w_1,w_2)(z_1,w_2))=[f_{h_1}(w_1)\vee f_{h_1}(z_1)\vee f_{h_2}(w_2)]\times {\vee }_{x_1}\{f_{h_2}(w_2)\vee f_{\overrightarrow{l_1}}(w_1{x}_1)\vee t_{\overrightarrow{l_1}}(z_1{x}_1)\},(w_1,w_2)(z_1,w_2)\in E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\square E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }},x_1\in {({\mathbb{N}}^{+}(w_1)\cap {\mathbb{N}}^{+}(z_1))}^{\ast }.$

9.

$$\begin{gathered} t_k((w_1,w_2)(z_1,z_2))=[t_{h_1}(w_1)\wedge t_{h_1}(z_1)\wedge t_{h_2}(w_2)\wedge t_{h_2}(z_2)]\times [t_{h_1}(w_1)\wedge t_{\overrightarrow{l_1}}(z_1{w}_1)\wedge t_{h_2}(z_2)\wedge t_{\overrightarrow{l_2}}(w_2{z}_2)], \\ (w_1,z_1)(w_2,z_2)\in E^{\square }. \end{gathered}$$

10.

$$\begin{gathered} i_k((w_1,w_2)(z_1,z_2))=[i_{h_1}(w_1)\wedge i_{h_1}(z_1)\wedge i_{h_2}(w_2)\wedge i_{h_2}(z_2)]\times [i_{h_1}(w_1)\wedge i_{\overrightarrow{l_1}}(z_1{w}_1)\wedge i_{h_2}(z_2)\wedge i_{\overrightarrow{l_2}}(w_2{z}_2)], \\ (w_1,z_1)(w_2,z_2)\in E^{\square }. \end{gathered}$$

11.

$$\begin{gathered} f_k((w_1,w_2)(z_1,z_2))=[f_{h_1}(w_1)\vee f_{h_1}(z_1)\vee f_{h_2}(w_2)\vee f_{h_2}(z_2)]\times [f_{h_1}(w_1)\vee f_{\overrightarrow{l_1}}(z_1{w}_1)\vee f_{h_2}(z_2)\vee f_{\overrightarrow{l_2}}(w_2{z}_2)], \\ (w_1,z_1)(w_2,z_2)\in E^{\square }. \end{gathered}$$

Proof. 

Using similar arguments as in Theorem 2.1. [39], it can be proven. ☐

Example 4.

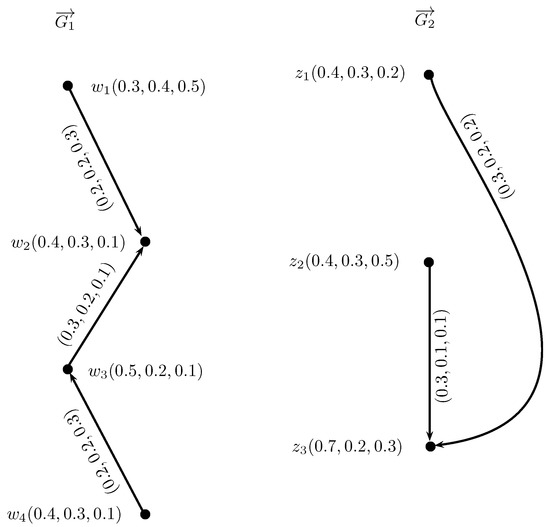
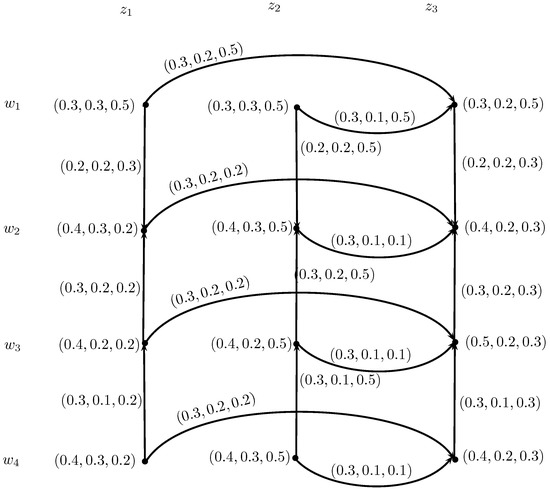
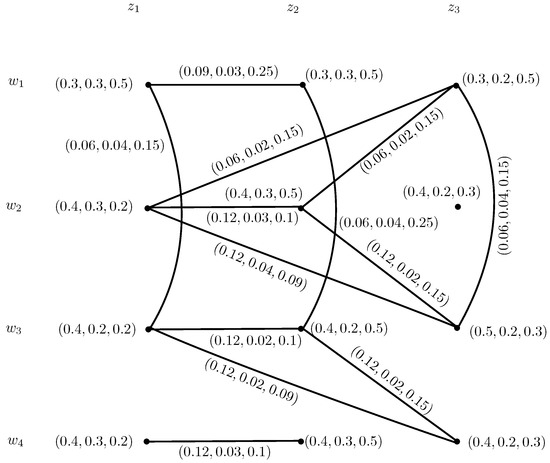
Consider $\overrightarrow{{\mathfrak{G}}_{\mathfrak{1}}}=(X_1$, $h_1$, $l_1)$ and $\overrightarrow{{\mathfrak{G}}_{\mathfrak{2}}}=(X_2$, $h_2$, $l_2)$ to be two IN-digraphs, respectively, as shown in Figure 6. The intuitionistic neutrosophic out and in-neighborhoods of $\overrightarrow{{\mathfrak{G}}_{\mathfrak{1}}}$ and $\overrightarrow{{\mathfrak{G}}_{\mathfrak{2}}}$ are given in Table 3 and Table 4. The INC-graphs $\mathbb{C}(\overrightarrow{{\mathfrak{G}}_1})$ and $\mathbb{C}(\overrightarrow{{\mathfrak{G}}_2})$ are given in Figure 7.

Figure 6. IN-digraphs.

Table 3. IN-out and in-neighborhoods of $\overrightarrow{{\mathfrak{G}}_1}$.

$\mathit{w}\in$${\mathit{X}}_{\mathbf{1}}$	${\mathbb{N}}^{+}(\mathit{w})$	${\mathbb{N}}^{-}(\mathit{w})$
$w_1$	$\{w_2(0.2,0.2,0.3)\}$	∅
$w_2$	∅	$\{w_1(0.2,0.2,0.3),w_3(0.3,0.1,0.1)\}$
$w_3$	$\{w_2(0.3,0.2,0.1)\}$	$\{w_4(0.3,0.1,0.1)\}$
$w_4$	$\{w_3(0.3,0.1,0.1)\}$	∅

Table 4. IN-out and in-neighborhoods of $\overrightarrow{{\mathfrak{G}}_2}$.

$\mathit{w}\in {\mathit{X}}_{\mathbf{2}}$	${\mathbb{N}}^{+}(\mathit{w})$	${\mathbb{N}}^{-}(\mathit{w})$
$z_1$	$\{z_3(0.3,0.2,0.2)\}$	∅
$z_2$	$\{z_3(0.3,0.1,0.1)\}$	∅
$z_3$	∅	$\{z_1(0.3,0.2,0.2),z_2(0.3,0.1,0.1)\}$

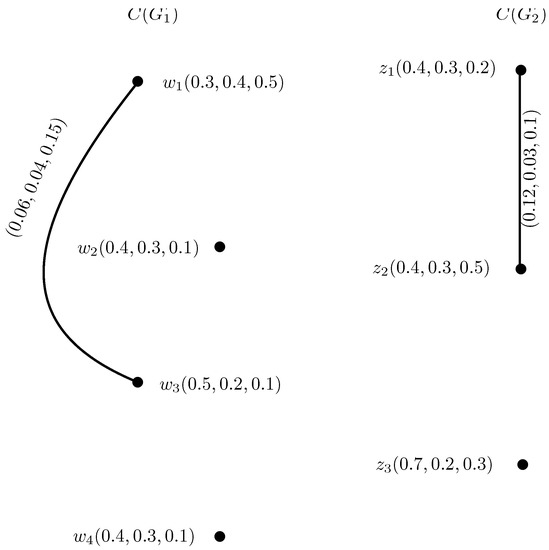
Figure 7. INC-graphs of $\overrightarrow{{\mathfrak{G}}_1}$ and $\overrightarrow{{\mathfrak{G}}_2}$.

We now construct the INC-graph ${\mathfrak{G}}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square \mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}\cup {\mathfrak{G}}^{\square }=(w$, $k)$, where $w=(t_w$, $i_w$, $f_w)$ and $k=(t_k$, $i_k$, $f_k)$, from $\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }$ and $\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }$ using Theorem $2.14$. We obtained two sets of edges by using Condition $(1)$.

$$\begin{array}{cc}\hfill E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }}\square E_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}=& \{(w_1,z_1)(w_1,z_2),(w_2,z_1)(w_2,z_2),(w_3,z_1)(w_3,z_2),\hfill \\ & (w_4,z_1)(w_4,z_2),(w_1,z_1)(w_3,z_1),\hfill \\ & (w_1,z_2)(w_3,z_2),(w_1,z_3)(w_3,z_3)\},\hfill \\ \hfill E^{\square }=& \{(w_2,z_1)(w_1,z_3),(w_2,z_1)(w_3,z_3),(w_2,z_2)(w_1,z_3)\hfill \\ & (w_2,z_2)(w_3,z_3),(w_3,z_1)(w_4,z_3),(w_3,z_2)(w_4,z_3)\}.\hfill \end{array}$$

The truth-membership, indeterminacy-membership and falsity-membership of edges can be calculated by using Conditions $(3)$ to $(11)$ as,

$$\begin{array}{c}k((w_1,z_1)(w_1,z_2))=(t_{h_1}(w_1)\wedge t_{h_2}(z_1)\wedge t_{h_2}(z_2),i_{h_1}(w_1)\wedge i_{h_2}(z_1)\wedge i_{h_2}(z_2),f_{h_1}(w_1)\vee f_{h_2}(z_1)\vee f_{h_2}(z_2))\hfill \\ \times (t_{h_1}(w_1)\wedge t_{l_2}(z_1{z}_3)\wedge t_{l_2}(z_2{z}_3),i_{h_1}(w_1)\wedge i_{l_2}(z_1{z}_3)\wedge i_{l_2}(z_2{z}_3),\hfill \\ f_{h_1}(w_1)\vee f_{l_2}(z_1{z}_3)\vee f_{l_2}(z_2{z}_3)\hfill \\ =(0.3,0.3,0.5)\times (0.3,0.1,0.5)\hfill \\ =(0.09,0.03,0.25),\hfill \\ k((w_2,z_1)(w_1,z_3))=(t_{h_1}(w_2)\wedge t_{h_2}(z_1)\wedge t_{h_1}(w_1)\wedge t_{h_2}(z_3),i_{h_1}(w_2)\wedge i_{h_2}(z_1)\wedge i_{h_1}(w_1)\wedge i_{h_2}(z_3),\hfill \\ f_{h_1}(w_2)\vee f_{h_2}(z_1)\vee f_{h_1}(w_1)\vee f_{h_2}(z_3))\hfill \\ \times (t_{h_1}(w_2)\wedge t_{l_1}(w_1{w}_2)\wedge t_{l_2}(z_3)\wedge t_{l_2}(z_1{z}_3),i_{h_1}(w_2)\wedge i_{l_1}(w_1{w}_2)\wedge i_{l_2}(z_3)\wedge i_{l_2}(z_1{z}_3),\hfill \\ f_{h_1}(w_2)\vee f_{l_1}(w_1{w}_2)\vee f_{l_2}(z_3)\vee f_{l_2}(z_1{z}_3))\hfill \\ =(0.3,0.2,0.5)\times (0.2,0.2,0.3)\hfill \\ =(0.06,0.04,0.15).\hfill \end{array}$$

All the truth-membership, indeterminacy-membership and falsity-membership degrees of adjacent edges of ${\mathfrak{G}}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square \mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}$ and ${\mathfrak{G}}^{\square }$ are given in Table 5.

Table 5. Adjacent edges of ${\mathfrak{G}}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square \mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}$∪${\mathfrak{G}}^{\square }$.

($\mathit{w}$, $\acute{\mathit{w}}$) ($\mathit{z}$, $\acute{\mathit{z}}$)	k ($\mathit{w}$, $\acute{\mathit{w}}$) ($\mathit{z}$, $\acute{\mathit{z}}$)
$(w_1$, $z_1)(w_1$, $z_2)$	$(0.09$, $0.03$, $0.25)$
$(w_2$, $z_1)(w_2$, $z_2)$	$(0.12$, $0.03$, $0.1)$
$(w_3$, $z_1)(w_3$, $z_2)$	$(0.12$, $0.02$, $0.1)$
$(w_4$, $z_1)(w_4$, $z_2)$	$(0.12$, $0.03$, $0.1)$
$(w_1$, $z_1)(w_3$, $z_1)$	$(0.06$, $0.04$, $0.15)$
$(w_1$, $z_3)(w_3$, $z_3)$	$(0.06$, $0.04$, $0.15)$
$(w_2$, $z_1)(w_1$, $z_3)$	$(0.06$, $0.04$, $0.15)$
$(w_2$, $z_1)(w_3$, $z_3)$	$(0.12$, $0.04$, $0.09)$
$(w_2$, $z_2)(w_1$, $z_3)$	$(0.06$, $0.02$, $0.15)$
$(w_2$, $z_2)(w_3$, $z_3)$	$(0.12$, $0.02$, $0.15)$
$(w_3$, $z_1)(w_4$, $z_3)$	$(0.12$, $0.02$, $0.09)$
$(w_3$, $z_2)(w_4$, $z_3)$	$(0.12$, $0.02$, $0.15)$
$(w_1$, $z_2)(w_3$, $z_2)$	$(0.06$, $0.04$, $0.25)$

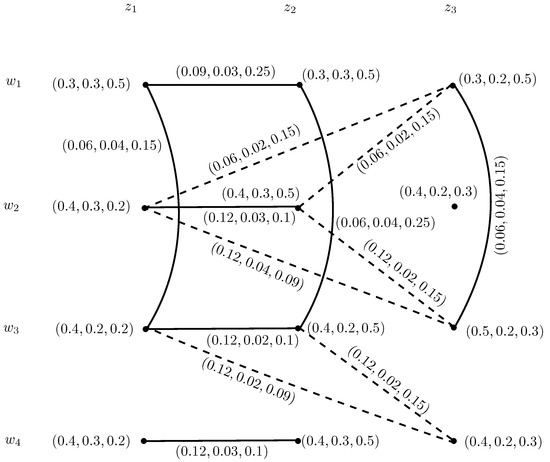
The INC-graph obtained by using this method is given in Figure 8 where solid lines indicate part of INC-graph obtained from ${\mathfrak{G}}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square \mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}$, and the dotted lines indicate the part of ${\mathfrak{G}}^{\square }$.

Figure 8. ${\mathfrak{G}}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square \mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}$∪${\mathfrak{G}}^{\square }$.

The Cartesian product $\overrightarrow{{\mathfrak{G}}_{\mathfrak{1}}}\square \overrightarrow{{\mathfrak{G}}_{\mathfrak{2}}}$ of IN-digraphs $\overrightarrow{{\mathfrak{G}}_{\mathfrak{1}}}$ and $\overrightarrow{{\mathfrak{G}}_{\mathfrak{2}}}$ is shown in Figure 9. The IN-out-neighborhoods of $\overrightarrow{{\mathfrak{G}}_{\mathfrak{1}}}\square \overrightarrow{{\mathfrak{G}}_{\mathfrak{2}}}$ are calculated in Table 6. The INC-graphs of $\overrightarrow{{\mathfrak{G}}_{\mathfrak{1}}}\square \overrightarrow{{\mathfrak{G}}_{\mathfrak{2}}}$ are shown in Figure 10.

Figure 9. $\overrightarrow{{\mathfrak{G}}_1}\square \overrightarrow{{\mathfrak{G}}_2}$.

Table 6. IN-out-neighborhoods of $\overrightarrow{{\mathfrak{G}}_1}\square \overrightarrow{{\mathfrak{G}}_2}$.

$(\mathit{w}$, $\mathit{z})$	${\mathbb{N}}^{+}(\mathit{w}$, $\mathit{z})$
$(w_1$, $z_1)$	$\{((w_2$, $z_1),0.2$, $0.2$, $0.3),((w_1$, $z_3),0.3$, $0.2$, $0.5)\}$
$(w_1$, $z_2)$	$\{((w_1$, $z_3),0.3$, $0.1$, $0.5),((w_2$, $z_2),0.2$, $0.2$, $0.5)\}$
$(w_1$, $z_3)$	$\{((w_2$, $z_3),$0.2, $0.2$, $0.3)\}$
$(w_2$, $z_1)$	$\{((w_2$, $z_3),$0.3, $0.2$, $0.2)\}$
$(w_2$, $z_2)$	$\{((w_2$, $z_3),$0.3, $0.1$, $0.1)\}$
$(w_2$, $z_3)$	∅
$(w_3$, $z_1)$	$\{((w_3$, $z_3),0.3$, $0.2$, $0.2),((w_2$, $z_1),0.3$, $0.2$, $0.2)\}$
$(w_3$, $z_2)$	$\{((w_2$, $z_2),0.3$, $0.2$, $0.5),((w_3$, $z_3),0.3$, $0.1$, $0.1)\}$
$(w_3$, $z_3)$	$\{((w_2$, $z_3),$0.3, $0.2$, $0.3)\}$
$(w_4$, $z_1)$	$\{((w_4$, $z_3),0.3$, $0.2$, $0.2),((w_3$, $z_1),0.3$, $0.1$, $0.2)\}$
$(w_4$, $z_2)$	$\{((w_4$, $z_3),0.3$, $0.1$, $0.1),((w_3$, $z_2),0.3$, $0.1$, $0.5)\}$
$(w_4$, $z_2)$	$\{((w_3$, $z_3),$0.3, $0.1$, $0.3)\}$

Figure 10. $\mathbb{C}(\overrightarrow{{\mathfrak{G}}_1}\square \overrightarrow{{\mathfrak{G}}_2})$.

It can be seen that $\mathbb{C}(\overrightarrow{{\mathfrak{G}}_1}\square \overrightarrow{{\mathfrak{G}}_2})\cong {\mathfrak{G}}_{\mathbb{C}{(\overrightarrow{{\mathfrak{G}}_1})}^{\ast }\square \mathbb{C}{(\overrightarrow{{\mathfrak{G}}_2})}^{\ast }}\cup {\mathfrak{G}}^{\square }$ from Figure 8 and Figure 10.

Definition 10.

The intuitionistic neutrosophic open-neighborhood of a vertex w of an IN-graph $\mathfrak{G}=(X$, h, $k)$ is IN-set $\mathbb{N}(w)=(X_w$, $t_w$, $i_w$, $f_w)$, where,

$$X_w=\{z|k_1(w,z)>0,k_2(w,z)>0,k_3(w,z)>0\},$$

and $t_w:X_w\to [0,1]$ defined by $t_w(z)=k_1(w$, $z)$, $i_w:X_w\to [0,1]$ defined by $i_w(z)=k_2(w$, $z)$ and $f_z:X_w\to [0,1]$ defined by $f_w(z)=k_3(w$, $z)$. For every vertex $w\in X$, the intuitionistic neutrosophic singleton set, $A_w=(w$, $h_1^{\prime }$, $h_2^{\prime }$, $h_3^{\prime })$, such that: $h_1^{\prime }:\{w\}\to [0,1]$, $h_2^{\prime }:\{w\}\to [0,1]$, $h_3^{\prime }:\{w\}\to [0,1]$ defined by $h_1^{\prime }(w)=h_1(w)$, $h_2^{\prime }(w)=h_2(w)$ and $h_3^{\prime }(w)=h_3(w)$, respectively. The intuitionistic neutrosophic closed-neighborhood of a vertex w is $\mathbb{N}[w]=\mathbb{N}(w)\cup A_w$.

Definition 11.

Suppose $\mathfrak{G}=(X$, h, $k)$ is an IN-graph. The single-valued intuitionistic neutrosophic open-neighborhood graph of $\mathfrak{G}$ is an IN-graph $\mathbb{N}(\mathfrak{G})=(X$, h, $k^{\prime })$, which has the same intuitionistic neutrosophic set of vertices in $\mathfrak{G}$ and has an intuitionistic neutrosophic edge between two vertices w, $z\in X$ in $\mathbb{N}(\mathfrak{G})$ if and only if $\mathbb{N}(w)\cap \mathbb{N}(z)$ is a non-empty IN-set in $\mathfrak{G}$. The truth-membership, indeterminacy-membership and falsity-membership values of the edge $(w$, $z)$ are given by:

$$\begin{array}{cc}\hfill k_1^{\prime }(w,z)& =[h_1(w)\wedge h_1(z)]H_1(\mathbb{N}(w)\cap \mathbb{N}(z)),\hfill \\ \hfill k_2^{\prime }(w,z)& =[h_2(w)\wedge h_2(z)]H_2(\mathbb{N}(w)\cap \mathbb{N}(z)),\hfill \\ \hfill k_3^{\prime }(w,z)& =[h_3(w)\vee h_3(z)]H_3(\mathbb{N}(w)\cap \mathbb{N}(z)),respectively.\hfill \end{array}$$

Definition 12.

Suppose $\mathfrak{G}=(X$, h, $k)$ is an IN-graph. The single-valued intuitionistic neutrosophic closed-neighborhood graph of $\mathfrak{G}$ is an IN-graph $\mathbb{N}(\mathfrak{G})=(X$, h, $k^{\prime })$, which has the same intuitionistic neutrosophic set of vertices in $\mathfrak{G}$ and has an intuitionistic neutrosophic edge between two vertices w, $z\in X$ in $\mathbb{N}[\mathfrak{G}]$ if and only if $\mathbb{N}[w]\cap \mathbb{N}[z]$ is a non-empty IN-set in $\mathfrak{G}$. The truth-membership, indeterminacy-membership and falsity-membership values of the edge $(w$, $z)$ are given by:

$$\begin{array}{cc}\hfill k_1^{\prime }(w,z)& =[h_1(w)\wedge h_1(z)]H_1(\mathbb{N}[w]\cap \mathbb{N}[z]),\hfill \\ \hfill k_2^{\prime }(w,z)& =[h_2(w)\wedge h_2(z)]H_2(\mathbb{N}[w]\cap \mathbb{N}[z]),\hfill \\ \hfill k_3^{\prime }(w,z)& =[h_3(w)\vee h_3(z)]H_3(\mathbb{N}[w]\cap \mathbb{N}[z]),respectively.\hfill \end{array}$$

Example 5.

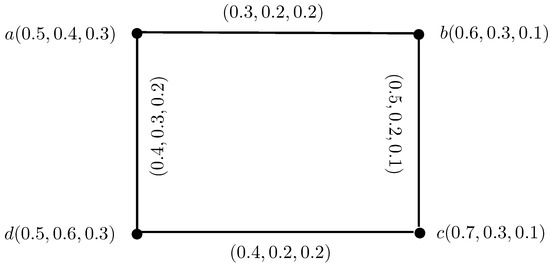
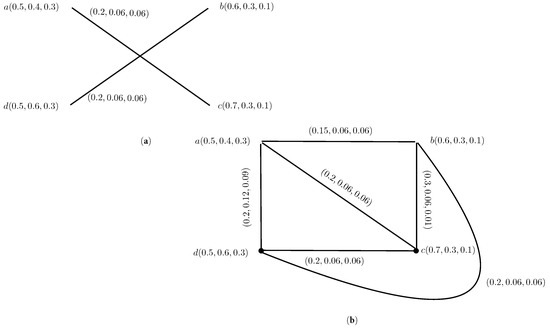
Consider $G=(X$, h, $k)$ to be an IN-graph, such that $X=\{a$, b, c, $d\}$, $h=\{(a$, $0.5$, $0.4$, $0.3)$, $(b$, $0.6$, $0.3$, $0.1)$, $(c$, $0.7$, $0.3$, $0.1)$, $(d$, $0.5$, $0.6$, $0.3)\}$, and $k=\{(ab$, $0.3$, $0.2$, $0.2)$, $(ad$, $0.4$, $0.3$, $0.2)$, $(bc$, $0.5$, $0.2$, $0.1)$, $(cd$, $0.4$, $0.2$, $0.2)\}$, as shown in Figure 11. Then, corresponding intuitionistic neutrosophic open and closed-neighborhood graphs are shown in Figure 12.

Figure 11. IN-digraph.

Figure 12. $(\mathbf{a})$$\mathbb{N}(\mathfrak{G})$; $(\mathbf{b})$$\mathbb{N}[\mathfrak{G}]$.

Theorem 4.

For each edge of an IN-graph $\mathfrak{G}$, there exists an edge in $\mathbb{N}[\mathfrak{G}]$.

Proof. 

Suppose $(w$, $z)$ is an edge of an IN-graph $\mathfrak{G}=(V$, h, $k)$. Suppose $\mathbb{N}[\mathfrak{G}]=(V$, h, $k^{\prime })$ is the corresponding closed neighborhood of an IN-graph. Suppose w, $z\in \mathbb{N}[w]$ and w, $z\in \mathbb{N}[z]$. Then, w, $z\in \mathbb{N}[w]\cap \mathbb{N}[z]$. Hence,

$$\begin{array}{cc}\hfill H_1(\mathbb{N}[w]\cap \mathbb{N}[z])& \ne 0,\hfill \\ \hfill H_2(\mathbb{N}[w]\cap \mathbb{N}[z])& \ne 0,\hfill \\ \hfill H_3(\mathbb{N}[w]\cap \mathbb{N}[z])& \ne 0.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill k_1^{\prime }(w,z)& =[h_1(w)\wedge h_1(z)]H_1(\mathbb{N}[w]\cap \mathbb{N}[z])\ne 0,\hfill \\ \hfill k_2^{\prime }(w,z)& =[h_2(w)\wedge h_2(z)]H_2(\mathbb{N}[w]\cap \mathbb{N}[z])\ne 0,\hfill \\ \hfill k_3^{\prime }(w,z)& =[h_3(w)\vee h_3(z)]H_3(\mathbb{N}[w]\cap \mathbb{N}[z])\ne 0.\hfill \end{array}$$

Thus, for each edge $(w$, $z)$ in IN-graph $\mathfrak{G}$, there exists an edge $(w$, $z)$ in $\mathbb{N}[\mathfrak{G}]$. ☐

Definition 13.

The support of an IN-set $\breve{A}=(w$, $t_{\breve{A}}$, $i_{\breve{A}}$, $f_{\breve{A}})$ in X is the subset $\widehat{A}$ of X defined by:

$$\widehat{A}=\{w\in X:t_{\breve{A}}(w)\ne 0,i_{\breve{A}}(w)\ne 0,f_{\breve{A}}(w)\ne 1\}$$

and $|supp(\widehat{A})|$ is the number of elements in the set.

We now discuss p-competition intuitionistic neutrosophic graphs.

Suppose p is a positive integer. Then, p-competition IN-graph ${\mathbb{C}}^p(\overrightarrow{\mathfrak{G}})$ of the IN-digraph $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is an undirected IN-graph $\mathfrak{G}=(X$, h, $k)$, which has the same intuitionistic neutrosophic set of vertices as in $\overrightarrow{\mathfrak{G}}$ and has an intuitionistic neutrosophic edge between two vertices w, z $\in X$ in ${\mathbb{C}}^p(\overrightarrow{\mathfrak{G}})$ if and only if $|supp({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z))|\ge p$. The truth-membership value of edge $(w$, $z)$ in ${\mathbb{C}}^p(\overrightarrow{\mathfrak{G}})$ is $t(w$, $z)=\frac{(i-p)+1}{i}[h_1(w)\wedge h_1(z)]H_1({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z))$; the indeterminacy-membership value of edge $(w$, $z)$ in ${\mathbb{C}}^p(\overrightarrow{\mathfrak{G}})$ is $i(w$, $z)=\frac{(i-p)+1}{i}[h_2(w)\wedge h_2(z)]H_2({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z))$; and the falsity-membership value of edge $(w$, $z)$ in ${\mathbb{C}}^p(\overrightarrow{\mathfrak{G}})$ is $f(w$, $z)=\frac{(i-p)+1}{i}[h_3(w)\vee h_3(z)]H_3({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z))$ where $i=|supp({\mathbb{N}}^{+}(w)\cap {\mathbb{N}}^{+}(z))|$.

The three-competition IN-graph is illustrated by the following example.

Example 6.

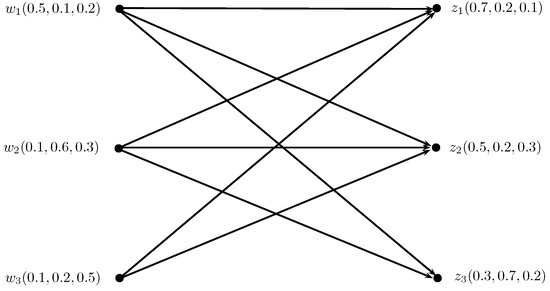
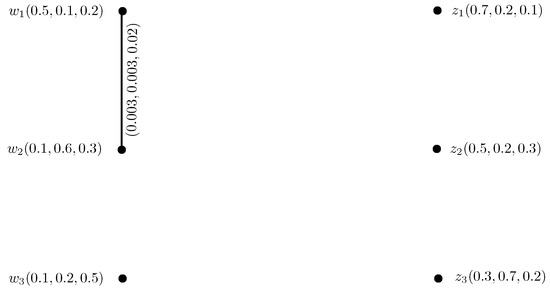
Consider $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ to be an IN-digraph, such that $X=\{w_1$, $w_2$, $w_3$, $z_1$, $z_2$, $z_3\}$, $h=\{(w_1$, $0.5$, $0.1$, $0.2)$, $(w_2$, $0.1$, $0.6$, $0.3)$, $(w_3$, $0.1$, $0.2$, $0.5)$, $(z_1$, $0.7$, $0.2$, $0.1)$, $(z_2$, $0.5$, $0.2$, $0.3)$, $(z_3$, $0.3$, $0.7$, $0.2)\}$ and $k=\{(\overrightarrow{(w_1,z_1)},0.4$, $0.1$, $0.1)$, $(\overrightarrow{(w_1,z_2)},0.5$, $0.1$, $0.3)$, $(\overrightarrow{(w_1,z_3)},0.2$, $0.1$, $0.1)$, $(\overrightarrow{(w_2,z_1)},0.1$, $0.1$, $0.2)$, $(\overrightarrow{(w_2,z_2)},0.1$, $0.1$, $0.2)$, $(\overrightarrow{(w_2,z_3)},0.1$, $0.5$, $0.2)$, $(\overrightarrow{(w_3,z_1)},0.1$, $0.1$, $0.1)$ $(\overrightarrow{(w_3,z_2)},0.1$, $0.1$, $0.2)\}$, as shown in Figure 13. Then, ${\mathbb{N}}^{+}(w_1)=\{(z_1$, $0.4$, $0.1$, $0.1)$, $(z_2$, $0.5$, $0.1$, $0.3)$, $(z_3$, $0.2$, $0.1$, $0.1)\}$, ${\mathbb{N}}^{+}(w_2)=\{(z_1$, $0.1$, $0.1$, $0.2)$, $(z_2$, $0.1$, $0.1$, $0.2)$, $(z_3$, $0.1$, $0.5$, $0.2)\}$ and ${\mathbb{N}}^{+}(w_3)=\{(z_1$, $0.1$, $0.1$, $0.1)$, $(z_2$, $0.1$, $0.1$, $0.2)\}$. Therefore, ${\mathbb{N}}^{+}(w_1)\cap {\mathbb{N}}^{+}(w_2)=\{(z_1$, $0.1$, $0.1$, $0.2)$, $(z_2$, $0.1$, $0.1$, $0.3)$, $(z_3$, $0.1$, $0.1$, $0.2)\}$, ${\mathbb{N}}^{+}(w_1)\cap {\mathbb{N}}^{+}(w_3)=\{(z_1$, $0.1$, $0.1$, $0.1)$, $(z_2$, $0.1$, $0.1$, $0.3)\}$ and ${\mathbb{N}}^{+}(w_2)\cap {\mathbb{N}}^{+}(w_3)=\{(z_1$, $0.1$, $0.1$, $0.2)$, $(z_2$, $0.1$, $0.1$, $0.2)\}$.

Figure 13. IN-digraph.

Now, $i=|supp({\mathbb{N}}^{+}(w_1)\cap {\mathbb{N}}^{+}(w_2))|=3$. For $p=3$, $t(w_1$, $w_2)=0.003$, $i(w_1$, $w_2)=0.003$ and $f(w_1$, $w_2)=0.02$. As shown in Figure 14.

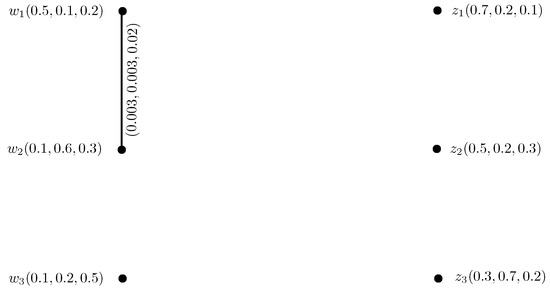
Figure 14. Three-competition IN-graph.

We now define another extension of INC-graph known as the m-step INC-graph.

• $\overrightarrow{P}{}_{z,w}^m$: a directed intuitionistic neutrosophic path of length m from z to w.
• ${\mathbb{N}}_m^{+}(z)$: single-valued intuitionistic neutrosophic m-step out-neighborhood of vertex z.
• ${\mathbb{N}}_m^{-}(z)$: single-valued intuitionistic neutrosophic m-step in-neighborhood of vertex z.
• ${\mathbb{C}}_m\overrightarrow{(\mathfrak{G})}$: m-step INC-graph of the IN-digraph $\overrightarrow{\mathfrak{G}}$.

Definition 14.

Suppose $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is an IN-digraph. The m-step IN-digraph of $\overrightarrow{\mathfrak{G}}$ is denoted by ${\overrightarrow{G}}_m=(X$, h, $k)$ where the intuitionistic neutrosophic set of vertices of $\overrightarrow{\mathfrak{G}}$ is the same as the intuitionistic neutrosophic set of vertices of ${\overrightarrow{G}}_m$ and has an edge between z and w in ${\overrightarrow{G}}_m$ if and only if there exists an intuitionistic neutrosophic directed path $\overrightarrow{P}{}_{z,w}^m$ in $\overrightarrow{\mathfrak{G}}$.

Definition 15.

The intuitionistic neutrosophic m-step out-neighborhood of vertex z of an IN-digraph $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is IN-set:

$${\mathbb{N}}_m^{+}(z)=(X_z^{+},t_z^{+},i_z^{+},f_z^{+}),\hspace{1em}where$$

$X_z^{+}=\{w|$ there exists a directed intuitionistic neutrosophic path of length m from z to w, $\overrightarrow{P}{}_{z,w}^m\}$, $t_z^{+}:X_z^{+}\to [0$, $1]$, $i_z^{+}:X_z^{+}\to [0$, $1]$ and $f_z^{+}:X_z^{+}\to [0$, $1]$ are defined by $t_z^{+}=min\{t\overrightarrow{(w_1,w_2)}$, $(w_1$, $w_2)$ is an edge of $\overrightarrow{P}{}_{z,w}^m\}$, $i_z^{+}=min\{i\overrightarrow{(w_1,w_2)}$, $(w_1$, $w_2)$ is an edge of $\overrightarrow{P}{}_{z,w}^m\}$ and $f_z^{+}=max\{f\overrightarrow{(w_1,w_2)}$, $(w_1$, $w_2)$ is an edge of $\overrightarrow{P}{}_{z,w}^m\}$, respectively.

Definition 16.

The intuitionistic neutrosophic m-step in-neighborhood of vertex z of an IN-digraph $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is IN-set:

$${\mathbb{N}}_m^{-}(z)=(X_z^{-},t_z^{-},i_z^{-},f_z^{-}),\hspace{1em}where$$

$X_z^{-}=\{w|$ there exists a directed intuitionistic neutrosophic path of length m from w to z, $\overrightarrow{P}{}_{z,w}^m\}$, $t_z^{-}:X_z^{-}\to [0$, $1]$, $i_z^{-}:X_z^{-}\to [0$, $1]$ and $f_z^{-}:X_z^{-}\to [0$, $1]$ are defined by $t_z^{-}=min\{t\overrightarrow{(w_1,w_2)}$, $(w_1$, $w_2)$ is an edge of $\overrightarrow{P}{}_{z,w}^m\}$, $i_z^{-}=min\{i\overrightarrow{(w_1,w_2)}$, $(w_1$, $w_2)$ is an edge of $\overrightarrow{P}{}_{z,w}^m\}$ and $f_z^{-}=max\{f\overrightarrow{(w_1,w_2)}$, $(w_1$, $w_2)$ is an edge of $\overrightarrow{P}{}_{z,w}^m\}$, respectively.

Definition 17.

Suppose $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is an IN-digraph. The m-step INC-graph of IN-digraph $\overrightarrow{\mathfrak{G}}$ is denoted by ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})=(X$, h, $k)$, which has the same intuitionistic neutrosophic set of vertices as in $\overrightarrow{\mathfrak{G}}$ and has an edge between two vertices w, $z\in X$ in ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})$ if and only if $({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))$ is a non-empty IN-set in $\overrightarrow{\mathfrak{G}}$. The truth-membership value of edge $(w$, $z)$ in ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})$ is $t(w$, $z)=[h_1(w)\wedge h_1(z)]H_1({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))$; the indeterminacy-membership value of edge $(w$, $z)$ in ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})$ is $i(w$, $z)=[h_2(w)\wedge h_2(z)]H_2({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))$; and the falsity-membership value of edge $(w$, $z)$ in ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})$ is $f(w$, $z)=[h_3(w)\vee h_3(z)]H_3({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))$.

The two-step INC-graph is illustrated by the following example.

Example 7.

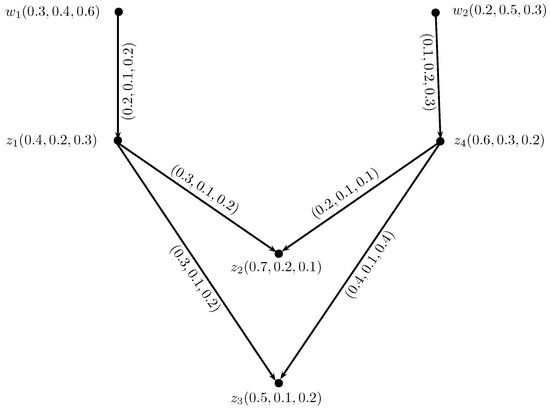
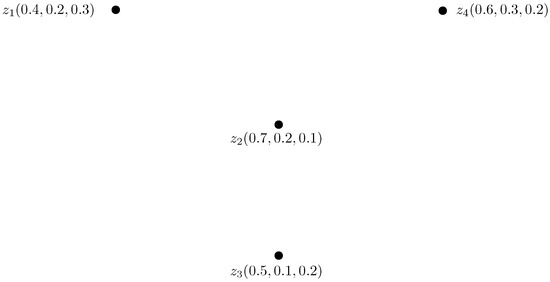
Consider $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is an IN-digraph, such that, $X=\{w_1$, $w_2$, $z_1$, $z_2$, $z_3\}$, $h=\{(w_1$, $0.3$, $0.4$, $0.6)$, $(w_2$, $0.2$, $0.5$, $0.3)$, $(z_1$, $0.4$, $0.2$, $0.3)$, $(z_2$, $0.7$, $0.2$, $0.1)$, $(z_3$, $0.5$, $0.1$, $0.2)$, $(z_4$, $0.6$, $0.3$, $0.2)\}$, and $k=\{(\overrightarrow{(w_1,z_1)}$, $0.2$, $0.1$, $0.2)$, $(\overrightarrow{(w_2,z_4)}$, $0.1$, $0.2$, $0.3)$, $(\overrightarrow{(z_1,z_3)}$, $0.3$, $0.1$, $0.2)$, $(\overrightarrow{(z_1,z_2)}$, $0.3$, $0.1$, $0.2)$, $(\overrightarrow{(z_4,z_2)}$, $0.2$, $0.1$, $0.1)$, and $(\overrightarrow{(z_4,z_3)}$, $0.4$, $0.1$, $0.4)\}$, as shown in Figure 15.

Figure 15. IN-digraph.

Then, ${\mathbb{N}}_2^{+}(w_1)=\{(z_2$, $0.2$, $0.1$, $0.2)$, $(z_3$, $0.2$, $0.1$, $0.2)\}$ and ${\mathbb{N}}_2^{+}(w_2)=\{(z_2$, $0.1$, $0.1$, $0.3)$, $(z_3$, $0.1$, $0.1$, $0.4)\}$. Therefore, ${\mathbb{N}}_2^{+}(w_1)\cap {\mathbb{N}}_2^{+}(w_2)=\{(z_2$, $0.1$, $0.1$, $0.3)$, $(z_3$, $0.1$, $0.1$, $0.4)\}$. Thus, $t(w_1,w_2)=0.02$, $i(w_1,w_2)=0.04$ and $f(w_1,w_2)=0.18$. This is shown in Figure 16.

Figure 16. Two-step INC-graph.

Definition 18.

The intuitionistic neutrosophic m-step out-neighborhood of vertex z of an IN-digraph $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is IN-set:

$${\mathbb{N}}_m(z)=(X_z,t_z,i_z,f_z),\hspace{1em}where$$

$X_z=\{w|$ there exists a directed intuitionistic neutrosophic path of length m from z to w, $P_{z,w}^m\}$, $t_z:X_z\to [0$, $1]$, $i_z:X_z\to [0$, $1]$ and $f_z:X_z\to [0$, $1]$ are defined by $t_z=min\{t(w_1$, $w_2)$, $(w_1$, $w_2)$ is an edge of $P_{z,w}^m\}$, $i_z=min\{i(w_1$, $w_2)$, $(w_1$, $w_2)$ is an edge of $P_{z,w}^m\}$ and $f_z=max\{f(w_1$, $w_2)$, $(w_1$, $w_2)$ is an edge of $P_{z,w}^m\}$, respectively.

Definition 19.

Suppose $\mathfrak{G}=(X$, h, $k)$ is an IN-graph. Then, the m-step intuitionistic neutrosophic neighborhood graph (IN-neighborhood-graph) ${\mathbb{N}}_m(\mathfrak{G})$ is defined by ${\mathbb{N}}_m(\mathfrak{G})=(X$, h, $\kappa )$, where $h=(h_1$, $h_2$, $h_3)$, $\kappa =({\kappa }_1$, ${\kappa }_2$, ${\kappa }_3)$, ${\kappa }_1:X\times X\to [0$, $1]$, ${\kappa }_2:X\times X\to [0$, $1]$ and ${\kappa }_3:X\times X\to [0,1]$ are such that:

$$\begin{array}{cc}\hfill {\kappa }_1(w,z)& =h_1(w)\wedge h_1(z)H_1({\mathbb{N}}_m(w)\cap {\mathbb{N}}_m(z)),\hfill \\ \hfill {\kappa }_2(w,z)& =h_2(w)\wedge h_2(z)H_2({\mathbb{N}}_m(w)\cap {\mathbb{N}}_m(z)),\hfill \\ \hfill {\kappa }_3(w,z)& =h_3(w)\vee h_3(z)H_3({\mathbb{N}}_m(w)\cap {\mathbb{N}}_m(z)),respectively.\hfill \end{array}$$

Theorem 5.

If all the edges of IN-digraph $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ are independent strong, then all the edges of ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})$ are independent strong.

Proof. 

Suppose $\overrightarrow{\mathfrak{G}}=(X$, h, $k)$ is an IN-digraph and ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})=(X$, h, $k)$ is the corresponding m-step INC-graph. Since all the edges of $\overrightarrow{\mathfrak{G}}$ are independent strong, then $H_1({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))>0.5$, $H_2({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))<0.5$ and $H_3({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))<0.5$. Then, $t(w,z)=(h_1(w)\wedge h_1(z))H_1({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))$, or $t(w,z)>0.5(h_1(w)\wedge h_1(z))$, or $\frac{t(w,z)}{(h_1(w)\wedge h_1(z))}>0.5$, $i(w,z)=(h_2(w)\wedge h_2(z))H_2({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))$, or $i(w,z)<0.5(h_2(w)\wedge h_2(z))$, or $\frac{i(w,z)}{(h_2(w)\wedge h_2(z))}<0.5$ and $f(w,z)=(h_3(w)\vee h_3(z))H_3({\mathbb{N}}_m^{+}(w)\cap {\mathbb{N}}_m^{+}(z))$, or $f(w,z)<0.5(h_3(w)\vee h_3(z))$, or $\frac{f(w,z)}{(h_3(w)\vee h_3(z))}<0.5$.

Hence, the edge $(w$, $z)$ is independent strong in ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})$. Since, $(w$, $z)$ is taken to be the arbitrary edge of ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})$, thus all the edges of ${\mathbb{C}}_m(\overrightarrow{\mathfrak{G}})$ are independent strong. ☐

3. Applications

Competition graphs are very important to represent the competition between objects. However, still, these representations are unsuccessful to deal with all the competitions of world; for that purpose, INC-graphs are introduced. Now, we discuss the applications of INC-graphs to study the competition along with algorithms. The INC-graphs have many utilizations in different areas.

3.1. Ecosystem

Consider a small ecosystem: human eats trout; bald eagle eats trout and salamander; trout eats phytoplankton, mayfly and dragonfly; salamander eats dragonfly and mayfly; snake eats salamander and frog; frog eats dragonfly and mayfly; mayfly eats phytoplankton; dragonfly eats phytoplankton. These nine species human, bald eagle, salamander, snake, frog, dragonfly, trout, mayfly and phytoplankton are taken as vertices. Let the degree of existence in the ecosystem of human be $60\%$, the degree of indeterminacy of existence be $30\%$ and the degree of false-existence be $10\%$, i.e., the truth-membership, indeterminacy-membership and falsity-membership values of the vertex human are $(0.6$, $0.3$, $0.1)$. Similarly, we assume the truth-membership, indeterminacy-membership and falsity-membership values of other vertices as $(0.7$, $0.3$, $0.2)$, $(0.4$, $0.3$, $0.5)$, $(0.3$, $0.5$, $0.1)$, $(0.3$, $0.4$, $0.5)$, $(0.3$, $0.5$, $0.2)$, $(0.7$, $0.3$, $0.2)$, $(0.6$, $0.4$, $0.2)$ and $(0.3$, $0.5$, $0.2)$. Suppose that human likes to eat trout $20\%$, indeterminate to eat $10\%$ and dislike to eat, say $10\%$. The likeness, indeterminacy and dislikeness of preys for predators are shown in Table 7.

Table 7. Likeness, indeterminacy and dislikeness of preys and predators.

Name of Predator	Name of Prey	Like to Eat	Indeterminate to Eat	Dislike to Eat
$Human$	$Trout$	20	10	10
$Bald$$eagle$	$Trout$	20	20	20
$Bald$$eagle$	$Salamander$	30	20	30
$Snake$	$Salamander$	20	20	10
$Snake$	$Frog$	30	20	40
$Salamander$	$Dragonfly$	20	20	20
$Salamander$	$Mayfly$	20	20	40
$Frog$	$Dragonfly$	30	30	30
$Trout$	$Dragonfly$	20	40	10
$Trout$	$Mayfly$	30	10	10
$Trout$	$Phytoplankton$	20	10	10
$Dragonfly$	$Phytoplankton$	10	10	10
$Mayfly$	$Phytoplankton$	30	30	20
$Frog$	$Mayfly$	10	10	10

It is clear that if trout is removed from the food cycle, then human must be lifeless, and in such a situation bald eagle, phytoplankton, dragonfly and mayfly grow in an undisciplined manner. Thus, we can evaluate the food cycle with the help of INC-graphs.

For this food web Figure 17, we have the following Table 8 of IN-out-neighborhoods.

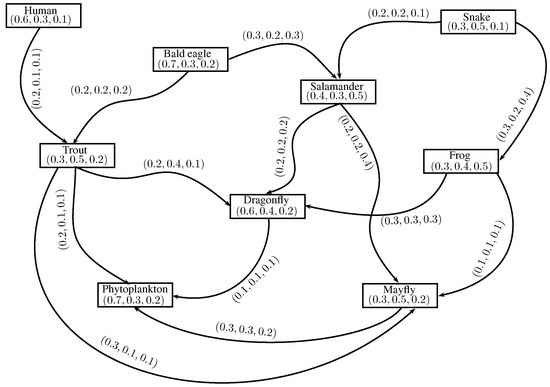
Figure 17. IN-food web.

Table 8. IN-out-neighborhoods.

$\mathit{w}\in \mathit{X}$	${\mathbb{N}}^{+}(\mathit{w})$
$Human$	$\{(Trout$, $0.2$, $0.1$, $0.1)\}$
$Bald$$eagle$	$\{(Trout$, $0.2$, $0.2$, $0.2)$, $(Salamander$, $0.3$, $0.2$, $0.3)\}$
$Salamander$	$\{(Dragonfly$, $0.2$, $0.2$, $0.2)$, $(Mayfly$, $0.2$, $0.2$, $0.4)\}$
$Snake$	$\{(Salamander$, $0.2$, $0.2$, $0.1)$, $(Frog$, $0.3$, $0.2$, $0.4)\}$
$Frog$	$\{(Dragonfly$, $0.3$, $0.3$, $0.3)$, $(Mayfly$, $0.1$, $0.1$, $0.1)\}$
$Mayfly$	$\{(Phytoplankton$, $0.3$, $0.3$, $0.2)\}$
$Phytoplankton$	∅
$Dragonfly$	$\{(Phytoplankton$, $0.1$, $0.1$, $0.1)\}$
$Trout$	$\{(Phytoplankton$, $0.2$, $0.1$, $0.1)$, $(Mayfly$, $0.3$, $0.1$, $0.1),(Dragonfly$, $0.2$, $0.4$, $0.1)\}$

Therefore, ${\mathbb{N}}^{+}(Human\cap Bald$ $eagle)=\{(Trout$, $0.2$, $0.1$, $0.2)\}$, ${\mathbb{N}}^{+}(Bald$ $eagle\cap Snake)=\{(Salamander$, $0.2$, $0.2$, $0.3)\}$, ${\mathbb{N}}^{+}(Salamander\cap Frog)=\{(Dragonfly$, $0.2$, $0.2$, $0.3)$, $(Mayfly$, $0.1$, $0.1$, $0.4)\}$, ${\mathbb{N}}^{+}(Salamander\cap Trout)=\{(Dragonfly$, $0.2$, $0.2$, $0.2)$, $(Mayfly$, $0.2$, $0.1$, $0.4)\}$, ${\mathbb{N}}^{+}(Trout\cap Frog)=\{(Dragonfly$, $0.2$, $0.3$, $0.3)$, $(Mayfly$, $0.1$, $0.1$, $0.1)\}$, ${\mathbb{N}}^{+}(Mayfly\cap Trout)=\{(Phytoplankton$, $0.2$, $0.1$, $0.2)\}$, ${\mathbb{N}}^{+}(Mayfly\cap Dragonfly)=\{(Phytoplankton$, $0.1$, $0.1$, $0.2)\}$ and ${\mathbb{N}}^{+}(Dragonfly\cap Trout)=\{(Phytoplankton$, $0.1$, $0.1$, $0.1)\}$.

Now, there is an edge between human and bald eagle; snake and bald eagle; salamander and trout; salamander and frog; trout and frog; trout and dragonfly; trout and mayfly; dragonfly and mayfly in the INC-graph, which highlights the competition between them; and for the other pair of species, there is no edge, which indicates that there is no competition in the INC-graph Figure 18. For example, there is an edge between human and bald eagle indicating a $12\%$ degree of likeness to prey on the same species, a $3\%$ degree of indeterminacy and a $4\%$ degree of non-likeness between them.

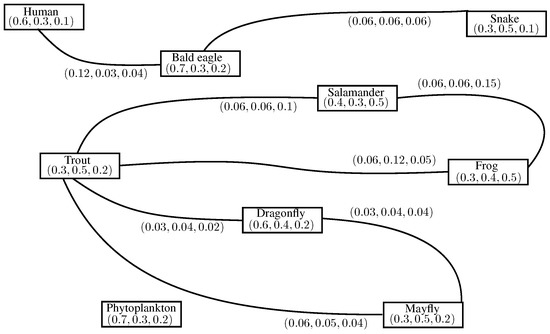
Figure 18. Corresponding INC-graph

We present our method, which is used in our ecosystem application in Algorithm 1.

Algorithm 1: Ecosystem.

Step 1. Input the truth-membership, indeterminacy-membership and falsity-membership values for set of n species. Step 2. If for any two distinct vertices $w_i$ and $w_j$, $t(w_i{w}_j)>0$, $i(w_i{w}_j)>0$, $f(w_i{w}_j)>0$, then $$(w_j,t(w_i{w}_j),i(w_i{w}_j),f(w_i{w}_j))\in {\mathbb{N}}^{+}(w_i).$$ Step 3. Repeat Step 2 for all vertices $w_i$ and $w_j$ to calculate IN-out-neighborhoods ${\mathbb{N}}^{+}(w_i)$. Step 4. Calculate ${\mathbb{N}}^{+}(w_i)\cap {\mathbb{N}}^{+}(w_j)$ for each pair of distinct vertices $w_i$ and $w_j$. Step 5. Calculate $H[{\mathbb{N}}^{+}(w_i)\cap {\mathbb{N}}^{+}(w_j)]$. Step 6. If ${\mathbb{N}}^{+}(w_i)\cap {\mathbb{N}}^{+}(w_j)\ne \varnothing$, then draw an edge $w_i{w}_j$. Step 7. Repeat Step 6 for all pairs of distinct vertices. Step 8. Assign membership values to each edge $w_i{w}_j$ using the conditions: $$t(w_i{w}_j)=(w_i\wedge w_j)H_1[{\mathbb{N}}^{+}(w_i)\cap {\mathbb{N}}^{+}(w_j)]$$

3.2. Career Competition

Consider the IN-digraph Figure 19 representing the competition between applicants for a career. Let $\{Rosaleen$, $Nazneen$, $Abner$, $Amara$, $Casper\}$ be the set of applicants for the particular careers $\{Medicine$, $Pharmacy$, $Anatomy$, $Surgery\}$. The truth-membership value of each applicant represents the degree of loyalty quality; the indeterminacy-value represents the indeterminate state of loyalty; and the false-membership value represents the disloyalty of each applicant towards their careers. Let the degree of truth-membership of Nazneen of her loyalty towards her career be $30\%$: degree of indeterminacy is $50\%$, and degree of disloyalty is $10\%$, i.e., the truth-membership, indeterminacy and falsity-membership values of the vertex Nazneen are $(0.3$, $0.5$, $0.1)$. The truth-membership value of each directed edge between an applicant and a career represents the eligibility for that career; the indeterminacy-value represents the indeterminate state of that career; and the false-membership value represents non-eligibility for that particular career.

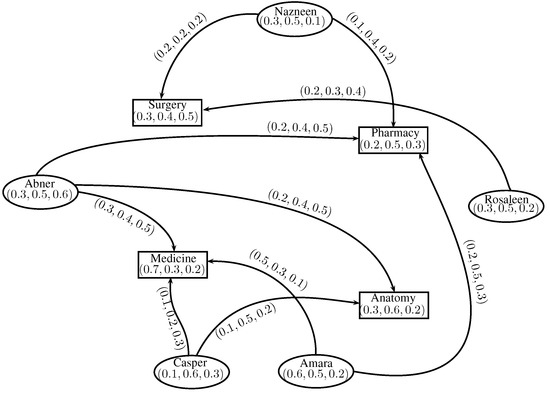
Figure 19. IN-digraph.

Thus, in Table 9, ${\mathbb{N}}^{+}(Nazneen)\cap {\mathbb{N}}^{+}(Rosaleen)=\{(Surgery$, $0.2$, $0.2$, $0.4)\}$, ${\mathbb{N}}^{+}(Nazneen)\cap {\mathbb{N}}^{+}(Amara)=\{(Pharmacy$, $0.1$, $0.4$, $0.3)\}$, ${\mathbb{N}}^{+}(Nazneen)\cap {\mathbb{N}}^{+}(Abner)=\{(Pharmacy$, $0.1$, $0.4$, $0.5)\}$, ${\mathbb{N}}^{+}(Nazneen)\cap {\mathbb{N}}^{+}(Casper)=\varnothing$, ${\mathbb{N}}^{+}(Rosaleen)\cap {\mathbb{N}}^{+}(Amara)=\varnothing$, ${\mathbb{N}}^{+}(Rosaleen)\cap {\mathbb{N}}^{+}(Casper)=\varnothing$, ${\mathbb{N}}^{+}(Rosaleen)\cap {\mathbb{N}}^{+}(Abner)=\varnothing$, ${\mathbb{N}}^{+}(Amara)\cap {\mathbb{N}}^{+}(Casper)=\{(Medicine$, $0.1$, $0.2$, $0.3)\}$, ${\mathbb{N}}^{+}(Amara)\cap {\mathbb{N}}^{+}(Abner)=\{(Medicine$, $0.3$, $0.3$, $0.5)$, $(Pharmacy$, $0.2$, $0.4$, $0.5)\}$ and ${\mathbb{N}}^{+}(Casper)\cap {\mathbb{N}}^{+}(Abner)=\{(Medicine$, $0.1$, $0.2$, $0.5)$, $(Anatomy$, $0.1$, $0.4$, $0.5)\}$.

Table 9. IN-out-neighborhoods.

$\mathit{w}\in \mathit{X}$	${\mathbb{N}}^{+}(\mathit{w})$
$Nazneen$	$\{(Surgery$, $0.2$, $0.2$, $0.2)$, $(Pharmacy$, $0.1$, $0.4$, $0.2)\}$
$Rosaleen$	$\{(Surgery$, $0.2$, $0.3$, $0.4)\}$
$Amara$	$\{(Medicine$, $0.5$, $0.3$, $0.1)$, $(Pharmacy$, $0.2$, $0.5$, $0.3)\}$
$Casper$	$\{(Medicine$, $0.1$, $0.2$, $0.3)$, $(Anatomy$, $0.1$, $0.5$, $0.2)\}$
$Abner$	$\{(Medicine$, $0.3$, $0.4$, $0.5)$, $(Anatomy$, $0.2$, $0.4$, $0.5)$, $(Pharmacy$, $0.2$, $0.4$, $0.5)\}$

The INC-graph is shown in Figure 20. The solids lines indicate the strength of competition between two applicants, and dashed lines indicate the applicant competing for the particular career. For example, Nazneen and Rosaleen both are competing for the career, surgery, and the strength of competition between them is $(0.06$, $0.1$, $0.08)$. In Table 10, $W(z$, $c)$ represents the competition of applicant z for career c with respect to loyalty quality, indeterminacy and disloyalty to compete with the others. The strength to compete with the other applicants with respect to a particular career is calculated in Table 10.

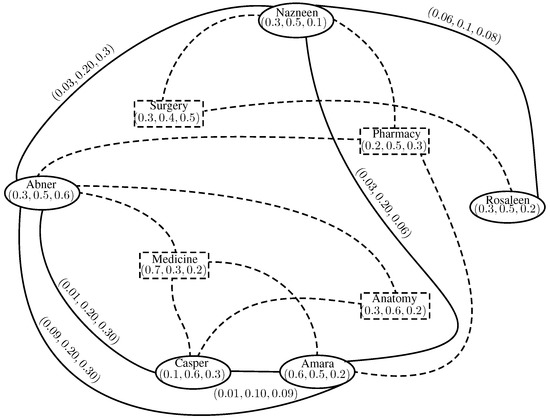
Figure 20. Corresponding INC-graph.

Table 10. Strength of competition of the applicant for a particular career.

$(\mathit{Applicant}$, $\mathit{Career})$	$\mathit{In}$ $\mathit{Competition}$	$\mathit{W}(\mathit{Applicant}$, $\mathit{Career})$	$\mathit{S}(\mathit{Applicant}$, $\mathit{Career})$
$(Nazneen$, $Surgery)$	$Rosaleen$	$(0.06$, $0.1$, $0.08)$	$0.88$
$(Rosaleen$, $Surgery)$	$Nazneen$	$(0.06$, $0.1$, $0.08)$	$0.88$
$(Abner$, $Anatomy)$	$Casper$	$(0.01$, $0.20$, $0.30)$	$0.51$
$(Casper$, $Anatomy)$	$Abner$	$(0.01$, $0.20$, $0.30)$	$0.51$
$(Nazneen$, $Pharmacy)$	$Abner$, $Amara$	$(0.03$, $0.20$, $0.18)$	$0.65$
$(Abner$, $Pharmacy)$	$Amara$, $Nazneen$	$(0.06$, $0.20$, $0.30)$	$0.56$
$(Amara$, $Pharmacy)$	$Nazneen$, $Abner$	$(0.06$, $0.20$, $0.18)$	$0.68$
$(Amara$, $Medicine)$	$Abner$, $Casper$	$(0.05$, $0.15$, $0.195)$	$0.705$
$(Casper$, $Medicine)$	$Abner$, $Amara$	$(0.01$, $0.15$, $0.195)$	0.665
$(Abner$, $Medicine)$	$Casper$, $Amara$	$(0.05$, $0.20$, $0.30)$	$0.55$

From Table 10, Nazneen and Rosaleen have equal strength to compete with the other for the career, surgery. Abner and Casper have equal strength of competition for the career, anatomy. Amara competes with the others for the career, pharmacy and medicine.

We present our method, which is used in our career competition application in Algorithm 2.

Algorithm 2: Career Competition

Step 1. Input the truth-membership, indeterminacy-membership and falsity-membership values for set of n applicants. Step 2. If for any two distinct vertices $z_i$ and $z_j$, $t(z_i{z}_j)>0$, $i(z_i{z}_j)>0$, $f(z_i{z}_j)>0$, then $$(z_j,t(z_i{z}_j),i(z_i{z}_j),f(z_i{z}_j))\in {\mathbb{N}}^{+}(z_i).$$ Step 3. Repeat Step 2 for all vertices $z_i$ and $z_j$ to calculate IN-out-neighborhoods ${\mathbb{N}}^{+}(z_i)$. Step 4. Calculate ${\mathbb{N}}^{+}(z_i)\cap {\mathbb{N}}^{+}(z_j)$ for each pair of distinct vertices $z_i$ and $z_j$. Step 5. Calculate $H[{\mathbb{N}}^{+}(z_i)\cap {\mathbb{N}}^{+}(z_j)]$. Step 6. If ${\mathbb{N}}^{+}(z_i)\cap {\mathbb{N}}^{+}(z_j)\ne \varnothing$, then draw an edge $z_i{z}_j$. Step 7. Repeat Step 6 for all pairs of distinct vertices. Step 8. Assign membership values to each edge $z_i{z}_j$ using the conditions: $$t(z_i{z}_j)=(z_i\wedge z_j)H_1[{\mathbb{N}}^{+}(z_i)\cap {\mathbb{N}}^{+}(z_j)]$$ $$i(z_i{z}_j)=(z_i\wedge z_j)H_2[{\mathbb{N}}^{+}(z_i)\cap {\mathbb{N}}^{+}(z_j)]$$ $$f(z_i{z}_j)=(z_i\vee z_j)H_3[{\mathbb{N}}^{+}(z_i)\cap {\mathbb{N}}^{+}(z_j)].$$ Step 9. If z, $r_1$, $r_2$, $r_3$, …, $r_n$ are the applicants competing for career c, then the strength of competition $W(z$, $c)=(t(z$, $c)$, $i(z$, $c)$, $f(z$, $c))$ of each applicant z for the career c is: $$W(z,c)=\frac{(t(z{r}_1)+t(z{r}_2)+\dots +t(z{r}_n),i(z{r}_1)+i(z{r}_2)+\dots +i(z{r}_n),f(z{r}_1)+f(z{r}_2)+\dots +f(z{r}_n))}{n}.$$ Step 10. Calculate $S(z,c)$, the strength of competition of each applicant z for career c. $$S(z,c)=t(z,c)-(i(z,c)+f(z,c))+1.$$

4. Conclusions

Graphs serve as mathematical models to analyze many concrete real-world problems successfully. Certain problems in physics, chemistry, communication science, computer technology, sociology and linguistics can be formulated as problems in graph theory. Intuitionistic neutrosophic set theory is a mathematical tool to deal with incomplete and vague information. Intuitionistic neutrosophic set theory deals with the problem of how to understand and manipulate imperfect knowledge. In this research paper, we have described the concept of intuitionistic neutrosophic competition graphs. We have also presented applications of intuitionistic neutrosophic competition graphs in ecosystem and career competition. We aim to extend our research work of fuzzification to (1) fuzzy soft competition graphs, (2) fuzzy rough soft competition graphs, (3) bipolar fuzzy soft competition graphs and (4) the application of fuzzy soft competition graphs in decision support systems.