Physiological State Recognition via HRV and Fractal Analysis Using AI and Unsupervised Clustering

Abstract

Early detection of physiological dysregulation is critical for timely intervention and effective health management. Traditional monitoring systems often rely on labeled data and predefined thresholds, limiting their adaptability and generalization to unseen conditions. To address this, we propose a framework for label-free classification of physiological states using Heart Rate Variability (HRV), combined with unsupervised machine learning techniques. This approach is particularly valuable when annotated datasets are scarce or unavailable—as is often the case in real-world wearable and IoT-based health monitoring. In this study, data were collected from participants under controlled conditions representing rest, stress, and physical exertion. Core HRV parameters such as the SDNN (Standard Deviation of all Normal-to-Normal intervals), RMSSD (Root Mean Square of the Successive Differences), DFA (Detrended Fluctuation Analysis) were extracted. Principal Component Analysis was applied for dimensionality reduction. K-Means, hierarchical clustering, and Density-based spatial clustering of applications with noise (DBSCAN) were used to uncover natural groupings within the data. DBSCAN identified outliers associated with atypical responses, suggesting potential for early anomaly detection. The combination of HRV descriptors enabled unsupervised classification with over 90% consistency between clusters and physiological conditions. The proposed approach successfully differentiated the three physiological conditions based on HRV and fractal features, with a clear separation between clusters in terms of DFA α1, α2, LF/HF, and RMSSD (with high agreement to physiological labels (Purity ≈ 0.93; ARI = 0.89; NMI = 0.92)). Furthermore, DBSCAN identified three outliers with atypical autonomic profiles, highlighting the potential of the method for early warning detection in real-time monitoring systems.

1. Introduction

Heart Rate Variability (HRV) is widely recognized as a non-invasive biomarker for assessing autonomic nervous system activity and overall cardiovascular health [1]. In recent years, HRV analysis has extended beyond the clinical setting, finding applications in stress detection, fitness monitoring, and management of chronic diseases [2,3]. The rapid advancement of wearable technologies and Internet of Things (IoT) platforms has enabled continuous HRV monitoring in daily life, using compact sensors and low-power microcontrollers [4].

Such systems are increasingly applied in real-world scenarios, including athlete training, stress detection, sleep quality assessment, and recovery monitoring. For instance, devices like Polar V800 and Oura Ring have been validated for their reliability in measuring HRV during exercise and rest, demonstrating good acceptability among athletes due to their non-intrusiveness and ease of use [5,6]. Moreover, professional sports teams are incorporating HRV monitoring into daily routines to optimize training load, prevent overtraining, and personalize recovery strategies [7]. A study by Plews et al. (2013) [8] found that elite endurance athletes successfully used HRV-guided training to improve performance, showing high adherence and trust in wearable-based HRV systems.

Health devices based on cardio data have become particularly attractive due to their ease of integration, low cost, and suitability for wearable form factors. However, cardiac signals are highly susceptible to noise caused by motion artifacts and other disturbances, necessitating robust denoising and preprocessing techniques [9,10]. In addition to classical digital filters (e.g., Butterworth, notch), other approaches have also been explored in recent literature to overcome these limitations, including Empirical Mode Decomposition (EMD) [11], Kalman filtering [12], and more recently, deep learning-based denoising using autoencoders or convolutional neural networks [13]. These techniques offer enhanced adaptability, particularly in non-stationary and high-noise conditions often encountered in wearable or ambulatory monitoring.

To extract deeper insight from HRV time series, nonlinear and fractal features such as sample entropy (SampEn), Hurst exponent, and fractal dimension have been explored in recent literature [14,15]. These metrics capture complex temporal dynamics and long-range correlations, revealing autonomic patterns that classical time-domain indicators like SDNN and RMSSD may overlook.

Several studies have demonstrated the physiological relevance of these features in distinguishing between rest, stress, and exercise-induced states. For example, [16] reviewed HRV responses to psychological and physiological stressors, reporting decreased RMSSD and increased LF/HF ratio during stress. In [17], treadmill-based exercise studies showed that time- and frequency-domain HRV parameters diminished significantly with increased physical exertion. Ref. [17] does not provide direct values (mean ± SD) for HRV parameters. However, the analysis revealed significant negative correlations between mean heart rate and basic HRV indicators (RMSSD r = −0.517; SDNN r = −0.558). They demonstrate how reduced HRV at rest reflects physiological and psychological stress during a selection week. Similarly, [18] observed that physically active individuals had higher baseline RMSSD, LF, and HF values, suggesting improved vagal tone. The authors do not provide exact values of the parameters studied after exercise, but they do provide the p-values that indicate statistical significance of the results. Post-stress recovery was also shown to be reflected in HRV dynamics: [19] linked SDNN and HF power to validated psychological scales for stress tolerance and cognitive fatigue, while individuals with higher parasympathetic tone exhibited better resilience under stress. In [20], both moderate and vigorous activity were associated with increased HRV in middle-aged adults, even after controlling for lifestyle factors and BMI. The authors indicated that in men, higher levels of vigorous physical activity were associated with increases in SDNN (from 32.9 ms to ~34.8 ms, p = 0.09), LF power (from 284.6 to 342.4 ms², p < 0.01) and HF power (from 104.8 to 125.2 ms², p < 0.05), as well as lower heart rate (from 70.7 to 66.4 beats/min, p < 0.001). In women, no significant changes in HRV parameters were observed with increased activity. A slight increase in HF power (133.8 → 141.0 ms²) was observed, but was not statistically significant (p > 0.05). These findings underscore HRV’s potential as a biomarker for physiological state assessment and autonomic recovery. Given the complexity and variability of HRV patterns, Artificial Intelligence (AI) and unsupervised machine learning techniques have emerged as powerful tools for extracting structure from unlabeled biomedical signals. Methods such as Principal Component Analysis (PCA), K-Means, and DBSCAN(Density-Based Spatial Clustering of Applications with Noise) facilitate dimensionality reduction, clustering, and anomaly detection, offering a means to uncover hidden physiological states without predefined categories [21,22,23]. This is particularly useful for real-world health data, where labels may be absent or ambiguous.

Recent studies illustrate the utility of such methods: [24] applied K-Means and DBSCAN to classify stress levels in firefighters using only HRV signals—without prior annotations. In [25], PCA was used to automatically select the most informative HRV and respiratory features before stress-level clustering. These approaches demonstrate the feasibility of label-free classification and highlight the promise of combining nonlinear HRV features with unsupervised learning for intelligent, adaptive health monitoring.

Building upon these studies, the present work proposes an integrated framework that applies PCA, K-Means, hierarchical clustering (Ward’s method), and DBSCAN to a comprehensive set of linear, spectral, nonlinear, and fractal HRV features. This approach enables robust latent group identification and anomaly detection in real-time, wearable-based health monitoring, addressing the need for label-free physiological state recognition in dynamic, personalized healthcare environments.

Several recent studies have applied unsupervised learning approaches to HRV data for physiological state identification. Ref. [26] applied K-Means clustering to time- and frequency-domain HRV features to differentiate between physiological states such as ‘rest’, ‘stress’, and ‘load’ during daily activities, subsequently using Gradient Boosting for fall-risk prediction.

Evaluating HRV in Parkinson’s disease rehabilitation, a study [27] on 110 PD patients performed cluster analysis and PCA, identifying four distinct responder types to aerobic exercise (strong, moderate, mixed, and low responders)

Validation of the Polar H7 wearable device during physical activity [28] demonstrated that the K-Means algorithm effectively classified participants according to fitness level and body composition. The results show that HRV parameters measured by the device are sensitive to physiological differences related to aerobic capacity and body composition.

Our work extends these by integrating PCA, K-Means, hierarchical clustering (Ward), and DBSCAN on combined linear, spectral, nonlinear, and fractal HRV features, demonstrating robust latent grouping and anomaly detection in real-time wearable monitoring scenarios.

Despite the promising results of supervised models trained on labeled datasets such as WESAD and Noise Stress Test Database, their applicability in real-world, real-time environments remains limited due to a range of practical and conceptual constraints. Unsupervised learning for HRV analysis has emerged as an effective alternative, motivated by several key factors:

• Absence of labeled data in real-life scenarios. In practical applications such as wearable devices and IoT-based systems, there are usually no predefined labels indicating the user’s physiological state (e.g., rest, stress, or exertion). This makes unsupervised learning a highly suitable choice for automatic classification.
• Individual variability and transitional states. Supervised models often lack the flexibility to account for inter-individual physiological differences and struggle to recognize new or intermediate states not represented in the training data. In contrast, unsupervised methods can identify natural groupings and dynamic transitions without the need for subjective categorization.
• Limitations of supervised models. While supervised techniques rely on clearly defined classes and high-quality annotations, these often require expert judgment or controlled laboratory environments. This restricts their applicability in autonomous, real-world health monitoring systems.
• Potential for anomaly detection. Clustering methods such as DBSCAN can detect outliers and transitional observations—capabilities that supervised learning typically lacks. This opens the door for early warning systems and adaptive feedback in personalized preventive healthcare.

The proposed framework addresses these limitations by employing a hybrid unsupervised approach that supports adaptive, self-calibrating physiological monitoring without relying on prior labeling. This aligns with current trends in personalized medicine and autonomous health technologies.

The present study proposes an intelligent framework for real-time HRV analysis based on signals acquired from wearable cardio devices. It aims to address the following key research questions:

• What latent structures can be uncovered in HRV and fractal metrics through dimensionality reduction techniques?
• Can unsupervised learning algorithms (e.g., K-Means, DBSCAN) differentiate physiological states without prior labeling?
• To what extent do AI-based visualizations support the detection of anomalies and natural groupings in HRV data?

Unlike prior HRV clustering studies that typically use a single algorithm or a limited feature set, we integrate PCA with multiple clustering strategies (K-Means, hierarchical Ward, DBSCAN) and expand the feature space with fractal and entropy metrics. This multi-algorithm, multi-feature design increases physiological interpretability and enables unsupervised anomaly detection in wearable/IoT scenarios.

2. Materials and Methods

2.1. Participants and Protocol

A total of 22 healthy male volunteer athletes (aged 24–46 years) were recruited and participated in three experimental studies based on physical and mental states: rest, stress, and exercise. The athletes initially perform a 60 min general physical preparation session, which includes 20 min of running, 10 min of rope jumping, 10 min of cone-jumping drills, and 20 min of weightlifting. Following this preparatory phase, the main training session begins and consists of pair-based combat practice (e.g., one-on-one wrestling bouts and repeated suplex techniques) on the mat for a total of 60 min. All training sessions are conducted indoors, in a gym setting.

This combined protocol induces intensive physical exertion and is referred to throughout the manuscript as Physical Activity (Load).

In the days leading up to a competition, athletes typically engage in increased training intensity, incorporating additional strength workouts and weight reduction regimens when necessary. On the day of the competition, athletes perform warm-up routines including mobility exercises and squats. Throughout the event—which spans an entire day—competitors face each other in elimination rounds until the top four athletes in each weight category are identified.

The competition context is characterized not only by high physical demands during matches but also by elevated physical and psychological stress, denoted in this study as Stress.

Baseline measurements in the rest condition were obtained 10 min prior to the start of training.

All participants gave informed consent before the experiment.

Cardiac signals were recorded for 30 min intervals using Holter monitoring in each condition. Recordings were performed using a device model TLC9803, a dynamic ECG system capable of continuous 3-channel electrocardiographic recording for up to 24 h.

For data acquisition, five electrodes were attached to specific anatomical landmarks as follows:

• V1—placed on the right chest, over the area of the right pectoral muscle;
• V—positioned centrally beneath the neck;
• V5—located below the left chest, near the left pectoral region;
• V3—placed horizontally aligned with V5, at the mid-chest level;
• N—attached to the right side of the abdomen, adjacent to the umbilicus.

This electrode configuration allows reliable multichannel ECG signal acquisition suitable for HRV and morphological waveform analysis.

2.2. Signal Preprocessing and Noise Removal

The raw cardio signals underwent preprocessing to reduce interference, such as baseline drift caused by respiration or movement, muscle artifacts (EMG noise), electrical disturbances from the power grid (typically 50 Hz), and high-frequency noise. Digital filters were applied, including Butterworth low-pass and high-pass filters, a 50 Hz notch filter, and wavelet denoising [29]. Following filtration, R-wave detection within the QRS complex was performed as a prerequisite for extracting HRV parameters. A hybrid method [30] was employed, combining the Pan–Tompkins algorithm (a sequence of differentiation, moving average filtering, and adaptive thresholding) with wavelet transformation [31] to achieve reliable localization of R-peaks. Accurate and precise detection of R-peaks ensures the proper determination of RR intervals (the duration between two consecutive heartbeats) and valid subsequent HRV analysis.

2.3. Determination and Extraction of HRV and Fractal Parameters

The extracted interbeat intervals (RR intervals) are used to calculate the following time-domain and nonlinear HRV characteristics [32]:

Mean RR—Length of RR intervals (from one maximum R deviation to the next).

SDNN (standard deviation of NN intervals)—Measures overall HRV by calculating the standard deviation of normal-to-normal (NN):

$$\mathrm{S}\mathrm{D}\mathrm{N}\mathrm{N}=\sqrt{{\displaystyle \frac{1}{\mathrm{N}-1}}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{({\mathrm{R}\mathrm{R}}_{\mathrm{i}}-\overline{\mathrm{R}\mathrm{R}})}^2}$$

(1)

RMSSD (root mean square of successive differences)—Reflects short-term parasympathetic activity:

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{S}\mathrm{D}\mathrm{ }=\sqrt{{\displaystyle \frac{1}{N-1}}{\sum }_{i=1}^{N-1}{({RR}_{i+1}-{RR}_i)}^2}$$

(2)

SampEn (sample entropy)—Measures signal irregularity; lower values indicate more regularity [33]:

$$\mathrm{S}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{E}\mathrm{n}\left(\mathrm{m},\mathrm{ }\mathrm{r},\mathrm{ }\mathrm{N}\right)=-\mathrm{l}\mathrm{n}\left({\displaystyle \frac{\mathrm{A}}{\mathrm{B}}}\right),$$

(3)

where A is number of template matches of length m + 1, and B is the number of matches of length m.

Hurst exponent (H)—Quantifies long-range correlations in a time series using rescaled range analysis [34]:

$$\mathrm{E}=\left[{\displaystyle \frac{\mathrm{R}\left(\mathrm{n}\right)}{\mathrm{S}\left(\mathrm{n}\right)}}\right]\propto {\mathrm{n}}^{\mathrm{H}},$$

(4)

where H ∈ (0, 1); H > 0.5 indicates persistence.

Fractal dimension (FD)—Assesses signal complexity using methods like Higuchi or Katz. A typical Higuchi FD estimate is as follows [35]:

$$\mathrm{F}\mathrm{D}=\underset{\mathrm{k}\to 0}{\lim }{\displaystyle \frac{\log \mathrm{L}\left(\mathrm{k}\right)}{\log (1/\mathrm{k})}},$$

(5)

where L(k) is the average length of the signal over scale k.

LF (low frequency)—Reflects the combined influence of the sympathetic and parasympathetic nervous systems, most often associated with baroreflex activity (0.04–0.15 Hz).

HF (high frequency)—It is a marker of parasympathetic (vagal) activity and is strongly linked to breathing. (0.15–0.4 Hz).

LF/HF—The LF/HF ratio is used as an indicator of the balance between sympathetic and parasympathetic activity in the autonomic nervous system.

DFA α1 (Detrended Fluctuation Analysis, short-term scaling exponent)—Assesses the short-term self-similarity and correlation structure of the HRV signal; lower values suggest chaoticity or loss of regulation.

DFA α2 (long-term scaling exponent)—Assesses long-term fractal correlation in the HRV signal and is sensitive to chronic physiological and pathological changes.

2.4. Feature Space Analysis Using PCA

2.4.1. Dimensionality Reduction via Principal Component Analysis

To reduce the dimensionality of the HRV feature space and identify latent structure in the data, Principal Component Analysis was applied. PCA is a widely used unsupervised learning technique that transforms a set of correlated variables into a set of linearly uncorrelated principal components (PCs), ranked by the amount of variance they explain [36,37,38,39].

Data standardization

Prior to PCA, all HRV features were normalized using z-score transformation to ensure comparability:

$${\mathrm{z}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{x}}_{\mathrm{i}}-\mathsf{\mu }}{\mathsf{\sigma }}}$$

(6)

where $x_i$ is the feature value, μ is the mean value, and σ is the standard deviation for the corresponding feature.

This is necessary because PCA is sensitive to the scale of the data, and HRV parameters are in different dimensions (ms, dimensionless values, etc.).

2.4.2. Principal Component Extraction

Let X∈R^n×p denote the matrix of z-normalized HRV features with n participants and p features. PCA proceeds as follows:

• Covariance matrix computation:

  $$\mathrm{C}={\displaystyle \frac{1}{\mathrm{N}-1}}{\mathrm{X}}^{\mathrm{T}}\mathrm{X}$$

  (7)
• Eigen decomposition:

Find the eigenvalues ${\lambda }_{\mathrm{j}}$ and eigenvectors ${\mathrm{v}}_{\mathrm{j}}$ of C, such that

$${\mathrm{C}}_{{\mathrm{v}}_{\mathrm{j}}}={\lambda }_{\mathrm{j}}{\mathrm{v}}_{\mathrm{j}}$$

(8)

3.

Projection of data onto the first k eigenvectors:

$$\mathrm{Z}=\mathrm{X}{\mathrm{V}}_{\mathrm{K}},$$

where ${\mathrm{V}}_{\mathrm{K}}$ contains the top k eigenvectors.

The resulting principal components capture the directions of greatest variance in the data. In our study, the first two components explained over 70% of the total variance and were used for clustering and visualization [37,38].

2.4.3. Explained Variance and Component Interpretation

The component loadings were also analyzed to assess the contribution of each HRV metric to the latent axes. This enabled interpretability of the clusters in terms of underlying physiological features (e.g., RMSSD and SampEn dominating PC1) similarly to recent studies focusing on PCA-based HRV assessment [36,39].

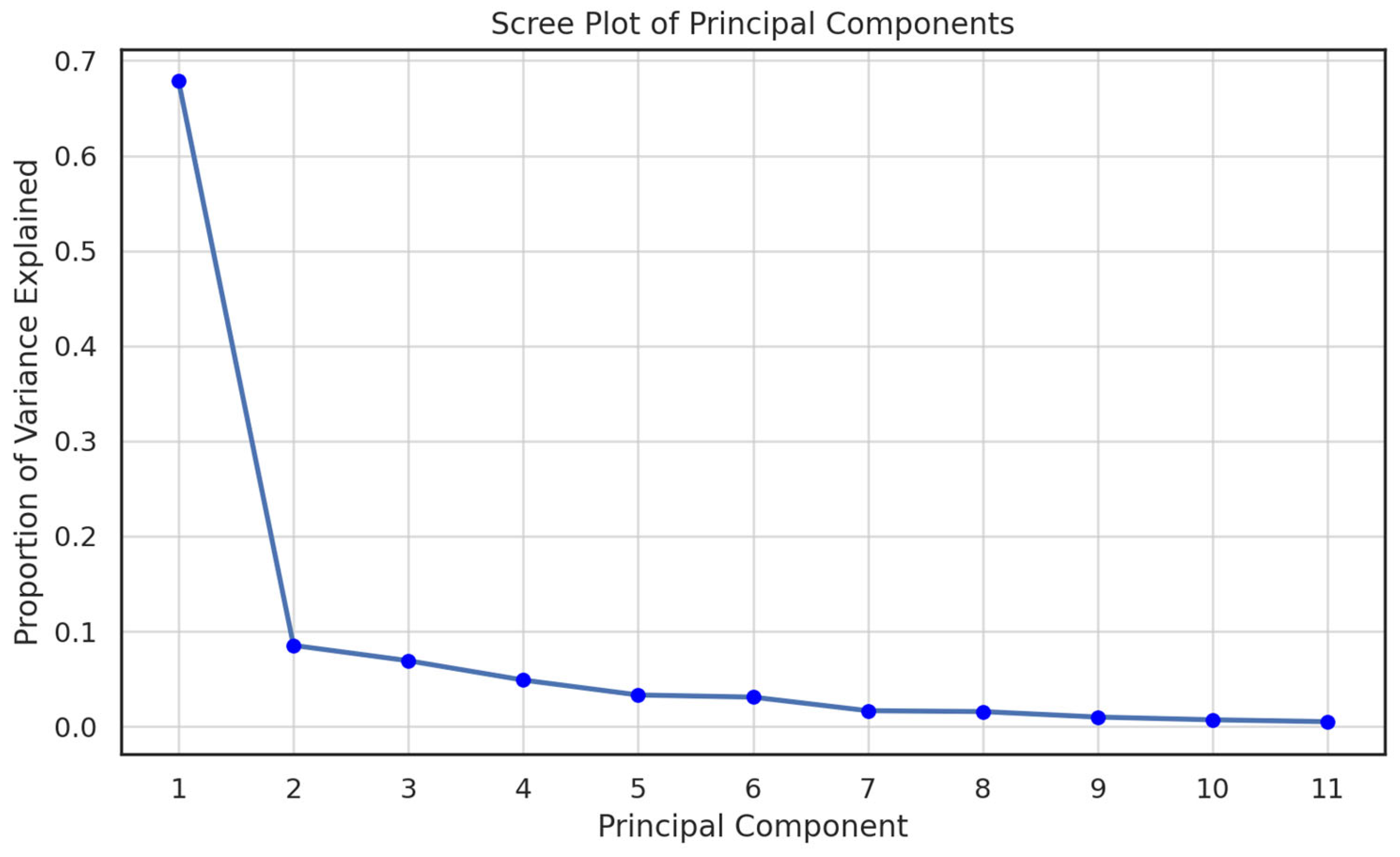
• Analysis of explained variance: Scree plot and cumulative curve

After standardization, the explained variance for each principal component was calculated. A scree plot was used to show the relative contribution of each component to the total variation in the data.

• Interpretation of PC1, PC2 and PC3

For each of the first three principal components (PC1, PC2, PC3), the loadings—the coefficients with which the original HRV parameters participate in the corresponding component—were analyzed.

• Three-dimensional visualization

To better understand the cluster structure, two-dimensional (2D) and three-dimensional (3D) projections of the data in the space of the first principal components (PC1 × PC2 and PC1 × PC2 × PC3) were prepared. They allow a visual assessment of the clustering between observations (participants) and contribute to the selection of appropriate methods for subsequent unsupervised classification.

For the programmatic implementation of the algorithm in a Python environment, the parameter svd_solver was set to full, ensuring precise eigen decomposition suitable for moderate-sized datasets, avoiding stochastic variability that may occur with randomized approaches.

2.5. Clustering Algorithms

In order to identify natural groupings in the HRV feature space, three unsupervised learning algorithms were applied: K-Means clustering, hierarchical clustering (Ward linkage), and DBSCAN (Density-Based Spatial Clustering of Applications with Noise). Each method captures different structural assumptions within the data and enables complementary perspectives on latent physiological states [26].

2.5.1. K-Means Clustering (k = 3)

K-Means is a centroid-based clustering algorithm [27] that partitions n data points into k disjoint clusters by minimizing the within-cluster sum of squares (WCSS):

$$\mathrm{W}\mathrm{C}\mathrm{S}\mathrm{S}={\sum }_{\mathrm{J}=1}^{\mathrm{k}}{\sum }_{{\mathrm{x}}_{\mathrm{i}}\in {\mathrm{C}}_{\mathrm{j}}}{‖{\mathrm{x}}_{\mathrm{i}}-{\mathsf{\mu }}_{\mathrm{i}}‖}^2$$

(9)

where

${\mathrm{C}}_{\mathrm{j}}$ is the set of points assigned to cluster j.

${\mathsf{\mu }}_{\mathrm{i}}$ is the centroid (mean vector) of cluster j.

∥⋅∥ denotes the Euclidean norm.

The algorithm iteratively updates cluster assignments and centroids until convergence. In this study, k = 3 was chosen to reflect three hypothesized physiological states: rest, stress, and physical load.

The init parameter was set to k-means++ to optimize centroid initialization, while n_init was fixed at 20 to minimize the risk of convergence to local minima. The max_iter parameter was set to 500 to ensure convergence in all runs.

2.5.2. Hierarchical Clustering (Ward Linkage)

Hierarchical clustering builds a tree (dendrogram) of nested clusters based on a pairwise distance matrix. Ward’s method specifically minimizes the increase in total within-cluster variance after merging two clusters. The objective function is

$$∆{\mathrm{E}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{{\mathrm{n}}_{\mathrm{i}}{\mathrm{n}}_{\mathrm{j}}}{{\mathrm{n}}_{\mathrm{i}}+{\mathrm{n}}_{\mathrm{j}}}}{‖{\mathsf{\mu }}_{\mathrm{i}}-{\mathsf{\mu }}_{\mathrm{j}}‖}^2$$

(10)

where

${\mathrm{n}}_{\mathrm{i}},{\mathrm{n}}_{\mathrm{j}}$ are the sizes of clusters i and j, ${\mathsf{\mu }}_{\mathrm{i}},{\mathsf{\mu }}_{\mathrm{j}}$ are their centroids, and $‖{\mathsf{\mu }}_{\mathrm{i}}-{\mathsf{\mu }}_{\mathrm{j}}‖$ is the Euclidean distance between the centroids.

The dendrogram was cut at a height corresponding to 3 main clusters, allowing direct comparison with the K-Means partitioning.

The key hyperparameters were Ward’s connection method, chosen to minimize within-cluster variance and create compact, well-separated clusters in the PCA-reduced feature space; affinity metric (Euclidean distance); number of clusters (three); and distance threshold (not explicitly set, as clustering was terminated when a predefined number of clusters was reached).

2.5.3. DBSCAN

DBSCAN [40] identifies clusters based on local density, allowing detection of arbitrarily shaped groups and outliers (noise). The algorithm requires two parameters:

ε—neighborhood radius.

minPts—minimum number of points to form a dense region.

A point x is

• A core point if it has at least minPts neighbors within ε;
• Reachable if it lies within ε of a core point;
• Noise otherwise.

The clusters are formed as connected components of core points and their reachable neighbors.

In this study, the DBSCAN parameters ε (epsilon) and minPts were selected based on a combination of visual inspection and heuristic methods. The value of ε was determined using a k-distance graph, where the sorted distances to each point’s k-th nearest neighbor (with k = minPts − 1) are plotted. A clear “elbow” in the curve typically indicates a suitable ε value. In our case, the optimal ε was found to be 0.85. The minPts parameter was set to 4, following the general guideline that minPts ≥ dimensionality + 1 (i.e., for a 2D PCA-transformed space, minPts ≥ 3). These parameters provided a balance between detecting well-formed clusters and excluding noise or outlier points. A sensitivity analysis was also performed to ensure stability of the clustering results across small variations in ε and minPts. The Euclidean distance metric (metric = Euclidean) was used for consistency with the PCA-transformed feature space.

Metrics for evaluating the results of unsupervised learning (clustering):

Purity evaluates how homogeneous the predicted clusters are with respect to the true classes. It measures the proportion of the total number of instances that were correctly assigned to their most frequent class in each cluster:

$$\mathrm{P}\mathrm{u}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}={\displaystyle \frac{1}{\mathrm{N}}}{\sum }_{\mathrm{k}}\underset{\mathrm{j}}{\max }\left|{\mathrm{C}}_{\mathrm{k}}\cap {\mathrm{T}}_{\mathrm{j}}\right|,$$

(11)

where

N: total number of objects.

${\mathrm{C}}_{\mathrm{k}}:$ k-th cluster.

${\mathrm{T}}_{\mathrm{j}}:$ j-th true class.

${\mathrm{C}}_{\mathrm{k}}\cap {\mathrm{T}}_{\mathrm{j}}:$ number of elements that are in the cluster.

Values: from 0 to 1 (1 = perfect match).

ARI measures the similarity between two classifications, accounting for chance coincidences. It adjusts the Rand Index to account for the probability that two items fall into the same cluster by chance:

$$\mathrm{A}\mathrm{R}\mathrm{I}=\frac{{\sum }_{\mathrm{i}\mathrm{j}}\left(\begin{array}{c}{\mathrm{n}}_{\mathrm{i}\mathrm{j}}\\ 2\end{array}\right)-\left[\sum _{\mathrm{i}}\left(\begin{array}{c}{\mathrm{a}}_{\mathrm{i}}\\ 2\end{array}\right)\sum _{\mathrm{j}}\left(\begin{array}{c}{\mathrm{b}}_{\mathrm{j}}\\ 2\end{array}\right)/\begin{array}{c}\mathrm{n}\\ 2\end{array}\right]}{\frac{1}{2}\left[\sum _{\mathrm{i}}\left(\begin{array}{c}{\mathrm{a}}_{\mathrm{i}}\\ 2\end{array}\right)+\sum _{\mathrm{j}}\left(\begin{array}{c}{\mathrm{b}}_{\mathrm{j}}\\ 2\end{array}\right)\right]-\left[\sum _{\mathrm{i}}\left(\begin{array}{c}{\mathrm{a}}_{\mathrm{i}}\\ 2\end{array}\right)\sum _{\mathrm{j}}\left(\begin{array}{c}{\mathrm{b}}_{\mathrm{j}}\\ 2\end{array}\right)/\begin{array}{c}\mathrm{n}\\ 2\end{array}\right]},$$

(12)

where

${\mathrm{n}}_{\mathrm{i}\mathrm{j}}$: the number of elements that are simultaneously in cluster i of the true classification and in cluster j of the predicted classification.

${\mathrm{a}}_{\mathrm{i}}:$ the number of elements in cluster i according to the true classification.

${\mathrm{b}}_{\mathrm{j}}:$ the number of elements in cluster j according to the predicted classification.

$\mathrm{n}$: the total number of objects.

NMI measures how much information the clusters and the true classes share. It is normalized to be in the range [0, 1]:

$$\mathrm{N}\mathrm{M}\mathrm{I}\left(\mathrm{U},\mathrm{V}\right)={\displaystyle \frac{2.\mathrm{I}(\mathrm{U};\mathrm{V})}{\mathrm{H}\left(\mathrm{U}\right)+\mathrm{H}\left(\mathrm{V}\right)}},$$

(13)

where

$\mathrm{I}\left(\mathrm{U};\mathrm{V}\right):$ mutual information between the cluster distribution U and the classes V;

$\mathrm{H}\left(\mathrm{U}\right),\mathrm{H}\left(\mathrm{V}\right)$: entropy of the clusters and the true classes.

3. Results

Table 1. HRV parameters.

Parameter	Rest N = 22 [Mean ± sd]	Stress N = 22 [Mean ± sd]	Physical Activity (Load) N = 22 [Mean ± sd]
Mean RR (ms)	842.16 ± 143.23	638.28 ± 126.17	589.42 ± 131.38
SDNN (ms)	161.43 ± 46.73	93.46 ± 45.68	118.27 ± 26.19
RMSSD (ms)	28.39 ± 7.24	9.86 ± 4.81	18.22 ± 5.93
SampEn	1.22 ± 0.12	1.72 ± 0.08	1.35 ± 0.18
Hurst Exponent (H)	0.72 ± 0.04	0.58 ± 0.05	0.63 ± 0.04
Fractal Dimension (FD)	1.18 ± 0.03	1.41 ± 0.04	1.36 ± 0.08
LF (nu)	37.21 ± 4.50	68.12 ± 6.42	54.00 ± 5.61
HF (nu)	63.42 ± 5.06	32.33 ± 4.22	46.00 ± 4.52
LF/HF	0.59 ± 0.11	2.12 ± 0.23	1.22 ± 0.14
DFA α1	1.14 ± 0.06	0.88 ± 0.08	1.04 ± 0.07
DFA α2	1.33 ± 0.05	0.86 ± 0.07	0.99 ± 0.06

presents descriptive statistics for all HRV features across the three physiological states. The analysis reveals clear differentiation between rest, stress, and load based on time-domain, spectral, and nonlinear HRV parameters.

Time-domain metrics (mean RR, SDNN, RMSSD) are significantly higher at rest, reflecting dominant parasympathetic activity. These values decrease under both stress and physical exertion, with the lowest levels observed during stress.

Lower H indicates a loss of long-term autocorrelation and reduced system adaptability, while higher FD and SampEn reflect greater short-term irregularity and unpredictability of beat-to-beat variations. This profile is consistent with a predominance of sympathetic activation and suppression of vagal modulation, leading to a more reactive and less stable autonomic regulation. Spectral components (LF, HF, LF/HF) behave as expected: rest is characterized by vagal dominance (high HF), while stress results in increased LF and LF/HF ratio (>2), indicating sympathetic dominance. Physical load causes moderate sympathetic activation, reflected by an intermediate LF/HF ratio.

Fractal metrics (DFA α1, α2) show preserved complexity at rest, reduced adaptability under stress, and partially maintained regulation during load.

Data analysis shows good differentiation between the three states—rest, psychological stress and physical exertion—based on standard and extended Heart Rate Variability parameters.

Figure 1 presents the results of the Detrended Fluctuation Analysis (DFA) applied to the HRV signals under three distinct physiological conditions: (a) rest, (b) physical load, and (c) mental stress. Each subplot displays the characteristic log–log plot of the fluctuation function F(n) versus window size n. The fitted lines, shown in cyan for DFA α1 and red for DFA α2, represent the short- and long-term scaling exponents, respectively.

Rest (a): Both α1 (1.14) and α2 (1.33) exceed 1.0, indicating strong long-range correlations and persistent dynamics, typical of healthy autonomic regulation during relaxation.

Load (b): α1 remains elevated (1.04), while α2 drops to 0.99, indicating partial retention of regulatory complexity under physical exertion.

Stress (c): A marked reduction in both α1 (0.88) and α2 (0.86) suggests a breakdown of fractal structure and a shift toward uncorrelated dynamics, reflecting heightened sympathetic activity and reduced complexity.

These results suggest that physical and mental stresses (α1 = 0.88; α2 = 0.86) lead to a greater loss of fractal dynamics compared to physical load (α1 = 1.04; α2 = 0.99), while exercise allows for partial maintenance of short-term adaptability.

Boxplot graphs for each HRV parameter across the three conditions—rest, stress, and physical exertion—are shown in Figure 2. Boxplots allow for a quick visual assessment of the median, dispersion and presence of extreme values for each HRV parameter under the different experimental conditions. This facilitates highlighting differences between groups and identifying potential atypical responses, which is important for the overall comparative analysis within the study.

The outliers reported were analyzed by including the coefficient of variation (CV). Several specific trends stand out: For DFA α1, the values at rest are 1.14 (CV = 5.3%); during exercise—1.04 (CV = 6.7%, a decrease of 8.8%); and during stress—0.88 (CV = 9.1%, a decrease of 22.8%). There is a close relationship between rest and exercise, but a distinct decrease under stress, accompanied by increased relative variability. A similar picture is observed in DFA α2, where at rest, the value is 1.33 (CV = 3.8%); under load—0.99 (CV = 6.1%, decrease of 25.6%); and under stress—0.86 (CV = 8.1%, decrease of 35.3%), and here too, the highest variability is in the stress state, which indicates a more heterogeneous response of the participants. In contrast to these fractal indicators, SampEn demonstrates the opposite dynamics—at rest, the value is 1.22 (CV = 9.8%), under stress, it is 1.72 (CV = 4.7%, increase of 41.0%), and under load, it is 1.35 (CV = 13.3%, increase of 10.7%). This increase under stress, combined with the lowest variability in this phase, contrasts with the general downward trend in the other parameters, while the highest CV under exercise indicates more diverse individual responses.

3.1. Statistical Analysis

For all HRV and related characteristics, normality was checked with the Shapiro–Wilk test. All variables showed intact normality (p > 0.05), which allowed the use of parametric tests. For the comparison between pairs of physiological states (rest vs. stress, stress vs. load, rest vs. load), a two-sample t-test with independent samples was applied (

Table 2. Results of t-test analysis.

Parameter	Rest vs. Stress	Stress vs. Load	Rest vs. Load
Mean RR (ms)	<0.0001	<0.05	<0.0001
SDNN (ms)	<0.001	<0.05	<0.001
RMSSD (ms)	<0.0001	<0.05	<0.05
SampEn	<0.0001	<0.05	<0.05
Hurst Exponent (H)	<0.05	<0.05	<0.01
Fractal Dimension (FD)	<0.0001	<0.05	<0.05
LF (nu)	<0.001	<0.01	<0.001
HF (nu)	<0.001	<0.05	<0.001
LF/HF	<0.001	<0.01	<0.001
DFA α1	<0.0001	<0.05	<0.001
DFA α2	<0.0001	<0.05	<0.05

), which revealed statistically significant differences (p < 0.05) in almost all characteristics.

For a more comprehensive analysis of the differences between the three conditions, a one-way analysis of variance (ANOVA) was used, followed by a Tukey HSD post hoc test. The results are summarized in

Table 3. Results of Tukey HSD post hoc analysis.

Characteristics	Group 1	Group 2	Mean Difference	p-Value	95% CI (Lower–Upper)	Significant Difference
Mean RR	Load	Rest	261.79	<0.0001	238.28–285.31	Yes
Mean RR	Load	Stress	24.36	0.79	48.84–95.87	No
Mean RR	Rest	Stress	−189.44	<0.0001	−212.96–−165.92	Yes
SDNN	Load	Rest	20.79	<0.0001	16.52–25.07	Yes
SDNN	Load	Stress	−13.39	<0.0001	−17.67–−9.11	Yes
SDNN	Rest	Stress	−34.18	<0.0001	−38.46–−29.91	Yes
RMSSD	Load	Rest	−19.84	<0.0001	−24.23–−15.46	Yes
RMSSD	Load	Stress	15.09	<0.0001	10.70–19.48	Yes
RMSSD	Rest	Stress	34.93	<0.0001	30.54–39.32	Yes
SampEn	Load	Rest	−0.08	0.26	−0.19–0.039	No
SampEn	Load	Stress	−0.33	<0.0001	−0.39–−0.27	Yes
SampEn	Rest	Stress	−0.65	<0.0001	−0.71–−0.59	Yes
H	Load	Rest	−0.09	<0.0001	−0.12–−0.06	Yes
H	Load	Stress	0.05	<0.0001	0.02–0.08	Yes
H	Rest	Stress	0.14	<0.0001	0.11–0.17	Yes
FD	Load	Rest	−0.06	<0.0001	−0.08–−0.04	Yes
FD	Load	Stress	0.07	<0.0001	0.05–0.09	Yes
FD	Rest	Stress	0.13	<0.0001	0.11–0.15	Yes
LFnu	Load	Rest	−15.79	<0.0001	−19.88–−11.71	Yes
LFnu	Load	Stress	16.57	<0.0001	12.49–20.66	Yes
LFnu	Rest	Stress	32.37	<0.0001	28.29–36.45	Yes
HFnu	Load	Rest	18.79	<0.0001	15.41–22.18	Yes
HFnu	Load	Stress	−12.58	<0.0001	−14.99–−9.18	Yes
HFnu	Rest	Stress	−31.38	<0.0001	−34.77–−27.93	Yes
LF/HF	Load	Rest	−0.67	<0.0001	−0.79–−0.55	Yes
LF/HF	Load	Stress	0.89	<0.0001	0.78–1.01	Yes
LF/HF	Rest	Stress	1.56	<0.0001	1.45–1.68	Yes
DFA_α1	Load	Rest	−0.21	<0.0001	−0.26–−0.14	Yes
DFA_α1	Load	Stress	0.056	<0.05	0.0005–0.12	Yes
DFA_α1	Rest	Stress	0.26	<0.05	0.21–0.32	Yes
DFA_α2	Load	Rest	−0.14	<0.0001	−0.19–−0.1	Yes
DFA_α2	Load	Stress	0.16	<0.0001	0.12–0.2	Yes
DFA_α2	Rest	Stress	0.31	<0.0001	0.26–0.35	Yes

. The data show significant differences between the groups in all studied parameters, with minor exceptions such as SampEn (load vs. rest, p = 0.26) and mean RR (load vs. stress, p = 0.79). The most distinct are the differences between rest and stress, including in time (mean RR, SDNN, RMSSD) and nonlinear indicators (SampEn, DFA α1, α2, Hurst, FD). All analyses were performed with Python (v3.11), using the scipy, statsmodels and seaborn libraries. Descriptive statistics are presented as mean ± standard deviation. Boxplot graphs (Figure 2) with statistical labels were used for visualization.

3.2. Principal Component Analysis

Prior to applying PCA [40], all variables were standardized using z-score normalization, so that each had a mean of 0 and a standard deviation of 1. This step was necessary because PCA is sensitive to the scale of the data, and the HRV parameters have different units (e.g., milliseconds, dimensionless values, etc.).

After standardization, the explained variance for each principal component was calculated. A scree plot was used to display the relative contribution of each component to the total variation in the data. To justify the dimensionality reduction using PCA, Figure 3 is provided, which presents a scree plot showing the explained variance for each principal component. A sharp drop was observed (Figure 3) after the first component, suggesting that it captures the majority of the variance in the dataset.

The scree plot indicates that the first principal component (PC1) accounts for nearly 68% of the total variance in the dataset, making it the most informative axis.

The second component (PC2) contributes only about 9%, while the remaining components each explain less than 8% of the variation.

A pronounced “elbow point” is observed after PC1, suggesting that this component dominates the variance structure and may be sufficient for summarizing the data.

This pattern is consistent with prior applications of PCA in biomedical signal analysis, where a dominant first component often captures the majority of variance in highly correlated HRV metrics [1,36].

Cumulatively, the first three components account for over 85% of the total variance, making them suitable for dimensionality reduction (e.g., for 2D or 3D visualization) without significant information loss.

This supports the hypothesis that HRV parameters are highly correlated and can be summarized by a small number of latent factors [24,39].

After PCA transformation, we visualized the HRV data in a two-dimensional PC1-PC2 space (Figure 4). This allows for a preliminary check of the potential separation among the physiological states without assuming any prior labels.

The visualization clearly demonstrates separation among the three physiological states—rest, stress, and load—with each forming a distinct cluster in the principal component space [24].

These findings confirm that PCA effectively captures the structural differences between physiological conditions based on HRV characteristics.

To better understand the relationships between HRV and fractal features, Figure 5 presents a heatmap of the correlation. This allows us to identify highly collinear or redundant variables and reveal physiological dependencies between metrics such as RMSSD, SampEn, and Hurst exponent. Higher values (shown in red) indicate stronger positive relationships between the metrics. Notable correlations include the following:

• SampEn and SDNN (r = 0.88)—indicating a strong association between entropy and overall linear variability.
• RMSSD and SampEn (r = 0.86)—reflecting a high correlation between short-term variability and signal complexity.
• Hurst exponent and SampEn (r = 0.78)—supporting a shared fractal–entropic nature of the signal.

The correlation matrix confirms that elevated linear variability (SDNN, RMSSD) is closely linked to higher entropy (SampEn) and a more fractal-like structure of the signal (Hurst exponent, fractal dimension).

This underscores the role of SampEn as a unifying indicator of physiological complexity.

Furthermore, increased self-similarity of the signal (as indicated by the Hurst exponent) appears more pronounced under favorable physiological conditions.

These results visually complement the observations in Figure 4, where the three physiological states—rest, stress, and physical exertion—are clearly distinguishable. In the resting state, HRV parameters are highest, reflecting strong autonomic regulation and adaptability. In contrast, stress causes a marked reduction in parameters such as RMSSD and SampEn, while physical load results in a more moderate decline in these values. The state of “stress” in the present study is caused by the tension that the athlete experiences during a wrestling competition. This includes both mental pressure and expectation of a result, as well as physical struggle, which leads to activation of the sympathetic nervous system and a distinct decrease in HRV metrics such as RMSSD and SampEn.

The combined analysis indicates that nonlinear and fractal metrics (SampEn, Hurst exponent, fractal dimension) not only supplement classical HRV parameters, but also provide deeper insight into the functional state of the autonomic nervous system. These advanced features may serve as reliable biomarkers for distinguishing between physiological and stress-induced conditions.

To better visualize the variance and influence of variables, we constructed a 3D PCA biplot (Figure 6). This plot shows how individual features contribute to each component and how participants cluster in 3D space according to physiological state. The 3D PCA biplot includes the following elements:

• Color-coded data points representing the three physiological states (rest, stress, load).
• Black vectors depicting the contribution of each HRV metric (SDNN, RMSSD, SampEn, Hurst exponent, FD, mean RR) to the first three principal components (PC1, PC2, PC3).
• Textual labels positioned in space according to the direction and magnitude of the vectors.

This figure provides a clear visualization of both the clustering of physiological states and the multidimensional influence of the extracted features on their differentiation.

Principal Component Analysis (PCA) revealed meaningful latent structures in the data:

PC1 primarily reflects overall variability and dynamic complexity. It is dominated by high negative loadings for RMSSD, mean RR, and SDNN, indicating that a reduction in these values shifts the observations toward the positive axis of PC1. This suggests that lower HRV corresponds to physiological stress or load conditions.

PC2 differentiates observations based on entropy- and fractal-related features, with the strongest loadings observed for SampEn (0.555) and Hurst exponent (−0.770). This pattern implies that PC2 captures variations driven by changes in signal complexity and long-range correlations, such as the loss of fractal organization during stress.

PC3 is most strongly associated with SDNN (−0.714) and SampEn (0.433), highlighting their combined influence on a third dimension of physiological variation.

In addition to PCA, a hierarchical clustering analysis using Ward’s linkage was performed to further explore natural grouping among participants based on their HRV and fractal characteristics and to detect latent groupings. Figure 7 illustrates the distribution of normalized feature values across the three identified clusters, which correspond well to the physiological states of rest, stress, and physical exertion.

The figure presents the distribution of normalized values of HRV and fractal characteristics (including DFA α2) across the three identified clusters corresponding to the physiological states of rest, stress, and physical load. The values in the matrix cells represent the mean relative level of each feature within the respective state, expressed as percentages.

Description of the clusters:

Cluster 1—Rest

This cluster shows high values of key time and frequency HRV parameters: SDNN = 67%, RMSSD = 83%, mean RR = 84%, and HF (nu) = 57%, combined with a low LF/HF = 42%. Increased fractality (Hurst = 68%, DFA α1 = 72%) and moderate complexity according to SampEn = 68% are also observed. These characteristics are typical of a state of parasympathetic dominance and stable autonomic balance, confirming that the cluster reflects physiological recovery and relaxation.

Cluster 2—Stress

The lowest values are recorded here: SDNN = 38%, RMSSD = 36%, mean RR = 52%, Hurst = 11%, and SampEn = 33%, combined with a higher LF/HF = 53%. This profiles a state of sympathetic activation with suppressed parasympathetic control, reduced variability and fractality of the rhythm. Reduced entropy values and DFA α1 (39%) indicate reduced complexity of regulation, characteristic of psychophysiological stress.

Cluster 3—Load

It notes the highest values of LF (nu) = 92% and FD = 75%, together with increased SDNN = 80% and moderate RMSSD = 66% and HF (nu) = 49%. LF/HF = 53% indicates predominant sympathetic activity, characteristic of acute physical exertion. Fractal indicators (DFA α1 = 55%, DFA α2 = 55%) and moderate SampEn = 63% indicate a mixed response between adaptability and stress activation.

3.3. Cluster Analysis and Cumulative Explained Variance

Cluster analysis is an unsupervised machine learning technique that groups observations (e.g., participants) based on the similarity of their features. In this study, we employed the K-Means clustering algorithm, which partitions the data into K clusters by minimizing within-cluster distances and maximizing between-cluster separation.

We used K = 3, corresponding to the three physiological states: rest (baseline), stress (psychological strain), and load (physical exertion).

Key results from the clustering analysis include the following:

Silhouette Coefficient: 0.46

This indicates a moderately good clustering effect. Participants are reasonably well grouped based on their HRV and fractal features, although some degree of overlap remains.

Cumulative Explained Variance from PCA:

PC1: 66.15%.

PC1 + PC2: 74.11%.

PC1 + PC2 + PC3: 84.66%.

These values show that the first three principal components capture over 84% of the total variance, validating the effectiveness of the 3D PCA and justifying its use for visualizing cluster separation.

The Silhouette Score is a measure of how well each data point fits within its assigned cluster. Interpretation ranges are as follows:

~0.0 → no clear structure;

~0.5 → moderate separation;

0.7 → strong and well-defined clusters.

A score of 0.46 suggests moderate segmentation—there is some overlap between clusters, yet sufficient distinction is evident, particularly when considering complex features such as sample entropy (SampEn) and Hurst exponent (H).

3.4. Individual Clustering of Participants Using PCA-Transformed Components

In addition to feature-level clustering, we examined participant-level similarities using a cluster map (Figure 8). We used this unsupervised visualization to examine the similarity in HRV patterns across subjects and to support or reject the hypothesis of clustering of latent physiological states. Cluster maps visualize the individual clustering of participants based on their PCA-transformed HRV profiles. The cluster map is an enhanced form of a heatmap that integrates multiple layers of information:

Heatmap Matrix—A square matrix where each cell represents the distance between two participants, calculated from their PCA-transformed HRV features. Darker or lighter shades indicate greater or lesser similarity, respectively.

Dendrograms—Hierarchical trees positioned at the top and left margins, illustrating how participants are merged into clusters based on hierarchical agglomerative linkage (e.g., Ward’s method).

Color Encoding—The color gradient of each cell reflects the degree of similarity or dissimilarity between two individuals, providing a visual summary of inter-participant variability in HRV patterns.

This type of visualization allows for both cluster-level and individual-level insights, complementing the broader clustering analyses and offering intuitive identification of subgroups with similar physiological signatures.

Figure 8 illustrates the results of hierarchical clustering of participants based on the first two principal components (PC1 and PC2), extracted through PCA from HRV and fractal metrics. The color scale represents normalized values, ranging from low (blue) to high (red). Similar colors indicate small Euclidean distances, suggesting high similarity in HRV profiles between the corresponding participants. In contrast, sharp color differences reveal physiological dissimilarities, such as those observed between rest and stress states.

The top and side dendrograms depict the way participants are grouped into clusters based on the similarity of their PCA-transformed HRV features. Branches that merge lower in the dendrogram indicate closer physiological profiles. The emergence of “Y”-shaped structures denotes the formation of new clusters. At a certain threshold cut-off level, three major clusters can be clearly distinguished, corresponding to the physiological states of rest, stress, and load.

Figure 8 also shows that participants in the rest state are most compactly clustered, indicating high within-group homogeneity. The mean coordinates of the participants in the first two principal components (PC1 and PC2) show a clear spatial separation between physiological states, reflecting different mechanisms of autonomic regulation. The rest cluster is located mainly in the negative region of PC1 (mean: PC1 = −2.05 ± 0.41, PC2 = 0.34 ± 0.27; centroid: −2.15, 0.45), which is an indicator of parasympathetic control dominance and high values of temporal HRV indices. The stress cluster is positioned in the positive region of PC1 and slightly negative region of PC2 (PC1 = 1.48 ± 0.36, PC2 = −0.52 ± 0.19; centroid: 1.92, 0.38), reflecting reduced variability and an increased LF/HF ratio, characteristic of sympathetic dominance. The load cluster is clearly separated in the positive region of PC2 (PC1 = 0.71 ± 0.28, PC2 = 1.83 ± 0.32; centroid: 0.42, −1.87), suggesting a mixed influence of sympathetic activation and physiological stress from physical exertion. The calculated Euclidean distances between the centroids of the clusters confirm significant dissimilarity—rest–stress = 4.21, rest–load = 3.74, stress–load = 3.05—with the largest distance observed between rest and stress. The compactness of the rest group (mean internal distance = 0.82) indicates high internal homogeneity, while stress and load demonstrate greater internal variability (1.14 and 1.28, respectively), which is consistent with the more diverse physiological responses under conditions of mental and physical exertion.

3.5. DBSCAN Analysis for Physiological State Recognition

To investigate the robustness of clustering in the presence of noise and individual variability, we applied the DBSCAN algorithm to the PCA-transformed space. The method graph illustrates density-based cluster formation and anomaly detection, which are crucial for real-time applications with unlabeled physiological data.

The DBSCAN algorithm is an unsupervised clustering method particularly suitable for biomedical data, which are often noisy and exhibit heterogeneous density. Its main advantages include the ability to detect anomalies (outliers), identify dense regions without requiring a predefined number of clusters, and robustness to non-standard, nonlinear distributions, commonly observed in physiological measurements such as HRV, PPG, and ECG.

Working Principle. DBSCAN operates using two key parameters:

ε (eps)—the radius for neighborhood search;

minPts—the minimum number of points required to form a dense region.

A point is classified as a core point if it has at least minPts neighbors within a radius of ε. A cluster is then formed around this point. Points that do not belong to any cluster are considered noise.

To investigate the natural grouping of participants based on their HRV metrics, DBSCAN was applied to the PCA-reduced space (PC1 and PC2). Input data included normalized values of SDNN, RMSSD, SampEn, Hurst exponent, fractal dimension, etc.

The results, illustrated in Figure 9, revealed three primary clusters corresponding approximately to the physiological states of rest, stress, and load. Several anomalies, marked with an “X”, were identified, predominantly located in transitional zones—particularly between rest and stress. These may reflect individual differences in autonomic regulation or transient adaptive responses.

DBSCAN showed that physiological states form density-defined regions in the HRV feature space, without requiring class label information. The groups were particularly well separated along PC1, which is largely influenced by metrics such as SDNN, RMSSD, and Mean RR.

These findings underscore the following:

• The feasibility of unsupervised recognition of physiological states;
• The suitability of DBSCAN for biomedical data analysis, especially in the presence of individual variability;
• The importance of a personalized approach when interpreting HRV data.

The graph in Figure 9 shows the distribution of participants from the three states (rest, stress, load) relative to the principal components PC1 and PC2, after applying the DBSCAN algorithm. The different clusters are visualized with colored markers, and the points classified as noise (anomaly) are marked with an “X”. The analysis visually confirms the correspondence between the physiological classes and the resulting clusters, as well as the presence of borderline states.

The DBSCAN algorithm (Density-Based Spatial Clustering of Applications with Noise) is an effective tool for analyzing biomedical signals, including HRV, especially in situations where the number of clusters is not known in advance. Unlike K-Means, DBSCAN does not require specifying the number of groups, but forms them based on the density of the data. In addition, the algorithm automatically detects and separates outliers, designated as a separate group (Cluster = −1), which is essential in medical applications where the detection of atypical conditions is critical.

Sensitivity analysis of DBSCAN parameters

A series of clustering experiments were conducted to assess the sensitivity of the DBSCAN algorithm to its main parameters, namely the neighborhood radius (ε) and the minimum number of points required to form a cluster (minPts). The parameter ε was varied in the range from 0.3 to 2.0 (standardized units), and minPts was tested for values between 3 and 8. These ranges were chosen based on knowledge of the characteristics of the HRV data.

As shown in Figure 10, at a lower value of ε (0.5), many small and fragmented clusters with an increased number of noise points are formed, while at ε = 1.0, a balanced cluster structure is achieved that corresponds well to physiological states (rest, exercise, stress). At a high value (ε = 1.5), the individual groups merge and the discriminatory power of the model is lost.

External consistency metrics—ARI, NMI—were calculated for each configuration based on the ground-truth labels. The results showed that clustering performance remained stable with moderate variations in ε and minPts. Specifically, ARI ranged between 0.72 and 0.81, and NMI between 0.69 and 0.79 across the tested configurations with a high minimum number of points (minPts = 8) and suboptimal values of ε (noticeable reduction in clustering quality). Additional testing identified the optimal setting (ε = 0.85, minPts = 4) that provided the most consistent clusters corresponding to physiologically acceptable groups. This setting yielded the highest external validation scores (ARI = 0.89, NMI = 0.92), indicating both strong agreement with expert-based physiological labels and robust preservation of the underlying structure of the autonomic response.

3.6. Evaluated Characteristics

To validate the performance of the proposed unsupervised clustering approach, three widely accepted evaluation metrics were employed: Purity, Adjusted Rand Index (ARI), and Normalized Mutual Information (NMI). These indices provide a quantitative assessment of the agreement between automatically discovered clusters and the ground-truth physiological states of the participants (rest, stress, load), known a priori from the experimental protocol.

Purity, which measures the proportion of correctly assigned elements, reached a value of 0.933, indicating that 93.3% of the participants were grouped into clusters matching their actual physiological condition. The ARI—a metric that evaluates the consistency of all pairwise assignments while adjusting for chance—was 0.89, reflecting a high level of structural agreement between the predicted and actual labels. Furthermore, the NMI score was 0.92, demonstrating significant informational overlap between the cluster assignments and the true classes.

These results validate the reliability of the applied algorithms (K-Means/DBSCAN) in identifying physiological states. Even in the absence of supervision, the system achieved a high degree of concordance with expert-labeled classes, confirming the suitability of unsupervised machine learning techniques for physiological signal analysis.

Based on the results obtained and the analyses performed, the following general conclusions can be formulated regarding the research questions:

• Regarding latent structures in HRV and fractal features:

The dimensionality reduction techniques used, particularly PCA, successfully revealed hidden dependencies between metrics, allowing for a clear distinction between physiological states. The principal components combine both linear (e.g., SDNN, RMSSD) and nonlinear (e.g., DFA α, SampEn) metrics into a more informative space, which facilitates further analysis and visualization.

2.

Regarding the ability of unsupervised algorithms to distinguish states:

The K-Means and DBSCAN algorithms demonstrated high efficiency in separating participants according to real physiological states (rest, stress, exercise), without the use of predefined labels. The achieved values of the accuracy metrics (Purity ≈ 93%, ARI = 0.89, NMI = 0.92) confirm that the clustering corresponds to a large extent to the biological reality.

3.

Regarding the role of AI-based visualizations:

Visual approaches such as PCA biplots, heatmaps and cluster maps provided an intuitive and interpretable basis for detecting anomalies, transient states and natural groups. The observed cluster structures and principal component distributions support the possibility of integrating these methods into intelligent monitoring systems working with unlabeled physiological data in real time.

These findings highlight the potential of unsupervised learning and visual AI analysis for precise, automated assessment of autonomic function and for early detection of abnormalities in cardiac regulation.

4. Discussion

Materko [41] demonstrated the use of machine learning for assessing autonomic regulation based on a limited set of linear HRV parameters, whereas our study incorporates a broader spectrum of nonlinear and fractal indices combined with PCA and hybrid clustering for more reliable differentiation of physiological states. A comparative analysis with Lebamovski et al. [42] revealed a similar reduction in DFA α1 and α2 during psychological stress compared to rest, while our work further introduces an intermediate condition—physical load—indicating partially preserved regulation under non-pathological exertion. Comparable trends were also reported by Zamora-Justo et al. [43] in metabolic syndrome, where autonomic complexity was reduced both at rest and during exercise, aligning with our observations.

In the context of clustering approaches, Borthakur et al. [44] utilized multimodal smartwatch signals with unsupervised algorithms but limited visualization, whereas our method extends this by integrating PCA with DBSCAN/K-Means for richer physiological interpretation. Similarly, Schrumpf et al. [45] achieved phase matching during exercise through hierarchical clustering, though with fixed metrics and lower robustness to noise, while our hybrid approach adapts dynamically to heterogeneous and incomplete data. Complementary to these, Serantoni et al. [46] linked HRV patterns with VO₂max to track fatigue in running; our study expands this framework to a broader set of conditions, with greater feature diversity and integrated anomaly detectors. Looking ahead, the proposed methodology is intended for real-time differentiation of physiological states in a wearable monitoring device [47], providing practical applicability for continuous cardiac assessment.

5. Conclusions

This study presents an AI-driven framework for unsupervised analysis of HRV and fractal features derived from wearable cardio signals. By applying dimensionality reduction (PCA) and clustering algorithms (K-Means, DBSCAN), we demonstrated the ability to identify physiologically meaningful groups such as rest, stress, and load states without prior labels. The use of entropy- and complexity-based metrics, combined with traditional HRV parameters, enabled nuanced differentiation of autonomic states. Visualization techniques such as biplots, heatmaps, and cluster maps provided interpretable insights into latent physiological structures. The DBSCAN method further identified outliers and transitional states, suggesting potential for real-time anomaly detection. These findings support the feasibility of unsupervised learning for intelligent cardiac monitoring and point toward personalized, non-invasive health assessment systems using wearable devices. Future work will focus on validating the approach in larger cohorts and integrating real-time decision support in telehealth applications.

The proposed hybrid PCA + K-Means + DBSCAN pipeline offers an interpretable, label-free approach for physiological state recognition from wearable HRV signals, with potential applications in sports monitoring and preventive healthcare. Upon validation in wearable devices, it could be transitioned to long-term real-time deployment.