Farmer Ants Optimization Algorithm: A Novel Metaheuristic for Solving Discrete Optimization Problems
Abstract
1. Introduction
- Presenting the new Optimization Algorithm based on the life of farmer ants;
- The concurrency feature of the algorithm that can solve complex problems with high accuracy and fast speed;
- The ability to share local knowledge to reach the best global solution;
- Ability to solve discrete NP-hard problems;
- Evaluation of the proposed method and comparing it with some state-of-the-art algorithms in solving engineering problems.
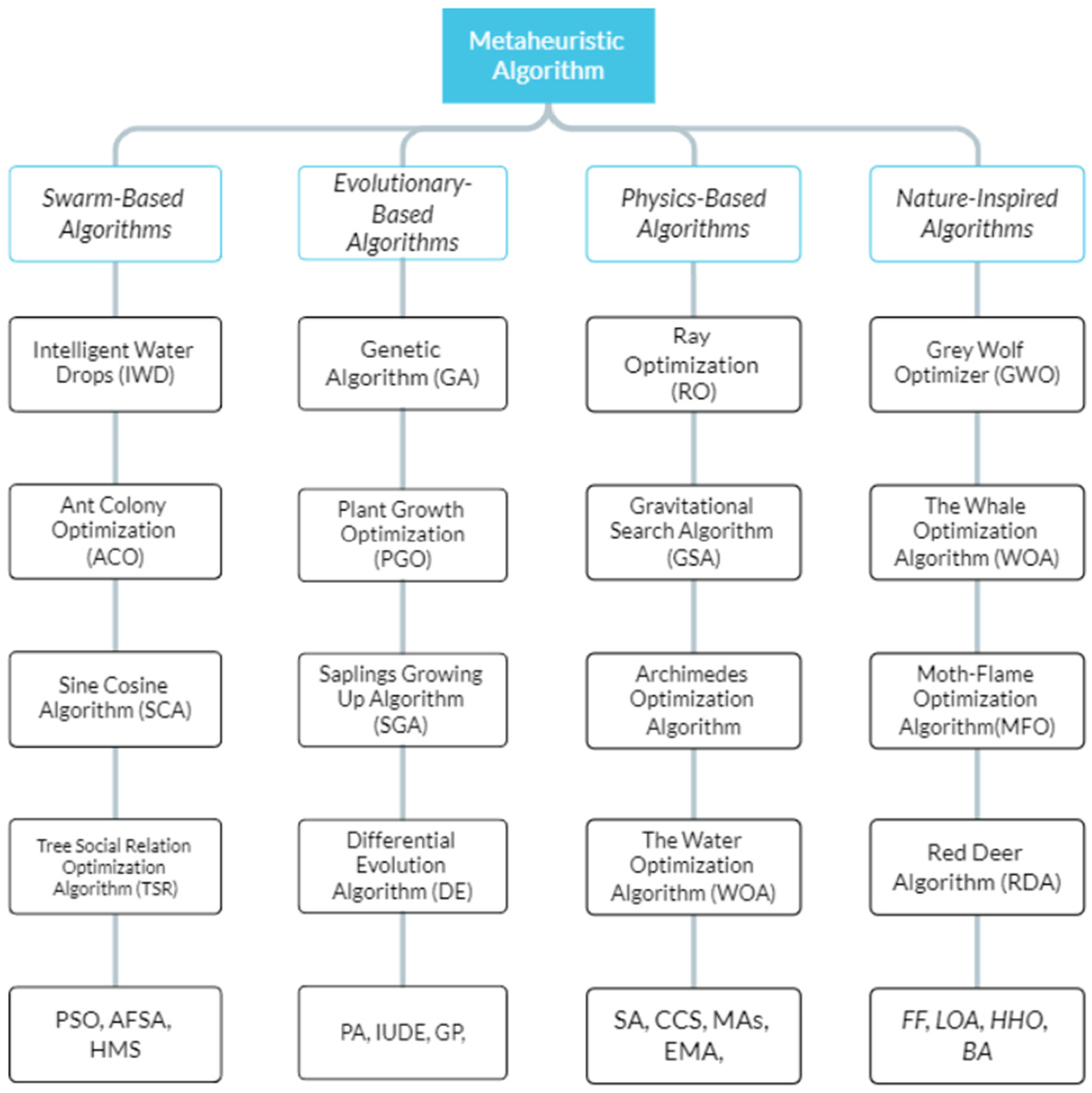
2. Related Works
3. Materials and Methods
3.1. Inspiration
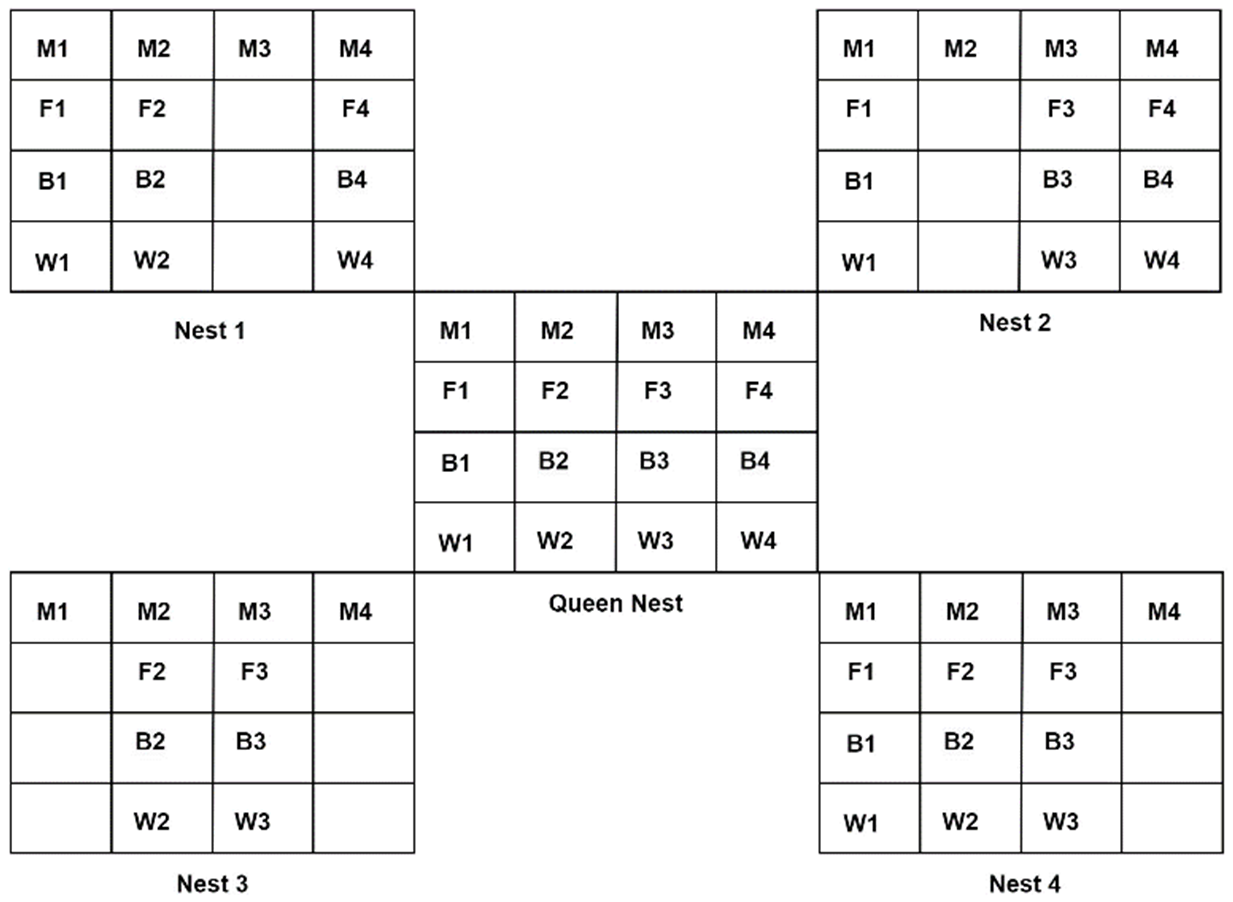
3.2. Farmer Ants Optimization Algorithm (FAOA)
- Step 1: Algorithm initialization including the number of ants, number of nests, types of mushrooms, foods, and bacteria;
- Step 2: Random distribution of mushrooms in nests and assigning ants to mushrooms;
- Step 3: Calculate the total weight of mushrooms in each nest using Equations (1)–(4);
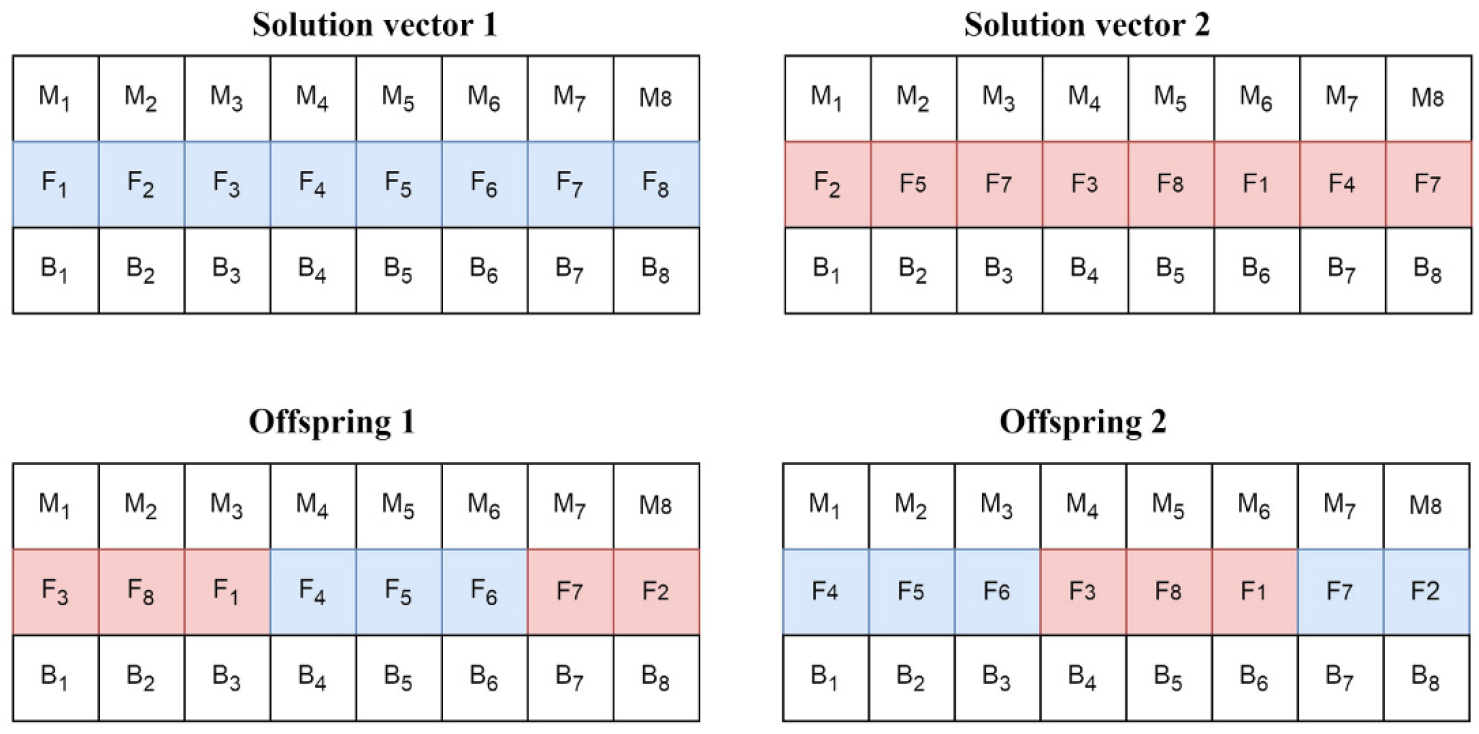
- Step 4: Do food change operations;
- Step 5: Do bacterial change operation on some mushrooms according to SP;
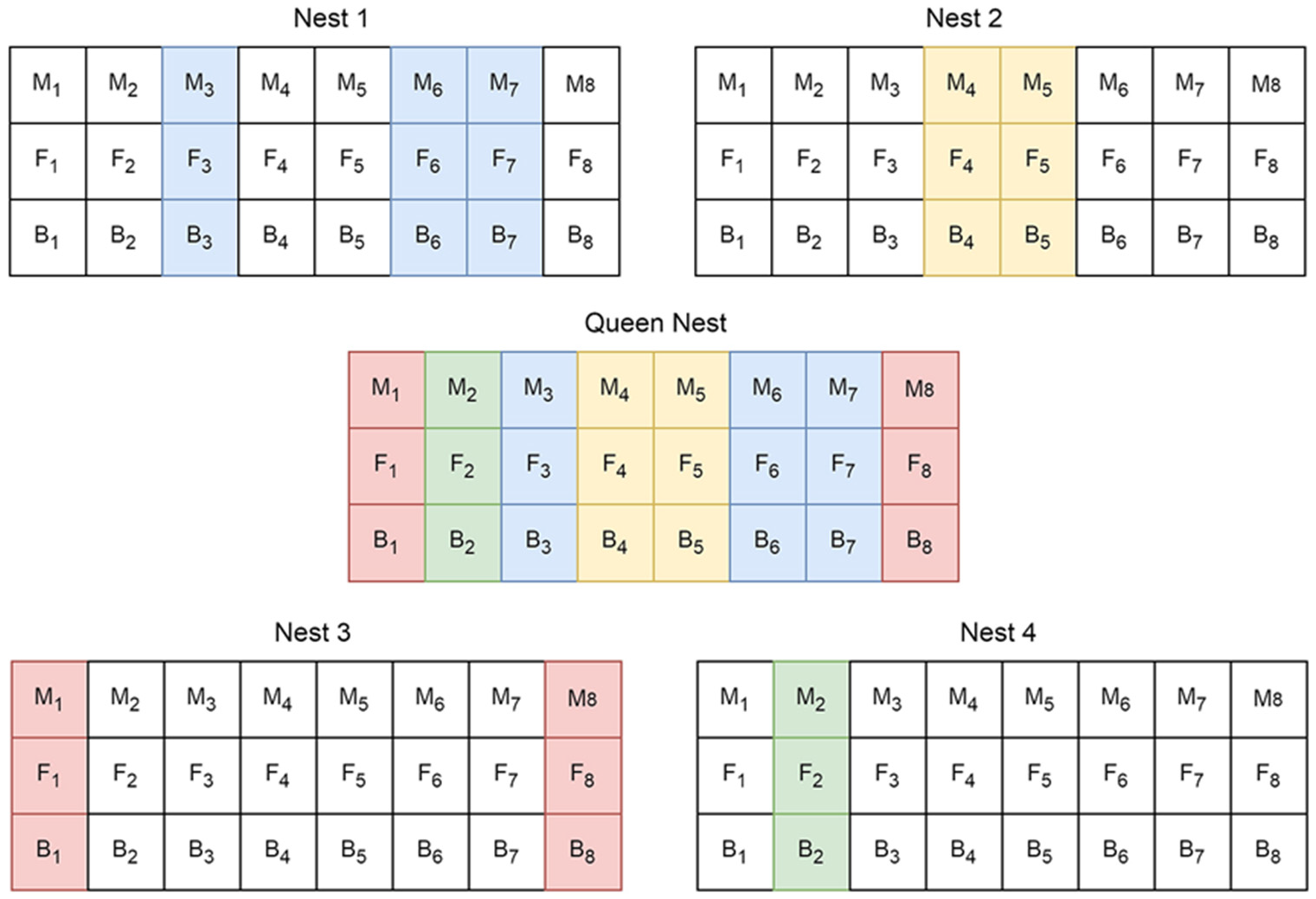
- Step 6: Participate 1 − SP percentage of ants in the global behavior of the algorithm;
- Step 7: Send the best relative pattern to the queen nest;
- Step 8: Calculate WK or the total weight of mushrooms in each nest using relations 1 to 4;
- Step 9: Calculate the total weight of mushrooms in the entire colony or W using equation 5;
- Step 10: Remove weak solutions;
- Step 11: Repeat the algorithm until the stop condition is reached.
| Algorithm 1: Farmer’s Side Process |
| Initialize parameters 1. For each nest K; 2. Generate the initial population; 3. Randomly assign ants to mushrooms; 4. 5. 6. Do food operation; 7. percent of mushrooms; 8. Do bacteria operation; 9. for new solutions; 10. 11. 12. 13. 14. Until the last iteration. |
| Algorithm 2: Queen Side Process |
| 1. Repeat; 2. For each iteration; 3. Receive partial solutions for all nests; 4. Compute by Equations (1), (5), and (6); 5. Do global food operation; 6. Do global bacteria operation; 7. Add solutions to the population; 8. best solutions; 9. End For; 10. Until the last iteration; 11. Return the final solution. |
4. Evaluation and Results
4.1. Problems and Compared Algorithms
4.2. Discrete Problems
4.2.1. The TSP Issue
4.2.2. Knapsack Problem (KP)
4.2.3. Server Placement Problem (SP)
4.2.4. Construction Site Layout Planning (CSLP)
4.2.5. AFP (Arable Field Problem)
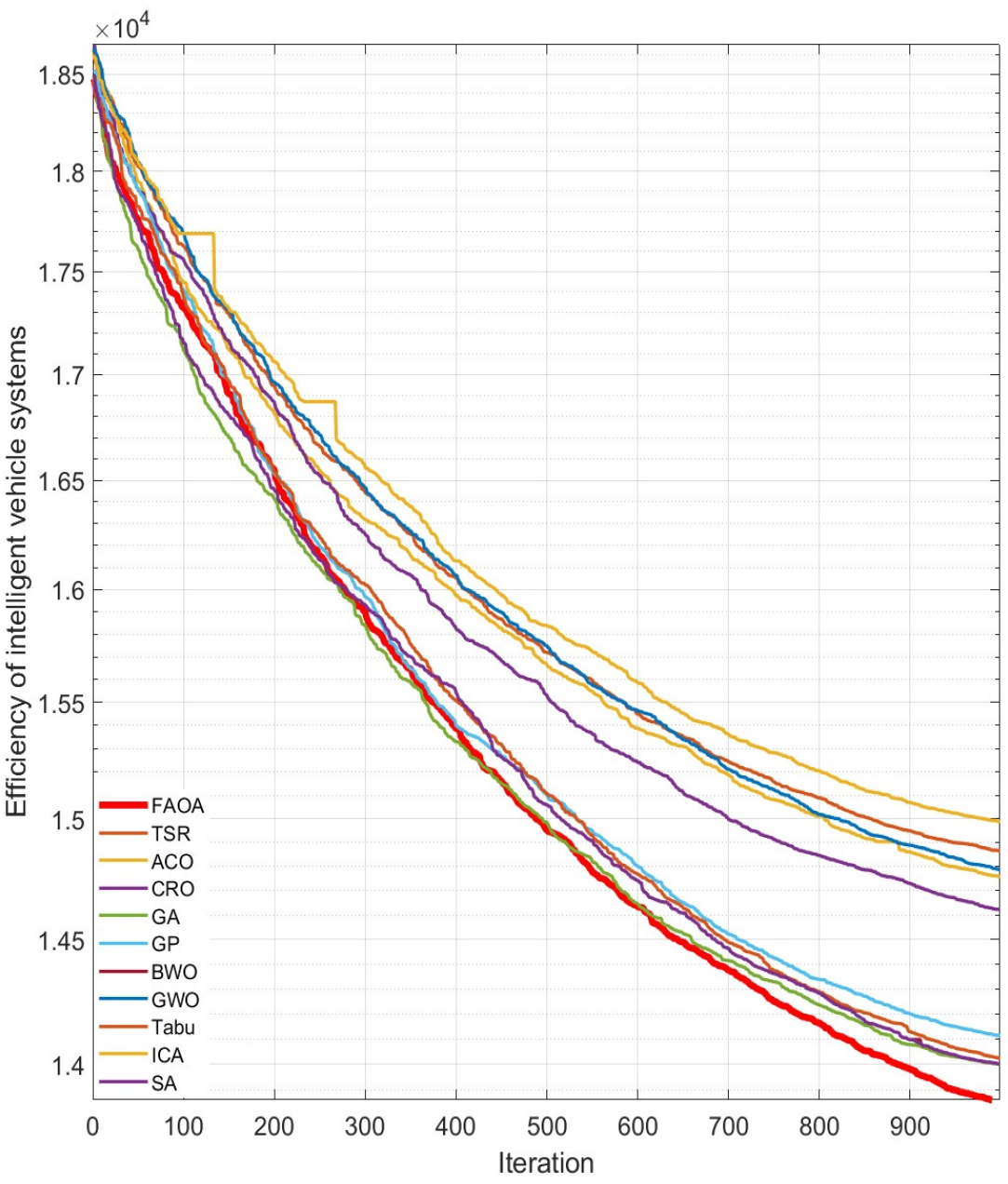
4.2.6. ES (Emblem System for Intelligent Vehicles)
4.2.7. FCS (Fog Computing System-Cloud Problem)
4.2.8. Truss Structures Problem (TS)
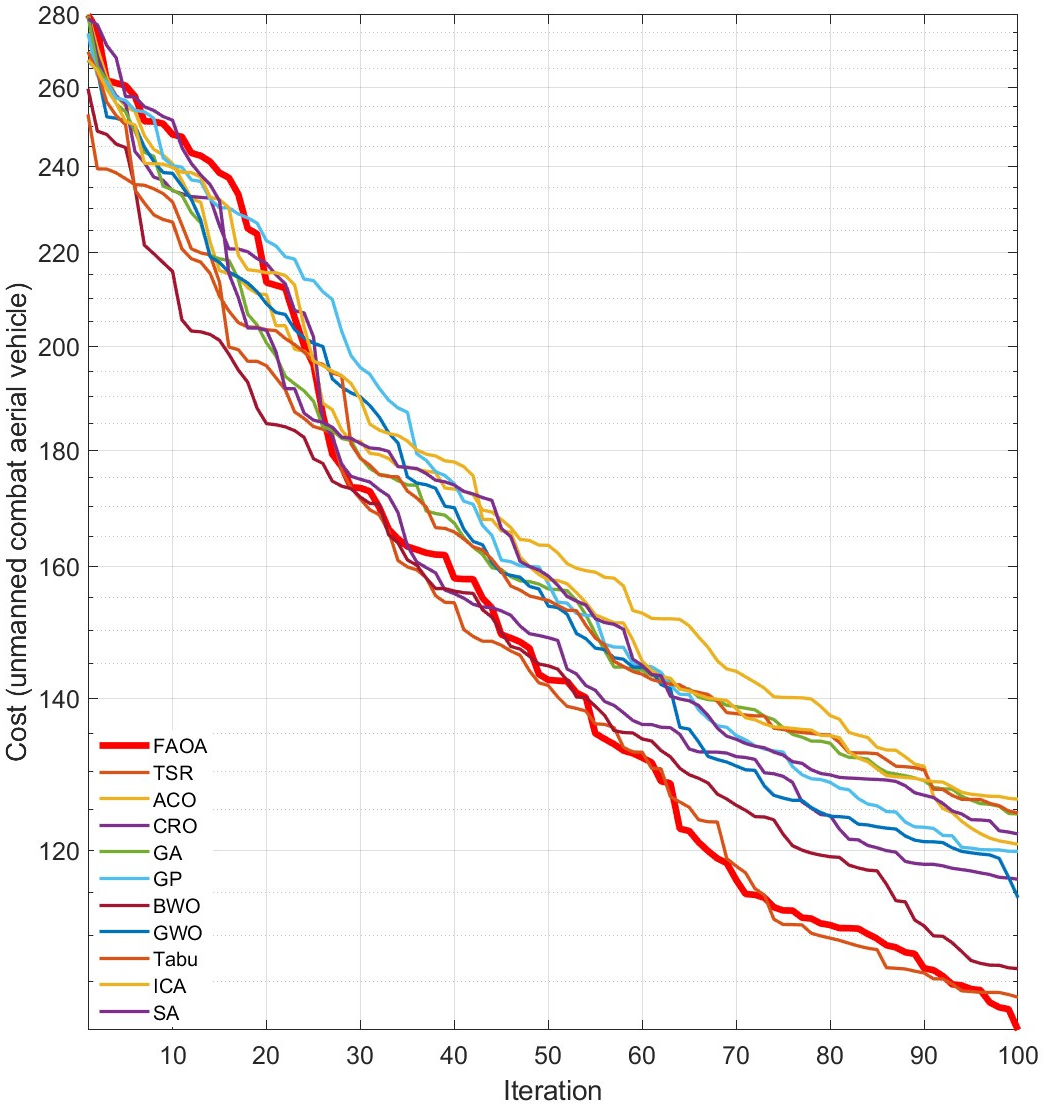
4.2.9. UCAV Problem (UCAV Three-Dimension Path Planning)
4.3. Benchmark Functions
4.4. Runtime
4.5. Performance Metrics
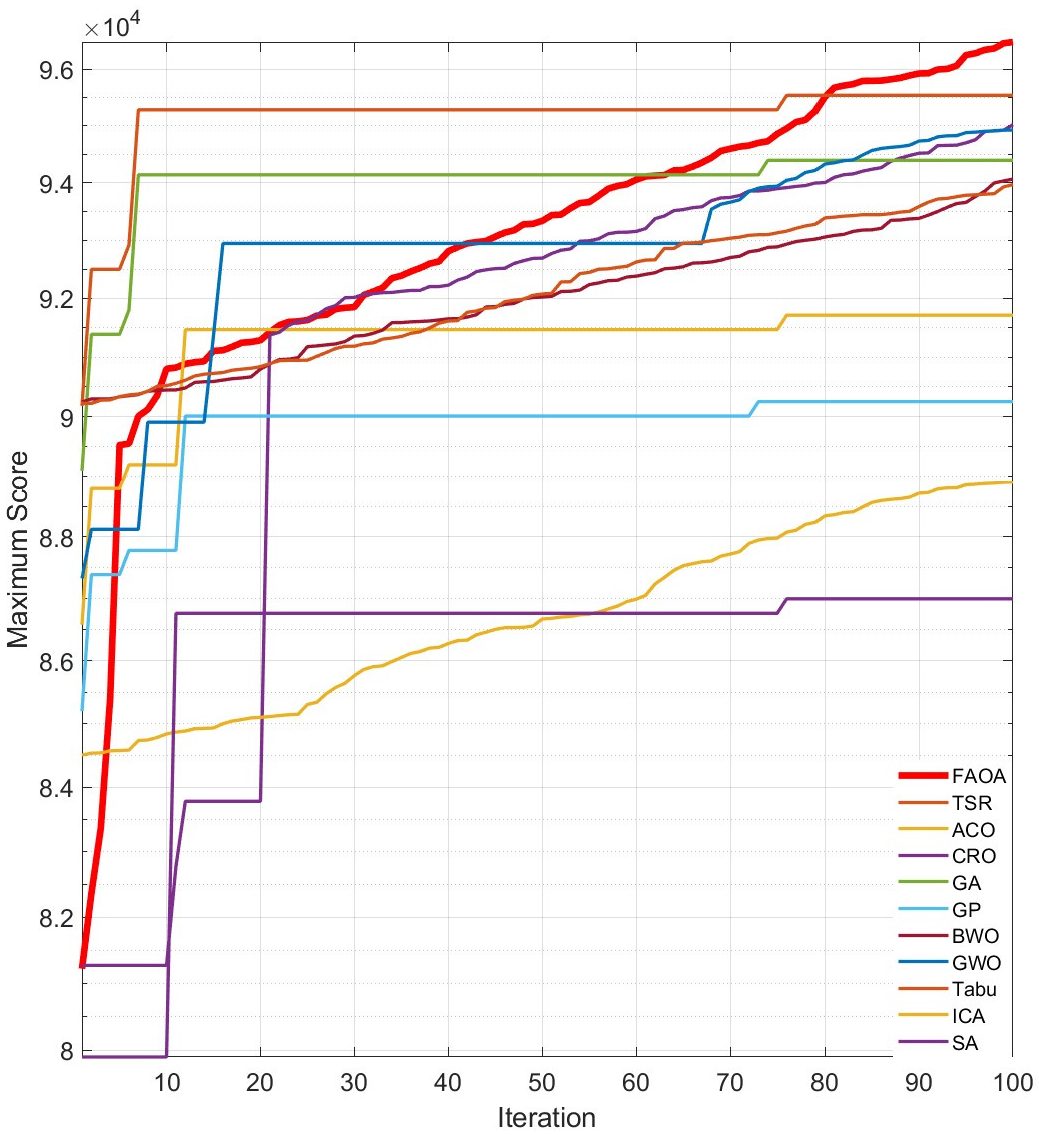
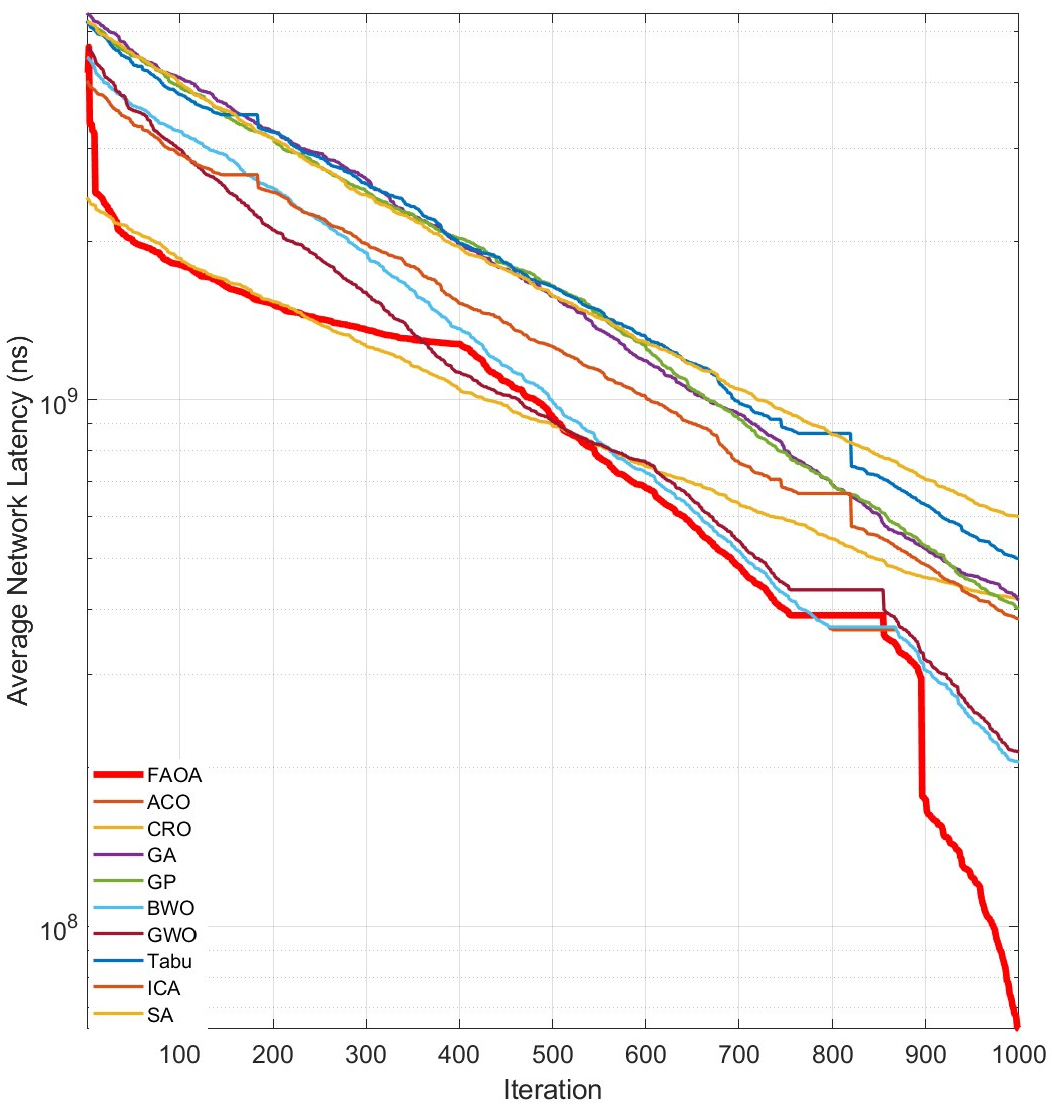
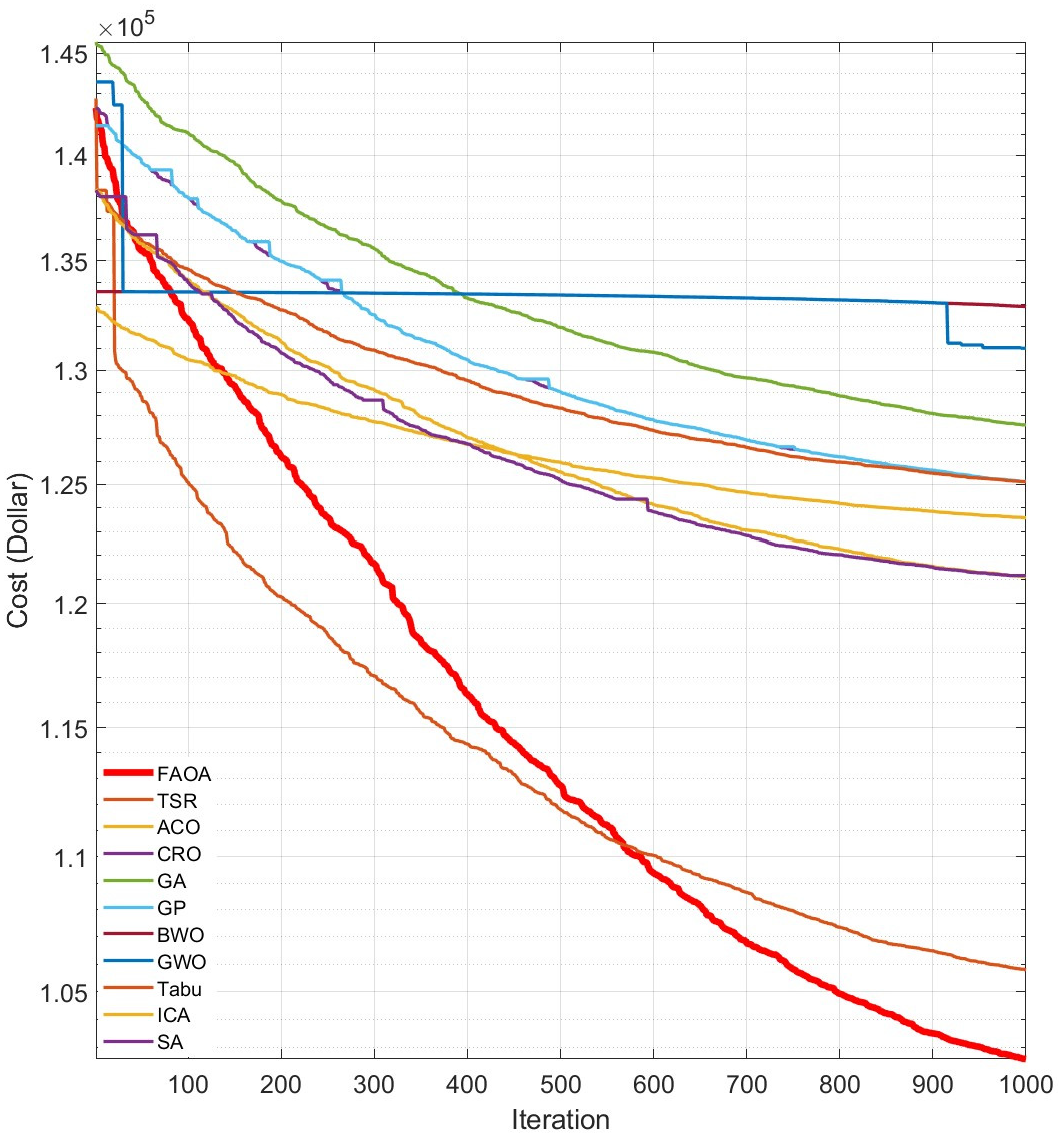
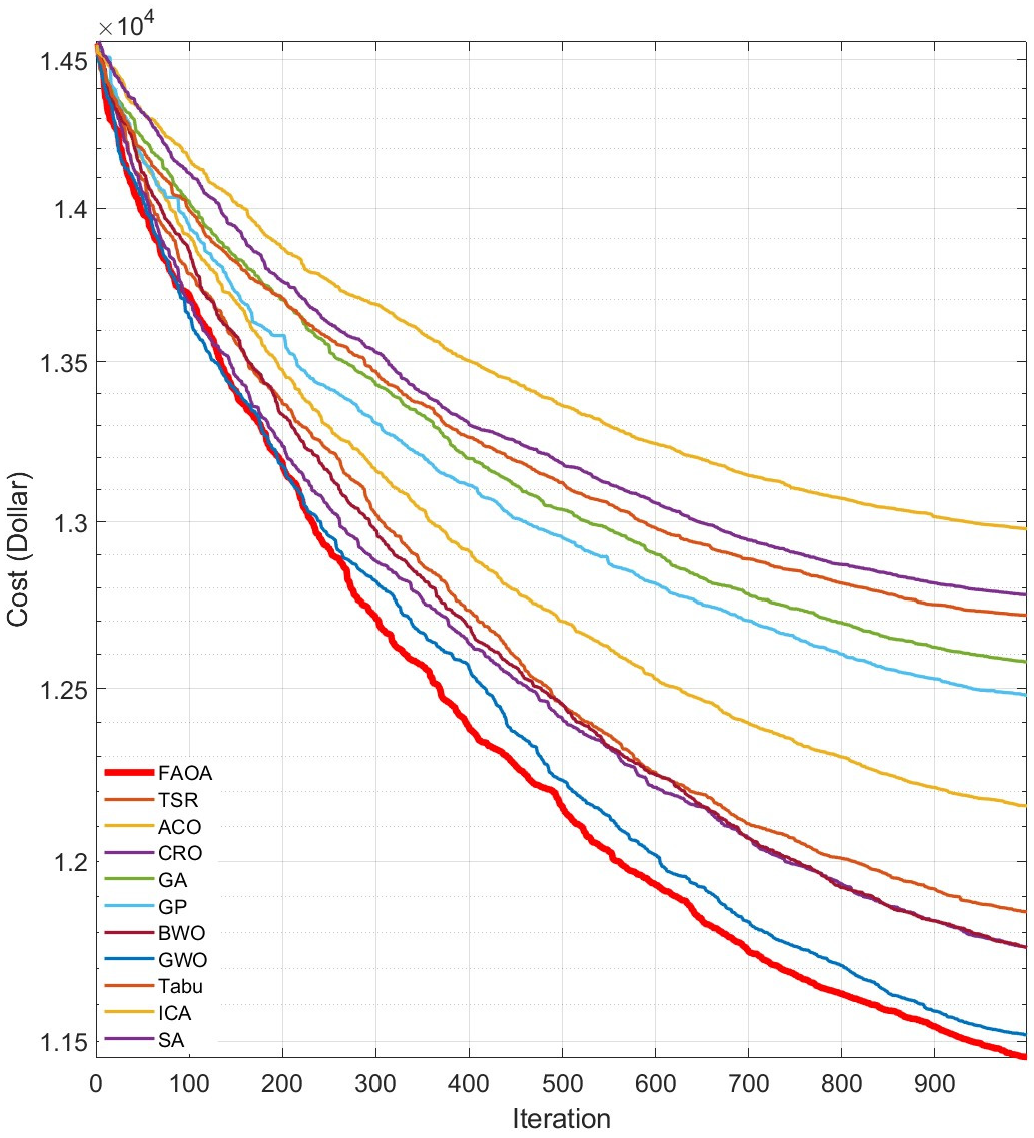
4.5.1. Convergence Rate
4.5.2. Computational Resource Utilization
4.5.3. Accuracy
4.5.4. Scalability
4.6. Discussion
4.7. Time Complexity
4.8. Limitation of the FAOA
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- ChandraBora, K.; Kalita, B. Exact Polynomial-time Algorithm for the Clique Problem and P = NP for Clique Problem. Int. J. Comput. Appl. 2013, 73, 19–23. [Google Scholar] [CrossRef][Green Version]
- Woeginger, G.J. Exact algorithms for NP-hard problems: A survey. In Combinatorial Optimization—Eureka, You Shrink; Springer: Berlin/Heidelberg, Germany, 2003; pp. 185–207. [Google Scholar]
- Lin, F.-T.; Kao, C.-Y.; Hsu, C.-C. Applying the Genetic Approach to Simulated Annealing in Solving Some NP-Hard Problems. IEEE Trans. Syst. Man Cybern. 1993, 26, 1752–1767. [Google Scholar]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Simpson, A.R.; Dandy, G.C.; Murphy, L.J. Genetic algorithms compared to other techniques for pipe optimization. J. Water Resour. Plan. Manag. 1994, 120, 423–443. [Google Scholar] [CrossRef]
- James, C. Introduction to Stochastics Search and Optimization; Wiley-Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Parejo, J.A.; Ruiz-Cortés, A.; Lozano, S.; Fernandez, P. Metaheuristic optimization frameworks: A survey and benchmarking. Soft Comput. 2012, 16, 527–561. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-Flame Optimization Algorithm: A Novel Nature-inspired Heuristic Paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Ensemble strategies for population-based optimization algorithms—A survey. Swarm Evol. Comput. 2019, 44, 695–711. [Google Scholar] [CrossRef]
- Mcculloch, W.S.; Pitts, W. A Logical Calculus Of The Ideas Immanent In Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Von Neumann, J.; Burks, A.W. Theory of self-reproducing automata. IEEE Trans. Neural Netw. 1966, 5, 3–14. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wu, G. Across neighborhood search for numerical optimization. Inf. Sci. 2016, 329, 597–618. [Google Scholar] [CrossRef]
- Wu, G.; Pedrycz, W.; Suganthan, P.N.; Mallipeddi, R. A variable reduction strategy for evolutionary algorithms handling equality constraints. Appl. Soft Comput. 2015, 37, 774–786. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Reeves, C.R. Modern Heuristic Techniques for Combinatorial Problems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Blum, C.; Puchinger, J.; Raidl, G.R.; Roli, A. Hybrid metaheuristics in combinatorial optimization: A survey. Appl. Soft Comput. 2011, 11, 4135–4151. [Google Scholar] [CrossRef]
- Daliri, A.; Asghari, A.; Azgomi, H. The water optimization algorithm: A novel metaheuristic for solving optimization problems. Appl. Intell. 2022, 52, 17990–18029. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- De Castro, L.N.; Timmis, J. Artificial Immune Systems: A New Computational Intelligence Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization (PSO). In Proceedings of the IEEE International Conference on Neural Networks; IEEE: Perth, Australia, 1995; pp. 1942–1948. [Google Scholar]
- Yang, X.-S. Flower Pollination Algorithm for Global Optimization. In Unconventional Computation and Natural Computation; Springer: Berlin/Heidelberg, Germany, 2012; pp. 240–249. [Google Scholar]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. In SAGA 2009: Stochastic Algorithms: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Alimoradi, M.; Azgomi, H.; Asghari, A. Trees Social Relations Optimization Algorithm: A new Swarm-Based metaheuristic technique to solve continuous and discrete optimization problems. Math. Comput. Simul. 2022, 194, 629–664. [Google Scholar] [CrossRef]
- Yazdani, M.; Jolai, F. Lion Optimization Algorithm (LOA): A NatureInspired Metaheuristic Algorithm. J. Comput. Des. Eng. 2016, 3, 24–36. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Oftadeh, R.; Mahjoob, M.J.; Shariatpanahi, M. A novel meta-heuristic optimization algorithm inspired by group hunting of animals: Hunting search. Comput. Math. Appl. 2010, 60, 2087–2098. [Google Scholar] [CrossRef]
- Yang, X.-S.; Dey, N.; Fong, S. Nature-Inspired Metaheuristic Algorithms for Engineering Optimization Applications; Springer: Singapore, 2010. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Ardleman, L. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
- De Jong, K.A. Evolutionary computation a unified approach. In GECCO Companion’15: Proceedings of the Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation; Association for Computing Machinery: New York, NY, USA, 2015; pp. 21–35. [Google Scholar] [CrossRef]
- Zheng, Y.-J. Water wave optimization: A new natureinspired metaheuristic. Comput. Oper. Res. 2015, 55, 1–11. [Google Scholar] [CrossRef]
- Shik, J.Z.; Kooij, P.W.; Donoso, D.A.; Santos, J.C.; Gomez, E.B.; Franco, M.; Crumiere, A.J.J.; Arnan, X.; Howe, J.; Wcislo, W.T.; et al. Nutritional niches reveal fundamental domestication trade-offs in fungus-farming ants. Nat. Ecol. Evol. 2021, 5, 122–134. [Google Scholar] [CrossRef]
- De Fine Licht, H.H.; Schiøtt, M.; Mueller, U.G.; Boomsma, J.J. Evolutionary Transitions in Enzyme Activity of ant Fungus Gardens. Evolution 2010, 64, 2055–2069. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Parpinelli, R.S.; Lopes, H.S. New inspirations in swarm intelligence: A survey. Int. J. Bio-Inspired Comput. 2011, 3, 1–16. [Google Scholar] [CrossRef]
- Shah-Hosseini, H. Optimization with the Nature-Inspired Intelligent Water Drops Algorithm. Evol. Comput. 2009, 57, 297–338. [Google Scholar]
- Liu, B.; Zhou, Y. Artificial fish swarm optimization algorithm based on genetic algorithm. Comput. Eng. Des. 2008, 62, 617–629. [Google Scholar]
- Hassanien, A.-E.; Taha, M.H.N.; Khalifa, N.E.M. Enabling AI Applications in Data Science; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2021; Volume 911. [Google Scholar]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray Optimization. Comput. Struct. 2012, 112–113, 283–294. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Knowles, D.; Corne, D.W. M-PAES: A Memetic Algorithm for Multiobjective Optimization. In Proceedings of the 2000 Congress on Evolutionary Computation. CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; IEEE: Piscataway, NJ, USA, 2000. [Google Scholar]
- Birbil, S.I.; Fang, S.C. An Electromagnetism-like Mechanism for Global Optimization. J. Glob. Optim. 2003, 25, 263–282. [Google Scholar] [CrossRef]
- Cai, W.; Yang, W.; Chen, X. A Global Optimization Algorithm Based on Plant Growth Theory: Plant Growth Optimization. In Proceedings of the 2008 International Conference on Intelligent Computation Technology and Automation (ICICTA), Changsha, China, 20–22 October 2008. [Google Scholar]
- Karci, A. Theory of Saplings Growing Up Algorithm. In Adaptive and Natural Computing Algorithms; Springer: Berlin/Heidelberg, Germany, 2007; pp. 450–460. [Google Scholar]
- Shukla, A.K.; Tripathi, D.; Reddy, B.R.; Chandramohan, D. A study on metaheuristics approaches for gene selection in microarray data: Algorithms. applications and open challenges. Evol. Intell. 2020, 13, 309–329. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm With Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Trivedi, A.; Sanyal, K.; Verma, P.; Srinivasan, D. A Unified Differential Evolution Algorithm for Constrained Optimization Problems. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Donostia/San Sebastian, Spain, 5–8 June 2017. [Google Scholar]
- Faradonbeh, R.S.; Monjezi, M.; Armaghani, D.J. Genetic programing and non-linear multiple regression techniques to predict backbreak in blasting operation. Eng. Comput. 2016, 32, 123–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M.; Tavakkoli-Moghaddam, R. Red deer algorithm (RDA): A new nature-inspired meta-heuristic. Soft Comput. 2020, 24, 14637–14665. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Diamond, J. Evolution, consequences and future of plant and animal domestication. Nature 2002, 418, 700–707. [Google Scholar] [CrossRef]
- Mehdiabadi, N.J.; Schultz, T.R. Natural history and phylogeny of the fungus-farming ants (Hymenoptera: Formicidae: Myrmicinae: Attini). Myrmecol. News 2009, 13, 37–55. [Google Scholar]
- Nygaard, S.; Hu, H.; Li, C.; Schiøtt, M.; Chen, Z.; Yang, Z.; Xie, Q.; Ma, C.; Deng, Y.; Dikow, R.B.; et al. Reciprocal genomic evolution in the ant–fungus agricultural symbiosis. Nat. Commun. 2016, 7, 12233. [Google Scholar] [CrossRef] [PubMed]
- Vellinga, E.C. Ecology and Distribution of Lepiotaceous Fungi (Agaricaceae). Nova Hedwig. 2004, 78, 273–299. [Google Scholar] [CrossRef]
- Mueller, U.G.; Rehner, S.A.; Schultz, T.R. The Evolution of Agriculture in Ants. Science 1998, 281, 2034–2038. [Google Scholar] [CrossRef]
- Mueller, U.G.; Gerardo, N.M.; Aanen, D.K.; Six, D.L.; Ted, R. Schultz The Evolution of Agriculture in Insects. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 563–595. [Google Scholar] [CrossRef]
- Hölldobler, B.; Wilson, E.O. The Leafcutter Ants: Civilization by Instinct; WW Norton & Company: New York, NY, USA, 2011. [Google Scholar]
- Currie, C.R.; Bot, A.N.M.; Boomsma, J.J. Experimental evidence of a tripartite mutualism: Bacteria protect ant fungus gardens from specialized parasites. Oikos 2003, 101, 91–102. [Google Scholar] [CrossRef]
- Van Borm, S.; Billen, J.; Boomsma, J.J. The diversity of microorganisms associated with Acromyrmex leafcutter ants. BMC Evol. Biol. 2002, 2, 9. [Google Scholar] [CrossRef]
- Ariniello, L. Protecting Paradise: Fungus-farming ants ensure crop survival with surprising strategies and partnerships. BioScience 1999, 49, 760–763. [Google Scholar] [CrossRef][Green Version]
- Ronque, M.U.; Feitosa, R.M.; Oliveira, P.S. Natural history and ecology of fungus-farming ants: A field study in Atlantic rainforest. Insectes Sociaux 2019, 66, 375–387. [Google Scholar] [CrossRef]
- Richard, F.-J.; Poulsen, M.; Drijfhout, F.; Jones, G.; Boomsma, J.J. Specificity in Chemical Profiles of Workers, Brood and Mutualistic Fungi in Atta, Acromyrmex, and Sericomyrmex Fungus-growing Ants. J. Chem. Ecol. 2007, 33, 2281–2292. [Google Scholar] [CrossRef] [PubMed]
- Poulsen, M.; Boomsma, J.J. Mutualistic Fungi Control Crop Diversity in Fungus-Growing Ants. Science 2005, 307, 741–744. [Google Scholar] [CrossRef]
- Wilson, E.O. The Insect Societies. In Insect Societies; Harvard University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Hughes, W.O.H.; Eilenberg, J.; Boomsma, J.J. Trade-offs in group living: Transmission and disease resistance in leaf-cutting ants. Proc. R. Soc. B Biol. Sci. 2002, 269, 1811–1819. [Google Scholar] [CrossRef]
- Aguilar-Colorado, Á.S.; Rivera-Cháve, J. Ants/Nest-Associated Fungi and Their Specialized Metabolites: Taxonomy, Chemistry, and Bioactivity. Rev. Bras. Farmacogn. 2023, 33, 901–923. [Google Scholar] [CrossRef]
- Moghadam, E.K.; Vahdanjoo, M.; Jensen, A.L.; Sharifi, M.; Sørensen, C.A.G. An Arable Field for Benchmarking of Metaheuristic Algorithms for Capacitated Coverage Path Planning Problems. Agronomy 2020, 10, 1454. [Google Scholar] [CrossRef]
- Kaveh, A.; Vazirinia, Y. Construction Site Layout Planning Problem Using Metaheuristic Algorithms: A Comparative Study. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 105–115. [Google Scholar] [CrossRef]
- Huang, H.-C. A Hybrid Metaheuristic Embedded System for Intelligent Vehicles Using Hypermutated Firefly Algorithm Optimized Radial Basis Function Neural Network. IEEE Trans. Ind. Inform. 2019, 15, 1062–1069. [Google Scholar] [CrossRef]
- Chen, H.; Chang, W.-Y.; Chiu, T.-L.; Chiang, M.-C.; Tsai, C.-W. SEFSD: An effective deployment algorithm for fog computing systems. J. Cloud Comput. 2023, 12, 105. [Google Scholar] [CrossRef]
- Leguizamon; Guillermo; Michalewicz, Z. A new version of ant system for subset problems. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 2, pp. 1459–1464.
- Khodadadi, N.; Çiftçioğlu, A.Ö.; Mirjalili, S.; Nanni, A. A comparison performance analysis of eight meta-heuristic algorithms for optimal design of truss structures with static constraints. Decis. Anal. J. 2023, 8, 100266. [Google Scholar] [CrossRef]
- Reinelt, G. The Traveling Salesman: Computational Solutions for TSP Applications; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Wang, G.; Guo, L.; Duan, H.; Wang, H.; Liu, L.; Shao, M. A HybridMetaheuristic DE/CS Algorithm for UCAV Three-Dimension Path Planning. Sci. J. 2012, 2012, 583973. [Google Scholar] [CrossRef]
- Hussien, A.G.; Hassanien, A.E.; Houssein, E.H.; Amin, M. New binary whale optimization algorithm for discrete optimization problems. Eng. Optim. 2020, 52, 945–959. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, S.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Del Ser, J.; Landa-Torres, I.; Gil-López, S.; Portilla-Figueras, J.A. The Coral Reefs Optimization Algorithm: A Novel Metaheuristic for Efficiently Solving Optimization Problems. Res. Artic. 2014, 2014, 739768. [Google Scholar] [CrossRef] [PubMed]
- Gallego, R.A.; Romero, R.; Monticelli, A.J. Tabu search algorithm for network synthesis. IEEE Trans. Power Syst. 2000, 15, 490–495. [Google Scholar] [CrossRef]
- Karna, S.K.; Sahai, R. An overview on Taguchi method. Int. J. Eng. Math. Sci. 2012, 1, 1–7. [Google Scholar]
- Available online: http://www.math.uwaterloo.ca/tsp/world/index.html (accessed on 16 January 2025).
- Asghari, A.; Sohrabi, M.K. Server placement in mobile cloud computing: A comprehensive survey for edge computing, fog computing and cloudlet. Comput. Sci. Rev. 2024, 51, 100616. [Google Scholar] [CrossRef]
- Asghari, A.; Azgomi, H.; Zoraghchian, A.A.; Barzegarinezhad, A. Energy-aware server placement in mobile edge computing using trees social relations optimization algorithm. J. Supercomput. 2024, 80, 6382–6410. [Google Scholar] [CrossRef]
- Asghari, A.; Sohrabi, M.K. Multiobjective edge server placement in mobile-edge computing using a combination of multiagent deep q-network and coral reefs optimization. IEEE Internet Things J. 2022, 9, 17503–17512. [Google Scholar] [CrossRef]
- Cheung, S.-O.; Tong, T.K.-L.; Tam, C.-M. Site pre-cast yard layout arrangement through genetic algorithms. Autom. Constr. 2002, 11, 35–46. [Google Scholar] [CrossRef]
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D. Introduction to Autonomous Mobile Robots, 2nd ed.; MIT Press: London, UK, 2011. [Google Scholar]
- Bonomi, F.; Milito, R.; Zhu, J. Fog computing and its role in the internet of things. In Proceedings of the Mobile Cloud Computing Workshop, Addepalli S (2012), Helsinki, Finland, 17 August 2012; ACM: New York, NY, USA, 2012; pp. 13–16. [Google Scholar]
- Kaveh, A.; Talatahari, S.; Khodadadi, N. The hybrid invasive weed optimizationshuffled frog-leaping algorithm applied to optimal design of frame structures. Period. Polytech. Civ. Eng. 2019, 63, 882–897. [Google Scholar]
- Kurnaz, S.; Cetin, O.; Kaynak, O. Adaptive neurofuzzy inference system based autonomous flight control of unmanned air vehicles. Expert Syst. Appl. 2010, 37, 1229–1234. [Google Scholar] [CrossRef]

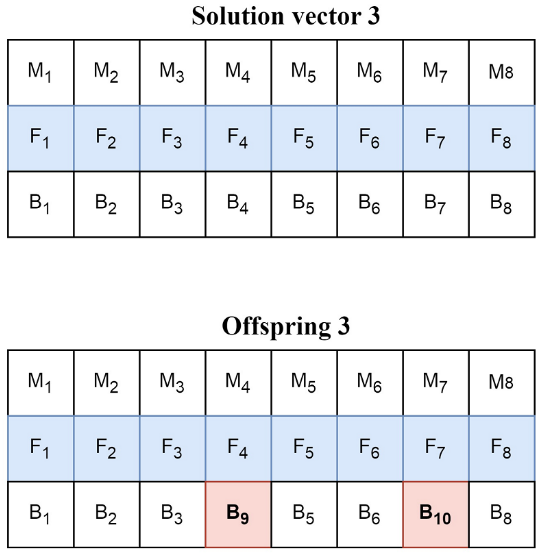
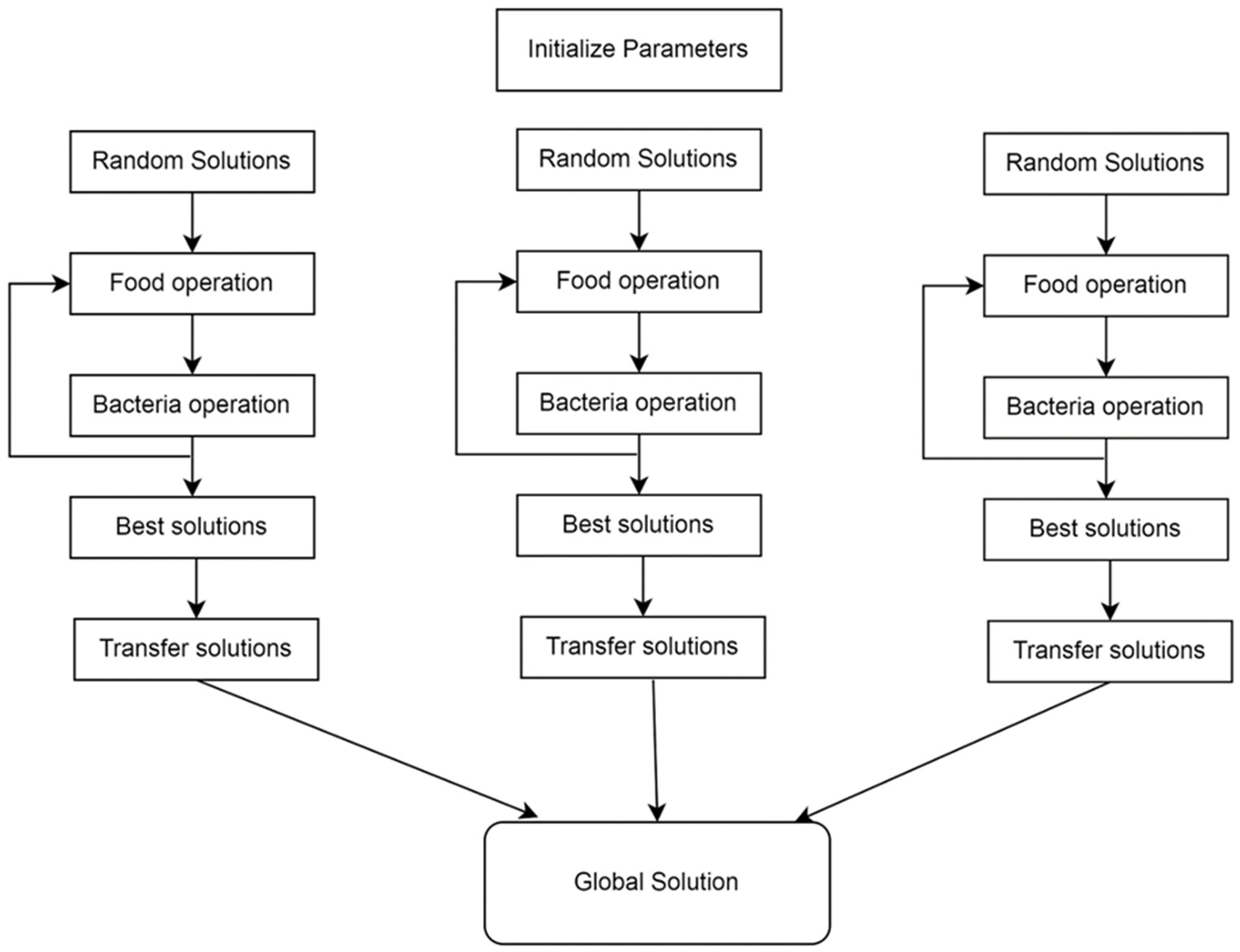



| Algorithms | Parameters | Values |
|---|---|---|
| Trees Social Relations Optimization Algorithm (TSR) | Population size | 50 |
| Number of generations of 10,000 cities | 1000 | |
| Number of generations of 1000 cities | 100 | |
| Genetic Algorithm (GA) | Population size | 50 |
| Number of generations of 10,000 cities | 1000 | |
| Number of generations for 1000 cities | 100 | |
| Gray Wolf Optimizer (GWO) | Control parameter a | [2,0] |
| Number of generations of 10,000 cities | 1000 | |
| Number of generations of 1000 cities | 100 | |
| Number of particles | 50 | |
| Imperialist Competitive Optimization Algorithm (ICA) | Number of countries | 50 |
| Number of generations of 10,000 cities | 1000 | |
| Number of generations of 1000 cities | 100 | |
| Number of nimps | 10 | |
| Simulated Annealing (SA) | Population size | 50 |
| Number of generations of 10,000 cities | 1000 | |
| Number of generations of 1000 cities | 100 | |
| Number of neighbors | 10 | |
| Ant Colony Optimization (ACO) | Population size | 50 |
| Number of generations | 100 | |
| Conversion ratio fitness | 100 | |
| Taboo (Tabu) | Population size | 50 |
| Number of generations of 10,000 cities | 1000 | |
| Number of generations of 1000 cities | 100 | |
| Genetic Programming (GP) | Population size | 5 |
| Number of generations of 10,000 cities | 1000 | |
| Number of generations of 1000 cities | 100 | |
| Coral Reefs Optimization (CRO) | Population size | 50 |
| Number of generations of 10,000 cities | 1000 | |
| Number of generations of 1000 cities | 100 | |
| Number of reefs | 10 | |
| Gray Wolf Optimizer (GWO) | Control parameter a | [0,2] |
| Number of generations | 1000 | |
| Search agent | 50 | |
| Binary Whale Optimization Algorithm (BWO) | Number of generations | 1000 |
| Parameter b | 1 | |
| Initial population | 100 |
| Function | Range | Dim | Minimum |
|---|---|---|---|
| [−100, 100] | 30 | 0 | |
| [−10, 10] | 5 | 0 | |
| [−100, 100] | 5 | 0 | |
| [−100, 100] | 5 | 0 | |
| [−30, 30] | 5 | 0 | |
| [−100, 100] | 5 | 0 | |
| [−1.28, 1.28] | 5 | 0 |
| Function | Range | Dim | Minimum |
|---|---|---|---|
| [−500, 500] | 30 | −2094.9 | |
| [−5.12, 5.12] | 30 | 0 | |
| [−32, 32] | 30 | 0 | |
| [−600, 600] | 30 | 0 | |
| [−50, 50] | 30 | 0 | |
| [−50, 50] | 30 | 0 | |
| [−100, 100] | 2 | −1 | |
| [−100, 100] | 2 | 0 | |
| [−5, 5] | 2 | −1.0316 |
| No. | Function | Range | Dim | Minimum |
|---|---|---|---|---|
| F17 | [5/100, 5/100, 5/100,…, 5/100] | [−100, 100] | 10 | 0 |
| F18 | [5/100, 5/100, 5/100,…, 5/100] | [−10, 10] | 10 | 0 |
| F19 | [1,1,1,…,1] | [−100, 100] | 10 | 0 |
| F20 | [5/32, 5/32, 1, 1, 5/0.5, 5/0.5, 5/100, 5/100, 5/100, 5/100] | [−100, 100] | 10 | 0 |
| F21 | [1/5, 1/5, 5/0.5, 5/0.5, 5/100, 5/100, 5/32, 5/32, 5/100, 5/100] | [−30, 30] | 10 | 0 |
| F22 | 0.1 × 1/5, 0.2 × 1/5, 0.3 × 5/0.5, 0.4× 5/0.5, 0.5 × 5/100, 0.6 × 5/100, 0.7 × 5/32, 0.8 × 5/32, 0.9 × 5/100, 1 × 5/100 | [−100, 100] | 10 | 0 |
| No. | Measure | FAOA | CRO | GA | GP | BWO | GWO | Tabu | ICA | SA | ACO | TSR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Worst Best Med | 1.2226 0.6405 0.8168 | 1.6567 0.7291 1.1465 | 1.6664 0.7739 1.1977 | 1.6664 0.8129 1.2719 | 1.6533 0.8290 1.1355 | 1.3074 0.4884 0.8993 | 1.3143 0.6468 1.2389 | 1.3066 0.6692 0.9187 | 1.3143 0.6156 0.8564 | 1.8590 0.8744 1.1923 | 1.3305 0.7902 0.9168 |
| F2 | Worst Best Med | 10.9587 5.3574 7.6834 | 11.3290 5.1686 7.7909 | 12.0828 5.7474 7.9445 | 12.4438 6.1975 9.8799 | 13.3660 5.9946 8.4458 | 12.7284 6.2801 8.8632 | 11.9477 5.2693 7.8180 | 12.7284 6.2801 8.8632 | 11.9585 5.6281 7.9842 | 13.3573 6.7918 9.0852 | 10.9977 5.2679 7.5280 |
| F3 | Worst Best Med | 10.9587 5.3574 8.6220 | 11.3290 5.3686 7.7909 | 12.0828 5.7474 7.9445 | 11.3641 6.1975 9.8799 | 13.3660 5.9946 8.4458 | 12.7284 6.8331 8.9541 | 10.9477 5.5673 7.3180 | 12.7284 6.2801 8.8632 | 11.9585 5.6281 7.9842 | 13.3573 6.7918 9.0852 | 9.9656 5.5673 7.4260 |
| F4 | Worst Best Med | 0.8994 0.4730 0.6402 | 1.0002 0.4993 0.7080 | 1.0070 0.4929 0.6871 | 1.3677 0.5203 0.7116 | 0.9981 0.4972 0.6902 | 1.0074 0.4884 0.6993 | 1.3143 0.6468 1.2389 | 1.1092 0.5506 0.8861 | 1.0843 0.5316 0.7818 | 1.0100 0.4701 0.6745 | 0.9892 0.6673 0.6415 |
| F5 | Worst Best Med | 3.1211 1.7522 2.80982 | 3.9431 2.2766 3.2650 | 4.1744 1.9454 3.002 | 3.9554 1.7936 2.8007 | 4.6525 2.2766 3.1870 | 4.0957 1.8504 2.6767 | 3.8584 1.9857 2.6913 | 3.8806 1.8863 2.6070 | 3.9971 1.7857 2.6988 | 4.6902 2.2492 3.0873 | 4.3219 1.8659 2.8098 |
| F6 | Worst Best Med | 2.0063 0.9854 1.4084 | 2.0262 1.0366 1.4639 | 2.1124 1.0150 1.4642 | 2.0513 1.2310 1.7264 | 2.1310 1.1456 1.5722 | 1.8285 1.0366 1.4639 | 2.2780 1.0513 1.5325 | 2.0669 1.3321 1.3991 | 2.0324 1.0224 1.3987 | 2.1038 0.9692 1.3658 | 1.9954 0.9942 1.3668 |
| F7 | Worst Best Med | 25.1211 10.2678 15.9337 | 21.9253 10.3068 14.7396 | 22.0878 10.6314 15.0474 | 22.0878 11.6009 17.6634 | 22.0424 10.8434 14.9337 | 21.9731 10.7293 15.2530 | 21.3654 11.1668 14.7483 | 21.9373 10.9716 14.1574 | 21.0684 11.1868 16.5789 | 21.8900 10.8703 14.7572 | 25.2519 11.9538 16.9507 |
| F8 | Worst Best Med | −4.5334 −607.59 −360.89 | 0.4053 −438.91 −259.36 | 0.7774 −479.62 −314.60 | 0.7730 −573.01 −302.37 | −9.0650 −526.75 −316.94 | −9.2331 −544.52 −345.38 | −18.2535 −477.41 −297.29 | −15.2535 −477.41 −302.33 | −64.666 −480.42 −300.59 | −2.2731 −475.46 −317.55 | −5.5324 −588.17 −371.12 |
| F9 | Worst Best Med | 20.9378 10.2199 14.5628 | 22.0333 10.8661 15.2704 | 21.6217 11.0292 15.5599 | 21.6335 13.4440 17.2383 | 22.0750 10.8661 15.2704 | 21.9096 10.7896 14.7859 | 21.9830 10.8292 14.6263 | 21.7611 11.0831 15.0769 | 21.9830 11.3330 14.7723 | 22.2724 10.9488 15.2834 | 21.7434 11.0184 14.9042 |
| F10 | Worst Best Med | 1.9797 0.9532 1.3296 | 1.6567 0.7291 1.1465 | 1.6664 0.8129 1.1593 | 1.9747 0.9327 1.3179 | 1.8862 0.9004 1.2712 | 1.0075 0.4884 0.6993 | 1.14453 0.6469 1.2389 | 1.3066 0.6693 0.9187 | 1.3143 0.6156 0.8564 | 1.8630 0.8532 1.2511 | 1.9446 0.9972 1.3318 |
| F11 | Worst Best Med | 11.5569 0.9532 1.0296 | 13.7779 0.7291 1.1465 | 13.7837 0.8129 1.1593 | 12.7673 0.9327 1.3179 | 13.8091 0.9004 1.2712 | 12.8441 0.4884 0.6993 | 12.1889 0.6469 1.2389 | 12.8139 0.6693 0.9187 | 12.9898 0.6156 0.8564 | 12.5548 08532 1.2511 | 12.8139 0.9532 1.3296 |
| F12 | Worst Best Med | 17.8449 10.1063 13.4438 | 20.8558 10.2402 14.2109 | 19.9719 9.3473 13.6702 | 19.9802 9.6638 13.6702 | 19.9472 9.8094 13.8010 | 19.6997 9.6014 13.9259 | 20.7629 10.3482 14.0935 | 19.6568 9.5607 13.5037 | 19.5704 9.1808 13.6570 | 20.9049 9.7175 13.6363 | 21.5133 9.9035 14.6050 |
| F13 | Worst Best Med | 31.8301 12.9900 22.8353 | 30.5145 15.0983 20.9827 | 30.4432 13.1165 19.1762 | 32.4154 16.0333 22.2618 | 35.4449 14.8222 22.2631 | 31.5799 14.5822 21.0264 | 30.9385 19.8335 27.2229 | 33.9556 21.3236 27.0829 | 34.7625 22.4064 28.0355 | 32.7230 15.3866 21.5134 | 43.9484 21.6129 30.9913 |
| F14 | Worst Best Med | 39.3650 20.3952 24.5581 | 58.8548 25.6390 40.5171 | 49.6172 24.9847 34.5394 | 49.6172 24.3202 41.4929 | 52.4141 25.3664 37.5636 | 54.8990 27.3500 36.4024 | 38.5144 18.0410 27.6067 | 38.6164 18.3310 26.6771 | 38.5144 19.9596 27.5412 | 48.8547 24.2191 33.2746 | 52.0969 26.5638 36.7144 |
| F15 | Worst Best Med | 27.5214 14.2108 19.4930 | 34.4763 18.2131 24.1748 | 32.4191 18.9884 27.1994 | 31.6964 14.7338 21.4537 | 31.0444 16.3008 25.3031 | 29.2296 14.7999 21.4487 | 27.8899 15.499 20.6888 | 31.3618 15.4935 18.6888 | 30.4080 15.4647 22.3304 | 31.0444 16.2108 26.6939 | 38.6854 18.7600 25.6250 |
| F16 | Worst Best Med | 147.695 55.630 100.913 | 148.143 65.864 95.735 | 138.968 64.498 131.242 | 130.987 66.907 105.476 | 137.410 69.659 99.322 | 128.2279 58.576 80.650 | 128.2250 59.8529 83.4341 | 128.197 58.576 123.008 | 127.805 62.131 90.170 | 146.083 69.777 99.6067 | 147.990 67.449 95.988 |
| F17 | Worst Best Med | 1.2797 0.3531 0.5296 | 1.6567 0.7290 1.1464 | 1.6663 0.8129 1.1592 | 1.9746 0.9327 1.3179 | 1.8999 0.9003 1.2711 | 1.0074 0.4884 0.6993 | 1.3903 0.6468 1.2389 | 1.3066 0.6692 0.9187 | 1.3143 0.6156 0.8564 | 1.8630 0.8532 1.6004 | 1.9445 0.9531 1.3296 |
| F18 | Worst Best Med | 88.065 40.778 49.580 | 89.672 43.001 60.250 | 99.672 62.503 57.737 | 97.302 60.683 60.683 | 98.360 45.543 65.191 | 111.545 45.543 65.191 | 81.339 42.754 54.845 | 89.608 44.930 65.226 | 89.786 44.812 64.332 | 97.932 47.233 66.505 | 117.736 56.591 80.496 |
| F19 | Worst Best Med | 1.3797 0.5532 0.7296 | 1.6567 0.7291 1.1465 | 1.6664 0.8129 1.1593 | 1.9747 0.9327 1.3179 | 1.8863 0.9004 1.2712 | 1.0075 0.4884 0.8993 | 1.3143 06469 1.2389 | 1.3066 0.6693 0.9187 | 1.3711 0.6156 0.8564 | 1.8630 0.8532 1.2511 | 1.9446 0.9532 1.3296 |
| F20 | Worst Best Med | 14.9639 7.3037 11.9414 | 21.8677 10.5102 14.3246 | 20.0637 9.6211 13.4553 | 22.7771 9.7146 15.7196 | 20.5455 11.4424 15.4901 | 17.9166 8.5933 12.2676 | 17.7144 8.8341 12.8070 | 15.7328 7.8003 12.8921 | 17.9709 8.0778 12.5988 | 21.7651 10.4934 14.4777 | 17.6642 8.8085 12.9201 |
| F21 | Worst Best Med | 17.5639 8.3037 11.9414 | 21.9898 10.5102 14.3246 | 20.0637 9.2611 13.4553 | 22.7771 9.6211 15.7196 | 23.0112 11.4424 15.4901 | 17.9166 8.5933 12.2676 | 17.7144 8.8341 12.8070 | 18.7328 7.8003 12.8921 | 17.9709 8.0778 12.5988 | 21.7651 10.4934 14.4777 | 17.6642 8.8085 12.9201 |
| F22 | Worst Best Med | 2.9258 0.9911 1.1071 | 4.9365 2.3619 3.2982 | 4.9832 2.4346 3.3766 | 1.9477 0.9327 1.3179 | 4.9631 2.5401 3.6015 | 5.9998 2.6400 3.3513 | 5.9865 2.9500 4.0263 | 4.9542 2.4413 3.711 | 5.0002 2.9500 4.1572 | 5.000 2.5401 3.6015 | 5.8980 2.8357 4.0007 |
| No. | FAOA | CRO | GA | GP | BWO | GWO | Tabu | ICA | SA | ACO | TSR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 37.2 | 41.5 | 42.3 | 49.2 | 47.2 | 41.9 | 46.5 | 48.8 | 41.1 | 42.5 | 36.2 |
| F2 | 39.5 | 44.8 | 46.7 | 51.6 | 48.3 | 44.1 | 48.9 | 47.1 | 47.5 | 47.1 | 42.6 |
| F3 | 41.0 | 48.2 | 50.2 | 53.3 | 50.1 | 46.2 | 54.6 | 52.6 | 49.3 | 46.8 | 44.1 |
| F4 | 38.6 | 45.1 | 45.6 | 51.5 | 43.5 | 41.5 | 49.1 | 50.2 | 44.0 | 43.3 | 40.3 |
| F5 | 33.8 | 38.3 | 43.3 | 46.9 | 44.0 | 39.0 | 42.9 | 43.1 | 40.4 | 39.1 | 37.5 |
| F6 | 33.2 | 37.8 | 42.5 | 45.3 | 42.9 | 36.7 | 42.5 | 43.9 | 39.1 | 40.2 | 33.1 |
| F7 | 35.9 | 41.9 | 42.6 | 43.0 | 39.1 | 34.9 | 43.7 | 44.5 | 38.7 | 39.5 | 35.9 |
| F8 | 50.8 | 55.5 | 61.5 | 62.5 | 61.2 | 52.2 | 58.1 | 60.0 | 56.4 | 55.7 | 52.3 |
| F9 | 42.7 | 46.7 | 52.9 | 54.4 | 48.5 | 46.3 | 51.6 | 53.8 | 47.2 | 46.0 | 44.0 |
| F10 | 45.9 | 48.4 | 57.7 | 57.1 | 52.4 | 48.6 | 54.2 | 56.3 | 51.3 | 51.2 | 47.1 |
| F11 | 54.2 | 59.6 | 62.2 | 69.2 | 67.3 | 57.1 | 63.3 | 66.2 | 59.8 | 58.8 | 55.7 |
| F12 | 47.0 | 61.4 | 55.4 | 64.7 | 61.9 | 51.4 | 60.5 | 62.4 | 53.2 | 54.3 | 49.9 |
| F13 | 48.3 | 52.2 | 57.8 | 58.7 | 57.7 | 52.0 | 54.7 | 58.6 | 55.5 | 53.4 | 50.8 |
| F14 | 50.1 | 55.3 | 62.6 | 61.8 | 60.5 | 53.5 | 56.0 | 59.4 | 58.6 | 57.5 | 50.0 |
| F15 | 49.6 | 55.0 | 63.5 | 65.7 | 61.4 | 54.2 | 55.2 | 57.1 | 59.9 | 60.4 | 52.6 |
| F16 | 52.8 | 56.9 | 65.1 | 65.0 | 63.8 | 57.4 | 58.8 | 62.0 | 62.7 | 62.7 | 55.5 |
| F17 | 78.8 | 8.2 | 92.4 | 94.2 | 89.8 | 82.1 | 85.4 | 89.7 | 87.8 | 86.3 | 80.8 |
| F18 | 81.4 | 86.1 | 97.0 | 96.5 | 92.6 | 80.6 | 87.7 | 90.3 | 91.7 | 91.8 | 83.7 |
| F19 | 82.7 | 88.0 | 98.7 | 100.5 | 98.9 | 84.3 | 88.1 | 96.5 | 92.6 | 90.4 | 84.2 |
| F20 | 75.6 | 81.3 | 99.5 | 102.4 | 91.0 | 77.9 | 85.5 | 89.9 | 85.5 | 85.9 | 77.3 |
| F21 | 74.8 | 79.6 | 98.3 | 103.8 | 90.2 | 79.7 | 84.3 | 88.7 | 84.9 | 83.0 | 77.6 |
| F22 | 81.2 | 85.7 | 97.2 | 101.3 | 97.6 | 86.6 | 90.1 | 95.2 | 90.1 | 91.7 | 84.4 |
| Problem | FAOA | CRO | GA | GP | BWO | GWO | Tabu | ICA | SA | ACO | TSR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TSP | 177 | 208 | 215 | 217 | 222 | 231 | 230 | 232 | 241 | 211 | 176 |
| KN | 89 | 112 | 119 | 114 | 126 | 130 | 123 | 141 | 133 | 129 | 106 |
| SP | 49 | 76 | 68 | 72 | 81 | 84 | 79 | 87 | 84 | 79 | 68 |
| CSLP | 92 | 127 | 143 | 150 | 162 | 171 | 159 | 163 | 149 | 138 | 77 |
| AFP | 116 | 138 | 156 | 173 | 180 | 189 | 167 | 175 | 150 | 139 | 131 |
| ES | 95 | 129 | 141 | 157 | 169 | 174 | 160 | 171 | 137 | 133 | 118 |
| FCS | 123 | 146 | 160 | 172 | 183 | 202 | 186 | 199 | 152 | 147 | 141 |
| TS | 119 | 149 | 181 | 196 | 203 | 218 | 191 | 206 | 160 | 137 | 132 |
| UCAV | 142 | 167 | 208 | 222 | 264 | 291 | 275 | 299 | 189 | 170 | 165 |
| Problem | FAOA | CRO | GA | GP | BWO | GWO | Tabu | ICA | SA | ACO | TSR |
| TSP | 8.1 | 12.9 | 15.6 | 12.7 | 13.5 | 11.7 | 12.7 | 11.5 | 14.2 | 12.1 | 9.9 |
| KN | 6.2 | 15.6 | 16.4 | 11.8 | 14.2 | 11.3 | 14.6 | 13.2 | 15.7 | 14.5 | 8.5 |
| SP | 8.5 | 16.8 | 17.8 | 13.1 | 16.0 | 12.8 | 15.9 | 14.8 | 16.3 | 14.8 | 8.3 |
| CSLP | 7.6 | 14.3 | 15.9 | 12.0 | 12.9 | 11.5 | 13.8 | 14.0 | 14.8 | 13.7 | 9.1 |
| AFP | 9.7 | 14.5 | 17.4 | 13.7 | 15.8 | 13.1 | 15.7 | 16.3 | 16.9 | 14.6 | 11.3 |
| ES | 11.2 | 16.9 | 19.3 | 15.9 | 17.5 | 15.6 | 18.0 | 17.8 | 18.5 | 17.8 | 11.2 |
| FCS | 13.0 | 18.2 | 22.5 | 18.5 | 20.3 | 17.1 | 20.1 | 19.4 | 21.2 | 19.9 | 15.0 |
| TS | 9.8 | 15.8 | 17.7 | 14.2 | 15.8 | 13.9 | 16.3 | 14.3 | 17.1 | 16.0 | 11.7 |
| UCAV | 11.8 | 16.9 | 18.3 | 15.7 | 16.2 | 14.8 | 19.0 | 17.5 | 16.6 | 15.4 | 11.6 |
| Problem | TSR | ACO | SA | ICA | Tabu | GWO | BWO | GP | GA | CRO | FAOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TSP | 92.5 | 93.2 | 91.3 | 90.4 | 91.6 | 92.3 | 90.8 | 89 | 91.4 | 92.1 | 95.5 |
| KN | 88.1 | 87.5 | 86.2 | 85.7 | 87.9 | 88.6 | 86.3 | 85.4 | 87 | 88.6 | 92.3 |
| SP | 90 | 89.4 | 88.8 | 87.5 | 89.1 | 90.4 | 88.2 | 87.7 | 89.2 | 90.5 | 94.1 |
| CSLP | 91.2 | 90.3 | 89.6 | 88.1 | 90.8 | 91 | 89.6 | 88.2 | 90.7 | 91.9 | 95.3 |
| AFP | 89.8 | 88.3 | 87.7 | 86.4 | 88.1 | 89.5 | 87.2 | 86.9 | 88.3 | 89.6 | 93.8 |
| ES | 90.5 | 89.2 | 88.7 | 87.3 | 89.1 | 90.4 | 88.5 | 87.1 | 89.6 | 90 | 94.5 |
| FCS | 91.3 | 90.1 | 89.7 | 88.9 | 90.7 | 91.7 | 89.2 | 88.3 | 90.4 | 91.6 | 95.4 |
| TS | 92.1 | 91.2 | 90.7 | 89.7 | 91.5 | 92 | 90.1 | 89.9 | 91.6 | 92.3 | 96 |
| UCAV | 90.5 | 89 | 88.5 | 87.8 | 90.3 | 91.6 | 89.2 | 87.4 | 89.5 | 90.8 | 94.9 |
| Problem | Dataset Size (n) | Runtime (ms) | Memory Utilization (%) |
|---|---|---|---|
| TSP | 200 cities | 37 | 8.1 |
| 500 cities | 40 | 8.5 | |
| 1000 cities | 43 | 9 | |
| Knapsack (KN) | 20 items | 33 | 6.2 |
| 50 items | 36 | 6.8 | |
| 100 items | 39 | 7.5 | |
| Server Placement (SP) | 300 antennas | 38 | 8.5 |
| 600 antennas | 42 | 9 | |
| 1000 antennas | 46 | 9.5 | |
| CSLP | 10 facilities | 38 | 7.6 |
| 20 facilities | 42 | 8 | |
| 50 facilities | 47 | 8.5 | |
| AFP | 8 trucks | 33 | 9.7 |
| 16 trucks | 37 | 10.2 | |
| 32 trucks | 41 | 10.8 | |
| ES | 4 wheels (small system) | 33 | 11.2 |
| 8 wheels | 37 | 11.8 | |
| 16 wheels | 42 | 12.5 | |
| FCS | 50 fog nodes | 47 | 13 |
| 100 fog nodes | 52 | 13.8 | |
| 200 fog nodes | 58 | 14.5 | |
| Truss Structures (TS) | 50 elements | 48 | 9.8 |
| 100 elements | 53 | 10.5 | |
| 200 elements | 60 | 11.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asghari, A.; Zeinalabedinmalekmian, M.; Azgomi, H.; Alimoradi, M.; Ghaziantafrishi, S. Farmer Ants Optimization Algorithm: A Novel Metaheuristic for Solving Discrete Optimization Problems. Information 2025, 16, 207. https://doi.org/10.3390/info16030207
Asghari A, Zeinalabedinmalekmian M, Azgomi H, Alimoradi M, Ghaziantafrishi S. Farmer Ants Optimization Algorithm: A Novel Metaheuristic for Solving Discrete Optimization Problems. Information. 2025; 16(3):207. https://doi.org/10.3390/info16030207
Chicago/Turabian StyleAsghari, Ali, Mahdi Zeinalabedinmalekmian, Hossein Azgomi, Mahmoud Alimoradi, and Shirin Ghaziantafrishi. 2025. "Farmer Ants Optimization Algorithm: A Novel Metaheuristic for Solving Discrete Optimization Problems" Information 16, no. 3: 207. https://doi.org/10.3390/info16030207
APA StyleAsghari, A., Zeinalabedinmalekmian, M., Azgomi, H., Alimoradi, M., & Ghaziantafrishi, S. (2025). Farmer Ants Optimization Algorithm: A Novel Metaheuristic for Solving Discrete Optimization Problems. Information, 16(3), 207. https://doi.org/10.3390/info16030207






