Error in Figure/Table
In the original publication [1], Table 2 contained errors. Specifically, there were mistakes in the time complexity of five matrices and in the formula for F. The corrected version of Table 2 is provided below.

Table 2.
The time complexity of each matrix in our proposed algorithm.
In the original publication [1], there were two errors in Table 3 as published. Specifically, there was a mistake in the algorithm complexity of SFS-AGGL and a mistake of the order of reference for FDEFS method. The corrected version of Table 3 is presented below.

Table 3.
Computational complexity of each iteration for FS methods.
In the original publication [1], there were errors in Table 4 as published. Specifically, mistakes were made in the first-order derivatives of F, the second-order derivatives of F, and S. The corrected version of Table 4 is provided below.

Table 4.
First- and second-order derivatives of each formula.
In the original publication [1], there were some mistakes in Figure 2 as published. Specifically, errors were made in the calculation and update process. The corrected version of Figure 2 is presented below.
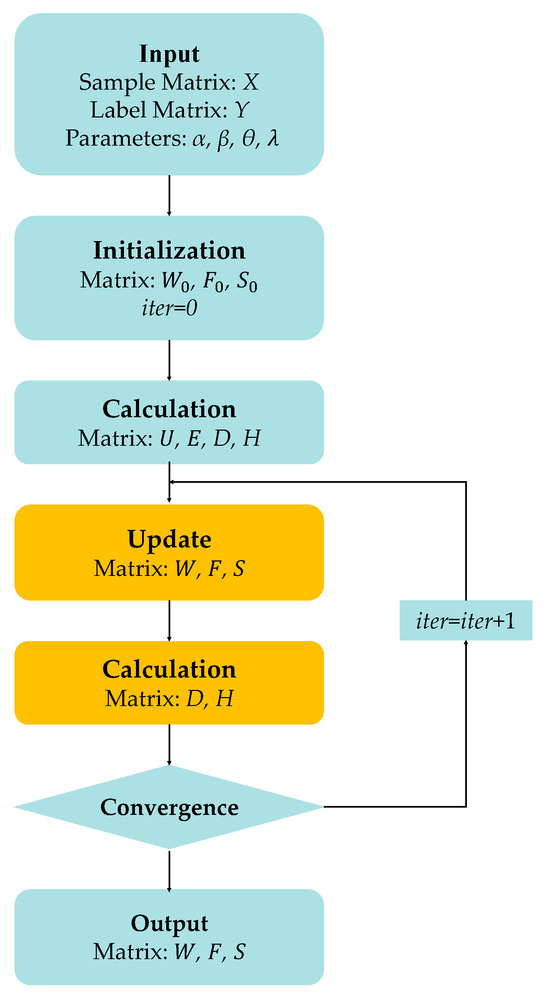
Figure 2.
Flow chart of SFS-AGGL algorithm.
In the original publication [1], there were some mistakes in sub-images of Figure 7 as published. Specifically, errors were made in the feature dimensions of the sub-images in Figure 7. The corrected version of Figure 7 is presented below.
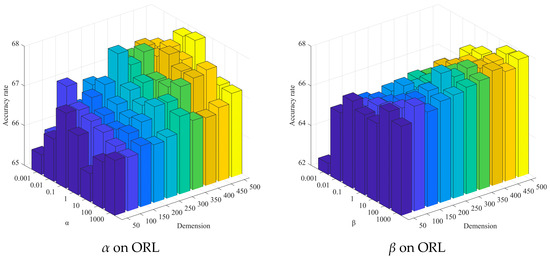
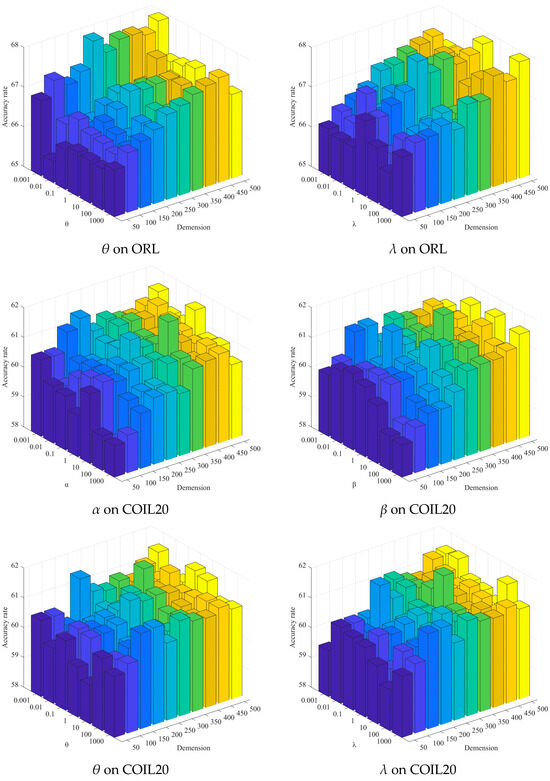
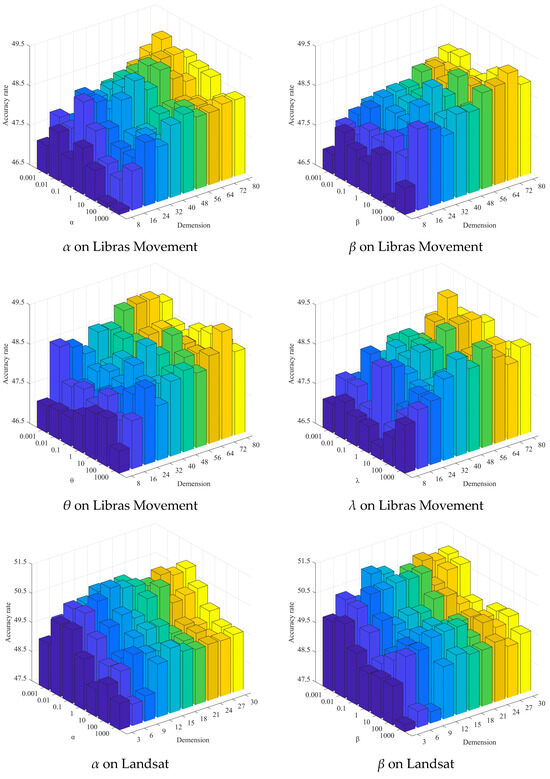
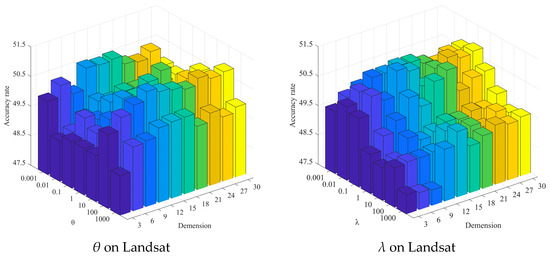
Figure 7.
Clustering results of SFS-AGGL under different parameter values and different feature dimensions, where different colors represent different feature dimensions.
Equations Correction
There were errors in some equations in the original publication [1]. Specifically, mistakes were made in the definition of symbol, the matrix transposition operation, or the absence of the matrix trace operation. The corrected equations are provided below.
Error in Algorithm
In the original publication [1], there were errors in Algorithm 1 as published. Specifically, mistakes were made in the calculation and update of the matrices. The corrected version of Algorithm 1 is presented below.
| Algorithm 1: SFS-AGGL |
| Input: Sample Matrix: Label Matrix: Parameters: Output: Feature Projection Matrix W Predictive Labeling Matrix F Similarity Matrix S |
| 1: Initialization: the initial non-negative matrix , ; 2: Calculation of the matrices U and E according to Equations (12) and (19), compute D and H according to S0 and W0; 3: Repeat 4: According to Equation (27) update as ; 5: According to Equation (33) update as ; 6: According to Equation (39) update as ; 7: According to and update matrices D and H; 8: Update ; 9: Until converges |
Text Correction
There were errors in the first paragraph of Section 2.1 in the original publication [1]. Mistakes were made regarding the sizes of matrices X and Y. The corrected content appears below.
Let denote the training samples, where denotes the i-th sample. is the label matrix, and denotes the true label of the labeled sample. If the sample belongs to the class j, then its corresponding class label is ; otherwise, . denotes the true label of the unlabeled sample. Since is unknown during the training process, it is set as a 0 matrix during training [49]. The main symbols in this paper are presented in Table 1.
There was an error in the first paragraph of Section 2.2 in the original publication [1]. Specifically, a mistake was made in the symbol X. The corrected content appears below.
Given a sample and a target dictionary , it is desired to find a coefficient vector such that the signal x can be represented as a linear combination of the basic elements of the target dictionary .
There was an error in the first paragraph of Section 2.3 in the original publication [1]. Specifically, a mistake was made in the definition of matrix S. The corrected content appears below.
Then, the weight matrix formed by the L1 graph is expressed as .
There was an error under Equation (11) in the first paragraph of Section 2.4 in the original publication [1]. Specifically, a mistake was made in the size of matrix U. The corrected content is provided below.
where can be computed by Equation (9) or Equation (10). is a diagonal matrix that effectively utilizes category information from all samples in SSL.
There was an error under Equation (23) in Section 3.2 in the original publication [1]. Specifically, there was a mistake in the definition of matrix H. The corrected content is provided below.
where is a matrix consisting of diagonal elements .
There was an error under the Equation (30) in Section 3.2 in the original publication [1]. Specifically, there was a mistake in the definition of matrix D. The corrected content is provided below.
where D is a diagonal matrix, whose diagonal elements are .
There were errors in Section 3.4.1 in the original publication [1]. Specifically, they are the matrix description and the total complexity of the SFS-AGGL algorithm. The corrected content is provided below.
Based on Algorithm 1, the SFS-AGGL algorithm’s computational complexity comprises two parts. The first part is the computation of the diagonal auxiliary matrices U and E in step 2, and the second part is the updating of three matrices (W, F, and S) during each iteration. The computational or updating components of each matrix are defined in Table 2. Therefore, the total complexity of the SFS-AGGL algorithm is , where iter is the iteration count. Furthermore, the computational complexities of other related FS methods are also presented in Table 3.
Error Citation
There was an error of references in the original publication [1]. Specifically, there was an incorrect information on reference [50]. The corrected content is provided below.
- 50.
- Zhu, R.; Dornaika, F.; Ruichek, Y. Learning a discriminant graph-based embedding with feature selection for image categorization. Neural Netw. 2019, 111, 35–46.
Missing ORCID
There was a missing orcid of an author in the original publication [1]. Specifically, there was a missing orcid of Gengsheng Xie. The corrected content is provided below.
The orcid of Gengsheng Xie is https://orcid.org/0000-0003-1224-6414.
The authors state that the scientific conclusions are unaffected. This correction was approved by the Academic Editor. The original publication has also been updated.
Reference
- Yi, Y.; Zhang, H.; Zhang, N.; Zhou, W.; Huang, X.; Xie, G.; Zheng, C. SFS-AGGL: Semi-Supervised Feature Selection Integrating Adaptive Graph with Global and Local Information. Information 2024, 15, 57. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).