Complexity Evaluation of Test Scenarios for Autonomous Vehicle Safety Validation Using Information Theory

Abstract

The validation of autonomous vehicles remains a vexing challenge for the automotive industry’s goal of fully autonomous driving. The systematic hierarchization of the test scenarios would provide valuable insights for the development, testing, and verification of autonomous vehicles, enabling nuanced performance evaluations based on scenario complexity. In this paper, an information entropy-based quantification method is proposed to evaluate the complexity of autonomous vehicle validation scenarios. The proposed method addresses the dynamic uncertainties within driving scenarios in a comprehensive way which includes the unpredictability of dynamic agents such as autonomous vehicles, human-driven vehicles, and pedestrians. The numerical complexity calculation of the approach and the ranking of the scenarios are presented through sample scenarios. To automate processes and assist with the calculations, a novel software tool with a user-friendly interface is developed. The performance of the approach is also evaluated through six example driving scenarios, then through extensive simulation using an open-source microscopic traffic simulator. The performance evaluation results confirm the numerical classification and demonstrate the method’s adaptability to diverse scenarios with a comparison of complexity calculation ranking to the ratio of collision, near collision, and normal operation tests observed during simulation testing. The proposed quantification method contributes to the improvement of autonomous vehicle validation procedures by addressing the multifaceted nature of scenario complexities. Beyond advancing the field of validation, the approach also aligns with the broad and active drive of the industry for the widespread deployment of fully autonomous driving.

1. Introduction

The automotive industry has undergone a significant transformation towards the development and integration of autonomous vehicles (AVs) and Advanced Driver Assistance Systems (ADAS) in recent years [1]. At the forefront of this technological evolution is the goal of fully autonomous driving, which corresponds to the Society of Automotive Engineers (SAE) level 5 classification [2]. This level envisions that the AV must be capable of driving independently in all driving situations. The driver is no longer required in the vehicle at this level and, therefore, cannot intervene with the system [3].

Central to the successful deployment of AVs is the validation of these systems [4]. Ensuring the reliability and safety of AVs requires the development of comprehensive testing processes that embrace a diverse range of situations that authentically mirror the intricacies of real-world driving [5,6]. This spectrum encompasses routine commute conditions, as well as rare and challenging scenarios that may be encountered infrequently but of substantial importance [7,8]. Scenario-based testing has been one of the main tools of AV validation approaches [9,10], in which it is required to explore and exploit a large number of scenarios in the scenario state space [11]. Hence, the complicated and critical task of quantifying the complexity of driving scenarios is a crucial aspect to guide the exploration of the scenario state space [12].

The assessment of the complexity of driving tasks constitutes a fundamental pillar in the design of test scenarios and the safety evaluation of AVs [8,13]. The complexity of the driving task can be a valuable parameter for selecting or designing test scenarios. Consequently, the use of high-complexity test scenarios and their variations in driving tasks becomes instrumental in enhancing overall test efficiency [14,15]. The hierarchization of testing scenarios becomes thus essential, requiring a thorough understanding of the complexity of individual scenarios. The multifaceted nature of scenario complexity involves variables such as unpredictable behaviors and interactions between the AV and its surroundings [16,17]. The acknowledgment of uncertainties introduced by dynamic and static entities in the operational range of AVs is important for this understanding [18].

In this paper, we propose COMP-AV-IT, a complexity evaluation of AV safety validation scenarios using information theory. It is important to note that the scenario complexity in our approach is calculated from the perspective of the vehicle under test in the safety validation process. COMP-AV-IT allows for a nuanced evaluation of AV or ADAS performance, allowing developers to prioritize testing based on the potential challenges posed by different scenarios. By subjecting AVs to a comprehensive battery of tests that span the entire spectrum of complexity, engineers can refine algorithms, identify vulnerabilities, and enhance the overall robustness of autonomous driving systems [18,19].

The main contributions of this paper are four-fold as follows:

• A novel quantification method is defined to evaluate the complexity of driving scenarios based on information entropy. The method includes the unpredictability of dynamic agents such as AVs, human-driven vehicles (HVs), and pedestrians.
• The numerical complexity calculation is performed by defining driving scenarios and evaluating their complexity scores.
• A software module with a user-friendly interface is developed to assist in complexity calculation and to allow users to try scenarios.
• Independent simulations are conducted in a microscopic traffic simulator, Simulation of Urban MObility (SUMO), to evaluate the performance of the proposed method.

The remainder of the paper is organized as follows. In Section 2, the existing related literature is presented, and the relevant quantification approaches are explained. Section 3 defines COMP-AV-IT, our quantification method, to evaluate the complexity of driving scenarios based on information entropy. Section 4 illustrates the results of multiple driving scenarios by applying the proposed method and simulating scenarios in microscopic traffic simulation. The results are then compared and discussed in Section 5. Finally, conclusions are summarized, and future research recommendations are derived in Section 6.

2. Related Work

In the context of information theory, the entropy of a random variable denotes the degree of information or uncertainty inherent to the possible outcomes of the variable [20]. Essentially, it quantifies the average uncertainty associated with a random variable. Even though there is a large number of approaches for the validation of AV functionalities [9,21,22,23], there are only several studies that propose the most relevant work to our approach, and hence they are discussed in this section. The analysis of these relevant approaches identifies the strengths and weaknesses of existing methods, as well as identifying unconsidered research aspects.

2.1. Complexity Quantification

The complexity quantification method by Zhang et al. defines the complexity of the scenario as a measurement of the motion uncertainties of all dynamic entities in a driving scenario [16]. In this method, the entropy of a vehicle is computed on the basis of feasible trajectories in a drivable area. The calculation is generated by a sample-based trajectory cluster generation algorithm to search the boundary trajectory of the maximum drivable area of a vehicle. The drivable area contains all feasible trajectories within the kinematic constraints of the road and the vehicle, and the complexity of the scenario is obtained by summarizing the entropies of all vehicles. This approach considers only four-wheel motor vehicles in a scenario and ensures that the trajectories are uniformly distributed. This means that the possibility of selecting any specific trajectory in the drivable area is viewed as equal to selecting any other. Another aspect is that a simplified vehicle kinematic model based on the bicycle model is used to describe vehicle motions. Therefore, the acceleration and steering angle of the front wheel are the only control inputs to compute trajectories.

The critical boundary scenario generation approach by Zhou et al. [19] builds upon the complexity quantification by Yu et al. [7] and calculates the overall scenario complexity based on static and dynamic scenarios while considering human driver cognition. The dynamic scenario complexity in this approach takes into account the AVs, human-driven vehicles, bicycles, and pedestrians. The influence range of the area around a vehicle is described as a semicircle. The dynamic scenario complexity only considers a vehicle-pair, and the influencing drivable area of a vehicle is defined as a rectangle based on the lateral and longitudinal range. Then, a vehicle-pair complexity quantification method based on encounter angle, relative velocity, and relative distance is used. The vehicle-pair complexity evaluates the interactions between the subject vehicle and surrounding dynamic entities. The scenario complexity of the subject vehicle is calculated considering all individual vehicle-pair complexities within the influencing area. Then, a smoothing step is included to reflect the characteristics of the human driver’s cognition.

2.1.1. Information Theory Based Approaches

Liu et al. focus on the evaluation of driving task complexity based on information theory [8]. The driving task complexity for AVs is evaluated from five aspects: the complexities of the number of driving operation steps, driving operation logic, traffic environment information, decision-making, motion planning, and tracking control. While first-order entropy measures the driving operation logic complexity, second-order entropy measures the complexities of the number of driving operation steps, the traffic environment information, the decision, planning and control. However, the method is verified only using a questionnaire and comparing the questionnaire results with the model calculation results. In the questionnaire, experts were asked about their evaluation of complexity for various test scenarios such as lane-change, roundabout, or overtaking. Zhang et al. proposed another approach in which the subject matter expert is required to determine the complexity [24]. This approach uses the analytic hierarchy process and information entropy to evaluate the complexity of test scenarios. The evaluation method calculates the overall complexity of a scenario considering the complexity of static and dynamic scenes. It takes into account weather, time, type of road segment, number of lanes, traffic signs, traffic markings, and other scene facilities and uses the Time to Collision (TTC) in x and y directions for dynamic scenario complexity. The approach ignores the relative motion relationship between a subject vehicle and surrounding traffic participants.

2.1.2. Alternative Approaches

There are also approaches in the literature that use no information theory-based calculation but still have aspects relevant to COMP-AV-IT. For instance, Ma et al. define the scenario complexity by taking the sum of three major uncertainties in the environment [15]. These are the uncertainties in environmental perception, uncertainties caused by the algorithm and database, and uncertainties in the prediction of the future state of the surrounding objects of the subject vehicle. The authors use inertia confinement, obedience to traffic laws, and other distinguishing features to rank the variety of paths of motion for different types of dynamic objects. The validation of this method was performed by five experts who conducted a survey. Cheng et al. define a method based on the theory of potential fields to define the environmental complexity of traffic [25]. The proposed method weighs the complexity of static and dynamic elements and calculates the overall complexity.

2.1.3. Summary

The relevant efforts in the literature show that it is essential to develop a novel quantification method that improves the evaluation of the complexity of driving scenarios. In this paper, a methodical and systematic approach is employed to address the missing aspects and identified weaknesses of the related approaches in the literature, through a novel approach using discretized, weighted trajectories of predicted motion centered around an ego vehicle in traffic situations. Furthermore, the approach is validated through scenario-based safety validation testing using microscopic traffic simulation, which is unique to this approach.

2.2. Scenario-Based Validation Testing

In this paper, safety validation scenarios are evaluated using the microscopic traffic simulator SUMO to evaluate the performance of the proposed complexity quantification method. As such, a discussion of scenario-based validation testing of AVs is included. Scenario-based testing is a strategy employed for testing AV autonomy and other artificial intelligence (AI) applications within the AV domain by constructing scenarios in which the AV autonomy or AI might encounter, then performing scenario tests to evaluate the performance of the AV or AI under test. Scenario tests may be conducted in a range of fidelity be it a toy model [5,8,11,24], via simulation [12,14,17,26,27], or testing within a live environment such as a university campus [28].

2.2.1. Scenario Design

The design of AV safety validation scenarios in this paper is influenced by the ASAM OpenScenario [29,30] format for AV validation scenario description and state-of-the-art research of contributors of ASAM OpenScenario in the form of scenario description languages. Scenario description languages define the environment, initial actor and obstacle positions, and sometimes behavior and missions of actors of the scenario in a format that is shareable and reproducible. Scenarios may be described explicitly using parameter ranges or concrete values to denote position and mission information, such as the case with ASAM OpenScenario v1.2 [29] format and within the PolyVerif [13] framework, a streamlined AV testing pipeline. Alternatively, some scenario description languages utilize a pseudo-code which mimics conversational descriptions of AV safety validation scenarios by using terms such as “in front, side of, behind, slower than, faster than”, etc., as is the case of Scenic [31], M-SDL by Foretellix [32], SCENEST [33], and ASAM OpenScenario v2.0 [30]. Finally, there are also simulator-specific means for describing scenarios when extensive micro-control within a specific simulator is required, such as using TraCI (Traffic Control Interface) [34] for SUMO to define custom AV safety validation scenarios in SUMO as is the case in this paper.

2.2.2. Scenario Testing and Evaluation

Once an AV safety validation scenario is described using a scenario description language or by simulator-specific means in a way that is reproduceable and shareable, the next step is to perform scenario tests to evaluate the AV performance. Scenario tests are derived from the scenario description and then tested in a scenario test environment. Software suites such as Foretify by Foretellix [35], Polyverif [13], SCENEST [33], and VerifAI [36] streamline the process of choosing, building, running, and evaluating scenario tests through a software pipeline for simulators such as LGSVL [37], SUMO, CARLA [38], etc. However, these pipelines are rigid, and alternating any step of the process requires creating an add-on to or refactoring one or multiple parts of the software to add a new unsupported performance metric or simulator.

2.2.3. Summary

In this paper, the design of the example driving scenarios is carefully considered to follow the structure and best practices of state-of-the-art research and development in AV safety validation scenario definition.

3. Methodology

It is necessary to define what is meant by “complexity” to develop a quantification method that evaluates the complexity of driving scenarios based on information entropy. Several definitions vary depending on the scope of the research. For intelligent transportation systems, Sussman defines a system complex when it is difficult to predict the behavior [39]. This means that from an observer’s perspective, the system deals with many uncertainties. Based on this idea, Zhang et al. achieve a more objective quantification method of driving scenario complexity by considering the evolution of driving scenarios and predicting the motions of dynamic traffic participants [16]. In this paper, the term “scenario complexity” is used based on the definitions in these two references. It describes the level of randomness in a scenario, and hence, entropy in information theory is introduced to measure the motion uncertainties of traffic participants.

The focus of our paper is on the dynamic scenario complexity as it is more challenging to consider the unpredictability of dynamic traffic participants and their interactions in a driving scenario [40]. Hence, the static scenario complexity, which refers to weather and environmental conditions, is not the main focus of the approach. The dynamic scenario complexity $C_D$ considers AVs, HVs, bicycles, and pedestrians. The calculation of the entropy of vehicle motion is based on the statistical probability distribution of feasible vehicle trajectories.

The methodology section is divided into three parts to present the quantification method for the complexity evaluation of driving scenarios based on information entropy. In Section 3.1, the fundamental kinematic model used in COMP-AV-IT for vehicle position and dynamics is described. In Section 3.2, the method for the dynamic scenario complexity calculation using information theory is described. In Section 3.3, a sample-based searching algorithm is introduced to determine the drivable area of the subject vehicle.

3.1. Kinematic Model for Vehicle Position and Dynamics

The drivable areas of subject vehicles are critical for the complexity calculation [41]. To generate the drivable area of a subject vehicle, a vehicle model is required. Zhang et al. introduced a kinematic bicycle model to describe the vehicle motions using relatively basic equations [16]. The vehicle model consists of equations that represent the lateral and longitudinal dynamics and the position on the road. In this paper, this model is extended and implemented to simulate and predict the behavior of the subject vehicle. The model is shown in Figure 1.

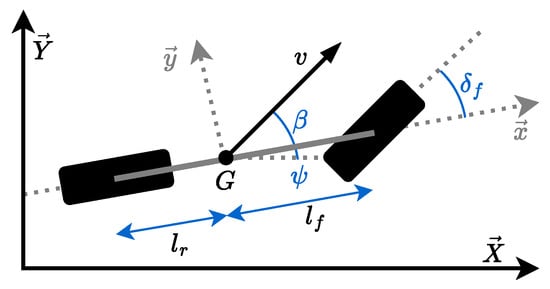
Figure 1. Kinematic bicycle model with tire slip.

The kinematic bicycle model with tire slip is used to predict the next state in a trajectory using the following state transition function:

$$\mathrm{KBM}(S_i)=S_{i+1}$$

where $S_i$ is the current state, and $S_{i+1}$ is the next state.

$$S_i=[x_i,y_i,v_i,{\psi }_i,a,\delta ,\Delta t,l_r,l_f,\underline{s},\overline{s}]$$

Each state S is a vector of multiple features. The state variables are as follows:

• $x_i$: longitudinal position (m)
• $y_i$: lateral position (m)
• $v_i$: velocity (mps)
• ${\psi }_i$: heading angle at the center of gravity G for a given iteration i (rad)
• $\Delta$t: time elapsed
• $l_r$: distance from the center of gravity to the rear axle
• $l_f$: distance from the center of gravity to the front axle
• $\underline{s}$: minimum operational speed of the vehicle
• $\overline{s}$: maximum operational speed of the vehicle

The control inputs are as follows:

• a: acceleration (mps²)
• $\delta$: steering angle of the front wheel, when assuming that only the front wheel can be steered (rad)

Knowing the slip angle at the center of gravity $\beta$, the next position ($x_{i+1}$, $y_{i+1}$) can be predicted using the following equations:

$$\begin{array}{cc}\hfill \beta & =arctan\left({\displaystyle \frac{l_r}{l_r+l_f}}tan\delta \right)\hfill \\ \hfill x_{i+1}& =x_i+v_{i}cos\left({\psi }_i+\beta \right)\Delta t\hfill \\ \hfill y_{i+1}& =y_i+v_{i}sin\left({\psi }_i+\beta \right)\Delta t\hfill \end{array}$$

The speed of the vehicle s at the next iteration i is predicted using the following equation:

$$s=v_i+a\Delta t$$

Then, the speed is confined to the operation speed of the vehicle such that s∈$\left[\underline{s},\overline{s}\right]$ and velocity $v_{i+1}$ is determined as follows:

$$v_{i+1}=\left\{\begin{array}{cc}s<\underline{s}\hfill & \underline{s},\hfill \\ s>\underline{s}\hfill & \overline{s},\hfill \\ \mathrm{otherwise}\hfill & \mathrm{s}\hfill \end{array}\right.$$

With vehicle speed, tires will slip slightly, altering the steering angle. The corrected angle is represented as $\vartheta$, which is given as follows:

$$\vartheta ={\displaystyle \frac{v_i}{l_r}}sin\left(\beta \right)\Delta t$$

Finally, the next heading angle ${\psi }_{i+1}$ is predicted as follows:

$${\psi }_{i+1}={\psi }_i+\vartheta$$

The kinematic bicycle model with tire slip is required to generate the drivable area of a vehicle. The calculation of the driving area is necessary to define the dynamic scenario complexity calculation in Section 3.2. Then, a sample-based search algorithm is introduced in Section 3.3 that is based on this model.

3.2. Dynamic Scenario Complexity Calculation

This section defines the process for the complexity calculation. To calculate the complexity value, the following definitions are made:

• The dynamic scenario complexity $C_D$ is calculated from the perspective of one of the vehicles in the scenario. This is the vehicle under test in the validation process.
• The drivable area of the subject vehicle is described as the combination of possible trajectories and is determined by applying the kinematic bicycle model. The possible trajectories form a fan-shaped drivable area and depend on the vehicle speed.
• The trajectories of the subject vehicle are Gaussian distributed with a mean equal to zero and variance equal to one.
• The motions of the surrounding traffic participants in a driving scenario are known. The trajectory that the subject vehicle selects is unknown. The reaction of the subject vehicle is investigated in a specific scenario.
• The entropy for selecting each trajectory of the subject vehicle is calculated to find the complexity of the whole scenario. For each trajectory, it must be defined which of the surrounding dynamic entities influences the motion of the subject vehicle and, therefore, must be considered in the entropy calculation for this specific trajectory. As soon as the trajectory of a surrounding traffic participant intersects with a trajectory within the fan-shaped drivable area of the subject vehicle, the object is included in the calculation. When a surrounding traffic participant is directly in the fan-shaped area, it is also considered in the calculation.

The entropy of a random variable measures the uncertainty and disorder of a system. The entropy is the sum of the variable’s possible values when given a discrete random variable X, which takes values in the alphabet $\mathcal{X}$ and is distributed according to p: $\mathcal{X}$$\to$$\left[0,1\right]$:

$$H(X)=-\sum _{x\in \mathcal{X}}p(x){log}_{2}p(x)$$

Based on this general idea of entropy, the entropy of a surrounding dynamic entity when the motion is known in a driving scenario is as follows:

$$H_i=-p({\tau }_i){log}_{2}p({\tau }_i)$$

(1)

where $H_i$ is the entropy of a dynamic traffic participant for selecting one specific trajectory ${\tau }_i$ and $p({\tau }_i)$ is the possibility of selecting a specific trajectory ${\tau }_i$.

For the calculation of the subject vehicle’s entropy in a driving scenario, it must be checked for each trajectory if other traffic participants influence its motion and, therefore, must be considered in the calculation. This decision depends on whether there are intersections of trajectories or if a traffic participant is in the fan-shaped area of the subject vehicle. The entropy of the subject vehicle for a specific trajectory $H_{Subject}(\tau =i)$ is described as follows:

$$H_{\mathrm{Subject}}(\tau =i)=-p({\tau }_i){log}_{2}p({\tau }_i)+\sum _{i=1}^N{\lambda }_i{H}_i$$

(2)

where N is the number of traffic participants that can influence the motion of the subject vehicle in a driving scenario and $H_i$ is the entropy of the ith surrounding dynamic entity in a driving scenario. ${\lambda }_i$ is the influence of a traffic participant and ${\lambda }_{vehicle}=1$, ${\lambda }_{bicycle}=0.9$, ${\lambda }_{pedestrian}=0.8$. $p({\tau }_i)$ is the possibility of selecting a specific trajectory ${\tau }_i$.

The dynamic scenario complexity $C_D$ for a subject vehicle is the sum of all entropies that are calculated for each trajectory of the subject vehicle:

$$C_D=\sum _{\tau =i}^n{H}_{Subject}\left(\tau =i\right)$$

(3)

where $H_{Subject}\left(\tau =i\right)$ is the entropy of the subject vehicle for a specific trajectory.

3.3. Sample-Based Search Algorithm

The computation of the drivable area of the subject vehicle is performed by our sample-based search algorithm, which is implemented as a software module specifically for this paper. The possible occupied drivable area of the subject vehicle is determined by generating trajectories that are represented as sequences of (x, y) positions in 2-dimensional space while adhering to vehicle kinematic constraints in a time window. The drivable area is made up of infinite feasible trajectories and is essential in quantifying the entropy of the vehicle. A novel sample-based search algorithm is introduced to identify the boundary trajectory of the maximum drivable area.

The model has two control parameter ranges, and all trajectories start at the root state $S_0$:

• Acceleration $a\in \left[\underline{a},\overline{a}\right]$ between the minimum acceleration $\underline{a}$ (i.e., max deceleration), and maximum acceleration $\overline{a}$.
• Steering angle of the front axle $\delta \in \left[\underline{\delta },\overline{\delta }\right]$ between the rightmost steering angle $\underline{\delta }$ and leftmost steering angle $\overline{\delta }$.

The number of trajectories generated is $n_a$$n_{\delta }$ where $n_a$ is the number of samples from a and $n_{\delta }$ is the number of samples from $\delta$. The duration of trajectories simulation time w and time step duration $\Delta$t is to be chosen. Each trajectory is simulated for a maximum of ${\displaystyle \frac{w}{\Delta t}}$ iterations. Each trajectory is uniquely identified by the ($a,\delta$) sample and is a sequence of $n_{xy}(x,y)$ points that form a polyline where $n_{xy}\in \left[1,{\displaystyle \frac{w}{\Delta t}}\right]$.

Figure 2 shows the designed user interface to determine the drivable area of a subject vehicle. In this configuration, the length of the time window is 3 s, and the time step duration $\Delta$t is 0.1 s. The initial state of the subject vehicle is described by the parameters initial x and y positions, initial speed, and the initial vehicle heading angle. The subject vehicle cannot move faster than 15 mps. The distances from the axles to the center of gravity are each 2.5 m. The control inputs are set as described in [16]. The control inputs of a and $\delta$ are, respectively, sampled from the range [−6, 4] (mps²) and [−10, 10] (deg). Three samples are between the minimum and maximum acceleration, and 15 samples are set for the number of samples between the minimum and maximum steering angles.

Figure 2. User interface to determine the drivable area.

To obtain a drivable area polygon, the boundary points are determined from all points generated during trajectory simulations. With a polygon identified, the drivable area can be calculated using the shoelace equation. The model works under the following assumptions:

• Minimum vehicle speed $\underline{s}$ > 0
• Acceleration a and steering angle $\delta$ are constant for each trajectory simulation.

The trajectories form a potentially asymmetrical and irregular fan shape. The acceleration a and steering angle $\delta$ are the IDs of a trajectory. There are n increments in accelerations where $a_0=\underline{a}$ and $a_n=\overline{a}$. Likewise, there are N increments in the steering angle where ${\delta }_0=\underline{\delta }$ and ${\delta }_n=\overline{\delta }$. The model uses the following strategy to find the boundary polygon starting from the origin and proceeding clockwise around the points of the trajectory cluster (Figure 3):

• The polyline that forms the boundary polygon starts with the leftmost trajectories, beginning with the trajectory with the smallest acceleration and largest steering angle ($a_0$,$\overline{\delta }$, i.e., $\underline{a},\overline{\delta }$). The polyline continues from the nearest point in $a_1.\overline{\delta }$ to the last point in $a_0,\overline{\delta }$ and continues to the end of $a_1,\overline{\delta }$. This is repeated through $a_n,\overline{\delta }$.
• Next, the front of the fan is added. This is the last point of trajectories with $\overline{a},\overline{\delta }$ to $\overline{a},\underline{\delta }$, excluding the leftmost and rightmost trajectories, i.e., $\overline{a},{\delta }_{n-1}$ to $\overline{a},{\delta }_1$.
• Finally, the polygon of the rightmost trajectories is added. To do so, the polyline from $\underline{a},\underline{\delta }$ to $\overline{a},\underline{\delta }$ is obtained. As this method finds the boundary points clockwise from the origin, the values of the rightmost trajectory polyline are appended to the boundary polyline from the last to the first index.

Figure 3. Trajectory boundary definition.

4. Scenario Complexities Using COMP-AV-IT

To demonstrate the performance of COMP-AV-IT, we define multiple sample driving scenarios and calculate their complexities. Hence, six (6) driving scenarios are selected to be presented and analyzed in this section for results. The complexity scores of these scenarios are first calculated according to the methodology presented in Section 3.2. The results are used to rank the driving scenarios from the most complex to the least complex scenario. Then, these scenarios are also modeled in SUMO [42] to see if the results align with the behavior in simulation and to evaluate the effectiveness and adaptability of the proposed framework.

Considerations are taken during scenario design to construct applicable driving scenarios that reflect real-life situations of driving conditions in traffic environments. Traffic environments are complex systems with many factors, e.g., the street network and the roads the vehicles travel on, as well as the vehicles that make up the traffic and their behaviors. There is an endless number of potential driving scenarios, which poses a problem when choosing which scenarios to test under time and resource constraints [12]. This is considered during the design of the scenario examples in this paper.

The driving scenarios focus on the behavior of vehicles and actors relative to an ego vehicle, Vehicle A. The scenarios are up to two other vehicle actors, Vehicles B and C, and a pedestrian actor P. The scenarios take place on a two (2) or three (3) lane segment of highway. A crosswalk is also present when pedestrians are included. The example scenarios are modeled in two forms, each with its own level of fidelity: In Section 4.1, the driving scenarios are modeled as lower-fidelity, theoretical scenarios, where vehicles are placed on a segment of the road relative to the ego Vehicle A, and their trajectories are given. In Section 4.2, the driving scenarios are modeled as higher-fidelity SUMO scenarios, where the actors operate along the edges (roads and sidewalks) of a street network.

4.1. Scenarios and Complexity Calculation

In the complexity calculation, the drivable area of the subject vehicle is determined using the sample-based search algorithm. The parameters are the same as shown in Figure 2. Then, six different scenarios are selected for the dynamic scenario complexity calculation. The steps to calculate the dynamic scenario complexity are described in Section 3.2. A figure for each scenario and the calculation steps are given in the following sections. In each scenario, Vehicle A is the subject vehicle, and the motions of the traffic participants surrounding the subject vehicle are predetermined. The subject vehicle can select any possible trajectory. For the sake of clarity and brevity, only the $\overline{a}$ trajectories are considered when calculating the drivable scenarios D1–D6.

D1.

Cut-in Scenario A: In this scenario, Vehicle A is in traffic behind Vehicle B, and another vehicle, C, is making a “cut-in” maneuver toward Vehicle A’s lane. Vehicle A is the subject vehicle, and the scenario complexity is calculated from the perspective of this vehicle. The vehicle motions of Vehicle B and Vehicle C are known as shown in Figure 4.

Figure 4. Design of driving scenario D1.

Table 1 below describes for each trajectory of the subject vehicle if other vehicles must be considered in the entropy calculation or not. This consideration depends on whether the vehicle motion intersects with a trajectory within the fan-shaped area of the subject vehicle or if a traffic participant is directly within the fan-shaped area. For example, Vehicle C is considered for the entropy calculation of the subject vehicle for the leftmost trajectory ($\tau$ = −5) because of the intersection. For the specific trajectory ($\tau$ = 0), just Vehicle B is considered because this vehicle is in the fan-shaped area of the subject Vehicle A.

Table 1. Overview of the influencing vehicles for the entropy calculation.

$H_{Subject}(\tau =-5)$: $H_C+H_A$	$H_{Subject}(\tau =-1)$: $H_A+H_B$	$H_{Subject}(\tau =1.5)$: $H_A+H_B$
$H_{Subject}(\tau =-4)$: $H_C+H_A$	$H_{Subject}(\tau =-0.5)$: $H_A+H_B$	$H_{Subject}(\tau =2)$: $H_A$
$H_{Subject}(\tau =-3)$: $H_C+H_A$	$H_{Subject}(\tau =0)$: $H_A+H_B$	$H_{Subject}(\tau =3)$: $H_A$
$H_{Subject}(\tau =-2)$: $H_C+H_A$	$H_{Subject}(\tau =0.5)$: $H_A+H_B$	$H_{Subject}(\tau =4)$: $H_A$
$H_{Subject}(\tau =-1.5)$: $H_C+H_A+H_B$	$H_{Subject}(\tau =1)$: $H_A+H_B$	$H_{Subject}(\tau =5)$: $H_A$

For all driving scenarios D1–D6, Vehicle A has the same trajectory choices and weights. The difference between scenarios is the placement, trajectory, and involvement of Vehicles B and C. To compare scenarios concisely, we adapt Equation (3) to reflect the pattern in Table 1:

$$C_{\mathrm{D}}=\sum H_{\mathrm{Subject}}\left(\tau =i\right)=\sum H_A\left(\tau =i\right)+\sum {\lambda }_B{H}_B\left(\tau =i\right)+\sum {\lambda }_C{H}_C\left(\tau =i\right)$$

(4)

where i is the index of the fifteen (15) possible discretized trajectories:

$$i\in \{-5,-4,-3,-2,-1.5,-1,-0.5,0,0.5,1,1.5,2,3,4,5\}$$

In this representation, $C_{\mathrm{D}}$ is the sum of all entity trajectories that overlap with the subject vehicle’s trajectories. Since the surrounding dynamic entities in this driving scenario are vehicles, the influence of those in scenarios D1–D5 is ${\lambda }_B={\lambda }_C=1$.

In this driving scenario example, we will calculate the entropy of the subject vehicle, Vehicle A, for all scenarios D1–D6. Vehicle A has 15 possible trajectories that it may select. In this step, we find the entropy $H_A$ of all potential trajectories for Vehicle A:

$$\begin{array}{c}{H}_A(\tau =-5)=-p({\tau }_{-5}){log}_2{(}_{-5})=-1.49({10}^{-6}){log}_2(1.49({10}^{-6}))=2.9({10}^{-5})\\ H_A(\tau =-4)=-p({\tau }_{-4}){log}_2{(}_{-4})=-0.000134{log}_2(0.000134)=0.001724\\ H_A(\tau =-3)=-p({\tau }_{-3}){log}_2{(}_{-3})=-0.004432{log}_2(0.004432)=0.034649\\ H_A(\tau =-2)=-p({\tau }_{-2}){log}_2{(}_{-2})=-0.053991{log}_2(0.053991)=0.227364\\ H_A(\tau =-1.5)=-p({\tau }_{-1.5}){log}_2{(}_{-1.5})=-0.129518{log}_2(0.129518)=0.38192\\ H_A(\tau =-1)=-p({\tau }_{-1}){log}_2{(}_{-1})=-0.241971{log}_2(0.241971)=0.495337\\ H_A(\tau =-0.5)=-p({\tau }_{-0.5}){log}_2{(}_{-0.5})=-0.352065{log}_2(0.352065)=0.53024\\ H_A(\tau =0)=-p({\tau }_0){log}_2{(}_0)=-0.398942{log}_2(0.398942)=0.528897\\ H_A(\tau =0.5)=-p({\tau }_{0.5}){log}_2{(}_{0.5})=-0.352065{log}_2(0.352065)=0.53024\\ H_A(\tau =1)=-p({\tau }_1){log}_2{(}_1)=-0.241971{log}_2(0.241971)=0.495337\\ H_A(\tau =1.5)=-p({\tau }_{1.5}){log}_2{(}_{1.5})=-0.129518{log}_2(0.129518)=0.38192\\ H_A(\tau =2)=-p({\tau }_2){log}_2{(}_2)=-0.053991{log}_2(0.053991)=0.227364\\ H_A(\tau =3)=-p({\tau }_3){log}_2{(}_3)=-0.004432{log}_2(0.004432)=0.034649\\ H_A(\tau =4)=-p({\tau }_4){log}_2{(}_4)=-0.000134{log}_2(0.000134)=0.001724\\ H_A(\tau =5)=-p({\tau }_5){log}_2{(}_5)=-1.49({10}^{-6}){log}_2(1.49({10}^{-6}))=2.9({10}^{-5})\end{array}$$

The trajectories of Vehicle A overlap only themselves. Thus, the total entropy for $H_A$ is:

$$\sum H_A\left(\tau =i\right)=3.871423$$

(5)

We apply our dynamic scenario complexity calculation and calculate the entropy of the surrounding Vehicle B and Vehicle C in this driving scenario. We know the motion of Vehicles B and C. Vehicle B follows its current path that corresponds to the trajectory $\tau =0$. The other vehicle, C, does a “cut-in” maneuver toward vehicle A’s lane. This movement corresponds to trajectory $\tau =3$. We solve the entropy equations for surrounding Vehicles B and C using Equation (1). The trajectory of vehicle B overlaps seven (7) trajectories of Vehicle A. We solve for the influence of vehicle B:

$$\sum {\lambda }_B{H}_B\left(\tau =i\right)=7{\lambda }_B{H}_B(\tau =0)=(7)(1)\left(-p({\tau }_0){log}_{2}p({\tau }_0)\right)=(7)(-0.398942){log}_2(0.398942)=3.70227$$

(6)

The trajectory of Vehicle C overlaps five (5) trajectories of Vehicle A. We solve for the influence of Vehicle C:

$$\sum {\lambda }_C{H}_C\left(\tau =i\right)=5{\lambda }_C{H}_C\left(\tau =i\right)=(5)(1)\left(-p({\tau }_3){log}_{2}p({\tau }_3)\right)=(5)(-0.004432){log}_2(0.004432)=0.17324$$

To calculate the scenario complicity for scenario D1, we sum the influence of all vehicles as described by Equation (4):

$$C_{\mathrm{D}1}=\sum H_{\mathrm{Subject}}\left(\tau =i\right)=3.871423+3.70227+0.17324=7.746933$$

The scenario complexity score is 7.746933.

D2.

Cut-in Scenario B: In this scenario, Vehicle A is in traffic behind Vehicle B, and another Vehicle C is making a “cut-in” maneuver towards Vehicle A’s lane. Compared to the previous cut-in scenario, Vehicle B is never considered in the calculation because it is not in the drivable area of the subject Vehicle A. Figure 5 shows that Vehicle C is considered for the calculation of the entropy of the subject vehicle for trajectories $\tau =-5$, $\tau =-4$, $\tau =-3$ and $\tau =-2$.

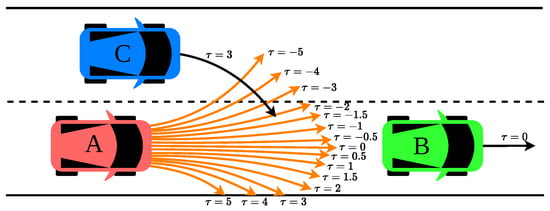Figure 5. Design of driving scenario D2.

The trajectory of Vehicle C overlaps with four (4) trajectories of Vehicle A. We solve for the influence of Vehicle C:

$$\sum {\lambda }_C{H}_C\left(\tau =i\right)=(4)(1)(-0.004432){log}_2(0.004432)=0.138596$$

$H_A$ is unchanged from Equation (5) and $H_B=0$. Thus, the scenario complexity is calculated as follows:

$$C_{\mathrm{D}2}=\sum H_{\mathrm{Subject}}\left(\tau =i\right)=3.871423+0+0.138596=4.010019$$

D3.

2-Lanes Traffic Scenario: In this scenario (Figure 6), Vehicle A is in traffic behind Vehicle B. Vehicle C continues straight in the lane next to the subject Vehicle A’s lane. Vehicle C is not considered in the scenario complexity calculation because it is not in the drivable area of the subject Vehicle A. Vehicle B is considered for the entropy calculation for the trajectories $\tau =-1.5$, $\tau =-1$, $\tau =-0.5$, $\tau =0$, $\tau =0.5$, $\tau =1$ and $\tau =1.5$.

Figure 6. Design of driving scenario D3.

The trajectory of vehicle B ($\tau =0$) overlaps with seven (7) trajectories of Vehicle A. The influence is already calculated in Equation (6) to be $H_B=3.70227$. Thus, the scenario complexity is calculated as follows:

$$C_{\mathrm{D}3}=\sum H_{\mathrm{Subject}}\left(\tau =i\right)=3.871423+3.70227+0=7.573693$$

D4.

2-Lanes No Traffic Scenario: In this scenario, there is no traffic participant other than subject Vehicle A (Figure 7), which means $H_B=H_C=0$. The scenario complexity is calculated as follows:

$$C_{\mathrm{D}4}=\sum H_{\mathrm{Subject}}\left(\tau =i\right)=3.871423+0+0=3.871423$$

Figure 7. Design of driving scenario D4.

D5.

3-Lanes Traffic Scenario: Figure 8 shows the configuration of the fifth scenario. In this scenario, Vehicle A is in the middle traffic lane between Vehicle B and Vehicle C. Vehicle A is the subject vehicle, and the scenario complexity is calculated from the perspective of this vehicle. Vehicle B and Vehicle C go straight into their lane. Vehicle B is not considered in the scenario complexity calculation because it is not in the drivable area of the subject Vehicle A. Vehicle C is considered for the entropy calculation of the subject vehicle for the trajectory $\tau =-5$.

Figure 8. Design of driving scenario D5.

The trajectory of Vehicle C ($\tau =0$) overlaps with one (1) trajectory of Vehicle A. We solve for the influence of Vehicle C:

$$\sum {\lambda }_C{H}_C\left(\tau =i\right)=(1)(1)(-0.398942){log}_2(0.398942)=0.528897$$

The scenario complexity is calculated as follows:

$$C_{\mathrm{D}5}=\sum H_{\mathrm{Subject}}\left(\tau =i\right)=3.871423+0+0.528897=4.40032$$

D6.

2-Lanes No Traffic with Pedestrian Crossing Scenario: In this last scenario, the subject vehicle is surrounded by no other vehicle, but a pedestrian is crossing the subject vehicle’s path (Figure 9). The pedestrian is considered for the entropy calculation of the subject vehicle for the trajectories $\tau =2$ and $\tau =3$.

Figure 9. Design of driving scenario D6.

The trajectory of Pedestrian P ($\tau =0$) overlaps with two trajectories of Vehicle A, and as a pedestrian, the influence is $\lambda =0.8$. We solve for the influence of Pedestrian P:

$$\sum {\lambda }_P{H}_P\left(\tau =i\right)=(0.8)(2)(-0.398942){log}_2(0.398942)=0.8462352$$

The scenario complexity is the sum of all influences in the scenario, which are $H_A$ and $H_P$. Thus, the scenario complexity is calculated:

$$C_{\mathrm{D}6}=\sum H_{\mathrm{Subject}}\left(\tau =i\right)=\sum {\lambda }_P{H}_P\left(\tau =i\right)+\sum {\lambda }_P{H}_P\left(\tau =i\right)=3.871423+0.8462352=4.717658$$

4.2. Simulation Scenarios and Complexity Classification

The performance of COMP-AV-IT is evaluated in simulation using the open-source microscopic traffic simulator SUMO v1.20.0 on Ubuntu v20.04.6 with Python v3.9.20 and the TraCI v1.19.0 Python package. SUMO is an open-source traffic simulation software that allows the modeling of traffic systems, including road vehicles, public transport, and pedestrians [42]. The scenarios that are used in the previous section are modeled and tested in SUMO. The implementation of scenario-based AV testing follows the approach of Goss et al. [26,27], where-in the modular, measurable, shareable, and general-case scenarios are derived from the scenarios of Section 4.1 then evaluated through extensive simulation tests.

4.2.1. Simulation Scenario Abstraction Levels

The scenarios in Section 4.1 are abstracted into five logical scenarios with parameter ranges for scenario-based testing. The parameter ranges are used to create variations of each simulation. Hence, an abstraction process is followed in the modeling and simulation process with the following three levels:

• Formal Abstraction Level: At this abstraction level, a scenario is defined in a human-readable format, often through forms or in a conversational tone, which describes the setting, mission, actors, and actions of participants in a scenario. The actions are described using atomic ideas of behavior or misbehavior, e.g., “Make a left turn”, or “Turn right at the traffic light”. At this level of abstraction, an expert in an operational design domain (ODD) may make a reasonable estimation of a scenario based on expert knowledge, e.g., vehicles confined to roads adhere to or close to road network rules and operate within definable physical constraints. An example scenario at the formal abstraction level is as follows:
  • “A vehicle turns right at a traffic light”.
• Logical Abstraction Level: At this abstraction level, a scenario is defined in a computer-readable formal with explicit instructions for scenario construction. Parameter ranges are used to represent multiple configurations with a single description. An example scenario at the logical abstraction level is as follows:
  • “Vehicle A is 0–100 m from an intersection with a traffic light, traveling at 0–5 mps. The vehicle under test will safely turn right at the intersection”.
• Concrete Abstraction Level: At this abstraction level, one configuration of a scenario is represented by selecting explicit, concrete values from each parameter range. An example scenario at the concrete abstraction level is as follows:
  • “Vehicle A is 27 m from an intersection with a traffic light, traveling at 4 mps. The vehicle under test will safely turn right at the intersection”.

4.2.2. Simulation Scenarios Setup

A summary of the scenario setups is presented in Table 2. The two drivable cut-in scenarios (D1 and D2) are combined in one scenario (L1) that satisfies both configurations (See Figure 10). The remaining drivable scenarios are also abstracted into logical scenarios:

• L2 is 2-lanes with traffic scenario (Figure 11).
  

  Figure 11. SUMO simulation of Scenario L2.
• L3 is 2-lanes without traffic scenario (Figure 12).
  

  Figure 12. SUMO simulation of Scenario L3.
• L4 is 3-lanes with traffic scenario (Figure 13).
  

  Figure 13. SUMO simulation of Scenario L4.
• L4 is a pedestrian crossing scenario (Figure 14).
  

  Figure 14. SUMO simulation of Scenario L5.

Figure 10. SUMO simulation of Scenario L1.

Table 2. Scenario Setup.

Logical
Scenario:	L1	L2	L3	L4	L5
Driving	D1
Scenario:	D2	D3	D4	D5	D6
Road Network Configuration
lanes	2	2	2	3	2
actors	3	3	1	3	2
ped X-ing					✔
Actor Placement
lane 2				C
lane 1	C	C		A
lane 0	AB	AB	A	B	A
sidewalk					P
Parameter Ranges
$s_{0_A}$	✔	✔	✔	✔	✔
$s_{0_B}$	✔	✔		✔
$s_{0_C}$	✔	✔		✔
${\mathrm{dist}}_{BA}$	✔	✔		✔
${\mathrm{dist}}_{CA}$	✔	✔		✔
${\mathrm{dist}}_{PA}$					✔
${\mathrm{dist}}_{P_0}$					✔
lcd	✔
Performance Metrics
$C_D$	✔	✔	✔	✔	✔
${\mathrm{collision}}_A$	✔	✔	✔	✔	✔
max(decelA)	✔	✔	✔	✔	✔
min(dtcAB)	✔	✔			✔
min(dtcAC)	✔	✔			✔
min(dtcAP)				✔
min(ttcAB)	✔	✔			✔
min(ttcAC)	✔	✔			✔
min(ttcAP)				✔

Table 2. Scenario Setup.

Logical
Scenario:	L1	L2	L3	L4	L5
Driving	D1
Scenario:	D2	D3	D4	D5	D6
Road Network Configuration
lanes	2	2	2	3	2
actors	3	3	1	3	2
ped X-ing					✔
Actor Placement
lane 2				C
lane 1	C	C		A
lane 0	AB	AB	A	B	A
sidewalk					P
Parameter Ranges
$s_{0_A}$	✔	✔	✔	✔	✔
$s_{0_B}$	✔	✔		✔
$s_{0_C}$	✔	✔		✔
${\mathrm{dist}}_{BA}$	✔	✔		✔
${\mathrm{dist}}_{CA}$	✔	✔		✔
${\mathrm{dist}}_{PA}$					✔
${\mathrm{dist}}_{P_0}$					✔
lcd	✔
Performance Metrics
$C_D$	✔	✔	✔	✔	✔
${\mathrm{collision}}_A$	✔	✔	✔	✔	✔
max(decelA)	✔	✔	✔	✔	✔
min(dtcAB)	✔	✔			✔
min(dtcAC)	✔	✔			✔
min(dtcAP)				✔
min(ttcAB)	✔	✔			✔
min(ttcAC)	✔	✔			✔
min(ttcAP)				✔

Using SUMO and TraCI, which allows micro-control of the SUMO simulator, scenarios are implemented on road networks with lanes 3.5 m wide, sidewalks 2 m wide, and maximum network speed set to 50 mps. The vehicle parameters used are a maximum speed of 15 mps, a wheelbase of 2.63 m, and a maximum steering angle of 10 degrees. The vehicle AI used is the SUMO no-collision AI, which attempts to keep a gap of 2.5 m between vehicles and utilizes a driving plan that prevents the need for excessive braking when possible, i.e., braking force > 4.5 mps². The pedestrian in the simulations always begins at a speed of 0 mps, has a maximum speed of 1.2 mps, and acceleration of 1.5 mps².

The parameter ranges used in the scenarios vary according to the scenario requirements, as shown in Table 2. For each scenario, as depicted in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, the blue vehicle is the subject Vehicle A, the red vehicle represents Vehicle B, and the green vehicle represents Vehicle C. The parameter ranges for these scenarios are defined as follows:

• The initial speed of Vehicle A 0 mps $\le s_{0_A}\le$ 15 mps by $0.27$ mps increments.
• The initial speed of Vehicle B 0 mps $\le s_{0_B}\le$ 15 mps by $0.27$ mps.
• The initial speed of Vehicle C 0 mps $\le s_{0_C}\le$ 15 mps by $0.27$ mps.
• The initial lateral distance of Vehicle B from Vehicle A ${\mathrm{dist}}_{BA}$. For scenarios L1 and L2. 10 m ≤ ${\mathrm{dist}}_{BA}\le$ 30 m by 1 m. For scenario L4 0 m ≤ ${\mathrm{dist}}_{BA}\le$ 30 m by 1.
• The initial lateral distance of Vehicle C from Vehicle A 0 m ≤ ${\mathrm{dist}}_{CA}\le$ 30 m by 1 m.
• The initial lateral distance of Pedestrian P from Vehicle A 0 m ≤ ${\mathrm{dist}}_{PA}\le$ 30 m by 1 m.
• The distance Pedestrian P begins from the start of the crosswalk measured from right-to-left of the front of Vehicle A 0 m ≤ ${\mathrm{dist}}_{P_0}\le$ 5 m by 1 m.
• The duration of time a vehicle takes to transition from one lane to another during a lane-change maneuver, i.e., lane-change duration (lcd), 0.5 s ≤ lcd ≤ 5 s by 0.1 s.

Scenarios are evaluated using several performance metrics. Distance to collision (DTC) and TTC are commonly used to define these metrics. Hence, it is important to define DTC and TTC. DTC is the Euclidean distance between two positions, p and q, at the time instant i:

$${\mathrm{dtc}}_i(p_i,q_i)=\sqrt{{(q_{x_i}-p_{x_i})}^2+{(q_{y_i}-p_{y_i})}^2}$$

The point of reference for the position is the center of the front of the vehicle or pedestrian. TTC at the time instant i for two vehicles is:

$${\mathrm{TTC}}_i={\displaystyle \frac{{\mathrm{dtc}}_i}{s_{{\mathrm{rel}}_i}}}$$

where $s_{{\mathrm{rel}}_i}$ is the relative speed between two vehicles at moment i. With DTC and TTC defined, the performance metrics can be listed as follows:

• $C_D$, scenario complexity prediction.
• collision_A, whether Vehicle A is involved in a collision (collision_A = 1) or not (collision_A = 0).
• max(decel_A), the maximum deceleration force of Vehicle A observed during the testing window.
• min(dtc_AB), the minimum DTC between Vehicles A and B observed during the testing window.
• min(dtc_AC), the minimum DTC between Vehicles A and C observed during the testing window.
• min(dtc_AP), the minimum DTC between Vehicle A and Pedestrian P observed during the testing window.
• min(ttc_AB), the minimum TTC between Vehicles A and B observed during the testing window.
• min(ttc_AC), the minimum TTC between Vehicles A and C observed during the testing window.
• min(ttc_AP), the minimum TTC between Vehicle A and Pedestrian P observed during the testing window.

Table 2 shows the performance metrics used for each simulation scenario. Both distance and time metrics are used as part of the performance metrics. DTC metrics provide a concise estimation of the closeness between actors using the terminology of the ODD, thus allowing the performance metric to be compared as a ratio to vehicle properties such as length and min gap. Likewise, TTC directly estimates the collision risk using DTC and the relative speed of actors, allowing the performance metric to be compared as a ratio of relative actor speeds and distances.

A limitation of the TTC metric is the assumption that the speed of actors is constant when calculating the time to a possible collision. However, the limitation comes with the trade-off of reduced time and resource costs during simulation tests. In this paper, no further performance metrics are used; however, there exist other supplementary performance metrics which may be considered:

• Deceleration Rate to Avoid Collision (DRAC) represents the rate at which a vehicle must decelerate to avoid a collision with another actor or object. DRAC may be defined as:

  $$\mathrm{DRAC}={\displaystyle \frac{v^2}{2d}}$$

  where v is the relative speed of the vehicle and d is the distance to the other actor or object.
• Modified Time to Collision (MTTC) takes into account relative acceleration a, which provides a more accurate estimation of TTC where relative velocity v is assumed to be constant. MTTC may be defined as:

  $$\mathrm{MTTC}={\displaystyle \frac{-v\pm \sqrt{v^2-2ad}}{a}}$$

  where v is relative velocity, a is relative acceleration, and d is relative distance between two actors. The MTTC equation is quadratic and, as such, evaluates to two solutions. The negative solution may be mathematically valid but physically irrelevant, e.g., the objects are not at their current positions.
• Proportion of Stopping Distance (PSD) quantifies the ratio of the distance available to stop a vehicle $d_a$ to the physically required stopping distance under current conditions $d_r$. PSD may be defined as:

  $$\mathrm{PSD}={\displaystyle \frac{d_a}{d_r}}$$

  where $d_a$ is the available stopping distance and $d_r$ is the required stopping distance. When PSD ≥ 1, the vehicle has adequate space to stop safely with normal braking force. When PSD < 1, the vehicle has inadequate space to stop safely, which means the vehicle must find another means to avoid a collision, e.g., going around the obstacle.

Using the performance metrics, a ranking system for the scenarios can be determined by categorizing the scenarios in three ways:

• Collision: The subject vehicle collides with another dynamic traffic participant. If an accident happens, the performance metrics TTC and DTC are both zero.
• Near Collision: In these scenarios, the subject vehicle is not involved in a collision, but the braking exceeds the normal braking force of 4.5 mps. This category represents situations in which the subject vehicle must make an immediate decision to slow down to avoid a collision.
• Normal Operation: The subject vehicle operates normally and as expected within the environment. The subject vehicle is not involved in any collision, and the braking forces do not exceed 4.5 mps.

A driving scenario is considered complex if collisions or near-collisions occur during simulation. By implementing simulation testing according to the explained approach, the driving scenarios are modeled and evaluated. Each scenario is tested 10,000 times using the parameter ranges, and the testing window is set to 3 s. The results for each of the scenarios are presented in the following subsections.

5. Results Summary and Discussion

The complexities of the six selected scenarios are calculated in Section 4.1, and these results are summarized in Table 3. The results in Table 3 show that COMP-AV-IT enables the ranking of driving scenarios. The value range of scenario complexity varies from the least complex scenario, i.e., 3.871423 for the 2-Lanes No Traffic scenario (D4), to the most complex scenario, i.e., 7.746933 for the cut-in scenario A (D1). A lower complexity score means a less complex scenario. The 2-Lanes No Traffic scenario only has one actor, i.e., Vehicle A, where only Vehicle A is considered in the complexity calculation—without any other actors involved, scenario D4 is the low end of the scenario complexity score range. The scenario complexity score may be affected in a number of ways:

• By adding more influential actors, i.e., actors whose possible trajectories overlap with Vehicle A. This causes the scenario to increase. For driving scenarios D1–D6, the additional actors are Vehicles B, C, and Pedestrian P.
• By adding, removing, or extending possible trajectories, e.g., removing trajectory $\tau =-5$ from Vehicle A in scenario D5 would remove Vehicle C from consideration in the scenario, and the complexity score would then be the same as scenario D4 as the other actors in the scenario no longer have overlapping trajectories. Likewise, extending trajectory $\tau =3$ from Vehicle A in scenario D5 into Vehicle B would increase the scenario complexity.
• By adjusting the trajectory weights. For these examples, the trajectory weights are determined using a Gaussian distribution where $\mu =0$ and $\sigma =1$. Alternatively, the $\tau$ values for trajectories may be adjusted to account for more situations, e.g., assigning leftmost trajectories a $\tau$ at or closer to zero (0) to notate the preference of making a left turn.
• By adjusting actor influence weight $\lambda$. A larger $\lambda$ value directly increases the scenario complexity score, while a smaller $\lambda$ value decreases the scenario complexity score.

Table 3. COMP-AV-IT scenario complexities.

#	Driving Scenario	Scenario Complexity
1	Cut-in Scenario A	7.746933
2	Cut-in Scenario B	4.010019
3	2-Lanes Traffic Scenario	7.573693
4	2-Lanes No Traffic Scenario	3.871423
5	3-Lanes Traffic Scenario	4.400320
6	Pedestrian Crossing	4.717658

Table 3. COMP-AV-IT scenario complexities.

#	Driving Scenario	Scenario Complexity
1	Cut-in Scenario A	7.746933
2	Cut-in Scenario B	4.010019
3	2-Lanes Traffic Scenario	7.573693
4	2-Lanes No Traffic Scenario	3.871423
5	3-Lanes Traffic Scenario	4.400320
6	Pedestrian Crossing	4.717658

The results of the simulation study are summarized in Table 4, where the percentage of collisions, near-collisions, and normal operations are given for each type of scenario. As already mentioned, the most complex scenario is considered to be the one with the highest percentages of collision and near-collision categories.

Table 4. Results of simulations using SUMO.

#	Driving Scenario	Collision	Normal Operation	Near Collision
1	Cut-in Scenario	35.48%	41.39%	23.23%
2	2-Lanes Traffic Scenario	6.69%	71.47%	21.84%
3	2-Lanes No Traffic Scenario	0%	100%	0%
4	3-Lanes Traffic Scenario	0%	100%	0%
5	Pedestrian Crossing	0%	80.05%	19.95%

The cut-in scenario has the highest collision rate for Vehicle A at 35.48%, while the 2-Lanes Traffic scenario has the next highest rate of 6.69%. Likewise, the near-collision rates of Vehicle A with another actor is 23.23% for the cut-in scenario and 21.84% for the 2-Lanes Traffic scenario. The 35.48% collision rate in the cut-in scenario indicates that three (3) to four (4) out of ten (10) vehicles would be involved in a collision. This may seem like an overestimation of collision risk when applied to a human driver—this is not an overestimation of collision risk, but actually a flaw in the AI of Vehicle A, which responds poorly to cut-in maneuvers. From a visual inspection of the vehicle AI during Cut-Scenario tests, Vehicle A does not recognize Vehicle C after a point in the merging maneuver, and thus, no preventative action is taken.

By comparing the results of the COMP-AV-IT calculations to the simulation results, it can be seen that the same ranking sequence of driving scenarios has been achieved. The cut-in traffic scenario is, in both cases, the most complex scenario configuration. The second most complex scenario is the 2-lane traffic scenario, followed by the 2-lane no-traffic scenario with pedestrian crossing. The 3-lane traffic scenario and the driving scenario with just the subject vehicle are the least complex scenarios.

This approach imposes some limitations to reduce the computational complexity such that it may be applied to simulation testing such as the SUMO scenario examples under time and resource constraints, e.g., in order to perform the 50,000 SUMO simulation tests within this paper, as well as the additional uncounted tests performed for debugging and tuning the approach. Rather than a drivable area, drivable trajectories are utilized at chosen at a discrete interval and assigned probabilities. The increase in performance of this decision comes at the cost of accuracy, e.g., in scenario D6, the pedestrian crosses trajectories $\tau =2$ and $\tau =3$ of Vehicle A and continues slightly farther towards trajectory $\tau =1.5$ which is not accounted for during complexity calculation.

In summary, independent simulations in SUMO have approved the quantification method to evaluate the complexity of driving scenarios based on information entropy. This demonstrates the adaptation and validity of the proposed method to diverse scenarios.

6. Conclusions

In this paper, a novel quantification method, COMP-AV-IT, is introduced to evaluate the complexity of driving scenarios based on information entropy. The proposed method addresses the dynamic uncertainties within driving scenarios in a comprehensive way. The evaluation of the quantification method is conducted with the comparison of the method’s calculations against simulation results. The evaluation scenarios are formally defined, and their complexity scores are calculated. By comparing the results of the numeric complexity calculations against the results of independent simulations in SUMO, the effectiveness, validity, and adaptability of the proposed framework are shown for various driving scenarios. Thus, the hierarchization and ranking of testing scenarios can be achieved based on their dynamic scenario complexity scores. This is essential to enable engineers to prioritize testing based on the potential challenges posed by different scenarios. Additionally, developers can design traffic scenarios and compare them without running complex simulations.

The paper contributes to the improvement of AV testing procedures by addressing the multifaceted nature of scenario complexities. Beyond advancing the field of AV testing, this paper also aligns with the larger industry push for the widespread deployment of fully autonomous driving. The paper opens up several future research directions. One of these could be the analysis of static uncertainties in the scenario complexity calculation. By integrating these factors into our model, the complexity of driving scenarios can be fully assessed. The change in dynamic scenario complexity scores could also be investigated by testing different statistical distributions and their influencing parameters.