RIS-Enabled UAV Cognitive Radio Networks: Trajectory Design and Resource Allocation

Abstract

Due to its flexible deployment and high mobility of unmanned aerial vehicles (UAVs), the UAV-assisted cognitive radio (CR) network has attracted a lot of attention as one of the most promising techniques to address spectrum congestion issues in futuristic networks. However, its performance can be severely affected by the blocked line-of-sight (LoS) channel in its air-to-ground (A2G) links. In this paper, we propose a UAV CR system enabled by a reconfigurable intelligent surface (RIS), which helps to reconstruct reliable links in UAV-assisted cognitive radio (CR) networks. Our goal is to maximize the achievable rate of a secondary receiver (SR) through the proper selection of the UAV trajectory, transmit power, and RIS phase shifts based on a given interference temperature threshold and other practical constraints. In addition, we solve the corresponding non-convex optimization problem using block coordinate descent (BCD) and successive convex approximation (SCA) algorithms. The simulation results will demonstrate the effectiveness of the proposed algorithms.

1. Introduction

In the upcoming B5G/6G networks, spectrum resources are still a constraint, which may further restrict the development of emerging wireless communication networks, such as internet of things (IoT), smart city, and unmanned aerial vehicle (UAV) communications [1,2,3,4]. In practice, allocating the spectrum to UAVs alone will exacerbate the shortage of spectrum resources. As one of the most effective techniques to tackle the spectrum shortage issue, cognitive radio (CR) has received extensive attention in UAV applications in recent years [5,6,7].

In a CR system, the authorized user (who owns the license of the spectrum) is usually called the primary user (PR), and the other users sharing the spectrum are called the secondary users (SRs). The main purpose of cognitive radio is to share the spectrum resources between the PR and the SRs by spectrum access based on spectrum cognition. On the physical (PHY) layer, the key design idea is that the interference from the SRs to the PR needs to be controlled below a certain threshold, namely, interference temperature (IT) [8,9,10,11]. Therefore, by utilizing the CR techniques, one can sense the external communication environment on a real-time basis and change the transmission parameters for reliable communications as well as the efficient use of limited spectrum resources [12]. On the other hand, UAV communication is considered one of the most promising techniques to establish temporal and flexible communication links between air-to-ground (A2G) terminals in practical wireless networks. Therefore, it is significant to implement CR techniques in the UAV networks to construct an intelligent device-to-device communication system [3] with the advantages of high mobility and fast deployment of the UAVs, as well as the line-of-sight (LoS) links in A2G communications [13,14,15,16].

However, it is not always possible to establish the LoS links in a UAV-assisted CR network since there are many large-scale blockages, such as high buildings, etc. [17]. Accordingly, severe blockage can incur huge performance losses in UAV communications. Fortunately, the reconfigurable intelligent surface (RIS) is helpful to reconstruct good wireless propagation channel links and can be potentially implemented in futuristic wireless networks [18,19,20,21] by reflecting the incident communications signals and adjusting its phase shifts to attain performance gain. The work reported in [22] studied RIS for multi-user communications in downlink channels, and the proposed RIS-based resource allocation method significantly improved the energy efficiency. The authors of [23], via studying the free-space path loss of RIS-assisted wireless communications, proposed and verified a RIS free-space path loss model, which was a great contribution to further research in this field. The RIS is able to actively reconfigure the wireless channel link between a transmitter and a receiver through controllable intelligent signal reflection, creating a virtual LoS link to bypass obstacles between the transceivers, which helps to improve the wireless link performance effectively [24,25]. More specifically, one can deploy RIS in UAV-assisted CR networks once the A2G LoS links are blocked, and thus mobile CR users can establish temporary or emergency communications via the cascaded channel links reconstructed by the RIS.

There are numerous works in the literature on UAV-assisted wireless communications. For example, a UAV-assisted CR scenario based on the spectrum sharing scheme was investigated in [3]. In [26], implementing multiple UAVs in an existing cellular network, the authors tried to maximize the minimum achievable rate among multiple ground devices with the given UAV mobility constraints and transmit power budget. On the other hand, addressing the issues on RIS-enabled wireless communications, the authors in [27] proposed simultaneous wireless power and information transfers. As a further step to establish the cascaded channel links when the LoS link is blocked between base station (BS) and receivers, the authors in [28] performed a power scaling law analysis to optimize the phase shift in RIS-aided massive multiple-input-multiple-output (MIMO) systems. Inspired by [2,4], we summarize the comparison of existing work in Table 1.

Table 1. Some existing work.

Ref.	Contributions	RIS	UAV	Cognitive
[3]	The scenario of sharing spectrum between the UAV and terrestrial wireless communication system is proposed, and the flight trajectory and the transmit power allocation are optimized to maximize the average achievable rate of the cognitive UAV.		√	√
[17]	The joint design of UAV trajectory for RIS-assisted UAV communication system and passive beamforming for RIS is researched to maximize the average reachable rate.	√	√
[22]	The work studies the RIS-assisted multi-user communications in downlink channels, and proposes RIS-based resource allocation method, which significantly improves the energy efficiency.	√
[23]	The authors study a RIS free-space path loss model, which is another great contribution to further research in this field.	√
[26]	In this work, by implementing multiple UAVs in an existing cellular network, the authors aim to maximize the minimum achievable rate among multiple ground devices with given UAV mobility constraints and transmit power budget.		√
[27]	The authors propose simultaneous wireless power and information transfers and study the weighted total power maximization problem in the RIS-assisted SWIPT system.	√
our work	We investigate several important issues on RIS enabled UAV CR networks and the joint design of phase shift matrix and transmission power as well as the flight trajectory of the UAV is performed to maximize the achievable average rate of SR.	√	√	√

The main contributions of this paper are summarized as follows:

• We investigate a practical application scenario, namely a RIS-enabled UAV CR network, where the LoS links between A2G terminals are largely blocked. Specifically, in this paper, the RIS is used to leverage and reconstruct the propagation links in A2G channels by reflecting the UAV transmit signals. The goal for maximizing the average achievable rate of SR is achieved via a joint optimization of the phase shifts of the RIS, the transmit power, as well as the UAV trajectory while satisfying the maximum interference threshold (IT) requirement and other operational constraints.
• The optimization problem in this paper is difficult to solve directly due to its non-convexity, and thus we design an iterative algorithm based on the block coordinate descent (BCD) and the successive convex approximation (SCA) algorithms to solve the problem. Additionally, to gain more insights from the analysis, a closed-form solution is attained. We solve the original optimization problem by dividing it into several sub-problems.
• The simulation results are provided to demonstrate that the average achievable rate can be improved significantly using the proposed algorithm, as compared to several comparison benchmarks.

The rest of this paper can be summarized as follows. In Section 2, we first introduce a basic system model and formulate an optimization problem. Then, we make use of the BCD and the SCA algorithms to solve the formulated non-convex and multi-variable optimization problem in Section 3. To this end, we verify the effectiveness of the proposed iterative algorithm according to the numerical results presented in Section 4. Finally, Section 5 gives the conclusions of this paper.

2. System Model and Problem Formulation

2.1. System Model

Let us consider a spectrum-sharing scenario in RIS-enabled UAV communications, as shown in Figure 1, where a cognitive UAV serves as a mobile aerial BS to communicate with one single ground SR in the presence of potential spectrum interference among K ground PRs. A set of PRs is represented by $\mathcal{K}\triangleq \{1,\dots ,K\}$. The horizontal coordinate of the ground SR is expressed as ${\mathit{w}}_s={(x_s,y_s)}^T$ and each ground PR $k\in \mathcal{K}$ is fixed at ${\mathit{w}}_k={(x_k,y_k)}^T$. In equally spaced N time slots, the step size of the time span T is set to ${\delta }_t$, where $T=N{\delta }_t$ and the time slot length is ${\delta }_t$. The time-varying horizontal coordinates of the UAV are represented by $\mathit{l}\left[n\right]={\left(x\left[n\right],y\left[n\right]\right)}^T$, $n\in \mathcal{N}=\{0,\dots ,N\}$. During the entire flight period T, the flight altitude of the UAV is fixed at $z_u$. In addition, the following mobility constraints should be used by the UAV:

$$\begin{array}{c}\mathit{l}\left[0\right]={\mathit{l}}_0,\mathit{l}\left[N\right]={\mathit{l}}_f,\hfill \end{array}$$

(1a)

$$\begin{array}{c}\parallel \mathit{l}[n+1]-\mathit{l}\left[n\right]\parallel \le V_{\max }{\delta }_t,n=1,\dots ,N,\hfill \end{array}$$

(1b)

where the original and final horizontal positions of the UAV are denoted by ${\mathit{l}}_0$ and ${\mathit{l}}_f$, and the limit of the flight speed of the UAV is represented as $V_{\max }$. The maximum distance between two consecutive slots is $V_{\max }{\delta }_t$.

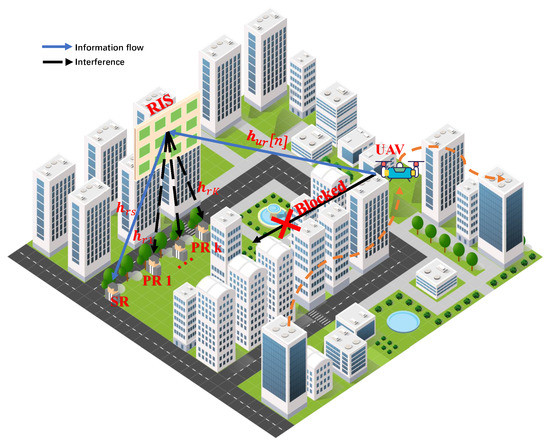
Figure 1. The RIS-enabled UAV CR scenario.

Assume that the RIS is implemented on buildings to reconstruct the cascaded A2G communication links. Furthermore, we assume that the RIS with M reflecting elements is used as one uniform linear array (ULA), which can reflect the signals adaptively from a UAV to PRs and SR. The RIS controller attunes the phase shifts of different elements accordingly, and the RIS fixed horizontal coordinates and its deployment altitude are denoted as ${\mathit{w}}_r={(x_r,y_r)}^T\in {\mathbb{R}}^{2\times 1}$ and $z_r$, respectively. The RIS phase shifts in the n-th time slot are denoted by a diagonal matrix $\mathsf{\theta }\left[n\right]=diag\{e^{j{\theta }_1\left[n\right]},e^{j{\theta }_2\left[n\right]},\dots ,e^{j{\theta }_M\left[n\right]}\}$, where ${\theta }_m\left[n\right]\in [0,2\pi )$, $m\in \mathcal{M}=\{1,\dots ,M\}$. Assume that the link between the UAV and the RIS (U-R link), the link between the RIS and the SR (R-S link), and the link between the RIS and the kth-PR (R-k link) are all LoS air-to-ground wireless channels, which follows the free-space pathloss model.

Therefore, the first hop channel power gain of the U-R link in the n-th time slot are represented by

$$\begin{array}{cc}\hfill & {\mathit{h}}_{ur}\left[n\right]=\sqrt{\beta d_{ur}^{-\alpha }\left[n\right]}\hfill \\ \hfill & \times {\left[1,e^{-j\frac{2\pi }{\lambda }\tilde{d}{\varphi }_{ur}\left[n\right]},\dots ,e^{-j\frac{2\pi }{\lambda }(M-1)\tilde{d}{\varphi }_{ur}\left[n\right]}\right]}^T,\hfill \end{array}$$

(2)

where the path loss at the reference distance $d_0=$ 1 m is denoted by $\beta$, $\alpha \ge 2$ is a path loss exponent, $d_{ur}\left[n\right]=\sqrt{{(z_r-z_u)}^2+{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2}$ is the distance between the UAV and the RIS, antenna separation and wavelength are denoted by $\tilde{d}$ and $\lambda$, respectively, ${\varphi }_{ur}\left[n\right]=\frac{x_r-x\left[n\right]}{d_{ur}\left[n\right]}$ denotes the cosine of the angle of arrival at RIS in each time slot, and its detailed description is given in Figure 2.

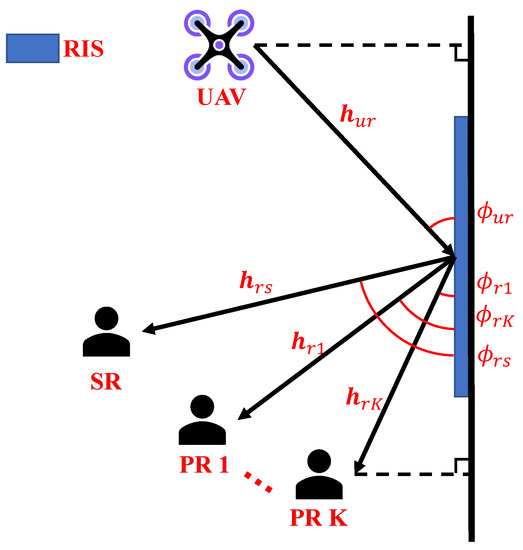
Figure 2. The geometrical diagram for a RIS-enabled UAV CR communication system.

Similarly, the second hop channel power gain of the R-S link, expressed as ${\mathit{h}}_{rs}$, can be represented by

$$\begin{array}{c}\hfill {\mathit{h}}_{rs}=\sqrt{\beta d_{rs}^{-\alpha }}{\left[1,e^{-j\frac{2\pi }{\lambda }\tilde{d}{\varphi }_{rs}},\dots ,e^{-j\frac{2\pi }{\lambda }(M-1)\tilde{d}{\varphi }_{rs}}\right]}^T,\end{array}$$

(3)

where $d_{rs}=\sqrt{{\left(z_r\right)}^2+{∥{\mathit{w}}_r-{\mathit{w}}_s∥}^2}$ is the distance between the RIS and the SR, and ${\varphi }_{rs}=\frac{x_s-x_r}{d_{rs}}$ denotes the cosine of angle of departure at RIS.

The channel power gain of the R-k link, expressed as ${\mathit{h}}_{rk}$, can be represented by

$$\begin{array}{c}\hfill {\mathit{h}}_{rk}=\sqrt{\beta d_{rk}^{-\alpha }}{\left[1,e^{-j\frac{2\pi }{\lambda }\tilde{d}{\varphi }_{rk}},\dots ,e^{-j\frac{2\pi }{\lambda }(M-1)\tilde{d}{\varphi }_{rk}}\right]}^T,\end{array}$$

(4)

where $d_{rk}=\sqrt{{\left(z_r\right)}^2+{∥{\mathit{w}}_r-{\mathit{w}}_k∥}^2}$ is the distance between RIS and the kth-PR, and ${\varphi }_{rk}=\frac{x_k-x_r}{d_{rk}}$ is the cosine of the angle of departure at RIS.

Based on the above discussion, the average achievable rate over N time slots can be written as

$$\begin{array}{c}\hfill \overline{R}=\frac{1}{N}\sum _{n=1}^N{log}_2(1+\frac{p\left[n\right]{\left|{\mathit{h}}_{rs}^H\mathsf{\theta }\left[n\right]{\mathit{h}}_{ur}\left[n\right]\right|}^2}{{\sigma }^2}),\end{array}$$

(5)

where $p\left[n\right]$ is the transmit power in the n-th time slot with a constraint $0\le p\left[n\right]\le P_{\max }$, and ${\sigma }^2$ is the noise power.

On the other hand, since the spectrum is shared amongst the SR and K PRs, we then need to derive the interference at the k-th PR caused by the UAV [3], which is known as the IT in CR networks and expressed by

$$\begin{array}{c}\hfill {IT}_k=p\left[n\right]{\left|{\mathit{h}}_{rk}^H\mathsf{\theta }\left[n\right]{\mathit{h}}_{ur}\left[n\right]\right|}^2.\end{array}$$

(6)

Based on the above analysis, we will then formulate the optimization problem and propose the corresponding algorithm to attain a numerical solution.

2.2. Problem Formulation

In this paper, our aim is to maximize the objective function $\overline{R}$ via the joint optimization of the UAV trajectory $\mathit{L}\triangleq \left\{\mathit{l}\right[n],n\in \mathcal{N}\}$, the phase shifts of the reflecting surface $\mathsf{\Theta }\triangleq \left\{\mathsf{\theta }\right[n],n\in \mathcal{N}\}$, and the power allocation $\mathit{P}\triangleq \left\{p\right[n],n\in \mathcal{N}\}$. Accordingly, the considered optimization problem can be expressed by

$$\begin{array}{cc}\hfill & \underset{\mathit{L},\mathsf{\Theta },\mathit{P}}{\max }\overline{R},\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left(1\right),\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill & 0\le {\theta }_i\left[n\right]<2\pi ,\forall n,i,\hfill \end{array}$$

(7b)

$$\begin{array}{cc}\hfill & {\mathrm{IT}}_k\le \mathsf{\Gamma },\forall k,\hfill \end{array}$$

(7c)

$$\begin{array}{cc}\hfill & 0\le p\left[n\right]\le P_{\max },\forall n,\hfill \end{array}$$

(7d)

where (1a) gives the original and final UAV location constraints, (1b) includes the maximum horizontal speed limit for UAV, (7b) denotes the phase-shift constraints, (7c) represents that the interference threshold of IT constraints is $\mathsf{\Gamma }$ for all PRs, and the transmit power constraint is denoted by (7d) with a maximum transmit power budget $P_{\max }$, respectively. Note that problem (7) is hard to solve directly because it is non-convex. As a further step in solving the proposed optimization problem, we elaborate more details to obtain a suboptimal solution in the sections followed.

3. Proposed Algorithm

In this work, we first divide the original optimization problem (7) into three sub-problems. Then, in each sub-problem, to tackle its non-convexity issue, the SCA algorithm is used to obtain a local optimal solution. Finally, we conclude that the whole algorithm can proceed in an iterative manner, where one of the variables $\{\mathit{L},\mathsf{\Theta },\mathit{P}\}$ is optimized at one iteration with the other two variables fixed.

3.1. Phase Shift Matrix Optimization

The optimization of $\mathsf{\Theta }$ with fixed $\mathit{L}$ and $\mathit{P}$ is considered in the first step. Based on (2) and (3), the formulation ${\mathit{h}}_{rs}^H\mathsf{\Theta }\left[n\right]{\mathit{h}}_{ur}\left[n\right]$ can be expressed by

$$\begin{array}{c}\hfill {\mathit{h}}_{rs}^H\mathsf{\theta }\left[n\right]{\mathit{h}}_{ur}\left[n\right]=\frac{{\displaystyle \beta \sum _{m=1}^M{e}^{j\left({\theta }_m\left[n\right]+\frac{2(m-1)\pi \tilde{d}}{\lambda }\left({\varphi }_{rs}-{\varphi }_{ur}\left[n\right]\right)\right)}}}{\sqrt{d_{rs}^{\alpha }{d}_{ur}^{\alpha }\left[n\right]}}.\end{array}$$

(8)

Recall that our aim is to maximize $\overline{R}$ with respect to the IT constraints; we only need to maximize the received signal energy. Thus, at the SR and PRs, the received signals from various paths are needed to be combined coherently.

We let ${\theta }_1\left[n\right]={\theta }_2\left[n\right]+\frac{2\pi \tilde{d}}{\lambda }\left({\varphi }_{rs}-{\varphi }_{ur}\left[n\right]\right)=\dots ={\theta }_M\left[n\right]+\frac{2\pi (M-1)\tilde{d}}{\lambda }\left({\varphi }_{rs}-{\varphi }_{ur}\left[n\right]\right)=\omega$, which can be reformulated as

$$\begin{array}{c}\hfill {\theta }_m\left[n\right]=\frac{2\pi (m-1)\tilde{d}}{\lambda }\left({\varphi }_{ur}\left[n\right]-{\varphi }_{rs}\right)+\omega ,\forall m,n,k.\end{array}$$

(9)

Substituting (9) into (8), we have

$$\begin{array}{c}\hfill {\mathit{h}}_{rs}^H\theta \left[n\right]{\mathit{h}}_{ur}\left[n\right]=\frac{\beta M{e}^{j\omega }}{\sqrt{d_{rs}^{\alpha }{d}_{ur}^{\alpha }\left[n\right]}}.\end{array}$$

(10)

Furthermore, based on (10), the achievable rate of SR at time slot n can be given by

$$\begin{array}{c}\hfill R_{us}\left[n\right]={log}_2\left(1+\frac{p\left[n\right]A}{{[{(z_r-z_u)}^2+{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2]}^{\alpha /2}}\right),\end{array}$$

(11)

where $A=\frac{{\left|\beta \right|}^2{M}^2}{d_{rs}^{\alpha }{\sigma }^2}$. Based on (9), ${\left|{\mathit{h}}_{rk}^H\mathsf{\theta }\left[n\right]{\mathit{h}}_{ur}\left[n\right]\right|}^2$ can be reformulated as

$$\begin{array}{c}\hfill {\left|{\mathit{h}}_{rk}^H\mathsf{\theta }\left[n\right]{\mathit{h}}_{ur}\left[n\right]\right|}^2=\frac{{\left|\beta \right|}^2{B}^2}{d_{rk}^{\alpha }{d}_{ur}^{\alpha }\left[n\right]},\end{array}$$

(12)

where $B={\sum }_{m=1}^M{e}^{j\left({\theta }_m\left[n\right]+\frac{2(m-1)\pi \tilde{d}}{\lambda }\left({\varphi }_{rk}-{\varphi }_{ur}\left[n\right]\right)\right)}$. To solve the sub-problem, we have the following upper bound for IT constraints, i.e.,

$$\begin{array}{c}\hfill p\left[n\right]{\left|{\mathit{h}}_{rk}^H\mathsf{\theta }\left[n\right]{\mathit{h}}_{ur}\left[n\right]\right|}^2\le \frac{p\left[n\right]C_k}{{[{(z_r-z_u)}^2+{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2]}^{\alpha /2}},\end{array}$$

(13)

where $C_k=\frac{{\left|\beta \right|}^2{M}^2}{d_{rk}^{\alpha }}$. Based on the above derivations, the sub-problem of (7) can be reformulated as

$$\begin{array}{cc}\hfill & \underset{\mathit{L},\mathit{P}}{\max }\frac{1}{N}\sum _{n=1}^N{log}_2\left(1+\frac{p\left[n\right]A}{{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}}\right),\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left(1\right),\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill & 0\le p\left[n\right]\le P_{\max },\forall n,\hfill \end{array}$$

(14b)

$$\begin{array}{cc}\hfill & \frac{p\left[n\right]C_k}{{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}}\le \mathsf{\Gamma },\forall n.\hfill \end{array}$$

(14c)

In the steps followed, we will elaborate more details to solve the above optimization problem as the following two subsections.

3.2. Power Optimization

In this subsection, we fix $\mathsf{\Theta }$ and $\mathit{L}$ to optimize $\mathit{P}$ in order to solve the subproblem. Accordingly, the optimization problem can be expressed by

$$\begin{array}{cc}\hfill & \underset{\mathit{P}}{\max }\frac{1}{N}\sum _{n=1}^N{log}_2\left(1+\frac{p\left[n\right]A}{{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}}\right),\hfill \end{array}$$

(15a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.\frac{p\left[n\right]C_k}{{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}}\le \mathsf{\Gamma },\forall n,\hfill \end{array}$$

(15b)

$$\begin{array}{cc}\hfill & 0\le p\left[n\right]\le P_{\max },\forall n.\hfill \end{array}$$

(15c)

Since each subproblem corresponds to a time slot $n\in N$, in order to facilitate the calculation, problem (15) consists of N subproblems, for which $1/N$ is ignored, or

$$\begin{array}{cc}\hfill & \underset{p\left[n\right]\ge 0}{\max }{log}_2\left(1+\frac{p\left[n\right]A}{{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}}\right),\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.p\left[n\right]\le min\left(P_{\max },\underset{k\in \mathcal{K}}{min}\frac{\mathsf{\Gamma }}{C_k}{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}\right).\hfill \end{array}$$

(16b)

When the constraint (16b) is tight, the optimality of problem (16) can be attained with the method given in [3]. Due to the page limit, the readers may refer to [3] for more details, and the related proof is omitted here. Therefore, we have the optimal solution to (16), which is a closed-form solution given as

$$\begin{array}{c}\hfill p{\left[n\right]}^{\ast }=min\left(P_{\max },\underset{k\in \mathcal{K}}{min}\frac{\mathsf{\Gamma }}{C_k}{[{(z_r-z_u)}^2+{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2]}^{\alpha /2}\right).\end{array}$$

(17)

In this part, we obtain the closed-form solution for the transmitted power, which we can then substitute into problem (7) to optimize the trajectory of the UAV.

3.3. Trajectory Optimization

In this subsection, let us consider the optimization subproblem of $\mathit{L}$, with the fixed $\mathsf{\Theta }$ and $\mathit{P}$. For given $\mathit{P}$ and $\mathsf{\Theta }$, we substitute (17) into (7), and then (7) can be transformed to

$$\begin{array}{cc}\hfill & \underset{\mathit{L}}{\max }\frac{1}{N}\sum _{n=1}^N\widehat{R}\left(\mathit{l}\left[n\right]\right),\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left(1\right),\hfill \end{array}$$

(18a)

$$\begin{array}{cc}\hfill & \frac{p\left[n\right]C_k}{{[{(z_r-z_u)}^2+{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2]}^{\alpha /2}}\le \mathsf{\Gamma },\forall n,k,\hfill \end{array}$$

(18b)

where we have

$$\begin{array}{cc}\hfill & \widehat{R}\left(\mathit{l}\left[n\right]\right)={log}_2(1+\hfill \\ \hfill & \frac{Amin\left(P_{\max },{min}_{k\in \mathcal{K}}\frac{\mathsf{\Gamma }}{C_k}{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}\right)}{{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}}).\hfill \end{array}$$

(19)

To tackle problem (18), we first introduce two sets of auxiliary variables, i.e., $\mathsf{\mu }={\left\{\mu \left[n\right]\right\}}_{n=1}^N$ and $\mathsf{\nu }={\left\{\nu \left[n\right]\right\}}_{n=1}^N$ to rewrite $\tilde{R}\left[n\right]={log}_2\left(1+A\mu \left[n\right]/\nu \left[n\right]\right)$. Accordingly, the problem (18) can be reformulated into

$$\begin{array}{cc}\hfill & \underset{\mathit{L},\mu ,\nu }{\max }\frac{1}{N}\sum _1^N\tilde{R}\left[n\right],\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left(1\right),\hfill \end{array}$$

(20a)

$$\begin{array}{cc}\hfill & 0\le \mu \left[n\right]\le P_{\max },\forall n,\hfill \end{array}$$

(20b)

$$\begin{array}{cc}\hfill & {[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}\le \nu \left[n\right],\forall n,\hfill \end{array}$$

(20c)

$$\begin{array}{cc}\hfill & \mu \left[n\right]\le \frac{\mathsf{\Gamma }}{C_k}{[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2},\forall n.\hfill \end{array}$$

(20d)

We can obtain a larger target value by reducing $\nu \left[n\right]$ without violation of the constraints, and thus we are confirmed that the constraint (20c) holds at the optimal point. Notice that (20) is a non-convex programming problem, as (20a) is non-concave and the constraint (20d) is non-convex. Then, by introducing the slack variables, the form of (20a) can be rewritten as

$$\begin{array}{c}\hfill \tilde{R}\left[n\right]={log}_2\left(\nu \left[n\right]+A\mu \left[n\right]\right)-{log}_2\left(\nu \left[n\right]\right).\end{array}$$

(21)

We can observe that (21) is a non-convex expression. When a function is convex, then its first-order Taylor expansion corresponds to the lower bound of the function [29]. Because $-{log}_2\left(\nu \left[n\right]\right)$ is convex with respect to $\left\{\nu \left[n\right]\right\}$, for any given local point $\left\{{\nu }^{\left(j\right)}\left[n\right]\right\}$, at the j-th iteration, it follows that $\tilde{R}\left[n\right]\ge {\tilde{R}}^{\mathrm{lb}}\left[n\right]$, where

$$\begin{array}{cc}\hfill {\tilde{R}}^{\mathrm{lb}}\left[n\right]& \triangleq {log}_2(\nu \left[n\right]+A\mu \left[n\right])-{log}_2\left({\nu }^{\left(j\right)}\left[n\right]\right)\hfill \\ \hfill & -\frac{\left(\nu \left[n\right]-{\nu }^{\left(j\right)}\left[n\right]\right){log}_2\left(e\right)}{{\nu }^{\left(j\right)}\left[n\right]}.\hfill \end{array}$$

(22)

For non-convex constraints (20d), note that ${[{(z_r-z_u)}^2+{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2]}^{\alpha /2}$ is convex with respect to $\mathit{l}\left[n\right]$. Using a first-order Taylor expansion at the given point ${\mathit{l}}^{\left(j\right)}\left[n\right]$, we can obtain the following inequality:

$$\begin{array}{cc}\hfill & {[{(z_r-z_u)}^2+{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2]}^{\alpha /2}\hfill \\ \hfill & \ge [{(z_r-z_u)}^2+\parallel {\mathit{l}}^{\left(j\right)}\left[n\right]-{\mathit{w}}_r{{\parallel }^2]}^{\alpha /2}\hfill \\ \hfill & +\alpha [{(z_r-z_u)}^2+\parallel {\mathit{l}}^{\left(j\right)}\left[n\right]-{\mathit{w}}_r{{\parallel }^2]}^{\frac{\alpha }{2}-1}\hfill \\ \hfill & \times {\left({\mathit{l}}^{\left(j\right)}\left[n\right]-{\mathit{w}}_r\right)}^T\left(\mathit{l}\left[n\right]-{\mathit{l}}^{\left(j\right)}\left[n\right]\right).\hfill \end{array}$$

(23)

The following slack constraints can be obtained by applying a similar derivation to the right-hand side of the inequality in (20d), i.e.,

$$\begin{array}{cc}\hfill \mu \left[n\right]& \le \frac{\mathsf{\Gamma }}{C_k}\left(\right[{(z_r-z_u)}^2+\parallel {\mathit{l}}^{\left(j\right)}\left[n\right]-{\mathit{w}}_r{{\parallel }^2]}^{\alpha /2}\hfill \\ \hfill & +\alpha [{(z_r-z_u)}^2+\parallel {\mathit{l}}^{\left(j\right)}\left[n\right]-{\mathit{w}}_r{{\parallel }^2]}^{\frac{\alpha }{2}-1}\hfill \\ \hfill & \times {\left({\mathit{l}}^{\left(j\right)}\left[n\right]-{\mathit{w}}_r\right)}^T\left(\mathit{l}\left[n\right]-{\mathit{l}}^{\left(j\right)}\left[n\right]\right))\triangleq S\left[n\right].\hfill \end{array}$$

(24)

Through the preceding analysis and derivations, the optimization problem is rewritten as

$$\begin{array}{cc}\hfill & \underset{\left\{\mathit{L},\mu ,\nu \right\}}{\max }\frac{1}{N}\sum _{n=1}^N{\tilde{R}}^{\mathrm{lb}}\left[n\right],\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left(1\right),\hfill \end{array}$$

(25a)

$$\begin{array}{cc}\hfill & 0\le \mu \left[n\right]\le P_{\max },\forall n,\hfill \end{array}$$

(25b)

$$\begin{array}{cc}\hfill & \mu \left[n\right]\le \frac{\mathsf{\Gamma }}{C_k}S\left[n\right],\forall n,k,\hfill \end{array}$$

(25c)

$$\begin{array}{cc}\hfill & {[{∥\mathit{l}\left[n\right]-{\mathit{w}}_r∥}^2+{(z_r-z_u)}^2]}^{\alpha /2}\le \nu \left[n\right],\forall n.\hfill \end{array}$$

(25d)

We find that the optimization problem (25) is convex. Thus, with the help of MATLAB toolbox, such as CVX, the pertinent problem can be solved effectively. In the $(j-1)$-th iteration, using the optimal solution $\{{\mathit{L}}^{(j-1)},{\mathsf{\mu }}^{(j-1)},{\mathsf{\nu }}^{(j-1)}\}$ obtained by solving problem (25), similarly in the j-th iteration, we can obtain the optimal solution of (25) at the local point $\{{\mathit{L}}^{(j-1)},{\mathsf{\mu }}^{(j-1)},{\mathsf{\nu }}^{(j-1)}\}$.

3.4. Overall Algorithm

To summarize the above optimization, in order to make problem (7) solvable, we used the BCD method to decompose the original problem (7) into three sub-problems. The proposed algorithm to solve problem (7) is shown in Algorithm 1. The solution obtained by (25) is expressed as ${\mathit{L}}^{\ast }={\left\{{\mathit{l}}^{\ast }\left[n\right]\right\}}_{n=1}^N$. Substituting ${\mathit{L}}^{\ast }$ into (17), we can obtain ${\mathit{P}}^{\ast }$. Similarly, we can obtain ${\mathsf{\Theta }}^{\ast }$ by substituting ${\mathit{L}}^{\ast }$ into (9). Combining $\left\{{\mathit{L}}^{\ast },{\mathit{P}}^{\ast },{\mathsf{\Theta }}^{\ast }\right\}$, we can obtain the solution to (7) finally. According to the results presented in [30], it is guaranteed that the average achievable rate will not decrease after a certain number of iterations.

Algorithm 1 The proposed algorithm for solving problem (7).

1: Initialization: Set the iteration number $j=0$, and the initial variables ${\mathit{L}}^{\left(0\right)},{\mathsf{\mu }}^{\left(0\right)},{\mathsf{\nu }}^{\left(0\right)},{\mathit{P}}^{\left(0\right)},{\mathsf{\Theta }}^{\left(0\right)}.$ 2: Repate: 3: Update $\{{\mathit{L}}^{\left(j\right)\ast },{\mathsf{\mu }}^{\left(j\right)\ast },{\mathsf{\nu }}^{\left(j\right)\ast }\}$ by sloving problem (25). 4: With given ${\mathit{L}}^{\left(j\right)\ast }$, update ${\mathsf{\Theta }}^{\left(j\right)\ast }$ by using (9). 5: With given ${\mathit{L}}^{\left(j\right)\ast }$, update ${\mathit{P}}^{\left(j\right)\ast }$ by using (17). 6: Update the variables as ${\mathit{L}}^{(j+1)}={\mathit{L}}^{\left(j\right)\ast }$, ${\mathsf{\mu }}^{(j+1)}=$ ${\mathsf{\mu }}^{\left(j\right)\ast }$, ${\mathsf{\nu }}^{(j+1)}={\mathsf{\nu }}^{\left(j\right)\ast }$ and ${\mathit{P}}^{(j+1)}={\mathit{P}}^{\left(j\right)\ast }$, ${\mathsf{\Theta }}^{(j+1)}={\mathsf{\Theta }}^{\left(j\right)\ast }$. 7: Update $j=j+1.$ 8: Until: The objective value of (25) will tend to converge after a certain number of iterations or with a given precision.

4. Numerical Results

In this section, we evaluate the performance of the proposed method to optimize the RIS phase shifts, the transmit power and the UAV trajectory by showing the obtained numerical results. We assume that the antenna separation is $\tilde{d}=\lambda /2$, and the rest of the parameters are set in Table 2. The fixed trajectory scheme serves as a benchmark that the UAV flies from its given original position to its final position at a fixed speed, i.e., $v=\frac{\parallel {\mathit{l}}_f-{\mathit{l}}_0\parallel }{T}$. Before performing the performance comparison, we first would like to show the convergence properties of Algorithm 1 from Figure 3. We can intuitively observe that the proposed BCD-based algorithm can converge within a finite iteration number.

Table 2. The major system parameters used in the paper.

Parameter	Value	Meaning
${\mathit{l}}_0$	$[-300,120]$ m	Initial horizontal positions
${\mathit{l}}_f$	$[300,120]$ m	Final horizontal positions
${\mathit{w}}_r$	$[0,0]$ m	The horizontal locations of the RIS
$z_r$	20 m	The height of the RIS
$z_u$	100 m	The height of UAV
${\mathit{w}}_s$	$[0,50]$ m	The horizontal locations of the SR
$V_{\max }$	10 m/s	The maximum speed of the UAV
${\delta }_t$	1 s	The time slot length
M	60	The number of reflecting elements
K	4	The number of ground PRs
${\sigma }^2$	$-110$ dBm	The power of AWGN
$P_{\max }$	500 mw	Max transmit power of UAV
$\alpha$	2	The pathloss exponent
$\beta$	$-20$ dB	The reference channel gain
$ϵ$	${10}^{-5}$	The accuracy for the iterations

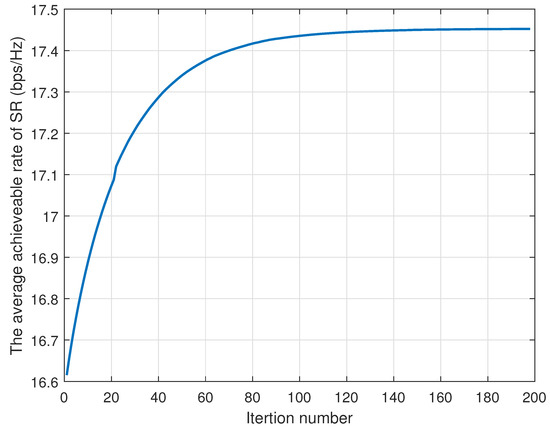
Figure 3. The convergence behavior of the proposed Algorithm 1.

Figure 4 illustrates the difference between the proposed algorithm and the benchmark algorithm from the perspective of flight trajectory. It can be seen that when the IT constraint $\mathsf{\Gamma }$ is easy to satisfy, the UAV can fly directly to RIS and transmit with its maximum power. If $\mathsf{\Gamma }$ decreases in the case of $\mathsf{\Gamma }=-60$ dBm, it can be seen that the UAV trajectory deviates from the $\mathsf{\Gamma }=-65$ dBm case. In particular, the UAV moves away from RIS at t = 28 s. When $\mathsf{\Gamma }=-65$ dBm, UAV moves away from RIS earlier at t = 15 s. Since $\mathsf{\Gamma }$ is relatively small, the IT constraints of the PR are too strict, and therefore, the UAV must stay away from RIS to satisfy more strict IT constraints.

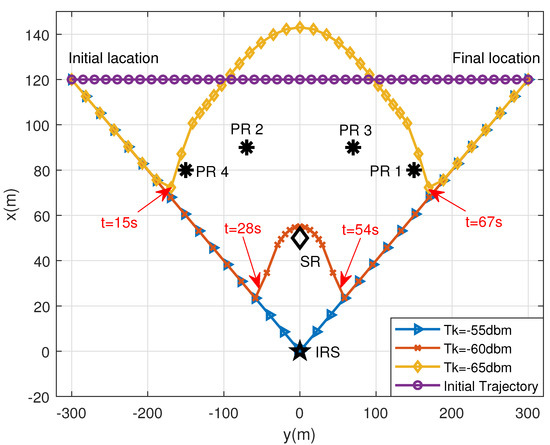
Figure 4. The UAV trajectory with different IT thresholds.

Figure 5 shows the transmit power over time with different parameter setups. When IT threshold $\mathsf{\Gamma }$ is large enough (e.g., $\mathsf{\Gamma }=-55$ dBm), the UAV always transmits with its full power $P_{\max }$. However, when $\mathsf{\Gamma }$ decreases to a value such as $\mathsf{\Gamma }=-60$ dBm, the UAV reduces its transmit power at $t=28$ s to satisfy the restrict IT constraint. After $t=54$ s, the UAV is far away from the RIS, and the transmit power of the UAV attains its maximum budget. When IT threshold $\mathsf{\Gamma }$ is small enough (e.g., $\mathsf{\Gamma }=-55$ dBm), the UAV transmit power decreases earlier and returns to its maximum level later (as shown in the time instants $t=15$ s and $t=67$ s, respectively).

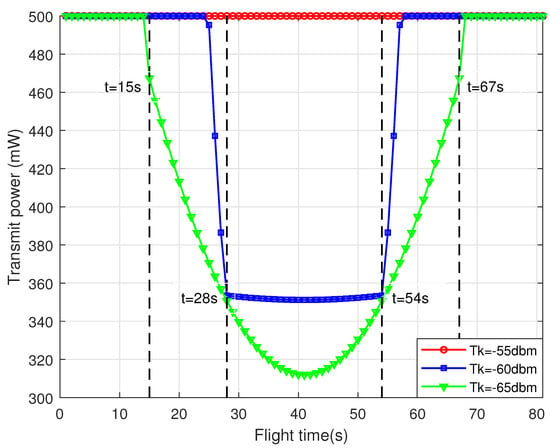
Figure 5. The transmit power versus time slots.

Let us take a look at Figure 4 and Figure 5 firstly. As discussed earlier, if the maximum IT threshold is set large enough (e.g., $\mathsf{\Gamma }\ge -55$ dBm), the IT constraint tends to be satisfied naturally, leading to full power transmission at the UAV. Therefore, the UAV can fly to RIS with its maximum speed and hover on the top of the RIS for a while to achieve a maximum achievable rate for the PR. However, when the IT constraint is set too strictly (e.g., $\mathsf{\Gamma }\ge -60$ dBm), the situation becomes a little bit different. For example, when $T=28$ s, the UAV begins to leave far away from the RIS to meet the strict IT constraint with its reduced transmit power. As the UAV is getting closer to the PR after $T=54$ s, in order to meet the IT constraints, the UAV may approach the RIS slowly to reduce its transmitting power. Finally, when the UAV is in a position that is the closest to RIS, it will hover near the RIS for a while. During this hovering period, the transmit power holds at the maximum level to attain the maximum achievable rate for the SR.

For a different IT threshold $\mathsf{\Gamma }$, the average achievable rate of the SR is shown in Figure 6. As shown, the proposed design outperforms the benchmark schemes when $\mathsf{\Gamma }$ becomes a bit larger (for example $\mathsf{\Gamma }\ge -65$ dBm). In particular, when $\mathsf{\Gamma }$ becomes large enough, the IT constraint can be satisfied easily, and the transmission power can reach $P_{\max }$ in all time slots. Therefore, the SR average achievable rate can also reach its upper bound to obtain the maximum rate. It is worth noting that the benchmark scheme, namely, the fixed trajectory, serves as a lower bound if compared to the proposed trajectory design, which demonstrates the performance gains attained by the optimal UAV trajectory design. With the introduced UAV trajectory design, we can see that the UAV can transmit signals at its maximum power, even with relatively tight IT constraints (e.g., $\mathsf{\Gamma }=-60$ dBm). As the flight duration T increases (e.g., $M=60$, $T=120$ s, and $T=81$ s), the UAV will stay in a position as long as possible, and thus the proposed design will help increase the average achievable rate. Similarly, when the number of RIS elements is larger (e.g., $T=120$, $M=60$, and $M=70$), the SR average achievable rate goes higher as well. Based on the above discussions, we can conclude that both the number of reflecting elements and the UAV trajectory can achieve a higher performance gain with the proposed optimization joint design method. To address the issues on the number the reflecting elements, we will elaborate more details in the next paragraph.

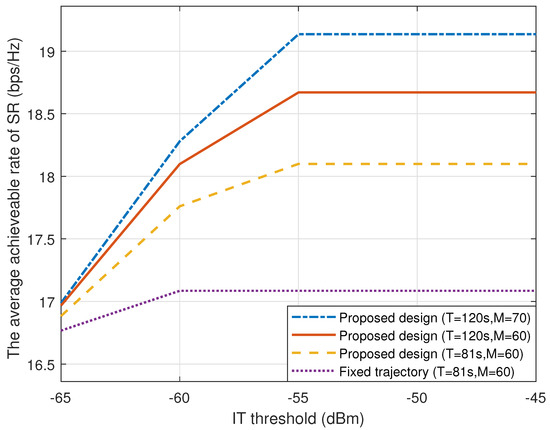
Figure 6. The average achievable rate versus different IT thresholds.

With a different number of the reflecting elements M, the average achievable rate of the SR is shown in Figure 7. It can be seen that with the increase in M, the average achievable rate of SR increases as well, and the proposed scheme also shows another significant improvement as compared to the benchmark scheme. When M is small enough (e.g., M = 40), the proposed scheme outperforms several benchmark schemes. We can see that when $\mathsf{\Gamma }=-55$ dBm and $\mathsf{\Gamma }=-60$ dBm, the performance is similar since the constraints can be satisfied naturally. With an increasing number of the reflecting elements M, although the constraints become more and more restricted, a large performance gain attained by the RIS might cover the IT threshold $\mathsf{\Gamma }$, leading to a higher achievable rate of the SR. Notably, when M is large enough (e.g., M = 100), the rate of the benchmark scheme at $\mathsf{\Gamma }=-55$ dBm is higher than that of the proposed scheme at $\mathsf{\Gamma }=-60$ dBm. This is because when M is relatively large, the IT constraints become more strict and more sensitive to $\mathsf{\Gamma }$.

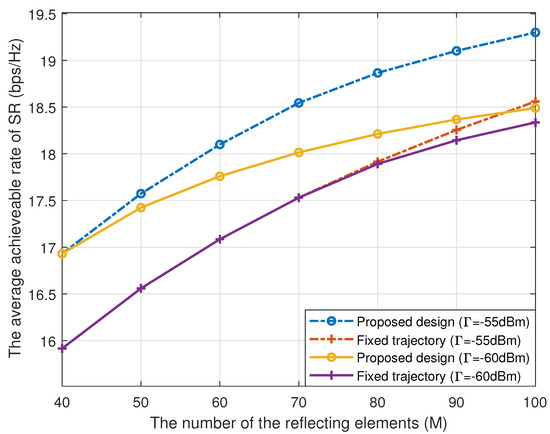
Figure 7. The average achievable rate versus the number of the reflecting elements.

5. Conclusions

In this paper, we investigated several important issues of RIS-enabled UAV CR networks, which is important for wireless communications when A2G LoS links are blocked. The aim of this work is to maximize the achievable average rate of SR, for which we proposed an optimization method to jointly design the RIS phase shifts, the transmission power, and the UAV trajectory. Unfortunately, the proposed optimization problem is non-convex. We introduced an iterative algorithm to solve this optimization problem with the help of the BCD and SCA algorithms. The simulation results were provided to testify that the proposed algorithm is effective to improve the transmission rate of a RIS enabled UAV CR network, if compared to several benchmark schemes. In our future work, our solution of the problem and the performance of the system can be extended into some other scenarios. For example, during the entire flight period, the UAV may establish a direct link with the ground user or there may exist a direct link between the UAV and the ground user. What is more, the main results of this paper can serve as a valuable reference for our future research points.