Simple Closed Quasigeodesics on Tetrahedra

Abstract

Pogorelov proved in 1949 that every convex polyhedron has at least three simple closed quasigeodesics. Whereas a geodesic has exactly a $\pi$ surface angle to either side at each point, a quasigeodesic has at most a $\pi$ surface angle to either side at each point. Pogorelov’s existence proof did not suggest a way to identify the three quasigeodesics, and it is only recently that a finite algorithm has been proposed. Here we identify three simple closed quasigeodesics on any tetrahedron: at least one through one vertex, at least one through two vertices, and at least one through three vertices. The only exception is that isosceles tetrahedra have simple closed geodesics but do not have a 1-vertex quasigeodesic. We also identify an infinite class of tetrahedra that each have at least 34 simple closed quasigeodesics.

1. Introduction

It is well-known that every convex polyhedron has at least three simple closed quasigeodesics [1], a counterpart to the Lusternik–Schnirelmann theorem that every smooth closed convex surface has at least three simple closed geodesics. Whereas a geodesic on a convex polyhedron has exactly $\pi$ surface angle to either side at each point, a quasigeodesic has at most $\pi$ surface angle to either side of any point. Unlike geodesics, quasigeodesics can pass through vertices.

As Pogorelov’s result does not lead directly to an algorithm, it was posed as an open problem to find a polynomial-time algorithm to construct at least one simple closed quasigeodesic: Open Prob. 24.2 [2]. Even a finite algorithm was not known. Recently there has been progress on this question [3], and an exponential-time algorithm has been developed [4].

In this paper, we describe the three quasigeodesics guaranteed by Pogorelov, in the particular case of tetrahedra.

In reference [5], we conjectured that every convex polyhedron has either a simple closed geodesic, or a simple closed quasigeodesic through exactly one vertex. We proved this conjecture for doubly-covered convex polygons [5], Chapter 17. Here we prove it for all tetrahedra.

Theorem 1.

Every tetrahedron has a 2-vertex quasigeodesic, a 3-vertex quasigeodesic, and a simple closed geodesic or a 1-vertex simple closed quasigeodesic.

Our result complements in some sense earlier work that determined closed geodesics on simplices [6,7].

Many ellipsoids admit only three simple closed geodesics. (However, not all ellipsoids: If sufficiently oblate, there are other simple closed geodesics [8].) Our second result establishes that many tetrahedra have an unexpected wealth of simple closed quasigeodesics.

Theorem 2.

There exists an open set $\mathcal{O}$ in the space of all tetrahedra, each element of which has at least 34 simple closed quasigeodesics.

All our proofs are constructive and lead to algorithms and constant-time in an appropriate model of computation. See [3] for a discussion of models of computation for quasigeodesics.

Alongside the above results, we also obtain a characterization of isosceles tetrahedra, defined in Section 2. It complements results in [9,10]. A geodesic loop is a simple closed curve that is a geodesic everywhere except at one point, the loop point.

Theorem 3.

A tetrahedron is isosceles if and only if it admits no geodesic loop at a vertex.

After presenting our proofs, we conclude the paper with a short section of remarks and open questions.

Notation

Here we list basic notation that we use throughout. More specialized notation and preliminaries will be introduced where needed.

• Vertices of tetrahedron T: $a,b,c,d$;
• Face A is opposite a; So: $A=bdc$, $B=cda$, $C=adb$, $D=abc$;
• Face angles are specified by vertex and face. So the three face angles incident to vertex a are: $aB,aC,aD$; etc. See Figure 1;
  

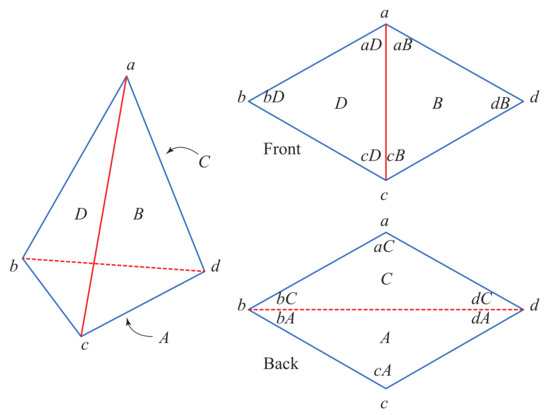  Figure 1. $A=bdc$, $B=cda$, $C=adb$, $D=abc$.
• Complete angle at a: ${\theta }_a=aB+aC+aD$;
• Vertex curvature at a: ${\omega }_a=2\pi -(aB+aC+aD)$.

For succinctness, we will often use the symbol $Q_k$ as shorthand for a “k-vertex simple closed quasigeodesic”.

2. ${\mathit{Q}}_{\mathbf{0}}$: Simple Closed Geodesics

We use the Gauss–Bonnet theorem in two forms:

1.

The total curvature at the four vertices sums to $4\pi$;

2.

The turn $\tau$ of a closed curve plus the curvature enclosed equals $2\pi$: $\tau +\omega =2\pi$.

By the first form of Gauss–Bonnet, a simple closed geodesic $Q_0$ splits the vertex set of a convex polyhedron into two subsets, the total curvature of each being $2\pi$. Alexandrov [11] (pp. 377–378) observed that such a condition is uncommon among all convex polyhedra. This fact was further refined by Gruber [12] (as a preliminary step of his general result proof) and by Gal’perin [13] (for polyhedra homeomorphic to the sphere). This led to a proof that, for a fixed number of vertices, the set of convex polyhedra having a simple closed geodesic is closed and has measure zero in the space of all convex polyhedra.

Particularizing to our framework, there is a special class of tetrahedra which do have many simple closed geodesics. An isosceles tetrahedron (also called an isotetrahedron, a tetramonohedron, or an isohedral tetrahedron) is a tetrahedron whose four vertices each have curvature $\pi$, or, equivalently, all four faces are congruent acute triangles.

It is a beautiful result that isosceles tetrahedra are the only convex surfaces that have arbitrarily long simple closed geodesics [6,14]. Consequently, they have infinitely many such geodesics. This wealth of $Q_0$s is balanced in some sense by the non-existence of $Q_1$s.

Lemma 1.

No isosceles tetrahedron has a 1-vertex quasigeodesic.

This lemma complements the remark in [9] and was reproved in [15], that a regular tetrahedron has no geodesic loop. See also [10] for a characterization of isosceles tetrahedra as the only tetrahedra having three distinct minimal loops through any point on the face.

Proof. 

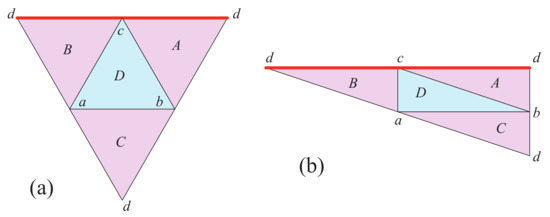
Refer to Figure 2. Here we use the second form of Gauss–Bonnet. Let Q be a 1-vertex quasigeodesic through vertex d, with a and b strictly to Q’s left, and c strictly to Q’s right. Since ${\omega }_a+{\omega }_b=2\pi$, Q must have no turn, $\tau =0$, to its left at d, and turn $\tau =\pi$ to its right at d. Having no turn to its left means the total angle of $\pi$ is to the left of Q at d. Turning $\pi$ to the right means that Q turns around completely, folding back on itself, which then forces Q to contain vertex c. Thus, c does not lie strictly to Q’s right: Q is a 2-vertex quasigeodesic, not a 1-vertex quasigeodesic.    □

Figure 2. (a,b) Unfoldings of two isosceles tetrahedra. Quasigeodesic Q (red) is a degenerate doubling of edge $dc$.

With a different argument, briefly presented next, one can prove a stronger result. No isosceles tetrahedron has a geodesic loop at a vertex.

To see this, assume the isosceles tetrahedron T admits a geodesic loop $\Lambda$ at its vertex a. Star-unfold T with respect to a, resulting in an acute triangle $\overline{T}$. The star-unfolding is discussed in Section 4.2. It cuts the three edges incident to a. Tile the plane with $\overline{T}$. In that tiling, $\Lambda$ corresponds to a segment $\tilde{\Lambda }$ joining two images of a, say $a_j$ and $a_k$. However, $a_j$ and $a_k$ are determining either a side or a diagonal apexed at images of a. In both cases, $\tilde{\Lambda }$ would contain the image of another vertex of T, showing that $\Lambda$ necessarily passes through the respective vertex.

3. ${\mathit{Q}}_{\mathbf{1}}$: 1-Vertex Quasigeodesics

We have just seen in Section 2 that isosceles tetrahedra have no 1-vertex quasigeodesic, but do have simple closed geodesics. The goal of this section is to prove this theorem:

Theorem 4.

Every non-isosceles tetrahedron has at least one 1-vertex simple closed quasigeodesic.

Notice that Theorem 3 follows immediately from the above result and the remark ending the previous section.

In the remainder of this section, we assume all tetrahedra are not isosceles.

• Properties of $Q_1$.

A quasigeodesic $Q_1$ through exactly one vertex v on a tetrahedron T must satisfy these conditions.

(1)

Q must form a geodesic loop with loop point v.

(2)

To satisfy the Gauss–Bonnet theorem, Q must partition the other three vertices two to one side and one to the other, such that the total curvatures to each side of Q are at most $2\pi$ (and not both sides equal to $2\pi$, for then there is no curvature at v and it is not a vertex).

Of course the quasigeodesic angle criterion must be satisfied at v.

• Sketch of Proof for Theorem 4.

The proof follows a case analysis based first on how many curvatures are greater than $\pi$, and second on the distances from low-curvature vertices to high-curvature vertices. The curvatures greater than $\pi$ lead to convex vertices in unfoldings, and which vertices are closest to these high-curvature vertices permits concluding that particular geodesic loops are inside certain disks and so live on T. Then the angles to either side at the geodesic loop vertex must be verified to be at most $\pi$ to conclude it is a quasigeodesic.

3.1. Case 1

For Case 1, assume exactly one vertex has curvature exceeding $\pi$: ${\omega }_a>\pi$. Let d be the closest vertex to a among $b,c,d$. Then star-unfold T with respect to d, as illustrated in Figure 3: Faces $C,D,B$ are incident to a, and face A is attached to face D along edge $bc$. Label the three images of d as $d_1,d_2,d_3$ as illustrated.

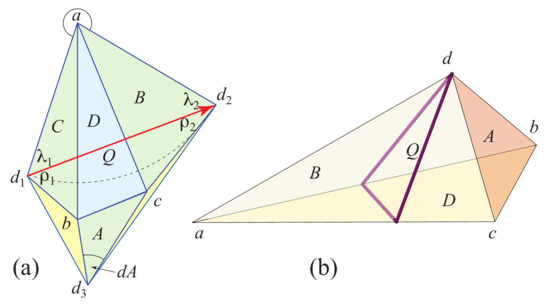
Figure 3. Case 1. (a) Unfolding of a tetrahedron when ${\omega }_a>\pi$ and the other three curvatures are <$\pi$. d is closest to a. Curvatures at $a,b,c,d$ are ${282}^{\circ },{140}^{\circ },{173}^{\circ },{124}^{\circ }$. Auxiliary yellow triangles added. (b) The quasigeodesic in 3D.

We claim that $Q=d_1{d}_2$ (red in the figure) is a simple closed quasigeodesic containing just the vertex d. It will help to view Q as directed from $d_1$ to $d_2$. Note that, because ${\omega }_a>\pi$, ${\theta }_a<\pi$.

First note that, because $\left|ad\right|$ is shorter than or equal to $\left|ab\right|$ and $\left|ac\right|$, Q separates $b,c$ from a: Q is a chord of a circle of radius $\left|ad\right|$ centered on a, and b and c lie on or outside that circle.

Next, Q is a straight segment between two images of vertex d in this unfolding, and so a geodesic loop on T includes d. It remains to show that the angle to either side of Q at d is ≤$\pi$.

Let ${\alpha }_1$ and ${\alpha }_2$ be the angles of $▵d_1{d}_{2}a$ above Q, as illustrated in the figures. Then it is immediate that ${\alpha }_1+{\alpha }_2<\pi$.

Let ${\beta }_1$ and ${\beta }_2$ be the angles $\angle d_2{d}_{1}b$ and $\angle d_1{d}_{2}c$ below Q, as illustrated. The angle of Q to the right side of d we seek to bound is ${\beta }_1+{\beta }_2+dA$. The reason angle $dA$ is to the right of Q is: (a) $dA$ is incident to vertex d, and (b) face $▵bc{d}_3$ is right of $d_1{d}_2$.

Now note that the external angles at b and c in the unfolding are ${\omega }_b$ and ${\omega }_c$ respectively. Because ${\omega }_b,{\omega }_c<\pi$, the triangle $▵d_1{d}_2{d}_3$ includes face A and so includes b and c. Therefore, ${\beta }_1+{\beta }_2+dA$ must be smaller than $\pi$ because those three angles are each smaller than the corresponding angles of $▵d_1{d}_2{d}_3$.

Therefore, we have proved that the angle to the right of Q at a is less than $\pi$, and so Q is a simple closed quasigeodesic as claimed.

3.2. Case 2

For Case 2, assume T has at least two vertices with curvatures more than $\pi$: ${\omega }_a\ge {\omega }_b\ge \pi$.

The reader may find it easier to follow the proof on the particular case of T, a doubly covered quadrilateral. The next argument, however, is valid for the general situation.

We will consider geodesic loops $Q_v$ at vertex v, with $v\in \{a,b,c,d\}$ suitably chosen, as constructed in Case 1.

Consider a closest vertex v to a among $b,c,d$.

• Case 2.1:

$v=b$: $\left|ab\right|\le \left|ac\right|,\left|ad\right|$: b is closest to a. Then there exists a geodesic loop $Q_b$ at b which separates a from $c,d$. We now justify this claim. As illustrated in Figure 4, the segment $Q_b=b_1{b}_2$ cannot be blocked by vertex a because ${\theta }_a\le \pi$, and cannot be blocked by vertices c or d, because they fall outside the circle centered at a of radius $\left|ab\right|$.

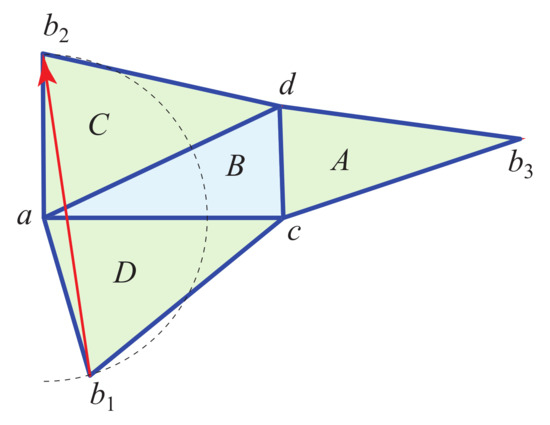
Figure 4. Case 2.1: b is closest to a. Curvatures at $a,b,c,d$ are ${196}^{\circ },{190}^{\circ },{159}^{\circ },{175}^{\circ }$.

An equivalent but different way to view this is as follows. View a as the apex of T, and remove the base $bcd$. Extend the faces $B,C,D$ incident to a to a cone $\mathcal{C}$. Then on $\mathcal{C}$ there are geodesic loops based on each of $b,c,d$. Because b is closest to a, the loop $Q_b$ lives on T.

Because ${\omega }_b\ge \pi$, the complete angle ${\theta }_b$ at b is at most $\pi$, hence $Q_b$ has less than $\pi$ to each side, and so is a simple closed quasigeodesic. This happens irrespective of ${\omega }_c,{\omega }_d$ being larger or smaller than $\pi$.

• Case 2.2:

$v=c$; i.e., c (or equivalently d) is closest to a: $\left|ac\right|\le \left|ab\right|,\left|ad\right|$.

Consider now a closest vertex w to b among $a,c,d$.

• Case 2.2.1:

This is handled by Case 2.1 with the roles of a and b reversed.

• Case 2.2.2:

$\left|bd\right|\le \left|ba\right|,\left|bc\right|$. $\left|ac\right|\le \left|ab\right|,\left|ad\right|$: c is closest to a and d is closest to b.

As illustrated in Figure 5a,b, the geodesic loop $Q_c$ at c separates a from $b,d$ because c is closest to a and so $b,d$ cannot interfere, and the geodesic loop $Q_d$ at d separates b from $a,c$, because d is closest to b and so $a,c$ cannot interfere.

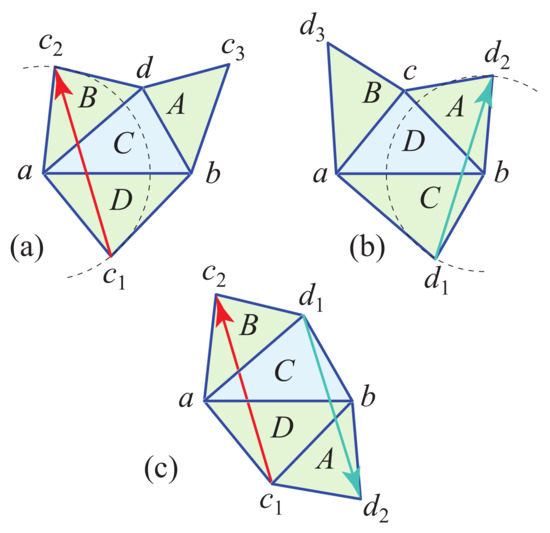
Figure 5. Case 2.2.2: c is closest to a and d is closest to b. (a) $Q_c$ red. (b) $Q_d$ green. Curvatures at $a,b,c,d$ are ${226}^{\circ },{205}^{\circ },{138}^{\circ },{151}^{\circ }$. (c) The two segments $c_1{c}_2$ and $d_1{d}_2$ are slightly non-parallel.

Now we argue that one or the other of $Q_c,Q_d$ is a quasigeodesic. Note first that, because ${\omega }_a,{\omega }_b\ge \pi$, the angle at c toward a (left in the figure), and the angle at d toward b (right in the figure), are $<\pi$ in $▵a{c}_1{c}_2$ and $▵b{d}_1{d}_2$ respectively. Next we examine the angles to the other side of $Q_c,Q_d$.

With $a,b$ separated by $Q_c$ and $Q_d$, those two geodesic loops bound a vertex-free region R on the surface of T, homeomorphic to a cylinder. As Figure 5c illustrates, cut R is isometric to a planar quadrilateral $c_1{c}_2{d}_1{d}_2$. Because the quadrilateral angles sum to $2\pi$, it cannot be that the two angles at c and the two angles at d both exceed $\pi$. At least one must be $\le \pi$. The respective geodesic loop is therefore a quasigeodesic. Figure 6 shows the two geodesic loops in 3D.

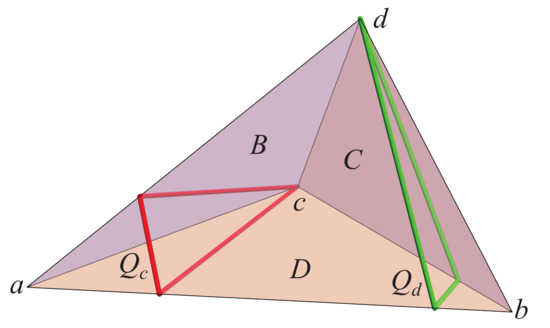
Figure 6. Case 2.2.2: $Q_c$ and $Q_d$ on the 3D tetrahedron unfolded in Figure 5. $Q_c$ is a quasigeodesic.

• Case 2.2.3:

$w=c$; i.e., c is closer than d to both a and b: $\left|bc\right|\le \left|ba\right|,\left|bd\right|$. $\left|ac\right|\le \left|ab\right|,\left|ad\right|$.

As illustrated in Figure 7a, just as in Case 1, because c is closest to both a and b, there exist geodesic loops $Q_c,Q_c^{\prime }$ at c such that $Q_c$ separates a from $b,d$ and $Q_c^{\prime }$ separates b from $a,d$: vertex d cannot interfere with either $Q_c=c_1{c}_2$ nor $Q_c^{\prime }=c_1{c}_3$.

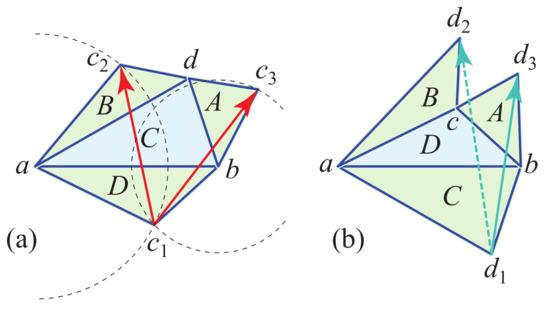
Figure 7. Case 2.2.3: c is closer than d to both a and b. $Q_c,Q_c^{\prime }$ red (a), $Q_d,Q_d^{\prime }$ green (b). Curvatures at $a,b,c,d$ are ${284}^{\circ },{200}^{\circ },{58}^{\circ },{178}^{\circ }$.

However, although one can construct two geodesic loops at d, $Q_d$ on the cone apexed at a and $Q_d^{\prime }$ on the cone apexed at b, they may not stay inside T. We now argue that at least one of $Q_d$, $Q_d^{\prime }$ lives on T.

Figure 7b illustrates the situation when one, in this case $Q_d=d_1{d}_2$, falls outside T. It should be clear that $d_1$ can see c, because ${\omega }_a,{\omega }_b\ge \pi$, so the two faces $C\cup D$ form a convex quadrilateral. The exterior angle gap at c can only block visibility from one of $d_2,d_3$. Another way to view this is that, if $Q_d=d_1{d}_2$ does not live on T, then it separates $a,c$ from b. However, then $Q_d^{\prime }=d_1{d}_3$ even more so separates $a,c$ from b, and lives on (remains inside the surface of) T.

So now we have two geodesic loops, say, $Q_c=c_1{c}_2$ and $Q_d=d_1{d}_2$. Then, just as in Case 2.2.2, we have identified a vertex-free region R, with one geodesic excluding a to the left, the other b to the right. Following the same logic as in Case 2.2.2, we conclude that at least one of the angles toward R at c or d must be $\le \pi$. It is straightforward that the angles to the other side are $\le \pi$: $▵a{c}_1{c}_2$ and $▵b{c}_1{c}_2$ and $▵b{d}_1{d}_3$.

This completes the proof of Theorem 4. There is a sense in which this theorem cannot be strengthened, because there are tetrahedra that have only one such $Q_1$. (That more complex “spiraling” geodesic loops are not possible is a consequence of Lemma 8 in [4]). We claim that Figure 8 is an example of a tetrahedron with only one simple $Q_1$.

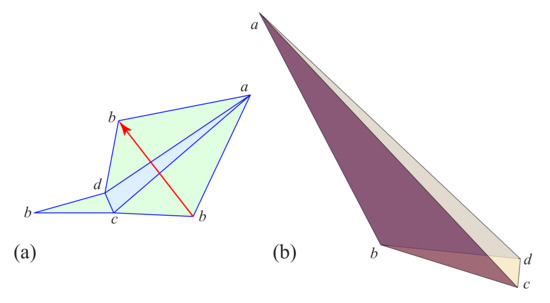
Figure 8. Tetrahedron with just one $Q_1$. (a) Unfolded. (b) Coordinates of $a,b,c,d$: $(-0.65,0,1.56),(0,0,0),(1,0,0),(0.89,0.25,0)$.

4. ${\mathit{Q}}_{\mathbf{2}}$: 2-Vertex Quasigeodesics

The goal of this section is to prove this theorem:

Theorem 5.

Every tetrahedron has a 2-vertex simple closed quasigeodesic.

4.1. Degenerate 2-Vertex Quasigeodesics

If a tetrahedron has at least two vertices with curvature of at least $\pi$, then the complete angle incident to those two vertices is each ≤$\pi$. So the double edge connecting them constitutes a degenerate simple closed quasigeodesic: at each endpoint, the angle to one side is 0, and to the other side at most $\pi$. We call such a degenerate quasigeodesic an edge-loop.

Define a tetrahedron as pointed if it has just one vertex with curvature exceeding $\pi$. We will consistently use the label a for that vertex, so it is pointed at a.

The remainder of this section concentrates on pointed tetrahedra. First, we review some tools used in the proof.

4.2. Star-Unfolding and Cut Locus

A geodesic segment on a P is a shortest path between its extremities.

The cut locus $C\left(x\right)$ of the point x on P is the set of endpoints (different from x) of all nonextendable geodesic segments (on the surface P) starting at x.

The star-unfolding of T with respect to its vertex v is obtained by cutting along the edges incident to v and unfolding to the plane.

We need one property of the star-unfolding that derives from [16] and is stated as Lemma 3.3 in [17]. To avoid introducing notation not needed here, we specialize this lemma to our situation:

Lemma 2.

Let $S_v$ be the star-unfolding of a tetrahedron from vertex v. Then the cut locus $C\left(v\right)$ is the restriction to $S_v$ of the Voronoi diagram of the images of v. Moreover, $C\left(v\right)$ lies entirely in the face opposite v. In particular, the degree-3 ramification point y lies in that face, and is connected by segments to that face’s three vertices.

One can see this intuitively: If y were interior to a face incident to v, then there would be three paths from v to y: one straight in 3D, but the other two with some 3D aspect, a contradiction.

• Sketch of Proof for Theorem 5.

The proof first establishes a visibility relation in the star-unfolding that yields an edge-loop. Second, the quasigeodesic condition is proved to hold at both ends of the geodesic, thereby establishing a 2-vertex simple closed quasigeodesic.

4.3. Visibility

Let T be a tetrahedron pointed at a, and $S_a$ the star-unfolding of T with respect to a. Label the three images of a as $a_b,a_c,a_d$, with $a_b$ opposite b, and similarly for $a_c$ and $a_d$. Say that two vertices $v,u\in S_a$ are visible to one another if the segment $vu$ is nowhere exterior to $S_a$, and touches $\partial S_a$ only at u and v. So $uv$ is a vertex-to-vertex diagonal of $S_a$.

Lemma 3.

If T is pointed at a, then at least one of $b,c,d$ is visible in $S_a$ to $a_b,a_c,a_d$ respectively. Sometimes there is only one such visibility relation.

Proof. 

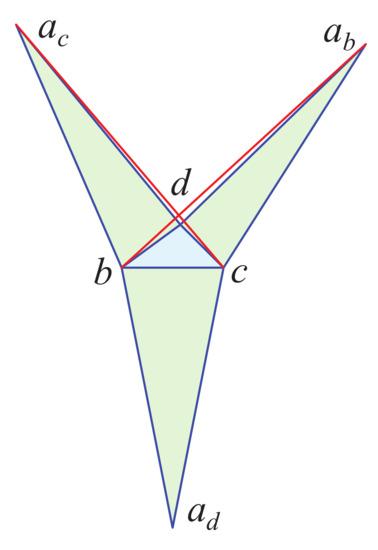
The tightness claim of the lemma is established by Figure 9.

Figure 9. Pointed T with just one visible segment, $a_{d}d$. Both $a_b$ and $a_c$ are blocked.

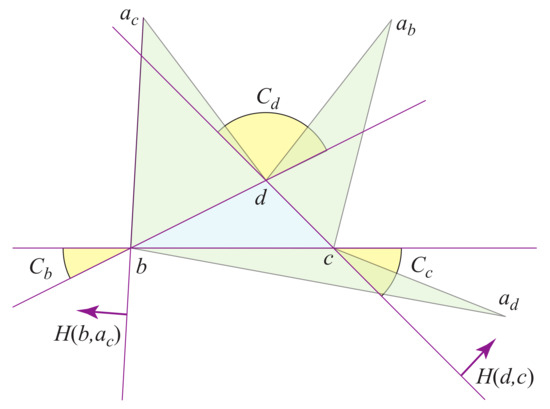
Because T is pointed at a, $S_a$ is reflex at $b,c,d$. Partition the plane into six regions by extending the three edges of $▵bcd$. Call the cone regions $C_b,C_c,C_d$ incident to $b,c,d$ respectively. If $a_b\in C_d$ or $a_b\in C_c$, then $a_b$ cannot see b, and similarly for c and d. So, for contradiction, we will show that if we have two visibility segments $a_{b}b,a_{c}c$ blocked, then $a_d$ can see d.

Let $H(x,y)$ be the halfplane to the left of the directed segment $xy$.

• Case 1: Two a-images in one cone.

Let $a_b,a_c\in C_d$, with no loss of generality. To contradict the claim of the lemma, we would need $a_d$ in either $C_c$ or $C_b$. Again with no loss of generality, let $a_d\in C_c$. This requires $a_d\in H(d,c)$, for the boundary of $H(d,c)$ is the (lower) boundary of $C_c$. See Figure 10. At the same time, it must be that $a_d\in H(b,a_c)$ in order for $S_a$ to be reflex at b. However, it is not possible for $a_d$ to be in both of those halfplanes below $bc$, for the intersection is only non-empty above $cd$.

Figure 10. Case 1. $a_d$ cannot be in both $C_c$ and $H(b,a_c)$.

• Case 2: Two a-images in two different cones.

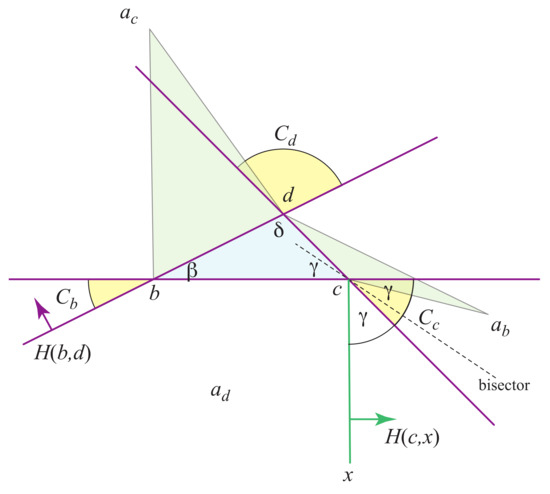
Let $a_b\in C_c$ and $a_c\in C_d$, with no loss of generality. Then we seek to show that $a_d$ can see d. If $a_d\in C_c$ or $a_d\in C_b$, then it is blocked from seeing d. If $a_d\in C_c$, then both $a_d$ and $a_b$ are in the same cone, already handled by Case 1. So we must have $a_d\in C_b$, which requires $a_d\in H(b,d)$, as the boundary of $H(b,d)$ is the lower boundary of $C_b$. See Figure 11.

Figure 11. Case 2: $a_d$ must lie in $H(c,x)$ for the bisector of $a_d$ and $a_b$ to penetrate $▵bcd$ at c.

By Lemma 2, the cut locus is entirely inside $▵bcd$. Thus, each of $b,c,d$ connects by a segment to the ramification point y. Each of these segments of the cut locus is a subsegment of a bisector. In particular, the bisector of $a_b$ and $a_d$ lies along the segment $cy$.

Let $\beta ,\gamma ,\delta$ be the angles of $▵bcd$. Now, in order for the bisector to penetrate into $▵bcd$ at c, $a_d$ must lie in the halfplane $H(c,x)$, where the ray $cx$ makes an angle of $\gamma$ with respect to the lower boundary of cone $Cc$. In the example shown in Figure 11, it is clear that it is impossible for $a_d$ to be in both $H(c,x)$ and in $H(b,d)$, because those halfplanes only intersect above $bc$.

However, if $\gamma$ is larger, then the two halfplanes could intersect below $bc$, and thus there is a possible placement of $a_d$ in $C_b$ satisfying the bisector condition. It is easy to see that the critical inequality is that we need $2\gamma >\pi -\beta$ for a placement to be available.

However, now a similar inequality is needed for the placements of $a_c$ and $a_b$, for each of those to both lie in the appropriate cones, and lead to bisectors that penetrate into $▵bcd$ at b and d respectively. Thus these three inequalities must hold:

$$\begin{array}{cc}\hfill 2\gamma & >\pi -\beta \hfill \\ \hfill 2\beta & >\pi -\delta \hfill \\ \hfill 2\delta & >\pi -\gamma .\hfill \end{array}$$

The reason that the inequalities are strict is that equality implies that the boundaries of $H(b,d)$ and $H(c,x)$ are parallel, and there is no spot at which to locate $a_d$ (and similarly for $a_c$ and $a_b$). Summing the three inequalities leads to $2\pi >2\pi$, a contradiction.

Therefore, it is not possible to have all three of $a_b,a_c,a_d$ located in three different cones.

Since the two Cases cover all possibilities, at least one image of a must lie in a region between cones, and so can see the corresponding vertex of $▵bcd$.    □

As a consequence of Lemma 3, we have established that every pointed tetrahedron has an edge-loop. Our next goal is to show that this edge-loop is in fact a simple closed quasigeodesic, which requires at most $\pi$ angle at the endpoints of the visibility segment.

Lemma 4.

Every pointed tetrahedron has a non-degenerate edge-loop forming a simple closed quasigeodesic.

Proof. 

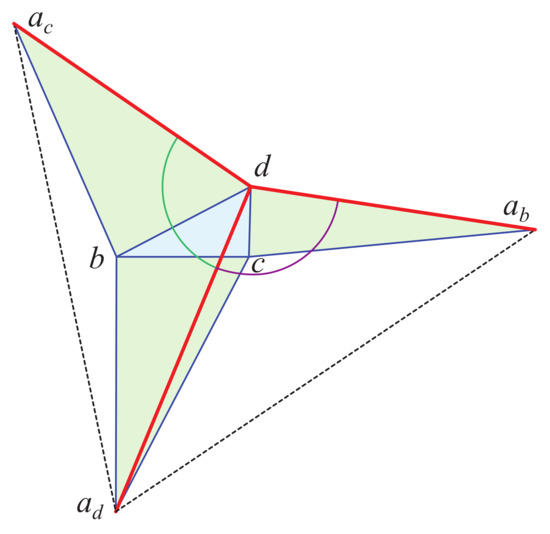
Let the visibility segment be $a_{d}d$ without loss of generality. First, because the curvature at a is >$\pi$, the total angle there is <$\pi$, and so the quasigeodesic condition is satisfied at that end. Now we turn to the other end at d.

Consider the segments incident to $a_d$. Segment $a_{d}b$ is left of and $a_{d}c$ is right of $a_{d}d$, just by the counterclockwise labeling convention for the base $bcd$. Now, because ${\omega }_b<\pi$ and ${\omega }_c<\pi$, the angles at b and at c in the unfolding $S_a$ are both reflex. See Figure 12. Therefore the segment endpoints incident to $a_d$ follow the counterclockwise order $a_b,c,d,b,a_c$. Therefore, the angle at d right of $a_{d}d$ is the apex of the triangle $▵a_{b}d{a}_d$ and the angle to the left is the apex of $▵a_{c}d{a}_d$. Because both angles are <$\pi$, we have established that the edge-loop is in fact a simple closed quasigeodesic.    □

Figure 12. $▵a_{b}d{a}_d$ and $▵a_{c}d{a}_d$: triangle angles at d are <$\pi$.

Note Lemma 4 holds for every visibility segment: although there is always at least one, there can be as many as three.

Together with the degenerate 2-vertex quasigeodesics on non-pointed tetrahedra, we have established Theorem 5.

4.4. A Geometrical Interpretation of Edge Loops

In this subsection, we provide a geometrical interpretation of edge loops of tetrahedra. Our construction is based on Alexandrov’s Gluing Theorem and the technique of vertex merging; see [5] for a description and other applications of these tools.

We are still in the case of tetrahedra T pointed at a, with an edge loop based on the edge $ad$, see Figure 12. Then we have ${\theta }_a+{\theta }_d<2\pi$.

Denote by n the mid-point of the edge $ad$. Cut T along $ad$ and glue back differently, via Alexandrov’s Gluing Theorem. Precisely, we identify a and d, and for the two banks of the cut, $an$ with $dn$. Because ${\theta }_a+{\theta }_d<2\pi$, the result after gluing is a convex polyhedron F with 5 vertices: b, c, $n_1$ and $n_2$ obtained from n, and $w=ab$ obtained from both a and b. By construction, the curvatures at $n_1,n_2$ are precisely $\pi$.

On F, we can merge the vertices c and $n_1$, and respectively d and $n_2$, to obtain a new convex polyhedron $\Delta$ with three vertices: w, u obtained from c and $n_1$, and v obtained from d and $n_2$. Therefore, $\Delta$ is a doubly covered (obtuse) triangle. See Figure 13.

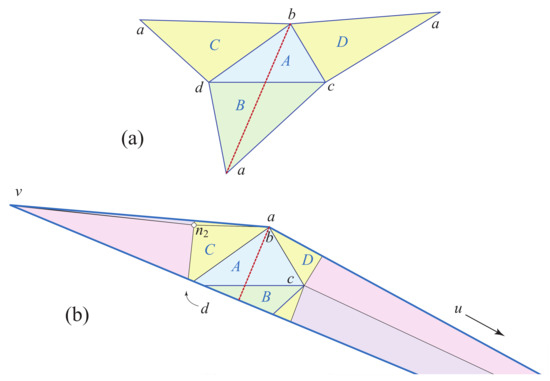
Figure 13. (a) Unfolding of a pointed tetrahedron, with edge-loop red. (b) One side of $\Delta$, an obtuse doubly-covered triangle with edge-loop along the altitude. ($n_1$ is on the back side.)

The edge loop of T based on $ad$ corresponds to the geodesic loop at w on $\Delta$ obtained by doubling the height h from w.

5. ${\mathit{Q}}_{\mathbf{3}}$: 3-Vertex Quasigeodesics

The goal of this section (a revision of [18]) is to prove this theorem:

Theorem 6.

Every tetrahedron T has at least one face F whose boundary $\partial F$ is a 3-vertex simple closed quasigeodesic $Q_3$.

We first establish two preliminary lemmas that will be used in the proof.

5.1. Preliminary Lemmas

Lemma 5.

Let ${\alpha }_1,{\alpha }_2,{\alpha }_3$ be the face angles incident to vertex v of a tetrahedron T. Then the angles satisfy the triangle inequality: ${\alpha }_1<{\alpha }_2+{\alpha }_3$, and similarly ${\alpha }_2<{\alpha }_1+{\alpha }_3$, and ${\alpha }_3<{\alpha }_1+{\alpha }_2$. The inequalities are strict unless T is flat.

Proof. 

See Lemma 2.8 in [5].    □

To simplify the calculations, angles will be represented in inequalities in units of $\pi$: $1\equiv \pi$, $2\equiv 2\pi$, etc. Thus, under this convention, each of the 12 face angles of a tetrahedron lies in $(0,1)$.

We say that “face F fails at vertex v” if the two angles incident to v not in F exceed $\pi$. So, for face A to fail on vertex b, then among the three face angles $bA,bC,bD$ incident to b, the two angles not in A satisfy $bC+bD>1$. This means that $\partial A$ is not a quasigeodesic, because to one side—the other side from $bA$—the angle exceeds $\pi$.

• Example.

Figure 14 shows a tetrahedron with $\partial C$ a quasigeodesic, but none of the other face boundaries is a quasigeodesic. Thus the “at least one” claim of Theorem 6 cannot be strengthened. Its vertex coordinates are:

$$a,b,c,d=(-3.54,1.98,4.58),(0,0,0),(1,0,0),(4.91,3.24,0).$$

Figure 14. The (red) boundary of shaded back face $C=abd$ is a quasigeodesic, but none of $\partial A,\partial B,\partial D$ are quasigeodesics.

For example, back face C does not fail at vertex b: $bD+bA={125}^{\circ }+{33}^{\circ }={159}^{\circ }<\pi$. Front face B fails at vertex c: $cD+cA={48}^{\circ }+{140}^{\circ }={188}^{\circ }>\pi$.

Lemma 6.

If a face A fails at a vertex b, then $\omega \left(b\right)<1$.

Proof. 

Since face A fails at b, by definition, $bC+bD>1$. Therefore

$$\begin{array}{ccc}\hfill \omega \left(b\right)& =& 2-(bA+bC+bD)\hfill \\ \hfill \omega \left(b\right)& =& 2-(bC+bD)-bA\hfill \\ \hfill \omega \left(b\right)& <& 1-bA\hfill \\ \hfill \omega \left(b\right)& <& 1\hfill \end{array}$$

This establishes the claim of the lemma.    □

5.2. Case Analysis

We now undertake a case analysis to show that it is not possible for all four faces of tetrahedron T to fail at vertices. The cases, illustrated in Figure 15, distinguish first the number of distinct vertices among the four face-failures, and second, the pattern of the failures.

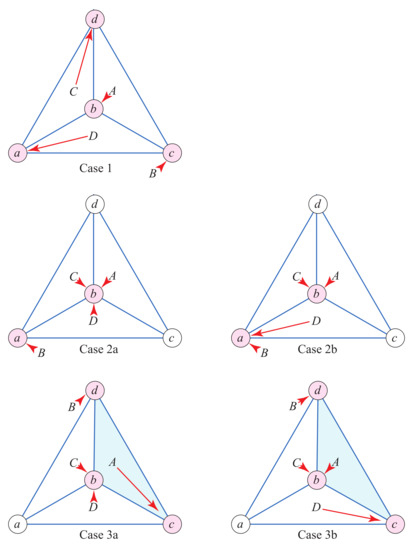
Figure 15. Failures. Case 1: at 4 vertices. Case 2: at 2 vertices. Case 3: at 3 vertices.

The proof analyzes the 12 face angles of T, and shows that the set of solutions in ${(0,1)}^{12}$ is empty (under the convention that each angle is in $(0,1)$). So we are representing tetrahedra by their 12 face angles. The four faces each have a total of $\pi$ angle, which reduces the dimension of the tetrahedron configuration space from 12 to 8. It is known that in fact the configuration space is 5-dimensional, not 8-dimensional [19], but the proof to follow works without including the various additional trigonometric relations that tetrahedron angles must satisfy. It suffices to use linear equalities and inequalities among the 12 face angles.

• Case 1: 4 vertices.

Suppose first that each of the four faces $A,B,C,D$ fail on four distinct vertices. Then Lemma 6 shows that $\omega \left(v\right)<1$ for each vertex v. But then $\sum \omega \left(v\right)<4$, contradicting the Gauss–Bonnet theorem.

• Case 2a: 2 vertices, $3+1$.

Suppose now that the four faces fail on a total of two vertices. This can occur in two distinct ways: three faces fail on one vertex, which we call Case 2a, or two faces fail each on two vertices, Case 2b. Say that b is the vertex at which three faces fail. We then have:

$$\begin{array}{ccc}\hfill A\mathrm{fails}\mathrm{at}b& :& bC+bD>1\hfill \\ \hfill B\mathrm{fails}\mathrm{at}a& :& aC+aD>1\hfill \\ \hfill C\mathrm{fails}\mathrm{at}b\\ \hfill D\mathrm{fails}\mathrm{at}b.\end{array}$$

It turns out that we do not need to use the fact that C and D fail at some vertices, so the implied inequalities are suppressed. Summing the failure inequalities above leads to a contradiction:

$$\begin{array}{ccc}\hfill (aC+bC)+(aD+bD)& >& 2\hfill \\ \hfill (1-dC)+(1-cD)& >& 2\hfill \\ \hfill 2& >& 2+(dC+cD)\hfill \\ \hfill 0& >& dC+cD.\hfill \end{array}$$

This is a contradiction because all angles have a positive measure.

• Case 2b: 2 vertices, $2+2$.

This follows the exact same proof, as again C and D failures are not needed to reach a contradiction.

• Case 3a: 3 vertices, double outside.

The three vertices at which faces fail bound a face, say A. One vertex of A, say b, is “doubled” in the sense that two faces fail at b. Case 3a is distinguished in that neither face failing on b is the three-vertex face A (Swapping B to fail on c and A to fail of d is symmetrically equivalent to the case illustrated).

We again do not need all failures, in particular, we only need those for faces B and D:

$$\begin{array}{c}\hfill A\mathrm{fails}\mathrm{at}c\\ \hfill B\mathrm{fails}\mathrm{at}d& :& dA+dC>1\hfill \\ \hfill C\mathrm{fails}\mathrm{at}b\\ \hfill D\mathrm{fails}\mathrm{at}b& :& bA+bC>1.\hfill \end{array}$$

Adding these inequalities leads to the same contradiction:

$$\begin{array}{ccc}\hfill (bA+dA)+(bC+dC)& >& 2\hfill \\ \hfill (1-cA)+(1-aC)& >& 2\hfill \\ \hfill 0& >& aC+cA;\hfill \end{array}$$

again a contradiction.

• Case 3b: 3 vertices, double inside.

In contrast to Case 3a, in this case, one of the faces that fail on b is the three-vertex face A. (Swapping B to fail on c, D to fail on b, and C to fail on d, is symmetrically equivalent.) This is the only difficult case, and the only case in which the triangle inequalities guaranteed by Lemma 5 are needed.

The angles of face A satisfy $bA+cA+dA=1$. Assume without loss of generality that $bA\le cA\le dA$. Three faces, $B,C,D$ fail at the three vertices of face A: $d,b,c$ respectively.

To build intuition, we first run through the proof for specific A-face angles:

$$\begin{array}{ccc}\hfill (bA,cA,dA)& =& (0.1,0.3,0.6)\hfill \\ \hfill A\mathrm{fails}\mathrm{at}b\\ \hfill B\mathrm{fails}\mathrm{at}d& :& dA+dC>1:dC>0.4\hfill \\ \hfill C\mathrm{fails}\mathrm{at}b& :& bA+bD>1:bD>0.9\hfill \\ \hfill D\mathrm{fails}\mathrm{at}c& :& cA+cB>1:cB>0.7\hfill \end{array}$$

Note $0.4+0.9+0.7=2$; this holds for arbitrary A angles. Now apply the triangle inequality to each of $dB,cB,dC$:

$$\begin{array}{ccc}\hfill bD& <& bA+bC:bC>bD-bA:bC>0.8\hfill \\ \hfill cB& <& cA+cD:cD>cB-cA:cD>0.4\hfill \\ \hfill dC& <& dA+dB:dB>dC-dA:dB>-0.2\hfill \end{array}$$

Note $0.8+0.4-0.2=1$; this again holds for arbitrary A angles.

Triangle face D satisfies: $bD+cD+aD=1$.

$$\begin{array}{ccc}\hfill bD& >& 0.9\hfill \\ \hfill cD& >& 0.4\hfill \\ \hfill bD+cD& >& 1.3\hfill \\ \hfill bD+cD+aD& >& 1.3>1,\hfill \end{array}$$

which contradicts $bD+cD+aD=1$.

Without specific angles assigned to $(bA,cA,dA)$, the argument is less transparent. Again assume that $bA\le cA\le dA$.

$$\begin{array}{c}\hfill A\mathrm{fails}\mathrm{at}b\\ \hfill B\mathrm{fails}\mathrm{at}d& :& dA+dC>1:dC>1-dA\hfill \\ \hfill C\mathrm{fails}\mathrm{at}b& :& bA+bD>1:bD>1-bA\hfill \\ \hfill D\mathrm{fails}\mathrm{at}c& :& cA+cB>1:cB>1-cA.\hfill \end{array}$$

Note the sum of the above three right-hand sides is $3-(dA+bA+cA)=2$. Now apply the triangle inequality to $dB,cB,dC$:

$$\begin{array}{ccc}\hfill bD& <& bA+bC:bC>bD-bA:bC>1-2·bA\hfill \\ \hfill cB& <& cA+cD:cD>cB-cA:cD>1-2·cA\hfill \\ \hfill dC& <& dA+dB:dB>dC-dA:dB>1-2·dA.\hfill \end{array}$$

Note the sum of the above three right-hand sides is $3-2(dA+bA+cA)=1$. Face D’s angles satisfy $bD+cD+aD=1$. Now we reach a contradiction using the inequalities above.

$$\begin{array}{ccc}\hfill bD& >& 1-bA\hfill \\ \hfill cD& >& 1-2·cA\hfill \\ \hfill bD+cD& >& 2-(bA+2·cA).\hfill \end{array}$$

We have $(bA+2·cA)\le 1$ because $bA+cA+dA=1$ and $cA\le dA$. Of course every angle is positive, so $aD>0$. So we have:

$$\begin{array}{ccc}\hfill bD+cD& >& 1\hfill \\ \hfill bD+cD+aD& >& 1,\hfill \end{array}$$

which contradicts $bD+cD+aD=1$.

That the inequalities for each of the above cases cannot be simultaneously satisfied has been verified by Mathematica’s FindInstance[] function, which uses Linear Programming over the rationals to conclude that the set of solutions in ${\mathbb{R}}^{12}$ is empty.

Replacing the triangle inequalities with equalities when the tetrahedron is flat (e.g., $aB=aC+aD$ instead of $aB<aC+aD$) again leads to the same contradiction.

We have thus established Theorem 6 and, together with remarks in Section 2, Theorems 4–6 establish Theorem 1.

6. Tetrahedra with Many ${\mathit{Q}}_{\mathbf{1},\mathbf{2},\mathbf{3}}$

As mentioned in the Introduction (Section 1), one cannot expect there to exist more than three simple closed quasigeodesics on a general convex surface, so one could expect that the same fact also holds for general tetrahedra.

In this section we provide an open subset of the space of tetrahedra, each tetrahedron of which has (unexpectedly) many such quasigeodesics.

Let $\mathcal{T}$ be the space of all tetrahedra in ${\mathbb{R}}^3$, with the topology induced by the usual Pompeiu–Hausdorff metric. Two polyhedra in $\mathcal{T}$ are then close to each other if and only if they have close respective vertices.

The goal of this section is to prove the theorem previously stated in the Introduction:

Theorem 2.

There exists an open set $\mathcal{O}$ of tetrahedra, each element of which has at least 34 simple closed quasigeodesics.

We call a tetrahedron f-acute if all its faces are acute triangles.

Lemma 7.

The set $\mathcal{F}$ of f-acute tetrahedra is open in $\mathcal{T}$.

Proof. 

The face angles at the vertices of T depend continuously on the vertex positions in ${\mathbb{R}}^3$. Once they are $<\pi$, they remain so in a neighborhood. □

We further restrict our study to a special open subset $\mathcal{O}$ of $\mathcal{F}$, of tetrahedra near a regular tetrahedron, all having three vertices of curvature $>\pi$. The introduction of these tetrahedra is justified by the considerations in Section 4.

We start with a regular tetrahedron of apex a and horizontal base $bcd$ and move a downward a short distance along a vertical line. The new tetrahedron N has base vertices of curvatures slightly larger than $\pi$ and top vertex a of curvature slightly less than $\pi$. Moreover, all faces of N remain acute triangles. So we consider $\mathcal{O}$ to be a small neighborhood of N.

The next lemma can be proved with an argument similar to Lemma 7’s proof.

Lemma 8.

All tetrahedra in $\mathcal{O}$ are f-acute and have three vertices of curvature $>\pi$.

The following is a particular case of Lemma 17.2 in [5].

Lemma 9.

Assume the tetrahedron T has a simple closed quasigeodesic $Q_k$ through $k\ge 1$ vertices, such that its left and right angles at each of the k vertices are all strictly less than π. Then, all tetrahedra sufficiently close to T in $\mathcal{T}$ have such a quasigeodesic.

In view of Lemmas 8 and 9, it suffices to count the simple closed quasigeodesics on our reference tetrahedron $N\in \mathcal{O}$

• We saw that a general tetrahedron has no $Q_0$;
• There exists at least one $Q_1$ on every tetrahedron. In fact, N has $\mathbf{6}$ such quasigeodesics. To see this, consider the four star-unfoldings of N with respect to its vertices. Because of the symmetry of N, three of the unfoldings from the base vertices $b,c,d$ are isometric. See Figure 16. One can then check that through each base vertex pass two $Q_1$s, as represented in Figure 16b. On the other hand, the three geodesic loops through apex a, represented in Figure 16a, are not quasigeodesics;
  

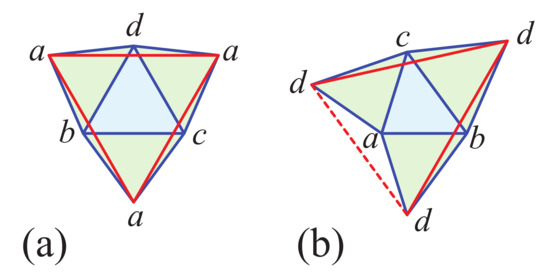  Figure 16. Two star unfoldings of a near-regular tetrahedron. In this example, ${\omega }_a={142}^{\circ }$ and ${\omega }_b={\omega }_c={\omega }_d={193}^{\circ }$. Geodesic loops are solid red segments. In (a), each loop has angle ${12}^{\circ }$ to one side of a and ${206}^{\circ }$ to the other side. In (b), ${\theta }_d={167}^{\circ }$, so the loops are quasigeodesics.
• Because N is chosen sufficiently close to a regular tetrahedron, Lemma 9 shows that every edge of N provides three non-degenerate $Q_2$s, as in Figure 17. The three vertices of curvatures $>\pi$ provide three more degenerate $Q_2$’s. They all sum up to $\mathbf{21}$$Q_2$s;
  

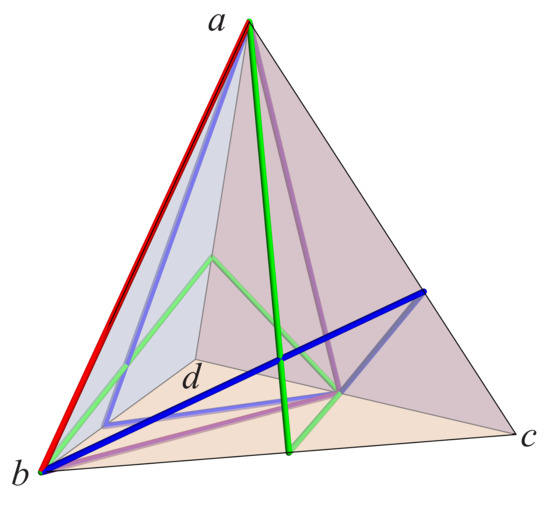  Figure 17. Three non-degenerate and one degenerate (red) $Q_2$ on a regular tetrahedron. The blue, green, and purple geodesic segments each connect to $ab$.
• The boundary of every face of N is a $Q_3$, because N is f-acute, hence there are $\mathbf{4}$ such $Q_3$ quasigeodesics;
• Every partition of the face set of N into two faces provides a $Q_4$, again because N is f-acute, hence there are $\mathbf{3}$$Q_4$s, namely corresponding to $AB:CD$, $AC:BD$, $AD:BC$.

Thus we have found a tetrahedron N in whose neighborhood $\mathcal{O}$, every tetrahedron has at least 34 quasigeodesics, verifying Theorem 2.

7. Remarks and Open Problems

Our work leaves open several questions of various natures.

Open Problem 1. The 2-vertex quasigeodesics that we identified in Section 4 are all edge-loops, i.e., they contain the edge joining the respective vertices. Is this necessarily the case?

According to Theorem 2, some tetrahedra have at least 34 simple closed quasigeodesics, and this happens on an open subset of the space $\mathcal{T}$ of tetrahedra.

Open Problem 2. Does there exist an upper bound on the number of simple closed quasigeodesics a tetrahedron can have? Of course, this is not the case for pure simple closed geodesics, see Section 2.

Open Problem 3. Find examples of tetrahedra with $k\ge 3$ simple closed quasigeodesics, for as many values of k as possible. For example, is there any tetrahedron that has only the $k=3$ simple closed quasigeodesics that Pogorelov guarantees and we describe in Theorem 1? Such a tetrahedron would be a polyhedral counterpart of an ellipsoid with exactly three simple closed geodesics.

Our quest for simple closed quasigeodesics on tetrahedra lead us to investigate the acuteness of face angles incident to a vertex. In this direction, we established the next elementary result of some independent interest.

Proposition 3.

Let $\overline{e}$ be a longest edge of the tetrahedron T. Then at least one extremity of $\overline{e}$ has all incident face angles acute, or T is a doubly covered rectangle.

Notice that the face angles incident to a vertex v of ${\omega }_v>\pi$ are all acute, directly from Lemma 5.

Proof. 

Assume $T=abcd$ and $\overline{e}=ab$. Then $ab$ is in particular a longest edge in the triangle faces C and D, hence the angles $aC,aD,bC,bD$ are all acute.

Assume now that the statement does not hold, hence $aB\ge \pi$, $bA\ge \pi$. Unfold the union of faces $A\cup B$ in the plane, to a quadrilateral $a^{\prime }{b}^{\prime }{c}^{\prime }{d}^{\prime }$. Clearly, the triangles $a^{\prime }{c}^{\prime }{d}^{\prime }$ and $acd$ are congruent, as are $b^{\prime }{c}^{\prime }{d}^{\prime }$ and $bcd$. However, $|a^{\prime }{b}^{\prime }|\ge |ab|$. The angle conditions $aB\ge \pi$, $bA\ge \pi$ imply, via an elementary geometry result, that the points $a^{\prime }$ and $b^{\prime }$ lie on, or in the interior of, the circle of diameter $cd$. Therefore, we get $|a^{\prime }{b}^{\prime }|\le |cd|\le |ab|\le |a^{\prime }{b}^{\prime }|$, impossible unless we have equalities everywhere. In this case, T is a doubly covered rectangle, and the conclusion holds. □

Our proofs involve the vertex of T of largest curvature.

Open Problem 4. Is the longest edge of a tetrahedron always incident to the vertex of largest curvature? This is indeed the case for degenerate tetrahedra, which correspond to planar quadrilaterals.