A Novel Clipping-Based Method to Reduce Peak-To-Average Power Ratio of OFDM Signals

Abstract

Orthogonal frequency division multiplexing (OFDM) is a widely used technology for wireless broadband communications. However, it also suffers from some drawbacks. One of the critical limitations is the problem of high peak-to-average power ratio (PAPR), which causes distortions of some nonlinear components such as power amplifiers. A number of techniques have been proposed to reduce the PAPR of OFDM signals, among which the clipping-based methods have gained a lot of attention due to the effective PAPR reduction and simplicity of implementation. This paper proposes a novel clipping-based method to reduce the PAPR of OFDM signals. Based on the recently proposed clipping noise compression (CNC) method, the proposed scheme introduces a preset normalization factor to replace the calculation of average amplitude of clipping noise in the original CNC method during compression processing. Comparative simulations were carried out, and the results exhibit that the proposed method achieves better bit-error-ratio performance with equal level of PAPR reduction compared to the original CNC method.

1. Introduction

Orthogonal frequency division multiplexing (OFDM) is widely used in modern broadband wireless communications such as Digital Video Broadcasting (DVB), IEEE 802.11, LTE-4G, 5G NR, and so on [1,2,3,4,5]. However, there are still some disadvantages for OFDM implementation, one of which is the problem of high peak-to-average power ratio (PAPR) [6]. Some nonlinear components of the communication equipment are sensitive to PAPR. For example, the high-power RF amplifier, which consumes a large part of the energy in the equipment, is usually expected to work near the saturation point to improve efficiency. In such situations, high PAPR will cause undesirable nonlinear distortions that degrade the performance of the communication systems [7,8]. In order to reduce the distortions, we can back-off the input power of the amplifier, or reduce the PAPR of the input signals. Since the solution of power back-off will lead to a decrease of energy efficiency, many researches have focused on the PAPR reduction of the OFDM signals [9,10].

A number of PAPR reduction techniques have been proposed in the literature. Depending on whether the signal is distorted, these techniques can be classified into two categories: distortion-based techniques and distortionless-based techniques [11,12,13]. The commonly used distortionless-based techniques include selective mapping (SLM), partial transmit sequence (PTS) and so on. They achieve the PAPR reduction by constructing multiple alternative signals and selecting the signal with the lowest PAPR signal for transmission [14]. These methods usually do not cause nonlinear distortion, but require high computational complexity and side-band information to be transmitted [15,16]. The distortion-based methods include clipping and filtering, companding, peak cancellation, etc., which would cause nonlinear distortions due to the direct modification of the signals [17,18,19]. In contrast, these methods have advantages of low computational complexity and no requirement of side-band information transmission.

The clipping and filtering based techniques have been extensively studied in recent years due to their simplicity of implementation. The traditional clipping and filtering technique reduces PAPR by directly limiting the amplitude of the signals to a predefined threshold, followed by a filter to suppress the out-of-band radiation. Since the filtering will cause the regrowth of peak, iterative clipping and filtering (ICF) was proposed to achieve a desired PAPR reduction [20]. However, this leads to an increase of computational complexity. Then, simplified clipping and filtering (SCF) was proposed and adopted a novel method to avoid iterative operations [21]. More recently, the clipping noise compression (CNC) method was proposed in [22], which further reduces computational complexity by reducing the number of fast Fourier transforms (FFTs). However, the CNC method uses the average amplitude of the clipping noise as the normalization factor in the noise compression processing. We found that both the normalization factor and the companding factor affect the performance of the CNC method, and tried to improve the compression algorithm to achieve better performance.

In this paper, we propose a novel method based on the analyses of the performance of the original CNC method. The proposed method improves the clipping-noise compression algorithm in the post-clipping processing. In the normalizing of clipping noise, the improved algorithm uses a preset fixed normalization factor rather than one that varies with the OFDM symbols. Since there is no requirement to calculate the normalization factor of the clipping noise for each OFDM symbol, the proposed method lowers the computational complexity. In addition, analyses and simulation results show that when the normalization factor and compression factor are properly selected, the proposed method can achieve an equivalent PAPR reduction and better bit-error-ratio (BER) performance compared to the original CNC method.

The rest of the paper is organized as follows. Section 2 gives the OFDM system model that is used in the analyses and simulations in this paper. In Section 3, we firstly present the description and analyses of the original CNC method, and then the proposed method is described and the analysis followed. Section 4 exhibits the results and the discussion of the simulations. Section 5 gives the conclusion.

2. System Model

In OFDM systems, the data to be transmitted usually needs to be mapped to complex symbols using phase shift keying (PSK) or quadrature amplitude modulation (QAM). Without loss of generality, it is assumed that the PSK or QAM constellations are scaled to average power of 1. That is to say, $\mathrm{E}[{|D|}^2]=1$, where $\mathrm{E}[\cdot ]$ denotes the expectation operation, and $D=[D_0,D_1,D_2,\dots ,D_k,\dots ,D_{N-1}]$ denotes the symbol vector with $N$ subcarriers, whose components are mapped data in the form of corresponding $M$-PSK or $M$-QAM constellation points [23].

In the baseband processing, oversampling techniques are generally applied to better approximate the continuous time-domain signals. With $L$-time oversampled, the symbol vector can be extended by zero padding to obtain the frequency-domain OFDM symbol as

$$S=[D_0,D_1,\dots ,D_{N-1},\underset{(L-1)N}{\underbrace{0,0,\dots ,0}}].$$

(1)

An inverse fast Fourier transform (IFFT) can be used to transform the OFDM symbol from the frequency domain to the time domain. Then, the discrete time-domain signal can be described as

$$s(n)=\frac{1}{\sqrt{LN}}{\displaystyle \sum _{k=0}^{LN-1}{S}_k{e}^{j\frac{2\pi nk}{LN}}},$$

(2)

where $S_k$ is the $k$-th subcarrier of the OFDM symbol. To simplify the analysis followed, without loss of generality, we can normalize the expected power of the OFDM symbol to 1. According to (1) and (2), there is

$$\mathrm{E}[{|s|}^2]={\left(\frac{1}{\sqrt{LN}}\right)}^2\cdot \mathrm{LN}\cdot \mathrm{E}[{|S|}^2]=\frac{1}{L}\mathrm{E}[{|D|}^2]=\frac{1}{L}.$$

(3)

Thus, we can obtain the discrete time-domain OFDM signal $x(n)$ with normalized power by scaling $s(n)$ as

$$x(n)=\sqrt{L}\cdot s(n)=\frac{1}{\sqrt{N}}{\displaystyle \sum _{k=0}^{LN-1}{S}_k{e}^{j\frac{2\pi nk}{LN}}}.$$

(4)

The amplitude envelope characteristic of the signal $x(n)$ is usually evaluated by the widely used metric PAPR, which is defined as

$$\xi =10{\log }_{10}\frac{\underset{0\le n\le LN-1}{\mathrm{MAX}}({|x(n)|}^2)}{P_{av}},$$

(5)

where $P_{av}$ is the average power of the OFDM symbol.

Since PAPR is a random variable for OFDM symbols, it is usually useful to study how often the random variable is above a particular level. We can use the complementary cumulative distribution function (CCDF) to investigate this problem [11]. The CCDF of PAPR is defined as

$$\mathrm{CCDF}(\xi )=\mathrm{prob}(\xi >{\xi }_0)$$

(6)

where ${\xi }_0$ is the reference level and prob(·) is the probability operator.

3. Description and Analysis of the Proposed Method

3.1. Description of Original CNC

The CNC method is effectively one of the clipping based techniques that focuses on the clipping noise modification to reduce the computational complexity. In clipping processing, the amplitude threshold can be calculated as

$$A=\gamma \sqrt{P_{av}},$$

(7)

where $\gamma$ is the clipping ratio and $P_{av}$ is the average power of the OFDM signal.

The clipping limits the amplitude of the OFDM signal to the threshold and keeps the phase unchanged. The processing can be descripted as

$$\overline{x}(n)=\{\begin{array}{cc}x(n),& |x(n)|\le A\\ A{e}^{j{\theta }_n},& |x(n)|>A\end{array},$$

(8)

where ${\theta }_n$ is the phase of $x(n)$, and $\overline{x}(n)$ is the clipped signal.

The difference between the original signal $x(n)$ and the clipped signal $\overline{x}(n)$ is defined as the clipping noise, which can be calculated as

$$c(n)=x(n)-\overline{x}(n).$$

(9)

Then the clipping noise is compressed by the compression function descripted as follows

$$\widehat{c}(n)=\frac{\mathrm{E}[c]e^{j{\vartheta }_n}}{\ln (1+\mu )}\ln (1+\frac{\mu }{\mathrm{E}[c]}|c(n)|),$$

(10)

where $\mu$ is the compression factor that determines the shape of compression curve, ${\vartheta }_n$ is the phase of $c\left(n\right)$, and $\mathrm{E}[c]$ is the average amplitude of $c\left(n\right)$. The compressed clipping noise is then used to modify the clipped OFDM signal to obtain the transmission signal as

$$\tilde{x}(n)=\overline{x}(n)+\widehat{c}(n).$$

(11)

3.2. The Proposed Method

According to the description of the original CNC method in the previous subsection, we can get that the compression function is derived from the general mu-law companding function that can be expressed as

$$g(x)=\frac{\ln (1+\mu x)}{\ln (1+\mu )}.$$

(12)

In the original CNC method, the term $\mathrm{E}[c]$ in (10) is used to normalize the clipping noise $c(n)$ such that the new variable $c^{\prime }(n)=c(n)/\mathrm{E}[c]$ can work in the appropriate compression interval. However, $\mathrm{E}[c]$ needs to be calculated according to the clipping noise signal $c(n)$, which varies with the OFDM symbols, resulting in different compression ratios even for the same value of samples. Therefore, we introduce a scale factor $\alpha$ in the compression function to normalize $c(n)$ and get $c^{\prime }(n)=c(n)/\alpha$. The factor $\alpha$ is a preset value, which can be adjusted according to the clipping ratio $\gamma$ and the compression factor $\mu$. The new compression function can be described as

$$\widehat{c}(n)=\frac{\alpha \ln (1+\mu \cdot \frac{|c(n)|}{\alpha })}{\ln (1+\mu )}{e}^{j{\vartheta }_n}.$$

(13)

According to (12) and (13), it can be seen that $\alpha$ is a scale factor that causes the signal to be linearly scaled, while $\mu$ is a compression factor that affects the shape of the compression curve, causing the signal to be nonlinearly scaled. Therefore, $\alpha$ and $\mu$ together determine the characteristics of the compression function, as shown in Figure 1.

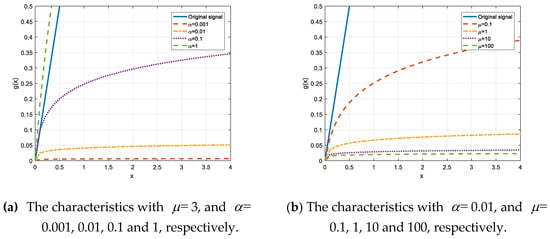
Figure 1. The characteristics of the modified $\mu$ law algorithm with different parameters.

Figure 1a depicts the characteristics for $\mu$ = 3, $\alpha$ = 0.001, 0.01, 0.1 and 1; Figure 1b shows the characteristics for $\alpha$ = 0.01, $\mu$ = 0.1, 1, 10, 100. As can be seen from the figure, $\alpha$ and $\mu$ together determine the characteristics of the compression function, which affects the performance of the CNC.

The new compression function in the proposed method adopts a predefined scale factor to replace the calculation of the expectation. The rest of the operations in the proposed method are the same as that in the original CNC. That is to say, the proposed method also performs the steps of clipping, clipping-noise calculation, clipping-noise compression, and transmission signal modification. The processing of clipping-noise compression is therefore improved for lower computational complexity and better performance of PAPR reduction.

The simplified block diagram of the proposed method is shown in Figure 2. The steps of the implementation are as follows.

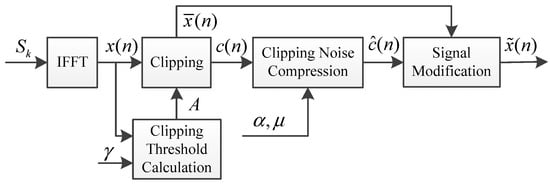
Figure 2. The simplified block diagram of the proposed method.

(1)

Use IFFT to transform the OFDM symbol $S_k$ to the time domain to obtain $x\left(n\right)$.

(2)

According to the preset clipping ratio $\gamma$ and the average power $P_{av}$, calculate the clipping threshold $A$ as shown in (7).

(3)

Clip the amplitude of $x\left(n\right)$ according to (8) to get the clipped signal $\overline{x}\left(n\right)$, then calculate the clipping noise $c\left(n\right)$ according to (9).

(4)

Compress the amplitude of $c\left(n\right)$ to get the compressed noise $\widehat{c}\left(n\right)$ according to (13).

(5)

Modify the clipped OFDM signal $\overline{x}\left(n\right)$ according to (11) to get the transmission signal $\tilde{x}\left(n\right)$.

3.3. Analysis of the Proposed Method

The discrete time-domain OFDM signal $x(n)$ can be written as $x(n)=x^R(n)+j{x}^I(n)$, where $x^R(n)$ and $x^I(n)$ respectively denote the real and imaginary parts. Generally, the input data symbols are statistically independent and identically distributed random variables with zero mean and variance of $\mathrm{E}[{|x|}^2]=1$ [24]. According to the central limit theorem, $x^R(n)$ and $x^I(n)$ are Gaussian variables with zero mean and variance ${\sigma }^2=\mathrm{E}[{|x|}^2]/2=1/2$. Therefore, the amplitude $|x(n)|=\sqrt{x^R{(n)}^2+x^I{(n)}^2}$ follows the Rayleigh distribution [25], and the probability density functions (PDFs) can be written as

$$f(|x(n)|)=\frac{|x(n)|}{{\sigma }^2}{e}^{-{|x(n)|}^2/(2{\sigma }^2)}=2|x(n)|e^{-{|x(n)|}^2}.$$

(14)

In order to describe the probability that the amplitude of the signal takes on the value less than or equal to a certain level, the cumulative distribution function (CDF) is commonly adopted [24]. According to (14), the CDF of $|x\left(n\right)|$ can be expressed as

$$F_{|x(n)|}(x)=\mathrm{Pr}(|x(n)|\le x)=1-e^{-x^2/(2{\sigma }^2)}.$$

(15)

where $\mathrm{Pr}(·)$ denotes the probability. This function is useful to investigate the probability distribution and calculate the probability of a certain interval. Sometimes, it is necessary to consider the opposite question (i.e., the probability of $|x\left(n\right)|$ above a certain level); at that point we usually adopt the CCDF probability, which is defined as

$$p=\mathrm{Pr}(|x(n)|>x)=1-F_{|x(n)|}(x).$$

(16)

Figure 3 gives an example of the PDF and CCDF of the amplitude of OFDM signals with 256 subcarriers and 64-QAM modulation.

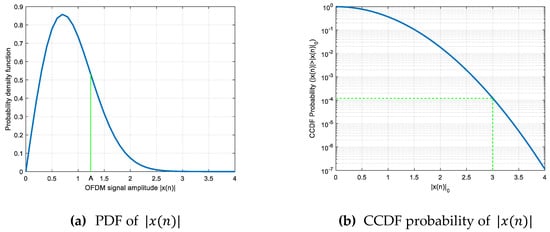
Figure 3. An example of the probability density function (PDF) and complementary cumulative distribution function (CCDF) of the amplitude of an orthogonal frequency division multiplexing (OFDM) signal.

As can be seen from Figure 3b, the samples with an amplitude lower than 3.8 account for approximately 99.99% of the total samples, so it is assumed that the amplitude of $x(n)$ that we need to deal with is in the interval (0, 3). Since the clipping ratio is defined as the ratio of the maximum amplitude to the square root of the average signal power, and is usually greater than 1, the value of the clipping threshold $A$ is greater than $\sqrt{P_{av}}$ = 1. Since the clipping noise is defined as $c\left(n\right)=x\left(n\right)-\overline{x}\left(n\right)$, according to Figure 3b, the amplitudes of most samples of the clipping noise are located in the interval (0,2).

Since the OFDM signal is normalized by average power as described in (4), we can obtain the clipping threshold $A_0$ for a given clipping ratio ${\gamma }_0$ as

$$A_0={\gamma }_0·\sqrt{P_{av}}={\gamma }_0.$$

(17)

According to (8) and (9), the clipping noise is actually the amplitudes that exceed the clipping threshold $A_0$, so we can calculate the expected amplitude of the clipping noise based on (13) as

$$\mathrm{E}[c_0]={\int }_{A_0}^{\infty }(|x(n)|-A_0)f(|x(n)|)d(|x(n)|)={\int }_{{\gamma }_0}^{\infty }(|x(n)|-{\gamma }_0)f(|x(n)|)d(|x(n)|).$$

(18)

According to (18), we can see that $\mathrm{E}[c]$ is related to $\gamma$. To achieve the equivalent PAPR reduction performance with the original CNC method, the proposed method should let the scale factor $\alpha$ be set depending on $\gamma$ and the compression factor $\mu$. That is to say, for a given ${\gamma }_0$, $\alpha$ can be set smaller than $\mathrm{E}[c_0]$ with a smaller $\mu$, or be set greater than $\mathrm{E}[c_0]$ with a greater $\mu$. Figure 4 shows an example of the equivalent compression ratio with different values of $\alpha$ and correspondingly selected values of $\mu$. From the figure we can see that the compression ratios of the function with the four sets of parameters are approximatively equivalent at $|c(n)|$ = 1.6. This means that in OFDM systems with a high probability of the clipping-noise peak amplitude of 1.6, the compression function with the four sets of parameters enables the compressed signal to have the equivalent amplitude peak with the same probability. Further, they will also have similar level of PAPR reductions, according to the definition of PAPR.

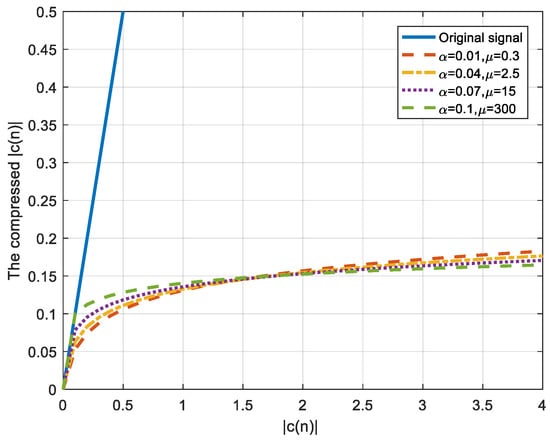
Figure 4. An example of the equivalent compression ratio with different values of $\alpha$ and correspondingly selected values of $\mu$.

However, according to (13) we can find that there is $\hat{c}(n)\to \alpha$ when $\mu \to \infty$, which means that $\alpha$ could not be arbitrarily large, otherwise it cannot be compressed to the desired amplitude. Specifically, there is

$$\alpha \le \frac{\mathrm{E}[c_0]}{\ln (1+{\mu }_0)}\ln (1+\frac{{\mu }_0}{\mathrm{E}[c_0]}|c(n_p)|).$$

(19)

where $c\left(n_p\right)$ is the sample with the maximum peak amplitude of the clipping noise and ${\mu }_0$ is the compressing factor of the original CNC. Since $\mathrm{E}[{\mathrm{c}}_0]$ is a function of $\gamma$, the upper bound of $\alpha$ is related to $\gamma$. For example, when $\gamma =1.4$ and ${\mu }_0=3$ is adopted by original CNC, we can determine that $\mathrm{E}[{\mathrm{c}}_0]=0.0423,\alpha \le 0.14$, and when $\gamma =1.8$, then $\mathrm{E}[{\mathrm{c}}_0]=0.0097,\alpha \le 0.041$. The proposed method with different values of $\mu$ and $\alpha$ is evaluated by simulations in the next section.

In addition, since the normalization factor in the proposed compression function is a preset constant instead of $\mathrm{E}[c]$, there is no need to calculate the average amplitude of the clipping noise of each OFDM symbol. Therefore, the proposed method requires lower computational complexity compared to the original CNC method.

4. Simulation Results and Discussion

As we adopt the normalization factor $\alpha$ in the proposed method, according to the previous analyses, we know that $\alpha$ and $\mu$ together affect the performance of the PAPR reduction. In this section, we evaluated the performance of the proposed method through simulations compared to the original CNC method. We also investigated the performance of the proposed method with different sets of the normalization factor $\alpha$ and the compression factor $\mu$. Specifically, we firstly used the CCDF curve of the PAPR obtained by the original CNC method as a reference. Then, with the same value of $\mu$ as that CNC adopted, we adjusted the value of $\alpha$ so that the CCDF of the signals using the proposed method was equivalent to that using CNC at a certain probability. Then, we compared the BER performance of the proposed method with the original CNC method, and a different value of $\mu$ was also considered. In addition, we also carried out evaluations for the proposed method in the OFDM systems with different modulation schemes and clipping ratios.

4.1. Simulation Results

In the simulations, pseudo random data is used as the input signal. The constellation diagram of the subcarrier modulation involved was normalized so that the mapped signal has an average power of 1. The power of the OFDM symbol is also normalized to 1 too as described in Section 2. At first, the original CNC method with compression factor ${\mu }_0$ was used to obtain the reference curve of CCDF of PAPR. Then, the value of the compression factor of the proposed method was selected keeping the same ${\mu }_0$, and the corresponding value of $\alpha$ chosen so that the level of PAPR reduction was approximately equal to the reference at the CCDF probability of ${10}^{-3}$. Then, we compared the BER performance of the proposed method with that of the original CNC method. In the simulations, the value of the compression factor was selected with $\mu =3$, and the larger value $\mu =30$ and the smaller one $\mu =0.3$ were also adopted for comparisons.

Figure 5 shows the performance of the proposed method for the OFDM system with 256 subcarriers and 64-QAM modulation, with the clipping ratio $\alpha$ set to 1.8. According to Figure 5a we can see that the performances of PAPR reduction using the original CNC method and the proposed method were approximately equivalent at the CCDF probability of ${10}^{-3}$, when the systems with $\mu =3,30,0.3$, and $\alpha =0.02,0.02,0.018$ were correspondingly adopted. It can be seen in Figure 5b that the proposed method achieved better BER performance than the original CNC method. Specifically, the required signal to noise ratio (SNR) of the proposed method with $\mu =0.3$ was about 0.4dB lower than that of original CNC when the BER was ${10}^{-3}$.

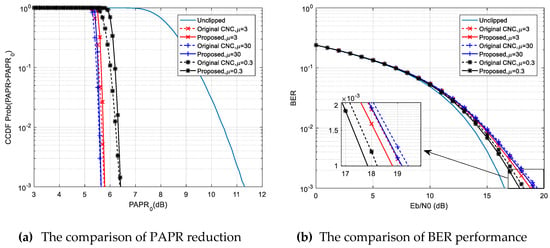
Figure 5. The CCDF probability of peak-to-average power ratio (PAPR) and bit-error-ratio (BER) performance of the original clipping noise compression (CNC) method and the proposed method with $\mu =3,30,0.3$, and $\alpha =0.02,0.02,0.018$ correspondingly, when $N=256$, $M=64$, and $\gamma =1.8$.

Figure 6 shows the performance of the proposed method for the OFDM system with different modulation schemes. Specifically, the number of subcarriers was set to 1024 and the modulation was 256-QAM. The clipping ratio $\gamma$ was also set to 1.8. According to Figure 6a we can see that the performances of PAPR reduction using original CNC and the proposed method were approximately equivalent at the CCDF probability of ${10}^{-3}$, when the systems with $\mu =3,30,0.3$, and $\alpha =0.014,0.015,0.013$ were correspondingly adopted. It can be seen in Figure 6b that the proposed method achieved obviously better BER performance than the original CNC method.

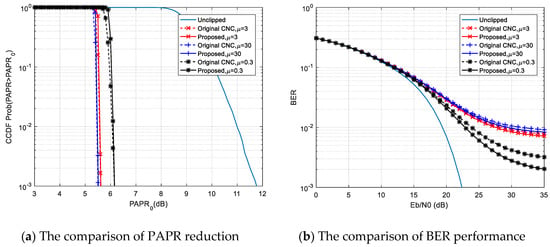
Figure 6. The CCDF probability of PAPR and the BER performance of the original CNC method and the proposed method with $\mu =3,30,0.3$, and $\alpha =0.014,0.015,0.013$ correspondingly, when $N=1024$, $M=256$, and $\gamma =1.8$.

Figure 7 shows the performance of the proposed method for the OFDM system with the clipping ratio $\gamma =1.5$, when the number of subcarriers was set to 256 and the modulation was 64-QAM. According to Figure 7a we can see that the performances of PAPR reduction using original CNC and the proposed method were approximately equivalent at the CCDF probability of ${10}^{-3}$, when the systems with $\mu =3,30,0.3$, and $\alpha =0.04,0.04,0.038$ were correspondingly adopted. Then, we can see in Figure 7b that the proposed method achieved better BER performance than the original CNC. With $\mu =0.3$, the proposed method achieved about 1.5dB better performance of BER compared to the original CNC according to Figure 7b.

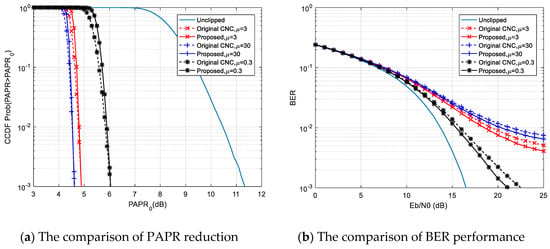
Figure 7. The CCDF probability of PAPR and the BER performance of the original CNC method and the proposed method with $\mu =3,30,0.3$, and $\alpha =0.04,0.04,0.038$ correspondingly, when $N=256$, $M=64$, and $\gamma =1.8$.

4.2. Discussion

According to the simulation results, the proposed method exhibits better BER performance than the original CNC when the same level of PAPR reduction achieved. This is because the proposed method introduces a preset normalization factor $\alpha$ that affects the performance along with the compression factor $\mu$. In the original CNC method, $\mathrm{E}[c]$ is used to normalize the clipping noise. Since the compression function is applied to each OFDM symbol separately, this causes $\mathrm{E}[c]$ to vary with the clipping noise of each symbol. As a result, the actual compression ratio of the clipping noise of each symbol is different from each other during the processing, which affects the PAPR reduction and the BER performance. The proposed method introduces a preset normalization factor that does not change throughout the PAPR reduction processing, resulting in consistent compression ratios for different symbols. The results show that properly selected normalization factor along with compression factor can improve the PAPR reduction performance compared to the original CNC method.

The evaluated OFDM systems in Figure 5 and Figure 6 adopted different modulation schemes and the same clipping ratio. However, they achieved equal level of PAPR reduction, by properly choosing the values of α and μ. As can be seen from the comparison of Figure 5b and Figure 6b, the promotion of the BER performance of the proposed method is more obvious in OFDM systems with high-order modulation of subcarriers.

The evaluated OFDM systems in Figure 5 and Figure 7 adopted the same modulation scheme and different clipping ratio, and they achieved an equivalent PAPR reduction as well when the proposed method adopted properly selected sets of α and μ. It can be seen from Figure 5b and Figure 7b that in both cases the proposed method has an improvement in BER performance compared to the original CNC method, and the improvement in Figure 7b is more obvious. This indicates that the proposed method has a more significant improvement compared to the original CNC method in the system with lower clipping ratio.

5. Conclusions

This paper proposes a novel clipping-based method to improve the performance of PAPR reduction for OFDM signals, on the basis of the CNC method. The original CNC method performs calculations of the average clipping-noise amplitude for each OFDM symbol before the compression operation, which makes the computational complexity high and the compression ratio vary with symbols. The proposed method instead uses a preset normalization factor to cancel the expectation calculation, and reduces the computational complexity. The analyses and simulations show that the proposed method achieves better BER performance with equal level of PAPR reduction compared to the original CNC method.

In future work, we will consider applying the techniques of PAPR reduction to some post-OFDM waveforms such as 5G NR, WiFi6, etc. We will also consider combining the proposed method with other linearization technique such as digital pre-distortion (DPD) to improve the linearity and efficiency of the high power amplifier.