Abstract
Formal concept analysis has proven to be a very effective method for data analysis and rule extraction, but how to build formal concept lattices is a difficult and hot topic. In this paper, an efficient and rapid incremental concept lattice construction algorithm is proposed. The algorithm, named FastAddExtent, is seen as a modification of AddIntent in which we improve two fundamental procedures, including fixing the covering relation and searching the canonical generator. The proposed algorithm can locate the desired concept quickly by adding data fields to every concept. The algorithm is depicted in detail, using a formal context to show how the new algorithm works and discussing time and space complexity issues. We also present an experimental evaluation of its performance and comparison with AddExtent. Experimental results show that the FastAddExtent algorithm can improve efficiency compared with the primitive AddExtent algorithm.
1. Introduction
In terms of formal concept analysis (FCA) [1,2], how to generate a relation diagram that is effectively and quickly built by the formal context has been extensively studied by scholars [3,4,5,6,7,8,9,10,11]
As an efficient tool for data analysis, FCA has attracted the attention of the majority of researchers [2], and has been applied to many areas [12]. In the past, FCA has been widely used in many different areas such as software engineering [13,14], linguistics [15,16], information retrieval [17,18], ontology engineering [19,20], bioinformatics [21,22], data mining [23,24], and complex network mining [23]. Intent and extent constitute every formal concept. The extent refers to the set of objects which has the same attributes, while the intent is the description of the concept (the set of attributes), which means the example has the common feature in this concept. This structure describes the essential relationship between objects and attributes and shows the formalization of all concepts in the category of philosophy [9].
The formation of a concept lattice is actually the formation of concept clusters. Since the concept lattice has been put forward, building a concept lattice from the formal context has become the focus in the field of conceptual research. According to the comparison of main classical algorithms, we can conclude that the matter of greatest concern is how to build the concept lattice efficiently [25]. The number of concepts growing exponentially will lead to considerable time consumption, so using and creating an efficient algorithm is important [26]. Existing concept lattice construction algorithms can be roughly divided into two categories: incremental and batch algorithms [3,4,26,27]. Batch algorithms [5,28,29] generally use two methods to construct a concept lattice: one of them is to build a concept lattice from top to bottom and the other is to build a concept lattice from bottom to top. On the other hand, incremental algorithms add objects or attributes one by one from the formal context progressively, which can change the concept lattice dynamically according to the changes made to a formal context. Consequently, it can reduce the unnecessary computational time by avoiding rebuilding the concept lattice.
2. The Basis of Formal Concept Lattice
The basis of concept lattice will be denoted in this section [25].
The formal context is shown by a triple K = (G, M, I) in FCA, in which G represents the set of objects, M represents the set of attributes, and I represents the binary relation between G and M. gIm denotes that the object g has the attribute m for an object and an attribute .
G and M are the object set and the attribute set in the formal context, respectively, and there are two reflections written as follows between and :
In the formal context, if a binary group C = (A, B) satisfies f(A) = B and g(B) = A, then we call C = (A, B) a formal concept. Here, A is a subset of G, which contains objects known as the extent of the formal concept; meanwhile, B is a subset of M, which contains attributes known as the intent of the formal concept.
All formal concepts are denoted as the set CS(K) of K. We take two concepts, C1 = (A1, B1) and C2 = (A2, B2). If A1 ⊆ A2, we say that C1 is a subconcept of C2 and C2 is a superconcept of C1. This relation can be expressed as (A1, B1) ≦ (A2, B2). If there is no C3 = (A3, B3) which satisfies (A1, B1) < (A3, B3) < (A2, B2), we denote C1 = (A1, B1) as the child of C2 = (A2, B2) and C2 as the parent of C1. Using this partial order relation, CS(K) can induce a concept lattice L(K), which is known as the concept lattice of K = (G, M, I).
A concept lattice can be visualized by a Hasse diagram, which draws a line segment or curve going upward from the child concept to the parent concept for each parent–child relationship.
Next, we will introduce some definitions and theories on the basis of incremental construction algorithm [1,4,18,19,20].
Let Mi = {m1, …, mi} ⊂ M, Ii = I∩(Gi × M), Mi+1 = Mi∪{m*}, Ii+1 = I∩(G × Mi+1), where m* is a newly added attribute. Given a formal context, Ki = (G, Mi, Ii) and the corresponding concept lattice is L(Ki). After adding m*, the new concept lattice is L(Ki+1) and the corresponding formal context is Ki+1 = (G, Mi+1, Ii+1).
Definition 1.
For the concept C = (A, B), if A = g(m*), then C is a modified concept. If C is a modified concept, the concept will be updated to be (A, B∪{m*}) in L(Ki+1).
Definition 2.
Let L1 and L2 be the concept lattice before and after inserting the new attribute m, respectively. The object set of m is denoted as m’ and (A, B) is a formal concept in L2. Then,
- (1)
- (A, B) is a new concept if A is not an extent of any concept in L1,
- (2)
- (A, B) is a modified concept if A ⊆ m’ and A is an extent of one concept in L1,
- (3)
- If (A, B) is unchanged from L1 to L2, it is an old concept,
- (4)
- Assuming that (X, Y) is a new concept and (A, B) is an old concept, if they satisfy A∩m’ = X ≠ A, the concept (A, B) is the generator of the concept (X, Y). Otherwise, it is a general old concept.
Proposition 1.
If (A1, B1) is the canonical generator of a new concept (A2, B2), and (A3, B3) is a non-canonical generator of (A2, B2), in the case that A1 ⊂ A3, A ⊂ A3 but A ⊄ A1, the concept (A, B) is neither a modified concept nor a canonical generator of any concept.
Proposition 2.
If (A3, B3) is an old concept and A3∩g(m*) = A1, and also in the condition of (A1, B1) ∈ L(Ki+1), which is a modified concept, and A ⊂ A3, A ⊄ A1, the concept (A, B) is neither a modified concept nor a canonical generator of any concept.
3. Related Work
Compared to batch algorithms, those advantages of incremental algorithms can make this algorithm more suitable to dynamic data sets. The Godin algorithm [4] and the AddIntent algorithm [3,27] are two classical incremental algorithms. Valtchev and other scholars [30] have improved the Godin algorithm, and the algorithm was also integrated into a very effective incremental mining framework of the closure frequent item-set. Nevertheless, Lingling and others refined the AddIntent algorithm, and what they did is add two fields to every concept, which are used to find new concepts at express speed. Empirical analysis shows what Lingling improved is better than the AddIntent algorithm at run time when the number of attributes is more than the objects in formal contexts.
The basic idea of incremental algorithms is to add a new object g (or a new attribute m) to an existing concept lattice L1. On the basis of the set of attributes which g has (or the set of objects which m has) L2 is built and the number of concepts of L2 is larger than that of L1. According to existing researches, the concepts are divided into three categories after inserting a new object (or a new attribute): old concepts, new concepts and modified concepts, where old concepts consist of general old concepts and generator concepts. Complete definitions are listed in [27].
In this paper, a new algorithm (the FastAddExtent algorithm) is proposed, which the AddAtom algorithm is the initial prototype [31,32]. The relationship between L1 and L2 is shown in Figure 1 as follows.
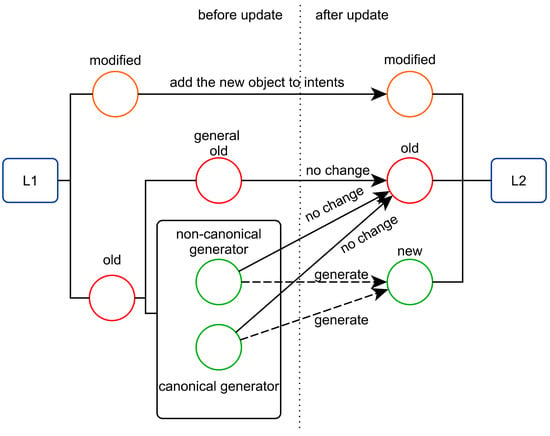
Figure 1.
Correspondences between concepts in L1 and L2.
4. A New Rapid AddExtent Algorithm
First, we summarize the AddExtent algorithm as follows: to add an attribute m (its object set is Extent), new concepts and modified concepts will be searched in a recursive way starting from the greatest upper bound. The concept MaximalConcept will be found repeatedly in the recursive function named GetMaximalConcept, and the extent of this concept is Extent. If the Extent of MaximalConcept equals to the function AddExtent’s parameters named extent, the resulting concept will be seen as a modified concept which is the greatest upper bound of the new concept. On the contrary, if the result concept’s Extent does not equal to the AddExtent’s extent, it will be identified as a canonical generator and a new concept called NewConcept will be generated. Meanwhile, the NewConcept will be returned as the greatest upper bound among all those modified. By marking every child of MaximalConcept as the initial GeneratorConcept and regarding MaximalConcept.Extent ∩ Extent as the initial object set extent, the AddExtent will receive the new two parameters and carry on a new round of recursion to find modified concepts and new concepts recursively. Next, the relationship between NewConcept and GeneratorConcept and the relationship between NewConcept and its children will be established. According to Proposition 1 and Proposition 2, any concept whose extent is smaller than MaximalConcept’s is neither a canonical generator nor a modified concept. That is to say, modified concepts and the canonical concept of the NewConcept is a MaximalConcept, so a canonical concept or a modified concept will turn up by a recursion through the AddExtent algorithm. To find other canonical generators and modified concepts, the function AddExtent will be used recursively to every child of the MaximalConcept.
A new rapid AddExtent algorithm: FastAddExtent algorithm is proposed in this paper, having a higher efficiency by avoiding a large part of comparisons.
Then, the detail of the FastAddExtent algorithm will be expressed: at one recursion of AddExtent, the descendants of all children of a MaximalConcept may be of the same concept and one concept will possibly be compared several times. At the same time, using the recursive function GetMaximalConcept to find MaximalConcept results in similar issues. In order to reduce comparisons and the number of recursive calls, every concept will be added four data fields.
4.1. The Overall Procedure
The FastAddExtent algorithm proposed in this paper, like the original AddIntent algorithm, uses a recursive way to construct a concept lattice. The FastAddExtent algorithm make refinements by adding four data fields to a concept: visited, NewConcept, doExtent, and MaximalConcept. Here, visited is a data field that stores an integer. The ID of a new attribute will be assigned to visited when the concept is being accessed. If visited of one concept is found equal to the id of a new attribute, we know this concept has been visited. The NewConcept field stores the returned new concept during the process of adding one attribute. If one concept is visited, the NewConcept field of the concept will be assigned to the candidate directly. Therefore, unnecessary recursive calls and comparisons can be avoided. The doExtent field stores the set of extent passed to the FastAddExtent procedure, and the canonical generator or the modified concept will be stored in the MaximalConcept of the GeneratorConcept. Obviously, the added fields doExtent and MaximalConcept make the parameter GeneratorConcept closer to the ClosureConcept so that we can decrease the time of search. Those refinements mentioned above are also the differences between FastAddExtent and FastAddIntent.
The Algorithm 1 will be described in which the lines with the mark {*} is are newly added compared to the AddExtent algorithm, while the lines with the mark {#} are modified.
| Algorithm 1: Procedure FastAddExtent(extent, generatorConcept, L, n) {#} |
| 1: tempConcept = generatorConcept {*} |
| 2: generatorConcept = GetClosureConcept(extent, generatorConcept, L, n) |
| 3: tempConcept.doExtent = extent {*} |
| 4: tempConcept.MaximalConcept = generatorConcept {*} |
| 5: if generatorConcept.Extent == extent then |
| 6: return generatorConcept |
| 7: end if |
| 8: GeneratorChildren = generatorConcept.Children |
| 9: newChildren = ∅ |
| 10: for each candidate in GeneratorChildren |
| 11: meet = candidate.Extent ∩ extent |
| 12: if meet != candidate.Extent then |
| 13: if candidate.visited == n then {*} |
| 14: candidate = candidate.NewConcept {*} |
| 15: else |
| 16: if meet ∩ candidate.doExtent == meet then {*} |
| 17: candidate = candidate.MaximalConcept {*} |
| 18: end if |
| 19: NC = FastAddExtent(meet, candidate, L, n) {#} |
| 20: candidate.NewConcept = NC {*} |
| 21: candidate.visited = n {*} |
| 22: candidate = NC {*} |
| 23: end if |
| 24: end if |
| 25: addChild = true |
| 26: for each Child in NewChildren |
| 27: if Candidate.Extent ⊆ Child.Extent then |
| 28: addChild = false |
| 29: exit for |
| 30: else if Child.Extent ⊆ Candidate.Extent then |
| 31: remove Child from NewChildren |
| 32: end if |
| 33: end for |
| 34: if addChild then |
| 35: add Candidate to NewChildren |
| 36: end if |
| 37: end for |
| 38: newConcept = (extent, generatorConcept.Intent) |
| 39: L = L∪{newConcept} |
| 40: for each Child in NewChildren |
| 41: removeLink(Child, generatorConcept, L) |
| 42: SetLink(Child, newConcept, L) |
| 43: end for |
| 44: SetLink(newConcept, generatorConcept, L) |
| 45: generatorConcept.NewConcept = newConcept {*} |
| 46: return newConcept |
The following paragraphs primarily explain the differences between the FastAddExtent algorithm and the AddExtent algorithm. The unchanged part of AddExtent and function can be referred to in [26], and this paper does not make a statement.
All the concepts which are accessed include new concepts, modified concepts, canonical generators, non-canonical generators in the whole process of running the algorithm. Since this algorithm is recursive, a new concept maybe be found as a modified concept in some recursive calls. We can see that an entry n is added to the parameters of the FastAddExtent algorithm, which is equal to the ID of the added attribute. This value n will be assigned to each accessed concept, indicating that the concept is last accessed by attribute n. In line 45, the last new concept called newConcept is given to the NewConcept field of the canonical generator GeneratorConcept that calls the earliest recursion in the process of adding an attribute. From line 19 to line 22, the NC is a newConcept returned by recursive calling FastAddExtent through the parameter candidate, and assigns NC to the candidate’s NewConcept field, and then changes the visited field of the candidate to the current attribute id, and finally sees the NC as a new candidate. All the operations of lines 19 to 22 serve for line 13 and line 14, and when the value of visited of a candidate equals to the id of the new attribute, we know the concept has been visited. Then the value of candidate.NewConcept is assigned directly to the candidate, eliminating a lot of unnecessary recursive calls and comparisons.
Here we use a case to explain the above added lines in the favor of reducing the running time. Table 1 shows the formal context before adding the attribute e, while Table 2 shows the formal context after adding the attribute e. Correspondingly, Figure 1 depicts the concept lattice based on Table 1 and Figure 2 depicts the concept lattice based on Table 2.

Table 1.
Example of the formal context before adding the attribute e.

Table 2.
Example of the formal context after adding the attribute e.
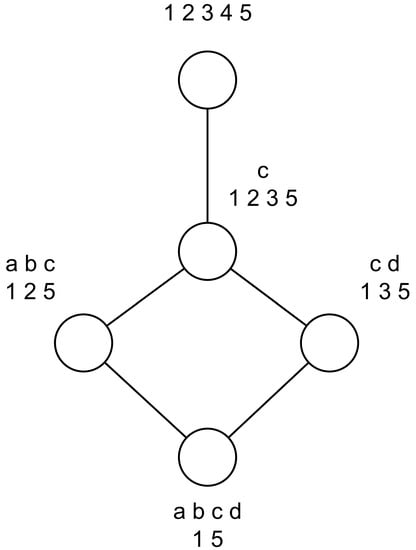
Figure 2.
Concept lattice of the formal context in Table 1.
All the concepts showed in Figure 3 have been marked to view easily and the labels are as follows:
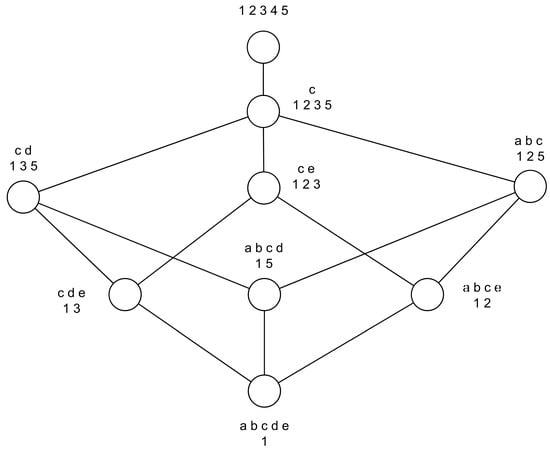
Figure 3.
Concept lattice of the formal context in Table 2.
- c0 ({1, 2, 3, 4, 5}, ∅)
- c1 ({1, 2, 3, 5}, {c})
- c2 ({1, 2, 5}, {a, b, c})
- c3 ({1, 3, 5}, {c, d})
- c4 ({1, 5}, {a, b, c, d})
- c5 ({1, 2, 3}, {c, e})
- c6 ({1, 2}, {a, b, c, e})
- c7 ({1, 3}, {c, d, e})
- c8 ({1}, {a, b, c, d, e})
In the process of adding attribute e whose object set is {1, 2, 3}, c1 is the canonical generator of the new concept c5. Visibly c1 has two candidates, and then the extent of two candidates need to do the intersection with {1, 2, 3}, respectively. At the same time, the results concluded from previous calls are that c2.NewConcept = c6, c3.NewConcept = c7, and the values of visited of c2 and c3 are both 5. Meanwhile, we suppose that c6 is built earlier than c7. In the process, c4 is a candidate of c2, and c8 is generated by c4 which is seen as the canonical generator, where c4.NewConcept = c8, c4.visited = 5. When creating c7, the candidate of c7 is c4. Because c4.visited = 5, c4 has been visited. Then, c4.NewConcept will be assigned directly to the candidate of c7. Eliminating a recursive call and many following comparisons greatly reduces the running time.
4.2. Find the Canonical Generator
As recursive calls consume time greatly, it is important to minimize the number of recursive calls in the search processes. The function GetClosureConcept finds canonical generators and modified concepts, so reducing the number of calling GetClosureConcept can help find canonical generators and modified concepts faster. There are two new fields added to every concept, doExtent and MaximalConcept, to achieve the desired effect. In lines 1, 3, and 4 of Algorithm 1, the value of the initial generatorConcept passed to the FastAddExtent function is assigned to tempConcept, and the GetClosureConcept function is called to find canonical generators or modified concepts under the extent value which is equal to extent. Then the result is assigned to GeneratorConcept. At the same time, to mark the initial GeneratorConcept assigned to tempConcept, the doExtent field of tempConcept is equal to extent, which equals the extent of the FastAddExtent. The MaximalConcept field stores the returned canonical generator. Lines 16–17 in Algorithm 1 are to judge the marks above: if the extent meet (candidate.Extent ∩ extent) is included in the doExtent field of one candidate of the GeneratorConcept, then the candidate.MaximalConcept will be assigned to the candidate. When the FastAddExtent function is called again, the number of recursive calls will be reduced because the candidate is now closer to the real ClosureConcept at this time The recursive times and the efficiency are even better in large data sets.
| Algorithm 2: Procedure GetClosureConcept (extent, generator, L): |
| 1: extentConcept = L.Find(extent) |
| 2: if extentConcept ≠ ∅then |
| 3: return extentConcept |
| 4: end if |
| 5: childIsMinimal = true |
| 6: while childIsMinimal |
| 7: childIsMinimal = false |
| 8: Children = GetChildren(GeneratorConcept, L) |
| 9: for each Child in Children |
| 10: if extent ⊆ Child.Extent |
| 11: GeneratorConcept = Child |
| 12: childIsMinimal = true |
| 13: end if |
| 14: end for |
| 15: return GeneratorConcept |
Most of Algorithm 2 in the FastAddExtent is identical to the function GetMaximalConcept. The GetClosureConcept has extra lines (line 1 to line 4) by adding the function L.Find(), which are used to find concepts in the concept lattice by indexes like hash values.
| Algorithm 3: Procedure CreateLatticeIncrementally(G, M, I |
| 1: topConcept = (G, ∅) |
| 2: L = {topConcept} |
| 3: i = 0 |
| 4: for each m in M |
| 5: i++ |
| 6: propertyConcept = FastAddIntent(m′,topConcept, L, i) |
| 7: Add m to the intent of propertyConcept and all concepts above |
| 8: end for |
| 9: return L |
Algorithm 3 is the beginning of the construction of a concept lattice. In Algorithm 3, The modified part is line 6 where the FastAddExtent algorithm adds a parameter i to the function CreateLatticeIncrementally compared to the AddExtent algorithm. This parameter i will be assigned to the visited of every concept to mark the concept whether it was visited when a new attribute is added.
5. Complexity Issues
Our algorithm showed above has a number of optimizations, i.e., adding new data fields to every concept. For example, lines 1–4, 13–23, and 45 of Algorithm 1 reduce unnecessary comparisons and traversal of the lattice.
Although our algorithm does not change the time complexity compared to the AddExtent, the running time is reduced so that the experimental results can come out quickly. Therefore, the FastAddExtent algorithm has a bound of O(|L||G||M|3) of a worst-case time complexity and the main details are discussed as follows [26]. The complexity relies on the number of invocations of the FastAddExtent function, while it calls the GetClosureConcept function only once for every extent of the lattice, as occurs in AddExtent. Since the length of the GeneratorChildren list never exceeds |M| [9] and the complexity of the GetClosureConcept function is restricted by O(|G||M|2) [26], the complexity of one call of FastAddExtent is roughly estimated as O(|G||M|3). Therefore, the total complexity is O(|L||G||M|3).
6. Experimental Evaluation and Analysis
In order to prove the efficiency of our algorithm proposed in this paper, we used the Python language to implement it and the original AddExtent algorithm. All experiments were run on the computer with an idle 64-bit system, AMD A6-3420M (1.5 GHz), and 6.0 GB RAM.
The data set used throughout the experiments was randomly generated with different fill ratios (i.e., |I|/|G||M|) and they are 10%, 24%, and 40% respectively. These data sets have 50 objects, but the number of attributes varies, and each attribute may have different number of objects.
Figure 4 demonstrates the runtime comparison between the FastAddExtent algorithm and the AddExtent algorithm on a 10% fill ratio (low density) data set. As we can see from the Figure, the number of attributes is increased gradually from 100 to 20,000. When the |M| is not large enough, the FastAddExtent algorithm differs from the AddExtent algorithm faintly. However, the FastAddExtent has a growing advantage along with the growing |M| and the gap becomes bigger.
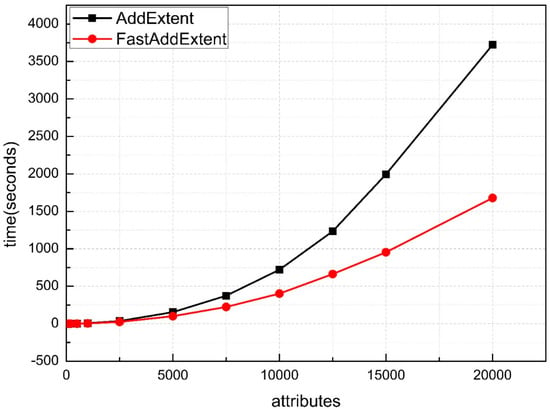
Figure 4.
Results for random datasets with low density.
Figure 5 shows the runtime comparison between the FastAddExtent algorithm and the AddExtent algorithm on a 24% fill ratio (medium density) data set. As we can see from the Figure, the number of attributes is increased gradually from 25 to 6000. The running time gap is bigger compared to Figure 4. The FastAddExtent has advantages whether the number of attributes is large (especially when |M| is around 1250) or small.
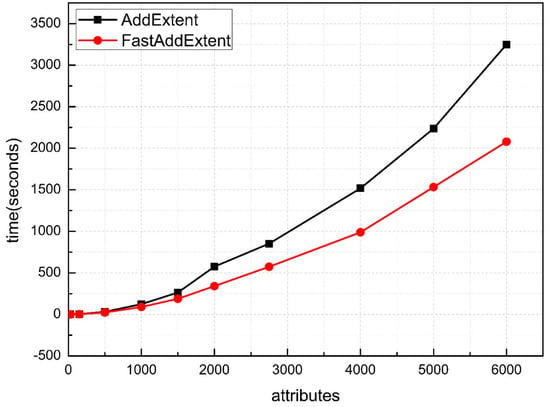
Figure 5.
Results for random datasets with medium density.
Figure 6 depicts the comparison between the FastAddExtent algorithm and the AddExtent algorithm on a 40% fill ratio (high density) data set. As we can see from the figure that the number of attributes is increased gradually from 10 to 425. Because the size of the concept lattice is very large and the consumption of memory resources is very fast, we can only run tests on 400 attributes. The line chart obtained from the experiment can be visually seen that the running time are rising rapidly. The intersecting point appears much earlier compared to Figure 4 and Figure 5. Meanwhile, the FastAddExtent has an obvious advantage at each test point.
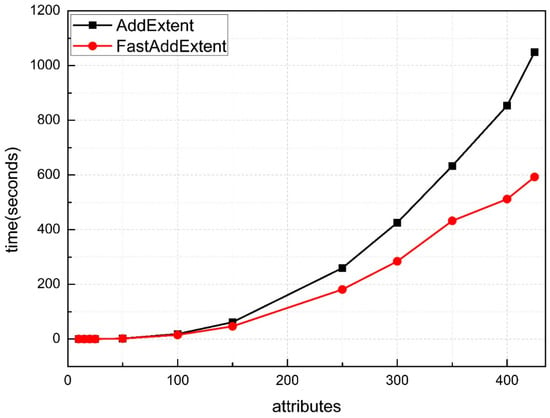
Figure 6.
Results for random datasets with high density.
7. Conclusions
Incremental algorithms that add attributes to concept lattices incrementally can be used to construct concept lattices and can also be used to update concept lattices. We introduce an efficient incremental algorithm called FastAddExtent in this paper. This algorithm adds four fields in the function FastAddExtent, which utilizes four new data fields to reduce unnecessary comparisons.
Compared to AddExtent, FastAddExtent can construct concept lattice faster at almost every test point even when the number of attributes is small and the data set has low fill ratio. Meanwhile, the performance gap between two algorithms will increase as the number of attributes increases. Both theoretical analysis and performance tests show that the FastAddExtent algorithm is a better choice than the AddExtent algorithm when we apply the FCA method with a large number of attributes and/or a high data fill ratio.
Author Contributions
Conceptualization, J.Z. and L.Z. (Ligeng Zou); Methodology, L.Z. (Ligeng Zou) and L.Z. (Licheng Zeng); Software, R.L.; Validation, L.Z. (Ligeng Zou) and L.Z. (Licheng Zeng); Visualization, L.Z. (Licheng Zeng); Writing—original draft, J.Z.; Writing—review and editing, R.L.
Funding
This research was funded by Major Project for Science and Technology Development of Henan Province, grant number (152102210093).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wille, R. Restructuring lattice theory: An approach based on hierarchies of concepts. In International Conference on Formal Concept Analysis; Springer: Berlin/Heidelberg, Germany, 2009; pp. 314–339. [Google Scholar]
- Ganter, B.; Wille, R. Formal Concept Analysis: Mathematical Foundations. (Translated from the German by Cornelia Franzke); Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Valtchev, P.; Missaoui, R. Building concept (Galois) lattices from parts: Generalizing the incremental methods. In International Conference on Conceptual Structures; Springer: Berlin/Heidelberg, Germany, 2001; pp. 290–303. [Google Scholar]
- Godin, R.; Missaoui, R.; Alaoui, H. Incremental concept formation algorithms based on Galois (concept) lattices. Comput. Intell. 1995, 11, 246–267. [Google Scholar] [CrossRef]
- Ganter, B. Two basic algorithms in concept analysis. In International Conference on Formal Concept Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 312–340. [Google Scholar]
- Bordat, J.-P. Calcul pratique du treillis de Galois d’une correspondance. Mathématiques et Sciences Humaines 1986, 96, 31–47. [Google Scholar]
- Norris, E.M. An algorithm for computing the maximal rectangles in a binary relation. Revue Roumaine de Mathématiques Pures et Appliquées 1978, 23, 243–250. [Google Scholar]
- Kuznetsov, S.O.; Obiedkov, S.A. Comparing performance of algorithms for generating concept lattices. J. Exp. Theor. Artif. Intell. 2002, 14, 189–216. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, Z.; Long, J.; Zhang, H. A fast incremental algorithm for deleting objects from a concept lattice. Knowl.-Based Syst. 2015, 89, 411–419. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, Z.; Long, J. An efficient algorithm for increasing the granularity levels of attributes in formal concept analysis. Expert Syst. Appl. 2016, 46, 224–235. [Google Scholar] [CrossRef]
- Wermelinger, M.; Yu, Y.; Strohmaier, M. Using formal concept analysis to construct and visualise hierarchies of socio-technical relations. In Proceedings of the 2009 31st International Conference on Software Engineering—Companion Volume, Vancouver, BC, Canada, 16–24 May 2009; pp. 327–330. [Google Scholar]
- Ganter, B.; Stumme, G.; Wille, R. Formal Concept Analysis: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3626. [Google Scholar]
- Priss, U. Linguistic applications of formal concept analysis. In Formal Concept Analysis; Springer: Berlin/Heidelberg, Germany, 2005; pp. 149–160. [Google Scholar]
- Ghani, I.; Jeong, S.R. Software Climate Change and its Disruptive Weather: A Potential Shift from”Software Engineering” to Vibrant/Dynamic Softology. KSII Trans. Internet Inf. Syst. 2016, 10, 3925–3942. [Google Scholar]
- Dau, F.; Ducrou, J.; Eklund, P. Concept similarity and related categories in SearchSleuth. In International Conference on Conceptual Structures; Springer: Berlin/Heidelberg, Germany, 2008; pp. 255–268. [Google Scholar]
- Hong, S.-S.; Kong, J.-H.; Han, M.-M. The Adaptive SPAM Mail Detection System using Clustering based on Text Mining. KSII Trans. Internet Inf. Syst. 2014, 8, 2186–2196. [Google Scholar]
- De Maio, C.; Fenza, G.; Gaeta, M.; Loia, V.; Orciuoli, F.; Senatore, S. RSS-based e-learning recommendations exploiting fuzzy FCA for Knowledge Modeling. Appl. Soft Comput. 2012, 12, 113–124. [Google Scholar] [CrossRef]
- Ahmad, I.S. Text-based Image Indexing and Retrieval using Formal Concept Analysis. KSII Trans. Internet Inf. Syst. 2008, 2, 150–170. [Google Scholar] [CrossRef]
- Amin, I.I.; Kassim, S.K.; ella Hassanien, A.; Hefny, H.A. Using formal concept analysis for mining hyomethylated genes among breast cancer tumors subtypes. In Proceedings of the 2013 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Mysore, India, 22–25 August 2013; pp. 521–526. [Google Scholar]
- Viji Rajendran, V.; Swamynathan, S. Enhanced Cloud Service Discovery for Naïve users with Ontology based Representation. KSII Trans. Internet Inf. Syst. 2016, 10, 38–57. [Google Scholar]
- Poelmans, J.; Kuznetsov, S.O.; Ignatov, D.I.; Dedene, G. Formal Concept Analysis in knowledge processing: A survey on models and techniques. Expert Syst. Appl. 2013, 40, 6601–6623. [Google Scholar] [CrossRef]
- Ahn, B.; Abbas, E.; Park, J.A.; Choi, H.-J. Increasing Splicing Site Prediction by Training Gene Set Based on Species. KSII Trans. Internet Inf. Syst. 2012, 6, 2784–2799. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, B.; Sheng, J.; Hu, Y.; Wang, Y.; Shao, J. Identifying Influential Nodes in Complex Networks Based on Weighted Formal Concept Analysis. IEEE Access 2017, 5, 3777–3789. [Google Scholar] [CrossRef]
- Song, G.Y.; Cheon, Y.; Lee, K.; Park, K.M.; Rim, H.C. Inter-category Map: Building Cognition Network of General Customers through Big Data Mining. KSII Trans. Internet Inf. Syst. 2014, 8, 583–600. [Google Scholar]
- Lv, L.; Zhang, L.; Zhu, A.; Zhou, F. An improved addintent algorithm for building concept lattice. In Proceedings of the 2011 2nd International Conference on Intelligent Control and Information Processing (ICICIP), Harbin, China, 25–28 July 2011; pp. 161–165. [Google Scholar]
- Van Der Merwe, D.; Obiedkov, S.; Kourie, D. AddIntent: A new incremental algorithm for constructing concept lattices. In International Conference on Formal Concept Analysis; Springer: Berlin/Heidelberg, Germany, 2004; pp. 372–385. [Google Scholar]
- Kourie, D.G.; Obiedkov, S.; Watson, B.W.; van der Merwe, D. An incremental algorithm to construct a lattice of set intersections. Sci. Comput. Programm. 2009, 74, 128–142. [Google Scholar] [CrossRef]
- Outrata, J.; Vychodil, V. Fast algorithm for computing fixpoints of Galois connections induced by object-attribute relational data. Inf. Sci. 2012, 185, 114–127. [Google Scholar] [CrossRef]
- Kuznetsov, S.O. A fast algorithm for computing all intersections of objects from an arbitrary semilattice. Nauchno-Tekh. Informatsiya Ser. 2-Informatsionnye Protsessy I Sist. 1993, 1, 17–20. [Google Scholar]
- Valtchev, P.; Missaoui, R.; Godin, R. A framework for incremental generation of closed itemsets. Discret. Appl. Math. 2008, 156, 924–949. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, Z.; Long, J. A fast incremental algorithm for constructing concept lattices. Expert Syst. Appl. 2015, 42, 4474–4481. [Google Scholar] [CrossRef]
- Van Der Merwe, F.; Kourie, D. AddAtom: An Incremental Algorithm for Constructing Concept Lattices and Concept Sublattices; Technical Report; Department of Computer Science, University of Pretoria: Pretoria, South Africa, 2002. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).