Research on Hypergeometric-Gaussian Vortex Beam Propagating under Oceanic Turbulence by Theoretical Derivation and Numerical Simulation

Abstract

In this paper, we use two methods to research the propagation characteristics of a Hypergeometric-Gaussian (HyGG) vortex beam under oceanic turbulence. One is numerical calculation based on the Rytov approximation theory, where the theoretical detection probability equation of the HyGG vortex beam propagating through oceanic turbulence is derived. The other is numerical simulation based on random phase screens model of oceanic turbulence, where the influences generated by oceanic turbulence on the phase and intensity of the propagation beam as well as the propagation of the beam through several independent phase screens, kept at the same distance, have the same effect. The effects of oceanic turbulence parameters and initial beam parameters on the detection probability of the HyGG vortex beam at the receiver are discussed. The results of theoretical derivation are well in agreement with those of numerical simulation, which demonstrated that the numerical simulation method could effectively simulate the complex theoretical derivation. Both results show that with higher dissipation rate of kinetic energy per unit mass of fluid, smaller dissipation rate of mean-squared temperature and lower temperature-salinity contribution ratio comes the better detection probability. Meanwhile, a HyGG vortex beam with smaller topological charge and longer wavelength has a superior turbulent resistance property. It provides a promising way to estimate the propagation characteristics of the optical beams in an underwater environment.

1. Introduction

In recent years, researches on underwater optical communication (UOC) have attracted much attention, and the need for large capacity and high speed UOC becomes more urgent due to the growing demand of human activities for scientific research and exploration in an underwater environment [1]. Vortex beams carrying orbital angular momentum (OAM) [2,3,4,5,6,7,8] are of great interest due to the potential applications that multiple OAM states can be used as different carriers for multiplexing, which can improve the system capacity of UOC greatly [9]. Despite the promising aspects, the existing studies have shown that when the beams carry OAM propagate through the underwater channel, OAM-spectrum would be spread and the crosstalk would be generated between the adjacent OAM modes. All these seriously limit the performance of OAM-based UOC system.

In order to obtain the desirable alternative for UOC communications, myriad work has been carried out in terms of the propagation properties of diverse OAM-carrying beams under oceanic turbulence theoretically and experimentally [10,11,12,13,14,15,16,17]. However, because some theoretical derivations are difficult to obtain analytical solutions and the underwater experimental environment is difficult to build, an intuitive and effective method called numerical simulation based on random phase screens model of oceanic turbulence is widely employed to analyze the evolution properties of vortex beams in an underwater environment [18,19,20]. Furthermore, for the purpose of mitigating the disturbance caused by turbulence, many efforts have been made to study the effects of nondiffracting and pseudo-nondiffracting vortex beams as to the resistance to turbulent disturbance [21,22,23,24], and the results show that the favorable characteristics of the beam can effectively reduce the influence of turbulence on the transmission of OAM modes.

As a member of pseudo-nondiffraction OAM-carrying beams family, Hypergeometric-Gaussian (HyGG) vortex beams [25,26,27,28,29,30] also have self-reconstruction and abruptly autofocusing properties [31]. Meanwhile, HyGG vortex beams could be separated as Gaussian mode, modefied exponential Gauss mode, modified Laguerre–Gaussian mode and modified Bessel Gauss mode for specific values of initial beam source parameters, which offers great potential in wireless optical communication. In this paper, we adopt theoretical derivation and numerical simulation two methods to study the propagation properties of the HyGG vortex beam under oceanic turbulence, and we compare the performance of the two methods through analyzing the influence of oceanic turbulence parameters and initial beam parameters on beam’s propagating.

The paper is organized as follows. Firstly, we present the detection probability of the HyGG vortex beam through oceanic turbulence by theoretical derivation. Secondly, we produce the detection probability of the HyGG vortex beam using the method of numerical simulation based on random phase screens model of oceanic turbulence. Then, we discuss the results in detail. Finally, we conclude the paper.

The extra contribution of this paper is that we use a different method of numerical simulation based on random phase screens model of oceanic turbulence to study the same problem in Ref. [27] and obtain highly consistent results, providing an effective way for similar studies when there is no direct theoretical solutions and experiments cannot be carried out.

2. Theoretical Derivation

In the case of paraxial propagation, the HyGG vortex beam at z plane in turbulence-free channel can be expressed as [26,27]

$$\begin{array}{cc}\hfill M_{m_0}(r,\varphi ,z)=& C{(\frac{z}{z_R}+i)}^{-[1+\left|m_0\right|+\frac{p}{2}]i^{\left|m_0\right|+1}}{\left(\frac{z}{z_R}\right)}^{\frac{p}{2}}{}_1{F}_1(-\frac{p}{2},\left|m_0\right|+1;\frac{z_R^2{r}^2}{{\omega }_0^2(z^2+iz{z}_R)})\hfill \\ \hfill & {\left(\frac{r}{{\omega }_0}\right)}^{\left|m_0\right|}exp[-\frac{i{z}_R{r}^2}{{\omega }_0^2(z+i{z}_R)}]exp\left(i{m}_0\varphi \right)\hfill \end{array}$$

(1)

where $r=\left|\mathbf{r}\right|$, $\mathbf{r}=(x,y)$ is the two-dimensional position vector in the receiver plane and $\varphi$ denotes the azimuthal angle. The normalized constant $C=\sqrt{2^{p+\left|m_0\right|+1}/[\pi \Gamma (p+\left|m_0\right|+1)]}\Gamma (p/2+\left|m_0\right|+1)/\Gamma (\left|m_0\right|+1)$ that ensures the HyGG vortex beam has finite power as long as the hollowness parameter $p\ge -\left|m_0\right|$, $m_0$ is the topological charge that corresponds to the value of the OAM mode. ${}_1{F}_1(a,b;x)$ is the confluent hypergeometric function and $\Gamma \left(x\right)$ is the Gamma function. $z_R=k{\omega }_0^2/2$ is Rayleigh range, and ${\omega }_0$ is the beam waist. k is wave number given by $k=2\pi /\lambda$, and $\lambda$ is wavelength.

When HyGG vortex beam propagates through weak oceanic turbulence at distance z, based on the Rytov approximation theory, its complex amplitude can be expressed as follows [27]

$$M(r,\varphi ,z)=M_{m_0}(r,\varphi ,z)exp\left[{\mathsf{\Psi }}_1(r,\varphi ,z)\right]$$

(2)

here, ${\mathsf{\Psi }}_1(r,\varphi ,z)$ is the complex phase term due to oceanic turbulence eddies. Owing to the disturbance of oceanic turbulence, the energy of single OAM mode spreads to the other OAM modes, resulting in the crosstalk among different OAM channels. Hence, the complex amplitude of the HyGG vortex beam propagating through the oceanic turbulence at distance z can be expressed as the superposition of various OAM modes

$$M(r,\varphi ,z)=\frac{1}{\sqrt{2\pi }}\sum _m{\beta }_m(r,z)exp\left(im\varphi \right)$$

(3)

${\beta }_m(r,z)$ in Equation (3) is the superposition coefficient, ${\beta }_m(r,z)=1/\sqrt{2\pi }{\int }_0^{2\pi }M(r,\varphi ,z)$$exp(-im\varphi )$, and the probability density of the HyGG vortex beam can be derived as [27]

$$\begin{array}{cc}\hfill <{\left|{\beta }_m(r,z)\right|}^2>=& \frac{1}{2\pi }{\int }_0^{2\pi }{\int }_0^{2\pi }{M}_{m_0}(r,\varphi ,z)M_{m_0}^{*}(r,{\varphi }^{{}^{\prime }},z)<exp\left[{\mathsf{\Psi }}_1(r,\varphi ,z)\right]+{\mathsf{\Psi }}_1^{*}(r,{\varphi }^{{}^{\prime }},z)]>\hfill \\ \hfill & exp[-i(m-m_0)(\varphi -{\varphi }^{{}^{\prime }})]d\varphi d{\varphi }^{{}^{\prime }}\hfill \\ \hfill =& \frac{2^{p+\left|m_0\right|+1}}{2{\pi }^2\Gamma (p+\left|m_0\right|+1)}·\frac{{\Gamma }^2(\frac{p}{2}+\left|m_0\right|+1)}{{\Gamma }^2(\left|m_0\right|+1)}{[1+{\left(\frac{z}{z_R}\right)}^2]}^{-(\frac{p}{2}+\left|m_0\right|+1)}{\left(\frac{r}{{\omega }_0}\right)}^{2\left|m_0\right|}\hfill \\ \hfill & {\left(\frac{z}{z_R}\right)}^p{\left|{}_1{F}_1(-\frac{p}{2},\left|m_0\right|+1;\frac{z_R^2{r}^2}{{\omega }_0^2(z^2+iz{z}_R)})\right|}^{2}exp[-\frac{2r^2{z}_R^2}{{\omega }_0^2(z_R^2+z^2)}]\hfill \\ \hfill & {\int }_0^{2\pi }{\int }_0^{2\pi }exp[-i(m-m_0)(\varphi -{\varphi }^{{}^{\prime }})-\frac{2r^2-2r^{2}cos(\varphi -{\varphi }^{{}^{\prime }})}{{\rho }_0^2}]d\varphi d{\varphi }^{{}^{\prime }}\hfill \\ \hfill =& \frac{2^{p+\left|m_0\right|+2}}{\Gamma (p+\left|m_0\right|+1)}·\frac{{\Gamma }^2(\frac{p}{2}+\left|m_0\right|+1)}{{\Gamma }^2(\left|m_0\right|+1)}{[1+{\left(\frac{z}{z_R}\right)}^2]}^{-(\frac{p}{2}+\left|m_0\right|+1)}{\left(\frac{r}{{\omega }_0}\right)}^{2\left|m_0\right|}{\left(\frac{z}{z_R}\right)}^p\hfill \\ \hfill & {\left|{}_1{F}_1(-\frac{p}{2},\left|m_0\right|+1;\frac{z_R^2{r}^2}{{\omega }_0^2(z^2+iz{z}_R)})\right|}^{2}exp[-\frac{2r^2{z}_R^2}{{\omega }_0^2(z_R^2+z^2)}]exp(-\frac{2r^2}{{\rho }_0^2})I_{m-m_0}\left(\frac{2r^2}{{\rho }_0^2}\right)\hfill \end{array}$$

(4)

where $I_{m-m_0(·)}$ is the modified Bessel function of the first kind, and ${\rho }_0$ is the spatial coherence length of the turbulent ocean medium that can be expressed as [11]

$$\begin{array}{cc}\hfill {\rho }_0^{-2}=\frac{1}{3}{\pi }^2{k}^{2}z{\int }_0^{\infty }{\kappa }^3{\varphi }_n\left(\kappa \right)d\kappa =8.705\times {10}^{-8}& k^2{\left(\epsilon \eta \right)}^{-1/3}{\chi }_{t}z(1-2.605{\varpi }^{-1}+7.007{\varpi }^{-2})\hfill \end{array}$$

(5)

${\varphi }_n\left(\kappa \right)$ is the refractive index spectrum of ocean turbulence, ${\chi }_t$ is the dissipation rate of mean-squared temperature, $\epsilon$ is the rate of dissipation of kinetic energy per unit mass of fluid and $\varpi$ is the temperature-salinity contribution ratio.

At the receiver, we use the following indicators to measure the transmission quality of the HyGG vortex beam [24]

$$\begin{array}{cc}\hfill P_m& =\frac{E_m}{{\sum }_{m^{{}^{\prime }}=-\infty }^{\infty }{E}_{m^{{}^{\prime }}}}\hfill \end{array}$$

(6)

where $E_{m^{{}^{\prime }}}$ is the energy of the OAM mode $m^{{}^{\prime }}$ that is calculated as $E_{m^{{}^{\prime }}}={\int }_0^R<{\left|{\beta }_{m^{{}^{\prime }}}(r,z)\right|}^2>rdr$, R is the size of the receiving aperture. If the detected OAM mode m is equal to the transmitted OAM mode $m_0$, $P_{m_0}$ represents the detection probability, the increase of which brings the transmission quality of the HyGG vortex beam.

3. Numerical Simulation

The random phase screens model of oceanic turbulence is an intuitive method to simulate the disturbance of oceanic turbulence on the optical beam propagation [16,17,18]. Here, the oceanic turbulence can be represented by a set of phase screens kept at regular distances, which can adjust the beam’s phase and intensity. Beam propagates freely between the space of adjacent phase screens and the phase perturbations caused by oceanic turbulence are achieved by multiplying the input field with a phase exponential function.

We assume that the beam passing through the Nth phase screen, the beam fields before and after are $M_{N-}(x,y,z)$ and $M_{N+}(x,y,z)$, and they have the following relationship

$$M_{N+}(x,y,z)=M_{N-}(x,y,z)){\theta }_N(x,y)$$

(7)

where ${\theta }_N(x,y)$ is the Nth phase screen. Generally, the phase screen spectrum $F_{\mathsf{\Phi }}(k_x,k_y)$ and the refractive index spectrum ${\varphi }_n(k_x,k_y)$ have the following relationship

$$F_{\mathsf{\Phi }}(k_x,k_y)=2\pi k^2\Delta z{\varphi }_n(k_x,k_y)$$

(8)

where $\Delta z$ is the distance between adjacent phase screens.

A phase screen, $\psi (m\Delta x,n\Delta y)$, in simulation can be described as [19]

$$\begin{array}{cc}\hfill \psi (m\Delta x,n\Delta y)=& FFT[p(j,l)+iq(j,l)]=\sum _{j=0}^{N_x}\sum _{l=0}^{N_y}[p(j,l)+iq(j,l)]exp\left[2\pi i(ml/N_x+nj/N_x)\right]\hfill \end{array}$$

(9)

The spatial-sampling intervals $\Delta x$, $\Delta y$ can be given as $\Delta x$=$L_x/N_x$, $\Delta y$=$L_y/N_y$. $L_x$ and $L_y$ are the sizes of the phase screen sampled uniformly with the sampling points $N_x\times N_y$. The expression of $p(j,l)$, $q(j,l)$ is given by

$$<p^2(j,l)>=<q^2(j,l)>=\Delta k_x\Delta k_y{F}_{\mathsf{\Phi }}(j\Delta k_x,l\Delta k_y)$$

(10)

the spectrum-sampling intervals $\Delta k_x$, $\Delta k_y$ can be given as $\Delta k_x=2\pi /L_x$, $\Delta k_y=2\pi /L_y$.

The above method of generating random phase screens of oceanic turbulence is called split-step method that has the problem of insufficient sampling of spatial low-frequency parts, which can be improved by subharmonic compensation method. Furthermore, the new phase screen can be indicated as [19]

$$\begin{array}{cc}\hfill {\theta }_{uv}(m\Delta x,n\Delta y)=& FFT\left[p\right(u,v,\xi )+iq(u,v,\xi \left)\right]\hfill \\ \hfill =& \sum _{\xi =1}^{N_{\xi }}\sum _{u=-1}^1\sum _{v=-1}^1[p(u,v,\xi )+iq(u,v,\xi )]exp\left[2\pi i(mu/\left(w^{\xi }{N}_x\right)+nv/\left(w^{\xi }{N}_y\right))\right]\hfill \end{array}$$

(11)

where $N_{\xi }$ represents the total order of compensation, $\xi$ is the variable of the compensation order($1\le \xi \le N_{\xi }$), u, v are variants u, v∈ [−1,0,1] and w is the sample level. $p(u,v,\xi )$, $q(u,v,\xi )$ are given by

$$<p^2(u,v,\xi )>=<q^2(u,v,\xi )>=\Delta k_{x\xi }\Delta k_{y\xi }{F}_{\mathsf{\Phi }}(u\Delta k_{x\xi },v\Delta k_{x\xi })$$

(12)

The final phase screen can take on the role of the superposition of the initial phase screen as well as the compensated phase screen

$$\theta =\psi +{\theta }_{uv}.$$

(13)

Based on the extended Huygens–Fresnel principle, the received light field $M_{m_0}^{{}^{\prime }}(r^{{}^{\prime }},{\varphi }^{{}^{\prime }},z)$ of the HyGG vortex beam though the oceanic turbulence can be expressed as [15]

$$\begin{array}{c}\hfill M_{m_0}^{{}^{\prime }}(r^{{}^{\prime }},{\varphi }^{{}^{\prime }},z)=\int M_{m_0}(r,\varphi ,z=0)\frac{exp(ikz+ik\frac{r^2+r^{\prime 2}-2r{r}^{\prime }cos(\varphi -{\varphi }^{\prime })}{2z})}{i\lambda z}exp\left(i\theta (r,\varphi ,r^{\prime },{\varphi }^{\prime })\right)r\mathbf{d}r\mathbf{d}\varphi \end{array}$$

(14)

$\theta$ is determined by Equation (13). Due to crosstalk between different OAM modes $M_m(r^{\prime },{\varphi }^{\prime },z)$ of the HyGG beam at the receiver, the detection probability of the detected OAM mode m can be given as

$$P_m=\frac{|\int M_m^{*}(r^{\prime },{\varphi }^{\prime },z)M_{m_0}^{\prime }(r^{\prime },{\varphi }^{\prime },z)r^{\prime }\mathbf{d}{r}^{\prime }\mathbf{d}{\varphi }^{\prime }{|}^2}{{\sum }_{m^{{}^{\prime }}=-\infty }^{+\infty }{|\int M_{m^{{}^{\prime }}}^{*}(r^{\prime },{\varphi }^{\prime },z)M_{m_0}^{\prime }(r^{\prime },{\varphi }^{\prime },z)r^{\prime }\mathbf{d}{r}^{\prime }\mathbf{d}{\varphi }^{\prime }|}^2}$$

(15)

When the value of the detected OAM mode m is equal to the value of the transmitted OAM mode $m_0$, $p_{m_0}$ represents the detection probability.

4. Results and Discussion

In this section, we use the two methods from the second and the third section to investigate the influences of different oceanic turbulence parameters and initial beam parameters on the detection probability when HyGG vortex beam is passing through oceanic turbulence channels, with the performance of the two methods compared through the research. Ten phase screens were used for simulation, the size of which is 0.8 × 0.8 m${}^2$ with $128\times 128$ points, and for computing each detection probability data point, 1000 realizations were used. The other parameters are set as follows without special instructions: $\epsilon ={10}^{-5}{\mathrm{m}}^2{\mathrm{s}}^{-3},{\chi }_t={10}^{-8}{\mathrm{K}}^2{\mathrm{s}}^{-1},\varpi =-3,\eta ={10}^{-3}\mathrm{m},{\omega }_0={10}^{-2}\mathrm{m},p=2,$$R=1.5\times {10}^{-2}\mathrm{m},m_0=1,\lambda =532\times {10}^{-9}\mathrm{m}$ and $z=50\mathrm{m}$, respectively.

The influence of different oceanic turbulence parameter of dissipation rate of kinetic energy per unit mass of fluid $\epsilon$ changing from ${10}^{-5}$ m${}^2$s${}^{-3}$ to ${10}^{-3}$ m${}^2$s${}^{-3}$ on the detection probability $p_{m_0}$ of the HyGG vortex beam is shown in Figure 1. As can be seen from Figure 1, when $\epsilon$ is given, the detection probability $p_{m_0}$ decreases with the increase of the transmission distance z. For given z, the detection probability $p_{m_0}$ decreases as $\epsilon$ decreases. This is because the turbulence intensity increases with the increase of z and the decrease of $\epsilon$, meaning that the increase of turbulent disturbance leads to a smaller detection probability. In addition, the curves of the two methods overlap at some specific points and such similar phenomenon can also be observed in other figures of this paper, which may arise from the way of simulation. The random numbers are used in the process of generating the random phase screens. Under the same conditions (parameters), different random phase screens would be generated according to the split-step method [19], and the fluctuation of the energy transmitted by the beam may cause such crossover phenomena.

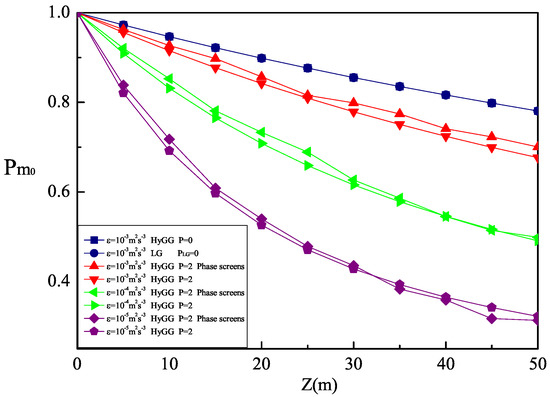
Figure 1. Detection probability $P_{m_0}$ of LG beam against z and that of the HyGG vortex beam against z versus the dissipation rate of kinetic energy per unit mass of fluid $\epsilon$.

Furthermore, we compare the detection probability of the HyGG vortex beam and Laguerre–Gaussian (LG) beam under the same conditions using theoretical derivation method. We note that when the parameter p of the HyGG vortex beam is set to 0, LG beam with radial mode order 0 can be regarded as the special case of the HyGG vortex beam [30], the curves of detection probability for the two beams are coincide with each other as shown in Figure 1, and the same results can also be obtained for the other different parameters which we do not show repeatedly. From Figure 1, we can see that the evolution of detection probability $p_{m_0}$ using the numerical calculation based on theoretical derivation and the numerical simulation based on random phase screens model of oceanic turbulence bear a large proportion of consistency.

Figure 2 shows the effect of dissipation rate of mean-squared temperature ${\chi }_t$, the oceanic turbulence parameter, varying from ${10}^{-9}{\mathrm{k}}^2{\mathrm{s}}^{-1}$ to ${10}^{-7}{\mathrm{k}}^2{\mathrm{s}}^{-1}$, on the detection probability $p_{m_0}$ of the HyGG vortex beam. As can be seen from Figure 2, for given z, the detection probability $P_{m_0}$ of the HyGG vortex beam increases as ${\chi }_t$ decreases, which is due to the fact that the strength of oceanic turbulence decreases as ${\chi }_t$ decreases. Similar to Figure 1, we can also find from Figure 2 that the results obtained by numerical calculation based on theoretical derivation are well in agreement with those obtained by numerical simulation based on random phase screens model of oceanic turbulence.

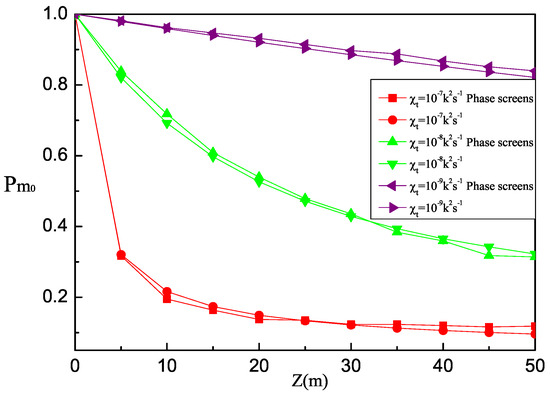
Figure 2. Detection probability $P_{m_0}$ of the HyGG vortex beam against z versus the dissipation rate of mean-squared temperature ${\chi }_t$.

Figure 3 plots the evolution of the detection probability $p_{m_0}$ of the HyGG vortex beam as a function of the temperature-salinity contribution ratio of oceanic turbulence $\varpi$ when the transmission distance z is 10 m, 30 m and 50 m. The value of $\varpi$ ranges from −5 to −1, correspondingly from temperature dominance to salinity dominance. As indicated in Figure 3, $P_{m_0}$ is inversely proportional to $\varpi$ for given z, which implies that the salinity fluctuation in turbulence is more influential to the propagation of the HyGG vortex beam than the temperature fluctuation. We note in Figure 3 that, when the transmission distance is less than 30 m and the value of $\varpi$ is closer to −1, the evolution trend of detection probability $p_{m_0}$ obtained by the two methods is consistent with each other, but the value of $p_{m_0}$ bears a deviation. We think the main reason of this phenomenon is that the random phase screens of oceanic turbulence has the problem of insufficient sampling of spatial low frequency parts, and the salinity fluctuation has more influence on the random phase screens model when the beam transmission distance is small.

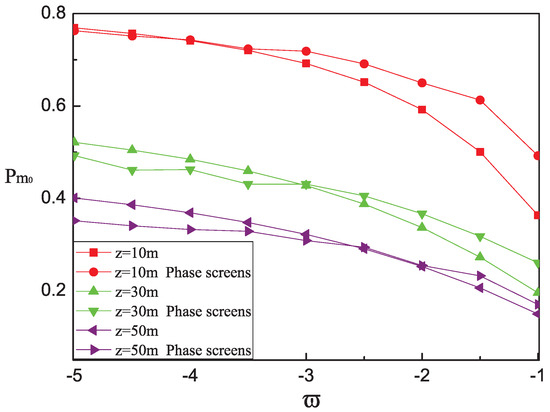
Figure 3. Detection probability $P_{m_0}$ of the HyGG vortex beam as a function of the temperature-salinity contribution ratio $\varpi$ when the transmission distance z is 10 m, 30 m and 50 m.

Next, we investigate the influence of initial beam source parameters on the propagation of the HyGG vortex beam through oceanic turbulence. Figure 4 and Figure 5 illustrate the behavior of detection probability $P_{m_0}$ as a function of z with different topological charge $m_0$ and wavelength $\lambda$, respectively. Because the radius of the beam rises up with the increase of topological charge, the values of the size of the receiving aperture for $m_0=3$ and $m_0=5$ are set as $R=0.17\mathrm{m}$ and $R=0.18\mathrm{m}$ when we carry out the numerical calculations with theoretical derivation. As Figure 4 shows, for given z, the detection probability $P_{m_0}$ is inversely proportional to $m_0$. Compared with HyGG vortex beam with shorter $\lambda$, we can see from Figure 5 that beam with longer $\lambda$ has higher detection probability $P_{m_0}$. According to these results, an anti-turbulence effect enhanced is obtained for the HyGG vortex beam with smaller topological charge and longer wavelengt, which can be considered as the profitable parameter for beam transmission underwater. Meanwhile, we can also see from Figure 4 and Figure 5 that the results through numerical calculation based on theoretical derivation correspond with those brought about by numerical simulation based on random phase screens model of oceanic turbulence.

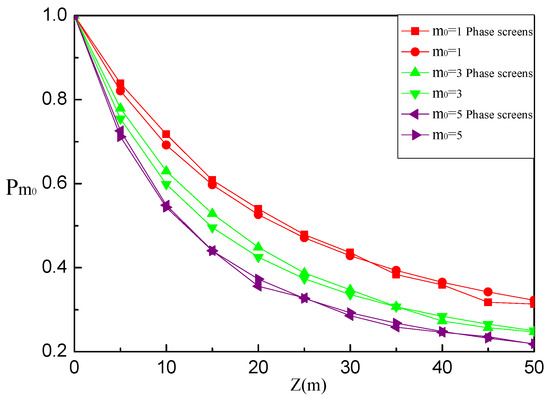
Figure 4. Detection probability $P_{m_0}$ of the HyGG vortex beam against z versus the initial beam parameter of topological charge $m_0$.

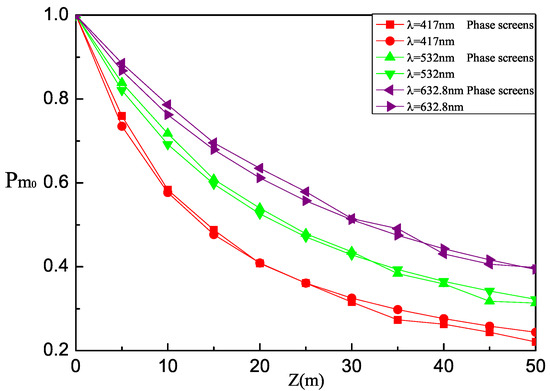
Figure 5. Detection probability $P_{m_0}$ of the HyGG vortex beam against z versus the initial beam parameter of wavelength $\lambda$.

5. Conclusions

In this paper, we have adopted theoretical derivation and numerical simulation to research the propagation properties of the HyGG vortex beam through oceanic turbulence, and the two methods are compared in details by analyzing the influence of different oceanic turbulence parameters together with different initial beam source parameters on the detection probability of the HyGG vortex beam at the receiver. The results have shown that the two methods are consistent in predicting the evolution of the detection probability of HgGG vortex beam propagating through the oceanic turbulence, which proves that numerical simulation method based on random phase screens model of oceanic turbulence is an intuitive and convenient method when it is difficult or even impossible to study the propagation characteristics of vortex beam in oceanic turbulence by theoretical derivation or experiment. Meanwhile, the impact of oceanic turbulence on the HyGG vortex beam has increased with the increase of the dissipation rate of mean-squared temperature and the temperature-salinity contribution ratio. In addition, the impact of oceanic turbulence has decreased with the increase of the dissipation rate of kinetic energy per unit mass of fluid. Furthermore, a HyGG vortex beam with smaller topological charge and longer wavelength can resist the disturbance of oceanic turbulence better. The obtained results are expected to serve as a valuable reference for the development and application of optical communication in the underwater environment.