L2-Gain Based Adaptive Robust Heel/Roll Reduction Control Using Fin Stabilizer during Ship Turns

Abstract

The rolling and heeling experienced by a ship during turning will be more severe under the interference of winds and waves, which will seriously affect the navigation safety of the ship. The fin stabilizer is currently the best active anti-rolling device, which is usually used to reduce the roll of the ship during straight-line sailing. The purpose of this work is to study the use of fin stabilizers to reduce the rolling and heeling during ship turning, considering the non-linearity and uncertainty during the rotation. The 4 degrees of freedom (4-DOF) nonlinear motion model of a multi-purpose naval vessel is established. The forces and moments produced by fin stabilizers, rudders, propellers, and waves are also considered. The nonlinear control model of rotation and roll is derived and established. Given the non-linearity and uncertainty in the ship turning process, an L2-gain based robust adaptive control is proposed to control the fin stabilizers to reduce the turning heel and roll motion. The proof of the stability and the detailed design process of the controller are also given. Simulations are carried out to verify the effectiveness of the proposed control strategy. For comparison purposes, the simulation results under a well-tuned PID controller are also given. The simulation results show that the developed control strategy can effectively reduce the heel and roll during ship turns, and it has good robustness against uncertainty and internal and external interference.

1. Introduction

When a ship is sailing at sea, it will experience movement in six degrees of freedom under the influence of winds, waves, and currents [1]. The roll motion, mainly caused by waves, has the largest impact on ship navigation safety [2]. Researchers and engineers have designed and manufactured a variety of passive or active anti-rolling devices to reduce ship rolling, such as bilge keel [1], anti-rolling tanks [3], moving weights [4], Magnus rotating roll stabilizers [5], and fin stabilizers [1,6,7]. The rudder can also be used to reduce the roll of the ship while maintaining or changing the course [8,9,10]. Among them, the fin stabilizer is currently the most effective active roll reduction device in the world [11].

In the traditional sense, the design and optimization of fin stabilizers are all aimed at minimizing the rolling motion of the ship caused by disturbances, such as sea waves during regular straight-line navigation, to ensure that the ship can sail smoothly and safely [6,12]. However, in some cases, ships also need to be steered for turning. The ship will also undergo a certain amount of rolling and heeling motions during turning in calm water [10]. For military ships, in order to avoid dangers, such as incoming torpedoes, emergency maneuvers with large rudder angles are required at high speeds [12]. At this time, the rolling and heeling motions experienced by the ship will be quite large. If there are certain disturbances, such as waves during the turning process, the rolling motion of the ship will be more severe, which will seriously affect the navigation safety of the ship. At the same time, the large-angle heeling will also affect the normal use of shipboard radar and weapons, and affect the normal work of ship personnel. This paper mainly studies the influence of fin stabilizers on the turning performance of ships and discusses the use of fin stabilizers to reduce the ship’s heeling and rolling during high-speed and large rudder angle turning.

Therefore, it is of more practical significance to use existing anti-rolling devices such as fin stabilizers to reduce roll and heel during ship turning. The French Charles de Gaulle aircraft carrier installed the Cogite system under the flight deck to reduce the heel during emergency turning to ensure a stable take-off and landing environment for the carrier aircraft [13]. Martin proposed a three-step control strategy to control the fin stabilizer to achieve the purpose of controlling heel and turning circle [12]. Wang designed a neuron adaptive PID controller to control the fin stabilizer to realize the roll reduction control during ship turns [14]. Zhang studied the influence of passive anti-rolling tanks on ship turning characteristics [15]. Liang et al. studied the influence of rudder type parameters on ship turning [16]. Liu proposed PID control based on particle swarm optimization to reduce the rolling motion during ship turning [17]. Liang et al. Developed an improved PID controller based on multi-island genetic algorithm to reduce the roll during ship turns [18]. The fin stabilizers of most ships are controlled by a PID controller developed using classical control theory [2,19]. The control parameters are usually designed and obtained using a simplified model for a limited number of environment conditions [19,20]. Uncertain parameters and environmental disturbances will decrease the control effect. Perez and Blanke pointed out that one of the key issues in roll reduction control is the adaptation to the changes in the environmental conditions [6]. Compared with the straight-line heading state, the nonlinearities and uncertainties of the ship in the turning process are more significant. For such a nonlinear system with uncertainty, it is difficult for conventional linear methods to achieve ideal control results.

So far, the control research on uncertain nonlinear systems can be divided into three categories: one is to use adaptive control methods to solve the uncertainty of non-matching conditions of nonlinear systems; the other is to use robust control methods to ensure the internal stability and disturbance attenuation of the closed-loop system; the third is a combination of the first two methods, that is, the adaptive robust control method. All of them can enhance the robustness of nonlinear systems to uncertainties, so they have attracted the attention of experts and scholars in the field of ship motion control with extensive uncertainty and non-linearity. Zhang et al. discussed the application of L2-gain robust adaptive control in force control fin stabilizer system [21]. Wang and Zhang designed the rudder-fin joint nonlinear robust controller based on backstepping and closed-loop gain shaping method and achieved good results through simulation [22]. Li et al. designed a robust adaptive control strategy for underwater remote-controlled submersibles with speed constraints [23]. Kahveci and Ioannou proposed an adaptive steering control method including linear quadratic controller and anti-saturation compensator based on Riccati for uncertain ship dynamics affected by input constraints [24]. Zhang et al. proposed a control scheme based on a simplified adaptive neural network to solve the problem of adaptive path following control of under-driven ships with model uncertainty and non-zero mean time-varying disturbances [25]. Considering the modeling error and the uncertainty of environmental interference, Hinostroza et al. proposed a robust fin controller based on L2-gain to reduce the rolling motion of surface ships [19]. Demirel and Alarcin designed H2 and H∞ state feedback controllers based on linear matrix inequalities for fin stabilization for the effects of roll nonlinearity and uncertainty [26]. Zwierzewice uses a robust adaptive feedback linearization method to complete the design of the ship’s automatic steering instrument controller [27]. Sun et al. proposed a nonlinear robust adaptive scheme based on PI sliding mode control and interference upper limit estimation to improve the robustness of the under-driven surface ship motion control system with model uncertainty and environmental disturbance [28]. Aiming at the uncertainty and environmental disturbance, in this paper, an adaptive robust control method based on L2-gain is adopted to design the fin controller to reduce the heeling and rolling during ship turns.

The structure of the paper is as follows. Section 2 establishes the mathematical models of the ship motion and the forces and moments acting on the hull. Section 3 discusses the effect of fin stabilizers on ship turning motion. Section 4 obtains the control model and designs the L2-gain adaptive robust controller. Section 5 gives the simulation results and discussion. Finally, the conclusion is given.

2. Ship Motion Model

2.1. 4-DOF Motion Model

In order to accurately describe the motion of the ship with six degrees of freedom, the inertial coordinate system and the body-fixed coordinate system are established, as shown in Figure 1.

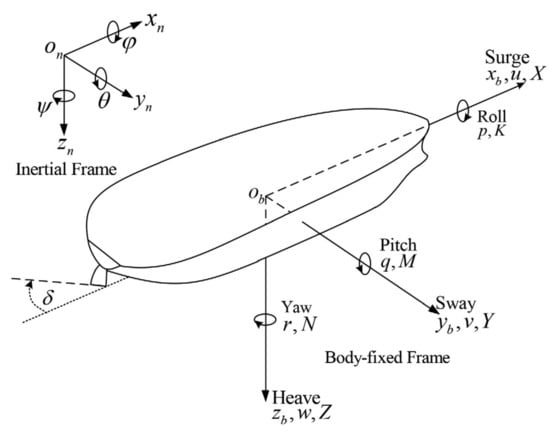
Figure 1. Coordinate system for ship modeling.

Regarding the ship as a rigid body, the 6-DOF nonlinear equations of ship motion can be obtained by Newton’s law [29]. Since this paper mainly studies the use of fin stabilizer to reduce the heeling and rolling motion caused by ship turning and environmental disturbance, the pitch and heave attitudes, and their influence on the other four degrees of freedom can be neglected [30]. Therefore, the 4-DOF ship motion model in the surge, sway, roll and yaw can be obtained by Equation (1):

$$\begin{array}{c}\hfill m\left(\dot{u}-vr-x_G{r}^2+z_{G}pr\right) = X\\ \hfill m\left(\dot{v}+ur-z_G\dot{p}+x_G\dot{r}\right) = Y\\ \hfill I_x\dot{p}-m{z}_G\left(\dot{v}+ur\right) = K\\ \hfill I_z\dot{r}+m{x}_G\left(\dot{v}+ur\right) = N\end{array}$$

(1)

where m is the ship mass, x_G and z_G are the coordinates of the center of gravity (CG) in x and z axes, respectively, I_x and I_z are the moments of inertia about the x and z axes, u and v are the surge and sway velocity, respectively, p and r are the roll and yaw angular velocity, X and Y are the forces acting on the hull in x and y axes direction, respectively, K and N are the moments acting on the hull about x and z axes, respectively.

2.2. Hydrodynamic Forces and Moments

The hydrodynamic forces and moments can be expressed in the form of nonlinear functions of the ship’s position, velocity and acceleration, and are influenced by the shipping state and fluid characteristics [29]. In this paper, the nonlinear hydrodynamic expression is adopted as [1]:

$$\begin{array}{cc}\hfill X_{hyd}=& X_{\dot{u}}\dot{u}+X_{u\left|u\right|}u\left|u\right|+X_{vr}vr\hfill \\ \hfill Y_{hyd}=& Y_{\dot{v}}\dot{v}+Y_{\dot{p}}\dot{p}+Y_{\dot{r}}\dot{r}+Y_{\left|u\right|v}\left|u\right|v+Y_{ur}ur+Y_{v\left|v\right|}v\left|v\right|+Y_{v\left|r\right|}v\left|r\right|+Y_{r\left|v\right|}r\left|v\right|+\hfill \\ & Y_{\phi \left|uv\right|}\phi \left|uv\right|+Y_{\phi \left|ur\right|}\phi \left|ur\right|+Y_{\phi uu}\phi uu\hspace{0.33em}\hfill \\ \hfill K_{hyd}=& K_{\dot{v}}\dot{v}+K_{\dot{p}}\dot{p}+K_{\left|u\right|v}\left|u\right|v+K_{ur}ur+K_{v\left|v\right|}v\left|v\right|+K_{v\left|r\right|}v\left|r\right|+K_{r\left|v\right|}r\left|v\right|+\hfill \\ & K_{\phi \left|uv\right|}\phi \left|uv\right|+K_{\phi \left|ur\right|}\phi \left|ur\right|+K_{\phi uu}\phi uu+K_{\left|u\right|p}\left|u\right|p+K_{\left|p\right|p}\left|p\right|p+K_{p}p+\hfill \\ & K_{\phi \phi \phi }\phi \phi \phi -\rho g\nabla GZ\left(\phi \right)\hfill \\ \hfill N_{hyd}=& N_{\dot{v}}\dot{v}+N_{\dot{r}}\dot{r}+N_{\left|u\right|v}\left|u\right|v+N_{\left|u\right|r}\left|u\right|r+N_{r\left|r\right|}r\left|r\right|+N_{r\left|v\right|}r\left|v\right|+N_{\phi \left|uv\right|}\phi \left|uv\right|+\hfill \\ & N_{\phi u\left|r\right|}\phi u\left|r\right|+N_{\left|p\right|p}\left|p\right|p+N_{p}p+N_{\left|u\right|p}\left|u\right|p+N_{\phi u\left|u\right|}\phi u\left|u\right|\hspace{0.33em}\hfill \end{array}$$

(2)

where ρ is the fluid density, g is the gravity acceleration, ∇ is the ship displacement, φ is the roll angle, GZ(φ) is the righting arm curve, and the multipliers are the ship’s hydrodynamic coefficients.

2.3. Wave Disturbance Forces and Moments

Disturbances experienced by ships sailing at sea are mainly caused by sea winds, waves, and currents. Among them, sea waves are the main cause of ship rolling. Considering the research content of this paper, the disturbance forces and moments produced by sea waves are considered, and the wave forces and moments model is adopted as [31]:

$$\begin{array}{l}{X}_{wave}=-\rho g\cos \chi {\displaystyle \sum _{n=1}^{NN}{E}_n}\frac{{\omega }_n^2}{g}[A_n\cos \left({\omega }_{e}t+{\epsilon }_n\right)\hspace{0.33em}\hspace{0.33em}-B_n\sin \left({\omega }_{e}t+{\epsilon }_n\right)]\\ Y_{wave}=\rho g\sin \chi {\displaystyle \sum _{n=1}^{NN}{E}_n}\frac{{\omega }_n^2}{g}[A_n\cos \left({\omega }_{e}t+{\epsilon }_n\right)\hspace{0.33em}\hspace{0.33em}-B_n\sin \left({\omega }_{e}t+{\epsilon }_n\right)]\\ K_{wave}=-\rho g\sin \chi {\displaystyle \sum _{n=1}^{NN}{E}_n}\frac{{\omega }_n^2}{g}[C_n\cos \left({\omega }_{e}t+{\epsilon }_n\right)\hspace{0.33em}\hspace{0.33em}-D_n\sin \left({\omega }_{e}t+{\epsilon }_n\right)]\\ N_{wave}=\rho g\sin \chi {\displaystyle \sum _{n=1}^{NN}{E}_n}\frac{{\omega }_n^2}{g}[G_n\cos \left({\omega }_{e}t+{\epsilon }_n\right)\hspace{0.33em}\hspace{0.33em}-H_n\sin \left({\omega }_{e}t+{\epsilon }_n\right)]\end{array}$$

(3)

where

$$A_n={\displaystyle \int F_n}\left(x\right)A\left(x\right)\sin \left(\frac{{\omega }_n^2}{g}x\cos \chi \right)dx,B_n={\displaystyle \int F_n}\left(x\right)A\left(x\right)\cos \left(\frac{{\omega }_n^2}{g}x\cos \chi \right)dx$$

$$C_n={\displaystyle \int F_n}\left(x\right)z_{B\left(x\right)}A\left(x\right)\sin \left(\frac{{\omega }_n^2}{g}x\cos \chi \right)dx,D_n={\displaystyle \int F_n}\left(x\right)z_{B\left(x\right)}A\left(x\right)\cos \left(\frac{{\omega }_n^2}{g}x\cos \chi \right)dx$$

$$G_n={\displaystyle \int F_n}\left(x\right)xA\left(x\right)\sin \left(\frac{{\omega }_n^2}{g}x\cos \chi \right)dx,H_n={\displaystyle \int F_n}\left(x\right)xA\left(x\right)\cos \left(\frac{{\omega }_n^2}{g}x\cos \chi \right)dx$$

$$F_n=\sin \left(\frac{{\omega }_n^2}{g}\frac{B\left(x\right)}{2}\sin \chi \right)e^{\frac{{\omega }_n^2}{g}d\left(x\right)}/\frac{{\omega }_n^2}{g}\frac{B\left(x\right)}{2}\sin \chi ,E_n=\sqrt{2S_{\zeta }\left({\omega }_n\right)\mathsf{\Delta }\omega }$$

where A_n, B_n, C_n, D_n, G_n and H_n are the corresponding coefficients of the first-order wave disturbance forces and moments. A(x), B(x), d(x) and z_B(x) are the cross-section area of water immersion, beam, draft and the z coordinate of the center of the cross-section area of water immersion at the ship’s longitudinal coordinate of x, respectively. ω_n and ω_e are the wave frequency and encounter frequency, respectively. χ is the encounter angle. ε_n and S_ζ(ωn) are the random phase and wave-height spectrum of the nth regular wave, respectively. NN is the number of regular waves.

2.4. Fin Forces and Moments

Fin stabilizers are installed in pairs on both sides of the bilge of the ship to have a large roll arm and anti-rolling moment. According to [1], the fin forces and moments can be approximated as:

$$\begin{array}{c}{X}_{fin}\approx -2T_f\hfill \\ Y_{fin}\approx 2N_f\cdot \sin \left({\beta }_{fin}\right)\hfill \\ K_{fin}\approx -2r_f\cdot N_f\hfill \\ N_{fin}\approx -2FCG\cdot N_f\cdot \sin \left({\beta }_{fin}\right)\hfill \end{array}$$

(4)

where r_f and FCG are the fin’s roll and yaw arms, respectively, β_fin is the fin’s tilt angle, T_f and N_f are the fin-induced tangential and normal forces, respectively, and can be calculated by Equation (5):

$$\begin{array}{l}{N}_f=D_f\sin {\alpha }_f+L_f\cos {\alpha }_f\\ T_f=D_f\cos {\alpha }_f-L_f\sin {\alpha }_f\end{array}$$

(5)

where L_f and D_f are the lift and drag forces generated on the fin, respectively, α_f is the effective fin angle of attack.

2.5. Rudder Forces and Moments

The vast majority of ships rely on one or more vertical installed rudders to accomplish all the maneuvers [12]. Rudders are usually installed after the propeller below the stern line of the ship. According to [14], the rudder-induced forces and moments can be obtained, as shown in Equation (6)

$$\begin{array}{c}{X}_{rud}=-D_r\cdot \delta \hfill \\ Y_{rud}=L_r\cdot \delta \hfill \\ K_{rud}=-r_r\cdot L_r\cdot \delta \hfill \\ N_{rud}=-LCG\cdot L_r\cdot \delta \hfill \end{array}$$

(6)

where r_r and LCG are the rudder’s roll and yaw arms, respectively, δ is the fin tilt angle, L_r and D_r are the lift and drag forces generated on the fin, respectively.

2.6. Propeller Forces and Moments

Most ships rely on propellers under the waterline of the stern to provide forward power. Under normal conditions, it can be considered that the propellers only produce a longitudinal force that drives the ship forward or backwards. When the ship sails straight at a constant speed, it can be considered that the effective thrust T_e generated by the propeller is equal to the ship resistance X_R. Perez suggested that the ship resistance can be considered to be approximately equal to X_|u|uU², where U is the ship sailing speed [1]. Martin pointed out through simulation that for ship turning at a fixed speed, the thrust generated by the propellers during the turning process can be approximately equal to the force before the turning and remains unchanged to simplify the study [12]. Therefore, according to [12], the forces and moments can be obtained, as shown in Equation (7):

$$\begin{array}{c}{X}_{prop}=-X_{\left|u\right|u}{U}_0^2\hfill \\ Y_{prop}=0\hfill \\ K_{prop}=0\hfill \\ N_{prop}=0\hfill \end{array}$$

(7)

where X_|u|u is the hydrodynamic coefficient related to the surge velocity, and U₀ is the initial speed before turning.

3. Ship Heel/Roll Control Using Fin

A multipurpose naval vessel with fin stabilizers and rudders is selected as the research object, the parameters of the vessel, fin and rudder are shown in Table 1 and Table 2, respectively. The fin angle that rolls the ship to port is defined as the positive fin angle. The rudder angle that turns the ship left is defined as the positive rudder angle. The seawater density is 1025 kg/m³. The hydrodynamic coefficients presented in Section 2.2 are shown in Table 3, where m is the mass of the ship and ∆ is the buoyancy of the ship.

Table 1. Parameters of the vessel.

Description	Value	Unit
Length between perpendiculars	51.5	m
Beam overall	8.6	m
Draft	2.3	m
Displacement	357	m3
Transverse metacentric height	1.1	m
Roll inertia	2.38 × 106	kg·m2
Yaw inertia	4.79 × 107	kg·m2
Coordinates of center of gravity	(−3.38, 0, −1.06)	m

Table 2. Parameters of the fin and rudder.

Description	Fin	Rudder	Unit
Area	1.6 × 2	1.5 × 2	m2
Aspect ratio	1	1.5	–
Max. angle of attack	25	35	°
Max. turning rate	15	10	°/s
Roll arm	4.22	3.3	m
Yaw arm	−2	20.4	m
Lift coefficient	0.042	0.044	/°
Tilt angle	34	90	°

Table 3. Hydrodynamic coefficients (from [1]).

Subscript	X	Y	K	N
$\dot{u}$	−1.74 × 104	0	0	0
$\dot{v}$	0	−1.90 × 106	2.96 × 105	5.38 × 105
$\dot{p}$	0	−2.96 × 105	−6.74 × 105	0
$\dot{r}$	0	−1.40 × 106	0	−4.40 × 107
$u\left|u\right|$	−1.96 × 103	0	0	0
$\left|u\right|v$	0	−1.18 × 104	9.26 × 103	−9.20 × 104
$\left|u\right|r$	0	1.31 × 105	−1.02 × 105	−4.71 × 106
$v\left|v\right|$	0	−3.70 × 103	2.93 × 104	0
$\left|r\right|r$	0	0	0	−2.02 × 108
$\left|v\right|r$	0.33 × m	−7.94 × 105	6.21 × 105	0
$r\left|v\right|$	0	−1.82 × 105	1.42 × 105	−1.56 × 107
$\phi \left|uv\right|$	0	−1.08 × 104	−8.40 × 103	−2.14 × 105
$\phi \left|ur\right|$	0	−2.51 × 105	−1.96 × 105	−4.98 × 106
$\phi uu$	0	−7.40 × 101	−1.18 × 103	−8.00 × 103
$\left|u\right|p$	0	0	−1.55 × 104	0
$\left|p\right|p$	0	0	−4.16 × 105	0
$p$	0	0	−5.00 × 105	0
$\phi \phi \phi$	0	0	−0.325∆	0

The correctness and applicability of the established model have been verified in our previous work [10]. Figure 2 shows the simulation results of ship turning motion under different sea states. The simulation parameters are as follows: the initial ship speed is 15 m/s, the fin angle is 0°, the rudder angle is 30°, the rudder rate is 10°/s, the initial encounter angle is 90°.

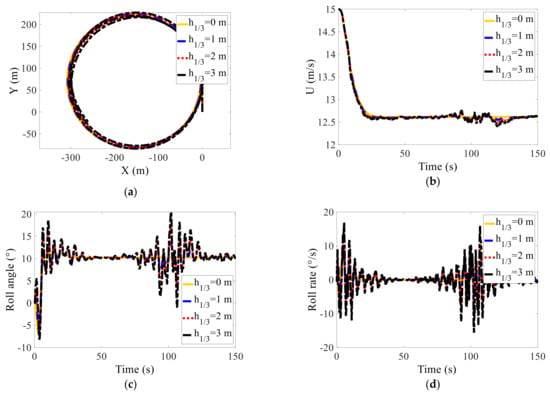
Figure 2. Simulation results of ship turning motion under different sea states. (a) Trajectory; (b) ship speed; (c) roll angle; (d) roll rate.

It can be seen from Figure 2 that the turning trajectory of the ship under the interference of sea waves has a slight deviation compared to that in calm water, and the turning diameter is basically unchanged. The outward heel and ship speed in the steady turning phase also changed irregularly on the basis of the steady outward heel angle and the steady sailing speed of the turning in clam water, respectively. As the level of sea conditions increases, the changes in the state of motion, especially the turning heel, are also intensified. Under the interference of the waves with a significant wave height of 3 m, the turning outward heel angle reaches a maximum of 20°, which seriously affects the navigation safety and comfort of the ship. Therefore, the ship should try to avoid turning manoeuvres in higher sea conditions. The sea state level of the subsequent heel/roll reduction control simulations in this paper is limited to sea state 3 with a significant wave height of 1.25 m.

3.1. Ship Turning Motion with Fin Stabilizer

To investigate the effect of fin stabilizer on ship turning motion, the simulation of the ship turning in calm water with different fin angles of attack is conducted. The initial ship speed is 15 m/s, the rudder angle of attack is 30° and the rudder turning rate is 10°/s. The simulation results with fin angle of −20°, −10°, 0°, 10°, and 20° are shown in Figure 3. The main results data are given in Table 4. It should be noted that the total simulation time is 100 s, and the simulation results of the first 50 s of the roll angular velocity are given to clearly show the changes in the transition process.

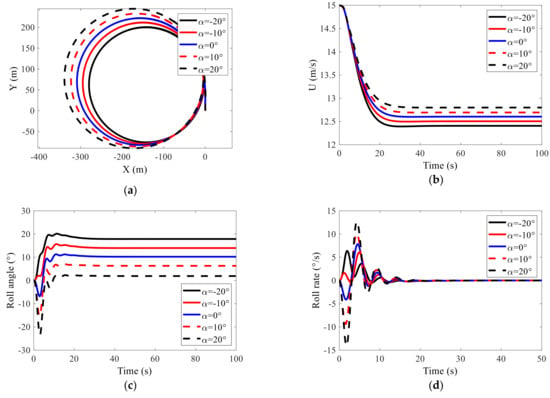
Figure 3. Simulation results of ship turning motion under different fin angles. (a) Trajectory; (b) ship speed; (c) roll angle; (d) roll rate.

Table 4. Simulation results of turning circle parameters under different fin angles.

Fin Angle (°)	Advance (m)	Steady Turning Diameter (m)	Max. Inward/Outward Heel Angle (°)	Steady Outward Heel Angle (°)	Steady Sailing Speed (m/s)
−20	198.63	276.29	0/20.14	17.86	12.41
−10	208.98	290.68	0/15.67	13.96	12.50
0	218.92	304.53	−6.79/11.29	10.22	12.60
10	229.45	318.57	−15.29/7.01	6.30	12.69
20	241.05	334.41	−23.36/2.30	1.91	12.80

It can be seen from Figure 3 and Table 4 that the positive and negative fin angles have opposite effects on the ship’s turning performance, and the strength of the influence increases as the fin angle increases. Under the action of a positive fin angle, the advance, turning radius and initial inward heel are increased compared to when the rudders act alone, while the maximum and steady outward heel angles are reduced. When the negative fin angle is acting, the opposite is true. In addition to the relatively small impact of the fin stabilizer on the speed reduction of turning, it also has a greater impact on other parameters such as the advance, turning diameter and turning heel. Therefore, the fin stabilizer can be used to assist the rudder to change the ship’s turning characteristics. In addition, it can be seen from the simulation results that the influence of the fin stabilizer on the steady turning diameter and steady outward heel is exactly the opposite. If one is reduced, the other is bound to increase. It is necessary to adjust the corresponding weight coefficients according to different control objectives to achieve relatively optimal control effects.

3.2. Fin Angle Speed Adjustment

It can be seen from the simulation results in Section 3.1 that fin stabilizers can be used to reduce the heel and roll motion during ship turns. It should be noted that to explore the law, the fin angle speed adjustment is not considered when setting the fin angle in the simulation of the front section. In the actual navigation of the ship, to protect the fin shaft from damage at high speeds, the speed adjustment problem must be considered when using fin stabilizers to reduce roll, which is, adjusting the maximum angle of attack of the fin according to the speed. In order to make the simulation results closer to the real situation, in this paper, the following fin angle speed adjustment law is adopted [32]:

$${\alpha }_{\max }^{*}=\left\{\begin{array}{cc}0\hfill & U<U_{L1},U<U_{L2}\hfill \\ {\alpha }_{\max }\hfill & U_{L1}\le U\le U_{design},U_{L2}\le U\le U_{design}\hfill \\ {\left(U_{design}/U\right)}^2{\alpha }_{\max }\hfill & U>U_{design}\hfill \end{array}\right.$$

(8)

where α*_max is the real-time maximum fin angle, α_max is the maximum fin angle corresponding to the design speed, U_design is the design speed. In this paper, U_design and α_max are set to 18 kn and 25°, respectively.

4. Heel/Roll Reduction Control Using Fin Stabilizers

Based on the above discussion, the diagram of the heel/roll reduction control system using fin stabilizers during ship turns, as shown in Figure 4, can be obtained.

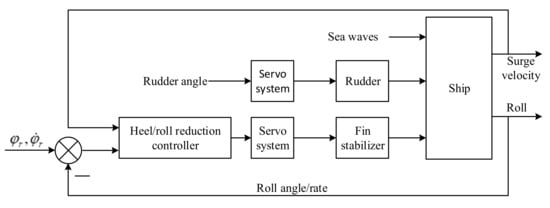
Figure 4. Diagram of heel/roll reduction control using fin stabilizers during ship turns.

4.1. Control Model Analysis

As mentioned earlier, when using fin stabilizers to reduce the heel during the turning process, it will inevitably increase the turning diameter of the ship. Therefore, in order to simplify the analysis, only one degree of freedom of roll is considered. From the mathematical model of ship motion established in Section 2, the ship’s roll model is given by Equation (9):

$$\begin{array}{cc}\hfill I_x\dot{p}-m{z}_G\left(\dot{v}+ur\right)=& K_{\dot{v}}\dot{v}+K_{\dot{p}}\dot{p}+K_{\left|u\right|v}\left|u\right|v+K_{ur}ur+K_{\left|v\right|v}\left|v\right|v+K_{\left|v\right|r}\left|v\right|r+\hfill \\ & K_{\varphi \left|uv\right|}\varphi \left|uv\right|+K_{\varphi \left|ur\right|}\varphi \left|ur\right|+K_{\varphi uu}\varphi uu+K_{\left|u\right|p}\left|u\right|p+K_{\left|p\right|p}\left|p\right|p+\hfill \\ & K_{p}p+K_{\varphi \varphi \varphi }\varphi \varphi \varphi -\rho g\nabla GMt\sin \left(\varphi \right)+K_{rud}+K_{fin}+K_{\mathrm{w}}\hfill \end{array}$$

(9)

Liang et al. pointed out that the sway acceleration term has little effect on the roll, and can be neglected [18]. In addition, when φ < 28°, sin(φ) can be approximately regarded as equal to φ. Therefore, ignoring the sway acceleration term and rewriting K_fin as K_fαf, Equation (9) can be rewritten as:

$$\begin{array}{ll}\hfill \left(I_x-K_{\dot{p}}\right)\dot{p}=& \left(K_{\left|u\right|p}\left|u\right|+K_p\right)p+K_{\left|p\right|p}\left|p\right|p+\hfill \\ & \left(K_{\varphi \left|uv\right|}\left|uv\right|+K_{\varphi \left|ur\right|}\left|ur\right|+K_{\varphi uu}uu-\rho g\nabla GMt\right)\varphi +K_{\varphi \varphi \varphi }\varphi \varphi \varphi +\hfill \\ & K_{\left|u\right|v}\left|u\right|v+K_{ur}ur+K_{\left|v\right|v}\left|v\right|v+K_{\left|v\right|r}\left|v\right|r+K_{\left|r\right|v}\left|r\right|v+m{z}_{G}ur+K_{rud}+K_f{\alpha }_f+K_{\mathrm{w}}\hfill \end{array}$$

(10)

where K_f = ρA_fu²C_Lr_f, C_L is the lift coefficient of the fin and A_f is the fin area.

Define υ = α_f, and Equation (10) can be further simplified as:

$$\dot{p}={\theta }_{1}p+{\theta }_2\left|p\right|p+{\theta }_3\varphi +{\theta }_4{\varphi }^3+b\upsilon +f_w$$

(11)

where

$${\theta }_1=\left(K_{\left|u\right|p}\left|u\right|+K_p\right)/\left(I_x-K_{\dot{p}}\right),{\theta }_2=K_{\left|p\right|p}/\left(I_x-K_{\dot{p}}\right)$$

$${\theta }_3=\left(K_{\varphi \left|uv\right|}\left|uv\right|+K_{\varphi \left|ur\right|}\left|ur\right|+K_{\varphi uu}uu-\rho g\nabla GMt\right)/\left(I_x-K_{\dot{p}}\right)$$

$$b=K_f/\left(I_x-K_{\dot{p}}\right)$$

$$f_w=\left(K_{\left|u\right|v}\left|u\right|v+K_{ur}ur+K_{\left|v\right|v}\left|v\right|v+K_{\left|v\right|r}\left|v\right|r+m{z}_{G}ur+K_{rud}+K_{\mathrm{w}}\right)/\left(I_x-K_{\dot{p}}\right)$$

It can be seen that the equation describing the roll motion in the turning process is strongly nonlinear, and the parameters of the equation still have greater uncertainty due to the speed reduction of turning and the influence of external interference. In this paper, the L2-gain based adaptive robust control method is adopted to design the fin controller to reduce the turning heel and roll motion.

4.2. Controller Design

4.2.1. L2-Gain Adaptive Robust Control

For the disturbed uncertain nonlinear system described in Equation (12), suppose it satisfies the following assumptions in a certain neighborhood of the origin of the state space [33].

$$\left\{\begin{array}{c}{\dot{x}}_i=x_{i+1}+{\gamma }_i^T\left(x_1,x_2,\cdots ,x_i\right),1\le i\le n-1\hfill \\ {\dot{x}}_n={\gamma }_0(x)+{\gamma }_n^T(x)\theta +\left({\beta }_0(x)-{\beta }^T(x)\theta \right)\upsilon +\eta \left(x,t\right)\hfill \\ y=x_1\hfill \end{array}\right.$$

(12)

where x∈Rⁿ, υ∈R, y∈R, and η∈R are the state vector, input, output and bounded disturbance of the system, respectively, γ_i(x) and β(x) are smooth vector fields with 0 ≤ i ≤ n, θ = (θ1,θ2,…,θp)^T∈L₂(0,∞) is the uncertain disturbance.

Hypothesis 1: (assumption of bounded interference) there is a constant d greater than zero, satisfying|η(x,t)| ≤ d;

Hypothesis 2: (achievable condition hypothesis) let $\widehat{\theta }$ be the estimate of θ, for any $\widehat{\theta }$∈B_θ and x∈B_x, it needs to satisfy |β₀(x) + β^T(x)$\widehat{\theta }$| > 0, where B_θ and B_x are the open balls that contain $\widehat{\theta }$ and x respectively in the parameter space. Compared with the control period, θ∈L₂(0,∞) is usually regarded as a slowly changing quantity, so it can be approximately equal to zero.

Then, introduce the following theorem as [34].

Theorem 1.

For any positive real constant γ > 0, if the perturbed nonlinear system described in Equation (12), for any T ≥ 0 and θ∈L₂(0,T), satisfy.

$${{\displaystyle {\int }_0^T‖y\left(t\right)‖}}^{2}dt\le {\gamma }^2{{\displaystyle {\int }_0^T‖\theta ‖}}^{2}dt+N$$

(13)

where N ≥ 0 is a finite constant, then the disturbing uncertain nonlinear system Equation (12) has L2-gain ≤ γ.

The design steps of L2-gain adaptive robust controller based on the backstepping method are briefly given below. For succinct description, let γ_i(x1, x2, …, xi) be γ_i, then when i = 1, we can get from Equation (12):

$${\dot{x}}_1=x_2+{\gamma }_1^T\theta$$

(14)

Assume x₂* is the control input of the subsystem (14), and defined by Equation (15)

$$x_2^{\ast }=-c_1{x}_1-\frac{1}{4}k{x}_1\left(1+{\gamma }_1^T{\gamma }_1\right)$$

(15)

where c₁ > 0 and k > 0 are undetermined coefficients.

Define the error term e₂ = x₂ − x₂*, then

$$x_2=e_2+x_2^{\ast }=e_2-c_1{x}_1-\frac{1}{4}k{x}_1\left(1+{\gamma }_1^T{\gamma }_1\right)$$

(16)

Define the Lyapunov function V₁ as

$$V_1=\frac{1}{2}{x}_1^2$$

(17)

Then we have Equation (18)

$${\dot{V}}_1=x_1{\dot{x}}_1=x_1\left(x_2+{\gamma }_1^T\theta \right)$$

(18)

Substitute Equation (16) into (18), we can get Equation (19)

$${\dot{V}}_1=x_1{e}_2-c_1{x}_1^2-\frac{1}{4}k{x}_1^2\left(1+{\gamma }_1^T{\gamma }_1\right)+x_1{\gamma }_1^T\theta$$

(19)

The last two terms on the right side of Equation (19) can be rewritten as

$$-\frac{1}{4}k{x}_1^2\left(1+{\gamma }_1^T{\gamma }_1\right)+x_1{\gamma }_1^T\theta =-k{\left(\frac{1}{2}{x}_1\sqrt{1+{\gamma }_1^T{\gamma }_1}-\frac{{\gamma }_1^T\theta }{k\sqrt{1+{\gamma }_1^T{\gamma }_1}}\right)}^2+\frac{{\left({\gamma }_1^T\theta \right)}^2}{k\left(1+{\gamma }_1^T{\gamma }_1\right)}\le \frac{1}{k}{‖\theta ‖}^2$$

(20)

Let e₁ = x₁, then we have Equation (21)

$${\dot{V}}_1\le -c_1{x}_1^2+\frac{1}{k}{‖\theta ‖}^2+e_1{e}_2$$

(21)

For i = 2, define the Lyapunov function V₂ as

$$V_2=V_1+\frac{1}{2}{e}_2^2$$

(22)

Then we have Equation (23)

$${\dot{V}}_2={\dot{V}}_1+e_2{\dot{e}}_2\le -c_1{e}_1^2+\frac{1}{k}{‖\theta ‖}^2+e_2{e}_1+e_2{\dot{e}}_2$$

(23)

From the definition of the previous error term e₂, we can get Equation (24)

$${\dot{e}}_2={\dot{x}}_2-{\dot{x}}_2^{\ast }=x_3-\frac{\partial x_2^{\ast }}{\partial x_1}{x}_2+{\left({\gamma }_2-\frac{\partial x_2^{\ast }}{\partial x_1}{\gamma }_1\right)}^T\theta$$

(24)

Substitute Equation (24) into (23), we have

$${\dot{V}}_2\le -c_1{e}_1^2+\frac{1}{k}{‖\theta ‖}^2+e_2{e}_1+e_2\left(x_3-\frac{\partial x_2^{\ast }}{\partial x_1}{x}_2+{\left({\gamma }_2-\frac{\partial x_2^{\ast }}{\partial x_1}{\gamma }_1\right)}^T\theta \right)$$

(25)

If α₂₁ and α₂₂ are

$${\alpha }_{21}=e_1-\frac{\partial x_2^{\ast }}{\partial x_1}{x}_2,\hspace{0.33em}\hspace{0.33em}{\alpha }_{22}={\gamma }_2-\frac{\partial x_2^{\ast }}{\partial x_1}{\gamma }_1$$

(26)

Then Equation (25) can be further written as

$${\dot{V}}_2\le -c_1{e}_1^2+\frac{1}{k}{‖\theta ‖}^2+e_2\left(x_3+{\alpha }_{21}+{\alpha }_{22}^T\theta \right)$$

(27)

Let $x_3^{*}$ be the control input of the second subsystem, and define

$$x_3^{*}=-c_2{e}_2-{\alpha }_{21}-\frac{1}{4}k{e}_2\left(1-{\alpha }_{22}^T{\alpha }_{22}\right)$$

(28)

Moreover, define the error term e₃ between x₃ and $x_3^{*}$ as

$$e_3=x_3-x_3^{\ast }=x_3+c_2{e}_2+{\alpha }_{21}+\frac{1}{4}k{e}_2\left(1-{\alpha }_{22}^T{\alpha }_{22}\right)$$

(29)

Substituting Equation (29) into (27), and performing a calculation similar to ${\dot{V}}_1$, we can get

$${\dot{V}}_2\le -c_1{e}_1^2+\frac{1}{k}{‖\theta ‖}^2+e_2\left(e_3+x_3^{\ast }+{\alpha }_{21}+{\alpha }_{22}^T\theta \right)\le -{\displaystyle \sum _{i=1}^2{c}_i{e}_i^2}+\frac{2}{k}{‖\theta ‖}^2+e_2{e}_3$$

(30)

Similarly, for 2 < i < n−1, define the Lyapunov function V_i as

$$V_i=V_{i-1}+\frac{1}{2}{e}_i^2$$

(31)

If α_i1, α_i2 and the error term e_i+1 between x_i+1 and the control input of the i^th subsystem $x_{i+1}^{\ast }$ are defined as

$${\alpha }_{i1}=e_{i-1}-{\displaystyle \sum _{j=1}^{i-1}\frac{\partial x_i^{\ast }}{\partial x_j}{x}_{j+1}},\hspace{0.33em}\hspace{0.33em}{\alpha }_{i2}={\gamma }_i-{\displaystyle \sum _{j=1}^{i-1}\frac{\partial x_i^{\ast }}{\partial x_j}{\gamma }_j}$$

(32)

$$x_{i+1}^{\ast }=-c_i{e}_i-{\alpha }_{i1}-\frac{1}{4}k{e}_i\left(1+{\alpha }_{i2}^T{\alpha }_{i2}\right),e_{i+1}=x_{i+1}-x_{i+1}^{\ast }$$

(33)

Similarly, we can get

$${\dot{V}}_i\le -{\displaystyle \sum _{j=1}^i{c}_j{e}_j^2}+\frac{i}{k}{‖\theta ‖}^2+e_i{e}_{i+1}$$

(34)

For the n^th subsystem, define the error term e_n as

$$e_n=x_n-x_n^{\ast }$$

(35)

Then we can have

$${\dot{e}}_n={\dot{x}}_n-{\dot{x}}_n^{\ast }={\gamma }_0-{\displaystyle \sum _{j=1}^{n-1}\frac{\partial x_n^{*}}{\partial x_j}}{x}_{j+1}+{\left({\gamma }_n-{\displaystyle \sum _{j=1}^{n-1}\frac{\partial x_n^{*}}{\partial x_j}}{\gamma }_j\right)}^T\theta +\left({\beta }_0+{\beta }^T\theta \right)u+\eta$$

(36)

Similarly, define α_n1 and α_n2 as

$${\alpha }_{n1}={\gamma }_0-{\displaystyle \sum _{j=1}^{n-1}\frac{\partial x_n^{\ast }}{\partial x_j}{x}_{j+1}},\hspace{0.33em}\hspace{0.33em}{\alpha }_{n2}={\gamma }_n-{\displaystyle \sum _{j=1}^{n-1}\frac{\partial x_n^{\ast }}{\partial x_j}{\gamma }_j}$$

(37)

Then Equation (36) can be further written as

$${\dot{e}}_n={\alpha }_{n1}+{\alpha }_{n2}^T\theta +\left({\beta }_0+{\beta }^T\theta \right)u+\eta$$

(38)

Define the Lyapunov function V_n as

$$V_n=V_{n-1}+\frac{1}{2}{e}_n^2+\frac{1}{2}{\left(\theta -\widehat{\theta }\right)}^T\left(\theta -\widehat{\theta }\right)$$

(39)

Then we have

$${\dot{V}}_n\le -{\displaystyle \sum _{i=1}^{n-1}{c}_i{e}_i^2}+\frac{n-1}{k}{‖\theta ‖}^2+e_n{e}_{n-1}+e_n\left({\alpha }_{n1}+{\alpha }_{n2}^T\theta +\left({\beta }_0+{\beta }^T\theta \right)u+\eta \right)-\left(\theta -\widehat{\theta }\right)\dot{\widehat{\theta }}$$

(40)

Define the adaptive control law as

$$\upsilon =\frac{1}{{\beta }_0+{\beta }^T\theta }\left(-{\alpha }_{n1}-c_n{e}_n-{\alpha }_{n2}^T\widehat{\theta }-\eta \right)$$

(41)

$$\dot{\widehat{\theta }}=\frac{-\left({\alpha }_{n1}+c_n{e}_n+{\widehat{\theta }}^T{\alpha }_{n2}+d\cdot \mathrm{sgn}\left(e_n\right)\right)\beta +\left({\beta }_0+{\beta }^T\widehat{\theta }\right){\alpha }_{n2}}{{\beta }_0+{\beta }^T\widehat{\theta }}{e}_n$$

(42)

Substituting the above adaptive control law into Equation (40), we can get

$${\dot{V}}_n\le -{\displaystyle \sum _{i=1}^{n-2}{c}_i{e}_i^2}+\frac{n-1}{k}{‖\theta ‖}^2+e_n{e}_{n-1}=-{\displaystyle \sum _{i=1}^{n-2}{c}_i{e}_i^2}-\left(c_{n-1}{e}_{n-1}^2+c_n{e}_n^2-e_n{e}_{n-1}\right)+\frac{n-1}{k}{‖\theta ‖}^2$$

(43)

Equation can be further written as follows if we choose c_i ≥ 1, 1 ≤ i ≤ n

$${\dot{V}}_n\le -c_1{e}_1^2+\frac{n-1}{k}{‖\theta ‖}^2$$

(44)

Moreover, because y = x₁ = e₁, integrating both ends of Equation (44), we can get

$${\displaystyle {\int }_0^T{‖y‖}^2}dt\le {\gamma }^2{\displaystyle {\int }_0^T{‖\theta ‖}^2}dt+N$$

(45)

where N > 0 is the initial value of V_n, γ² = (n−1)/k.

It can be seen that, under the effect of the designed adaptive control law, the disturbed uncertain nonlinear system has L2-gain ≤ γ.

4.2.2. Design of Turning Heel/Roll Reduction Controller

For the disturbed and uncertain nonlinear turning heel/roll reduction system described in Equation (11), Let x₁ = φ, x₂ = p, then Equation (11) can be rewritten as:

$$\begin{array}{c}{\dot{x}}_1=x_2\hfill \\ {\dot{x}}_2={\theta }_1{x}_2+{\theta }_2\left|x_2\right|x_2+{\theta }_3{x}_1+{\theta }_4{x}_1^3+b\upsilon +f_w\hfill \end{array}$$

(46)

Comparing the disturbed uncertain nonlinear system (46) and (12), it can be seen that the order of the turning hell/roll reduction system n is 2, and we can get

$${\gamma }_1\left(x_1\right)=0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\gamma }_0=0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\gamma }_2={\left[\begin{array}{cccc}{x}_2& \left|x_2\right|x_2& x_1& x_1^3\end{array}\right]}^T$$

(47)

$${\beta }_0=b,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\beta }_2=0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\eta =f_w$$

(48)

According to the design steps of the L2-gain adaptive robust law described in Section 4.2.1, we can get

$$x_2^{\ast }=-\left(c_1+\frac{1}{4}k\right)x_1$$

(49)

$${\alpha }_{21}=\left(c_1+\frac{1}{4}k\right)x_2$$

(50)

$${\alpha }_{22}={\left[\begin{array}{cccc}{x}_2& \left|x_2\right|x_2& x_1& x_1^3\end{array}\right]}^T$$

(51)

$$e_2=x_2+\left(c_1+\frac{1}{4}k\right)x_1$$

(52)

The hyperbolic tangent function tanh(·) is used instead of the sign function sgn(·) to eliminate the chattering of the control signal caused by the hard handoff. The adaptive control law can be expressed as:

$$\upsilon =\frac{1}{b}\left[-\left(c_1+c_2+\frac{1}{4}k\right)x_2-c_2\left(c_1+\frac{1}{4}k\right)x_1-{\alpha }_{22}^T\widehat{\theta }-d\cdot \tanh \left(e_2\right)\right]$$

(53)

$$\dot{\widehat{\theta }}={\alpha }_{22}{e}_2$$

(54)

where c₁ ≥ 1, c₂ ≥ 1 and k > 0 are undetermined control parameters.

5. Result and Discussion

In this section, the simulation of the ship turning under wave disturbance are performed to verify the effectiveness of the designed L2-gain based adaptive robust controller. The simulation parameters are as follows: the significant wave height is 1.25 m, the initial encounter angle is 135°, the initial sailing speed is 15 m/s, the turning rudder angle is 30°. The other parameters can be found in Table 1 and Table 2. It can be seen from the simulation results in Section 3.1, the surge velocity during the turning process gradually decreases from the initial sailing speed of 15 m/s to about 12.6 m/s, and changes slightly on this basis. Considering the short duration of the steering phase and the transition phase during the turning process, the parameters of the steady-state turning is used to calculate the parameters of the disturbed and uncertain nonlinear turning heel/roll reduction system. Based on the above analysis, we can get b = 0.0146 and d = 0.2786. Design c₁ = c₂ = k = 4, then the adaptive control law can be obtained from Equations (52)–(54):

$$u=\frac{1}{b}\left(-20x_1-9x_2-{\alpha }_{22}^T\widehat{\theta }+0.2786sign\left(e_2\right)\right)$$

(55)

$$e_2=5x_1+x_2$$

(56)

The simulation results of turning heel/roll reduction control using fin stabilizers based on the design L2-gain based adaptive robust controller are shown in Figure 5 and Figure 6. For comparison purposes, the simulation results a well-tuned PID controller are also given. NC, PID and L2ARC stand for “No control”, “PID control” and “L2-gain based adaptive robust control” respectively.

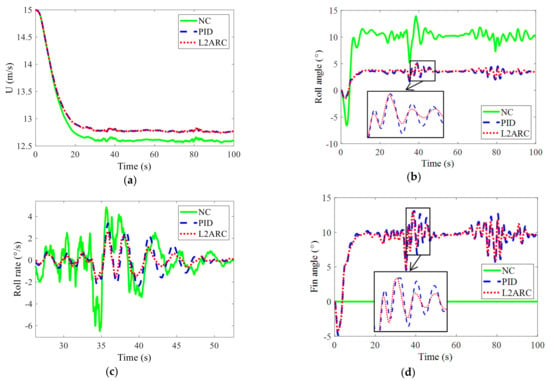
Figure 5. Simulation results of L2-gain adaptive robust control under wave disturbance. (a) Ship speed; (b) roll angle; (c) roll rate; (d) fin angle.

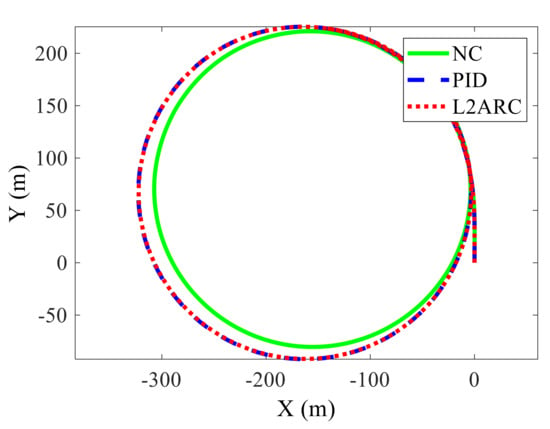
Figure 6. Trajectory of L2-gain adaptive robust control under wave disturbance.

It can be seen from Figure 5 that both the designed L2-gain based adaptive robust controller (L2ARC) and a well-tuned PID controller can effectively reduce the heel and roll motion during ship turns. It can be seen from Figure 5a that the sailing speed of the ship under the action of the controller is slightly increased than that without control, from 12.6 m/s to 12.8 m/s. From Figure 5b,c, it can be seen that the roll and heel reduction control effect of the designed L2ARC is slightly better than a well-tuned PID controller, which shows the superiority of the proposed control strategy. The steady outward heel angle with L2ARC is reduced from 10.19° to 3.01°, and the heel reduction effect can be easily calculated to be about 70.5%. The mean square value of the roll angle during the steady turning phase is reduced from 1.26° to 0.52°, and the roll reduction effect can be easily calculated to be 58.7%. As the encounter angle changes continuously with the progress of the turning, so that the amplitude of the roll motion of the ship also changes periodically. The ship roll is more severe when the encounter angle is 90° or 270°, while other angles are gentler. The control effect of the two controllers is almost the same when the roll is small, but the control effect of L2ARC is better than that of the PID when the roll is large, which is more obvious in Figure 5c. It can be seen from Figure 5d that the fin angle under the action of L2ARC is significant smaller than that under the action of PID. The movement of the fins in the steady turning phase is reduced by approximately 10%, which means the reduction of energy consumption and the effectiveness of the designed L2ARC. The overall effect of the designed L2-gain based adaptive controller is slightly better than well-tuned PID control. In addition, due to the opposite effect of the fin stabilizer on the steady outward heel and turning diameter, the steady turning diameter increases by about 15 m compared with the situation without control, as shown in Figure 6. The simulation results show that the designed controller has good robustness against uncertainties caused by a speed reduction of turning and internal and external disturbance.

6. Conclusions

In this paper, the use of fin stabilizers to reduce the heel and roll during ship turns under wave disturbance is investigated. The 4-DOF nonlinear mathematical model of a multipurpose naval vessel with forces and moments caused by hydrodynamics, waves, fin stabilizers, rudders and propellers is established. Based on the analysis of ship turning motion with different fin angles in calm water, it is found that the fin stabilizer can be used to reduce the heel and roll motion during ship turns, and it has the opposite effect on the steady outward heel and steady turning diameter. Through the analysis, the model of the turning heel/roll reduction system, which is convenient for controller design is obtained. For this disturbed uncertain nonlinear system, the L2-gain based adaptive robust controller is adopted to realize the control of fin stabilizers to reduce the heel and roll during ship turns. Considering the influence of ship speed on the maximum fin angle, fin angle speed adjustment is added in the simulation to get close to the real situation. The simulation results show that both the design L2-based adaptive robust controller and the well-tuned PID controller can effectively reduce the heel and roll motion during ship turns, and the overall effect of the designed controller is slightly better than the well-tuned PID controller.

In the future, we will make further research on the current basis. If possible, we will conduct ship model and even real ship experiments to verify the effectiveness of our proposed method.