Abstract
Accurately estimating air–water gas exchanges requires considering other factors besides wind speed. These are particularly useful for coastal ocean applications, where the sea-state varies at fine spatial and temporal resolutions. We upgrade FuGas 2.5 with improved formulations of the gas transfer velocity parametrized based on friction velocity, kinetic energy dissipation, roughness length, air-flow conditions, drift current and wave field. We then test the algorithm with field survey data collected in the Baltic Sea during spring–summer of 2014 and 2015. Collapsing turbulence was observed when gravity waves were the roughness elements on the sea-surface, travelling at a speed identical to the wind. In such cases, the turbulence driven transfer velocities (from surface renewal and micro-scale wave breaking) could be reduced from ≈20 cm∙h−1 to ≤ 5 cm∙h−1. However, when peak gravity waves were too flat, they were presumably replaced by capillary-gravity waves as roughness elements. Then, a substantial increase in the turbulence and roughness length was observed, despite the low and moderate winds, leading to transfer velocities up to twice as large as those predicted by empirical u10-based formulations.
1. Introduction
The dynamics of atmosphere–ocean gas exchanges are fundamental to the Earth’s climate, because the ocean acts as both sink and source of greenhouse gases and dimethyl sulfide (DMS) to the atmosphere. It is generally assumed that the open ocean uptakes CO2 from the atmosphere, despite the observed seasonal, inter-annual and regional variability [1,2,3]. On the other hand, the balances and fluxes of CO2, CH4, N2O and DMS across the coastal oceans’ surface are heterogenic, due to processes such as upwelling, plankton productivity, and continental loads of organic matter and nutrients, from both natural and anthropogenic sources. Consequently, the coastal ocean can be a source of CO2 [1,2,3,4,5,6,7,8,9,10], CH4 [2,9,11,12], N2O [2,9,13,14,15] and DMS [16] to the atmosphere, at least on a seasonal basis. The uncertainty about the atmosphere–coastal ocean exchange of CO2 led scientists to question the overall CO2 budget of the global ocean [3,17].
The atmosphere–ocean gas flux depends on the imbalance of its concentrations in liquid and gas phases, and on the transfer velocity across the air–water interface. Turbulence is the key factor governing the transfer velocity, while wind is attributed to be one of the main drivers of turbulence [18,19,20,21,22,23,24,25,26,27,28,29,30,31]. The wind is most often low or moderate over the world’s oceans [18,24,32,33], and particularly in tropical regions [34], resulting in large gas exchange between atmosphere and ocean [18,24,33]. Hence, accurate estimates of gas transfer velocities under low and moderate winds are fundamental for improving global air chemistry models [35]. Both regional and global models estimate the transfer velocity from quadratic or cubic dependencies on the wind velocity 10 m above the sea surface (u10), the most widely used formulation given by Wanninkhof [18]. However, the scientific community became increasingly aware that the accurate estimation of the atmosphere–ocean gas transfer velocities and fluxes requires standard universal formulations. Consequently, many studies emerged, assessing near-surface turbulence [22,23,26,27,28,29,30,31], focusing on alternative factors like the effect of bubbles from breaking waves [33,36,37,38,39], and even proposing that the sea-surface roughness, resulting from the wave field, is an overall better proxy for the turbulence mediating the transfer velocity [22,39,40,41,42,43,44].
Overall, the literature suggests that the transfer velocities of gases and transfer coefficients of heat, moisture and momentum may depend on the bubble formation by breaking gravity waves (i: the kbubble term) and the turbulent surface renewal (ii + iii: the kwind term) [21,24,25,33,36,37,38,39]. The latter has two drivers, namely the small eddies set by wind stress (ii) and the turbulence generated by breaking gravity waves (iii). The effects of breaking gravity waves on the transfer velocity (i.e., i + iii) dominates under high winds, whereas the effects of small eddies (ii) dominate under low and moderate winds. Because these small eddies are set by wind drag, they have been considered proportional to the friction velocity. However, their occurrence and magnitude depend on whether micro-scale (or short wind-) waves break, depending on the relative velocities of surface wind and water. The relation is slightly more intricate as, depending on the relative directions and velocities of wind and gravity waves, either gravity waves or capillary-gravity waves act as the roughness elements on the sea-surface. These roughness elements have a direct effect on the wind stress and momentum transfer to the sea-surface, and, consequently, on the turbulence mediating the transfer velocity. On the air-side, the roughness elements affect the roughness length and friction velocity [25,26,27,35].
This work focuses on the turbulence-driven gas transfer velocity. Integrating all the related knowledge is a complex task, particularly when studying the coastal ocean, where the relevant factors have been demonstrated to vary at shorter spatial and temporal scales. Illustrating this challenge, the relative proportion between the transfer velocity due to turbulent surface renewal (kwind hereafter) and to wave breaking (kbubble hereafter) under similar wind velocities depends significantly on the age of gravity waves under aerodynamic rough air-flow [22]. Wave age is commonly given by the ratio between the peak wave phase velocity (cp) and 10-m wind speed (u10), or friction velocity (u*). Representing wave age by cp/u10 [23,45] facilitates the identification of swell, as in fully developed wind-seas both velocities should be approximate. The difference between wind and wave directions was also demonstrated as a determinant factor. Hence the failure of traditional models for the gas transfer velocities and drag coefficients under cross and counter swell [46,47,48,49,50,51]. Lange et al. [52] stated the need to estimate the wind velocity relative to the velocity of the surface water. Soloviev et al. [22] advanced the frequency-direction spectrum of surface waves as a future research direction. Zavarsky and Marandino [49] corrected the wind velocity by its direction relative to waves to estimate the transfer velocity. Terray et al. [53] provided a comprehensive formulation where the effective wave velocity depends on the frequency-direction spectrum of the waves. Pan et al. [51] estimated a wind-stress component specific to counter-swell. The most complex algorithms for atmosphere–ocean interactions consider the relative velocities of wind and gravity waves to determine which part of the wave spectrum—from millimeter scale capillary waves to large gravity breaking waves and swell—act as roughness elements at the sea-surface [54,55,56]. Further, evidence emerged on limitations to the turbulence-mediated transfer velocity under high winds [49,57,58,59,60,61]. Low wind speeds at ~5 ms−1 lead to the smoothest sea surfaces as per the surface tension relation, but the sea becomes rougher under lower wind speeds. Consequently, below ~ 5 ms−1, the air-flow gets rougher and the wind stress coefficient larger [35,62,63,64,65].
Several numerical schemes have been developed aggregating many of the drivers of gas transfer velocity. The COARE is probably the most widely used [63,64,66,67,68,69,70], competing with alternatives such as the MESSy-Airsea [71] and the FluxEngine [43,44,55,72]. Built upon the original scheme by Johnson [73], we developed the FuGas (Flux of Gases) numerical scheme [74,75,76] with over 150 available formulations, some competing, others complementary, allowing the users to tune their model from a wide range of driving factors and degrees of complexity. This work reports on a FuGas update (version 2.5) with formulations that, either directly or indirectly, account for the effects of the wind, wave field and air-flow type on the gas transfer velocity. The development of the most comprehensive physically-based alternatives followed Goddard’s [21] statement that “wind is only an external forcing of the aqueous boundary; although it influences surface waves and near-surface turbulence, it does not influence gas exchange directly”. Hence, in a FuGas exclusive, the transfer velocity is only dependent on u*, while the relative air and water motions are considered in the estimation of surface velocity (us) and roughness length (z0), and then applied to aerodynamically rough-flow and smooth-flow formulations to estimate u*. Alternative and complementary formulations were tested and compared using field observations described in the following section.
2. Field Surveys
‘Observed’ CO2 transfer velocities (kw) were inferred from kw = F/(kHcp∙Δppm). F is the CO2 vertical fluxes measured by Eddy–Covariance (E-C) methods. Δppm is the difference between atmospheric and oceanic CO2 measured concentrations. The parameter kHcp is the Henry’s constant, providing the CO2 solubility in its cwater/ρair form (mol∙L−1∙atm−1), and estimated from the measured surface water temperature and salinity [73,74,75,76]. Simultaneously, we measured the atmospheric and oceanic variables related with turbulence and commonly used in formulations estimating gas transfer velocities. The surveys took place in the Baltic Sea during May 2014 and May to September 2015, with data sampled at the atmospheric tower at Östergarnsholm (57°27′ N, 18°59′ E), and with the Submersible Autonomous Moored Instrument (SAMI–CO2) 1 km away and the Directional Waverider (DWR) 3.5 km away, both south-eastward from the tower [7,12,45,77,78,79]. The vertical CO2 fluxes measured by E-C were averaged over 30 min bins, and subject to the Webb–Pearman–Leuning (WPL) correction [80]. The DWR measured temperatures at 0.5 m depth, taken as representative of the sea-surface warm layer while not accounting for its cool skin effect. Only the fluxes for which the wind direction set the SAMI–CO2 and DWR in the footprint of the atmospheric tower (80° < wind direction < 160°) were used for CO2 transfer velocity estimates. For the u* estimates, we used only the wind data without flow distortion from land or from our own atmospheric tower (80° < wind direction < 220°). For an extensive description of the data processing, quality control and selection of data from open sea sectors, we refer to Nilsson et al. [78] and Rutgersson et al. [79]. Furthermore, time sequences with abrupt changes in wind properties were discarded, assuming that the homogeneity of conditions had been severely violated.
3. Modelling with the FuGas
The FuGas framework [74,75,76] was developed for the estimation of the air–water fluxes of virtually any gas in the atmosphere, currently having 110 alternative or complementary formulations. The details about its application are provided in its software tutorial (see Section 5: Code and Data Availability). The estimation of the transfer velocity from atmospheric and oceanic variables [Equation (1)] takes into consideration the chemical enhancement by the hydration reaction under low wind speeds (bt), the turbulence generated by wind drag and wave breaking (kwind), as well as by currents (kcurrent), and the air entrapment in bubbles from breaking waves (kbubble). The first three of these forcing functions are weighted by the observed water viscosity, as given by the Schmidt number (Scw), and scaled to the reference Schmidt number for CO2 in freshwater (Scw = 600) or for CO2 in seawater (Scw = 660) at 20 °C, depending on the original formulations being used [21,24,38,49,81].
Historically, the transfer velocity has been demonstrated to scale with the turbulent kinetic energy dissipation at the sea-surface (ε), the wind drag being its main driver [22,23,24,27,28,30,31,39,53,82]. Emulating this process, the kwind is often estimated from simple empirical formulations, considering the wind speed at 10 m heights (u10), usually under atmospherically neutral conditions [18,81,83,84,85,86,87,88,89,90,91] and disregarding the remaining factors. Some more elaborate formulations rely on the speed of the wind effectively exerting drag over the sea-surface, i.e., u* [20,31,92,93,94]. In the FuGas most comprehensive physically-based formulation, when kwind is estimated directly from u*, the effects of the wave-state and atmospheric stability become implicit. This is demonstrated in the proceeding sections. Despite the predominant use of wind-based formulations, both kwind and ε have been proposed to correlate with the sea-surface roughness better than with the wind [20,22,23,29,40,41,42,43,44,49,57,95].
3.1. Air-Flow Regime
The u* can be estimated from several principles of fluid mechanics applied to the surface boundary layer and air–water interface. These require a preliminary definition of the air-flow regime over the sea-surface. Rough air-flow (or turbulent flow) is characterized by the air moving with strong lateral mixing between adjacent layers. The occurrence of eddies and swirls enhances exchanges perpendicular to the flow direction, i.e., vertically. The roughness length (z0) and u* scale with this turbulence (hence z0 and u* are positively correlated); z0 being the theoretical height at which u* becomes zero (see Section 3.4 for a more detailed explanation on z0). In smooth air-flow (or laminar flow) the air moves along parallel layers, with the least lateral mixing between adjacent layers. Due to the lack of flow separation, z0 is expected to increase with decreasing u* [35,55,56,57,58,96]. The air-flow regime is usually estimated from the roughness Reynolds number (Rr = z0·u*/νa), a dimensionless quantity measuring the ratio of inertial forces (z0·u* in m2∙s−1) to viscous forces (υa also in m2∙s−1). Exclusively turbulent rough flow has been proposed above Rr = 1 [63], Rr = 2 [96], Rr = 2.3 [52,65,97,98,99], Rr = 2.33 [100], Rr = 2.5 [101], or Rr = 3 [102]. Below this threshold is a transient region between rough and smooth air flows [52,58]. Smooth air-flow has been proposed to occur below Rr = 0.1 [63], Rr = 0.11 [103], Rr = 0.135 [65] or Rr = 0.5 [100]. Its predominance over the sea-surface increases the shorter the fetch [52], and thus transient and smooth air flow conditions may be particularly important at the coastal ocean.
3.2. Friction Velocity
The friction velocity (u*) at the air–water interface is the fluctuating component of the velocity of turbulent wind. Reworking the traditional formulation for wind stress τ = u*2ρ, the u* is a function of the shear stress (τ) exerted by air dragging over the sea-surface and of the fluid’s density (ρ). Due to momentum conservation, the shear stress must be equal at both sides of the interface, the result being that u*a × ρa0.5 = u*w × ρw0.5, where subscripts a and w stand for the air and water sides, respectively. Therefore, u*w = u*a(ρa/ρw)0.5 [20,21,24,30,53,93]. Henceforth, u* refers to u*a. In this section are presented formulations for the estimation of u*, valid for any air-flow regime or exclusive to a specific air-flow regime.
3.2.1. Friction Velocities under Rough Air-Flow
The FuGas allows u* to be estimated from the uw and vw wind components measured by the EC method. One frequent option is Equation (2a) [26,52,66,67,95,100,104,105]. The u’, v’ and w’ are the longitudinal, lateral and vertical wind fluctuations, with the overbars corresponding to the bin averaged second order crossed central moments. This formulation is implemented in the COARE 2.5. Because it may lead to biased estimates of individual u* measurements [64], Equation (2b) has been used instead [20,28,39,45,46,51,106,107] and implemented in the COARE 3.0 [64]. Because the estimates of u* from E-C measurements at different heights may show subtle differences [46,52,103,106], the u* measured at height z is converted to the u*s expected at the sea-surface by u*s = u*−0.0007z [52]. From then on, the former u* is replaced by the u*s value.
The Baltic Sea experiment provided a total of 1304 valid {uw,vw} observations, which, when applied to these equations, generally yielded resembling values of u* (Figure 1a,b). In only a few situations, mainly under low winds, did both formulations provide conspicuously different estimates. In only rare occasions, Equation (2a) yielded complex numbers with negligible imaginary components. For comparison among formulations, these u* were used together with the u10n to obtain the observed drag coefficients (CD = u*2/u102). The CD, often increasing with the lowest wind speeds (ranging from 1 m∙s−1 to 3 m∙s−1) (Figure 1c), matched previous observations done worldwide [35,46,62,63,64,65]. This dynamic has been advanced as a consequence of capillary-gravity waves replacing peak gravity waves as roughness elements on the sea-surface [35,62], and/or the occurrence of cross or counter swell [46,50,51,54], and led to u* peaking at u10n ≈ 2 m∙s−1.
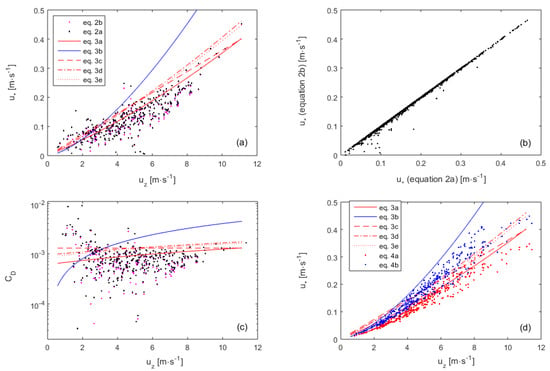
Figure 1.
Estimated u* from E-C data [Equation (2a,b)], from wind speed at 10 m heights under atmospherically neutral conditions (u10n) and using drag coefficient (CD) empirical formulations [Equation (3a–e)], or from the wave age [Equation (4a,b)]. Figure panels are: (a,d) estimated u* and its relation with wind observed at height z, (b) comparison between u* estimated by Equation (2a,b), (c) estimated drag coefficients.
Alternatively, the FuGas allows the u* to be estimated from the Drag Coefficient. In this case, the u* is estimated from u10, the definition of drag coefficient (also frequently mentioned in the literature as ‘wind stress coefficient’) reversed to u* = u10 × CD0.5, and one among the several empirical formulations for the estimation of CD from u10, namely Equation (3a) [108], Equation (3b) [92], Equation (3c) [109], Equation (3d) [46], or Equation (3e) [110]. In the case of Equation (3b), its application clearly departed from the observations as well as all other formulations (Figure 1a,c), and thus should be rejected. Mackay and Yeun [92] developed this CD parameterization simultaneously with a formulation that also widely overestimated transfer velocities (debated in Section 3.6). The CD and u* forecasted by the remaining formulations, although reasonably close to each other, (i) tended to slightly overestimate relative to the bulk of the observations, and (ii) were unable to account for the large CD and u* episodically occurring under low winds.
The FuGas also allows u* to be estimated from the wave field following the formulations developed by Gao et al. [111] for the coastal ocean [Equation (4a)] or offshore conditions [Equation (4b)]. These formulations use the wind measured at 10 m under atmospherically neutral conditions (u10n), and the celerity of peak gravity waves (cp). Both formulations predict u* reasonably close to that predicted by the former CD-based formulations (Figure 1d).
3.2.2. Friction Velocities Estimated from the WLLP (under Rough Air-Flow)
In a FuGas exclusive [73,74,75], u* was estimated from the wind measured at height z (uz) by solving the Wind Log-Linear Profile (WLLP) backwards [Equation (5)]. This solution congregates the effects of wind speed, wave state and atmospheric stability, and thus is central to the most comprehensive physically-based numerical scheme provided in FuGas. The WLLP is the air-side complementary of the Velocity Defect Law for the aqueous boundary layer [26,27], the boundary condition being that at height z = 0 the uz−us = 0. Thus, theoretically, the collinear surface velocity us should not be neglected [63,106]. These laws report to turbulent flow. In the WLLP’s case, that is the rough air-flow regime.
The estimation of us from the sea-state is presented in Section 3.3. The sea-state effect over the aerodynamic roughness length (z0) is presented in Section 3.4. The atmospheric stability function (ψm) was presented in previous FuGas applications [73,74,75], but new parameterizations derived from data specific to this Baltic Sea site [45] were added to FuGas 2.5. The von Kármán constant (κ) is 0.4, although 0.41 is also frequently used. As the WLLP must be iteratively solved for convergence [63,64,74,75], a preliminary guess for u* was required. This could be taken from one of the former solutions: E-C data, CD-based formulations or wave-based formulations. Only afterwards could the definite u* be estimated from Equation (5).
3.2.3. Friction Velocities upon Smooth and Transient Air-Flow Regimes
Given that under smooth-flow, u* and z0 are negatively correlated, the u* may be estimated as u* = Rr·νa/z0. This is the principle also applied to the z0 estimation under smooth-flow [52,63,64,65,112], being usually applied the same Rr of the smooth-flow threshold (see Section 3.1). Under transient-flow, u* is a compromise between rough-flow and smooth-flow formulations. Because the u* estimation under smooth-flow requires other properties (such as z0) that need be estimated ahead, it will be addressed later in Section 3.5.
3.3. Surface Velocity
The wind at 0 heights (u0 ≈ 0) over the sea-surface has a movement relative to the moving surface water [26,27,52,62,63,106,113,114,115,116]. The surface water velocity (us) was shown to affect the wind stress over the sea-surface, even in the open ocean, most often reducing it, and with an impact on the transfer velocities [27,114,115,116]. Hence, FuGas provides four options for its estimation:
- (i)
- Disregarding the velocity of the sea-surface, in which case us = 0.
- (ii)
- Using the collinear component of the water current; this being most suited for estuaries and tidal lagoon systems. In this case us = w × cosθ, where w is the current speed and θ is the angle between the wind and current directions.
- (iii)
- Using the collinear component of the sea-surface drift currents induced by waves, estimated adapting Stokes transport law [117]. In this case us = 4π2∙fp∙Hs2/Lp∙cosθ. Note that this is the average horizontal velocity, i.e., disregarding both the vertical movement and the back-and-forth horizontal movement of particles on the sea-surface as waves pass by.
- (iv)
- Estimating the surface drift currents adapting Wu’s [62,114] algorithm us = Vn + Vv, where (Vn) are the wind and (Vv) the wave forcings. The wind-induced drift current is estimated by Vn = 22∙uc, where uc is the drift current component of u* estimated from Equation (6a). CD is the u10-based drag coefficient and Cv the wave drag coefficient [Equation (6b)]. The wave-induced drift current, dependent on the wave age, was reworked to Equation (6c).
During the Baltic Sea experiment the surface water velocity was always very low, and only on rare occasions the estimates from available formulations slightly exceeded 10% of the wind velocity (Figure 2a). This is in accordance with the bulk of the observations reported in previous works. According to Wu’s formulation, the wind-induced drift currents are a fundamental component of us (Figure 2b). Nevertheless, us has little relevance for the estimation of u* from Equation (5), and is particularly irrelevant under low winds (Figure 2c).
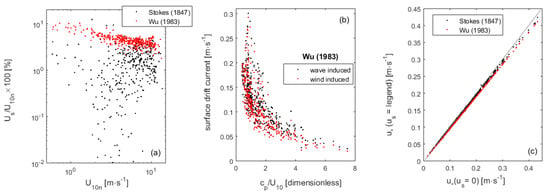
Figure 2.
Surface velocity (us) and its effect on the estimation of u*. (a) The us is estimated from Stokes’ [117] and Wu’s [62,114] algorithms, shown as a percentage of the wind velocity at a 10 m height under atmospherically neutral conditions (u10n). (b) The wind- and wave-induced drift currents estimated from Wu [62,114] are related with the wave age (cp/u10), where cp is the celerity of peak waves. (c) The resulting u* is compared with the estimated neglecting the us.
3.4. Roughness Length
Both the Law of the Wall (LOW) and the Velocity Defect Law assume that in contact with the surface there is a sub-layer with laminar flow. Within this sublayer, stress is predominately carried by viscous transfer and, although there may be an effective wind velocity (i.e., uz > 0 with z ≈ 0), the turbulent velocity tends to be zero (i.e., u* = 0). The depth of this sub-layer corresponds to the roughness length z0, and may tend to be infinitesimal depending on air-flow regime and roughness elements over the sea-surface. Upon rough-flow the roughness elements protrude the laminar flow sub-layer, i.e., z0 is smaller than the height of the roughness elements, causing the air-flow to separate from the sea-surface. In this case, z0 increases with increasing u*. Upon transient-flow the roughness elements have approximately the same height as in the laminar flow sub-layer. Upon smooth-flow the roughness elements stay within the laminar flow sub-layer, i.e., z0 is larger than the height of the roughness elements, causing the air-flow to not separate from the sea-surface. In this case, z0 increases with decreasing u*. Either peak gravity waves or shorter waves, even on the capillary-gravity range, can be the roughness elements on the sea-surface. Wu [100,113] proposed that the roughness elements are the waves travelling sufficiently slower than the wind for wakes to generate in their front, and the flow to separate.
3.4.1. Roughness Length under Rough Air-Flow
Under rough (turbulent) air-flow, the roughness length (z0) scales with turbulence, and thus with u*. The bulk of the empirical formulations assume that the roughness length depends exclusively on gravity waves as the roughness elements on the sea-surface. The simplest of them, by Charnock [118], proposes a z0 (units in m) dependency on u* [Equation (7) and Figure 3]. Here, g is the gravitational acceleration constant, and Charnock’s coefficient is 0.01 < αCh < 0.02 over water surfaces [52,53,64,103,112].
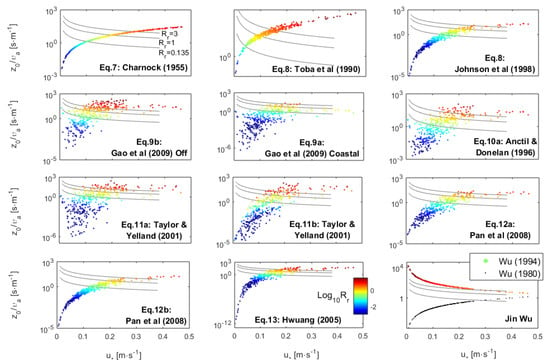
Figure 3.
Roughness length (z0) predicted by empirical formulations. Additional parameters used in the plot are u*, kinematic viscosity of air (υa) and roughness Reynolds number (Rr = z0·u*/νa). Wu (1994) label represents Wu [35] formulation for z0 under rough air-flow. Wu (1980) label represents Wu [100] formulation for z0 under any air-flow regime.
Because Charnock’s [118] formulation could not reflect the influence of the wave field, several authors proposed updating this classical formulation with a αCh dependency on the wave age (cp/u*), as given by Equation (8) [97,98,99,107,119,120,121]. The wave age is given by the celerity of peak waves (cp) relative to u*. Usually, 1 < cp/u* < 1000. The larger the ratio, the older the waves. Different ACh and BCh constants were proposed by the respective authors. Their values usually mean z0 increasing with younger waves [98,99,107,119,120,121] [Figure 3/‘Johnson et al. (1998)’]. Only the coefficients proposed by Toba et al. [97] opposed it, yielding a z0 increasing with older waves [Figure 3/‘Toba et al. (1990)’].
Representing wave age by cp/u10 instead facilitates the identification of swell, as in fully developed (mature) wind-seas both velocities should be approximate [97]. Swell corresponds to older waves travelling faster than the wind, and in this case aged > 1, obviously aside from waves traveling in other directions. Gao et al. [111] developed a z0 parameterization relying exclusively on this wave age, with a calibration for the coastal ocean [Equation (9a)] and another for offshore conditions [Equation (9b)]. Both formulations showed a z0 generally scaling with u*. Nevertheless, matching the smooth flow theory, under the lowest u* and z0, typical of smooth air-flows, the inverse scaling took place, i.e., z0 increased with decreasing u* and Rr (Figure 3). The off-shore formulation fit particularly well the Baltic Sea data: under the lowest u* it predicted z0 matching exactly that expected for smooth air-flows. The larger z0 variability under similar u*, but given different wave ages, demonstrated an enhanced ability of this formulation to adapt to local conditions.
Anctil and Donelan [106] added extra factors to the z0 dependency on wave age. First, they found that the dimensionless roughness length scaled with the inverse wave age. Solved for z0, it leads to Equation (10a). This formulation also showed a z0 generally scaling with u*, but inverting the scaling under conditions corresponding to smooth air-flows (Figure 3). This formulation also fit well the Baltic Sea data sampled under the lowest u*, predicting z0 matching the expected for smooth air-flows. This formulation also showed an enhanced ability to adapt to local conditions, demonstrated by the larger variability of z0 estimated under similar u*, but given different wave ages. Anctil and Donelan [106] found that the dimensionless roughness length scaled equally well with the mean squared slope of the wave field (θS, but also named <S2> [20,27]). Solved for z0, it leads to Equation (10b). Finally, they merged both factors in a multiple regression, which, solved for z0, leads to Equation (10c). Our data did not include measurements of θS necessary for the implementation of Equation (10b,c).
Taylor and Yelland [110] (following Hsu [122]) proposed a z0 dependency on the wave slope as estimated from the peak wave length (Lp) and significant wave height (Hs) [Equation (11a)], and calibrated by Aw = 1200 and Bw = 4.5. This formulation also showed a z0 generally scaling with u*, but inverting the scaling under conditions corresponding to smooth air-flows (Figure 3); it also fit well the Baltic Sea data sampled under the lowest u*, predicting z0 matching that expected for smooth air-flows. This formulation also showed an enhanced ability to adapt to local conditions, demonstrated by the larger variability of z0 estimated under similar u*, but given different wave ages. Taylor and Yelland [110] (following Donelan [103] and Anctil and Donelan [106]) presented an alternative formulation for a z0 dependency on, simultaneously, the wave age and slope [Equation (11b)]. However, this formulation was subsidiary, with its authors not attributing a value for Cw. Preliminary tests showed that the Bw and Cw terms could easily become antagonistic. We tested the calibration Aw = 1200, Bw = 1.5 and Cw = 3.5. This calibration lost the good fit to the transient-smooth air-flow conditions, bringing back the behavior more characteristic of the Charnock-based formulations (Figure 3).
Pan et al. [123] went back to the z0 dependency on the inverse wave age and size, proposing a new three-parameter formulation where the dimensionless roughness length scales with the u*-based inverse wave age, i.e., z0/Hs u*/cp. We reformulated it into Equation (12a). In a secondary formulation, they also revived the αCh u*/cp. We reformulated it into Equation (12b), which is basically Equation (8) with new coefficients. These formulations brought back the behavior more characteristic of the Charnock-based formulations (Figure 3).
Hwang [124] proposed that the vertical scales of properties of the air–water interface, like the drag coefficient or z0, should depend on the (horizontal) wave length. Consequently, both the drag coefficient and z0 increase non-linearly with wave age for very young waves, while decreasing non-linearly with wave age for very old waves. Hwang [124] tuned his formulation for deep water conditions. We adapted it for any water depth [Equation (13)]. In this case, ω* is the inverse wave age. This formulation uses the same parameters (wave age and length) as COARE [64] z0 formulation adapted from Oost et al. [125].
The Baltic Sea data only comprehended the range of older waves, for which Hwang [122] predicted that z0 decreases with wave age. Our data did not comprehend the extremely young waves for which Hwang [122] proposed a z0 increasing with wave age. For waves with different Lp to be similarly old, the faster travelling, longer waves occurred under higher winds, and attained higher heights. Therefore, although here was used Lp, other metrics such as Hs or the peak wave frequency (fp) worked similarly. Due to this similitude, within the range of older waves, our adaptation of the formulation by Hwang [122] behaved reasonably similarly to our adaptation of the formulation by Pan et al. [123] (Figure 3), and thus this formulation also showed a behavior more characteristic of the Charnock-based formulations.
3.4.2. Roughness Length under Smooth Air-Flows
Contrary to the rough-flow regime, upon smooth-flow, the roughness length (z0) increases with decreasing u*, due to the lack of flow separation [35,62,63,64,65,112]. The most usual parametrization is z0 = Rr × νa/u*, with the Rr value given by the smooth-flow threshold, namely Rr = 0.11 [52,64,103,112] or Rr = 0.135 [65] (Figure 3). An alternative formulation with unconstrained Rr was advanced by Wu [35,62]. It proposes that at u10 ≈ 5 m∙s−1 actually occurs the smoothest air-flows over the sea-surface, below which the sea-surface gets rougher with decreasing winds, because capillary waves (whose restoring force is the surface tension σ) replace the mild gravity waves (whose restoring force is the acceleration constant g) as roughness elements. This shift leads to both drag and z0 increasing with decreasing u*. However, once the shift is done, the drag increase can be so intense as to turn the air-flow rough again, even upon light breezes (Figure 3). Wu’s algorithm [Equation (14a)] has the water surface tension (σ) governing the wind–wave interactions. The surface tension (N∙m−1) of pure water (σ0) was estimated from Equation (14b), accounting for the water temperature (Tw in K) and considering a critical water temperature Tc = 647.1K [126]. Rectification for salt water surface tension (σw) was done by Equation (14c), using the surface salinity (S in ppt) [127].
3.4.3. Definite Estimation of Roughness Length
Theory says that under typical smooth flows, z0 should be exclusively set by the smooth-flow term, under typical rough flows z0 should be exclusively set by the rough-flow term, and only under the transient regime should it be a function of both. Yet COARE [64] always adds both terms. Since when one term is maximized the other is minimized—tending to infinitesimal—always adding them yielded results almost identical to using exclusively the term adequate for each regime (Figure 4a–c). Besides, it is computationally simpler and more efficient. Choosing the maximum between each term also yielded almost identical results. Another option was averaging between both terms. Using the arithmetic mean yielded slightly different results (Figure 4d–f). The fundamental difference was that z0 was estimated slightly smaller. However, using the geometric mean yielded widely different results as the rough-flow infinitesimal terms became preponderant. Consequently, with low u* the definite z0 also becomes infinitesimal (Figure 4g–i), contradicting general theory on laminar flows. Geometric means never yielding infinitesimal z0 could only be obtained if the rough-flow term also never yield infinitesimal z0, which was only satisfied by the formulations by Actil and Donelan [106] [Equation (10a)], Taylor and Yelland [110] [Equation (11b)] and Gao et al. [111] [Equation (9a)]. Using an analogous to the double resistance estimator (i.e., 1/z0 = 1/zrough + 1/zsmooth) yielded results similar to those when using the geometric mean. The smooth-flow term can be estimated from a fixed-Rr formulation or from the formulation by Wu [35,62]. Either application yielded widely different results (Figure 3). Since z0 cannot be directly measured, it was impossible to determine which numerical scheme provided the best estimates.
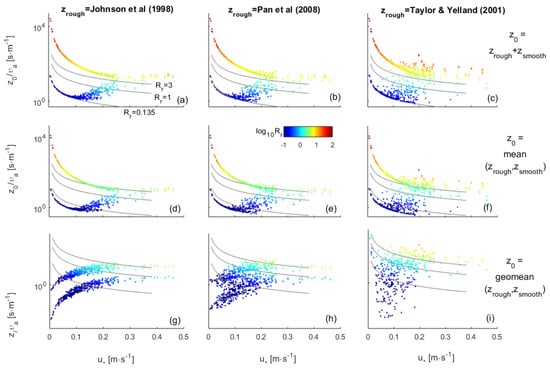
Figure 4.
Definite estimation of roughness length (z0) congregating the smooth and rough air-flow regimes. Congregation of zsmooth and zrough was additive (a–c), their arithmetic mean (d–f) or their geometric mean (g–i). Roughness length under rough air-flow (zrough) was estimated from the formulations by Johnson et al. [98] [Equations (7) and (8)], Pan et al. [123] [Equation (12a)] or Taylor and Yelland [110] [Equation (11a)]. Roughness length under smooth air-flow (zsmooth) was estimated from the formulation by Wu [35,62] [Equation (14)] (upper trajectories with larger Rr) or formulations relying on a fixed Rr (bottom trajectories closer to the Rr = 0.135 threshold). In bottom-right panel is only shown the geometric mean between Taylor & Yelland [110] and Wu [35,62]. Roughness Reynold number estimated from Rr = z0 × u*/υa.
Alternatively, Wu [100] also advanced a general formulation for z0 under any air-flow regime by combining the formulations related with rough and smooth air-flows [Equation (15)]. The υw is the kinematic viscosity of water and β is a constant. Wu proposed αCh = 0.0185 and 2 < β< 2.5. These β values implied that gravity waves dominate the determination of z0. Oddly, the smooth-flow component of Equation (15) was inversed relative to the previous smooth-flow formulations. The resulting z0 was far off the predicted values given by other algorithms (Figure 3), and followed a narrow logarithmic trend that was basically dependent on u*, while the kinematic viscosity and surface tension of water were irrelevant.
Our analysis suggests that, although larger gravity waves are determinant of z0 for coastal ocean, other factors are equally important, namely the waves on the capillary-gravity range [20,28,30,31,35,62,94,128] and the smooth air-flow [35,62,63,64,65,112].
3.5. Converging Friction Velocities
One of the purposes of FuGas is to be applied to atmospheric and oceanic L4 data with large spatial and temporal coverage. In such cases, since direct observations are not available, u* must alternatively be estimated from empirical formulations. The FuGas user may opt for one simple parameterization, or its comprehensive iterative estimation involving the wind log-linear profile: first, a preliminary u* is estimated, and then z0 and u* must be solved for convergence. In both COARE [63,64] and previous FuGas algorithms [74,75,76], convergence was generally attained after three iterations. Although the new FuGas schemes could be substantially more complex, convergence was still attained within three iterations, at most, and often with only one or two. Once convergence was achieved, we compared the forecasted u* with the u* estimated from direct observation obtained through the EC method. Yet, there was no guarantee that the EC-based u* reflected the true u*, particularly under the low winds, when turbulence is reduced and EC method is prone to failure, as previously demonstrated for this Baltic Sea station [7].
The estimation of the preliminary u* from a CD-based formulation was an important step. Following the Smith [108] formulation in Equation (3a) leads to the best fits (Root Mean Square Deviation RMSD ≈ 0.0348 m∙s−1). The worst estimation was from the formulation by Mackay and Yeun [92] given in Equation (3b) (RMSD ≈ 0.155 m∙s−1). The z0 estimation was also determinant. Its smooth-flow term was better estimated from a fixed-Rr formulation (RMSD ≈ 0.0343 m∙s−1) than from Wu’s [35,62] smooth-flow formulation given in Equation (14) (RMSD ≈ 0.0376 m∙s−1) (Figure 5). The z0’s rough-flow term was best estimated from the Pan et al. [123] formulation in Equation (12) or the Gao et al. [111] formulation for the coastal ocean in Equation (9a) (RMSD ≈ 0.0343 m∙s−1), and was worst estimated from the Toba et al. [97] formulation in Equations (7) and (8), or Gao et al. [111] formulation for the open ocean in Equation (9b) (RMSD ≈ 0.0355 m∙s−1) (Figure 5). The rough-flow and smooth-flow terms need to be merged under transient air-flows. The tests were not conclusive about which z0 integration method should be preferred. Yet, estimating their geometric average generally provided the best fits (RMSD ≈ 0.0343 m∙s−1). On the opposite extreme, integrating z0 rough-flow and smooth-flow terms in Equation (15) [Wu 100] led to largely overestimated u* (RMSD ≈ 0.141 m∙s−1). The choice of critical Rr for smooth-flow or rough-flow thresholds was of little relevance, and so was the choice of surface velocity from drift currents.
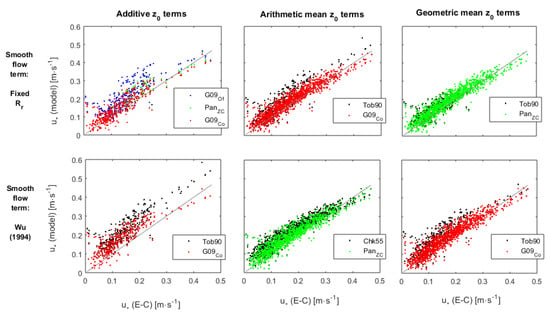
Figure 5.
Definite estimation of u* iterating for convergence together with roughness length (z0). Colored marks represent the roughness length under rough air-flow estimated following, Charnock [118] [Chk55, Equation (7)], Gao et al. [111] formulations for the coastal ocean [G09Co, Equation (9a)] or off-shore [G09Of, Equation (9b)], Pan et al. [123] [PanZC, Equation (12b)] or Toba et al. [97] [Tob90, Equations (7) and (8]). Roughness length under smooth air-flow was estimated following Wu [35,62] [Equation (14)] or formulations relying on a fixed Rr. Smooth and rough air-flow terms under transient air-flow regimes were added, arithmetically averaged or geometrically averaged.
When the numerical scheme was fine-tuned, the empirical estimation of u* was generally close to its estimation from direct observation obtained through the EC method (Figure 5), although often slightly overestimated. Most of this overestimation occurred under lower wind speeds, when the air-flow should be transient or smooth, and the EC-based estimations may be biased. Melville [129] proposed that the shift from rough to transient air-flows occurs at u* from 0.15 to 0.3 m∙s−1. Wu [35] proposed this threshold at u10 ≈ 5 m∙s−1, which in our data corresponded to u* predominantly between 0.05 and 0.2 m∙s−1, and median at ≈ 0.13 m∙s−1. Below this transient region, the empirically estimated u* was larger than that estimated from direct observation (Figure 5). The lack of precision of EC methods under such low winds was already debated. The present observations match previous observations and models where, under low winds, the u* decreases less sharply associated with decreasing wind velocity [58], while drag and transfer coefficients increase [35,62,63,64,65,98]. To justify such an effect, Wu [35] proposed that the sea surface is aerodynamically rough even under light winds, on the account of capillary-gravity waves replacing gravity waves as roughness elements on the sea-surface.
3.6. The kwind Term
The experiment provided a total of 163 observations with valid transfer velocities, of which only 94 included the wave properties necessary for simulations using the most advanced algorithms available in the FuGas. Still, starting with the simplest, i.e., the empirical u10-based formulations, the formulations by Jacobs et al. [83] and Wanninkhof and McGillis [84] estimated respectively the largest and the lowest transfer velocities under the observed wind range (Figure 6a). The formulation by Wanninkhof [18] is the standard in Earth-System Models, and roughly represents the average behavior of u10-based formulations. Their application should use the wind speed at a 10 m height under atmospherically neutral conditions (u10n). If that is not the case during field experiment, the equivalent u10n must be estimated from the data. These standard transformations, although derived from the wind log-linear profile, neglect the surface velocity, and that z0 is variable. However, the FuGas numerical scheme allows accounting for them. Wanninkhof’s [18] formulation applied to this u10n yields RMSD = 9.42 cm∙h−1 (Figure 6a). All u10-based formulations largely misfit the observed transfer velocities under the lowest winds and swell. This had already been demonstrated for the Östergarnsholm setup [7]. Several explanations have been advanced for the swell interference in the transfer velocities. The older and larger waves have been demonstrated as having a direct interaction with the atmosphere, and as interfering in the properties of the shorter wind-waves that often regulate the turbulence and air-flow over the sea-surface [77,78,79]. The interference of swell was demonstrated to be stronger with lower winds, steeper waves and/or when opposing the wind direction [50,51,54], which was precisely our case. Disregarding the wave-state has already been shown to introduce systematic bias to the calibration of bulk flux formulations for the transfer of heat and moisture from direct observation obtained through EC method, particularly under near-collapsed turbulence [48].
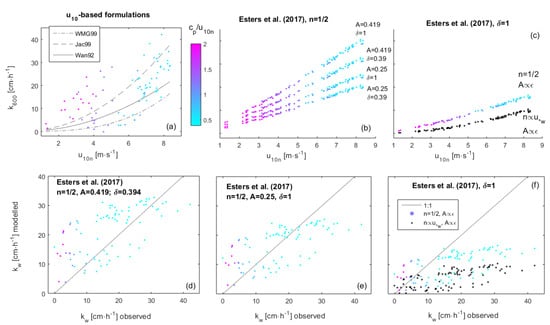
Figure 6.
Estimation of kwind term. (a) The transfer velocity standardized for CO2 in fresh-water at 20 °C (k600) estimated from (EC data) direct observation obtained through EC method for 2014 and 2015, and relation with (u10n) wind speed (cp/u10n) and wave age. Waves aged cp/u10n > 1 correspond to overdeveloped sea. The EC transfer velocities were compared with (a) those estimated from the u10-based formulations by Jacobs et al. [83] (Jac99), Wanninkhof [18] (Wan92) and Wanninkhof and McGillis [84] (WMG99), and (b–f) with comprehensive physically-based algorithms (u*-based) by Esters et al. [30]. [Equations (17) and (18)]. (a,b) k600 estimated from Esters et al. [30] algorithm and its relation with u*. (d–f) validation of k600 estimated from from Esters et al. [30] algorithm against k600 estimated from direct observation obtained through EC method.
Turbulence-driven transfer velocities should be more accurately inferred from the wind effectively exerting drag on the sea-surface, i.e., u*. The most frequently used u*-based formulation was developed by Jähne et al. [94] [Equation (16a)] from wave tank experiments. In this formulation the transfer velocities were attributed to surface renewal by micro-scale wave breaking. Hence, this formulation is adequate for comprehensive physically-based algorithm splitting the kwind and kbubble components of transfer velocity [37,38,39], being usually conjugated with the kbubble formulation by Woolf [38]. This specific ensemble yields RMSD = 9.33 cm∙h−1. Mackay and Yeun [92] performed wave tank experiments to measure the transfer velocities of 11 organic solutes with solubilities ranging from extremely low to extremely high. Their formulation [Equation (16b)], representing the average behavior of these organic molecules, yields extreme transfer velocities about 10 times higher than everything else ever reported. Zhao et al. [40] used data from the open ocean, coastal ocean and lakes, with wind speeds ranging from 1 m∙s−1 to 34 m∙s−1. They calibrated a generalist formulation [Equation (16c)] with the effect of wave breaking implicit, and thus unsuited for comprehensive physically-based algorithms. Under the stronger winds, this formulation estimated too low transfer velocities, resulting in RMSD = 12.5 cm∙h−1. Landwehr et al. [31] developed two formulations with similar structures but calibrated to different data sets [Equation (16d,e)]. Their negative intercepts led to kwind estimates lower than those by the previous formulations, and to the estimation of kwind = 0 for u10 = 2.5 m∙s−1 and u10 = 2 m∙s−1, respectively. This opposes the general acceptance of effective transfer velocities even under zero winds. Thus, despite RMSD of 8.7 cm∙h−1 and 8.24 cm∙h−1, respectively, they are unsuited for application at the coastal ocean featuring frequent low winds. Other formulations use Equation (16f) to relate the transfer velocity to the water-side friction velocity (u*w) [20,93,94]. In this case, the βs and ns parameters reflect the effects of capillary-gravity waves, surface tension and surfactants. Scw is the Schmidt number of water, dependent on temperature and salinity. We could not test these formulations due to the lack of data on shorter waves. All these equations yield kwind in units of m∙s−1.
Evidence points to kwind scaling preferably with the turbulent kinetic energy dissipation rate ε [19,22,23,24,27,28,30,31,39,53,82] than with u*. The major difficulty with this approach is to determine the vertical profile of ε and its integration depth. In their recent algorithm, Esters et al. [30] start from Equation (17a), where A is a scaling constant and υw the kinematic viscosity of water. Following the Law of the Wall, ε at the surface (εs) was given by Equation (17b) [21,27,30,39,53]. However, this formulation only accounts for shear-induced turbulence, and not for turbulence from wave breaking. The integration depth z corresponds to the thickness of the viscous sub-layer, being inversely proportional to the wind speed [Equation (17c)]. Esters et al. [30] observed an off-set (here named δ) ≈ 0.394 between model forecasts and their observations. Equation (17a–c) were integrated into Equation (17d). However, its incorporation in FuGas 2.5 conjugated with Equation (1) required a constant with the value 660.
A can either be a proportionality constant or scale allometrically with ε as A = βεγ, β and γ being fixed coefficients. Esters et al. [30] propose specific A for CO2 and DMS, and list the coefficients for their alternative calibrations. Beware the typo in Esters et al. [30] publication, with β erroneously having negative signs. The CO2 coefficients are also provided in FuGas, whereas for other gases these must be updated from the literature. This formulation calibrated with n = 1/2, constant A, z0 estimated from the wave field, and conjugated with the kbubble formulation by Woolf [38], showed a mild variability in the gas transfer velocities forecasted under similar wind speeds, since they now depended on ε instead (Figure 6). However, they did not differ much from the previous formulations, and still largely misfitted the observed transfer velocities (Figure 6). The best fit was provided when A = 0.25 and δ = 1, yielding RMSD = 7.62 cm∙h−1. Given the large variability in the observed transfer velocities, the uncertainty about their accuracy, and their systematic bias under swell, no solution can be considered overall better. The model implementation where A scaled with ε did not improve the fit, yielding RMSD = 10.28 cm∙h−1 (Figure 6).
The kwind effect on transfer velocity is regulated by the Schimdt number, i.e., the ratio between the kinematic viscosity of water and the molecular diffusivity of the trace gas in water [see Equation (1)]. Its exponent n was demonstrated to scale with the wave field, being usually considered 2/3 for a smooth solid wall model to 1/2 for a free wavy surface [20,21,30,49,93,94]. Esters et al. [30] also provide the possibility of n depending on u*w instead of the wave field [Equation (18)]. However, when included in FuGas 2.5, this represents an implicit dependency of n from the wave field.
Applied to the Baltic Sea data, the variable n exponent was generally 0.58 < n < 0.71 with just four exceptions going beyond to a maximum of 0.86. This update did not improve the model fit to our data (Figure 6), yielding a RMSD = 13.9 cm∙h−1. This was not surprising, since the Esters et al. [30] LOW formulation is only valid in situations in which no waves are present, so that the prevailing turbulence is purely shear induced. It was conjugated with the kbubble formulation by Woolf [38], which considers only the whitecap fraction relation with bubble-mediated gas transfer, and not with turbulence induced by breaking waves, as some other kbubble formulations do. Therefore, this ensemble neglects the gas transfer mediated by turbulence from wave breaking.
Terray et al. [53] estimated the depth profile of ε accounting for breaking waves and for a transition layer dependent on the wave size. From it, Esters et al. [30] developed an alternative formulation that we adapted [Equation (19a)]. In this case, ċ is the effective wave velocity, related with the energy flux from wind to waves, and given by Equation (19b) after reworking the original model. However, the original fit by Terray et al. [83], based exclusively on young waves, applied to old waves, led to negative ċ/cp and consequently negative ċ, both being illogical. This happened in most of the observations in our survey. We re-fit Terray’s data to a Weibull curve (Figure 7a) and reworked to estimate ċ [Equation (19c)]. Under low and moderate winds, the waves were generally old (u*/cp < 0.05) and the kwind was particularly sensitive to the x-axis displacement of the Weibull (= 18) and to its increment rate (= 2) determining the shape of this side of the function. Under higher winds the waves were younger (u*/cp > 0.05) and the kwind became also sensitive to the asymptotic y (= 0.5).
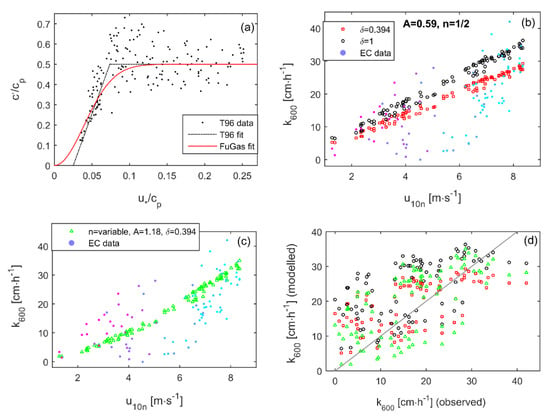
Figure 7.
Estimation of kwind term adapting the algorithm by Esters et al. [30] based on the formulation by Terray et al. [53] for the ε depth profile [Equation (19)]. (a) Terray et al. [53] function and FuGas re-fit; (b) and (c) Esters et al. [30] calibration; (d) Esters et al. [30] validation against EC-derived transfer velocities. (T96 data) Terray et al. [53] data, (T96 fit) Terray et al. [53] fit, and (FuGas fit) FuGas re-fit of effective wave velocity. (EC data) transfer velocities estimated from the Eddy-Covariance fluxes.
This formulation showed an improved ability to adapt the transfer velocity forecasts to the local conditions (Figure 7a,b). However, different calibrations adapted better to different groups of observations, and no specific calibration could adjust better to the whole set of observations. Consequently, the new transfer velocity fits to the transfer velocities estimated from direct observation obtained through the EC method were not better than the fits provided by the previous algorithms (Figure 7d, RMSD = 8.4 cm∙h−1).
4. Conclusions
Transfer velocities obtained through the EC method are inherently subject to large uncertainty, making model calibration, validation and comparisons among formulations difficult. Nevertheless, our simulations showed that comprehensive physical-based algorithms are more sensitive, and better adaptable to local conditions, than simpler u10-based empirical formulations (Figure 8a). The more comprehensive algorithms in FuGas 2.5 included factors besides the wind speed that have been proved fundamental drivers of transfer velocities, such as sea-surface roughness and atmospheric stability. In the coastal ocean, and particularly under low winds, these factors lead to gas transfer velocity estimates systematically larger than the estimates by empirical u10-based formulations. Nevertheless, many other factors are still to be added, and those included can still be improved. One such important update is the effect of shorter (capillary) waves, when these act as roughness elements on the sea-surface [130,131,132], leading the air-flow to separate. Other potentially important updates are the saturation of the turbulent transfer velocities [49,57,58,59,60,61] and its dependency on the relative air and water motions [49]. Empirical u10-based formulations can see their predictive ability improved if using the wind speed under atmospherically neutral conditions (u10n) (Figure 8b). In fact, after wind speed, atmospheric stability is probably the most important factor governing gas transfer velocity across the atmosphere–ocean interface.
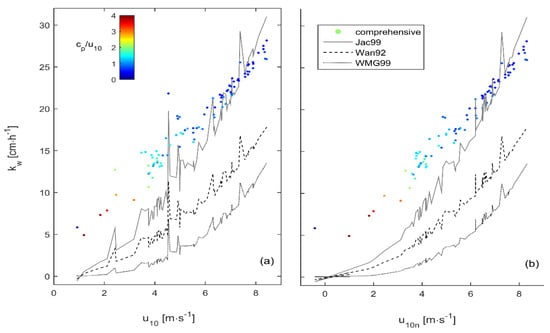
Figure 8.
Comparing transfer velocities predicted by comprehensive physical-based algorithms and empirical u10-based algorithms. Comprehensive algorithm included kwind term by Terray et al. [53] and kbubble term by Woolf [38]. Empirical u10-based algorithms by Jacobs et al. (1999) [83], Wanninkhof (1992) [18] and Wanninkhof and McGillis (1999) [84]. Please confirm if the (a) and (b) should be added in this figure caption.
5. Code and Data Availability
The FuGas was first published by Vasco Vieira in 2012. The latest FuGas 2.5, data and videos related with previous publications are available at http://www.maretec.org/en/models/fugas.
Author Contributions
Conceptualization, V.M.N.C.S.V. and M.M.; Formal analysis, V.M.N.C.S.V. and R.C.; Funding acquisition, M.M. and F.L.; Investigation, V.M.N.C.S.V. and R.C.; Methodology, V.M.N.C.S.V. and R.C.; Project administration, M.M. and F.L.; Resources, M.M.; Software, V.M.N.C.S.V.; Supervision, V.M.N.C.S.V.; Validation, V.M.N.C.S.V. and R.C.; Visualization, V.M.N.C.S.V.; Writing—Original draft, V.M.N.C.S.V.; Writing—Review & editing, V.M.N.C.S.V., M.M., R.C. and F.L. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by FCT/MCTES (PIDDAC) through project LARSyS: FCT Pluriannual funding 2020-2023 (UIDB/EEA/50009/2020). F.L. was funded by national funds by FCT under the Transitional Norm (DL57/2016/CP [1361]/CT[0008].
Acknowledgments
We are thankful to Anna Rutgersson and Erik Nilsson at Uppsala University for providing data from the marine field station Östergarnsholm funded by ICOS Sweden and Vetenskapsrådet Grants 2012-03902 and 2013-02044. The Directional Waverider (DWR) data was provided by Heidi Pettersson at Finnish Meteorological Institute. The wave measurements are part of the Finnish Marine Research Infrastructure Network FINMARI. This research was supported by CLIMFISH project (PTDC/ASP-PES/28518/2017), founded by Portugal 2020, n2/SAICT/2017—SAICT (Projetos de IC&DT).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Takahashi, T.; Sutherland, S.C.; Sweeney, C.; Poisson, A.; Metzl, N.; Tilbrook, B.; Bates, N.; Wanninkhof, R.; Feely, R.A.; Sabine, C.; et al. Global sea–air CO2 flux based on climatological surface ocean pCO2, and seasonal biological and temperature effects. Deep-Sea Res. 2002, 49, 1601–1622. [Google Scholar] [CrossRef]
- Sarmiento, J.L.; Gruber, N. Ocean Biogeochemical Dynamics; Princeton University Press: Princeton, NJ, USA, 2013; pp. 73–100. [Google Scholar]
- Borges, A.V. Do we have enough pieces of the jigsaw to integrate CO2 fluxes in the coastal ocean? Estuaries 2005, 28, 3–27. [Google Scholar] [CrossRef]
- Cole, J.J.; Caraco, N.F. Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of SF. Limnol. Oceanogr. 1998, 43, 647–656. [Google Scholar] [CrossRef]
- Cole, J.J.; Caraco, N.F. Carbon in catchments: Connecting terrestrial carbon losses with aquatic metabolism. Mar. Freshw. Res. 2001, 52, 101–110. [Google Scholar] [CrossRef]
- Borges, A.V.; Delille, B.; Frankignoulle, M. Budgeting sinks and sources of CO2 in the coastal ocean: Diversity of ecosystems counts. Geophys. Res. Lett. 2005, 32, L14601. [Google Scholar] [CrossRef]
- Rutgersson, A.; Norman, M.; Schneider, B.; Petterson, H.; Sahlée, E. The annual cycle of carbon dioxide and parameters influencing the air–sea carbon exchange in the Baltic Proper. J. Mar. Syst. 2008, 74, 381–394. [Google Scholar] [CrossRef]
- Norman, M.; Parampil, S.R.; Rutgersson, A.; Sahlée, E. Influence of coastal upwelling on the air–sea gas exchange of CO2 in a Baltic Sea Basin. Tellus B 2013, 65, 21831. [Google Scholar] [CrossRef]
- Harley, J.F.; Carvalho, L.; Dudley, B.; Heal, K.V.; Rees, R.M.; Skiba, U. Spatial and seasonal fluxes of the greenhouse gases N2O, CO2 and CH4 in a UK macrotidal estuary. Estuar. Coast. Shelf Sci. 2015, 153, 62–73. [Google Scholar] [CrossRef]
- Lansø, A.S.; Bendtsen, J.; Christensen, J.H.; Sørensen, L.L.; Chen, H.; Meijer, H.A.J.; Geels, C. Sensitivity of the air–sea CO2 exchange in the Baltic Sea and Danish inner waters to atmospheric short-term variability. Biogeosciences 2015, 12, 2753–2772. [Google Scholar] [CrossRef]
- Dutta, M.K.; Mukherjee, R.; Jana, T.K.; Mukhopadhyay, S.K. Biogeochemical dynamics of exogenous methane in an estuary associated to a mangrove biosphere; The Sundarbans, NE coast of India. Mar. Chem. 2015, 170, 1–10. [Google Scholar] [CrossRef]
- Gutiérrez-Loza, L.; Wallin, M.B.; Sahlée, E.; Nilsson, E.; Bange, H.W.; Kock, A.; Rutgersson, A. Measurement of air-sea methane fluxes in the Baltic Sea using the Eddy Covariance method. Front. Earth Sci. 2019, 7. [Google Scholar] [CrossRef]
- Nevison, C.D.; Weiss, R.F.; Erickson, D.J., III. Global oceanic emissions of nitrous oxide. J. Geophys. Res. 1995, 100, 15809–15820. [Google Scholar] [CrossRef]
- Nevison, C.D.; Lueker, T.J.; Weiss, R.F. Quantifying the nitrous oxide source from coastal upwelling. Glob. Biogeochem. Cycles 2004, 18, GB1018. [Google Scholar] [CrossRef]
- Barnes, J.; Upstill-Goddard, R.C. N2O seasonal distributions and air-sea exchange in UK estuaries: Implications for the tropospheric N2O source from European coastal waters. J. Geophys. Res. 2011, 116, G01006. [Google Scholar] [CrossRef]
- Gypens, N.; Borges, A.V. Increase in dimethylsulfide (DMS) emissions due to eutrophication of coastal waters offsets their reduction due to ocean acidification. Front. Mar. Sci. 2015. [Google Scholar] [CrossRef]
- Smith, S.V.; Hollibaugh, J.T. Coastal metabolism and the oceanic organic carbon balance. Rev. Geophys. 1993, 31, 75–89. [Google Scholar] [CrossRef]
- Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean. J. Geophys. Res. 1992, 97, 7373–7382. [Google Scholar] [CrossRef]
- Clayson, C.A.; Fairall, C.W.; Curry, J.A. Evaluation of turbulent fluxes at the ocean surface using surface renewal theory. J. Geophys. Res. 1996, 101, 28503–28513. [Google Scholar] [CrossRef]
- Frew, N.M.; Bock, E.J.; Schimpf, U.; Hara, T.; Haußecker, H.; Edson, J.B.; McGillis, W.R.; Nelson, R.K.; McKenna, S.P.; Uz, B.M.; et al. Air-sea gas transfer: Its dependence on wind stress, small-scale roughness, and surface films. J. Geophys. Res. 2004, 109, C08S17. [Google Scholar] [CrossRef]
- Upstill-Goddard, R.C. Air-sea gas exchange in the coastal zone. Estuar. Coast. Shelf Sci. 2006, 70, 388–404. [Google Scholar] [CrossRef]
- Soloviev, A.; Donelan, M.; Graber, H.; Haus, B.; Schlüssel, P. An approach to estimation of near-surface turbulence and CO2 transfer velocity from remote sensing data. J. Mar. Syst. 2007, 66, 182–194. [Google Scholar] [CrossRef]
- Zappa, C.J.; McGillis, W.R.; Raymond, P.A.; Edson, J.B.; Hintsa, E.J.; Zemmelik, H.J.; Dacey, J.W.H.; Ho, D.T. Environmental turbulent mixing controls on air-water gas exchange in marine and aquatic systems. Geophys. Res. Lett. 2007, 34, L10601. [Google Scholar] [CrossRef]
- Wanninkhof, R.; Asher, W.E.; Ho, D.T.; Sweeney, C.S.; McGillis, W.R. Advances in quantifying air-sea gas exchange and environmental forcing. Ann. Rev. Mar. Sci. 2009, 1, 213–244. [Google Scholar] [CrossRef] [PubMed]
- Soloviev, A.; Lukas, R. The Near-Surface Layer of the Ocean. Structure, Dynamics and Applications; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Bourassa, M.A. Shear stress model for the aqueous boundary layer near the air-sea interface. J. Geophys. Res. 2000, 105, 1167–1176. [Google Scholar] [CrossRef]
- Sidiqui, M.H.K.; Loewen, M.R. Characteristics of the wind drift layer and microscale breaking waves. J. Fluid Mech. 2007, 573, 417–456. [Google Scholar] [CrossRef]
- Sutherland, G.; Ward, B.; Christensen, K.H. Wave-turbulence scaling in the ocean mixed layer. Ocean Sci. 2013, 9, 597–608. [Google Scholar] [CrossRef]
- Brumer, S.E.; Zappa, C.J.; Blomquist, B.W.; Fairall, C.W.; Cifuentes-Lorenzen, A.; Edson, J.B.; Brooks, I.M.; Huebert, B.J. Wave-related Reynolds number parameterizations of CO2 and DMS transfer velocities: Reynolds number parameterizations. Geophys. Res. Lett. 2017. [Google Scholar] [CrossRef]
- Esters, L.; Landwehr, S.; Sutherland, G.; Bell, T.; Christensen, K.H.; Saltzman, E.S.; Miller, S.D.; Brian, W. Parameterizing air-sea gas transfer velocity with dissipation. J. Geophys. Res. Ocean. 2017, 122, 3041–3056. [Google Scholar] [CrossRef]
- Landwehr, S.; Miller, S.D.; Smith, M.J.; Bell, T.G.; Saltzman, E.S.; Ward, B. Using eddy covariance to measure the dependence of air–sea CO2 exchange rate on friction velocity. Atmos. Chem. Phys. 2018, 18, 4297–4315. [Google Scholar] [CrossRef]
- Harrison, D.E. On climatological monthly mean wind stress and wind stress curl field over the world ocean. J. Clim. 1989, 2, 57–70. [Google Scholar] [CrossRef]
- Jeffery, C.; Robinson, I.; Woolf, D. Tuning a physically-based model of the air-sea gas transfer velocity. Ocean Modell. 2010, 31, 28–35. [Google Scholar] [CrossRef]
- Sadler, J.C.; Lander, M.A.; Hot, A.M.; Oda, L.K. Tropical Marine Climate Atlas, Volume II—Pacific Ocean; UHMET 87-02; University of Hawaii: Honolulu, HI, USA, 1987. [Google Scholar]
- Wu, J. The sea surface is aerodynamically rough even under light winds. Bound. Layer Meteorol. 1994, 69, 149–158. [Google Scholar] [CrossRef]
- Asher, W.E.; Farley, P.J. Phase-Doppler anemometer measurement of bubble concentrations in laboratory-simulated breaking waves. J. Geophys. Res. 1995, 100C, 7045–7056. [Google Scholar] [CrossRef]
- Woolf, D.K. Bubbles and their role in gas exchange. In The Sea Surface and Global Change; Duce, R.A., Liss, P.S., Eds.; Cambridge Univ. Press: New York, NY, USA, 1997; pp. 173–205. [Google Scholar]
- Woolf, D.K. Parameterization of gas transfer velocities and sea state-dependent wave breaking. Tellus B 2005, 57, 87–94. [Google Scholar] [CrossRef]
- Shuiqing, L.; Dongliang, Z. Gas transfer velocity in the presence of wave breaking. Tellus B 2016, 68, 27034. [Google Scholar] [CrossRef]
- Zhao, D.; Toba, Y.; Suzuki, Y.; Komori, S. Effect of wind waves on air-sea gas exchange: Proposal of an overall CO2 transfer velocity formula as a function of breaking-wave parameter. Tellus B 2003, 55, 478–487. [Google Scholar] [CrossRef]
- Zhang, W.; Perrie, W.; Vagle, S. Impacts of winter storms on air-sea gas exchange. Geophys. Res. Lett. 2006, 33, L14803. [Google Scholar] [CrossRef]
- Zhao, D.; Xie, L. A practical bi-parameter formula of gas transfer velocity depending on wave states. J. Oceanogr. 2010, 66, 663–671. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Woolf, D.K.; Marandino, C. Space-based retrievals of air-sea gas transfer velocities using altimeters: Calibration for dimethyl sulphide. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Woolf, D.K.; Chapron, B.; Queffeulou, P. Improvements to estimating the air–sea gas transfer velocity by using dual-frequency, altimeter backscatter. Remote Sens. Environ. 2013, 139, 1–5. [Google Scholar] [CrossRef][Green Version]
- Högström, U.; Sahlée, E.; Drennan, W.M.; Kahma, K.K.; Smedman, A.-S.; Johansson, C.; Pettersson, H.; Rutgersson, A.; Tuomi, L.; Zhang, F.; et al. Momentum fluxes and wind gradients in the marine boundary layer – a multi-platform study. Boreal. Environ. Res. 2008, 13, 475–502. [Google Scholar]
- Donelan, M.A.; Drennan, W.M.; Katsaros, K.B. The air–sea momentum flux in conditions of wind sea and swell. J. Phys. Oceanogr. 1997, 27, 2087–2099. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Woolf, D.K.; Callaghan, A.H. Parameterizations and algorithms for oceanic whitecap coverage. J. Phys. Oceanogr. 2011, 41, 742–756. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Evaluation of the air-sea bulk formula and sea-surface temperature variability from observations. J. Geophys. Res. 2006, 111, C05002. [Google Scholar] [CrossRef]
- Zavarsky, A.; Marandino, C.A. The influence of transformed Reynolds number suppression on gas transfer parameterizations and global DMS and CO2 fluxes. Atmos. Chem. Phys. 2019, 19, 1819–1834. [Google Scholar] [CrossRef]
- Drennan, W.M.; Graber, H.C.; Donelan, M.A. Evidence for the effects of swell and unsteady winds on marine wind stress. J. Phys. Oceanogr. 1999, 29, 1853–1864. [Google Scholar] [CrossRef]
- Pan, J.; Wang, D.W.; Hwang, P.A. A study of wave effects on wind stress over the ocean in a fetch-limited case. J. Geophys. Res. C Ocean. 2005, 110. [Google Scholar] [CrossRef]
- Lange, B.; Johnson, H.K.; Larsen, S.; Hojstrup, J.; Kofoed-Hansen, H.; Yelland, M.J. On detection of a wave age dependency for the sea surface roughness. J. Phys. Oceanogr. 2004, 34, 1441–1458. [Google Scholar] [CrossRef]
- Terray, E.A.; Donelan, M.A.; Agrawal, Y.C.; Drennan, W.M.; Kahma, K.K.; Williams, A.J., III; Hwang, P.A.; Kitaigorodskii, S.A. Estimates of kinetic energy dissipation under breaking waves. J. Phys. Ocean. 1996, 26, 792–806. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Makin, V.K. Impact of Swell on the Marine Atmospheric Boundary Layer. J. Phys. Oceanogr. 2004, 3, 934–949. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Chapron, B.; Makin, V. Impact of wind waves on the air-sea fluxes: A coupled model. J. Geophys. Res. Ocean. 2014, 119, 1217–1236. [Google Scholar] [CrossRef]
- Kukulka, T.; Hara, T.; Belcher, S.E. A Model of the Air–Sea Momentum Flux and Breaking-Wave Distribution for Strongly Forced Wind Waves. J. Phys. Oceanogr. 2007, 37, 1811–1828. [Google Scholar] [CrossRef]
- Bell, T.G.; De Bruyn, W.; Miller, S.D.; Ward, B.; Christensen, K.H.; Saltzman, E.S. Air-sea dimethylsulfide (DMS) gas transfer in the North Atlantic: Evidence for limited interfacial gas exchange at high wind speed. Atmos. Chem. Phys. 2013, 13, 11073–11087. [Google Scholar] [CrossRef]
- Bell, T.G.; De Bruyn, W.; Marandino, C.A.; Miller, S.D.; Law, C.S.; Smith, M.J.; Saltzman, E.S. Dimethylsulfide gas transfer coefficients from algal blooms in the Southern Ocean. Atmos. Chem. Phys. 2015, 15, 1783–1794. [Google Scholar] [CrossRef]
- Blomquist, B.W.; Brumer, S.E.; Fairall, C.W.; Huebert, B.J.; Zappa, C.J.; Brooks, I.M.; Yang, M.; Bariteau, L.; Prytherch, J.; Hare, J.E.; et al. Wind Speed and Sea State Dependencies of Air-Sea Gas Transfer: Results From the High Wind Speed Gas Exchange Study (HiWinGS). J. Geophys. Res. Ocean. 2017. [Google Scholar] [CrossRef]
- Yang, M.; Bell, T.G.; Blomquist, B.W.; Fairall, C.W.; Brooks, I.M.; Nightingale, P.D. Air-sea transfer of gas phase controlled compounds. IOP Conf. Ser. Earth Environ. Sci. 2016, 35, 012011. [Google Scholar] [CrossRef]
- Zavarsky, A.; Goodijn-Murphy, L.; Steinhoff, T.; Marandino, C. Bubble-Mediated Gas Transfer and Gas Transfer Suppression of DMS and CO2. J. Geophys. Res. Atmos. 2018, 123, 6624–6647. [Google Scholar] [CrossRef]
- Wu, J. Laboratory studies of wind-wave interactions. J. Fluid Mech. 1968, 34, 91–112. [Google Scholar] [CrossRef]
- Fairall, C.W.; Hare, J.E.; Edson, J.B.; McGillis, W. Parameterization and micrometerological measurements of air-sea gas transfer. Bound. Layer Meteorol. 2000, 96, 63–105. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Andreas, E.L.; Mahrt, L.; Vickers, D. A new drag relation for aerodynamically rough flow over the ocean. J. Atmos. Sci. 2012, 69, 2520–2537. [Google Scholar] [CrossRef]
- Edson, J.B.; Fairall, C.W. Similarity Relationships in the Marine Atmospheric Surface Layer for Terms in the TKE and Scalar Variance Budgets. J. Atmos. Sci. 1998, 55, 2311–2328. [Google Scholar] [CrossRef]
- Edson, J.B.; Hinton, A.A.; Prada, K.E.; Hare, J.E.; Fairall, C.W. Direct covariance flux estimates from mobile platforms at sea. J. Atmos. Ocean. Technol. 1998, 15, 547–562. [Google Scholar] [CrossRef]
- Blomquist, B.W.; Fairall, C.W.; Huebert, B.J.; Kieber, D.J.; Westby, G.R. DMS sea-air transfer velocity: Direct measurements by eddy covariance and parameterization based on the NOAA/COARE gas transfer model. Geophys. Res. Lett. 2006, 33, L07601. [Google Scholar] [CrossRef]
- Jackson, D.L.; Wick, G.A.; Hare, J.E. A comparison of satellite-derived carbon dioxide transfer velocities from a physically based model with GasEx cruise observations. J. Geophys. Res. 2012, 117, G00F13. [Google Scholar] [CrossRef]
- Blomquist, B.W.; Huebert, B.J.; Fairall, C.W.; Bariteau, L.; Edson, J.B.; Hare, J.E.; McGillis, W.R. Advances in Air–Sea CO2 Flux Measurement by Eddy Correlation. Bound. Layer Meteorol. 2014, 152, 245–276. [Google Scholar] [CrossRef]
- Pozzer, A.; Jockel, P.; Sander, R.; Williams, J.; Ganzeveld, L.; Lelieveld, J. Technical Note: The MESSy-submodel AIRSEA calculating the air-sea exchange of chemical species. Atmos. Chem. Phys. 2006, 6, 5435–5444. [Google Scholar] [CrossRef]
- Shutler, J.D.; Land, P.E.; Piolle, J.-F.; Woolf, D.K.; Goddijn-Murphy, L.; Paul, F.; Girard-Ardhuin, F.; Chapron, B.; Donlon, C.J. FluxEngine: A flexible processing system for calculating atmosphere-ocean carbon dioxide gas fluxes and climatologies. J. Atmos. Ocean. Technol. 2016. [Google Scholar] [CrossRef]
- Johnson, M.T. A numerical scheme to calculate temperature and salinity dependent air-water transfer velocities for any gas. Ocean Sci. 2010, 6, 913–932. [Google Scholar] [CrossRef]
- Vieira, V.M.; Martins, F.; Silva, J.; Santos, R. Numerical tools to estimate the flux of a gas across the air–water interface and assess the heterogeneity of its forcing functions. Ocean Sci. 2013, 9, 355–375. [Google Scholar] [CrossRef]
- Vieira, V.M.; Sahlée, E.; Jurus, P.; Clementi, E.; Pettersson, H.; Mateus, M. Improving estimates of atmosphere-ocean greenhouse gas fluxes for Earth-System modelling. In Proceedings of the Living Planet Symposium, European Space Agency, Prague, Czeck Republic, 9–13 May 2016. SP-740, ATMO-100. [Google Scholar]
- Vieira, V.M.; Jurus, P.; Clementi, E.; Mateus, M. The FuGas 2.3 framework for atmosphere–ocean coupling: Comparing algorithms for the estimation of solubilities and gas fluxes. Atmosphere 2018, 9, 310. [Google Scholar] [CrossRef]
- Rutgersson, A.; Smedman, A. Enhanced air– sea CO2 transfer due to water-side convection. J. Mar. Syst. 2010, 80, 125–134. [Google Scholar] [CrossRef]
- Nilsson, E.; Bergström, H.; Rutgersson, A.; Podgrajsek, E.; Wallin, M.B.; Bergström, G.; Dellwik, E.; Landwehr, S.; Ward, B. Evaluating Humidity and Sea Salt Disturbances on CO2 Flux Measurements. J. Atmos. Ocean. Technol. 2018, 35, 859–875. [Google Scholar] [CrossRef]
- Rutgersson, A.; Pettersson, H.; Nilsson, E.; Bergström, H.; Wallin, M.; Nilsson, E.D.; Sahlée, E.; Wu, L.; Mårtensson, E.M. Using land-based stations for air-sea interaction studies. Tellus 2018. (Submitted). [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Borges, A.V.; Vanderborght, J.P.; Schiettecatte, L.S.; Gazeau, F.; Ferrón-Smith, S.; Delille, B.; Frankignoulle, M. Variability of the Gas Transfer Velocity of CO2 in a Macrotidal Estuary (the Scheldt). Estuaries 2004, 27, 593–603. [Google Scholar] [CrossRef]
- Wang, B.; Liao, Q.; Fillingham, J.; Bootsma, H.A. On the coefficients of small eddy and surface divergence models for the air-water gas transfer velocity. J. Geophys. Res. Ocean. 2015, 120. [Google Scholar] [CrossRef]
- Jacobs, C.M.J.; Kohsiek, W.; Oost, W.A. Air’sea fluxes and transfer velocity of CO2 over the North Sea: Results from ASGAMAGE. Tellus B Chem. Phys. Meteorol. 1999, 51, 629–641. [Google Scholar] [CrossRef]
- Wanninkhof, R.; McGillis, W.R. A cubic relationship between air-sea CO2 exchange and wind speed. Geophys. Res. Lett. 1999, 26, 1889–1892. [Google Scholar] [CrossRef]
- Carini, S.; Weston, N.; Hopkinson, C.; Tucker, J.; Giblin, A.; Vallino, J. Gas exchange rates in the Parker River estuary, Massachusetts. Biol. Bull. 1996, 191, 333–334. [Google Scholar] [CrossRef]
- Nightingale, P.D.; Malin, G.; Law, C.S.; Watson, A.J.; Liss, P.S.; Liddicoat, M.I.; Boutin, J.; Upstill-Goddard, R.C. In Situ Evaluation of Air-Sea Gas Exchange Parameterizations Using Novel Conservative and Volatile Tracers. Glob. Biogeochem. Cycles 2000, 14, 373–387. [Google Scholar] [CrossRef]
- McGillis, W.R.; Edson, J.B.; Ware, J.D.; Dacey, J.W.; Hare, J.E.; Fairall, C.W.; Wanninkhof, R. Carbon dioxide flux techniques performed during GasEx-98. Mar. Chem. 2001, 75, 267–280. [Google Scholar] [CrossRef]
- Raymond, P.A.; Cole, J.J. Gas exchange in rivers and estuaries: Choosing a gas transfer velocity. Estuaries 2001, 24, 312–317. [Google Scholar] [CrossRef]
- Ho, D.T.; Law, C.S.; Smith, M.J.; Schlosser, P.; Harvey, M.; Hill, P. Measurements of air-sea gas exchange at high wind speeds in the Southern Ocean: Implications for global parameterizations. Geophys. Res. Lett. 2006, 33, L16611. [Google Scholar] [CrossRef]
- Sweeney, C.; Gloor, E.; Jacobson, A.R.; Key, R.M.; McKinley, G.; Sarmiento, J.L.; Wanninkhof, R. Constraining global air-sea gas exchange for CO2 with recent bomb 14C measurements. Glob. Biogeochem. Cycles 2007, 21, GB2015. [Google Scholar] [CrossRef]
- Weiss, A.; Kuss, J.; Peters, G.; Schneider, B. Evaluating transfer velocity-wind speed relationship using a long-term series of direct eddy correlation CO2 flux measurements. J. Mar. Syst. 2007, 66, 130–139. [Google Scholar] [CrossRef]
- Mackay, D.; Yeun, A.T.K. Mass transfer coefficient correlations for volatilization of organic solutes from water. Environ. Sci. Technol. 1983, 17, 211–217. [Google Scholar] [CrossRef]
- Jähne, B.; Huber, W.; Dutzi, A.; Wais, T.; Lamberger, J. Wind/wave-tunnel experiment on the Schmidt number—And wave field dependence of air/water gas exchange. In Gas Transfers at Water Surfaces; Brutsaert, W., Jirka, G.H., Eds.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1984; pp. 303–309. [Google Scholar]
- Jähne, B.; Münnich, K.O.; Bösinger, R.; Dutzi, A.; Huber, W.; Libner, P. On the parameters influencing air-water gas exchange. J. Geophys. Res. 1987, 92, 1937–1949. [Google Scholar] [CrossRef]
- Gutiérrez-Loza, L.; Ocampo-Torres, F.J.; García-Nava, H. The Effect of Breaking Waves on CO2 Air–Sea Fluxes in the Coastal Zone. Bound. Layer Meteorol. 2018. [Google Scholar] [CrossRef]
- Wu, J. On critical roughness Reynolds numbers of the atmospheric surface layer. J. Geophys. Res. 1981, 86, 6661–6665. [Google Scholar] [CrossRef]
- Toba, Y.; Iida, N.; Kawamura, H.; Ebuchi, N.; Jones, I.S.F. Wave dependence on sea-surface wind stress. J. Phys. Oceanogr. 1990, 20, 705–721. [Google Scholar] [CrossRef]
- Johnson, H.K.; Hoejstrup, J.; Vested, H.J.; Larsen, S.E. Dependence of sea surface roughness on wind waves. J. Phys. Oceanogr. 1998, 28, 1702–1716. [Google Scholar] [CrossRef]
- Drennan, W.M.; Graber, H.C.; Hauser, D.; Quentin, C. On the wave age dependence of wind stress over pure wind seas. J. Geophys. Res. 2003, 108, 8062. [Google Scholar] [CrossRef]
- Wu, J. Wind-Stress Coefficients over Sea Surface near Neutral Conditions—A Revisit. J. Phys. Oceanogr. 1980, 10, 727. [Google Scholar] [CrossRef]
- Kraus, E.B.; Businger, J.A. Atmosphere-Ocean Interaction; Oxford University Press: Oxford, UK, 1994; 352p. [Google Scholar]
- Kitaigorodskii, S.A. The Physics of Air–Sea Interaction; Israel Program for Scientific Translations: Jerualem, Israel, 1970; 237p, (Translated from Russian by A. Baruch). [Google Scholar]
- Donelan, M.A. Air-sea interaction. In Ocean Engineering Science, vol.9, The Sea; Le Mehaute, B., Hanes, D.M., Eds.; John Wiley: Hoboken, NJ, USA, 1990; pp. 239–292. [Google Scholar]
- Lettvin, E.E.; Vesecky, J.F. Estimation of wind friction velocity and direction at the ocean surface from physical models and space-borne radar scatterometer measurements. Geophys. Res. Lett. 2001, 106, 22503–22519. [Google Scholar] [CrossRef]
- Brunke, M.A.; Fairall, C.W.; Zeng, X.; Eymard, L.; Curry, J.A. Which bulk aerodynamic algorithms are least problematic in computing ocean surface turbulent fluxes? J. Clim. 2003, 16, 619–635. [Google Scholar] [CrossRef]
- Anctil, F.; Donelan, M.A. Air–water momentum flux observations over shoaling waves. J. Phys. Oceanogr. 1996, 26, 1344–1353. [Google Scholar] [CrossRef]
- Oost, W.A.; Komen, G.J.; Jacobs, C.M.J.; van Oort, C.; Bonekamp, H. Indications for a wave dependent Charnock parameter from measurements during ASGAMAGE. Geophys. Res. Lett. 2001, 28, 2795–2797. [Google Scholar] [CrossRef]
- Smith, S.D. Wind stress and heat flux over the ocean in gale force winds. J. Phys. Oceanogr. 1980, 10, 709–726. [Google Scholar] [CrossRef]
- Duce, R.A.; Liss, P.S.; Merrill, J.T.; Atlas, E.L.; Buat-Menard, P.; Hicks, B.B.; Miller, J.M.; Prospero, J.M.; Arimoto, R.C.; Church, T.M.; et al. The Atmospheric Input of Trace Species to the World Ocean. Glob. Biogeochem. Cycles 1991, 5, 193–259. [Google Scholar] [CrossRef]
- Taylor, P.K.; Yelland, M.J. The dependence of sea surface roughness on the height and steepness of the waves. J. Phys. Oceanogr. 2001, 31, 572–590. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, Q.; Zhou, M. Wave-dependence of friction velocity, roughness length, and drag coefficient over coastal and open water surfaces by using three databases. Adv. Atmos. Sci. 2009, 26, 887–894. [Google Scholar] [CrossRef]
- Smith, S.D. Coefficients for sea surface wind stress, heat flux, and wind profiles as a function of wind speed and temperature. J. Geophys. Res. 1988, 93, 15467–15472. [Google Scholar] [CrossRef]
- Wu, J. A criterion for determining air-flow separation from wind waves. Tellus 1969, 21, 707–714. [Google Scholar] [CrossRef][Green Version]
- Wu, J. Sea-surface drift currents induced by wind and waves. J. Phys. Oceanogr. 1983, 13, 1441–1451. [Google Scholar] [CrossRef]
- Kara, A.B.; Metzger, E.J.; Bourassa, M.A. Ocean current and wave effects on wind stress drag coefficient over the global ocean. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Deng, Z.; Zhao, D.; Wu, K.; Yu, T.; Shi, J. Impacts of Wave and Current on Drag Coefficient and Wind Stress over the Tropical and Northern Pacific. J. Ocean Univ. Chin. 2008, 7, 373–378. [Google Scholar] [CrossRef]
- Stokes, G.G. On the theory of oscillating waves. Trans. Cambridge Phil. Soc. 1847, 8, 441–445. [Google Scholar]
- Charnock, H. Wind stress over a water surface. Q. J. R. Meteorol. Soc. 1955, 81, 639–640. [Google Scholar] [CrossRef]
- Maat, N.; Kraan, C.; Oost, W.A. The roughness of wind waves. Bound.-Layer Meteorol. 1991, 54, 89–103. [Google Scholar] [CrossRef]
- Smith, S.D.; Anderson, R.J.; Oost, W.A.; Kraan, C.; Maat, N.; DeCosmo, J.; Katsaros, K.B.; Davidson, K.L.; Bumke, K.; Hasse, L.; et al. Sea surface wind stress and drag coefficients: The HEXOS results. Bound.-Layer Meteorol. 1992, 60, 109–142. [Google Scholar] [CrossRef]
- Monbaliu, J. On the use of the Donelan wave spectral parameter as a measure for the roughness of wind waves. Bound.-Layer Meteorol. 1994, 67, 277–291. [Google Scholar] [CrossRef]
- Hsu, S.A. A dynamic roughness equation and its application to wind stress determination at the air–sea interface. J. Phys. Oceanogr. 1974, 4, 116–120. [Google Scholar] [CrossRef]
- Pan, Y.; Sha, W.; Zhu, S.; Ge, S. A new parameterization for sea surface aerodynamic roughness. Prog. Nat. Sci. 2008, 18, 1365–1373. [Google Scholar] [CrossRef]
- Hwang, P. Drag coefficient, dynamic roughness and reference wind speed. J. Oceanogr. 2005, 61, 399–413. [Google Scholar] [CrossRef]
- Oost, W.A.; Komen, G.J.; Jacobs, C.M.J.; van Oort, C. New evidence for a relation between wind stress and wave age from measurements during ASGAMAGE. Bound.-Layer Meteorol. 2002, 103, 409–438. [Google Scholar] [CrossRef]
- Vargaftik, N.B.; Volkov, B.N.; Voljak, L.D. International tables of the surface tension of water. J. Phys. Chem. 1983, 12. [Google Scholar] [CrossRef]
- Nayar, K.G.; Panchanathan, G.H.; McKinley, G.H.; Lienhard, J.H. Surface tension of seawater. J. Phys. Chem. 2014, 4. [Google Scholar] [CrossRef]
- Zappa, C.J.; Asher, W.E.; Jessup, A.T.; Klinke, J.; Long, S.R. Microbreaking and the enhancement of air-water transfer velocity. J. Geophys. Res. 2004, 109, C08S16. [Google Scholar] [CrossRef]
- Melville, W.K. Wind stress and roughness length over breaking waves. J. Phys. Oceanogr. 1977, 7, 702–710. [Google Scholar] [CrossRef]
- Coantic, M. A Model of gas transfer across air-water interfaces with capillary waves. J. Geophys. Res. 1986, 91, 3925–3943. [Google Scholar] [CrossRef]
- Back, D.D.; McCready, M. Effect of small-wavelength waves on gas transfer across the ocean surface. J. Geophys. Res. Ocean. 1988, 93, 5143–5152. [Google Scholar] [CrossRef]
- Szeri, A.J. Capillary waves and air-sea gas transfer. J Fluid Mech. 1997, 332, 341–358. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).