Delayed Fuzzy Output Feedback H∞ Control for Offshore Structures
Abstract
1. Introduction
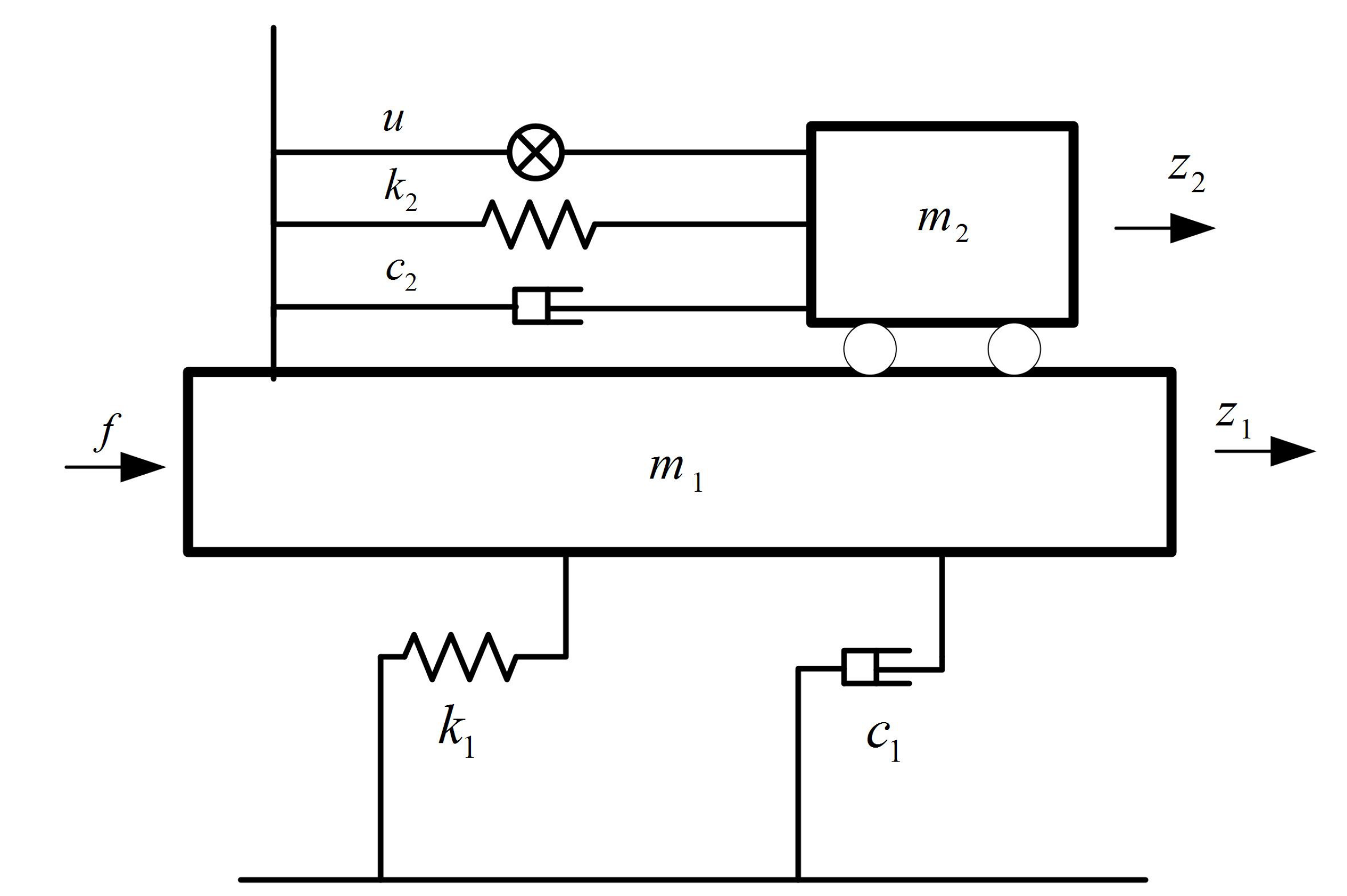
2. Problem Formulation
3. Fuzzy Output Feedback Control Design
3.1. Mixed Delayed Fuzzy Output Feedback Control Design
3.2. Pure Delayed Fuzzy Output Feedback Control Design
3.3. Fuzzy Output Feedback Control Design
4. Simulation Results
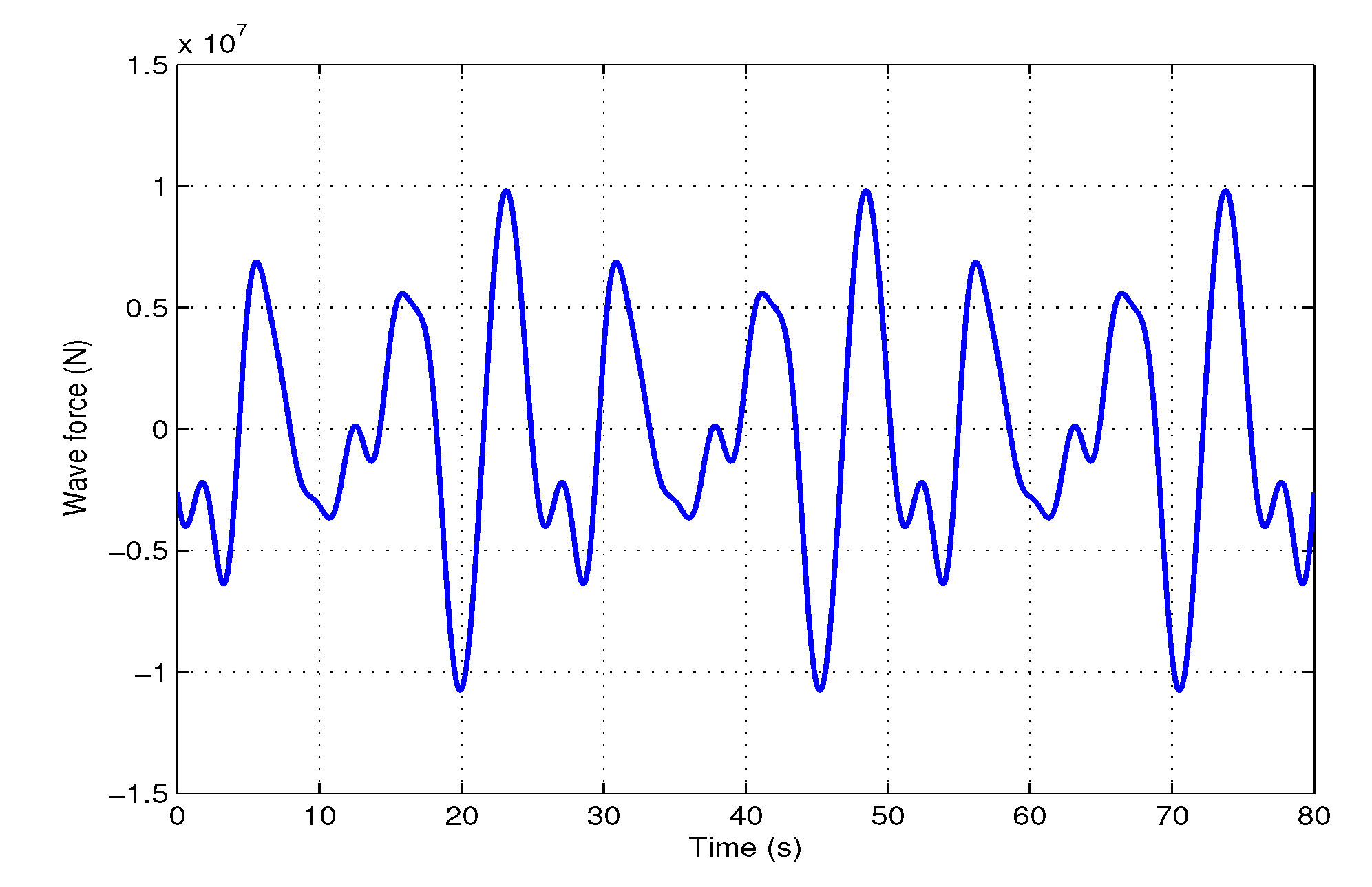
4.1. Parameters of an Offshore Structure
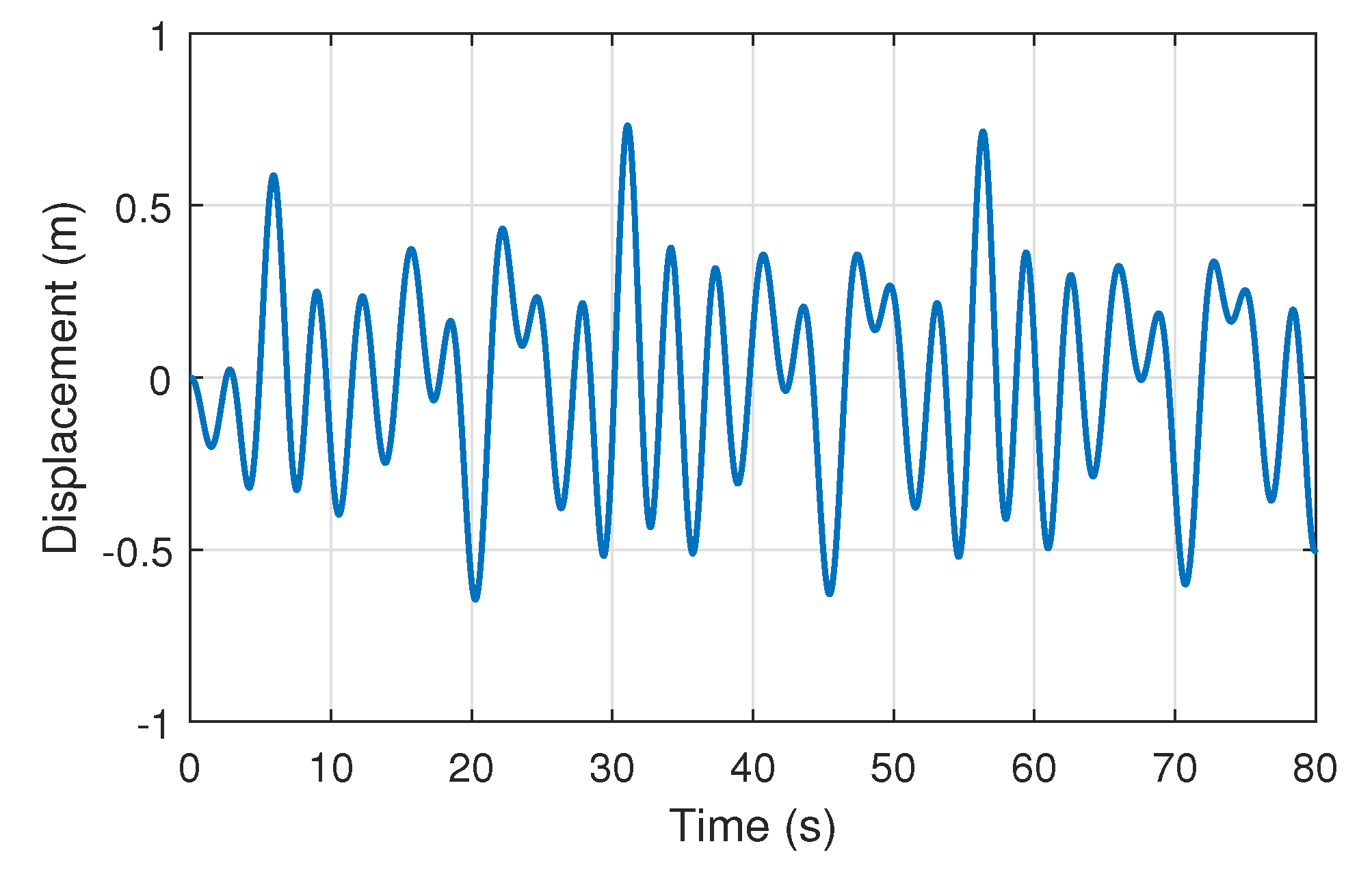
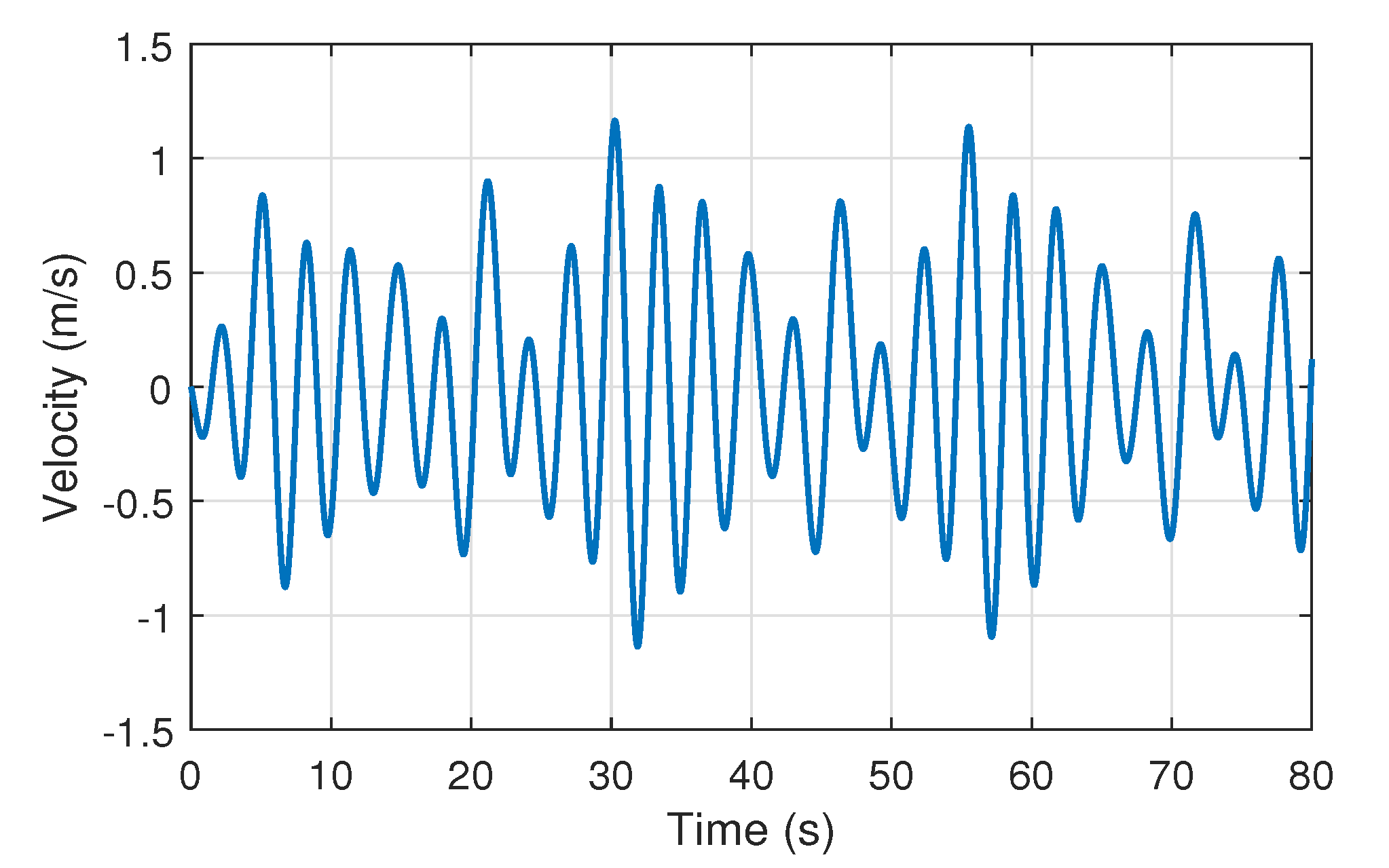
4.2. Responses of the Offshore Structure with Different Fuzzy Output Feedback Control Schemes
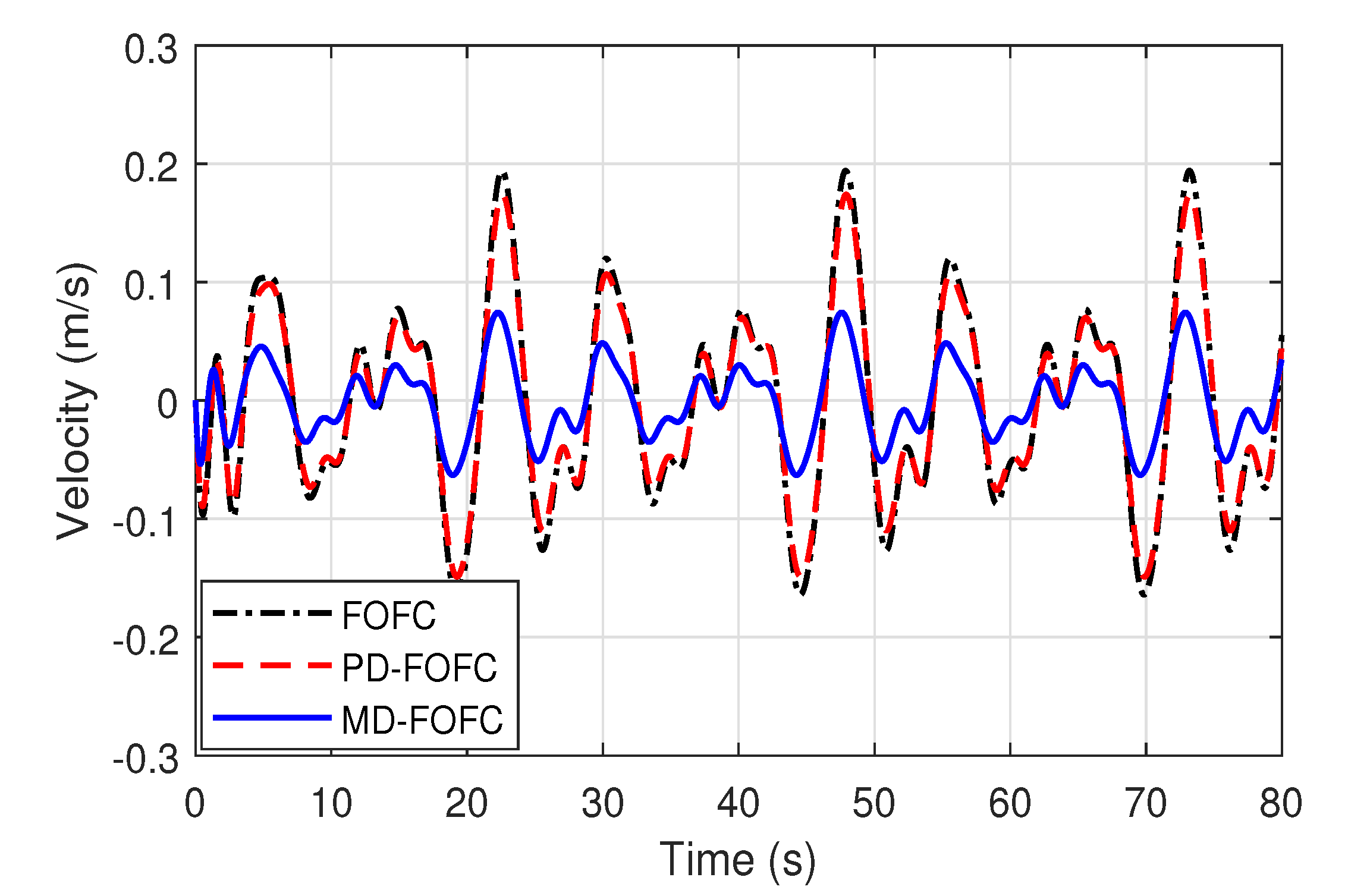
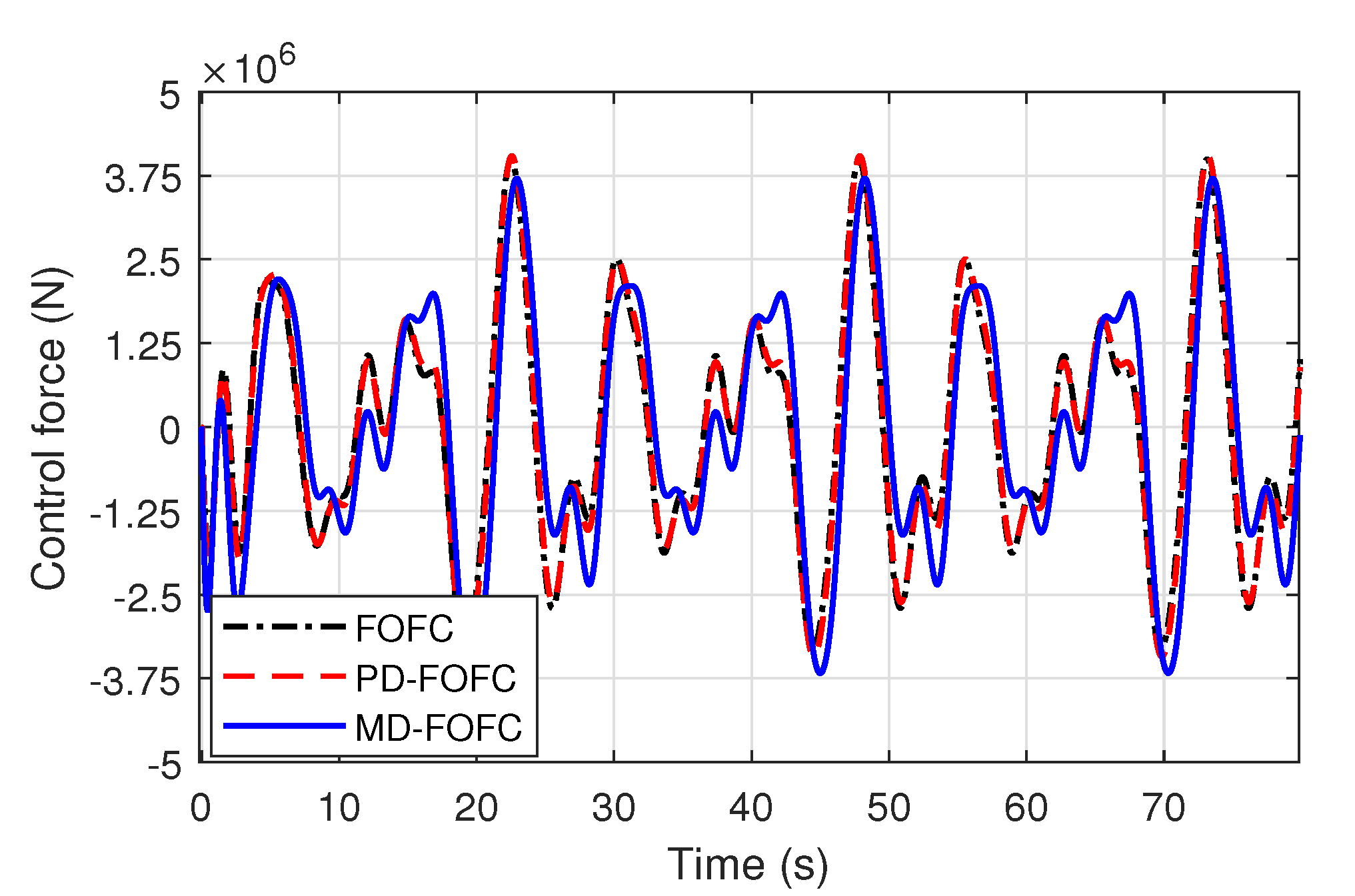
4.3. Comparisons of FOFC, PD-FOFC, and MD-FOFC
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zribi, M.; Almutairi, N.; Abdel-Rohman, M.; Terro, M. Nonlinear and robust control schemes for offshore steel jacket platforms. Nonlinear Dyn. 2004, 35, 61–80. [Google Scholar] [CrossRef]
- Ghassempour, M.; Failla, G.; Arena, F. Vibration mitigation in offshore wind turbines via tuned mass damper. Eng. Struct. 2019, 183, 610–636. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, X.; Zheng, R.; Minagawa, K. High response performance of a Tuned-Mass damper for vibration suppression of offshore platform under earthquake loads. Shock Vib. 2016, 4, 7383679. [Google Scholar] [CrossRef]
- Sun, C.; Jahangiri, V. Fatigue damage mitigation of offshore wind turbines under real wind and wave conditions. Eng. Struct. 2019, 178, 472–483. [Google Scholar] [CrossRef]
- Ma, H.; Tang, G.-Y.; Ding, X.-Q. Modified-transformation-based networked controller for offshore platforms under multiple outloads. Ocean Eng. 2019, 190. [Google Scholar] [CrossRef]
- Huang, S.; Cai, M.; Xiang, Z. Sampled-data H∞ control for offshore platforms subject to irregular wave forces and actuator saturation. Nonlinear Dyn. 2017, 88, 2705–2721. [Google Scholar] [CrossRef]
- Ma, H.; Hu, W.; Tang, G.-Y. Networked predictive vibration control for offshore platforms with random time delays, packet dropouts and disordering. J. Sound Vib. 2019, 441, 187–203. [Google Scholar] [CrossRef]
- Ou, J.; Long, X.; Li, Q.S.; Xiao, Y.Q. Vibration control of steel jacket offshore platform structures with damping isolation systems. Eng. Struct. 2007, 29, 1525–1538. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M. Recent advances in vibration control of offshore platforms. Nonlinear Dyn. 2017, 89, 755–771. [Google Scholar] [CrossRef]
- Reza Ghasemi, M.; Shabakhty, N.; Hadi Enferadi, M. Vibration control of offshore jacket platforms through shape memory alloy pounding tuned mass damper (SMA-PTMD). Ocean Eng. 2019, 191, 106348. [Google Scholar] [CrossRef]
- Hadi Enferadi, M.; Reza Ghasemi, M.; Shabakhty, N. Wave-induced vibration control of offshore jacket platforms through SMA dampers. Appl. Ocean Res. 2019, 90, 101848. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M.; Tang, G.-Y. Active Control of Offshore Steel Jacket Platforms; Springer: Gateway East, Singapore, 2019. [Google Scholar]
- Ma, H.; Tang, G.-Y.; Zhao, Y.-D. Feedforward and feedback optimal control for offshore structures subjected to irregular wave forces. Ocean Eng. 2006, 33, 1105–1117. [Google Scholar] [CrossRef]
- Li, H.-J.; Hu, S.-L.; Jakubiak, C. H2 active vibration control for offshore platform subjected to wave loading. J. Sound Vib. 2003, 263, 709–724. [Google Scholar] [CrossRef]
- Kim, D.H. Neuro-control of fixed offshore structures under earthquake. Eng. Struct. 2009, 31, 517–522. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Li, M.; Han, Q.-L. Sliding mode H∞ control for offshore steel jacket platforms subject to nonlinear self-excited wave force and external disturbance. Nonlinear Anal. Real World Appl. 2013, 14, 163–178. [Google Scholar] [CrossRef]
- Nourisola, H.; Ahmadi, B.; Tavakoli, S. Delayed adaptive output feedback sliding mode control for offshore platforms subject to nonlinear wave-induced force. Ocean Eng. 2015, 104, 1–9. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M. Sliding mode control with mixed current and delayed states for offshore steel jacket platforms. IEEE Trans. Control Syst. Technol. 2014, 22, 1769–1783. [Google Scholar] [CrossRef]
- Sivaranjani, K.; Rakkiyappan, R.; Lakshmanan, S.; Lim, C.P. Robust stochastic sampled-data control for offshore steel jacket platforms with non-linear perturbations. IMA J. Math. Control Inf. 2015, 34, 337–357. [Google Scholar] [CrossRef]
- Sakthivel, R.; Selvaraj, P.; Mathiyalagan, K.; Park, J.H. Robust fault-tolerant H∞ control for offshore steel jacket platforms via sampled-data approach. J. Frankl. Inst. Eng. Appl. Math. 2015, 352, 2259–2279. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M. Event-triggered H∞ reliable control for offshore structures in network environments. J. Sound Vib. 2016, 368, 1–21. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Wei, H.-M.; Cai, Z.H.; Li, Q.; Tang, G.-Y. Resilience analysis and design of event-triggered offshore steel jacket structure. Neurocomputing 2019, 400, 429–439. [Google Scholar] [CrossRef]
- Rush, D.R.; Petterson, B.J.; Fahrenholtz, J.C. Lag-stabilized force feedback damping. J. Intell. Robot. Syst. 1998, 21, 277–285. [Google Scholar]
- Zhang, X.-M.; Han, Q.-L.; Han, D.S. Effects of small time-delays on dynamic output feedback control of offshore steel jacket structures. J. Sound Vib. 2001, 30, 3883–3900. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Cai, Z.H.; Gao, S.W.; Tang, G.-Y. Delayed proportional-integral control for offshore steel jacket platforms. J. Frankl. Inst. Eng. Appl. Math. 2019, 356, 6373–6387. [Google Scholar] [CrossRef]
- Li, H.Y.; Yu, J.Y.; Liu, H.H. Adaptive sliding-mode control for nonlinear active suspension vehicle systems using T–S fuzzy approach. IEEE Trans. Ind. Electron. 2012, 60, 3328–3338. [Google Scholar] [CrossRef]
- Peng, C.; Han, Q.-L.; Yue, D. To transmit or not to transmit: A discrete event-triggered communication scheme for networked Takagi-Sugeno fuzzy systems. IEEE Trans. Fuzzy Syst. 2013, 21, 164–170. [Google Scholar] [CrossRef]
- Zhang, D.W.; Han, Q.-L.; Jia, X.-C. Network-based output tracking control for a class of TS fuzzy systems that can not be stabilized by nondelayed output feedback controllers. IEEE Trans. Cybern. 2015, 45, 1511–1524. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.-L. Global asymptotic stability analysis for delayed neural networks using a matrix quadratic convex approach. Neural Netw. 2014, 54, 57–69. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.-L.; Ge, X.; Ding, D. An overview of recent developments in Lyapunov–Krasovskii functionals and stability criteria for recurrent neural networks with time-varying delays. Neurocomputing 2018, 313, 392–401. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.-L.; Wang, J. Admissible delay upper bounds for global asymptotic stability of neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5319–5329. [Google Scholar] [CrossRef]
- Lian, H.-H.; Xiao, S.-P.; Yan, H.; Yang, F.; Zeng, H.-B. Dissipativity analysis for neural networks with time-varying delays via a delay-product-type Lyapunov functional approach. IEEE Trans. Neural Netw. Learn. Syst. 2020. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-M.; Han, Q.-L.; Ge, X.; Ding, L. Resilient control design based on a sampled-data model for a class of networked control systems under denial-of-service attacks. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; She, J.; Zhang, X.; Cao, Z.; Zhang, Z. Performance enhancement of RCS and application to tracking control of chuck-workpiece systems. IEEE Trans. Ind. Electron. 2020, 67, 4056–4065. [Google Scholar] [CrossRef]
- Zhou, L.; She, J.; Zhou, S.; Li, C. Compensation for state-dependent nonlinearity in a modified repetitive-control system. Int. J. Robust Nonlin. Control 2018, 28, 213–226. [Google Scholar] [CrossRef]
- Zhou, L.; She, J.; Zhou, S. Robust H∞ control of an observer-based repetitive-control system. J. Franklin Inst. 2018, 355, 4952–4969. [Google Scholar] [CrossRef]

| Controllers | Peak Values | RMS Values | ||||
|---|---|---|---|---|---|---|
| Dis. (m) | Vel. (m/s) | u (10 N) | Dis. (m) | Vel. (m/s) | u (10 N) | |
| No Control | 0.7320 | 1.1648 | – | 0.2831 | 0.4785 | – |
| FOFC | 0.2120 | 0.1940 | 3.9925 | 0.1012 | 0.0841 | 1.7169 |
| d (s) | Peak Values | RMS Values | ||||
|---|---|---|---|---|---|---|
| Dis. (m) | Vel. (m/s) | u (10 N) | Dis. (m) | Vel. (m/s) | u (10 N) | |
| 0.01 | 0.0393 | 0.0376 | 4.0354 | 0.0187 | 0.0162 | 1.9460 |
| 0.02 | 0.0518 | 0.0490 | 3.9232 | 0.0246 | 0.0211 | 1.8962 |
| 0.03 | 0.1064 | 0.0981 | 3.7403 | 0.0507 | 0.0425 | 1.7432 |
| 0.04 | 0.1927 | 0.1739 | 4.0412 | 0.0920 | 0.0760 | 1.7574 |
| 0.05 | 0.2679 | 0.2375 | 4.7104 | 0.1282 | 0.1050 | 2.0294 |
| 0.06 | 0.2956 | 0.2633 | 4.8960 | 0.1416 | 0.1159 | 2.1104 |
| 0.07 | 0.3597 | 0.3277 | 5.2523 | 0.1728 | 0.1421 | 2.2810 |
| 0.10 | 0.5282 | 0.5238 | 4.0183 | 0.2379 | 0.2171 | 1.8024 |
| 0.15 | 0.5321 | 0.5597 | 2.0533 | 0.2241 | 0.2422 | 0.8497 |
| 0.60 | 0.6887 | 1.0773 | 0.0847 | 0.2644 | 0.4325 | 0.3192 |
| d (s) | Peak Values | RMS Values | ||||
|---|---|---|---|---|---|---|
| Dis. (m) | Vel. (m/s) | u (10 N) | Dis. (m) | Vel. (m/s) | u (10 N) | |
| 0.01 | 0.1506 | 0.1393 | 3.6803 | 0.0717 | 0.0602 | 1.6498 |
| 0.02 | 0.1806 | 0.1668 | 3.7523 | 0.0861 | 0.0720 | 1.6416 |
| 0.03 | 0.0787 | 0.0743 | 3.7035 | 0.0374 | 0.0319 | 1.7856 |
| 0.04 | 0.1462 | 0.1346 | 3.7199 | 0.0697 | 0.0583 | 1.6720 |
| 0.05 | 0.2081 | 0.1923 | 3.8471 | 0.0992 | 0.0830 | 1.6552 |
| 0.06 | 0.1690 | 0.1552 | 3.7840 | 0.0806 | 0.0672 | 1.6688 |
| 0.07 | 0.1118 | 0.1029 | 3.7337 | 0.0532 | 0.0446 | 1.7317 |
| 0.10 | 0.2640 | 0.2391 | 4.4164 | 0.1262 | 0.1042 | 1.8866 |
| 0.15 | 0.2547 | 0.2282 | 4.4678 | 0.1218 | 0.1002 | 1.9172 |
| 4.00 | 0.3074 | 0.6380 | 9.9099 | 0.0351 | 0.0627 | 3.2455 |
| 5.50 | 0.4896 | 0.8379 | 52.554 | 0.0696 | 0.1078 | 2.5903 |
| Controllers | Peak Values | RMS Values | ||||
|---|---|---|---|---|---|---|
| Dis. (m) | Vel. (m/s) | u (10 N) | Dis. (m) | Vel. (m/s) | u (10 N) | |
| FOFC | 0.2120 | 0.1940 | 3.9925 | 0.1012 | 0.0841 | 1.7169 |
| PD-FOFC () | 0.1064 | 0.0981 | 3.7403 | 0.0507 | 0.0425 | 1.7432 |
| MD-FOFC () | 0.0787 | 0.0743 | 3.7035 | 0.0374 | 0.0319 | 1.7856 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, H.-N.; Zhang, B.-L.; Li, Q.; Tang, G.-Y. Delayed Fuzzy Output Feedback H∞ Control for Offshore Structures. J. Mar. Sci. Eng. 2020, 8, 434. https://doi.org/10.3390/jmse8060434
Feng H-N, Zhang B-L, Li Q, Tang G-Y. Delayed Fuzzy Output Feedback H∞ Control for Offshore Structures. Journal of Marine Science and Engineering. 2020; 8(6):434. https://doi.org/10.3390/jmse8060434
Chicago/Turabian StyleFeng, Hua-Nv, Bao-Lin Zhang, Qing Li, and Gong-You Tang. 2020. "Delayed Fuzzy Output Feedback H∞ Control for Offshore Structures" Journal of Marine Science and Engineering 8, no. 6: 434. https://doi.org/10.3390/jmse8060434
APA StyleFeng, H.-N., Zhang, B.-L., Li, Q., & Tang, G.-Y. (2020). Delayed Fuzzy Output Feedback H∞ Control for Offshore Structures. Journal of Marine Science and Engineering, 8(6), 434. https://doi.org/10.3390/jmse8060434





