Abstract
This study aims to develop a simple but effective approach to investigate the stability of an unsaturated and multilayered coastal-embankment slope during the rainfall, in which a Random Search Algorithm (RSA) based on the random sampling idea of the Monte Carlo method was employed to obtain the most dangerous circular sliding surface, whereas the safety factor of the unsaturated slope was calculated by the modified Morgenstern–Price method. Firstly, two typical distributions of matric suction were illustrated and the associated methods for determining the strength parameters of unsaturated soil were developed. Based on this, the Morgenstern–Price method was further modified to calculate the safety factor, and RSA was adopted to locate the most dangerous sliding surface of the unsaturated multilayered coastal-embankment slope. Finally, the slope breaking process under rainfall infiltration was simulated through continuously searching the critical slip surfaces under different groundwater levels by RSA. The results indicated that the stability of the unsaturated embankment slope was gradually deteriorated with the increase of rainfall infiltration. It was also found that both of the distributions of the matrix suction (ua-uw) and the suction angle (φb) had significant effects on the safety factor of the embankment slope. Basically, linear distribution of (ua-uw) along the depth and linear relationship between φb and (ua-uw) should be adopted in assessing the stability of the unsaturated multilayered coastal-embankment slope.
1. Introduction
As one of the effective defensing coastal structures, embankment slope or breakwater is widely used to protect ashore human life and property from severe environment (storm, rainfall, long-term wave loading, etc.). Therefore, the instability of the embankment slope has attracted more and more attention in coastal engineering with the failure modes of scour [1,2,3,4] and shear failure [5,6,7,8]. Moreover, most of the above literature has mainly focused on wave-induced seabed instability, in which the soil was considered as saturated material [4,6,9,10,11,12,13]. However, in practical coastal engineering, the coastal-embankment slope is always unsaturated and multilayered. Its stability suffers from huge challenges, especially during rainfall, which has proven to be the key factor linked to landslides [14,15,16,17,18].
As shown in Figure 1, rainfall usually results in a rising of the water table, and a decreasing in matric suction [19,20,21,22]. In addition, as the moisture content increases, the unit weight increases. The combined factors mentioned above may reduce the stability of an unsaturated-soil slope. The occurrence of instabilities of unsaturated slopes during wet periods is quite common all over the world [23,24] and has an expectable increasing trend in intensity and frequency due to the warming climate [22,24]. Therefore, it becomes more and more urgent to develop a simple but effective method to assess the stability of the unsaturated-soil slope during rainfall infiltration.
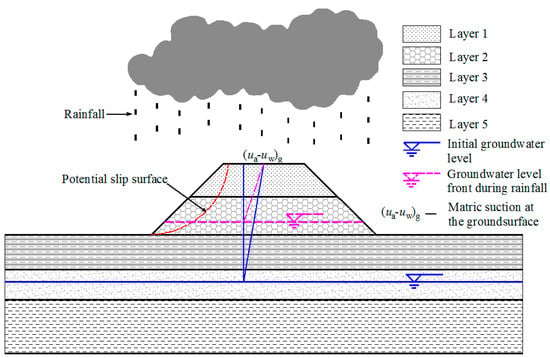
Figure 1.
Cross section of unsaturated multilayered coastal-embankment slope under rainfall infiltration.
To comprehensively investigate the stability of an unsaturated-soil slope, three key issues should be addressed, as follows: (1) an appropriate method to determine the matric suction and its associated strength parameters; (2) a reasonable approach to evaluate the stability of a trial unsaturated-soil slope; (3) an effective algorithm to search for the critical slip surface. Fredlund and Rahardjo [25] pointed out that the presence and the magnitude of matric suction (ua-uw), which were critical to the stability of unsaturated-soil slopes, were dependent on the practical environmental conditions. For the sake of simplicity, the distribution of matric suction in general is considered to be uniformed or linearly decreased along the buried depth [26,27]. Recently, Zhang et al. [28] investigated the effect of the different distributions of matric suction on the overturning stability of the retaining wall with homogeneous, continuous and non-layered surrounding soils. It was found that the influence of uniformed suction was more remarkable than that of linear suction. Xu and Yang [21] found that there is a little difference between the effect of the distribution pattern of matric suction on stability of three-dimensional unsaturated, homogeneous, continuous and non-layered soil slope. However, in practice, the ground conditions in the unsaturated region are generally multilayered, which results in the uncertainty of influence of the matric suction distribution patterns on the stability of unsaturated-soil slope. Moreover, the existence of the multilayered behavior will significantly increase the difficulty in the determination of strength parameters when the rigorous limit equilibrium method was adopted to investigate the safety of the unsaturated-soil slope, which will be analyzed in detail in a later section.
In practical slope engineering design, the limit equilibrium method (LEM) has proven to be an efficient tool to investigate the stability of a saturated soil slope under two-dimensional (2-D) plane strain conditions by computing the safety factor of a given slip surface with some calculation models (Simplified Bishop method [29], Spencer method [30], Morgenstern–Price method [31], etc.). As the most rigorous theoretical approach in LEM under 2-D conditions, Morgenstern–Price (represented by M–P for short) method was firstly developed by Morgenstern and Price in 1965 with the integral form, which resulted in difficulty in programming. Then, M–P method was improved for the convenience of programming by Chen et al. [32], Chen et al. [33] and Zhu and Chen [34] with the discrete pattern. However, both of the improved M–P methods were applicable to compute the safety factor of the saturated soil slope, which should be modified to investigate the stability of the unsaturated-soil slope by combined with the failure criterion of unsaturated soil as suggested by Fredlund and Rahardjo [25].
After determining the safety factor of a given slip surface, another work to investigate the stability of an unsaturated multilayered coastal-embankment slope is to adopt an effect global optimization algorithm to locate the most dangerous slip surface. In the last few decades, nonlinear programming approaches were usually adopted to address the failure surface of saturated slope both in practice and in academic research [35,36]. However, their efficiencies in locating the most dangerous sliding surface have proven to be poor in the case of multilayered slopes with discontinuous soil properties [37]. The Random Search Algorithm (RSA), developed based on the Monte Carlo principle, behaves much better in solving complicated optimization problems in comparison to nonlinear programming approaches [38]. Within the framework of RSA, the global optimal solution can be addressed without iteration by generating a series of trial solutions randomly and comparing them with current optimum solution one by one until reaching the maximum number of locating. The main shortcoming of RSA is the generation of the large number of trial solutions which reduces the calculation efficiency in the past and has become of secondary importance due to the rapid development of computational technology. Currently, it has been widely used in determining the most dangerous sliding surface by search adequate times [39,40].
It should be noted that the stability of coastal-embankment slope with the unsaturated and multilayered feature during rainfall were greatly different from those of dry or saturated soils and should be investigated by a simple and effective approach in consideration of effect of matric suction distributions and underground water levels. As a consequence, in the framework of this research (shown in Figure 2), the influence of rainfall infiltration on unsaturated-soil slope was simulated by the gradual rise of the groundwater level and strength parameters under different distributions of matric suction were determined. Then, the M–P method was modified to investigate the safety of the unsaturated multilayered coastal-embankment slope by combined the rigorous limit equilibrium theory with failure criterion of unsaturated soil. Furthermore, the RSA developed by Malkawi’s method [40] was adopted to locate the critical slip surface of the unsaturated multilayered coastal-embankment slope. Finally, the failure process under the rainfall infiltration was reproduced by searching for the critical slip surface and the associated safety factor, on which the effect of distribution of the matric suction was also investigated. In addition, the influence of the determined method of suction angle on the safety factor is discussed in detail.
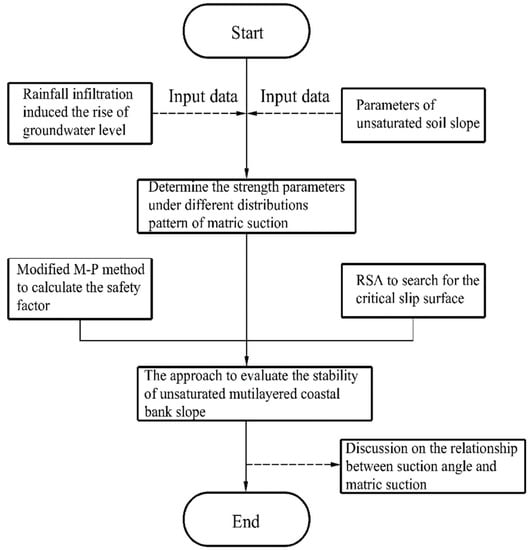
Figure 2.
Framework of the present study.
2. A Simple Approach to Simulate Rainfall Infiltration
When the rainfall is heavy enough to overcome the hydraulic conductivity of the sub-layer, the groundwater table will move upward gradually; however, assuming capillarity rising to the ground surface, the distribution depth of matric suction will decrease until the soil becomes fully saturated, as depicted in Figure 1. Moreover, the density of Layers 2–3 will lose the effective density from its natural pattern and the pore-water pressure will decrease with the associated reduction in the effective stress. Then, the shear strength of soil will drop and the stability of the soil slope will in turn deteriorate. Actually, the effect of rainfall on stability of unsaturated-soil slope is dependent on many of factors (rainfall amount, average intensity, duration, pattern, vegetation) [16,19,41]. For more detailed investigations, it is necessary to address the soil-water profile with 1-D or 2-D infiltration model to address the effect of infiltration on unsaturated-soil slope’s stability [42], which will make the problem become more complicated, laborious and computationally expensive [43]. Since the groundwater level will gradual rise during long-term rainfall infiltration, the effect of rainfall on the unsaturated coastal-embankment slope can be alternatively reproduced by the progressive elevation of the groundwater level without considering the interaction between soil and water. For the sake of simplicity, the phreatic line is assumed to be horizontal in this study as shown in Figure 1.
3. Limit Equilibrium Method of Unsaturated-Multilayered-Soil Slope
3.1. Failure Criterion of Unsaturated-Soil
Fredlund and Rahardjo [25] developed the Mohr–Coulomb criterion to evaluate the failure of the unsaturated soil through introducing matric suction:
where τu = the shear strength; c’ = the effective cohesion; σn = the total normal stress; uw = the pore-water pressure; φ’ = the effective internal friction angle associated with (σn-uw); (ua-uw) = the matric suction; φb = the suction angle. (ua-uw) and φb are the key parameters of unsaturated-soil failure criterion. Furthermore, the value of φb is always dependent on (ua-uw) [44], the (ua-uw) has become a crucial issue unsaturated soil theory [25,26,27,28].
3.2. Distributions of Matric Suction
As shown in Equation (1), (ua-uw) and φb are the key parameters of unsaturated-soil failure criterion. Furthermore, the value of φb is always dependent on (ua-uw) [44], the accurate determination of (ua-uw), therefore, is of great important to the failure criterion of unsaturated soil, which has become a crucial issue in unsaturated-soil theory.
Although the matric suctions at the ground surface (ua-uw)g can be easily tested by tensiometer, the underground matric suctions are difficult to test in practical engineering. For the sake of simplicity, the matric suction is assumed to be distributed along the buried depth by following two patterns [21,25,26,27,28]:
(1) Distribution I
As shown in Figure 3a, the matric suction is uniform along the depth and its value can be half of the matric suction at the ground surface in a general stratified unsaturated-soil slope.
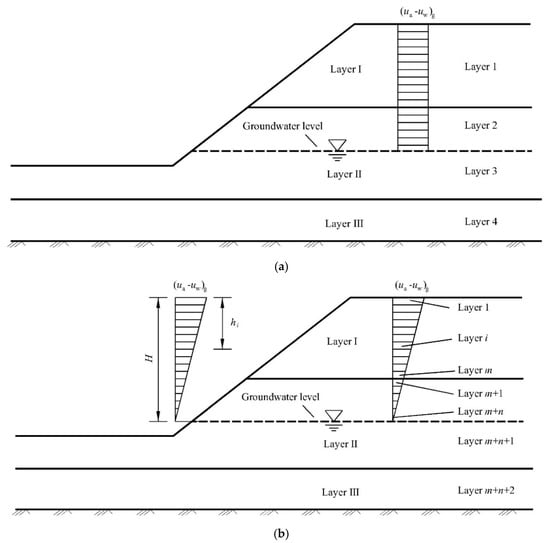
Figure 3.
Distributions of the (ua-uw) along the depth in unsaturated-multilayered-soil slope (a) Distribution I: uniform distribution of (ua-uw); (b) Distribution II: linear distribution of (ua-uw).
(2) Distribution II
As shown in Figure 3b, the matric suctions decrease linearly along the depth and attained their minimum value at the groundwater level.
3.3. Determination of the Strength Parameters under Different Distributions of Matric Suction
For the sake of simplicity, the total cohesion C of unsaturated soil is always considered to be composed of the effective cohesion and the contribution of suction to strength. Then, Equation (1) can be reduced to
where C is the total cohesion and C = c’+(ua-uw)tanφb.
The associated soil strength parameters at different depths can be calculated as follows:
(1) For Distribution I
As shown in Figure 3a, assume that the soil slope is composed of three layers (Layer I, Layer II, Layer III) and for each layer the strength parameters are c’i, φ’i (i = 1,2,3). Because of the existence of (ua-uw) in the soil layers above the groundwater level, the correspondent strength parameters can be determined as follows:
(2) For Distribution II
As shown in Figure 3b, the soil layer above the groundwater level can be divided into (m+n) small soil layers. In each small layer, the strength parameters are supposed to be uniform and to be determined as follows,
where c’i, φ’i(j = I, II, III) = the strength parameters of the original soil layers; (ua-uw)g = the matric suction at the ground surface; Ci, φ’i (i = 1,2,…,m+n+2) = the strength parameters of the divided small layers; H = the distance between the groundwater level and the top of the slope, hi (i = 1,2,…,m+n+2) = the distance between the ith small soil layers and the top of the slope.
3.4. Modified M-P Method
As shown in Figure 4a, a trial sliding mass was generally divided into several small slices based on the principle of slice method. The inter-slice forces imposing on the typical slice was further illustrated in Figure 4b. Within the framework of two-dimensional (2-D) limit equilibrium analysis, M-P method [31] and its improved pattern [32,33,34] had proven to be the most rigorous theoretical approach due to its excellent performance in satisfying both force and moment equilibrium conditions. However, the aforementioned M–P method and its improved pattern were developed within the framework of saturated soil and should be modified with reference to the unsaturated soil strength criterion to exactly address the stability of a two-dimensional unsaturated-soil slope.
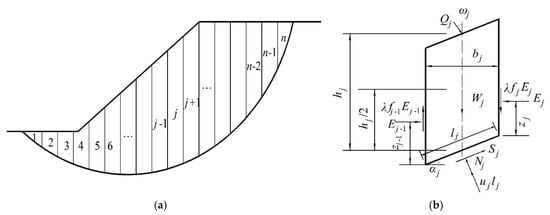
Figure 4.
Discrete model and inter-slice forces in the slip surface of an unsaturated-soil slope (a) discrete model of a slip surface, (b) inter-slice forces.
Based on both of the forces and moment equilibrium of a typical slice (as shown in Figure 4b), the safety factor with the iteration form can be addressed by the following equations [34]:
where Fs = the safety factor of the trial sliding surface; λ = the scaling factor; Ej-1 and Ej = the inter-slice force for slice j-1 and j; Wj = the weight of jth slice; Qj = the external loading; Sj = the shear force; Nj = the normal pressure; uj = the pore-water pressure at slice-base; φ’j and Cj = the mobilized internal friction angle and total cohesion along; fj-1 and fj = the inter-slice force function for slice j-1 and j which can be determined by relating them with the horizontal coordinate. Other detailed information about the model parameters can be found in Reference [34]. The safety factor of a trial sliding surface in the unsaturated multilayered coastal-embankment slope can be performed as shown in Figure 5.
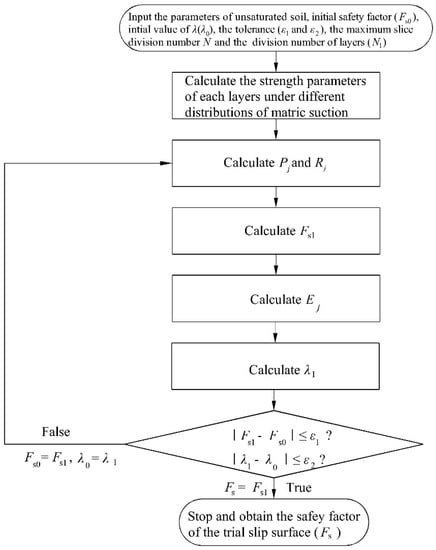
Figure 5.
Flow diagram of modified M–P method.
4. A Global Algorithm to Search for the Critical Slip Surface of Unsaturated Coastal-Embankment Slope
As a typical failure mechanism in practical geotechnical engineering, circular sliding surfaces are widely employed in the stability analysis of saturated soil slopes with both single layer [45,46,47] and multilayer [34,48,49]. Then, the aforementioned problem of determining a trial circular failure surface can be represented by locating the two control intersections (L(xL, yL), R(xR, yR)) and a radius (Rc) shown in Figure 6, in which the potential sliding surface should be addressed in order to satisfy the boundary conditions represented by y = g(x) and y = r(x), the hydraulic conditions y = w(x) and the discontinuity between the layers demonstrated by y = lj(x). Then, the potential sliding surface represented by S can be expressed as functions of xL, yL, xR, yR and Rc in the following form:
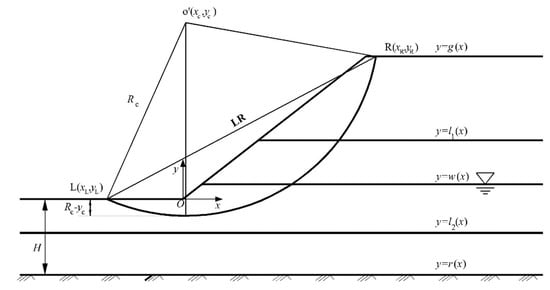
Figure 6.
Cross section of a typical multilayered slope with circular sliding surface.
On the basis of LEM, the safety factor (Fs) with respect to the most dangerous sliding surface should be minimized among all of the trial failure surfaces. The issue in terms of locating the most dangerous slip surface can be mathematically represented by addressing the minimum of Fs with regard to S as follows:
Theoretically speaking, the trial circular failure surface can be generated with any combination of intersections (L(xL, yL), R(xR, yR)) and Rc. However, most of these are invalid due to their impossible occurrence in practical engineering. To improve the searching efficiency, the control parameters should be empirically constrained as:
where xLmax and xLmin = the upper and lower limits of horizontal ordinate of point L; xRmax and xRmin = the upper and lower limits of horizontal ordinate of point R; Rcmax and Rcmin = the upper and lower limits of radius. It should be noted that definitions of these parameters should be dependent on the experience of the researcher.
As shown in Figure 6, the following constraints are considered:
where H = the distance between the bottom and the lower boundary; ‖LR‖ = the length of LR; yc = the vertical ordinate of the center of the circular slip surface.
To resolve the problem mentioned above, a trial sliding surface should be firstly addressed by locating two points and the radius (represented by L, R and Rc shown in Figure 6) within the range of [xLmin, xLmax], [xRmin, xRmax] and [Rcmin, Rcmax], in which points L and R can be located stochastically in the following forms:
where r1, r2 and r3 = stochastic numbers which can be obtained randomly from 0 to 1.
The horizontal and vertical ordinate of O’ can be addressed by the following equations:
where xc = the horizontal ordinate of O’. There are two groups of solution for Equation (22), and to make sure the trial slip surface to be reliable, the smaller value of xc and the lager value of yc are used.
The Random Search Algorithm (RSA) is adopted to obtain the most dangerous sliding surface and the associated minimum safety factor for the unsaturated-soil slope. The detailed procedure for the RSA can be schematically illustrated in Figure 7.
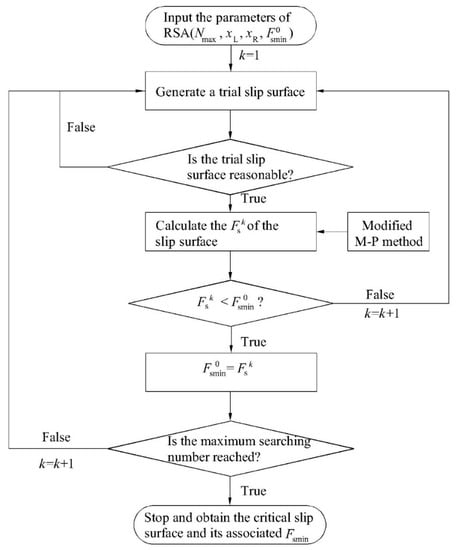
Figure 7.
The flowchart of locating the critical slip surface.
5. Application
5.1. Comparison with the Existing Model
The feasibility of the developed model is assessed by comparison with the numerical results predicted by Zhang et al. [50], in which both the linear and nonlinear relationship between the unsaturated shear strength and matric suction determined by the soil-water characteristic curve (SWCC) were adopted to investigate the effect of matric suction on the slope stability, for a steep unsaturated-soil slope with 30 m high and 50° inclination angle, as illustrated in Figure 8. The parameters for both models are illustrated in Table 1. In addition, the inclined groundwater table in the research of Zhang et al. [50] is assumed to be horizontal with an average 5 m below the toe of the slope for simplicity.
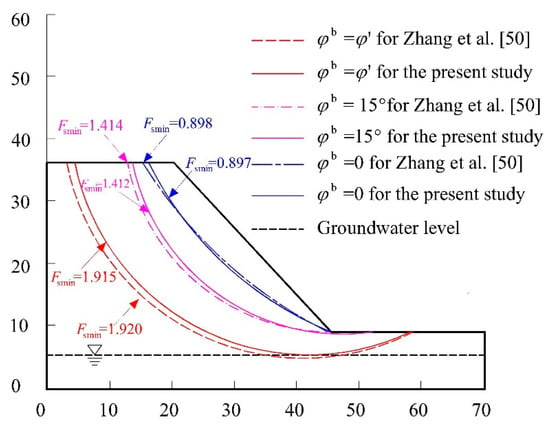
Figure 8.
Comparison of the critical slip surface.

Table 1.
Parameters of soil.
As shown in Figure 8, the critical slip surfaces predicted by both models become gradually deeper and their associated minimum safety factors progressively decrease with the increase of φb. This is because of the amplification of φb which significantly increases the total cohesion (shown in Equations (3)–(8), and enhances the shear strength (Equation (2)), which in turn improves the safety factor. Moreover, both the critical slip surfaces (marked by the solid line) and the associated safety factor always agree well with those (marked by other line type) predicted by Zhang et al. [50]. Therefore, the present method performs well in investigating the stability of the unsaturated-soil slope.
5.2. Case Study
As shown in Figure 9, an unsaturated coastal-embankment slope with the inclination of 1:1.5 and four layers is subject to long-term rainfall, the stability of which is facing a great challenge. The physical-mechanical parameters of each layer are illustrated in Table 2.
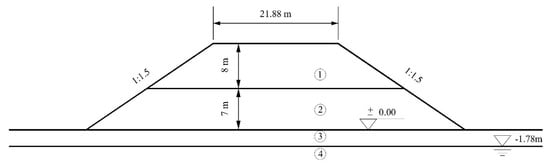
Figure 9.
The geological profile of a high road fill.

Table 2.
Physic-mechanical properties of soil.
To investigate the stability of the unsaturated coastal-embankment slope under rainfall, the failure surface under different groundwater levels and the associated minimum safety factor have been searched 100,000 times by RSA. Two matric suction distributions along the depth: namely the linear distribution (Distribution I); and uniformed distribution (Distribution II) are used in the analysis. Meanwhile, the most dangerous sliding surface and its associated minimum safety factor determined by the traditional saturated M–P method in which the matric suction along the depth is zero (Distribution III) are also addressed by RSA. Based on the comparison results shown in Figure 10, it can be summarized as follows:
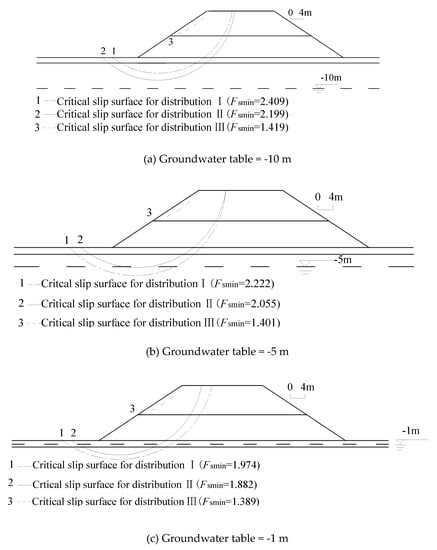
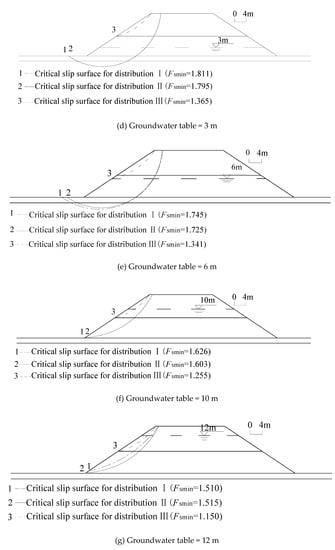
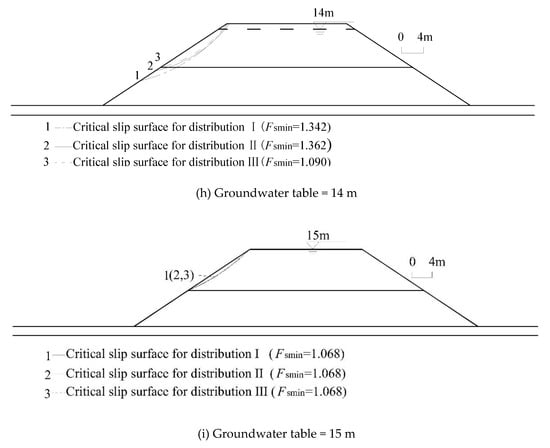
Figure 10.
Critical slip surfaces associated with each distribution pattern of matric suction under rainfall infiltration.
(1) There is an apparent discrepancy among Distribution I, Distribution II and Distribution III with respect to the critical slip surfaces. The critical slip surfaces associated with the above three distributions do not coincide until the groundwater level reaches the top of slope in which the soil is fully saturated.
(2) The most dangerous sliding surface of Distribution III is always located at the shallow depth of the slope and it is independent on the fluctuation of the groundwater level. Unfortunately, these results do not coincide with the practical results. The location of critical slip surface of Distribution I and Distribution II are close and both of them change from deep slip to shallow slip with the rising of the groundwater level and these predicted results coincide well with the practical results.
5.3. Discussion on the Effect of Distribution of (ua-uw) on Fsmin
In this section, the minimum safety factor (Fsmin) under different groundwater level shown in Figure 10 was adopted to investigate the effects of the different distributions of matric suction (ua-uw) on the stability of unsaturated-soil slope. As shown in Figure 11, Fsmin is intensively related to the distribution of (ua-uw) along the buried depth. Overall, all of the three values of Fsmin corresponding to different distributions show gradual decrease with the rise of the groundwater level. However, the reduced rate of Distribution III without suction, which keeps constant (approaches to 0) under the condition that the groundwater level is below 6 m, is remarkable lower that of the other two distributions. Moreover, both of the amplitude and reduced rate of Distribution I are greater than those of Distribution II. When the groundwater level approaches to 15 m, Fsmin of the three distributions coincides with each other, in which the soil is fully saturated. The effects of distributions of (ua-uw) on Fsmin varies accordingly to the distributions. For Distribution I and II with consideration of (ua-uw), the reduction in Fsmin is due to the decrease of distributed depth of (ua-uw) (shown in Figure 1) and the increase of the pore-water pressure (Equations (13) and (16)) with the increase of groundwater level. However, the decrease of Fsmin for Distribution III regardless of (ua-uw) is mainly attributed to the increase of the pore-water pressure. Therefore, the reduced rate and amplitude of Fsmin for Distribution I and II are much greater than that for Distribution III.
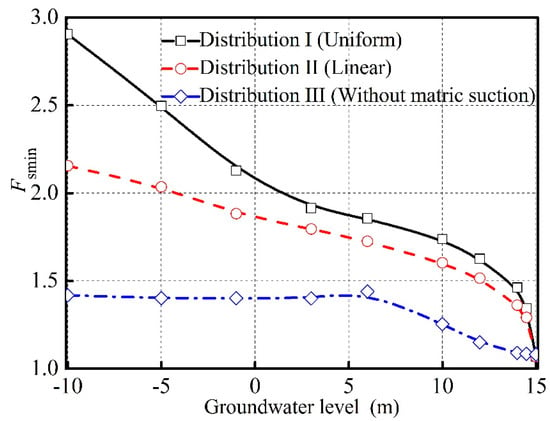
Figure 11.
Effect of distribution pattern of matric suction on safety factor under rainfall infiltration.
Above all, it can be concluded that the Distribution III in traditional saturated limit equilibrium analysis is unexpected which may significantly increase the cost of solidified unsaturated-soil slope and the other two distributions are more rational. Moreover, the safety factor for uniformed distribution (Distribution I) of (ua-uw) is always greater than that for linear distribution (Distribution II), which may result in an unsafe design of the unsaturated-soil slope. With the comprehensive consideration of safety and economy, it is suggested that Distribution II can be used in addressing the stability of unsaturated coastal-embankment slope in practical engineering.
5.4. Discussion on the Relationship between φb and (ua-uw)
The suction angle φb was conventionally supposed to be constant and independent on (ua-uw) in the previous literature [19,51,52,53,54]. However, the multistage direct shear test results [44] showed that the relationship between φb and (ua-uw) could be depicted by Curve 3, as shown in Figure 12. When (ua-uw) is small, φb is supposed to be the maximum value φbmax. With the increase of (ua-uw), φb gradually decreases and when (ua-uw) increases to a certain value φb reaches the minimum value φbmin. Some researchers [25,55,56] used the Curve 1 and Curve 2 to simulate the relationship between φb and (ua-uw) as shown in Figure 12. Curve 1, Curve 2 and Curve 3 can be described by the following functions:
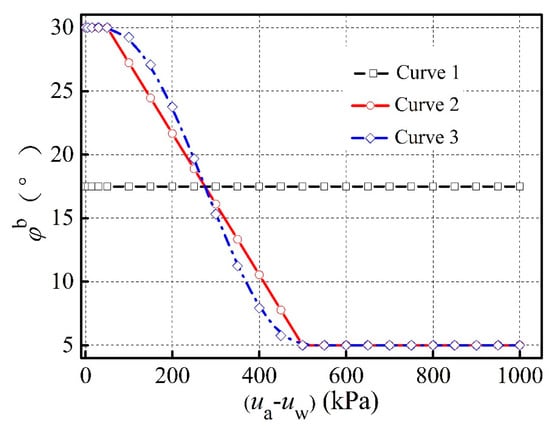
Figure 12.
Correlation curves between φb and (ua-uw).
(1) For Curve 1
(2) For Curve 2
(3) For Curve 3
where φbmax and φbmin are the upper and lower limit respectively. Herein, φbmax is 30°and φbmin is 5°.
Now, two conditions in which the groundwater level reaches up to 6 m and 12 m are considered associated with the Distribution II of matric suction, respectively. Their correspondent critical slip surface is Surface 2 in Figure 10. The influence of the distribution of φb on safety factor in different (ua-uw)g is shown in Figure 13. It can be seen that when φb is supposed to be constant, the safety factor(F1s) associated with Curve 1 is almost linearly increased with the increasing of (ua-uw)g. When the distribution of φb is linear (Curve 2) and nonlinear (Curve 3) both the safety factor (F2s) associated with Curve 2 and (F3s) associated with Curve 3 show the same change trend with the increase of (ua-uw)g. At first, F2s and F3s have a dramatic rise until reaching the maxima. This is because that (ua-uw)g is smaller in this stage and the matric suction on the slip surface is smaller than 50 kPa. Meanwhile, the correspondent value of φb always equals to φbmax and the total cohesion on the slip surface increases with the increasing of (ua-uw)g. Therefore, F2s and F3s become larger and larger. When (ua-uw)g increases to a certain value (about 450 kPa in the example) the matric suction on the slip surface will exceed to 50kPa and the correspondent φb will decrease accordingly to Equation (24) and Equation (25). The value of (ua-uw) will increase but the value of φb will decrease on the slip surface and the total cohesion slightly decreases. Therefore, F2s and F3s decrease slightly at this stage. When (ua-uw)g is kept increasing to a certain value (about 750 kPa in the example), (ua-uw) in the slip surface always exceed to 500 kPa and the correspondent value of φb no longer change. Then, the total cohesion keeps increasing with the increase of (ua-uw)g and F2s and F3s will increase at this stage.
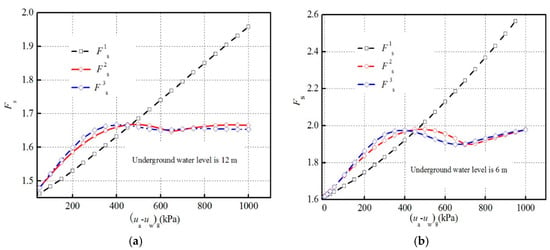
Figure 13.
The influence of the distribution of φb on the safety factor, (a) Underground water level = 6 m; (b) Underground water level = 12 m.
Above all, it can be found that the safety factor is sensitive to the distribution of φb and Curve 2 and Curve 3 are more rational than Curve 1 shown in Figure 13. For the sake of simplicity, it is more reasonable to adopt the linear relationship between φb and (ua-uw) in addressing the unsaturated-soil slope’s safety factor.
6. Conclusions
In this study, the modified Morgenstern–Price (M–P) method coupled with Random Search Algorithm (RSA) was developed to investigate the stability of an unsaturated and multilayered embankment slope considering the effects of matric suction distributions, determinations of suction angle and rainfall infiltration. A convenient programmable M–P method was developed to address the unsaturated-multilayered-soil slope’s safety factor. Based on RSA without iteration, the critical slip surface of unsaturated-multilayered-soil slope could be located. Assuming that the effect of rainfall infiltration could be simulated by the gradual increase in groundwater level, the stability of an unsaturated-multilayered-soil slope under rainfall infiltration was evaluated by introducing different matric suction distribution patterns. Finally, the effect of the determined method of suction angle (φb) on the safety factor was investigated. It was found that the fluctuation of the groundwater level has a significant influence on the location of the most dangerous sliding surface. The associated minimum safety factor and the sliding modes of unsaturated-soil slope gradually change from deep sliding to shallow sliding with the rise of groundwater level. Moreover, the traditional slope stability method regardless of the matric suction is conservative to the predicted results. It is more reasonable to adopt the linear distribution of matric suction in practical calculation of the safety factor (Fs). In addition, Fs is sensitive to the distribution of φb and the linear relationship between φb and (ua-uw) is more beneficial in addressing the stability of the unsaturated multilayered coastal slope. It should be noted that the present approach is simple and a lot of factors such as the effect of soil layering on the matric suction and non-circular failure surface are not covered, which will be addressed in detail in future work.
Author Contributions
Methodology and Writing-original draft, J.-f.Z. Supervision, C.-f.C.; Writing-Review and Editing, H.-y.-Z.
Funding
This research was funded by National Natural Science Foundation of China (51879133, 51409142, 41572298), Natural Science Foundation of Zhejiang Province (LY17E080006). The APC was funded by K.C. Wong Magna Fund in Ningbo University of China.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tofany, N.; Ahmad, M.F.; Mamat, M.; Mohd-Lokman, H. The effects of wave activity on overtopping and scouring on a vertical breakwater. Ocean Eng. 2016, 116, 295–311. [Google Scholar] [CrossRef]
- Pourzangbara, A.; Brocchinib, M.; Saberc, A.; Mahjoobid, J.; Mirzaaghasie, M.; Barzegar, M. Prediction of scour depth at breakwaters due to non-breaking wavesusing machine learning approaches. Appl. Ocean Res. 2017, 63, 120–128. [Google Scholar] [CrossRef]
- Li, K.; Guo, Z.; Wang, L.Z.; Jiang, H.Y. Effect of Seepage Flow on Shields Number around a Fixed and Sagging Pipeline. Ocean Eng. 2019, 172, 487–500. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, W.J.; Zhu, C.B.; Yuan, F.; Rui, S.J. Numerical simulations of wave-induced soil erosion in silty sand seabeds. J. Mar. Sci. Eng. 2019, 7, 52. [Google Scholar] [CrossRef]
- Henkel, D.H. The role of waves in causing submarine landslides. Géotechnique 1970, 20, 75–80. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Jeng, D.-S. Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness. Int. J. Numer. Meth. Eng. 1994, 18, 785–807. [Google Scholar] [CrossRef]
- Jeng, D.-S. Wave-induced seabed instability in front of a breakwater. Ocean Eng. 1997, 24, 887–917. [Google Scholar] [CrossRef]
- Fukuoka, M. Landslides associated with rainfall. Can. Geotech. J. 1980, 11, 1–29. [Google Scholar]
- Guo, Z.; Jeng, D.-S.; Zhao, H.Y.; Guo, W.; Wang, L.Z. Effect of Seepage Flow on Sediment Incipient Motion around a Free Spanning Pipeline. Coast. Eng. 2019, 143, 50–62. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Liang, Z.D.; Jeng, D.-S.; Zhu, J.F.; Guo, Z.; Chen, W.Y. Numerical investigation of dynamic soil response around a submerged rubble mound breakwater. Ocean Eng. 2018, 156, 406–423. [Google Scholar] [CrossRef]
- Chen, W.Y.; Chen, G.X.; Chen, W.; Liao, C.C.; Gao, H.M. Numerical simulation of the nonlinear wave-induced dynamic response of anisotropic poro-elastoplastic seabed. Mar. Georesour. Geotechnol. 2018. [Google Scholar] [CrossRef]
- Zhu, J.F.; Zhao, H.Y.; Jeng, D.-S. Effects of principal stress rotation on wave-induced soil response in a poro-elastoplastic sandy seabed. Acta Geotech. 2019. [Google Scholar] [CrossRef]
- Zhu, J.F.; Zhao, H.Y.; Jeng, D.-S. Dynamic characteristics of a sandy seabed under storm wave loading considering the effect of principal stress rotation. Eng. Geol. 2019. [Google Scholar] [CrossRef]
- Lim, T.T.; Rahardjo, H.; Chang, M.F.; Fredlund, D.G. Effect of rainfall on matrix suctions in residual soil slope. Can. Geotech. J. 1996, 33, 618–628. [Google Scholar] [CrossRef]
- Cho, S.E. Stability analysis of unsaturated soil slopes considering water-air flow caused by rainfall infiltration. Eng. Geol. 2016, 211, 184–197. [Google Scholar] [CrossRef]
- Tang, G.P.; Huanga, J.S.; Sheng, D.C.; Sloan, S.W. Stability analysis of unsaturated soil slopes under random rainfall patterns. Eng. Geol. 2018, 245, 322–332. [Google Scholar] [CrossRef]
- Wu, J.H.; Chen, J.H.; Lu, C.W. Investigation of the Hsien-du-shan Landslide Caused by Typhoon Morakot at Kaohsiung, Taiwan. Int. J. Rock Mech. Min. Sci. 2013, 60, 148–159. [Google Scholar] [CrossRef]
- Chen, K.T.; Wu, J.H. Simulating the failure process of the Xinmo landslide using discontinuous deformation analysis. Eng. Geol. 2018, 239, 269–281. [Google Scholar] [CrossRef]
- Rahardjo, H.; Ong, T.H.; Rezaur, R.B.; Leong, E.C. Factors controlling instability of homogeneous soil slopes under rainfall. J. Geotech. Geoenviron. Eng. 2007, 133, 1532–1543. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, S.; Regueiro, R.A. Instability of partially saturated soil slopes due to alteration of rainfall pattern. Eng. Geol. 2012, 147–148, 28–36. [Google Scholar] [CrossRef]
- Xu, J.S.; Yang, X.L. Three-dimensional stability analysis of slope in unsaturated soils considering strength nonlinearity under water drawdown. Eng. Geol. 2018, 237, 102–115. [Google Scholar] [CrossRef]
- Chowdhury, R.K.; Beecham, S. Australian rainfall trends and their relation to the southern oscillation index. Hydrol. Process. 2010, 24, 504–514. [Google Scholar] [CrossRef]
- Su, L.-J.; Hu, K.-H.; Zhang, W.-F.; Wang, J.; Lei, Y.; Zhang, C.-L.; Cui, P.; Pasuto, A.; Zheng, Q.-H. Characteristics and triggering mechanism of Xinmo landslide on 24 June 2017 in Sichuan, China. J. Mt. Sci. 2017, 14, 1689–1700. [Google Scholar] [CrossRef]
- Robinson, J.D.; Vahedifard, F.; AghaKouchak, A. Rainfall-triggered slope instabilities under a changing climate: comparative study using historical and projected precipitation extremes. Can. Geotech. J. 2017, 54, 117–127. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Oh, W.T.; Vanapalli, S.K. Influence of rain infiltration on the stability of compacted soil slopes. Comput. Geotech. 2010, 37, 649–657. [Google Scholar] [CrossRef]
- Zhang, C.G.; Chen, X.D.; Fan, W. Overturning stability of a rigid retaining wall for foundation pits in unsaturated soils. Int. J. Geomech. 2016, 16, 06015013. [Google Scholar] [CrossRef]
- Bishop, A.W. The use of the slip circle in the stability analysis of earth slopes. Géotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Spencer, E. A method of analysis of the stability of embankments assuming parallel interslice forces. Géotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The analysis of the stability of general slip surfaces. Géotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Morgenstern, N.R. Extensions to the generalized method of slices for stability analysis. Can. Geotech. J. 1983, 20, 104–109. [Google Scholar] [CrossRef]
- Chen, C.F.; Zhu, J.F.; Gong, X.N. Calculation method of earth slope reliability based on response surface method and Morgenstern-Price procedure. Eng. Mech. 2008, 28, 166–172. (In Chinese) [Google Scholar]
- Zhu, J.F.; Chen, C.F. Search for circular and noncircular critical slip surfaces in slope stability analysis by hybrid genetic algorithm. J. Cent. South Univ. 2014, 21, 387–397. [Google Scholar] [CrossRef]
- Nguyen, V.U. Determination of critical slope failure surfaces. J. Geotech. Eng. ASCE 1985, 111, 238–250. [Google Scholar] [CrossRef]
- Yamagami, T.; Ueta, Y. Search for noncircular slip surfaces by the Morgenstern-Price method. In Proceedings of the 6th International Conference on Numerical Methods in Geomechanics, Innsbruck, Austria, 16–20 June 1986; pp. 1335–1340. [Google Scholar]
- Greco, V.R. Numerical methods for locating the critical slip surface in slope-stability analysis. In Proceedings of the 6th International Conference on Numerical Methods in Geomechanics, Innsbruck, Austria, 11–15 April 1988; pp. 1219–1223. [Google Scholar]
- Boutrup, E.; Lovell, C.W. Search techniques in slope stability analysis. Eng. Geol. 1980, 16, 51–61. [Google Scholar] [CrossRef]
- Greco, V.R. Efficient Monte-Carlo technique for locating critical slip surface. J. Geotech. Eng. ASCE 1996, 122, 517–525. [Google Scholar] [CrossRef]
- Malkawi, A.H.; Hassan, W.F.; Sarma, S.K. An efficient search method for finding the critical circular slip surface using the Monte Carlo technique. Can. Geotech. J. 2001, 38, 1081–1089. [Google Scholar] [CrossRef]
- Li, W.C.; Lee, L.M.; Cai, H.; Li, H.J.; Dai, F.C.; Wang, M.L. Combined roles of saturated permeability and rainfall characteristics on surficial failure of homogeneous soil slope. Eng. Geol. 2013, 153, 105–113. [Google Scholar] [CrossRef]
- Gavin, K.; Xue, J. A simple method to analyze infiltration into unsaturated soil slopes. Comput. Geotech. 2008, 35, 223–230. [Google Scholar] [CrossRef]
- Cho, S.E. Infiltration analysis to evaluate the surficial stability of two-layered slopes considering rainfall characteristics. Eng. Geol. 2009, 105, 32–43. [Google Scholar] [CrossRef]
- Gan, J.K.M.; Fredlund, D.G.; Rahardjo, H. Determination of the shear strength parameters of an unsaturated soil using the direct shear test. Can. Geotech. J. 1988, 25, 500–510. [Google Scholar] [CrossRef]
- Loukidis, D.; Bandini, P.; Salgado, R. Stability of seismically loaded slopes using limit analysis. Géotechnique 2003, 53, 463–479. [Google Scholar] [CrossRef]
- Wang, J.P.; Yang, Z.J.; Huang, D.R. New pole-searching algorithm with applications to probabilistic circular slope stability assessment. Comput. Geosci. 2013, 51, 83–89. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.Y.; Wang, N.X.; Sun, P.; Yu, S.; Li, S.Y.; Du, X.H. Modeling lateral enlargement in dam breaches using slope stability analysis based on circular slip mode. Eng. Geol. 2016, 209, 70–81. [Google Scholar] [CrossRef]
- Li, D.Q.; Jiang, S.H.; Qi, X.H.; Cao, Z.J. Efficient system reliability analysis of multi-layered soil slopes using multiple stochastic response surfaces. Geotech. Saf. Reliab. 2017, 164–172. [Google Scholar]
- Deng, D.P.; Li, L.; Zhao, L.H. Stability analysis of a layered slope with failure mechanism of a composite slip surface. Int. J. Geomech. 2019, 19, 04019050. [Google Scholar] [CrossRef]
- Zhang, L.L.; Fredlund, D.G.; Fredlund, M.D.; Ward Wilson, G. Modeling the unsaturated soil zone in slope stability analysis. Can. Geotech. J. 2014, 51, 1384–1398. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, Q. A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage. Comput. Geotech. 1998, 22, 1–28. [Google Scholar] [CrossRef]
- Tsaparas, I.; Rahardjo, H.; Toll, D.G.; Leong, E.C. Controlling parameters for rainfall-induced landslides. Comput. Geotech. 2002, 29, 1–27. [Google Scholar] [CrossRef]
- Blatz, J.A.; Ferreira, N.J.; Graham, J. Effects of near-surface environmental conditions on instability of an unsaturated soil slope. Can. Geotech. J. 2004, 41, 1111–1126. [Google Scholar] [CrossRef]
- Cascini, L.; Cuomo, S.; Pastor, M.; Sorbin, G. Modelling of rainfall induced shallow landslides of the flow-type. J. Geotech. Geoenviron. Eng. 2010, 136, 85–98. [Google Scholar] [CrossRef]
- Wang, R.G.; Yan, S.W.; Deng, W.D. Analysis of seepage stability of high-filled embankment slope due to rainfall infiltration. Chin. J. Highw. Transp. 2004, 17, 25–30. (In Chinese) [Google Scholar]
- Xu, H.; Zhu, Y.W.; Cai, Y.Q.; Zhu, F.M. Stability analysis of unsaturated soil slopes under rainfall infiltration. Rock Soil Mech. 2005, 26, 1957–1962. (In Chinese) [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).