Multi-Mode Joint Equalization Scheme for Low Frequency and Long Range Shallow Water Communications
Abstract
1. Introduction
2. The Acoustic Field Model and Channel Characteristic
3. The Communication Receiver Design
3.1. Part 1: Modal Depth Function Estimation
3.2. Part 2: Mode Filtering
3.3. Part 3: The Multi-Input Equalization
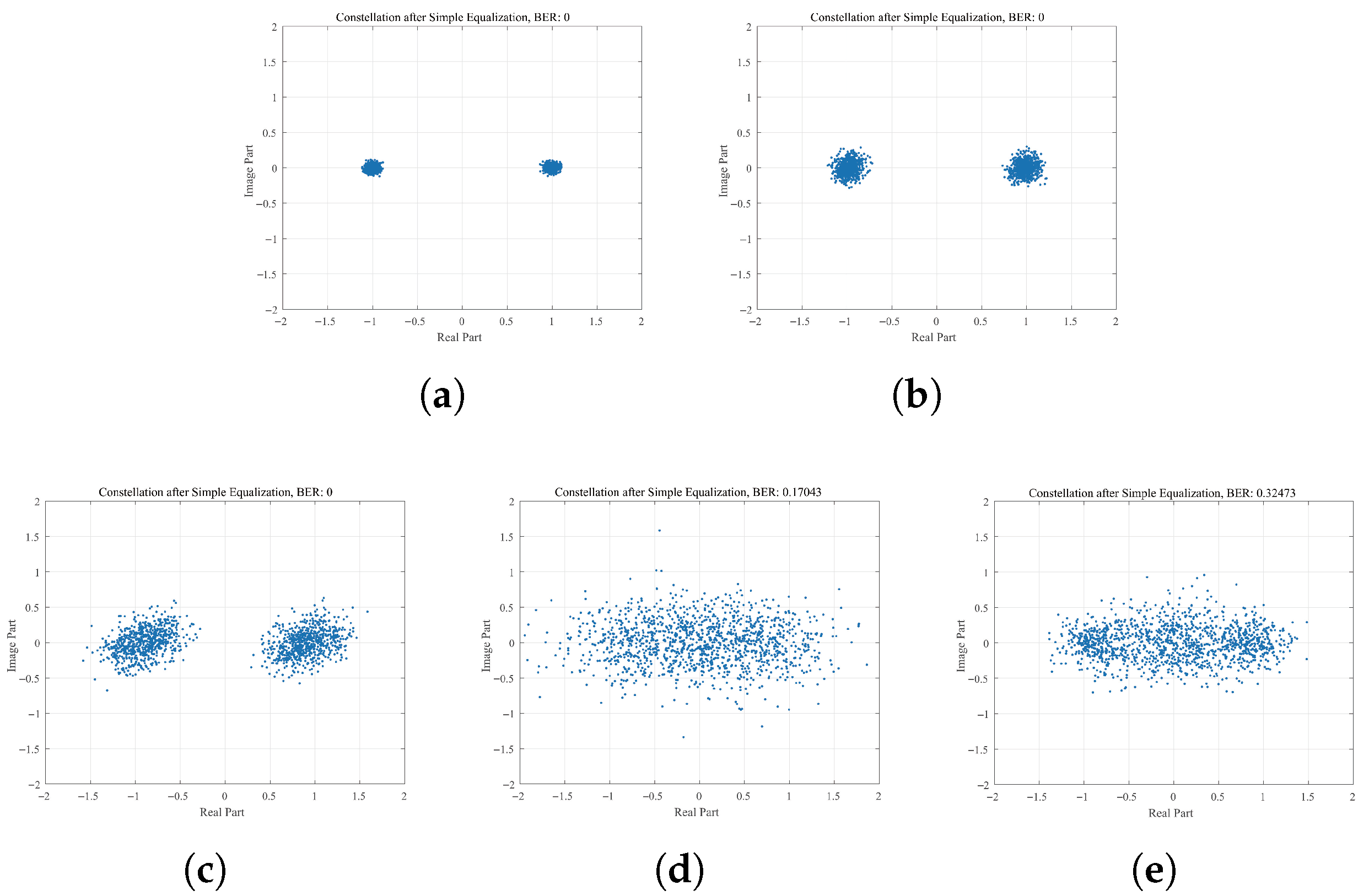
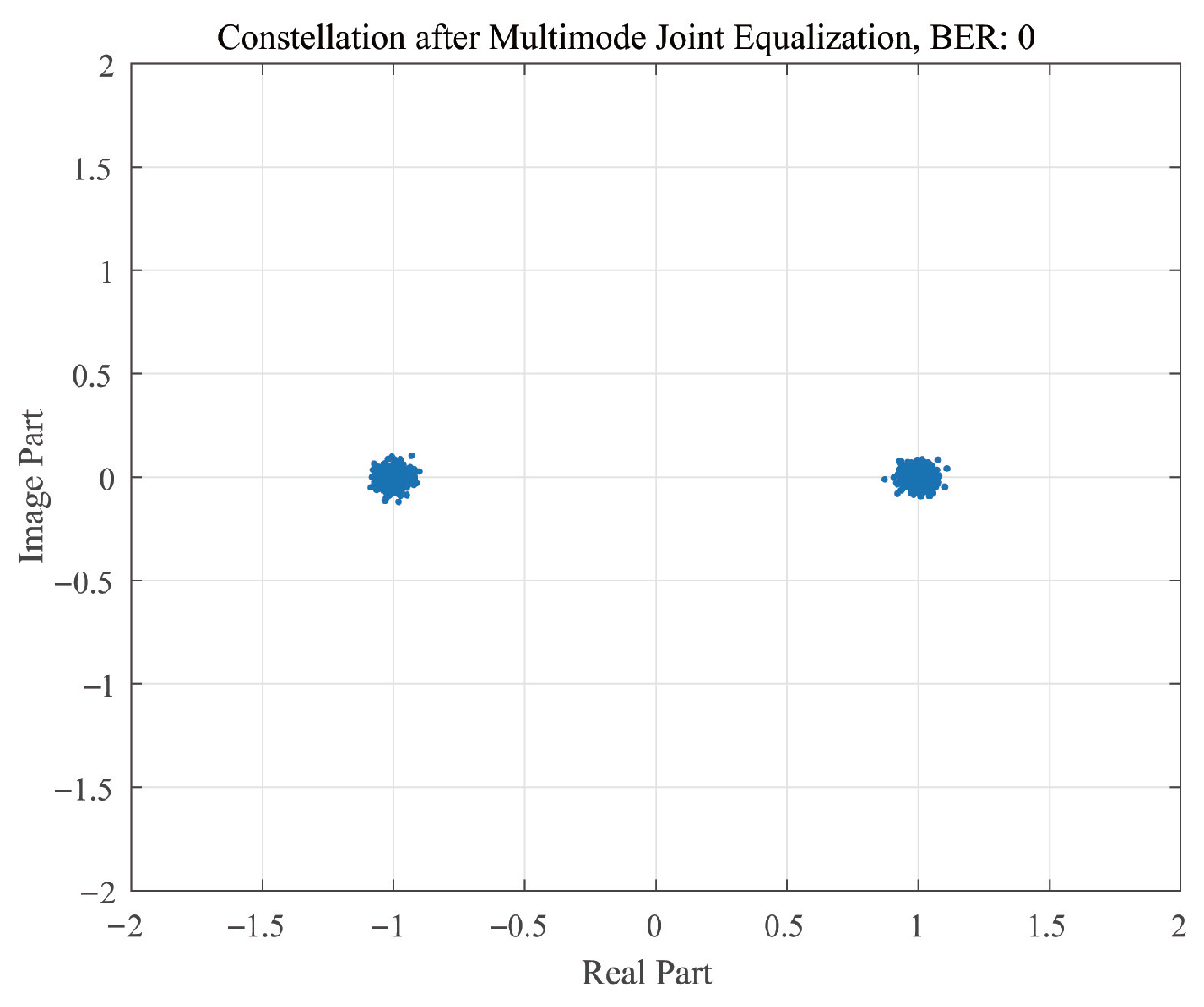
4. Simulation Results and Analysis
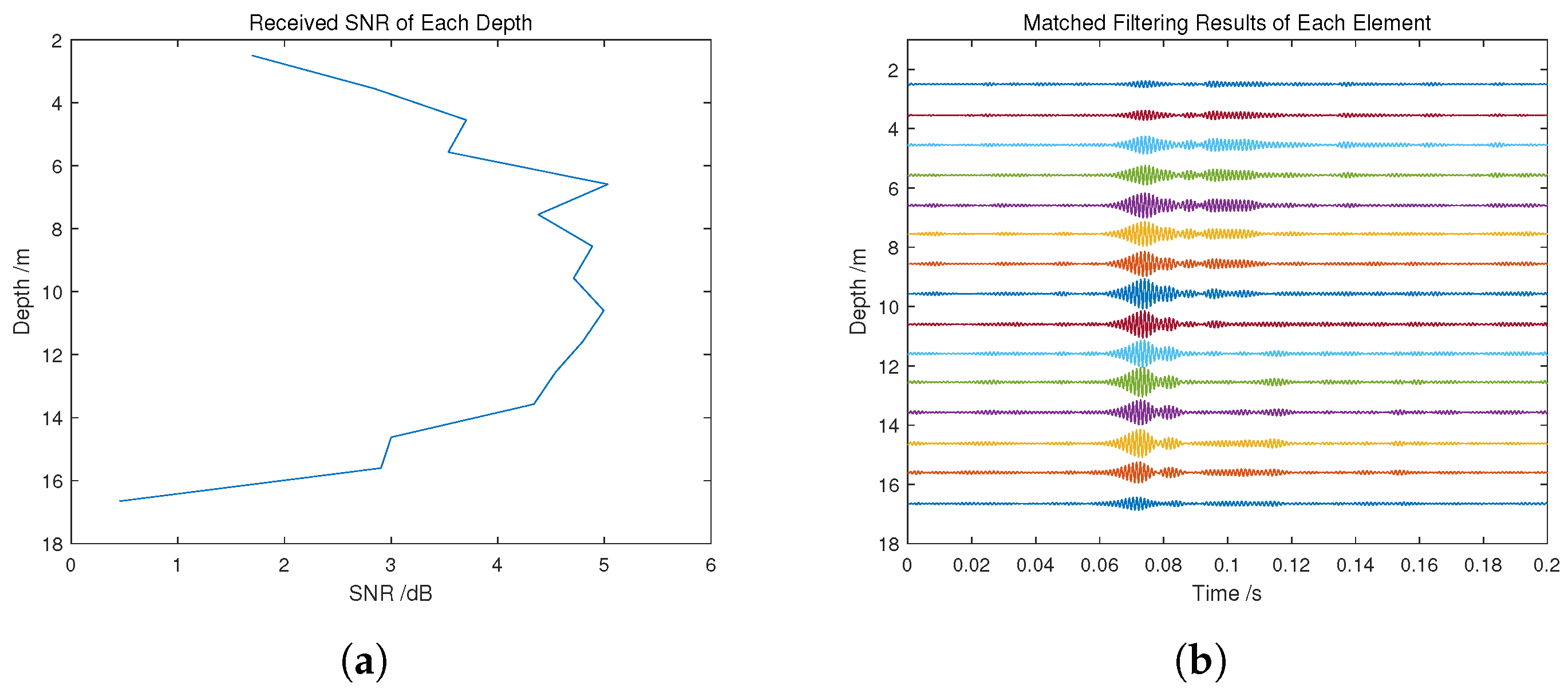
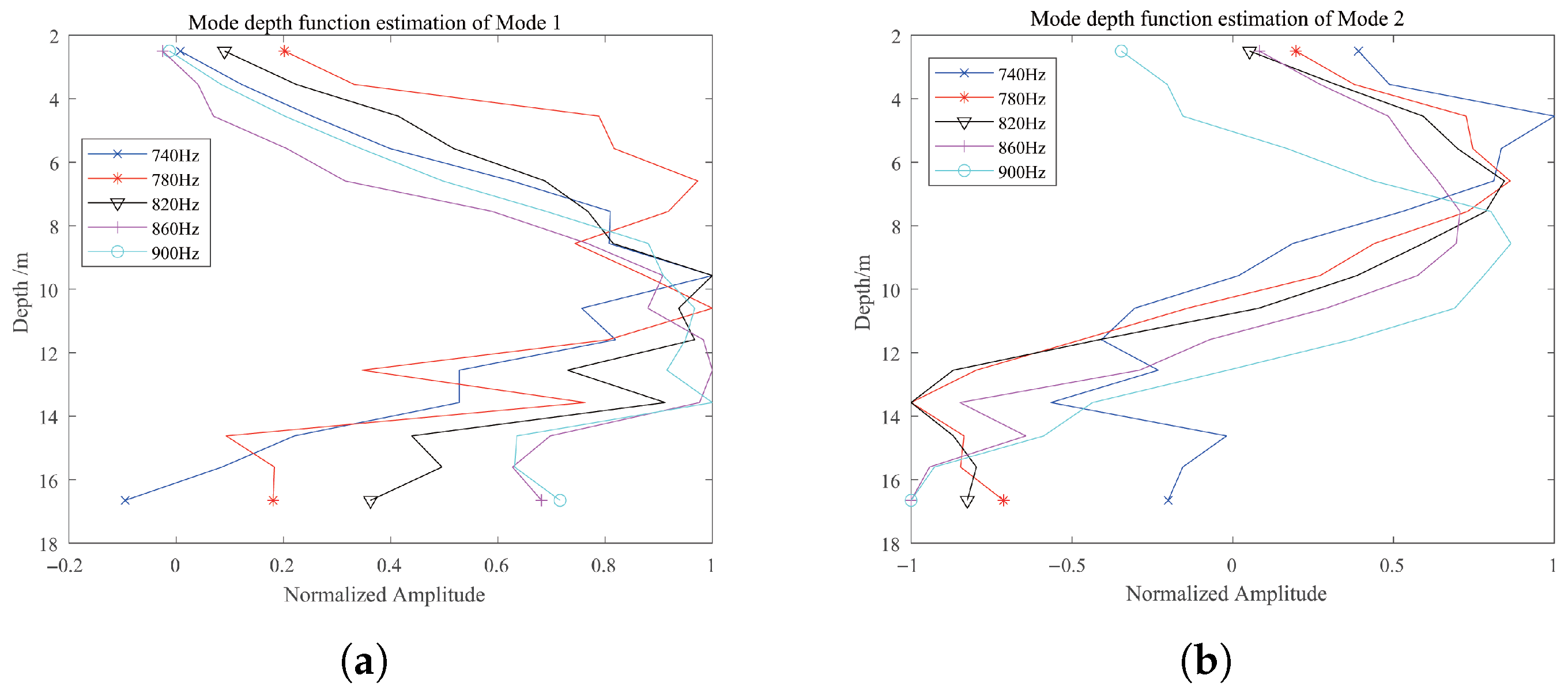
5. Analysis with Field Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilfoyle, D.B.; Baggeroer, A.B. The state of the art in underwater acoustic telemetry. IEEE J. Ocean. Eng. 2000, 25, 4–27. [Google Scholar] [CrossRef]
- Yang, T.C. A Study of Spatial Processing Gain in Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2007, 32, 689–709. [Google Scholar] [CrossRef]
- Stojanovic, M.; Catipovic, J.; Proakis, J.G. Adaptive multichannel combining and equalization for underwater acoustic communications. J. Acoust. Soc. Am. 1998, 94, 1621–1631. [Google Scholar] [CrossRef]
- LeBlanc, L.R.; Beaujean, P.J. Spatio-temporal processing of coherent acoustic communication data in shallow water. IEEE J. Ocean. Eng. 2000, 25, 40–51. [Google Scholar] [CrossRef]
- Kanga, T.; Song, H.C.; Hodgkiss, W.S.; Soo, K.J. Long-range multi-carrier acoustic communications in shallow water based on iterative sparse channel estimation. J. Acoust. Soc. Am. 2010, 126, EL372–EL377. [Google Scholar] [CrossRef]
- Singer, A.C.; Nelson, J.K.; Kozat, S.S. Signal processing for underwater acoustic communications. IEEE Commun. Mag. 2009, 47, 90–96. [Google Scholar] [CrossRef]
- Pajovic, M.; Preisig, J.C. Performance Analysis and Optimal Design of Multichannel Equalizer for Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2015, 40, 759–774. [Google Scholar] [CrossRef]
- Liu, Z.; Yoo, K.; Yang, T.C.; Cho, S.E.; Song, H.C.; Ensberg, D.E. Long-Range Double-Differentially Coded Spread-Spectrum Acoustic Communications with a Towed Array. IEEE J. Ocean. Eng. 2014, 39, 482–490. [Google Scholar] [CrossRef]
- Zhang, D.L.; Xiao, S.; Cui, H.Y.; Gao, D.Z.; Cui, H.Y. Performance analysis of an improved modal dispersion compensation receiver for low-frequency and long-range shallow water communication experiment. Appl. Acoust. 2020, 159, 107–117. [Google Scholar] [CrossRef]
- Yang, T.C. Measurements of temporal coherence of sound transmissions through shallow water. J. Acoust. Soc. Am. 2006, 120, 2595–2614. [Google Scholar] [CrossRef]
- Rouseff, D.; Turgut, A.; Wolf, S.N.; Finette, S.; Orr, M.H.; Pasewark, B.H.; Apel, J.R.; Badiey, M.; Chiu, C.S.; Headrick, R.H.; et al. Coherence of acoustic modes propagating through shallow water internal waves. J. Acoust. Soc. Am. 2002, 111, 1655–1666. [Google Scholar] [CrossRef]
- Baggeroer, A.B.; Kuperman, W.A. An overview of matched field methods in ocean acoustics. IEEE J. Ocean. Eng. 1993, 18, 401–424. [Google Scholar] [CrossRef]
- Yang, T.C. A method of range and depth estimation by modal decomposition. J. Acoust. Soc. Am. 1987, 82, 1736–1745. [Google Scholar] [CrossRef]
- Bucka, J.R.; Preisig, J.C.; Wage, K.E. A unified framework for mode filtering and the maximum a posteriori mode filter. J. Acoust. Soc. Am. 1998, 103, 1813–1824. [Google Scholar] [CrossRef]
- Collison, N.; Dosso, S. A comparison of modal decomposition algorithms for matched-mode processing. Can. Acoust. 2000, 28, 15–26. Available online: https://api.semanticscholar.org/CorpusID:54729552 (accessed on 14 August 2025).
- Papp, J.C.; Preisig, J.C.; Morozov, A.K. Physically constrained maximum likelihood mode filtering. J. Acoust. Soc. Am. 2010, 127, 2385–2391. [Google Scholar] [CrossRef] [PubMed]
- Morozov, A.K.; Preisig, J.C.; Papp, J. Modal processing for acoustic communications in shallow water experiment. J. Acoust. Soc. Am. 2008, 124, 177–181. [Google Scholar] [CrossRef]
- Morozov, A.K.; Preisig, J.C.; Papp, J.C. Investigation of Mode Filtering as a Preprocessing Method for Shallow-Water Acoustic Communications. IEEE J. Ocean. Eng. 2010, 35, 744–755. [Google Scholar] [CrossRef]
- Udovydchenkov, I.A.; Rypina, I.I.; Brown, M.G. Mode filters and energy conservation. J. Acoust. Soc. Am. 2010, 127, 185–191. [Google Scholar] [CrossRef]
- Brown, M.G.; Udovydchenkov, I.A. Underwater communication using weakly dispersive modal pulses. Acoust. Phys. 2013, 59, 533–538. [Google Scholar] [CrossRef]
- Udovydchenkov, I.A. Array design considerations for exploitation of stable weakly dispersive modal pulses in the deep ocean. J. Sound Vib. 2017, 400, 402–416. [Google Scholar] [CrossRef]
- Udovydchenkov, I.A.; Brown, M.G.; Duda, T.F.; Worcester, P.F.; Dzieciuch, M.A.; Mercer, J.A.; Andrew, R.K.; Howe, N.M.; Colosi, J.A. Weakly dispersive modal pulse propagation in the North Pacific Ocean. J. Acoust. Soc. Am. 2013, 134, 3386–3394. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F.B.; Kuperman, W.A. Computational Ocean Acoustics; Springer: New York, NY, USA, 2000. [Google Scholar]
- Zhang, D.L.; Xiao, S.; Cui, H.Y.; Gao, D.Z.; Sun, D.J. Modal dispersion compensation receiver for the long range shallow water acoustic communications. J. Acoust. Soc. Am. 2019, 145, EL483–EL487. [Google Scholar] [CrossRef]
- Porter, M. Acoustic Toolbox—A Matlab Version of KRAKEN. 2018. Available online: https://oalib-acoustics.org/ (accessed on 14 August 2025).
- Neilsen, T.B.; Westwood, E.K.; Udagawa, T. Mode function extraction from a VLA using singular value decomposition. J. Acoust. Soc. Am. 1997, 101, 3025–3032. [Google Scholar] [CrossRef]
- Neilsen, T.B.; Westwood, E.K. Extraction of acoustic normal mode depth functions using vertical line array data. J. Acoust. Soc. Am. 2002, 111, 748–756. [Google Scholar] [CrossRef]
- Wage, K.E.; Baggeroer, A.B.; Preisig, J.C. Modal analysis of broadband acoustic receptions at 3515-km range in the North Pacific using short-time Fourier techniques. J. Acoust. Soc. Am. 2003, 113, 801–817. [Google Scholar] [CrossRef]
- Zhu, Z.L.; Tong, F.; Zhou, Y.H.; Wu, F.Y. Dual parameters optimization lp-LMS for estimating underwater acoustic channel with uncertain sparsity. Appl. Acoust. 2023, 202, 109150. [Google Scholar] [CrossRef]
- Gong, G.Y.; Yao, W.B. Adaptive estimation of sparse channel based on modified RLS for coherent underwater acoustics communications. Appl. Acoust. 2022, 192, 108745. [Google Scholar] [CrossRef]
- Jin, Y.W.; Friedlander, B. Reduced-Rank Adaptive Detection of Distributed Sources Using Subarrays. IEEE Trans. Sig. Process. 2005, 53, 13–25. [Google Scholar] [CrossRef]
- Sheng, X.L.; Dong, C.P.; Guo, L.X.; Wang, X. High-resolution frequency-difference beamforming for a short linear array. J. Acoust. Soc. Am. 2023, 154, 1191–1201. [Google Scholar] [CrossRef]
- Liu, C.X.; Tao, J.; Huang, W.M. A Recursive Gaussian Newton Based Variable Parameter Adaptive Receiver for Single-Carrier Underwater Acoustic Communications. IEEE Trans. Veh. Technol. 2025, 73, 19275–19286. [Google Scholar] [CrossRef]
- Gao, D.Z.; Wang, N.; Wang, H.Z. A Dedispersion Transform for Sound Propagation in Shallow Water Waveguide. J. Comp. Acoust. 2010, 18, 245–257. [Google Scholar] [CrossRef]
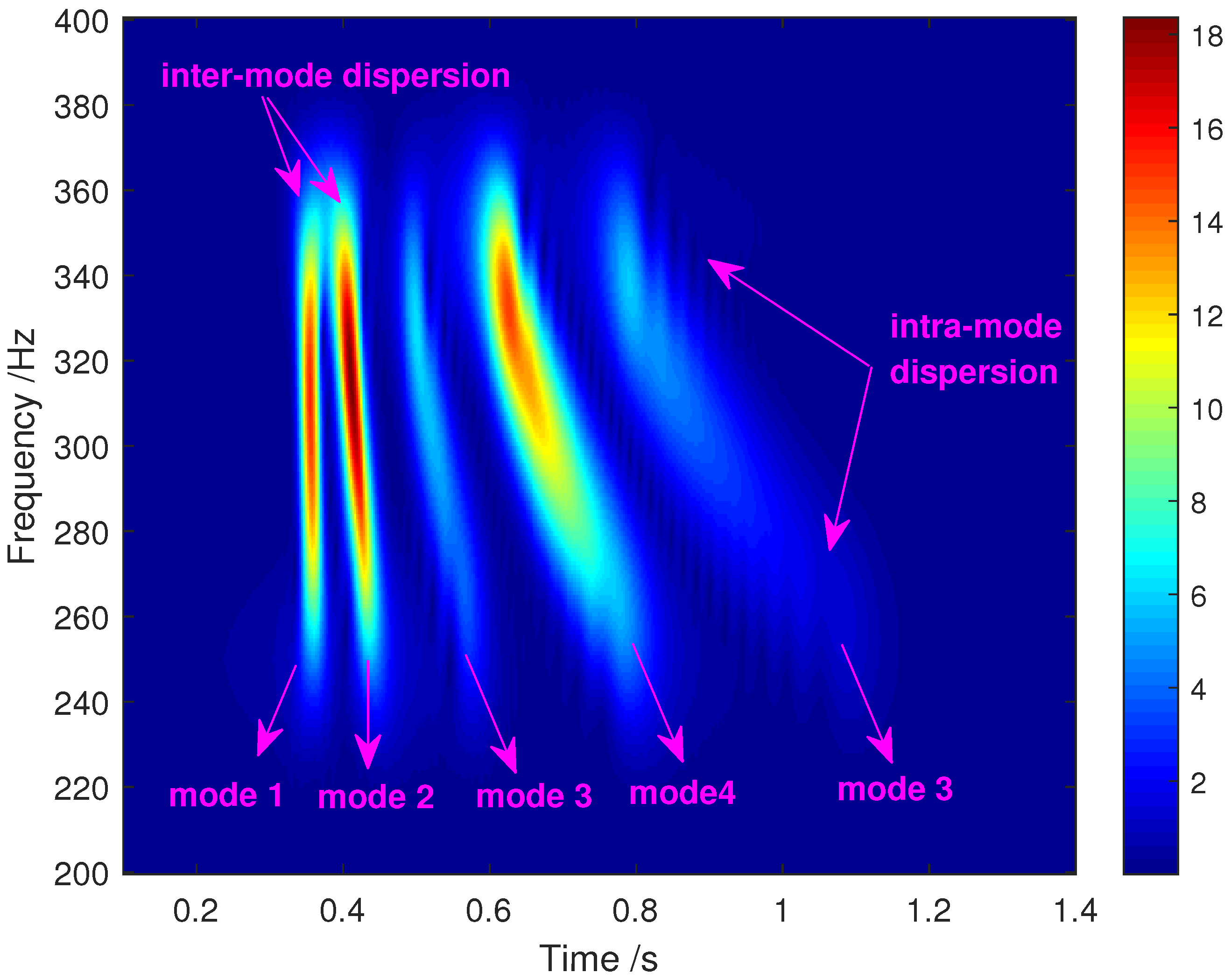

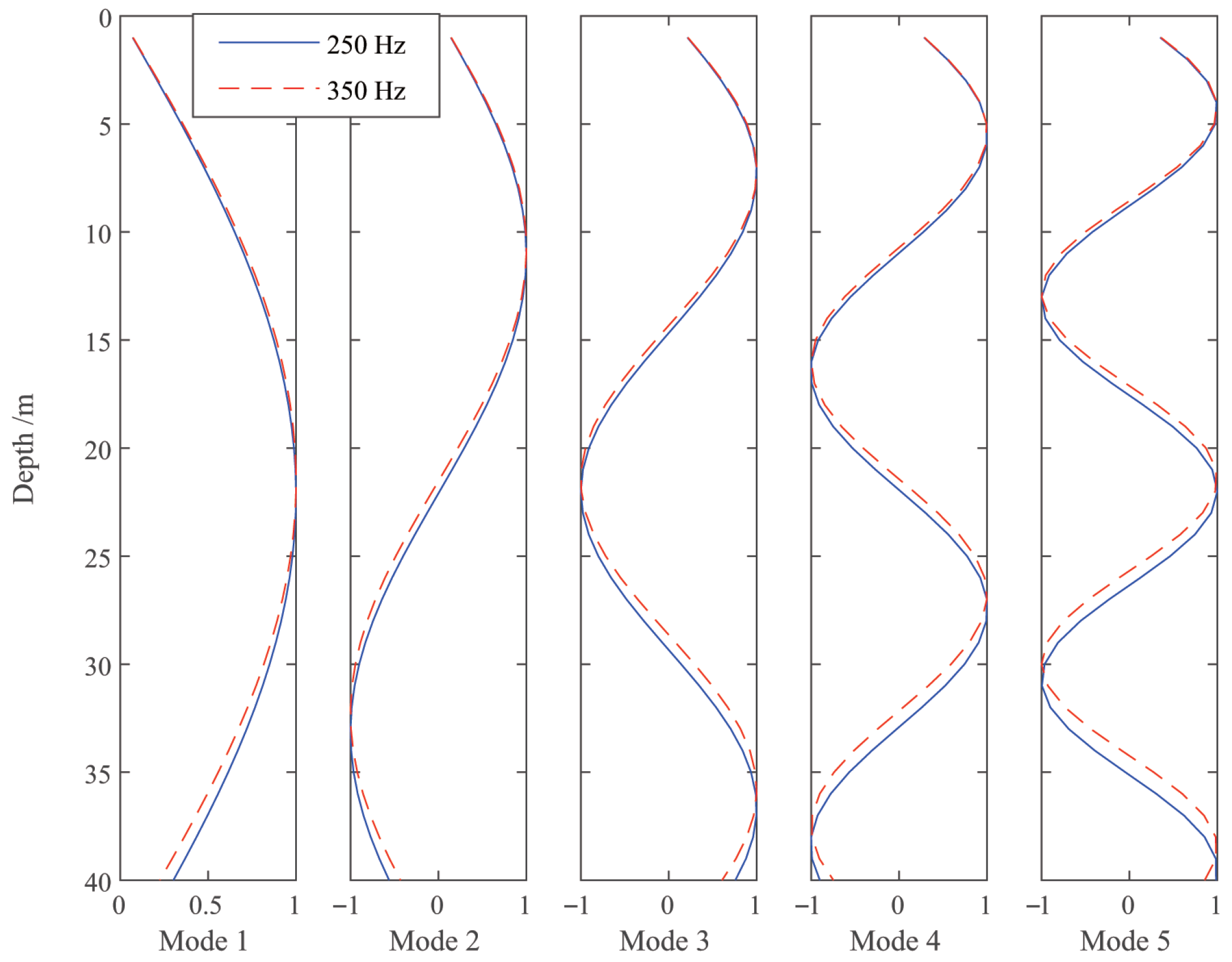
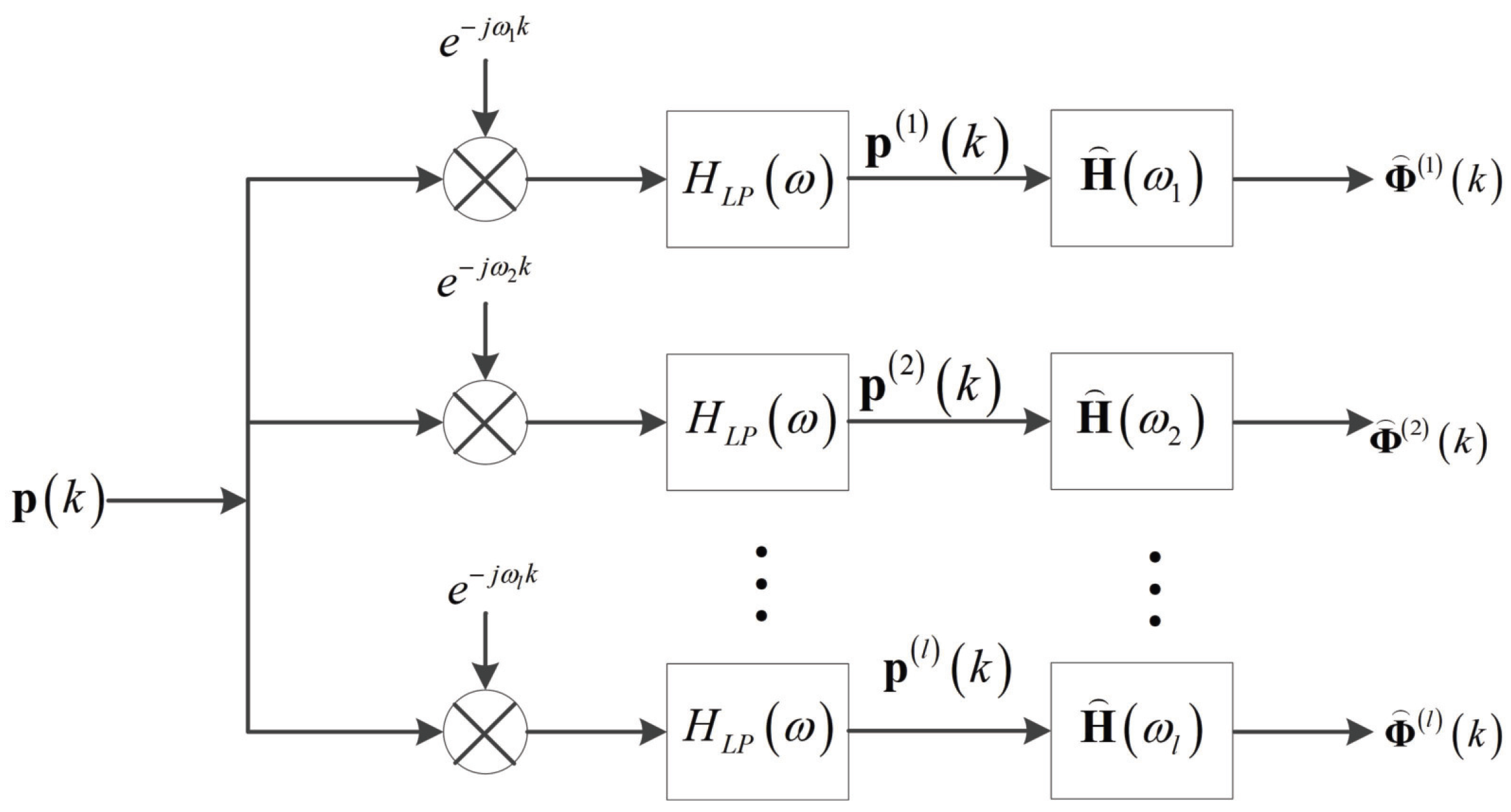
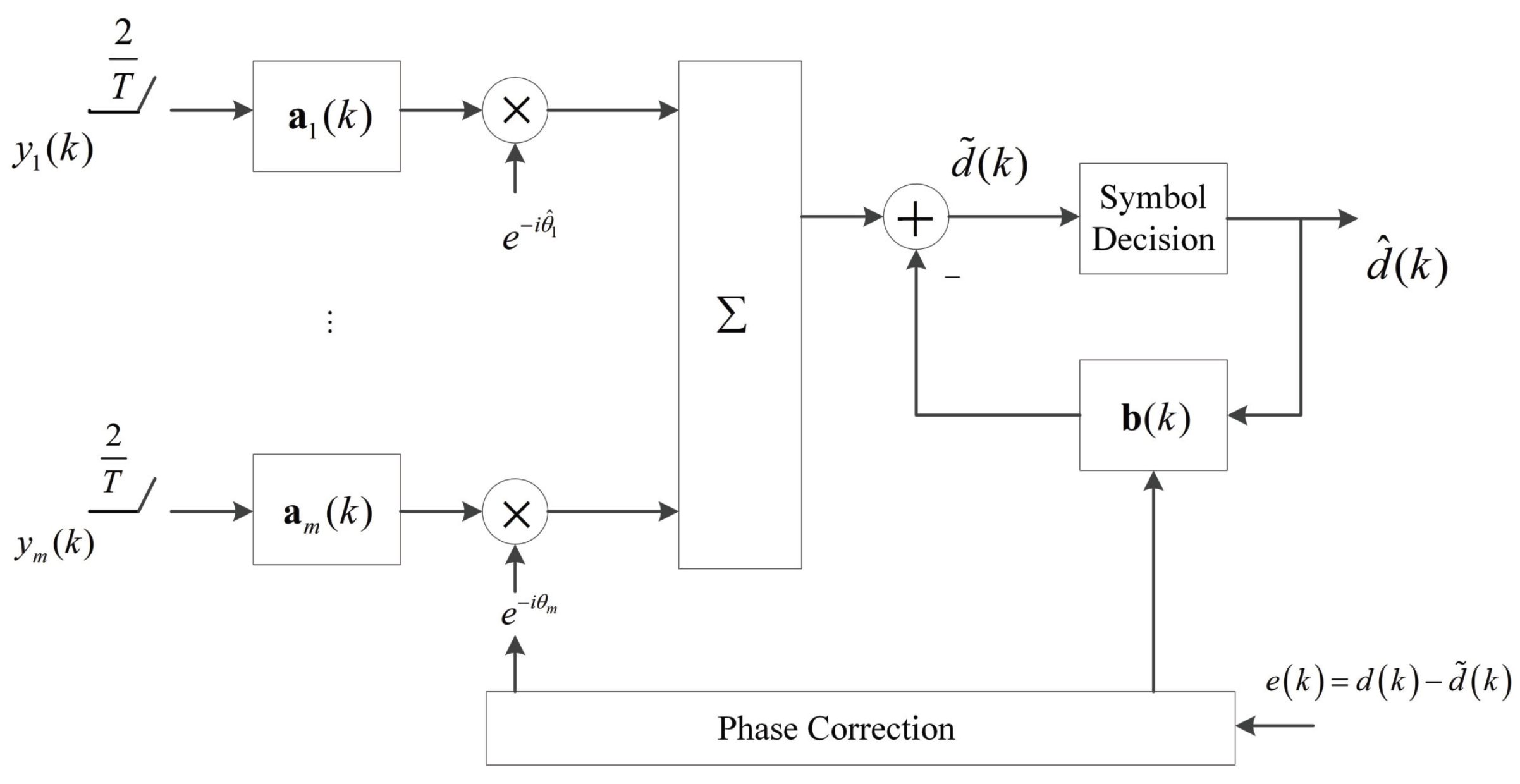
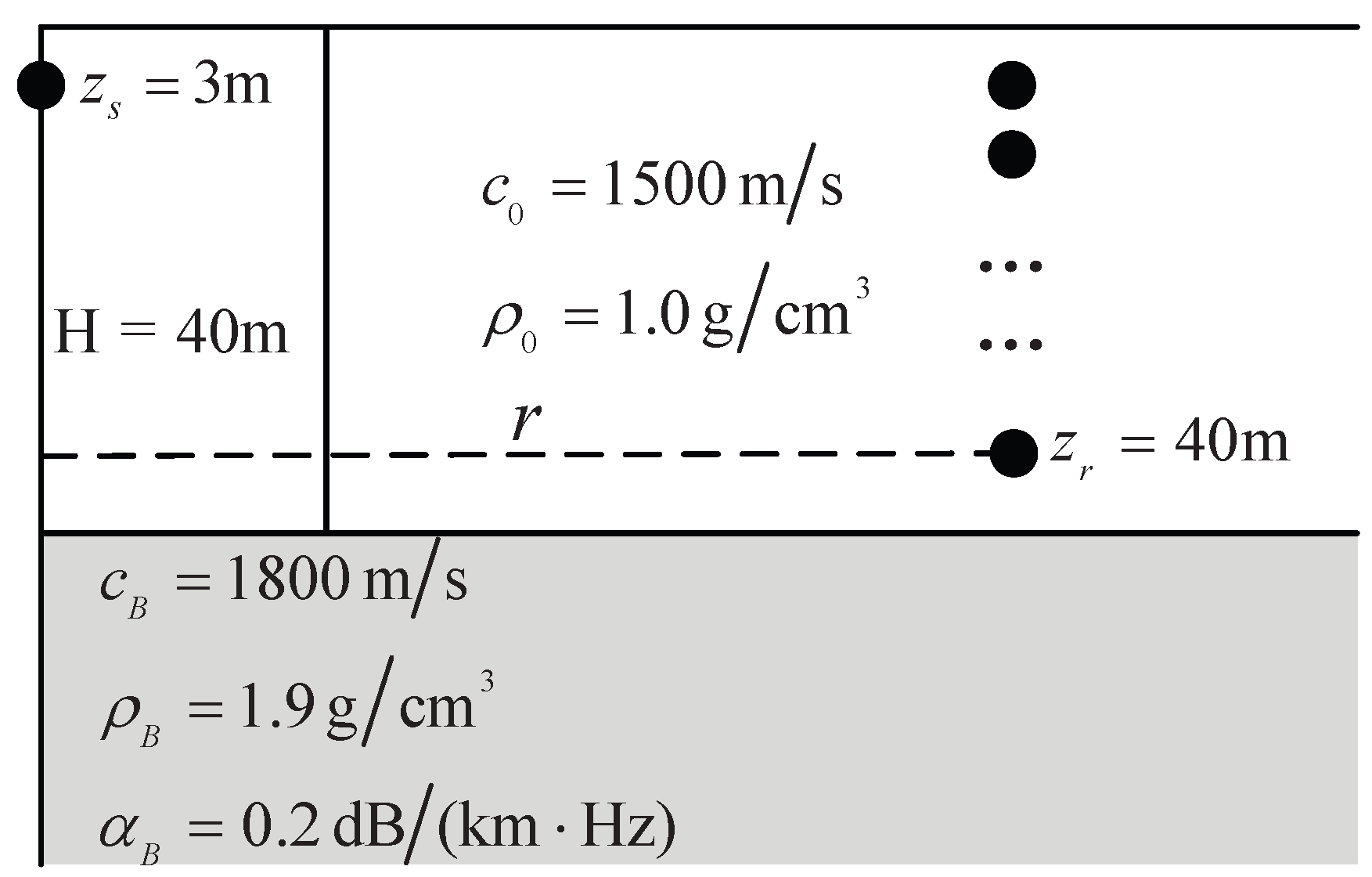
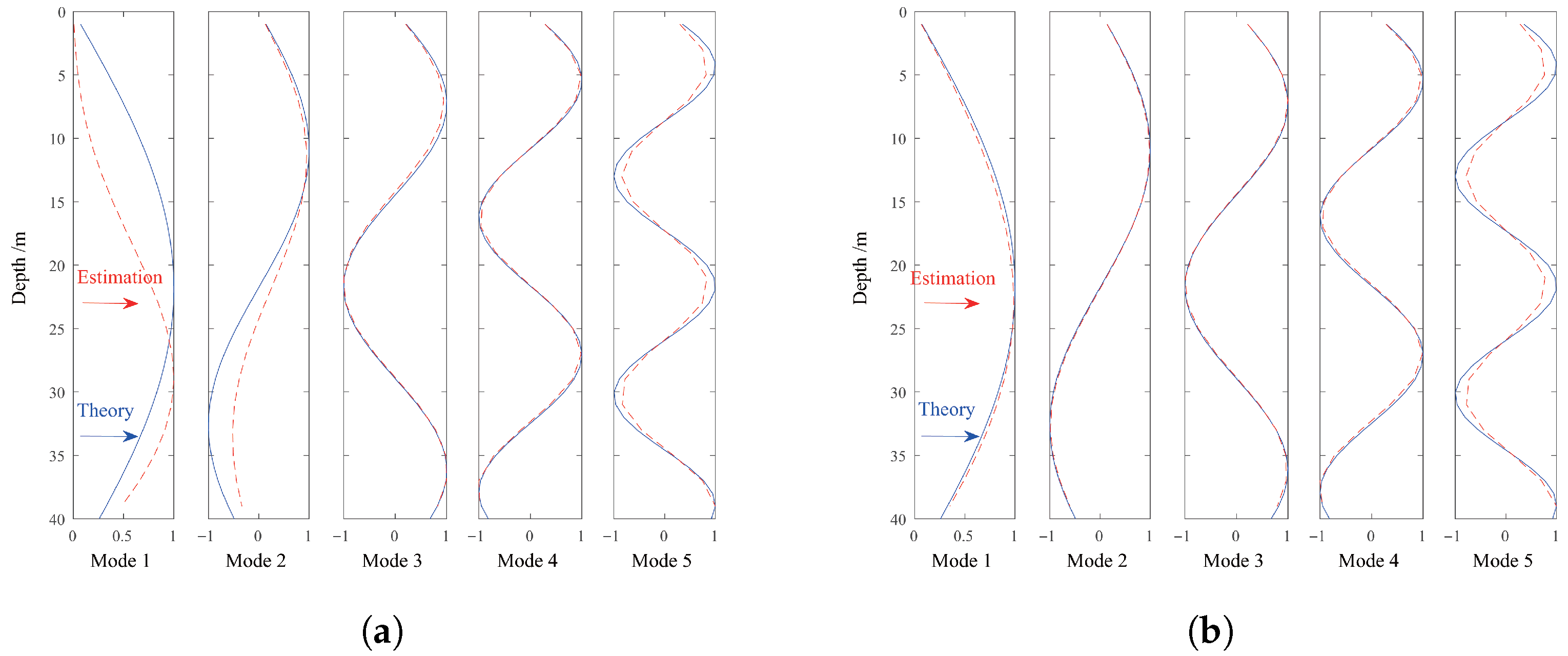
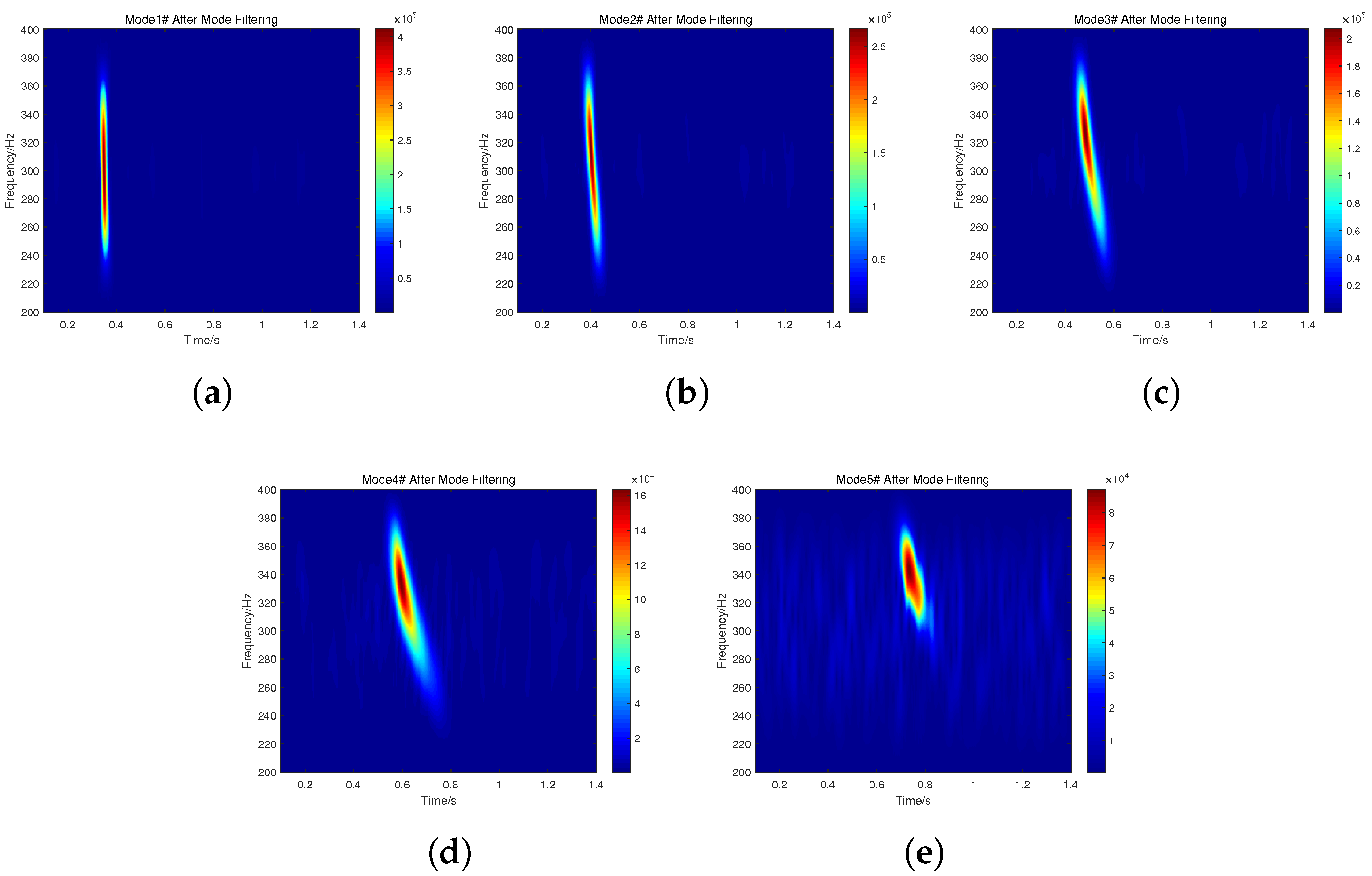
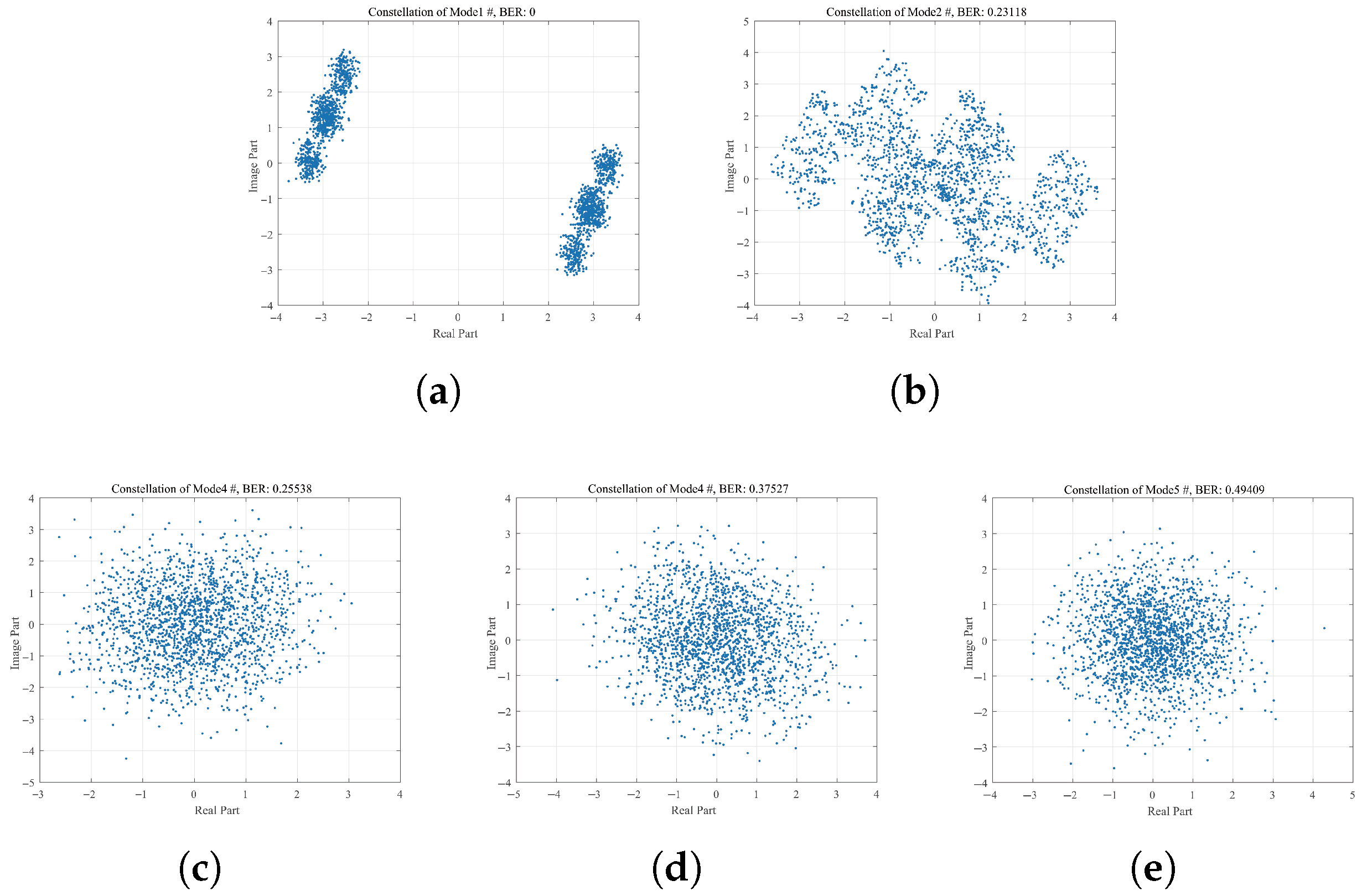


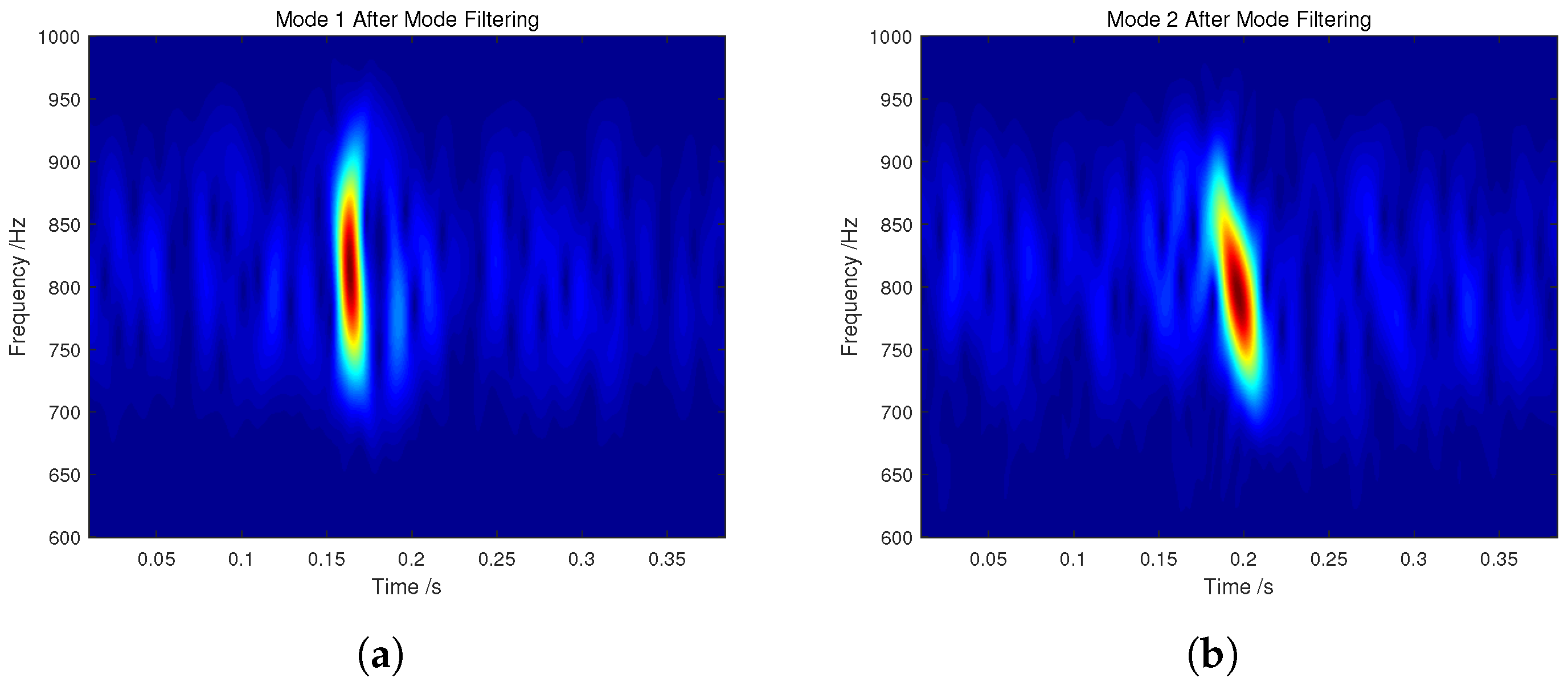
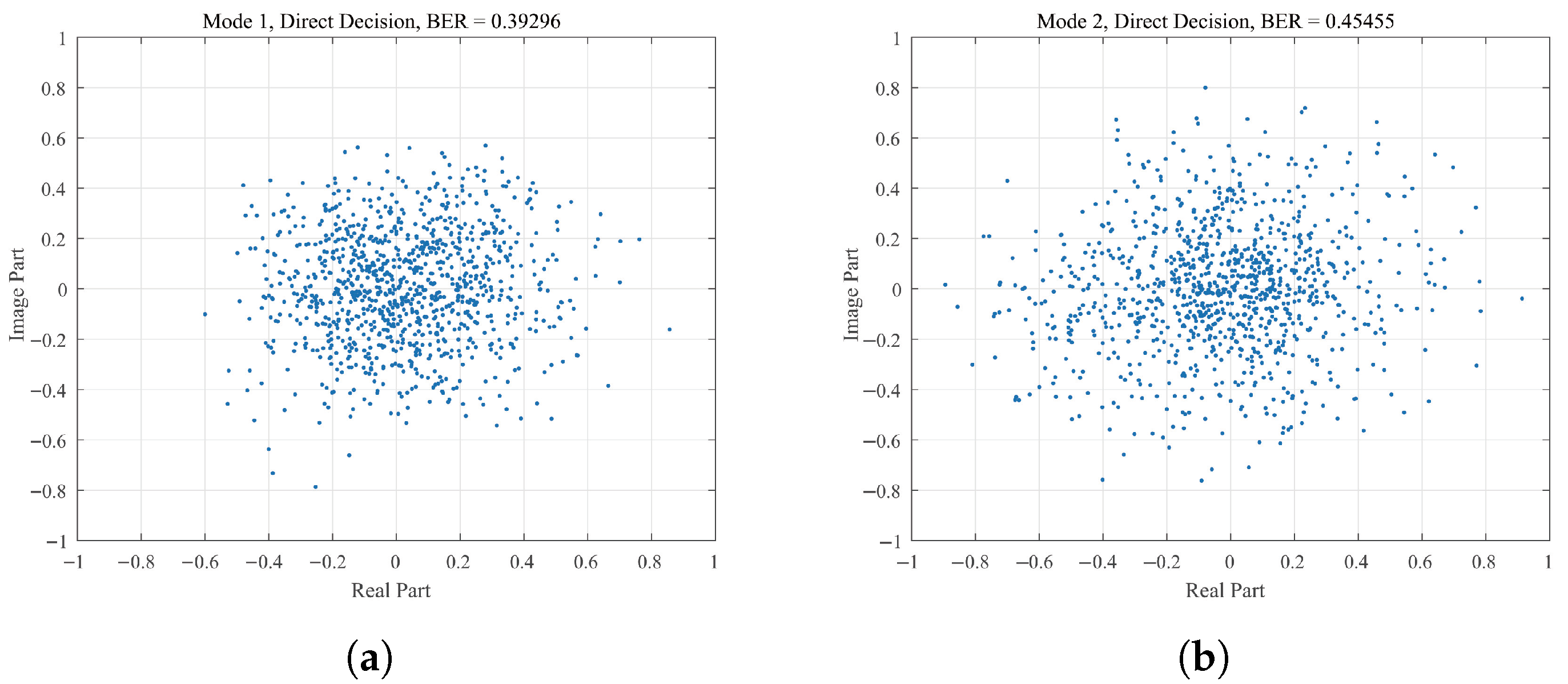
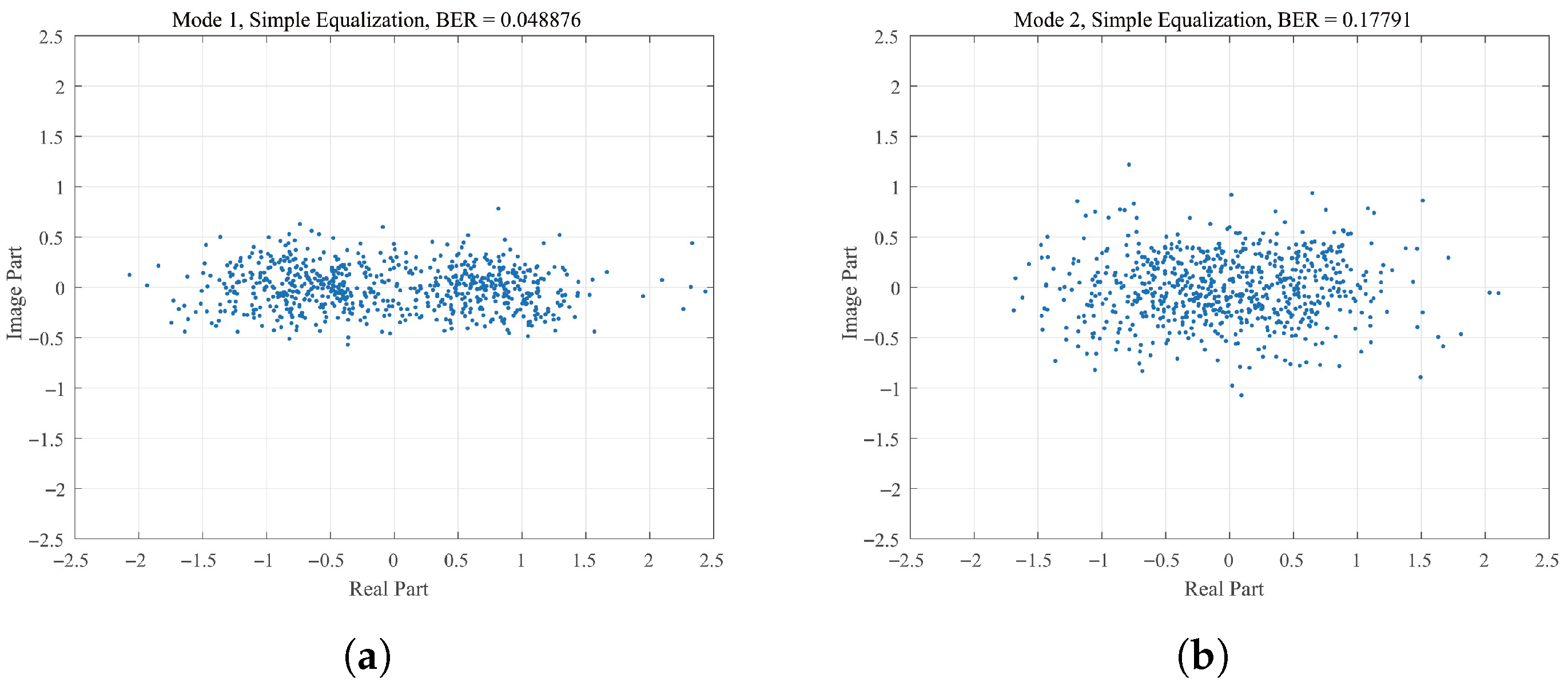
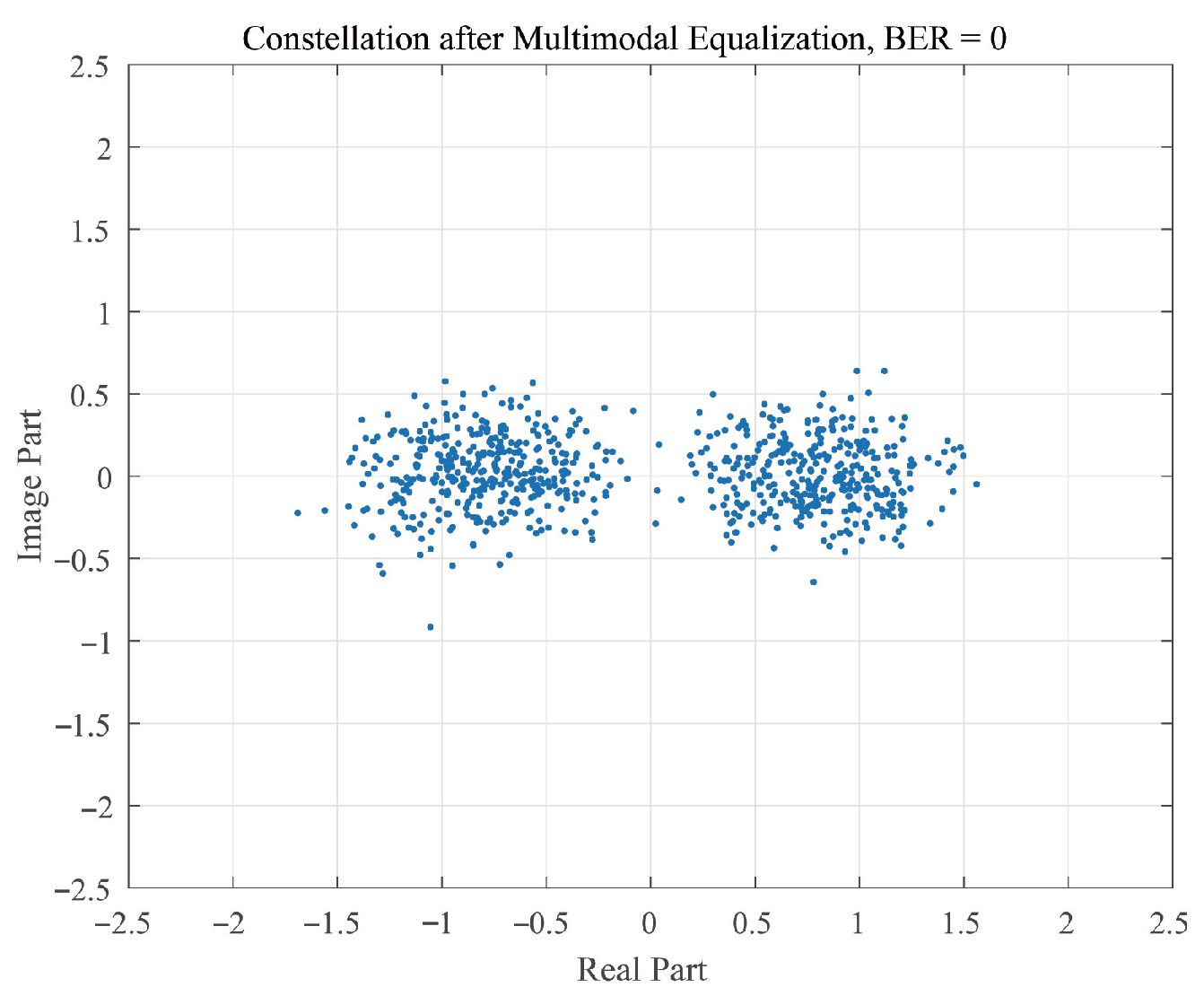
| Water Depth | 40 m | Range | 20 km |
| Water Density | 1 | Number of Efficient modes | 5 |
| Sound Velocity of Water | 1500 | Number of array elements | 20 |
| Sound Velocity of Bottom | SNR | 10 dB | |
| Density of Bottom | Carrier Frequency | 300 Hz | |
| Attenuation of Bottom | Bandwidth | 200 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, S.; Zhang, Y.; Liu, B.; Cui, H.; Gao, D. Multi-Mode Joint Equalization Scheme for Low Frequency and Long Range Shallow Water Communications. J. Mar. Sci. Eng. 2025, 13, 1587. https://doi.org/10.3390/jmse13081587
Xiao S, Zhang Y, Liu B, Cui H, Gao D. Multi-Mode Joint Equalization Scheme for Low Frequency and Long Range Shallow Water Communications. Journal of Marine Science and Engineering. 2025; 13(8):1587. https://doi.org/10.3390/jmse13081587
Chicago/Turabian StyleXiao, Shuang, Yaqi Zhang, Bin Liu, Hongyu Cui, and Dazhi Gao. 2025. "Multi-Mode Joint Equalization Scheme for Low Frequency and Long Range Shallow Water Communications" Journal of Marine Science and Engineering 13, no. 8: 1587. https://doi.org/10.3390/jmse13081587
APA StyleXiao, S., Zhang, Y., Liu, B., Cui, H., & Gao, D. (2025). Multi-Mode Joint Equalization Scheme for Low Frequency and Long Range Shallow Water Communications. Journal of Marine Science and Engineering, 13(8), 1587. https://doi.org/10.3390/jmse13081587







