Abstract
Merchant vessels often feature numerous perforations in their web frames. To enhance the buckling resistance of these perforated panels, it is customary to install local reinforcements around the openings. This research introduces a novel approach that segments perforated panels into separated unstiffened panels (SUPs) and applies recently updated classification rules for buckling strength assessment, supplemented by inelastic FEA. This research aims to show a case study on how to reduce shipbuilding expenses by conducting a quantitative analysis of the buckling strength of such panels. The study treated perforated panels as separated unstiffened panels (SUPs) in accordance with Common Structural Rules (CSR). The authors examined web frames from various types of carriers, including those for liquefied petroleum gas, containers, products, and crude oil. They gathered data on dimensions, materials, and applied loads for 96 SUPs in total. To assess the buckling strength of these SUPs, IACS rules, eigenvalue finite element analysis (FEA), and inelastic FEA were employed. We performed element size convergence analyses on a square unstiffened panel with simple support on all four edges, ultimately deciding on a 10 mm element size for both eigenvalue and inelastic FEAs. Additionally, inelastic FEAs were performed on the rectangular, unstiffened panels with various aspect ratios, and it was decided to use the average level of initial imperfection for the inelastic FEAs. The SUPs under investigation were classified into Method A and Method B based on CSR recommendations. The ultimate buckling strengths of the categorized SUPs were evaluated by CSR and inelastic FEA. CSR rules provided more conservative ultimate buckling strengths for SUPs corresponding to Method A, while inelastic FEA did for SUPs that were classified into Method B. On the other hand, the inelastic FEAs and CSR rules provided similar ultimate buckling strengths for SUPs requiring Method B. The eigenvalue FEA confirmed that Method B can be an alternative method to inelastic FEA and CSR rules. Significant cost savings were demonstrated by selectively applying CSR and inelastic FEAs for SUPs requiring Method A. The originality of this work lies in its application of the latest classification rule logic, detailed finite element validation using real ship data, and a cost-benefit analysis of reinforcement strategies.
1. Introduction
The buckling strength of unstiffened panels is controlled by the slenderness ratio. If the slenderness ratio is low, the buckling strength approximates the yield strength. In this case, the elastic buckling strength can be greater than the proportional limit or yield strength, and a portion of the unstiffened panel reaches yield before the elastic buckling strength is reached. Due to this problem, the elastic buckling strength is used with plasticity correction. The plasticity-corrected elastic buckling strength is commonly referred to as the critical buckling strength. The Johnson–Ostenfeld plasticity correction equation is the most widely used [1]. On the other hand, as the slenderness ratio increases, the compressive stress of the unstiffened panel reaches the elastic buckling strength before reaching the yield strength, so the elastic buckling strength is equivalent to the critical buckling strength. Unstiffened panels in large merchant ships are designed to have an intermediate slenderness ratio. The International Association of Classification Societies (IACS) has historically used the critical buckling strength of unstiffened panels as the buckling strength, but has recently allowed the use of the ultimate buckling strength [2,3]. This means that the buckling limit states of unstiffened panels are based on the ultimate buckling strength.
Finite element analysis (FEA) has been widely used to obtain the elastic buckling strength of unstiffened or stiffened panels [4]. The FEA that has been commonly used to obtain the elastic buckling strength is called eigenvalue FEA. For the evaluation of elastic buckling strength, eigenvalue FEA is interpreted in the same sense as elastic FEA. On the other hand, inelastic FEA is required to determine the post-buckling behavior. Inelastic FEA has been used interchangeably with nonlinear FEA to evaluate post-buckling strength. Recent numerical studies to obtain the ultimate buckling strength rely on either inelastic FEA or nonlinear FEA.
There are many openings and cutouts in the web frames and double-bottom bulkheads of large merchant ships. Most of the cutouts in web frames are for the penetration of longitudinal stiffeners and are relatively small in size, and the cutouts are close to the primary support members (PSMs), such as stringers and double girders, which are not known to have a significant effect on the reduction of buckling strength. Openings, on the other hand, are needed to provide access for ship inspections, passage of pipes, routing of wires, etc. Depending on the presence or absence of local stiffeners around the openings, they are referred to as unstiffened perforated panels or stiffened perforated panels. It is known that the buckling strength of perforated panels can be significantly reduced depending on the size or shape of the opening.
The work of Fujita et al. [5,6] is considered a pioneering example of research on the buckling strength of unstiffened perforated panels. They evaluated the buckling strength of unstiffened perforated panels through compression experiments. Nishihara et al. [7] and Nishihara and Sawayabagi [8] presented empirical formulas for estimating the shear buckling strength from shear experiments of unstiffened perforated panels. Narayanan and Der Avanessian [9] studied the elastic buckling behavior of perforated panels subjected to shear load as a function of the location of the circular openings. Shanmugam et al. [10] conducted compression experiments on stiffened perforated panels with circular and square openings. They presented a method for estimating the effective width of stiffened perforated panels. Alagusundaramoorthy et al. [11] investigated the ultimate buckling strength of simply-supported stiffened perforated panels with a square cutout. They compared their method to experimental results through a series of compressive tests for the stiffened perforated panels. Shanmugam et al. [12] developed a predictive model for determining the ultimate buckling strength of unstiffened perforated panels under uniaxial and biaxial compressions. The study also considered various boundary condition effects. Durban and Zuckerman [13] studied the inelastic buckling of a perforated panel with different boundary conditions.
Betten and Shin [14] studied the effect of aspect ratio and biaxial load ratio on the ultimate buckling strength of a perforated plate. El-Sawy and Nazmy [15] examined how the shape, size, and placement of the off-center rectangle and round openings in the unstiffened perforated panels influence their elastic buckling resistance when subjected to compression along a longitudinal axis. Harada and Fujikubo [16] proposed a modified ultimate buckling strength empirical expression based on the size of the opening when a simply-supported unreinforced hollow plate is subjected to uniaxial compressive loading. It has been demonstrated through nonlinear FEA that the behavior of an unstiffened perforated panel with a circular opening until the ultimate strength is reached after elastic buckling depends on the plate dimensions, opening geometry and dimensions, boundary conditions, loading conditions, and yield strength [17]. Kumar et al. [18] investigated how a centrally located rectangular hole impacts the ultimate buckling capacity of a square plate subjected to axial compressive loads. They employed nonlinear finite element analysis (FEA) to examine the influence of two key factors: the plate’s slenderness ratio and the proportion of the plate’s area occupied by the opening.
Paik [19] proposed an empirical formula through nonlinear structural analyses for simply-supported unstiffened plates with a circular opening at the center subjected to pure shear loading. Subsequently, he employed the same method to perform nonlinear FEAs on unstiffened perforated panels subjected to uniaxial compressive loads, and based on these results, proposed an empirical formula for ultimate buckling strength [20]. Combining previous studies [19], he derived the ultimate buckling strength of an unstiffened perforated panel under simultaneous biaxial compressive and shear loading by nonlinear FEA and proposed a closed-form empirical formula [21]. A reference [22] focused on the elastic buckling of rectangular plates with a circular cutout under linearly varying in-plane normal load. The study also investigated the effects of boundary conditions, plate aspect ratios, and perforation sizes on the elastic buckling strength of these perforated plates. Wang et al. [23] investigated the double bottoms of 137 bulk carriers and then collected the unstiffened perforated panels with elongated circular openings. Eigenvalue FEAs and inelastic FEAs were performed on the collected panels subjected to uniaxial compression and shear loads to derive the elastic buckling strength and ultimate buckling strength, respectively. Kim et al. [24,25] conducted experimental studies on unstiffened and stiffened perforated panels. The study focuses on three types of stiffeners: longitudinal stiffeners, transverse stiffeners, and combined longitudinal and transverse stiffeners. The results showed that the type of stiffener has a significant impact on the buckling capacity of the stiffened panel.
Cheng and Zhao [26] conducted nonlinear FEAs on four different reinforcement methods to improve the ultimate buckling strength of square perforated panels with circular openings. They considered uniaxial compressive loading conditions and simply-supported boundary conditions on all four sides. They proposed a reinforcement method dependent on the thickness of the perforated panel and the size of the opening. A similar study to [26] was performed by Kim et al. [27]. They classified reinforcement methods for perforated panels with elongated circular holes and performed nonlinear FEA on these panels. Based on the findings from the FEAs, they developed an empirical formula. Additionally, they validated the FEA results and the empirical formula through experimental tests. Yu and Lee [28] conducted inelastic FEAs on unstiffened panels with rectangular openings of varying shapes and sizes. Through nonlinear regression analysis, they proposed and validated design formulas that are practical for engineering applications. Dadrasi [29] investigated the buckling behavior of the perforated plates with circular and square cutouts under uniaxial compressive loading.
Saad-Eldeen et al. conducted compression experiments on unreinforced perforated panels with elongated circular openings [30]. They experimentally evaluated the effect of the size of the cracks around the elongated circular opening on the compressive strength [31]., conducted compression experiments on reinforced perforated panels with elongated circular openings [32], and conducted compression experiments on unreinforced and reinforced perforated panels with circular openings [33]. They found that the ultimate load-carrying capacity of the perforated panels decreases with increasing opening size. The perforated panels with circular openings tend to have better strength compared to those with elongated circular openings. High-tensile steel plates exhibit higher ultimate strength compared to mild steel plates. Perforated, stiffened panels are less affected by openings compared to perforated, unstiffened plates.
Lorenzini et al. [34,35] analyzed the effect of the geometry and location of the openings on the elastic and inelastic buckling behavior and presented stress limit curves to prevent the occurrence of the perforated panel buckling. Cui and Wang [36] applied inelastic finite element analysis (FEA) to evaluate the ultimate buckling strength of perforated longitudinal girders located in the double bottom of container ships. They proposed simplified prediction formulas for ultimate buckling strength based on variables such as opening size, location, boundary conditions, and initial imperfections. Yanli et al. [37] conducted a numerical analysis to examine the effects of aspect ratio, slenderness ratio, and the size and location of holes on the elastic buckling strength of unstiffened, perforated panels. Based on their analysis, they proposed a buckling coefficient for the unstiffened, perforated panels.
Research on the ultimate buckling strength of perforated plates made of composite materials has also been conducted by Li et al. [38]. They classified the shapes of openings into categories such as square, rhombus, ellipse, and circle, and performed nonlinear FEAs on these configurations. Nonlinear FEAs were conducted to determine the ultimate buckling strength of grillage structures incorporating web frames with openings (Doan et al. [39]). Their study focused on grillage structures with perforated web frames, rather than unstiffened or stiffened perforated panels. In addition, the analysis was performed for both steel and aluminum materials. Liu et al. [40] conducted a study on the ultimate buckling strength of a deck structure with large openings in a passenger ship. They carried out experiments on full-scale stiffened perforated plates using a large testing apparatus, followed by nonlinear FEA.
Silva-Campillo et al. [41] experimentally and numerically evaluated the elastic buckling strength of perforated panels in the web frames of container ship double bottoms when subjected to biaxial loads. After reinforcing the areas around the openings of a 1/6 scale model using various methods, compression tests were conducted. Additionally, optimal reinforcement solutions were proposed through topology optimization.
Despite the extensive research on perforated panels, most prior studies have evaluated the buckling behavior by treating the panel as a single entity, focusing on geometric parameter studies such as opening shape, size, and location. However, such an approach lacks alignment with recent structural design practices in the shipbuilding industry. The present study distinguishes itself by applying the latest revision of the common structural rules [42], which mandates a novel segmentation approach—dividing perforated panels into SUPs—for regulatory-compliant buckling assessment. This regulatory shift introduces a fundamentally different evaluation methodology, one that has not been thoroughly implemented or validated in existing literature. Moreover, by collecting and analyzing real design data from four merchant vessels, our study not only adheres to the updated rules but also proposes a cost-optimized methodology that balances structural integrity with economic efficiency.
In this study, the elastic buckling strength and ultimate buckling strength are evaluated according to the newly revised classification rules. For this purpose, perforated panels in transverse web frames were investigated on four actually built and operated merchant ships: a liquefied petroleum gas carrier, a container carrier, a product carrier, and a crude oil carrier. The stress obtained from cargo hold analyses with loading conditions corresponding to the ultimate limit state (ULS), which had already been performed during the design phase of the four vessels, was used as the loads acting on the investigated perforated panels. The buckling strength of the perforated panels was then derived using the classification rule [42], eigenvalue FEA, and inelastic FEA. The importance of the buckling strength evaluation methodology is emphasized by analyzing the cost of construction based on the selective application of each methodology.
2. Application of Classification Rules to Perforated Panels
This section introduces the updated classification rules and explains how they are applied to the evaluation of buckling strength for perforated panels in transverse web frames.
2.1. Definition of Separated Unstiffened Panel
The buckling strength of unstiffened panels can be evaluated based on empirical equations presented by various researchers or classification rules [42]. According to the classification rules, when static and dynamic loads exert simultaneously on the unstiffened panel of the web frame, the buckling utilization factor , which considers the interaction of longitudinal compressive load and shear load , cannot exceed 1.0, as shown in Equation (1). If exceeds 1.0, it is considered to have buckled and collapsed. is determined from the stress multiplier factor given in Equation (2), where is the stress multiplier factor when both longitudinal compressive and shear loads are applied simultaneously, while is the stress multiplier factor when only shear loads are applied. and are determined from Equations (3) and (4), respectively. is the slenderness ratio of the plate, which is determined from Equation (5).
IACS [42] requires a buckling strength assessment for each of the SUPs separated by an opening in the perforated panel. For example, the opening in Figure 1 creates two SUPs (SUP1 and SUP2) and requires a buckling strength assessment for each SUP. Depending on whether stiffeners are placed around the opening, the boundary condition at the edge of the SUPs can be either simply-supported or free, i.e., if stiffeners are placed along the opening to improve the buckling strength, the SUPs are considered to be four-sided simply-supported, otherwise three-sided simply-supported. In this study, the buckling safety is evaluated by considering both and acting on the SUP simultaneously.
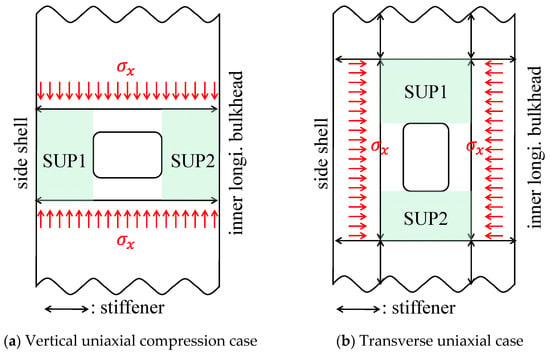
Figure 1.
Definition of SUPs in the transverse web frame.
2.2. Load and Boundary Conditions
As shown in Figure 2, the IACS [42] specifies that the buckling strength evaluation approach for three-side simply-supported SUPs is divided into Method A and Method B. For example, as shown in Figure 1a, if one of the unloaded edges of SUP1 is supported by primary support members (PSMs) with sufficient stiffness, SUP1 is classified as Method A and the corresponding buckling strength assessment method is applied. PSMs are typically large longitudinal members such as side shells, inner longitudinal bulkheads, stringers, deck plates, inner bottom plates, bottom plates, etc.
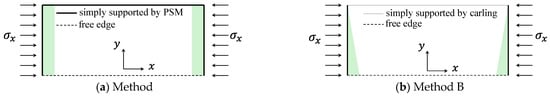
Figure 2.
Illustration of boundary conditions required for Method A and Method B.
Method A assumes that the one unloaded edge is supported by the PSM, such as a side shell, inner bottom, or stringer, so the loaded edges are compressed while remaining horizontal, as shown in Figure 2a. For Method A, the stresses in the plane are redistributed as the uniaxial compressive load is continuously increased, and the ultimate buckling strength can be significantly increased compared to the elastic buckling strength. To improve the convergence of inelastic FEA for the Method A case, displacement control is applied rather than load control.
In Method B, shown in Figure 2b, the light green color means the shortened region is applied when one of the unloaded edges of the SUP is supported by a local stiffener, such as a carling, which is not sufficiently rigid to prevent out-of-plane deformation, as shown in Figure 1b. In this case, it is assumed that the stiffeners are not stiff enough, so that the loaded edges are not leveled and the free edge compresses faster. For the cases where Method B should be applied, a nonlinear FEA based on load control techniques is more suitable to cause compressive deformation of the free edge. Due to the lower load carrying capacity at the free edge, the buckling strength is lower with Method B than with Method A.
2.3. Ultimate Buckling Strength Based on IACS
As shown in Equations (6) and (7), the ultimate buckling strengths and for compressive and shear loads that may be applied to the SUP are determined by multiplying the yield strength by a reduction factor . The reduction factor is determined depending on the boundary conditions and the type of load. For a four-edge simple support panel, the reduction factor and buckling factor provided in Table 1 can be used to determine the ultimate buckling strength. On the other hand, the reduction and buckling factors for a three-sided simple support SUP are determined from Table 2. The used in Table 1 and Table 2 is the slenderness ratio of the unstiffened panel, which is determined using Equation (8), where and are the elastic buckling strength and aspect ratio, respectively, as seen in Equations (9) and (10).

Table 1.
Buckling and reduction factors for four-edge simply-supported panel.

Table 2.
Buckling and reduction factors for three-edge simply-supported panel.
3. Preparation for Finite Element Analyses
This section presents the procedures undertaken to establish reliable finite element models, including mesh size determination and the modeling of initial imperfections.
3.1. Determination of Element Size
In this study, the mesh size was determined by observing the elastic buckling strength as a function of element size. For this purpose, a square, flat plate with dimensions × × of 800 mm × 800 mm × 10 mm was divided into 15 different element sizes, from 0.5 mm to 80 mm. Uniaxial compressive loads were applied to the loaded sides of the square unstiffened panels with four-edge simply-supported condition, as shown in Figure 3. For the elastic buckling strength analysis, Abaqus/Standard [43] was used. The quadrilateral shell element of S4R with a reduced integration scheme was used for geometry modeling. The material constants applied to the element size convergence analyses are presented in Table 3. Note that the yield strength was not applied to the convergence analysis. The first mode eigenvalues are presented in Figure 4a. It can be seen that the elastic buckling strength is overestimated for element sizes larger than 10 mm. Therefore, the element size determined in this study is 10 mm. Figure 4a,b illustrate the mode shapes corresponding to the first and second mode eigenvalues. The buckling strength used in the convergence analysis corresponds to the first mode.
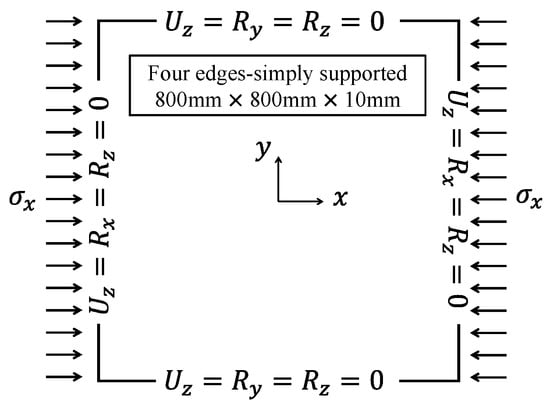
Figure 3.
Model for mesh convergence analyses.

Table 3.
Material constants for element size convergence analyses.
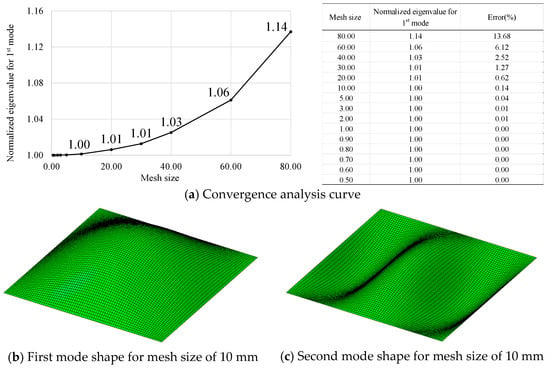
Figure 4.
Convergence analysis result.
3.2. Determination of Initial Imperfection Level
Initial imperfections usually refer to residual stresses and initial deformations caused by welding, transportation, etc. It is known that the residual stresses are redistributed by launching, cargo loading, etc. Furthermore, numerous researchers [44,45] have investigated the initial deformation of ships and offshore structures.
Therefore, in this study, the initial deformation is considered the initial imperfection. The initial deformation can be alternatively represented by the Fourier series in Equation (11) or by the buckling modes obtained through eigenvalue FEAs. In this study, the initial deformation was realized through eigenvalue FEAs.
According to Ghavami and Khedmati [46], the severity of the amplitude of the initial deformation has a great influence on the elastic buckling strength and the ultimate buckling strength. Therefore, to determine the amplitude , Equation (12), proposed by Smith et al. [47], was employed, where the terms “slight,” “average,” and “severe” refer to typical levels of initial deformation caused by welding-induced imperfections in ship structures.
To determine the severity of the amplitude in Equation (12), seven benchmark models presented in reference [48] were generated. As shown in Table 4, the width of a rectangular flat plate with a constant a × t of 800 mm × 10 mm was reduced in seven steps from 1000 mm to 400 mm to determine the magnitude of the initial deformation. The elements used were S4R, with a 10 mm element size determined from the convergence analysis. The boundary conditions shown in Figure 5, i.e., three-edge simply-supported boundary conditions, were applied. The loading conditions corresponding to Method A, i.e., prescribed compressive displacement, were applied to the loaded sides of the FEA model. The material constants from Table 3 were applied where an elastic-perfect plastic material was assumed, since the plastic strain at the ultimate buckling strength does not exceed the Lüders plateau.

Table 4.
Models to determine initial imperfection level from inelastic FEAs.
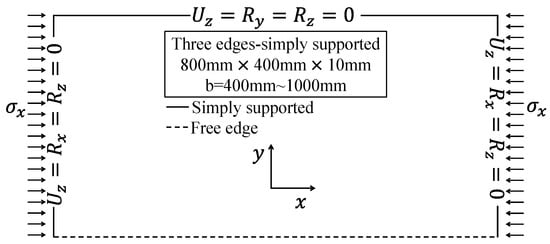
Figure 5.
Model for determination of initial imperfection level.
For the seven models, the buckling modes were obtained by eigenvalue FEAs and used as initial deformations for the inelastic FEAs. The initial deformations corresponding to the slight and average levels in Equation (12) were applied to the inelastic FEA models. After obtaining the deformed geometries by performing the eigenvalue FEAs for the B10 and B04 models, the initial deformation magnitude of an average level was applied to the buckling mode, as illustrated in Figure 6. For visualization purposes, the amplitudes in Figure 6 are exaggerated by a factor of 100.

Figure 6.
Average level of initial imperfection.
The load shortening results obtained by performing the inelastic FEAs for the B10 and B04 models are illustrated in Figure 7. Here, the vertical axis is defined as the average compressive stress, , which is the compressive load divided by the cross-sectional area, normalized by SMYS . The horizontal axis is defined as the average shortening strain , which is the shortening displacement divided by the length of the unstiffened panel and then normalized by the SMYS equivalent yield strain .
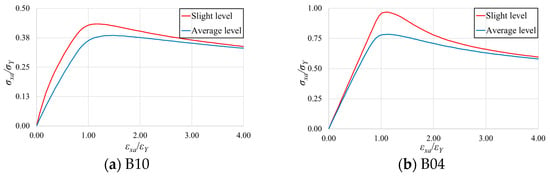
Figure 7.
Load-shortening curves for determination of initial imperfection level.
The ultimate buckling strengths obtained from the inelastic FEAs for the seven models were compared with the results obtained by IACS rules. As shown in Figure 8, the ultimate buckling strength when applying the slight level was more consistent with that of IACS than when applying the average level. It can be concluded that IACS’s ultimate buckling strength formula was likely determined based on the slight level.
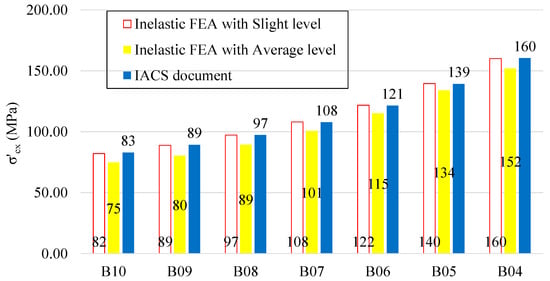
Figure 8.
Comparison of ultimate compressive buckling strengths by IACS and inelastic FEAs for determination of initial deformation level.
4. Evaluation of Buckling Limit State for Investigated Perforated Plates
This section describes the evaluation of buckling limit states for SUPs collected from four commercial vessels using various analysis methods, including IACS rules, eigenvalue FEA, and inelastic FEA.
4.1. Investigated Perforated Plates in Medium-Range Merchant Vessels
The web plates of four recently built medium-range merchant ships in Korea were examined to collect SUPs isolated by openings. The four ships included a 45,000 m3 capacity liquefied petroleum gas carrier (45K LPGC), a 2000 twenty equivalent unit (TEU) capacity container carrier (2K TEU CC), a 50,000 ton capacity product carrier (50K PC), and a 115,000 ton capacity crude oil carrier (115K COC). The investigated opening types were an elongated circle in Figure 9a,d, a true circle in Figure 9b, and a keyhole in Figure 9c. For non-rectangular SUPs, due to inclined local stiffeners and bottom curvatures as shown in Figure 9d, they were idealized as extended rectangular SUPs for conservative buckling limit state assessment.
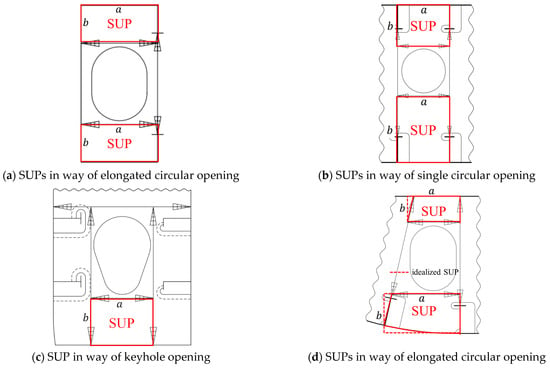
Figure 9.
Typical SUPs in way of various openings.
From the investigation of the four merchant vessels, the number of SUPs and their dimensions are presented in Table 5. FEAs for three-hold models considering both static and dynamic loads according to classification society rules were previously performed on the cargo holds of these ships. The longitudinal stress and shear stress that occurred in the investigated SUPs are presented in Table 5, where positive indicates compressive stress. Detailed information on the dimensions of the investigated SUPs and applied loads is provided in Table A1, Table A2, Table A3 and Table A4.

Table 5.
Dimensions and applied loads in investigated SUPs.
4.2. Buckling Limit State by Classification Rules
Using Equations (6) and (7), the ultimate buckling strengths of and were calculated. Then, the stress multiplier factor was derived using Equations (3) and (4). Subsequently, was determined using Equation (2), and the buckling limit states were evaluated using Equation (1). The results are summarized in Table 6. More SUPs were found to not meet the criterion when the loading conditions of Method A were applied compared to when those of Method B were applied. The highest number of failed SUPs occurred at 115K COC.

Table 6.
Buckling limit state results by IACS.
4.3. Buckling Limit State by Eigenvalue Analyses
To obtain the elastic buckling strengths of the SUPs, the FEA models used four-node shell elements with reduced integration (S4R). The applied boundary conditions were identical to those shown in Figure 5, with simple support on three edges. Axial compressive force and shear force per unit length were applied to the eigenvalue FEA model separately. The material constants presented in Table 3 were applied to the eigenvalue FEA models. For eigenvalue FEAs, linear stiffness and elastic material are assumed, so Method A and Method B could not be distinguished. Therefore, considering 18, 26, 28, and 24 panels from four types of commercial vessels and two loading conditions, a total of 192 eigenvalue FEAs were performed. The elastic buckling strengths obtained through eigenvalue FEAs were considered as and in Equations (6) and (7). Using these values, stress multiplier factors and were derived using Equations (3) and (4). Subsequently, was determined using Equation (2), and the buckling utilization factor was evaluated using Equation (1).
The results were summarized in Table 7 (case-specific values are presented in Table A1, Table A2, Table A3 and Table A4). Among the cases where Method B was applied, 51 cases failed to satisfy Equation (1). By vessel type, the 115K COC had the most failed cases, followed by 50K PC, 2K TEU CC, and 45K LPGC, in that order.

Table 7.
Buckling limit state results by eigenvalue FEAs.
4.4. Buckling Limit State by Inelastic Analyses
Eigenvalue FEAs revealed 51 SUPs that failed to satisfy Equation (1), as presented in Table 7. Inelastic FEAs were subsequently performed on these failed SUPs. To obtain conservative ultimate buckling strengths, initial imperfections of an average level were applied to the inelastic FEA models. The elements used in the inelastic FEA model to obtain the ultimate buckling strength of SUPs were four-node shell elements with a reduced integration scheme (S4R).
The steel grades used for the SUPs investigated in the four ships were A, AH32, and AH36. Poisson’s ratio and the elastic modulus from Table 3 were applied to these steels. The SMYSs for these three steel grades were 235 MPa, 315 MPa, and 355 MPa, respectively. Plastic hardening was ignored; thus, elastic-perfect plastic behavior was assumed.
Unlike the boundary conditions applied to the eigenvalue FEA model, the boundary conditions for the inelastic FEA model are considerably more complex. This complexity arises from the need to use various displacement coupling elements to individually apply compressive and shear loads to inelastic FEA models supported by common boundary conditions. As shown in Figure 10, simple support boundary conditions, as presented in Table 8, were applied to the loaded edges and and the unloaded edge . No boundary conditions were applied to the free edge .
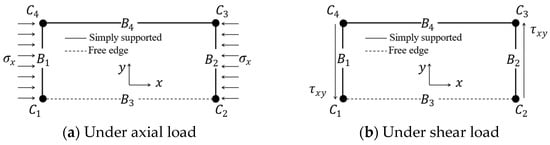
Figure 10.
Load and boundary conditions applied to inelastic FEA models.

Table 8.
Boundary conditions at each edge and vertex applied to inelastic FEAs.
As shown in Table 9, a displacement coupling element (EQUATION) was arranged so that the longitudinal displacements at the nodes placed on the loaded edge follow along the displacement at the corner . To maintain a straight line on the unloaded edge , a second EQUATION element was located so that the transverse displacement at the corner was same as the displacement at the corner . To maintain symmetry with respect to the x-plane, a third EQUATION element was arranged so that of corner equaled the sum of the rotational displacements of corners and . A displacement coupling element (SLIDER) was used so that the nodes placed on the unloaded edge followed the straight-line connecting corners and .

Table 9.
Degrees of freedom in coupling elements.
For the Method A loading condition, as shown in Figure 10, prescribed compressive displacement and prescribed shear displacement were applied separately to maintain the loaded edges horizontally. For the Method B loading condition, compressive force per unit length and shear line load per unit length were applied. To improve the convergence of the load increment analysis based on the Newton–Raphson method, the Riks method was used in conjunction.
As a result of inelastic FEAs, eight SUPs did not satisfy Equation (1). These are shown in Table 10 in order of decreasing . The three SUPs with the largest occurred because Method B loading conditions were applied, resulting in quite large values, exceeding 3.0. In particular, the yield strength of 235 MPa for the two SUPs with the largest was presumed to be the cause of the high . Among the SUPs to which Method A loading conditions were applied, the largest (4th in order) was likely due to the highly developed longitudinal compressive stress of 165.53 MPa.

Table 10.
Detailed information on failed SUPs through inelastic FEAs.
4.5. Cost Reduction
As described in Table 11, when evaluating the buckling limit state using IACS, structural reinforcement is required for a total of 22 SUPs, but when applying inelastic FEA, reinforcement is required for only eight SUPs. Therefore, the cost of reinforcing the 14 SUPs was analyzed. The average length of SUPs requiring reinforcement was 820.36 mm. It was assumed that these SUPs would be reinforced with carlings of size 100 mm × 10 mm. The steel grade of the carling was assumed to be the same as that of the SUP. As shown in Table 12, the steel price, welder’s hourly wage, and welding speed proposed by Do and Lee [49] were applied. The welding cost was calculated assuming the length of the carling as the welding length. As presented in Table 13, as a result of this study, shipbuilding costs could be reduced by approximately $38,000.

Table 11.
The number of failed SUPs by IACS and inelastic FEA.

Table 12.
Material and welding costs.

Table 13.
Reduction of ship construction costs.
5. Discussions
The relationship between / and for SUPs is shown in Figure 11. When is approximately 2.4 or greater, eigenvalue FEA provides results equivalent to CSR–Method B or Inelastic FEA–Method B. When Method B’s loading conditions are applied, CSR and inelastic FEA predict similar ultimate buckling strengths across the entire range of . When applying inelastic FEA to SUPs that require Method B, the average ultimate buckling strength approximates the CSR–Method B curve, making the application of CSR helpful for quickly determining the ultimate buckling strength.
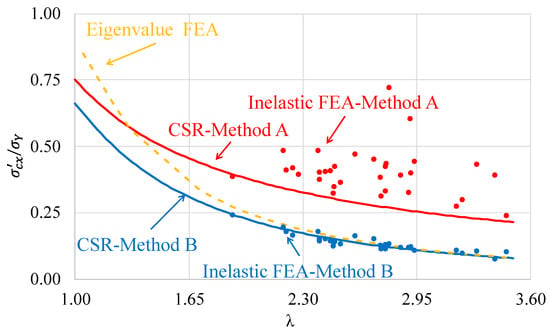
Figure 11.
Normalized ultimate buckling strengths for 51 failed SUPs.
On the other hand, when Method A loading conditions are applied, there is a considerable difference between the results of CSR and inelastic FEA. For most of the SUPs used in this study, inelastic FEA presented higher ultimate buckling strengths than CSR. Therefore, for SUPs where Method A should be applied, it is predicted that using inelastic FEA rather than CSR would allow for design weight reduction.
It was demonstrated that the selective application of ultimate buckling strength evaluation methods in actual ship design can lead to significant cost savings. When applying CSR to SUPs that require Method A, it was confirmed that there is considerable design margin, and future research is needed to develop design equations that can reduce this gap.
6. Conclusions
This research introduced a comprehensive evaluation framework for assessing the ultimate buckling capacity of perforated panels in commercial ships, incorporating the latest IACS classification standards combined with eigenvalue and inelastic FEAs.
The investigation approached perforated panels as SUPs following CSR rules. These SUPs were categorized into Method A or Method B configurations depending on their support conditions, with corresponding assessment techniques applied to each category. The inelastic FEA models incorporated average-level initial imperfections to provide conservative estimates of post-buckling response.
The findings revealed that CSR approaches yielded more cautious predictions for Method A-classified SUPs, while inelastic FEA typically demonstrated superior buckling resistance, particularly for Method A configurations, indicating opportunities for structural optimization. Conversely, Method B-classified SUPs showed good agreement between CSR and inelastic FEA results, confirming the suitability of CSR for streamlined assessments in these scenarios.
The strategic implementation of inelastic FEA decreased the required structural reinforcements from 22 panels (using CSR methodology) to just eight panels, resulting in cost reductions of approximately $38,000 across the four examined vessel categories.
The targeted application of CSR and inelastic FEA methodologies based on SUP classification enables enhanced structural performance and eliminates excessive reinforcement requirements, supporting economical ship construction practices. For Method A panels, refinements to CSR-derived formulations are suggested to achieve better correlation with inelastic FEA predictions.
To advance design accuracy and economic efficiency, subsequent research should focus on establishing improved empirical design relationships for Method A-type SUPs through comprehensive inelastic FEA datasets. Furthermore, experimental verification of inelastic buckling characteristics for SUPs subjected to combined loading conditions and varying imperfection magnitudes remains crucial for validation. While this study focused on medium-range merchant vessels, future research should investigate the applicability of the proposed SUP-based evaluation framework to larger vessels or offshore structures, where different load conditions and failure mechanisms may require further calibration or refinement of the current methodology.
Author Contributions
Conceptualization, J.C. and I.C.; methodology, J.C., I.C. and G.T.T.; software, G.K.; validation, J.C., I.C. and G.T.T.; formal analysis, J.C. and G.K.; investigation, J.C., I.C. and G.K.; resources, I.C.; data curation, J.C., I.C. and G.K.; writing—original draft preparation, J.C. and G.K.; writing—review and editing, J.C. and G.K.; visualization, G.K.; supervision, J.C.; project administration, J.C.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by an INHA research grant. (Grant number 75583).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Inhwan Cha is employed by the company Structural Design Department, HD Hyundai Mipo. Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
The following abbreviations are used in this manuscript:
| Length of the longer side of the plate panel | |
| Length of the shorter side of the plate panel | |
| Reduction factor | |
| Elastic modulus | |
| Buckling factor | |
| Partial safety factor | |
| Thickness of panel | |
| Initial imperfection | |
| Magnitude of initial imperfection | |
| Aspect ratio | |
| Slenderness ratio for unstiffened panel | |
| Stress multiplier factor | |
| Stress multiplier factor for combined compressive and shear load | |
| Stress multiplier factor for shear load | |
| Yield strain corresponding to specified minimum yield strength | |
| Average shortening strain | |
| Utilization factor | |
| Reference degree of slenderness | |
| Poisson ratio | |
| Elastic buckling strength | |
| Specified minimum yield strength | |
| Applied compressive stress | |
| Average shortening stress | |
| Ultimate buckling strength under uniaxial compression load | |
| Applied shear stress | |
| Ultimate buckling strength under shear load |
Appendix A
Appendix A.1

Table A1.
Investigated SUPs for 45K LPGC.
Table A1.
Investigated SUPs for 45K LPGC.
| No | Method | α | β | σY (MPa) | σx (MPa) | τxy (MPa) | η by | ||
|---|---|---|---|---|---|---|---|---|---|
| CSR (2023) | Eigenvalue FEA | Inelastic FEA | |||||||
| 1 | A | 2.02 | 1.70 | 355.00 | 80.55 | −88.94 | 0.85 | 1.49 | 0.57 |
| 2 | A | 2.02 | 1.70 | 355.00 | 75.75 | −19.15 | 0.46 | 1.09 | 0.26 |
| 3 | A | 2.02 | 1.70 | 355.00 | 42.84 | 107.22 | 0.66 | 0.81 | 0.81 |
| 4 | A | 2.02 | 1.70 | 355.00 | 31.63 | 70.35 | 0.33 | 0.43 | 0.43 |
| 5 | A | 2.02 | 1.42 | 355.00 | −85.66 | −117.78 | 0.36 | 0.25 | 0.25 |
| 6 | A | 2.02 | 1.42 | 355.00 | 31.07 | 49.75 | 0.14 | 0.16 | 0.16 |
| 7 | A | 2.02 | 1.42 | 355.00 | 65.79 | 117.18 | 0.64 | 0.67 | 0.67 |
| 8 | A | 2.02 | 1.42 | 355.00 | 28.05 | 53.77 | 0.15 | 0.15 | 0.15 |
| 9 | A | 2.02 | 0.81 | 355.00 | 66.73 | −98.41 | 0.27 | 0.05 | 0.05 |
| 10 | A | 2.02 | 0.95 | 355.00 | 59.63 | 0.60 | 0.07 | 0.06 | 0.06 |
| 11 | A | 2.02 | 0.81 | 355.00 | 33.64 | −125.49 | 0.37 | 0.03 | 0.03 |
| 12 | A | 2.02 | 0.95 | 355.00 | 28.40 | −45.44 | 0.06 | 0.02 | 0.02 |
| 13 | B | 1.33 | 1.25 | 355.00 | 32.28 | −152.97 | 0.62 | 0.11 | 0.11 |
| 14 | B | 1.33 | 1.25 | 355.00 | −20.36 | −94.23 | 0.23 | 0.03 | 0.03 |
| 15 | B | 1.21 | 2.74 | 315.00 | −50.68 | −51.41 | 0.14 | 0.23 | 0.23 |
| 16 | B | 1.21 | 2.74 | 315.00 | −63.15 | −34.44 | 0.08 | 0.12 | 0.12 |
| 17 | B | 1.21 | 2.43 | 315.00 | 4.56 | 132.53 | 0.91 | 0.72 | 0.72 |
| 18 | B | 1.21 | 2.43 | 315.00 | 5.58 | 60.81 | 0.29 | 0.23 | 0.23 |
Appendix A.2

Table A2.
Investigated SUPs for 2K TEU CC.
Table A2.
Investigated SUPs for 2K TEU CC.
| No | Method | α | β | σY (MPa) | σx (MPa) | τxy (MPa) | η by | ||
|---|---|---|---|---|---|---|---|---|---|
| CSR (2023) | Eigenvalue FEA | Inelastic FEA | |||||||
| 1 | A | 2.53 | 1.88 | 355.00 | 78.14 | 12.57 | 0.65 | 2.03 | 0.28 |
| 2 | A | 2.53 | 1.88 | 355.00 | 40.03 | 18.34 | 0.24 | 0.68 | 0.68 |
| 3 | A | 2.39 | 1.99 | 355.00 | 61.50 | −56.63 | 0.72 | 1.86 | 0.51 |
| 4 | A | 2.39 | 1.99 | 355.00 | 68.17 | 1.18 | 0.54 | 1.81 | 0.22 |
| 5 | A | 2.53 | 1.88 | 355.00 | 68.40 | −87.69 | 1.03 | 2.23 | 0.83 |
| 6 | A | 2.53 | 1.88 | 355.00 | 42.39 | −28.11 | 0.30 | 0.80 | 0.80 |
| 7 | A | 2.39 | 1.99 | 355.00 | 65.61 | −72.48 | 0.91 | 2.21 | 0.70 |
| 8 | A | 2.39 | 1.99 | 355.00 | 67.96 | −2.57 | 0.54 | 1.80 | 0.22 |
| 9 | A | 2.53 | 1.66 | 355.00 | −26.31 | −133.91 | 0.85 | 0.85 | 0.85 |
| 10 | A | 2.53 | 1.66 | 355.00 | 57.77 | −2.36 | 0.29 | 0.78 | 0.78 |
| 11 | A | 2.39 | 1.76 | 355.00 | 33.01 | −120.72 | 0.90 | 1.13 | 0.84 |
| 12 | A | 2.39 | 1.76 | 355.00 | 65.91 | −3.31 | 0.40 | 1.13 | 0.19 |
| 13 | A | 1.89 | 1.37 | 355.00 | 100.60 | −69.04 | 0.58 | 0.80 | 0.80 |
| 14 | A | 1.89 | 1.37 | 355.00 | 24.63 | 53.68 | 0.12 | 0.10 | 0.10 |
| 15 | A | 1.85 | 2.05 | 355.00 | 29.62 | 76.20 | 0.48 | 0.74 | 0.74 |
| 16 | A | 1.85 | 2.05 | 355.00 | 50.00 | −0.22 | 0.29 | 0.88 | 0.88 |
| 17 | B | 1.26 | 2.12 | 315.00 | 9.11 | 113.64 | 0.61 | 0.43 | 0.43 |
| 18 | B | 1.41 | 1.89 | 315.00 | 12.84 | −3.79 | 0.06 | 0.05 | 0.05 |
| 19 | A | 1.61 | 2.35 | 315.00 | 24.28 | −96.67 | 0.84 | 1.22 | 0.84 |
| 20 | A | 1.61 | 2.35 | 315.00 | 26.95 | −24.48 | 0.23 | 0.59 | 0.59 |
| 21 | A | 1.61 | 2.35 | 315.00 | 22.40 | −95.58 | 0.81 | 1.16 | 0.82 |
| 22 | A | 1.61 | 2.35 | 315.00 | 27.42 | 2.44 | 0.16 | 0.52 | 0.52 |
| 23 | A | 1.61 | 2.35 | 315.00 | 25.27 | 120.80 | 1.16 | 1.60 | 1.22 |
| 24 | A | 1.61 | 2.35 | 315.00 | 48.89 | 10.26 | 0.42 | 1.34 | 0.21 |
| 25 | A | 1.61 | 2.35 | 315.00 | 72.54 | −77.17 | 1.25 | 3.04 | 0.92 |
| 26 | A | 1.61 | 2.35 | 315.00 | 47.29 | −7.14 | 0.39 | 1.26 | 0.20 |
Appendix A.3

Table A3.
Investigated SUPs for 50K PC.
Table A3.
Investigated SUPs for 50K PC.
| No | Method | α | β | σY (MPa) | σx (MPa) | τxy (MPa) | η by | ||
|---|---|---|---|---|---|---|---|---|---|
| CSR (2023) | Eigenvalue FEA | Inelastic FEA | |||||||
| 1 | A | 1.39 | 1.91 | 355.00 | 48.60 | 117.43 | 0.66 | 0.73 | 0.73 |
| 2 | A | 1.39 | 2.00 | 315.00 | 32.17 | 57.48 | 0.31 | 0.43 | 0.43 |
| 3 | A | 0.99 | 3.27 | 355.00 | 49.60 | 125.56 | 1.22 | 2.05 | 0.92 |
| 4 | A | 1.61 | 2.35 | 315.00 | 26.95 | −24.48 | 0.23 | 0.59 | 0.59 |
| 5 | A | 1.25 | 1.29 | 355.00 | 22.40 | −95.58 | 0.26 | 0.06 | 0.06 |
| 6 | A | 1.61 | 2.35 | 315.00 | 27.42 | 2.44 | 0.16 | 0.52 | 0.52 |
| 7 | A | 1.28 | 3.10 | 355.00 | −5.67 | 117.89 | 0.43 | 1.25 | 0.39 |
| 8 | A | 1.28 | 2.81 | 355.00 | 74.31 | 22.51 | 0.79 | 2.54 | 0.50 |
| 9 | A | 1.27 | 2.45 | 355.00 | 73.45 | 115.17 | 1.18 | 2.14 | 0.88 |
| 10 | A | 1.27 | 2.21 | 355.00 | 44.19 | 30.26 | 0.26 | 0.55 | 0.16 |
| 11 | A | 1.00 | 2.81 | 355.00 | 89.30 | 17.22 | 0.78 | 2.03 | 0.65 |
| 12 | A | 1.00 | 3.93 | 355.00 | 72.16 | 10.14 | 0.94 | 3.44 | 0.75 |
| 13 | A | 1.27 | 2.45 | 355.00 | 101.11 | 39.36 | 1.04 | 2.74 | 0.72 |
| 14 | A | 1.27 | 2.21 | 355.00 | 42.93 | 10.94 | 0.20 | 0.49 | 0.49 |
| 15 | A | 1.27 | 2.45 | 355.00 | 66.39 | 60.62 | 0.70 | 1.55 | 0.47 |
| 16 | A | 1.27 | 2.21 | 355.00 | 35.81 | 25.97 | 0.19 | 0.39 | 0.39 |
| 17 | A | 1.28 | 3.10 | 355.00 | 42.08 | 57.24 | 0.68 | 1.81 | 0.54 |
| 18 | A | 1.28 | 2.81 | 355.00 | 8.65 | 3.97 | 0.03 | 0.09 | 0.09 |
| 19 | A | 1.24 | 2.74 | 315.00 | 88.78 | 55.26 | 1.34 | 3.46 | 0.98 |
| 20 | A | 1.24 | 2.74 | 315.00 | 82.35 | 36.62 | 1.10 | 3.19 | 0.76 |
| 21 | A | 1.10 | 3.38 | 315.00 | 43.42 | 59.69 | 0.85 | 2.14 | 0.68 |
| 22 | A | 1.10 | 3.38 | 315.00 | 41.81 | 50.91 | 0.74 | 1.95 | 0.56 |
| 23 | B | 1.51 | 1.90 | 235.00 | 37.26 | 35.69 | 0.84 | 0.71 | 0.71 |
| 24 | B | 1.51 | 1.90 | 235.00 | 41.69 | 27.52 | 0.94 | 0.80 | 0.80 |
| 25 | A | 1.24 | 2.36 | 235.00 | 83.64 | 47.51 | 1.49 | 3.46 | 1.09 |
| 26 | A | 1.24 | 2.36 | 235.00 | 57.26 | 38.70 | 0.86 | 1.92 | 0.59 |
| 27 | A | 1.10 | 2.92 | 235.00 | 56.56 | 34.75 | 1.03 | 2.75 | 0.77 |
| 28 | A | 1.10 | 2.92 | 235.00 | 37.96 | 37.59 | 0.68 | 1.61 | 0.48 |
Appendix A.4

Table A4.
Investigated SUPs for 115K COC.
Table A4.
Investigated SUPs for 115K COC.
| No | Method | α | β | σY (MPa) | σx (MPa) | τxy (MPa) | η by | ||
|---|---|---|---|---|---|---|---|---|---|
| CSR (2023) | Eigenvalue FEA | Inelastic FEA | |||||||
| 1 | A | 2.07 | 2.15 | 355.00 | 60.79 | 82.06 | 0.98 | 2.29 | 0.70 |
| 2 | A | 2.07 | 2.15 | 355.00 | 61.08 | 75.06 | 0.92 | 2.21 | 0.61 |
| 3 | A | 1.27 | 2.17 | 355.00 | 104.89 | 56.96 | 0.97 | 2.09 | 0.64 |
| 4 | A | 1.27 | 1.69 | 355.00 | 110.10 | 17.17 | 0.58 | 0.94 | 0.94 |
| 5 | A | 1.46 | 2.15 | 315.00 | 81.25 | 22.61 | 0.78 | 2.01 | 0.49 |
| 6 | A | 1.46 | 1.90 | 355.00 | 74.53 | 14.54 | 0.43 | 0.94 | 0.94 |
| 7 | A | 1.30 | 3.15 | 315.00 | 66.96 | 25.18 | 1.02 | 3.75 | 0.39 |
| 8 | A | 1.30 | 2.78 | 355.00 | 56.97 | 46.87 | 0.68 | 1.88 | 0.27 |
| 9 | A | 1.01 | 3.13 | 315.00 | 87.40 | 61.63 | 1.36 | 3.50 | 0.70 |
| 10 | A | 1.01 | 3.13 | 315.00 | 70.66 | 59.47 | 1.06 | 2.61 | 0.54 |
| 11 | A | 1.39 | 2.29 | 355.00 | 165.53 | 42.45 | 2.15 | 5.83 | 1.27 |
| 12 | A | 1.39 | 2.27 | 315.00 | 133.42 | 26.36 | 1.77 | 4.80 | 1.11 |
| 13 | A | 1.67 | 2.45 | 355.00 | 98.00 | 37.70 | 1.27 | 4.19 | 0.67 |
| 14 | A | 1.67 | 2.33 | 355.00 | 96.10 | 39.17 | 1.14 | 3.53 | 0.57 |
| 15 | B | 1.27 | 2.40 | 355.00 | 66.92 | 141.02 | 1.31 | 2.03 | 2.44 |
| 16 | B | 1.27 | 1.90 | 355.00 | 22.53 | 129.22 | 0.53 | 0.37 | 0.37 |
| 17 | A | 1.50 | 1.96 | 235.00 | 89.00 | 62.18 | 1.57 | 3.17 | 1.13 |
| 18 | A | 1.50 | 2.15 | 315.00 | 70.66 | 59.47 | 0.84 | 1.85 | 0.56 |
| 19 | A | 1.21 | 2.93 | 235.00 | 35.72 | 61.56 | 1.02 | 2.18 | 0.73 |
| 20 | A | 1.21 | 3.40 | 315.00 | 61.02 | 16.91 | 0.89 | 3.45 | 0.33 |
| 21 | B | 2.00 | 1.44 | 315.00 | 37.30 | 110.29 | 0.71 | 0.48 | 0.48 |
| 22 | B | 2.00 | 1.44 | 315.00 | 19.74 | 82.08 | 0.35 | 0.23 | 0.23 |
| 23 | B | 1.67 | 1.60 | 235.00 | 121.26 | 36.61 | 3.93 | 3.18 | 3.76 |
| 24 | B | 1.67 | 1.60 | 235.00 | 109.05 | 3.41 | 3.16 | 2.58 | 3.07 |
References
- Paik, J.K.; Thayamballi, A.K. Ultimate Limit State Design of Steel-Plated Structures; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 978-0-471-48632-9. [Google Scholar]
- IACS. Common Structural Rules for Bulk Carriers; International Association of Classification Societies (IACS): London, UK, 2006. [Google Scholar]
- IACS. Common Structural Rules for Double Hull Oil Tankers; International Association of Classification Societies (IACS): London, UK, 2006. [Google Scholar]
- Kim, J.H.; Baeg, D.Y.; Seo, J.K. Numerical Investigation of Residual Strength of Steel Stiffened Panel Exposed to Hydrocarbon Fire. J. Ocean. Eng. Technol. 2021, 35, 203–215. [Google Scholar] [CrossRef]
- Fujita, Y.; Yoshida, K.; Arai, H. Instability of Plates with Holes (2nd Report). J. SNAJ Nihon Zousen Gakkai Ronbunshu 1969, 1969, 285–294. [Google Scholar] [CrossRef] [PubMed]
- Fujita, Y.; Yoshida, K.; Arai, H. Instability of Plates with Holes (3rd Report). J. SNAJ Nihon Zousen Gakkai Ronbunshu 1970, 1970, a161–a169. [Google Scholar] [CrossRef]
- Nishihara, S.; Imakita, A.; Sawayanagi, M. On the Shear Buckling Strength of Perforated Plates and their Reinforcements. J. SNAJ Nihon Zousen Gakkai Ronbunshu 1978, 1978, 301–307. [Google Scholar] [CrossRef]
- Nishihara, S.; Sawayanagi, M. On the Shear Buckling Strength of Perforated Plates and Their Reinforcements (2nd Report). J. SNAJ Nihon Zousen Gakkai Ronbunshu 1980, 1980, 276–282. [Google Scholar] [CrossRef]
- Narayanan, R.; der Avanessian, N.G.V. Buckling of Perforated Plates under Shear. Thin-Walled Struct. 1984, 2, 51–73. [Google Scholar] [CrossRef]
- Shanmugam, N.E.; Paramasivam, P.; Lee, S.-L. Stiffened Flanges Containing Openings. J. Struct. Eng. 1986, 112, 2234–2246. [Google Scholar] [CrossRef]
- Alagusundaramoorthy, P.; Sundaravadivelu, R.; Ganapathy, C. Ultimate Strength of Stiffened Panels with Cutouts under Uniaxial Compression. Mar. Struct. 1995, 8, 279–308. [Google Scholar] [CrossRef]
- Shanmugam, N.E.; Thevendran, V.; Tan, Y.H. Formula for Axially Compressed Perforated Plates. Thin-Walled Struct. 1999, 34, 1–20. [Google Scholar] [CrossRef]
- Durban, D.; Zuckerman, Z. Elastoplastic Buckling of Rectangular Plates in Biaxial Compression/Tension. Int. J. Mech. Sci. 1999, 41, 751–765. [Google Scholar] [CrossRef]
- Betten, J.; Shin, C.H. Elastic-Plastic Buckling Analysis of Rectangular Plates Subjected to Biaxial Loads. Forsch. Ingenieurwesen 2000, 65, 273–278. [Google Scholar] [CrossRef]
- El-Sawy, K.M.; Nazmy, A.S. Effect of Aspect Ratio on the Elastic Buckling of Uniaxially Loaded Plates with Eccentric Holes. Thin-Walled Struct. 2001, 39, 983–998. [Google Scholar] [CrossRef]
- Harada, M.; Fujikubo, M. Estimation of buckling and ultimate strength of rectangular plate with cutout. J. SNAJ Nihon Zousen Gakkai Ronbunshu 2001, 2001, 723–729. [Google Scholar] [CrossRef] [PubMed][Green Version]
- El-Sawy, K.M.; Nazmy, A.S.; Martini, M.I. Elasto-Plastic Buckling of Perforated Plates under Uniaxial Compression. Thin-Walled Struct. 2004, 42, 1083–1101. [Google Scholar] [CrossRef]
- Kumar, M.S.; Alagusundaramoorthy, P.; Sundaravadivelu, R. Ultimate Strength of Square Plate with Rectangular Opening under Axial Compression. J. Nav. Arch. Mar. Eng. 2007, 4, 15–26. [Google Scholar] [CrossRef]
- Paik, J.K. Ultimate Strength of Perforated Steel Plates under Edge Shear Loading. Thin-Walled Struct. 2007, 45, 301–306. [Google Scholar] [CrossRef]
- Paik, J.K. Ultimate Strength of Steel Plates with a Single Circular Hole under Axial Compressive Loading along Short Edges. Ships Offshore Struct. 2007, 2, 355–360. [Google Scholar] [CrossRef]
- Paik, J.K. Ultimate Strength of Perforated Steel Plates under Combined Biaxial Compression and Edge Shear Loads. Thin-Walled Struct. 2008, 46, 207–213. [Google Scholar] [CrossRef]
- Aydin Komur, M.; Sonmez, M. Elastic Buckling of Rectangular Plates under Linearly Varying In-Plane Normal Load with a Circular Cutout. Mech. Res. Commun. 2008, 35, 361–371. [Google Scholar] [CrossRef]
- Wang, G.; Sun, H.; Peng, H.; Uemori, R. Buckling and Ultimate Strength of Plates with Openings. Ships Offshore Struct. 2009, 4, 43–53. [Google Scholar] [CrossRef]
- Kim, U.-N.; Choe, I.-H.; Paik, J.K. On Buckling and Ultimate Strength of Perforated Plate Panels Under Axial Compression: Experimental and Numerical Investigations with Design Formulations; OnePetro: Richardson, TX, USA, 2008. [Google Scholar]
- Kim, U.-N.; Choe, I.-H.; Paik, J.K. Buckling and Ultimate Strength of Perforated Plate Panels Subject to Axial Compression: Experimental and Numerical Investigations with Design Formulations. Ships Offshore Struct. 2009, 4, 337–361. [Google Scholar] [CrossRef]
- Cheng, B.; Zhao, J. Strengthening of Perforated Plates under Uniaxial Compression: Buckling Analysis. Thin-Walled Struct. 2010, 48, 905–914. [Google Scholar] [CrossRef]
- Kim, J.-H.; Jeon, J.-H.; Park, J.-S.; Seo, H.-D.; Ahn, H.-J.; Lee, J.-M. Effect of Reinforcement on Buckling and Ultimate Strength of Perforated Plates. Int. J. Mech. Sci. 2015, 92, 194–205. [Google Scholar] [CrossRef]
- Yu, C.-L.; Lee, J.-S. Ultimate Strength of Simply Supported Plate with Opening under Uniaxial Compression. Int. J. Nav. Archit. Ocean Eng. 2012, 4, 423–436. [Google Scholar] [CrossRef]
- Dadrasi, A. On the Effect of Imperfection on Buckling Load of Perforated Rectangular Steel Plates. Res. J. Recent Sci. 2013, 2, 36–43. [Google Scholar]
- Saad-Eldeen, S.; Garbatov, Y.; Guedes Soares, C. Experimental Strength Assessment of Thin Steel Plates with a Central Elongated Circular Opening. J. Constr. Steel Res. 2016, 118, 135–144. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Guedes Soares, C. Experimental Investigation on the Residual Strength of Thin Steel Plates with a Central Elliptic Opening and Locked Cracks. Ocean Eng. 2016, 115, 19–29. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Guedes Soares, C. Experimental Compressive Strength Analyses of High Tensile Steel Thin-Walled Stiffened Panels with a Large Lightening Opening. Thin-Walled Struct. 2017, 113, 61–68. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Guedes Soares, C. Structural Capacity of Plates and Stiffened Panels of Different Materials with Opening. Ocean Eng. 2018, 167, 45–54. [Google Scholar] [CrossRef]
- Lorenzini, G.; Helbig, D.; Real, M.d.V.; dos Santos, E.D.; Isoldi, L.A.; Rocha, L.A.O. Computational Modeling and Constructal Design Method Applied to the Mechanical Behavior Improvement of Thin Perforated Steel Plates Subject to Buckling. J. Eng. Thermophys. 2016, 25, 197–215. [Google Scholar] [CrossRef]
- Lorenzini, G.; Helbig, D.; Silva, C.; Real, M.; dos Santos, E.; Isoldi, L.; Rocha, L.A.O. Numerical Evaluation of the Effect of Type and Shape of Perforations on the Buckling of Thin Steel Plates by Means of the Constructal Design Method. Int. J. Heat Technol. 2016, 34, S9–S20. [Google Scholar] [CrossRef]
- Cui, J.; Wang, D. A Study of Ultimate Strengths of Typical Longitudinal Girders With Openings in Container Ships. In Volume 3: Structures, Safety, and Reliability, Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: Madrid, Spain, 2018; p. V003T02A088. [Google Scholar]
- Guo, Y.; Song, X.; Li, X.; Yao, X.; Xia, Z.; Xu, B.; Su, J. Elastic Buckling of Thin Plate with Circular Holes in Bending. E3S Web Conf. 2019, 136, 04043. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Z.; Li, Y.; Chen, Q.; Zhang, X. Mechanical Behavior of Composite Ship Structures with Open-Hole. IOP Conf. Ser. Mater. Sci. Eng. 2020, 892, 012033. [Google Scholar] [CrossRef]
- Doan, V.T.; Liu, B.; Garbatov, Y.; Wu, W.; Guedes Soares, C. Strength Assessment of Aluminium and Steel Stiffened Panels with Openings on Longitudinal Girders. Ocean Eng. 2020, 200, 107047. [Google Scholar] [CrossRef]
- Liu, B.; Gao, L.; Ao, L.; Wu, W. Experimental and Numerical Analysis of Ultimate Compressive Strength of Stiffened Panel with Openings. Ocean Eng. 2021, 220, 108453. [Google Scholar] [CrossRef]
- Silva-Campillo, A.; Suárez-Bermejo, J.C.; Herreros-Sierra, M.A. An Experimental and Numerical Investigation on Buckling Strength Assessment of Perforated Plates under Combined In-Plane Loads. Ocean Eng. 2022, 259, 111919. [Google Scholar] [CrossRef]
- IACS. Common Structural Rules for Bulk Carriers and Oil Tankers; International Association of Classification Societies (IACS): London, UK, 2023. [Google Scholar]
- Simulia Abaqus User Manual. Available online: https://www.3ds.com/support/documentation/user-guides (accessed on 25 August 2024).
- Jeong, H.K.; Kim, S.H.; Hwang, S.P. Study on Stiffened-Plate Structure Response in Marine Nuclear Reactor Operation Environment. J. Ocean Eng. Technol. 2023, 37, 205–214. [Google Scholar] [CrossRef]
- Yu, Y.-J.; Park, S.-H.; Cho, S.-R. Collision-Damage Analysis of a Floating Offshore Wind Turbine Considering Ship-Collision Risk. J. Ocean Eng. Technol. 2024, 38, 124–136. [Google Scholar] [CrossRef]
- Ghavami, K.; Khedmati, M.R. Numerical and Experimental Investigations on the Compression Behaviour of Stiffened Plates. J. Constr. Steel Res. 2006, 62, 1087–1100. [Google Scholar] [CrossRef]
- Smith, C.S.; Davidson, P.C.; Chapman, J.C. Strength and Stiffness of Ships’ Plating Under In-plane Compression and Tension. R. Inst. Nav. Archit. Trans. 1988, 130, 277–296. [Google Scholar]
- IACS. Technical Background Report & Consequence Assessment (CA) Report; International Association of Classification Societies (IACS): London, UK, 2021. [Google Scholar]
- Do, H.-S.; Lee, T.-K. Economic Feasibility Analysis According to Seam Location of Ship Pieces. J. Ocean Eng. Technol. 2023, 37, 266–272. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).