Abstract
This paper proposes a convolutional multi-agent deep deterministic policy gradient method with prioritized experience replay (PER-CMADDPG) for the problem of multi-AUV cooperative search for moving targets. A comprehensive mathematical model of the multi-AUV cooperative search for moving targets is first established, which includes the environment model, the AUV model, and the information update and fusion model. Building upon the MADDPG framework, the proposed PER-CMADDPG method introduces two major enhancements. Convolutional neural networks (CNNs) are integrated into both the actor and critic networks to extract spatial features from local observation maps and global states, enabling agents to better perceive the spatial structure of the environment. In addition, a prioritized experience replay (PER) mechanism is incorporated to improve learning efficiency by emphasizing informative experiences during training, thereby accelerating policy convergence. Simulation experiments demonstrate that the proposed method achieves faster convergence and higher rewards compared with MADDPG. Furthermore, the influences of the multi-AUV cluster system’s scale, AUV speed, and sonar detection radius on performance are analyzed. The results verify the effectiveness of the proposed PER-CMADDPG method for the multi-AUV cooperative search for moving targets.
1. Introduction
As an intelligent piece of equipment working underwater autonomously, autonomous underwater vehicles (AUVs) are widely used in fields such as marine environment monitoring [1], resource exploration [2], seabed mapping [3], underwater rescue [4], and military applications [5]. In recent years, with the rapid development of AUV technology, multi-AUV cluster systems have become a prominent research focus [6]. Compared with a single AUV, a multi-AUV cluster system can significantly enhance mission efficiency and improve system robustness through redundancy. Multi-AUV cooperative target search is an important application field of the multi-AUV cluster system, which aims to detect and localize targets within the mission area through coordinated operations among multiple AUVs. It is a highly challenging problem. First, during the target search process, the mission environment is often unknown and dynamically changing due to factors such as unknown obstacles, target movement, and inter-AUV communication constraints. Therefore, it is essential to design an effective search strategy for the multi-AUV cluster system to operate efficiently in an unknown and dynamic environment. Second, as the number of individuals in the multi-AUV cluster system increases, the joint state space grows exponentially, leading to a significant rise in computational complexity, which affects the real-time performance of the system.
There are primarily two classes of methods for the multi-AUV cooperative target search problem: traditional methods based on heuristic algorithms and intelligent methods based on reinforcement learning. Traditional methods for addressing the problem of multi-AUV cooperative target search uses optimization theory, which converts the multi-AUV cooperative target search problem into a multi-objective optimization problem and uses heuristic algorithms to maximize or minimize optimization objectives. Wang et al. proposed a knowledge hierarchy-based dynamic multi-objective optimization method to enhance multi-AUV cooperative search performance under unstable communication conditions [7]. Li et al. introduced a hierarchical strategy for static target search that optimizes cumulative search rewards [8]. You et al. addressed the limited-time static search challenge by developing an improved particle swarm optimization algorithm, employing a Voronoi diagram and biological competition models to efficiently allocate AUVs and subregions, thus transforming the multi-AUV search into multiple single-AUV searches and improving overall efficiency [9]. Wang et al. proposed a hierarchical method based on maximizing cumulative detection rewards or search efficiency to solve the path-planning problem of AUVs in static target search missions under marine environments [10]. Traditional methods can quickly provide a search strategy and yield satisfactory outcomes in a specific environment. However, when confronted with dynamically changing environments, traditional methods exhibit limited flexibility and adaptability, which is due to the reliance on prior knowledge of the environment during the algorithm design process.
In recent years, the development of reinforcement learning (RL) has provided a new solution for addressing the problem of multi-AUV cooperative target searches. RL enables the agent to learn the optimal strategy through interactive training between the agent and the environment, which has significant advantages in dynamically changing environments. It has been widely applied across various fields, including robotics [11], unmanned aerial vehicles [12], unmanned ground vehicles [13], and AUVs [14,15,16]. Liu et al. proposed a controller based on the DDPG algorithm to improve the control performance of vectored-thruster AUVs operating in complex marine environments [14]. Ren et al. designed a controller based on the proximal policy optimization (PPO) algorithm to achieve hovering control of large-displacement AUVs [15]. Lin et al. designed an image-based deep deterministic policy gradient (I-DDPG) intelligent docking control system for AUVs, which provides excellent adaptability and continuous control for vision-based underwater docking [16]. Multi-agent reinforcement learning (MARL) is an extension of RL, which exhibits superior performance in environments that involve complex dynamics of multi-agent cooperation and competition compared with RL. In multi-agent environments, agents influence each other; the strategy change of one agent affects the decision-making of other agents. The multi-AUV cooperative target search problem can be modeled as a decentralized partially observable Markov decision process (Dec-POMDP), making it solvable with a MARL method.
This paper investigates multi-AUV cooperative search for moving target problems and proposes a convolutional multi-agent deep deterministic policy gradient method with prioritized experience replay. The main contributions of this work are as follows:
- The multi-AUV cooperative search for the moving target problem is formulated mathematically, including the environment model, the AUV model, and the information update and fusion model. In the multi-AUV cluster system, each AUV obtains environmental cognitive information from other AUVs within its communication range, processes it through the information update and fusion model, and utilizes the fused information to guide its actions. The information update and fusion model not only enhances the environmental perception capability of individual AUVs but also strengthens the cooperation among members of the multi-AUV cluster system. Subsequently, the multi-AUV cooperative search for moving targets is reformulated as a multi-objective optimization problem, where the optimization objectives include the uncertainty of the mission area, the exploration rate, and the number of detected moving targets.
- A convolutional multi-agent deep deterministic policy gradient method with prioritized experience replay is proposed to address the problem of multi-AUV cooperative search for moving targets. This method employs a CNN to extract spatial features from states and observations, thereby enabling more effective information processing. In addition, a prioritized experience replay mechanism is adopted to accelerate strategy convergence.
- To evaluate the performance of the proposed PER-CMADDPG method, simulation experiments are conducted, and the results are compared with those obtained using MADDPG and the convolutional multi-agent deep deterministic policy gradient (CMADDPG). The comparative analysis verifies the effectiveness and advantages of the proposed method. In addition, the influences of factors such as the multi-AUV cluster system scales, AUV speed, and sonar detection radius on the performance of the proposed PER-CMADDPG method are analyzed.
The remainder of this paper is organized as follows. Section 2 presents the current related work. Section 3 defines the multi-AUV cooperative search for the moving target model. Section 4 presents the proposed PER-CMADDPG method in detail. Section 5 carries out simulation experiments and analyzes the results. Section 6 summarizes this paper and points out directions for future research. The list of important notations used in this paper is shown in Table 1.

Table 1.
List of important notations used in this paper.
2. Related Works
This section analyzes the related work on multi-AUV cooperative search for moving targets in two parts. The first part presents a comprehensive review of research on target search, while the second part discusses related works in the field of MARL.
2.1. Target Search
As a branch of search theory study, target search focuses on the cooperation of multiple agents to detect as many targets as possible within a limited time in the mission area. A common method in target search problems is to divide the mission area into cells, with each cell associated with a target presence probability, thereby forming a probability map of the entire area [17]. Ji et al. proposed a collaborative particle swarm optimization genetic algorithm to address collaborative target search for multiple UAVs, which establishes a search probability map model and uses a collaborative particle swarm optimization genetic algorithm to generate a search path [18]. Lu et al. proposed an improved pigeon-inspired optimization (IPIO) algorithm based on natural selection and Gauss–Cauchy mutation, which achieves cooperative dynamic target search and rapidly obtains the full age of the target area under an uncertain environment [19]. Yue et al. improved the multi-wolf pack algorithm and employed it to address collaborative search for multi-intelligent targets by multi-AUV in a complex underwater environment [20]. Jiang et al. proposed a dynamic target search path planning method based on the Glasius biologically inspired neural network, which effectively addresses the problem of dynamic target search in marine environments by utilizing a constructed target presence probability map [21].
However, as the scale of the multi-AUV cluster system increases, traditional methods based on heuristic algorithms encounter escalating computational complexity for obtaining the optimal solution. To reduce computational complexity, an intelligent algorithm based on MARL is proposed. Zhang et al. proposed a new deep reinforcement learning method called double-critic deep deterministic policy gradient (DCDDPG) for the multi-UAV cooperative reconnaissance search problem [22]. Wu et al. proposed an MADRL method based on parameter sharing and action masks, which significantly improved the search efficiency of UAVs [23]. Song et al. combined particle swarm optimization with RL and proposed a new collaborative search method, which effectively solved the problem of multi-USV cooperative search in complex ocean environments [24]. Li et al. proposed an SAC-QMIX algorithm for solving the multi-AUV cooperative search problem [25]. Wang et al. proposed a multi-AUV maritime target search method for moving and invisible objects based on the MADDPG algorithm [10]. Compared with traditional methods, the proposed method achieves a higher target detection success rate and reduced search time.
2.2. Multi-Agent Reinforcement Learning
MARL refers to placing multiple agents in the same environment, and each agent independently interacts with the environment and improves its own strategy based on the rewards received from environmental feedback, aiming to obtain a higher return. In multi-agent environments, the strategy of each agent depends not only on its own observations and actions but also on the observations and actions of other agents. One solution to solving the MARL problem is to model each agent as an independent RL agent and optimize its strategy separately. Common algorithms include independent Q-Learning (IQL) [26] and independent proximal policy optimization (IPPO) [27]. The primary advantages of such algorithms are that they are simple to implement, as they can directly reuse the corresponding single-agent algorithms without requiring complex multi-agent cooperation mechanisms. However, as the number of agents in the multi-agent environments increases, the non-stationarity of the environment can make learning unstable and hinder the convergence of agents’ strategies to the optimal. The centralized training and decentralized execution architecture can effectively alleviate the impact of environmental non-stationarity, which uses global states to optimize agents’ strategies during training and makes decisions based on local observation of each agent during execution. Representative MARL algorithms adopting the CTDE architecture include value decomposition networks (VDNs) [28], QMIX [29], and the multi-agent deep deterministic policy gradient (MADDPG) [30]. As a variant of the deep deterministic policy gradient (DDPG) [31], MADDPG exhibits outstanding performance compared to other MARL algorithms in complex and dynamic environments involving multi-agent cooperation and competition. In this work, we propose an improved version of the MADDPG algorithm to enable its application to the multi-AUV cooperative search for the moving target problem.
3. Problem Formulation
This section presents the mathematical formation of the multi-AUV cooperative search for the moving target problem. The multi-AUV cooperative search for the moving target problem is first introduced, and subsequently, the corresponding mathematical model is established and explained in detail.
3.1. Multi-AUV Cooperative Search for Moving Targets
The mission scenario of the multi-AUV cooperative search for moving targets is shown in Figure 1. The objective of the multi-AUV cluster system is to detect as many moving targets as possible in the mission area within a limited time. Furthermore, since the number of targets is unknown, the mission area must be continuously explored to improve the multi-AUV cluster system’s knowledge of the environment. To simplify the mission scenario and focus on the primary issue, some assumptions are made in this paper as follows:
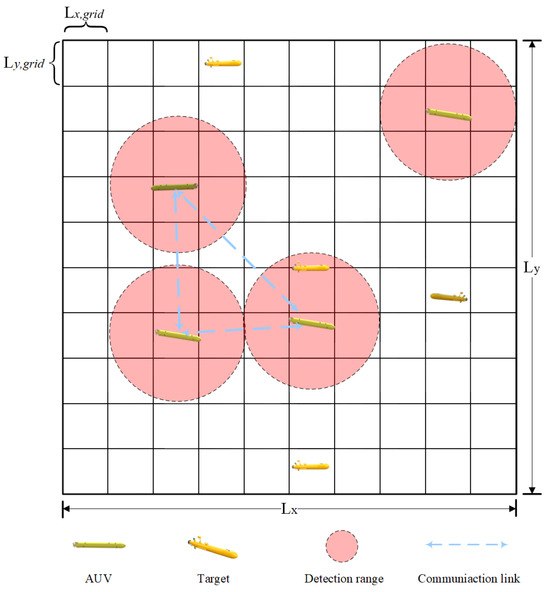
Figure 1.
Multi-AUV cooperative search for moving target scenario.
- 1.
- Both the multi-AUV cluster system and the targets operate at fixed but different depths, thereby simplifying the movement of the multi-AUV cluster system and the targets from three-dimensional space movement to two-dimensional planar movement. Since the multi-AUV cluster system and the targets move at different depths, only intra-AUV collisions are considered due to fixed depths; inter-vehicle vertical separation remains constant.
- 2.
- Each individual in the multi-AUV cluster system has a fixed initial position and moves at a constant speed. Each AUV is equipped with a series of detection sonars. When a target enters the detection range of the sonar of an AUV, the AUV is capable of detecting the target. However, due to the inherent detection probability and false alarm probability of the equipped sonar, the result of a single detection is unreliable. Therefore, the multi-AUV cluster system must cooperate to perform repeated detections to improve the reliability of the detection results. In addition, each AUV can only share detection information with neighboring AUVs within its communication range.
- 3.
- The targets are initially randomly distributed within the mission area and move randomly at a constant speed within the same area. The targets are assumed to employ evasion strategies to avoid detection by the multi-AUV cluster system and to prevent collisions with other targets.
3.2. Mathematical Model
The mathematical model of the multi-AUV cooperative search for the moving target problem consists of the environment model, the AUV model, and the information update and fusion model. Based on these components, the mathematical formulation of the problem is established.
3.2.1. Environment Model
As shown in Figure 1, the mission area is modeled as a two-dimensional rectangular plane with a length of and a width of , which is divided into grid areas. The mission area is defined as follows:
where M and N represent the number of grid areas in the rows and columns of the mission area, respectively. Each grid area is denoted by , and the coordinate of the grid area is indicated as , where ,. The length and width of each grid area are and , respectively, where and .
Let be the set of moving targets. The position of the target at time step is denoted by , and the corresponding grid area coordinate is . The target presence state of the grid area is denoted as ; means that there is no target in this grid area, and means that there is at least one target in this grid area. At each time step, each target can occupy only one grid area, although multiple targets may occupy the same grid area simultaneously.
Let denote the multi-AUV cluster system, where , and is the number of individuals. The position of the AUV at time step is denoted by , and the corresponding grid area coordinate is . The detection radius of each AUV is . The detection area of the AUV is defined as follows:
The detection result of AUV at time step t for grid area is denoted by , where indicates that no target is detected in the grid area, and indicates that a target is detected. It is important to note that, due to the inherent detection probability and false alarm probability of the sonar, a single detection is hardly enough to ensure the detection of the target. Therefore, multiple detections are necessary to obtain reliable detection results. The detection probability of sonar is defined as follows [32]:
where is the false alarm probability of the sonar, and it is considered a constant value. represents the true detection probability of the sonar, which is defined as a function of the distance between the sonar and the target as follows:
The communication capability of the multi-AUV cluster system is limited. Each AUV can only communicate with neighboring AUVs within its communication range. The set of neighbors for AUV at time step t is denoted as follows:
where represents the communication radius of the AUV.
3.2.2. AUV Model
This section assumes that all individuals in the multi-AUV cluster system move at a constant speed v and maintain a fixed depth. Let denote the state of AUV at time step t, where represents the position of AUV and denotes the heading angle of AUV . The simplified kinematic model of the AUV is given by the following:
where indicates the change in the heading angle per unit time .
3.2.3. Information Update and Fusion Model
The information update and fusion model includes the target probability map, uncertainty map, environment search map, and AUV position map. The components are described in detail below.
(1) Target Probability Map
The target probability map describes the probability of a target’s existence within each grid area. In the multi-AUV cluster system, each AUV maintains a target probability map for the whole mission area, which is represented as follows:
where represents the probability of a target existing in the grid area at time step t, while means that a target exists in the grid area , and means that there are no targets existing. Since no prior information is available regarding the spatial distribution of targets, the initial probability for each grid area is set to 0.5, which represents the probability that the target exists in any grid area is 50%.
In the process of searching for moving targets, the multi-AUV cluster system collects detection data and updates the target probability maps based on new detection results. The target probability update is represented as follows:
The target probability map update process is nonlinear, resulting in high computational complexity. To improve computational efficiency, ref. [17] proposes a linear update method. By introducing the nonlinear conversion described in Equation (9), the update rule can be reformulated as shown in Equation (10):
During the search process of the multi-AUV cluster system, each AUV can share detection information with neighboring AUVs to facilitate information fusion and cooperation. The update of each AUV’s target probability map is performed in two steps. First, according to the sonar detection result, each AUV updates its own target probability map using the Bayesian rule described in Equation (11):
where is a decay factor that regulates the weight of information from the previous time step in the update process. When the grid area satisfies and , ; otherwise, .
Then, each AUV shares its updated target probability map with neighboring AUVs, and it updates its own target probability map again by Equation (12):
where
(2) Uncertainty Map
The uncertainty map represents the degree of knowledge of an AUV possesses about the mission area. For each AUV in the multi-AUV cluster system, its uncertainty map is defined as follows:
According to Equation (15), the value of the uncertainty map is a function of the corresponding target probability value from the target probability map. The relationship between and is shown in Figure 2.

Figure 2.
The relationship between target probability and uncertainty.
It is seen that when the grid area is , the uncertainty has a maximum uncertainty of 1, which indicates that the grid area is completely unknown to the AUV . Conversely, when or , the uncertainty has a minimum uncertainty of 0, which represents that the AUV is completely certain about whether the target exists or not in the grid area .
(3) Environment Search Map
The environment search map stores the last detection time for each grid area, which is defined as follows:
where represents the last detection time of the grid area at time step t according to the perception of the AUV . For each AUV in the multi-AUV cluster system, the environment search map is updated in two steps. First, each AUV updates its own environment search map based on the detection result at time step t, which can be represented as follows:
Then, each AUV shares its updated environment search map with neighboring AUVs and updates its own environment search map again according to Equation (18).
(4) AUV Position Map
The AUV position map stores the positions of all AUVs in the multi-AUV cluster system, which is defined as follows:
where represents the existence status of the AUV in the grid area at time step t. means that there is an AUV in the grid area , and means that there is no AUV.
The update of the AUV position map for each AUV is accomplished in two steps. First, each AUV updates its own AUV position map according to Equation (20).
Then, each AUV shares the updated AUV position map with neighboring AUVs, and it updates its own AUV position map again using Equation (21).
3.2.4. Mathematical Formulation of the Problem
This section formulates the multi-AUV cooperative search for the moving target problem as a multi-objective optimization problem. Since the number of moving targets is unknown to the multi-AUV cluster system, the mission area must be continuously explored to discover new targets. Consequently, one of the optimization objectives is to maximize the exploration rate of the mission area, which can be expressed as follows:
where represents the last detection time of the grid area at time step t. The maximum value of is 1, which means that all grid areas in the mission are being observed by the multi-AUV cluster system at time step t. However, it is unrealistic since the maximum sensing area of the multi-AUV cluster system is less than the mission area, i.e., .
Another optimization objective is to minimize the overall uncertainty of the mission area, which can be defined as follows:
where represents the uncertainty value of the grid area at time step t.
The last optimization objective is to maximize the number of detected moving targets, which can be expressed as follows:
where represents the probability of a target existing in the grid area at time step t, and is a predetermined detection threshold.
It is important to take into account the constraints. First, since the multi-AUV cluster system moves within the mission area, the boundary constraint is expressed as follows:
In addition, the safety of the multi-AUV cluster system is very important. Collisions between individuals in the multi-AUV cluster system must be avoided, so the collision avoidance constraint is expressed as follows:
where denotes the safe distance between individuals in the multi-AUV cluster system.
Thus, the multi-AUV cooperative search for moving targets problem can be described as follows:
4. Reformulation and Algorithm
This section reformulates the multi-AUV cooperative search for the moving target problem within the framework of the Dec-POMDP. The state space, observation space, and action space and the reward function are designed. Finally, the PER-CMADDPG method is introduced, followed by a detailed description of its training process.
4.1. Dec-POMDP
In the multi-AUV cooperative search for the moving target mission, each AUV operates as an independent decision-making unit, determining its action strategy based on the local observation. Then, the environment executes the joint action of all agents to update the current rewards and the next global state. The multi-AUV cooperative search for the moving target problem is modeled as Dec-POMDP, defined as a tuple , where the following are the provided definitions:
- N represents the number of agents;
- is the global state space, and is the current state of the environment;
- is the joint action space of all agents, and is the action of the i-th agent;
- is the joint reward by executing the joint action given the state s;
- is the joint observation space of all agents, and is the local observation of the i-th agent;
- : is the state transition probability function;
- : is the local observation probability function;
- is the discount factor.
4.2. State Space
The environment state at time step t is defined as follows:
where denotes the probability of the target existing in all grid areas, denotes the uncertainty values in all grid areas, denotes the last detection time for all grid areas, and denotes the existence status of the individuals in the multi-AUV cluster system in all grid areas.
4.3. Observation Space
In a multi-AUV cluster system, each AUV maintains individual cognitive information about the mission area and makes decisions based on its own cognitive information. However, if the AUV uses cognitive information of the entire mission area, an excessive amount of inaccurate information will make it difficult for the AUV to make the right decision. To enhance the decision-making ability of the AUV, the observation field is defined as a square area centered in the AUV’s current grid area, for which its side length is . At time step t, cognitive information in the observation field is used as an element of the observation space. Similarly to the environment’s state, the joint observation space of the multi-AUV cluster system at time step t is represented as follows:
where represents the local observation of the i-th AUV. It consists of four parts:
- is obtained from the target probability map , assuming that the target existence probability outside the mission area is 0, which means that there is no target outside the mission.
- is obtained from the uncertainty map . The uncertainty outside the mission area is assumed to be 0, which indicates that the AUV has complete knowledge of the outside of the mission area.
- is obtained from the environment search map , where is normalized by dividing by t. The environment search information outside the mission area is assumed to be 1, which means that there is no need to explore.
- is extracted from the AUV position map , and the value outside of the mission area is assumed to be 0, which means that there is no AUV.
4.4. Action Space
The joint action space of the multi-AUV cluster system at time step t is defined as follows:
where denotes the action space of the i-th AUV, which indicates the change in heading angle of the i-th AUV per unit time.
4.5. Reward Function
To enable the multi-AUV cluster system to detect as many moving targets as possible within a limited time in the mission area, it is essential to design a reasonable reward function. The reward function consists of cognitive reward, exploring reward, target discovery reward, collision punishment, and out-of-bounds punishment, and it is given as follows:
where represents the reward for the i-th AUV at time step t. , ,, , and represent weight coefficients.
(1) Cognitive reward
The purpose of the cognitive reward is to guide the AUV to reduce the uncertainty of the whole mission area. The cognitive reward is designed as follows:
(2) Exploring reward
The purpose of the exploration reward is to encourage the AUV to explore the mission area. Exploring reward is designed as follows:
where denotes the local exploration rate of the mission area of the i-th AUV at time step t.
(3) Target discovery reward
The purpose of the target discovery reward is to encourage the multi-AUV cluster system to search for more targets, noting that each target yields a reward only upon its initial detection by any agent. The target discovery reward is designed as follows:
(4) Collision punishment
To avoid collisions between individuals in the multi-AUV cluster system, the collision punishment is designed as follows:
where denotes the safe distance between individuals in the multi-AUV cluster system.
(5) Out-of-bounds punishment
To ensure that the AUV always moves within the mission area, an out-of-bounds punishment is introduced as follows:
4.6. Multi-AUV Cooperative Search for Moving Targets Method
4.6.1. MADDPG
MADDPG is a variant of DDPG designed to address MARL problems, adopting the CTDE architecture. Each agent consists of four deep neural networks: an actor network, a target actor network, a critic network, and a target critic network. During the centralized training phase, the critic network has access to the states and actions of all agents and estimates the expected return for the current action given the states. In the decentralized execution phase, each agent makes decisions and executes actions independently based on its local observations and its own actor network.
Assume that the agent i is equipped with a policy , referred to as the actor, which is parameterized by . The actor network generates an action based on a given observation. Each agent then executes the generated action, receiving a reward from the environment and transitioning from state to the next state . The experience tuple is stored in the experience replay buffer . Note that the state is composed of all agents’ observations, i.e., .
When the experience replay buffer contains sufficient samples, a mini-batch of experiences is randomly sampled to update the actor and critic networks. The critic network takes the states and actions of all agents as input and outputs the Q-value for the agent i. The target Q-value can be expressed as follows:
where is the discount factor. The critic network is updated by minimizing the loss function:
The gradient of the expected return for the agent i can be expressed as follows:
The parameters of the target actor and target critic networks for the agent i are updated via soft updates from the parameters of the corresponding actor and critic networks, which can be expressed as follows:
4.6.2. Actor–Critic Networks Based on CNN
CNN is a type of neural network specifically designed to process data with a grid-like structure. By simulating the local receptive mechanism of the human visual system, it automatically extracts local features from the data and combines them through a hierarchical structure to form higher-level abstract representations [33]. To enhance the spatial feature extraction capability of the observation space, CNNs are incorporated into both the actor and critic networks. Within the MARL framework, each agent is equipped with an individual actor network that receives its local observation as input. The CNN module in the actor network extracts spatial features from the local observation, which are subsequently processed by fully connected layers to generate continuous actions for decentralized decision-making. During centralized training, the critic network takes as input the global state and the joint actions of all agents. Its CNN module extracts spatial representations from the global state, while the fully connected layers integrate these spatial features with the joint action information to estimate the Q-value.
In the proposed architecture, both the actor and critic networks adopt identical CNN encoder configurations. The first convolutional layer contains 16 filters with a kernel size of , a stride of 1, and a padding of 1, followed by a max-pooling layer with a kernel size of and a stride of 2. The second convolutional layer employs 32 filters with the same kernel, stride, and padding settings, followed by a max-pooling layer with a kernel size of , a stride of 1, and a padding of 1; this is followed by a max-pooling layer with a kernel size of and a stride of 1. The resulting feature maps are flattened and fed into two fully connected layers, each with 64 hidden units. All hidden layers in both networks use the ReLU activation function, while the output layer of the actor network applies the tanh activation function to generate continuous actions. This design ensures consistent spatial feature extraction between the actor and critic networks while adhering to the CTDE architecture. Consequently, it enhances the model’s ability to represent complex spatial structures and improves cooperative decision-making performance in multi-agent environments. The overall architectures of the actor and critic networks are illustrated in Figure 3.
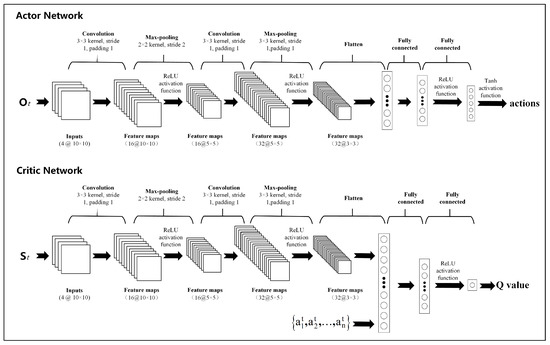
Figure 3.
The architecture of the actor and critic networks.
4.6.3. Prioritized Experience Replay
As a core technique in reinforcement learning, experience replay significantly improves training efficiency by systematically storing and reusing historical interaction data. However, traditional experience replay adopts a uniform sampling strategy, which ignores the differences in learning value among samples. Consequently, crucial experiences may be overwhelmed by a large number of ordinary samples, leading to low learning efficiency, especially in environments with sparse rewards. To overcome the above problems, prioritized experience replay (PER) is proposed [34]. PER introduces a priority-based sampling mechanism that leverages the temporal difference (TD) error to determine the importance of each experience sample. The sampling probability of the transition sample is defined as follows:
where represents the priority of transition i, calculated using proportional prioritization as follows:
where is the TD error of the transition, and is a small positive constant that ensures all samples have non-zero probability of being selected, thereby maintaining exploration for low-priority experiences. is a weighting factor that determines the degree of prioritization; when , the sampling simplifies to uniform sampling.
Since PER changes the distribution of sampled states, it inevitably introduces bias. To eliminate bias, importance sampling with an annealing factor is applied, and it is defined as follows:
where is a factor that controls the impact of importance sampling weights . As increases, the weights of low-priority samples gradually grow, compensating for the bias introduced by non-uniform sampling. When increases to 1, the bias is completely eliminated. The sampling weights are normalized to obtain better stability. After introducing the PER, the loss function of the critic network in Equation (44) becomes the following:
4.6.4. PER-CMADDPG
This section proposes a convolutional multi-agent deep deterministic policy gradient method with prioritized experience replay (PER-CMADDPG) for the mutli-AUV cooperative search for the moving targets problem. The training framework of the PER-CMADDPG is illustrated in Figure 4. During training, the multi-AUV cooperative search for a moving target environment generates a state , and each agent receives its own local observation derived from . Then, the actor network of each agent generates an action based on its observations. The environment executes the joint actions of all agents and returns the next state along with the rewards for each agent. Finally, the interaction data are stored in the PER buffer. Once the PER buffer has accumulated a sufficient number of samples, prioritized sampling is performed, and the parameters of both the actor and critic networks are updated. The pseudocode of the PER-CMADDPG method is presented in Algorithm 1.
| Algorithm 1 The PER-CMADDPG Algorithm |
|

Figure 4.
The training framework of PER-CMADDPG.
5. Experimental Results and Analysis
In this section, the parameters of the simulation environment are first introduced, followed by a series of experimental comparisons to verify the performance of the proposed PER-CMADDPG method.
5.1. Simulation Settings
The multi-AUV cooperative search for the moving target problem studied in this section is as follows. The mission area is defined as a 1000 m × 1000 m square, divided into 10 × 10 cells, with each cell having a side length of 100 m. At the initial time, the prior information of the mission area is missing, and the target existence probability in each cell is set to 0.5, the uncertainty value is set to 1, and the environment search map value is set to 0. To evaluate the proposed PER-CMADDPG method’s performance under different cluster scales, the number of individuals in the multi-AUV cluster system is set to 3, 6 and 9, while the number of moving targets is fixed at 6. To analyze the influence of the AUV speed, the speed of the AUV is set to 1 m/s, 2 m/s, and 3 m/s, while the speed of moving targets is fixed at 2 m/s. In addition, since the sonar detection radius is an important factor influencing multi-AUV cooperative search performance, its effect is analyzed by setting it to 100 m, 200 m, and 300 m. The true detection probability and false alarm probability are set to 0.7 and 0.3, respectively. The communication radius of each AUV is 500 m, and the safety distance is set to 100 m. The other simulation parameters are listed in Table 2.

Table 2.
Simulation parameters.
The simulation environment setting is as follows: CPU Intel Core i9-14900HX 2.20 GHz; GPU NVIDIA GeForce RTX 4070, RAM 32 GB. The simulation programs are developed based on Python 3.12 and PyTorch 2.6.0.
5.2. Result Analysis
5.2.1. Performance Analysis of the PER-CMADDPG Method
This section compares the performance of the MADDPG, convolutional multi-agent deep deterministic policy gradient (CMADDPG), and PER-CMADDPG methods. Figure 5 illustrates the reward curves of different methods. The results shown in Figure 5 are obtained from a multi-AUV cooperative search for the moving target mission, in which six AUVs are used for detecting six moving targets within a 1000 m × 1000 m mission area. The speed of the AUV and the moving target is set to 2 m/s. The sonar detection radius is set to 200 m, and the communication radius is set to 500 m.
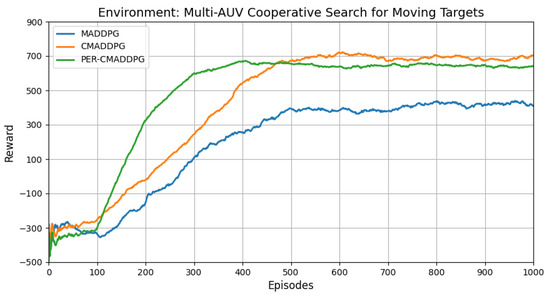
Figure 5.
The reward curves of different methods.
As shown in Figure 5, the rewards obtained using the CMADDPG and PER-CMADDPG methods are much higher than those obtained by the MADDPG method. This is because CNNs can more effectively extract the spatial features of states and observations, thereby providing better guidance for agent motion. Moreover, the PER-CMADDPG method converges the fastest, requiring only about 400 episodes, whereas the MADDPG and CMADDPG methods converge at approximately 750 and 690 episodes, respectively. This improvement can be attributed to the introduction of PER, which enables the agent to learn high-value samples first and thus accelerates the training process.To ensure that the experience replay buffer contains sufficient data before agent training, random actions are executed during the first 100 episodes to collect enough experiences. Training of the agents begins after these 100 episodes.
5.2.2. Influence of Environmental Parameters
(1) Influence of the multi-AUV cluster system scale
To evaluate the influence of the scale of the multi-AUV cluster system on the performance of the PER-CMADDPG method, this section sets the number of individuals in the multi-AUV cluster system to three, six, and nine, while the number of moving targets is fixed at six. The speeds of both the multi-AUV cluster system and the moving targets are set to 2 m/s. The sonar detection radius is fixed at 200 m. The performance of the PER-CMADDPG method is observed in five different scenarios. Table 3 gives the experimental results under different multi-AUV cluster system scales. For a clearer and more intuitive comparison, the data presented in Table 3 are visualized in Figure 6.

Table 3.
Experimental results under different multi-AUV cluster system scales.

Figure 6.
Experimental result curves under different multi-AUV cluster system scales.
As shown in Figure 6, with an increase in the number of individuals in the multi-AUV cluster system, both the number of detected targets and the exploration rate increase, while environmental uncertainty decreases. When the number of individuals in the multi-AUV cluster system is three, it fails to detect all targets in the environment. In contrast, when the number of individuals in the multi-AUV cluster system is six or nine, all targets can be successfully detected. From the perspective of improving the exploration rate and reducing uncertainty, larger cluster scales generally achieve better performance. However, considering both the number of detected targets and economic efficiency, a cluster scale of six AUVs represents a reasonable choice for the multi-AUV cooperative search for the moving target problem studied in this section.
(2) Influence of the AUV speed.
To explore the influence of the AUV speed on the performance of the PER-CMADDPG method, experiments are conducted with AUV speeds as set to 1 m/s, 2 m/s, and 3 m/s, while the speed of the moving targets is fixed at 2 m/s. The number of individuals in both the multi-AUV cluster system and moving targets is set to six, and the sonar detection radius is fixed at 200 m. The performance of the PER-CMADDPG method is observed in five different scenarios. Table 4 presents the performance of the PER-CMADDPG method under different AUV speeds. To facilitate a more intuitive understanding, the data in Table 4 are illustrated in Figure 7.

Table 4.
Experimental results under different AUV speeds.

Figure 7.
Experimental result curves under different AUV speeds.
As shown in Figure 7, with the increase in AUV speed, the number of detected targets rises, and the exploration rate improves. When the AUV speed increases from 1 m/s to 2 m/s, the average uncertainty decreases significantly from 54.5474 to 39.0417. However, a further increase from 2 m/s to 3 m/s results in a slight rise in average uncertainty from 39.0417 to 39.3437. This is because higher speeds enhance the mobility of the multi-AUV cluster system, enabling them to cover a wider area within the same time period. However, increased mobility also reduces the duration within which an AUV can continuously monitor a specific region, which results in a slight rise in uncertainty values at speeds of 3 m/s compared with that at 2 m/s. For the mission scenario considered in this paper, from the perspective of detecting moving targets, an AUV speed of either 2 m/s or 3 m/s is sufficient for meeting mission requirements. If greater exploration capability of the mission area is desired, a speed of 3 m/s is recommended.
(3) Influence of the sonar detection radius
To assess the influence of the sonar detection radius on the performance of the PER-CMADDPG method, experiments are conducted with the sonar detection radius set at 100 m, 200 m, and 300 m. The speeds of both the multi-AUV cluster system and the moving targets are set to 2 m/s. The numbers of both the multi-AUV cluster system and moving targets are set to six. The performance of the PER-CMADDPG method is observed in five different scenarios. Table 5 gives the performance of the PER-CMADDPG method under different sonar detection radii. For a more intuitive presentation of the results, the data in Table 5 are plotted in Figure 8.

Table 5.
Experimental results under different sonar detection radii.

Figure 8.
Experimental result curves under different sonar detection radii.
As shown in Figure 8, when the sonar detection radius is 200 m, the multi-AUV cluster system can detect all targets in the mission area, and uncertainty reaches its lowest level. When the sonar detection radius is increased to 300 m, the coverage of the multi-AUV cluster system becomes the maximum. This is because, with a larger detection radius, certain regions are simultaneously detected by multiple AUVs. Owing to the inherent detection probability and false alarm probability of the equipped sonar, erroneous information may affect the multi-AUV cluster system’s judgment of these regions. For the mission scenario considered in this section, a sonar detection radius of 200 m provides good performance.
6. Conclusions
This paper investigates the multi-AUV cooperative search for the moving target problem and proposes a convolutional multi-agent deep deterministic policy gradient method with prioritized experience replay. CNNs are integrated into the actor and critic networks to improve feature extraction from observations and states, while the PER mechanism is employed to accelerate training. The effectiveness of the proposed method was validated through comparisons with other methods, and the influences of factors such as multi-AUV cluster system scales, AUV speed, and sonar detection radius were also analyzed. Future work will consider more complex scenarios involving three-dimensional spatial motion and will focus on the problem of multi-AUV cooperative search for moving targets under conditions of limited communication.
Author Contributions
Conceptualization, L.L. and R.A.; methodology, L.L. and R.A.; software, R.A. and Z.G.; validation, Z.G. and J.G.; formal analysis, Z.G. and J.G.; writing—original draft preparation, L.L. and R.A.; writing—review and editing, L.L., R.A., Z.G. and J.G.; funding acquisition, L.L. and J.G. All authors have read and agreed to the published version of this manuscript.
Funding
This work is supported by in part by the National Key Research and Development Program (project number 2021YFC280300); the National Natural Science Foundation of China (project number 61903304); and the Fundamental Research Funds for the Central Universities, China, under project number 3102020HHZY030010.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Torabi, P.; Hemmati, A. A synchronized vessel and autonomous vehicle model for environmental monitoring: Mixed integer linear programming model and adaptive matheuristic. Comput. Oper. Res. 2025, 183, 107188. [Google Scholar] [CrossRef]
- Pervukhin, D.; Kotov, D.; Trushnikov, V. Development of a Conceptual Model for the Information and Control System of an Autonomous Underwater Vehicle for Solving Problems in the Mineral and Raw Materials Complex. Energies 2024, 17, 5916. [Google Scholar] [CrossRef]
- Richmond, K.; Haden, T.; Siegel, V.; Alexander, M.; Gulley, J.; Adame, T.; Heaton, T.; Monteleone, K.; Worl, R. Field Demonstrations of Precision Mapping and Control by the SUNFISH® AUV in Support of Marine Archaeology. In Proceedings of the OCEANS 2023-MTS/IEEE US Gulf Coast, Biloxi, MI, USA, 25–28 September 2023; pp. 1–8. [Google Scholar]
- Qin, H.; Zhou, N.; Han, S.; Xue, Y. An environment information-driven online Bi-level path planning algorithm for underwater search and rescue AUV. Ocean Eng. 2024, 296, 116949. [Google Scholar] [CrossRef]
- Gan, W.; Qiao, L. Many-Versus-Many UUV Attack-Defense Game in 3D Scenarios Using Hierarchical Multi-Agent Reinforcement Learning. IEEE Internet Things J. 2025, 12, 23479–23494. [Google Scholar] [CrossRef]
- Wang, T.; Peng, X.; Hu, H.; Xu, D. Maritime Manned/unmanned Collaborative Systems and Key Technologies: A Survey. Acta Armamentarii 2024, 45, 3317. [Google Scholar]
- Wang, Y.; Liu, K.; Geng, L.; Zhang, S. Knowledge hierarchy-based dynamic multi-objective optimization method for AUV path planning in cooperative search missions. Ocean Eng. 2024, 312, 119267. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Y.; Zou, Z.; Yu, Q.; Zhang, Z.; Sun, Q. Multi-AUV underwater static target search method based on consensus-based bundle algorithm and improved Glasius bio-inspired neural network. Inf. Sci. 2024, 673, 120684. [Google Scholar] [CrossRef]
- You, Y.; Xing, W.; Xie, F.; Yao, Y. Multi-AUV Static Target Search Based on Improved PSO. In Proceedings of the 2023 8th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Singapore, 16–18 June 2023; pp. 84–90. [Google Scholar]
- Wang, G.; Wei, F.; Jiang, Y.; Zhao, M.; Wang, K.; Qi, H. A multi-auv maritime target search method for moving and invisible objects based on multi-agent deep reinforcement learning. Sensors 2022, 22, 8562. [Google Scholar] [CrossRef]
- Karthikeyan, R.; Rani, B.S. An innovative approach for obstacle avoidance and path planning of mobile robot using adaptive deep reinforcement learning for indoor environment. Knowl.-Based Syst. 2025, 326, 114058. [Google Scholar] [CrossRef]
- Kuo, P.H.; Chen, K.L.; Lin, Y.S.; Chiu, Y.C.; Peng, C.C. Deep reinforcement learning–based collision avoidance strategy for multiple unmanned aerial vehicles. Eng. Appl. Artif. Intell. 2025, 160, 111862. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Q. Online Unmanned Ground Vehicle Path Planning Based on Multi-Attribute Intelligent Reinforcement Learning for Mine Search and Rescue. Appl. Sci. 2024, 14, 9127. [Google Scholar] [CrossRef]
- Liu, T.; Hu, Y.; Xu, H. Deep reinforcement learning for vectored thruster autonomous underwater vehicle control. Complexity 2021, 2021, 6649625. [Google Scholar] [CrossRef]
- Ren, H.; Gao, J.; Gao, L.; Wang, J.; He, J.; Li, S. Reinforcement Learning based Hovering Control of a Buoyancy Driven Unmanned Underwater Vehicle with Discrete Inputs. In Proceedings of the 2025 10th International Conference on Control and Robotics Engineering (ICCRE), Nagoya, Japan, 9–11 May 2025; pp. 165–170. [Google Scholar]
- Lin, Y.H.; Chiang, C.H.; Yu, C.M.; Huang, J.Y.T. Intelligent docking control of autonomous underwater vehicles using deep reinforcement learning and a digital twin system. Expert Syst. Appl. 2026, 296, 129085. [Google Scholar] [CrossRef]
- Hu, J.; Xie, L.; Lum, K.Y.; Xu, J. Multiagent information fusion and cooperative control in target search. IEEE Trans. Control Syst. Technol. 2012, 21, 1223–1235. [Google Scholar] [CrossRef]
- Ji, H.; Yao, J.; Pei, C.; Liang, H. Collaborative target search for multiple UAVs based on collaborative particle swarm optimization genetic algorithm. In International Conference on Autonomous Unmanned Systems; Springer: Berlin/Heidelberg, Germany, 2021; pp. 900–909. [Google Scholar]
- Lu, J.; Jiang, J.; Han, B.; Liu, J.; Lu, X. Dynamic target search of UAV swarm based on improved pigeon-inspired optimization. In 2021 5th Chinese Conference on Swarm Intelligence and Cooperative Control; Springer: Berlin/Heidelberg, Germany, 2022; pp. 361–371. [Google Scholar]
- Yue, W.; Xin, H.; Lin, B.; Liu, Z.C.; Li, L.L. Path planning of MAUV cooperative search for multi-intelligent targets. Kongzhi Lilun Yu Yingyong/Control Theory Appl. 2022, 39, 2065–2073. [Google Scholar] [CrossRef]
- Jiang, Z.; Sun, X.; Wang, W.; Zhou, S.; Li, Q.; Da, L. Path planning method for maritime dynamic target search based on improved GBNN. Complex Intell. Syst. 2025, 11, 296. [Google Scholar] [CrossRef]
- Zhang, B.; Lin, X.; Zhu, Y.; Tian, J.; Zhu, Z. Enhancing multi-UAV reconnaissance and search through double critic DDPG with belief probability maps. IEEE Trans. Intell. Veh. 2024, 9, 3827–3842. [Google Scholar] [CrossRef]
- Wu, J.; Luo, J.; Jiang, C.; Gao, L. A multi-agent deep reinforcement learning approach for multi-UAV cooperative search in multi-layered aerial computing networks. IEEE Internet Things J. 2024, 12, 5807–5821. [Google Scholar] [CrossRef]
- Song, R.; Gao, S.; Li, Y. A novel approach to multi-USV cooperative search in unknown dynamic marine environment using reinforcement learning. Neural Comput. Appl. 2024, 37, 16055–16070. [Google Scholar] [CrossRef]
- Li, Y.; Ma, M.; Cao, J.; Luo, G.; Wang, D.; Chen, W. A method for multi-AUV cooperative area search in unknown environment based on reinforcement learning. J. Mar. Sci. Eng. 2024, 12, 1194. [Google Scholar] [CrossRef]
- Tan, M. Multi-agent reinforcement learning: Independent vs. cooperative agents. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 June 1993; pp. 330–337. [Google Scholar]
- De Witt, C.S.; Gupta, T.; Makoviichuk, D.; Makoviychuk, V.; Torr, P.H.; Sun, M.; Whiteson, S. Is independent learning all you need in the starcraft multi-agent challenge? arXiv 2020, arXiv:2011.09533. [Google Scholar]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-decomposition networks for cooperative multi-agent learning. arXiv 2017, arXiv:1706.05296. [Google Scholar]
- Rashid, T.; Samvelyan, M.; De Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. Monotonic value function factorisation for deep multi-agent reinforcement learning. J. Mach. Learn. Res. 2020, 21, 1–51. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6380–6391. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Su, K.; Qian, F. Multi-UAV cooperative searching and tracking for moving targets based on multi-agent reinforcement learning. Appl. Sci. 2023, 13, 11905. [Google Scholar] [CrossRef]
- Yang, T.; Chi, Q.; Xu, N.; Bai, J.; Wei, W.; Chen, H.; Wu, H.; Yao, Z.; Chen, W.; Lin, Y. Integrating deep Q-networks, convolutional neural networks, and artificial potential fields for enhanced search path planning of unmanned surface vessels. Ocean Eng. 2025, 335, 121338. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).