Pursuing Optimization Using Multimodal Transportation System: A Strategic Approach to Minimizing Costs and CO₂ Emissions

Abstract

The core problem of a multimodal transportation system is integrating various transportation modes into a cohesive, efficient, and user-friendly network. This study introduces a novel centralized load concentration approach for regions facing geographic challenges. The principal aim is improving multimodal transportation systems by mitigating CO₂ emissions and improving operational efficiency. This will significantly reduce high logistics costs and the environmental impact caused by greenhouse gas emissions, particularly in land transportation, aligning with the global sustainable development goals and offering a promising path towards a more sustainable future. The proposed method implicates direct cargo transportation from its origin to the export ports without passing through intermediate centers. The mathematical model determines the most efficient means of transportation for each route, considering variables such as distance, volume, and type of cargo. Research results indicate that multiple hubs may not be necessary in scenarios with high freight concentration, which could streamline transportation and logistics operations. The modal preferences vary depending on regional dynamics and cargo characteristics, with rail and sea transport emerging as preferable options in specific circumstances, outperforming road transport. The proposed model shows reductions in logistics costs and CO₂ emissions compared to road-focused scenarios. This study provides an adaptable framework for optimizing multimodal transportation systems in regions with similar geographic and logistical attributes. It offers a versatile solution to various contexts and needs. Lastly, the strategic integration of multiple modes of transportation is fundamental to improving efficiency and sustainability.

1. Introduction

Addressing emissions in the transportation sector is essential, and the optimization of its structure has emerged as a pivotal strategy toward achieving this. According to the International Energy Agency, in 2018, emissions from transportation constituted 25% of global emissions [1]. Without effective interventions, projections suggest that this figure could escalate to 30% by 2030 and 50% by 2050 [2]. Notably, despite road transport representing over 70% of total transportation, its carbon intensity exceeds that of rail transport by fourfold and that of inland waterway transport by tenfold [2].

In the domain of multimodal port transportation, the strategic placement of hubs emerges as a critical factor for cargo consolidation, optimizing both time and operating costs and contributing significantly to reducing CO₂ emissions. This approach not only fortifies linkages between importing/exporting entities and port terminals, thereby bolstering their competitiveness and customer satisfaction [3], but also plays a pivotal role in crafting efficient supply chain networks and multimodal transportation systems. These networks, modeled on a hub-and-spoke paradigm, centralize operations and facilitate the transshipment, consolidation, and sorting of cargo [4], achieving economies of scale and optimizing variable transportation costs. Such optimization improves shipping capabilities concerning weight, volume, accessibility, and transit times [5]. Moreover, this structured approach fosters cargo mobility, slashes greenhouse gas emissions, and augments efficiency in long-haul transportation, amplifying the advantages of local transportation [5,6,7].

The embrace of multimodal transportation hinges on several factors, including geographical attributes, the allocation of public funds, and effective coordination among ports. This decision necessitates a comprehensive evaluation of the pros and cons inherent in each transportation mode [8]. Despite entailing substantial upfront investments, the multimodal system stands out for its operational efficiency and reduced environmental impact, outstripping the advantages of solely land-based transportation. This preference is substantiated by its capability to curtail greenhouse gas emissions and preserve road infrastructure due to the alleviated burden on truck traffic [9].

The allocation and distribution of cargo in mathematical models have been widely studied in the literature. These models encompass location and routing schemes crucial for optimizing transport in multimodal ports. Notably, the Vehicle Routing Problem (VRP) and its variants, such as the Capacitated Vehicle Routing Problem (CVRP), have been extensively studied [10]. The CVRP involves a fleet of homogeneous vehicles with limited capacity, while an extension, the Vehicle Routing Problem with Time Windows (VRPTW), focuses on deliveries within predefined time windows [11]. Unlike the Traveling Salesman Problem (TSP), where a single vehicle visits all points in the network, in the VRP, each vehicle serves a specific subset of points, adding complexity to the problem [12]. The VRP is a common application in distributing goods and end products from factories to multiple customers, utilizing a fleet of vehicles without intermediate storage [13]. However, integrating intermediate warehouses into logistics network design, known as the Capacitated Locations Routing Problem (CLRP), can significantly enhance efficiency [14]. The CLRP, combining the Facility Location Problem (FLP) with the VRP [15], presents a complex logistical challenge in supply chain management, involving the selection of distribution centers; customer assignment; and the determination of optimal delivery sequences to minimize total costs, including distribution and depot location [16].

In the field of route optimization in port contexts, various methods have been deployed to enhance operational efficiency. Deep reinforcement learning has been utilized to minimize empty truck trips, while genetic algorithms and greedy-type heuristics have aided in reducing bottlenecks and pollutant emissions [17,18]. Additionally, the amalgamation of Monte Carlo simulation with linear programming has proven effective in curtailing carbon footprints [19,20].

1.1. Contribution

This study introduces a new multimodal transportation model tailored to the geographic characteristics of Chile, a country that extends 4270 km in length with width variations between 445 and 90 km. Based on research by [13], the model responds to high freight concentrations in the central zone, where traditional hub models prove ineffective.

The principal contribution of this research is the direct transportation of cargo from its origin to export ports, thus eliminating the necessity for intermediate hubs. This strategy represents a redefinition of traditional multimodal transportation approaches and their adaptation to the specific characteristics of Chile. A modified hub-and-spoke model has been developed that integrates new variables for different types of cargo and distinguishes between concentration and consolidation hubs. This new formulation has been demonstrated to markedly enhance cargo handling efficiency, reducing logistics costs and CO₂ emissions by 70% and 81%, respectively.

This approach not only offers substantial economic and environmental benefits but also contributes to the Sustainable Development Goals. Its implementation in Chilean ports could provide logistics stakeholders with a valuable tool to enhance transport efficiency and sustainability. The adaptability of the model indicates its potential applicability in other regions with similar geographical and logistical challenges.

Furthermore, this study establishes a precedent for the adaptation of logistics models in countries with similar geographic constraints. The inclusion of integer variables in a quadratic formulation optimizes the model, ensuring that each scenario is handled optimally, which represents a significant contribution to global sustainable development initiatives. This modified model, which incorporates four load types and distinguishes between concentration and distribution hubs, improves upon the classic formulation documented by O’Kelly [21], which generally did not differentiate between load types and hub types.

1.2. Motivation

The present study centers on optimizing transportation routes within Chilean ports, aligning with strategic objectives outlined by the Chilean government. This strategic approach aims to strengthen national export and import logistics chains by 2030, highlighting the necessity of adapting to global sustainability trends while tackling existing challenges within freight transportation. Notably, in 2021, logistics costs in Chile constituted 18% of the GDP, a figure markedly higher than the OECD average of 9% [22]. In response to this scenario, the Chilean government’s Budget Directorate has been promoting innovation in research and development to enhance the country’s productivity, competitiveness, and diversification of production [23]. Furthermore, the Chilean Economic Development Agency identified deficiencies in the intermodal network as early as 2017, thereby driving initiatives aimed at fostering smarter port infrastructure development [24].

The aim is to answer key questions:

• What are the factors that influence the choice of transportation mode for cargo transshipment and temporary storage warehouses in the route from the south of the country to the ports of San Antonio and Valparaiso?
• How does the optimization model affect the costs and emissions associated with transshipment and temporary storage facilities along the route?
• What are the potential benefits and challenges of locating transshipment and temporary storage facilities in different locations?

This study provides a methodological framework to answer the research questions posed, focusing on adapting existing transportation models to Chile’s particularities and specific needs.

In the global context, the European Union’s study emphasizes the significance of multimodal transportation, predicting a possible 40% decrease in greenhouse gas emissions by 2030 in comparison to 1990 [25]. Additionally, Elbert et al.  [8] underscores the significance of multimodal transportation, delineating its three integral segments: collection, main transportation, and distribution within logistics frameworks. In addition, Liu [26] examines the complexities of the Chinese agricultural transportation system. His findings indicate that traffic congestion results in a 20% increase in carbon emissions. This highlights the significance of optimizing routes for cold chain containers to reduce the adverse consequences.

This research is structured into several sections: Section 1 introduces the study’s context, contribution, and motivation. Section 2 covers the theoretical background, providing a description of the transportation network in Chile and an exhaustive literature review. Section 3 details the materials and methods used. Section 3.1 details the optimization modeling. Section 3.2 is dedicated to the practical application development of the study. Finally, Section 4 and Section 5 present the results, discuss the findings, and provide the conclusions of the research.

2. Background

2.1. Description of System

Chile’s transportation network is a linchpin of its open economy, constituting 11.7% of GDP in 2022, encompassing roads, railways, and coastal shipping. In 2023, cargo distribution comprised solid bulk (47%), liquid bulk (22%), general cargo containers (24%), refrigerated cargo (4.4%), and other types (2.6%) [27]. These goods traverse a comprehensive network of land, rail, and maritime infrastructure to reach public and private ports, which collectively manage 96.4% of the country’s imports and exports [27]. Despite its pivotal role, multimodal transportation remains underdeveloped compared to individual modes.

Chile boasts 3570 km of paved dual-carriageway roads and a total road network spanning 28,700 km, with 15,441 km being asphalted [28]. Additionally, its national road infrastructure extends to 88,510 km [28]. The railway infrastructure, predominantly linking central zones with maritime ports, plays a pivotal role in facilitating the transportation of a wide array of cargo.

Regarding port infrastructure, Chile harbors 56 ports, comprising 10 state-owned public ports, 14 privately-owned public ports, and 32 private ports. Among them, the ports of Valparaíso, featuring 8 docking sites across 5 docks, and San Antonio, with 3 docks and 8 docking sites, hold prominence in this study [29]. Seven out of the ten state-owned port companies operate under active concession contracts [30].

The country’s domestic transportation primarily relies on road, rail, and coastal shipping, with 88% of tonnage destined for international trade and 12% for the domestic market [31]. Containerized cargo is distributed as follows: 42.7% in imports, 45.1% in exports, 8.6% in transit, and 3.4% in coastal shipping, mobilizing 12% of domestic trade in containers [32]. Major cargo types include solid waste, cellulose, copper concentrate, general cargo containers, metallic copper, and agricultural products, among others, transported from production and distribution centers to port facilities.

In Figure 1a,b, the percentages by type of cargo for the ports of San Antonio and Valparaíso are shown.

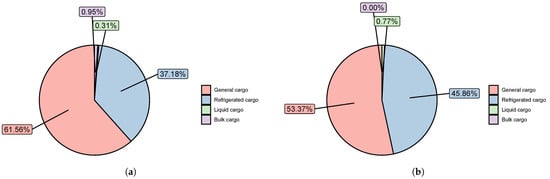
Figure 1. Types of cargo from origin to port. (a) San Antonio Port. (b) Valparaíso Port.

2.2. Related Works

To understand how to model routes in freight transport networks considering port and multimodal limitations, optimize the location of distribution centers with a space-time approach, and comprehend the challenges and decisions related to reducing pollutant emissions and logistic inefficiencies, an exhaustive literature review was conducted using the Web of Science and SCOPUS databases. The query used was: (TS=((“Freight transport” or “Logistics planning” or “Route optimization” or “Freight consolidation”) and (“Multimodal” or “transport optimization” or “Transport network”) and (“port”)). The resulting research from the search was qualitatively analyzed, selecting those presented in Table 1.

Table 1. Limitations and contributions of multimodal transportation networks.

Author	Method/Model/Technique	Limitations	Contributions
Transport industry:
[5]	Multi-objective planning model	Exploring model applicability in various regions, incorporating diverse transport modes, and managing dynamic supply chain and logistics uncertainties are essential areas for research.	Rail transport is the most efficient mode for long distances, surpassing other methods in terms of cost and carbon emissions.
[33]	Mathematical modeling to design service schedules for synchromodal freight transport systems.	Examines a case of the Port of Rotterdam hinterland network, limiting generalizability. The study lacks information on barriers to synchromodal freight transport systems.	Improved performance of the intermodal freight system, achieving cost savings equivalent to a reduction of more than 20%.
[34]	SynchroMO algorithm	The study of the Port of Rotterdam hinterland network could limit the results’ relevance. Analysis is required for infrastructure, stakeholder collaboration, and regulations.	It allows simulations and comparisons to be made between different routes and schedules, depending on the goods transiting the Rotterdam hinterland container transport.
[35]	Genetic algorithm	The study examines 10 regional capitals in Ghana, limiting generalizability. The genetic algorithm model considers time, distance, and CO2 emissions but overlooks other sustainability factors.	By optimizing the system, total cost savings were achieved, representing a reduction of 4.5% compared to the same amount of cargo transported with the traditional system.
[36]	ArcGIS and event model	The research centers on GIS modeling of freight transportation and logistics in Russia. It does not mention the specific event model employed or the constraints of the GIS model. The absence of exploration into potential biases of the data utilized.	Optimizes the planning and coordination of the transportation and logistics system in the city of St. Petersburg, thus improving regional connectivity within Europe.
[37]	Stochastic integer programming model	The paper presents an optimization model for load allocation in synchromodal transport but lacks detailed information on solution techniques, focuses on a specific problem, and lacks assumptions in the model.	Improves sustainability, increases flexibility, and reduces costs, among other benefits, in the field of freight transportation.
[38]	Multi-objective optimization and genetic algorithm	The investigation focuses on transportation cost, fixed cost, and CO2 emissions while overlooking social impacts, land use, and noise pollution factors. Challenges and limitations in applying the model for real-world decisions are not analyzed.	Inland ports are positioned in a multimodal freight transport network to optimize transport and operational costs while lowering CO2 emissions. The growth of inland ports is linked to cost and emission reductions.
[39]	Multimodal environment evaluation tool (MEET)	The study examines how modal shifts in Shenzhen affect air quality without considering social impacts, land use changes, or noise pollution. More research is required to assess the success of accompanying strategies and measure extra advantages.	Replacing road transport with sustainable options such as rail and river transport can benefit port cities in terms of transport efficiency and environmental quality. Stricter emission standards for vehicles can improve air quality by reducing NOX and O3 levels.
[40]	Data envelopment analysis (DEA) model	The research explores carbon emissions efficiency of rail–water intermodal transport in China, but findings may not be generalizable. It concentrates on CO2 emissions and overlooks other environmental impacts or pollutants.	Evaluates the carbon emission efficiency of rail–water intermodal transport in 14 Chinese ports, facilitating sustainable transport planning and decision making.
[41]	Multi-objective optimization	The research on a European port freight transport network may limit generalizability. Other factors like infrastructural constraints and regulatory policies could affect CO2 emissions and logistics costs balance.	Examines the relationship between logistics costs and CO2 emissions in various freight transport networks. Evaluates the effects of changing modes and routes on the balance between costs and emissions, emphasizing the role of the demands and capacities of the freight transport system.
[42]	Integrates Dijkstra’s algorithm and a pattern search algorithm in a bi-level programming model	It is necessary to examine the risks of implementing the subsidy mechanism in the various transport and logistics planning modes. Further analysis is required to understand the proposal’s economic, social, environmental, and political effects.	Utilizes Yangtze River data to optimize China Railway Express freight subsidy system in multimodal transportation setup, improving decision-making and policy development for sustainable transport. Sets specific intervals for adjusting unit subsidy based on the transported cargo type.
Industria Portuaria
[43]	Linear optimization	An in-depth examination of transport strategies, associated risks, and subsidy mechanisms implications is needed. Real-world uncertainties like personnel performance in port operations and current regulations must be evaluated.	Examines carbon reduction methods in supply chains of London Gateway, studying alternative ports and transport modes like short sea shipping. Decreasing travel distances and CO2 e emissions leads to lower costs.
[44]	Logistic regression model	The logistic regression model of the case study needs to study service reliability and environmental impact to improve the effectiveness of the service design.	Optimizing SSS services in intermodal transport chains involves designing the optimal vessel size based on demand estimation. A case study of a Ro-Pax service in Portugal shows how design adjustments can improve economic performance.
[45]	Stochastic network assignment model and global logistics intermodal network simulation model	The model neglects external factors like politics or economics affecting logistics flow. Simulation results are restricted by data availability and accuracy for comparison with observed flows.	Evaluates logistics infrastructure policies in the Greater Mekong subregion of Myanmar and tests various scenarios to determine their effects on goods movement and container traffic. Analyzes the environmental and economic impact of increased truck speed and the opening of the Dawei port on transport modes.
[46]	Two-stage stochastic mixed integer model (MIP)	Lack of consideration of weather conditions, port congestion, and labor availability, which affects throughput and operating costs. More accurate costing is required for various scenarios and terminals.	Examines how uncertainty affects barge transportation by analyzing real data from a land terminal and evaluating long-term performance through simulated weekly operations for one year. Creates a stochastic program for transportation planning that demonstrates that uncertainty can influence total costs.
[47]	Interport Model (network programming tool)	The model examines the rationality of economic agents and perfect competition. Studying the uncertainty of factors such as container demand, costs, capacity constraints, and regulatory changes is convenient.	Investigates the link between sustainability and container logistics in Campania ports. Examines the impact of policies and measures on the competitiveness and sustainability of container distribution. Emphasizes the reduction of transport costs and suggests public and private strategies for green transport.

Table 1 illustrates the main applications of multimodal transportation in the transportation and port industry, revealing a variety of employed mathematical models. However, these models focus on specific aspects and do not address the vehicle routing problem, such as the Vehicle Routing Problem (VRP), its variants like the Capacitated Vehicle Routing Problem (CVRP) [10], or the hub and spoke model, utilized in this study [13,21].

A review of the literature on multimodal transportation systems reveals a significant advance in the applied methodology compared to traditional approaches. This integration of complex logistics management tailored to specific needs represents a notable advancement. However, studies such as those by Dini et al. [48] and Yang et al. [49] have developed models that, while simplifying real-world complexities, may compromise the optimality of the proposed solutions. For instance, the model proposed by Dini et al. [48] significantly reduces the number of routes analyzed from 59 to only 6. Similarly, Yang et al. [49] employ a two-level genetic algorithm to specifically handle time windows in container transport.

Furthermore, Hu et al. [50] investigate the impact of economic and regulatory factors, such as regulatory costs and carbon taxes, on environmental sustainability and economic efficiency. They propose a balanced approach that aligns incentives for cost and emission reductions. However, the effectiveness of these models may depend on alignment among stakeholders. Conversely, Ge and Sun [51] address uncertainties in transportation networks using a fuzzy optimization model. While seeking practical solvability through a linear reformulation, this approach may lose optimality due to the assumption of independence among variables.

In contrast, our research employs a more holistic and direct approach, considering all possible routes, nodes, and hubs without reducing or simplifying the model. This method not only preserves the integrity and depth of the analysis but also improves the accuracy of route selection and maximizes both cost efficiency and environmental sustainability. This approach provides a robust framework for logistics management in complex multimodal transportation scenarios.

3. Materials and Methods

The methodological framework used in this study follows a structured sequence of steps typical of operations research in transportation logistics:

• Identify the research motivation, which is rooted in addressing a national logistics problem.
• Exploration of possible solutions to the problem and the decision to use a mathematical optimization model.
• Review and analyze various mathematical models, including the Capacitated Vehicle Routing Problem (CVRP) and discrete simulation, and compare how similar problems have been addressed in other regional contexts.
• Select the Hub and Spoke model as the most appropriate framework for this study.
• Collect freight data categorized by freight type and distances between cities and ports, with a focus on consolidating these data by freight type and mode.
• Conceptual design and development of the mathematical model, followed by its implementation using the GAMS programming language.
• Programming of several model formulations and iterative runs to derive the optimal solution.
• Analysis and discussion of the results, including further adjustments based on sensitivity analysis and additional calculations.

3.1. Optimization Modeling

3.1.1. Model Assumptions

This study employed classical optimization due to its ability to generate interpretable and transparent solutions. It is suitable in scenarios with limited data where machine learning methods are not applicable due to the lack of high-quality data. Classical optimization, efficient due to its simplicity and lower demand for computational resources, proves to be particularly effective compared to techniques such as deep learning in contexts with clear deterministic rules, providing analytical solutions without the need for large volumes of information.

A mathematical model is used to determine the distribution of loads and warehouses, identifying concentration and distribution nodes, as shown in the conceptual diagram of the multimodal system in Figure 2. The diagram illustrates the conceptual organization of the mathematical model. On the left, cities from the center to the south of the country are shown within a rectangle, indicating the origin points for cargo headed towards central zone ports. The ports of San Antonio and Valparaiso are depicted on the right within a square. The diagram is centered on two ellipses representing potential intermediate nodes. The left ellipse symbolizes a potential cargo consolidation node, where various cargo types such as general, bulk, and liquid can be integrated to exploit economies of scale. This is done by factoring in both investment and annual operational costs within the model. The right ellipse suggests a potential cargo distribution node, tasked with deconsolidating and forwarding cargo received via road, rail, or ship to the ports.

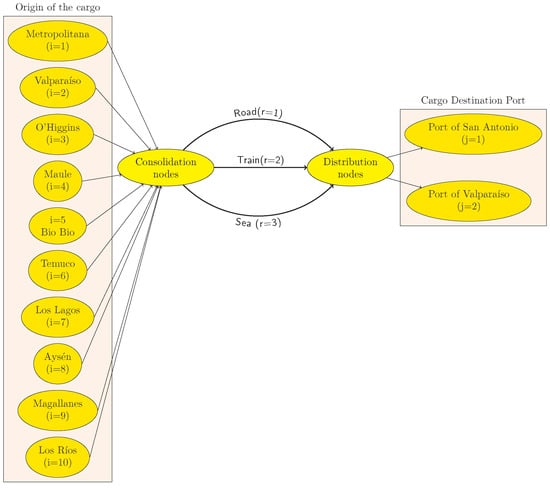
Figure 2. Conceptual diagram multimodal system.

The model employs binary decision variables $z_1$ and $z_2$ to determine the use of consolidation ($z_1$) and distribution ($z_2$) nodes, respectively. Additionally, it utilizes binary variables $y_0$, $y_k$, $y_m$, and $y_{km}$, each representing different system configurations. Specifically, if the model solves with $y_0=1$ (and all other y variables set to 0), this indicates the optimal route is direct shipment from the origin to the destination ports without intermediate nodes. Conversely, if $y_k=1$ (with $y_m=y_{km}=0$), this indicates that a consolidation node should be used to aggregate cargo before shipping it to the ports. If $y_m$ = 1 (with $y_0$ = $y_k$ = $y_{km}$ = 0), it indicates that a single distribution node is optimal, directing cargo from this node to the ports. In the event that $y_{km}=1$ (with $y_0=y_k=y_m=0$), the cargo is consolidated and subsequently routed through a distribution node to the ports.

The objective function comprises 6 terms, reflecting different cost elements associated with node operations. The term with $y_0$ represents the cost when bypassing both consolidation and distribution nodes. The term with $y_k$ adds the transportation cost associated with using a consolidation node, factoring in the fixed costs from the initial term. The $y_m$ term accounts for the costs associated with the processing of cargo through both consolidation at the origin and distribution at the destination.

The model consists of various entities representing its indexes:

• Zones of origin of the load (index i):

  -

  Metropolitan Region, Santiago (i = 1),

  -

  Valparaíso Region, Valparaíso (i = 2),

  -

  O’Higgins Region, Rancagua (i = 3),

  -

  Maule Region, Talca (i = 4),

  -

  Bío Bío Region, Concepción (i = 5),

  -

  Temuco Region, Temuco (i = 6),

  -

  Los Lagos Region, Puerto Montt (i = 7),

  -

  General Carlos Ibáñez del Campo Region of Aysén, Coyhaique (i = 8),

  -

  Magallanes and Antarctica Chilen Region, Punta Arenas (i = 9)

  -

  Los Lagos Region, Valdivia (i = 10)

• Port cargo destination zones (index j):

  -

  San Antonio (j = 1),

  -

  Valparaíso (j = 2)

• Consolidation node installation zones (index k):

  -

  Metropolitana Region, Santiago (k = 1),

  -

  Valparaíso Region, Valparaíso (k = 2),

  -

  O’Higgins Region, Rancagua (k = 3),

  -

  Maule Region, Talca (k = 4),

  -

  Bío Bío Region, Concepción (k = 5),

  -

  Temuco Region, Temuco (k = 6),

  -

  Los Lagos Region, Puerto Montt (k = 7),

  -

  General Carlos Ibáñez del Campo Region of Aysén, Coyhaique Region (k = 8),

  -

  Magallanes and Antarctica Chilen Region, Punta Arenas (k = 9)

  -

  Los Lagos Region, Valdivia (k = 10)

• Distribution node zones (index m)

  -

  San Antonio (m = 1),

  -

  Zeal Zone of Valparaíso (m = 2),

  -

  Midpoint between San Antonio and Valparaíso (m = 3),

  -

  Calera (m = 4)

• Modes of transport (index r):

  -

  Road (r = 1),

  -

  Train (r = 2),

  -

  Ship (r = 3)

• Type of product (index p ):

  -

  General cargo (p = 1),

  -

  Refrigerated cargo (p = 2),

  -

  Liquid cargo (p = 3),

  -

  Bulk cargo (p = 4)

Table 2 and Table 3 present the parameters and variables.

Table 2. Parameters.

Symbol	Description
$W_{ijp}$	Transport of cargo from origin node i to port of embarkation j for product type p.
$C{1}_{ik}^{pr}$	Unit cost of transport from the origin node i to the consolidation node k for product type p along route r [dollars per ton-kilometer].
$C{2}_{km}^{pr}$	Unit transport cost from consolidation node k to distribution node m for product type p on route r [dollars per ton-kilometer].
$C{3}_{mj}^{pr}$	Unit cost of transportation between distribution node m and port j for product type p along route r [dollars per ton-kilometer]
$C{4}_{im}^{pr}$	Unit transport cost from origin node i to consolidation node m for product type p via the route.
$C{5}_{kj}^{pr}$	Unit transport cost from origin node i to consolidation node m for product type p via the route r.
$C{6}_{ij}^{pr}$	Unit cost of transportation between node i and port of embarkation j for product p and route r.
$d{1}_{ik}$	Generic expression for the distance between the origin node i and the consolidation center at node k.
$d{2}_{kj}$	Generic expression for the distance from consolidation center k to destination node j.
$d{4}_{mj}$	Generic expression for the distance from consolidation center m to destination node j.
$d{6}_{km}$	Generic expression for the distance between the consolidation center k and the distribution center at node m.
$C{c}_k$	Investment for the setup, operation, and maintenance of a consolidation node.
$C{d}_m$	Investment for the setup, operation, and maintenance of a distribution node.
a	Project evaluation period.

Table 3. Variables.

Symbol	Description
$x{0}_{ij}^{pr}$	A binary variable that equals 1 if product type p is shipped directly from origin i to destination j via route r, and 0 otherwise.
$x{1}_{ik}^{pr}$	Binary variable is 1 if transport is from origin i to node k for product type p via route r, and 0 otherwise.
$x{2}_{kj}^{pr}$	Binary variable equals 1 if cargo is transported from node k to j for product type p along route r, and 0 otherwise.
$x{3}_{km}^{pr}$	Binary variable is 1 if cargo moves from consolidation node k to distribution node m for product type p via route r, and otherwise 0.
$x{4}_{mj}^{pr}$	Binary variable equal to 1 if the cargo is transported from node m to port j for product type p via route r, and 0 otherwise.
$x{5}_{kj}^{pr}$	Binary variable is 1 if cargo is transported from node k to port j for product type p via route r, and 0 otherwise.
$z{1}_k$	Binary variable that is 1 if a consolidation node is installed at node k, and 0 otherwise.
$z{2}_m$	Binary variable is 1 if a distribution node is installed at node m, and 0 otherwise.
$y_0$	Binary variable: 1 if no consolidation or distribution nodes are installed, and 0 otherwise.
$y_k$	Binary variable set to 1 for installing consolidation node at node k and distribution node at node m, and 0 otherwise.
$y_m$	A binary variable indicating 1 for a distribution node installation at node m, and 0 otherwise.
$y_{km}$	Binary variable equal to 1 if a consolidation node is installed at node k, and 0 otherwise.

3.1.2. Objective Function

The objective function integrates six terms: The first two penalize the cost of opening and operating a distribution and cargo consolidation center for 20 years. The remaining four, linked to potential solutions of the problem, incorporate binary variables (with a value of 1 if the solution is employed and 0 otherwise). For example, the third term, multiplied by the binary variable $y_0$, represents a solution that excludes distribution and consolidation nodes. The fourth term represents the interaction between a distribution center at node k and a consolidation center at node m, multiplied by the binary variable $y_k$. The fifth term refers to the solution that consolidates at a single node, k, represented by $y_m$. Finally, the sixth term implies a unique solution with a consolidation center at node m, represented by the variable $y_{km}$.

$$\begin{array}{cc}\hfill \mathrm{Min}:& \sum _{k}C{c}_k\ast z1k+\sum _{m}C{d}_m\ast z2m+\hfill \\ \hfill & y_0\ast \left(\sum _i\sum _j\sum _k\sum _m\sum _p\sum _{r}a\ast w_{ij}^{p}C{6}_{ij}^{pr}d{5}_{ij}\ast x{0}_{ij}^{pr}\right)+\hfill \\ \hfill & y_k\ast \left(\sum _i\sum _j\sum _k\sum _m\sum _p\sum _{r}a\ast w_{ij}^{p}C{1}_{ik}^{pr}d{1}_{ij}\ast x{1}_{ik}^{pr}+a\ast w_{ij}^{p}C{2}_{km}^{pr}d{6}_{km}\ast x{3}_{km}^{pr}+a\ast w_{ij}^{p}C{3}_{mj}^{pr}d{4}_{mj}\ast x{4}_{mj}^{pr}\right)+\hfill \\ \hfill & y_m\ast \left(\sum _i\sum _j\sum _k\sum _m\sum _p\sum _{r}a\ast w_{ij}^p\left(C{4}_{im}^{pr}d{3}_{im}\ast x{5}_{im}^{pr}+C{3}_{mj}^{pr}d{4}_{mj}\ast x{4}_{mj}^{pr}\right)\right)+\hfill \\ \hfill & y_{km}\ast \left(\sum _i\sum _j\sum _k\sum _m\sum _p\sum _{r}a\ast w_{ij}^p\left(C{1}_{ik}^{pr}d{1}_{ik}\ast x{1}_{ik}^{pr}+C{5}_{kj}^{pr}d{2}_{kj}\ast x{2}_{kj}^{pr}\right)\right)\hfill \end{array}$$

(1)

Subject to:

$$\begin{array}{c}{y}_0+y_k+y_m+y_{km}=1\end{array}$$

(2a)

$$\begin{array}{c}x{1}_{ik}^{pr}\le z{1}_k\forall k\end{array}$$

(2b)

$$\begin{array}{c}x{2}_{kj}^{pr}\le z{1}_k\forall k\end{array}$$

(2c)

$$\begin{array}{c}x{3}_{km}^{pr}\le z{1}_k\forall k\end{array}$$

(2d)

$$\begin{array}{c}x{3}_{km}^{pr}\le z{2}_m\forall k\end{array}$$

(2e)

$$\begin{array}{c}\sum _{k}z{1}_k\le 1\end{array}$$

(2f)

$$\begin{array}{c}\sum _{m}z{2}_m\le 1\end{array}$$

(2g)

$$\begin{array}{c}x{0}_{ij}^{pr}+x{1}_{ik}^{pr}+x{5}_{im}^{pr}=1\end{array}$$

(2h)

$$\begin{array}{c}x{0}_{ij}^{pr}\le y_0\forall i,j\end{array}$$

(2i)

$$\begin{array}{c}x{1}_{ik}^{pr}\le y_{ym}\forall i,k\end{array}$$

(2j)

$$\begin{array}{c}x{2}_{kj}^{pr}\le y_{km}\forall k,j\end{array}$$

(2k)

$$\begin{array}{c}x{3}_{km}^{pr}\le y_{km}\forall k,m\end{array}$$

(2l)

$$\begin{array}{c}x{3}_{km}^{pr}\le y_m\forall k,m\end{array}$$

(2m)

$$\begin{array}{c}x{4}_{mj}^{pr}\le y_m\forall m,j\end{array}$$

(2n)

$$\begin{array}{c}x{5}_{im}^{pr}\le y_m\forall m,i\end{array}$$

(2o)

Constraint (2a) limits the choice to a single solution among the four possible ones, represented by the variables $y_0,y_k,y_m,y_{km}$. Constraint (2b) ensures the connection from the source node i to the consolidation node k only if the latter is operational. Constraint (2c) establishes transit from consolidation node k to destination node j only if k is operational. Constraint (2d) ensures the connection of node k to m only when consolidation node k is operational. Constraint (2e) guarantees transit from node k to node m only when the latter is operational. Constraint (2f) ensures the existence of at most one distribution center. Constraint (2g) limits the number of consolidation centers to one. Constraint (2h) ensures that cargo transportation proceeds directly from the source node i to a final destination j or through consolidation nodes k or m. Constraint (2i) establishes that direct cargo transportation from i to j is feasible only if binary variable $y_0$ is one; otherwise, this route is discarded. Constraint (2j) guarantees that cargo transportation from source node i to consolidation node k is only feasible if binary variable $y_3$ is one; otherwise, this transportation is unviable. Constraints (2k) and (2l) specify that cargo can only be transported directly from k to destination node j and distribution node m, respectively, under the same condition of $y_3$ being one. Constraint (2m) determines that cargo transportation from node k to distribution node m is only allowed if $y_2$ is one, prohibiting it otherwise. Constraint (2n) ensures direct cargo transportation from node m to destination node j only when binary variable $y_2$ is one. Constraint (2o) ensures a similar condition for transportation from node i to distribution node m. If it is not one, the corresponding transportation is not allowed.

The proposed model, based on the Hub and Spoke strategy and without a predefined value of p, overcomes the limitations of a fixed number of hubs, providing flexibility in the allocation of stations for cargo consolidation or deconsolidation. This adaptability is evidenced in Figure 2, where two optional hubs are highlighted, whose selection depends on factors such as cargo, costs, and distances. Given Chile’s elongated geography, it is suggested that these hubs be located in strategic regions: one in the central-south and another in a central area close to the main ports.

3.2. Data for the Chilean Multimodal System

3.2.1. Freight Transport Data: Distances and Volumes

Table 4 and Table 5 present the 2019 TEU loads transported from regional cities to the ports of San Antonio and Valparaíso, respectively [52].

Table 4. Cargo transportation from origins to San Antonio Port [TEUS] [52].

ID	Region, Capital City	General	Refrigerated	Liquid	Granel
1	Metropolitan Region, Santiago	7,543,212	640,633	15,897	17,683
2	Valparaíso Region, Valparaíso	880,155	1,153,233	19,576	0
3	O’Higgins Region, Rancagua	1,491,447	3,949,870	6456	0
4	Maule Region, Talca	2,457,589	1,545,269	22,395	0
5	Bío Bío Region, Concepción	320,855	48,966	144	179,314
6	Temuco Region, Temuco	4345	58,460	0	0
7	Los Lagos Region, Puerto Montt	27,845	48,016	0	0
8	General Carlos Ibáñez del Campo Region of Aysén, Coyhaique	8914	60,266	0	0
9	Magallanes and Antarctica Chilen Region	38,078	210,935	0	0
10	Los Ríos Region, Valdivia	24,358	12,794	0	0

Table 5. Cargo transportation from origins to Valparaíso Port [TEUS] [52].

ID	Region, Capital City	General	Refrigerated	Liquid	Granel
1	Metropolitan Region, Santiago	4,133,243	530,133	6408	1
2	Valparaíso Region, Valparaíso	773,020	991,239	67,241	0
3	O’Higgins Region, Rancagua	673,554	3,208,655	2836	0
4	Maule Region, Talca	809,974	749,697	15,123	45
5	Bío Bío Region, Concepción	39,073	22,206	2133	0
6	Temuco Region, Temuco	22,980	22,543	0	0
7	Los Lagos Region, Puerto Montt	7486	15,817	0	0
8	General Carlos Ibáñez del Campo Region of Aysén, Coyhaique	0	2185	0	0
9	Magallanes and Antarctica Chilen Region, Punta Arenas	531	6863	0	0
10	Los Ríos Region, Valdivia	1769	1646	0	0

Table 6, Table 7 and Table 8, I confirm. respectively, present the distances between the origin nodes and the consolidation nodes, the origin nodes, and the distribution locations, as well as between the consolidation nodes and the shipping ports.

Table 6. Distances between origin and cargo consolidation nodes ¹.

		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
ID	Region	RM 2	Valparaíso	O’Higgins	Maule	Bio Bio	Temuco	The Lakes	Aysén	Magallanes	Los Lagos
1	Metropolitan	0	116	84	257	500	690	1036	1898	3023	855
2	Valparaíso	116	0	194	367	610	800	1203	2066	3191	1023
3	O’Higgins	84	194	0	173	416	606	948	1810	2935	767
4	Maule	257	367	173	0	247	437	777	1639	2764	596
5	Bio Bio	500	610	416	247	0	305	644	1506	2632	464
6	Temuco	690	800	606	437	305	0	353	1215	1255	172
7	Los Lagos	1036	1203	948	777	644	1032	0	1042	2167	211
8	Aysén	1898	2066	1810	1639	1506	1215	1042	0	1254	1073
9	Magallanes	3023	3191	2935	2764	2632	1255	2167	1254	0	2199
10	Los Ríos	855	1023	767	596	464	172	211	1073	2199	0

¹ Calculate the distance between cities in Chile. https://sitios.cl/servicios/distancias.htm, access 26 March 2024. ² RM: Metropolitan Region.

Table 7. Distances between initial, final, and intermediate distribution nodes ¹.

ID	Origin Node 2	San Antonio 3	Valparaiso 3	Center of Gravity 4	La Calera
1	Metropolitan	117	125	121	127
2	Valparaíso	88	10	39	47
3	O’Higgins	141	98	120	208
4	Maule	265	366	315	381
5	Bio Bio	508	609	558	624
6	Temuco	698	810	754	815
7	Los Lagos	1040	1142	1091	1143
8	Aysén	1717	1818	1767	1833
9	Magallanes	3012	3123	3067	3128
10	Los Ríos	856	957	906	958

¹ Calculate distance between cities in Chile https://sitios.cl/servicios/distancias.htm, access 26 March 2024. ² Consolidation. ³ Final destination and possible distribution node. ⁴ Possible distribution node.

Table 8. Distances between potential consolidation nodes and shipping ports ¹.

Origin	San Antonio	Valparaiso (Zeal 2)
San Antonio	0	88
Valparaiso (Zeal)	88	10
Center of gravity	8	8
Calera	113	57

¹ Calculate the distance between cities in Chile https://sitios.cl/servicios/distancias.htm, access 26 March 2024. ² Logistics Support Extension Zone.

3.2.2. Costs of Different Means of Transportation

Table 9 provides a detailed account of the variable costs associated with railway transportation for cargo and containers in southern Chile. Table 10 and Table 11 offer a comprehensive overview of the unit costs associated with road and maritime transportation, respectively, categorized by cargo type [53]. All calculations are based on a fixed exchange rate of 700 CLP per dollar [54].

Table 9. Rail transportation costs for different types of cargo 2018 [ton-km]; data from [53].

Cargo	Trailer	Cost [CLP/tn-km]	Cost [dollars/tn-km]
General	Flat Trolley	24	0.03428
Refrigerated	Reefer container	26	0.03714
Liquid	Pond	25	0.03571
Granel	Bulk hopper	24	0.03428

Table 10. Road transportation costs for different types of freight 2018 [km-ton]; data from [53].

Cargo	Tractor	Cost [CLP/tn-km]	Cost[dollars/tn-km]
General	Flat	49	0.070
Refrigerated	Refrigerated	53	0.075
Liquid	Pond	52	0.074
Granel	Hopper	53	0.0757

Table 11. Maritime transportation costs for different types of cargo [tn-km] ¹.

Cargo	Storage	Cost [CLP/tn]	Cost [dollars/tn-km] 2
General	Container	145	0.007631579
Refrigerated	Container reef	175	0.009210526
Liquid	Pond	58	0.003052632
Granel	Pond	35	0.001842105

¹ Shipping cost information [53]. ² Average international trade values, calculated on the basis of the most frequent trip to Beijing, China, indicate a distance of 19,000 km.

3.2.3. Warehousing Costs

To obtain the storage costs shown in Table 12, the reference data from the Barrancas multimodal terminal are used. This terminal is primarily intended for the Costanera Espigón dock at the Port of San Antonio, which is under construction by DP World [55].

Table 12. Costanera Espigón Pier [55].

Items	Values	Units
Investment	19	millions of dollars
Warehouse capacity	250.000	TEU/año
Train capacity	600	mt de largo

4. Results

The results presented in Table 13 are derived from the data contained in Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12 and are based on the proposed mathematical model, consisting of a non-linear integer binary programming. This model employs 2369 binary variables and 6932 constraints, implemented in GAMS [56] and solved using SCIP version 3.1 [57] in the same environment through a specific MIQCP routine of SCIP.

Table 13. Optimisation results.

		San Antonio				Valparaíso
Region	Tipo	General	Reeffer	Liquid	Granel	General	Reeffer	Liquid	Granel
1 RM	Train	1	1	1	1	1	1	1	1
2 Valparaiso	Road	0	0	0	1	0	0	0	1
2 Valparaiso	Train	1	1	1	0	1	1	1	0
3 O’Higgins	Road	0	0	0	1	0	0	0	1
3 O’Higgins	Train	1	1	1	0	1	1	1	0
4 Maule	Road	0	0	0	1	0	0	0	0
4 Maule	Ship	1	1	1	0	1	1	1	1
5 Bio Bio	Road	0	0	0	0	0	0	0	1
5 Bio Bio	Ship	1	1	1	1	1	1	1	0
6 Temuco	Road	0	0	1	1	0	0	1	1
6 Temuco	Ship	1	1	0	0	1	1	0	0
7 Los Lagos	Road	0	0	1	1	0	0	1	1
7 Los Lagos	Ship	1	1	0	0	1	1	0	0
8 Aysén	Road	0	0	1	1	1	0	1	1
8 Aysén	Ship	1	1	0	0	0	1	0	0
9 Magallanes	Road	0	0	1	1	0	0	1	1
9 Magallanes	Ship	1	1	0	0	1	1	0	0
10 Los Ríos	Road	0	0	1	1	0	0	1	1
10 Los Ríos	Ship	1	1	0	0	1	1	0	0

The equations employed in the calculations for Table 14 are presented in detail below.

Table 14. Summary of the proposed solution in 20 years.

	Port	San Antonio Port				Valparaíso Port				Totals
	Type of Charge	General	Reefer	Liquid	Granel	General	Reefer	Liquid	Granel	by Region
RM	Charge in tons	7,543,212	640,633	15,897	18	4,133,243	530,133	6408	1	12,869,545
	Distances (km)	117	117	117	117	125	125	125	125
	Proposed solution in millions of USD	620.9	57.1	1.4	0.0	362.9	50.4	0.6	0.0	1093.3
	Actual solution in millions of USD	1251.4	113.9	2.8	0.0	732.0	100.6	1.2	0.0	2201.9
	Savings with the proposed solution in millions of USD	630.5	56.8	1.4	0.0	369.1	50.2	0.6	0.0	1108.6
	Savings in dollars per ton-km	0.7	0.8	0.8	0.8	0.7	0.8	0.8	0.8
	CO2 emission current system (Ton CO2)	10,590.7	899.4	22.3	0.0	6199.9	795.2	9.6	0.0	18,517.1
	Optimized CO2 emission (Ton CO2)	2647.7	224.9	5.6	0.0	1550.0	198.8	2.4	0.0	4629.3
VALPARAISO	Charge in tons	880,155	1,153,233	19,576	0	773,020	991,239	67,241	0	3,884,464
	Distances (km)	88	88	88	88	10	10	10	10
	Proposed solution in millions of USD	55.2	78.3	1.4	0.2	6.9	9.6	0.6	0.0	152.1
	Actual solution in millions of USD	110.3	154.8	2.6	0.0	12.4	17.1	1.1	0.0	298.4
	Savings with the proposed solution in millions of USD	55.1	76.5	1.2	0.0	5.5	7.5	0.5	0.0	146.4
	Savings in dollars per ton-km	0.7	0.8	0.7	0.0	0.7	0.8	0.8	0.0
	CO2 emission current system (Ton CO2)	929.4	1217.8	20.7	0.0	92.8	118.9	8.1	0.0	2387.7
	Optimized CO2 emission (Ton CO2)	232.4	304.5	5.2	0.0	23.2	29.7	2.0	0.0	596.9
O’HIGGINS	Charge in tons	1,491,447	3,949,870	6456	0	673,554	3,208,655	0	1	9,329,983
	Distances (km)	141	141	141	141	98	98	98	98
	Proposed solution in millions of USD	147.6	422.9	0.7	0.0	46.8	240.8	0.0	0.0	858.7
	Actual solution in millions of USD	297.5	844.3	1.4	0.0	93.8	478.9	0.0	0.0	1715.9
	Savings with the proposed solution in millions of USD	149.9	421.4	0.7	0.0	47.1	238.1	0.0	0.0	857.2
	Savings in dollars per ton-km	0.7	0.8	0.8	0.0	0.7	0.8	0.0	0.0
	CO2 emission current system (Ton CO2)	2523.5	6683.2	10.9	0.0	792.1	3,773.4	0.0	0.0	13,783.1
	Optimized CO2 emission (Ton CO2)	630.9	1670.8	2.7	0.0	198.0	943.3	0.0	0.0	3445.8
MAULE	Charge in tons	2,457,589	1,545,269	22,395	0	809,974	749,697	15,123	45	5,600,092
	Distances (km)	265	265	265	265	366	366	366	366
	Proposed solution in millions of USD	104.6	78.9	0.4	0.0	46.9	52.2	0.4	0.0	283.4
	Actual solution in millions of USD	916.9	617.7	8.8	0.0	416.7	413.3	8.2	0.0	2381.7
	Savings with the proposed solution in millions of USD	812.4	538.8	8.4	0.0	369.8	361.0	7.9	0.0	2098.3
	Savings in dollars per ton-km	1.2	1.3	1.4	0.0	1.2	1.3	1.4	1.5
	CO2 emission current system (Ton CO2)	7815.1	4914.0	71.2	0.0	3557.4	3292.7	66.4	0.2	19,717.0
	Optimized CO2 emission (Ton CO2)	976.9	614.2	8.9	0.0	444.7	411.6	8.3	0.0	2464.6
BIO BIO	Charge in tons	320,855.0	48,966.0	144.0	179,314.0	39,073.0	22,206.0	2133.0	0.0	612,691
	Distances (km)	508	508	508	508	609	609	609	609
	Proposed solution in millions of USD	25.6	4.7	0.0	3.8	3.7	2.5	0.1	0.0	40.4
	Actual solution in millions of USD	228.9	37.4	0.1	138.3	33.4	20.3	1.9	0.0	460.4
	Savings with the proposed solution in millions of USD	203.3	32.7	0.1	134.6	29.7	17.8	1.8	0.0	420.0
	Savings in dollars per ton-km	1.2	1.3	1.4	0.0	1.2	1.3	1.4	0.0
	CO2 emission current system (Ton CO2)	1955.9	298.5	0.9	1093.1	285.5	162.3	15.6	0.0	3811.8
	Optimized CO2 emission (Ton CO2)	244.5	37.3	0.1	136.6	35.7	20.3	1.9	0.0	476.5
TEMUCO	Charge in tons	4345	58,460	0	0	22,980	22,543	0	0	108,328
	Distances (km)	698	698	698	698	800	800	800	800
	Proposed solution in millions of USD	0.5	7.6	0.0	0.0	2.9	3.4	0.0	0.0	14.3
	Actual solution in millions of USD	4.3	61.3	0.0	0.0	25.8	27.1	0.0	0.0	118.5
	Savings with the proposed solution in millions of USD	3.8	53.7	0.0	0.0	22.9	23.7	0.0	0.0	104.1
	Savings in dollars per ton-km	1.2	1.3	0.0	0.0	1.2	1.3	0.0	0.0
	CO2 emission current system (Ton CO2)	36.4	489.7	0.0	0.0	220.6	216.4	0.0	0.0	963.1
	Optimized CO2 emission (Ton CO2)	4.5	61.2	0.0	0.0	27.6	27.1	0.0	0.0	120.4
LOS LAGOS	Charge in tons	27,845	48,016	0	0	7486	15,817	0	0	99,164
	Distances (km)	1040	1040	1040	1040	1142	1142	1142	1142
	Proposed solution in millions of USD	4.8	9.5	0.0	0.0	1.3	3.4	0.0	0.0	19.0
	Actual solution in millions of USD	40.6	75.0	0.0	0.0	12.0	27.1	0.0	0.0	154.7
	Savings with the proposed solution in millions of USD	35.8	65.5	0.0	0.0	10.7	23.8	0.0	0.0	135.8
	Savings in dollars per ton-km	1.2	1.3	0.0	0.0	1.2	1.3	0.0	0.0
	CO2 emission current system (Ton CO2)	347.5	599.2	0.0	0.0	102.6	216.8	0.0	0.0	1266.1
	Optimized CO2 emission (Ton CO2)	43.4	74.9	0.0	0.0	12.8	27.1	0.0	0.0	158.3
AYSEN	Charge in tons	8914	60,266	0	0	0	2185	0	0	71,365
	Distances (km)	1717	1717	1717	1717	1818	1818	1818	1818
	Proposed solution in millions of USD	2.4	19.2	0.0	0.0	0.0	0.7	0.0	0.0	22.3
	Actual solution in millions of USD	21.4	155.4	0.0	0.0	0.0	6.0	0.0	0.0	182.8
	Savings with the proposed solution in millions of USD	19.1	136.2	0.0	0.0	0.0	5.2	0.0	0.0	160.5
	Savings in dollars per ton-km	1.2	1.3	0.0	0.0	0.0	1.3	0.0	0.0
	CO2 emission current system (Ton CO2)	183.7	1241.7	0.0	0.0	0.0	47.7	0.0	0.0	1473.1
	Optimized CO2 emission (Ton CO2)	23.0	155.2	0.0	0.0	0.0	6.0	0.0	0.0	184.1
MAGALLANES	Charge in tons	38,078	210,935	0	0	531	6863	0	0	256,407
	Distances (km)	3012	3012	3012	3012	3113	3113	3113	3113
	Proposed solution in millions of USD	17.5	117.5	0.0	0.0	0.3	4.0	0.0	0.0	139.2
	Actual solution in millions of USD	160.6	953.5	0.0	0.0	2.3	32.1	0.0	0.0	1148.4
	Savings with the proposed solution in millions of USD	143.1	836.0	0.0	0.0	2.1	28.1	0.0	0.0	1009.2
	Savings in dollars per ton-km	1.2	1.3	0.0	0.0	1.2	1.3	0.0	0.0
	CO2 emission current system (Ton CO2)	1376.3	7624.0	0.0	0.0	19.8	256.4	0.0	0.0	9276.5
	Optimized CO2 emission (Ton CO2)	172.0	953.0	0.0	0.0	2.5	32.0	0.0	0.0	1159.6
LOS RIOS	Charge in tons	24,358	12,794	0	0	1769	1646	0	0	40,567
	Distances (km)	856	856	856	856	957	957	957	957
	Proposed solution in millions of USD	3.2	2.0	0.0	0.0	0.5	0.5	0.0	0.0	6.2
	Actual solution in millions of USD	29.2	16.5	0.0	0.0	2.4	2.4	0.0	0.0	50.4
	Savings with the proposed solution in millions of USD	26.0	14.4	0.0	0.0	1.9	1.9	0.0	0.0	44.2
	Savings in dollars per ton-km	1.2	1.3	0.0	0.0	1.1	1.2	0.0	0.0
	CO2 emission current system (Ton CO2)	250.2	131.4	0.0	0.0	20.3	18.9	0.0	0.0	420.8
	Optimized CO2 emission (Ton CO2)	31.3	16.4	0.0	0.0	2.5	2.4	0.0	0.0	52.6
TOTAL	Charge in tons	12,796,798	7,728,442	64,468	179,332	6,461,630	5,550,984	90,905	47	32,872,606
	Distances (km)	8442	8442	8442	8442	9038	9038	9038	9038
	Proposed solution in millions of USD	982.1	797.8	3.8	4.0	472.1	367.5	1.7	0.0	2629.0
	Actual solution in millions of USD	3061.1	3029.8	15.7	138.3	1330.9	1124.8	12.5	0.0	8713.1
	Savings with the proposed solution in millions of USD	2079.0	2232.0	11.9	134.6	858.7	757.3	10.8	0.0	6084.3
	Savings in dollars per ton-km	10.9	11.5	5.1	0.8	9.5	11.4	4.4	2.3
	CO2 emission current system (Ton CO2)	26,008.8	24,099.0	126.0	1093.1	11,291.0	8898.6	99.7	0.2	71,616.4
	Optimized CO2 emission (Ton CO2)	5006.6	4112.4	22.5	136.6	2297.0	1698.3	14.7	0.0	13,288.0

Equation (3) corresponds to the third term in Equation (1). The model assumes the optimal scenario where the variables $z_{1k}=z_{2m}=y_k=y_m=y_{km}=0$ and $y_0=1$.

$$\begin{array}{cc}\hfill \mathrm{Proposed}\mathrm{solution}\mathrm{in}\mathrm{millions}\mathrm{of}\mathrm{USD}=& \sum _i\sum _j\sum _k\sum _m\sum _p\sum _{r}a\ast w_{ij}^{p}C{6}_{ij}^{pr}d{5}_{ij}\ast x{0}_{ij}^{pr}\hfill \end{array}$$

(3)

Equation (4) corresponds to the current situation where only road transportation is used, so in Equation (1), r = 1 was considered.

$$\begin{array}{cc}\hfill \mathrm{Actual}\mathrm{solution}\mathrm{in}\mathrm{millions}\mathrm{of}\mathrm{USD}=& \sum _i\sum _j\sum _k\sum _m\sum _{p}a\ast w_{ij}^{p}C{6}_{ij}^{p1}d{5}_{ij}\ast x{0}_{ij}^{p1}\hfill \end{array}$$

(4)

Equation (5) is the difference between the current cost and the proposed solution.

$$\begin{array}{cc}\hfill & \mathrm{Proposed}\mathrm{Solution}\mathrm{Savings}\left(\mathrm{SWPS}\right)\mathrm{in}\mathrm{millions}\mathrm{of}\mathrm{USD}\hfill \\ \hfill & \sum _i\sum _j\sum _k\sum _m\sum _p\sum _{r}a\ast w_{ij}^{p}C{6}_{ij}^{pr}d{5}_{ij}\ast x{0}_{ij}^{pr}-\sum _i\sum _j\sum _k\sum _m\sum _{p}a\ast w_{ij}^{p}C{6}_{ij}^{p1}d{5}_{ij}\ast x{0}_{ij}^{p1}\hfill \end{array}$$

(5)

Equation (6) represents the quotient between the savings resulting from the optimized solution (SWPS) and the tons transported and the distance traveled.

$$\begin{array}{cc}\hfill \mathrm{Savings}\mathrm{in}\mathrm{dollars}\mathrm{per}\mathrm{ton}-\mathrm{km}=& \frac{\mathrm{SWPS}}{\mathrm{Charge}\mathrm{in}\mathrm{tons}\ast \mathrm{Distances}\left(\mathrm{km}\right)}\hfill \end{array}$$

(6)

Equation (7) corresponds to the CO₂ emission with the proposed optimal function. Equation (7) was used as a basis for this equation, and then the cost was replaced by the CO₂ emission, using the term Er for this value. This term is defined as $E_r={\mathrm{CO}}_2$ emission * ton-km for transport type r.

Equation (3) was used as a basis, and then the cost was replaced by the CO₂ emission, using the term $E_r$ for this value, according to the following definition:

$E_r$ = CO₂ emission * ton-km for transport type r.

The values of $E_r=\{$Road (r = 1) = 0.012, Train (r = 2) = 0.003, and Sea (r = 3) = 0.0015} [58].

$$\begin{array}{cc}\hfill \mathrm{Optimized}{\mathrm{CO}}_2\mathrm{emissions}\left(\mathrm{tons}{\mathrm{CO}}_2\right)=& \sum _i\sum _j\sum _k\sum _m\sum _p\sum _{r}a\ast w_{ij}^p{E}_{r}d{5}_{ij}\ast x{0}_{ij}^{pr}\hfill \end{array}$$

(7)

Equation (8) represents the emission of pollutants when only road transport is utilized ($r=1$).

$$\begin{array}{cc}\hfill {\mathrm{CO}}_2\mathrm{emission}\mathrm{current}\mathrm{system}\left(\mathrm{ton}{\mathrm{CO}}_2\right)=& \sum _i\sum _j\sum _k\sum _m\sum _{p}a\ast w_{ij}^p{E}_{1}d{5}_{ij}\ast x{0}_{ij}^{p1}\hfill \end{array}$$

(8)

The results indicate that, for the metropolitan region, the transport of cargo by rail to both ports is the most appropriate. In regions five and six, bulk cargo shipping via train is advised, while road transport proves more efficient for other cargo types. Conversely, in the seventh region, maritime transport to both ports is preferred for most cargo types, with the exception of bulk cargoes destined for San Antonio, which are better served by road.

For the eighth region, maritime transportation is favored, while regions nine through fourteen demonstrate enhanced efficiency through a blend of maritime and land transport. Notably, the model eschews cargo consolidation or distribution centers due to the substantial volume of cargo (39.4%) originating from the metropolitan region situated further north. Establishing centers there would entail redundant movements and an additional estimated cost of $19 million per center.

Over a 20-year span, the solution without centers incurred costs of $2626 billion, representing only 30.1% compared to the $8713 billion from an exclusive road transport model. Furthermore, this multimodal strategy led to a notable reduction in CO₂ emissions, totaling 13,288 tons of CO₂ compared to the 71,616 tons of CO₂ generated by the current model, reflecting a decrease of 18.5%. It is important to note that this analysis factored in a 30-km increase in road transportation for all regions from their respective capitals.

In Chile, transportation costs have a significant impact on overall logistics expenses due to the country’s extensive size. The implementation of the proposed multimodal transportation system could result in a significant reduction in these costs, from $8.713 billion to $2.629 billion, representing a 69.8% decrease. Additionally, the reduction of greenhouse gas emissions is of equal importance. In response, the country is developing new emissions standards [58]. The projected reduction in CO₂ emissions from the implementation of the new multimodal system is 81.5%, from 71,616.4 tons to 13,288 tons. This reduction will significantly mitigate the environmental impact.

5. Discussion and Conclusions

5.1. Limitations and Optimization Model

• Data Limitations: The applicability of the study is limited to the specific data used, particularly the load data at current rates, which are subject to annual variation.
• Data Availability and Accuracy: The data, such as cargo volumes reported by ports, is sourced from local customs and may contain errors due to regional processing discrepancies or data recording inconsistencies.
• Accuracy of Distance Measurements: Calculated origin-to-port distances are based on official records, which may not accurately reflect the actual routes taken by trucks or cargo, potentially leading to inaccuracies in distance-based analyses.
• Stakeholder Involvement: The study does not consider the involvement of key stakeholders, including local communities [59], in the development and implementation of the multimodal transportation system.
• Uncertainty Factors: The model does not account for uncertainties inherent in the transportation system, such as weather variations; accidents; or the overall volatility, uncertainty, complexity, and ambiguity [60] of the system.

The classical “hub and spoke” model is applied to logistic networks through hubs that function as multimodal warehouses. In the study of the model applied to Chile, the optimal solution dispenses with these hubs, favoring a hub-less exchange approach. This mathematical model, which distinguished between concentrating and deconcentrating hubs, opted for a multimodal strategy with multiple modes of transportation. This decision is justified by Chile’s elongated geography and the clustering of cargo generators near Santiago, the capital [61].

The application of this research addressed an adaptation of the hub and spoke model to the specific context of a country with a territorial concentration in cargo generation and distribution. The general version of the model, in its p-hub version, selects an optimal quantity of hubs [62]. However, given the country’s particular geographical characteristics, the possibility of establishing a maximum of two hubs was considered: one in the south to concentrate cargo and another in the central zone, near the ports, for unloading. Contrary to this hypothesis, the optimal results of the model suggest dispensing with these hubs, favoring the direct transportation of cargo from generation points to ports. This approach not only optimizes logistics but also significantly contributes to reducing greenhouse gas emissions.

5.2. Conclusions

This study emphasizes the need to optimize road transportation in Chile, especially in the central and southern regions of the country, and contrasts its advantages and limitations with those of railway and maritime transportation. It is highlighted that although the railway is efficient for large volumes and long distances, and maritime transport excels in certain conditions, each mode has specific characteristics and costs that influence logistics efficiency [63].

The ratio of savings in dollars per ton-km in Equation (6) shows that the savings with the proposed system are greater for the more remote regions due to the greater distances involved in transportation.

The State Railways Company (EFE) plays a key role in logistics, connecting productive regions with ports, but faces challenges such as a lack of direct connections in some areas. Railway transport is highlighted for its sustainability, especially when using renewable energies, offering an alternative with lower environmental impact compared to road transport [64]. However, limited flexibility and the need for truck transshipment, which increases loading and unloading costs, mark disadvantages compared to the versatility of road transport.

In terms of operational efficiency and CO₂ emissions, railway transport, powered by unconventional renewable energies (ERNC), emerges as a significantly cleaner option compared to the emissions capacity of the truck fleet [65].

In conclusion, transportation optimization in Chile requires the strategic integration of road, railway, and maritime modes, aiming to maximize efficiency, sustainability, and emissions reduction in freight transportation.

5.3. Future Research

Exploring the impact of integrating emerging technologies, such as automation and digitization, on the efficiency of multimodal transportation is essential. In the future, it will be possible to assess the viability of replicating the model in regions with similar geographical and logistical characteristics, adapting solutions to different national or international contexts. Additionally, it is crucial to investigate the role of public–private cooperation in developing and implementing these transportation solutions and analyzing their long-term socioeconomic and environmental impact. Considering a new routing model and possible consolidation, as well as integrating it with neighboring countries in the multinational project “bioceanic corridor”, involving Argentina, Brazil, Chile, and Paraguay, is proposed [66].

A forthcoming study could evaluate the impact of increased volume on Chile’s ports and cities, considering both economic benefits and potential port overloads. It is essential to analyze the current infrastructure’s capacity to efficiently manage the anticipated increase in international cargo using a routing model with limited capacity that considers customs restrictions and points of loading.

Explore dynamic models that track the evolution of multimodal transportation over time, incorporating fluctuating demand, technological advances, and infrastructure changes. These models facilitate simulations to evaluate the impact of different strategies on the efficiency and sustainability of multimodal transportation systems, thereby improving our understanding of their effects.

It is proposed to adapt the static model to seamlessly integrate new input parameters as they become available, allowing for real-time updates and continuous refinement. This approach will enhance the model’s adaptability to changing conditions and maintain its applicability in a dynamic environment. Alternatively, probabilistic methods could be used to quantify confidence levels in the predictions and facilitate risk assessment.