An Adaptive Large Neighborhood Search Algorithm for Equipment Scheduling in the Railway Yard of an Automated Container Terminal

Abstract

In container sea–rail combined transport, the railway yard in an automated container terminal (RYACT) is the link in the whole logistics transportation process, and its operation and scheduling efficiency directly affect the efficiency of logistics. To improve the equipment scheduling efficiency of an RYACT, this study examines the “RYACT–train” cooperative optimization problem in the mode of “unloading before loading” for train containers. A mixed-integer programming model with the objective of minimizing the maximum completion time of automated rail-mounted gantry crane (ARMG) tasks is established. An adaptive large neighborhood search (ALNS) algorithm and random search algorithm (RSA) are designed to solve the abovementioned problem, and the feasibility of the model and algorithm is verified by experiments. At the same time, the target value and calculation time of the model and algorithms are compared. The experimental results show that the model and the proposed algorithms are feasible and can effectively solve the “RYACT–train” cooperative optimization problem. The model only obtains the optimal solution of the “RYACT–train” cooperative scheduling problem with no more than 50 tasks within a limited time, and the ALNS algorithm can solve examples of various scales within a reasonable amount of time. The target value of the ALNS solution is smaller than that of the RSA solution.

1. Introduction

With the tangible growth of the “Belt and Road Initiative”, the volume of China’s sea–rail combined transport has increased year by year, and an increasing number of ports have begun to pay attention to and expand the construction and development of their sea–rail combined transport business. At present, the railway center station and dock yard are separated in most of China’s sea–rail combined transport ports, but this configuration inevitably increases the operating cost and transfer time of sea–rail combined transport. To solve the above problems, newly built sea–rail combined transport ports began to adopt the “sea–rail” operation mode to bring railway lines into the port. For example, the railway line under construction in the Yuanhai Automated Container Terminal of Xiamen Port is located in the port area, and the railway yard is adjacent to the dock yard; the trains directly enter the port area to load and unload containers to the railway central station yard. The railway central station yard plays an important role as a buffer, and it forms a good connection between railway and water transport, as well as reducing logistics time and costs. However, joint dispatch between the port and railway is still time-consuming and inefficient. Improving the dispatch level can help the port, railway, and logistics departments improve the utilization rate of the site and save time.

A container yard can be divided into a front yard and a rear yard, and it can also be divided into a port general container yard and a railway yard in a sea–rail automated container terminal. Because of the long railway line, an RYACT has the characteristics of a long length and a low container storage height. Therefore, it is different from other rear yards in terms of mechanical scheduling. The mechanical scheduling efficiency of the railway central station has a direct impact on the departure time of trains and ships in the port. Improving the mechanical scheduling level of this link is of great significance to improving the status of container ports in sea–rail combined transportation. Through a literature review, we found that yard scheduling, ship scheduling, and joint scheduling between yards and ships in automated container terminals have attracted the attention of many scholars. However, there are few studies on scheduling optimization between trains and RYACTs in sea–rail combined transportation. Railways and ports are important connecting points for sea–rail combined transportation, and their joint scheduling efficiency affects the efficiency of the entire logistics chain. This study examines the “RYACT–train” collaborative optimization problem in the mode of “unloading before loading” for train containers in an automated container terminal’s railway central station. Furthermore, a mixed-integer programming model is established, and an ALNS algorithm is designed to solve the approximate optimal solution of the problem. Finally, the ALNS algorithm is compared with the model and the RSA in terms of computational performance and solution results. The experiment results show that the designed ALNS algorithm can be used to solve the “ARMG–train” cooperative optimization problem. The remainder of this paper is organized as follows: Section 2 provides a comprehensive review of the relevant literature. The problem is described and modeled in Section 3. The algorithm is designed in Section 4. Section 5 provides a series of computational experiments and shows the relevant results, and conclusions are drawn in Section 6.

2. Literature Review

As an interface of shipping and land transportation, container terminals play an important role in the global supply chain [1]. The operation process of container terminals includes the loading and unloading of vessels at the wharf front, horizontal transportation between the wharf front and the yard and between the yard and the yard, and the stacking and palletizing of goods in the yard. The loading and unloading of vessels are carried out by quay cranes (QCs). Horizontal transport machinery includes an automated guided vehicle (AGV) or an autonomous straddle carrier, and stacking machinery usually comprises a yard crane (YC), an ARMG, or an automatic stacking crane (ASC). Many scholars have conducted research on the mechanical scheduling of automated container terminals. The scheduling of a single machine, the joint scheduling of multiple machines, the space allocation of a storage yard, and the charging scheduling have been widely examined by scholars.

Regarding a single mechanical scheduling problem, Vallada et al. [2] and Iris et al. [3] researched the QC scheduling problem. Iris et al. [3] presented an adaptive large-neighborhood-based heuristic framework to solve the weekly berth and quay crane assignment problem. References [4,5,6] studied the YC scheduling problem, and Chu et al. [4] studied the management of three yard cranes in two adjacent container blocks in line. Gharehgozli et al. [5] researched the problems of both stacking and lifting tasks in a container yard. Hu et al. [6] considered the delayed trans-shipment of containers caused by the heterogeneous periodicities of vessels. References [7,8,9,10] researched the ASC scheduling problem, while Gao et al. [8] developed a virtual container yard that was synced with a physical container yard in an automated container terminal digital twin system for observation and validation. Reference [10] explored the influences of the locations of handshake areas. References [11,12,13,14,15] studied the AGV scheduling problem. Wang et al. [13] investigated the AGV dispatching and routing problem with multiple bidirectional paths to generate conflict-free routes. Drungilas et al. [15] proposed an AGV speed control algorithm based on deep reinforcement learning to optimize the energy consumption of container transportation. Cai et al. [16] presented a rescheduling combination of new and unexecuted jobs policy and compared the scheduling of long-term autonomous straddle carriers under the uncertainty of new job arrivals by using a multi-objective cost function. Yang et al. [17] studied the flexible allocation of yard space using unilateral cantilever rail-mounted gantry cranes and established a mixed-integer quadratic programming model with the objective of minimizing the total AGV transportation cost and the penalty cost of unmet demand.

Regarding the joint scheduling of machinery, Lau et al. [18] proposed a heuristic method called the multi-layer genetic algorithm to obtain a near-optimal solution to the integrated scheduling problem, including QCs, AGVs, and YCs. Shouwen et al. [19] considered the integrated scheduling problem of QCs, AGVs, and ASCs and the conflict-free path planning problem of AGVs. Considering the bidirectional flow caused by the synchronous loading and unloading operation mode, Zhuang et al. [20] examined the integrated scheduling of double-trolley quay cranes, AGVs, and ARMGs. Liu et al. [21] analyzed the yard crane, AGV, and truck scheduling problem based on a U-shaped yard layout and established a bi-level programming model with the goal of achieving the minimum completion time and minimum total waiting time. Skaf et al. [22] solved the scheduling problem for a single quay crane and multiple yard trucks in the port of Tripoli, Lebanon. Considering the transport of the direct, buffer, and hybrid modes, Wang et al. [23] established three continuous time integer programming models for the scheduling of ASCs and AGVs. Aiming to increase terminal efficiency through the coordination of multiple sub-operations, Zhang et al. [24] focused on the integrated optimization of AGVs and double yard cranes in automated container terminals. Cao et al. [25] regarded the joint scheduling problem of yard trucks and YCs as a two-stage flexible flow shop to establish mixed-integer programming with the minimum loading operation time.

There are many studies on the mechanical scheduling of automated container terminals. Some studies have examined the charging management of automated container terminals, but few have focused on the equipment scheduling of RYACTs. References [26,27,28] researched the storage space allocation problem in a container terminal. Xiang et al. [29] analyzed an automated container terminal considering battery management. Some scholars have conducted research on the operation of automated container terminals for sea–rail combined transportation. Considering that the rail gantry crane, intelligent guided vehicle, and double-cantilever rail crane usually work in groups, Li et al. [30] introduced a cluster scheduling method applied in a U-shaped automated terminal and attempted to improve the efficiency of automated terminal and the sea–rail intermodal transport. Yang et al. [31] addressed the cooperative scheduling challenges of rail gantry cranes, YCs, and AGVs in the loading and unloading mode in a sea–rail automated container terminal. Liu et al. [21] optimized the yard crane scheduling problem, AGV task assignment problem, and AGV path planning problem simultaneously. Niu et al. [32] optimized the dispatch efficiency of quay cranes, automatic double cantilevers, intelligent guided transport vehicles, and external trucks of a U-shaped automatic terminal from the aspect of reducing energy consumption. These studies focus on the machine scheduling problem within ports or between ports and external vehicles in sea–rail combined transport, but they do not pay attention to the scheduling problem between the railway yards and trains in automated container terminals.

In summary, the scheduling of a single machine, the joint scheduling of multiple machines, storage yard space allocation, charging scheduling, and other topics of automated container terminals have attracted extensive attention from scholars, but there are few studies on the equipment scheduling of RYACTs. In particular, there is almost a gap in the research on the “RYACT–train” cooperative optimization problem. Therefore, this study attempts to fill this gap and examines the “RYACT–train” cooperative optimization problem in the “unloading before loading” mode of train containers in an RYACT. The main contributions are as follows: 1. For the “RYACT–train” cooperative optimization problem, a mixed-integer programming model with the objective of minimizing the maximum completion time of ARMG tasks is constructed. 2. The designed ALNS algorithm can be used to solve cooperative optimization problems in RYACTs, and it takes less time to obtain a near-optimal solution and to complete tasks for ARMG than the RSA.

3. Model Establishment

In this section, we present a mixed-integer programming model for the “RYACT–train” cooperative optimization problem.

3.1. Problem Description

The loading and unloading process of a train in an RYACT is shown in Figure 1, and it includes the following: (1) The unloading operation: an empty ARMG moves to the top of the container carriage of a train to grab a container. Then, the ARMG is driven to the target bay in the RYACT. Finally, the ARMG trolley moves to the target row to release the container, thereby completing the task. (2) The loading operation: an empty ARMG drives to the container storage location in the RYACT to grab a container. Then, the ARMG is driven to the position of the target carriage. Finally, the ARMG trolley places the container on top of the carriage, thereby completing the task.

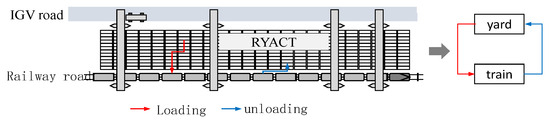
Figure 1. ARMG loading/unloading of a train in an RYACT.

3.2. Assumption

In an RYACT, multiple ARMGs run on the same track and work together on the incoming train. When scheduling the container tasks assigned to multiple ARMGs, mutual interference should be avoided. According to the freight plan of the incoming train, the same operation volume rule can be used to predetermine the job assignment of each ARMG, which can reduce the maximum job completion time and the complexity of scheduling. However, at the same time, the scheduling plan of multiple ARMGs is still subject to interference. To improve the operation efficiency of a railway central station, the objective of this problem is to minimize the maximum completion time of all tasks during ARMG operation. Without the loss of generality, the following assumptions can be made:

(1)

Overturning activity is not considered when an ARMG moves containers in the RYACT.

(2)

To avoid interference between loading and unloading, the operation mode of unloading before loading is adopted.

(3)

The horizontal moving speed of ARMG carts remains unchanged.

(4)

In the RYACT (or train), the operation time required for an ARMG to grab a container is equal to that required to release a container.

(5)

The container tasks for each ARMG are known.

(6)

To ensure the safety of the container handling operation, the cart does not move during the movement of the ARMG trolley.

3.3. Mathematical Model Formulation

A mixed-integer programming model is used for ARMG scheduling in an RYACT. As previously mentioned, the goal is to minimize the maximum completion time for all tasks. The main operational decisions are made to determine when and in what order an ARMG loads and unloads containers on a train. Table 1 and Table 2 present the notations related to this problem.

Table 1. Sets and parameters.

Sets/Parameters	Definitions
$S$	Set of ARMGs, indexed by s
$I_s^L$	Set of ARMG $s$ tasks for loading containers, indexed by$i$ and $j$
$I_s^U$	Set of ARMG $s$ tasks for unloading containers, indexed by$i$ and $j$
$I_s$	Set of ARMG $s$ tasks for loading and unloading containers, indexed by$i$ and $j{I}_s=I_s^L\cup I_s^U$
$I$	Set of all tasks; $I={\bigcup }_{s\in S}{I}_s$;
$I_s^O$	Set of tasks for loading and unloading containers;$I_s^O=I_s\cup \left\{O\right\}$, where $\left\{O\right\}$ represents the virtual start task and can be similarly defined in $I_s^{LO}$ and $I_s^{UO}$
$I_s^F$	Set of tasks for loading and unloading containers; $I_s^F=I_s\cup \left\{F\right\}$, where $\left\{F\right\}$ represents the virtual start task and can be similarly defined in$I_s^{LF}$ and $I_s^{UF}$
$C$	Set of tasks that may conflict with job tasks of adjacent ARMG, thereinto$\left(i,j\right)\in C,$ which indicates that, if an ARMG carries out container task i at the same time that another ARMG carries out container task j, then the two ARMGs will interfere with each other
$A_i$	The ARMG assigned to task $i$
$\left({\alpha }_i,{\alpha }_j^{\prime }\right)$	The conflict of tasks $\left(i,j\right)\in C$ between the nodes selected in the middle of the moment; when its value is 0, it is the middle time of ARMG operation in the RYACT, and, when it is 1, it is the middle time of ARMG operation in the train carriage
$\left({\beta }_i,{\beta }_j^{\prime }\right)$	The middle of the moment to avoid the conflict of tasks$\left(i,j\right)\in C;$ when its value is 0, it refers to the middle moment of the starting position, and, when it is 1, it refers to the middle moment of the ending position
$2T_i^B$	The operation time required for the ARMG to grab/release a container in the RYACT
$2T_i^R$	The operation time required for the ARMG to grab/release a container on the train
$T_i^S$	Time required in operation task $i$ for the ARMG to grab/release a container on the train
$T_{ij}^{Int}$	The minimum time interval between ARMG container tasks $i$ and $j$
$T_{ij}^{ET}$	The time taken by the ARMG to move from the end position of container task $i$ to the start position of container task $j$
$T_i^G$	The moving time of the sprig trolley when the ARMG completes task$i$
$M_n$	A positive number that is large enough, $n\in \left\{\mathrm{1,2},\dots ,5\right\}$

Table 2. Decision variables.

Variables	Definitions
$x_{ij}$	If the value is $1$, it indicates that the ARMG starts container task $j$ immediately after completing container task $i$; otherwise, it is 0.
$z_{ij}$	If the value is $1$, it indicates that interference task $\left(i,j\right)\in C$ the task $i$ is completed before task $j$; otherwise, it is 0.
$t_i^S$	The start time of task $i$, which is a real variable.
$t_i^E$	The end time of the task $i$, which is a real variable.
$t_i^M$	The middle of the moment to grab or release a container for ARMG operating conflict task $i$. If it is in railway yard, it can be calculated via $t_i^S+T_i^B$; if it is on the train, it can be calculated via $t_i^E-T_i^R$, which is a real variable.

3.4. Mathematical Model

According to the above descriptions and the settings of the parameters and decision variables, the following mathematical model [M1] is constructed:

$$\begin{array}{ccc}\hfill \left[\mathrm{M}1\right]& f^{Min}=\min \left(\underset{i\in I}{\max }{t}_i^E\right)\hfill & \mathrm{(1)}\\ s.t.\hfill & \hfill & \\ \hfill & t_i^S\ge T_0+T_{Oi}^{ET},\forall i\in I_s^U,s\in S\hfill & \mathrm{(2)}\\ \hfill & {{\displaystyle \sum }}_{i\in I_s^{UF}}{x}_{O,i}=1,\forall s\in S\hfill & \mathrm{(3)}\\ \hfill & {{\displaystyle \sum }}_{i\in I_s^{UO}}{x}_{i,F}=1,\forall s\in S\hfill & \mathrm{(4)}\\ \hfill & {{\displaystyle \sum }}_{i\in I_s^{UO},i\ne j}{x}_{ij}={{\displaystyle \sum }}_{i\in I_s^{UF},i\ne j}{x}_{ji}=1,\forall j\in I_s^U,s\in S\hfill & \mathrm{(5)}\\ \hfill & {{\displaystyle \sum }}_{i\in I_s^U}{{\displaystyle \sum }}_{j\in I_s^L}{x}_{ij}=1,\forall i\in I_s^U,j\in I_s^L,s\in S\hfill & \mathrm{(6)}\\ \hfill & t_j^S\ge t_i^E+T_{ij}^{ET},\forall i\in I_s^U,j\in I_s^L,s\in S\hfill & \mathrm{(7)}\\ \hfill & {{\displaystyle \sum }}_{i\in I_s^{LO}}{x}_{O,i}=1,\forall s\in S\hfill & \mathrm{(8)}\\ \hfill & {{\displaystyle \sum }}_{i\in I_s^{LF}}{x}_{i,F}=1,\forall s\in S\hfill & \mathrm{(9)}\\ \hfill & {{\displaystyle \sum }}_{i\in I^{LO},i\ne j}{x}_{ij}={{\displaystyle \sum }}_{i\in I^{LF},i\ne j}{x}_{ji}=1,\forall j\in I_s^L,s\in S\hfill & \mathrm{(10)}\\ \hfill & t_j^S\ge t_i^E+T_{ij}^{ET}+M_1\left(x_{ij}-1\right),\forall i,j\in I_s,i\ne j,s\in S\hfill & \mathrm{(11)}\\ \hfill & t_i^E\ge t_i^S+T_i^S,\forall i\in I_s,s\in S\hfill & \mathrm{(12)}\\ \hfill & z_{ij}+z_{ji}=1,\forall \left(i,j\right)\in C\hfill & \mathrm{(13)}\\ \hfill & \left\{\begin{array}{l}{t}_i^M=\left(1-{\alpha }_i\right)\left(t_i^S+T_i^B\right)+{\alpha }_i\left(t_i^E-T_i^R-{0.5\beta }_i{T}_i^G\right)\\ t_j^M=\left(1-{\alpha }_j^{\prime }\right)\left(t_j^S+T_j^B\right)+{\alpha }_j^{\prime }\left(t_j^E-T_j^R-{0.5\beta }_j^{\prime }{T}_j^G\right)\\ t_j^M-t_i^M\ge T_{ij}^{Int}{z}_{ij}+M_2\left(z_{ij}-1\right)\end{array},\forall \left(i,j\right)\in C\right.\hfill & \mathrm{(14)}\\ \hfill & x_{ij},z_{ij}\in \left\{\mathrm{0,1}\right\},\forall i,j\in I\hfill & \mathrm{(15)}\\ \hfill & t_i^S,t_i^E,t_i^M\ge 0,\forall i\in I\hfill & \mathrm{(16)}\end{array}$$

The objective function is shown in Equation (1), which is used to minimize the maximum completion time of the tasks. Formulas (2)–(6) are the constraints of the ARMG unloading task phase. Formula (2) is used to limit the start time of the initial task of the ARMG unloading operation, where $T_0=0$. Formulas (3) and (4) indicate that the ARMG unloading operation starts with a virtual start task and ends with a virtual end task, respectively. Formula (5) is used to limit task $j\in I_s^U$ flow balancing for ARMG tasks. Formula (6) is used to restrict the ARMG to complete the unloading task first and the loading task later. The constraints of the ARMG loading task phase include the following: Formula (7) is used to limit the start time of the initial task of the ARMG loading operation, and Equations (8) and (9) indicate that the ARMG loading operation starts with a virtual start task and ends with a virtual end task, respectively. Formula (10) is used to limit task $j\in I_s^L$ ARMG flow balancing for ARMG tasks. When the ARMG is continuously working on tasks i and j, Formula (11) is used to determine the relationship between the ARMG end time for task i and the ARMG start time for task j. Formula (12) is used to determine the relationship between the start time and the end time of ARMG task i. Formula (13) represents the order in which any two tasks, i and j, should be completed. Formula (14) is used to avoid interference between adjacent ARMGs. Formulas (15) and (16) limit the ranges of the variable values.

4. Proposed Algorithms

From the above model, the ARMG scheduling problem can be regarded as an extension of the vehicle routing problem, which is an NP problem. To solve medium- and large-scale examples of this problem, this study adopts a heuristic algorithm that can be solved quickly—the ALNS algorithm. The ALNS algorithm was first proposed by Ropke and Pisinger [33], and it has been widely used to solve various VRPs in recent years ([34,35,36,37]). Zhang et al. [38] used ALNS to solve the multi-objective optimization problem of synchromodal transport. Wu et al. [39] used ALNS to solve the multi-allocation hub location routing problem for the design of an intra-city express service system. Li et al. [40] used a hybrid ALNS to solve the large-scale heterogeneous container loading problem. Wang et al. compared the results of ALNS with the model when solving the tugboat scheduling problem [41]. Compared with other algorithms, ALNS has the characteristics of self-adaptability and multi-neighborhood search, has a good effect on the solving speed and the solving result, and has rarely been applied in the optimization of machinery scheduling. This study attempts to verify the performance of the ALNS algorithm in terms of the “RYACT–train” cooperative optimization problem through experiments. In this section, we design an ALNS algorithm to obtain an approximate optimal solution to the problem, and we finally compare ALNS with the model and the RSA in terms of computational performance and solution results.

4.1. Encoding Method

As can be seen in the decision content of the problem, in this study, the relative order of ARMG tasks is encoded using the sequential encoding method, and it is called the ARMG task sequence, where the encoded value represents the task number and the position of the value represents the task order. According to the requirements of ARMG job assignment and unloading before loading, each task subsequence can be predetermined, as shown in Figure 2. An ARMG can work according to its task subsequence, and, when there is interference between tasks, the priority of its job tasks can be determined according to its job sequence. Since the start and finish positions of tasks are not the same, each task carried out by an ARMG has two critical time nodes—the start time ($t_i^S$) and the end time ($t_i^E$). According to the mathematical model constructed above, the time node of the task can be calculated using Equations (2), (7) and (14), and the time node obtained here is the earliest feasible operating time (for example, the earliest start time and the earliest finish time).

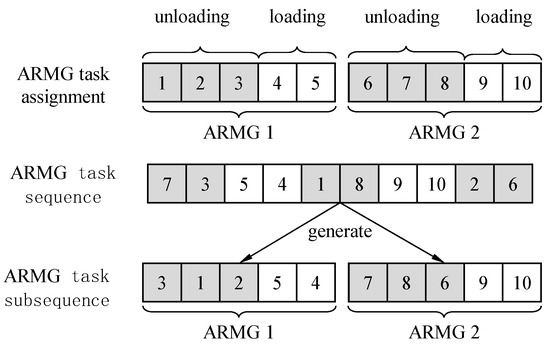
Figure 2. Generation of a subsequence of ARMG tasks.

4.2. RSA

A fixed number of iterations is set in the RSA, and a new ARMG task sequence is randomly generated in each iteration. This task sequence is simulated to calculate the time required for ARMG tasks, and the maximum completion time of all ARMG tasks is taken as the score value of this sequence. The optimal sequence is determined by comparing the current sequence score with the current minimum score. Finally, the stopping algorithm is set according to the stopping condition of the number of iterations, and the minimum result is returned. The result contains the score value for the encoding and the time nodes (start time and end time) for the ARMG tasks. The steps are shown in Table 3.

Table 3. RSA steps.

Step 1	Input parameter: $S,I,I_s^L,I_s^U,I_s,I_s^O,I_s^F,C,A_i,2T_i^B,2T_i^R,T_i^S,T_{ij}^{Int},T_{ij}^{ET},T_i^G$; Set the maximum number of iterations $N^{Max}$;
Step 2	Initialize the data:  set iteration number $n=1$;  The score of the n sequence $f_n;$  Initialize the minimum score $f^{best}$and the corresponding $Z^{best}$;
Step 3	While $n\le N^{Max}$
Step 3.1	Randomly generate a sequence $Z$ of ARMG tasks;
Step 3.2	According to tasks assignment $I_s^L$ and $I_s^U$, the task subsequence $X_s$ of each ARMG is determined.
Step 3.3	Calculate the earliest start and end time $\left\{t_i^{ES},t_i^{EE},\forall i\in I\right\}$ of the ARMG task according to the calculation method in mathematical model $\left\{t_i^{ES},t_i^{EE},\forall i\in I\right\};$
Step 3.4	Determine the score of the task sequence $f_n=\underset{i\in I}{\max }\left\{t_i^{EE}\right\}$;
Step 3.5	$n\leftarrow n+1$;
Step 3.6	If $f_n<f^{best}$, there is $f^{best}=f_n$ and $Z^{best}=Z$, otherwise, go to Step 3.1;
	End while
Step 4	Calculate $\left\{t_i^S,t_i^E,\forall i\in I\right\}$according to the optimal sequence $Z^{best}$; $f\leftarrow f^{best}$;
Step 5	Return $f,t_i^S,t_i^E$

4.3. ALNS Algorithm

Based on the given initial ARMG task sequence, ALNS is designed to adjust the task sequence, the neighborhood transformation is implemented adaptively by setting the neighborhood search operator, a new sequence with a better target value is generated based on the given coding evaluation method, the ARMG task sequence is iteratively optimized, and the completion time and scheduling schedule are returned. The initial ALNS solution is generated by the RSA with a given number of iterations. The encoding method adopts the integer encoding method shown in Figure 2, and the steps of the decoding method are shown in Table 4.

Table 4. The decoding method steps of integer encoding for ALNS.

Step 1	Input data: integer encoding $Z$ Initialize the data:  Task location number $n^Z=1$  The start time of the virtual task $t_O^S=t_O^E=0$
Step 2	Generate the task subsequence $X_s$ for each ARMG according to the code $Z$ and the task assignment ($I_s^L$ and $I_s^U$)
Step 3.1	While $n^Z<\left|I\right|$
Step 3.2	Determine the insert task $i$
Step 3.3	Calculate the earliest start and end times $\left\{t_i^{ES},t_i^{EE}\right\}$ for ARMG task $i$ according to the method described in Section 3.1
Step 3.4	$n^Z\leftarrow n^Z+1$
	End while
Step 4	Determine the score of the task sequence $f=\underset{i\in I}{\max }\left\{t_i^{EE}\right\},$ and the time node of the task $t_i^S\leftarrow t_i^{ES}$ and $t_i^E\leftarrow t_i^{EE}$
Step 5	Return $f,t_i^S,t_i^E$

The neighborhood search operators include (A) single-point reinsertion, (B) fragment reinsertion, (C) local reverse order, (D) two-point exchange, (E) fore-and-aft interchange, and (F) regeneration.

The stopping conditions of this algorithm include the following: First, the maximum number of iterations ($N^G$) is set, and, when the iteration number of the algorithm reaches this value, the algorithm will stop and return the output result. Second, the maximum number of iterations ($N^{St}$) is set, and the optimal value remains unchanged. When the number of iterations in which the optimal value remains unchanged reaches this value, the algorithm will stop and return the output result.

ALNS can adaptively select a neighborhood search operator in each iteration to generate a new neighborhood code to improve the current solution. The steps of ALNS are shown in Table 5.

Table 5. ALNS steps.

Step 1	Input data: $S,I,I_s^L,I_s^U,I_s,I_s^O,I_s^F,C,A_i,2T_i^B,2T_i^R,T_i^S,T_{ij}^{Int},T_{ij}^{ET},T_i^G$; Set algorithm parameters:  The number of solutions generated per iteration: $N^P$;  Maximum number of iterations $N^G$;  The maximum number of iterations with the same optimal value $N^{St}$;
Step 2	The initial solution $Z$ is generated by RSA, and its score $f_0$ is calculated;
Step 3	Initialize the data:  Set iteration number $n=1$;  The score $f_{nm}$ and sequence $Z_{nm}$ of the m code of the n iteration  Optimal score $f^{best}$ and corresponding sequence $Z^{best}$
Step 4	While $n\le N^G$
Step 4.1	Determine the list of domain search operators;
Step 4.2	Search the neighborhood of $Z^{best}$ to generate $N^P$ new encodings $Z_{nm},\forall m\in \left\{1,\dots ,N^P\right\}$;
Step 4.3	For $m\in \left\{1,\dots ,N^P\right\}$
Step 4.3.1	Calculate score $f_{nm}$ of $Z_{nm}$ according to Table 3;
	End for
Step 4.4	Determine the optimal score $f^{best}\leftarrow \min \left\{f^{best},\underset{m\in \left\{1,\dots ,N^P\right\}}{\mathit{min}}\left\{f_{nm}\right\}\right\}$ and corresponding sequence $Z^{best}$;
	End while
Step 5	Calculate $\left\{t_i^S,t_i^E,\forall i\in I\right\}$ according to the optimal sequence $Z^{best}$; $f\leftarrow f^{best}$;
Step 6	Return $f,t_i^S,t_i^E$

5. Experiment and Result Analysis

To evaluate the feasibility and computational performance of the model and algorithm in this study, two experiments are designed. The technical parameters of an ARMG are shown in Table 6, and the initial parameter settings of ALNS are given in Table 7.

Table 6. The technical parameters of ARMG.

Parameters	Value
ARMG cart moving speed	0.56 m/s
ARMG trolley moving speed	2 m/s
The amount of time ARMG spends on vertical operations in the yard ($2T_i^B$)	80 s
The amount of time ARMG spends on vertical operations on the train ($2T_i^R$)	100 s

Table 7. Initial parameter settings of ALNS.

Parameter	Value
The number of solutions per generation ($N^P$)	24
Maximum number of iterations ($N^G$)	600
The maximum number of iterations in which the minimum solution remains unchanged ($N^{St}$)	100
Operator class ($\left|R\right|$)	6
The initial value of the operator weight ($w_r$)	50

5.1. Experimental Design

• Experiment 1: Verify the feasibility of the model and algorithm

The specific steps of this experiment are as follows: (1) The number of ARMG and container tasks ($S\times I$) is set to $2\times 15$, and the input parameters are set according to the initial data set. (2) The model solution time is limited to 1200 s. (3) The model is solved, and the RSA is run according to the given ARMG task sequence to obtain the experimental results.

• Experiment 2: Compare the optimality and computation time of the model [2-1] and the algorithm

The specific steps of this experiment are as follows: (1) The number of tasks is set to 10, 12, …, 50, 60, …, 160 to generate corresponding examples. (2) The iteration number of the RSA is $N^{Max}={10}^3$. (3) The parameters in ALNS are set according to Table 5. (4) For each example, the model [M1] is solved, and the RSA and ALNS algorithm are run to obtain the experimental results.

5.2. Result Analysis

In experiment 1, the target value of the model to solve a given example is 2251.88 s, and the ARMG operation process corresponding to the result is shown in Figure 3. According to the given ARMG task sequence, the target value of the RSA to solve the given example is 2735.66 s, and the ARMG task process corresponding to the result is shown in Figure 4. It can be seen in Figure 3 and Figure 4 that many tasks assigned to each ARMG do not cause conflict. There is no interference between multiple ARMGs; thus, the ARMG operation process meets the operation requirements of train unloading before loading. Therefore, the proposed model [M1] and algorithm are feasible and can be used to make scheduling plans for the equipment in an RYACT.

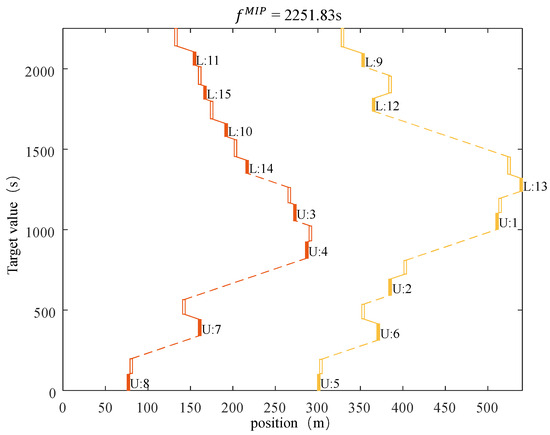
Figure 3. The result of solving the model in experiment 1.

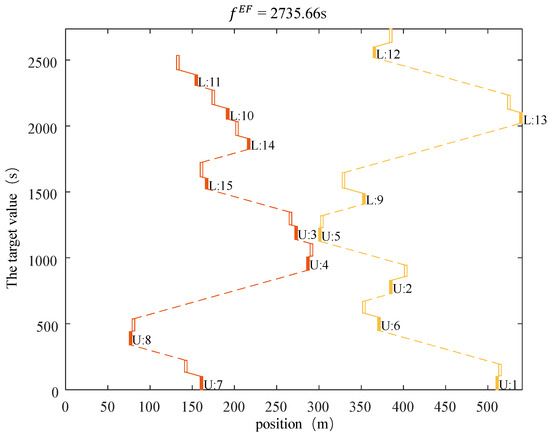
Figure 4. Results of RSA in experiment 1.

To compare the computational performance of the model, the RSA, and the ALNS algorithm, the target value and computation time of the three methods were compared in experiment 2, and the results are shown in Table 8. Firstly, the model [M1] shows excellent computational performance in small- and medium-sized examples. For example, in the case of no more than 60 tasks, the model can obtain the result quickly in a limited time. In the case of the number of tasks being from 60 to 90, the solution time of the model exceeds the 1200 s set in the experiment, so only feasible solutions can be obtained within 1200 s. Secondly, the RSA can quickly solve examples of various scales, but the target value obtained by the RSA is greater than or equal to the target value obtained by the other two methods, so the optimization of the solution results is poor. Finally, the solving speed of ALNS is less than 8 s, and it can quickly solve examples of various scales and has excellent computational performance. The target value obtained by ALNS is larger than that obtained by the model, but the gap is not large. In the small- and medium-sized example of no more than 90 tasks, the solved target value is less than 6% compared with the target value of the model. Moreover, its multiple solution convergence is good. Figure 5 shows the results of multiple ALNS solution examples. As can be seen in Figure 5, there is not much difference between the upper limit, lower limit, upper quartile, lower quartile, and median of each group of results, and the convergence of the target value of multiple solutions is good.

Table 8. The computational performance of [M1], RSA, and ALNS.

Number of Tasks	[M1]			RSA			ALNS
	${\mathit{f}}^{\mathit{M}\mathit{I}\mathit{P}}$	$\mathit{G}\mathit{a}{\mathit{p}}^{\mathit{a}}$	$\mathit{C}\mathit{p}\mathit{u}$	${\mathit{f}}^{\mathit{R}\mathit{S}\mathit{A}}$	$\mathit{G}\mathit{a}{\mathit{p}}^{\mathit{a}}$	$\mathit{C}\mathit{p}\mathit{u}$	${\mathit{f}}^{\mathit{M}\mathit{i}\mathit{n}}$	${{\mathit{f}}^{\mathit{M}\mathit{e}\mathit{a}\mathit{n}}}^{\mathit{b}}$	$\mathit{C}\mathit{p}\mathit{u}$
10	1878.54	0.00	0.10	1878.54	0.00	<0.01	1878.54	1878.54	3.02
12	1986.96	0.00	0.05	1986.96	0.00	<0.01	1986.96	1986.96	3.22
14	2049.12	0.00	0.05	2049.12	0.00	<0.01	2049.12	2049.12	2.84
16	2475.43	0.00	0.12	2475.43	0.00	<0.01	2475.43	2478.07	2.86
18	2612.16	0.00	0.27	2656.45	1.70	<0.01	2612.16	2620.24	3.29
20	2830.07	0.00	1.07	3130.36	10.61	<0.01	2830.07	2867.49	2.68
22	2105.69	0.00	1.78	2130.69	1.19	<0.01	2105.69	2110.97	3.36
24	2155.51	0.00	0.87	2284.17	5.97	<0.01	2155.51	2165.71	2.72
26	2413.94	0.00	1.33	2552.51	5.74	<0.01	2413.94	2468.51	2.73
28	2621.93	0.00	19.82	2726.21	3.98	<0.01	2621.93	2651.93	2.80
30	2691.53	0.00	1.01	2978.81	10.67	<0.01	2691.53	2762.16	3.87
32	2151.26	0.00	0.45	2273.40	5.68	<0.01	2151.26	2152.58	4.02
34	2252.36	0.00	0.64	2412.36	7.10	<0.01	2252.36	2298.24	4.24
36	2387.88	0.00	0.63	2582.88	8.17	<0.01	2387.88	2399.74	4.39
38	2627.73	0.00	147.15	2712.16	3.21	<0.01	2627.73	2640.80	4.79
40	2615.44	0.00	64.27	2810.44	7.46	<0.01	2615.44	2661.64	4.57
42	2180.71	0.00	0.74	2247.14	3.05	<0.01	2180.71	2186.28	4.42
44	2236.34	−1.03	61.14	2474.91	9.53	<0.01	2259.65	2340.62	4.83
46	2357.44	0.00	145.45	2465.14	4.57	<0.01	2357.44	2361.30	4.24
48	2400.13	0.00	5.41	2576.76	7.36	<0.01	2400.13	2429.35	4.65
50	2510.53	0.00	5.33	2695.39	7.36	<0.01	2510.53	2536.04	5.14
60	3553.20	−0.12	1200.11	4166.77	17.13	<0.01	3557.49	3690.65	4.89
70	3978.53	−2.26	1133.98	5063.13	24.38	<0.01	4070.67	4362.10	5.22
80	4478.54	−5.73	1203.72	5847.83	20.98	<0.01	4750.69	4993.32	6.27
90	5376.27	−3.83	1231.24	6477.87	15.87	<0.01	5590.56	5751.43	5.94
100	—		—	7059.66	17.48	<0.01	6009.37	6291.13	5.68
110	—		—	8002.13	17.11	<0.01	6833.24	7046.66	6.77
120	—		—	8793.97	15.99	<0.01	7581.89	7724.49	8.25
130	—		—	9644.81	20.17	<0.01	8025.91	8389.71	8.12
140	—		—	10,098.89	17.16	<0.01	8620.06	8999.28	7.61
150	—		—	10,892.59	15.04	<0.01	9468.16	9818.32	8.56
160	—		—	11,716.71	18.28	<0.01	9906.03	10,384.06	7.96

^a This value is calculated as follows: $Gap=\left(f\left(\mathsf{\Theta }\right)-f\left(\mathrm{A}\mathrm{L}\mathrm{N}\mathrm{S}\right)\right)/f\left(ALNS\right)\times 100\%$, where $\mathsf{\Theta }$ represents model [M1] and RSA; ^b the calculation time of RSA does not exceed 0.01 s.

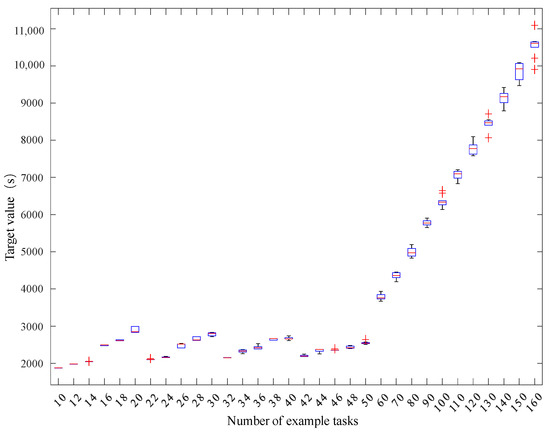
Figure 5. Results of multiple examples of ALNS in experiment 2.

6. Conclusions

This study examines how to dispatch multiple ARMGs to simultaneously load/unload incoming trains in an RYACT, and it establishes a mixed-integer programming model with the aim of minimizing the maximum completion time of work tasks. According to the decision content and constraints of the model, an RSA and an ALNS algorithm are designed to solve the problem quickly. Through experimental verification, the following conclusions are obtained: The proposed model and algorithms are feasible and can solve the “RYACT–train” cooperative optimization problem. The proposed ALNS algorithm can quickly solve examples of various scales. Compared with the RSA, the target value of the solution is smaller, and the calculation performance is better. The model only obtains the optimal solution of the cooperative scheduling problem with no more than 50 tasks within a limited time. Although the algorithm can effectively solve this problem, with an increase in container freight volume, a large railway station in an automated container terminal will inevitably need to handle more trains; mechanical scheduling will become more complicated, and more problems related to the optimization of mechanical operation efficiency will be encountered, such as the operation sequence of arriving trains and the selection of the train operation mode. Other methods can be explored, such as digital twin technology, and these are valuable research directions for us to investigate in the future.