Abstract
In this paper, the effectiveness of transplanted (either created or restored) seagrass meadows as a coastal protection measure is assessed through a five-step methodology. The analysis is focused on a stretch of the Catalan coast (NW Mediterranean) which is a fetch-limited environment. The results show that even considering conservative values for the meadow parameters (plant diameter, meadow density and canopy height), significant reductions of the annual average wave heights reaching the beach may be obtained, reducing flooding and erosion risks. Therefore, the investment in the conservation and restauration of seagrass meadows for protecting coastal areas from erosion and flooding is a measure that must be considered, due to the multiple benefits that they provide including ecosystem services. In addition, the proposed methodology may be a useful tool for coastal managers to help them in the design of seagrass meadows for coastal protection.
1. Introduction
Coastal areas are hazard prone and their risk is expected to increase in the next future as a consequence of sea level rise and other climate-related threats coinciding with population growth [1,2,3,4,5,6,7,8,9]. Therefore, building resilient communities is a challenge for populations living along the coast [10]. To address this challenge, communities usually build barriers along the coast to protect their assets [11,12,13,14]. Nevertheless, engineered solutions may cause negative impacts on sediment dynamics [15,16]. In addition, there is a growing perception that conventional approaches to coastal protection (seawalls, groins, bulkheads, etc.) are unsustainable [17]. Such measures may be very expensive to construct and maintain and can generate undesired impacts including degradation of habitats and shoreline erosion [14,18,19], affecting communities that depend on healthy coastal ecosystems [20].
These concerns about traditional engineering works for coastal protection are increasing the search for alternatives as, among others, nature-based solutions (NBS), which are more environmentally friendly, more cost-effective to maintain in the long-term [21,22,23,24] and can provide additional benefits as ecosystem services [25,26,27,28]. Such NBS include seagrass beds [29,30], coral reefs [31,32,33], shellfish reefs [34,35,36], wetlands [37,38,39] and mangroves [40,41,42] and have the potential to attenuate surges and waves associated with storms, reducing coastal erosion and flooding [6,22].
Among the aforementioned NBS, seagrasses stand out due to their presence on the coast of all continents except Antarctica and are among the most productive ecosystems on Earth [43], providing a number of ecosystem services such as nutrient fixation, carbon sequestration, sediment stabilization, habitat for many species, water quality improvement and reduction of coastal erosion [44,45,46,47]. In particular, seagrass meadows can dissipate wave energy [48,49,50,51], reduce current velocity and favor sediment stabilization [52,53,54], leading to local sediment trapping and stabilization and contributing to coastal protection [55,56,57,58,59,60]. Recent laboratory experiments [61] have shown that besides lessening the amount of wave energy that reaches a beach, seagrass meadows also reduce cross-shore sediment transport and shoreline retreat. These effects are a consequence of the wave attenuation generated by the presence of the meadow.
Despite their importance, seagrass is often not considered in coastal management decisions [62,63,64]. In addition, seagrass ecosystems are experiencing a global crisis due to anthropogenic activities such as coastal development (generating their removal in ports, marinas and beach nourishments), land erosion (increasing sedimentation), destructive fishing methods (such as trawling), water quality reduction and eutrophication (due to run-off of nutrients and other pollutants from land), mechanical damage (due to dredging and boat anchoring) and climate change [47,65]. These activities lead to the worldwide degradation of seagrass habitats [66] including the Mediterranean [67]. The total seagrass surface is estimated to have declined by 7–19% between the mid-1980s and the mid-1990s including the generation of dead seagrass patches with both spatial and temporal heterogeneity [68] or its disappearance in some locations [47]. Loss of seagrass meadows entails ecological and socio-economic impacts such as reduction of fisheries, a decline of biodiversity, loss of carbon sinks and enhancement of coastal erosion [69,70].
Since habitat creation, conservation or restoration does not exclude alternative actions later, NBS can be considered no- or low-regret coastal adaptation options regardless of the future climate [25]. Conservation, restoration and, in some cases, habitat creation are generally cheaper than coastal protection infrastructure and, in general, are very cost effective [22]. In addition, the improvement of transplanting methodologies used for seagrass restoration has increased the probability of successful seagrass restoration [71,72,73].
Another point in favor of using NBS is that many coastal ecosystems can adapt to climate change, potentially being more effective in the long term than coastal structures [17]. Nevertheless, the capacity of NBS to protect coastal areas is highly context-dependent and the performance of ecosystems may be very different depending on the conditions [74] and sometimes they may not provide the required defense [57]. Among the limitations of seagrass meadows to provide coastal protection, it is worth mentioning their limited effectiveness under high wave energy [75], since percent cover, patch size and number of patches decline with increasing wave energy [76]. This is because seagrass can be uprooted when sediment erodes around the rhizoids and roots [54,77], massive defoliation can occur as the leaves of the seagrass break as a consequence of the strong drag forces of the waves [54] or seagrass communities can be suffocated or buried due to the movement of large quantities of sediment [78,79]. In addition, some studies point out that seagrass value for coastal protection strongly depends on conditions such as water depth and seasonal shoot density [80,81]. On the contrary, in coastal zones with mid and low wave energy such as fetch limited areas, wave effects on plants and sediments should be less intense and, therefore, most of the time, this protection function could be fulfilled [48,82].
For this reason, decision-makers need tools that can help them to identify where these ecosystems may be an effective alternative to select the best option in a timely manner [83]. Hence, the main objective and motivation of this work is the assessment of the suitability and effectiveness of transplanted (restored, rehabilitated or created) marine seagrass meadows as a measure for coastal protection, using a Digital Twin strategy similar to that of Pillai et al. [84]. Up to now, studies about the effectiveness of seagrass meadows on coastal protection have been focused on assessing their wave attenuation under individual (specific) wave conditions [49,50,84,85,86,87], i.e., at the event time scale. In this work, the focus is on assessing the protective role of the seagrass in the mid-term (an average wave climate year), not under singular wave conditions as conducted in previous works. This means considering all the wave conditions recorded in the area (including storm waves) but weighted according to their frequency of occurrence.
Another innovation of the work is the development of a framework to help coastal managers to assess if the use of seagrass meadows is a feasible coastal protection option and, in this case, to select the best location and configuration of the meadow. The methodological framework developed for this aim is applied to a case study of the Catalan coast (NW Mediterranean). This includes the selection of the plant and the site location (considering areas where this plant can be developed), the definition of the features and dimensions of the meadow and assessment (by means of a numerical model) of its performance, taking into account the local wave climate. In addition, the feasibility of its application to coastal management is discussed.
2. Materials and Methods
2.1. Study Area
The study focuses on the NW Mediterranean coast from latitude 40°45′ N to 42°25′ N and from longitude 0°45′ E to 3°15′ E, a 700 km coastal stretch also known as Catalan coast (Figure 1). The reason for selecting this littoral zone is because it is a fetch-limited environment and, as a consequence, it is submitted to medium wave energy conditions. In this coastal area, there are already some sections in which the presence of seagrass meadows is noticeable being the two most abundant seagrass species Posidonia oceanica and Cymodocea nodosa. As pointed out by Vacchi et al. [44,88,89], the location of the seagrass meadows is conditioned by hydrodynamic conditions. In the study area, P. oceanica is located in coastal areas from water depths of 0.5 m up to 26–27 m (although, in general, they are located at depths of less than 20 m) occupying a surface of 61.23 km2. C. nodosa extends over 36.12 km2 between the surface and water depths greater than 15 m [90].
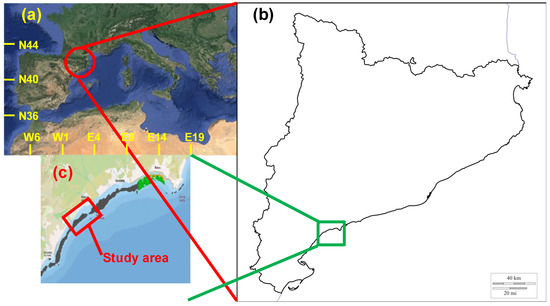
Figure 1.
Location of the study area. (a) Situation of the Catalan coast in the NW Mediterranean; (b) the Catalan coast; (c) the studied stretch, with spots indicating the presence of seagrass, where green corresponds to P. oceanica and black to unidentified species.
Another factor considered for selecting this area is the recent evolution of seagrass meadows there. In previous decades, between 1960 and 2010, seagrass meadows and particularly P. oceanica, have experienced a considerable regression in both occupied surface and number of plants. Currently, the surface of seagrass meadows of 75–80% compared to that of the pre-industrial era is estimated [90]. In the last years, surface losses have been barely perceptible [91] or even, in certain areas, there is a positive trend of seagrass surface evolution [92]. This improvement is probably due to a number of actions and the application of environmental regulations, as well as an increased awareness of the value of marine ecosystems [90].
In this coastal area, the wave climate is complex, and some strong events are controlled by large-scale synoptic activity [93], but local topography features (in particular orographic barriers such as the Pyrenees) condition the wind climate and, as a consequence, the wave patterns [94]. In addition, irregular bathymetry also contributes to local wave modification [95]. The directional distribution of waves indicates a predominance of NW and N wave conditions at the northern and southern stretches of the area, with E and S wave conditions prevailing in the central part. The most energetic waves are those from the E or E-NE because the stronger winds coincide with the largest fetches [95].
Finally, this area is a fetch-limited and a micro-tidal environment, with mixed tides predominantly semidiurnal and tidal ranges of about 20 cm [96].
2.2. Framework
The proposed methodology to determine the feasibility of seagrass meadows as a coastal protection measure is structured in five steps.
- Step 1. Analysis of the feasibility of using seagrass meadows at the selected site.
- Step 2. Assessment of the species suitable for this area and selection of the most appropriate.
- Step 3. Definition of different meadow configurations.
- Step 4. Simulation, using a numerical model of the wave propagation on the littoral area, considering the local wave climate corresponding to an average year.
- Step 5. Comparison of the numerical model results and selection, if applicable, of the best alternative.
To analyze the feasibility (step 1) of using seagrass meadows as a coastal protection measure in a coastal area, such area must fulfill several conditions. First of all, it must be a sandy coast susceptible to being eroded. Secondly, it should preferably be located in an area of medium- or low-wave energy because, as indicated before, high-energy environments reduce the density and effectiveness of the meadows [54,57,75,76,77,78]. Third, it must be an area with limited anthropogenic pressure affecting water quality, since its degradation may hinder meadow development. In particular, discharges of submarine outfalls and desalination plants must be avoided near the area of study to prevent such degradation. Finally, the historical presence of meadows in the area is not essential but it provides added value to the feasibility because it indicates the suitability of seagrass growth.
Taking into account these factors, a 3.1 km long coastal stretch located on the Catalan coast has been selected. As can be seen in Figure 1c, in this stretch there are already seagrass meadows, indicating that the use of seagrass in this region is possible. In the selected area, where a sandy coast exists, there are no desalination plants. In addition, the two submarine outfalls existing in this coastal stretch are connected to treatment plants and discharge to depths greater than 30 m, that are beyond the area where some seagrass species (e.g., P. oceanica) may exist. Finally, it can be considered a medium-wave energy area, due to the limited fetch conditions. All these considerations lead to the conclusion that the existence of seagrass meadows at the selected site is feasible (step 1).
For step 2, a list of seagrass species existing in similar or neighboring areas must be elaborated because among them are those that are more likely to succeed in a meadow creation or restoration process. As indicated in the previous section, in this region two main seagrass species are relatively abundant: P. oceanica and C. nodosa, which account for 63% and 37%, respectively, of the total seagrass surface on the Catalan coast, estimated at 97.35 km2 [90]. These two species have different plant features that can influence their contribution to wave attenuation such as leaf length and width, canopy height, root length or growth rate, among others. In particular, P. oceanica leaves are longer (1 m or more vs. 20–45 cm) and wider (1 cm vs. 0.6 cm) than those of C. nodosa. As pointed out by different authors [97], the attenuation of waves and currents depends on the meadow biomass, which is related to plant density and the size and number of leaves, being P. oceanica, the European species with the longest and widest leaves, the highest number of leaves per shoot and, as a consequence, the species with the greatest biomass. In addition, P. oceanica is more independent of seasonal variations than other species, so its biomass is more constant throughout the year [57]. Therefore, P. oceanica wave attenuation capacity should be higher, and, for this reason, this species has been selected for this study. In addition, the use and effectiveness of P. oceanica for wave attenuation have been widely studied in flume [49,50,85] or field experiments [98,99].
Step 3 consists of defining the different meadow configurations. This mainly includes meadow location (range of water depths), dimensions (surface occupied) and plant features (stem density and height). In addition, seagrass distribution is spatially heterogeneous, ranging from continuous to patchy meadows [100]. In this case, to limit the number of simulations to be carried out, only variations in stem density and height have been considered, keeping constant the dimensions of the meadow that extends along 3.1 km of coastline and 0.8 km in the cross-shore direction and assuming that the plants are uniformly distributed (Figure 2). The chosen setting is one of many possible options and has been selected just to illustrate the application of this methodology. Nevertheless, the limits of the meadow are within the range suggested by Vacchi et al. [88,89]. In the next section, the scenarios used in this study are described.
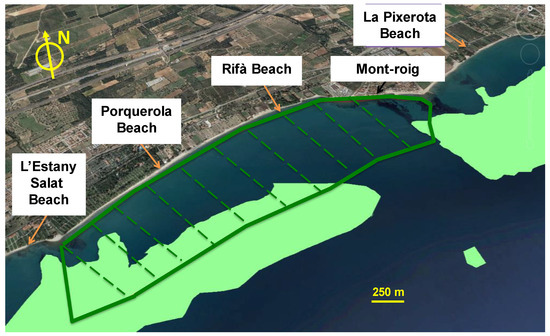
Figure 2.
Extension of the proposed meadow (dark green) and existing meadows (light green) in the study area.
For step 4, the wave propagation to the coast, there are different types of models that can be used such as Boussinesq-type models, which have been widely used to study coastal disaster reduction and protection [101,102,103]. In this case, the analysis has been carried out with the numerical model SWAN [104,105]. This model has been chosen because it is one of the common tools used worldwide for wave propagation and due to its ability to reproduce energy dissipation due to vegetation [38]. The influence of seagrass on hydrodynamics has been assessed through the vegetation module validated by Suzuki et al. [106].
Step 5 consists of the comparison of numerical model results between those of the selected scenarios and the reference situation to assess the effect of seagrass on hydrodynamics. In this way, at each node, the absolute difference in significant wave height (Hs) has been calculated, as well as the relative attenuation (in percentage). In addition, the maximum and average attenuation values in the points located in the meadow have been obtained.
2.3. Model Validation
The model has been validated without vegetation for different storms that occurred in the study area [107,108]. In particular, using data from a buoy located in the area, the SWAN model was validated for different events. Thus, for a storm that occurred in 2013 between February 27 and March 3, with Hs between 1 m and 4.5 m, the model achieved the following metrics that measure the deviation of the numerical results from the observations: RMSE = 0.22 m, bias = 0.01 m, scatter index = 0.11 and correlation coefficient r = 0.98.
In addition, for wave propagation on seagrass, the SWAN model was validated with data from flume experiments [109]. The data used for such validation were obtained from experiments conducted on the large-scale flume CIEM located at the Universitat Politècnica de Catalunya. In these experiments, the effect of P. oceanica on wave parameters and beach profile morphology was analyzed using a 10 m long seagrass meadow with 40 cm and 60 cm high leaves and 269 stems/m2 in a 2 m deep area.
Two series of tests were carried out with Tp = 3.71 s for both series and Hs = 0.41 m (R1) and Hs = 0.60 m (R2), respectively. The tests consisted of 12 time series of 500 waves and duration of 30 min each at prototype scale. Wave heights across the profile were recorded using different wave sensors (pressure transducers and acoustic and resistive wave gauges). For further details about the experiments and the recorded data, see Astudillo et al. [61].
The model was calibrated trying to fit the model results to the measured data, using the drag coefficient CD (which is closely related to the flexibility of the plant) as a calibration parameter. To this aim, the values of the drag coefficient were based on the estimated ranges of earlier experiments: Sánchez-González et al. [110] obtained CD values between 0.1–1.0, Cavallaro et al. [111] between 0.2–4.0 and Koftis et al. [50] between 0.75–2.0. Recently, Twomey et al. [112] reported values of CD in the range 0.18–2.30 for P. oceanica. The CD values used in the model calibration were 0.3, 0.7, 1.0 and 1.5, finding that the value that best fit the experimental data was 0.7.
This process showed the importance of this coefficient since, depending on the value adopted, differences in the significant wave height given by the model of up to 10 cm were obtained, which represents differences of up to 15%. For further details about the calibration process, see the work of Russek [109].
Figure 3 presents the comparison between experimental data and numerical model results, showing that the model fits the data reasonably well although it shows a slight tendency to overpredict the measured data, in particular, over and behind the meadow. The metrics measuring goodness-of-fit also reflect the good performance of the model. For experiment R1: RMSE = 0.022 m, normalized RMSE = 0.06, bias = 0.012 m, normalized bias = 0.03 and scatter index = 0.051 and for experiment R2: RMSE = 0.027 m, normalized RMSE = 0.05, bias = 0.003 m, normalized bias = 0.006 and scatter index = 0.050. Notice that the positive bias confirms this overprediction trend of the model.
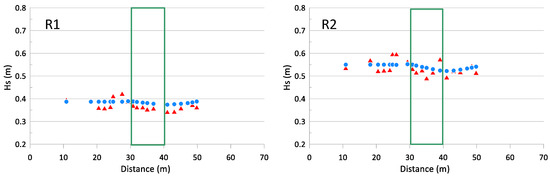
Figure 3.
Validation of the SWAN model with flume experiments. Red triangles: laboratory measurements; blue circles: model results; the green rectangle indicates the position of the seagrass meadow in the flume. R1: Waves with Hs = 0.41 m; R2: Waves with Hs = 0.60 m.
2.4. Model Configuration
For the modeling of the selected coastal stretch, the study considers four littoral scenarios:
- -
- Scenario 0. Absence of seagrass meadows. This is used as reference scenario for comparing the amount of energy reaching the coastal area and, thus, the efficiency of the different meadow configurations in dissipating wave energy.
- -
- Scenario A. Existence of a meadow of P. oceanica in the study area, with an average meadow height of 0.5 m and a density of 150 stems/m2.
- -
- Scenario B. Existence of a meadow of P. oceanica in the study area, with an average prairie height of 0.25 m and a density of 150 stems/m2.
- -
- Scenario C. Existence of P. oceanica meadows in the study area, with an average meadow height of 0.5 m and a density of 500 stems/m2.
In the area of study, some presence of seagrass meadows has been identified (Figure 1c), but their state of conservation is unknown. For this reason, the effect that the existing natural meadows may have on hydrodynamics has been disregarded and, accordingly, the reference case of the numerical simulation (Scenario 0) is characterized by the total absence of seagrass. On the contrary, seagrass configurations A, B and C represent different degrees of maturity and only have to be understood as tests for long-term action strategies. Scenarios A and B are representative of the initial stages of the intervention whereas scenario C is representative of a well-developed meadow achieved at a longer time scale. Thus, the numerical modeling for scenarios A, B and C contemplates the existence of a meadow artificially restored, with the values of seagrass height and density previously indicated and dimensions 3.1 × 0.8 km, whose location is shown in Figure 2.
The set-up of the SWAN model for its application to the study area requires the definition of several seagrass parameters to carry out the interaction between hydrodynamics and the meadow:
- -
- Meadow density: Studies carried out by Ruiz et al. [90] reported that the average density of P. oceanica meadows in the Catalan coast ranged between 150 and 1000 stems/m2. Some local studies of characterization showed a local density of 455 stems/m2, with a coverage of 30%. For this reason, a conservative value of 150 stems/m2 has been selected for scenarios A and B. For scenario C, a density of 500 stems/m2 has been assumed, simulating a successful case of seagrass artificial planting.
- -
- Canopy height: Although the leaf heights have up to 1 m in the study area [90], what matters is the canopy height, which is lower than the length of the leaves due to their bending. As indicated above, two values have been considered: 0.5 m and 0.25 m, corresponding, respectively to mature or young plants.
- -
- Plant diameter: For the three scenarios with plants, an equivalent diameter of 0.01 m has been assumed considering the data of Dalla Via et al. [113] and Zeller et al. [114]. Nevertheless, according to data of Ruiz et al. [90], this hypothesis is conservative, and the obtained results can be considered a lower bound of the wave attenuation obtained by the analyzed seagrass meadows.
- -
- Drag coefficient: The literature indicates that the coefficient of friction, defined as CD, is a function of the hydrodynamic conditions, water depth and intrinsic properties of the meadow (which determine the plant flexibility) [115]. In this study, CD has been obtained from the results of the calibration process.
Wave propagation has been performed nesting three domains, with progressive reduction of mesh dimensions and results of the coarser grids providing boundary conditions for the finer ones (Figure 4). The outer grid (DOM 3) is rectangular and has a spatial resolution of 200 × 200 m; the intermediate grid (DOM 2) is also rectangular and 70 × 70 m; the finer mesh (DOM 1) is curvilinear of dimensions of 15 × 18 m if the water depth is greater than 14 m and 8 × 18 m for shallower depths.
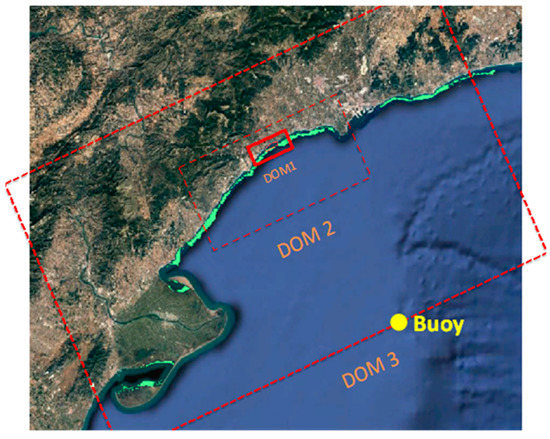
Figure 4.
Location of the three domains used in numerical modelling and the buoy where the wave data were recorded.
To analyze the performance of the different meadow configurations, the local wave climate has been considered. To this aim, wave data recorded at a buoy located in the study area (Figure 4) and managed by the Spanish Port Authority (Puertos del Estado) have been used [116]. These data have been grouped by directions (in sectors of 22.5°) and wave heights (in bins of 1 m), obtaining the frequency of each combination. Each hydrodynamic condition has been propagated towards the coast, considering the combinations (with the frequency of occurrence greater than 0) of Hs and directions that generate incident waves towards the coast, as shown in Table 1. Between parenthesis, the number of wave periods considered for each combination of wave height and direction is indicated. Accordingly, 74 different wave conditions have been considered for each scenario, giving a total of 296 numerical simulations (74 wave conditions x 4 scenarios).

Table 1.
Combinations of directions and wave heights were considered in the study.
The output of the numerical simulations are the values of significant wave height (Hs) at each node of the domain. With the aim of obtaining representative results for an average wave climate, an integration of all the matrices resulting for each of the scenarios has been conducted, as explained in the next section. The obtained results correspond to the annual average of Hs at each node for each scenario.
3. Results
Figure 5 shows the annual average Hs at each point i (Ĥsi) for the DOM2 obtained by multiplying the Hsij obtained at each point i in each simulation j by the frequency of presentation (fj) of the wave conditions simulated and making the addition of the values corresponding to all simulations (74) at each node, as shown in Equation (1).
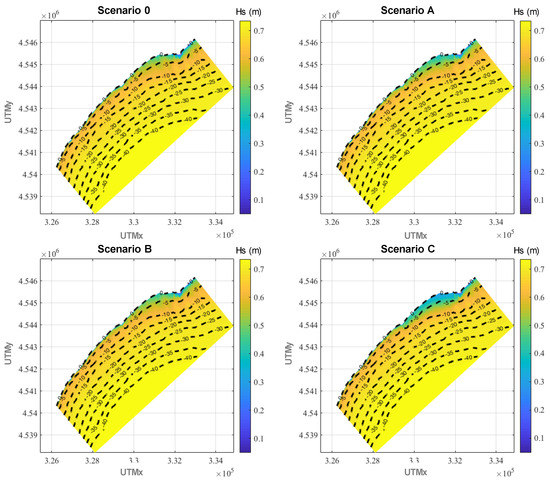
Figure 5.
Annual average significant wave height in the nearshore area for the four scenarios analyzed.
As can be seen, the annual average Hs is relatively small, with values of around 0.7 m or even smaller in the entire studied domain. This is because this is a fetch-limited area (in all directions) and the intensity, in terms of Hs, the biggest storms are constrained by these bounded fetches. Although extreme events with Hs greater than 3 m are recorded in the area, their frequency of presentation is very small (around 2%) and they hardly contribute to the annual average [116], while waves with Hs ≤ 2 m represent almost the 95%, as shown in Figure 6.
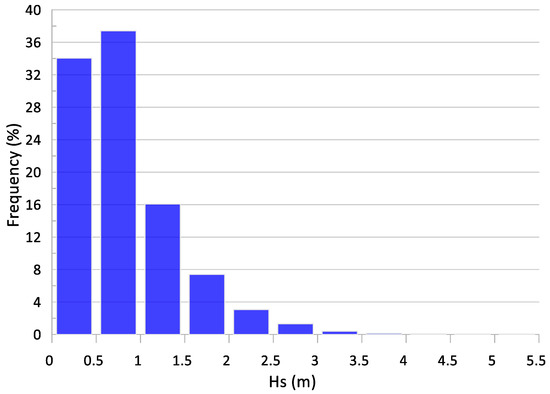
Figure 6.
Histogram of waves recorded in the buoy during the period 2004–2021.
In particular, for all scenarios, a Hs of 0.7 m is observed between the outer limit of the domain and water depths of 15 m. From there towards the shoreline, Hs progressively decreases due to bottom friction and wave breaking. This wave attenuation is more intense in the area where the seagrass meadow is located (water depths between 10 and 3 m).
On the other hand, a superficial comparison of the annual average Hs of the four scenarios does not show any appreciable difference among them in most of the plotted areas. This happens because the seagrass meadow (where the greatest differences could take place) only covers a small fraction of such area. Nevertheless, if the differences in annual average Hs are plotted in the area where the meadow is located (Figure 7, Figure 8 and Figure 9), the wave attenuation due to the presence of the meadow is clearly perceptible and major differences in annual averaged Hs are found where the seagrass is located.
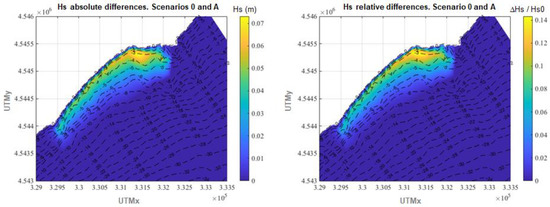
Figure 7.
Differences in annual average Hs between scenario 0 and scenario A. Left panel: absolute differences. Right panel: relative differences.
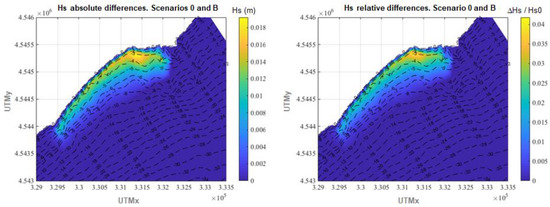
Figure 8.
Differences in annual average Hs between scenario 0 and scenario B. Left panel: absolute differences. Right panel: relative differences.
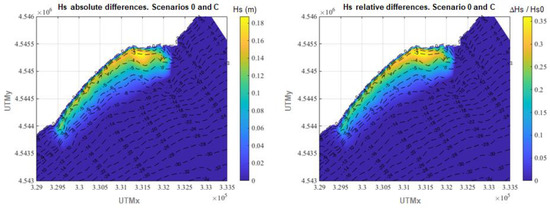
Figure 9.
Differences in annual average Hs between scenario 0 and scenario C. Left panel: absolute differences. Right panel: relative differences.
Thus, Figure 7 which represents differences in average Hs in scenario A with respect to scenario 0 shows how the average Hs reduction over the area where the meadow is located is 2.1 cm, which represents in relative terms 3.7%. The maximum attenuation values reached in such area are 7.3 cm or 14.3% with respect to the reference scenario. Although the average wave attenuation may seem poor, if the 75th percentile is considered, the Hs decrease ranges between 6.0% and 14.3%, mainly concentrated between isobaths −1 and −5 m.
In Figure 8, the differences in annual average Hs between scenarios 0 and B are presented. The results show an average reduction of the annual Hs over the meadow of 0.5 cm, which represents a relative decrease of 1.0%. The maximum reduction of annual average Hs reached is 1.9 cm, which represents 4.2%. If the 75th percentile of the obtained values is taken into account, the wave attenuation ranges between 1.6% and 4.2%, also concentrated in water depths between 1 m and 5 m.
Finally, in Figure 9, the differences in annual average Hs between scenario 0 and scenario C are shown. In these cases, the average Hs reduction over the meadow is 5.9 cm representing, in relative terms, 10.5%. The maximum values of attenuation recorded are 18.8 cm and 36.1%. If the 75th percentile of the obtained results is considered, the Hs reduction ranges between 17.4% and 36.1%, mostly located between isobaths −1 m and −5 m.
4. Discussion
4.1. Wave Attenuation Due to Seagrass
Results show that, even considering plant and seagrass conservative parameters (plant diameter, stem density, plant height), a significant reduction of annual average wave heights reaching the beach can be achieved by placing seagrass meadows (through implantation or restoration) in front of a sandy beach. These reductions range between 1% and 10.5% of all the meadow area is considered and between 1.6% and 36.1% if only the area with greater submergence ratios is considered. As both wave set-up and sediment transport are dependent on wave height, this leads to a reduction of the flooding and erosive potential of waves in this area and, accordingly, contributes to coastal protection. The obtained results, based on numerical modeling are in agreement with observations in flume tests [49,50,61,85], field experiments [98,99] or other numerical studies [117,118,119].
Although the wave reduction achieved with the presence of the meadow may seem modest, as shown by Astudillo et al. [61] in field experiments at the prototype scale, a decrease in wave height of about 8% can lead to significant reductions of sediment transport and shoreline retreat. In addition, it must be stressed that the obtained values refer to the annual average wave energy reaching the beach so that the protection effect on the beach extends over time.
The wave attenuation attained is strongly related to the meadow concentration, in particular stem density and canopy height. Thus, if the stem density is the same, the wave attenuation is greater for greater canopy heights, as shown in Figure 10, where the relative differences between scenarios B and A are shown, reaching values up to 11%.
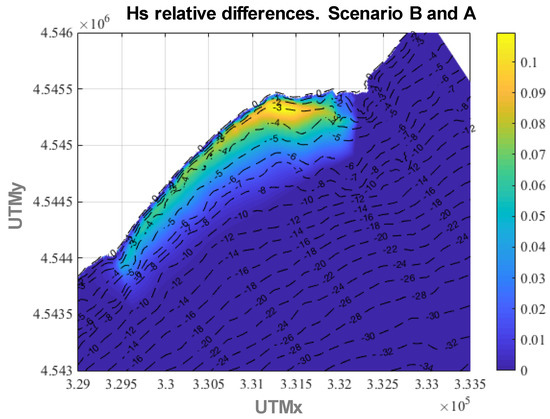
Figure 10.
Relative differences in annual average Hs between scenario B and scenario A.
In the same way, if the canopy height is the same but the density is larger, wave attenuation is greater, as shown in Figure 11, where the relative differences in Hs between scenarios A and C are presented, attaining values up to 26%. This is in line with Paul and Amos [80] who indicated that a minimum shoot density is necessary to achieve wave damping.
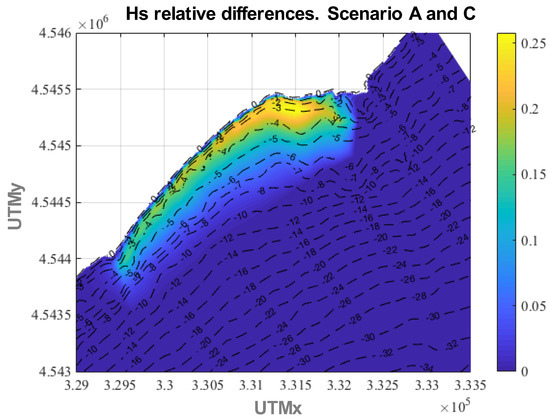
Figure 11.
Relative differences in annual average Hs between scenario C and scenario A.
Another remarkable feature of the results is that the largest wave damping is concentrated in water depths between 1 and 5 m. This is because the reduction takes place mainly when the submergence ratio (canopy height over water depth) is greater than 0.19, as shown by several authors [49,50,85,120]. For water depths greater than 5 m, the submergence ratio is smaller than 0.1, greatly reducing the effectiveness of the meadow in attenuating waves. On the other hand, for water depths less than 1 m, most of the energy is dissipated by bottom friction and wave breaking and, as a consequence, the differences in average wave heights are negligible among the studied scenarios.
Another factor analyzed in this study is the wave attenuation carried out by seagrass meadows as a function of the incident wave direction. With this aim, results between scenario A and scenario 0 (reference) have been compared for the six wave directions considered (ENE, E, ESE, SE, SSE and S), being the results shown in Figure 12. Although there are slight differences between the wave damping reached in each direction (values between 7.25% for the E and 8.51% for the ESE), the differences are small, indicating that the wave direction is not significant in the wave attenuation process. This is because the wave height reduction takes place in the areas with greater submergence ratios in the wave path over the meadow. Anyway, whatever the direction of the waves, the distance traveled over the area of the meadow with greater submergence ratios is long enough for the waves to feel the effect of the plants.
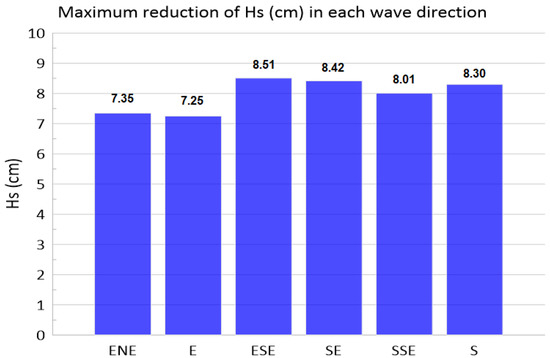
Figure 12.
Results of wave attenuation for the wave directions were taken into account in the study.
4.2. Limitations of the Study
The presented results are illustrative of the potential of seagrass meadows for coastal protection, but the limitations of the modeling process and associated uncertainties must be taken into account. The model is a simplification of a very complex reality and cannot accurately reproduce the wave behavior as it interacts with the meadow. This is due to the difficulty of reproducing some factors such as plant flexibility, which is closely linked to the drag coefficient [111]. The overall trend is that the drag coefficient (and as a consequence the wave height reduction) decreases with plant flexibility [109,111]. This is a very important point since, as noted in Section 2.3, variations in the drag coefficient can lead to differences in model results of up to 15%. Nevertheless, in some scenarios, the impact of plant flexibility may be irrelevant because it is overshadowed by others. Thus, Dijkstra and Uittenbogaard [121] pointed out that in a very dense meadow plant flexibility may not matter anymore since plant position is unlikely to change because it has no space to do it.
Another potential source of uncertainty would be the presence of tidal currents, which would modify wave propagation patterns and wave–meadow interactions. Nevertheless, in open coasts located in micro-tidal environments such as the case studied here, tidal currents are negligible and do not affect the results.
Another uncertainty factor is associated with the accuracy of the numerical model. Although, as shown when comparing the model results with experimental data, the degree of approximation obtained is reasonable, the model tends to slightly overpredict the wave height. In particular, this happens over and behind the meadow. However, it is to be expected that the error made in evaluating Hs is bounded. In addition, for comparative purposes as here, in which the aim is to determine which is the best option among several settings, the final result obtained will be the best alternative.
4.3. Implications for Coastal Protection
It must be stressed that the studied area is not a high-wave energy environment, due to the aforementioned limited fetches. As pointed out by several authors [57,122,123] in areas of large wave energy, the effectiveness of seagrass meadows as a coastal protection measure is reduced because large storms generate a decline in meadow density. This is due to the high level of sediment movement generated by large wave energy, which exposes seagrass to considerable erosion with subsequent exposure of roots and rhizomes [124]. In addition, as pointed out by other authors [125,126], the shelter of seedlings plays an important role in the success of restauration. In our case, the studied area can be considered a medium-wave energy environment (95% of sea states with Hs ≤ 2 m, as indicated in Section 3) and, for this reason, the coastal protection provided by the meadow is greater than in more energetic coastal regions.
Therefore, although some of the parameters used to characterize the meadow are conservative and the model tends to overpredict wave heights, so that the obtained results may be considered a lower bound of what might be expected, significant wave damping can be achieved by using seagrass meadows in coastal zones with limited wave energy but placing them in areas where the submergence ratio is relatively large (greater than 0.1). Thus, as shown in this study, the annual average amount of wave energy reaching coastal areas can be reduced by such meadows and, hence, beach erosion and flooding decreased.
Taking into account the previous considerations, we can conclude that seagrass meadows may be an effective littoral protection measure and it is worth considering them in coastal defense projects.
As indicated above, the use of seagrass as a coastal protection measure requires the conservation, restoration or creation of new seagrass meadows. Although seagrass rehabilitation has failed in some cases due to a variety of factors [127,128,129,130], recent successful projects have demonstrated that active restoration facilitates the recovery of seagrass meadows [126,130,131,132,133,134,135,136]. Consequently, in fetch-limited areas where the wave energy is limited and where the environmental conditions allow the restoration or implantation of seagrass meadows, coastal managers should consider its use as a coastal protection measure. In this way, the methodology described here can be a useful tool for coastal stakeholders to help them in the design of seagrass meadows with the aim of coastal protection. In addition, a project focused on the use of seagrass for coastal defense could consider more scenarios, so that the wider variety of meadow typologies and configurations analyzed could increase the probability of success.
The study should be completed with a cost-benefit analysis. This analysis is not addressed in this case due to the difficulty of assessing the value of all ecosystem services provided by the seagrass meadow. Anyway, in the long term, as pointed out by different authors [21,22], the lower maintenance costs associated with NBS with respect to conventional engineering alternatives plus the additional (besides coastal protection) ecosystem services that they provide, make it very likely that the benefits using seagrass meadows as a coastal defense measure far exceed their costs. Finally, seagrass meadows can contribute to climate change mitigation through carbon sequestration and, in contrast to artificial structures, they may naturally adapt to climate change maintaining their coastal protection function [137].
5. Conclusions
A methodological framework to assess the effectiveness of transplanted seagrass meadows as a coastal protection measure has been developed. It includes the analysis of the feasibility of using seagrass at a certain site, the selection of the most suitable species, the definition of different meadow configurations, the numerical simulation of wave propagation over the meadows (over an average wave climate year) and the selection of the best alternative.
To illustrate the usefulness of the proposed methodology, it has been applied to a coastal stretch of the Catalan coast (NW Mediterranean). Although only a reduced number of meadow configurations and conservative plant parameters have been simulated, the results show that significant reductions (up to 10.5% on average over the meadow and up to 36.1% in the areas with maximum attenuation) in the average annual wave height can be achieved in the nearshore area due to the presence of the seagrass meadow. The wave damping depends largely on canopy height and meadow density. The greater the value of these parameters, the greater the wave attenuation reached. Another fact to be taken into account is that the meadow is particularly effective in dissipating wave energy if the submergence ratio is relatively large (greater than 0.19). The main implications for coastal protection are the following:
- -
- The presence of seagrass meadows reduces the amount of energy reaching the beach, which contributes to its defense against flooding and erosion.
- -
- The seagrass meadow creation or restoration can be an effective coastal protection measure. In addition, such measures provide other ecosystem services that enhance their suitability,
- -
- The use of seagrass meadows as a coastal protection measure is especially suitable in fetch-limited areas, where the intensity of storms is conditioned by such bounded fetches.
- -
- Restoration and implantation of meadows are more likely to succeed and prevail if a large density of shoots or seeds is used. This, in turn, increases the effectiveness of the meadow to reduce wave heights reaching the coast, so the additional cost of planting more seagrass is widely compensated by its enhanced coastal protection function and the ecosystem services it provides.
- -
- Coastal managers can use the methodology described here to assess whether the use of seagrass meadows is feasible in their areas of jurisdiction and, if possible, decide on the optimal meadow layout to achieve the desired level of protection.
Author Contributions
Conceptualization, J.P.S. and V.G.; methodology, V.G.; software, X.C., M.G.-L. and J.L.-Y.; validation, X.C., M.G.-L. and J.L.-Y.; formal analysis, V.G. and C.M.; investigation, X.C., M.G.-L. and C.M.; resources, M.G.-L., C.M. and J.L.-Y.; data curation, X.C., M.G.-L., C.M. and J.L.-Y.; writing—original draft preparation, J.P.S., V.G. and X.C.; writing—review and editing, J.P.S. and V.G.; visualization, J.P.S. and X.C.; supervision, J.P.S. and V.G.; project administration, J.P.S. and V.G.; funding acquisition, J.P.S., V.G. and C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded by the Spanish Government within the Research, Development and Innovation Program through the grant to COBALTO project (REF CTM2017-88036-R).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available upon request to the authors.
Acknowledgments
The support of the Secretaria d’Universitats i Recerca del Departament d’Economia i Coneixement de la Generalitat de Catalunya (Ref 2014SGR1253) is also acknowledged. The authors also wish to acknowledge Puertos del Estado for providing wave data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nicholls, R.J.; Marinova, N.; Lowe, J.A.; Brown, S.; Vellinga, P.; De Gusmão, D.; Hinkel, J.; Tol, R.S.J. Sea-level rise and its possible impacts given a ‘beyond 4 °C world’ in the twenty-first century. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 161–181. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Arcilla, A.; Mösso, C.; Sierra, J.P.; Mestres, M.; Harzallah, A.; Senouci, M.; El Raey, M. Climate drivers of potential hazards in Mediterranean coasts. Reg. Environ. Chang. 2011, 11, 617–636. [Google Scholar] [CrossRef]
- Sierra, J.P.; Casas-Prat, M. Analysis of potential impacts on coastal areas due to changes in wave conditions. Clim. Chang. 2014, 124, 861–876. [Google Scholar] [CrossRef]
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R. Future coastal population growth and exposure to sea-level rise and coastal flooding—A global assessment. PLoS ONE 2015, 10, e0118571. [Google Scholar] [CrossRef] [PubMed]
- Casas-Prat, M.; McInnes, K.L.; Hemer, M.A.; Sierra, J.P. Future wave-driven coastal sediment transport along the Catalan coast (NW Mediterranean). Reg. Environ. Chang. 2016, 16, 1739–1750. [Google Scholar] [CrossRef]
- Di Risio, M.; Bruschi, A.; Lisi, I.; Pesarino, V.; Pasquali, D. Comparative analysis of coastal flooding vulnerability and hazard assessment at national scale. J. Mar. Sci. Eng. 2017, 5, 51. [Google Scholar] [CrossRef]
- Wahl, T.; Haigh, I.D.; Nicholls, R.J.; Arns, A.; Dangendorf, S.; Hinkel, J.; Slangen, A.B.A. Understanding extreme sea levels for broad-scale coastal impact and adaptation analysis. Nat. Commun. 2017, 8, 16075. [Google Scholar] [CrossRef]
- Grases, A.; Gracia, V.; García-León, M.; Lin-Ye, J.; Sierra, J.P. Coastal flooding and erosion under a changing climate: Implications at a low-lying coast (Ebro Delta). Water 2020, 12, 346. [Google Scholar] [CrossRef]
- Molina, R.; Manno, G.; Lo Re, C.; Anfuso, G.; Ciraolo, G. A methodological approach to determine sound response modalities to coastal erosion processes in Mediterranean Andalusia (Spain). J. Mar. Sci. Eng. 2020, 8, 154. [Google Scholar] [CrossRef]
- Kron, W. Coasts: The high-risk areas of the world. Nat. Hazards 2013, 66, 1363–1382. [Google Scholar] [CrossRef]
- Sierra, J.P.; Dowding, D.D.; Persetto, V.; Oliveira, T.A.C.; Gironella, X.; Mösso, C.; Mestres, M. Wave reflection, transmission and spectral changes at permeable low-crested structures. J. Coast. Res. 2011, SI 64, 593–597. [Google Scholar]
- Linham, M.M.; Nicholls, R.J. Adaptation technologies for coastal erosion and flooding: A review. Proc. Inst. Civ. Eng. Marit. Eng. 2012, 165, 95–112. [Google Scholar] [CrossRef]
- Sauvé, P.; Bernatchez, P.; Glaus, M. Identification of coastal defence measures best adapted to mitigate hazards in specific coastal systems: Development of a dynamic literature meta-analysis methodology. J. Mar. Sci. Eng. 2022, 10, 394. [Google Scholar] [CrossRef]
- Qu, K.; Lie, Y.; Wang, X.; Li, X. Numerical analysis of influences of emergent vegetation patch on runup processes of focused wave groups. J. Mar. Sci. Eng. 2023, 11, 8. [Google Scholar] [CrossRef]
- Nguyen, T.P. Malaleuca entrapping microsites as a nature based solution to coastal erosion: A pilot study in Kien Giang, Vietnam. Ocean Coast. Manag. 2018, 155, 98–103. [Google Scholar] [CrossRef]
- Vieira, B.F.V.; Pinho, J.L.S.; Barros, J.A.O.; do Carmo, J.S.A. Hudrodynamics and morphodynamics performance assessment of three coastal protection structures. J. Mar. Sci. Eng. 2020, 8, 175. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.; Ysebaert, T.; De Vriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef]
- Patrick, C.J.; Weller, D.E.; Li, X.; Ryder, M. Effects of shoreline alteration and other stressors on submerged aquatic vegetation in subestuaries of Chesapeake Bay and the Mid-Atlantic coastal bays. Estuaries Coasts 2014, 37, 1516–1531. [Google Scholar] [CrossRef]
- Temmerman, S.; Kirwan, M.L. Building land with a rising sea. Science 2015, 349, 588–589. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Williams, A.; Anfuso, G. Hard protection structures as a principal coastal erosion management strategy along the Caribbean coast of Colombia. A chronicle of pitfalls. Ocean Coast. Manag. 2018, 156, 58–75. [Google Scholar] [CrossRef]
- Sutton-Grier, A.E.; Wowk, K.; Bamford, H. Future of our coasts: The potential for natural and hybrid infrastructure to enhance the resilience of our coastal communities, economies and ecosystems. Environ. Sci. Policy 2015, 51, 137–148. [Google Scholar] [CrossRef]
- Narayan, S.; Beck, M.W.; Reguero, B.G.; Losada, I.J.; Van Wesenbeeck, B.; Pontee, N.; Sanchirico, J.N.; Ingram, J.C.; Lange, G.M.; Burks-Copes, K.A. The effectiveness, costs and coastal protection benefits of natural and nature-based defences. PLoS ONE 2016, 11, e0154735. [Google Scholar] [CrossRef] [PubMed]
- Saleh, F.; Weinstein, M.P. The role of nature-based infrastructure (NBI) in coastal resilience planning: A literature review. J. Environ. Manag. 2016, 183, 1088–1098. [Google Scholar] [CrossRef] [PubMed]
- Gracia, V.; Sierra, J.P.; Caballero, A.; García-León, M.; Mösso, C. A methodological framework for selecting an optimal sediment source within a littoral cell. J. Environ. Manag. 2021, 296, 113207. [Google Scholar] [CrossRef]
- Cheong, S.M.; Silliman, B.; Wong, P.P.; Van Wesenbeeck, B.; Kim, C.K.; Guannel, G. Coastal adaptation with ecological engineering. Nat. Clim. Chang. 2013, 3, 787–791. [Google Scholar] [CrossRef]
- Belhassen, Y.; Rousseau, M.; Tynyakov, J.; Shashar, N. Evaluating the attractiveness and effectiveness of artificial coral reefs as a recreational ecosystem service. J. Environ. Manag. 2017, 203, 448–456. [Google Scholar] [CrossRef]
- Varin, M.; Théau, J.; Fournier, R.A. Mapping ecosystem services provided by wetlands at multiple spatiotemporal scales: A case study in Quebec, Canada. J. Environ. Manag. 2019, 246, 334–344. [Google Scholar] [CrossRef]
- Hafezi, M.; Stewart, R.A.; Sahin, O.; Giffin, A.L.; Mackey, B. Evaluating coral reef ecosystem services outcomes from climate change adaptation strategies using integrative system dynamics. J. Environ. Manag. 2021, 285, 112082. [Google Scholar] [CrossRef]
- Gacia, E.; Duarte, C.M. Sediment retention by a Mediterranean Posidonia oceanica meadow: The balance between deposition and resuspension. Estuar. Coast. Shelf Sci. 2001, 52, 505–514. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields, Coast. Eng. 2004, 51, 103–118. [Google Scholar]
- Lentz, S.J.; Churchill, J.H.; Davis, K.A.; Farrar, J.T. Surface gravity wave transformation across a platform coral reef in the Red Sea. J. Geophys. Res. Oceans 2016, 121, 693–705. [Google Scholar] [CrossRef]
- Reguero, B.G.; Beck, M.W.; Agostini, V.N.; Kramer, P.; Hancock, B. Coral reefs for coastal protection: A new methodological approach and engineering case study in Grenada. J. Environ. Manag. 2018, 210, 146–161. [Google Scholar] [CrossRef] [PubMed]
- La Hausse de Lalouvière, C.; Gracia, V.; Sierra, J.P.; Lin-Ye, J.; García-León, M. Impact of climate change on nearshore waves at a beach protected by a barrier reef. Water 2020, 12, 1681. [Google Scholar] [CrossRef]
- Piazza, B.P.; Banks, P.D.; La Peyre, M.K. The potential for created oyster shell reefs as a sustainable shoreline protection strategy in Lousiana. Restor. Ecol. 2005, 13, 499–506. [Google Scholar] [CrossRef]
- Scyphers, S.B.; Powers, S.P.; Heck, K.L., Jr.; Byron, D. Oyster reefs as natural breakwaters mitigate shoreline loss and facilitate fisheries. PLoS ONE 2011, 6, e22396. [Google Scholar] [CrossRef]
- Donker, J.J.A.; van der Vegt, M.; Hoekstra, P. Wave forcing over an intertidal mussel bed. J. Sea Res. 2013, 82, 54–66. [Google Scholar] [CrossRef]
- Gedan, K.B.; Kirwan, M.L.; Wolanski, E.; Barbier, E.B.; Silliman, B.R. The present and future role of coastal wetland vegetation in protecting shorelines: Answering recent challenges to the paradigm. Clim. Chang. 2011, 106, 7–29. [Google Scholar] [CrossRef]
- Vuik, V.; Jonkman, S.N.; Borsje, B.W.; Suzuki, T. Nature-based flood protection: The efficiency of vegetated foreshores for reducing wave loads on coastal dikes. Coast. Eng. 2016, 116, 42–56. [Google Scholar] [CrossRef]
- Gijsman, R.; Horstman, E.M.; van der Wal, D.; Friess, D.A.; Swales, A.; Wijnberg, K.M. Nature-based engineering: A review on reducing coastal flood risk with mangroves. Front. Mar. Sci. 2021, 8, 702412. [Google Scholar] [CrossRef]
- Das, S.; Vincent, J.R. Mangroves protected villages and reduced death toll during Indian super cyclone. Proc. Natl. Acad. Sci. USA 2009, 106, 7357–7360. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, H.; Li, Y.; Xu, H.; Shen, J.; Rhome, J.; Smith III, T.J. The role of mangroves in attenuating storm surges. Estuar. Coast. Shelf Sci. 2012, 102–103, 11–23. [Google Scholar] [CrossRef]
- Kelty, K.; Tomiczek, T.; Cox, D.T.; Lomonaco, P.; Mitchell, W. Prototype-scale ophysical model of wave attenuation through a mangrove forest of moderate cross-shore thickness: LiDAR-based characterization and Reynolds scaling for engineering with Nature. Front. Mar. Sci. 2022, 8, 780946. [Google Scholar] [CrossRef]
- Hemminga, M.; Duarte, C.M. Seagrass Ecology; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Vacchi, M.; De Falco, G.; Simeone, S.; Montefalcone, M.; Morri, C.; Ferrari, M.; Bianchi, C.N. Biogeomorphology of the Mediterranean Posidonia oceanica seagrass meadows. Earth Surf. Proc. Landf. 2017, 42, 42–54. [Google Scholar] [CrossRef]
- Githaiga, M.N.; Frouws, A.M.; Kairo, J.G.; Huxham, M. Seagrass removal leads to rapid changes in fauna and loss of carbon. Front. Ecol. Evol. 2019, 7, 62. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Yadav, N.S.; Barak, S.; Lima, F.P.; Sapir, Y.; Winters, G. Responses of invasive and native populations of the seagrass Halophila stipulacea to simulated climate change. Front. Mar. Sci. 2020, 6, 812. [Google Scholar] [CrossRef]
- Valdez, S.R.; Zhang, Y.S.; van der Heide, T.; Vanderklift, M.A.; Tarquinio, F.; Orth, R.J.; Solliman, B.R. Positive ecological interactions and the success of seagrass restoration. Front. Mar. Sci. 2020, 7, 91. [Google Scholar] [CrossRef]
- Infantes, E.; Orfila, A.; Simarro, G.; Terrados, J.; Luhar, M.; Nepf, H. Effect of seagrass (Posidonia oceánica) meadow on wave propagation. Mar. Ecol. Prog. Ser. 2012, 456, 63–72. [Google Scholar] [CrossRef]
- Manca, E.; Cáceres, I.; Alsina, J.M.; Stratigaki, V.; Townend, I.; Amos, C.L. Wave energy and wave-induced flow reduction by full-scale model Posidonia oceanica seagrass. Cont. Shelf Res. 2012, 50–51, 100–116. [Google Scholar] [CrossRef]
- Koftis, T.; Prinos, P.; Stratigaki, V. Wave damping over artificial Posidonia oceanica meadow: A large-scale experimental study. Coast. Eng. 2013, 73, 71–83. [Google Scholar] [CrossRef]
- Reidenbach, M.A.; Thomas, E.L. Influence of the seagrass Zoostera marina, on wave attenuation and bed shear stress within a shallow bay. Front. Mar. Sci. 2018, 5, 397. [Google Scholar] [CrossRef]
- Hansen, J.C.R.; Reidenbach, M.A. Wave and tidally driven flows in eelgrass beds and their effect on sediment suspension. Mar. Ecol. Prog. Ser. 2012, 448, 271–287. [Google Scholar] [CrossRef]
- Christianen, M.J.A.; van Belzen, J.; Herman, P.M.J.; van Katwijk, M.M.; Lamers, L.P.M.; van Leent, P.J.M.; Bouma, T.J. Low-canopy seagrass beds still provide important coastal protection services. PLoS ONE 2013, 8, e62413. [Google Scholar] [CrossRef]
- James, R.K.; Lynch, A.; Herman, P.M.J.; van Katwijk, M.M.; van Tussenbroek, B.I.; Dijkstra, H.A.; van Westen, R.M.; van der Boog, C.G.; Klees, R.; Pietrzak, J.D.; et al. Tropical biogeomorphic seagrass landscapes for coastal protection: Persistence and wave attenuation during major storm events. Ecosystems 2021, 24, 301–318. [Google Scholar] [CrossRef]
- De Boer, W.F. Seagrass–sediment interactions, positive feedbacks and critical thresholds for occurrence: A review. Hydrobiologia 2007, 591, 5–24. [Google Scholar] [CrossRef]
- Hendriks, I.E.; Bouma, T.J.; Morris, E.P.; Duarte, C.M. Effects of seagrasses and algae of the Caulerpa family on hydrodynamics and particle-trapping rates. Mar. Biol. 2010, 157, 473–481. [Google Scholar] [CrossRef]
- Ondiviela, B.; Losada, I.J.; Lara, J.L.; Maza, M.; Galván, C.; Bouma, T.J.; van Belzen, J. The role of seagrasses in coastal protection in a changing climate. Coast. Eng. 2014, 87, 158–168. [Google Scholar] [CrossRef]
- Potouroglou, M.; Bull, J.C.; Krauss, K.W.; Kennedy, H.A.; Fusi, M.; Daffonchio, D.; Mangora, M.M.; Githaiga, M.N.; Diele, K.; Huxham, M. Measuring the role of seagrasses in regulating sediment surface elevation. Sci. Rep. 2017, 7, 11917. [Google Scholar] [CrossRef]
- Paul, M. The protection of sandy shores—Can we afford to ignore the contribution of seagrass? Mar. Pollut. Bull. 2018, 134, 152–159. [Google Scholar] [CrossRef] [PubMed]
- James, R.K.; Silva, R.; van Tussenbroek, B.I.; Escudero-Castillo, M.; Mariño-Tapia, I.; Dijkstra, H.A.; van Westen, R.M.; Pietrzak, J.D.; Candy, A.S.; Katsman, C.A.; et al. Maintaining tropical beaches with seagrass and algae: A promising alternative to engineering solutions. Bioscience 2019, 69, 136–142. [Google Scholar] [CrossRef]
- Astudillo, C.; Gracia, V.; Cáceres, I.; Sierra, J.P.; Sánchez-Arcilla, A. Beach profile changes induced by surrogate Posidonia oceánica: Laboratory experiments. Coast. Eng. 2022, 175, 104144. [Google Scholar] [CrossRef]
- Duarte, C.M.; Dennison, W.C.; Orth, R.J.W.; Carruthers, T.J.B. The charisma of coastal ecosystems: Addressing the imbalance. Estuaries Coast 2008, 31, 233–238. [Google Scholar] [CrossRef]
- Nordlund, L.; de la Torre-Castro, M.; Erlandsson, J.; Conand, C.; Muthiga, N.; Jiddawi, N.; Gullström, M. Intertidal zone management in the western Indian Ocean: Assessing current status and future possibilities using expert opinions. Ambio 2014, 43, 1006–1019. [Google Scholar] [CrossRef] [PubMed]
- Nordlund, L.M.; Jackson, E.L.; Nakaoka, M.; Samper-Villareal, J.; Beca-Carretero, P.; Creed, J.C. Seagrass ecosystem services—What’s next? Mar. Pollut. Bull. 2018, 134, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Zabarte-Maeztu, I.; Matheson, F.; Manley-Harris, M.; Davies-Colley, R.; Oliver, M.; Hawes, I. Effects of fine sediment on seagrass meadows: A case study of Zostera muelleri in Pauatahanui Inlet, New Zealand. J. Mar. Sci. Eng. 2020, 8, 645. [Google Scholar] [CrossRef]
- Grech, A.; Chartrand-Miller, K.; Erftemeijer, P.; Fonseca, M.; McKenzie, L.; Rasheed, M.; Taylor, H.; Coles, R.A. comparison of threats, vulnerabilities and management approaches in global seagrass bioregions. Environ. Res. Lett. 2012, 7, 024006. [Google Scholar] [CrossRef]
- Montefalcone, M.; Parravicini, V.; Vacchi, M.; Albertelli, G.; Ferrari, M.; Morri, C.; Bianchi, C.N. Human influence on seagrass hábitat fragmentation in NW Mediterranean Sea. Estuar. Coast. Shelf Sci. 2010, 86, 292–298. [Google Scholar] [CrossRef]
- Boudouresque, C.F.; Bernard, G.; Pergent, G.; Shili, A.; Verlaque, M. Regression of Mediterranean seagrasses caused by natural processes and anthropogenic disturbances and stress: A critical review. Bot. Mar. 2009, 52, 395–418. [Google Scholar] [CrossRef]
- Costanza, R.; de Groot, R.; Sutton, P.; van der Ploeg, S.; Anderson, S.J.; Kubiszewski, I.; Farber, S.; Turner, R.K. Changes in the global value of ecosystem services. Glob. Environ. Chang. 2014, 26, 152–158. [Google Scholar] [CrossRef]
- Arias-Ortiz, A.; Serrano, O.; Masqué, P.; Lavery, P.S.; Mueller, U.; Kendrick, G.A.; Rozaimi, M.; Esteban, A.; Fourqurean, J.W.; Marbà, N.; et al. A marine heatwave drives massive losses from the world’s largest seagrass carbon stocks. Nat. Clim. Chang. 2018, 8, 338–344. [Google Scholar] [CrossRef]
- Park, J.I.; Lee, K.S. Site-specific success of three transplanting methods and the effect of planting time on the establishment of Zostera marina transplants. Mar. Pollut. Bull. 2007, 54, 1238–1248. [Google Scholar] [CrossRef]
- Li, W.T.; Kim, Y.K.; Park, J.I.; Zhang, X.; Du, G.Y.; Lee, K.S. Comparison of seasonal growth responses of Zostera marina transplants to determine the optimal transplant season for habitat restoration. Ecol. Eng. 2014, 71, 56–65. [Google Scholar] [CrossRef]
- Park, H.J.; Park, T.H.; Kang, H.Y.; Lee, K.S.; Kim, Y.K.; Kang, C.K. Assessment of restoration success in a transplanted seagrass bed based on isotopic niche metrics. Ecol. Eng. 2021, 166, 106239. [Google Scholar] [CrossRef]
- Ruckelshaus, M.; Guannel, G.; Arkema, K.; Verutes, G.; Griffin, R.; Guerry, A.; Silver, J.; Faries, J.; Brenner, J.; Rosenthal, A. Evaluating the benefits of green infrastructure for coastal areas: Location, location, location. Coast. Manag. 2016, 44, 504–516. [Google Scholar] [CrossRef]
- Oprandi, A.; Mucerino, L.; De Leo, F.; Bianchi, C.N.; Morri, C.; Azzola, A.; Benelli, F.; Besio, G.; Ferrari, M.; Montefalcone, M. Effects of severe storm on seagrass meadows. Sci. Total Environ. 2020, 748, 141373. [Google Scholar] [CrossRef]
- Uhrin, A.V.; Turner, M.G. Physical drivers of seagrass spatial configuration: The role of thresholds. Landsc. Ecol. 2018, 33, 2253–2272. [Google Scholar] [CrossRef]
- Fourqurean, J.W.; Rutten, L.M. The impact of Hurricane Georges on soft-bottom, back reef communities: Site- and species-specific effects in south Florida. Bull. Mar. Sci. 2004, 75, 239–257. [Google Scholar]
- Van Tussenbroek, B.I.; Barba Santos, M.G.; van Dijk, J.K.; Sanabria Alcaraz, S.N.M.; Téllez Calderón, M.L. Selective elimination of rooted plants from a tropical seagrass bed in a back-reef lagoon: A hypothesis tested by Hurricane Wilma (2005). J. Coast. Res. 2008, 241, 278–281. [Google Scholar] [CrossRef]
- Van Tussenbroek, B.I.; Cortés, J.; Collin, R.; Fonseca, A.C.; Gayle, P.M.H.; Guzmán, H.M.; Jácome, G.E.; Juman, R.; Koltes, K.H.; Oxenford, H.A.; et al. Caribbean-wide, long-term study of seagrass beds reveals local variations, shifts in community structure and occasional collapse. PLoS ONE 2014, 9, e89377. [Google Scholar] [CrossRef]
- Paul, M.; Amos, C.L. Spatial and seasonal variation in wave attenuation over Zoostera nolti. J. Geophys. Res. 2011, 116, C08019. [Google Scholar] [CrossRef]
- Bouma, T.J.; van Beelzen, J.; Balke, T.; Zhu, Z.; Airoldi, L.; Blight, A.J.; Davies, A.J.; Galvan, C.; Hawkins, S.J.; Hoggart, S.P.G.; et al. Identifying knowledge gaps hampering application of intertidal habitats in coastal protection: Opportunities & steps to take. Coast. Eng. 2014, 87, 147–157. [Google Scholar]
- Pinsky, M.L.; Guannel, G.; Arkema, K.K. Quantifying wave attenuation to inform coastal habitat conservation. Ecosphere 2013, 4, 95. [Google Scholar] [CrossRef]
- Silver, J.M.; Arkema, K.K.; Griffin, R.M.; Lashley, B.; Lemay, M.; Maldonado, S.; Moultrie, S.H.; Ruckelhaus, M.; Schill, S.; Thomas, A.; et al. Advancing coastal risk reduction science and implementation by accounting for climate, ecosystems and people. Front. Mar. Sci. 2019, 6, 556. [Google Scholar] [CrossRef]
- Pillai, U.P.A.; Pinardi, N.; Alessandri, J.; Federico, I.; Causio, S.; Unguendoli, S.; Valentini, A.; Staneva, J. A Digital Twin modelling framework for the assessment of seagrass Nature Based Solutions against storm surges. Sci. Total Environ. 2022, 847, 157603. [Google Scholar] [CrossRef] [PubMed]
- Stratigaki, V.; Manca, E.; Prinos, P.; Losada, I.J.; Lara, J.L.; Sclavo, M.; Amos, C.L.; Cáceres, I.; Sánchez-Arcilla, A. Large-scale experiments on wave propagation over Posidonia oceánica. J. Hydraul. Res. 2011, 49 (Suppl. S1), 31–43. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. A coupled model of submerged vegetation under oscillatory flow using Navier–Stokes equations. Coast. Eng. 2013, 80, 16–34. [Google Scholar] [CrossRef]
- Chen, W.L.; Muller, P.; Grabowski, R.C.; Dodd, N. Green nourishment: An innovative nature-based solution for coastal erosion. Front. Mar. Sci. 2022, 8, 814589. [Google Scholar] [CrossRef]
- Vacchi, M.; Montefalcone, M.; Bianchi, C.N.; Morri, C.; Ferrari, M. Hydrodynamic constraints to the seaward development of Posidonia Oceanica meadows. Estuar. Coast. Shelf Sci. 2012, 97, 58–65. [Google Scholar] [CrossRef]
- Vacchi, M.; Montefalcone, M.; Schiaffino, C.F.; Parravicini, V.; Bianchi, C.N.; Morri, C.; Ferrari, M. Towards a predictive model to assess the natural position of the Posedonia oceanica seagrass meadows upper limit. Mar. Pollut. Bull. 2014, 83, 458–466. [Google Scholar] [CrossRef]
- Ruiz, J.M.; Guillén, J.E.; Ramos-Segura, A.; Otero, M.M. (Eds.) . Atlas de las Praderas Marinas de España; IEO/IEL/UICN: Murcia-Alicante-Málaga, Spain, 2015. [Google Scholar]
- Romero, J.; Pérez, M.; Alcoverro, T. The seagrass (Posidonia oceánica) meadows in the Catalán coast: Past trends and present status. In Proceedings of the 3rd Mediterranean Symposium on Marine Vegetation, Marseilles, France, 27–29 March 2007. [Google Scholar]
- Pinedo, S.; Zabala, M.; Ballesteros, E. Long-term changes in sublitoral macroalgal assemblages related to water quality improvement. Bot. Mar. 2013, 56, 461–469. [Google Scholar] [CrossRef]
- Casas-Prat, M.; Sierra, J.P. Trend analysis of wave storminess: Wave direction and its impact on harbour agitation. Nat. Hazards Earth Syst. Sci. 2010, 10, 2327–2340. [Google Scholar] [CrossRef]
- Bertotti, L.; Cavaleri, L. The predictability of the “Voyager” accident. Nat. Hazards Earth Syst. Sci. 2008, 8, 533–537. [Google Scholar] [CrossRef]
- Sánchez-Arcilla, A.; González-Marco, D.; Bolaños, R. A review of wave climate and prediction along the Spanish Mediterranean coast. Nat. Hazards Earth Syst. Sci. 2008, 8, 1217–1228. [Google Scholar] [CrossRef]
- Sánchez-Arcilla, A.; Lin-Ye, J.; García-León, M.; Gracia, V.; Pallarés, E. The land-sea coastal border: A quantitative definition by considering the wind and wave conditions in a wave-dominated, micro-tidal environment. Ocean Sci. 2019, 15, 113–126. [Google Scholar] [CrossRef]
- Paul, M.; Bouma, T.J.; Amos, C.L. Wave attenuation by submerged vegetation: Combining the effect of organism traits and tidal current. Mar. Ecol. Prog. Ser. 2012, 444, 31–41. [Google Scholar] [CrossRef]
- Luhar, M.; Infantes, E.; Orfila, A.; Terrados, J.; Nepf, H.M. Field observations of wave-induced streaming through a submerged seagrass (Posidonia oceanica) meadow. J. Geophys. Res. Oceans 2013, 118, 1955–1968. [Google Scholar] [CrossRef]
- Colomer, J.; Soler, M.; Serra, T.; Casamitjana, X.; Oldham, C. Impact of anthropogenically created canopy gaps on wave attenuation in a Posidonia oceanica seagrass meadow. Mar. Ecol. Prog. Ser. 2017, 569, 103–116. [Google Scholar] [CrossRef]
- Abadie, A.; Richir, J.; Lejeune, P.; Leduc, M.; Gobert, S. Structural changes of seagrass seascapes driven by natural and anthropogenic factors: A multidisciplinary approach. Front. Ecol. Evol. 2019, 7, 190. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Ma, X.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection qon harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Gao, J.; Zhou, X.; Zhou, L.; Zang, J.; Chen, H. Numerical investigation on effects of fringing reefs on low-frequency oscillations within a harbor. Ocean Eng. 2019, 172, 86–95. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Oceans 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions: 2. Verification. J. Geophys. Res. Oceans 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Suzuki, T.; Zijlema, M.; Burger, B.; Meijer, M.C.; Narayan, S. Wave dissipation by vegetation with layer schematization in SWAN. Coast. Eng. 2012, 59, 64–71. [Google Scholar] [CrossRef]
- Alomar, M. Improving wave forecasting in variable wind conditions: The effect of resolution and growth rate for the Catalan coast. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2012. [Google Scholar]
- Pallarés, E. High-resolution wave forecasting. The Catalan coast case modelling, coupling and validation. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2016. [Google Scholar]
- Russek, N. Influence of seagrass meadows on hydrodynamics: A modelling approach. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2020. [Google Scholar]
- Sánchez-González, J.F.; Sánchez-Rojas, V.; Memos, C.D. Wave attenuation due to Posidonia oceanica meadows. J. Hydraul. Res. 2011, 49, 503–514. [Google Scholar] [CrossRef]
- Cavallaro, L.; Viviano, A.; Paratore, G.; Foti, E. Experiments on surface waves interacting with flexible aquatic vegetation. Ocean Sci. J. 2018, 53, 461–474. [Google Scholar] [CrossRef]
- Twomey, A.J.; O’Brien, K.R.; Callaghan, D.P.; Saunders, M.I. Synthesising wave attenuation for seagrass: Drag coefficient as a unifying indicator. Mar. Pollut. Bull. 2020, 160, 111661. [Google Scholar] [CrossRef]
- Dalla Via, J.; Sturmbauer, C.; Schönweger, G.; Sötz, E.; Mathekowitsch, S.; Stifter, M.; Rieger, R. Light gradients and meadow structure in Posidonia oceanica: Ecomorphological and functional correlates. Mar. Ecol. Prog. Ser. 1998, 163, 267–278. [Google Scholar] [CrossRef]
- Zeller, R.B.; Weitzman, J.S.; Abbett, M.E.; Zarama, F.J.; Fringer, O.B.; Koseff, J.R. Improved parametrizations of seagrass blade dynamics and wave attenuation based on numerical and laboratory experiments. Limnol. Oceanogr. 2014, 59, 251–266. [Google Scholar] [CrossRef]
- Myrhaug, D.; Holmedal, L.E. Drag force on a vegetation field due to long-crested and short-crested nonlinear random waves. Coast. Eng. 2011, 58, 562–566. [Google Scholar] [CrossRef]
- EPPE. Clima Medio de Oleaje. Boya de Tarragona; Puertos del Estado: Madrid, Spain, 2022. [Google Scholar]
- Cao, H.; Feng, W.; Hu, Z.; Suzuki, T.; Stive, M.J.F. Numerical modeling of vegetation-induced dissipation using an extended mild-slope equation. Ocean Eng. 2015, 110, 258–269. [Google Scholar] [CrossRef]
- Sierra, J.P.; García-León, M.; Gracia, V.; Sánchez-Arcilla, A. Green measures for Mediterranean harbours under a changing climate. Proc. Inst. Civ. Eng. Mar. Eng. 2017, 170, 55–66. [Google Scholar] [CrossRef]
- Vu, M.T.; Lacroix, Y.; Nguyen, V.T. Investigating the impacts of the regression of Posidonia oceanica on hydrodynamics and sediment transport in Giens Gulf. Ocean Eng. 2017, 146, 70–86. [Google Scholar] [CrossRef]
- Chastel, T.; Botten, K.; Durand, N.; Goutal, N. Bulk drag coefficient of a subaquatic vegetation subjected to irregular waves: Influence of Reynolds and Keulegan-Carpenter numbers. Houille Blanche 2020, 2, 34–42. [Google Scholar] [CrossRef]
- Dijkstra, J.; Uittenbogaard, R. Modeling the interaction between flow and highly flexible aquatic vegetation. Water Resour. Res. 2010, 46, W12547. [Google Scholar] [CrossRef]
- Bradley, K.; Houser, C. Relative velocity of seagrass blades: Implications for wave attenuation in low energy environments. J. Geophys. Res. 2009, 114, F01004.g. [Google Scholar] [CrossRef]
- Paulo, D.; Cunha, A.H.; Boavida, J.; Serrão, E.A.; Gonçalves, E.J.; Fonseca, M. Open coast seagrass restoration. Can we do it? Large scale seagrass transplants. Front. Mar. Sci. 2019, 6, 52. [Google Scholar] [CrossRef]
- Paling, E.I.; van Keulen, M.; Wheeler, K.D.; Phillips, J.; Dyhrberg, R. Influence of spacing on mechanically transplanted seagrass survival in a high wave energy regime. Restor. Ecol. 2003, 11, 56–61. [Google Scholar] [CrossRef]
- Villanueva, R.; Paul, M.; Schlurmann, T. Anchor forces on coir-based artificial seagrass mats: Dependence on wave dynamics and their potential use in seagrass restoration. Front. Mar. Sci. 2022, 9, 802343. [Google Scholar] [CrossRef]
- Villanueva, R.; Thom, M.; Visscher, J.; Paul, M.; Schlurmann, T. Wake length of an artificial seagrass meadow: A study of shelter and its feasibility for restoration. J. Ecohydraul. 2021, 7, 77–91. [Google Scholar] [CrossRef]
- Valdemarsen, T.; Canal-Vergés, P.; Kristensen, E.; Holmer, M.; Kristiansen, M.D.; Flindt, M.R. Vulnerability of Zostera marina seedlings to physical stress. Mar. Ecol. Prog. Ser. 2010, 418, 119–130. [Google Scholar] [CrossRef]
- Kendrick, G.A.; Waycott, M.; Carruthers, T.J.B.; Cambridge, M.L.; Hovey, R.K.; Krauss, S.L.; Lavery, P.S.; Les, D.H.; Lowe, R.J.; Mascaró I Vidal, O.; et al. The central role of dispersal in the maintenance and persistence of seagrass populations. Bioscience 2012, 62, 56–65. [Google Scholar] [CrossRef]
- Carstensen, J.; Krause-Jensen, D.; Markager, S.; Timmermann, K.; Windolf, J. Water clarity and eelgrass responses to nitrogen reductions in the eutrophic Skive Fjord. Denmark. Hydrobiologia 2013, 704, 293–309. [Google Scholar] [CrossRef]
- van Katwijk, M.M.; van Thorhaug, A.; Marbà, N.; Orth, R.J.; Duarte, C.M.; Kendrick, G.A.; Althuizen, I.H.J.; Balestri, E.; Bernard, G.; Cambridge, M.L.; et al. Global analysis of seagrass restoration: The importance of large-scale planting. J. Appl. Ecol. 2016, 53, 567–578. [Google Scholar] [CrossRef]
- Orth, R.J.; Moore, K.A.; Marion, S.R.; Wilcox, D.J.; Parrish, D.P. Seed addition facilitates eelgrass recovery in a coastal bay system. Mar. Ecol. Prog. Ser. 2012, 448, 177–195. [Google Scholar] [CrossRef]
- Statton, J.; Kendrick, G.A.; Dixon, K.W.; Cambridge, M.L. Inorganic nutrient supplements constrain restoration potential of seedlings of the seagrass, Posidonia australis. Restor. Ecol. 2013, 22, 196–203. [Google Scholar] [CrossRef]
- Hotaling-Hagan, A.; Swett, R.; Ellis, L.R.; Frazer, T.K. A spatial model to improve site selection for seagrass restoration in shallow boating environments. J. Environ. Manag. 2017, 186, 42–54. [Google Scholar] [CrossRef]
- Rezek, R.J.; Furman, B.T.; Jung, R.P.; Hall, M.O.; Bell, S.S. Long-term performance of seagrass restoration projects in Florida, USA. Sci. Rep. 2019, 9, 15514. [Google Scholar] [CrossRef]
- Tan, Y.M.; Dalby, O.; Kendrick, G.A.; Statton, J.; Sinclair, E.A.; Fraser, M.W.; Macreadie, P.I.; Gillies, C.L.; Coleman, R.A.; Waycott, M.; et al. Seagrass restoration is possible: Insights and lessons from Australia and New Zealand. Front. Mar. Sci. 2020, 7, 617. [Google Scholar] [CrossRef]
- Sinclair, E.A.; Sherman, C.D.H.; Statton, J.; Copeland, C.; Matthews, A.; Waycott, M.; van Dijk, K.J.; Vergés, A.; Kajlich, L.; McLeod, I.M.; et al. Advances in approaches to seagrass restoration in Australia. Ecol. Manag. Restor 2021, 22, 10–21. [Google Scholar] [CrossRef]
- Borsje, B.W.; van Wesenbeeck, B.K.; Dekkerc, F.; Paalvastd, P.; Bouma, T.J.; van Katwijk, M.M.; de Vries, M.B. How ecological engineering can serve in coastal protection. Ecol. Eng. 2011, 37, 113–122. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).