Abstract
The identification of longitudinal bending moments is a critical component in the health monitoring of ship structures. This study examines the effect of the failure of measurement points on the accuracy of bending moment identification and presents a solution using an XGboost fitting method. The impact of failure point position and quantity on strain fitting accuracy and bending moment identification was investigated by performing a four-point bending experiment in typical failure scenarios. Further numerical analysis was conducted to identify potential sources of errors in the measurement process. Additionally, several XGBoost-based fitting schemes were tested under practical conditions to provide reliable fitting suggestions. The results indicated that the XGboost strain fitting method outperforms conventional methods for removing failed measurement points, resulting in improved accuracy of identification. When the most critical failure condition occurs (i.e., the deck plate measurement points and deck stiffener measurement points fail), the XGboost method can still estimate the strain at the failure points with acceptable accuracy. These results also hold in complex load scenarios. Moreover, in the practical measurement conditions, the arrangement of measuring points includes two sections that are sufficient to support the fitting of failed measurement points by using the XGboost method. The XGboost strain fitting method exhibits promising potential in strain fitting applications.
1. Introduction
To this day, safety and lightweight hull structures remain the primary objectives pursued by ship designers. In order to accurately adjust hull design parameters, a high level of proficiency in assessing the navigation environment is essential. With this in mind, the structural health monitoring (SHM) system was introduced. In recent years, interest in SHM has increased with the development of large-scale and intelligent ships [1,2]. Generally, the hull can be regarded as an ultra-long, hollow, and thin-walled beam with distinctive structural characteristics that challenge its ability to withstand longitudinal bending. The issue of the longitudinal bending of the hull has been a subject of great concern among researchers for many years [3,4]. Therefore, the monitoring of longitudinal bending is one of the most important modules of hull structural health monitoring [5,6,7].
At present, the methods to monitor longitudinal bending fall into two common categories, namely, longitudinal stress monitoring and longitudinal bending moment identification. Compared with the method of stress monitoring, longitudinal bending moment identification can be applied to not only provide design loads but also learn lessons in order to enhance requirements for next-generation vessels, exhibiting a brighter outlook [8,9,10,11]. During navigation, irregular wave loads would produce vertical, lateral, and torsional moments on the hull girder [12]. These moments can be determined via the relationship between the theoretical influence coefficient function and the strain value measured on a section. For years, researchers have verified this principle and adopted it in practical applications. Liu [13] proposed several methods for establishing the influence coefficient matrix based on this principle. The method based on FEM analysis is highly efficient in constructing the influence coefficient matrix of complex ship hulls. In view of this principle, Li et al. [14,15] referenced beam theory and proposed a construction method of the influence coefficient matrix for longitudinal bending moment identification. They conducted hull girder experiments and verified that this method is effective. By using this principle, Yu et al. [12] established a longitudinal bending identification method based on LBSG (long base strain gauges) and monitored the longitudinal bending moment time history of a large container ship during navigation. However, in practical cases, strain signals display faults due to the failure of measuring points. This limitation would reduce the identification accuracy and significantly mislead the safety assessment of the hull structure.
Up to now, the strategy to address the issue of measuring point failure in practical structures did not gained much attention [16,17]. In general, removing failed points is a widely used strategy to reduce the identification error to a certain extent in practical engineering due to its simplicity [16]. Nevertheless, the information on stress near the failed point is still inaccessible. To this end, estimating the strain of failed measure points was found to be more beneficial to ice load identification than the method of removing failed points on a typical polar ship’s side grillage [17]. Aided by FEM analysis, the researchers adopted cubic function to estimate the strain value at any position by investigating the potential relationships between the coordinates of measuring points. This scheme is similar to the method of fitting missing values. Nowadays, in some datasets where the correlation between data points is low, it is typical to establish direct mappings between values in order to estimate missing values. Previous research studies have concluded that mean imputation and K-nearest neighbor (KNN) methods [18,19] are effective for missing value fitting. However, due to the lack of consideration of the correlation between different variables, the fitting performance of these methods has potential for further improvement.
In order to enhance the fitting accuracy of missing values, ensemble learning methods such as MissForest and XGboost are introduced to fit missing values [20]. Compared with the XGboost method, the solution efficiency of MissForest is not satisfactory due to the requirement of establishing multiple random forest models. It is worth mentioning that the XGBoost method has become widely adopted in recent years due to its efficient and flexible characteristics, which enable it to capture complex data dependencies with high precision [21]. Thanks to its robustness to outliers, XGboost has demonstrated the applicability of large-scale data and performs well in predicting static travel time [22]. In addition, XGboost shows a better fitting ability of missed values compared to the D-GEX algorithm and linear regression method [23]. In summary, the methods to process the situation with failed measuring points deserve intensive exploration.
This work aims to utilize a strain fitting method based on XGboost to improve the identification accuracy of longitudinal bending moment. Different from missing value fitting, strain fitting presents unique challenges due to the limited number of measurement points, resulting in a small-scale dataset that makes it difficult to capture dependencies. In addition, the involvement of measurement errors and the intricate stress distribution under longitudinal bending exacerbates the level of difficulty even further. Nevertheless, by exploring the relationship between bending moment identification and the positions of measurement points, along with a comprehensive evaluation of XGboost, it becomes possible to establish a simplified training set comprising highly correlated measurement points. Through this approach, the fitting method can be brought closer to practical requirements while effectively mitigating failure issues.
As shown in Figure 1, to investigate the issue of failed measurement points in the context of longitudinal bending moment identification under a practical scenario, we conducted some experiments which are organized as follows:
- (1)
- A four-point bending experiment based on a box girder was conducted to realize the loading identification based on the measured signals.
- (2)
- The correlation between the measurement point position and identification accuracy is explored in the experiment scenario to investigate the impact of measuring point failure on longitudinal bending moment identification.
- (3)
- Based on the investigation of correlation, 17 failure conditions were designed to assess the effectiveness of the fitting method based on XGboost, and the method’s fitting capabilities were thoroughly evaluated.
- (4)
- To clarify the sources of fitting errors and further explore the applicability of fitting method, the connections between the fitting values and the training set were comprehensively studied under typical load cases using finite element analysis. Then, the minimum training set required for fitting was determined for the simplification of the training set.
- (5)
- Recommendations were provided for the implementation of the strain fitting method for longitudinal bending moment identification.
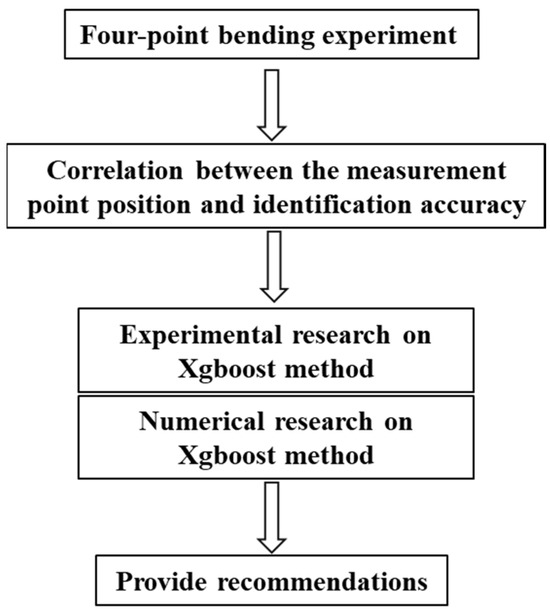
Figure 1.
Workflow.
2. Experiment on Longitudinal Bending Moment Identification
2.1. Experimental Details
At present, researchers primarily investigate longitudinal bending through designing four-point bending box girder experiments [24,25,26,27]. Therefore, we conduct a four-point bending experiment utilizing a stiffened box girder model for longitudinal bending moment identification research. By subjecting the middle section of the model to a four-point bending configuration, the longitudinal bending of a cabin in ship hull can be simulated.
2.1.1. Design of the Box Girder
To ensure that the model’s structure closely resembles that of a ship, the design of the stiffened plate on the box girder is based on the relevant literature [28]. The geometric dimensions of the model are illustrated in Figure 2 and Table 1. The model consists of two extension parts and a middle part, with bulkheads installed to separate them. To simulate the practical ship structure, except bulkheads, longitudinal and transverse stiffeners are arranged on the box girder. The stiffeners are arranged on the outer surface of the model to facilitate the installation of measuring points. Throughout the entire length of the model, the longitudinal stiffeners remain continuous, and the structures of sections are strengthened by transverse stiffeners. The elastic modulus of steel of the model is 206 GPa.
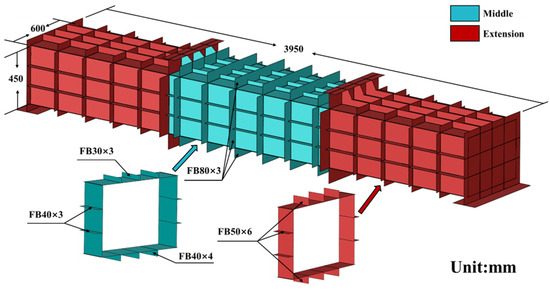
Figure 2.
Design of the stiffened box girder.

Table 1.
Dimensions of the components.
2.1.2. Experiment Setup
As shown in Figure 3, the box girder is placed on two rigid support seats with a round bar at the bottom. The whole model is loaded using the MTS loading system, and the vertical force is equally divided by a square beam to the two bulkheads of the box girder. During the experiment, loads on bulkheads are kept at the same value and increased by the same step to ensure that the middle part is under bending conditions. The bending moment is calculated as follows:
where is the bending load on a bulkhead and is the length of an extension part. The load conditions of this experiment are 5t , 10t, 15t, 20t, 25t, and 30t, which are the safety load levels for this box girder (after applying the load, the box girder did not fail).

Figure 3.
Experimental setup. (a) Four-point bending. (b) Test model. (c) Loading tool.
The layout of measuring points is shown in Figure 4, where S (…) is the number of points on the stiffener and P (…) is the number of points on the deck. All measuring points are in the center of the panel. In our quest to explore the correlation between measuring point position and the accuracy of longitudinal bending moment identification, it is necessary to monitor the longitudinal strain across all panels and stiffeners. For this purpose, a substantial number of measuring points were arranged on the left side and deck. This extensive placement of measuring points ensures comprehensive data collection for a comprehensive analysis of the longitudinal strain distribution throughout the structure. The scale of arrangement on the right side and the bottom is small, as they are used to verify the symmetry of the model. The strain gauge we adopted is a unidirectional resistance strain gauge with a resistance of 120 Ω and a sensitivity of 2%.
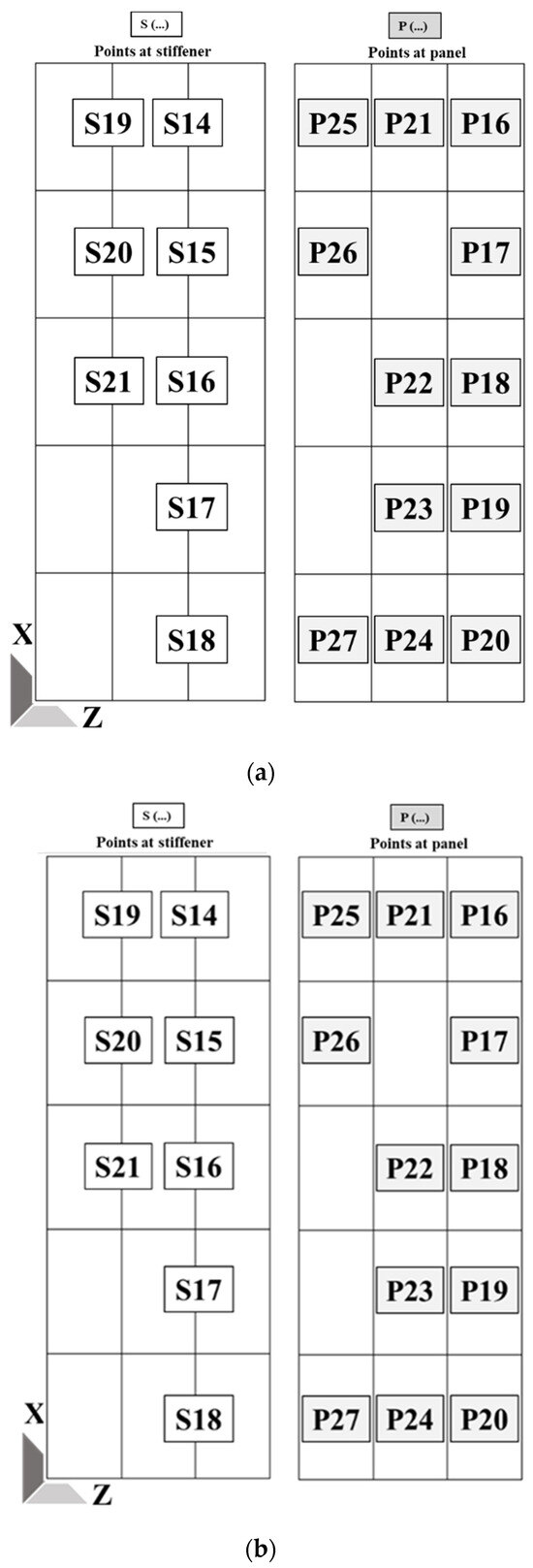
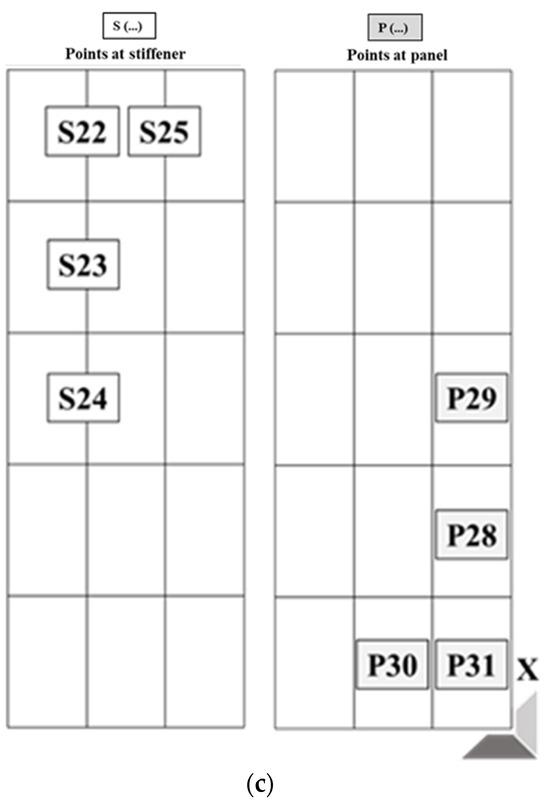
Figure 4.
Layout of strain gauges on the box girder. (a) Layout of strain gauges on the deck. (b) Layout of strain gauges on the left side. (c) Layout of strain gauges on the right side.
2.2. Longitudinal Bending Moment Identification Method
During navigation, the normal stress on a section of the hull girder is balanced. The relationship between strain and bending moment is as follows:
where is the elastic modulus; σ is the longitudinal strain of a measuring point on the section; is the section moment of inertia; and is the vertical distance between the measuring point and the neutral axis. Therefore, the load–strain transfer matrix can be estimated as follows [14,15]:
where is the vector which is made up of the measured longitudinal strain on a section, is the longitudinal bending moment, and is the longitudinal moment–strain transfer vector composed of the ideal longitudinal strain.
2.3. Gradient Descent Method for Load Identification
According to Equation (3), the key to moment identification is to obtain the least squares solution of the bending moment. To this end, we adopt the adaptive gradient descent method to identify the bending moment in this study, which is as follows [29]:
First, operate the initial parameters: , , , .
When n > 1,
where is the load to be identified; and are the intermediate variables. The relative error of bending moment identification of each section is as follows:
where is the relative error, is the identified bending moment, and is the test bending moment which can be calculated as follows:
Figure 5a–e present the results of the longitudinal bending moment identification, along with the corresponding relative errors, for various load conditions ranging from 5t to 30t. The sectional interval between each measurement is set at 200 mm. The maximum relative error of the identification result is less than 4%, while the average relative error is calculated to be 2.3%. These identification errors stem from the deviation between the strain measuring value and the simulated value. During the experiment, due to the existence of unavoidable geometric defects in the structure and interference from the practical environment, the deviation of the strain value is hard to be eliminated. In this study, the identification error is very low. This indicates that the accuracy of strain measurement is within an acceptable range, and the longitudinal moments can be accurately identified in the practical scenario.
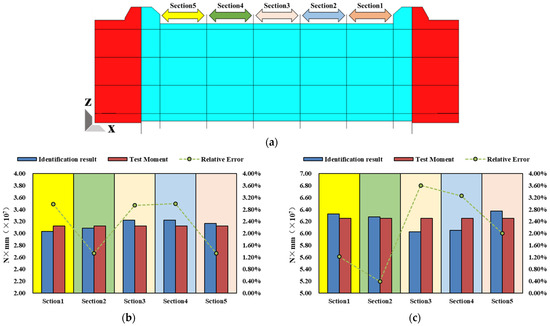
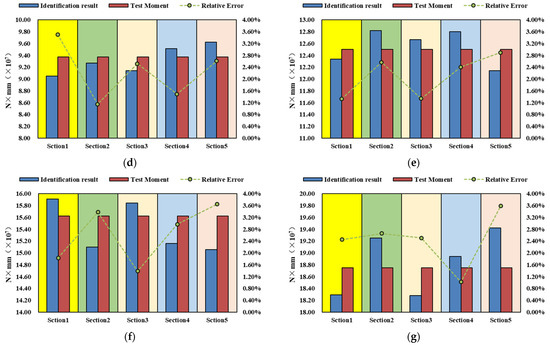
Figure 5.
Bending moment identification of different sections. (a) Distribution of identified sections. (b) 5t. (c) 10t. (d) 15t. (e) 20t. (f) 25t. (g) 30t.
3. XGboost Fitting of the Strains at Measuring Points
XGboost integrates the cart tree model, which is a weak regression model to form a strong regression model. A cart tree model can be built as follows [21]:
where is the divided input space and is the corresponding output value. By repeating Equation (12) for until the stopping criterion is met, the input space is divided into areas. generates a decision tree. In this study, the stopping criterion is restricted by setting the maximum depth of the cart tree.
As shown in Figure 6, the principle of the XGboost method is building a new cart tree model which is learning a new function to fit the residual predicted last iteration. The final regression result can be obtained by adding the regression values of all cart tree models.
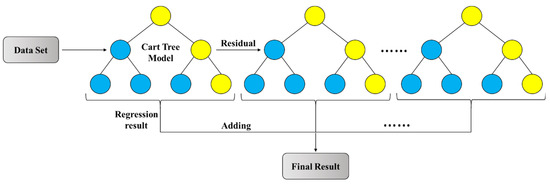
Figure 6.
XGboost regression method.
The objective function of XGboost to predict residual consists of the loss function and the regularization term, as follows [21]:
where is the loss function; is the regularization term; is the sample; and is the predicted value of . In this study, the loss function is a linear function which is as follows:
For each iteration, the objective function is optimized as follows:
(1) By expending the second-order Taylor of loss function term and removing the constant term , the loss function term can be optimized as follows:
where .
(2) By expanding the regularization term and removing the constant term, the regularization term can be optimized as follows:
where is the number of leaf nodes and is the score of leaf nodes. γ, λ are regularization parameters. As is a function about , the objective functions can be converted to functions about , that is, , as follows:
(3) By solving the minimum value of the objective function, the optimal tree structure can be obtained as follows:
By utilizing the unfailed points as the training set, it is possible to perform regression analysis to estimate the strain values at the failed points. For the parameter options of the XGboost method, when the fitting residual is less than 104 or the number of iterations exceeds 1000, the iteration stops. And the maximum depth of the tree is 10.
4. Investigations into Strain Fitting Method Based on the XGboost Method
4.1. Correlation between Measuring Point Position and Identification Accuracy
In practical load monitoring, positioning measurement points at locations exhibiting strong correlation is more effective in accurately identifying bending moments. This viewpoint is similar to the results of related research studies focused on identifying ice loads [30] and impulse loads [14]. Moreover, measurement points with strong correlation can be used to build training sets for strain fitting with strong features. Therefore, it becomes imperative to investigate the correlation between the positions of measurement points and the identification accuracy of the bending moment.
Based on the above moment identification method, the accuracy of moment identification is related to the strain on a section of the hull. Consequently, this study specifically examines the impact of measuring point position on a single section. By substituting the functional measuring points with failed points (the strains at failed points are replaced with zero), several failure conditions of measuring points are introduced. The degree of correlation between the failed measuring point position and moment identification can be regarded as increasing as the error in moment identification becomes greater. Through this approach, we investigate the effect of measuring point failures on the accuracy of longitudinal bending moment identification, thereby obtaining insights into the correlation between measuring point position and identification.
4.1.1. Correlation between Measuring Points at Different Locations and Identification Accuracy
As shown in Figure 7, under the condition of longitudinal bending, the longitudinal strain distribution on the hull’s side exhibits a linear function distribution, assuming ideal conditions, while the deck displays a uniform distribution. This indicates differences in the strain distribution characteristics between the side and the deck of the hull. Hence, this study categorizes the locations of failed measuring points into two types: deck and side.
Figure 7.
Strain distribution on the hull under longitudinal bending.
In order to investigate the underlying correlations, section 1 was regarded as the failure section due to its arrangement of a relatively higher number of measuring points compared to other sections. Seven failed conditions are designed, as shown in Figure 8.
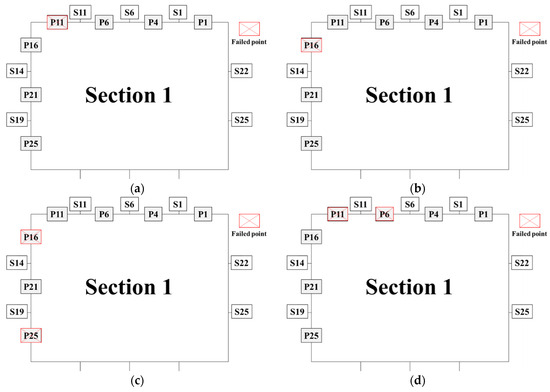
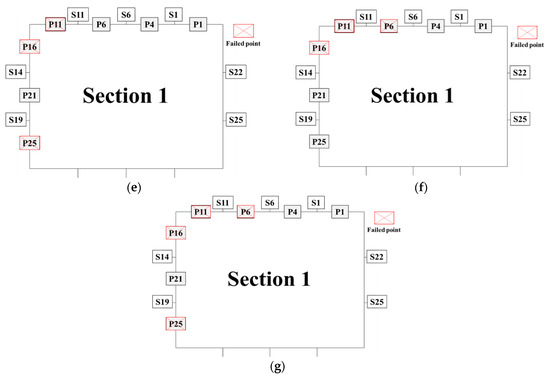
Figure 8.
Failure conditions at different locations. (a) One failed point (deck). (b) One failed point (side). (c) Two failed points (side). (d) Two failed points (deck). (e) Three failed points (deck: one, side: two). (f) Three failed points (deck: two, side: one). (g) Four failed points (deck: two, side: two).
The failed points are considered for longitudinal bending moment identification. The identification results and relative error of different conditions are shown in Figure 9a–f; the variables are the conditions a–g shown in Figure 7. As the number of failed points increases, the relative error also rises. Once the failed test points exceed two, the identification relative error surpasses 7%. Among these seven conditions, the maximum identification relative error is more than 30%, which emphasizes that the failed points significantly affect the identification of the bending moment. By exploring the trend of the error curve, when there are more failed points on the deck, the relative error of identification is greater (the relative error of condition a is greater than that of condition b; the relative error of condition d is greater than that of condition c; the relative error of condition f is greater than that of condition e; and the relative error of condition e is smaller than that of condition d). This suggests a stronger correlation between failed points on the deck plate and bending moment identification, as opposed to failed points on the side.
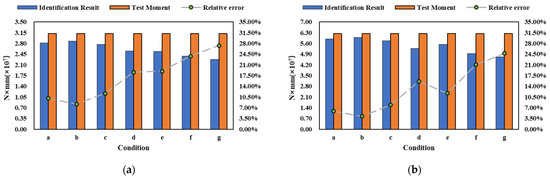
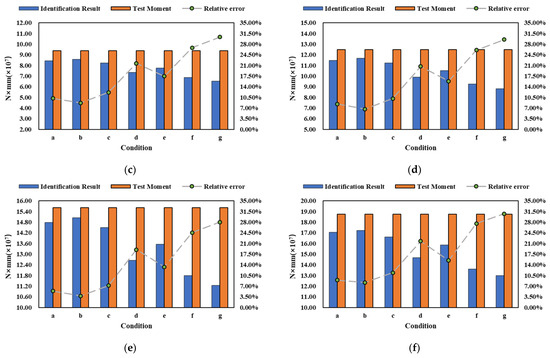
Figure 9.
Bending moment identification of point failures at different locations. (a) 5t. (b) 10t. (c) 15t. (d) 20t. (e) 25t. (f) 30t.
4.1.2. Correlation between Measuring Points at Different Structures and Identification Accuracy
In general, the bearing capacity of the plate and the stiffener on a stiffened plate is different [31]. The failed points on the stiffener and the failed points on the plate have different correlations with moment identification. To this end, in this study, the located structures of failed points are divided into two types: plate and stiffener. As shown in Figure 10, six failure conditions were designed to investigate the correlation between measuring points at different structures and identification accuracy.
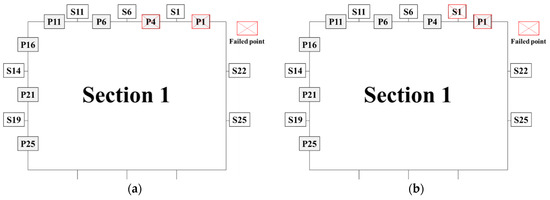
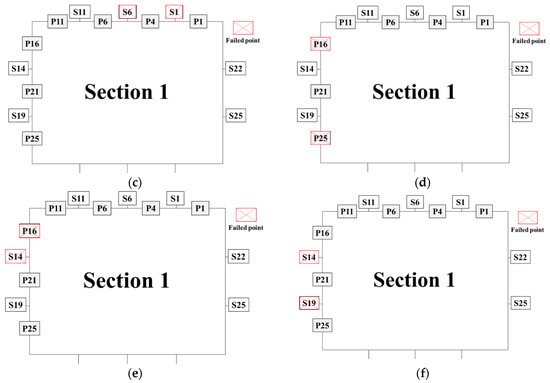
Figure 10.
Failure conditions at different structures. (a) Two failed points on the deck (plate). (b) Two failed points on the deck (plate, stiffener). (c) Two failed points on the deck (stiffener). (d) Two failed points on the side (plate). (e) Two failed points on the side (plate, stiffener). (f) Two failed points on the side (stiffener).
The identification results and relative error of different conditions are shown in Figure 11. Among the identification results of conditions a to c, the relative error in condition a is the lowest, whereas condition c exhibits the highest relative error. This indicates that the measuring points located on the deck stiffener have a more pronounced influence on the accuracy of moment identification compared to those on the deck plate. Similarly, when examining the identification results of conditions d to f, it becomes evident that condition d displays the highest relative error, whereas condition f demonstrates the lowest relative error. This suggests that the measuring point on the side plate exhibits a stronger correlation with the identification of the bending moment as compared to the measuring point on the side stiffener. Furthermore, the relative error observed in conditions a to c is greater than that observed in conditions d to f, which further substantiates that the deck measuring points are more strongly correlated with the accurate identification of the bending moment.
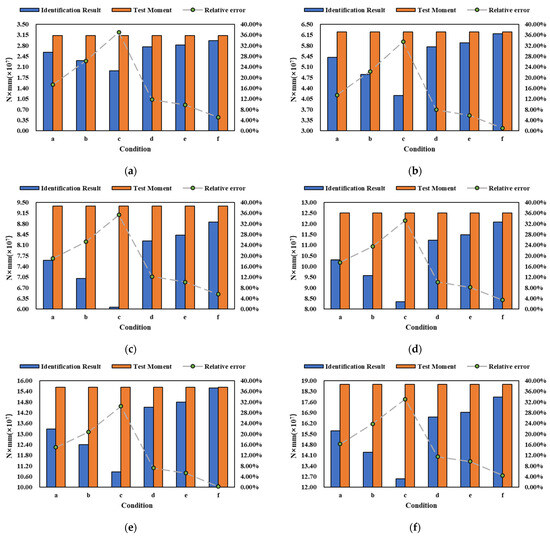
Figure 11.
Bending moment identification of point failure at different structures. (a) 5t. (b) 10t. (c) 15t. (d) 20t. (e) 25t. (f) 30t.
The identification error as shown in cases a–c indicates that the failure of highly correlated measuring points can significantly impact the accuracy of bending moment identification which requires further investigation. On the other hand, it should be noted that the aforementioned conclusion may not be universally applicable across all ships. Since the identification results are obtained by inverting the influence coefficient matrix, this investigation is synonymous with the correlation between the measurement point position and the influence coefficient matrix.
According to beam theory, the strain on a section increases in proportion to its distance from the neutral axis. Consequently, influence coefficients within the matrix are also proportionately greater when measurement points are positioned further from the neutral axis. In situations where a portion of the input vector signal is lost, the related influence coefficient can have a notable impact on the accuracy of the identification results. This impact is particularly significant when the influence coefficient is higher. In the experimental model tested in this study, the neutral axis is in close proximity to P21. Consequently, the highest influence coefficient within the matrix falls on the deck stiffener (S1, S6, and S11), followed by the deck plate (P1, P4, P6, and P11), with the side plate (P16 and P25) ranking third, and the side stiffener (S14 and S19) exhibiting the lowest coefficient of influence. This order is in complete agreement with the previously established correlation conclusions.
4.2. Strain Fitting Based on Experiment Results
Removing failed measuring points is a common method for processing failed signals. To explore the improvement of the XGboost method on moment identification, this study adopts two methods to process failure signals as follows:
- (a)
- Remove failed points.
- (b)
The effectiveness of strain fitting is examined by comparing the improvement of moment identification accuracy under various failure conditions. Strain fitting is performed on the above failure conditions.
4.2.1. Strain Fitting of Failed Points on Different Positions
Strain Fitting at Different Locations
The bending moment identification results after fitting the failed points at different locations are shown in Figure 12. After implementing strain fitting, the range of relative error decreases significantly from 4–31% to 0–5%. This enhancement in accuracy underscores the effectiveness of strain fitting in improving the identification of the bending moment. In parallel, the method of removing failed points also demonstrates an improvement in identification accuracy. Following the removal of failed points, the range of relative error decreases to 0–8%. In conditions a, b, and c, it becomes challenging to determine a superior method solely by comparing the identification errors of experimental results. However, in conditions d to g, as the number of failed points increases, the method of removing failed points yields higher identification errors. Furthermore, compared to the method of removing failed points, the relative error trend after strain fitting displays a smoother pattern. This indicates that the strain fitting method not only enhances identification accuracy but also renders the bending moment identification results more stable and reliable, albeit with a slight sacrifice in identification accuracy.
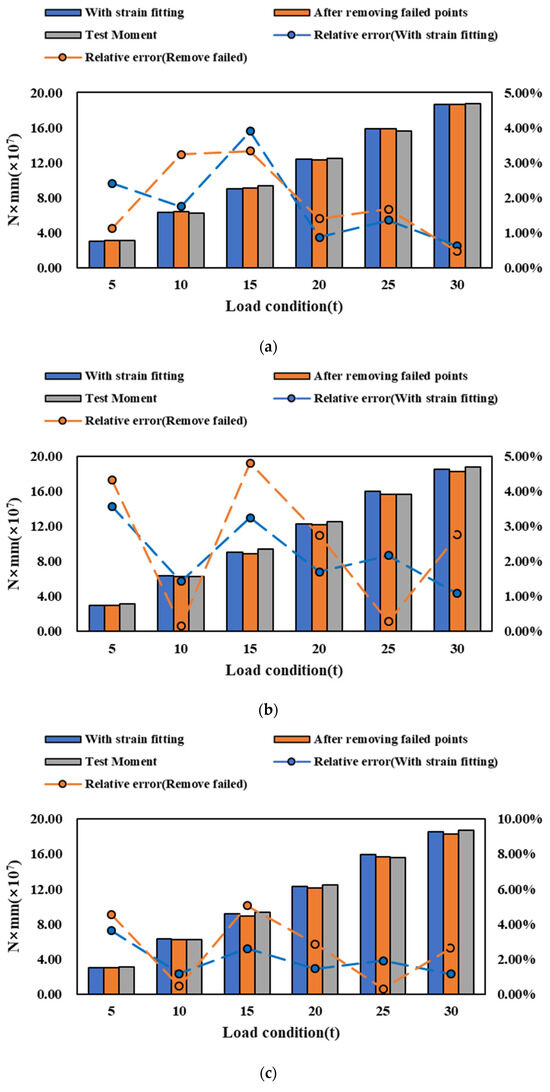
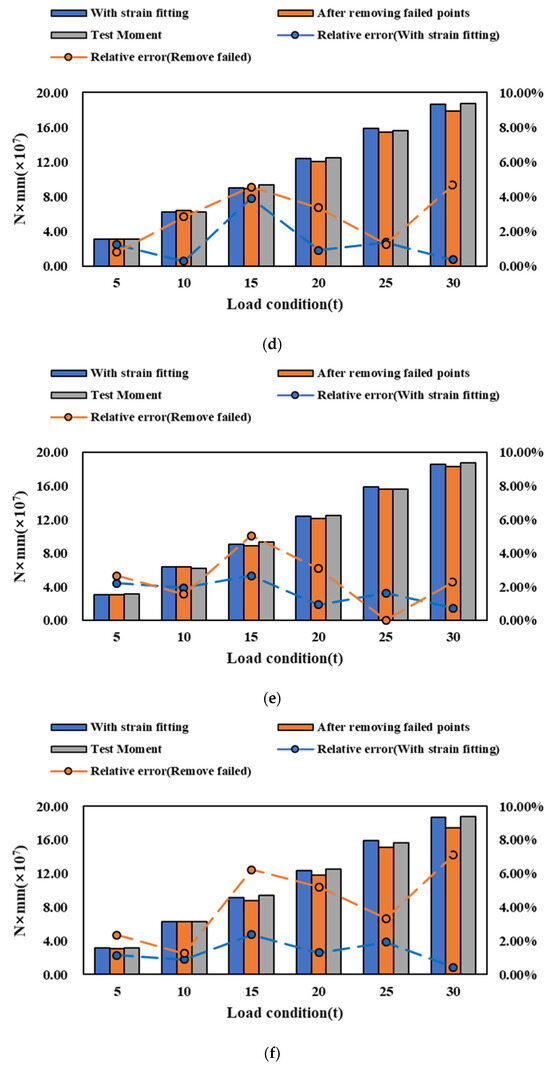
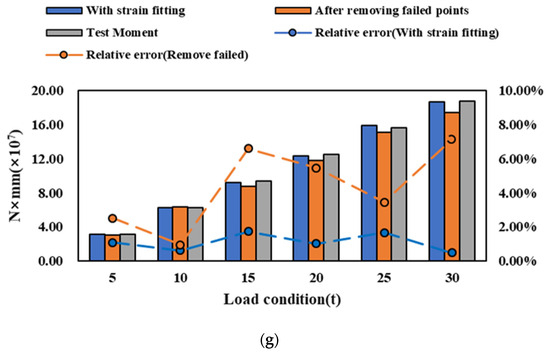
Figure 12.
Bending moment identification of strain fitting at different locations. (a) Condition a. (b) Condition b. (c) Condition c. (d) Condition d. (e) Condition e. (f) Condition f. (g) Condition g.
The strain values of each failed point at different locations before and after XGboost fitting are shown in Figure 13. Despite a certain degree of error between the fitted strain values and the actual values, the fitted strain can still provide a reasonable estimation of the strain values at each measuring point. In conditions where failures occur on a small scale (e.g., conditions a to d), the fitted strain values for points P16 and P11 remain unchanged. However, as the scale of failure at the measuring points increases (e.g., conditions e to g), particularly when adjacent measuring points such as P11, P16, and P6 are affected, the strain fitting values differ from those observed under small-scale failure conditions due to the changes in the training set.
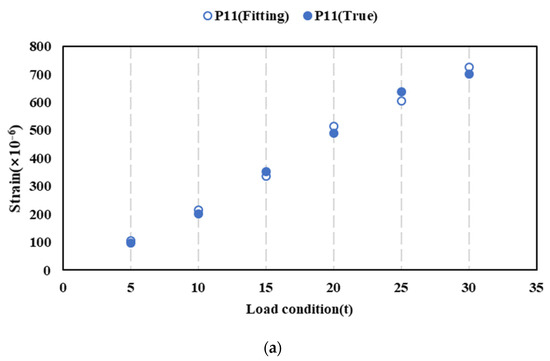
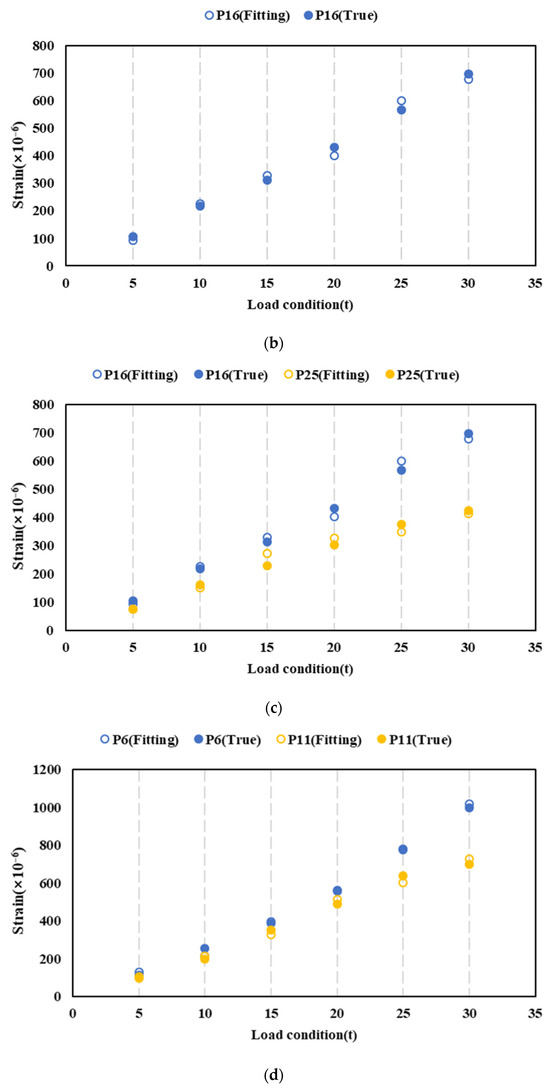
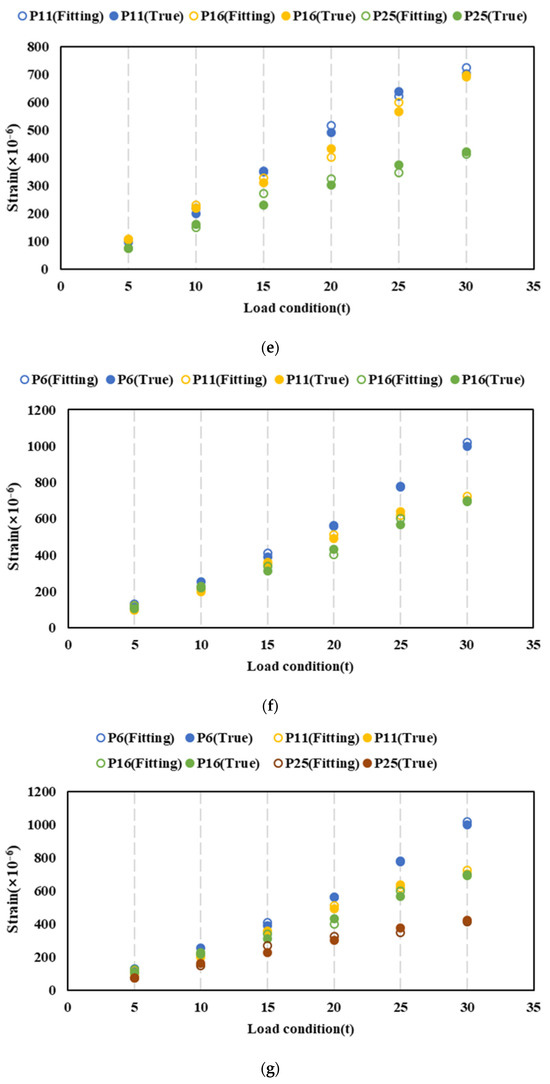
Figure 13.
Strain fitting at different locations. (a) Condition a. (b) Condition b. (c) Condition c. (d) Condition d. (e) Condition e. (f) Condition f. (g) Condition g.
Strain Fitting at Different Structures
The bending moment identification results after fitting the failed points at different structures are shown in Figure 14. The range of relative error in the identification results decreases from 0–40% to 0–4% through the implementation of strain fitting. Removing the failed points also improves bending moment identification, and the range of relative error reduces to 0–10%. When the failed points are located on the deck stiffener (conditions b and c), the strain fitting method outperforms the method of removing the points. However, both methods prove effective in improving identification accuracy in the other conditions (conditions d to f). Taking overall performance into consideration, the strain fitting method is deemed more suitable for enhancing identification accuracy.
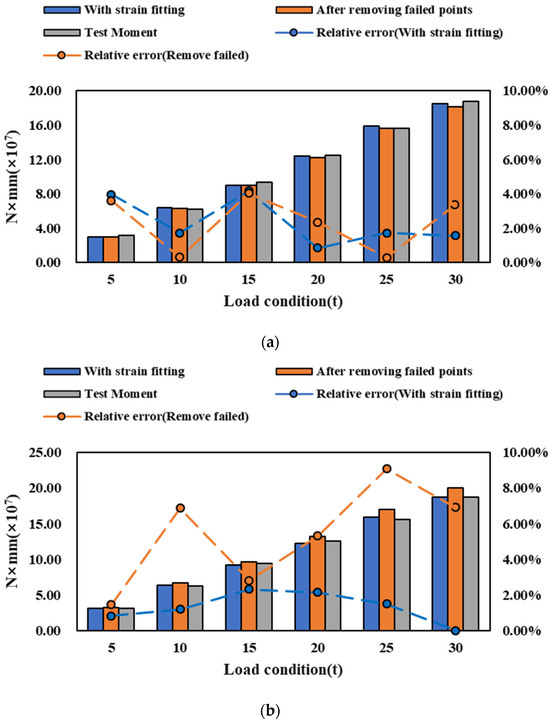
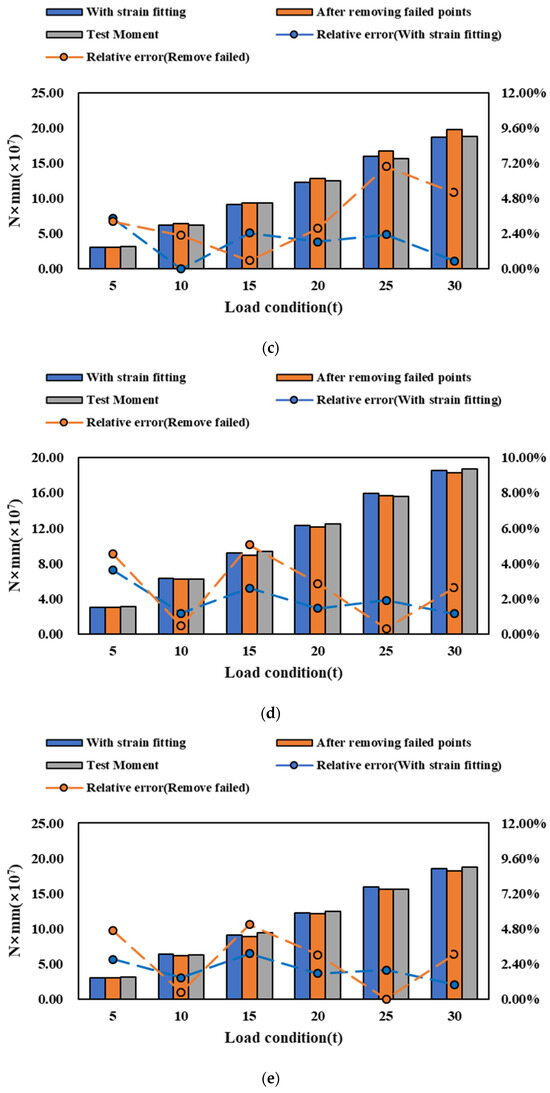
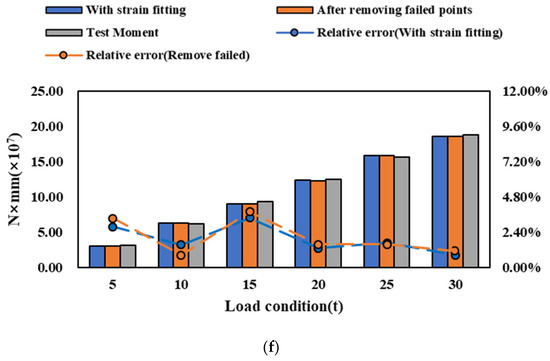
Figure 14.
Bending moment identification of strain fitting at different structures. (a) Condition a. (b) Condition b. (c) Condition c. (d) Condition d. (e) Condition e. (f) Condition f.
The strain values of each failed point at different structures before and after XGboost fitting are shown in Figure 15. The estimated value is close to the valid and actual value. The fitting accuracy of condition f is worse than the others under low load conditions (condition e and f, 5t).
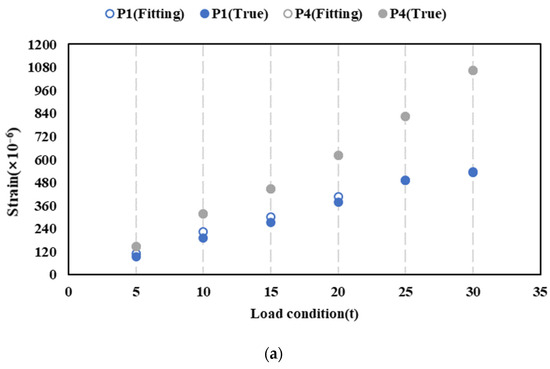
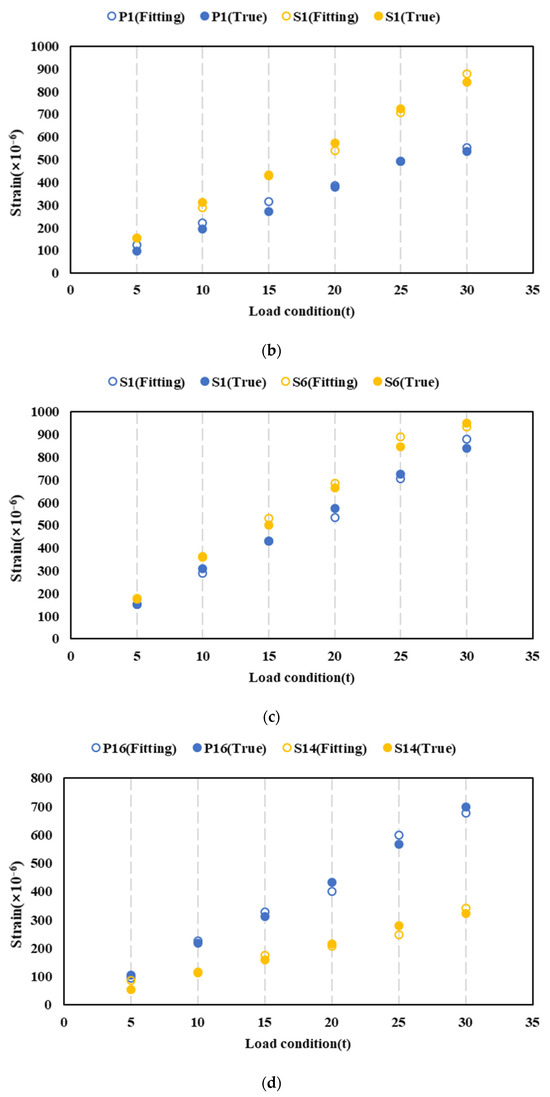
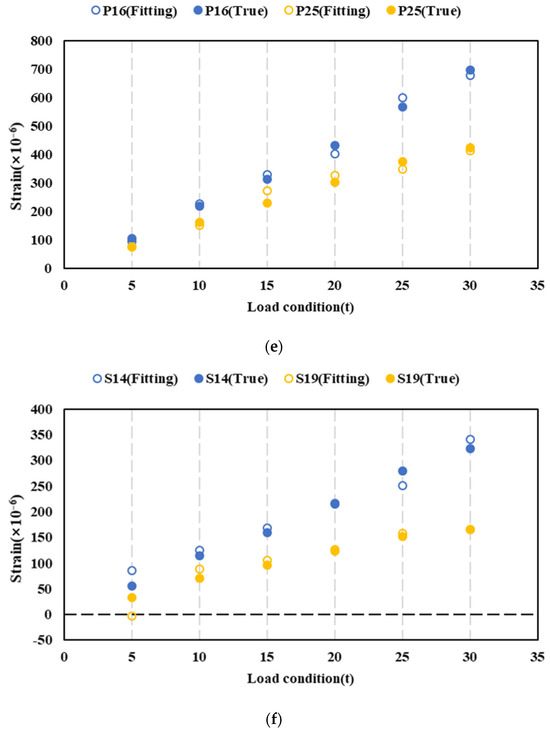
Figure 15.
Strain fitting at different structures. (a) Condition a. (b) Condition b. (c) Condition c. (d) Condition d. (e) Condition e. (f) Condition f.
4.2.2. Strain Fitting on Different Sections
Based on the above exploration, the XGboost method is effective in improving bending moment identification under the failure of section 1. To further verify the effectiveness of the XGboost method, random failure conditions are designed on other sections which are shown in Figure 16.
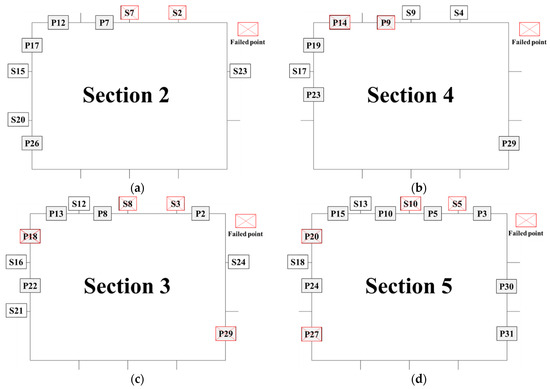
Figure 16.
Conditions of lack of points. (a) Two points deleted on the deck stiffener. (b) Two points deleted on the side plate. (c) Four points deleted (deck: two; side: two). (d) Four points deleted (deck: two; side: two).
The longitudinal bending moment identification results are shown in Figure 17. By employing two different methods to handle failure measurement points, the relative error in bending moment identification is reduced to less than 10%. In conditions characterized by a small-scale layout of measurement points (conditions a to c), the strain fitting method outperforms the method of removing measurement points when the load is low (0–15t). Removing measurement points diminishes the number of signals involved in the identification process. When the load is low and the true strain is small, the measured values become more susceptible to interference from other factors. Under such circumstances, a reduced number of measurement points leads to lower identification accuracy. In contrast, regardless of the layout of measuring points, the strain fitting method consistently exhibits a more stable trend in identification error.
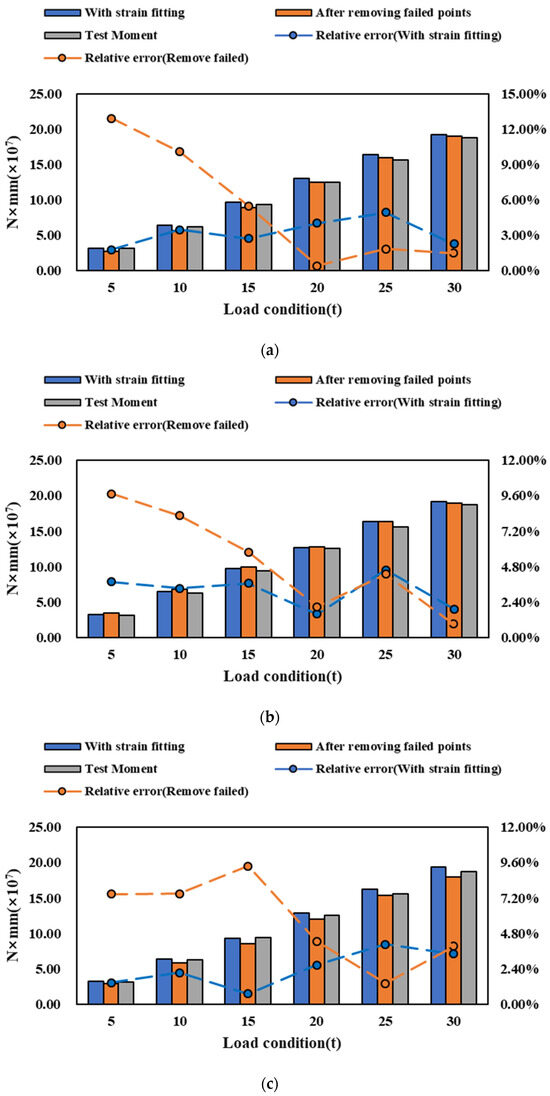
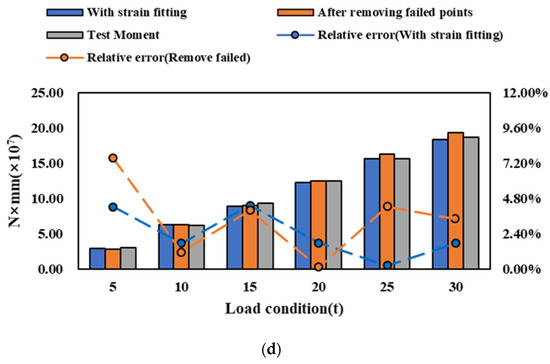
Figure 17.
Longitudinal bending moment of strain fitting under different layouts of points. (a) Condition a. (b) Condition b. (c) Condition c. (d) Condition d.
The fitting strain of measuring points is shown in Figure 18. The strain of other conditions is almost consistent with the actual values. Based on the above analysis, the XGboost method can effectively improve the identification of the longitudinal bending moment in the case of failure of the measuring points. Compared to common methods of removing failed points, the advantages of this method are as follows:
- (a)
- It makes the identification results more stable.
- (b)
- It shows a better improvement capability in cases of high-correlation measurement point failure and small-scale measurement point layouts.
- (c)
- Using strain fitting can estimate the approximate strain of failed points, which is more conducive to structural safety assessment.
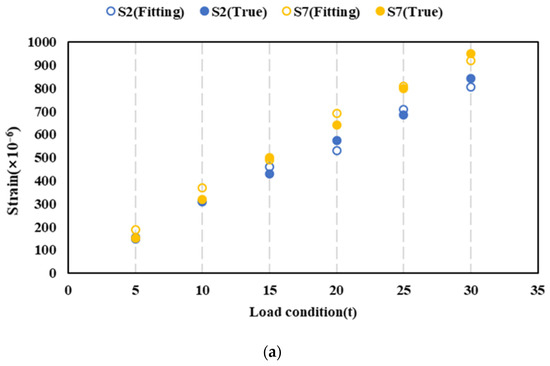
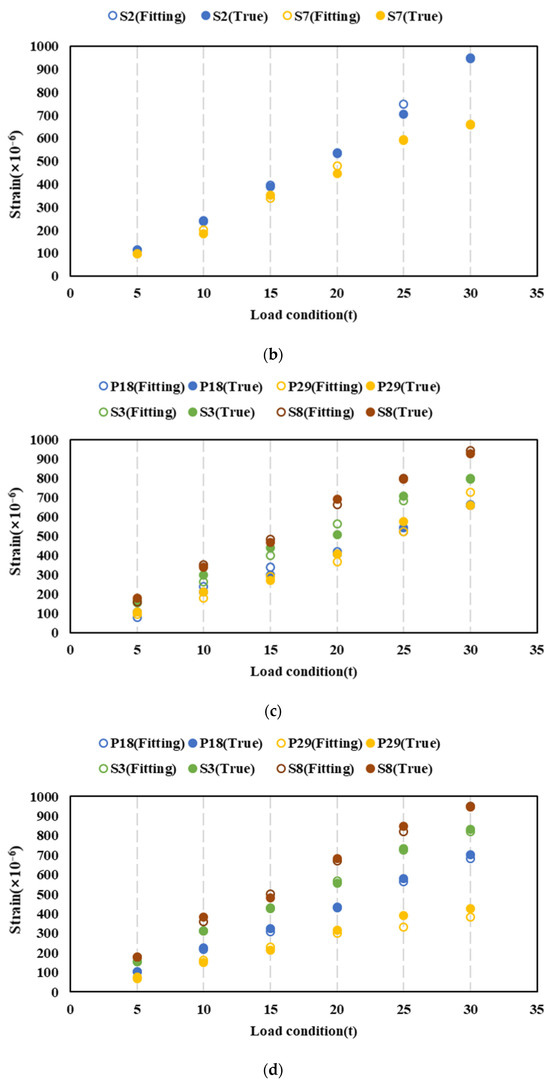
Figure 18.
Strain fitting under the layout of points. (a) Condition a. (b) Condition b. (c) Condition c. (d) Condition d.
4.3. Strain Fitting Based on Numerical Analysis
Based on the above experimental results, discrepancies persist between the fitted strain values and the actual values, and it is hard to determine whether these arise from measurement errors or the algorithm itself, based solely on the experimental results. Moreover, in addition to the longitudinal bending moment, the ship is affected by other types of load such as the lateral bending moment and torsion during navigation [12]. This makes the strain distribution on the different sections more complex, and the difficulty of fitting increases. Therefore, further numerical research is necessary, utilizing finite element analysis to provide additional insights.
4.3.1. Finite Element Model
The finite element model consists of shell elements. As the preloading cycles were used to eliminate the residual stresses, the numerical analysis did not consider the influence caused by residual stress. For the numerical analysis, the support boundary of the finite element model is free only with the x-displacement at one end and the y-rotation at both ends. This condition is to generate the actual boundary of the box girder in the experiment. The bending loads are applied at the bulkheads of the model. In this study, the numerical results of longitudinal strain on the sections are extracted to establish the moment–strain transfer matrix.
4.3.2. Convergence Study on the Mesh Size of Finite Elements
This study adopted ABAQUS 14.0 for numerical analysis. To study the convergence of the mesh size of finite element model, nine sizes (i.e., 10, 15, 20, 25, 30, 35, 40, 50, and 80 mm) are set to analyze the mean square error () between the solutions of the z-displacement in the middle of the box girder under two adjacent sizes. In this study, the can be calculated as follows [17]:
where is the z-displacement of the former size and is the z-displacement of the latter size. As shown in Figure 19, when a bending load of 1 × 105 N is applied to the box girder, the increases with the increase of the mesh size. When the mesh size is less than 40 mm, the grows slowly. Therefore, the mesh size of 20 mm is adopted for numerical analysis. The number of elements for the model is 11,511.
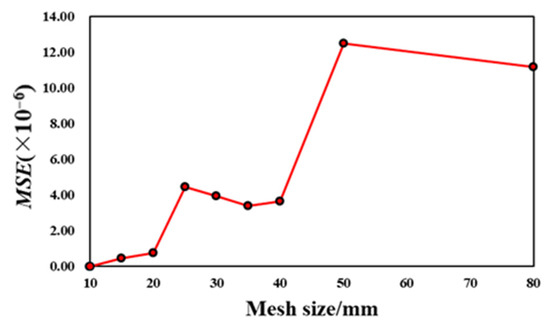
Figure 19.
MSE under different mesh sizes.
4.3.3. Analysis of the Sources of Fitting Errors
A finite element model was adopted to explore the influence of lateral bending moment and torsion on the XGboost fitting method. Based on the above research, under the longitudinal bending condition, the effect of the failed measuring points on the deck stiffener is greater than that on the deck plate, and the opposite is true on the side. Thus, two failed points are designed on the deck stiffener and the others are on the side plate, as shown in Figure 20.
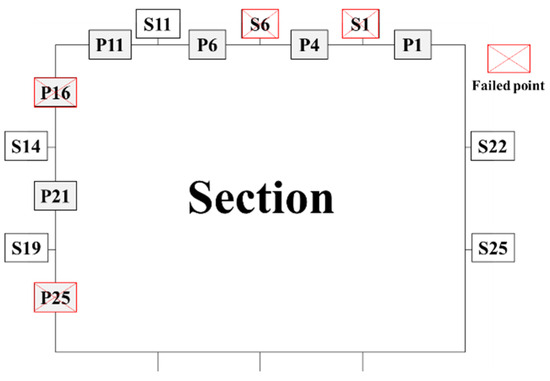
Figure 20.
Measuring point failure under different loading types.
In order to identify the longitudinal bending moment, the influence of other loads is required to be restrained as follows [14,15]:
where is the longitudinal bending moment of the section, is the lateral bending moment of the section, and is the torque of the section. is the longitudinal moment–strain transfer matrix composed of longitudinal bending moment–strain transfer vectors (), lateral bending moment–strain vectors (), and torque–strain vectors (). To investigate the reason of the experimental errors, the conditions of loading under longitudinal bending are designed as shown in Table 2.

Table 2.
Conditions of loading without interfering.
The results of longitudinal bending moment identification after strain fitting are shown in Table 3. The relative error is below 0.1% which is not shown in the table. The strain fitting results, which are almost consistent with the actual values, are shown in Figure 21. This result suggests the reliability of the finite element model, with most of the fitting errors in the experimental results originating from measurement errors.

Table 3.
Identification results without interfering.
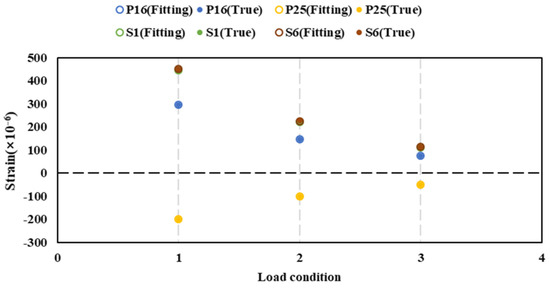
Figure 21.
Strain fitting without interfering.
4.3.4. Impact of Lateral Bending
To explore the impact of lateral bending on the XGboost fitting method, lateral bending is applied to the model and it is enhanced. The loading conditions are shown in Table 4. We designed some cases where the lateral bending moment is greater than the longitudinal bending moment. The finite element analysis results of condition 1 are shown in Figure 22a. The maximum longitudinal strain is situated in the corner of the box girder, whereas the strain in the middle of the deck and sides is relatively lower. The lateral strain and shear strain experienced by the model are significantly smaller in magnitude compared to the longitudinal strain. The longitudinal strains on the model deck display a linear distribution, indicating that the influence of lateral bending cannot be disregarded. To account for the impact of lateral bending moment, the above mentioned influence coefficient matrix (Equation (23)) can be utilized to decrease its effects.

Table 4.
Conditions of loading under lateral bending.
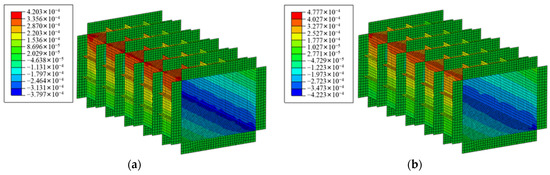
Figure 22.
Longitudinal strain under different conditions. (a) Lateral bending. (b) Torsion-lateral bending.
The longitudinal bending moment identification results under different conditions are shown in Table 5. After strain fitting, the relative error of bending moment identification results is very small. Figure 23 shows the strain fitting results under different conditions. The fitted value is almost consistent with the actual value. Therefore, the XGboost method is effective under the condition of lateral-longitudinal bending.

Table 5.
Identification results under lateral bending.
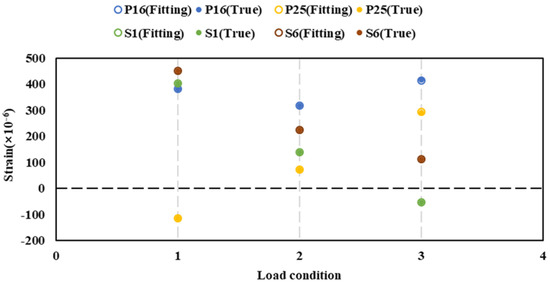
Figure 23.
Strain fitting under lateral bending.
4.3.5. Impact of Torsion-Lateral Bending
To explore the influence of torsion on the identification of the longitudinal bending moment based on the XGboost fitting method, torsion is applied to the model as shown in Table 6.

Table 6.
Conditions of loading under torsion-lateral bending.
Figure 24 shows the relationship between the longitudinal strain distribution of the deck under torsion-lateral bending and that under lateral bending on a section. The relationship between cases is linear. The slope of the liner function in Figure 24 is 1.002, and the intercept is −0.3921. The slope close to 1 and the low intercept indicate that the strain in the two cases is close to being the same. Therefore, the influence of torsion on the longitudinal strain of the model is small.
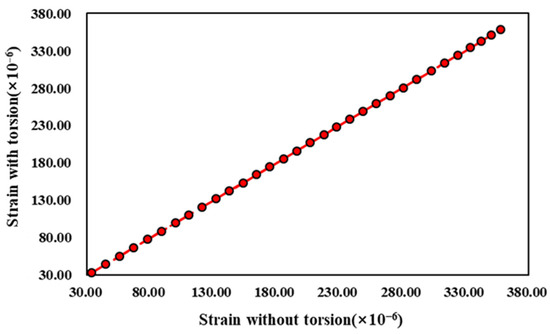
Figure 24.
Relationship between strain distribution of two cases.
The longitudinal bending moment identification results under different conditions are shown in Table 7 and the strain fitting results are shown in Figure 25. The identification accuracy and fitting accuracy are good. For this model, torsion has little effect on the identification of the longitudinal bending moment and strain fitting.

Table 7.
Identification results under torsion-lateral bending.
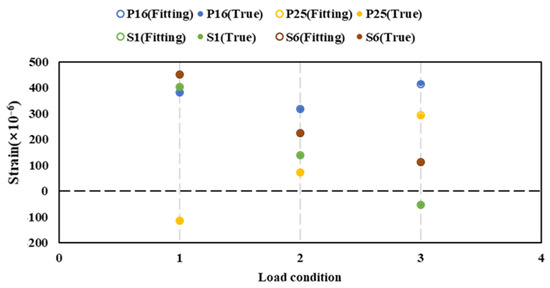
Figure 25.
Strain fitting under torsion-lateral bending.
4.4. Investigation of Fitting Schemes
Based on the above exploration, the XGboost fitting method has excellent performance in improving the accuracy of moment identification. However, in practical moment monitoring, parts of the monitored sections are far away. Using strain signals from all sections as the training set might reduce the accuracy of longitudinal bending moment identification. Therefore, the training set requires to be streamlined, and its connection with fitting value should be further investigated. To this end, based on the FEM analysis under longitudinal bending-lateral bending-torsion (conditions in Section 4.3.5), training conditions are proposed as shown in Table 8 to investigate the fitting schemes. The section number in the table represents the section included in the training set. The layout of measuring points on each section is shown in Figure 20. Through reducing the number of measuring points involved in the training set, the minimum number of sections required for strain fitting can be determined.

Table 8.
Training condition.
The strain fitting results under different training conditions are shown in Figure 26. As the strain fitting point value is almost consistent with the true value based on schemes 2 to 5, we just show one figure. Meanwhile, the fitting value displays an undeniable error based on scheme 1. This indicates that only two measurement points from the section are needed to accurately fit the failed points on a failure section. In other word, scheme 2 appears to be the optimal choice, taking into account the quest for the number of measurement points balanced against the required fitting accuracy.
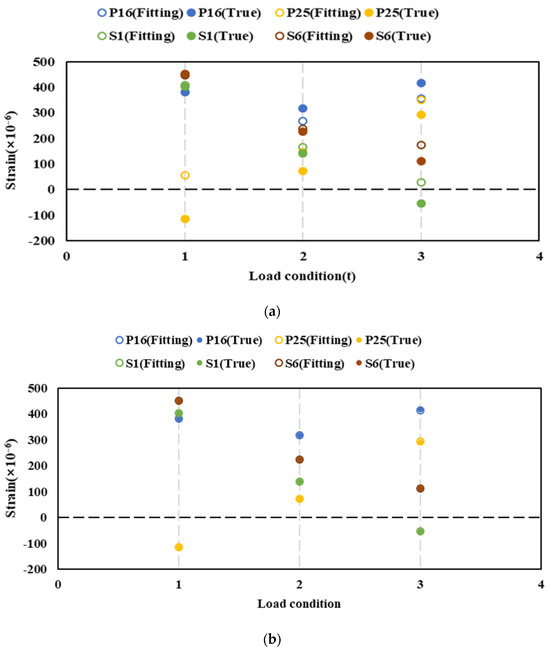
Figure 26.
Strain fitting of different schemes. (a) Scheme 1. (b) Schemes 2–5.
5. Discussion
5.1. Strain Fitting Model Based on XGboost in the Case of Failed Points
In general, the ideal fitting strategy would involve capturing the spatial strain distribution of the entire model to achieve a precise estimation of strain fitting values. However, given the challenges posed by the complex strain distribution, the extensive monitoring range, and economic constraints, employing a global fitting method is not practical in the specific scenario of longitudinal bending moment identification. Therefore, we adopted a fitting principle based on local points for dealing with the problem of measuring point failure in identifying the longitudinal bending moment, rather than global estimation.
From the perspective of the XGboost fitting principle, owing to the implementation of cart tree regression models [21,32], the XGboost strain fitting method is a suitable approach for fulfilling our requirements. By using the XGboost method, similar values in the training set will be divided into the same group of strain value. Due to the stress transfer continuity within the structure, strain values at adjacent measuring points are similar. In other words, the groups of strain value established by using the XGboost method consist mostly of measuring points with similar spatial positions. Based on this principle, accurate fitting values can be obtained by including the points surrounding the failed point in the training set, with the coordinates of the failed points serving as the test set. As a result, the strain fitting values obtained through the XGboost fitting method are greatly influenced by the local measuring points instead of global points. Our numerical results in scheme 2 verified this feature of the XGboost method. As shown in Figure 26b, the fitting results obtained from the different schemes are similar, suggesting that the impact of non-adjacent sections on strain fitting is insignificant. Other researchers also demonstrated that this feature of XGboost could support its high reliability in predicting unrelated data, such as patient laboratory test results and gene amplification [23,33]. They employed the XGboost method to capture the correlations among the samples in close proximity to the missing data, thus achieving a reliable estimation of the missing values. Therefore, the XGboost fitting method is suitable for fitting strain values as its characteristic aligns with the idea of employing local point fitting.
In particular, it should be pointed out that the XGboost fitting method operates on the principle of reducing the influence of adjacent outlier values on the fitted points. This principle has been substantiated by the fitting results obtained from our experimental and numerical investigations. As shown in Figure 12a–d, a comparison of the fitting outcomes under small-scale failure conditions (conditions a and d) reveals that the fitted strain value of P11 remains nearly unchanged even after the failure of P6 (which is in close spatial proximity to P11). Due to the existence of initial defects in the experimental model, the strain value at P6 differed from that at P11, ultimately leading them to be assigned to separate groups of value during the training regression model. The numerical results also present similar observations. For instance, as depicted in Figure 26, despite P11 and S14 being the closest points to the failed point P16, the fitting value of P16 aligns more closely with the corresponding point in the adjacent section. Due to the fact that P11, P16, and S14 are situated on distinct structures, significant disparities in stress components exist among these three positions under combined bending and torsion conditions, thereby hindering their regression into the same group of strain values. This characteristic of the XGboost fitting method mitigates interference from neighboring outliers during the fitting process of failed points. In summary, the XGboost fitting method not only fulfills the demands of local fitting but also exhibits robustness which is suitable for strain fitting.
5.2. Application Prospects of the XGboost Method for the Treatment of Failed Points
Compared to common methods of removing failed points, the XGboost method makes the identification results more stable and shows a better improvement capability in the case of high-correlation measurement point failure. For the establishment of the training set, according to the aforementioned investigation in Section 4.1, it is recommended to position the measurement points in the areas of the structure that exhibit high correlation, such as the deck stiffener or deck plate. These suggestions ensure the establishment of a training set with strong features to effectively fit failed points, which align with the guidelines set by classification societies [6,7]. On the other hand, for strain fitting based on XGboost, arranging the measurement points into two sections, which is a common method employed in practical longitudinal bending moment monitoring [12,13,34,35,36], is deemed sufficient. Consequently, the strain fitting method does not impose any special requirements on the layout of measurement points, making it widely applicable for longitudinal bending moment monitoring systems on ships. Additionally, apart from improving the identification of the longitudinal bending moment, the XGboost fitting method extends its potential applications in the supplement strain values to help load identification (such as ice load identification [37,38]) or deformation monitoring (such as iFEM [39,40]).
6. Conclusions
In this study, a novel method, the XGboost fitting method, is proposed to reduce the impact of the failure of measuring points on the identification of the longitudinal bending moment. Suggestions for point arrangement and the scheme for strain fitting were deeply investigated by experimental and numerical analysis. The main conclusions are as follows:
- (1)
- The failure of highly correlated measuring points has a significant impact on the accuracy of identifying the total longitudinal bending moment. This result indicates that the points on the deck stiffener have the highest correlation, followed by the deck plate, the side plate, and the side stiffener.
- (2)
- Based on the experimental results, the XGboost fitting method can effectively improve the identification accuracy of the longitudinal bending moment in the case of the failure of measuring points. Compared to common methods of removing failed points, the XGboost method makes the identification results more stable and shows a better improvement capability in the case of high-correlation measurement point failure. In this study, after using the strain fitting method, the relative error decreased to less than 6%, and that was less than 5% in most conditions. By contrast, the relative error of some conditions still reaches 10% by removing failed points.
- (3)
- There is a fitting error between the fitted strain and the measured strain due to the measurement error. However, the trend of the fitted values is almost consistent with the actual values. Therefore, this method is able to estimate strain to an approximate value.
- (4)
- Based on the FEM analysis, the XGboost fitting method is effective for complex load conditions. After further numerical investigation, it is suggested as the optimal fitting scheme which adopts the failed section and its adjacent section as the training set.
Author Contributions
Conceptualization, G.X. and J.G.; Methodology, G.X. and J.G.; Software, G.X.; Formal analysis, G.X.; Data curation, J.L.; Writing—original draft, G.X.; Writing—review & editing, H.L.; Supervision, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Katsoudas, A.S.; Silionis, N.E.; Anyfantis, K.N. Structural Health Monitoring for Corrosion Induced Thickness Loss in Marine Plates Subjected to Random Loads. Ocean Eng. 2023, 273, 114037. [Google Scholar] [CrossRef]
- Rahgozar, R.; Bitaraf, M. A Summary Evaluation of Output-Only Damage-Sensitive Features for Structural Health Monitoring of Offshore Platforms Subjected to Ambient Loads. Ocean Eng. 2022, 266, 112892. [Google Scholar] [CrossRef]
- Gordo, J.; Guedes Soares, C.; Faulkner, D. Approximate Assessment of the Ultimate Longitudinal Strength of the Hull Girder. J. Ship Res. 1996, 40, 60–69. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ando, T.; Anai, Y.; Yao, T.; Fujikubo, M.; Iijima, K. Longitudinal Strength of Container Ships Under Combined Torsional and Bending Moments. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009; OnePetro: Richardson, TX, USA, 2009. [Google Scholar]
- American Bureau of Shipping. Guide for Hull Condition Monitoring System 2020. Available online: https://ww2.eagle.org/content/dam/eagle/rules-and-guides/current/conventional_ocean_service/73_Hull_Condition_Monitoring_2016/hull-condition-monitoring-guide-july20.pdf (accessed on 23 February 2023).
- China Classification Society. Rules for Intelligent Ship. Available online: https://www.ccs.org.cn/ccswz/specialDetail?id=201900001000009739 (accessed on 23 February 2023).
- Nippon Kaiji Kyokai. Rules for Hull Monitoring Systems. Available online: https://www.classnk.or.jp/account/zh/Rules_Guidance/ssl/tech_rules.aspx (accessed on 24 February 2023).
- Li, M.; Boulougouris, E.; Lazakis, I.; Theotokatos, G. Wave-Induced Vertical Bending Moment Estimation by Onboard Tiltmeters Units on Container Ship. In Proceedings of the International Conference on Maritime Safety and Operations, Glasgow, UK, 13–14 October 2016; Available online: https://strathprints.strath.ac.uk/58370/1/Li_etal_MSO2016_Wave_induced_vertical_bending_moment_estimation_by_onboard_tiltmeters.pdf (accessed on 24 February 2023).
- Tatsumi, A.; Iijima, K.; Fujikubo, M. Estimation of Still-Water Bending Moment of Ship Hull Girder Using Beam Finite Element Model and Ensemble Kalman Filter. In Proceedings of the ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering, Hamburg, Germany, 5–10 June 2022; American Society of Mechanical Engineers Digital Collection: Washington, DC, USA, 2022. [Google Scholar]
- Cusano, G.; La Marca, L.S. Evaluation and Forecasting of Elapsed Fatigue Life of Ship Structures by Analyzing Data from Full Scale Ship Structural Monitoring. J. Shipp. Ocean Eng. 2015, 5, 59–74. [Google Scholar] [CrossRef][Green Version]
- Moreira, L.; Soares, C.G. Neural Network Model for Estimation of Hull Bending Moment and Shear Force of Ships in Waves. Ocean Eng. 2020, 206, 107347. [Google Scholar] [CrossRef]
- Yu, H.; Ha, M.; Choi, J.; Tai, J.S. Design and Implementation of a Comprehensive Full-Scale Measurement System for a Large Container Carrier. In Proceedings of the Design & Operation of Container Ships conference, London, UK, 22–23 November 2006; RINA: Genoa, Italy, 2006; pp. 51–60. [Google Scholar]
- Liu, D. Fatigue Assessment Methodfor Hull Structure Based on Strength Monitoring System. Master’s Thesis, Harbin Engineering University, Harbin, China, 2018. [Google Scholar]
- Li, J. Research on Load Inversion Method and Model Experiment of Ultra Large Ships. Master’s Thesis, Harbin Engineering University, Harbin, China, 2021. [Google Scholar]
- Li, J.; Dong, W.; Liu, N.; Feng, G.; Ren, H. Theoretical and Experimental Study on Load Inversion of Ship Hull Girder. Shipengineering 2022, 44, 41–46. [Google Scholar] [CrossRef]
- Liu, Y.; Xing, Y.; Shen, Z. Identification of Cross-section Loads Based on Measured Strain of Missile Body. Acta Amamentaii 2016, 37, 332–337. [Google Scholar]
- Wang, J.; Chen, X.; Duan, Q.; Ji, S. Eliminating the Influence of Measuring Point Failure in Ice Load Identification of Polar Ship Structures. Ocean Eng. 2022, 261, 112082. [Google Scholar] [CrossRef]
- Shrive, F.M.; Stuart, H.; Quan, H.; Ghali, W.A. Dealing with Missing Data in a Multi-Question Depression Scale: A Comparison of Imputation Methods. BMC Med. Res. Methodol. 2006, 6, 57. [Google Scholar] [CrossRef] [PubMed]
- Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing Value Estimation Methods for DNA Microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef] [PubMed]
- Stekhoven, D.J.; Buhlmann, P. MissForest-Non-Parametric Missing Value Imputation for Mixed-Type Data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Kankanamge, K.D.; Witharanage, Y.R.; Withanage, C.S.; Hansini, M.; Lakmal, D.; Thayasivam, U. Taxi Trip Travel Time Prediction with Isolated XGBoost Regression. In Proceedings of the 2019 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 3–5 July 2019; pp. 54–59. [Google Scholar]
- Li, W.; Yin, Y.; Quan, X.; Zhang, H. Gene Expression Value Prediction Based on XGBoost Algorithm. Front. Genet. 2019, 10, 1077. [Google Scholar] [CrossRef] [PubMed]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Experimental Assessment of the Ultimate Strength of a Box Girder Subjected to Severe Corrosion. Mar. Struct. 2011, 24, 338–357. [Google Scholar] [CrossRef]
- Xu, W.; Iijima, K.; Wada, R.; Fujikubo, M. Experimental Evaluation of the Post-Ultimate Strength Behavior of a Ship’s Hull Girder in Waves. J. Mar. Sci. Appl. 2012, 11, 34–43. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Guedes Soares, C. Effect of Corrosion Severity on the Ultimate Strength of a Steel Box Girder. Eng. Struct. 2013, 49, 560–571. [Google Scholar] [CrossRef]
- Akhras, G.; Gibson, S.; Yang, S.; Morchat, R. Ultimate Strength of a Box Girder Simulating the Hull of a Ship. Can. J. Civ. Eng. 1998, 25, 829–843. [Google Scholar] [CrossRef]
- Hughes, O. Ship Structural Design: A Rationally-Based, Computer-Aided Optimization Approach; Wiley-Interscience: New York, NY, USA, 1983. [Google Scholar]
- Hauser, R. Line Search Methods for Unconstrained Optimisation, Lecture 8; Oxford University Computing Laboratory: Oxford, UK, 2007. [Google Scholar]
- Kong, S.; Cui, H.; Tian, Y.; Ji, S. Identification of Ice Loads on Shell Structure of Ice-Going Vessel with Green Kernel and Regularization Method. Mar. Struct. 2020, 74, 102820. [Google Scholar] [CrossRef]
- Ma, H.; Xiong, Q.; Wang, D. Experimental and Numerical Study on the Ultimate Strength of Stiffened Plates Subjected to Combined Biaxial Compression and Lateral Loads. Ocean Eng. 2021, 228, 108928. [Google Scholar] [CrossRef]
- Santhanam, R.; Uzir, N.; Raman, S.; Banerjee, S. Experimenting XGBoost Algorithm for Prediction and Classification of Different Datasets. In Proceedings of the National Conference on Recent Innovations in Software Engineering and Computer Technologies (NCRISECT), Pittsburgh, PA, USA, 23–24 March 2017. [Google Scholar]
- Zhang, X.; Yan, C.; Gao, C.; Malin, B.A.; Chen, Y. Predicting Missing Values in Medical Data Via XGBoost Regression. J. Healthc. Inform. Res. 2020, 4, 383–394. [Google Scholar] [CrossRef]
- Choi, J.; Kang, Y. Two-Plane Hull Girder Stress Monitoring System for Container Ship. J. Ship Ocean Technol. 2004, 8, 17–25. [Google Scholar]
- Park, J.; Kang, Y.-T. Strain Decomposition Method in Hull Stress Monitoring System for Container Ship. J. Ship Ocean Technol. 2003, 7, 56–65. [Google Scholar]
- Yu, H.; Choi, J.; Park, G.; Han, S.; Tai, S.; Ha, M. Full Scale Measurement of a Large Container Carrier on the Far East—Europe Route. In Proceedings of the SNAME Maritime Convention, Houston, TX, USA, 15–17 October 2008; OnePetro: Richardson, TX, USA, 2008. [Google Scholar]
- Suominen, M.; Kujala, P.; Romanoff, J.; Remes, H. Influence of Load Length on Short-Term Ice Load Statistics in Full-Scale. Mar. Struct. 2017, 52, 153–172. [Google Scholar] [CrossRef]
- Lee, T.; Lee, J.; Kim, H.; Rim, C. Field Measurement of Local Ice Pressures on the ARAON in the Beaufort Sea. Int. J. Nav. Archit. Ocean Eng. 2014, 6, 788–799. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and Stress Monitoring of a Chemical Tanker Based on Inverse Finite Element Method. Ocean Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and Stress Monitoring of a Panamax Containership Using Inverse Finite Element Method. Ocean Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).