Influence of Auxiliary Pipelines of the Deepwater Drilling Riser on the Dynamic Characteristics of the Subsea Wellhead

Abstract

During deepwater drilling, the subsea wellhead will be subjected to dynamic loads transmitted from the marine environment, floating drilling platform, riser, and blowout preventer (BOP). Therefore, complex dynamic responses will be induced, which will seriously affect the safety of the subsea wellhead. In this paper, considering the effect of auxiliary pipelines on the riser, a novel entire mechanical model of the floating platform–riser–BOP–subsea wellhead is established. By using the finite-difference method, the governing equations are solved. Finally, the dynamic bending moment and stress distribution of the subsea wellhead are obtained. Moreover, the model is verified by numerical simulation in Orcaflex. On this basis, the influence of the wave height, wave period, sludge height of the subsea wellhead, rotational stiffness of the lower flexible joint, and wall thickness of the conductor on the dynamic characteristics of the subsea wellhead is discussed. Analysis results show that the theoretical analysis results are in good agreement with the numerical simulation. The auxiliary pipelines have important influence on the dynamic characteristics of the subsea wellhead. Wave period is the most important factor affecting the mechanical behavior of the subsea wellhead. Wave height, wall thickness of the conductor, and sludge height are secondary factors affecting the mechanical behavior of the subsea wellhead. The rotational stiffness of the lower flexible joint has little influence on the mechanical behavior of the subsea wellhead. By solving the optimized mechanical model proposed in this paper, the dynamic characteristic of the subsea wellhead conforms more to the actual deepwater drilling conditions. This study has reference significance for the design and mechanical control of the subsea wellhead in deepwater drilling.

1. Introduction

With the increase in the world demand for oil and gas resources, the exploration and development of oil and gas in deepwater areas have received more and more attention [1,2,3]. The deepwater drilling riser and subsea wellhead are indispensable equipment for deepwater drilling engineering, and its safety and efficiency are the premise for developing deepwater oil and gas resources [4,5,6]. However, the riser will generate complex mechanical behavior under the combined action of the marine environment, floating platform, and operating load, and will transmit the vibration load to the subsea wellhead through the BOP, inducing a dynamic response on the subsea wellhead, which seriously affects the safety of the subsea wellhead [7,8,9,10]. Therefore, it is of great significance to analyze the dynamic response of the subsea wellhead and obtain the main control factors of the dynamic behavior.

At present, much research has been carried out on the mechanical analysis of the deepwater drilling riser and subsea wellhead, which provides significant basis for the safe and efficient development of oil and gas in deepwater areas. In terms of riser mechanics, Burke [11] established the dynamic analysis equation of the riser, where the Morison equation was used to describe the wave current, and the dynamic response of the riser was solved and discussed. Egeland et al. [12] modified the lateral vibration governing equation of the riser by changing the boundary conditions at the top of the riser, with consideration of the random wave and drilling platform, and analyzed the influence of random wave parameters on the vibration characteristics of the riser. Tian et al. [13] simulated the vortex-induced vibration of a riser system with 4~10 auxiliary pipelines, which showed that the auxiliary pipelines have an obvious effect on the dynamic response of the riser. Wu et al. [14] obtained the f-vortex-induced vibration characteristics of the deepwater drilling riser considering the auxiliary pipelines. Han et al. [15] established the mechanical model of the deepwater drilling riser considering the effect of buoyancy blocks and the nonlinear dynamic characteristic effects of drilling fluid in the riser. Gao et al. [16] studied the dynamic behavior of the deepwater drilling riser by using the principle of vibration mechanics. Kong et al. [17] studied the vortex-induced vibration of the riser system considering six auxiliary pipelines of the drilling riser by numerical simulation. Wang et al. [18] proposed the dynamic model for the riser-recoil response, which was solved by the finite-element model and the Newmark–β method. Yang et al. [19] proposed a model for the natural frequency and vibration of the deepwater drilling riser to avoid resonance. Karun et al. [20] carried out a theoretical analysis of the deepwater drilling riser, and studied the effect of the internal wave on the large-amplitude dynamic response of the riser. Zhang et al. [21] proposed an assessment method for the deepwater drilling riser under the influence of extreme sea conditions. Zhao et al. [22] studied the dynamic model on the recoil control of the deepwater drilling riser system. Liu et al. [23] proposed a deepwater drilling riser recoil-control method based on the control theory. Chen et al. [24] established an analysis method to determine the safe operation window of the deepwater riser based on the allowable offset of the drilling platform in different directions. Wang et al. [25,26,27,28,29,30,31] established a systematic analysis method for the mechanical behavior of the deepwater drilling riser under complex marine environments and drilling loads, which provided a scientific basis for the design and control of the deepwater drilling riser. The mechanical analysis on the riser system, including static analysis, vibration analysis, and recoil analysis, is related to the resilience issue. It is necessary to discuss and study the current research on the resilience of pipelines and other systems. Argyroudis et al. [32] proposed a novel framework for the quantitative resilience assessment of critical infrastructure. Mina et al. [33] studied the resilience of unburied high-pressure/high-temperature pipelines with different outside diameter-to-wall thickness ratios and subjected to the action of thermal loads. Ouyang et al. [34] proposed a novel resilience-assessment method of interdependent infrastructure systems. Zelaschi et al. [35] studied the resilience response of the bridges in a road network based on a three-dimensional finite-element model.

In terms of the subsea wellhead, Valka et al. [36] discussed the transfer mechanism of loads acting on the subsea wellhead, and introduced the key points to be considered in the entire mechanical modeling of the subsea wellhead. Evans et al. [37] discussed the influence of the riser system configuration and operation parameters on subsea wellhead fatigue damage. Williams et al. [38,39] studied the transmission mechanism of stress acting on the subsea wellhead, and evaluated the effect of the motion of the floating drilling platform on the fatigue damage of the subsea wellhead. Pedro et al. [40] studied the dynamic bending moment of the subsea wellhead, and pointed out that the frequency-domain method has certain limitations in the global response analysis. Det Norske Veritas GL (DNVGL) proposed two recommended practices for the fatigue-damage evaluation of the subsea wellhead [41,42]. Jaiswal et al. [43] conducted a numerical simulation study on the mechanical behavior of the floating drilling platform–riser–BOP–subsea wellhead, and evaluated the effect of the dynamic wave load on the fatigue damage of the subsea wellhead. McNeill et al. [44,45,46] analyzed the fatigue damage of the subsea wellhead using a semianalytical method. Li et al. [47] simulated the wave and current loads with finite-element software, and calculated the fatigue life of the subsea wellhead. Wang et al. [48] proposed a subsea wellhead fatigue analysis method which is more suitable for practical engineering applications. Li et al. [49] developed a local stress–strain method based on a semidecoupled model to predict the fatigue damage of the subsea wellhead. Chen et al. [50] summarized the factors affecting the fatigue damage of the subsea wellhead system qualitatively and quantitatively. Pestana et al. [51,52] conducted a theoretical analysis of the recoil response of the riser after emergency detachment using a nonlinear damping-spring model. Mai et al. [53,54] presented new modeling of the behavior of an underwater vehicle operating in the littoral sea, and a new simulation method of the full equations of the combined rigid-body motion of an underwater vehicle, and the flexible motion of the umbilical cable was derived. Wang et al. [55,56,57] established an analysis frame for the fatigue assessment of the subsea wellhead with consideration of the coupling effect of temperature and pressure.

To sum up, a lot of research has been carried out on the mechanical analysis and design control of the deepwater drilling riser and subsea wellhead, which provides scientific guidance for the safety of deepwater drilling engineering. However, the rare published literature on the mechanical characteristics of the riser and subsea wellhead has considered the influence of the auxiliary pipelines of the drilling riser, which results in analysis results different from the reality situation. The former method models for the riser dynamic usually ignored the influence of auxiliary pipelines on the riser. Ignoring the auxiliary pipelines may reduce the calculation time to solving the models, but the results do not conform to the actual deepwater drilling conditions. Therefore, it is necessary to establish a practical mechanical model to analyze the mechanical behavior of the riser and the subsea wellhead. Therefore, considering the influence of the auxiliary pipelines of the riser and the movement of the floating platform, the novel entire dynamic analysis model and governing equations of the floating platform–riser–BOP–subsea wellhead are established in this paper. On this basis, the influence of auxiliary pipelines on the dynamic response of the subsea wellhead has been analyzed emphatically. This study has guiding significance for the accurate analysis of the mechanical response of the subsea wellhead.

The subsequent sections of the paper are structured as follows: Section 2 considers the auxiliary pipelines of the drilling riser, and establishes the novel entire mechanical model of the floating platform–riser–BOP–subsea wellhead. Section 3 elaborates the solution process of the mechanical model by the finite-difference method. Section 4 first compares the theoretical calculation and numerical simulation results to validate the model proposed in this paper. Then, the influence of the wave height, wave period, sludge height of the subsea wellhead, rotational stiffness of the lower flexible joint, and wall thickness of the conductor on the dynamic behavior of the subsea wellhead are discussed by sensitivity analysis. Finally, the main controlling factors which affect the dynamic characteristics of the subsea wellhead are revealed by orthogonal experiments. Section 5 discusses all the results of this paper, including the model establishment, validation, and sensitivity analysis results. Finally, the primary conclusions of the paper are summarized in Section 6.

2. Mechanical Model

2.1. Mechanical Model of the Floating Platform–Riser–BOP–Subsea Wellhead

In order to simplify the mechanical model and mathematical derivation, the following assumptions are adopted in this paper. The riser is assumed as an isotropic linear elastic material, and the mechanical characteristics are regarded as constant along the water depth. The propagation directions of the wave and current are in the same plane. The top and the bottom of the riser are connected to the floating drilling platform and BOP through the upper and lower flexible joint, respectively, which is considered as a hinged restraint, as shown in Figure 1.

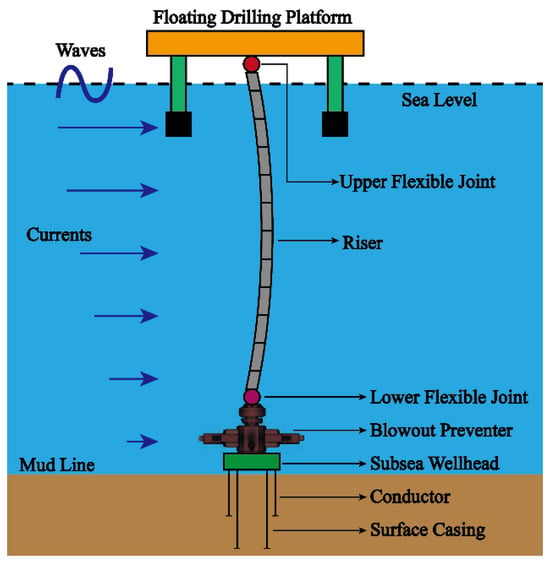
Figure 1. The system of the floating drilling platform–riser–BOP–subsea wellhead.

Based on the above assumptions, the mechanical model of the riser is established based on the principles of elasticity. In the governing Equation (1), the elastic modulus does not vary with the length of the riser, and the mechanical model established in this article is in a two-dimensional plane. The governing equation of the riser can be expressed as [58]:

$$EI\frac{{\partial }^{4}y(x,t)}{\partial x^4}-T\left(x\right)\frac{{\partial }^{2}y\left(x,t\right)}{\partial x^2}+m\frac{{\partial }^{2}y}{\partial t^2}=f(x,t)$$

(1)

where E is the elastic modulus of the riser, Pa; I is the inertia moment of riser, m⁴; y(x,t) is the lateral displacement of the riser, m; x is the axial length of the riser, m; f(x,t) is the wave current force on the riser, N/m; T(x) is the axial tension of the riser per length, N/m; m is the total weight of the riser per length, kg/m.

The top of the riser is connected to the floating platform through the upper flexible joint, which can be considered as a hinged restraint. The displacement at the top of the riser is equal to the displacement of the platform; additionally, the bending moment is equal to the rotational stiffness of the upper flexible joint. Therefore, the top boundary condition of Equation (1) can be expressed as:

$$\left\{\begin{array}{c}y\left(0,t\right)=S(t)\hfill \\ EI\frac{{\partial }^{2}y(0,t)}{\partial x^2}-K_1\frac{\partial y\left(0,t\right)}{\partial x}=0\hfill \end{array}\right.$$

(2)

where S(t) is the dynamic motion of the floating platform, m; K₁ is the rotational stiffness of the upper flexible joint, N·m/rad.

The bottom of the riser is connected to the BOP through the lower flexible joint, which can be considered as a hinged restraint. The displacement at the bottom of the riser is 0; additionally, the bending moment is equal to the rotational stiffness of the lower flexible joint. Therefore, the bottom boundary condition of Equation (1) can be expressed as:

$$\left\{\begin{array}{c}y\left(L,t\right)=0\hfill \\ EI\frac{{\partial }^{2}y(L,t)}{\partial x^2}-K_2\frac{\partial y\left(L,t\right)}{\partial x}=0\hfill \end{array}\right.$$

(3)

where K₂ is the rotational stiffness of the lower flexible joint, N·m/rad; L is the riser length, m.

The forces acting on the riser system include axial forces and wave–current forces. The axial force includes the floating weight of the main rise and auxiliary pipelines, as well as the weight of drilling fluid inside the riser.

The top tension of the riser can be expressed as [59]:

$$T_0=W_s{f}_{wt}-B_n{f}_{bt}+A_{i}L({\rho }_m-{\rho }_w)$$

(4)

where W_s is the weight of the riser in seawater, N; f_wt is the submersion coefficient, which is 1.05 in this paper; B_n is the buoyancy force of the buoyancy joint, N; f_bt is the effective coefficient, which is 0.96 in this paper; A_i is the area of the riser inner diameter, m²; ρ_m is the density of drilling fluid, kg/m³; ρ_w is the density of seawater, kg/m³.

2.2. Model of the Auxiliary Pipelines

The auxiliary pipelines mainly include kill lines, hydraulic lines, choke lines, and booster lines. The function of the choke and kill lines is to reduce the pressure loss caused by fluid flow in the riser. The booster line, which is connected with the mud pump on the floating platform, is used to increase the flow rate of the drilling fluid in the riser. The hydraulic pipelines are used to control the BOP in drilling engineering [60]. The distribution of the main riser pipe and auxiliary pipelines are shown in Figure 2.

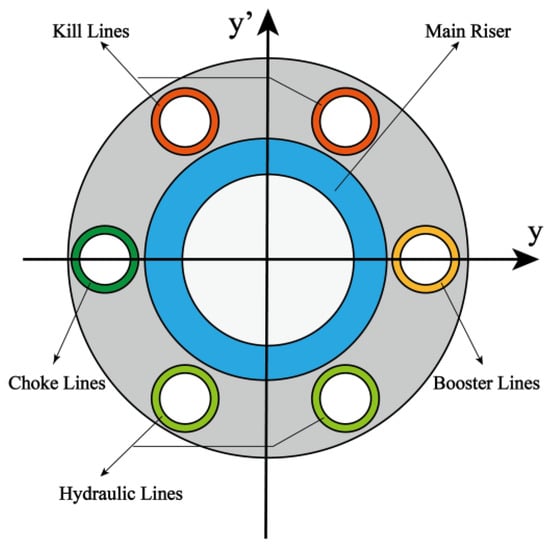
Figure 2. The main riser pipe and auxiliary pipelines.

The auxiliary pipelines are distributed around the main riser pipe, which will affect the bending stiffness of the riser system. Therefore, considering the auxiliary pipelines of the riser, the governing Equation (1) can be written as:

$$E\left(I+I_a\right)\frac{{\partial }^{4}y\left(x,t\right)}{\partial x^4}-T\left(x\right)\frac{{\partial }^{2}y\left(x,t\right)}{\partial x^2}+(m+m_a)\frac{{\partial }^{2}y}{\partial t^2}=f(x,t)$$

(5)

where I_a is the inertia moment of the riser auxiliary pipelines, m⁴; m_a is the weight of the auxiliary pipelines per length, kg/m.

$$\left\{\begin{array}{c}\hfill I_a=I_1+I_2+I_3+I_4\hfill \\ I_1=a[\frac{\pi \left(D_1^4-d_1^4\right)}{64}+{\alpha }^2\frac{\pi (D_1^2-d_1^2)}{4}]\hfill \\ I_2=b[\frac{\pi \left(D_2^4-d_2^4\right)}{64}+{\beta }^2\frac{\pi (D_2^2-d_2^2)}{4}]\hfill \\ I_3=c[\frac{\pi \left(D_3^4-d_3^4\right)}{64}+{\gamma }^2\frac{\pi (D_3^2-d_3^2)}{4}]\hfill \\ I_4=e[\frac{\pi \left(D_4^4-d_4^4\right)}{64}+{\delta }^2\frac{\pi (D_4^2-d_4^2)}{4}]\hfill \end{array}\right.$$

(6)

where a is the number of kill lines, dimensionless; D₁ is the outer diameter of the kill lines, m; d₁ is the inner diameter of kill lines, m; b is the number of hydraulic lines, dimensionless; D₂ is the outer diameter of the hydraulic lines, m; d₂ is the inner diameter of the hydraulic lines, m; c is the number of choke lines, dimensionless; D₃ is the outer diameter of the choke lines, m; d₃ is the inner diameter of the choke lines, m; e is the number of booster lines, dimensionless; D₄ is the outer diameter of the booster lines, m; d₄ is the inner diameter of the booster lines, m; α is the distance between the kill lines center and the y-axis, m; β is the distance between the hydraulic lines center and the y-axis, m; γ is the distance between the choke lines center and the y-axis, m; δ is the distance between the booster lines center and the y-axis, m.

When considering the auxiliary pipelines, Equation (2) can be written as:

$$\left\{\begin{array}{c}y\left(0,t\right)=S(t)\hfill \\ E\left(I+I_a\right)\frac{{\partial }^{2}y(0,t)}{\partial x^2}-K_1\frac{\partial y\left(0,t\right)}{\partial x}=0\hfill \end{array}\right.$$

(7)

Equation (3) can be written as:

$$\left\{\begin{array}{c}y\left(L,t\right)=0\hfill \\ E\left(I+I_a\right)\frac{{\partial }^{2}y(L,t)}{\partial x^2}-K_2\frac{\partial y\left(L,t\right)}{\partial x}=0\hfill \end{array}\right.$$

(8)

In Section 2.2, considering the auxiliary pipelines, a novel entire mechanical model of the deepwater drilling riser is established. The novel governing equation is shown as Equation (5), and the novel boundary conditions are shown as Equations (7) and (8).

2.3. Marine Environmental Loads and Platform Motion

The wave–current force on the riser can be calculated by the Morrison equation [61], which is:

$$f\left(x,t\right)=\frac{\pi }{4}{\rho }_w{C}_M{D}^2\frac{\partial v_w}{\partial t}+\frac{1}{2}{\rho }_w{C}_{D}D(v_w+v_c)\left|v_w+v_c\right|$$

(9)

where C_M is the inertial coefficient, dimensionless; C_D is the drag coefficient, dimensionless; v_c is the current velocity, m/s; v_w is the horizontal velocity of wave particle, m/s.

Generally, the lateral motion of the floating platform will affect the dynamic characteristics of the deepwater drilling riser. The motion of the platform can be described by Equation (10) [62]:

$$S\left(t\right)=S_0+S_L\sin \left(\frac{2\pi t}{T_L}-{\alpha }_L\right)+\sum _{n-1}^N{A}_n\cos (k_n{x}_p-{\omega }_{n}t+{\phi }_n)$$

(10)

where S_L is the amplitude drift of the platform, m; T_L is the drift period of the platform, s; S₀ is the static offset of the platform, m; α_L is the phase angle of the drift motion, usually taken as 0; A_n is the amplitude of the random wave, m; k_n is the wave number, dimensionless; x_p is the horizontal position of the platform, m; ω_n is the wave circle frequency, rad/s; t is the time, s; φ_n is the phase angle of the wave, rad.

2.4. Mechanical Model of the Subsea Wellhead

The physical structure and mechanical load of the subsea wellhead are shown in Figure 3.

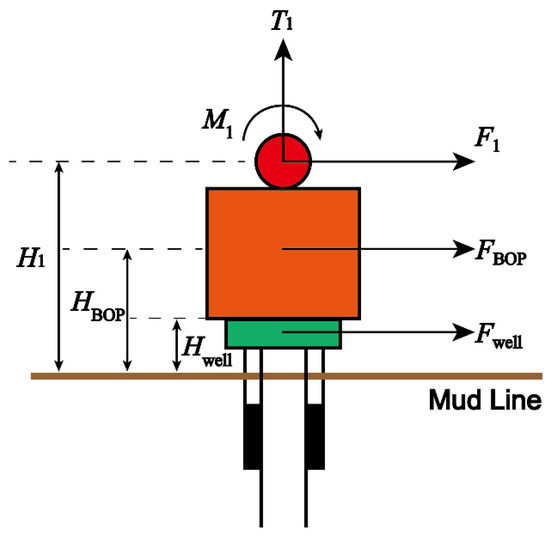
Figure 3. Mechanical model of the subsea wellhead.

The total bending moment on the subsea wellhead is:

$$M=F_{BOP}·H_{BOP}+F_{well}·H_{well}+F_1·H_1+M_1$$

(11)

where F_BOP is the current force on the BOP, N; H_BOP is the height from the mud line to the center of gravity of the BOP, m; F₁ is the current force on the lower flexible joint, N; H₁ is the distance between the mud line and the lower flexible joint, m; M₁ is the bending moment on the subsea wellhead transmitted from the riser, N·m; F_well is the current force on the subsea wellhead, N; H_well is the sludge height of the subsea wellhead, m.

After mathematical derivation, Equation (11) can be written as:

$$M={\int }_0^{H_{BOP}}\frac{1}{2}{C}_D{\rho }_w{v}_c^2{D}_{BOP}dy\times H_{BOP}+{\int }_0^{H_{well}}\frac{1}{2}{C}_D{\rho }_w{v}_c^2{D}_{well}dy\times H_{well}+{\int }_0^{H_1}\frac{1}{2}{C}_D{\rho }_w{v}_c^2{D}_{\mathrm{F}}dy\times H_1+M_1$$

(12)

where M is the total bending moment on the subsea wellhead, N·m; D_F is the diameter of the lower flexible joint, m.

After the bending moment on the subsea wellhead is obtained, the maximum stress, located at the outer wall of the subsea wellhead, generated by the bending moment can be calculated according to the basic principles of material mechanics, which is:

$${\sigma }_{max}=\frac{M·H_{well}}{I_{well}}$$

(13)

where I_well is the inertia moment of the conductor, m⁴.

3. Model Solution

In this paper, the finite-difference method is used to solve the governing Equation (5). The riser is divided into n segments in the x direction, and n + 1 nodes are obtained. The length of each segment is h, and the nodes are numbered from top to bottom. The first node at the top is 1, and the last node at the bottom is n + 1, and i is the node number. The time is divided into m segments, and m + 1 time nodes are obtained. The time scale of each segment is k, and j is the time node. Therefore, y(i,j) can be used to represent the riser displacement at position i and time j, and f(i,j) represents the external load at position i at time j.

The discretized governing equation of Equation (5) can be written as:

$$E\left(I+I_a\right)\frac{y_{i+2}^j-4y_{i+1}^j+6y_i^j-4y_{i-1}^j+y_{i-2}^j}{h^4}-T\left(i\right)\frac{y_{i+1}^j-2y_i^j+y_{i-1}^j}{h^2}+\left(m+m_a\right)\frac{y_i^{j+1}-2y_i^j+y_i^{j-1}}{k^2}=f(i,j)$$

(14)

where the axial force at position i can be written as:

$$T\left(i\right)=T_0-i[A_i{\rho }_{m}g+\left(A_o-A_i\right){\rho }_{s}g+A_F{\rho }_{s}g]$$

(15)

where ρ_s is the density of the riser, kg/m³; A_o is the area of the riser outer diameter, m²; A_F is the cross-sectional area of the auxiliary pipelines, m².

After mathematical derivation, Equation (14) can be expressed as:

$$A{y}_{i+2}^j+B_i{y}_{i+1}^j+C_i{y}_i^j+D_i{y}_{i-1}^j+E{y}_{i-2}^j=Ff(i,j)$$

(16)

where,

$$\left\{\begin{array}{c}A=k^{2}E(I+I_a)\hfill \\ B_i=-4k^{2}E\left(I+I_a\right)-k^2{h}^{2}T(i)\hfill \\ C_i=6k^{2}E\left(I+I_a\right)+2k^2{h}^{2}T\left(i\right)-2h^4(m+m_a)\hfill \\ D_i=-4k^{2}E\left(I+I_a\right)-k^2{h}^{2}T(i)\hfill \\ E=k^{2}E\left(I+I_a\right)\hfill \\ F=k^2\hfill \end{array}\right.$$

(17)

The top boundary condition can be written as:

$$\left\{\begin{array}{c}y(0,j)=S(j)\hfill \\ E\left(I+I_a\right)\frac{{\partial }^{2}y(0,j)}{\partial x^2}-K_1\frac{\partial y\left(0,j\right)}{\partial x}=E\left(I+I_a\right)\frac{y_1^j-2y_0^j+6y_{-1}^j}{h^2}-K_1\frac{y_1^j-y_0^j}{h}\hfill \end{array}\right.$$

(18)

The bottom boundary condition can be written as:

$$\left\{\begin{array}{c}y(L,j)=0\hfill \\ E\left(I+I_a\right)\frac{{\partial }^{2}y(L,j)}{\partial x^2}-K_2\frac{\partial y\left(L,j\right)}{\partial x}=E\left(I+I_a\right)\frac{y_{L+1}^j-2y_L^j+y_{L-1}^j}{h^2}-K_2\frac{y_{L+1}^j-y_L^j}{h}\hfill \end{array}\right.$$

(19)

The matrix form of the governing equation can be expressed as:

$$\left[\begin{array}{ccccccccc}0& 1& 0& 0& 0& \cdots & 0& 0& 0\\ 1& -2& 1& 0& 0& \cdots & 0& 0& 0\\ E& D_1& C_1& B_1& A& \cdots & 0& 0& 0\\ 0& E& D_2& C_2& B_2& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& \cdots & C_{n+1}& B_{n+1}& A\\ 0& 0& 0& 0& 0& \cdots & -2& 1& 0\\ 0& 0& 0& 0& 0& \cdots & 2& -2& 1\end{array}\right]\left[\begin{array}{c}{y}_{-1}\\ y_0\\ y_1\\ y_2\\ ⋮\\ y_{n+1}\\ y_{n+2}\\ y_{n+3}\end{array}\right]=\left[\begin{array}{c}S(j)\\ 0\\ Fy(1,j)\\ Fy(2,j)\\ ⋮\\ Fy(n+1,j)\\ 0\\ 0\end{array}\right]$$

(20)

In order to demonstrate the process of model solving more clearly, the computational flow chart of the model solution is shown in Figure 4.

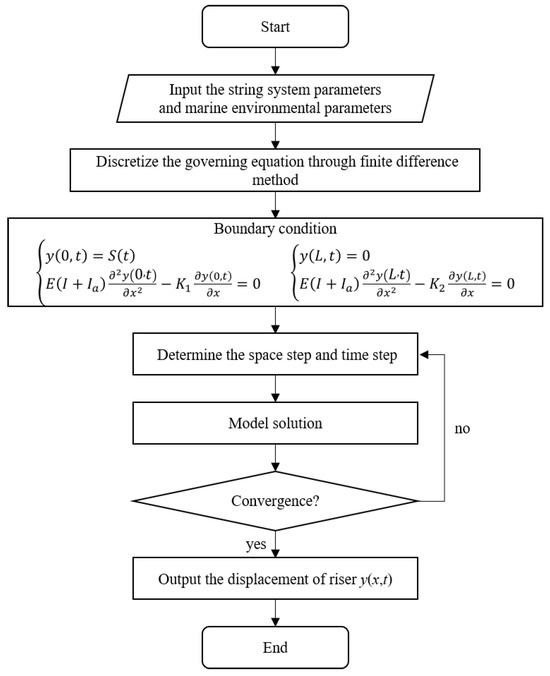
Figure 4. Computational flow chart of the model solution.

4. Case Study

4.1. Case Study

4.1.1. Model Validation

Taking a deepwater drilling as an example, the parameters of the marine environment and platform are shown in Table 1, and the configuration parameters of the riser system are shown in Table 2. Five auxiliary pipelines are arranged around the main riser pipe, including one choke line, one kill line, one booster line, and two hydraulic lines. The auxiliary pipelines configuration is shown in Table 3.

Table 1. Marine environmental and platform parameters.

Parameter	Value
Water depth (m)	1524
Density of seawater (kg/m3)	1025
Density of drilling fluid (kg/m3)	1200
Rotational stiffness of the upper flexible joint (kN·m/rad)	573
Rotational stiffness of the lower flexible joint (kN·m/rad)	5500
Drag coefficient	1.2
Added mass coefficient	1
Wave height (m)	8 m
Wave period (s)	13 s
Sea surface current velocity (m/s)	1 m/s
The static offset of the platform (m)	0 m
The amplitude drift of the platform (m)	10 m
The drift period of the platform (s)	200 s
Outer diameter of the conductor (m)	0.162
Wall thickness of the conductor (m)	0.0254
The sludge height of the subsea wellhead (m)	3 m

Table 2. Riser system configuration.

Riser Components	Number	Length/m	Weight/t
BOP	1	16.780	331.640
Riser joint (bare)	12	22.860	12.831
Buoyancy joint 1	27	22.860	0.415
Buoyancy joint 2	26	22.860	2.540
Riser joint 1	1	6.096	5.510
Riser joint 2	1	4.572	4.520
Riser joint 3	1	3.048	3.448
Riser joint 4	1	1.524	2.458

Table 3. Auxiliary pipelines configuration.

Name	Number	Outer Diameter/m	Inner Diameter/m
Main riser pipe	1	0.5334	0.4890
Choke line	1	0.1715	0.1143
Kill line	1	0.1715	0.1143
Booster line	1	0.1270	0.1016
Hydraulic line	2	0.1080	0.0889

The model validation has been carried out through comparing the results obtained by the method proposed in this paper and the numerical simulation in Orcaflex. In order to make the comparison results more intuitive, in the process of model verification, the bending moment and stress of the first half of the platform drift period have been chosen. The comparison results are shown in Figure 5 and Figure 6.

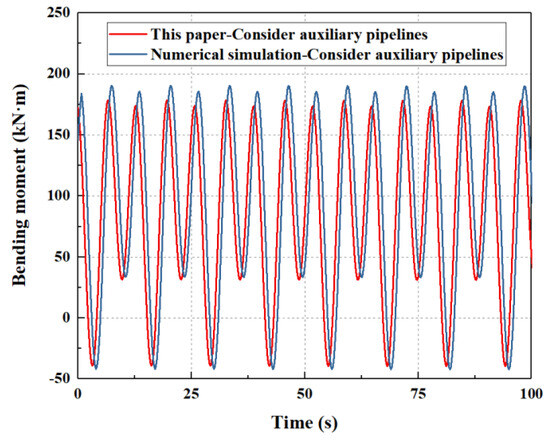
Figure 5. Model validation considering auxiliary pipelines.

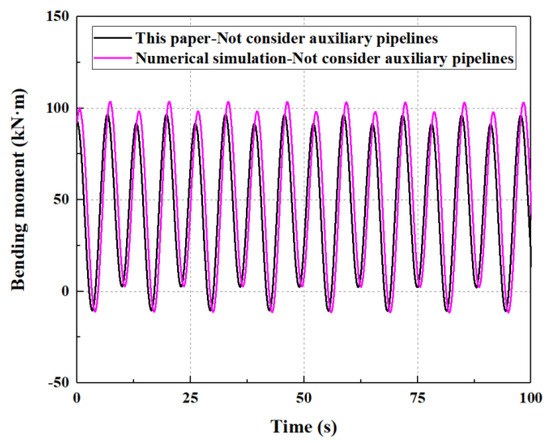
Figure 6. Model validation not considering auxiliary pipelines.

The results show that, if the auxiliary pipelines are considered, the maximum bending moment is 178.5 kN·m calculated by the method proposed in this paper, while the maximum bending moment is 190.5 kN·m calculated by the numerical simulation. If the auxiliary pipelines are not considered, the maximum bending moment is 96.6 kN·m by the method proposed in this paper, while the maximum bending moment is 103.6 kN·m by the numerical simulation. If the auxiliary pipeline of the riser is considered, the error between the theoretical results and the numerical simulation is about 6.7%, while the error between the theoretical results and the numerical simulation is about 7.2% if the auxiliary pipelines are not considered. Additionally, the results between the numerical simulation and the theoretical calculation have the same order of the amplitude, and the oscillation periods between the numerical simulation and the theoretical calculation are the same. Therefore, the correctness of the model proposed in this paper has been verified.

4.1.2. Results of the Case Study

The total bending moment of the subsea wellhead consists of the bending moment transmitted from the riser system, the bending moment at the lower flexible joint, the bending moment at the BOP, and the bending moment generated by the current at the subsea wellhead. The bending moments generated by the above four aspects are shown in Figure 7 and Figure 8.

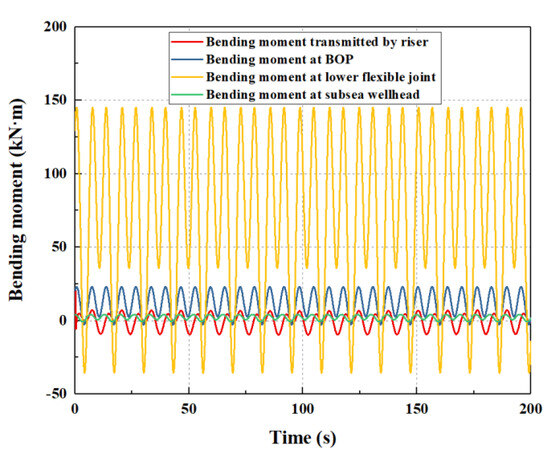
Figure 7. Bending moment on the subsea wellhead considering the auxiliary pipelines.

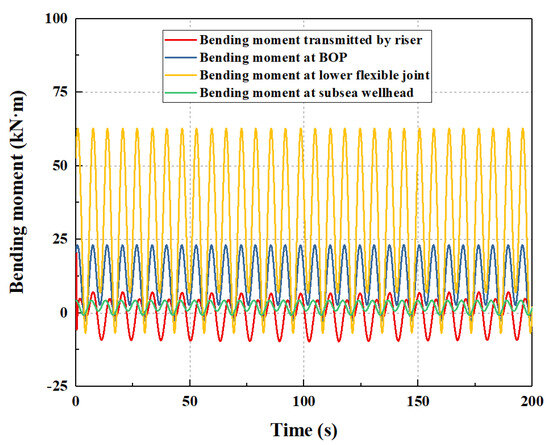
Figure 8. Bending moment on the subsea wellhead without considering the auxiliary pipelines.

As shown in Figure 7 and Figure 8, on the whole, the auxiliary pipelines have great influence on the bending moment of the subsea wellhead. In particular, the bending moment at the lower flexible joint has the greatest effect on the total bending moment of the subsea wellhead, successively followed by the bending moment at the BOP, the bending moment at the riser, and the bending moment on the subsea wellhead.

The total time-varying bending moment and stress on the subsea wellhead are shown in Figure 9 and Figure 10, respectively.

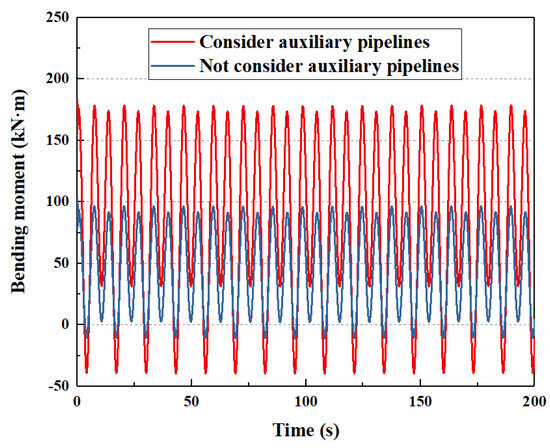
Figure 9. Total bending moment on the subsea wellhead.

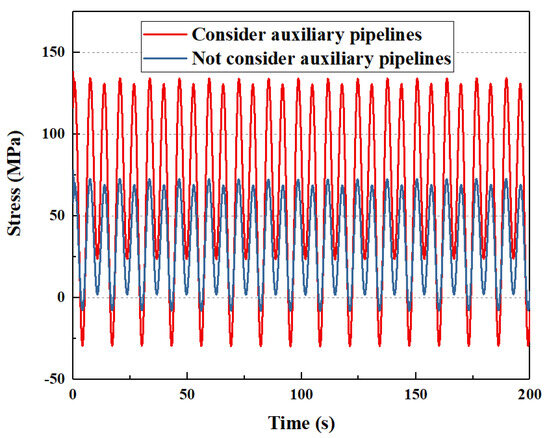
Figure 10. Bending stress on the subsea wellhead.

As shown in Figure 9 and Figure 10, the auxiliary pipelines have a significant effect on the mechanical characteristics of the subsea wellhead. If the auxiliary pipelines are not considered, the maximum bending moment and bending stress on the subsea wellhead are 96.6 kN·m and 72.6 MPa. If the auxiliary pipelines are considered, the maximum bending moment and bending stress on the subsea wellhead are 178.5 kN·m and 134.2 MPa. The results show that the maximum difference between the bending moment and the bending stress of the subsea wellhead are 81.9 kN·m and 61.6 MPa, and the bending moment and bending stress on the subsea wellhead increase by 84.8% if the auxiliary pipelines are considered. Therefore, this paper suggests that the auxiliary pipelines should be considered in the process of the subsea wellhead dynamic analysis.

4.2. Sensitivity Analysis

4.2.1. Auxiliary Pipelines

Due to different drilling conditions, the types and numbers of auxiliary pipelines are different. This paper selects four types of auxiliary pipeline configurations, which are three auxiliary pipelines (choke line, kill line, and booster line), four auxiliary pipelines (choke line, kill line, booster line, and hydraulic line), five auxiliary pipelines (choke line, kill line, booster line, and two hydraulic lines), and six auxiliary pipelines (choke line, two kill lines, booster line, and two hydraulic lines). The influence of auxiliary pipelines on the dynamic response of the subsea wellhead is shown in Figure 11 and Figure 12.

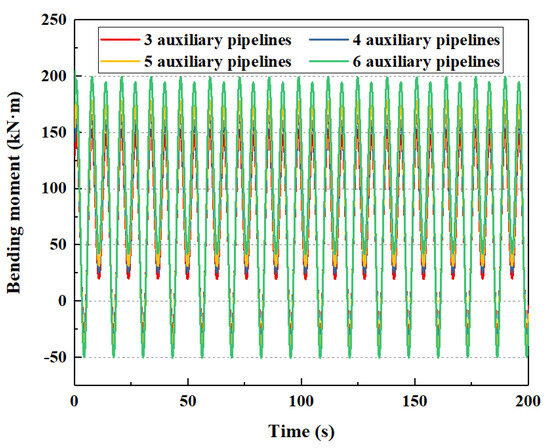
Figure 11. The influence of auxiliary pipelines of bending moment on the subsea wellhead.

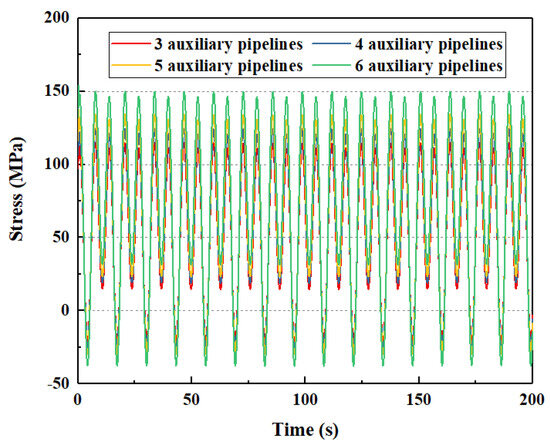
Figure 12. The influence of auxiliary pipelines of bending stress on the subsea wellhead.

As shown in Figure 11 and Figure 12, the auxiliary pipelines have an influence on the total bending moment and bending stress on the subsea wellhead. As shown in Table 4, when the number of auxiliary pipelines increases from three to six, the maximum bending moment at the subsea wellhead increases from 152.6 kN·m to 199.3 kN·m, and the maximum bending stress increases from 114.7 MPa to 149.8 Mpa.

Table 4. The maximum bending moment and stress on the subsea wellhead under different configurations of auxiliary pipelines.

The Number of Auxiliary Pipelines	The Maximum Bending Moment/kN·m	The Maximum Bending Stress/MPa
3	152.6	114.7
4	165.5	124.4
5	178.5	134.2
6	199.3	149.8

4.2.2. Sludge Height of the Subsea Wellhead

If the sludge height of the subsea wellhead is 2 m, 3 m, 4 m, and 5 m, respectively, the mechanical behavior of the subsea wellhead is shown in Figure 13 and Figure 14.

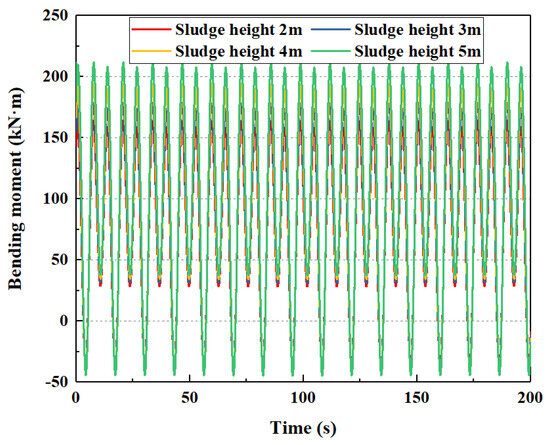
Figure 13. The influence of sludge height of bending moment on the subsea wellhead.

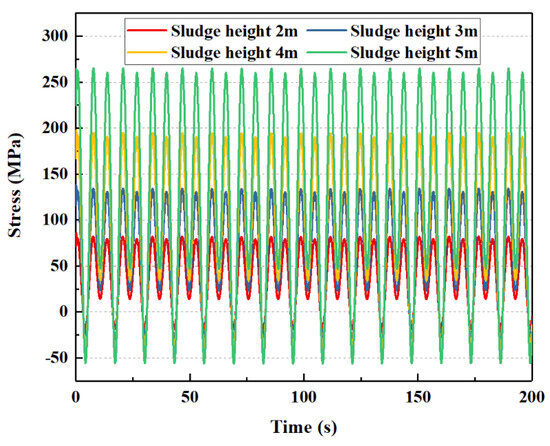
Figure 14. The influence of sludge height of bending stress on the subsea wellhead.

As shown in Figure 13 and Figure 14, the sludge height has effect on the bending moment and stress of the subsea wellhead, and the effect on the bending stress is more significant. As shown in Table 5,when the sludge height increases from 2 m to 5 m, the maximum bending moment at the wellhead increases from 163.8 kN·m to 211.7 kN·m. The maximum bending stress increases from 82.1 Mpa to 265.2 Mpa.

Table 5. The maximum bending moment and stress on the subsea wellhead under different sludge heights.

Sludge Height	The Maximum Bending Moment/kN·m	The Maximum Bending Stress/MPa
2 m	163.8	82.1
3 m	178.5	134.2
4 m	194.3	194.7
5 m	211.7	265.2

4.2.3. Wall Thickness of the Conductor

If the wall thickness of the conductor is 0.5 in, 1.0 in, 1.5 in, and 2.0 in, respectively, the mechanical behavior of the subsea wellhead is shown in Figure 15 and Figure 16.

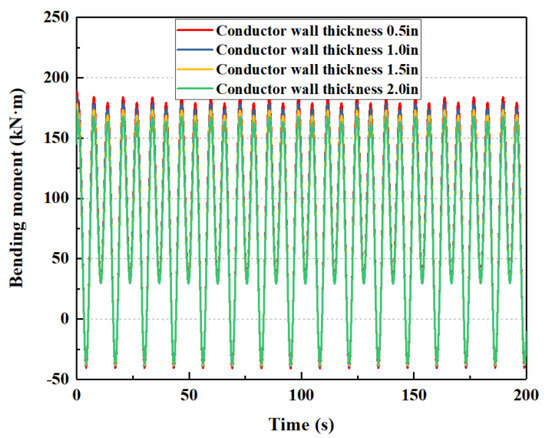
Figure 15. The influence of conductor wall thickness of bending moment on the subsea wellhead.

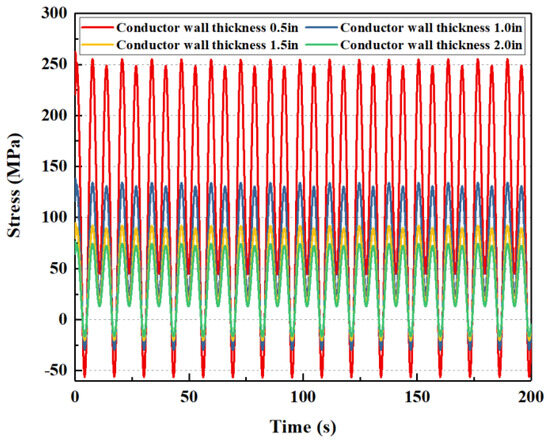
Figure 16. The influence of conductor wall thickness of bending stress on the subsea wellhead.

As shown in Figure 15 and Figure 16, the wall thickness of the conductor has little effect on the total bending moment of the subsea wellhead, and has a certain effect on the bending stress. As shown in Table 6, When the wall thickness of the conductor increases from 0.5 in to 2.0 in, the maximum bending moment is reduced from 183.9 kN·m to 167.8 kN·m, while the maximum bending stress is reduced from 255.2 MPa to 74.2 MPa.

Table 6. The maximum bending moment and stress on the subsea wellhead under different wall thicknesses of the conductor.

Wall Thickness of Conductor	The Maximum Bending Moment/kN·m	The Maximum Bending Stress/MPa
0.5 in	183.9	255.2
1.0 in	178.5	134.2
1.5 in	173.1	92.1
2.0 in	167.8	74.2

4.2.4. Rotational Stiffness of the Lower Flexible Joint

If the rotational stiffness of the lower flexible joint is 4000 kN·m, 5500 kN·m, 7000 kN·m, and 8500 kN·m, respectively, the mechanical behavior of the subsea wellhead is shown in Figure 17 and Figure 18.

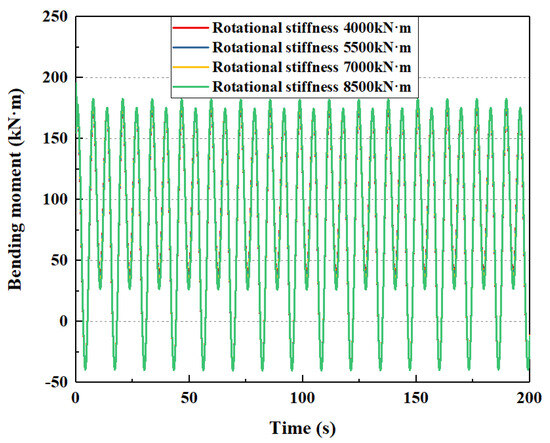
Figure 17. The influence of rotational stiffness of bending moment on the subsea wellhead.

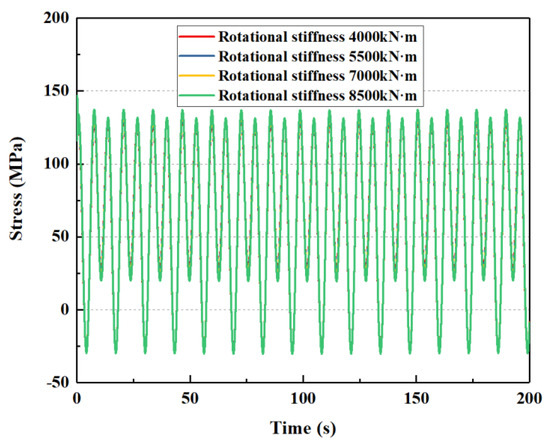
Figure 18. The influence of rotational stiffness of bending stress on the subsea wellhead.

As shown in Figure 17 and Figure 18, the rotational stiffness of the lower flexible joint has little influence on the total bending moment and stress on the subsea wellhead. As shown in Table 7, when the rotational stiffness of the lower flexible joint increases from 4000 kN·m to 8500 kN·m, the maximum bending moment at the wellhead increases from 176.5 kN·m to 182.6 kN·m, and the maximum bending stress increases from 24.2 Mpa to 28.2 Mpa.

Table 7. The maximum bending moment and stress on the subsea wellhead under different rotational stiffnesses of the flexible joint.

Rotational Stiffness of Flexible Joint	The Maximum Bending Moment/kN·m	The Maximum Bending Stress/MPa
4000 kN·m	176.5	132.7
5500 kN·m	178.5	134.2
7000 kN·m	180.5	135.7
8500 kN·m	182.6	137.3

4.2.5. Wave Height

If the wave height is 6 m, 8 m, 10 m, and 12 m, respectively, the mechanical behavior of the subsea wellhead is shown in Figure 19 and Figure 20.

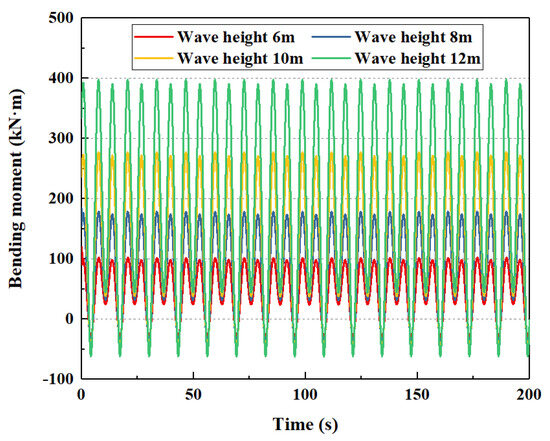
Figure 19. The influence of wave height of bending moment on the subsea wellhead.

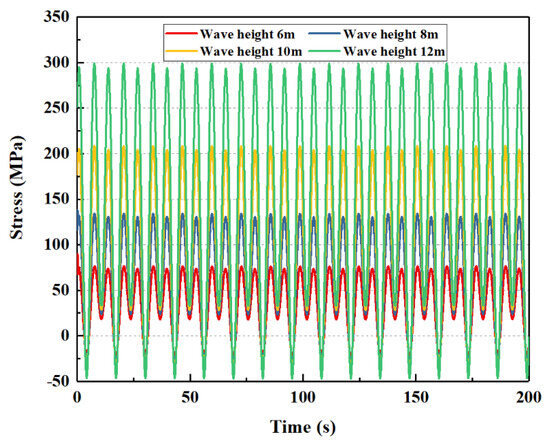
Figure 20. The influence of wave height of bending stress on the subsea wellhead.

As shown in Figure 19 and Figure 20, the wave height has a great influence on the total bending moment and the stress on the subsea wellhead. As shown in Table 8, when the wave height increases from 6 m to 12 m, the maximum bending moment at the wellhead increases from 101.7 N·m to 397.9 kN·m, and the maximum bending stress increases from 76.5 MPa to 299.1 MPa.

Table 8. The maximum bending moment and stress of the subsea wellhead under different wave heights.

Wave Height	The Maximum Bending Moment/kN·m	The Maximum Bending Stress/MPa
6 m	101.7	76.5
8 m	178.5	134.2
10 m	277.3	208.5
12 m	397.9	299.1

4.2.6. Wave Period

If the wave period is 10 s, 13 s, 16 s, and 19 s, respectively, the mechanical behavior of the subsea wellhead is shown in Figure 21 and Figure 22.

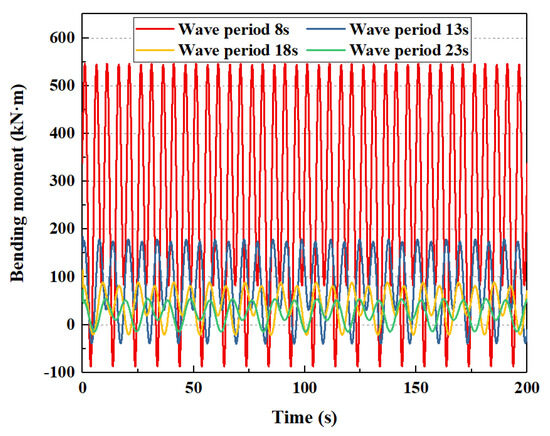
Figure 21. The influence of wave period of bending moment on the subsea wellhead.

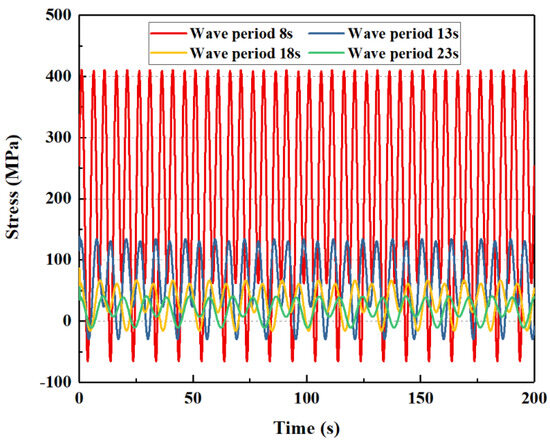
Figure 22. The influence of wave period of bending stress on the subsea wellhead.

As shown in Figure 21 and Figure 22, the wave period has a significant effect on the total bending moment and the stress on the subsea wellhead. As shown in Table 9, when the wave period increases from 10 s to 19 s, the maximum value of the wellhead bending moment decreases from 545.5 kN·m to 54.0 kN·m, and the maximum bending stress increases from 410.0 Mpa to 40.6 Mpa.

Table 9. The maximum bending moment and stress of subsea wellhead under different wave periods.

Wave Periods	The Maximum Bending Moment/kN·m	The Maximum Bending Stress/MPa	Cycle Periods/s
10 s	545.5	410.0	10 s
13 s	178.5	134.2	13 s
16 s	88.5	66.5	16 s
19 s	54.0	40.6	19 s

4.3. Orthogonal Experiment

The influence of the sludge height, wall thickness of the conductor, rotational stiffness of the lower flexible joint, wave height, and wave period on the mechanical behavior of the subsea wellhead are obtained through the analysis of numerical examples. However, the grade of the main control factors affecting the bending stress of the subsea wellhead is still unclear. It is necessary to use an orthogonal experimental method to determine the main control factors affecting the bending stress of the subsea wellhead. The orthogonal experiment results are shown in Table 10.

Table 10. The results of the orthogonal experimental.

Number		Sludge Height (m)	Wall Thickness of Conductor (in)	Rotational Stiffness of Lower Flexible Joint (kN·m)	Wave Height (m)	Wave Period (s)	The Maximum Bending Moment (kN·m)	The Maximum Bending Stress (MPa)
1		2	0.5	4000	6	10	275.4	262.4
2		2	1.0	5500	8	13	170.5	85.4
3		2	1.5	7000	10	16	128.0	45.0
4		2	2.0	8500	12	19	115.9	32.2
5		3	0.5	5500	10	19	83.5	119.4
6		3	1.0	4000	12	16	192.6	144.8
7		3	1.5	8500	6	13	104.2	54.9
8		3	2.0	7000	8	10	547.8	227.9
9		4	0.5	7000	12	16	212.0	404.1
10		4	1.0	8500	10	19	92.4	92.6
11		4	1.5	4000	8	10	611.0	429.4
12		4	2.0	5500	6	13	110.8	61.4
13		5	0.5	8500	8	13	215.7	514.0
14		5	1.0	7000	6	10	390.2	488.8
15		5	1.5	5500	12	19	136.3	119.7
16		5	2.0	4000	10	16	156.3	108.3
Stress level	K1	106.25	324.975	236.225	216.875	352.125
	K2	136.75	202.9	96.475	314.175	178.925
	K3	246.875	162.25	291.45	91.325	175.55
	K4	307.7	107.45	173.425	175.2	90.975
Difference between maximum and minimum		201.45	217.525	194.975	222.85	261.15
Grade of main control factors		4	3	5	2	1

The results show that the wave period is the most important factor affecting the mechanical behavior of the subsea wellhead. Wave height, wall thickness of the conductor, and sludge height are the secondary factors, and the rotational stiffness of the lower flexible joint has the least influence. The bending stress increases with the increase in the sludge height, the rotational stiffness of the lower flexible joint, and the wave height, while the bending stress decreases with the increase in the wall thickness of the conductor and the wave period. Through the orthogonal experimental analysis, it can be seen that the marine environmental parameters have the most obvious influence on the mechanical behavior of the subsea wellhead. Therefore, in addition to selecting a small wave height and large wave period, it is particularly important to optimize the sludge height of the wellhead, the wall thickness of the conductor, and the rotational stiffness of the lower flexible joint to control the safety of the subsea wellhead.

5. Discussion

(1)

The mechanical model and analysis method of the dynamic response of the subsea wellhead have been established, considering the auxiliary pipelines and floating drilling platform. The model is verified by numerical simulation. The dynamic bending moment and stress of the subsea wellhead have been obtained;

(2)

The auxiliary pipelines have an important influence on the dynamic characteristics of the subsea wellhead. If the auxiliary pipelines are considered, the bending moment and stress on the subsea wellhead are significantly increased. Therefore, this study suggests that the auxiliary pipelines should be considered in the dynamic analysis of the subsea wellhead to obtain a more realistic dynamic response of the subsea wellhead;

(3)

Wave period is the most important factor affecting the mechanical behavior of the subsea wellhead. Wave height, wall thickness of the conductor, and sludge height are secondary factors affecting the mechanical behavior of the subsea wellhead. The rotational stiffness of the lower flexible joint has little influence on the mechanical behavior of the subsea wellhead.

6. Conclusions

(1)

The contribution of this paper is to optimize the entire mechanical model of the floating platform–riser–BOP–subsea wellhead by considering the effect of auxiliary pipelines on the riser. Furthermore, the more accurate bending moment and stress transmitted to the subsea wellhead have been obtained. Comparing the theoretical calculation results with the numerical simulation results, the calculation accuracy is 93.3%. Subsequently, through sensitivity analysis and orthogonal experiments, the influence factors of the mechanical characteristics of the subsea wellhead have been discussed, and the main controlling factors affecting the mechanical characteristics of the subsea wellhead have been obtained;

(2)

In the future, in order to further verify the reliability of the theoretical model, indoor testing or ocean tests can be carried out subsequently to obtain real subsea wellhead mechanical-response results. By comparing the test results with the theoretical calculation results, the confidence of the theoretical model can be increased;

(3)

This research can lay the foundation for developing independent mechanical analysis software for the deepwater subsea wellhead system, and ultimately achieve application in deepwater drilling engineering.