Analytical Investigation of Tension Loads Acting on a TLP Floating Wind Turbine

Abstract

The purpose of this study is to scrutinize the coupled hydroaeroelastic problem for a TLP design of a floating structure consisting of multiple vertical truncated cylinders which support a $10 \mathrm{MW}$ wind turbine (WT). The platform is exposed to the combined effects of water waves and wind loading. The motions of the platform are examined for seven different directions of the incident waves. The hydrodynamic problem was solved analytically by combining the physical idea of multiple scattering and the method of matched axisymmetric eigenfunction expansions in order to obtain analytical representations of the velocity potential around the cylindrical members of the platform, while the contribution of the WT is considered within the six degrees of motion of the floater. Numerical results are initially presented for the exciting forces acting on the platform, the added masses, and the hydrodynamic damping coefficients, as well as the RAOs of the platform’s motions. Furthermore, the shear forces and bending moments are calculated at the point where the WT is assembled with the floater. Finally, results for the total mooring forces are given.

1. Introduction

The worldwide continuously increasing needs for renewable energy have led to a thorough investigation of methods and structures exploiting solar, wind, and wave energy. In the field of offshore engineering, considerable efforts have been made to design floating structures supporting a WT. Since they have to be competitive against other existing methods of clean energy, the development and, accordingly, the evolution on this issue has led to a cost-effective solution for the exploitation of natural sources. However, taking into account the possible installation areas of offshore structures (UK, Denmark, Germany, Japan, and China), they must survive extreme environmental conditions very often, which is of critical importance for their survival and operability [1,2]. Offshore WTs can be either fixed on the seabed for shallow or intermediate depths as a monopile, or can be floating, attached to a mooring system, for larger water depths in the open ocean, where they can harvest higher wind and, consequently, wave power.

A general classification of the floating structure supporting a WT is as follows: spar-buoy type, pontoon-type, tension-leg platform (TLP), and semi-submersible. In the spar-buoy type, the floater, which is usually a cylindrical body made of steel, supports the tower of the WT and the rotor–nacelle assembly. Several studies have been conducted for this type [3,4,5,6,7,8,9] of floating WT. Pontoon-type floaters are sometimes preferred due to their simplicity and the stability they offer to the structure. Fully coupled hydroaeroelastic analysis has been accomplished either in time or frequency domain including the influence of the WT, in the works [10,11,12,13,14]. TLP platforms are widely used to support WTs which are permanently moored by means of tendons. This kind of mooring offers extremely small heave motions of the platform due to the high pretension of the tendons in the vertical $z$ direction. Among many studies of this subject are those of references [15,16,17,18,19,20,21]. More complex configurations have been also investigated, encompassing oscillating water column (OWC) devices along with the WT. These structures can be very efficient, in a sense that they can exploit wind and wave energy at the same time. For this reason, they are widely called multipurpose floating structures. Representative research efforts on such an intriguing issue have been presented in [22,23,24,25,26]. Finally, semi-submersible designs carrying three WTs in a special configuration have been investigated in [27,28,29].

A fully coupled hydroaeroelastic analysis of the problem under consideration, as well as integrated tank testing of the corresponding model, is of great importance to secure reliability of the whole structure in the real environmental conditions. This can be achieved by a combination of analytical and numerical methods, along with experimental results, as clearly demonstrated, among others, in [30,31]. Analytical methods focus mainly on extracting closed-form solutions for the corresponding hydrodynamic boundary value problem by means of the velocity potential, while numerical methods treat the problem of the nonlinear analysis of the aerodynamic loading of the WT, which is explicitly considered as external loading to the floating structure and must be taken into account during the design stage. The aforementioned methods should be validated against experimental results. Tank testing of the corresponding model, based on similarity principle through Froude scaling law, allows, through measurements and observations, the correlation between the behavior of the model and the structure in real sea states, via sea spectral analysis.

The fully coupled hydroaeroelastic analysis of the structure is a very complicated procedure. In order to take into account the contribution of the WT to the total dynamic behavior of the floating structure, we made use of Hamiltonian dynamic analysis and blade element momentum theory. By this approach, we obtain estimations about the added mass, damping, and stiffness matrices which directly contribute to the inertial, gyroscopic, gravitational, and aerodynamic loading on the structure [13,14,18]. In that direction, several CFD models have been also developed. These complicated numerical models deal with the unsteady aerodynamic characteristics of the flow around a rotating WT, which is supported by a floating platform subjected to surge, pitch, and yaw motions, due to the incoming waves [32,33,34,35]. The part of the hydrodynamic analysis of the problem was executed by the in-house developed code HAMVAB [36]. It is an efficient software which is based on analytical representations of the hydrodynamic parameters of the boundary value problem.

The purpose of this paper is to investigate the impact of a TLP mooring system on the dynamic behavior of a semi-submersible platform supporting a $10\mathrm{MW}$ WT. Numerical results concerning the nondimensional response amplitude operators (RAOs) of the floater’s motions at the six degrees of freedom (DOF), the exciting wave forces, the added masses, and the hydrodynamic damping are presented. Furthermore, results are given for the shear forces at the point where the WT is assumed to be connected to the floating structure and the total forces at each branch of the mooring system. All the results are derived for several wave directions.

The paper is organized as follows: in Section 2, we describe in detail the geometry of the rectangular floating platform. Next, in Section 3, we proceed to the formulation and solution of the hydrodynamic problem, and we discuss thoroughly the effect that the WT has on the dynamics of the platform as a whole, while in Section 4, we present the TLP mooring system under consideration. Furthermore, in Section 5, the dynamic equation of motion of the floater is employed and numerical results for the exciting forces and moments acting on the structure, the added masses, and damping coefficients, along with the RAOs of the motions of the floater, are given. Section 6 discusses and presents results for the shear forces and bending moments calculated at the section where the WT is assumed to be integrated to the floating platform. Section 7 deals with the mooring tensions acting on each tendon of the TLP system, and finally the major conclusions are drawn in Section 8.

2. Description of the Floating Platform

The examined floating system is proposed to support a $10 \mathrm{MW}$ DTU WT. The draft of the platform is $20 \mathrm{m}$. The floating platform consists of four column-cylindrical tubes mounted at the corners of a rectangular floater, contributing the necessary buoyance, linked together with thinner, horizontal, and inclined tubular members, which provide stiffness to the floating structure. There are five sets of these smaller members. Particularly, two sets of four horizontal tubes each (upper and lower for a total of eight members) connect the offset buoy cylinders to each other at the top and the bottom of the structure. Two sets of four inclined tubes on the horizontal $xy$-plane (upper and lower for a total of eight members) connect the offset buoy columns to the main vertical column at the top and the bottom of the structure. Finally, four cross-cylindrical braces connect the bottom of the main column to the upper part of the offset columns. The tower of the WT is supported by a cylindrical member in the geometrical center of the rectangular deck of the floater and is cantilevered at $10 \mathrm{m}$ above the still water level (SWL) to the top of the main column of the floating platform. The WT encompasses the tower, the blades, and the rotor–nacelle assembly. The whole structure is depicted in Figure 1 and Figure 2. Details about the dimensions of the main structural members of the floater are given in Table 1 and details about the secondary members are given in Table 2.

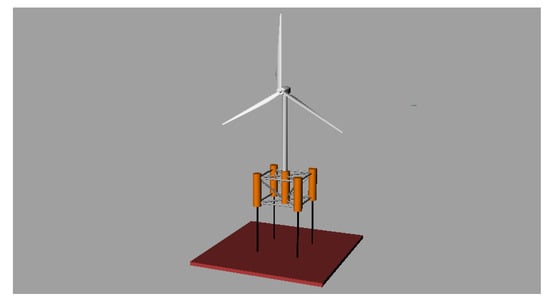
Figure 1. The floating platform with the encompassed WT in 3D.

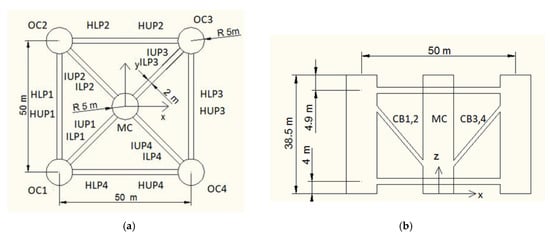
Figure 2. (a) Plan view; (b) side view of the semi-submersible platform.

Table 1. Floating platform geometry.

Element	Length (m)	Diameter (m)	Number of Elements
Main Column	38.5	10	1
Offset Buoy Columns	38.5	10	4
Horizontal Upper Tubes	40	2	4
Horizontal Lower Tubes	40	2	4
Inclined Upper Tubes	25.355	2	4
Inclined Lower Tubes	25.355	2	4
Cross Brace	23.188	2	4

Table 2. Member geometry.

Column Name	Abbreviation	Start Location (X,Y,Z)	End Location (X,Y,Z)	Length (m)
Main Column	MC	0, 0, −20	0, 0, 18.5	38.5
Offset Column 1	OC1	−25, −25, −20	−25, −25, 18.5	38.5
Offset Column 2	OC2	−25, 25, −20	−25, 25, 18.5	38.5
Offset Column 3	OC3	25, 25, −20	25, 25, 18.5	38.5
Offset Column 4	OC4	25, −25, −20	25, −25, 18.5	38.5
Horizontal Upper Tube 1	HUP1	−25, −20, 13.6	−25, 20, 13.6	40.0
Horizontal Upper Tube 2	HUP2	−20, 25, 13.6	20, 25, 13.6	40.0
Horizontal Upper Tube 3	HUP3	25, 20, 13.6	25, −20, 13.6	40.0
Horizontal Upper Tube 4	HUP4	20, −25, 13.6	−20, −25, 13.6	40.0
Horizontal Lower Tube 1	HLP1	−25, −20, −16.0	−25, 20, −16.0	40.0
Horizontal Lower Tube 2	HLP2	−20, 25, −16.0	20, 25, −16.0	40.0
Horizontal Lower Tube 3	HLP3	25, 20, −16.0	25, −20, −16.0	40.0
Horizontal Lower Tube 4	HLP4	20, −25, −16.0	−20, −25, −16.0	40.0
Inclined Upper Tube 1	IUP1	−21.464, −21.464, 13.6	−3.565, −3.565, 13.6	25.355
Inclined Upper Tube 2	IUP2	−21.464, 21.464, 13.6	−3.565, 3.565, 13.6	25.355
Inclined Upper Tube 3	IUP3	21.464, 21.464, 13.6	3.565, 3.565, 13.6	25.355
Inclined Upper Tube 4	IUP4	21.464, −21.464, 13.6	3.565, −3.565, 13.6	25.355
Inclined Lower Tube 1	ILP1	−21.464, −21.464, −16.0	−3.565, −3.565, −16.0	25.355
Inclined Lower Tube 2	ILP2	−21.464, 21.464, −16.0	−3.565, 3.565, −16.0	25.355
Inclined Lower Tube 3	ILP3	21.464, 21.464, −16.0	3.565, 3.565, −16.0	25.355
Inclined Lower Tube 4	ILP4	21.464, −21.464, −16.0	3.565, −3.565, −16.0	25.355
Cross Brace 1	CB1	−21.464, −21.464, 7.68	−3.565, −3.565, −10.036	23.188
Cross Brace 2	CB2	−21.464, 21.464, 7.68	−3.565, 3.565, −10, 036	23.188
Cross Brace 3	CB3	21.464, 21.464, 7.68	3.565, 3.565, −10, 036	23.188
Cross Brace 4	CB4	21.464, −21.464, 7.68	3.565, −3.565, −10, 036	23.188

For mooring purposes, each tendon of the TLP is attached to the center of the corresponding offset column. The mass of the platform, including the ballast, if needed, is $2.1671\times {10}^6 \mathrm{kg}$. This mass was calculated as the sum of the weights: tower of the WT, the rotor–nacelle assembly, platform, and mooring system; plus, the applied pretension equals the buoyancy in the static equilibrium position in still water. From a mathematical perspective, for a TLP mooring system, this can be expressed as

$${\displaystyle \sum }_{n=1}^4{T}_n+W_{total}=B,$$

(1)

where $T_n$ is the pretension of each tendon, $W_{total}$ is the sum of all the aforementioned weights, and $B$ denotes the buoyancy (which is equal to the weight of the displaced water). The CM of the platform, including the ballast, is located at $9.91 \mathrm{m}$ below the SWL along the platform centerline. The roll and pitch inertias, which correspond to the rotation about the $x$-axis and $y$-axis, respectively, are $3.89\times {10}^9 {\mathrm{kgm}}^2$, while the yaw inertia is $7.32\times {10}^9 {\mathrm{kgm}}^2$. The properties of the floating platform are summarized in Table 3.

Table 3. Floating platform structural properties.

Platform Mass Including Ballast (kg)	Draft (m)	Water Density (kg/m3)	CM Location below SWL Waterline (m)	Platform Roll Inertia about CM (kgm2)	Platform Pitch Inertia about CM (kgm2)	Platform Yaw Inertia about CM (kgm2)
$2.1671\times {10}^6$	$20$	$1025$	$9.91$	$3.89\times {10}^9$	$3.89\times {10}^9$	$7.32\times {10}^9$

3. Formulation of the Hydrodynamic Problem and the Role of the WT

The solution of the hydrodynamic boundary value problem is provided within the framework of analytical approaches. The Cartesian coordinate system is located at the SWL and in the geometrical center of the rectangular floater, with the vertical $z$-axis showing positive upwards. The fluid is assumed inviscid, irrotational, and incompressible, so that the flow around the structure can be described by the linear potential theory. This assumption will be used to evaluate the coefficients for the added mass and hydrodynamic damping, as well as for the exciting forces. The velocity potential around each cylindrical member accounts for the hydrodynamic interactions among the members of the multicylinder arrangement using the physical idea of multiple scattering. According to this approach, various orders of propagating and evanescent wave modes, scattered by all the cylinders, are superimposed, leading to a series representation for the potential. This theory has been proved to be valid for any random multibody configuration and is independent of the number of elements included. Since it has already been thoroughly described in [37], no further elaboration is accordingly needed in the present. The method of matched axisymmetric eigenfunction expansions was used to derive the first-order single-body hydrodynamic characteristics. The series representation for the diffraction potential around an arbitrary body $q$ of the structure is given by

$${\phi }_D^{\left(q\right)}=\left(r_q,{\theta }_q,z\right)=-i\omega \left(H/2\right){\displaystyle \sum }_{m=-\infty }^{\infty }{\Psi }_{D,m}\left(r_q,z\right)e^{im{\theta }_q},$$

(2)

where

$$\begin{array}{r}{\Psi }_{D,m}\left(r_q,z\right)=h{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}[Q_{D,mn}^{\left(q\right)}\left(I_m\left({\alpha }_n{r}_q\right)/I_m\left({\alpha }_n{b}_q\right)\right)\\ +F_{D,mn}^{\left(q\right)}\left(K_m\left({\alpha }_n{r}_q\right)/K_m\left({\alpha }_n{b}_q\right)\right)]Z_n\left(z\right),\end{array}$$

(3)

where $h$ is the water depth, $b_q$ is the radius of the $q-th$ cylinder, and $I_m$ and $K_m$ denote the $m-th$ order modified Bessel functions of the first and second kind, respectively. The first term in (3) corresponds to the contribution of the incident wave field to the total wave potential around the $q-th$ body. In the case of isolated body–wave interaction, it holds that

$$Q_{D,mn}^{\left(q\right)}=\frac{e^{ik{l}_{0q}cos\left({\theta }_{0q}-\beta \right)}}{{{hz}^{\prime }}_0\left(0\right)}{e}^{-im\left(\beta -\pi /2\right)}{I}_m\left({\alpha }_n{b}_q\right){\delta }_{0,n}$$

(4)

where $\beta$ is the angle of wave incidence, $l_{0q}$ and ${\theta }_{0q}$ are the distance and azimuthal angle of the $q-th$ body coordinate system with respect to an inertial frame, $k$ is the wave number, and ${\delta }_{0,n}$ is the Kronecker’s delta function. The unknown complex coefficients $F_{D,mn}^{\left(q\right)}$ in (3) are calculated using the method of matched eigenfunction expansion. Moreover, the $Z_n\left(z\right)$ are orthogonal functions in $\left[-h,0\right]$ and are defined by

$$Z_n\left(z\right)={\left\{\frac{1}{2}[1+sinh\left(2{\alpha }_{n}h\right)/\left(2{\alpha }_{n}h\right)\right\}}^{-1/2}cos\left({\alpha }_{n}h\right),$$

(5)

The eigenvalues ${\alpha }_n$ are the roots of the nonlinear equation

$$\left({\omega }^2/g\right)+{\alpha }_{n}tan\left({\alpha }_{n}h\right)=0,$$

(6)

which has to be solved iteratively, while the notation ${\alpha }_0=-ik$ is used for the imaginary root.

The contribution of the WT to the dynamic behavior of the floater is expressed via the inclusion of the matrices for the added mass, damping, and stiffness to the dynamic equation of motion of the floater. These coefficients, actually, superinduce the external loads due to the presence (gravity) and operation (inertial/gyroscopic effects, aerodynamic loading) of the WT. In order to derive these matrices, we consider the problem within the Hamiltonian approach, by using the Lagrange’s equations. The dynamic behavior of the system can be described by the second-order differential equation

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q_j}}\right)-\left(\frac{\partial L}{\partial q_j}\right)=Q_j={\displaystyle \sum }_i^{}\frac{\partial \left({\mathit{F}}_i·{\mathit{r}}_i\right)}{\partial q_j},$$

(7)

where $q_j$ are the generalized coordinates which prescribe the position $r_j$ of a specific point, $L$ is the Lagrangian of the system which is defined as the difference between its kinetic and potential energy, and $Q_j$ are the generalized loads associated with the real loads (forces or moments). It should be mentioned that by defining the Lagrangian of a system, one can derive its equation of motion. The WT is modeled as a collection of concentrated masses for the blades, the hub, the nacelle, and the tower. The aerodynamic loads on the WT blades are calculated in the context of the blade element momentum theory, which accounts for the angular momentum of the rotor. However, this issue has already been scrutinized and for a complete discussion on it, the reader can refer to the publications [14,26].

The total mass of the WT is $1.2\times {10}^6 \mathrm{kg}$. The total tower height is $105.63 \mathrm{m}$ and its mass is $0.563\times {10}^6 \mathrm{kg}$. The hub mass is $0.106\times {10}^6 \mathrm{kg}$ and the nacelle mass is $0.406\times {10}^6 \mathrm{kg}$ (Figure 1). As far as the three blades are concerned, the total mass of them is $0.126\times {10}^6 \mathrm{kg}$($3\times 0.042\times {10}^6 \mathrm{kg}$) and its length, excluding the hub, is $86.35 \mathrm{m}$ [38]. All these details are summarized in Table 4.

Table 4. WT properties.

Total Mass (kg)	Total Tower Height (m)	Tower Mass (kg)	Hub Mass (kg)	Nacelle Mass (kg)	Mass of the Blades (#3) (kg)	Length of the Blades (without the Hub) (m)
$1.2\times {10}^6$	$105.63$	$0.563\times {10}^6$	$0.106\times {10}^6$	$0.406\times {10}^6$	$0.126\times {10}^6$	$86.35$

4. The Mooring System

The dynamic behavior of the platform is examined under a TLP mooring system. The base of the anchoring system is located at the sea bottom, at a depth of $200 \mathrm{m}$. For a TLP system, the mooring forces, $F_{i,mooring}$, acting on the platform in the $i-th$ direction are given explicitly by

$$F_{i,mooring}=C_{ijmooring}·x_{j0}, i,j=1,\dots ,6,$$

(8)

where the coefficients $C_{ij, mooring}$ express the platform’s mooring line stiffness, given by a six by six matrix. Indicatively, the $C_{11}$, $C_{22}$, and $C_{33}$ are given, which are defined as

$$C_{11mooring=}{C}_{22mooring=}{\displaystyle \sum }_{n=1}^4\frac{T_n}{L},$$

(9)

$$C_{33mooring=}\frac{EA}{L},$$

(10)

where $T_n$ is the pretension force, $L$ is the unstretched length of each tendon, $E$ is the elasticity modulus, and $A$ is the total cross-section area. The pretension of each tendon is $987.5 \mathrm{t}$. The TLP mooring system increases the vertical stiffness of the system while reduces the heave period. Consequently, it can be used to avoid the resonance between the structure’s heave period and the incident’s wave period. It is anticipated that the motions of the TLP platform will be horizontal due to the large pretension in the vertical $z$-direction. Table 5 and Table 6 summarize the main properties of the examined mooring system and cite the coordinates of the attachment points of the tendons, respectively.

Table 5. Mooring system properties.

Number of Mooring Lines	Depth to Anchors below SWL (Water Depth) (m)	Depth to Fairleads below SWL (Water Depth) (m)	Mooring Line Length (m)	Mooring Line Diameter (mm)	Equivalent Mooring Line Mass Density (kg/m)	Submerged Weight Per Unit Length (N/m)	Mooring Line Stiffness Cxx of Each Tendon (kN/m)	Mooring Line Stiffness Czz of Each Tendon (kN/m)	Total Pretension (kN)
4	200	20	180	239	136.10	895.00	53.83	2067	9690

Table 6. Coordinates of the upper and lower attachment points of the tendons.

Tendon (#)	Upper Attachment Point $(\mathit{x}, \mathit{y},\mathit{z})$	Lower Attachment Point $(\mathit{x},\mathit{y},\mathit{z})$
1	(−25, −25, −20)	(−25, −25, −200)
2	(−25, 25, −20)	(−25, 25, −200)
3	(25, 25, −20)	(25, 25, −200)
4	(25, −25, −20)	(25, −25, −200)

5. Coupled Motion Equations

For a moored floating platform, including the influence of the WT on the dynamic behavior of the system, the coupled equations of motion can be expressed by the following system of differential equations [26] by using Newton’s second law,

$$\begin{array}{c}{\displaystyle {\displaystyle \sum }_{j=1}^6}\{-{\omega }^2\left[({{\rm M}}_{ij}+A_{ij})+A_{ij}^{WT}+\frac{i}{\omega }\left(B_{ij}+B_{ij}^{WT}\right)\right]+C_{ij hydro}+C_{ij mooring}\\ +C_{ij}^{WT}\}{x}_{j0}=F_i, i=1,\dots ,6,\end{array}$$

(11)

where $A_{ij}^{WT}$, $B_{ij}^{WT}, C_{ij}^{WT}$ are the six by six matrices of the WT’s added mass, damping, and stiffness, respectively. The coupling of the WT’s dynamic behavior to the response of the floater is ensured by including the WT’s added mass, damping, and stiffness matrices into the governing equations of motions of the floating system. The accounting of these matrices into the equation of motion of the floater reduces the contribution of the WT to an external loading to the floating structure, attributing to inertial-gyroscopic effects, gravity, and aerodynamic forces. $A_{ij}$, $B_{ij}$, $C_{ij hydro}$ are the six by six matrices of the added mass, damping, and stiffness of the floating platform, respectively. ${{\rm M}}_{ij}$ is the mass of the platform, $C_{ij mooring}$ are the stiffness coefficients of the mooring lines, and, finally, $F_i$ are the external hydrodynamic forces acting on the $i-th$ direction expressed by a six by one column matrix. The solution of the equations of motions is carried out in the frequency domain.

5.1. Exciting Forces and Moments

The exciting wave forces are derived by the integration of the hydrodynamic pressures over the wetted surface of the structure. The potential of the incident wave and the diffraction potential are those which contribute to the calculation of the hydrodynamic pressures, by exploiting the linearized Bernoulli equation. In the general form, they are given by Equation (12):

$$F_i=-\underset{S}{\overset{}{{\displaystyle \iint }}}pndS,$$

(12)

where $n$ is the normal vector pointing outwards from the wetted surface into the fluid, and $S$ holds for the wetted surface. Similarly, the overturning moments acting on the floating structure are given by

$$M_i=-\underset{S}{\overset{}{{\displaystyle \iint }}}p\left(x\times n\right)dS.$$

(13)

Figure 3, Figure 4, Figure 5 and Figure 6 demonstrate the normalized exciting forces and moments for a range of angular frequencies and for several directions of the incident wave. The exciting forces are nondimensionalized by the term $5\rho g{b}^2 \left(H/2\right)$, where the factor five holds for the number of bodies (NUBO), i.e., four offset columns and one main, $\rho =1025 \mathrm{kg}/{\mathrm{m}}^2$ is the water density, $b=5 \mathrm{m}$ is the radius of the offset and main columns, and, finally, $H/2$ is the wave amplitude. In an analogous manner, the moments are normalized by the term $5\rho g{b}^3 \left(H/2\right)$. The exciting forces in the transverse direction $F_y$ and the moment $M_x$ are omitted owing to the double symmetry of the rectangular floater. It can be seen that for increasing wave frequencies, or equivalently smaller wavelengths, the exciting wave loads reduce.

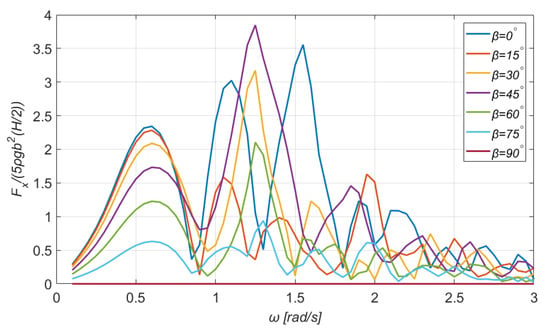
Figure 3. The horizontal exciting wave force on the TLP floating platform for a wide range of directions of the incident wave.

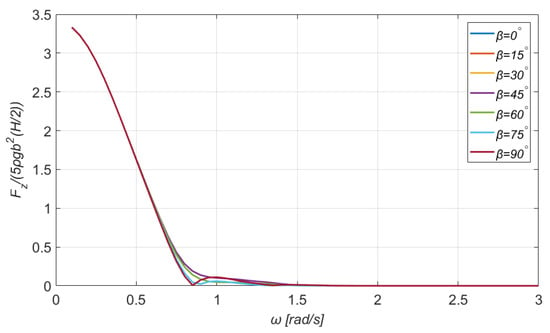
Figure 4. The vertical exciting wave force on the TLP floating platform for a wide range of directions of the incident wave.

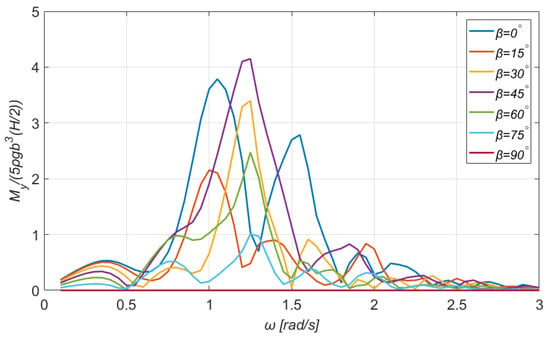
Figure 5. The exciting overturning moment along the $y$-axis on the TLP floating platform for a wide range of directions of the incident wave.

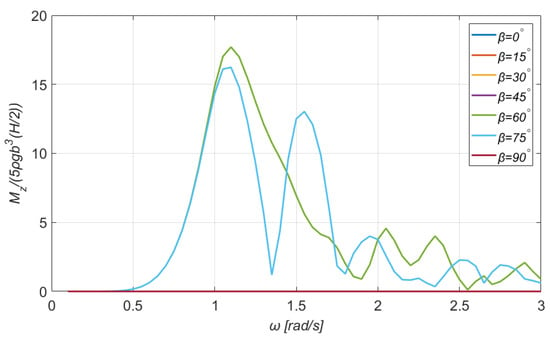
Figure 6. The exciting wave moment around the $z$-axis on the TLP floating platform for a wide range of directions of the incident wave.

Particularly, Figure 3 and Figure 4 show the normalized exciting forces along the $x,z$-axes as a function of the incident wave’s angular frequency, for seven different angles of attack, ranging from $0–{90}^{°}$. The maximum horizontal exciting force obtains the value 3.84, which occurs for a wave frequency of $\omega =1.25 \mathrm{rad}/\mathrm{s}$ and for direction of the incident wave $\beta ={45}^{°}$. Moreover, it is noticed that for waves propagating along the $y$-axis, the loads in the $x$ direction are zero. On the other hand, the maximum vertical exciting force is 3.33 for wave frequency of $\omega =0.1 \mathrm{rad}/\mathrm{s}$ (see Figure 4).

As depicted in Figure 5, the maximum exciting overturning moment along the $y$-axis attains the value of 4.15 for the same pair of data with the corresponding exciting force, i.e., $\beta ={45}^{°}$ and $\omega =1.25 \mathrm{rad}/\sec$. A feature that should be mentioned is the fact that when the wave direction is $\beta ={90}^{°}$, the loads in the direction of the roll DOF (i.e., the $M_y$ overturning moment) are zero. Next, the exciting wave moment around the $z$-axis, see Figure 6, demonstrates an interesting behavior. Particularly, when symmetry exists (for angles $\beta =0^{°},{45}^{°},{90}^{°}$), it is practically zero. It attains the maximum value of 17.30 for $\beta ={30}^{°},{60}^{°}$ and $\omega =1.1 \mathrm{rad}/\sec$. Furthermore, it is noticed that the curves for $\beta ={15}^{°},{75}^{°}$ coincide also, and they form a pronounced secondary peak.

5.2. Added Masses, Hydrodynamic Damping, and Motions of the Floater

Figure 7 and Figure 8 demonstrate the behavior of added mass coefficients as a function of the incident wave frequency, while Figure 9 and Figure 10 show the behavior of several damping coefficients. Given that our analysis is performed in the frequency domain, the added masses and the damping coefficients are given explicitly by Equations (14) and (15), as follows:

$$A_{ij}=-\rho \mathrm{Re}[\underset{S}{\overset{}{{\displaystyle \iint }}}{\phi }_j{n}_{i}dS],$$

(14)

and

$$B_{ij}=-\rho \omega \mathrm{Im}[\underset{S}{\overset{}{{\displaystyle \iint }}}{\phi }_j{n}_{i}dS],$$

(15)

respectively. The added mass and damping matrices are related to the solution of the radiation problem, which deals with the hydrodynamic loads on the platform owing to its forced oscillation in all six DOFs in otherwise calm water. All these coefficients are frequency-dependent and are listed below. The $A_{11}$ and $A_{33}$ added masses have been normalized by the term $5\rho b^3$,whereas the $A_{55}$ and $A_{66}$ by the term $5\rho b^5$.

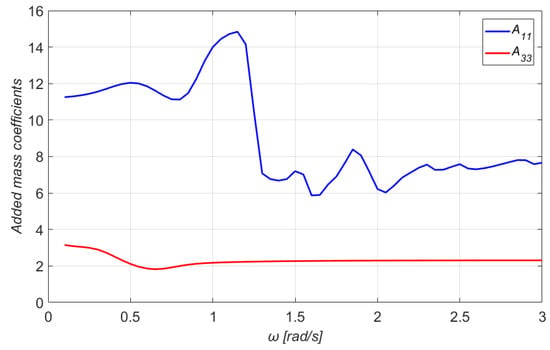
Figure 7. The $A_{11}$ and $A_{33}$ added mass coefficients of the floater.

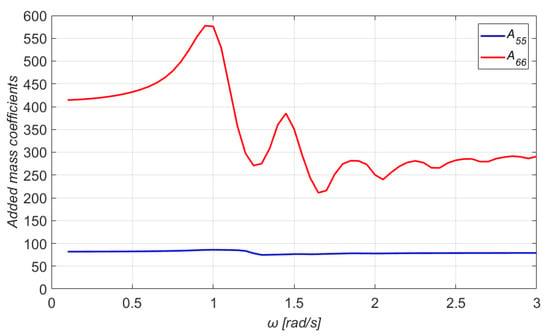
Figure 8. The $A_{55}$ and $A_{66}$ added mass coefficients of the floater.

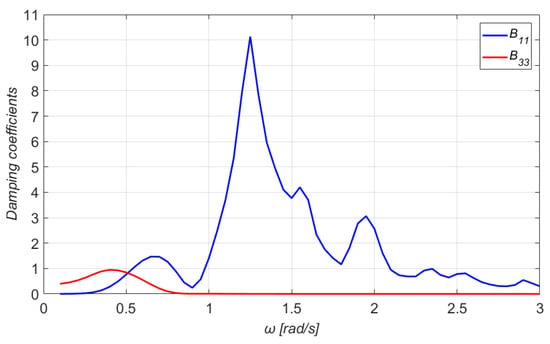
Figure 9. The $B_{11}$ and $B_{33}$ damping coefficients of the floater.

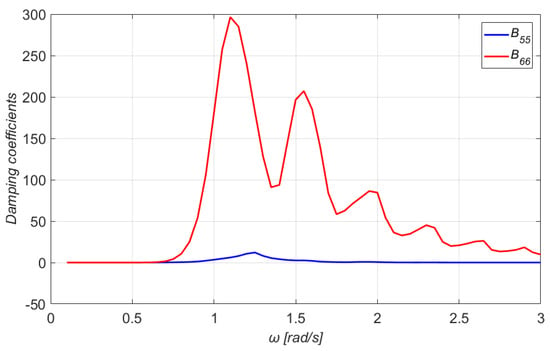
Figure 10. The $B_{55}$ and $B_{66}$ damping coefficients of the floater.

At this point, it should be mentioned that $A_{11}$ and $B_{11}$ coincide with $A_{22}$ and $B_{22}$, due to the platform’s symmetry. This observation holds also for the elements $A_{44}$, $B_{44}$ and $A_{55}$, $B_{55}$. Moreover, as it can be noticed from Figure 9 and Figure 10, the asymptotic values of the damping coefficients for zero and infinite wave frequencies tend to zero for all modes of motions, but the damping coefficient in heave for wave frequencies tending to zero attains a nonzero limiting value. The latter is related to the nonzero vertical exciting force in the low-frequency regime (see Figure 4) through the Newman–Haskind relation [39]

$$B_{ii}=\frac{k}{8\pi \rho g{c}_g}\underset{0}{\overset{2\pi }{{\displaystyle \int }}}{\left|F_i\left(\theta \right)\right|}^{2}d\theta$$

(16)

where $F_i$ is the excitation force and $c_g$ is the group velocity given by

$$c_g=\frac{1}{2}\frac{\omega }{k}\left(1+\frac{2kh}{\sin \mathrm{h}\left(2kh\right)}\right)$$

(17)

It should also be mentioned that the damping coefficients form a main peak at intermediate frequencies. The $B_{11}$ and $B_{33}$ damping coefficients have been normalized by the term $5\omega \rho b^3$, whereas the $B_{55}$ and $B_{66}$ by the term $5\omega \rho b^5$.

Next, some numerical results for the RAOs of the motions of the floater are given. Similar to the comment of Section 5.1, the graphs for the sway and roll motions are omitted, owing to the double symmetry of the rectangular floater. The wind speed was taken as equal to $11.4 \mathrm{m}/\mathrm{s}$. Figure 11, Figure 12, Figure 13 and Figure 14 show, graphically, the RAOs of the motions of the rectangular floater. As it is expected, the surge (and sway) motions are larger in the horizontal and transverse direction of the incoming wave, respectively. Consequently, their magnitude is reduced while the wave’s angle of attack deviates from these anticipated directions.

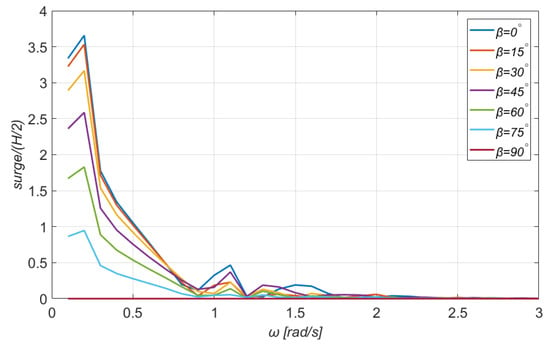
Figure 11. Surge motion of the TLP combined floating platform and WT system for a wide range of directions of the incident wave. Wind speed: $11.4 \mathrm{m}/\mathrm{s}$.

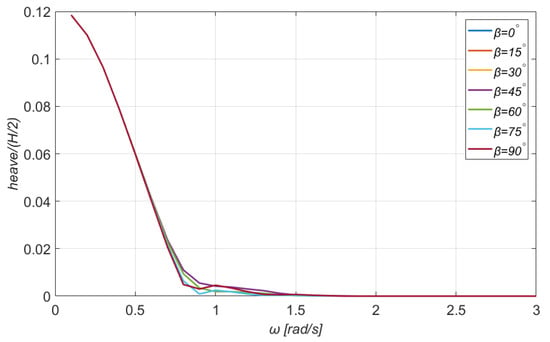
Figure 12. Heave motion of the TLP combined floating platform and WT system for a wide range of directions of the incident wave. Wind speed: $11.4 \mathrm{m}/\mathrm{s}$.

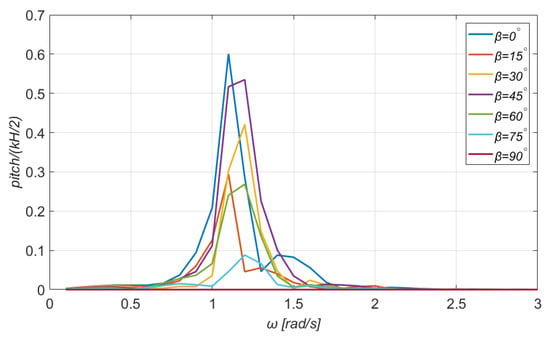
Figure 13. Pitch motion of the TLP combined floating platform and WT system for a wide range of directions of the incident wave. Wind speed: $11.4 \mathrm{m}/\mathrm{s}$.

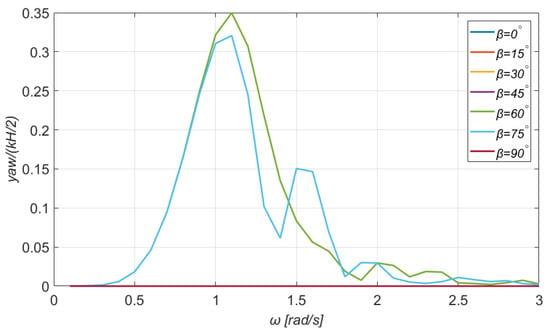
Figure 14. Yaw motion of the TLP combined floating platform and WT system for a wide range of directions of the incident wave. Wind speed: $11.4 \mathrm{m}/\mathrm{s}$.

From Figure 12, the heave motion is proved to be rather independent of the wave direction and it also obtains much smaller values compared to surge and sway motions. This is a reasonable outcome, since a TLP mooring system sets significant constraints to the motion of the platform along the $z$-axis. Finally, Figure 13 and Figure 14 depict the normalized rotational motions of the platform. The pitch motion is more intense when the incoming wave is parallel to the $x$-axis and is zero when the direction of the incoming wave is $\beta ={90}^{°}$. The maximum RAO of the pitch motion is 0.6 for $\omega =1.1 \mathrm{rad}/\sec$. Regarding the yaw motion, it is zero for $\beta =0^{°}$, $\beta ={45}^{°}$, and $\beta ={90}^{°}$. In addition, the curves for $\beta ={15}^{°}$, $\beta ={75}^{°}$ and $\beta ={30}^{°}$, $\beta ={60}^{°}$ are identical, while the maximum RAO of the yaw motion is identified in the latter case.

6. Shear Forces

In order to calculate the local displacement of the structure at a specific intersection point $r=\left(x,y,z\right)$, we follow the analysis provided in the publication [40]. The local motion of each body can be calculated by the following equations:

$$s_1=x_{10}+z·x_{50}-y·x_{60}$$

(18)

$$s_2=x_{20}+x·x_{60}-z·x_{40}$$

(19)

$$s_3=x_{30}+y·x_{40}-x·x_{50}$$

(20)

$$s_4=x_{40}$$

(21)

$$s_5=x_{50}$$

(22)

$$s_6=x_{60}$$

(23)

where $x_{j0}, j=1,\dots ,6$ are the motions and rotations of the body relatively to the initial coordinate system (see Figure 2a), and $s_j, j=1,\dots ,6$ denote the motions and rotations referring to the section point.

In order to calculate the shear forces, we consider the moored floating structure and the WT as a system of two bodies with kinematic coupling. The shear forces at the intersection point can be calculated by summing the forces $\left(F_{xi}, F_{yi},F_{zi}\right)$ acting on each body ($i=1$ for the floating structure, and $i=2$ for the WT) (Figure 15). We examine the case where the section $AA$ is at the point where the WT is assembled to the floating structure, i.e., $18.5 \mathrm{m}$ above the SWL.

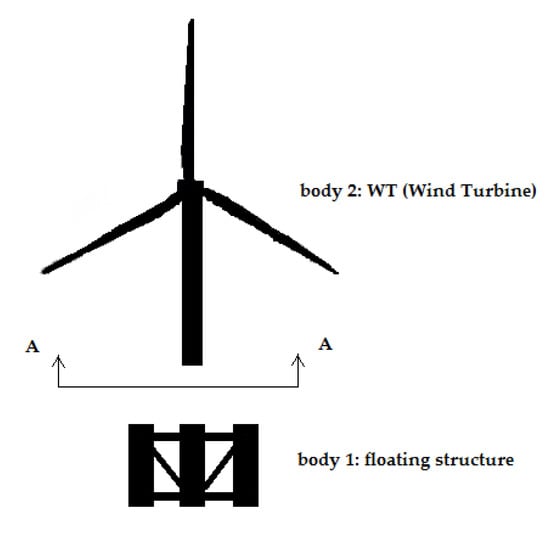
Figure 15. The shear forces and bending moments are calculated at the point where the WT is incorporated in the floating system (section $AA$).

In a similar manner, the bending moments $\left(M_{xi}, M_{yi},M_{zi}\right)$ are the sum of the external moments acting on each body and the moments generated by the previously mentioned forces, given by the cross product of the force and the distance from the section point, as follows in a vectoral form:

$$\mathit{M}={\mathit{M}}_{\mathit{i}}+\mathit{r}\times {\mathit{F}}_{\mathit{i}}$$

(24)

The shear forces and bending moments at the section $AA$ of the column which supports the WT are shown graphically in Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. The maximum value of the horizontal shear force is 902 kNm/m for $\beta =0^{°}$ and $\omega =1.1 \mathrm{rad}/\mathrm{s}$, while the maximum transverse shear force is 941 kNm/m for $\beta ={90}^{°}$ and the same wave frequency. Furthermore, from Figure 18, it is noticed that the maximum vertical shear force is much smaller and seems to be slightly affected by the wave direction. In detail, the maximum value is 19.60 kNm/m at all cases, for $\omega =0.5 \mathrm{rad}/\mathrm{s}$.

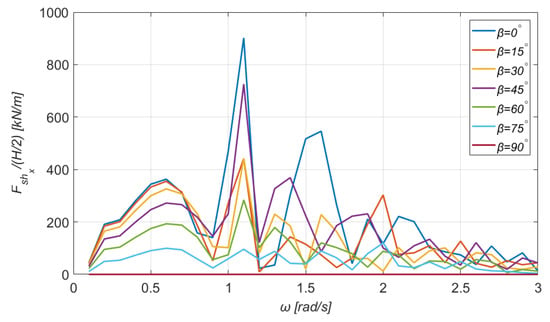
Figure 16. Horizontal shear force for the section $AA$ (see Figure 15) for a wide range of directions of the incident wave.

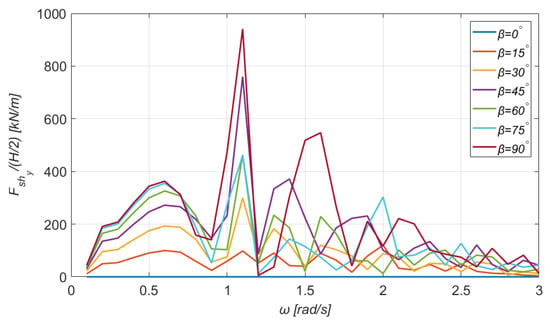
Figure 17. Transverse shear force for the section $AA$ (see Figure 15) for a wide range of directions of the incident wave.

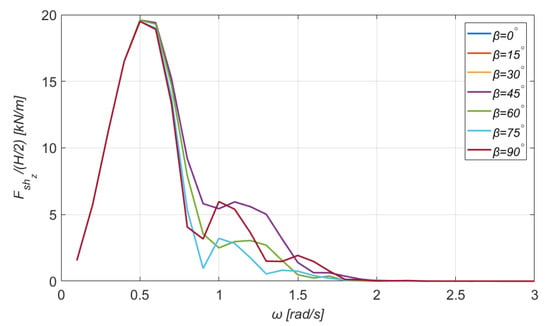
Figure 18. Vertical shear force for the section $AA$ (see Figure 15) for a wide range of directions of the incident wave.

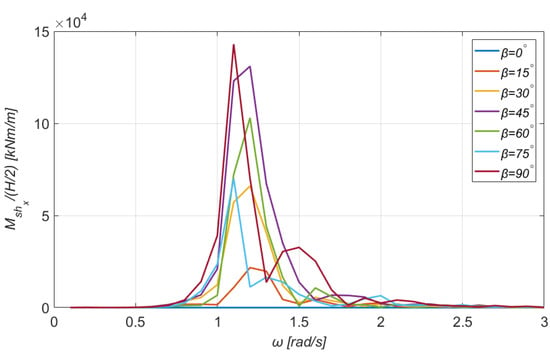
Figure 19. Horizontal bending moment for the section $AA$ (see Figure 15) for a wide range of directions of the incident wave.

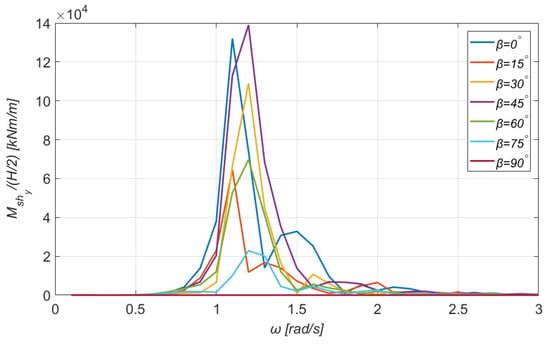
Figure 20. Transverse bending moment for the section $AA$ (see Figure 15) for a wide range of directions of the incident wave.

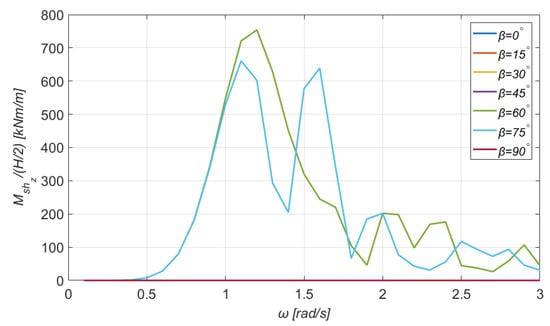
Figure 21. Vertical bending moment for the section $AA$ (see Figure 15) for a wide range of directions of the incident wave.

As far as the bending moments are concerned, the maximum value of the horizontal bending moment is 143,000 kNm/m and is obtained for $\beta ={90}^{°}$ and $\omega =1.1 \mathrm{rad}/\sec$, and that of the transverse bending moment is 139,000 kNm/m, but it is obtained for the pair of parameters $\beta ={45}^{°}$ and $\omega =1.2 \mathrm{rad}/\mathrm{s}$. Finally, one can easily notice that the magnitude of the vertical bending moments is significantly smaller. Particularly, the curves for $\beta ={30}^{°}$ and ${60}^{°}$ coincide; the same observation holds for the curves corresponding to $\beta ={15}^{°}$ and ${75}^{°}$. For orientations of the wave at $\beta =0^{°}, {45}^{°}, {90}^{°}$, the vertical bending moment is practically zero. On this occasion, it should be pointed out that the units for the shear forces and the total tensions (in the following section) are kNm/m because the analysis is performed in the frequency domain and under the harmonic waves’ action. Consequently, these physical quantities are expressed in terms of the incident wave’s amplitude. The same comment holds for the bending moments as well.

7. Calculation of the Total Mooring Tensions

In this section, the total mooring tensions at the top of each tendon are given in Figure 22, Figure 23, Figure 24 and Figure 25. With a careful observation of Figure 22 and Figure 23, we immediately notice that the curves of $T_1$ and $T_2$ which correspond to a completely horizontal direction of the incoming wave ($\beta =0^{°}$) are identical, as expected.

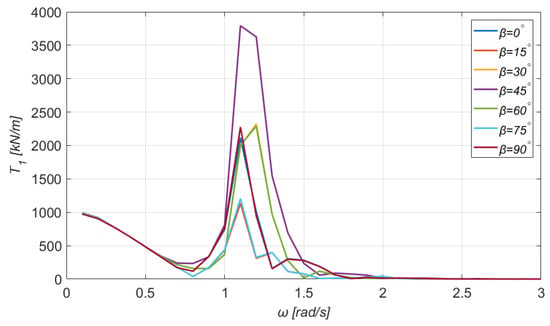
Figure 22. Total mooring forces at the first tendon of the TLP.

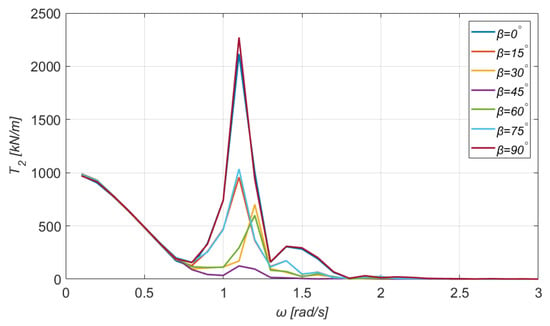
Figure 23. Total mooring forces at the second tendon of the TLP.

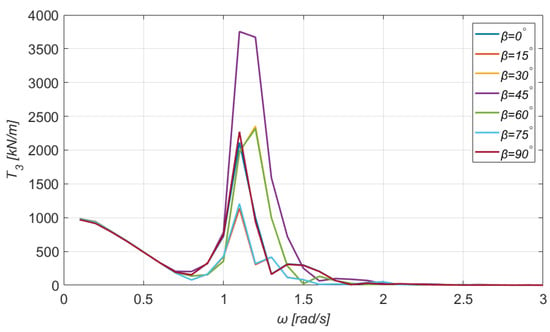
Figure 24. Total mooring forces at the third tendon of the TLP.

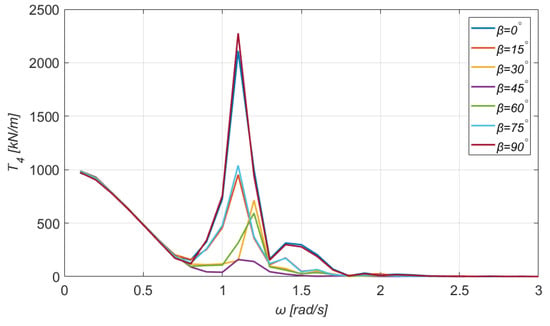
Figure 25. Total mooring forces at the fourth tendon of the TLP.

Similar deductions can be obtained for different angles as well, owing to the double symmetry of the rectangular floating structure, along the $xy$ plane. Moreover, the values of the mooring tensions at the first and third branch (see Figure 22 and Figure 24) are considerably higher, compared to the second and fourth. Furthermore, it is interesting to mention that the maximum value of the tension at each tendon is obtained for the angular frequency $\omega =1.1 \mathrm{rad}/\mathrm{s}$. Finally, the tension at the first and third tendon is higher when the angle of the incoming wave is $\beta ={45}^{°}$, whereas at the second and fourth, the tension is higher when $\beta ={90}^{°}$.

8. Discussion and Conclusions

The purpose of this study was to formulate and solve the coupled hydroaeroelastic problem for a TLP floating WT in the frequency domain. The examined floating structure is rectangular. The hydrodynamic problem was solved by exploiting the method of matched axisymmetric eigenfunction expansions and the physical idea of multiple scattering. The contribution of the WT to the formulation of the dynamic equation of motion and its coupling to the floater was discussed sufficiently. Numerical results concerning the exciting forces and bending moments acting on the floating structure, along with the added masses and damping coefficients and the RAOs of the floater’s motions, have been presented. Moreover, the shear forces and moments at the interconnection of the WT tower with the floating structure have been evaluated. In addition, particular attention was paid to the tension at each branch of the TLP mooring system. Finally, the effect of the angle of wave incidence and of the angular frequency on the maximum values of the examined physical quantities has been examined in detail.