Abstract
Breaching or overtopping of coastal dunes is associated with greater upland damages. Reliable tools are needed to efficiently assess the likelihood of dune erosion during storm events. Existing methods rely on numerical modeling (extensive investment) or insufficiently parameterize the system. To fill this gap, a fragility curve model using a newly developed dune Engineering Demand Parameter (EDP) is introduced. Conceptually, the EDP is similar to the Shield’s parameter in that it represents the ratio of mobilizing terms to stabilizing terms. Physically, the EDP is a measure of storm intensity over the dune’s resilience. To highlight potential applications, the proposed EDP fragility curve models are fit to a spatially and temporally robust dataset and used to predict dune response subjected to varying storm intensities including both extratropical and tropical storm. This approach allows for the probabilistic prediction of dune impacts through an innovative, computationally efficient model. Several different forms of the EDP are tested to determine the best schematization of the dune resilience. The final recommended EDP is the Peak Erosion Intensity (PEI) raised to the fourth power over the product of the dune volume and berm-width squared. Including both storm intensity and resilience terms in the EDP enables comparison of different beach configurations in different storm events fulfilling a need existing vulnerability assessors cannot currently account for directly.
1. Introduction
1.1. Motivation
The performance of the combined beach and dune system subjected to coastal storms is of importance to engineers, coastal managers and underwriters alike. Breaches, overwash or significant overtopping of a dune are associated with greater impacts to upland infrastructures. This has in part led to the development and widespread use of categorical scales for predicting/assessing storm impact such as the Sallenger [1] Storm Impact Scale. Alternatively, dune and beach performance can be predicted numerically using models of varying complexity and fidelity (e.g., DUROS, SBEACH, XBeach, CShore, etc.). However numerical methods require significant effort through model initialization (pre-event bathymetry and topography), calibration and, for the 2D models over large domains, significant computational run times. These traits require significant investment and preclude the widespread implementation in real-time forecasting applications. Furthermore, performance of cross-shore models is highly dependent on the calibration and even with a calibrated model, the skill of a model may not be uniform if applied over wide range of storm severity (e.g., moderate to severe events) [2]. Fragility curves, which have been used extensively in the field of seismic design, have more recently been applied to coastal engineering problems [3,4]. These methods allow for the consideration of probabilistic estimates and can be extended beyond the binary ‘survive’ or ‘fail’ models.
Despite extensive advancements in numerical simulations, there is still a demonstrated need to predict dune impacts in storm events using analytic or index-based equations. However, the approaches available in the existing literature have one or more deficiencies that can broadly be categorized as follows:
- The parameters account for either the dune resilience parameters or the storm intensity, but not both;
- Provide a categorical response only (e.g., the scale is not a continuous number which limits the usefulness in statistical fitting);
- Incomplete parameterization of the resilience terms (e.g., consider dune volume but not position of the dune);
- Incomplete consideration for storm intensity parameters (e.g., account for peak storm intensity but not duration effects).
A summary of current approaches is presented in the following subsections, where they are grouped according to the interdependence of beach width and volume in the design of coastal defense projects (Section 1.2), widely used parameters to describe dune resilience (Section 1.3) and lastly parameterization of storm intensity (Section 1.4 and Section 1.5).
Here, the dune EDP is proposed to fulfill the need for a single variable that simultaneously parameterizes both the storm intensity and the resilience of a beach and dune in a physically meaningful way. The EDP is ideally suited to applications within a fragility curve framework by preserving the underlying physics and not exclusively relying on a statistical fit. The parameter considers both the mobilizing terms (intensity) and the stabilizing terms (resilience) to capture the demand placed on the dune. Characterizing the demand enables better estimation of the vulnerability over a range of storm intensities and beach configurations. The intended application of the EDP is in the evaluation of dunes with incomplete or partially defined data (e.g., cases where the dune volume may be estimated but offshore bathymetry is unknown). While the methods do not, and should not, replace numerical modeling, they have uses in forecasting, rapid or regional scale assessments, and as a design tool in conceptual design.
1.2. Quantifying the Combined Effects of the Beach Width and Dune Volume
The protective benefit afforded by the dunes and berm in the broader beach system are deeply intertwined. However, despite the consensus that dunes are a primary defense feature to coastal storms, the design and quantification of the protection afforded by dunes and, more specifically, the combined effect of beach width and dune volume is limited in the existing literature. Consider that in Dean’s textbook [5], appropriately considered the seminal work in the beach nourishment design, the benefit of dunes is not included in either the chapter or appendix dedicated to quantification of the benefit of nourishment. Instead, the quantification of benefit is focused exclusively on beach width. Additional gold standards for consulting engineering including [6,7,8] provide an excellent description of the physical processes and role of dunes as a reserve volume in the beach–dune system. However, none provide explicit guidance on the design of dunes in relationship to the beach width. Bruun [9] highlighted the necessity for the beach and dune to be considered comprehensively and described considerations for geometric shape and placement. The often cited FEMA 540-rule [10] is used in assessment of existing dunes for the National Flood Insurance program, though has been adapted to provide guidance for construction as well [11]. Some of the most relevant quantification on dune design stems from The Netherlands starting with Vellinga [12] and resulting in technical guidance, e.g., [13]. A more expansive summary can be found in [14].
1.3. Resilence or Vulnerbility Assessors
One of the first comprehensive methods to identify areas with increased susceptibly to storm-driven morphology changes (e.g., breaches, overtopping, etc.) at a regional scale was performed by Morgan and Stone [15]. Morgan and Stone developed the Storm Wave Susceptibility Quotient (SWS), an index used to quantify the vulnerability of sandy coasts located along Florida’s barrier islands. The schematization of the wave climate was simple but precludes assessment to a specific storm or event.
First-order estimates, such as the 540-rule rule [10] are delightfully simple to apply. However, they poorly resolve the risk of dune failure for return periods above or below 100-years, fail to account for the position of the dune (setback) and do not quantify the uncertainty and spread in possible outcomes. Consequently, guidance for best practice has been to double the expected median eroded volumes to account for the significant uncertainty [11].
Sallenger [1] introduced the Storm Impact Scale for barrier islands that categorically classified impacts for both tropical and extra-tropical storms based on wave runup. Four regimes are classified as ‘swash’, ‘impact’, ‘overwash’ and ‘inundation’. Each regime characterizes when different physical processes dominate, and the magnitude of impacts change dramatically. The category is determined between the ratio of the maximum run-up elevation and the dune toe and crest elevations. The scale is useful in qualitatively describing the dominant physics, but it does not consider duration, the volume of the dune, nor does it a provide the magnitude of the expected consequences (e.g., dune volume loss). The scale has been tested in hindcasting historical storms by Stockdon, et al. [16]. Leaman, et al. [17] expanded this scale to create a storm hazard matrix including the effects of storm duration and thus erosion-dominated events.
The Sallenger [1] Storm Impact Sale has been used by the U.S. Geological Survey (USGS) to predict shoreline changes through the Coastal Change Hazard Portal [18]. The portal is unique in that it is one of the few available sources for forecasting storm impacts during storm events. When applied through forecasting, the model uses LiDAR measurements for pre-storm dune elevations and real-time forecasts of wave and water level conditions. However, consistent with the original Storm Impact Scale, the USGS model is based on peak run-up and does not consider duration effects. This shortcoming has been acknowledged by USGS and has been attributed as a potential cause of the underprediction of overwash regimes [19]. At the time of this writing, updates to the Coastal Change Hazard Portal are expected to be released in the near future to improve the performance. Recent advances include applications of machine learning to estimate the likely beach impacts [20] by combining both the storm intensity and vulnerability of the beach–dune system.
Judge, et al. [21] assessed the vulnerability parameters to characterize the performance of coastal dunes subjected to a Category 3 (SSHWS) hurricane at 110 profiles along the coast of North Carolina. Dune performance was assessed categorically as ‘failed’ (greater than 50% eroded volume) or ‘survived’ (less than 50% eroded volume). Vulnerability parameters included median erosion [10], erosion potential [22], Strom Impact Scales [1], and traditional dune geometries including crest height, dune centroid and a new Erosion Resistance (ER) term (Equation (1)). Use of the ER term improved the prediction of survival and failure classification. The ER parameter is a surrogate for mass moment of inertia and accounts for the dune’s cross-sectional area (A) and the centroid (Zc) in reference to mean high water.
It is worth noting alongshore transects were spaced at approximately 300 m. Alongshore variation in storm intensity was not quantified. While the paper includes estimates of Hurricane Fran’s storm surge, wave heights and duration, these parameters are not directly accounted for in the ER parameter.
1.4. Storm Intensity Measures
Numerous indices or scales exist to quantify and communicate storm intensity. However, most of these indices cannot be used in fragility functions. Often, the scales are not continuous and, in some cases, are not representative of the physics of the hazard. For example, application of the ubiquitous Saffir–Simpson Hurricane Wind Scale (SSHWS) applied to dune erosion is neither continuous (although wind-speed is), nor does it represent the principal hazard (elevated water levels, wave heights) as it relates to dune erosion. It is therefore unsurprising that the SSHWS storm classification is poorly corelated with dune erosion, e.g., [23] and only loosely correlated with monetary damages [24].
A summary of available storm intensity parameters is presented in Table 1. Note they are separated by storm type (i.e., tropical, extratropical or both) and intensity measure (peak, cumulative or both). The only parameters suitable for use with fragility functions that have a continuous numeric scale, are physically based and consider both duration and peak effects are the COSI [25] and SEI parameters. While either could be utilized within a fragility function framework, SEI was chosen due to its demonstrated use in literature including spatial and temporal considerations.

Table 1.
Summary of available measures of Storm Intensity and key characteristics. Note variables are identified in ‘Parameters Considered’ column.
1.5. Storm Erosion Index (SEI)
SEI developed by Miller and Livermont [37] and refined by Lemke and Miller [38] combines the three primary drivers of coastal erosion (wave height, total water level, and storm duration) into a physically meaningful index. The index is both continuous and physically based, enabling evaluation of storms based on their erosion potential. The storm’s erosion potential is defined by the sum of an instantaneous erosion intensity (IEI) over the duration of the storm (td):
where Hb is the depth-limited breaking wave height (Hb = 0.8 hb), W* is the width of the active surfzone (approximated as the distance to the breakpoint), B is the berm height, S is the water level height above the mean sea level, and ti is a time index.
The foundation of the Storm Erosion Index (SEI) is the physical response of a beach profile due to increased water levels. SEI is based on a form of the well-known Bruun Rule [39] modified by Dean and Dalrymple [6] to predict the equilibrium shoreline recession due to an increase in water level, and cross-shore varying wave set-up due to breaking waves. Miller and Dean [40] utilized a time-varying form of this modified Bruun Rule to predict equilibrium shoreline change based on wave height, water level, and storm duration. Miller and Livermont [37] suggested that the time varying form could be interpreted as the Instantaneous Erosion Intensity (IEI) and that the maximum value of IEI represented a measure of storm intensity they termed the Peak Erosion Intensity (PEI).
Notably, IEI has units of length and represents a theoretical landward progression of the equilibrium shoreline position if storm conditions were to persist indefinitely. While it is not realistic to expect SEI or IEI to directly represent shoreline change, it provides a quantifiable metric for erosive potential; including both instantaneous and duration effects. Though subtle, this is important for parameterization of the physics involved. Numerous studies have found the primary factor for predicting structural damages is the cross-shore distance from the mean sea level elevation or shoreline (e.g., Walling, et al. [41], FEMA [11], Dean [5]). Thus, using a quantifiable metric that represents a theoretical landward progression of the shoreline position in terms of a length scale provides a physically meaningful parameter.
Unlike many other indices, IEI/PEI/SEI makes no distinction between tropical and extratropical storms. It has been successfully applied to a number of locations, including but not limited to, the Gulf of Mexico [42]; Atlantic coast of Florida [43,44]; Gulf coast of Florida [45]; North and South Carolina [46]; New Jersey [37,38,47,48]. SEI has been shown to be more closely related to observed erosion than traditional indices.
2. Study Area and Storm Climate
The New Jersey coast provides a rich blend of high-quality datasets over a spatially diverse domain exposed to both tropical and extra-tropical storms. The oceanfront coast of New Jersey extends roughly 210 km over a predominately sandy coast including natural and nourished beaches, and both undeveloped and developed barrier islands. Lemke and Miller [38] characterized the climate of the region’s storms through the lens of the erosion potential over a 34-year period. The historical record of storms [38] is provided at 13 Segments located along the New Jersey Coast. An extensive collection of beach surveys is available through the New Jersey Beach Profile Network (NJBPN) collected bi-annually by the Coastal Research Center at Stockton University. The extents of these segments and the locations of the individual profiles from the NJBPN are shown in Figure 1.
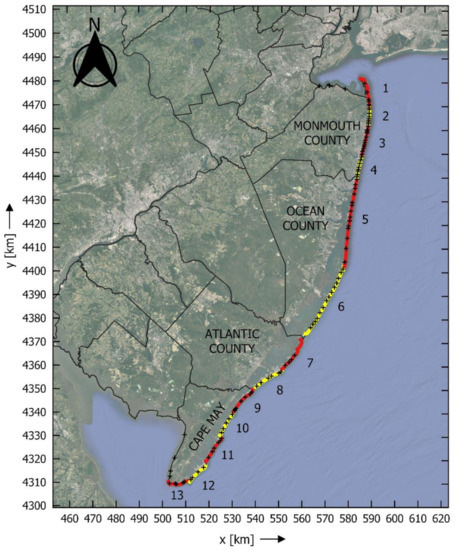
Figure 1.
Study area location. Alternating red and yellow lines depict NJ Shoreline Segments utilized by Lemke and Miller [38] to produce the storm erosion potential climatology. Segments are numbered from north to south with #1 at Sandy Hook and #13 at Cape May. NJ coastal are counties labeled accordingly. Black + markers depict NJBPN survey locations. Map coordinate system is NAD83/UTM Zone 18N in kilometers. Courtesy of [20].
Typical attributes of the beach including dune crest elevations, berm widths, slopes and dune volumes associated with these segments are presented in Figure 2. Median grain sizes range from 0.2 mm to 0.6 mm. Typically, the region experiences three to four storms per year [38]. A list of notable storms is provided in Table 2 with corresponding averaged return periods based on SEI. The aggregated observed impacts of each storm (limited to dune volume loss) is presented in Figure 3.
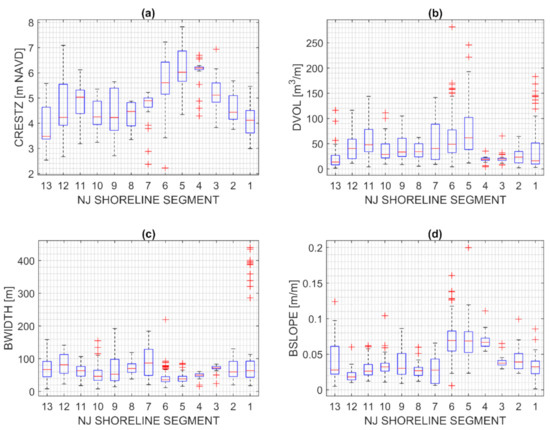
Figure 2.
Spatial variance for select Resilience parameters by segment. (a) Dune crest elevation; (b) Dune volume; (c) Berm width; (d) Beach slope. Presented by segment, south (13) to north (1). Red horizontal bar—median value, blue box—25th and 75th percentiles. Outliers defined by 1.5 × IQR away from 25th/75th percentiles. Courtesy of [48].

Table 2.
Average SEI and PEI values, and associated return periods (tr), for eighteen historical storms in New Jersey. Storm data from [20]. Return periods are based on frequency of occurrence curves by [49].
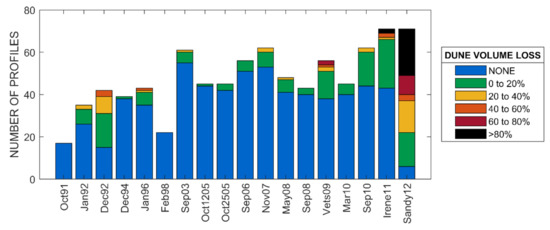
Figure 3.
Aggregated summary of quantity of profiles available and corresponding dune volume loss percentage by storm for the New Jersey coast. Courtesy of [20].
Storms within the region have been classified into Categories representing intensity [38]. The scale ranges from 1 (low intensity) to 5 (high intensity). The numerical break points for each category and the associated annual probability of exceedance are presented in Table 3. These Categories are used throughout this paper.

Table 3.
Storm Categories based on SEI and PEI including parameter value, return period (Tr) and annual probability of exceedance. Storm categories determined by [38], return period calculated from [49].
3. Methodology
This paper can be broken down into two components:
- Development of the EDP;
- Application of the EDP to develop probabilistic fragility curves of dune impacts in storm events.
This workflow is visually summarized in Figure 4. This paper makes extensive use of two existing datasets characterizing the storm intensity measures (IM) [38] and beach morphology parameters [20]. Morphology parameters include both the Resilience (Rf) parameters (e.g., beach characteristics including width, volume, etc.) and the Impact (i.e., observed dune volume loss for a given storm). The data are recast into the EDP by combining the IM and Rf from previously published datasets. The EDP is then used as a physically based parameter to fit fragility curves to predict the observed Impact classes. The EDP is the argument, and the probability of class is the return.
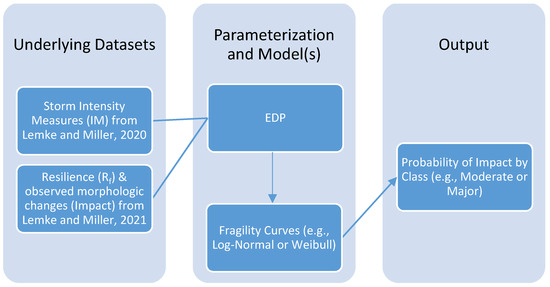
Figure 4.
Conceptual flowchart to highlight sources of previously published data used to generate the EDP and subsequent fragility curves.
3.1. Development of the Engineering Demand Parameter
In the most general from, the EDP is a non-dimensional parameter representing the ratio of Storm Intensity (‘IM’) to the Resilience factors (‘Rf’). The general form of the EDP is presented in Equation (3) with arbitrary variables. In theory, any combination of any Rf or IM parameters may be included in an EDP with corresponding power variables (e.g., ‘i’, ‘j’, ‘k’) selected to ensure non-dimensionality.
In all, 21 different IM, Rf and Impact parameters were considered. Reduction of variables was selected based on two guiding principles. The first was to ensure the most physically meaningful parameters were included both from a qualitative and quantitative means. The second was to the extent possible, include only parameters that are easily measured or estimated without specialized tools or equipment. This is a necessary compromise to make the curves more useful in real-time forecasting with limited time and resources to collect data.
Quantitative comparison was completed using Spearman correlation between the parameters and impact (i.e., dune loss percentage). In the cases of highly correlated parameters (e.g., berm volume and berm width) only the most easily measured parameter was used. A summary of parameters used is presented in Table 4.

Table 4.
Reduced parameters of interest. Note FB denotes freeboard or vertical distance between parameter and mean sea level, WL—water level, vol—volume, Hb—breaking wave height, cumE—cumulative energy (H2), Z denotes elevation, Max denotes the maximum hourly value over a single storm duration and Bslope/Islope denote beach and intertidal slope.
Several forms of the EDP were considered. The EDPs and underlying parameters are presented in the third column of Table 5. Care has been taken to ensure the selection of parameters used in the various cases of the EDP are physically meaningful and not based exclusively on best fit.

Table 5.
Considered EDPs, underlying parameters (IM and Rf) and physical meaning.
3.2. Physical Meaning of Various EDP Cases
EDP cases 1 through 4 isolate the Resilience as function of a single parameter (i.e., setback or volume). Two common measures of dune volume are tested. Cases 5 and 6 model the resilience of the dune in a conceptually similar method to shear (L2) and moment (L3). Cases 7 and 8 model the dune as a mass-moment of inertia (L4) with the distinction being Case 7 that uses a simplified measure of the moment arm (neglects vertical component of the moment arm), whereas Case 8 estimates the centroid of the dune by modeling the dune as a triangular shape. The vertical location of the centroid is then estimated as one third the difference between the crest and toe elevations. The resultant centroid is estimated using the Pythagoras theorem; adding the berm width and the crest width together. The equation shown in Case 8 in Table 5 shows the redundant square of the square-root for clarity. This is a slightly simplified approach of the Erosive Resistance (ER) parameter introduced by Judge, Overton and Fisher [21].
The significance of the physical proxy (shear, moment, etc.) has implications to potential optimization of the dune configuration. Consider an analogy between a dune and a beam. If shear controls, then the cross-sectional area of the beam must be increased. Now, consider if the moment controls and two separate beams, each with identical cross-sectional areas but with different W-shapes. The beam with a deeper section will be able to span a greater distance even if the total material is the same by taking advantage of the geometric properties. Now, consider the berm (depth) and dune volume (area) as the web and the flange of a beam, respectively. If the volume of the dune is analogous to the cross-sectional area of steel and both an indicator of material cost, then a more efficient geometric shape can potentially imply more cost-effective dunes.
3.3. The Fragility Model
The fragility models have been developed using the EDP as the argument. The fragility curves are fit to a long-term and spatially diverse record. The observational record was developed and first presented by Lemke [20,48]. This record is the combination of two datasets parameterizing both storm intensity and dune morphology, respectively. Historical storms are extracted from the dataset published by Lemke and Miller [38]. Dune morphology, including pre- and post-event indicators, are based on bi-annual beach surveys. The combination of each of these respective datasets allows for the characterization of the beach parameters pre and post storm, quantifiable measures of storm impacts and parameterization of the responsible storm intensity.
This dataset provides a unique long-term (>20-year) and spatial diverse (200-km) dataset to fit the model to. However, the dataset has some limitations identified by Lemke [48]. The median time between the ‘storm’ and pre/post- surveys was approximately 5 months. This introduces some uncertainty around the quantification of the loss (e.g., percent volume loss) and the resilience parameters (particularly berm width which fluctuates seasonally) that were present at the time of the storm.
To reduce the influence of this uncertainty, the fragility models are fit to predict categorical response of the dune impacts for a given storm intensity in lieu of a regression analysis (e.g., predicting percent dune loss or volume loss). Categories for response are based on the percentage of dune volume loss as presented in Table 6 and are identical to those established by Lemke and Miller [20]. The Major threshold was based on empirical evidence in the aftermath of Hurricane Sandy dunes with volume losses greater than 40% generally exhibited evidence of overwash, as characterized by a lowering of the post-storm dune crest elevation. The onset of overwash is attributed with greater impacts (damages) to upland assets and, thus, a useful delineation in the prediction of storm damages.

Table 6.
Classification of storm-induced dune impacts based on quantitative changes.
3.4. Fragility Function and Fitting Techniques
Two forms of fragility functions were considered. The first, is a fragility curve based on a log-normal cumulative distribution function. This form is commonly used to represent fragility functions for structural dynamic analysis, particularly in applications predicting the probability of collapse during seismic events, e.g., [50]. Herein, the return of the argument is the probability of the respective damage classification. Each categorical classification (e.g., Moderate, Major) has its own curve which is a function of the EDP.
The log-normal distribution is shown in Equation (4). The left-hand side of the equation states that the probability of category can be estimated by the EDP. The probability is estimated as the log-normal cdf evaluated at a given EDP and two fit parameters, θ and β. The parameters θ and β define the median of the distribution (i.e., the EDP measure corresponding to 50% probability classification) and the standard distribution (commonly referred to as the dispersion), respectively.
These parameters are estimated by fitting observed classifications using a multiple stripe analysis (MSA). In MSA, the data are binned into groups for similar intensity measures. The percentage of observed moderate and major categories within each bin is plotted against the EDP and are then fit using the Maximum Likelihood Estimation (MLE) method.
Using MSA, the curve is fit to the percent observations corresponding to each classification in each bin. The advantage is that all data from the record are retained. In traditional curve fit failure analysis, only the cases in which an observed failure (or classification in this context) are used. For the dataset used herein, approximately 15% of the available data are classified as Moderate or Major.
As an alternative to the log-normal distribution, a Weibull distribution was fit to the Moderate and Major classifications using only the observations corresponding to each classification. The CDF of the two-parameter Weibull function, as modified to use the EDP, is shown in Equation (5):
The two fit variables of the distribution are the scale (λ) and shape (κ). The scale factor shifts the distribution, with the shape parameter influencing the shape. Parameters are estimated using the MLE fitting techniques.
The Weibull distribution is one of the most commonly applied distributions to model predicted failure. The distribution has been shown to be remarkably flexible, with the ability to characterize the failure based on multiple inputs (e.g., time to failure, length of elongation, stress, cycles, number of units, etc.). There are only two limitations in fitting a Weibull distribution to the data that are of particular concern to the data presented.
- The confidence of the fit distribution is proportional to the number of samples at failure. With the consensus that more than 20 samples are needed to have reasonable performance. Each sample must be independent.
- The samples must be tested to failure, with the demand (i.e., value of ‘x’) at failure known.
Two separate distributions and fitting techniques were used to assess the influence of asymmetry in the distribution. Advantages and limitations of each method is discussed further in Section 5.2.
3.5. Data Screening, Fitting Techniques and Sensitivity Analysis
The original data [20] contained 865 datapoints and were screened to eliminate smaller local storms and beaches that were clearly manipulated between surveys.
The first condition was the identification of morphologic changes but for a storm intensity so low (i.e., low water level and/or wave heights) that the storm fails to meet the criteria of a storm based on the definitions provided by Lemke and Miller [38]. This occurs when the spatial variation in the storm is such that it may qualify as a storm in either the northern sections or southern limits of the state, but not both. This phenomenon occurred only for two storms in the dataset and reduced the dataset to 852 points.
The second screened condition were profiles with volume changes that indicated post-storm manipulation. Volume changes indicating greater than or equal to 10% net positive volume change (i.e., highly accretional events) were flagged as likely attributed to beach scrapping or manipulation. Beach management within New Jersey typically falls under local jurisdictions, with many local municipalities opting, or having previously experimented, with beach scraping and winter dunes.
To reduce the influence of potential Type II errors attributed to beach manipulation, all cases in which the dune loss returned a post-storm accretion of 10% or greater were removed from the dataset. This amounted to 172 datapoints. The value of 10% was chosen based on engineering judgement. The idea being that collision regime and/or berm rollover events that could lead to accretional volumes at the toe of the dune would be allowed to remain in the dataset while egregious volume accretions that would likely be attributed to a measurement error or anthropogenic beach management activities (e.g., beach scraping) would be removed from the dataset. This is a slight departure from the screening process presented in Lemke [48].
3.6. Comparision of the EDPs and Evaluation of Curves
3.6.1. Log-Normal and MSA Curves
For the MSA, the dataset was split into a training and test dataset using a 70–30 split. Evaluation metrics included: Mean Absolute Error (MAE); Bias; and Root Mean Squared Error (RMSE). Sensitivity analysis on bin width was performed including variable and constant bin widths. The selected model was determined by minimizing the RMSE for training and testing datasets for each classification. MAE and Bias for the test and training set are reported for context.
The error is calculated based on difference between the expected (predicted) probability of damage based on class and the observed fraction of damage class corresponding to the bin. The error is calculated at each bin. Due to the variable width of the bin, the median value of the EDP within the bin is used; not the mean value EDP of the bin. For small values of EDP, in the well-resolved portion of the data, the mean EDP of the bin and median EDP of the data contained within the bin are nearly identical. That is to say, the EDPs of the binned samples are relatively evenly distributed over the bin. However, for large values of EDP, the number of observations within each bin decreases while the bin width increases. In these cases, the median EDP of the samples within the bin are used to better characterize the data with the training and testing datasets.
3.6.2. Weibull Distribution
For the Weibull distribution, the curves were fit using only the observations corresponding to classification (i.e., Moderate or Major). A 70–30 split in the data would not be possible while maintaining sufficient datapoints for fitting each class.
4. Results
4.1. Preliminary Analysis
The observed dune loss percent vs. storm intensity for the entire dataset is presented in Figure 5. Colored dots denote observed Major (red) and Moderate (blue) damage classifications. Minimal impacts are denoted by x’s. Negative dune loss denotes accretion of the dune. (Potential causes and the treatment of these datapoints are discussed in Section 3.5). While the storm intensity measure alone (PEI) appears to separate the data, use of the EDP (Figure 6) improves the clustering by damage classifications. In Figure 6, the storm Categories (measure of PEI alone) are converted into an EDP using the median dune volume and berm width. Other EDPs (Cases 1–6, 8) had similar effect. However, generally speaking, clustering was improved for EDP cases that considered both berm width and dune volumes.
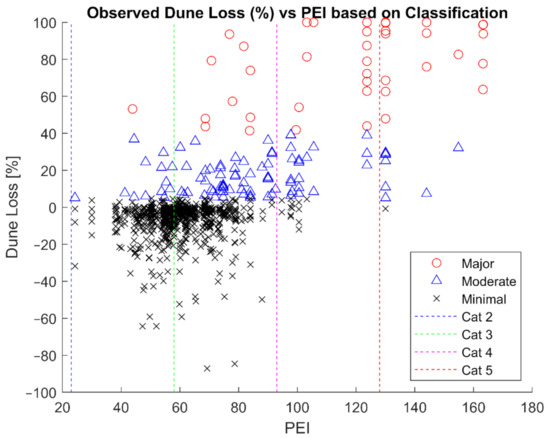
Figure 5.
Observed dune loss percentage as a function of storm intensity (PEI) alone; each data point represents observations from a single profile. X-axis is storm intensity (PEI). Storm categories are denoted by colored vertical dashed lines. The Y-axis is dune loss percentage. Red circles indicate Major loss (>40%), blue circles indicate Moderate (>5% but <40%). Negative dune loss indicates accretion.
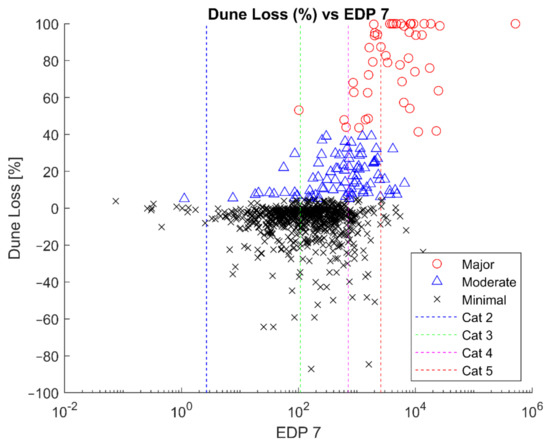
Figure 6.
Observed dune loss percentage as a function of EDP Case 7; each data point represents observations from a single profile. X-axis is the EDP. Storm categories are denoted by colored vertical dashed lines. Storm category PEI values converted to an EDP using median resilience parameters. The Y-axis is dune loss percentage. Red circles indicate Major loss (>40%), blue circles indicate Moderate (>5% but <40%). Negative dune loss indicates accretion.
Low values of EDP indicate a low demand placed on a beach through either extremely resilient beaches (i.e., high volume and wide berms) or low intensity storms (i.e., low PEI and, therefore, low water levels and wave heights). Conversely, high EDP values denote high intensity storms or beach–dune systems that are very vulnerable.
Data corresponding to each classification were extracted and plotted in a Q-Q plot. This was done for all EDP cases. Figure 7 and Figure 8 illustrate these results using the Weibull distribution for Moderate and Major classification, respectively. The performance of the Major classification (Figure 8) is distorted by a single outlier. Removal of this datapoint improves the fit drastically (Figure 9). Justification for this is discussed in Section 5.1.
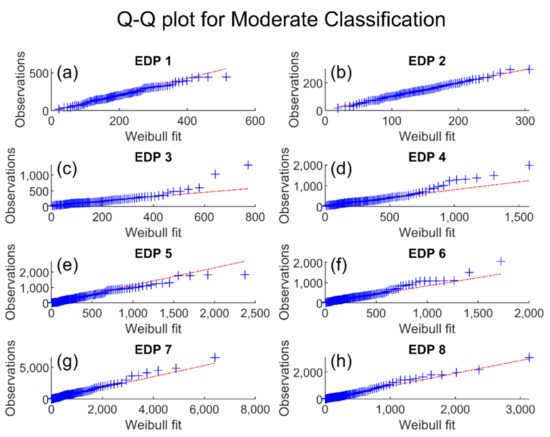
Figure 7.
Weibull distribution quantile plots for all observations corresponding to Moderate classification. (a) EDP 1—Berm Width; (b) EDP 2—Berm and Dune width; (c) EDP 3—Dune Volume; (d) EDP 4—Foredune Volume; (e) EDP 5—Shear; (f) EDP 6—Moment; (g) EDP 7—Simplified Mass-moment of Inertia; (h) EDP 8—Mass-moment of Inertia.
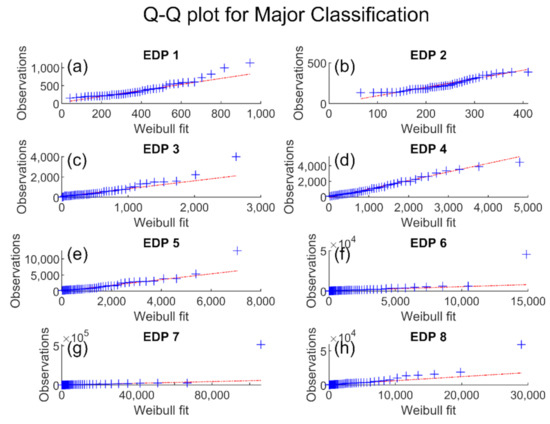
Figure 8.
Weibull distribution quantile plots for all observations corresponding to Major classification. (a) EDP 1—Berm Width; (b) EDP 2—Berm and Dune width; (c) EDP 3—Dune Volume; (d) EDP 4—Foredune Volume; (e) EDP 5—Shear; (f) EDP 6—Moment; (g) EDP 7—Simplified Mass-moment of Inertia; (h) EDP 8—Mass-moment of Inertia.
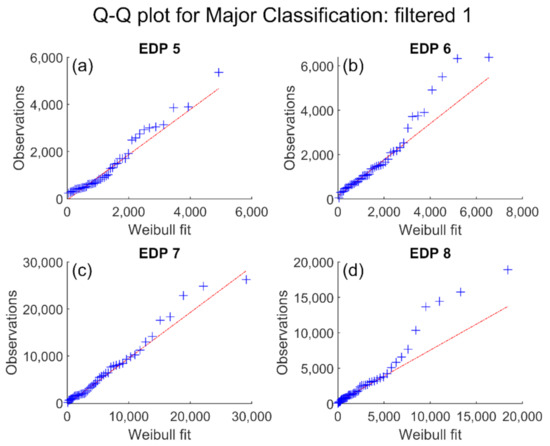
Figure 9.
Weibull distribution quantile plots removing maximum observation corresponding to Major classification with a single datapoint removed. Only EDP cases 5 to 8 are shown for clarity. (a) EDP 5—Shear; (b) EDP 6—Moment; (c) EDP 7—Simplified Mass-moment of Inertia; (d) EDP 8—Mass-moment of Inertia.
4.2. EDP Curves
The selected curves for both the log-normal and Weibull distributions are shown in Figure 10 and Figure 11, respectively. For brevity, only EDP Case 7 is shown. Note in Figure 10, the fit curve describes the onset of damage. That is to say, the predicted probability and fraction of observed classifications are in better agreement for low values of EDP than at the upper EDP values.
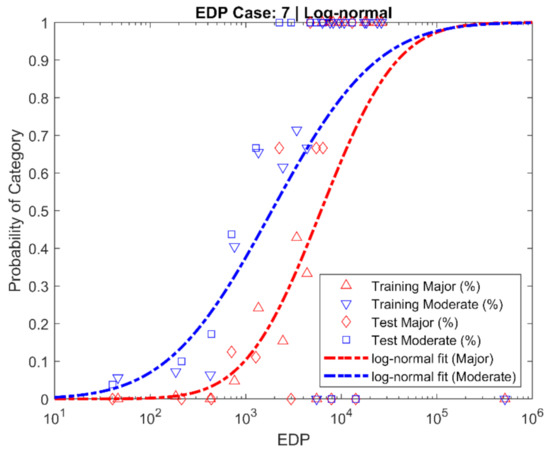
Figure 10.
Example log-normal distribution for EDP 7 for calibration/training (triangular shapes) and test datasets (square/diamond). Dashed curves represent MLE log-normal fit curves with red denoting Major and blue denoting Moderate classification.
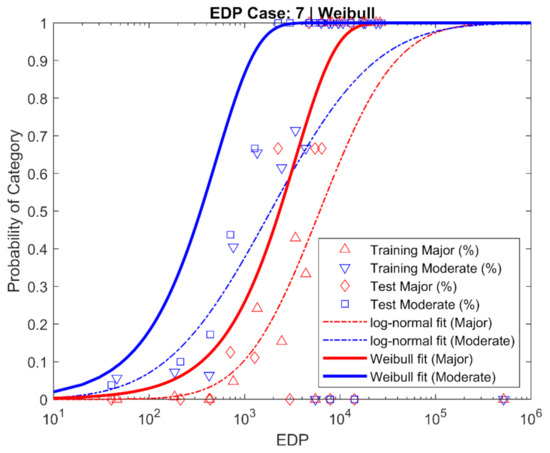
Figure 11.
Comparation of Weibull (solid line) vs. log-normal distribution (dashed) for EDP 7. Observed fractions of classification are denoted by shapes and retained from previous figure to illustrate performance. Red denotes Major, Blue denotes Moderate classification.
4.3. Comparison of EDPs and Fragility Functions
To enable comparison of the EDPs and the respective fitting techniques, the entire dataset (combined training and test) is then re-grouped by storm intensity corresponding to the PEI Categories defined by Lemke and Miller [38]. The mean hindcasted probabilities and the observed fractions of each classification are presented. Figure 12 illustrates all EDP cases using the log-normal distribution. In Figure 13, the most physically relevant EDPs (5–8) are shown for both the log-normal MSA and the Weibull fitting technique.
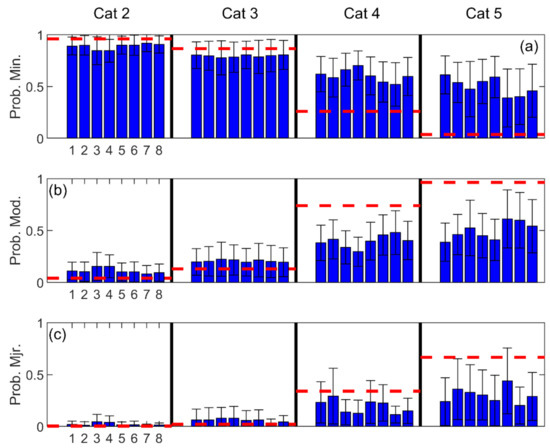
Figure 12.
Log-normal predicted and observed fractions of damage classification by storm category (vertical columns). Each subplot corresponds to a damage classification: (a) Minimal; (b) Moderate; (c) Major. Vertical bars correspond to EDP case (1 to 8 in each box), whiskers are standard deviation in predicted probabilities for storms within the Category. Dashed red horizontal bar is the fraction of observed classifications corresponding to the appropriate storm category.
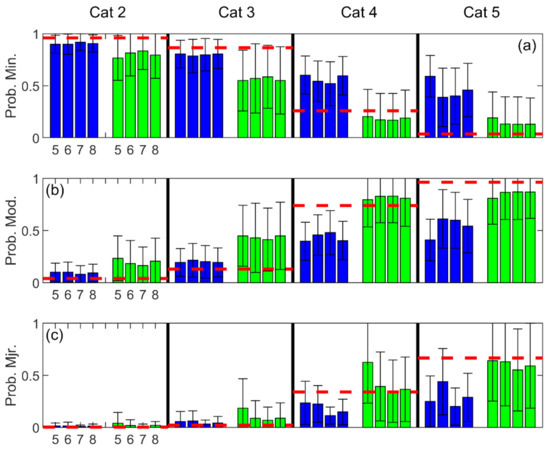
Figure 13.
Comparison of Weibull (green/right) and log-normal (blue/left) models by storm category (vertical columns). Each subplot corresponds to a damage classification: (a) Minimal; (b) Moderate; (c) Major. Each vertical bar corresponds to an EDP case and model. Note only EDPs 5–8 are shown. Whiskers are standard deviation in predicted probabilities for the corresponding category of storms. Dashed red horizontal bar is the actual observed fraction corresponding to the appropriate storm category.
Both figures display a 3 × 4 matrix, each row corresponds to the classification (i.e., Minimal, Moderate and Major). Each column corresponds to the storm category (i.e., Category 2, 3, 4 and 5). Each EDP case is represented by a vertical bar. The vertical bar represents the estimated mean probability of the damage classification for the storms contained within the respective storm category groups. The whiskers represent the standard deviation in the predicted probabilities. The dashed red horizontal bar represents the fraction of observed classification within the storm category.
The estimated best fit parameters are shown in Table 7 and Table 8 for the log-normal and Weibull distributions, respectively. Estimates of errors for the combined training and test datasets are shown in Table 9.

Table 7.
Best Estimate Normal Distribution parameters.

Table 8.
Best Estimate Weibull Distribution parameters.

Table 9.
Error metrics for log-normal MSA curves.
5. Discussion
5.1. General Assessment of the EDP
The relatively strong performance of a wide range of EDP cases in the Q-Q plots shown in Figure 7, Figure 8 and Figure 9 indicates the strength of the EDP in parameterizing the physical demands placed on the beach and dune systems subjected to coastal storms. The dataset is robust by combing both tropical and extra-tropical storms which extends the applicability of the presented EDP.
However, the observational dataset has one import shortcoming—the temporal resolution. It is impossible to discern the timestep within the storm that leads to onset of the classification. Consideration for these cases can be depicted in the removal of a single point from Figure 8 and Figure 9. Note that removal of the datapoint prevents over-estimation of the resilience of the beach–dune system. If the removed datapoint is used as an evaluation point, the performance of the curves is substantially better than if the point is used to define the onset of failure. The distinction is due to the use of the cdf used in the validation of the curves vs. the assignment of failure at a defined EDP in the pdf. A subtle distinction, however important.
The EDP represents the ratio of the peak intensity of the storm to the resiliency of the beach and dune system. Consider a theoretical beach with low resiliency terms subjected to a moderate event (PEI ~ 80) that results in an observed Major classification. Now, consider the identical beach subjected to a more intense storm (say, PEI ~ 100) which results in Major classification. However, using EDP 7, the change in EDP is ~2.5 larger for the second event. The classification is assigned to this PEI. In reality, the beach–dune system is subjected to a ramp up in the IEI over the course the storm. The limitation of the dataset is that it is impossible to discern at which timestep the classification occurs. This is a limitation of the dataset and not the EDP.
The implicit assumption is that the damage classification occurs at or nearly at the peak of the storm. Mathematically, that is to say, the IEI resulting in classification is approximately equal to the PEI. This is likely true for most events. However, for high value EDPs, the likelihood increases that classification occurs at some IEI value less than the PEI. This is the justification for removing the highest EDP values in the Weibull curve fitting (i.e., Figure 8 and Figure 9).
5.2. Fragility Model Performance
When presented using the Q-Q plots, outliers discussed above are more readily seen. The concern becomes more apparent using the MSA analysis when individual events become obscured by the binning procedure and data aggregation. Uncertainties within the dataset can lead to miss-binning. The influence of this was attempted to be counteracted through extensive sensitivity testing of the bin widths, including variable bin width sizing which improved the fit slightly. However, the underprediction of Major classification seen in Figure 10 and Figure 12 is a significant impediment to the applicability of the curves if not accounted for.
Herein, the underprediction has been addressed by fitting a Weibull distribution and removing the MSA. Use of the Weibull distribution allows for the more flexibility in the shape of the distribution over a log-normal distribution. The performance for Major impacts in severe storms (e.g., Cat 4 or 5) is markedly improved in Figure 12.
Consider the two assumptions stated for the Weibull distribution. The presented dataset has 865 independent observations, but only contains 88 instances of moderate and 45 instances of major impacts. The number of observations (sample size) for each category therefore exceeds the minimum number required even if ~20 observations would be removed. However, the combined samples only account for roughly 15% of the total data. Undoubtedly, meaningful information contained with those datapoints is ignored by this fitting process.
5.3. Limitations of the Curves and Potential Improvements
Reduction of data is less than ideal, but necessary due to limitations of the temporal resolution of the underlying observational data. The presented curves, particularly the Weibull fits, are still useful given these limitations. This is particularly true because they fill a niche exhibiting ease of application while providing probabilistic outputs. Consider the proposed curves in comparison to the widely used methods such as the 540-rule [10].
It is postulated that the fragility curves using EDPs, particularly Cases 6, 7 and 8 could be improved through the use numerical or physical tests that can resolve the temporal response of the beach–dune system within the storm duration. Resolution on a storm time scales (i.e., hourly) through numerical or physical modeling could better quantify duration effects. The observational dataset used herein could then be used exclusively for evaluation of the experimentally determined curves.
5.4. Comparing EDP Cases and the Physical Meaning
Despite the limitations of the dataset, the strength of the EDP is the physically meaningful proxy. Similar to the methods presented by Judge, Overton and Fisher [21], the EDPs are presented based on a physical surrogate. The results herein further substantiate the findings by Judge, Overton and Fisher [21] that the resilience of the dune can be modeled using the volume and berm widths as a surrogate for the mass-moment of inertia (EDP Cases 7 and 8). With an eye towards extending the usefulness of the curves without the need for specialized measurements, a simplified version (EDP 7) was tested with comparable performance. In the simplified estimation of the centroid of the dune, the vertical component is omitted. Thus, for cases where the berm width >> dune toe elevation, the performance should be comparable. It should be noted that in the derivation of SEI, the berm elevation is included, thus somewhat accounting for the erosive potential of the storm as related to the position of the dune toe and berm height.
The performance gap between EDP 6 and 7 narrows and eventually even reverses for high intensity storms (Figure 13, Table 9). Under Swash or Collision regimes, the berm width would need to be significantly eroded to allow higher wave heights to impact the dunes. However, during significantly elevated high-water levels associated with Overwash and/or Inundation regimes, the berm will be fully submerged. It is postulated that protective benefit of the berm is therefore reduced, while the importance of the dune volume is magnified. This is conceptually similar to the reduced protection afforded by a drowned offshore bar (or coastal structure) during elevated water levels. There appears to be some evidence to support this in the performance of the single-parameter EDPs. EDPs using setback alone (EDP 1 and 2) appeared better than volume alone (EDP 3 and 4) for lower magnitude events (Category 2 and 3). However, the performance was narrowed or even reversed for Category 5 storms (Figure 12). Admittedly, this is not exhaustive, but conceptually shows the flexibility of the EDP in parameterizing the physics governing the demands placed on a beach and dune system during erosive events.
6. Conclusions
6.1. Thematic
The Engineering Demand Parameter has been introduced to address the need for a physically based, continuous parameter that simultaneously accounts for the most important Resilience terms (e.g., dune volume and setback) and the storm intensity (e.g., erosive potential). The advantage of the presented form of the EDP is that it can, if needed, be easily modified where additional parameters may be needed. The only explicit assumptions are:
- The EDP must represent the ratio of storm intensity over the resilience terms;
- Terms in numerator and denominator must be combined in a way that produces a non-dimensional parameter.
To demonstrate the potential usefulness of the parameter, the EDP has been applied to a categorical fragility model. The model is fit to a robust (but imperfect) observational dataset that includes a wide range of storm intensities (moderate to severe); tropical and extratropical storms; and a wide variation in beach/dune morphology. The relative skill of the EDP is indicative of the robustness of the approach in parameterizing the physics in a simple, yet meaningful way.
Several forms of the EDP with different fitting techniques and distributions were tested. Curves were generated using MSA with log-normal distribution and a Weibull distribution. Both curves were fit using MLE techniques.
6.2. Recommended EDP and Fragility Function
Based on the observed data, the recommended form the EDP is Case 7, which is the PEI [37] over a modified version of the Erosive Resistance parameter [21]. In the event Major impacts are the primary concern, the Weibull distribution (i.e., λ = 4428, κ = 1.32) is the recommended form.
In general, the hindcasted probabilities of Major (i.e., dune volume loss > 40%) impacts are well resolved by the Weibull distribution for all storm intensities (e.g., Cat 2 through Cat 5). However, if the prediction of the onset of moderate impacts (i.e., dune volume loss > 5% but <40%) during lower intensity storms (e.g., Cat 2 or 3) is of paramount concern, the curves fit using the log-normal and MSA analysis are superior. The reason is not the distribution but rather from the fitting technique. When using MSA the curve is fit to the fraction of observations corresponding to the classification in the record. Consequently, the fit dataset retains both ‘failed’ and ‘resilient’ observations whereas the Weibull distributions only consider a limited subset of the full dataset and only those resulting in the appropriate classification.
6.3. Limitations, Compromises and Potential Improvements
The development of the EDP has been specifically tailored for the application of fragility function in a forecasting application. This need has led to necessary compromises in the selection of underlying parameters. Care has been taken to include Resilience parameters (e.g., volume, berm width) that are easily estimated with simple tools or remote sensing (e.g., satellite, aerial photographs, UAVs, etc.). This has led to a conscious decision to remove factors that are important (e.g., crest, toe, centroid elevations, slope, etc.) but require expensive or specialized equipment (e.g., RTK GPS). Attempts to quantify the impact of these omission (e.g., EDP Case 7 and 8) suggest the increased complexity may not be warranted for the curves intended application (e.g., forecasting)—following the adage of “everything must be made as simple as possible, but not simpler.”
At extreme events with high storm intensity, the resilience may decrease from EDP Case 7 to 6 (i.e., the product of the dune volume and berm width vs. berm width squared). It is hypothesized that at high water levels (therefore high PEI values and high EDPs), the berm may be fully submerged, allowing higher wave heights to impact the dunes. This is conceptually similar to attenuating protection afforded by a drowned offshore bar during elevated water levels. Admittedly, this has not been conclusively tested, but warrants further investigation.
Author Contributions
Conceptualization, M.S.J.; methodology, M.S.J. and J.K.M.; formal analysis, M.S.J.; data curation, M.S.J.; writing—original draft preparation, M.S.J.; writing—review and editing, J.K.M.; visualization, M.S.J.; supervision, J.K.M.; project administration, J.K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the New Jersey Department of Environmental Protection (NJDEP) through the New Jersey Coastal Protection Technical Assistance Service (N.J.S.A. 18A:64L-1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. Details regarding these sources can be found at The Stockton University Coastal Research Center (Welcome-Coastal Research Center | Stockton University) and in Lemke and Miller [20] and Lemke and Miller [38].
Acknowledgments
The authors would like to acknowledge and express sincere gratitude to Laura Lemke who graciously provided unfettered access and insights into her datasets. The authors would also like to thank the reviewers whose meaningful feedback improved the presentation of the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Sallenger, A.H. Storm impact scale for barrier islands. J. Coast. Res. 2000, 16, 890–895. [Google Scholar]
- Kalligeris, N.; Smit, P.B.; Ludka, B.C.; Guza, R.T.; Gallien, T.W. Calibration and assessment of process-based numerical models for beach profile evolution in southern California. Coast. Eng. 2020, 158, 103650. [Google Scholar] [CrossRef] [Green Version]
- Tomiczek, T.; Kennedy, A.; Zhang, Y.; Owensby, M.; Hope, M.E.; Lin, N.; Flory, A. Hurricane Damage Classification Methodology and Fragility Functions Derived from Hurricane Sandy’s Effects in Coastal New Jersey. J. Waterw. Port Coast. Ocean Eng. 2017, 143, 17. [Google Scholar] [CrossRef]
- Tomiczek, T.; Kennedy, A.; Rogers, S. Collapse Limit State Fragilities of Wood-Framed Residences from Storm Surge and Waves during Hurricane Ike. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 43–55. [Google Scholar] [CrossRef] [Green Version]
- Dean, R.G. Beach Nourishment; World Scientific: Singapore, 2003; Volume 18, p. 420. [Google Scholar]
- Dean, R.G.; Dalrymple, R.A. Coastal Processess with Enginerring Applications; Cambridge University Press: New York, NY, USA, 2004; p. 475. [Google Scholar]
- Kamphuis, J.W. Introduction to Coastal Engineering and Management; World Scientific: Singapore, 1999. [Google Scholar]
- Reeve, D.; Chadwick, A.; Fleming, C. Coastal Engineering: Processes, Theory and Design Practice, 3rd ed.; Spon Press: New York, NY, USA, 2012. [Google Scholar]
- Bruun, P. Dunes—Their Function and Design. J. Coast. Res. 1998, 26, 26–31. [Google Scholar]
- Hallermeier, R.J.; Rhodes, P.J. Description and Assessment of Coastal Dune Erosion; Dewberry & Davis, Inc.: Fairfax, VA, USA, 1986. [Google Scholar]
- FEMA. Coastal Construction Manual Principles and Practices of Planning, Siting, Designing, Construction and Maintaining Residential Buildings in Coastal Areas, 4th ed.; FEMA: Washington, DC, USA, 2011. [Google Scholar]
- Vellinga, P. Beach and Dune Erosion during Storm Surges; Hydraulics Laboratory: Delft, The Netherlands, 1982. [Google Scholar]
- ENW. Technical Report on Dune Erosion (in Dutch); Delft Hydraulics: Delft, The Netherlands, 2007. [Google Scholar]
- Van Koningsveld, M.; Otten, C.J.; Mulder, J.P.M. Dunes: The Netherland’s Soft but Secure Sea Defences. In Proceedings of the 18th World dreding congress (WODCON XVIII), Lake Buena Vista, Florida, USA, 27 May–1 June 2007; WODA: Lake Buena Vista, Florida, USA, 2007; pp. 167–184. [Google Scholar]
- Morgan, J.P.; Stone, G.W. A technique for quantifying the coastal geomorphology of Florida’s barrier island and sandy beaches. Shore Beach 1985, 53, 19–26. [Google Scholar]
- Stockdon, H.F.; Sallenger, A.H.; Holman, R.A.; Howd, P.A. A simple model for the spatially-variable coastal response to hurricanes. Mar. Geol. 2007, 238, 1–20. [Google Scholar] [CrossRef]
- Leaman, C.K.; Harley, M.D.; Splinter, K.D.; Thran, M.C.; Kinsela, M.A.; Turner, I.L. A storm hazard matrix combining coastal flooding and beach erosion. Coast. Eng. 2021, 170, 104001. [Google Scholar] [CrossRef]
- United States Geological Survey (USGS). Coastal Change Hazards Portal; USGS: Reston, VA, USA, 2019.
- United States Geological Survey (USGS). Before and After: Coastal Change Caused by Hurricane Michael. Available online: https://www.usgs.gov/news/featured-story/and-after-coastal-change-caused-hurricane-michael (accessed on 1 December 2019).
- Lemke, L.; Miller, J.K. Role of Storm Erosion Potential and Beach Morphology in Controlling Dune Erosion. J. Mar. Sci. Eng. 2021, 9, 1428. [Google Scholar] [CrossRef]
- Judge, E.K.; Overton, M.F.; Fisher, J.S. Vulnerability indicators for coastal dunes. J. Waterw. Port Coast. Ocean Eng. Asce 2003, 129, 270–278. [Google Scholar] [CrossRef]
- Kriebel, D.L.; Dalrymple, R.A.; Pratt, A.P.; Sakovich, V. Shoreline risk index for noreasters. In Proceedings of 1996 Conference on Natural Disaster Reduction, Washington, DC, USA, 3–5 December 1996; pp. 251–252. [Google Scholar]
- Ellis, J.T.; Harris, M.E.; Román-Rivera, M.A.; Ferguson, J.B.; Tereszkiewicz, P.A.; McGill, S.P. Application of the Saffir-Simpson Hurricane Wind Scale to Assess Sand Dune Response to Tropical Storms. J. Mar. Sci. Eng. 2020, 8, 670. [Google Scholar] [CrossRef]
- The National Oceanic and Atmospheric Administration, N. Billion-Dollar Weather and Climate Disasters: Events. Available online: https://www.ncdc.noaa.gov/billions/events/US/1980-2019 (accessed on 14 October 2021).
- Basco, D.R.; Mahmoudpour, N. The modified Coastal Storm Impulse (COSI) parameter and quantification of fragility curves for coastal design. Coast. Eng. Proc. 2012, 1. [Google Scholar] [CrossRef]
- Schott, T.; Landsea, C.; Hafele, G.; Lorens, J.; Taylor, A.; Thurm, H.; Ward, B.; Willis, M.; Zaleski, W. The Saffir-Simpson Hurricane Wind Scale; NOAA/National Weather Service: Silver Spring, MD, USA, 2012. [Google Scholar]
- Kantha, L. Time to replace the Saffir-Simpson hurricane scale? Eos Trans. Am. Geophys. Union 2006, 87, 3–6. [Google Scholar] [CrossRef] [Green Version]
- Powell, M.D.; Reinhold, T.A. Tropical cyclone destructive potential by intergrated kinetic energy. Bull. Am. Meteorol. Soc. 2007, 88, 513–526. [Google Scholar] [CrossRef] [Green Version]
- Hebert, C.; Weinzapfel, B.; Chambers, M. Hurricane Severity Index: A new way of estimating a tropical cyclones destructive potential. In Proceedings of the 29th Conference on Hurricanes and Tropical Meteorology, Tucson, AZ, USA, 10–14 May 2010. [Google Scholar]
- Irish, J.L.; Resio, D.T. A hydrodynamics-based surge scale for hurricanes. Ocean Eng. 2010, 37, 69–81. [Google Scholar] [CrossRef]
- Done, J.M.; PaiMazumder, D.; Towler, E.; Kishtawal, C.M. Estimating impacts of North Atlantic tropical cyclones using an index of damage potential. Clim. Change 2018, 146, 561–573. [Google Scholar] [CrossRef] [Green Version]
- Dolan, R.; Davis, R.E. An intensity scale for atlantic coast northeast storms. J. Coast. Res. 1992, 8, 840–853. [Google Scholar]
- Mendoza, E.T.; Jimenez, J.A.; Mateo, J. A coastal storms intensity scale for the Catalan sea (NW Mediterranean). Nat. Hazards Earth Syst. Sci. 2011, 11, 2453–2462. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Douglas, B.C.; Leatherman, S.P. Beach Erosion Potential for Severe Nor’easters. J. Coast. Res. 2001, 17, 309–321. [Google Scholar]
- Balsillie, J.H. Beach and coast erosion due to extreme event impact. Shore Beach 1986, 54, 15. [Google Scholar]
- Kraus, N.C.; Wise, R.A. Simulation of 4 January 1992 storm erosion at Ocean City, Maryland. Shore Beach 1993, 61, 34–41. [Google Scholar]
- Miller, J.K.; Livermont, E. An index form Predicting Storm Erosion Due to Increased Waves and Water Levels. In Proceedings of the Solutions to Coastal Disasters, Turtle Bay, Oahu, HI, USA, 13–16 April 2008; p. 16. [Google Scholar]
- Lemke, L.; Miller, J.K. Evaluation of storms through the lens of erosion potential along the New Jersey, USA coast. Coast. Eng. 2020, 158, 103699. [Google Scholar] [CrossRef]
- Bruun, P. Sea-level rise as a cause of shore erosion. J. Waterw. Port Coast 1962, 88, 117–132. [Google Scholar] [CrossRef]
- Miller, J.K.; Dean, R.G. A simple new shoreline change model. Coast Eng. 2004, 51, 531–556. [Google Scholar] [CrossRef]
- Walling, K.; Herrington, T.O.; Miller, J.K. Hurricane Sandy damage comparison: Oceanfront houses protected by a beach and dune system with vs. without a rock seawall. Shore Beach 2016, 84, 35–41. [Google Scholar]
- Janssen, M.S.; Lemke, L.; Miller, J.K. Application of Storm Erosion Index (SEI) to parameterize spatial storm intensity and impacts from Hurricane Michael. Shore Beach 2019, 87, 41–50. [Google Scholar] [CrossRef]
- Wehof, J.; Miller, J.K.; Engle, J. Application of the Storm Erosion Index (SEI) to three unique storms. In Proceedings of the 34th International Conference on Coastal Engineering, Seoul, Korea, 15–20 June 2014. [Google Scholar]
- Miller, J.K.; Wehof, J. Evaluation of Storm Severity Based on the Storm Erosion Index along the Southeast Atlantic Coast of Florida in the wake of Hurricane Sandy. Technical Report Prepared for the Jacksonville District of the USACE; Stevens Insitute of Technology, Davidson Laboratory: Hoboken, NJ, USA, 2013; p. 14. [Google Scholar]
- Cheng, J.; Cossu, F.C.; Wang, P. Factors controlling longshore variations of beach changes induced by Tropical Storm Eta (2020) along Pinellas County beaches, west-central Florida. Shore Beach 2021, 89, 10. [Google Scholar] [CrossRef]
- Miller, J.K. Evaluation of Storm Severity Based on the Storm Erosion Index along the Atlantic Coasts of North Carolina and South Carolina. Technical Report Prepared for the Charleston District of the USACE; Stevens Insitute of Technology, Davidson Laboratory: Hoboken, NJ, USA, 2015; p. 14. [Google Scholar]
- Lemke, L.; Miller, J.K. Development of a storm erosion climatology for the New Jersey Coast, US. In Proceedings of the 36th International Conference on Coastal Engineering, Baltimore, MD, USA, 30 December 2018; p. 14. [Google Scholar]
- Lemke, L. Hybrid Approach for Evaluating the Erosion Potential of Coastal Storms; Stevens Institute of Technology: Hoboken, NJ, USA, 2021. [Google Scholar]
- Janssen, M.S. Risk-Based Assessment of Coastal Defense Projects: Quantifying Hazard, Vulnerability, and Parametric Design Applications; Stevens Institute of Technology: Hoboken, NJ, USA, 2022. [Google Scholar]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).