On Formulae for Wave Transmission at Submerged and Low-Crested Breakwaters

Abstract

Submerged and low-crested breakwaters are nearshore barriers with an underwater or slightly emergent crest, designed to reduce the energy of wave attacks and, consequently, to protect the coast from erosion and flooding. Their performance in reducing the wave energy can be evaluated by the value of the wave transmission coefficient, which thus requires accurate prediction. In the last few decades, several experimental investigations allowed the development of several formulae to predict this coefficient that agreed well within the given range of validity. In the present study, a comprehensive review of the existing formulae has been reported and the influence of input design variables has been highlighted. Moreover, an extensive set of experimental data has been collected and critically examined and re-analyzed to obtain a homogenous up-to-date database. Special attention has been addressed to the assessment of the reliability of each existing formula for and to evaluate its performance beyond the validity limits for which it was developed.

1. Introduction

Submerged and low-crested breakwaters are nearshore barriers with an underwater or slightly emergent crest, designed to reduce energy of wave attacks and, consequently, to protect the coast from erosion and flooding. Over time, submerged and low-crested breakwaters have become more popular compared to the conventional high-crested structures due to their own advantages such as an enhanced water circulation, reduced visual impact and an increased biodiversity [1]. When the incident waves reach the structure, a process of energy transformation occurs. One part of this energy is dissipated by wave breaking and by friction with the structure, while another part is transmitted above the crest and through its interior in the case of permeable submerged breakwaters and the remaining energy is reflected seaward. To design efficient submerged and low-crested breakwaters as coastal protection, an assessment of these hydraulic performances is necessary.

In the last few decades, experimental observations have been conducted at both a small and large scale, many of which led to the development of predictive formulae for the wave transmission coefficient at the rear side of the structure. A variety of submerged and low-crested breakwaters have been tested, such as rubble-mound structures with natural and concrete units (permeable and impermeable) as well as smooth structures (impermeable). All these structures with their own characteristics have been tested at different test facilities and under different wave conditions, behaving differently for wave transmission. Within the EU-projects CLASH [2] and DELOS [3], an extensive database was generated for submerged and low-crested structures and new empirical formulae were obtained focusing on wave transmission and wave reflection phenomena. Later, artificial neural networks (ANNs) [4] were adopted to predict the hydraulic performance in terms of wave transmission for a wide range of wave conditions and for a variety of structure geometries. Research for these types of breakwaters is still very active [5,6].

In the present study, an attempt is made to give a comprehensive state-of-the-art review of the research in the field of submerged and low crested structures. The objectives of this paper are as it follows:

• Define the most important hydraulic and structural parameters involved in wave transmission phenomenon.
• Describe the existing formulae and give insight to them by means of an in-depth description of all the involved parameters.
• Produce an up-to-date experimental wave transmission database, with the largest amount of data to date (4144).
• Develop a user-friendly MATLAB script for calculating wave transmission coefficient implementing the existing formulae that consider all the validity limits for which the formulae were derived.
• Use the up-to-date experimental database to assess the validity of the existing formulae for wave transmission prediction.

2. Materials and Methods

2.1. Governing Parameters

The principal wave characteristics and structural parameters involved in the transmission phenomenon are listed in Table 1 and reported in Figure 1, which shows a definition sketch of a typical breakwater. Other parameters which influence the hydraulic performance are the roughness of the armor layer, the permeability of the mound, the slope roughness, the type of armor units (natural or artificial stones) and the angle of wave attack [7]. The wave transmission coefficient, K_t, is equal to the ratio of transmitted and incident wave height K_t = H_t/H_i.

Table 1. Principal influencing wave characteristics and structural parameters involved in the wave transmission phenomenon.

Symbol	Unit	Definitions
Hi	[m]	Incident wave height, typically the spectral significant wave height Hmoi, at the toe of the structure
Ht	[m]	Transmitted wave height, typically the spectral significant wave height Hmot, at the toe of the structure
Tp	[s]	Spectral peak wave period
hs	[m]	Water depth at the toe of the structure
hc	[m]	Structure height
Rc	[m]	Crest freeboard Rc = hc − hs
Bc	[m]	Crest width of the structure
tan(α)	[-]	Seaward structure slope
sop	[-]	Wave steepness, $s_{op}=\frac{2\pi ·H_i}{g·T_p^2}$
ξop	[-]	Surf similarity parameter, ${\xi }_{op}=\frac{tan\alpha }{{\left(s_{op}\right)}^{0.5} }$
Dn50	[m]	Nominal diameter of the armor units
n	[-]	Porosity of the structure
β	[°]	Angle of wave attack

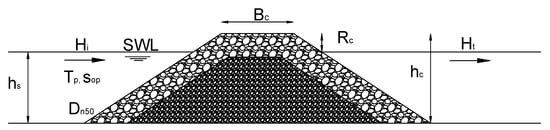
Figure 1. Definition sketch for wave transmission.

2.2. Existing Transmission Formulae

Based on a number of different datasets, several authors have proposed a series of wave transmission formulae. In the present section, the existing formulae with the relative description are reported. Subsequently, some of these formulae with their validity range have been implemented in a MATLAB script and applied to the largest database to date. In the following, the considered formulae are reported.

In 1990, Van der Meer [8] developed a simplified method prediction for emerged and submerged rubble-mound breakwaters which relates linearly the relative crest freeboard (R_c/H_i) to the wave transmission coefficient K_t, without taking into account the influence of crest width. The formula is in the first edition of The Rock Manual [9].

$$K_t=0.80\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}for-2.00<\frac{R_c}{H_i}<-1.13$$

(1)

$$K_t=0.46-0.3\frac{R_c}{H_{i }}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}for-1.13<\frac{R_c}{H_i}<1.2$$

(2)

$$K_t=0.1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}for 1.2<\frac{R_c}{H_i}<2$$

(3)

In 1987, Ahrens [10] improved the prediction method [8] including the analysis of laboratory test results for a reef-type emerged breakwater characterized by small waves (low values of H_i/D_n50) and relatively large freeboards (R_c/H_i > 1).

$$K_t=\frac{1}{1.0+X^{0.592}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{with} X=\frac{H_{s,i}}{L_p} \frac{A_t}{D_{n50}^2}\hspace{1em}\hspace{1em}for 1.2<\frac{R_c}{H_i}<2$$

(4)

where L_p is the local wavelength related to T_p and A_t is the total cross-sectional area of the structure.

In 1994, Van der Meer and Daemen [11] proposed a different relative crest freeboard which considers the permeability of the armor layer by relating the freeboard to the nominal diameter of the armor stones (R_c/D_n50). The formula has been developed assuming the linear dependency of K_t on the relative crest freeboard with the parameters a and b, where the latter is the intercept that represents the transmission coefficient for structure with no crest freeboard (R_c = 0). The formula considers the crest width and is valid for emerged and submerged rubble-mound breakwaters and for $1<H_i/D_{n50}<6$ and $0.01<s_{op}<0.05$.

$$K_t=a \frac{R_c}{D_{n50}}+b\hspace{1em}\hspace{1em}for 0.075\le K_t\le 0.75$$

(5)

where:

$$a=0.031 \frac{H_i}{D_{n50}}-0.024$$

(6)

$$b=-5.42 s_{op}+0.0323 \frac{H_i}{D_{n50}}-0.0017 {\left(\frac{B_c}{D_{n50}}\right)}^{1.84}+0.51$$

(7)

In 1996, D’Angremond et al. [12] performed the analysis for low-crested rubble-mound structures by neglecting data with high steepness (i.e., s_op > 0.06), breaking waves (i.e., H_i/h > 0.54), and structures highly submerged (i.e., R_c/H_i < −2.5), and highly emerged (R_c/H_i > 2.5). The formula reads:

$$K_t=-0.4 \frac{R_c}{H_i}+C {\left(\frac{B_c}{H_i}\right)}^{-0.31}\left(1-exp(-0.5{ \xi }_{op}\right))$$

(8)

where C is a coefficient equal to 0.80 for impermeable structures, and equal to 0.64 for permeable ones. The formula is valid for $0.075\le K_t\le 0.80$.

In 1998, Seabrook and Hall [13] proposed a formula for submerged rubble-mound breakwaters only, calibrated for a wide range of relative crest width values:

$$K_t=1-\left[exp\left(-0.65\frac{R_c}{H_i}-1.09\frac{H_i}{B_c}\right)+0.047\frac{B_c R_c}{L D_{n50}}-0.067\frac{R_c{H}_i }{B_c D_{n50}} \right]$$

(9)

The formula is valid within the following validity ranges:

$$5\le B_c/H_i\le 74.47, 0<\frac{B_c R_c}{L D_{n50}}<7.08 \mathrm{and} 0<\frac{H_i R_c}{B_c D_{n50}}<2.14$$

In 2002, Calabrese et al. [14] proposed a formula for low-crested and submerged rubble-mound breakwaters in the presence of broken waves, based on large-scale tests by resembling the formula of Van der Meer and Daemen [11] and replacing D_n50 with B_c.

$$K_t=a \frac{R_c}{B_{c }}+b$$

(10)

where:

$$a=\left(0.6957 \frac{H_i}{h_s}-0.7012\right) exp \left(0.2568 \frac{B_c}{H_i}\right)$$

(11)

$$b=\left[1-0.562exp \left(-0.0507{\xi }_{op}\right)\right]\left(-0.0854 \frac{B_c}{H_i}\right)$$

(12)

The validity ranges are: $-0.4 \le \frac{R_c}{B_c}\le 0.3$, $1\le \frac{B_c}{H_i}\le 8.13$, $0.31\le \frac{H_i}{h_s}\le 0.61$ and $3\le {\xi }_{op} \le 5.2$.

In 2003, Briganti et al. [15] re-analyzed the D’Angremond formula using the European DELOS project database [3] for rubble-mound low-crested structures because it was observed that (8) overestimates 𝐾_𝑡 when 𝐵_𝑐/𝐻_i is larger than 10. To improve the prediction of wave transmission when 𝐵_𝑐/𝐻_i > 10, the authors proposed the following relationship:

$$K_t=-0.35 \frac{R_c}{H_i}+0.51 {\left(\frac{B_c}{H_i}\right)}^{-0.65}\left(1-exp(-0.41{ \xi }_{op}\right))$$

(13)

For structures with 𝐵_𝑐/𝐻_i < 10, Equation (4) is still considered accurate. It is worth noting that the Formulae (8) and (13) give a discontinuity for 𝐵_𝑐/𝐻_i = 10.

In 2005, Van der Meer et al. [7] developed a formula for wave transmission over smooth structures using a database from the European DELOS project [3] and considered, for the first time, the influence of angle of wave attack $\beta$. The formula is based on measurements at smooth slopes, so it is not suitable for rubble mound breakwaters.

$$K_t=\left[-0.3 \frac{R_c}{H_i}+0.75 \left(1-exp(-0.5 {\xi }_{op}\right))\right]{\left(cos\beta \right)}^{\frac{2}{3}}$$

(14)

Its validity ranges are:

$$1\le s_{op}\le 3, 0°\le \beta \le 70°,1\le \frac{B_c}{H_i}\le 4 \mathrm{and} 0.075\le K_t\le 0.80$$

Given the discontinuity found by Briganti et al. [15] for 𝐵_𝑐/𝐻_i = 10, authors suggested for practical applications to use (8) for 𝐵_𝑐/𝐻_i = 10 and (14) for 𝐵_𝑐/𝐻_i = 12, and in the range 8 < 𝐵_𝑐/𝐻_i < 12 to perform an interpolation between both equations. Because a larger crest width determines a lower wave transmission, the upper limit of K_t is obtained considering the influence of the non-dimensional parameter 𝐵_𝑐/𝐻_i instead of a constant value; it follows that the limits are: $0.05\le K_t\le -0.006\frac{B}{H_i}+0.93$.

In 2007, Buccino et al. [16] proposed a set of several formulae combined, which are based on a schematization of the physical processes governing wave transmission. The method is different for submerged and emerged rubble-mound structures. The present study considers the Buccino et al. [16] formulae for submerged breakwaters solely, where the submergence is defined based on two threshold factors indicating high, S₁, and low, S₂, submergence, respectively.

$$K_t=\frac{1}{\begin{array}{c}1.18 {\left(\frac{H_i}{R_c}\right)}^{0.12}+0.33{\left(\frac{H_i}{R_c}\right)}^{1.5}\frac{B_c}{\sqrt{H_i{L}_o}} \\ \end{array}} \hspace{1em}for\frac{R_c}{H_i}\ge S_1$$

(15)

$$K_t={\left[\min \left(0.74;0.62{\xi }_{op}^{0.17}\right)-0.25\min (2.2; \frac{B}{\sqrt{H_i{L}_o}})\right]}^2 for \frac{R_c}{H_i}\le S_2$$

(16)

$$Eq.\left(16\right)\frac{R_c}{H_i}=S_2+\frac{Eq.\left(15\right)\frac{R_c}{H_i}=S_1-Eq.\left(16\right)\frac{R_c}{H_i}=S_2}{S_1-S_2} \left(\frac{R_c}{H_i}-S_2\right)for S_1>\frac{R_c}{H_i}>S_2$$

(17)

Equation (15) is valid for high relative submergence, where $R_c/H_i\ge S_1$, while Equation (16) is for breakwaters with the crest close to the mean water level, $R_c/H_i\le S_2$. In the range between these values, the wave transmission coefficient could be estimated by an interpolation of Equations (15) and (16), resulting in Equation (17). For practical application, the authors assumed $S_1$ = 1.2 and $S_2=0.5$.

In 2008, Goda and Ahrens [17] developed a relationship for the wave transmission coefficient for low-crested rubble-mound structures. It distinguishes, for the first time, the contribution of transmission due to overtopping over the structure from the contribution of infiltration through the structure.

$${\left(K_t\right)}_{over}=\max \left\{0;(1-exp\left[a \left(\frac{R_c}{H_i}-R_{c,0 }\right)\right]\right\}$$

(18)

$${\left(K_t\right)}_{thru}=\frac{1}{{\left[1+C {\left(\frac{H_i}{L}\right)}^{0.5}\right]}^2}$$

(19)

$${\left(K_t\right)}_{all}=\min \left\{1.0;\sqrt{{\left(K_t\right)}_{over}^2+K_h^2 {\left(K_t\right)}_{thru}^2}\right\} \mathrm{with} K_h=\min \left\{1.0;\frac{h_c}{h_s+H_i}\right\}$$

(20)

where:

$$R_{c,0 }=\{\begin{array}{cc}1.0\hfill & \hfill for D_{eff}=0\\ max \left\{0.5;min \left\{1.0;\frac{H_i}{D_{eff}}\right\}\right\} \hfill & \hfill for D_{eff}>0\end{array}$$

$$C=1.135 {\left(\frac{B_{eff}}{D_{eff}}\right)}^{0.65}$$

where B_eff and D_eff represent the relative crest width and the effective diameter of materials composing the low crested structure, respectively [17].

Later in 2013, [17,18] based on an extensive database for low-crested rubble-mound structures, larger than [17], Tomasicchio and D’Alessandro [18] re-calibrated Equations (18)–(20). They found that (K_t)_all from Goda and Ahrens is overestimated in the range K_t < 0.4 and they further calibrated the formula for different values of K_h, C, and R_c,0 as it follows:

$$K_h=\left\{0.8;\frac{h_c}{h_s+H_i}\right\}$$

(21)

$$R_{c,0 }=\{\begin{array}{cc}1.0\hfill & \hfill for D_{eff}=0\\ max \left\{0.6;min \left\{0.8;\frac{H_i}{D_{eff}}\right\}\right\} \hfill & \hfill for D_{eff}>0\end{array}$$

$$C=3.450 {\left(\frac{B_{eff}}{D_{eff}}\right)}^{0.65}$$

In 2014, Zhang et al. [19] proposed two equations to determine the wave transmission coefficient for emerged porous rubble mound breakwaters and for submerged breakwater by using the shape function. The formulae are developed based on the laboratory data from [7]; Equations (22) and (23) are for emerged and submerged breakwaters, respectively

$$\begin{array}{l}{K}_t={\beta }_1\frac{\left(1-{\mathsf{\alpha }}_1\frac{R_c}{H_i}\right)}{\left(1+{\mathsf{\alpha }}_1\frac{R_c}{H_i}\right)} \exp \left(-0.18 \frac{B_c}{H_i}\right) \left[1-\exp (-0.5{\xi }_{op}\right)]\\ \mathrm{with} {\mathsf{\alpha }}_1=1.0 \mathrm{and} {\mathsf{\beta }}_1=0.90\end{array}$$

(22)

$$\begin{array}{l}{K}_t={\beta }_2 \frac{\left(1-{\mathsf{\alpha }}_2\frac{R_c}{H_i}\right)}{\left(1+{\mathsf{\alpha }}_2\frac{R_c}{H_i}\right)} \exp \left(-0.18 \frac{B_c}{H_i}\right) \\ \mathrm{with} {\alpha }_1=0.23 \mathrm{and} {\beta }_1=0.50\end{array}$$

(23)

In 2015, Sindhu et al. [20] established a semi-empirical approach to calculate K_t for submerged reef-type breakwaters where the value of the crest freeboard R_c must be negative, and no range of validity has been mentioned.

$$K_t=\left(0.02 \frac{-R_c}{B_c}+0.035 \frac{h_c}{h_s}\right) \left(\frac{h_s}{D_{n50}}+\frac{0.45}{\sqrt{s_{op}}}\right)$$

(24)

In 2022, Kurdistani et al. [21] developed a method for prediction of the wave transmission coefficient valid for submerged structures solely and including the pore pressure distribution inside the mound. The formula includes, for the first time, the influence of the porosity of the structure.

$$K_t=0.576\ln \left(0.428{\left(1+z\right)}^{0.042}{\left(1+\frac{R_c}{H_i}\right)}^{0.75}{\left(\frac{B_{eff}}{D_{n50}}\right)}^{0.125}{L}^{*0.39}{\omega }^{0.413}{\mathit{\phi }}^{-0.18}\right)+0.923$$

(25)

where z is the seaward slope, L* = L/B_eff, ω = (1/2π) tanh(2π h_s/L), φ = (n 0.5h_s x)/(B_cH_i), n is the porosity of the structure and x is the horizontal coordinate inside the breakwater core [22].

Table 2 shows a list of the considered formulae, including the type of structure for which they have been calibrated and the involved dimensional parameters. It is intended that although the formulae have been calibrated for a specific type of structure, in the present study, unless expressly restricted by the validity limits, the formulae have been also applied for different structure geometries and wave conditions.

Table 2. Features of existing formulae including the type of the structures for which they have been calibrated and the considered parameters.

Formula	Structure Type					Input Parameters
	E	S	RM	RT	Sm	Hi	Tp	Rc	Bc	Dn50	hs	β	n
Van der Meer (1990)
Van der Meer and Deamen (1994)
Ahrens (1987)
d’Angremond et al. (1996)
Seabrook and Hall (1998)
Calabrese et al. (2002)
Briganti et al. (2003)
Van der Meer et al. (2005)
Buccino et al. (2007)
Goda and Ahrens (2008)
Tomasicchio and D’Alessandro (2013)
Zhang et al. (2014)
Sindhu et al. (2015)
Kurdistani et al. (2022)

Note: E = Emerged; S = Submerged; RM = Rubble mound; RT = Reef-Type structures; SI = Smooth Impermeable structures.

2.3. Existing Data Sets

Numerous experimental investigations have been performed for various low-crested and submerged structure configurations and materials by several investigators in the last few decades. An attempt to group and give a comprehensive description of these data is given in the present section. Among the first reported physical experiments on the wave transmission behind submerged breakwaters, Seelig [23] focused on waves with large wave steepness, Allsop [24] limited his studies to structures with a relatively high crest level, Daemrich and Kale [25] used Tetrapods as armor units, Powell and Allsop [26] carried out their tests at extremely shallow water depths and Ahrens [10] studied reef type breakwaters behavior. Investigations at Delft Hydraulics by Van der Meer [27] and Daemen [28] have been conducted for Tetrapods and Accropodes armor layers. Supplementary data sets, mostly on specific breakwater models, have been added by de Jong [29] to enlarge the database (in the following, these data sets will be indicated with the Delft Hydraulics report number M2090, H524, H2061, H1872, H2014, H1974). Taveira-Pinto [30] carried out an experimental campaign on smooth low-crested breakwaters, under random waves. Seabrook and Hall [13] conducted an extensive experimental study on rock-armored, nonemergent structures only and focused on the importance of the relative submergence, incident wave height and structure crest width as design variables. Later, within the European project DELOS, the following experimental investigations were performed: at the University of Cantabria [31], experimental tests included wide-crested breakwaters exposed to long waves; at the Polytechnic University of Catalonia [32], experiments on barriers with the crest near the still-water level have been considered. The armor layer of the breakwater models adopted for both previous tests groups was made of rock. Daemrich, Mai and Ohle [33] measured wave transmission at submerged structures with special interest beyond the upper limit of the formula of d’Angremond et al. [12]. Hirose et al. [34] proposed and tested the reef-type concrete armor units, Aquareef, designed for submerged structures. Wang et al. [35] studied the three-dimensional wave transmission at rubble and smooth structures subjected to direct long crested wave attack. Melito and Melby [36] conducted model tests to investigate the hydraulic response of structures armored with Coreloc, for submerged and emerged conditions with the relative freeboard varying in a wide range. The GWK experiments [14] have been conducted to study the behavior of rock-armored rubble mound breakwaters, with different crown widths at intermediate/shallow waters exposed to breaking/broken waves. Experimental tests have been carried out by Ruol et al. [37] to estimate the water piling up behind low-crested structures. Kimura et al. [38] investigated the behavior for wide submerged breakwater with armor blocks. The influence of the berm width of emerged and submerged structures has been investigated by Mori and Cappietti [39]. Amongst the more recent experimental investigations, Koraim et al. [40] and Lokesha et al. [41] investigated experimentally the efficiency of smooth and stepped submerged breakwaters; Teh et al. [42] tested a trapezoidal breakwater whose porosity is enabled by circular pipes. Recently, Kubowicz-Grajewska et al. [43] and Koley et al. [44] studied the wave interaction with multilayered trapezoidal porous breakwaters; Kim and Lee [45] studied the role of the superstructures on rubble mound structures in reducing the wave overtopping and improving the stability; Metallinos et al. [46] focused on permeable structures with steep slopes; Liu et al. [47] compared experimental data to a CIP-based model to accurately predict the wave deformation and the distribution of the velocity and the dynamic pressure over a submerged bar; Mahmoudof and Hajivalie [48] focused on the hydraulic response of smooth impermeable submerged breakwaters with a rectangular cross section.

The total amount of data collected and reported in the present study is extended in respect to the previous studies, leading to a total number of 4144 tests. All datasets are summarized in Table 3 in terms of wave conditions and structural parameters together with the dimensionless parameters that relate dimensional parameters and can identify the relevant physical processes. The type of the investigated breakwaters is also defined to give insight to the diversity of the tested structures. Of these tests, 67.4% of the total amount concerns permeable mound breakwaters, 28.0% concerns impermeable breakwater structures and only 4.6% of tests refer to reef-type breakwaters. It is also noteworthy that a number of the datasets, specifically 21%, consider only emerged structures, 34% of the datasets consider only submerged structures, and the majority (43%) refer to both emerged and submerged structures, thus including low-crested structures.

Table 3. Characteristics of the existing Data Sets.

Dataset	Type of Structure	No	Hi (m)	Tp (s)	sop (-)	Rc (m)	Bc (m)	Dn50 (m)	$\frac{{\mathit{H}}_{\mathit{m}0}}{{\mathit{D}}_{\mathit{n}50}}$	$\frac{{\mathit{R}}_{\mathit{c}}}{{\mathit{H}}_{\mathit{m}0}}$	$\frac{\mathit{B}}{{\mathit{H}}_{\mathit{m}0}}$
Seelig (1980)	SI (1)–E (2)	13	0.13∼0.17	1.33∼3.32	0.01∼0.07	0.00∼0.15	0.30	/	/	0.00∼1.33	1.74∼2.65
Seelig (1980)	RMn, RMa–E,S	69	0.08∼0.18	0.91∼3.46	0.01∼0.08	−0.42∼0.21	0.30∼0.40	0.11∼0.16	0.64∼1.60	−4.42∼1.74	1.76∼5.00
Allsop (1983)	RMn–E	21	0.05∼0.16	1.02∼3.17	0.01∼0.04	0.08∼0.16	0.16	0.04∼0.05	0.96∼4.03	0.50∼3.14	0.99∼3.27
Daemrich & Kahle (1985)	SI–S	147	0.02∼0.24	1.23∼3.27	0.01∼0.04	−0.20∼0.00	0.20	/	/	−8.11∼0.00	0.82∼8.46
Daemrich & Kahle (1985)	Rma–S	196	0.02∼0.22	1.23∼3.27	0.01∼0.04	−0.20∼0.00	0.20∼1.00	0.08	0.28∼2.88	−8.80∼0.00	0.89∼45.72
Powell & Allsop (1985)	RMn–S	42	0.09∼0.22	1.39∼2.30	0.03∼0.04	−0.28∼0.08	0.07∼0.32	0.08∼0.09	1.16∼2.90	−2.43∼0.68	0.38∼3.61
DH-M2090 (1985)	SI–E	7	0.07∼0.21	1.30∼2.28	0.02∼0.04	0.06∼0.21	0.43	/	/	0.30∼1.66	2.02∼6.16
DH-M2090 (1985)	RMn–E	31	0.05∼0.20	1.07∼2.26	0.02∼0.04	0.05∼0.20	0.15	0.04	1.03∼4.60	0.36∼3.39	0.75∼3.33
Ahrens (1987)	RTn–E,S	201	0.01∼0.18	1.33∼3.64	0.001∼0.04	−0.09∼0.11	0.16∼0.36	0.02∼0.03	0.37∼8.47	−2.58∼5.91	1.35∼25.90
Van der Meer (1988)	RTn–E,S	31	0.08∼0.23	1.94∼2.60	0.01∼0.05	−0.10∼0.13	0.30	0.04	2.08∼6.42	−0.89∼1.68	1.30∼4.00
DH-H524 (1990)	RTn–E	14	0.06∼0.14	1.83∼2.56	0.01∼0.03	0.12∼0.20	0.08∼0.17	0.02∼0.03	2.16∼6.53	0.90∼2.31	0.66∼2.99
Daemen (1991)	RTn–E,S	53	0.03∼0.15	0.98∼2.88	0.01∼0.05	−0.06∼0.20	0.34	0.04∼0.06	0.80∼3.70	−0.65∼4.03	2.30∼10.63
DH-H1872 (1994)	Rma–E	39	0.07∼0.17	1.02∼2.22	0.02∼0.05	0.11∼0.19	0.14	0.04∼0.05	1.38∼3.71	0.66∼1.82	0.83∼2.14
DH-H2061 (1994)	RMn–E,S	32	0.09∼0.25	1.24∼2.89	0.02∼0.04	−0.05∼0.20	0.20	0.04∼0.05	2.54∼6.23	−0.43∼2.25	0.82∼2.25
DH-H2014 (1994)	SI–E,S	11	0.14∼0.21	1.80∼2.16	0.02∼0.05	−0.16∼0.08	0.20	/	/	−1.00∼0.41	0.97∼1.39
DH-H1974 (1994)	Rma–E	10	0.09∼0.19	1.57∼2.45	0.02∼0.03	0.10–0.15	0.35	0.05	1.73∼3.62	0.55∼1.65	1.90∼3.98
TU Delft (1997)	Rma–E	137	0.05∼0.20	1.03∼2.50	0.01∼0.05	0.00∼0.34	0.11∼0.40	0.03∼0.05	1.24∼5.94	0.00∼5.22	0.56∼6.45
Taviera Pinto (1997)	SI–S	552	0.02∼0.10	0.80∼1.50	0.01∼0.12	−0.04∼0.00	0.05∼0.10	/	/	−1.82∼0.00	0.51∼4.55
Seebrook & Hall (1998)	RMn–S	633	0.05∼0.19	1.16∼2.13	0.01∼0.08	−0.20∼0.00	0.30∼3.50	0.06	0.78∼3.20	−3.92∼0.00	1.59∼74.47
Zannutigh (2000)	RMn–E,S	56	0.02∼0.15	0.74∼1.97	0.02∼0.05	−0.07∼0.03	0.20∼0.60	0.05	0.43∼3.22	−1.58∼1.53	1.44∼30.70
Van der Meer (2000)	SI–E,S	28	0.04∼0.15	1.03∼1.75	0.01∼0.06	−0.01∼0.13	0.13∼1.33	/	/	−0.10∼1.10	0.99∼33.78
UCA (2001)	RMn–E,S	53	0.03∼0.09	1.60∼3.20	0.003∼0.03	−0.05∼0.05	0.25∼1.00	0.04	0.84∼2.40	−1.50∼1.53	2.67∼30.66
Daemrich, Mai, Ohle (2001)	RMn–E,S	100	0.02∼0.15	1.00∼1.75	0.01∼0.07	−0.20∼0.05	0.20	0.04	0.48∼3.51	−9.84∼0.78	1.36∼9.95
Kimura (2002)	Rma–S	90	0.10∼0.15	1.62∼2.84	0.01∼0.04	−0.02	0.24∼1.14	0.09	1.11∼1.66	−0.22∼−0.15	1.57∼11.38
Aquareef (2002)	Rta–S	1063	0.03∼0.14	1.07∼2.39	0.004–0.08	−0.11∼−0.01	0.12–2.35	0.04	0.65–3.55	−4.09∼−0.05	0.93∼90.48
UPC (2002)	RMn–E,S	20	0.28∼0.46	2.56∼3.41	0.02∼0.04	−0.11∼0.15	1.22∼1.83	0.11	2.59∼4.27	−0.37∼0.38	2.64∼6.53
Wang (2002)	RMn–E,S	84	0.06∼0.17	1.02∼2.33	0.02∼0.06	−0.05∼0.05	0.10	0.05	1.28∼3.51	−0.66∼0.83	0.60∼1.67
Wang (2002)	SI–E,S	84	0.06∼0.20	1.02∼2.33	0.02∼0.06	−0.05∼0.05	0.20	/	/	−0.59∼0.83	1.00∼3.33
Melito & Melby (2002)	Rma–E,S	122	0.03∼0.23	1.07∼3.36	0.01∼0.06	−0.30∼0.30	0.243	0.05	0.69∼4.65	−8.25∼8.87	1.06∼7.19
GWK (2002)	RMn–E,S	45	0.45∼0.96	3.50∼6.50	0.01∼0.03	−0.40∼0.30	1.00∼4.00	0.23	2.02∼4.26	−0.76∼0.66	1.06∼8.13
DH-H4087 (2002)	RMn–S	20	0.09∼0.12	1.61∼1.80	0.026∼0.029	−0.14∼−0.05	1.00∼2.50	0.02∼0.03	3.50∼4.82	−1.21∼−0.37	8.66∼22.86
DH−4171 (2003)	SI–E,S	9	0.68∼1.36	3.38∼4.46	0.04∼0.06	−0.21∼0.50	1.75	/	/	−0.18∼0.73	1.29∼2.57
Ruol and Faedo (2004)	RMn–E	11	0.03∼0.15	0.97∼2.44	0.02∼0.05	0.05	0.20	0.05	0.46∼2.70	0.34∼2.00	1.37∼8.00
Mori and Cappietti (2006)	RMn–E,S	57	0.07∼0.10	1.50∼1.80	0.03∼0.04	−0.03∼0.03	0.01∼0.21	0.03	2.31∼3.38	−0.45∼0.45	0.10∼3.13
Koraim (2014)	SI–S	∼70	0.03∼0.10	0.80∼1.80	0.01∼0.08	−0.35∼−0.05	0.30∼0.90	/	/	−11.67∼−0.50	3.00∼30.00
The (2014)	Rma–S	nd	0.03∼0.13	0.60∼2.00	0.001∼0.04	−0.15∼0.00	0.15	/	/	−5.77∼0.00	1.19∼5.77
Lokesha (2015)	SI, Sist–S	80	0.03∼0.09	0.55∼0.95	0.003∼0.03	−0.05∼0.00	0.10∼0.30	/	/	−1.67∼0.00	1.11∼10.00
Grajewska (2017)	RMn–S	48	0.06∼0.11	1.60∼2.14	0.01∼0.03	−0.10∼−0.05	0.30	0.09	0.69∼1.27	−1.59∼−0.46	2.62∼4.81
Kim (2018)	Rma–E	nd	0.05∼0.15	1.13∼1.60	0.02∼0.04	0.05∼0.20	0.3∼0.4	0.34	0.15∼0.44	0.33∼4.00	2.00∼8.00
Metallinos (2019)	RMn–S	8	0.05∼0.08	1.25∼2.00	0.001∼0.005	−0.05	0.50	0.05	0.90∼1.60	−1.11∼−0.63	6.25∼11.11
Liu (2019)	SI–S	18	0.05∼0.10	1.47∼2.94	0.001∼0.005	−0.24∼−0.14	1.50	/	/	−4.80∼−1.40	15.00∼30.00
Koley (2020)	RMn–E,S	30	0.05∼0.15	0.95∼5.43	0.004∼0.11	−0.10∼0.10	0.20	nd	nd	−2.00∼2.00	1.33∼4.00
Mohmoudof (2021)	SI–S	15	0.04∼0.08	1.10∼1.90	0.01∼0.03	−0.15∼−0.05	0.90	/	/	−3.44∼−0.65	11.63∼20.64
	TOT	4144	0.01∼1.36	0.55∼6.50	0.001∼0.12	−0.42∼0.34	0.01∼4.00	0.02∼0.34	0.15∼8.47	−11.67∼8.87	0.10∼90.48

Note: ⁽¹⁾ RMn = Rubble Mound with natural stones; Rma = Rubble Mound with artificial stones; SI = Smooth Impermeable structures; Sist = Smooth Impermeable steeped structures; RTn = natural Reef-Type structures; Rta = articial Reef-Type structures. ⁽²⁾ E = Emerged; S = Submerged.

3. Analysis

In the present study, all formulae for calculating the transmission coefficient have been applied to the entire collected available database (4144), respecting the validity ranges for which each formula was developed.

Figure 2 shows the comparison between the observed (K_t,obs) and calculated (K_t,calc) wave transmission coefficients. N_t represents the total amount of tests that fall within the validity ranges of each formula.

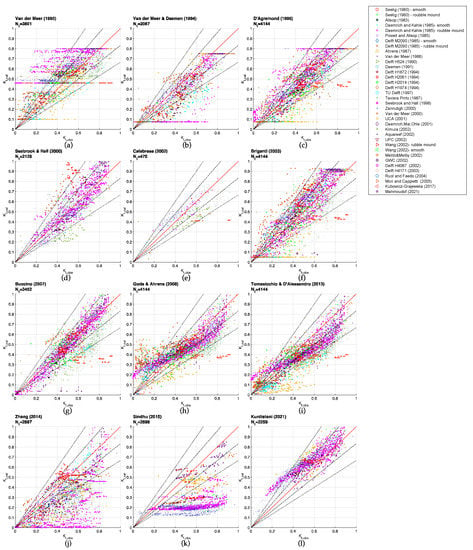
Figure 2. Comparison between Kt calculated and observed against the full database for (a) Van der Meer (1990) (b) Van der Meer and Daemen (1991) (c) D’Agremond et al. (1996) (d) Seabrook & Hall (1998) (e) Calabrese et al. (2002) (f) Briganti et al. (2003) (g) Buccino et al. (2007) (h) Goda & Ahrens (2008) (i) Tomasicchio & D’Alessandro (2013) (j) Zhang et al. (2014) (k) Sindhu et al. (2015) (l) Kurdistani et al. (2022).

The diagonal red line represents the condition of perfect agreement where K_{t_obs} = K_{t_calc}. The dotted lines represent the confidence levels of ±20% and ±50%, respectively. Table 4 and Table 5 show the amount and the percentage of the calculated data that fall in the interval of ±20% and ±50% in respect to K_t,obs. Table 6 reports the root mean square error (RMSE) for each formula and single datasets. The gradation of colors, from green to orange, is associated with the value of RMSE ranging from 0.015 (best agreement, in correspondence of green) to 0.494 (worst agreement, in correspondence of orange).

Table 4. Number and percentage of calculated data K_t,cal in the interval ±20% respect to K_t,obs.

	Total Data	Van der Meer (1990)	Van der Meer & Daemen (1994)	Seabrook & Hall (1998)	Calabrese (2002)	Buccino (2007)	D’Angremond (1996)	Briganti (2003)	Goda & Ahrens (2008)	Tomasicchio & D’Alessandro (2013)	Zhang (2014)	Sindhu (2015)	Kurdistani (2022)
Seelig (1980)-smooth	13	2	0	0	0	3	4	4	5	5	0	0	0
Seelig (1980)-rubble mound	69	26	25	28	2	30	51	27	32	44	32	0	24
Allsop (1983)	21	8	3	0	0	0	3	11	3	5	0	0	0
Daemrich and Kahle (1985)-smooth	147	73	0	0	0	84	137	111	73	73	0	0	0
Daemrich and Kahle (1985)- rubble mound	196	114	110	79	4	123	147	109	157	109	59	0	96
Powell and Allsop (1985)	42	38	25	20	5	35	37	24	37	26	25	0	29
Delft M2090 (1985)-smooth	7	1	0	0	0	0	0	1	4	4	0	0	0
Delft M2090 (1985)-rubble mound	31	7	8	0	0	0	16	2	0	12	2	0	0
Ahrens (1987)	201	124	59	0	0	75	79	82	107	52	14	38	46
Van der Meer (1988)	31	23	20	9	0	13	21	26	17	14	12	0	9
Delft H524 (1990)	14	0	4	0	0	0	7	4	0	2	0	0	0
Daemen (1991)	53	17	26	10	3	14	35	14	19	21	10	8	11
Delft H1872 (1994)	39	19	10	0	0	0	21	9	1	8	0	0	0
Delft H2061 (1994)	32	24	12	3	3	24	23	2	24	10	13	10	6
Delft H2014 (1994)	11	5	0	0	0	7	7	7	10	10	0	0	0
Delft H1974 (1994)	10	0	2	0	0	0	4	2	0	2	3	0	0
TU Delft (1997)	137	30	1	0	0	0	50	56	29	11	37	0	0
Taveira Pinto (1987)	552	224	0	0	13	217	426	399	87	87	0	0	0
Seebrook and Hall (1998)	633	147	107	444	21	538	333	407	376	304	67	34	299
Zannutigh (2000)	56	22	8	12	0	17	28	27	24	20	11	0	9
Van der Meer (2000)	28	5	0	0	0	0	3	2	10	10	0	0	0
UCA (2001)	53	20	21	16	1	25	25	22	29	26	8	3	10
Daemrich,Mai,Ohle (2001)	100	43	65	52	0	91	93	36	82	66	45	65	68
Kimura (2002)	90	58	7	9	35	9	43	78	40	7	0	0	0
Aquareef (2002)	1063	430	444	782	129	902	751	405	830	800	240	53	389
UPC (2002)	20	5	5	5	0	10	14	16	12	5	3	2	5
Wang (2002)-rubble mound	84	76	21	3	0	61	65	26	68	48	55	0	19
Wang (2002)-smooth	84	44	0	0	0	38	44	44	50	50	0	0	0
Melito&Melby (2002)	122	42	35	11	0	21	59	41	16	33	10	1	16
Calabrese and Buccino (2002)	45	23	10	14	0	25	34	44	35	21	5	0	12
Delft H4087 (2002)	20	1	0	3	0	9	20	6	15	9	0	4	5
Delft H4171 (2003)	9	0	0	0	0	0	0	0	3	3	0	0	0
Ruol and Faedo (2004)	11	7	0	0	0	0	1	9	11	0	0	0	0
Mori and Cappietti (2005)	57	16	19	0	0	9	0	0	15	22	32	5	0
Kubowicz-Grajewska (2017)	48	4	0	0	0	0	1	1	0	0	0	0	0
Mahmoudof (2021)	15	5	0	0	0	0	2	0	2	2	0	0	0
Number of data	4144	3801	2087	2129	470	3452	4144	4144	4144	4144	2887	2698	2259
N° of calculated data Kt,cal in the interval ±20% Kt,obs		1683	1047	1500	216	2380	2584	2054	2223	1921	683	223	1053
% of calculated data Kt,cal in the interval ±20% Kt,obs		44%	50%	70%	46%	69%	62%	50%	54%	46%	24%	8%	47%

Table 5. Number and percentage of calculated data K_t,cal in the interval ±50% respect to K_t,obs.

	Total Data	Van der Meer (1990)	Van der Meer & Daemen (1994)	Seabrook & Hall (1998)	Calabrese (2002)	Buccino (2007)	D’Agremond (1996)	Briganti (2003)	Goda & Ahrens (2008)	Tomasicchio & D’Alessandro (2013)	Zhang (2014)	Sindhu (2015)	Kurdistani (2022)
Seelig (1980)-smooth	13	7	0	0	0	6	8	10	6	6	0	0	0
Seelig (1980)-rubble mound	69	43	33	38	2	41	65	52	43	64	50	8	40
Allsop (1983)	21	16	12	0	0	0	16	16	5	14	0	0	0
Daemrich and Kahle (1985)-smooth	147	123	0	0	0	147	147	147	147	147	0	0	0
Daemrich and Kahle (1985)- rubble mound	196	149	153	128	5	187	192	183	187	191	112	67	132
Powell and Allsop (1985)	42	39	35	26	5	36	41	42	42	41	37	1	33
Delft M2090 (1985)-smooth	7	1	0	0	0	0	1	3	4	4	0	0	0
Delft M2090 (1985)-rubble mound	31	17	24	0	0	0	24	14	0	24	10	0	0
Ahrens (1987)	201	165	98	0	0	91	131	150	183	129	111	91	91
Van der Meer (1988)	31	24	27	11	0	13	29	30	22	31	22	11	11
Delft H524 (1990)	14	1	7	0	0	0	8	11	0	7	0	0	0
Daemen (1991)	53	34	48	15	4	15	50	36	35	43	33	15	15
Delft H1872 (1994)	39	34	22	0	0	0	37	26	7	25	2	0	0
Delft H2061 (1994)	32	24	13	9	3	24	24	24	24	25	25	16	16
Delft H2014 (1994)	11	11	0	0	0	10	11	11	11	11	0	0	0
Delft H1974 (1994)	10	0	9	0	3	0	10	3	1	8	4	0	0
TU Delft (1997)	137	98	66	0	0	34	105	81	86	93	53	0	0
Taveira Pinto (1987)	552	552	0	0	42	537	536	536	549	549	0	0	0
Seebrook and Hall (1998)	633	255	117	503	23	586	488	562	532	547	226	93	446
Zannutigh (2000)	56	38	22	16	0	29	47	43	52	48	33	0	16
Van der Meer (2000)	28	14	0	0	0	0	16	14	15	15	0	0	0
UCA (2001)	53	27	25	18	3	32	35	41	35	31	24	17	18
Daemrich, Mai, Ohle (2001)	100	66	68	66	0	92	98	94	92	98	82	71	71
Kimura (2002)	90	86	69	64	71	69	87	82	87	87	31	0	0
Aquareef (2002)	1063	773	593	1019	192	1037	971	954	1008	1028	693	277	853
UPC (2002)	20	15	14	10	0	10	20	19	15	20	17	10	10
Wang (2002)-rubble mound	84	84	44	10	0	62	80	77	80	80	78	15	26
Wang (2002)-smooth	84	73	0	0	0	59	72	72	75	75	0	0	0
Melito & Melby (2002)	122	63	83	11	5	31	98	89	38	79	36	20	22
Calabrese and Buccino (2002)	45	43	25	25	0	35	44	45	43	44	39	14	25
Delft H4087 (2002)	20	10	0	20	0	20	20	20	20	20	0	14	15
Delft H4171 (2003)	9	1	0	0	0	1	2	2	6	6	0	0	0
Ruol and Faedo (2004)	11	10	2	0	0	0	9	9	11	9	9	0	0
Mori and Cappietti (2005)	57	29	39	0	0	23	26	9	28	41	44	33	0
Kubowicz-Grajewska (2017)	48	46	0	0	8	19	45	45	24	24	0	0	0
Mahmoudof (2021)	15	10	0	0	0	0	12	0	13	13	0	0	0
Number of data	4144	3801	2087	2129	470	3452	4144	4144	4144	4144	2887	2698	2259
N° of calculated data Kt,cal in the interval ±50% Kt,obs		2981	1648	1989	366	3246	3605	3552	3526	3677	1771	773	1840
% of calculated data Kt,cal in the interval ±50% Kt,obs		78%	79%	93%	78%	94%	87%	86%	85%	89%	61%	29%	81%

Table 6. RMSE of each formula for single dataset and mean value for each formula.

	Van der Meer (1990)	Van der Meer & Daemen (1994)	Seabrook & Hall (1998)	Calabrese (2002)	Buccino (2007)	D’Agremond (1996)	Briganti (2003)	Goda & Ahrens (2008)	Tomasicchio & D’Alessandro (2013)	Zhang (2014)	Sindhu (2015)	Kurdistani (2022)
Seelig (1980)-smooth	0.097	/	/	/	0.064	0.117	0.116	0.069	0.069	/	/	/
Seelig (1980)-rubble mound	0.110	0.091	0.120	0.015	0.122	0.086	0.155	0.179	0.111	0.144	0.468	0.171
Allsop (1983)	0.042	0.080	/	/	/	0.073	0.042	0.168	0.080	0.154	/	/
Daemrich and Kahle (1985)-smooth	0.157	/	/	/	0.150	0.076	0.118	0.171	0.171	/	/	/
Daemrich and Kahle (1985)-rubble mound	0.132	0.098	0.134	0.086	0.111	0.093	0.130	0.092	0.123	0.262	0.338	0.113
Powell and Allsop (1985)	0.047	0.122	0.115	0.029	0.052	0.075	0.134	0.082	0.124	0.129	0.494	0.096
Delft M2090 (1985)-smooth	0.094	/	/	/	/	0.112	0.110	0.022	0.022	/	/	/
Delft M2090 (1985)-rubble mound	0.068	0.054	/	/	/	0.039	0.087	0.202	0.048	0.085	/	/
Ahrens (1987)	0.115	0.126	/	/	0.093	0.183	0.179	0.120	0.199	0.237	0.161	0.142
Van der Meer (1988)	0.055	0.058	0.119	/	0.051	0.063	0.035	0.114	0.114	0.166	0.278	0.082
Delft H524 (1990)	0.079	0.027	/	/	/	0.024	0.035	0.226	0.035	0.064	/	/
Daemen (1991)	0.098	0.056	0.097	0.050	0.053	0.041	0.093	0.090	0.081	0.139	0.137	0.078
Delft H1872 (1994)	0.035	0.102	/	/	/	0.050	0.084	0.187	0.077	0.158	/	/
Delft H2061 (1994)	0.043	0.070	0.255	0.044	0.029	0.057	0.159	0.132	0.100	0.098	0.088	0.128
Delft H2014 (1994)	0.090	/	/	/	0.077	0.068	0.073	0.065	0.065	/	/	/
Delft H1974 (1994)	0.102	0.050	/	0.110	/	0.028	0.090	0.103	0.048	0.059	/	/
TU Delft (1997)	0.130	0.190	/	/	0.206	0.091	0.096	0.136	0.168	0.123	/	/
Taviera Pinto (1987)	0.177	/	/	0.186	0.197	0.133	0.142	0.233	0.233	/	/	/
Seebrook and Hall (1998)	0.279	0.262	0.076	0.043	0.040	0.132	0.084	0.114	0.122	0.368	0.399	0.116
Zannutigh (2000)	0.146	0.140	0.115	/	0.123	0.105	0.121	0.095	0.129	0.216	0.406	0.119
Van der Meer (2000)	0.155	/	/	/	0.214	0.104	0.107	0.098	0.098	/	/	/
UCA (2001)	0.194	0.148	0.070	0.052	0.055	0.098	0.086	0.101	0.087	0.243	0.226	0.109
Daemrich, Mai, Ohle (2001)	0.110	0.050	0.102	/	0.073	0.051	0.122	0.098	0.109	0.134	0.091	0.074
Kimura (2002)	0.123	0.204	0.220	0.130	0.205	0.131	0.104	0.145	0.194	0.302	/	/
Aquareef (2002)	0.174	0.132	0.093	0.076	0.061	0.097	0.130	0.075	0.083	0.248	0.349	0.138
UPC (2002)	0.120	0.138	0.091	/	0.051	0.061	0.048	0.095	0.082	0.149	0.133	0.096
Wang (2002)-rubble mound	0.037	0.108	0.323	/	0.041	0.064	0.135	0.066	0.095	0.090	0.291	0.095
Wang (2002)-smooth	0.116	/	/	/	0.106	0.120	0.121	0.096	0.096	/	/	/
Melito & Melby (2002)	0.111	0.116	0.083	0.198	0.178	0.100	0.082	0.281	0.132	0.205	0.321	0.155
GWK (2002)	0.104	0.188	0.098	/	0.091	0.075	0.042	0.081	0.112	0.171	0.274	0.104
Delft H4087 (2002)	0.248	0.390	0.108	/	0.096	0.039	0.108	0.085	0.112	0.401	0.221	0.145
Delft H4171 (2003)	0.269	/	/	/	0.217	0.223	0.223	0.130	0.130	/	/	/
Ruol and Faedo (2004)	0.045	0.159	/	/	/	0.101	0.068	0.026	0.096	0.107	/	/
Mori and Cappietti (2005)	0.179	0.110	0.291	/	0.153	0.176	0.293	0.187	0.107	0.078	0.162	/
Kubowicz-Grajewska (2017)	0.304	/	/	0.378	0.404	0.319	0.319	0.374	0.374	/	/	/
Mahmoudof (2021)	0.154	/	/	/	0.415	0.183	0.379	0.203	0.203	/	/	/
RMSE	0.126	0.126	0.139	0.107	0.129	0.100	0.124	0.132	0.117	0.174	0.269	0.115

Van der Meer’s formula [8] (Figure 2a) considers N_t = 3801 and shows an overestimation of the wave transmission coefficient, since the formula does not consider the crest width, the effect of porosity and material size. It is noted that there is a noticeable concentration of data at K_t,calc = 0.8 and K_t,calc = 0.1, respectively, due to the upper and lower limits imposed by the formula. At K_t,calc = 0.46 there is also a noticeable a concentration of data which refers to the structure with no freeboard (R_c = 0).

The prediction formula of Van der Meer and Daemen [11] (Figure 2b) considers N_t = 2087, mainly since nominal diameter D_n50 is used to obtain the dimensionless parameter R_c/D_n50 in the calculation and, consequently, structures where the value of D_n50 is not known are not taken into account. (e.g., smooth structures). In addition, the transmission coefficient is underestimated for tests characterized by a high value of crest width B_c, which is not considered in the formula. Seabrook and Hall (Figure 2d) [13] counts N_t = 2129, as the formula is only valid for submerged barriers, but it is worth noting that the formula has the highest percentage of data that fall in both confidence levels of ±20% and ±50%, reaching 70% and 93%, respectively. The accuracy of the transmission coefficient prediction decreases for zero freeboard (R_c = 0); the accuracy increases for tests characterized by high submergence.

The developed prediction method of Calabrese et al. [14] (Figure 2e) considers the smallest number of data (N_t = 470) because tests with relatively high submergence, relatively large crest widths and breaking waves have been excluded by the imposed validity ranges. Despite this, the percentage of data that fall in ± 20% confidence level is the highest and the RMSE shows a good agreement for barriers that respect all the validity ranges for shallow water.

D’Angremond et al. [12] (Figure 2c) counts the number of tests equal to the full available database (N_t = 4144) and, similarly, Briganti et al. [15] (Figure 2f) consider the same number of data, since both formulae do not have a validity range and they are valid for any condition; both show a concentration of values at the lower and upper limits, but the Briganti’s limits are wider since the upper limit depends on the relative crest width. Although Briganti’s formula has been calibrated to improve D’Angremond’s prediction for tests with B_c/H_i > 10, the latter shows the lowest RMSE, equal to 0.100, and has a higher percentage of data falling within the ±20% and ±50% confidence levels compared to Briganti’s. In detail, for d’Angremond’s, 62% and 87% of data fall in ±20% and ±50% confidence levels, respectively; for Briganti’s, 50% and 86% of data fall in ±20% and ±50% confidence levels, respectively.

Buccino et al. [16] (Figure 2g) selected N_t =3452 tests, considering tests with submerged barriers solely as for the Seabrook and Hall formula, with which it shows a similar accuracy in terms of data falling within the ±20% and ±50% confidence levels, reaching, respectively, 69% and 94%, and RMSE, equal to 0.129. However, with respect to Seabrook and Hall, Buccino et al. adopted a larger set of data.

The Goda and Ahrens formula [17] (Figure 2h) shows a fairly good agreement between the calculated and observed transmission coefficient values, with a RMSE equal to 0.132, but there is a noticeable overestimation for K_t < 0.4 for tests with a small submergence. The re-calibrated formula of Tomasicchio and D’Alessandro [18] (Figure 2i) provides an improvement for those cases where K_t is less than 0.4. In the present study, both formulae consider the entire database (N_t = 4144) as they can be applied for any condition. Goda and Ahrens’s [17] includes more data that fall within the ±20% confidence level, while Tomasicchio and D’Alessandro present a larger amount of data in the ±50% confidence level; therefore, Tomasicchio and D’Alessandro’s leads to a lower RMSE, as shown in Table 6.

The method proposed by Zhang et al. [19] (Figure 2j) considers N_t = 2881, of which 27% and 63% fall within the ±20% and ±50% confidence bands, respectively. The overall trend shows a large scatter below the line of perfect agreement due to the influence of R_c/H_i and B_c/H_i: the prediction accuracy decreases as the crest width increases and the crest freeboard approaches zero.

Sindhu et al. [20] (Figure 2k) count N_t = 2629 and it is valid only for submerged barriers. Developed for reef-type structures, the formula has also been applied to rubble-mound structures. The trend of the results is far from the line of perfect agreement and, as can be seen in Table 4 and Table 5, the percentage of data that falls in ±20% and ±50% confidence levels is the lowest in respect to other formulae: 8% and 30%, respectively. Accordingly, RMSE is the highest for each single dataset.

The Kurdistani et al. [21] (Figure 2l) formula is applicable for submerged porous breakwater data without any limitations; for K_t,obs < 0.4, the calculated transmission coefficient is higher than the observed one. The data that fall in confidence levels ±20% and ±50% are lower than the formula of Seabrook and Hall [13], which considers the same datasets and structure type, but the RMSE shows an improved accuracy in prediction due to the inclusion of the pore pressure attenuation inside the breakwater.

4. Conclusions

In the present study, a comprehensive analysis has been conducted with the aim of describing and comparing the performance of the existing formulae for wave transmission at submerged and low-crested breakwaters. The formulae have been implemented in a user-friendly MatLab script, taking into account the validity range for each formula and have been applied for the largest database collected from all available laboratory tests, including 4144 data. The statistical analysis of the values of the predicted wave transmission coefficient have given insight to the reliability of the existing formulae; in general, it can be stated that the larger the standard deviation, the more unreliable the prediction is. The analysis indicates that for submerged rubble-mound breakwaters, the best agreement in prediction is given by Kurdistani et al. [21], with RMSE equal to 0.115 in respect to Buccino et al. [16] and Seabrook and Hall [13]. However, Buccino’s considers a larger amount of data than Kurdistani and Seabrook and Hall. For all the structure types (i.e., submerged, emerged and low-crested), Calabrese’s formula [14] provides a good agreement in terms of mean square deviation (RMSE = 0.107), but it is found to be applicable for a small number of data compared to the total database (N_t = 470). Formula from Tomasicchio and D’Alessandro [18], which presents a relative low mean square deviation (RMSE = 0.117) for the entire dataset, allows the separation of contributions due to overtopping and due to infiltration through the structure, while requiring a larger number of input parameters.

Finally, the analysis indicated that the D’Angremond et al. [12] formula provides the smallest mean square deviation (RMSE = 0.100), taking into account the full number of data (N_t = 4144), where 62% of data falls within a confidence level of 20% and 87% of data falls within a confidence level of 50%.