Modeling the Thermal Conditions in a Piglet Area with Infrared Heating

Abstract

A pressing task is to develop a mathematical model and calculation method that most accurately describes the radiant component of heat exchange between an animal and its environment. This will help determine the optimal design parameters and temperature conditions for infrared (IR) heaters in livestock premises. The mathematical models considered describe the animal’s heat exchange with the environment during IR heating. However, they do not take into account the hidden surface temperature of the premises’ enclosing structures and their emissivity factor, or the relationship between animal thermal comfort and the IR heater surface temperature. The proposed radiant heat exchange mathematical model is applicable to diffusely absorbing and radiating isothermic surface system typical of pigsties. It takes into account the emissivity factors of all of the enclosing structures’ surfaces and determines the effective (apparent) premises temperature value t_ef, corresponding to the thermal comfort conditions. The IR heater surface temperature’s dependence on the emissivity of the pigsty’s enclosing structures (walls, ceiling, and floor) is given, calculated using three methods. As the emissivity of the premises’ enclosing structures decreases, the difference between the results obtained via methods 1, 2, and 3 increases significantly and reaches 50…60% at ε = 0.8. The IR heater radiating surface temperature range is defined in order to create suitable thermal conditions on premises designed for keeping 1- to 4-week-old newborn piglets depending on the enclosing structure temperature and emissivity, taking into account hidden heat exchange surfaces.

1. Introduction

Managing animals of different age grades (i.e., pigs and suckling piglets) on the same premises within the pork industry, as well as in animal transport situations, requires the adoption of specific and differentiated thermal conditions infrared (IR) heating [1,2]. Thus, the air temperature for breeding pigs must be maintained in the range of 16 °C to 20 °C, while in areas where piglets are kept, it has to be between 32 °C and 34 °C, decreasing to 24 °C by the 26-day point, the moment of their weaning. By the end of the first month, the ambient air temperature must be about 23 °C, and it can be reduced to 21 °C by the age of two months [3,4]. This presents a complex challenge, particularly in light of the demands posed by global climate change.

Creating different localized temperature zones in animal housing areas, particularly in those where young animals are kept, has always been and remains a standard solution to the task set above. Various technical means can be applied today for heating young animals in a localized manner, including heated floor panels and mats, brooders, underfloor heating, and IR heaters (lamps, panels, films, etc.) [5]. Modern heating installations in farrowing houses feature unique designs, and their heating systems make it possible to satisfy the required thermal demand for breeding pigs, newborn piglets, and post-weaning pigs simultaneously with a fair degree of accuracy.

In engineering practice, simplified techniques are commonly used for calculating local heaters. The reason for this is that animals are able to adapt their metabolic reactions to changes in various thermal environments in a certain temperature range [6]. But in the very first hours and days of their life, the biological thermoregulation mechanism of young animals is still in the formative stage. Therefore, the thermal parameters of systems affecting the level of heat flows in areas where animals are housed must be varied within a rather narrow specific range. Therefore, calculation methods for local heaters designed for young animals, particularly newborn piglets, must account for the functional interrelations among all elements of the biotechnical system to the fullest extent possible [4,5,7].

1.1. Current Research Analysis

Boltyanska [8] studied a great number of possible heating system options for pig-breeding farms. She reported statistical values for the share of electricity and fuel costs associated with heat provision on pig-breeding premises as a part of the total energy and fuel consumption costs. She also defined the major factors that have to be taken into account while selecting heating and ventilation systems for a pig-breeding farm. She gave an analysis of the major advantages and drawbacks of infrared heating systems, heated floors, and electric heat exchangers.

Vasdal et al. [4,9] carried out a series of experimental studies on the thermoregulatory behavior of newborn (one-day-old) suckling piglets while being heated with the help of infrared heater lamps in the temperature range of 26 °C to 42 °C. In addition, they observed lying poses and a huddling-together tendency for 1- to 3-week-old piglets depending on the temperature deviation in the ranges of ±4 °C and ±8 °C from standard temperature values for the corresponding ages (34 °C, 27 °C, and 25 °C). Experimental studies of the influence of various local devices designed for heating piglets on their weight gain and survival indicators have been performed. The values of temperature in the kennel and absolute and average daily liveweight gain were compared for three local heating system types: electrically heated floors, infrared heater lamps, and the combination of the first two methods. The best indicators were observed for a combined local heating system with infrared heater lamps and heated floors [10,11]. Komarov and Fain [12] calculated the energy-related parameters for local electric heating and performed a comparative economic assessment for local heating appliances per year with and without the account of liveweight gain, for suckling piglets.

The basic principles for analytical evaluation of the temperature felt by animals while being heated with the use of infrared heater lamps, as well as those for their body surface, have been considered. Conditions of heat emission by animals exposed to external heat sources in standing and lying positions have been studied. A thermal balance calculation scheme has been presented with a piglet as an example. Provisions for determining thermal comfort conditions have been defined for young animals while using radiant heaters, along with the necessary and sufficient conditions that have to be applied for comparing various heating installations in the process of selecting a particular animal heating method [13,14]. A two-dimensional thermophysical model of piglet heat exchange in combined heating conditions for a floor-mounted environment has been presented, forming the basis for developing a mathematical model making it possible to calculate the thermal condition parameters in areas for heating piglets [15]. An analysis of studies on piglets’ thermal state and local heating is presented in Table 1.

Table 1. Comparative analysis of piglet thermal state research and the effectiveness of local heating methods.

Authors	Study Object	Primary Objective	Model Type	Heat Transfer Mechanisms Considered	Validation	Key Findings
Huang et al. [16]	Thermal balance of adult pigs in hot climates	To develop a mechanistic model for predicting thermal state and preventing heat stress	Mechanistic, dynamic, two-node (core–skin)	Convection, radiation, respiratory evaporation, conduction (internal, via blood flow)	Literature data (Stombaugh and Roller, 1977 (https://doi.org/10.13031/2013.35712); Huynh, 2005)	A detailed approach to modeling vasodilation and thermal tachypnea is applied. Linking physiological responses to core temperature
Zhang and Xin [17]	Newborn piglets under localized heating	To model the performance of a heat mat for determining optimal energy use and surface temperature	Mechanistic, steady-state, one-dimensional	Conduction (primary), convection, radiation	Experimental data under controlled conditions	The optimal power range for heat mats (100–188 W/m2) and the permissible surface temperature (up to 46 °C) were determined
Smith et al. [18]	Microclimate parameters in the lying area of newborn piglets under localized heating	To develop and refine a thermal state model using an expanded Effective Environment Temperature (EET) index for assessing the microclimate in the piglet zone	Mechanistic, steady-state, extended for a group of animals	Conduction (primary focus), convection, radiation	Data collected in laboratory settings using sensors	An expanded Effective Environment Temperature (EET) index was proposed, accounting for conduction and animal age (mass). A comparative analysis was conducted, evaluating the effectiveness of heat lamps versus semi-enclosed heated crates
Fialho et al. [19]	Growing–finishing pigs	To develop a theoretical model of the animal thermal balance and body temperature	Deterministic model based on differential equations	Convection, conduction, long-wave radiation, short-wave radiation, skin evaporation, respiratory evaporation, heating of feed and water	The accuracy of the model forecasts was verified by the authors in the following article: Fialho et al. (https://doi.org/10.1017/S1357729800054606)	A comprehensive theoretical model of thermal balance was created, utilizing body temperature as the primary regulatory mechanism. The model was integrated with models of metabolism and growth
Milan et al. [20]	Newborn piglets	To determine optimal parameters for piglets’ supplemental heating	Hybrid model: Machine Learning (ML) and biophysical model	Convection, conduction, radiation, evaporative heat loss (partial)	Experimental data	A hybrid approach (ML + biophysical model) was proposed for the precise determination of optimal heating power (266–344 W for 1 kg piglets and 44–128 W for 20 kg piglets). A practical model for energy-saving climate control management was developed
Opderbeck et al. [21]	Weaned piglets in Germany’s temperate climate	To compare the impact of two types of heating systems and a floor cooling system on behavior, pen cleanliness, and piglet performance	Empirical, based on experimental design	Combined heating and cooling: radiation (heated crate); water-based floor heating and cooling	Repeated trials, mixed statistical models, temperature monitoring in compared groups.	The combined heating and cooling system in a zoned pen was demonstrated to be a highly effective solution for meeting the changing thermal needs of weaned piglets in a temperate climate
Spodyniuk et al. [22]	Young pigs and poultry under localized heating	To evaluate a combined heating system performance with an IR heater and supply ventilation	Empirical, based on experimental design	Radiation (primary, IR heating), convection (ventilation)	Laboratory and field experiments	Empirical relationships for predicting temperature in the animal zone were established, and the efficacy of the combined infrared heating and supply ventilation system was confirmed
Kostov et al. [23]	A sow farrowing house	To develop a simplified calculation method for assessing the heating and cooling load of livestock farm buildings	A criterion-based model founded on similarity theory	Building envelope transmission losses, ventilation losses, internal heat gains (from animals), solar radiation	Comparison with results from standard calculation methodologies (deviation within 5%)	Derived a criterion equation for estimating the specific heating/cooling capacity, taking into account the influence of wind speed on the heat loss of a building

1.2. Problem Analysis, Research Goal, and Objectives

Current research analysis (see Table 1) reveals significant limitations in existing mathematical models of piglet heat exchange during IR heating. These models fail to account for the hidden surface temperature of the premises’ enclosing structures and their emissivity factor. Furthermore, these studies overlook the relationship between piglets’ thermal comfort, the IR heater’s surface temperature, and the effective temperature in the premises. In all the reviewed studies (except [18,20]), radiant heat transfer is calculated primarily using the Stefan–Boltzmann equation in its most general form, ignoring the effects of temperature and the emissivity of the premises’ enclosing structures. In this model, the radiant component of heat transfer is calculated similarly to the convective heat transfer component [20]. The extended Effective Environment Temperature (EET) index is used, which takes into account convection, radiation, and additionally thermal conductivity and piglet mass. Radiative heat transfer calculations are also presented in a simplified form [18].

The proposed calculation model allows us to describe the dependence of piglets’ thermal state on the thermophysical parameters set (radiation temperature and enclosing structure materials’ emissivity factor, air temperature). The supplemented calculation model describes the animal radiant heat exchange in a system of diffusely absorbing and radiating isothermic bodies, typical for pigsties. This model will provide a more comprehensive description of the heat exchange processes that occur during IR heating of piglets. The expansion of existing radiant heat exchange models to include the effects of diffusely absorbing and radiating bodies in a closed system will help substantiate the design and thermal parameters, as well as the operating modes, of IR heaters.

2. Materials and Methods

Thermal sensation for a certain animal activity level is a function of the organism’s thermal balance. Thermal comfort is the heat exchange balance in conditions of minimum physiological activity, that is, the state when all of the metabolic heat is dissipated into the environment without considerable negative physiological reactions (such as shivering, high respiratory rate, and so on). Suitable thermal conditions are characterized by an effective temperature value t_ef that is optimal with regard to the physiological demand of the organism to achieve the maximum productivity (survival ability) for a reasonable feed consumption rate (economically optimal productivity) under the stipulation that animals are not exposed to either overheating or excessive cold in areas where they are located. The temperature value t_ap corresponds to that of an idealized homogeneous environment having a uniform temperature of both the system shell and gaseous medium, provided that the animal organism’s heat exchange in this idealized environment is identical to that in real conditions [7,14].

A biotechnical system is a complex of technical equipment interacting with the animal organism and having a certain impact on the thermal conditions within the environment area under consideration.

2.1. Comparative Analysis of Calculation Methods for Young Animal Heating with the Use of Radiant Heater Panels

Early age piglets (up to one month old) are most sensitive to the ambient temperature variations [24,25]. Animals’ thermal balance is strongly influenced by radiant heat energy in the process of heat exchange with the enclosing structures of the premises where they are kept. Therefore, it is essential to create an artificial environment with thermophysical parameters in a certain value range to ensure suitable conditions for managing animals [26,27]. Selecting mathematical models that most adequately describe all physical links and their interaction within the “animal–environment” biotechnical system makes it possible to define the infrared heater’s parameters and operation modes to provide the required thermal conditions in areas where young animals have to be kept.

An animal’s heat emission rate depends on the temperature of the enclosing structure surfaces as well as on its position and size. Suitable environments can only be implemented in a system where the thermal equilibrium is achieved and where there is no organism stress in the process of its thermoregulation [1,28].

One universally accepted mathematical representation of such conditions for industrial and residential premises has the following form [27]:

$$\begin{array}{l}{Q}_{\mathrm{an}}^{\text{r-con}}=F_{\mathrm{r}}{\displaystyle \sum C}{\phi }_{\mathrm{i}}{b}_{\mathrm{i}}\left(t_{\mathrm{an}}-t_{\mathrm{i}}\right)+F_{\mathrm{con}}{\alpha }_{\mathrm{con}}\left(t_{\mathrm{an}}-t_{\mathrm{a}}\right)+F_{\mathrm{cond}}{K}_{\text{an-f}}\left(t_{\mathrm{an}}-t_{\mathrm{f}}\right)\\ Q_{\mathrm{an}}^{\text{r-con}}\subset U\end{array},$$

(1)

where Q_an^r-con is aggregate radiant, convective, and conductive animal heat emission into the environment (W); F_r is animal surface area (m²) participating in radiant heat transfer; C is reduced radiation coefficient (4.65 W·m⁻²·K⁻⁴) [29]; φ_i is angular coefficient for irradiance from the elementary animal surface towards the i-th surface; b_i is a corrective factor; F_con is the animal surface area (m²) participating in convective thermal transfer; α_con is the convective heat transfer rate (W∙m⁻²∙K⁻¹); F_cond is the animal surface area (m²) participating in conductive heat transfer; K_an-f is the heat transfer rate from the animal body surface towards the floor (W∙m⁻²∙K⁻¹); t_i is the temperature of the i-th surface (°C); t_an, t_a, and t_f are the temperatures of the animal skin, ambient air, and floor (°C), respectively; and U is the heat exchange rate in the area of the animal’s major heat exchange (W) [26,27].

Evaporative heat exchange in the piglet’s heat balance is of significant importance under hyperthermia (overheating) conditions. Under thermal conditions close to comfortable, the animal’s heart rate and pulse are normal, so the vaporization latent heat during breathing is not taken into account (it can be neglected).

The average specific value of the heat emission from the elementary animal surface area equals

$$q_{\mathrm{an}}={\displaystyle \frac{Q_{\mathrm{an}}^{\text{r-con}}}{F_{\mathrm{an}}}},$$

(2)

where F_an is the animal surface area (m²).

It follows from relationships (1) and (2) that

$$q_{\mathrm{r}}\subset (Q_{\mathrm{sen}.\min }/F_{\mathrm{an}}\dots Q_{\mathrm{sen}.\max }/F_{\mathrm{an}}),$$

(3)

where q_r is a specific value or radiant heat emission from the animal’s elementary surface area (W/m²), Q_sen.min…Q_sen.max is the sensible heat emission Q_sen range for animals of a particular species and age in thermal comfort conditions in the areas of their major heat exchange U (W).

If animals are located close to heated or cooled surfaces, the rate of the radiant heat exchange over the body surface area most sensitive to radiation will be a determining factor.

The radiant heat exchange equation for heat emission from the animal’s elementary surface area in a system of radiating surfaces has the following form [29]:

$$q_{\mathrm{r}}=\Sigma C{\phi }_{\mathrm{i}}{b}_{\text{an-i}}(t_{\mathrm{an}}-t_{\mathrm{i}})+C(1-\Sigma {\phi }_{\mathrm{i}})b_{\text{an-en}}(t_{\mathrm{an}}-t_{\mathrm{en}}),$$

(4)

where φ_i is the angular coefficient of irradiance from the animal’s elementary surface towards the i-th surface, b_an-i = 0.81 + 0.01τ_med.i is the temperature corrective factor, τ_cpi = 0.5 (t_an + t_i), t_i is the temperature of the i-surface (°C), b_an-es = 0.81 + 0.01τ_med._es is the temperature corrective factor (°C), τ_med.es = 0.5 (t_an + t_es) (°C), and t_es is the average temperature of the premises’ enclosing structure (°C).

Values of sensible heat emission Q_sen and those of heat production for a particular animal Q_hp as well as surface temperature t_an have to correspond to the major heat exchange area U [1,28].

The value of specific heat flow q_r, transferred by the premises enclosure to the elementary animal surface is defined from the following formula [22,29,30]:

$$q_{\mathrm{r}}={\displaystyle \sum C_{\text{red-i}}}\left[{\left({\displaystyle \frac{T_{\mathrm{an}}}{100}}\right)}^4-{\left({\displaystyle \frac{T_{\mathrm{i}}}{100}}\right)}^4\right]{\phi }_{\mathrm{i}}+C_{\mathrm{red}}(1-\Sigma {\phi }_{\mathrm{i}})\left[{\left({\displaystyle \frac{T_{\mathrm{an}}}{100}}\right)}^4-{\left({\displaystyle \frac{T_{\mathrm{s}.\mathrm{sh}}}{100}}\right)}^4\right],$$

(5)

where C_red-i = С₀ (1/ε_an + 1/ε_i − 1) and C_red = С₀ (1/ε_an + 1/ε_s.sh − 1) are reduced radiation rates; С₀ is the blackbody coefficient (W∙m⁻²∙K⁻⁴); ε_an, ε_i, and ε_s.sh are the emissivity factors of the animal surface, i-th surface, and system shell, respectively; T_an is the animal surface temperature (K); T_i is the temperature of the i-surface (K); and T_s.sh is the temperature of the system shell (K).

Let us consider the generalized model for animal heat exchange with a radiator panel (see Figure 1). Based on expression (4), the radiant heat exchange equation will be written for this case as follows:

$$\begin{array}{l}{q}_{\mathrm{r}}=C{\phi }_{\mathrm{rp}}{b}_{\text{an-rp}}(t_{\mathrm{an}}-t_{\mathrm{rp}})+C(1-\Sigma {\phi }_{\mathrm{rp}})b_{\text{an-s.sh}}(t_{\mathrm{an}}-t_{\mathrm{s}.\mathrm{sh}})\\ t_{\mathrm{rp}}=t_{\mathrm{an}}+{\displaystyle \frac{1-{\phi }_{\mathrm{rp}}}{{\phi }_{\mathrm{rp}}}}{\displaystyle \frac{b_{\text{an-rp}}}{b_{\text{an-s.sh}}}}\left(t_{\mathrm{an}}-t_{\mathrm{s}.\mathrm{sh}}\right)-{\displaystyle \frac{q_{\mathrm{r}}}{C{\phi }_{\mathrm{rp}}{b}_{\text{an-rp}}}}\end{array},$$

(6)

where b_{an-rp and} b_an-s.sh are temperature coefficients, t_rp is the temperature of the IR radiator panel surface (°C), and φ_rp is the angular coefficient for irradiance from the animal elementary surface towards the radiator panel surface.

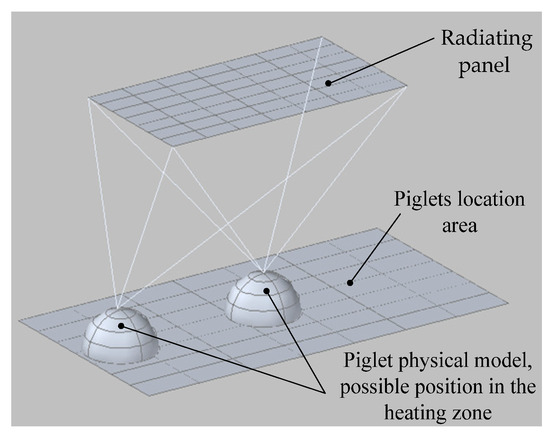
Figure 1. Model for animal heat exchange with radiating panel.

Formula (6) describes the heat exchange for an elementary surface area on the animal’s surface with a radiating panel. This expression is based on the literature [29] (Figure 1).

Based on relationship (5), we can write the following radiant heat exchange equation for the variant under consideration:

$$q_{\mathrm{r}}={С}_0\left({\displaystyle \frac{1}{{\epsilon }_{\mathrm{an}}}}+{\displaystyle \frac{1}{{\epsilon }_{\mathrm{rp}}}}-1\right)\left[{\left({\displaystyle \frac{T_{\mathrm{an}}}{100}}\right)}^4-{\left({\displaystyle \frac{T_{\mathrm{rp}}}{100}}\right)}^4\right]{\phi }_{\mathrm{rp}}+C_0\left({\displaystyle \frac{1}{{\epsilon }_{\mathrm{an}}}}+{\displaystyle \frac{1}{{\epsilon }_{\mathrm{s}.\mathrm{sh}}}}-1\right)(1-{\phi }_{\mathrm{rp}})\left[{\left({\displaystyle \frac{T_{\mathrm{an}}}{100}}\right)}^4-{\left({\displaystyle \frac{T_{\mathrm{s}.\mathrm{sh}}}{100}}\right)}^4\right].$$

(7)

The radiant heat exchange model based on relationships (4) to (7) is applicable only to the radiant heat transfer flows for “apparent” surfaces, but it does not take into account the diffuse component of radiant heat flux from hidden surfaces that is typical for diffusely absorbing and radiating bodies. Therefore, the above radiant heat exchange model has to be extended to involve diffusely absorbing and radiating isothermic bodies in the system, which will make it possible to obtain a much more complete description of the thermophysical processes (see Figure 2 and Figure 3).

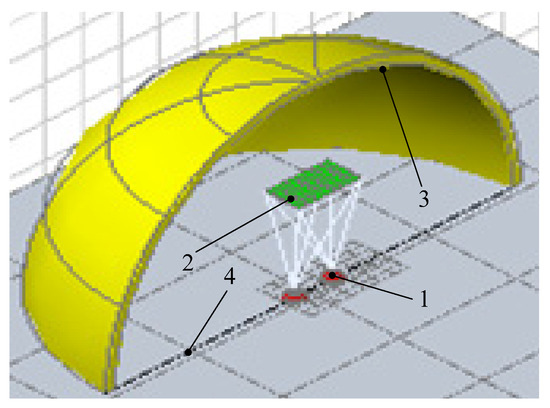
Figure 2. Heat exchange physical model in the system of diffusely absorbing and radiating isothermic surfaces: 1—animal body elementary surface; 2—radiating panel; 3—enclosing structure surface; 4—floor surface.

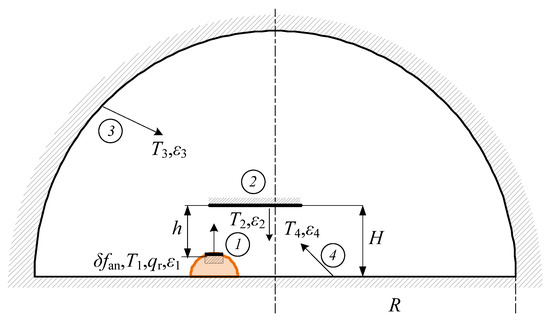
Figure 3. Thermophysical model for radiant heat exchange between various surfaces: 1—elementary animal surface area δf_an, T₁ (t₁) is surface temperature, q_r is total radiation rate from elementary surface, ε₁ is its emissivity factor; 2—radiating panel, T₂ (t_rp) is its surface temperature, ε₂ is its emissivity factor; 3—premises’ enclosing structure surface (ceiling, walls), T₃ (t₃) is enclosure temperature, ε₃ is enclosure emissivity factor; 4—floor surface, T₄ (t₄) is floor temperature, ε₄ is floor emissivity factor, H is radiator suspension height, h is radiator suspension height above the animal surface δf_an, R is premises’ generalized dimension.

An animal’s thermal comfort depends substantially on the radiant heat component in its entire thermal balance with the environment. In this context, radiant heat exchange of animals located close to heated or cooled surfaces (particularly, the radiant heat balance of the animal body surface area most unfavorably located in relation to the radiation sources) shall be regarded as a decisive factor. For any biological system, there exist the maximum permitted values of the radiant heat exchange rate between an organism’s surface and that of a radiation source [31,32]. That is why it is necessary to control the intensity of the radiant heat exchange in areas where animals are managed wherever infrared heating has to be applied. In this regard, an essential task is to study technical environments having their thermophysical parameters in accordance with expression (3) to set the borders of the animals’ major heat exchange area. This refers to the equilibrium between the heat production and heat emission by an animal organism in the process of its interaction with the radiating panel surface in areas where it is located.

The thermal exchange physical–mathematical problem for radiations in a system of isolated gray surfaces can be considered as a complete one provided that the temperature values for some of these surfaces are defined while values of thermal flows are known for the other surfaces. The reference condition is either a specified animal thermal state or that of its model representation, i.e., the effective temperature value and those of the following parameters corresponding to this value: sensible heat emissions Q_sen, model surface temperature t_sm, and surface area f_an.

The heat exchange model for an isolated thermodynamic system composed of N finite-dimensional surfaces (see Figure 3) has to be built with consideration of the following assumptions [33]: each surface is isothermic, each system surface is gray, radiation reflected from surfaces is distributed diffusely in space, radiation emitted by each surface is distributed diffusely in semi-space, effective radiation flow surface density is uniform in all points of each system surface, and angular coefficients do not depend on the value and surface distribution of radiation flows. We consider the case where the temperatures on all N system surfaces are given and it is necessary to determine the corresponding heat fluxes of the resulting radiation.

For an arbitrary i-surface, total radiation flow density can be defined for the specified values of system surface temperatures based on research [34] on the expression:

$${\displaystyle \frac{Q_{\mathrm{i}}}{F_{\mathrm{i}}}}={\displaystyle \sum _{\mathrm{j}=1}^N{А}_{\mathrm{ij}}\sigma T_{\mathrm{j}}^4},\hspace{0.17em}1\le i\le N,\hspace{0.17em}{A}_{\mathrm{ij}}=\left({\displaystyle \frac{{\epsilon }_{\mathrm{i}}}{1-{\epsilon }_{\mathrm{i}}}}\right)({\delta }_{\mathrm{ij}}-{\psi }_{\mathrm{ij}}),$$

(8)

where δ_ij is the Kronecker index, δ_ij = 1 for I = j, δ_ij = 0 for I ≠ j, and Q_i is the total radiation flow from surface F_i (W).

The coefficients ψ_ij included in Equation (8) are determined based on the inverse matrix calculation ψ = χ⁻¹ [34]:

$$\begin{array}{l}\psi ={\chi }^{-1}=\left[\begin{array}{ccc}{\psi }_{11}& \dots & {\psi }_{1\mathrm{N}}\\ ⋮& \ddots & ⋮\\ {\psi }_{\mathrm{N}1}& \dots & {\psi }_{\mathrm{NN}}\end{array}\right],\hspace{0.17em}\\ {\chi }_{\mathrm{ij}}={\displaystyle \frac{{\delta }_{\mathrm{ij}}-(1-{\epsilon }_{\mathrm{i}}){\phi }_{\mathrm{ij}}}{{\epsilon }_{\mathrm{i}}}},\hspace{0.17em}\hspace{0.17em}\chi =\left[\begin{array}{ccc}{\chi }_{11}& \dots & {\chi }_{1\mathrm{N}}\\ ⋮& \ddots & ⋮\\ {\chi }_{\mathrm{N}1}& \dots & {\chi }_{\mathrm{NN}}\end{array}\right]\end{array}.$$

(9)

where φ_ij is the angular coefficient of irradiance from surface i to surface j.

Expression 8 is the general equation for calculating the IR radiating panel surface temperature. The coefficients ψ_ij included in Equation (8) are determined using expression (9). Expression (9) includes the angular coefficients φ_ij.

In the model under consideration, angular coefficients can be calculated on the basis of the reciprocity and congruence theorem [33,35].

The following definition and assumptions were introduced: the premises’ generalized size will be expressed with use of the parameter R = (ΣF_st/3π)^0.5 where ΣF_st is the aggregate surface area of the walls, ceiling, and floor; linear dimensions of surfaces 1 and 2 are substantially smaller compared to those of surfaces 3 and 4 of the system shell; and the shield effect on the IR flows between the system shell surfaces can be neglected (see Figure 3).

Analytical calculations can be substantially simplified by considering an isolated system composed of only N = 4 finite-size gray surfaces (floor, walls–ceiling, animal, radiant IR heater). Nevertheless, such a model can be regarded as a generalizing structure for livestock premises that vary widely in their geometry and size (see Figure 3). Increasing the number of surfaces (5 or more) significantly complicates the calculations. However, this has virtually no effect on the accuracy of the obtained results, such as the IR radiating panel temperature t_rp.

The angular radiation coefficients φ_ij between the interacting surfaces are expressed by the following relations (10):

$$\begin{array}{l}{\phi }_{11}=0;\\ {\phi }_{12}={\displaystyle \frac{1}{2\pi }}\left[{\displaystyle \frac{X}{{\left(1+X^2\right)}^{-2}}}{\tan }^{-1}\left({\displaystyle \frac{Y}{{\left(1+X^2\right)}^{-2}}}\right)+{\displaystyle \frac{Y}{{\left(1+Y^2\right)}^{-2}}}{\tan }^{-1}\left({\displaystyle \frac{X}{{\left(1+Y^2\right)}^{-2}}}\right)\right];\\ {\phi }_{13} =1-{\phi }_{12};{\phi }_{14}=0;\\ {\phi }_{21}={\displaystyle \frac{1}{2\pi }}\left[{\displaystyle \frac{X}{{\left(1+X^2\right)}^{-2}}}{\tan }^{-1}\left({\displaystyle \frac{Y}{{\left(1+X^2\right)}^{-2}}}\right)+{\displaystyle \frac{Y}{{\left(1+Y^2\right)}^{-2}}}{\tan }^{-1}\left({\displaystyle \frac{X}{{\left(1+Y^2\right)}^{-2}}}\right)\right]{\displaystyle \frac{\delta f}{F}},\hspace{0.17em}{\phi }_{22}=0;\\ {\phi }_{23}={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{H}{\int }}\frac{h{\left(R^2-{\left(H-h\right)}^2\right)}^{-2}}{\pi R^3}}}dhd\phi ,\hspace{0.17em}{\phi }_{24}=1- {\phi }_{23};\\ {\phi }_{31}=\left(1-{\phi }_{12}\right){\displaystyle \frac{\delta f}{F_{31}}},\hspace{0.17em}{\phi }_{32}=0.5{\phi }_{23}{F}_2/\pi RH,\hspace{0.17em}{\phi }_{33}=1-(F_4/F_3),{\phi }_{34}=F_4/F_3;\\ {\phi }_{41}=0,\hspace{0.17em}{\phi }_{42}=(1-{\phi }_{23})(F_2/\pi R^2),{\phi }_{43}=1,{\phi }_{44}=0,\end{array}$$

(10)

where X = a/c, Y = b/c, a and b are dimensions of rectangular radiating surface (m), c is distance between the radiating surface end-face and the animal’s elementary surface δf_an (m), δf_an is the elementary animal surface area, F₃₁ is the “apparent” surface F₃ having elementary area δf_an, H is the radiator suspension height (m), h is the radiator suspension height above the animal elementary surface δf_an (m).

The above relationships serve as a basis for determining the required surface temperature of the IR radiating panel and thermal energy emission. They can also be applied to perform a comparative evaluation of the calculation results for the methods under consideration. Further on, we will assume that expressions (5), (6), and (8) represent calculation methods 1 to 3, respectively (see Table 2).

Table 2. A comparison of the calculation methods (calculation models) for radiant heat exchange between an animal and the environment.

No.	Purpose	Theoretical Basis	Feature	Application	Mathematical Description
Method 1	Radiant heat exchange calculation of an animal (using a piglet as an example) in an enclosure with an artificial IR heating source	Stefan–Boltzmann law	This model describes the radiant heat exchange between visible surfaces; it does not account for the temperature and emissivity ε of the hidden surfaces of the premises’ enclosing structures	To analyze the heat exchange processes involved in microclimate formation in industrial, residential, and agricultural premises	Equation (5)
Method 2	Radiant heat exchange calculation of an animal (using a piglet as an example) in an enclosure with an artificial IR heating source	Stefan–Boltzmann law		To consider the heat exchange processes involved in the formation of the premises’ microclimate. Widely used in engineering calculations	Equation (6)
Method 3	Radiant heat exchange calculation of an animal (using a piglet as an example) in an enclosure with an artificial IR heating source	Stefan–Boltzmann law	It describes the dependence of the piglets’ thermal state on a set of thermophysical parameters of the premises (radiation temperature, enclosing structure materials’ emissivity factor, air temperature) and makes it possible to determine the effective temperature values that correspond to comfortable conditions for the animals. The model takes into account radiant heat exchange with all the enclosing structures of the premises. It will allow for a more complete description of the heat exchange processes that occur during animals’ IR heating	Calculation of radiant heat exchange for an animal in a closed system of diffusely absorbing and radiating bodies, typical for pig farms. This approach makes it possible to calculate the IR heater’s surface temperature and select its power. Rarely used in practice	Equation (8)

2.2. Piglet Heat Exchange Physical Model

The physical model for piglet heat exchange with an environment comprises the relationships presented below. Piglet body surface area and weight (age) correlate in accordance with the following experimental expression:

$$f_{\mathrm{an}} =r_{\mathrm{d}}{m}^{2/3},$$

(11)

where f_an is the animal surface area (m²), m is the animal weight (kg), and r_d is a corrective factor (r_d = 0.0998 [36], r_d = 0.09 [18], r_d = 0.092 [37]). According to other sources, f_an = 0.097m^0.633 [38].

Piglet geometric parameters are as follows:

$$m=72.4d^{2.93 }or m=71.9l^{1.79},$$

(12)

where d is chest girth (m) and l is barrel length (m) [36].

In regulatory documents, as well as in some zoohygienic study reports, the values of sensible heat Q_sen for animals in standing posture are specified as a function of a limited number of parameters [7]. In accordance with the statement above, the piglet thermophysical calculation model has to be based on the standardized data for heat production Q_st and sensible heat emission into the environment Q_sen. For the equilibrium state Q_st = Q_sen, Q_sen depends on the animal weight (age) and effective t_ef in premises. Various representations of this dependence have been reported in the literature [18]. One of such representations is based on the following power polynomial approximation of initial data [28]:

$$\begin{array}{l}m=Q_{\mathrm{sen}}(m,t_{\mathrm{ef}})= (0.0102m^4-0.4319m^3+4.5771m^2+24.969m-1.8333)k_{\mathrm{t}}; \\ 1\le m\le 20;\\ k_{\mathrm{t}}(t_{\mathrm{ef}})=0.000005t^4-0.0003t^3+0.0051t^2-0.052t+1.2494;\\ t\in \left[\mathrm{10\dots 30}\right],\end{array}$$

(13)

where k_t (t_ef) is the conversion factor for various effective temperature values in premises and t_ef is the effective temperature in premises (°C).

2.3. Mathematical Description of the Piglet Heat Exchange Model

Modeling animal heat exchange with the environment is performed with the help of analogies in which the real animal body geometric shape is normally represented in the form of a cylinder, a solid sphere, or another form [39,40] invariant with respect to the variables f_an (m), Q_sen (m,t_ef), l (m), and d (m) integrated into the thermophysical model.

The mathematical description of the piglet model heat exchange (Figure 4) in a homogeneous environment system with temperature t_ef can be represented by the following equation with consideration of the deduced expressions and criterial relationships determining convective and radiant heat emission conditions:

$$\begin{array}{l}{Q}_{\mathrm{sen}}={\alpha }_{\mathrm{con}}(t_{\mathrm{sm}}-t_{\mathrm{ef}})f_{\mathrm{an}}+\left[{\left({\displaystyle \frac{273+t_{\mathrm{sm}}}{100}}\right)}^4- {\left({\displaystyle \frac{273+t_{\mathrm{ef}}}{100}}\right)}^4\right]{\phi }_{\mathrm{en}}{\epsilon }_{\mathrm{red}}{C}_0{f}_{\mathrm{an}}; \hfill \\ \mathrm{Nu}={\displaystyle \frac{{\alpha }_{\mathrm{con}}d}{\lambda }},\hfill \end{array}$$

(14)

where Q_sen is the piglet’s sensible heat emission (W), f_an is the piglet model’s surface area (m²), m is the piglet weight (kg), τ is the piglet age (days), α_con is the average coefficient of convective heat emission from the piglet body surface (W·m⁻²·°K⁻¹), λ is the air’s thermal conductivity (W·m⁻¹·°K⁻¹), t_sm is the piglet physical model’s surface temperature (°C), φ_en is the rate of mutual irradiance between the organism and the external enclosure, ε_red is the reduced emissivity factor for the animal surface and the enclosure’s internal surfaces, C₀ is the blackbody coefficient (W·m⁻²·K⁻⁴), Nu is the Nusselt number.

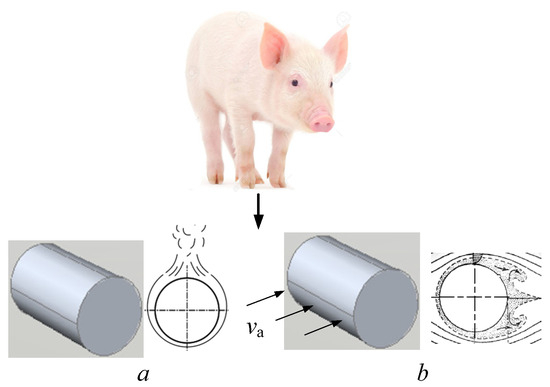
Figure 4. Physical model for piglet heat exchange with the environment: (a) natural convection, (b) forced convection, ν_an—air flow velocity (air speed in the area where piglets are kept).

Depending on the air medium circulation mode in premises, either natural or forced convection heat transfer conditions may occur in areas where animals are managed. These can be represented by the following criterial equations [41,42]:

-

For natural convection mode,

$$\mathrm{Nu}=0.50{\left({\mathrm{GrPr}}_{\mathrm{liq}}\right)}^{0.25},$$

(15)

-

For forced convection mode (laminar air motion 2 × 10³ ≤ Re ≤ 1 × 10⁴),

$$\mathrm{Nu}=0.26{\mathrm{Re}}^{0.5}{\mathrm{Pr}}^{0.37}{\epsilon }_{\mathrm{t}}{\epsilon }_{\mathsf{\phi }},$$

(16)

where Re, Gr, and Pr are Reynolds, Grashof, and Prandtl numbers, respectively; ε_t = (Pr_liq/Pr_w)^0.25 is corrective value that takes the dependence of the air’s physical properties on temperature into account; Pr_liq corresponds to a certain air temperature; the Pr_W value has to correspond to a particular medium and given wall temperature; ε_φ is a corrective value taking account of incident flow angle (angle φ between the air velocity vector and cylinder axis); either expression ε_φ = 1 − 0.54cos²φ or ε_φ = (sinφ)^0.5 can be applied to calculate ε_φ.

The values of heat emission from the animal surface depend on the particular medium’s thermal properties and on air flow velocity:

$$Q_{\mathrm{loss}}=f(t_{\mathrm{r}},t_{\mathrm{f}},t_{\mathrm{a}},{\nu }_{\mathrm{a}},Q_{\mathrm{input}}),$$

(17)

where t_r is the radiant temperature in the premises (area-averaged temperature of internal surfaces) (°C), t_f is the floor temperature (°C), t_a is the air temperature (°C), ν_a is the air flow velocity (m/s), and Q_input is heat gain from other sources (W).

Thermal conditions will correspond to actual values of effective temperature t_ef when equation Q_sen (m,t_ef) = Q_loss (t_r,t_f,t_a,ν_a,Q_input) is valid, in the thermodynamic equilibrium state.

The thermodynamic state of a real animal as well as that of its physical model can be described by a certain complex of parameters.

For a real animal,

$$Q_{\mathrm{sen}}=f(Q_{\mathrm{hp}},U{t}_{\mathrm{an}},t_{\mathrm{r}},t_{\mathrm{f}},t_{\mathrm{a}},{\nu }_{\mathrm{a}},Q_{\mathrm{input}}),$$

(18)

where Ut_an is the temperature field distribution over the animal skin surface (°C).

For an animal model,

$$Q_{\mathrm{sen}}^{\mathrm{m}}=f_{\mathrm{m}}(Q_{\mathrm{hp}}^{\mathrm{m}},t_{\mathrm{sm}},t_{\mathrm{ef}})$$

(19)

where Q_hp^m is heat production (W) and Q_sen^m is model heat loss (W).

For Q_hp = Q_sen = Q_hp^m = Q_sen^m, the real animal’s thermal state can be expressed with the use of model temperature parameters t_sm and t_ef for various external thermal states of the environment.

3. Results and Discussion

The general formulation of the calculation problem for heating areas intended for managing young animals is defined by the system of equations for total heat exchange in premises and by the thermal comfort conditions. The radiant temperature situation in premises is governed by the following major surface groups: heating, cooling, and neutral surfaces. The radiant heat transfer flows in premises have to be calculated with the consideration of the enclosure’s internal surface temperature. In this case, the mathematical description for calculating the heating surface areas and temperatures may be substantially simplified. One specific feature of composing relationships for the above different surface groups relates to defining the values of coefficients for irradiance between the interacting surfaces, values of averaged coefficients for the reduced radiation, effective radiation flows, and other process parameters.

Solutions for complete systems composed of a number of equations may be rather complicated. That is why we will apply simplified calculation procedures. For this purpose, we will determine the temperatures of both internal enclosures and external ones facing the interior space of the premises. Therefore, either the temperature or the surface area of the heating IR radiator will be a target value. Such an approach to solving this problem enables us to replace the entire heat exchange equation system for premises with just one single equation.

A radiation field in a system of arbitrarily assigned configuration of surfaces having various sizes and separated from each other by a diathermic medium represents the function of temperature fields and optical constants on the system borders. A local system configuration is typical. It is normally an area within the entire system comprising an infrared radiation source (see Figure 2) [43]. Livestock-dedicated premises are characterized by a rather wide size range and configuration variety (from small farms to large livestock complexes). Therefore, there is a reason to reduce this diversity of objects’ geometric shapes to one single generalized parameter R representing the size of particular premises (see Figure 3).

With this background, the problem has to be set as follows:

-

Determining radiating surface temperature (or surface area) in an isolated system composed of diffusely radiating bodies; in addition, temperature and total radiation from the elementary animal surface δf_an have to be maintained in the ranges t₁⊂ (t_1min…t_1max) and q_r⊂ (q_rmin…q_rmax);

-

Defining variation intervals for calculated parameter values depending on the corresponding variables: enclosure and floor temperatures, emissivity factor of surfaces;

-

Evaluating interacting bodies’ emissivity factor;

-

Setting limiting conditions for calculation models’ validity.

3.1. Calculating IR Radiating Panel Surface Temperature, Accounting for Enclosing Surface Emissivity Factor and Premises’ Size

The following design and technological parameters of thermophysical systems were selected as the initial data with respect to technological design standards for farrowing houses [44]:

-

The radiating panel’s dimensions are 0.5 m wide and 1 m long, and its suspension height h over the surface δf_an is 1 m;

-

The total radiation rate from the elementary surface is δf q_r = 18 W/m², for body surface temperature t₁ = 33 °C;

-

The emissivity factor of the radiating system varies in the ranges of ε_i = 0.80 to 0.96, i = 1 to 4, and temperatures of thermally homogeneous surfaces 3 and 4 range within the limits of t₃ = 10 °C to 25 °C and t₄ = 5 °C to 25 °C, respectively.

The dependences of radiating panel surface temperature t_rp on the temperature of the enclosure t₃ (wall and ceiling temperature) calculated with the application of the first and the second methods do not practically differ from one another, and the corresponding enclosure temperature values’ variation does not exceed 10% for the specified temperature range (see Figure 5a). For surfaces 1 and 2, method 3 has to be applied within the t_rp variation range limited by the interval ε = ε₁ = ε₂ = ε₃ = ε₄ = 0.80 to 0.96 (see Figure 5b).

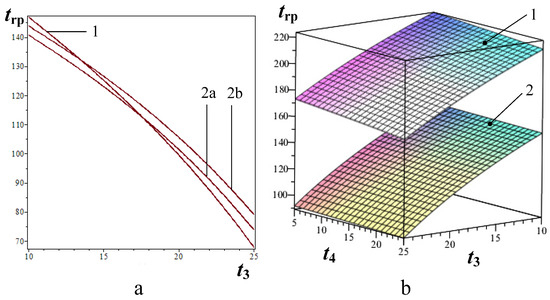
Figure 5. Dependence of panel surface temperature t_rp (°C) on the temperature of the enclosure (walls and ceiling) surface t₃ in premises (а): 1—for calculation method 1; 2a and 2b—for calculation method 2 (ε₃ = 0.96 and ε₃ = 0.80, respectively). The value range for panel surface temperature t_rp (°C) depending on t₃ (temperature of ceiling and walls) and t₄ (floor temperature) (b): 1—for ε₁ = ε₂ = ε₃ = ε₄ = 0.80; 2—for ε₁ = ε₂ = ε₃ = ε₄ = 0.96.

For total radiation q_r from animal body elementary surface δf_an and its temperature t₁, specified in mathematical models, the values of the radiating panel surface temperature calculated by methods 2 and 3 differ significantly (the difference amounts to 50% to 60%) as a result of the effect of reflected diffused thermal flows and interacting surfaces’ emissivity factor (see Figure 6). Given that emissivity factor values of the system shell are close to those of the absolute black body (ε ≈ 1), temperature values t_rp calculated using methods 2 and 3 are in close agreement (3% to 5%) (see Figure 6).

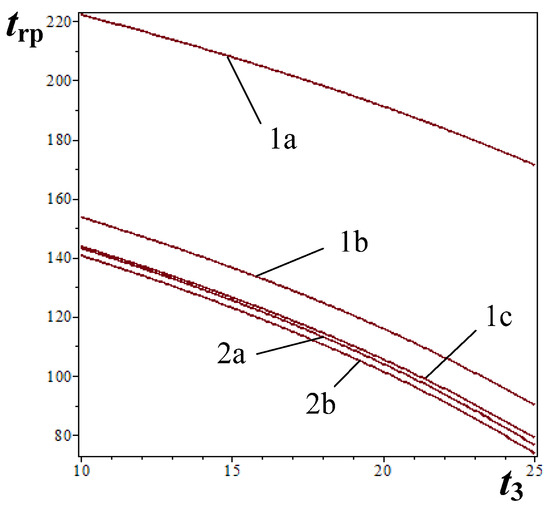
Figure 6. Dependence of radiating panel surface temperature t_rp (°C) on the temperature of the enclosure t₃: 1a and 1b—in accordance with method 3 for the following values of parameters involved in the calculation model: ε₁ = ε₂ = ε₃ = ε₄ = 0.80 (t₄ = 10 °C, R = 15 m) and ε₁ = ε₂ = ε₃ = ε₄ = 0.96, respectively; curves 2a and 2b apply to method 2 for ε₃ = 0.96 and ε₃ = 0.80, respectively: curve 1с applies to method 3 for t₄ = 20 °C, R = 15 m, and ε₁ = ε₂ = ε₃ = ε₄ → 1.

The calculated dependence of radiating panel surface temperature t_rp on the system shell emissivity in accordance with relationship (7) (see Figure 7) indicated the essential influence of the system shell emissivity factor on the thermal environment in areas where animals are located.

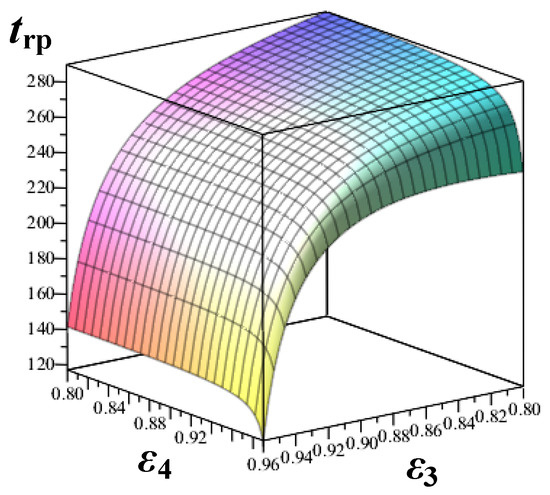
Figure 7. Dependence of radiating panel surface temperature t_rp on the system shell emissivity factor: ε₃ is the enclosure emissivity factor (that of ceiling and walls); ε₄ is the floor emissivity factor.

As ε decreases to values ≤ 0.9, a significant portion of the radiant heat fluxes reflected from hidden surfaces interacts with the animal’s body. Accordingly, as ε increases, the magnitude of the reflected heat fluxes decreases significantly, and the influence of hidden surfaces is reduced by a factor of several. Therefore, at ε ≥ 0.95, traditional methods for calculating radiant heat exchange between the animal and the environment can be used (Equations (4)–(7)).

A relationship between the IR heating panel temperature (t_rp) and the emissivity of the enclosing structures has been established. A decrease in the emissivity of the enclosing structures (ε_i ≤ 0.9) significantly influences the increase in t_rp. For ε ≈ 1, the t_rp values calculated using the proposed methodology and established methods are in close agreement, with a difference of ≤5% (see Figure 7).

In order to ensure the required thermal conditions and irradiation levels in heated zones, one has to take into account the type and configuration of particular premises. The calculations carried out have shown that for any fixed emissivity factor values of the system surfaces integrated in calculation model (7) and their temperatures (for example, for ε₁ = ε₂ = ε₃ = ε₄ = 0.8, t₃ = 15 °C, and t₄ = 10 °C), the premises’ size and configuration described by generalized parameter R do not practically have an effect on radiating panel temperature t_rp (see Figure 8).

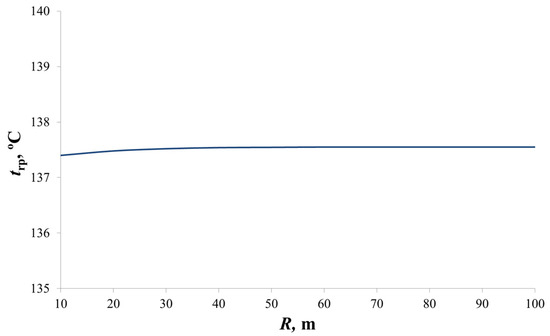
Figure 8. Dependence of radiating panel surface temperature t_rp on parameter R.

As shown in Figure 2 and Figure 3, the actual configuration of the livestock premises is replaced by a hemisphere inscribed in these premises. The projection of the premises’ enclosing structures onto the hemisphere does not depend on the premises’ dimensions. The dimensions and configuration of the premises, characterized by the generalized parameter R, do not significantly affect the IR heater surface temperature t_rp, as shown in Figure 8. It follows from this that the proposed mathematical model is applicable to livestock premises of virtually any configuration and size.

Calculations for the surface temperature were performed for a particular radiating panel in a system of diffusely absorbing and radiating isothermic surfaces having the given geometry and specific value of total radiation flow from the elementary surface at a certain specified point.

3.2. Calculating IR Radiating Panel Surface Temperature for Piglets of Various Ages, Accounting for Premises’ Enclosing Structure Temperature

In engineering practice, the first two calculation methods for evaluating thermal comfort normally prevail. This is explained by the fact that animals are capable of adapting their metabolic reactions to the thermal environment change, within a certain range. Calculations performed with the use of such models can determine the thermophysical characteristics of biotechnical systems, within their permissible borders, with accuracy sufficient to define optimal parameters of IR radiators.

A vast amount of experimental data related to the maintenance conditions for piglets belonging to various age groups has been accumulated, particularly data concerning arranging location areas having specific thermal characteristics [21,22,45,46,47].

The role of an integrated parameter representing various thermal environments is played by the effective (apparent) temperature in premises, i.e., a complex parameter depending on the ambient air temperature and velocity as well as on the premises’ radiant temperature.

Within the entire range of possible effective temperature values, there exist intervals ensuring the maximum productivity for a certain animal group corresponding to the lowest possible specific reduced production cost. Such value ranges are defined by biologists and have to be treated as the standard ones for all animal species.

It is clear from the analysis of studies in which data and recommendations were reported concerning temperature conditions’ control that the optimal air temperatures may vary in a rather wide range according to a number of research results. It was reported in works [7,48] that the optimal air temperature values in areas where piglets have to be kept are in the following ranges: 26 °C to 30 °C, 24 °C to 26 °C, and 22 °C to 24 °C for the second, third, and fourth week, respectively. According to other sources, air temperature in areas where piglets are housed has to be maintained in the following intervals: 32 °C to 34 °C, 26 °C to 28 °C, 24 °C to 26 °C, 22 °C to 24 °C, and 20 °C to 22 °C, during the second, third, fourth, and fifth week, respectively [4,9].

In addition to the microclimate requirements mentioned above, it is essential to implement the heating system operation modes in correspondence with particular animal group biological rhythms, i.e., with the consideration of their cyclic metabolism intensity variations governed by natural daily alternation between the activity and rest periods. According to some sources, piglets’ metabolism reduces by 15% during their rest time.

These air temperature values as well as the experimentally obtained data on animal metabolism variations were integrated into the initial calculation model as the input parameters contributing to the calculation results. Selecting actual values of variables included in expressions (13) and (14) depends on the specific features of animal production and management technologies focused on achieving the maximum technological effect [37].

These calculations determined the dependence of the IR panel surface temperature (t₂) on the temperature of the enclosing structures (ceiling, walls, and floor), which is required to ensure a comfortable thermal state for piglets of different ages at a given effective temperature t_ef in the heating zone (Figure 9).

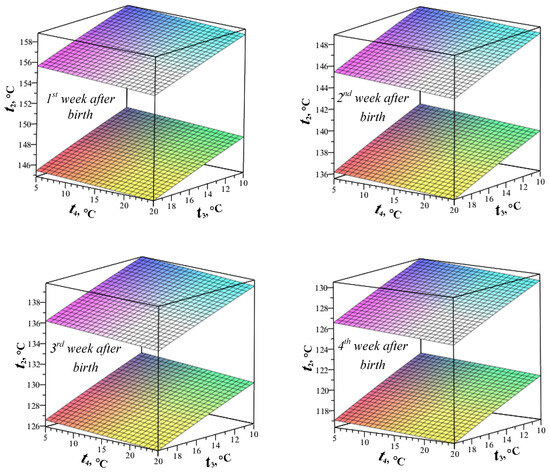
Figure 9. Value range for panel surface temperature t₂ depending on temperatures t₃ (ceiling, walls) and t₄ (floor) corresponding to the thermal comfort state in heating areas for piglets aged from 1 to 4 weeks.

The optimal effective temperature was established for different age groups: 30–26 °C for 1–7 days, 26–24 °C for 8–14 days, 24–22 °C for 15–21 days, and 22–20 °C for 22–28-day-old piglets [44]. These ranges are maintained by adjusting the infrared panel temperature (t_rp) in response to the surface temperatures and emissivity of the enclosure structures.

Figure 10 shows the algorithm for calculating the surface temperature of the radiating panel t₂, which creates comfortable conditions in the piglet placement area with a given effective temperature t_ef.

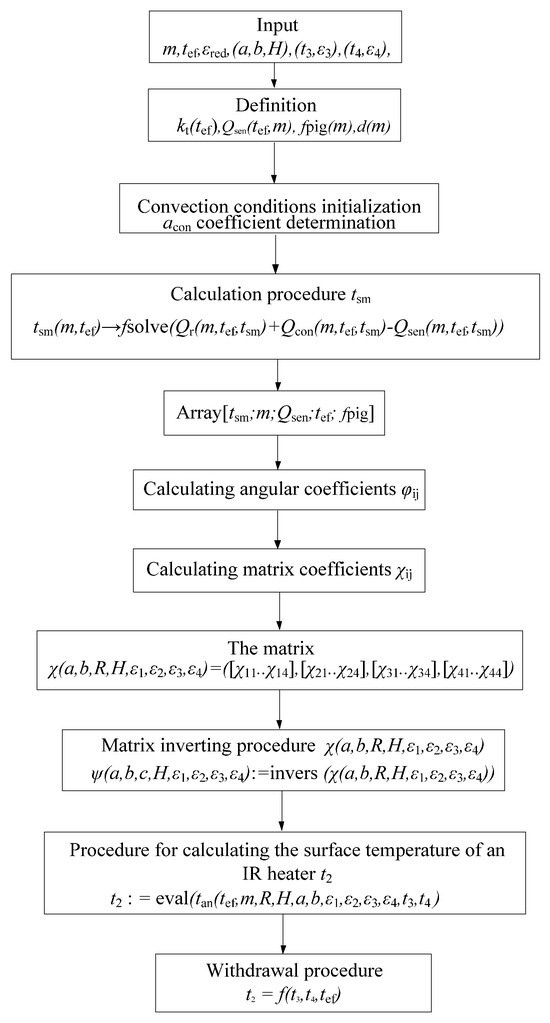
Figure 10. Algorithm for calculating the radiating panel surface temperature.

The objective of computational blocks 1–5 is to determine the surface temperature of the physical piglet model (t_sm) as a function of body mass (age) and the effective temperature (t_ef). The objective of computational blocks 6–10 is to determine the radiating panel surface temperature required to establish comfortable conditions in the piglet occupancy zone.

The angular radiation coefficients and the IR heater surface temperature calculations were carried out using the Maple 17 software package. The primary objective is to determine the infrared radiating panel surface temperature required to maintain a comfortable effective temperature in the piglet occupancy zone. The temperature and emissivity of the enclosing structures (walls, ceiling, and floor) have a significant influence on the animals. This influence can be mitigated through the implementation of a radiant heating system utilizing panel-type IR heaters.

4. Conclusions

A mathematical model and a methodology for calculating the radiant heat exchange of young animals (using piglets as an example) in a closed system of diffusely absorbing and radiating isothermic surfaces have been developed. The model accounts for the emissivity (ε_i) of the enclosing structures and the interrelationship between the effective temperature t_ef inside the premises and the surface temperature of the animal model (t_sm).

The relationship between the infrared heating panel temperature (t_rp) and the emissivity of the enclosing structures has been established. A decrease in the emissivity of these surfaces (ε_i ≤ 0.9) significantly leads to an increase in t_rp. For ε ≈ 1, the t_rp values calculated using the proposed methodology are in close agreement with those obtained by established methods (difference ≤ 5%).

It has been demonstrated that the size and configuration of the premises (generalized by the parameter R) do not significantly affect the required t_rp. Thus, the proposed mathematical model is applicable to livestock premises of virtually any configuration and size.

The required range for the infrared panel surface temperature (t₂) has been determined based on the radiant temperature and emissivity of the enclosing structures for four age groups of piglets (from 1 to 4 weeks) at specified effective temperature (t_ef) values.

Applying the developed methodology allows for rationalization of the parameters, operational modes, and infrared heater design. This ensures the required thermal regime, which contributes to improved animal survival and weight gain while reducing energy consumption.

Promising research directions include the experimental verification of the theoretical results, development of a prototype infrared heating panel with a uniform heat flux, integration of localized heating into an automatic climate control system, and study of animal behavioral responses.