Enhanced Prediction of Broiler Shipment Weight Using Vision-Assisted Load Cell Analysis
Abstract
1. Introduction
2. Background
2.1. Overview of Broiler Weight Prediction Methods
2.2. Object Detection for Broiler Counting on the Weighing Platform
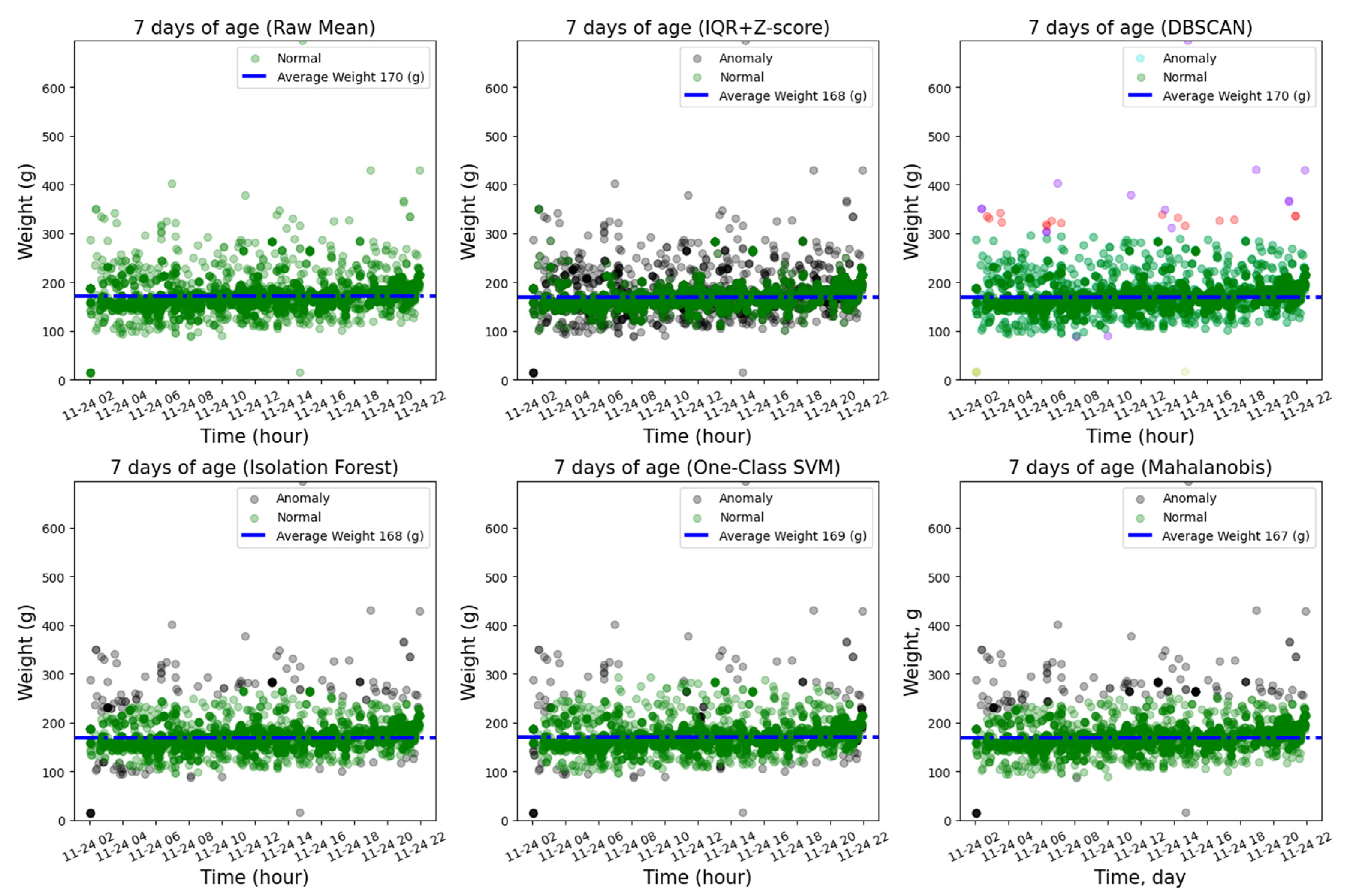
2.3. Outlier Handling
2.3.1. IQR and Z-Score
2.3.2. DBSCAN
2.3.3. Isolation Forest
- 1.
- Construct binary trees (Isolation Trees, iTrees) randomly from the training dataset;
- 2.
- For a test sample , input it into all iTrees and record the path length required from the root node to complete isolation (reaching a leaf node) in each tree. Then, calculate the average path length across all trees (Equation (3)):
- 3.
- The anomaly score is calculated according to Equation (4), where represents the theoretical expected path length for a sample size of , serving as a normalization factor for path lengths, as defined in Equation (5), where represents the approximation of the i-th harmonic number, with the constant being the Euler–Mascheroni constant:
- 4.
- If , the sample is highly likely to be an anomaly. If s, the sample x is generally considered normal. When all samples in the dataset yield scores close to 0.5, it indicates no significant anomalies exist in the dataset:
2.3.4. One-Class Support Vector Machines
2.3.5. Mahalanobis
3. Materials and Methods
3.1. Data Collection
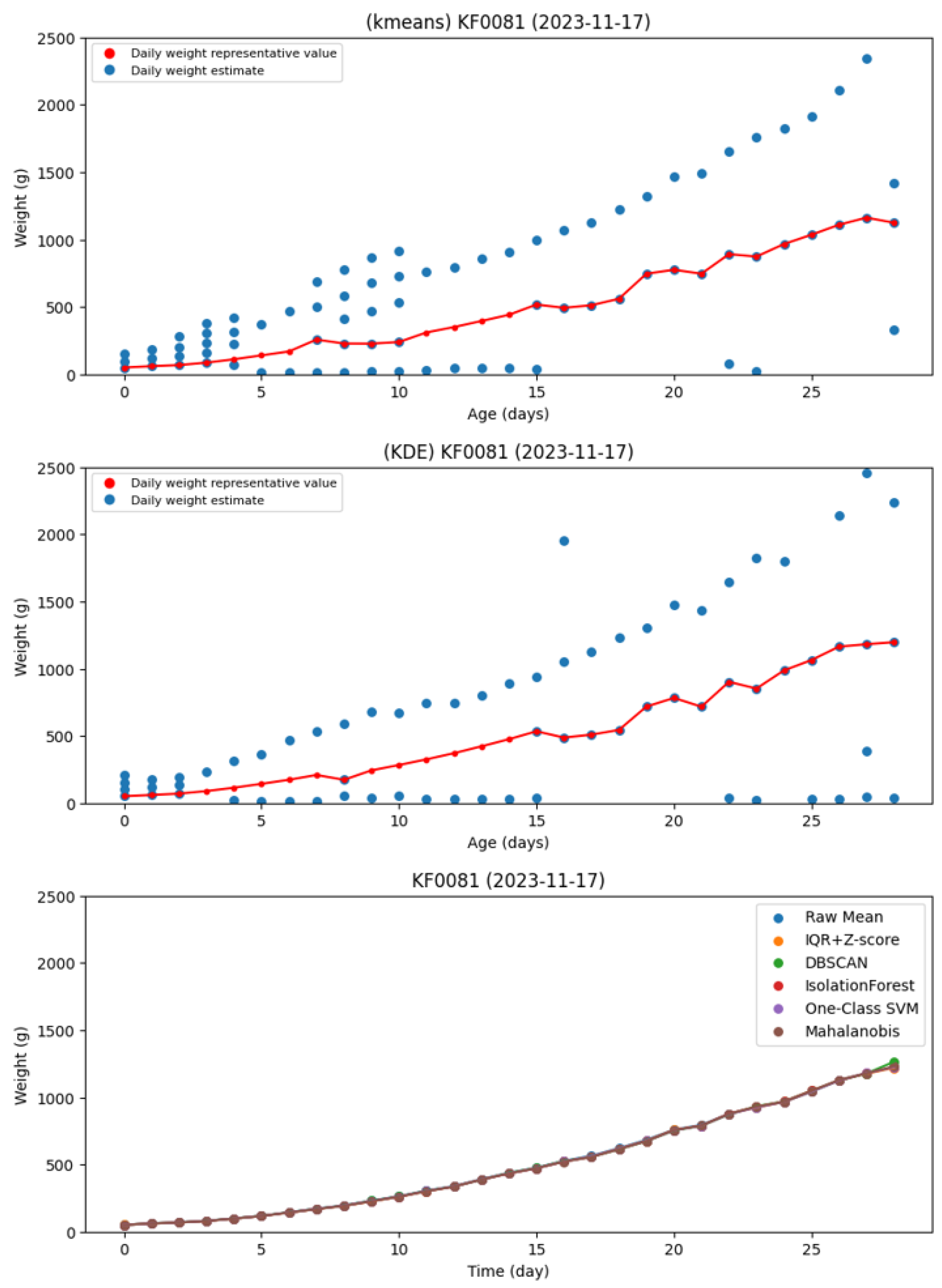
3.2. Algorithm Composition and Design
- Raw Mean: Direct calculation without any preprocessing;
- IQR + Z-score;
- DBSCAN;
- Isolation Forest;
- One-Class SVM;
- Mahalanobis.
- Experiment A (Basic Configuration):
- Experiment B (Center Contraction):
- Experiment C (Edge Expansion):
3.3. Performance Evaluation of the Algorithm
4. Results
4.1. Experiments in Object Detection Evaluation
4.2. Evaluation Experiments of Edge/Center Region Strategy
4.3. Experiments in the Shipping Weight Prediction Step
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, H.-C.; Kim, D.-H.; Kim, E.-T.; Lee, H.-J.; Park, J.-H.; Kim, J.-B.; Lee, J.-Y.; Jeon, J.-H.; Ki, K.-S.; Kwon, K.-S. Livestock Production in Korea: Recent Trend and Future Prospects of ICT Technology Livestock Production in Korea: Recent Trend and Future Prospects of ICT Technology. FFTC Agric. Policy Platf. 2019. Available online: https://ap.fftc.org.tw/article/1616 (accessed on 1 September 2025).
- Korea Meat Distribution and Export Association. Available online: http://www.kmta.or.kr/kr/data/stats_import_chicken_month.php (accessed on 7 July 2025).
- Oh, Y.; Lyu, P.; Ko, S.; Min, J.; Song, J. Enhancing Broiler Weight Estimation through Gaussian Kernel Density Estimation Modeling. Agriculture 2024, 14, 809. [Google Scholar] [CrossRef]
- Lee, B.; Song, J. Development of an Algorithm for Predicting Broiler Shipment Weight in a Smart Farm Environment. Agriculture 2025, 15, 539. [Google Scholar] [CrossRef]
- Beiki, H.; Pakdel, A.; Moradi-Shahrbabak, M.; Mehrban, H. Evaluation of Growth Functions on Japanese Quail Lines. J. Poult. Sci. 2013, 50, 20–27. [Google Scholar] [CrossRef]
- Al-Samarai, F.R. Growth Curve of Commercial Broiler as Predicted by Different Nonlinear Functions. Am. J. Appl. Sci. Res. 2015, 1, 6–9. [Google Scholar]
- Araújo, C.C.; Rodrigues, K.F.; Vaz, R.G.M.V.; Conti, A.C.M.; Amorim, A.F.; Campos, C.F.A. Analysis of Growth Curves in Different Lineages of Caipira Broiler Type. Acta Scientiarum. Anim. Sci. 2018, 40, 38806. [Google Scholar] [CrossRef]
- Johansen, S.V.; Bendtsen, J.D.; Martin, R.; Mogensen, J. Broiler Weight Forecasting Using Dynamic Neural Network Models with Input Variable Selection. Comput. Electron. Agric. 2019, 159, 97–109. [Google Scholar] [CrossRef]
- Mouffok, C.; Semara, L.; Ghoualmi, N.; Belkasmi, F. Comparison of Some Nonlinear Functions for Describing Broiler Growth Curves of Cobb 500 Strain. Poult. Sci. J. 2019, 7, 51–61. [Google Scholar] [CrossRef]
- Koushandeh, A.; Chamani, M.; Yaghobfar, A.; Sadeghi, A.A.; Baneh, H. Comparison of the Accuracy of Nonlinear Models and Artificial Neural Network in the Performance Prediction of Ross 308 Broiler Chickens. Poult. Sci. J. 2019, 7, 151–161. [Google Scholar] [CrossRef]
- Kucukonder, H.; Demirarslan, P.C.; Alkan, S.; Özgur, B.B. Curve Fitting with Nonlinear Regression and Grey Prediction Model of Broiler Growth in Chickens. Pak. J. Zool. 2020, 52, 347. [Google Scholar] [CrossRef]
- Zuidhof, M.J. Multiphasic Poultry Growth Models: Method and Application. Poult. Sci. 2020, 99, 5607–5614. [Google Scholar] [CrossRef]
- Yalcin, S.; Settar, P.; Ozkan, S.; Cahaner, A. Comparative Evaluation of Three Commercial Broiler Stocks in Hot versus Temperate Climates. Poult. Sci. 1997, 76, 921–929. [Google Scholar] [CrossRef]
- Wang, D.Q.; Lu, L.Z.; Ye, W.C.; Shen, J.D.; Tao, Z.R.; Tao, Z.L.; Ma, F.L.; Chen, Y.C.; Zhao, A.Z.; Xu, J. Study on the Growth Regularity of Jinyun Muscovy Duck. Zhejiang J. Anim. Sci. Vet. Med. 2004, 6, 3–5. [Google Scholar]
- Yang, Y.; Mekki, D.M.; Lv, S.J.; Wang, L.Y.; Yu, J.H.; Wang, J.Y. Analysis of Fitting Growth Models in Jinghai Mixed-Sex Yellow Chicken. Int. J. Poult. Sci. 2006, 5, 517–521. [Google Scholar] [CrossRef]
- De Wet, L.; Vranken, E.; Chedad, A.; Aerts, J.-M.; Ceunen, J.; Berckmans, D. Computer-Assisted Image Analysis to Quantify Daily Growth Rates of Broiler Chickens. Br. Poult. Sci. 2003, 44, 524–532. [Google Scholar] [CrossRef] [PubMed]
- Mortensen, A.K.; Lisouski, P.; Ahrendt, P. Weight Prediction of Broiler Chickens Using 3D Computer Vision. Comput. Electron. Agric. 2016, 123, 319–326. [Google Scholar] [CrossRef]
- Amraei, S.; Abdanan Mehdizadeh, S.; Salari, S. Broiler Weight Estimation Based on Machine Vision and Artificial Neural Network. Br. Poult. Sci. 2017, 58, 200–205. [Google Scholar] [CrossRef]
- Liu, D.; Vranken, E.; Van Den Berg, G.; Carpentier, L.; Fernández, A.P.; He, D.; Norton, T. Separate Weighing of Male and Female Broiler Breeders by Electronic Platform Weigher Using Camera Technologies. Comput. Electron. Agric. 2021, 182, 106009. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Chen, Y.-J.; Chien, C.-F. Industry 3.5 to Empower Smart Production for Poultry Farming and an Empirical Study for Broiler Live Weight Prediction. Comput. Ind. Eng. 2021, 151, 106931. [Google Scholar] [CrossRef]
- Guo, Y.; Chai, L.; Aggrey, S.E.; Oladeinde, A.; Johnson, J.; Zock, G. A Machine Vision-Based Method for Monitoring Broiler Chicken Floor Distribution. Sensors 2020, 20, 3179. [Google Scholar] [CrossRef]
- Geffen, O.; Yitzhaky, Y.; Barchilon, N.; Druyan, S.; Halachmi, I. A Machine Vision System to Detect and Count Laying Hens in Battery Cages. Animal 2020, 14, 2628–2634. [Google Scholar] [CrossRef]
- Siriani, A.L.R.; Kodaira, V.; Mehdizadeh, S.A.; de Alencar Nääs, I.; de Moura, D.J.; Pereira, D.F. Detection and Tracking of Chickens in Low-Light Images Using YOLO Network and Kalman Filter. Neural Comput. Appl. 2022, 34, 21987–21997. [Google Scholar] [CrossRef]
- Cruz, E.; Hidalgo-Rodriguez, M.; Acosta-Reyes, A.M.; Rangel, J.C.; Boniche, K. AI-Based Monitoring for Enhanced Poultry Flock Management. Agriculture 2024, 14, 2187. [Google Scholar] [CrossRef]
- Ultralytics YOLOv8. Available online: https://docs.ultralytics.com/models/yolov8 (accessed on 30 June 2025).
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. ACM Comput. Surv. (CSUR) 2009, 41, 3. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Kdd, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 413–422. [Google Scholar]
- Schölkopf, B.; Williamson, R.C.; Smola, A.; Shawe-Taylor, J.; Platt, J. Support Vector Method for Novelty Detection. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 1999; MIT Press: Cambridge, MA, USA, 1999; Volume 12. [Google Scholar]
- McLachlan, G.J. Mahalanobis Distance. Resonance 1999, 4, 20–26. [Google Scholar] [CrossRef]
- Satopaa, V.; Albrecht, J.; Irwin, D.; Raghavan, B. Finding a “Kneedle” in a Haystack: Detecting Knee Points in System Behavior. In Proceedings of the 2011 31st International Conference on Distributed Computing Systems Workshops, Minneapolis, MN, USA, 20–24 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 166–171. [Google Scholar]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN. ACM Trans. Database Syst. (TODS) 2017, 42, 3. [Google Scholar] [CrossRef]
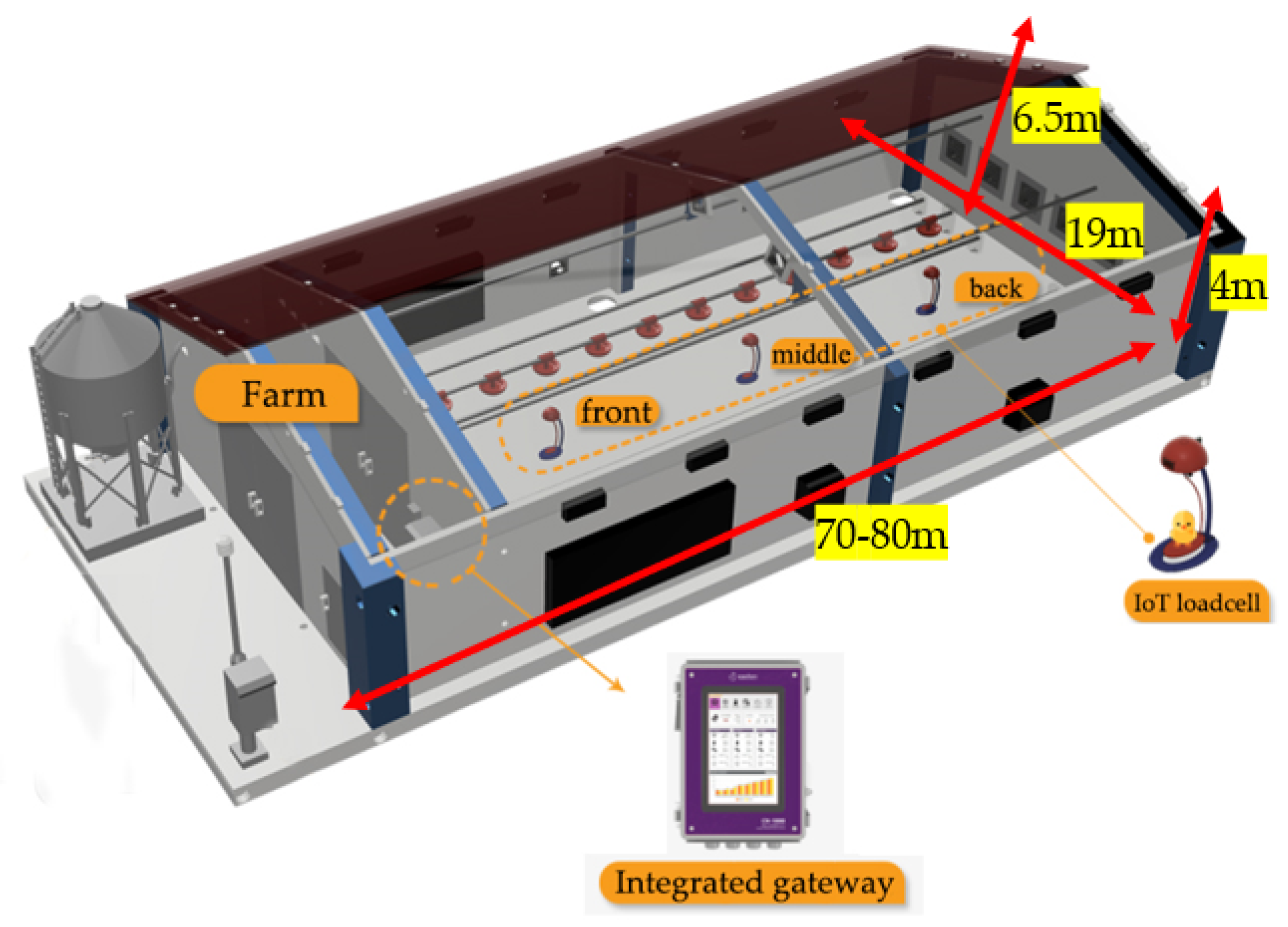

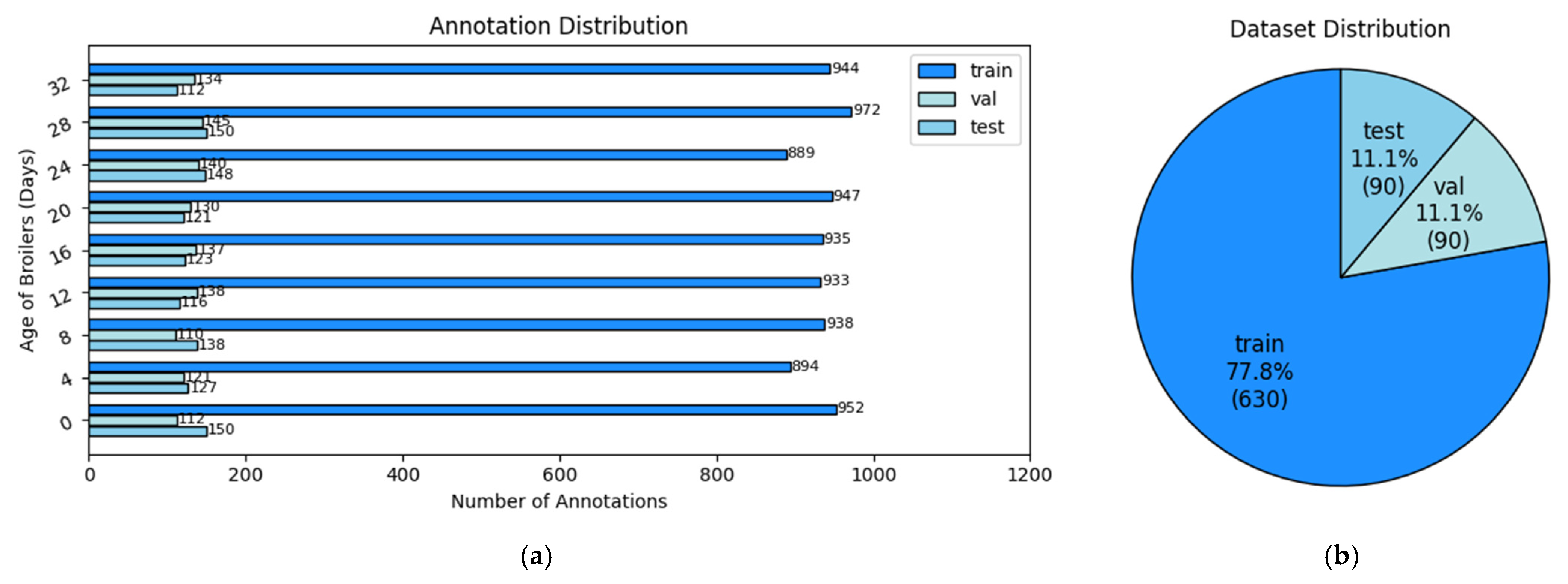
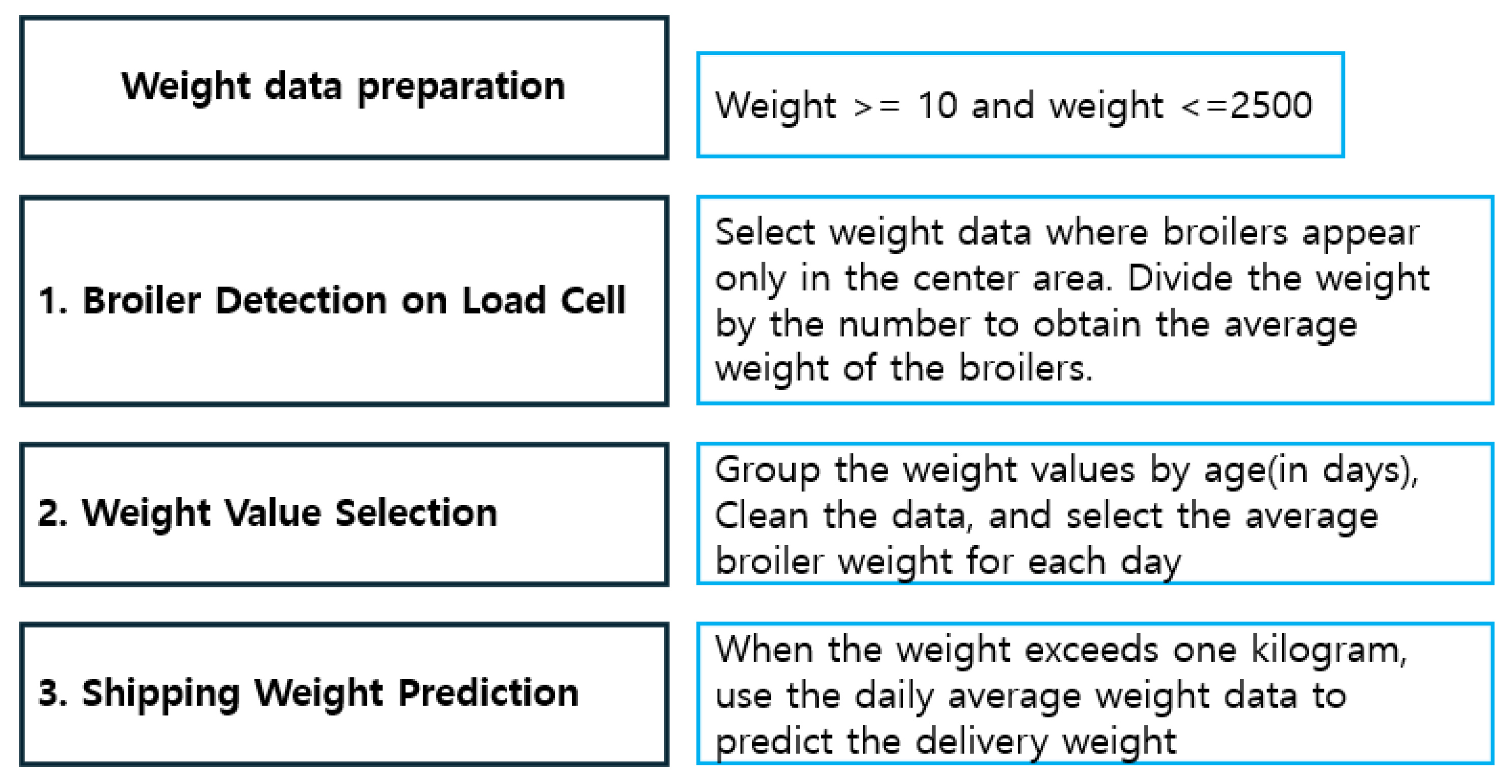

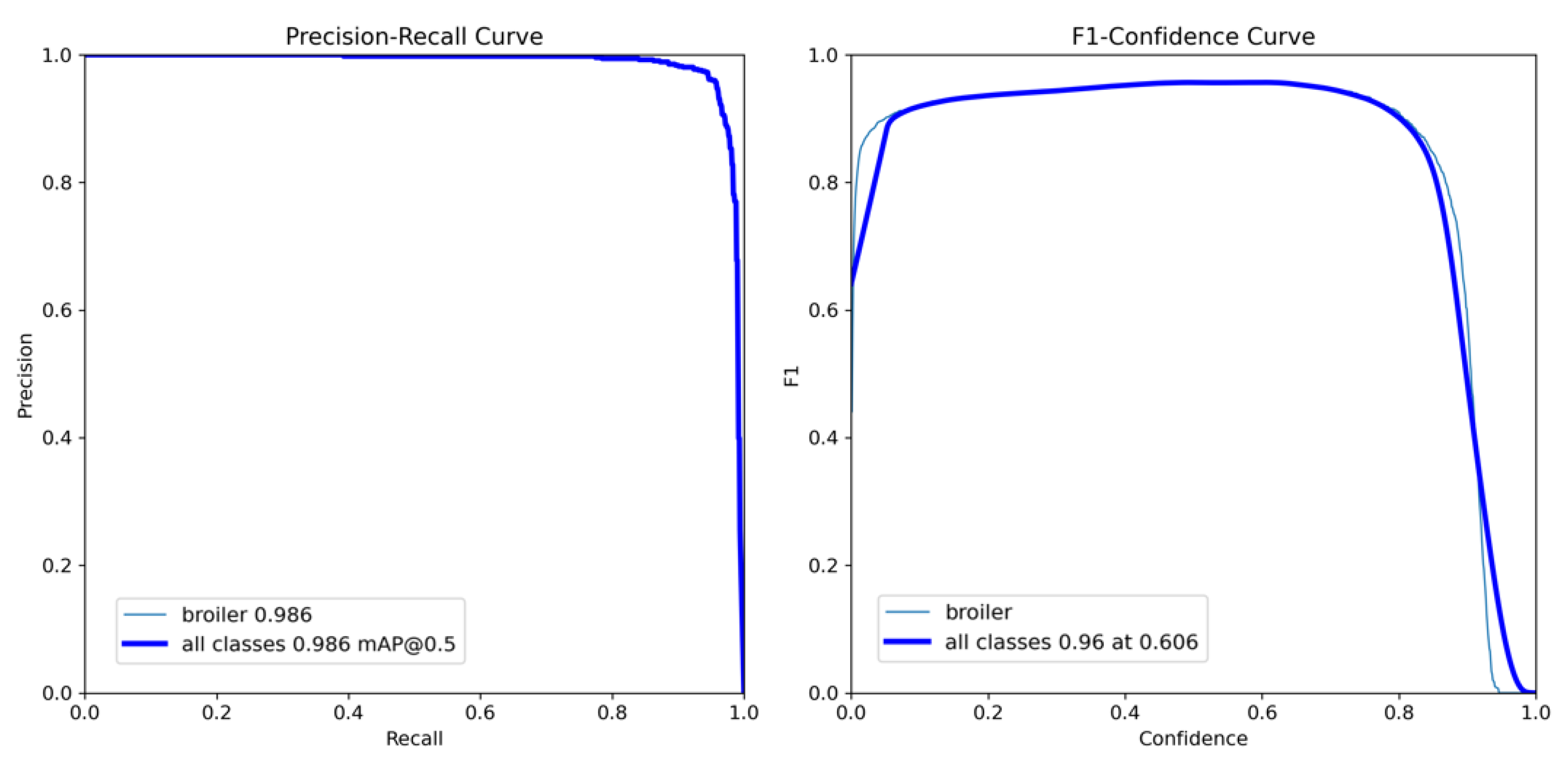
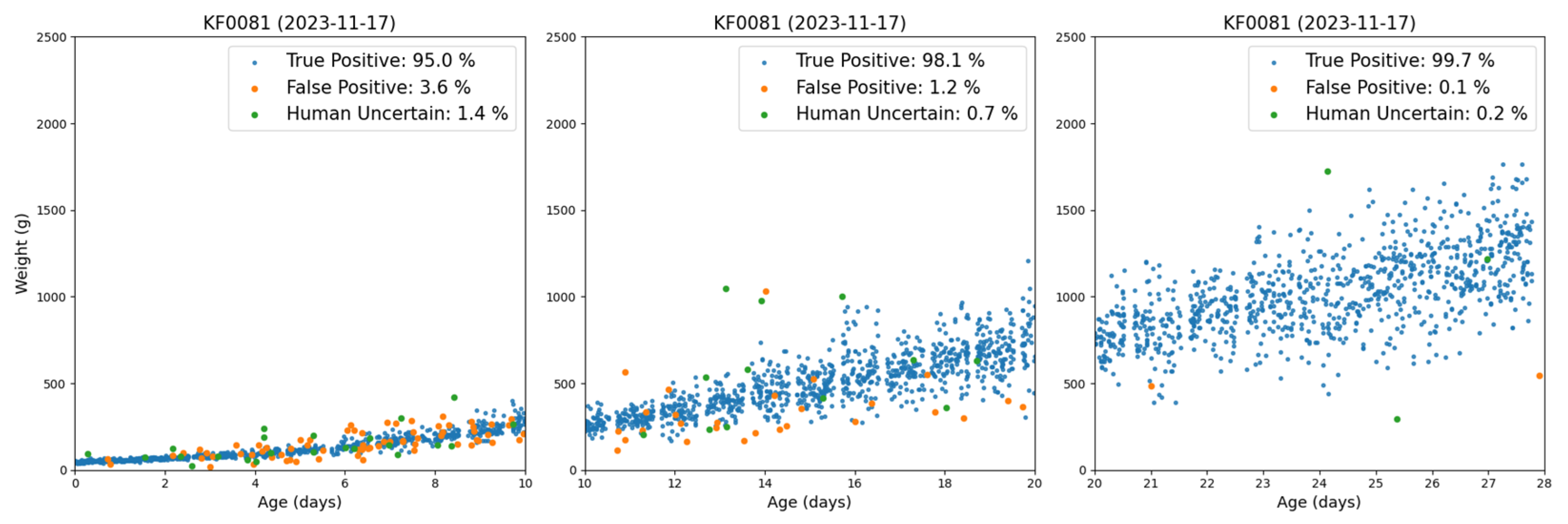
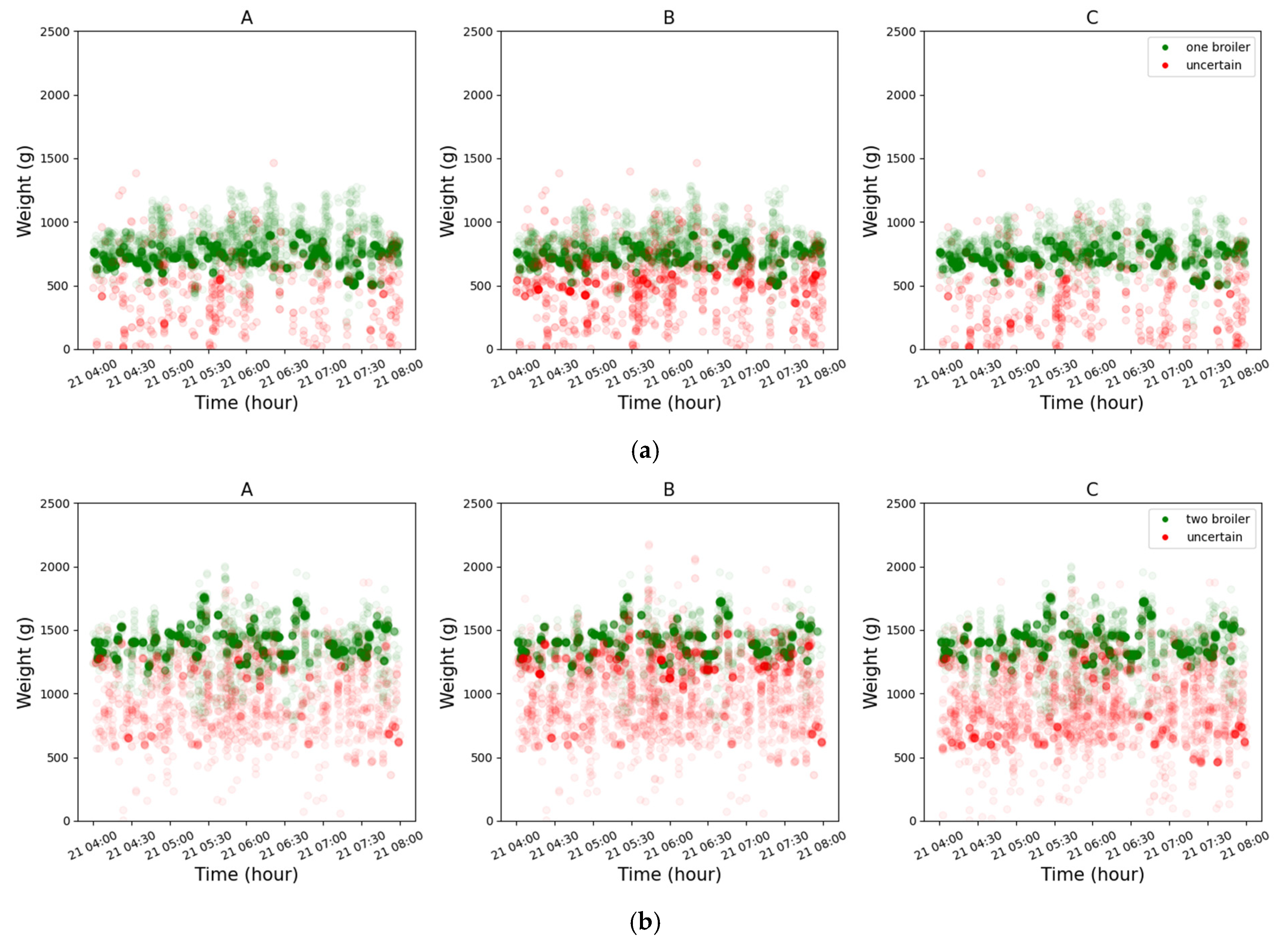
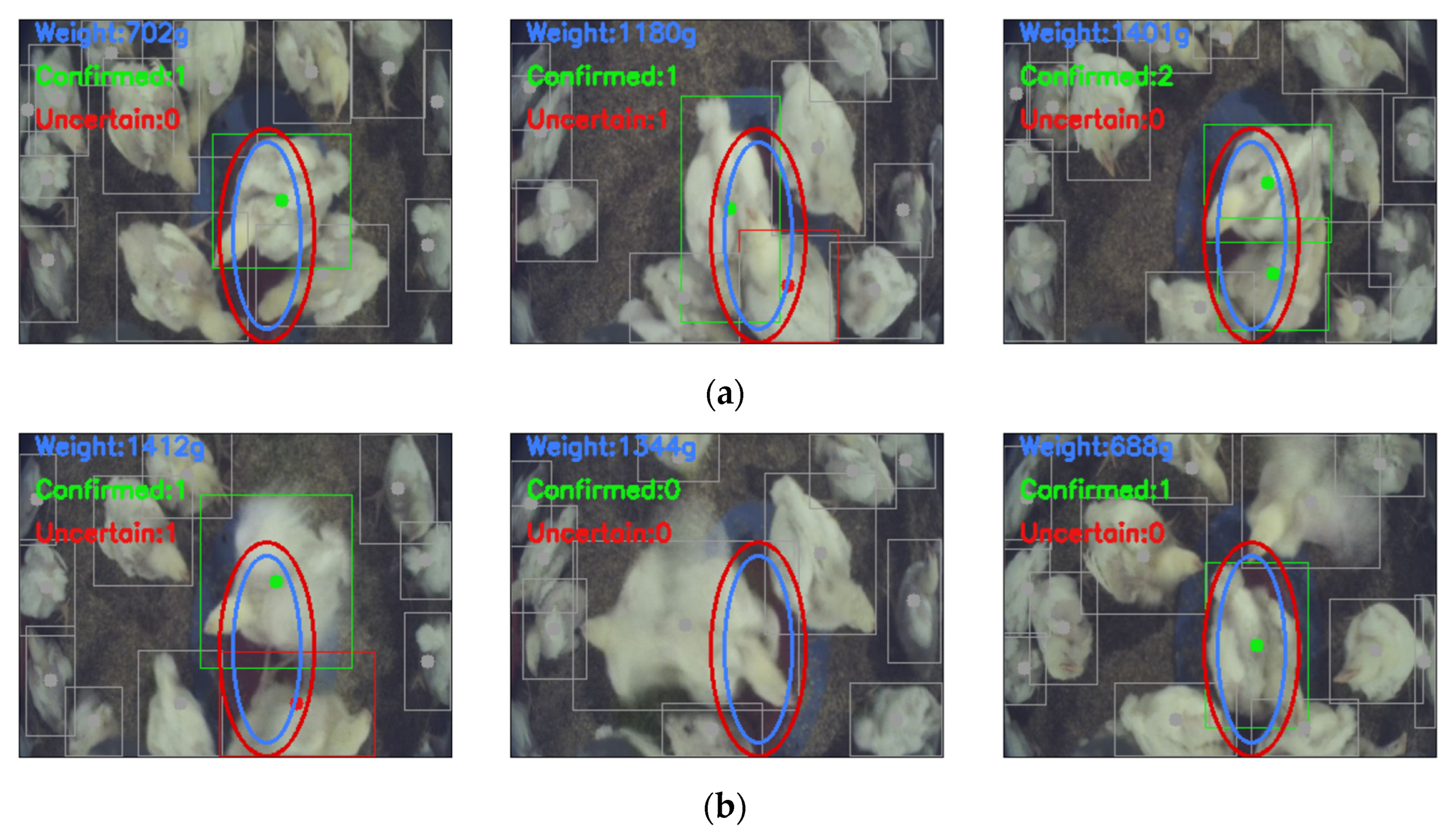
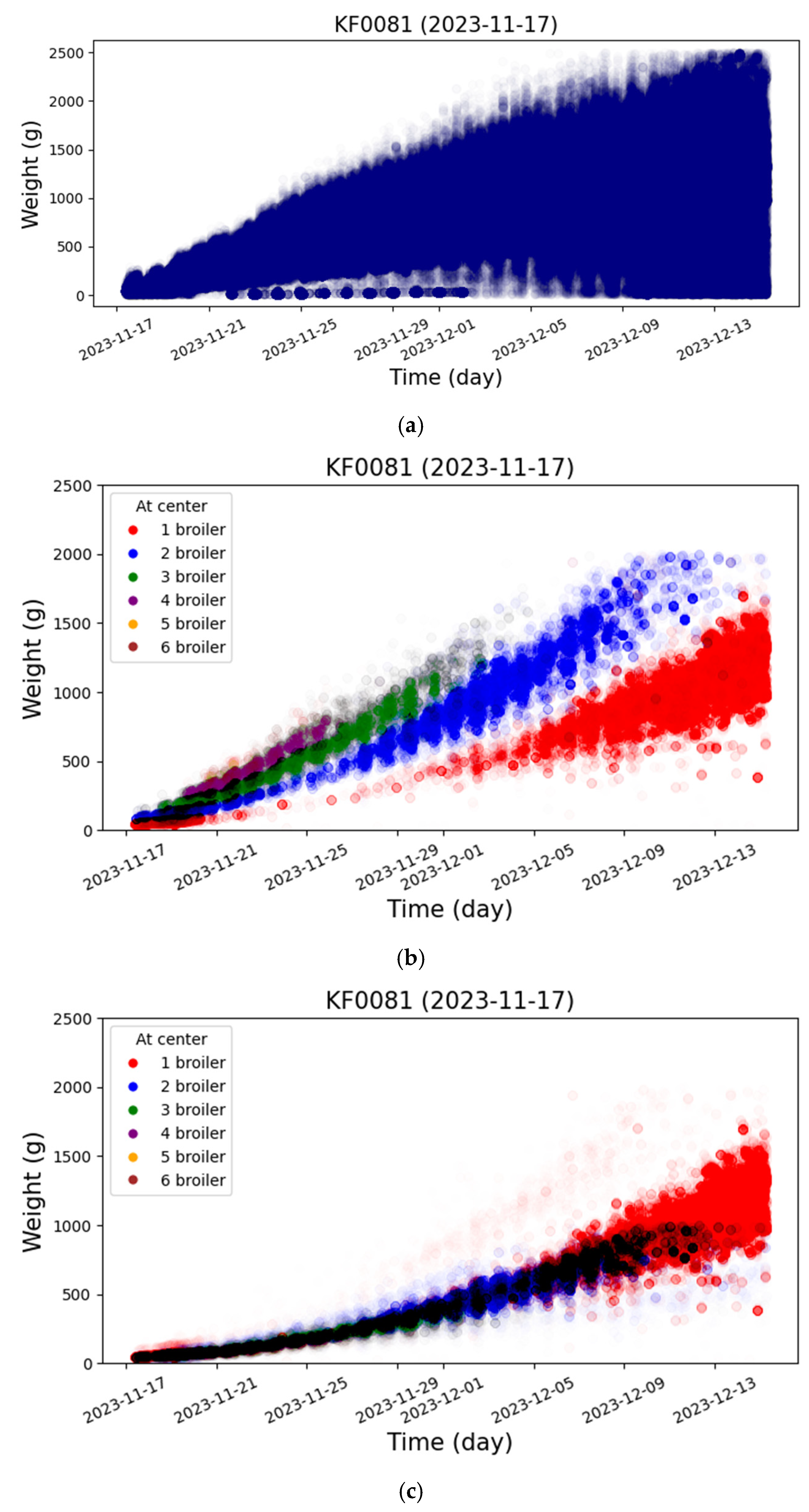
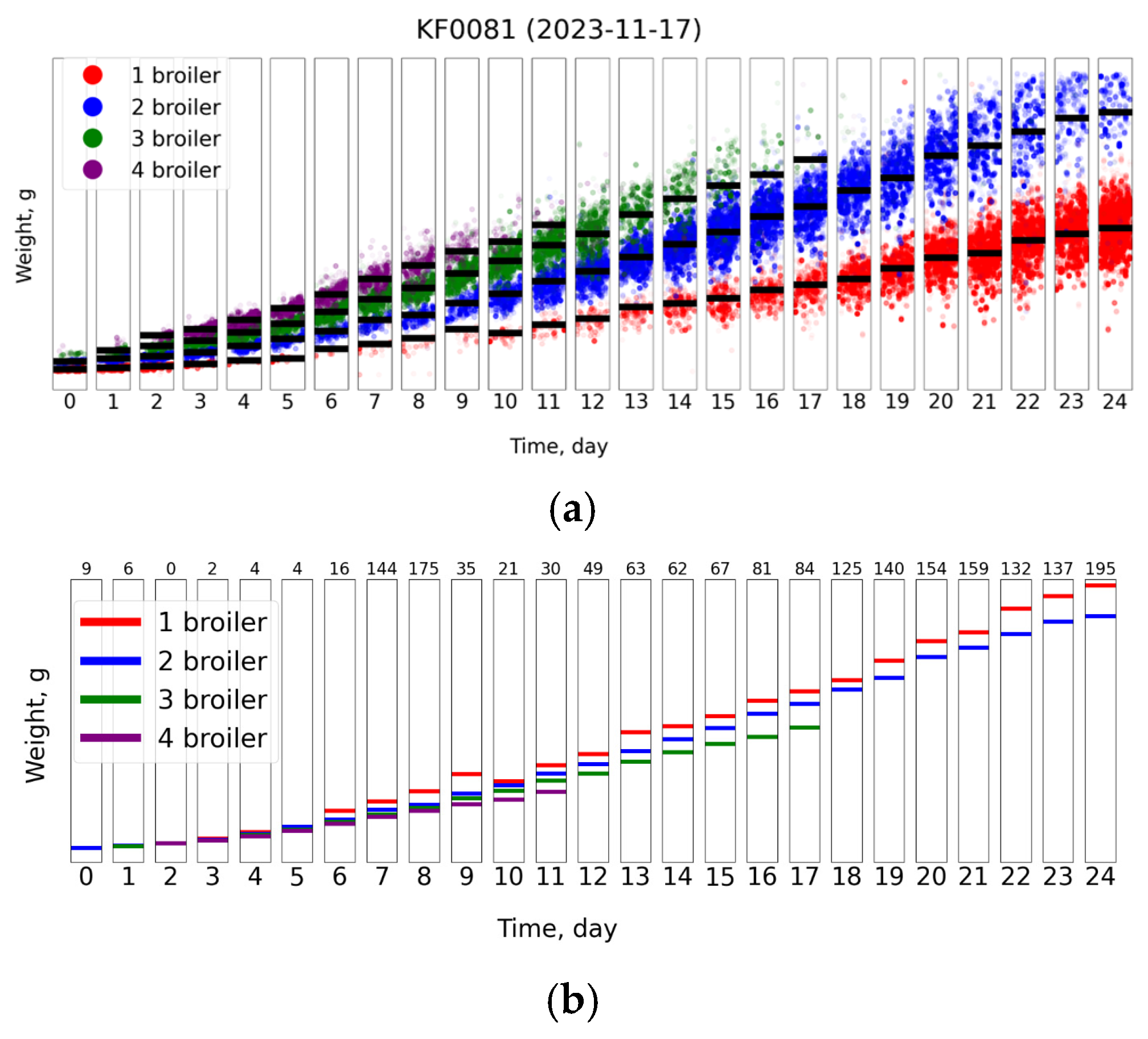
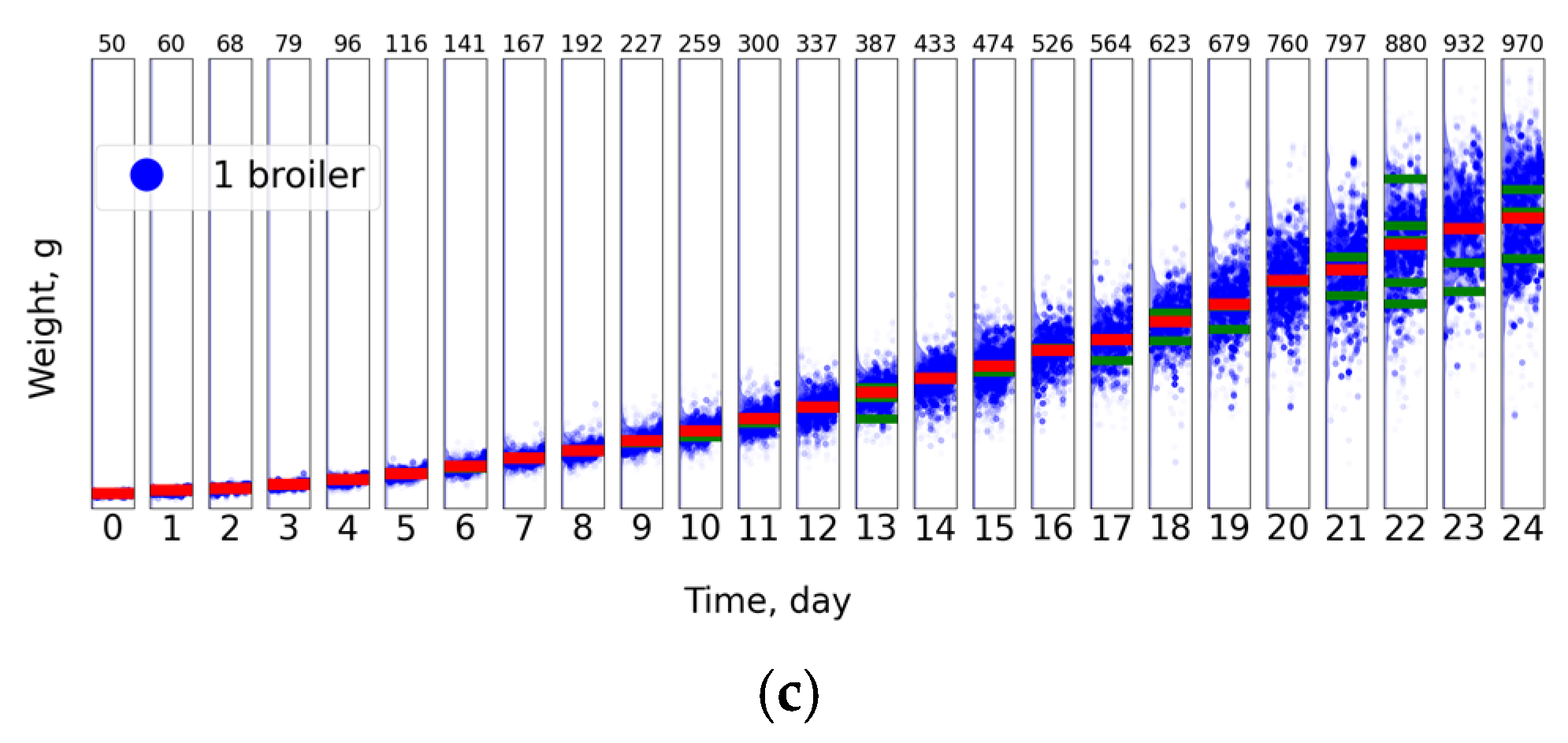
| File Name | Start Date | Delivery Date | Avg. Weight (g) | Images |
|---|---|---|---|---|
| 2023_1117_KF0081_01-Img_Data | 17 November 2023 9:13 | 21 December 2023 7:59 | 1703.5 | 2,191,039 |
| 2024_0105_KF0081_01-Img_Data | 5 January 2024 11:30 | 8 February 2024 3:59 | 1810 | 2,745,771 |
| 2024_0502_KF0081_01-Img_Data | 2 May 2024 10:09 | 6 June 2024 23:45 | 1910 | 2,589,510 |
| 2024_0502_KF0081_02-Img_Data | 2 May 2024 10:09 | 6 June 2024 23:45 | 1910 | 2,461,297 |
| 2024_1226_KF0081_01-Img_Data | 26 December 2024 11:04 | 24 January 2025 19:59 | 1366 | 2,030,085 |
| Age (Days) | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 |
|---|---|---|---|---|---|---|---|---|---|
| train | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 |
| val | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| test | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Equipment | Model | Manufacturer (Location) |
|---|---|---|
| Processor | Intel Xeon Gold 5218R CPU Processor NVidia a100-pcie-80gb | Intel Corporation (Santa Clara, CA, USA) NVIDIA Corporation (Santa Clara, CA, USA) |
| RAM | 256 GB | Samsung Electronics (Suwon, Republic of Korea) |
| SSD | 6 TB | Samsung Electronics (Suwon, Republic of Korea) |
| OS | Ubuntu 20.04 LTS | Canonical Ltd. (London, UK) |
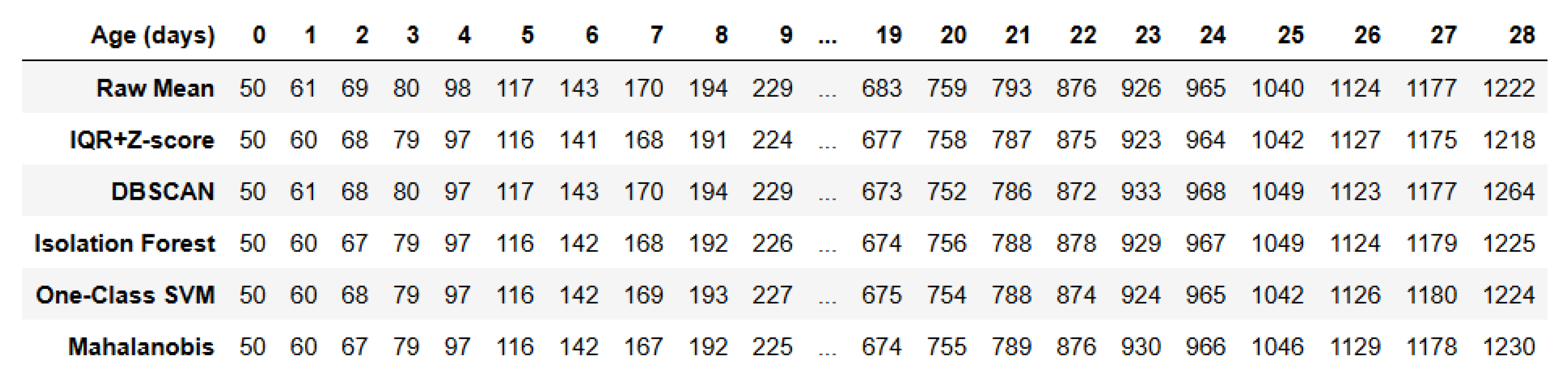
| Data | K-Means | KDE | Raw Mean | IQR + Z-Score | DBSCAN | Isolation Forest | One-Class SVM | Mahalanobis | Avg. Weight (g) |
|---|---|---|---|---|---|---|---|---|---|
| 2023_1117_KF0081_01-Img_Data | 1677.9 | 1643.3 | 1589.2 | 1598.4 | 1623.5 | 1616.5 | 1600.6 | 1615.6 | 1703.5 |
| (error%) 1.50% | 3.53% | 6.71% | 6.17% | 4.70% | 5.11% | 6.04% | 5.16% | ||
| 2024_0105_KF0081_01-Img_Data | 1755.4 | 1692.8 | 1773.9 | 1768 | 1774.7 | 1782.1 | 1776 | 1776.9 | 1810 |
| (error%) 3.02% | 6.48% | 1.99% | 2.32% | 1.95% | 1.54% | 1.88% | 1.83% | ||
| 2024_0502_KF0081_01-Img_Data | 1574.3 | 1609.2 | 1856 | 1859.3 | 1867.5 | 1867.2 | 1867.6 | 1874.9 | 1910 |
| (error%) 17.58% | 15.75% | 2.83% | 2.65% | 2.23% | 2.24% | 2.22% | 1.84% | ||
| 2024_0502_KF0081_02-Img_Data | 1902.5 | 1929.3 | 1931.2 | 1938.4 | 1945.2 | 1944.4 | 1933.2 | 1935.7 | 1910 |
| (error%) 0.39% | 1.01% | 1.11% | 1.49% | 1.84% | 1.80% | 1.21% | 1.35% | ||
| 2024_1226_KF0081_01-Img_Data | 1314.7 | 1276.7 | 1339 | 1342.2 | 1339.2 | 1341.9 | 1335.8 | 1344.7 | 1366 |
| (error%) 3.76% | 6.54% | 1.98% | 1.74% | 1.96% | 1.76% | 2.21% | 1.56% |
| Method | MAE (g) | MAPE (%) | RMSE | STD | MEAN |
|---|---|---|---|---|---|
| K-Means | 94.94 | 5.25% | 154.28 | 136.0 | 94.9 |
| KDE | 117.36 | 6.66% | 152.44 | 118.4 | 109.6 |
| Raw Mean | 50.52 | 2.92% | 60.77 | 49.1 | 42.0 |
| IQR + Z-score | 50.00 | 2.87% | 57.89 | 48.2 | 38.6 |
| DBSCAN | 43.96 | 2.54% | 47.77 | 41.7 | 29.9 |
| Isolation Forest | 43.24 | 2.49% | 48.87 | 43.6 | 29.5 |
| One-Class SVM | 46.54 | 2.71% | 54.76 | 44.9 | 37.3 |
| Mahalanobis | 40.62 | 2.35% | 47.26 | 40.5 | 30.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Song, J. Enhanced Prediction of Broiler Shipment Weight Using Vision-Assisted Load Cell Analysis. Agriculture 2025, 15, 1947. https://doi.org/10.3390/agriculture15181947
Yang L, Song J. Enhanced Prediction of Broiler Shipment Weight Using Vision-Assisted Load Cell Analysis. Agriculture. 2025; 15(18):1947. https://doi.org/10.3390/agriculture15181947
Chicago/Turabian StyleYang, Lunfei, and Juwhan Song. 2025. "Enhanced Prediction of Broiler Shipment Weight Using Vision-Assisted Load Cell Analysis" Agriculture 15, no. 18: 1947. https://doi.org/10.3390/agriculture15181947
APA StyleYang, L., & Song, J. (2025). Enhanced Prediction of Broiler Shipment Weight Using Vision-Assisted Load Cell Analysis. Agriculture, 15(18), 1947. https://doi.org/10.3390/agriculture15181947







