A High-Accuracy Contour Segmentation and Reconstruction of a Dense Cluster of Mushrooms Based on Improved SOLOv2

Abstract

This study addresses challenges related to imprecise edge segmentation and low center point accuracy, particularly when mushrooms are heavily occluded or deformed within dense clusters. A high-precision mushroom contour segmentation algorithm is proposed that builds upon the improved SOLOv2, along with a contour reconstruction method using instance segmentation masks. The enhanced segmentation algorithm, PR-SOLOv2, incorporates the PointRend module during the up-sampling stage, introducing fine features and enhancing segmentation details. This addresses the difficulty of accurately segmenting densely overlapping mushrooms. Furthermore, a contour reconstruction method based on the PR-SOLOv2 instance segmentation mask is presented. This approach accurately segments mushrooms, extracts individual mushroom masks and their contour data, and classifies reconstruction contours based on average curvature and length. Regular contours are fitted using least-squares ellipses, while irregular ones are reconstructed by extracting the longest sub-contour from the original irregular contour based on its corners. Experimental results demonstrate strong generalization and superior performance in contour segmentation and reconstruction, particularly for densely clustered mushrooms in complex environments. The proposed approach achieves a 93.04% segmentation accuracy and a 98.13% successful segmentation rate, surpassing Mask RCNN and YOLACT by approximately 10%. The center point positioning accuracy of mushrooms is 0.3%. This method better meets the high positioning requirements for efficient and non-destructive picking of densely clustered mushrooms.

1. Introduction

Mushrooms, recognized as one of the edible fungi with the most extensive cultivated areas and found in some of the world’s largest cultivation countries, exhibit a significant output. In China alone, they boast an annual production of nearly 2 million tonnes. Currently, the mainstream production mode of mushrooms in developed countries is factory production, and most of the processes have realized mechanization and automation. Only picking still relies on manual labor [1,2]. Due to the decline in the rural labor force, manual mushroom picking is experiencing a significant shortage of labor, posing a serious obstacle to the industry’s continued growth. Scholars have researched the autonomous picking technology of mushrooms and achieved phased development. The relevant research has developed from the exploration stage [3,4], limited to the laboratory under ideal conditions, to the field experiment test stage [5,6] in the actual factory mushroom house. However, due to the heterogeneity of the realistic growing environment of mushroom houses and the randomness of fruiting body growth, it is challenging to achieve efficient and nondestructive picking, especially for densely overlapping mushrooms [7]. Clusters of mushrooms has become the main reason that prevents the practical application of mushroom havesting robots. Therefore, identifying and locating densely overlapping mushrooms with high precision is one of the keys to realizing more efficient, nondestructive mushroom picking.

Mushrooms are a kind of natural high-cluster crop. It is effortless for fruiting bodies to grow together densely and overlappingly. Due to the limited space for dense growth, the mushroom shape can easily vary from round to oval or irregular, or vertical to inclined. Many mushrooms are seriously overlapping, which makes it difficult to segment and reconstruct the mushroom contour with high accuracy. For example, since densely growing mushrooms are easily squeezed and stacked, the contour segmentation between them will become complex, and it is not easy to obtain accurate edge contours of mushrooms, as shown in Figure 1, Mushrooms 1, 2, 3, and 4. For another example, densely growing mushrooms are prone to appearing heavily obscured, such as mushrooms 9 and 10 in the figure. Their shapes are no longer round or elliptical but are missing and irregular. It is often difficult to restore the contour based on these missing or irregular shapes to the actual contour, such as contour 9. The deviation between the generated and accurate contours is significant, resulting in a considerable variation between the identified and actual mushroom center points. In addition, a few small mushrooms are easily overlooked, such as Mushroom 5, 6, 7, and 8. Therefore, to achieve efficient and lossless picking of densely overlapping mushrooms, it is necessary to study further and improve the segmentation and contour reconstruction algorithms of densely overlapping mushrooms to obtain high-precision positioning.

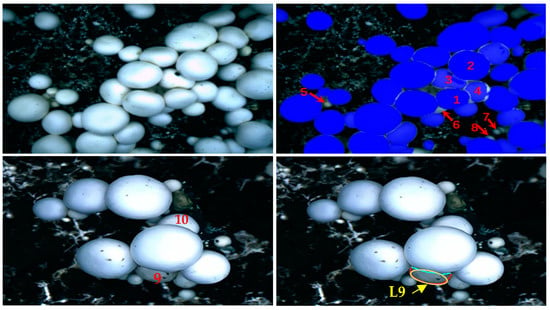
Figure 1. Main problems in segmentation and localization of densely overlapping mushrooms.

The existing system faces several challenges in accurately segmenting and recon-structing mushroom contours:

Dense Overlapping Growth: Generally, mushrooms grow in clusters with densely overlapping caps. Conventional segmentation methods encounter difficulties in distinguishing individual mushrooms within these clusters, resulting in inaccurate boundary delineation.

Deformation and Irregular Shapes: Due to mutual adhesion, extrusion, or varying growth conditions, mushrooms can exhibit irregular shapes and deformities. Most of the methods, fitting with circles only, are not very accurate in fitting the contours of irregular shapes and deformities.

Incomplete and Occluded Contours: When mushrooms are partially covered by other mushrooms, the segmentation process may yield incomplete or occluded contours, making it challenging to obtain an accurate representation of each mushroom’s shape.

Variable Lighting and Impurities: Non-uniform lighting conditions and the presence of surface impurities, such as soil and lesions, can adversely affect the quality of mushroom images, leading to additional segmentation difficulties.

To address these problems, the proposed work makes significant contributions:

(1)

The PR-SOLOv2 instance segmentation model is introduced that leverages PointRend to improve segmentation accuracy. This model effectively handles dense overlapping mushrooms and enhances boundary accuracy, achieving a segmentation accuracy of 93.04%.

(2)

The work proposes a novel contour reconstruction method based on the curvature and length of mask contours obtained through instance segmentation. This approach enables the reconstruction of mushroom contours with high precision.

(3)

The work introduces a least-squares ellipse fitting technique for mushrooms with regular shapes. For irregularly shaped or occluded mushrooms, a corner-based segmentation method is applied to accurately reconstruct contours. This classification and fitting approach significantly improves the quality of contour reconstruction.

(4)

The proposed work demonstrates a successful segmentation rate of 98.92%. This high success rate shows the effectiveness of the proposed methods.

The manuscript is structured as follows: Section 2 reviews existing research and methodologies related to mushroom segmentation and contour reconstruction. Section 3 elucidates mushroom instance segmentation dataset construction. Section 4 introduces the PR-SOLOv2 instance segmentation model. The contour construction of mushrooms using the proposed approach is presented in Section 5. It explains the classification and fitting approach based on curvature and length. Section 6 presents the experimental results of the proposed methods and compares them to other segmentation algorithms, highlighting the accuracy and effectiveness of PR-SOLOv2. Section 7 summarizes the major contributions of the research, emphasizing the improvements in mushroom segmentation and contour reconstruction.

2. Related Work

In 1968, American researchers Schertz et al. initially suggested the utilization of image processing technology for citrus detection and picking [8]. Subsequently, computer vision started to be extensively employed in detecting fruits and vegetables. The research on identifying and positioning single fruits and vegetables also started with traditional visual technology and developed rapidly [9,10,11,12]. Several researchers [10,13] adopted the machine learning method to detect and locate apples and citrus fruits by extracting the features of the target in the image. However, it was not easy to simultaneously ensure high precision, high efficiency, and detection robustness.

As deep learning technology has advanced, the application of convolutional neural network (CNN)-based architectures and their variations has progressively been employed in the detection of fruits and vegetables, demonstrating notable advantages [14]. Researchers have suggested employing enhanced target detection algorithms, such as the Faster RCNN (Faster Region-based Convolutional Neural Network) algorithm, the Single Shot MultiBox Detector (SSD) algorithm, and You Only Look Once (YOLO), to identify the locations of strawberries, apples, and other fruits. These algorithms have demonstrated a recognition success rate exceeding 83%. It has been proven that it is quite feasible to use the target detection class deep learning algorithm to calculate the quantity and judge the quality of plant phenotypes [15,16]. In recent years, due to the improvement of people’s requirements for target positioning and the need to distinguish different individuals in the map, instance segmentation methods have emerged as the times require. Among these, the Mask Region-based Convolutional Neural Network (Mask RCNN), a convolutional neural network based on regions, has also been explored for its application in recognizing the picking of grapes, oranges, strawberries, apples, and other fruits and vegetables, and, in different light intensities, multi-fruit adhesion and overlapping. The success rate of fruit recognition under complex growth conditions such as tree occlusion can reach more than 90%, which shows that the case segmentation method has significant robustness in agricultural fruit detection [17,18,19,20].

In the exploration of recognizing and locating edible fungi, researchers have exper-imented with traditional image processing methods. Morphological target detection algorithms, including threshold methods based on grayscale [21], sequential scanning algorithms [22], watershed algorithms based on angular density features [23], segmentation and recognition methods based on edge grayscale gradient features, and contour grouping [24] have been employed to identify and pinpoint mushroom contours. As a result, the recognition success rate has risen from approximately 80% to around 95%. However, the generalization ability of traditional visual methods is poor, and they are vulnerable to illumination and other objective factors. This kind of method’s segmentation and positioning effect for mushrooms with sparse or general growth density is acceptable. However, the segmentation and positioning effect for mushrooms with complex adhesion and high-density overlap will be significantly reduced, which cannot meet the high-precision positioning requirements for efficient and nondestructive picking of densely overlapping mushrooms.

The advancement of machine learning has extensively promoted the research pro-gress in recognizing edible fungi [25]. However, it is used in the classification of edible fungi varieties or growth stages [26,27,28]. Deep learning models are becoming a new trend in edible fungus detection, which further optimize the effectiveness of edible fungus identification, classification, and localization. At present, the significance of deep learning technology in the field of edible fungi is more focused on classification research [29,30,31,32,33], and only a few scholars have carried out in-depth studies on the segmentation and localization of mushroom fruiting bodies by using this technology. Lee et al. [34] established a faster RCNN target detection model to identify mushrooms and obtained three-dimensional point cloud data through a depth camera to segment a single mushroom. The identification accuracy of this algorithm was 70.93%. The oyster mushroom harvesting robot designed by Rong et al. [35] adopted the SSD target detection algorithm improved by MobileNet-v2 to identify oyster mushrooms, with a 95% success rate and improved detection speed.

Zheng et al. [36] used two detection network models, YOLOv3 and YOLOv4, to de-tect the head of Flammulina and found that the test time of the YOLOv4 algorithm was 0.8 s and the test accuracy was 81.54%, which was superior to YOLOv3. Lu et al. [37] applied the YOLOv3 algorithm for the identification of Agaricaria bisporus and introduced a positioning correction method to enhance the results. They devised the fractional penalty algorithm to compute the circle diameter of the mushroom cap, assess the fruiting body’s growth rate, and estimate harvest time, thereby enhancing the efficiency of mushroom growth management. Nevertheless, the accuracy of the algorithm can be influenced by the clarity of the contour in the mushroom region. The contour reconstruction method based on the circle has a specific deviation for the edge fitting of rare mushrooms with severe adhesion and extrusion deformation.

Missourian [38] focused on image classification and segmentation in the context of a harvesting robot’s 3D vision system. This work employs a Support Vector Machine (SVM) to identify mushrooms as either class one or class two. Image segmentation is addressed through a multi-step process using HSV color space, image gradient information, and the Hough transform to locate individual mushrooms in the XY plane. Sert and Okumus [39] studied segmenting mushrooms in images and measuring their cap width. They make use of a customized K-Means clustering method, enhancing classical K-Means for better segmentation. Image preprocessing includes filtering and histogram balancing, followed by segmentation. Soomro et al. [40] presented a two-stage image segmentation method for intensity inhomogeneous images. The first stage combines global intensity and geodesic edge terms, producing a rough segmentation. The second stage refines the segmentation using local intensity and geodesic edge terms. They use image gradient information and a Gaussian kernel for regularization in their energy function.

Pchitskaya and Bezprozvanny [41] examined the shapes of dendritic spines, empha-sizing their dynamic nature and advocating for clusterization approaches over classifi-cation. They explore algorithms that rely on clusterization to enable new levels of spine shape analysis. Ref. [42] presented a method for detecting and measuring the diameter of mushroom caps using depth image processing. They proposed a novel approach based on the three-dimensional structure of mushrooms to segment them from the background and measure their diameters using the Hough transform. Arjun et al. [43] analyzed visual cues for white button mushrooms using image processing tools. It assesses chromatic and morphological characteristics and predicts the onset of mushroom discoloration through hyperspectral image analysis.

Baisa and Al-Diri [44] presented an algorithm for detecting, localizing, and estimat-ing the 3D pose of mushrooms using RGB-D data from a consumer RGB-D sensor. It combines RGB and depth information for these purposes and employs advanced techniques for 3D pose estimation. Zhao et al. [45] proposed a white measurement method for Agaricus bisporus based on image analysis. It involves the construction of an imaging system, color calibration, and the application of CIE Ganz whiteness formula to assess the whiteness of the mushrooms. Retsinas et al. [46] concentrated on developing a vision module for 3D pose estimation of mushrooms in an industrial mushroom farm. It uses multiple RealSense active-stereo cameras and employs a novel pipeline for mushroom instance segmentation and template matching.

Zhang et al. [47] investigated more than 62 articles related to microorganism biovolume measurement using digital image analysis methods. It tracks the development of this approach since the 1980s. Chen et al. [48] introduced an improved YOLOv5s algorithm for accurate Agaricus bisporus detection. The algorithm combines a deep learning network with the Convolutional Block Attention Module (CBAM) to enhance detection accuracy. Chen et al. [49] focused on accurately recognizing Agaricus bisporus in complex backgrounds by proposing a watershed-based segmentation recognition algorithm. It includes various image processing techniques for accurate mushroom segmentation and recognition. Table 1 illustrates a detailed summary of the existing works related to the proposed work.

Table 1. Summary of the state-of-the-art works.

Author	Approach	Major Findings	Segmentation Success Rate	Mean Time
Masoudian [38]	SVM for image classification, multi-step segmentation	This approach is not well suited for large datasets.	88.57%	0.49 s
Soomro et al. [40]	Two-stage segmentation for intensity inhomogeneous images	The two-stage segmentation technique overcomes issues related to the initial contour, making it suitable for inhomogeneous image segmentation.	97.99%	1.41 s
Ji et al. [42]	Depth image processing for mushroom diameter measurement	The method detects mushrooms and provides essential information for robotic selective harvesting, improving production quality and efficiency.	92.37%	0.5 s
Baisa and Al-Diri [44]	RGB-D data for mushroom detection and 3D pose estimation	The algorithm provides a robust method for mushroom detection, localization, and 3D pose estimation, which can be valuable for robotic picking applications.	98.99%	-
Retsinas et al. [46]	Vision module for 3D pose estimation using Intel RealSense cameras	The method aims to accurately detect the 3D pose of mushrooms without relying on 3D annotation data, which can facilitate mushroom harvesting by robotic systems.	96.31%	3 s
Zhang et al. [47]	Review of microorganism biovolume measurement methods	The work has research significance and application value, offering insights into microorganism biovolume measurement using digital image analysis methods.	-	-
Chen et al. [48]	Improved YOLOv5s algorithm for Agaricus bisporus detection	The improved algorithm shows convincing recognition accuracy, robustness, and low error rates in Agaricus bisporus detection.	98%	0.018 s
Chen et al. [49]	Watershed-based segmentation for Agaricus bisporus recognition	The proposed algorithm demonstrates recognition of Agaricus bisporus with low error rates and real-time processing capabilities.	95.7%	0.706
Tillett et al. [21]	Algorithm for locating mushrooms in growing beds	The algorithm is designed for use in robotic harvesting systems and provides a basis for identifying and tracking mushrooms in a growing bed.	93%	-
Yang et al. [23]	Corner density-based localization algorithm for overlapping mushrooms	The algorithm demonstrates a success rate of 86.3% in locating overlapping mushrooms, providing an efficient solution for mushroom localization.	96.37%	0.712 s
Yang et al. [24]	Improved segmentation recognition algorithm for overlapping Agaricus bisporus	The algorithm achieves over 90% recognition rate for Agaricus bisporus in overlapping situations, making it suitable for complex planting environments.	97.25%	0.212 s
Lu and Liaw [37]	CNN-based mushroom cap diameter measurement	The algorithm provides an estimation of mushroom cap diameters and outperforms the Circle Hough Transform.	82.7%	-

To sum up, traditional image recognition methods are still widely used in mushroom recognition and positioning, and the recognition effect has been continuously improved. However, due to the influence of model generalization, there is little room for further improvement. In contrast, the algorithm based on depth learning dramatically improves the accuracy and generalization ability of the recognition algorithm. Currently, the mainstream methods are YOLO, faster RCNN, and other target detection methods. Recently, Mask RCNN has begun to emerge in recognition of fruits and vegetables and has achieved better results. Yin et al. [50,51] also attempted to use instance segmentation to segment caps of Oudemansiella raphanipes and Agrocybe cylindracea. Moreover, instance segmentation proves especially effective in detecting fruits in complex growth states, including varying light intensities and instances of multi-fruit adhesion, overlap, and occlusion. The instance segmentation algorithm will become the next research hotspot in the recognition and positioning of fruits, vegetables, and edible fungi during picking.

However, two-stage algorithms, which normally have low efficiency, are mainly used at present. In contrast, the single-stage instance segmentation algorithm SOLO (Segmenting Objects by Locations) was simplified compared with the two-stage method of first detection and then segmentation; it claims a more straightforward design to achieve greater efficiency and better segmentation performance [52,53]. Furthermore, the improved version of the SOLO model, SOLOv2, uses dynamic convolution to enhance the quality of the mask segmentation and the model’s efficiency [54]. In SOLOv2, the category branch and mask branch are integrated, and the matrix non-maximum suppression is proposed to inhibit the repetitive prediction after multi-scale feature extraction of the input image by Full Convolutional Networks (FCN), thus realizing faster mask processing [55]. Therefore, the SOLOv2 network structure is used as the segmentation framework for more and more tasks requiring efficient and accurate segmentation between the object and the background. For instance, Li et al. [56] utilized the SOLOv2 algorithm to segment the perimeter of the offshore area in the oilfield operation site and then took the segmentation result as the key to detecting the intrusion of the offshore perimeter area. The accuracy rate of the designed model was up to 94.7%; Ji et al. [57] used the method based on the SOLOv2 network and point cloud cavity characteristics to automatically score the rumen filling of dairy cows. The average segmentation accuracy on the test set images was 86.29%, showing robustness to individual differences.

Therefore, given the shortcomings of low segmentation and positioning accuracy in visual recognition of densely overlapping mushrooms, this paper proposes a novel high-accuracy positioning method for densely overlapping mushrooms based on the instance segmentation model SOLOv2. This method has the following characteristics: (1) It solves the fuzzy problem of densely overlapping mushroom edge segmentation; (2) the most extended contour classification reconstruction algorithm based on the mask contour of instance segmentation can better eliminate the interference sub-contour in the irregular contour that is seriously occluded and extruded, and effectively improves the contour reconstruction effect and mushroom center point positioning accuracy through classification fitting.

3. Mushroom Instance Segmentation Dataset Construction

This paper takes mushrooms as the research object and collects images of mushrooms growing in the mushroom house of Shanghai Lianzhong Edible Fungus Professional Cooperative to construct the dataset. Mushrooms are raised in factory production environments and standard culture racks. The culture racks are 31 m long, 1440 mm wide, and 6 storeys high, with the storeys spaced 600 mm apart. The temperature, humidity, carbon dioxide concentration, and light in the mushroom room are intelligently controlled by an intelligent control system under conditions suitable for the growth of mushrooms, as shown in Figure 2. Three MV-GE300C-T GigE color industrial cameras, with a focal length of 4 mm, a pixel depth of 10 bits of colour and image resolution of 1280*720 is used, were installed transversely on the picking robot to traverse each layer of mushrooms and capture mushroom images.

Figure 2. Field image of mushroom image acquisition.

Mushrooms quickly form dense clusters, especially the mushrooms in the early picking stage, whose growth is particularly lush, resulting in mutual extrusion, shielding, staggering, and other phenomena among mushrooms. In addition, the fruiting bodies of mushrooms may appear on the surface of scales during the growth process or the browning phenomenon due to poor anti-browning ability, thus affecting the shape of mushrooms. Therefore, the construction of the data set should fully consider these differences in mushroom growth shape and posture. In this paper, a total of 480 images of eight typical forms of mushrooms were collected, and 60 shots were gathered for each category, as shown in Figure 3.

Figure 3. Datasets of different forms of mushrooms. (a) With scales on caps; (b) With brown spots on caps; (c) With soil on caps; (d) Serious interleaving, clumping, and adhesion; (e) Large differences in size and height; (f) Adhesion and extrusion deformation between mushrooms; (g) Heavily tilted to expose its stalk; (h) With mechanical damage on caps.

This paper also considers the images under different light source conditions when constructing the dataset. Specific composition (Figure 4): 160 images with uniform light and high brightness collected under the top light source, 160 pictures with uneven light under the side light source, and 160 images with low brightness under the dark light source.

Figure 4. Datasets for different light sources: (a) Top light source; (b) Side light source; (c) Dark light source.

The images in this paper are labeled with labelme. To ensure that the labeled polygons try to fit the real contours of the mushrooms, the number of basic labeling points for each mushroom example is stipulated, following the definition of a COCO dataset for s, m, l to divide the mushroom model: s-type mushrooms at least 10 labeling points, m-type at least 20 labeling points, and l-type mushrooms at least 25 points, to improve the degree of labeling and fit to the real contours of the mushrooms. After labeling all the initial images to obtain the initial data set, we used data enhancement to process the images to improve the generalization ability and robustness of the model. Specific image data enhancement methods included: image brightness change, horizontal flipping of the image, vertical mirroring, and random rotation. Finally, 1920 mushroom images obtained after performing the image enhancement process were randomly divided into training and validation sets in a ratio of 7:3.

4. Research on High-Accuracy Mushroom Segmentation

The SOLOv2 algorithm, shown in Figure 5, was used to segment the mushrooms first.

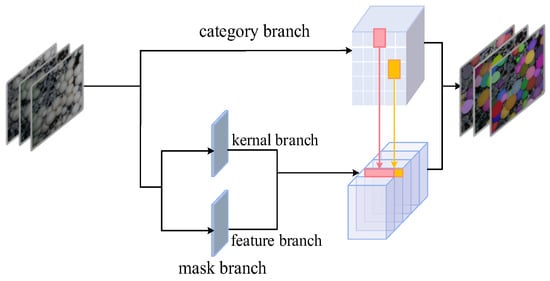
Figure 5. SOLOv2 network structure.

The segmentation results are as follows: for the mushrooms with a general aggregation degree and good growth form, the segmentation effect is good. The recognition rate of the mushrooms in Figure 6a is high, especially since some tiny mushrooms are segmented. The mask boundary fits well with the contour of the actual mushroom. However, the segmentation effect will be affected for mushrooms with a high aggregation degree and complex growth morphology, resulting in a rough mask and inaccurate segmentation of mushroom edges, as shown in Figure 6b. Especially in the densely overlapping area of mushrooms, the positioning accuracy of the mushroom picking center will be affected. Therefore, SOLOv2 needs to be improved to obtain more precise and accurate segmentation of mask edges.

Figure 6. Result of SOLOv2 segmented mushrooms: (a) Ordinary aggregation; (b) Complex polymerization.

The PointRend neural network can optimize object edge segmentation, treat segmentation of an image as a rendering problem, and perform the prediction of image segmentation based on an adaptive point selection iterative subdivision algorithm [58]. The structure of the network is shown in Figure 7. A lightweight prediction head generates a rough prediction mask, and bilinear interpolation is utilized for upsampling the rough prediction mask to obtain a prediction mask with twice the resolution. N points distributed on the edge are selected, and point-by-point features are constructed on the points chosen by combining fine-grained features and coarse prediction features. Finally, a simple multi-layer perceptron is used to predict these points. All points share the weight of the multi-layer perceptron. The multi-layer perceptron can be trained by standard task-specific segmental losses and finally output the classification label of each point. This is iterated until the mask at the desired resolution is upsampled. Therefore, this paper uses the PointRend network structure, which can solve the edge segmentation accuracy that is not high enough to improve the SOLOv2 network. In SOLOv2, to obtain the semantic information of the segmentation target, multiple convolutions and pooling operations on the original image will reduce the image resolution. Then, if the image with high semantic and low key is directly upsampled to be consistent with the size of the original image, information in specific areas will be lost, resulting in rough segmentation results. In addition, the method of predicting each pixel in a regular grid and inferring the instance category to which it belongs has the conditions of over-sampling and under-sampling. In particular, too many sampling points in low-frequency areas belonging to the same object in the image leads to over-sampling, and the under-sampling of such high-frequency regions close to the object boundary in the picture makes the segmented border too smooth and unreal. This will inevitably lead to rough segmentation results, especially at the edge of the segmentation object.

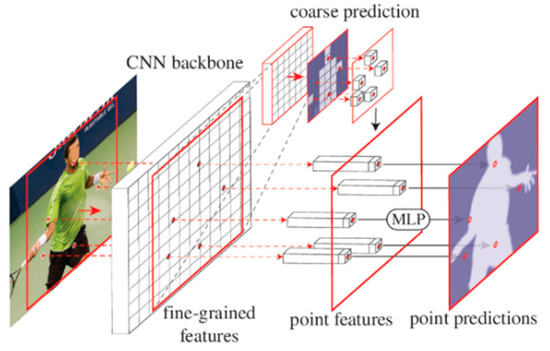
Figure 7. PointRend network structure.

Therefore, this paper combines the SOLOv2 network structure with the PointRend neural network module to build an improved SOLOv2 algorithm, which is called the PR-SOLOv2 algorithm in this paper. Its network structure is shown in Figure 8. After the Fully Convolution Network (FCN) of SOLOv2’s feature extraction backbone network, the PointRend module is introduced before the mask prediction branch to improve the image up-sampling method. To solve the information loss in local areas and render fine segmentation details, the delicate features of the second layer of the FCN network are introduced, combined with the rough features of the fourth layer, and sent to the taught PointRend module.

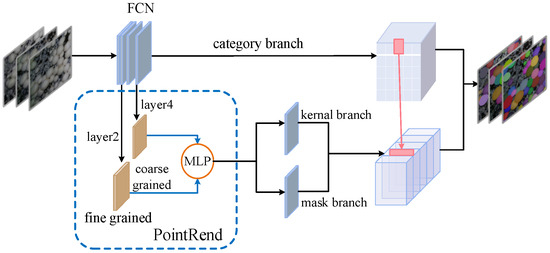
Figure 8. PR-SOLOv2 network structure.

The top-N feature pixels are extracted adaptively from the feature map of low spatial resolution and the corresponding fine feature map of high spatial resolution. The multi-layer perceptron is used to iterate and optimize each point continuously, and the instance is connected to the segmentation prediction branch to predict the instance mask. By this method, low-level and high-level features are combined layer by layer. The output image is iteratively rendered from coarse–fine to coarse–fine to solve the boundary inauthenticity caused by the over-sampling of the smooth region and under-sampling of the boundary region, which can improve the misjudgment of boundary pixels caused by the original network structure and improve the accuracy of the image segmentation edge.

The model’s total loss function L is composed of the loss $L_{\mathrm{cate}}$ generated by instance classification and the loss $L_{\mathrm{Mask}}$ generated by mask prediction. λ is the coefficient that balances the two losses, and the calculation is shown in Equation (1).

$$L=L_{\mathrm{cate}}+\lambda L_{\mathrm{Mask}}$$

(1)

$$L_{\mathrm{Mask}}={\displaystyle \frac{1}{N_{\mathrm{pos}}}}\sum 1{\{P_{i,j}^{*}>0\}}^{d_{\mathrm{Mask}}},i,j\in M$$

(2)

$$d_{\mathrm{Mask}}=1-D\left(p,q\right)=1-{\displaystyle \frac{2{{\displaystyle \sum }}_{x,y}\left(p_{x,y}•q_{x,y}\right)}{{{\displaystyle \sum }}_{x,y}{p}_{x,y}^2+{{\displaystyle \sum }}_{x,y}{q}_{x,y}^2}}$$

(3)

where $L_{\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{e}}$ is the Focal Loss function for classification [59] for the calculation of $L_{\mathrm{M}\mathrm{a}\mathrm{s}\mathrm{k}}$ (Equation (2)). S is the number of grid units divided into the input image. i and j respectively represent the subscripts of indexes from left to right and from top to bottom on $M\times M$ grids on the input image, traversing all grids on the picture; Npos is the number of positive samples; $P^{\mathrm{*}}$ represents the instance category. $1\{P_{i,j}^{\mathrm{*}}>0\}$ is the indicator function; if $P_{i,j}^{\mathrm{*}}>0$, the indicator function value is 1, otherwise it is 0; $d_{\mathrm{M}\mathrm{a}\mathrm{s}\mathrm{k}}$ is the Dice Loss function, and its definition is shown in Equation (3), where D is the Dice coefficient, which is used to measure the similarity of two sets. $p$ and $q$ represent the predicted Dice Loss mask and the natural mask, respectively, and $p_{x,y}$ and $q_{x,y}$ are the pixel values of the point $\left(x,y\right)$ of the predicted mask and the natural mask on the image, respectively.

5. Contour Reconstruction of Mushroom

In the process of mushroom growth, due to its natural cluster growth characteristics, it is common for mushrooms to overlap and extrude each other, leading to the pileus’s deformation. The PR-SOLOv2 instance segmentation model can more accurately separate them from the complex situations of adhesion between mushrooms, inclination, soil shielding on the surface, and uneven light, and obtain their masks. However, for mushrooms that are occluded or deformed due to aggregation growth, the mask obtained according to the image is only part of the shape of the mushroom. If the mask center point is directly extracted from the mushroom center point, there will be a significant error.

Therefore, given the above non-uniform and irregular mushroom growth shapes, especially the severe deformation and shape loss of densely overlapping mushroom contours, to better restore the actual mushroom contour and improve the center point positioning accuracy, this paper proposes a mushroom contour classification reconstruction method based on PR-SOLOv2 segmentation mask contour curvature and length, as shown in Figure 9.

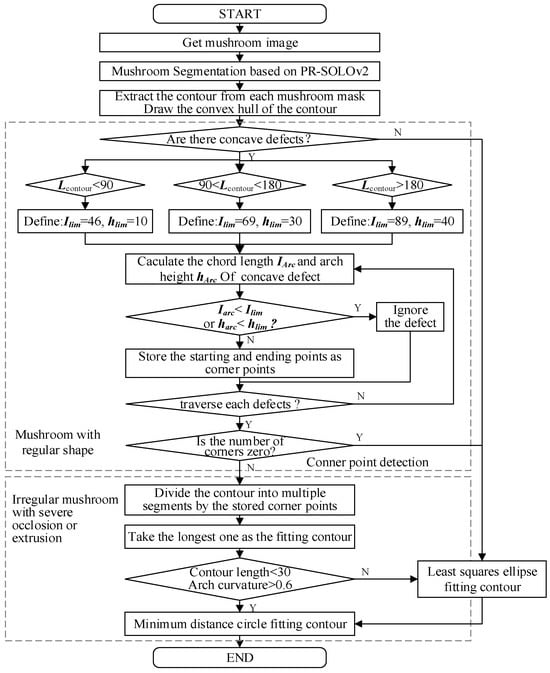
Figure 9. Flow chart of high-precision contour reconstruction based on PR-SOLOv2.

In this method, firstly, the PR-SOLOv2 algorithm is used to segment mushrooms and obtain their masks. Then, the mushroom mask contour based on the mask is extracted. Next, mushrooms are classified into regular and irregular shapes according to the concave defect length of the extracted contour. A mushroom with a regular shape is fitted with the least square ellipse. In contrast, a mushroom with an irregular shape and difficult contour fitting, seriously occluded or squeezed, is reconstructed with the longest contour extraction and classification reconstruction method based on corner segmentation.

5.1. Reconstruction of Regular Contours

The contour is considered regular with no or only shallow concave defects.

Firstly, the convex hull method is used to find out if there are any concave defects in the contour. Contours without concave defects are considered regular contours. In addition, although some mushrooms have concave defects, the chord length ($I_{Arc}$) and arch height ($h_{Arc}$) of the concave contour are relatively small compared to the entire mushroom length (_r$L_{contour}$), so such concave defects can be ignored. Mushroom contours that meet the above conditions can still be considered regular contours. Due to the varying sizes of mushrooms, to better determine the impact of concave contours on the fitting of mushrooms of different sizes, mushrooms are divided into three types based on the contour length ($L_{contour}$): small, medium, and large. Different boundary values are used to determine mushrooms of different sizes. A mushroom with a contour length in the range [0,90) is defined as a small mushroom, [90,180) as a medium mushroom, and above 180 as a large mushroom. When $I_{Arc}$ is less than 46 or $h_{Arc}$ is less than 10 for a small mushroom, a concave contour can be ignored; when $I_{Arc}$ is less than 69 or h_Arc is less than 30 for a medium mushroom, a concave contour can be ignored; when $I_{Arc}$ is less than 89 or $h_{Arc}$ is less than 40 for a large mushroom, a concave contour can be ignored. After the above judgment, if the concavities of the mushroom contour can be ignored, then this mushroom is defined as having a regular mushroom contour. Otherwise, it has an irregular contour.

For mushrooms with regular contours, they can be fitted by the least-squares ellipse method: Take the $n$ contour points above it as $P_i\left(x_i,y_i\right)\left(i=\mathrm{1,2},\dots ,n\right)$, perform fitting operation according to the least-squares ellipse fitting objective function, calculate the ellipse position parameters and shape parameters, and reconstruct the contour of the bisporus mushroom with a smooth contour and regular shape.

5.2. Reconstruction of Irregular Contours

After segmenting the irregular contour of the overlapping mushroom, the obtained contour contains the contour fragment of the overlapping part of the other mushrooms covered. Suppose it is not processed and allowed to participate in the fitting together with the effective contour, such as the least-squares ellipse fitting. In that case, the fitted contour will differ from the actual contour. And the overlapped part cannot be well restored to the actual contour.

Given the above situation, this paper proposes the longest contour extraction and classification reconstruction approach relying on corner segmentation. The specific process is as follows:

(1)

Detect corner points at abrupt changes in contour shape. If the concave contours cannot be ignored, define its start and end point as corner points;

(2)

By corner coordinates, the coordinate line between adjacent corner coordinates is regarded as a sub-contour segment, and the whole mushroom contour is divided into N sub-contour segments;

(3)

Calculate the length of each sub-contour segment and choose the longest sub-contour segment;

(4)

Based on the longest sub-contour, the mushroom contour is classified and fitted according to the difference in arch curvature and length of the longest sub-contour.

(5)

Calculate the arch curvature C of the contour (Equation (4)).

$$C={\displaystyle \frac{1}{R}}$$

(4)

$$R=0.5*\left({\displaystyle \frac{z^2}{h_{Arc}}}+h_{Arc}\right)$$

(5)

$$z=\sqrt{{\left(x_n-x_1\right)}^2+{\left(y_n-y_1\right)}^2}$$

(6)

$$h_{Arc}=\underset{i}{\max (}{\displaystyle \frac{S_i*2}{z}})$$

(7)

$$S_i=\sqrt{p_i\left(p_i-z\right)\left(p_i-v_i\right)\left(p_i-m_i\right)},i=1,\dots n$$

(8)

where $R$ is the arcuate curvature radius of the longest sub-contour, v_i and m_i are, respectively, the length of both sides of the inscribed triangle formed by any point i (i = 1,2,…,n) on the longest sub-contour and its two upper endpoints, $I_{Arc}$ is the chord length of the longest sub-contour and is also the bottom length of all inscribed triangles in the longest sub-contour, $p_i$ is the half circumference of the inscribed triangle, $S_i$ is the area of the inscribed triangle, $h_{Arc}$ is the height of the longest arch in the inscribed triangle on the longest sub-contour.

For the longest sub-contour with an arch curvature exceeding 0.6 and a length surpassing 30, the least-squares ellipse is employed to fit the contour. However, when dealing with the longest sub-contour having an arch curvature less than 0.6 or a length below 100, using the least-squares ellipse fitting method would result in a significant deviation of the fitting contour and its center point from the actual values. Consequently, the minimum-distance circle-fitting method is applied to reconstruct the mushroom contour in these two scenarios. N points $\left(x_j,y_j\right)$ on the contour are selected, and the circle parameters are determined based on the sum of the absolute values of the distances between the data points and the circle, as depicted in Equation (9):

$$f=\sum \left|\sqrt{{\left(x_j-x_c\right)}^2+{\left(y_j-y_c\right)}^2}-r\right|$$

(9)

where $x_c$ and $y_c$ are the center point of the fitted circle, r is the radius of the fitted circle, f is the minimum value of $x_c$, $y_c$ and r are the best-fit parameters. For irregular contours, the longest sub-contour is extracted based on the corner segmentation proposed above, and then the target contours of overlapping and irregular mushrooms are reconstructed separately by least-squares ellipse fitting and minimum-distance circle-fitting according to the different situations of the bow curvature and length of the longest sub-contour.

6. Experimental Results and Discussion

6.1. Segmentation Experiment and Discussion Based on PR-SOLOv2

6.1.1. Model Training

To validate the results and advantages of the enhanced algorithm, this article uses Mask RCNN, YOLACT, SOLOv2, and PR-SOLOv2 image segmentation networks for training based on the mushroom datasets mentioned above to compare and verify their segmentation effects.

The model training environment was built under the Windows 10 operating system and a 1×GeForceRTX3090 NVIDIA graphics card from the United States, and the running memory was 24 GB. Framework Detectron2 of Facebook under the running architecture CUDA10.1 and CUDNN7.6.5 acceleration libraries of Python3.7, PyTorch1.6, and GPU were configured as the running framework of the model.

Training parameters were configured with a training batch size of 4. The neural network optimization algorithm employed stochastic gradient descent (SGD) to progress in the direction of the maximum slope at the current location. The initial learning rate was set at 0.01 and the momentum size at 0.9, and 5000 iterations of iterative training were carried out. In addition, the mesh size S of SOLOv2 and PR-SOLOv2 algorithms was (12,16,24,36,40).

6.1.2. Model Evaluation Metrics

The instance segmentation algorithm is essentially a problem of pixel classification and category recognition. Its evaluation metrics include Average Precision (AP), Intersection over Union (IOU), forecast time, and other common metrics.

AP represents the area value of the curve enclosed by the coordinate axis, and the precision–recall (PR) curve is plotted with the recall rate as the horizontal coordinate and the accuracy rate as the vertical coordinate. IOU denotes the intersection area of the target mask predicted by the model and the actual annotation box, along with the ratio of their combination. A preset judgment threshold is utilized, and when the IOU value exceeds this threshold, the model’s prediction for the target is deemed relatively accurate.

The mushroom segmentation task necessitates predicting categories at the pixel level. Therefore, evaluation indicators such as the IOU threshold and the corresponding AP value are adopted. These metrics help distinguish the intersection ratio between the predicted segment and the ground truth. The average accuracies ${\mathrm{A}\mathrm{P}}_{50}$ and ${\mathrm{A}\mathrm{P}}_{75}$, obtained using the commonly used decision thresholds of 0.5 and 0.75 in the example segmentation task, are used to evaluate the segmentation accuracy of the model under different confidence levels.

6.1.3. Instance Segmentation Results and Discussion

(1)

Experiment and result of dense overlapping mushroom segmentation

For the mushrooms that grow densely and form mutual adhesion or even mutual extrusion, the segmentation effect of different instance segmentation methods is shown in Figure 10. The segmentation result of Mask RCNN shows inaccurate segmentation of mushroom masks and missing identification of some mushrooms, as shown in Figure 10b. No. 1, 2, 3, and 4 mushrooms gather and grow, stick together, squeeze, and deform each other. There is no height difference between mushrooms, which leads to their indistinct boundary. No. 6 and No. 8 mushrooms were not identified because they were severely obscured by their neighbors, with only a small amount of fungus cap exposed and uneven light exposure. Due to the limited growth space of No. 5 and No. 7 mushrooms, the fruiting body can only grow slightly inclined, exposing the stalk. It is difficult to distinguish between the mushroom cap to be identified and the stem. Mask RCNN cannot handle these complex instance segmentation cases.

Figure 10. Segmentation results of densely overlapping mushrooms: (a) Original; (b) Mask RCNN; (c) YOLACT; (d) PR-SOLOv2.

The segmentation effect of the YOLACT algorithm is shown in Figure 10c. There were some cases in which the stalk was misidentified as a mushroom, some mushrooms were not identified, and the shape of the generated mushroom mask was very different from the actual mushroom shape. The stalk of mushroom No. 14, marked in yellow box in the picture, is misidentified as a mushroom; No. 5, 7, and 9 mushrooms that grow slightly at an angle and expose their stalks are missed; No. 6 and No. 8 mushrooms were seriously blocked by the large mushrooms growing around them, resulting in a small imaging area and uneven illumination and not being recognized. The shape of the segmentation mask generated by No. 2, 10, 11, 12, and 13 mushrooms is rectangular, greatly different from the actual mushroom shape. Like Mask RCNN, the YOLACT algorithm cannot solve the complex and challenging high-precision segmentation problems mentioned above.

In contrast is the PR-SOLOV2 algorithm for dense adhesion and extrusion deformation. It can be accurately segmented in complex segmentation situations, such as non-obvious features of the fungus cap and stalk, as shown in Figure 10d. The PR-SOLOv2 can accurately segment No. 1, 2, 3, and 4 mushrooms that grow densely and extrude each other without blurred edges. It can also separate No. 6 and No. 8 mushrooms that can be heavily obscured and not easily identified. In addition, an excellent segmentation effect was also shown on No. 5, 7, and 9 mushrooms with no obvious characteristics of fungus cap and stalk, and no fungus stalk was misidentified as fungus cap. The mask shapes generated on No. 10, 11, 12 and 14 mushrooms will not appear rectangular like the YOLACT but will generate masks that conform to the actual shape of the mushrooms.

(2)

Segmentation of a tilting mushroom

For the tilted mushroom, the segmentation problems of the Mask RCNN algorithm and the YOLACT algorithm are similar, as shown in Figure 11b,c. No. 1 and 2 mushrooms grow at a full tilt to the soil surface, exposing most of the stalks. The stalks look like tiny mushrooms. The growth posture of No. 3, 4, and 5 mushrooms was slightly inclined, revealing a small amount of stem. With inaccurate segmentation results, the mask RCNN and YOLACT algorithms also divided part of the stalk into the cap. No. 6 mushroom grows together with other mushrooms and hides on the stem of another mushroom. When the Mask RCNN and YOLACT algorithm segment the mushroom, in this case, part of the stalk is also divided into the fungus cap to obtain an unclear mask. The PR-SOLOv2 as shown in Figure 11d can correctly segment the stem with similar characteristics to the mushroom cap due to oblique growth, which increases the difficulty of identifying the mushroom. Including the correct segmentation of No. 1 and No. 2 of this oblique growthwhich is difficult to accurately identify. It can also accurately divide mushrooms No. 3, 4, 5, and 6, whose stalk and cap characteristics are difficult to distinguish, and get their precise edge.

Figure 11. Segmentation result of tilting mushrooms: (a) Original; (b) Mask RCNN; (c) YOLACT; (d) PR-SOLOv2.

(3)

Segmentation result of tiny mushrooms

The identification effect of small mushrooms is shown in Figure 12. Mask RCNN and YOLACT have similar products in small mushroom recognition, as shown in Figure 12b,c. No. 1, 3, 4, 7, 8, 9, 11, 12, 13, 16, 17, and 19 mushrooms are not exposed to uniform light, the individual mushroom is small, and the characteristics of the fungus cap are not prominent. Therefore, it is easy to be mistaken for mycelium and miss recognition. Individual mushrooms No. 2, 5, 6, 10, 14, 15, 18, 20, and 21 are slightly larger, belonging to the small mushroom and large mushroom adhesion with a certain height difference. It is easy to identify the small mushroom in the stalk of the large mushroom, which also missed identification. However, the effect of the PR-SOLOv2 algorithm is shown in Figure 12d; it can correctly segment the mushrooms with smaller individuals and fewer features, whose characteristics are similar to mycelia. In addition, it can also accurately segment small mushrooms that are adhered to large mushrooms and have different heights and similar features.

Figure 12. Segmentation result of tiny mushrooms: (a) Original; (b) Mask RCNN; (c) YOLACT; (d) PR-SOLOv2.

(4)

Comparison of segmentation effects

The effect of instance segmentation on mushroom segmentation is tabulated in Table 2. The average segmentation accuracy of the Mask RCNN on the dense mushroom image segmentation task is 83.510%. The AP of YOLACT is 80.743%, while that of SOLOv2 is more than 90% (90.279%). The PR-SOLOv2 proposed in this paper has the highest AP among the four segmentation methods in dense mushroom segmentation, reaching 93.037%, which is about 10% higher than Mask RCNN and YOLACT, and about 3% higher than that of SOLOv2. When the IOU threshold is set to 50%, the AP performance of PR-SOLOv2 in the mushroom image segmentation task is as high as 99.056%. In addition, the average segmentation time is 0.39 s, which is still better than the Mask RCNN and YOLACT algorithms.

Table 2. Effect of instance segmentation on mushroom segmentation.

Algorithm	P	R	AP (%)	AP50 (%)	AP75 (%)	$\mathbf{Mean} \mathbf{Time}\left(\mathbf{s}\right)$
Mask RCNN	0.933	0.852	83.510	95.061	89.006	0.68
YOLACT	0.901	0.838	80.743	93.451	87.853	0.41
SOLOv2	0.959	0.917	90.279	96.103	92.747	0.36
PR-SOLOv2	0.982	0.945	93.037	99.056	95.249	0.39

(5)

Comparison of segmentation effect under different light sources

In order to compare the segmentation effect of the model under the three light sources, this paper selects 60 pictures for experiment; the pictures are all from the camera used in the experiment; each picture has the same resolution and is divided into three groups according to the light sources. The overall results of the experiment are as follows: 651 examples of top light source images, 638 successful segmentations, segmentation success rate of 97.81%; 794 examples of side light source images, 772 successful segmentations, segmentation success rate of 97.23%; 1102 examples of dark light source images, 1088 successful segmentations, segmentation success rate of 98.73%, as shown in Figure 13.

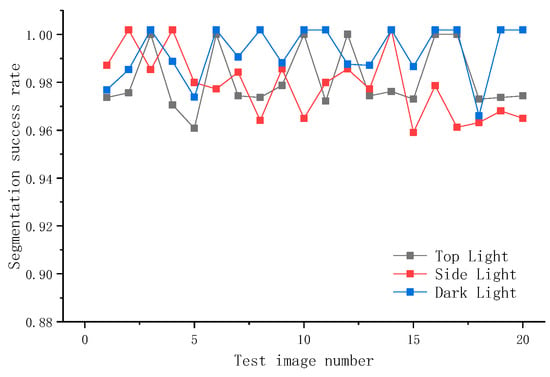
Figure 13. Segmentation results under different light sources.

The result shows that the segmentation accuracy of the side light source is the lowest, lower than that of the top light source, and lower than that of the dark light source. This paper concludes that since the side light source produces shadows on the mushroom surface when irradiating the mushroom, the light and dark demarcation line will affect the extraction of the mushroom edge features to a certain extent, so it will affect the final segmentation success rate. Based on the results of this experiment, considering that in the natural state, most of the stacked mushroom racks are illuminated by lights with side light sources, the direct photographs will affect the subsequent recognition and contour reconstruction. Therefore, in this paper, the camera is equipped with a parallel light source to assist illumination when taking pictures, to eliminate the influence of the side light source on the subsequent recognition and segmentation of mushrooms, and to improve the accuracy of recognition and contour reconstruction.

(6)

Further validation of PR-SOLOv2 algorithm

There are 260 mushroom sample images of different mushroom rooms and layers collected in the actual production environment from two plants, totaling 9362 mushrooms. The mask RCNN, YOLACT, SOLOV2, and PR-SOLOv2 algorithms were used to segment the sample images. The experimental outcomes are shown in Table 3. It is observed that the proposed approach achieves a segmentation success rate of 98.13%, which is significantly higher than those of the other existing works.

Table 3. Mushroom segmentation success rate of different algorithms.

Plant	Algorithm	Number	Num of Successful Segment Mushroom	Segmentation Success Rate (%)
Plant 1	Mask RCNN	4865	4209	86.52
	YOLACT	4865	3908	80.33
	SOLOv2	4865	4407	90.59
	PR-SOLOv2	4865	4784	98.34
Plant 2	Mask RCNN	4497	3853	85.68
	YOLACT	4497	3617	80.43
	SOLOv2	4497	4077	90.66
	PR-SOLOv2	4497	4403	97.91

There are two main reasons for the unsuccessful segmentation: first, multiple large mushrooms are blocked at the same time, resulting in too serious small mushrooms; Second, a small mushroom with a large area of dark lines on the surface. In the marking of the dataset, the two cases are not common, resulting in poor learning effect of the segmentation features of the model for these two cases. In the future, the segmentation efficiency of the model can be improved by adding the marking of special cases.

6.2. Experimental Results and Discussion of Contour Reconstruction

The mask contour obtained by segmentation mask based on the PR-SOLOv2 algorithm proposed in this paper is adopted. The process and effect of the classification and reconstruction method according to the curvature and arc length of the mask contour are shown in Figure 14: (a) the fruit-body mask obtained by PR-SOLOv2 segmentation network processing proposed in this paper; (b) the extracted mask contour. Among them, No. 1, 5, and 8 are mushrooms whose average curvatures are 0.01317, 0.01367, and 0.02313, respectively, and corresponding lengths are 444, 427, and 246 pixels, respectively. They are all mushrooms whose average curvature is less than 0.103 and whose contour length is more than 100. No. 2, 3, 4, 6 and 7 are partially occluded fruiting bodies, whose average curvatures are 0.02378, 0.01787, 0.01648, 0.02087, and 0.02252, respectively, and corresponding contour lengths are 291, 257,335, 239,and 316 pixels, respectively, belonging to non-smooth occluded contours. Among them, the arch curvature of the largest contour fragment of No. 2, No.4, and No. 7 mushrooms is more significant than 0.9. The least-squares ellipse fitting was used. The No. 3 and No. 6 mushrooms were extruded to produce a large deformation, and their contour shape was irregular. However, the arch curvature of their longest contour was greater than 0.9, so the ellipse fitting was also adopted. The figure illustrates that both the regular mushroom and the severely blocked mushroom exhibit a well-matched contour when employing the contour reconstruction method proposed in this paper. The reconstruction effect is satisfactory.

Figure 14. Reconstruction effect of overlapping extruded mushrooms: (a) PR-SOLOv2 mask; (b) Extract mask edges; (c) Contour reconstruction.

More reconstruction effects of the mushroom cluster neutron entity are shown in Figure 15. In general, the contour reconstruction method in this paper can fit the contour of the densely overlapped fruit body well. For example, the surface damage of No. 1, 7, 8, 12, and 26 mushrooms and the surface dirt of No. 3 mushrooms will affect the image segmentation effect and lead to a poor subsequent reconstruction effect. The SOLOv2-PR algorithm proposed in this paper can accurately segment the mushroom mask and extract the edge of the mask. On this basis, the mushroom contour reconstruction can have a good effect. No. 6, 10, 13, 17, 18, 19, 20, 21, 22, 26, 23, 27, 28, and 29 mushrooms are mainly adhered to a mushroom around them or are partially blocked by a single mushroom next to them. Although these mushrooms are blocked or squeezed, the deformation of the mushrooms is not severe, and the extracted mushroom outline is roughly smooth and regular. The contour reconstruction method proposed in this paper can achieve a better effect than mushroom contour reconstruction. In addition, for the mushrooms squeezed by two surrounding mushrooms, such as No. 4, 5, 9, 12, 15, 14, 16, 25, 31, 32, 34, and 33, the contour edge deformation is large, and the shape is irregular, so it is not easy to reconstruct the contour. The mushroom contour reconstruction method realized in this paper can restore the mushroom’s true contour.

Figure 15. Mushroom contour reconstruction effect.

However, in cases of extremely dense growth, a majority of the fruiting bodies, like mushrooms numbered 2, 11, 15, 24, 30, and 35, are either blocked or severely deformed by the presence of multiple surrounding mushrooms. The PR-SOLOv2 algorithm is employed to segment the mask contour of these severely deformed mushrooms and subsequently reconstruct their contours. There may be some deviation between the fitted contour and the actual contour. However, there will be missed recognition for the mushroom fruiting bodies smaller than 30 pixels, such as the mushrooms in the area marked by the yellow rectangle box. However, these are tiny mushrooms with fresh buds, so the missing identification does not affect the picking or monitoring.

6.3. Verification of Center Coordinates

6.3.1. Center Point Ground Truth Determination Method

In order to find the ground true of center point of each fruiting body in the mushroom image, we use manual marking to determine the center point of each fruiting body, as shown in the Figure 16. The center point of the daughter body with regular contour is directly obtained by using circle annotation in labelme, and the daughter body with irregular contour is obtained by using polygon annotation in labelme, as close as possible to its true contour, as shown in Figure 16b. After all mushrooms are marked, the center point of the child body marked with a circle is directly output as its benchmark, and the center point of the child body marked with a polygon is obtained by ellipse fitting output, as shown in Figure 16c. The coordinates of all the central green ‘x’ in the final output image are used as the reference point of each sub-entity center.

Figure 16. Benchmarking process for determining mushroom centers: (a) Original image; (b) Marking image; (c) Fitting contour map.

6.3.2. Calculation of Fitting Accuracy

In order to quantify the contour reconstruction accuracy, the center point positioning accuracy of the contour is used to characterize it. Firstly, the deviation from the center datum is compared from the actual fitting effect graph, as shown in Figure 17: the center point of the actual contour using manual labeling, as shown in Figure 17a; and the center point of the contour reconstructed by PR-SOLOv2, as shown in Figure 17b; for comparison, the comparison effect is shown in Figure 17c. It can be seen that the contour reconstructed by PR-SOLOv2 fits better with the actual contour manually labeled, and the center point deviation is very small.

Figure 17. Comparative effect of fitting: (a) Manually labeled contours; (b) Reconstructed contours by this paper’s method; (c) Comparison result.

In order to calculate the deviation more quantitatively, the center point positioning accuracy is calculated using the 2D coordinate deviation rate (CDR) [24] as depicted in Equation (10).

$$E=\left(\left|{\displaystyle \frac{c_j-c_i}{W}}\right|+\left|{\displaystyle \frac{r_j-r_i}{H}}\right|\right)\times 100\%$$

(10)

where r_j and c_j are the row and column coordinates of the center point of the mushroom contour fitted by manual marking, r_i and c_i are the row and column coordinates of the center point of the mushroom obtained by the research method in this paper, and W and H are the width and height of the mushroom image, respectively.

The contour reconstruction comparison results of three more dense onsite mushroom images (169 mushrooms in total) are provided to further verify the effectiveness of the contour reconstruction method in this paper, as shown in Figure 18. The corresponding CDR comparison of the four images is shown in Figure 19.

Figure 18. Comparison effect of contour reconstruction by this paper’s method and manually labeled contours: (a) Manually labeled contours; (b) Reconstructed contours by this paper’s method; (c) Comparison result.

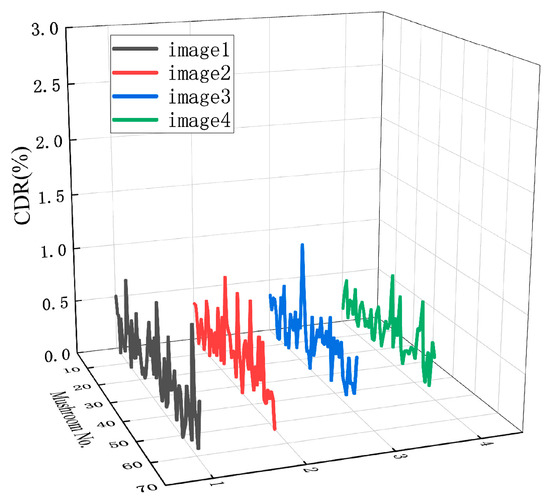
Figure 19. CDR plots of the four pictures.

As shown in Table 4, the average CDR between the centroid of the contour fitted by the method in this paper and the actual contour is 0.30%, which shows that the centroid positioning accuracy is higher, with better results.

Table 4. Mean deviation statistics for the average CDR coordinates of the four pictures.

Image Number	1	2	3	4	Average
The contour number	63	54	52	50
Average CDR	0.28%	0.32%	0.31%	0.30%	0.3%

7. Conclusions

This paper presents a high-precision segmentation and contour reconstruction method for densely overlapping mushrooms based on an improved SOLOv2 model (PR-SOLOv2), aiming to improve the segmentation accuracy and center point positioning accuracy of highly dense mushrooms. The experimental results show significant improvement. The PR-SOLOv2 model improves segmentation accuracy to 93.04% and segmentation rate by 98.13%, about 10% higher than Mask RCNN and YOLACT. Meanwhile, the center positioning error is as low as 0.3%, which proved that the proposed contour reconstruction method in this study could accurately segment dense, overlapped, extruded, and tilting fruiting bodies, effectively reconstruct mushroom contours that are severely occluded and compressed, and achieve accurate center point positions. It is not only suitable for the high-precision identification and positioning of the fruiting bodies of various edible fungi but also those of other densely overlapping spherical-like fruits. However, there are still some limitations. For example, for mushrooms with too a high tilt angle, occasionally it will be mistaken to identify the stalk of the mushroom as a fungus cap. When the fruiting body of the mushroom is severely obstructed, the reconstructed mushroom contour may have some relatively larger deviations from the actual mushroom contour, which needs to be further improved. In the future, we will continue to improve the structure of the segmentation model, and even try some new occlusion segmentation algorithms such as amodal instance segmentation, to further enhance the segmentation effect and reduce processing time, and optimize the reconstruction fitness of the contour reconstruction algorithm for contours covered by multiple positions or severely obstructed, to further enhance center point position accuracy.